Effect of Surface Topography on Particle Deposition from Liquid Suspensions in Channel Flow

Abstract

A Eulerian—Lagrangian model has been developed to simulate particle attachment to surfaces with arc-shaped ribs in a two-dimensional channel flow at low Reynolds numbers. Numerical simulation has been performed to improve the quantitative understanding of how rib geometries enhance shear rates and particle-surface interact for various particle sizes and flow velocities. The enhanced shear rate is attributed to the wavy flows that develop over the ribbed surface and the weak vortices that form between adjacent ribs. Varying pitch-to-height ratio can alter the amplitude of the wavy flow and the angle of attack of the fluid on the ribs. In the presence of these two competing factors, the rib geometry with a pitch-to-height ratio of two demonstrates the greatest shear rate and the lowest fraction of particle attachment. However, the ribbed surfaces have negligible effects on small particles at low velocities. A force analysis identifies a threshold shear rate to reduce particle attachment. The simulated particle distributions over the ribbed surfaces are highly non-uniform for larger particles at higher velocities. The understanding of the effect of surface topography on particle attachment will benefit the design of surface textures for mitigating particulate fouling in a wide range of applications.

1. Introduction

Understanding deposition of particles from liquid or gas suspensions on a solid surface is important in numerous engineering applications, such as oil refineries, food and pharmaceutical industries, and environmental science. Three mechanisms have been identified in the deposition process: particle transport from bulk flow to the surface, particle attachment on the surface, and particle re-entrainment from the surface [1,2,3,4]. Depending on particle sizes, particle transport can be divided into three regimes: diffusion, inertia, and impact [2,4]. Near the surface, particle attachment and resuspension are determined by the interplay among adhesive particle-surface interactions, hydrodynamic drag, lift force, gravity, surface roughness, etc. Among many factors, surface topography, such as random roughness, grooves, and ribs, can change contact geometries and hydrodynamics near the surface, thus, having substantial influence on the particle deposition [5]. While extensive research effort has been made towards understanding the effect of random or designed surface roughness on particle deposition from gas flows [4], particle interactions with surface topography in liquid suspensions are less addressed, despite the considerably great hydrodynamic lift force near the wall [2].

A case of interest is ribbed surfaces for heat exchangers. Developed for enhancing heat transfer [6,7,8,9] and/or mitigating crystallization fouling [10,11], these structures may exacerbate particulate fouling. Assuming an analogy between particle transport and heat transfer, theoretical studies [6,12] suggest that rib structures intensify particle transport to the surface, but, in the meantime, the enhanced local shear rate reduces the fraction of the particles sticking to the surface. Thereby, it is possible to achieve both enhanced heat transfer and mitigated particle deposition with surface structures [12]. However, this conclusion is not completely supported by the experimental studies. Kim and Webb [6] studied particulate fouling of three types of ribbed tubes and a smooth tube for 14,000 < Re < 26,000 using ferric oxide particles (0.64 micron in diameter) and aluminum oxide particles (3 microns in diameter) dispersed in water. All ribbed tubes were found to increase particulate fouling with the only exception of fouling at a high Re (26,000) where the extent of fouling was approximately the same as the smooth tube. Based on the experimental study, the first accelerated particulate fouling model was developed for helically ribbed tubes. Somerscales et al. [8,9] reviewed the particulate fouling characteristics of five different in-tube heat transfer enhancement surfaces. Their study suggests that certain surface geometries (e.g., roped surfaces) are effective in battling particulate fouling especially at high velocities. Li [13] studied particulate fouling of helically ribbed surfaces using an accelerated particle fouling test. More particle deposition occurs on all ribbed surfaces with different geometrical parameters at a Reynolds number around 16,000. More review on experimental studies of particulate fouling of surfaces with structures for heat transfer enhancement can be found in the References [7,8,9]. Textured surfaces used to suppress attachment of bio-organisms through enhanced shear [14] are out of the scope of this work, and thus, are not reviewed.

The differential behaviors of particle deposition near surface structures in previous studies [6,7,8,9] reveal the complicated interplay among particles, fluid flow, and surface topography. As an alternative to experimental studies, computational models of various complexities have been developed to acquire quantitative understanding of particle attachment to complex surfaces. Lu and Lu [15,16,17,18] performed Computational Fluid Dynamics (CFD) simulations of particle deposition from an air flow on three different surfaces with circular, triangular, and square ribs, respectively. Their studies suggest that particle deposition increases with short rib spacing and increased rib height, although the latter has less influence. Most particles accumulate on the windward area of the ribs. Among the three different rib shapes, the circular shape demonstrates the least particle deposition, while the square-shaped rib has the highest. Hong et al. [19] conducted a two-dimensional numerical study on particle deposition on structured elements from gas flow. The range of the height and the spacing of the elements are 0.4~2 mm and 4~16 mm, respectively, and the diameter of the channel is 20 mm. This study shows more particle deposition on surfaces with increased element height and spacing. Xu et al. [20] studied the submicron particle deposition on a semi-circular structured surface and suggested that the recirculation wake is the main mechanism for more particle deposition. Kasper et al. [21,22] developed numerical models with the capability of studying particle deposition on structured surfaces from turbulent liquid flow, and the predicted particle deposition agrees with their experimental study. More computational studies for particle transport and deposition are given in the review paper by Guha [4]. Compared with computational studies of gas suspensions, particle deposition from liquid suspensions on surfaces with various topographies are less-frequently addressed, especially for low-Reynolds-number flows.

In this paper, a Eulerian—Lagrangian model is developed to simulate particle attachment to surfaces with arc-shaped ribs in a two-dimensional channel flow at low Reynolds numbers. Numerical simulations are performed to improve the quantitative understanding of how rib geometries enhance shear rates and particle-surface interactions for various particle sizes and flow velocities. Of special interest is how the geometrical parameters of these ribs, such as pitch-to-height ratios, modify the hydrodynamics and particle-surface interactions for various particle sizes and flow velocities. A force analysis is performed to identify a threshold shear rate for reduction of particle attachment. The model is also used to predict particle distributions over the ribbed surfaces for different particle sizes and flow velocities. It is anticipated that the understanding of the effect of surface topography on particle attachment will benefit design of surface textures for mitigating particulate fouling in a wide range of applications.

2. Mathematical Models

We develop a Eulerian-Lagrangian model to describe the attachment of micrometer-sized particles on surfaces from liquid suspensions moving at low Reynolds numbers. Assuming a low volumetric particle concentration (<5%), the liquid suspension is treated as an incompressible and Newtonian fluid. The effects of particles and particle-particle collisions on the fluid flow are considered negligible. The dynamics of the fluid flow is described by the mass conservation and the Navier-Stokes equations, which are:

$$\nabla ·u_f=0$$

(1)

$${\rho }_f\frac{\partial u_f}{\partial t}+\nabla ·\left({\rho }_f{u}_f{u}_f\right)=-\nabla P+\nabla ·\left[{\mu }_f\nabla \left(u_f+u_f{}^T\right)\right]+{\rho }_{f}g$$

(2)

where $u_f$ is the fluid velocity vector, ${\rho }_f$ is the fluid density, ${\mu }_f$ is the fluid viscosity, P is the pressure, and g is the acceleration due to gravity. The Lagrangian method is used to describe the motion of the particles with diameters in the range of 10~75 microns. The position and velocity of a particle are determined based on Newton’s second law of motion:

$$\frac{d{X}_{\mathrm{p},\mathrm{i}}}{dt}= u_{\mathrm{p},\mathrm{i}}\mathrm{and}{m}_{p,i} \frac{d{u}_{p.i}}{dt}={\displaystyle {\sum }_1^N}{F}_{\mathrm{i}}$$

(3)

where X_p,i is the position of a particle, u_p,i is the particle velocity vector, m_p,i is the mass of the particle, F_i is the force acting on the particle, and N is the total number of the forces. The particles are assumed to be spherical and rigid. For liquid suspensions passing a channel at low Reynolds numbers, forces acting on the particles are drag, buoyancy, gravity, pressure gradient, Saffman lift force, and wall-induced lift force. As the main focus of this study is the effect of surface topography on particle attachment to a solid surface, particles are assumed to be neutrally charged and the electrostatic double layer force is not included. Brownian force is not considered because its magnitude is relatively weak compared with other forces for the particle size of interest in this study. The acceleration, velocity, and location of a discrete particle are calculated at each time step by numerical integration of Equation (3).

The general form of the drag force F_D acting on a particle developed for a wide range of Reynolds numbers is expressed in terms of a drag coefficient C_D, which is [23]:

$$F_D=C_D\frac{\pi d_p^2}{8}{\rho }_f\left(u_f-u_p\right)\left|u_f-u_p\right|$$

(4)

where d_p is the diameter of the particle, $u_f$ is the fluid velocity at the point where the center of a particle is located, $u_p$ is the particle velocity, and $\left|u_f-u_p\right|$ is the magnitude of the relative slip velocity. The drag coefficient C_D depends on the particle Reynolds number, which is defined as:

$$R{e}_p=\frac{{\rho }_f{d}_p }{{\mu }_f}\left|u_f-u_p\right|$$

(5)

The correlation for the drag coefficient proposed by Putnam [24] is used in this study due to its suitability for a wide range of particle Reynolds numbers while imposing the correct limiting drag force within the Newtonian regime:

$$C_D=\left\{\begin{array}{c}\frac{24}{R{e}_p}\left(1+\frac{1}{6}R{e}_p^{\frac{2}{3}}\right) if R{e}_p<1000 \left(Laminar regime\right)\\ 0.424 if R{e}_p \ge 1000 \left(Turbulent regime\right) \end{array}\right\}.$$

(6)

While this correlation is limited to smooth particles, the calculated drag force can be extended to rough particles in this study because the effect of surface roughness is negligible under the conditions of laminar flow and low Re_p, which is the case of the current study.

The buoyancy and the gravitational forces on a particle are combined as one total force F_g:

$$F_g=m_{p}g(1-\frac{{\rho }_f}{{\rho }_p})$$

(7)

where ${\rho }_p$ is the density of the particle. The pressure gradient force resulted from local pressure change is important for solid particles suspended in liquid [23]:

$$F_p=-\frac{\pi d_p^3}{6}\nabla p$$

(8)

A non-uniform velocity field gives rise to the Saffman lift force in the direction normal to the fluid flow. Mathematical description of this shear induced lift force was first developed by Saffman [25,26] and advanced by Mei [27]. The Saffman lift force F_L,S is expressed as:

$$F_{L,S}=C_L\frac{\pi D_p^3}{6}{\rho }_f\left(u_f-u_p\right)\times \left(\nabla \times u_f\right)$$

(9)

where C_L is the Saffman lift force coefficient. Formulations to calculate C_L can be found in the reference [27].

In addition to the Saffman lift force, a particle moving close to a wall is subject to a viscous lift force because of the progressively increasing friction between the two approaching surfaces. The expression for the wall-induced lift force that is normal to the surface [28,29] is:

$$F_L= f_L {\rho }_f {\gamma }^2{d}_p{}^4$$

(10)

where $f_L$ is lift coefficient, and $\gamma$ is local shear rate. The lift coefficient depends on the local Reynolds number [29]:

$$f_L=3.4368 R{e}^{-0.714}$$

(11)

The adhesive van der Waals force between a spherical particle and a surface has the form of [30,31,32,33]

$$F_{vdw}= \frac{A_H{d}_p }{12 z^2}$$

(12)

where A_H is the Hamaker constant and z is the surface-to-surface distance between the particle and the wall. The Combining Relation method [34] can be used to evaluate $A_{H }$ in Equation (12) based on the experimental and theoretical values of the related materials [35].

Upon contact, a particle may adhere to or bounce back from the surface.

The collision outcome is dependent on the approaching velocity of a particle and the particle-surface interactions. The principle of the conservation of energy has been widely used to describe the states of a particle before and after the particle-wall collision [36]:

$$E_{kin,1}+E_{el,1}=E_{vdW}+E_{kin,2}+E_{el,2}+E_{Loss}$$

(13)

where $E_{kin}$ is the kinetic energy, $E_{el}$ is the electrostatic energy, $E_{vdW}$ is the van der Waals attraction energy between the particle and the surface, and $E_{Loss}$ is the dissipation energy. $E_{Loss}$ is resulted from particle deformation and friction during the collision. Subscripts 1 and 2 represent the states before and after a collision, respectively. It is generally accepted that a particle will adhere to the surface if its kinetic energy after the collision is zero, i.e., $E_{kin,2}=0$ [36,37]. Based on this criterion, the critical approaching velocity U_cr for particle adherence can be derived from Equation (13). When the electrostatic energy and the energy loss are not considered [37] for neutrally charged and rigid particles, the critical velocity U_cr for particle adherence has the form of:

$$U_{cr= }\sqrt{\frac{12 E_{vdw}}{\pi d_p{}^3 {\rho }_p}}.$$

(14)

Particles approaching the surface at velocities greater than U_cr will result in $E_{kin,2}> 0,$ and are predicted to bounce back. The van der Waals energy is calculated by integrating of the product of the van der Waals pressure and the contact area over the distance to the wall [38]. The van der Waal energy of a particle in Equation (14) at the wall is [38]:

$$E_{vdw}= \frac{A_H{}^2 d_p}{144 \pi z_0{}^4\sigma }$$

(15)

where $z_0$ is the distance between the particle and the surface upon contact and $\sigma$ is the yield strength of polystyrene particles. The values of A_H, z₀, and $\sigma$ used in this study are given in

Table 1. Physical properties and simulation parameters.

Variable	Value
Height of the channel, h	20 mm
Height of the rib, H	1 mm
Density of water, ${\rho }_f$ [39]	998.2 kg/m3
Viscosity of water, ${\mu }_f$ [39]	0.001003 Pa s
Density of particle, ${\rho }_p$	1040 kg/m3
Yield strength of polystyrene particles, $\sigma$ [40]	40 MPa
Contact distance, z0 [41]	0.4 nm
Hamaker constant, AH [34,35]	1.69 × 10−20 J
Maximum channel velocity, umax	3 cm/s, 8 cm/s, and 13 cm/s
Diameter of particles, dp	10 µm, 50 µm, and 75 µm
Critical velocity of particle adherence, Ucr	0.36, 0.079, 0.048 cm/s
Channel Reynolds number	500~3000
Particle relaxation time	5.76 × 10−6 ~ 3.24 × 10−4 s
Particle Reynolds number, Rep	0.299~9.70

.

3. Problem Setup and Numerical Issues

The deposition of polystyrene particles from an aqueous suspension is studied in a two-dimensional copper channel. The channel is 20 mm in height and 140 mm in length. As shown in Figure 1a, it has a 20 mm long entry region, a 100 mm long test surface with repeated arc-shaped ribs, and a 20 mm long region for exit. The arc-shaped two-dimensional ribs with identical height but four different pitch-to-height ratios (λ/H) are shown in Figure 1b.

A fully developed flow with a parabolic velocity profile is applied at the inlet:

$$u_{inlet}\left(y\right)= \frac{4 u_{max} y \left(h-y\right)}{h^2},$$

(16)

where h is the height of the channel and u_max is the maximum inlet velocity. At the outlet, p = 0. On the channel wall, a no slip condition is applied, which is $u_{f }$= 0. Due to the symmetry, only half of the domain is simulated, and the symmetric boundary condition is applied at the centerline. The deposition of particles of three different sizes, which are 10, 50, and 75 microns, on ribbed and flat channel surfaces, are tested for u_max of 3, 8, and 13 cm/s. The Reynolds numbers of the channel flow, the particle Reynolds numbers, and the particle relaxation time are listed in Table 1. The corresponding critical approaching velocities are calculated to be 0.36, 0.079, and 0.048 cm/s for particles with diameters of 10, 50, and 75 microns, respectively. A particle is considered adhering to the surface if its velocity normal to the surface is lower than the critical velocity upon contact. The fluid and particle properties, geometrical parameters, and simulation parameters are given in Table 1.

Complex surface textures can induce instability even at low velocities. To capture the smallest structure of the hydrodynamics near the surface, very fine meshes that meet the requirement of Direct Numerical Simulation (DNS) are used in this study. In DNS, the mesh size Δx and time step Δt can be estimated as [42]:

$$\mathsf{\Delta }x~ {\left(Re\right)}^{-3/4}L and \mathsf{\Delta }t~ \mathsf{\Delta }x/U$$

(17)

where L is the characteristic length of the problem and U is the velocity. Based on the velocity of 13 cm/s and the channel height of 0.02 m, Δx is approximately 50 microns and Δt is 300 µs. In this study, a maximum mesh size of 40 microns is used in a 1 mm thick layer above the surface as shown in Figure 2. Outside of this near surface layer, the maximum mesh size is 100 microns. The total number of elements in the near surface layer is 150,000. Further reduction of mesh size by 50% yields 0.1% difference in the velocity at the location of 0.1 mm above the apex of a rib. A time step of $\mathsf{\Delta }t$ < 300 µs is used in the transient simulation of the fluid flow before a steady state velocity field is established.

Well-mixed particle-laden fluids are used in many studies of particle transport and deposition in channel flows. To ensure a nearly uniform particle concentration, a flowrate-weighted particle distribution is applied when injecting particles from the inlet. However, this approach is not employed in this study because of the dependence of particle placement over the inlet on the flow velocity and the velocity profile. As our focus in the current study is how surface features affect the attachment of the particles, we aim to conduct numerical tests that highlight the effect of surface structures while minimizing the influence of other factors such as initial placement of the particles and particle concentrations. In light of this consideration, 1000 particles that are uniformly distributed in space are injected from the inlet of the channel every 0.5 s for 150 s in the numerical tests. Further increasing the number of the injected particles to 2000 every 0.5 s leads to less than 1% difference in the fraction of the particles that adhere to the surface. A time step of 10⁻⁴ s is chosen for the numerical integration of Equation (3). Further halving the time step yields a less than 0.1% difference in the fraction of particle deposition. A second-order implicit scheme is used to integrate Equation (3) for particle velocity and location.

Considering the assumption of a low particle concentration, a one-way coupling scheme is used in this study. The steady-state velocity field is obtained first, followed by the calculation of the acceleration, the velocity, and the location of each particle at each time step using Equation (3). For the numerical study of fluid flow, the pressure-velocity coupling scheme is used for pressure and momentum equation and the second-order upwind scheme is used for discretization. The simulation is performed using the software ANSYS-Fluent with user-defined subroutines or functions to implement additional forces for particle-surface interactions.

4. Results

In this study, simulations of fluid flow and particle attachment have been performed in a two-dimensional (2D) channel illustrated in Figure 1a with surface topographies shown in Figure 1b. The ribs shown in Figure 1b share the same height (H) with various pitches (λ). To provide a reference for the ribbed surfaces, simulations are also conducted in the 2D channel with a flat test surface. This reference channel has a height of h-2H as the area for the fluid flow in the ribbed channel is reduced. 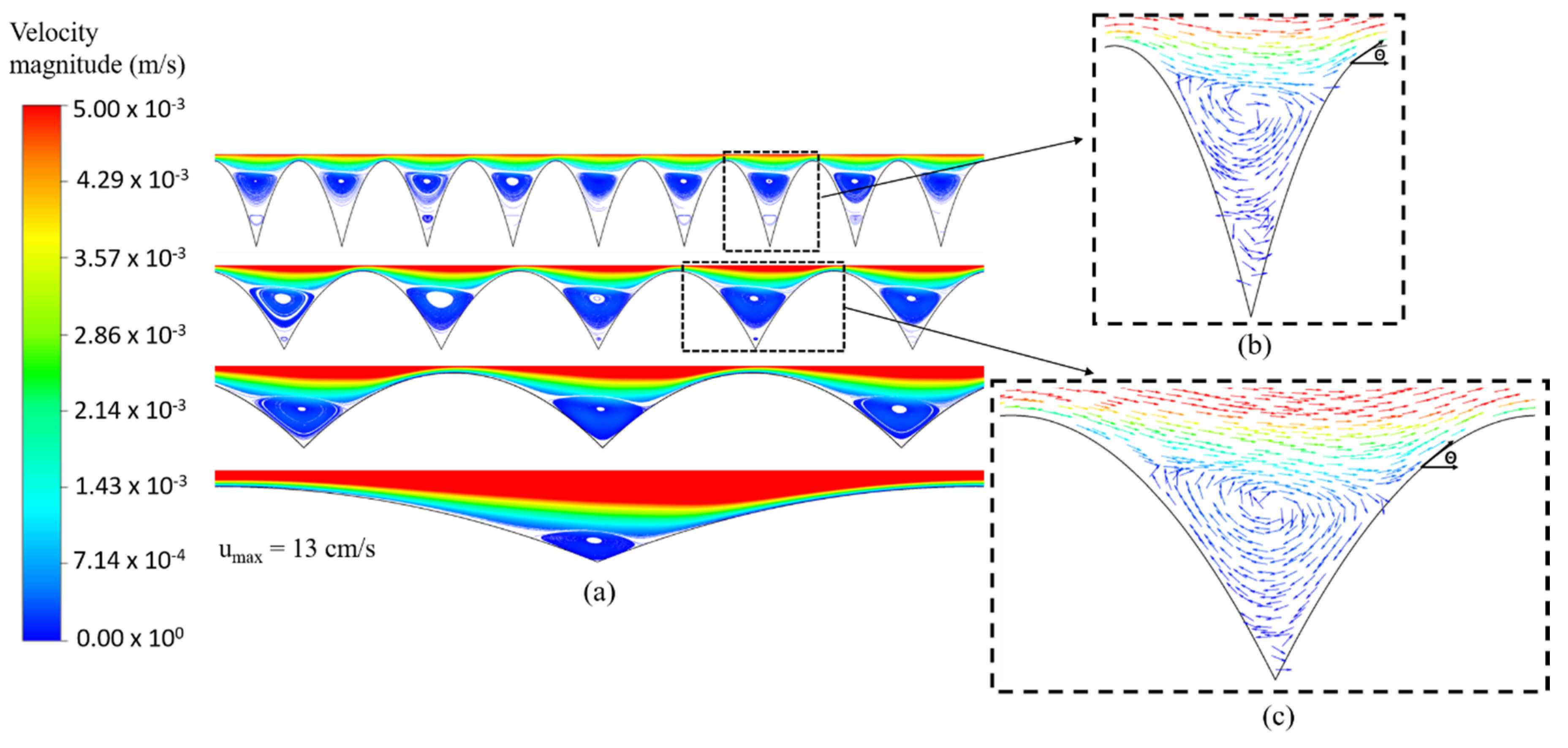Figure 3 shows the complex flow patterns near the arc-shaped ribs of different λ/H ratios. The velocity fields demonstrate vortices formed between adjacent ribs and a wavy pattern of shear flows above the surface. Both the height of the vortex and the amplitude of the wavy flow are dependent on the λ/H ratio of the ribs.

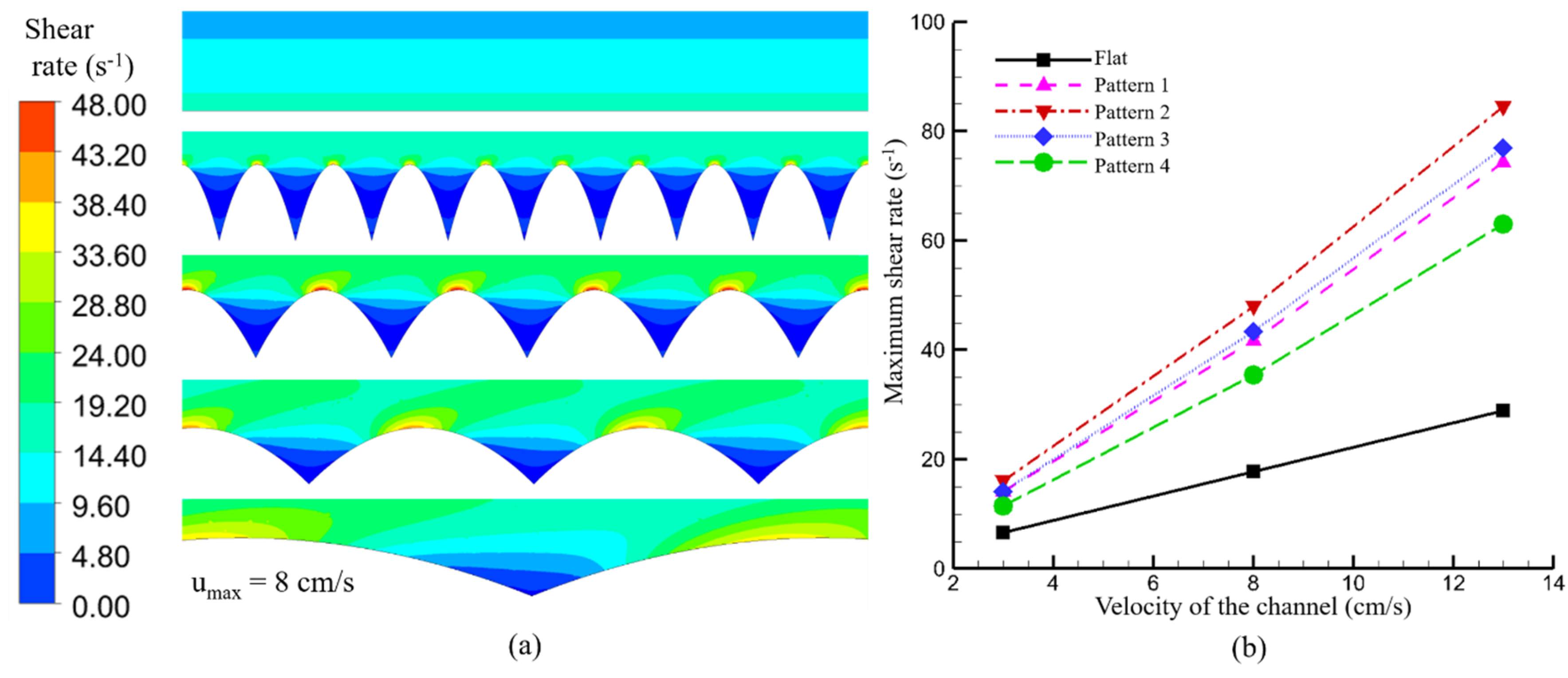
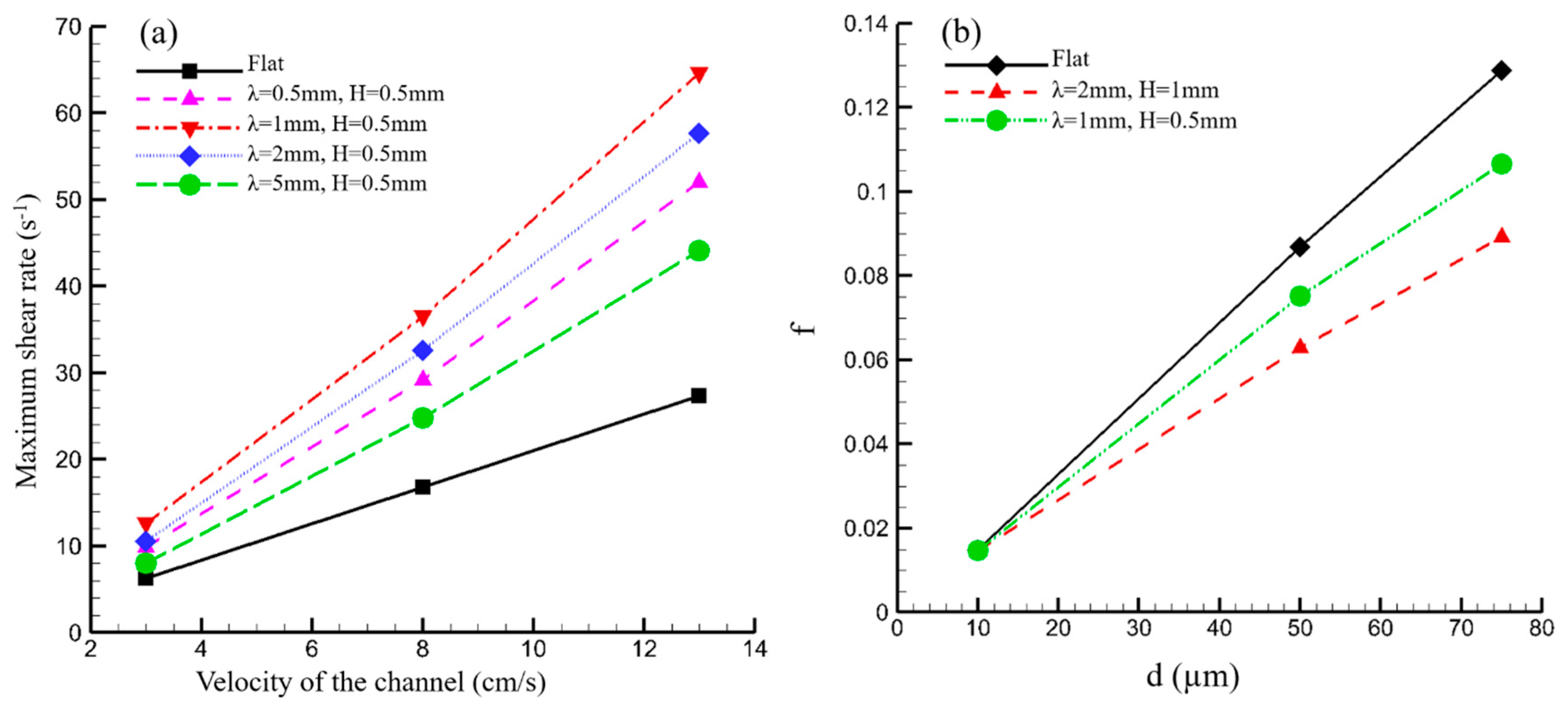
The shear rate distributions over the ribbed surfaces at a velocity of 8 cm/s are shown in Figure 4a. The maximum shear rates generated by these surfaces at velocities ranging from 3 to 13 cm/s are compared in Figure 4b. While the highest shear rate all occurs at the apex of the arc-shaped ribs, its magnitude varies over a large range despite the same height of the ribs. The ribs with a λ/H = 2 is identified to yield the highest maximum shear rate. Additionally, the shear rate enhancement is more pronounced at high velocities as evidenced by the slopes of the plots in Figure 4b.

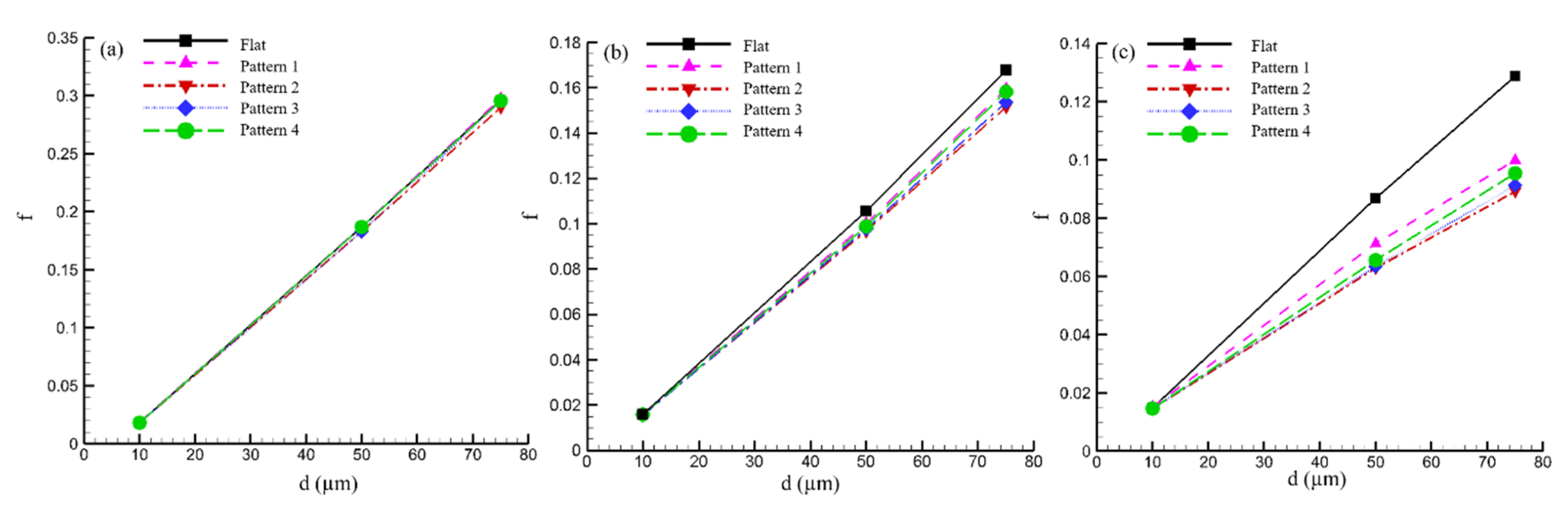
In this study, particle deposition is measured by the fraction of particle attachment, f, defined as the fraction of the injected particles that adheres to the test surface. At a low velocity of 3 cm/s, the ribs show negligible effect on the particle attachment regardless of particle size, as observed in Figure 5a. At a higher velocity of 8 cm/s, the f values for 50 and 75 micron particles decline on the ribs as displayed in Figure 5b. The attachment of 50 and 75 micron particles is further reduced by the ribs when the velocity is increased to 13 cm/s as shown in Figure 5c. Interestingly, 10 micron particles remain insensitive to the ribbed surface topographies even at the higher velocities. The reduction in particle attachment is dependent on both the velocity and the particle size.

Among the four ribbed surfaces, the rib geometry with a λ/H = 2 is the most effective in reducing particle attachment for 50 and 75 micron particles as shown in Figure 6. Compared with the flat surface, this rib geometry reduces particle attachment for 50 and 75 micron particles, respectively, by 8.62% and 9.54% at the velocity of 8 cm/s, and by 27.6% and 30.54% at a velocity of 13 cm/s. Additionally, the simulation results show that regardless of surface topographies, particle attachment decreases with increasing velocity and decreasing particle size. This observation agrees with other theoretical and experimental studies [43].

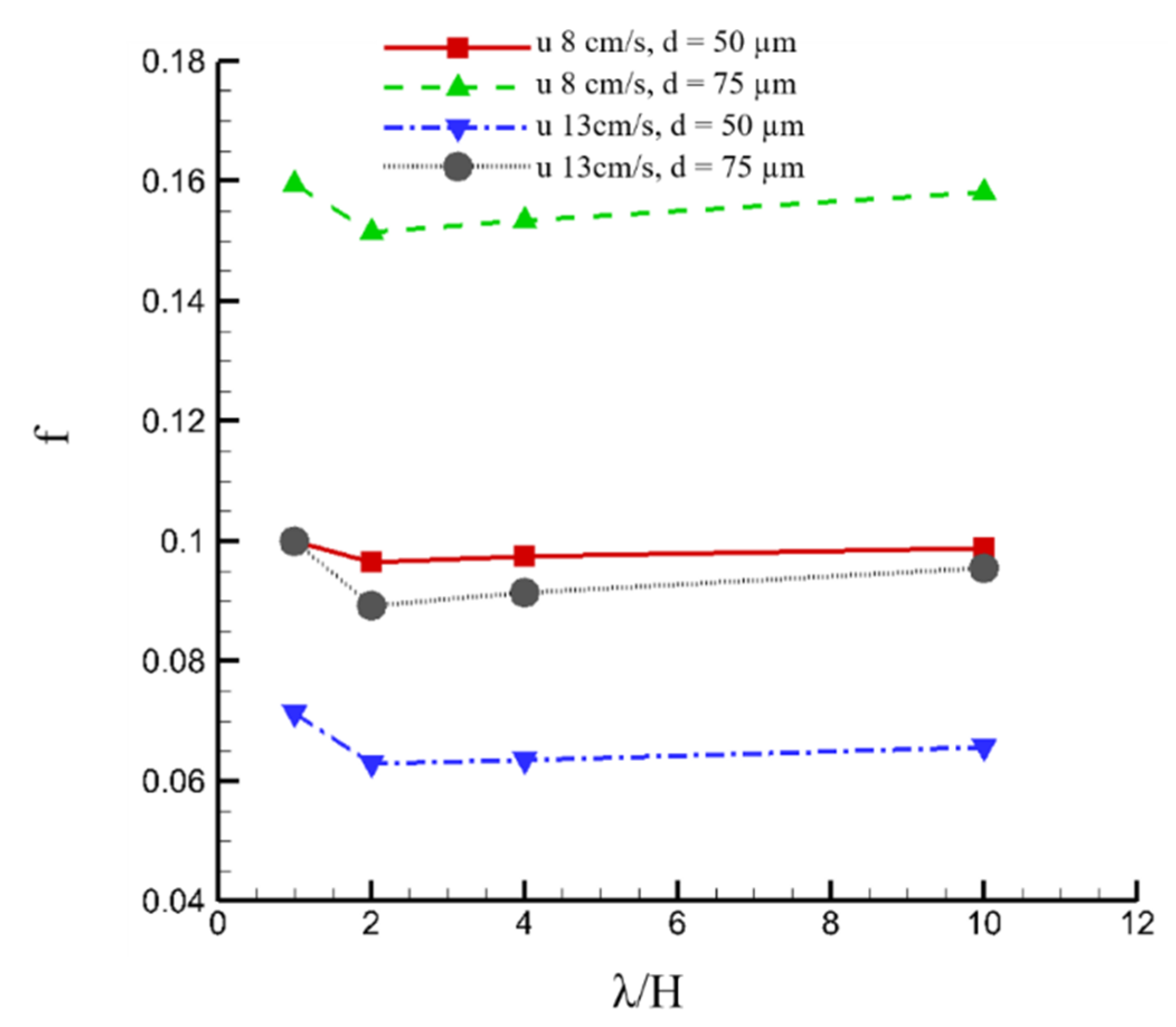
We have also performed simulation of particle attachment to ribbed surfaces with the rib height (H) of 0.5 mm and λ/H ratios of 1, 2, 4, and 10. Again, the surface with a λ/H = 2 demonstrates the highest shear rate enhancement shown in Figure 7a and the lowest fraction of particle attachment. However, the reduction in particle attachment is not as effective as the 1 mm-height ribs of the same λ/H ratio, as displayed in Figure 7b.

The distributions of 50 and 75 micron particles are also characterized on the arc-shaped ribs with a λ/H value of 2. As shown in Figure 8, a unit surface structure can be divided by a midline into two sub-areas: apex and valley. The total number of particles that attach to each of the sub-areas over the entire test surface is calculated and compared for different velocities. Figure 8 shows that at 8 cm/s, the amount of 50 micron particles settled in the valley is slightly higher than that in the apex. In contrast, most 75 micron particles fall in the valley at 13 cm/s. The distribution of the larger particles in the high velocity flow is more sensitive to the surface topography.

5. Discussion

The behavior of particle attachment to a surface is determined by the complicated interplay between the particle, the hydrodynamics, and the surface topography. When a stream of liquid is passed over a ribbed surface, complex hydrodynamics is created even at moderate flow velocities. The enhanced shear rate, the flow pattern, the contact geometry, and the particle size are important factors that determine the fraction of particle attachment to the surface as well as the particle distribution over the surface.

Our simulation shows that the maximum shear rates generated at the ribbed surfaces are significantly higher than the flat surface under an identical flow velocity. As the height of the flat-surfaced channel is reduced, the observed shear enhancement can only be attributed to the wavy flow and the surface topography illustrated in Figure 3. As the fluid follows the contour of the ribs, the upward acceleration of the fluid along the front side of the rib maximizes the shear rate near the apex. The magnitude of the shear is dependent on both the wavy flow amplitude and the angle of attack at the front of the rib. For the surface with a λ/H = 1, the close spacing between the ribs results in a small wavy flow amplitude and a limited amount of the fluid interacting with the ribs. In the opposite case of a large λ/H = 10, the effect of the large wave amplitude is weakened by the small slope of the rib surface. With these competing mechanisms at play, the surface topography with a λ/H = 2 yields the highest maximum shear rate for all velocities. When the height of the arc-shaped ribs is reduced to 0.5 mm, the highest shear rate is again yielded at a λ/H value of 2, illustrating the same mechanisms at play. To further improve the shear rate, topographical parameters that can suppress the stagnant zones between the ribs while maintaining an optimal angle of attack should be developed in the future study.

High shear rates near a surface will reduce the fraction of particle attachment. However, this is only observed in our study for 50 and 75 micron particles at the velocities of 8 and 13 cm/s. This discrepancy can be explained by the threshold shear rate. For deposition of micrometer-sized particles in laminar flows, the van der Waals force only dominates over a short particle-surface distance of hundreds of nanometers. Beyond this distance, it has negligible influence on the particle trajectory. The role of the Saffman force in laminar flows is also insignificant. Thereby, the motion of the particles is dictated by the competition between the magnitudes of the buoyancy force, F_g, and the wall-induced lift forces, F_L, in the direction normal to the surface. A particle will move away from the surface when the lift force overpowers gravity. The ratio of the magnitudes of these two forces near a surface is expressed as:

$$\left|\frac{ {\mathrm{F}}_L}{ {\mathrm{F}}_g}\right|= \frac{6 f_L {\gamma }^2 d_p {\rho }_{f }}{\pi (1-\frac{{\rho }_f}{{\rho }_p }) g \pi {\rho }_p}$$

(18)

Based on $\left|{\mathrm{F}}_L/{\mathrm{F}}_g\right|<1$, a threshold shear rate, ${\gamma }_{cr}$, can be calculated. The threshold shear rate for polystyrene particles of various diameters in water is given in Figure 9. For 10 micron particles, the threshold shear rate is 140 s⁻¹, higher than any maximum shear rate presented in Figure 4. This explains the reason why 10 micron particles are insensitive to increasing velocities and surface topographies. On the other hand, for the lowest fluid velocity of 3 cm/s, the ribbed surfaces are unable to raise shear rates above the respective threshold values for all three particles sizes; therefore, no reduction in the particle attachment is observed.

The reduction in the particle attachment by the ribs is most effective for large particles at high velocities due to the decline in threshold shear rates and the nonlinear dependence of the magnitude of F_L on the shear rate $\left({\mathit{F}}_L\propto {\gamma }^2\right)$. Considering the pivotal role of the shear rate in particle adherence to a surface, it is not surprising that the ribbed surface yielding the highest maximum shear rate is associated with the most reduction in particle attachment.

Besides the reduced particle attachment to the surface, a non-uniform shear rate also affects the distribution of the attached particles on the surface. While it has been established that more particles fall in the valley area than the apex, our study shows that the disproportionality is very sensitive to particle size and velocity. With more particles accumulating in the valley, the adhesive particle-surface interaction will be replaced by the cohesive particle-particle interactions. This change has significant influence on the evolution of particle deposition rate with time. Quantitative information on the particle distribution over a rib is also very helpful for understanding particle resuspension from the surface.

One limitation of our numerical models is the idealized representation of real situations such as spherical and rigid particles, two-dimensional laminar flows, zero electrostatic forces, and no energy loss with collision. While these assumptions may compromise the accuracy of the predicted particle fouling rate, the results can still elucidate the physics underlying the particle-rib interactions and the effect of surface topographical features on particle attachment. Such understanding and knowledge is still valuable for surface texture choice and design. In addition, this study focuses only on particle attachment to clean surfaces, and the effect of particle interaction with the previously attached particle and the change of surface topographies by particle accumulation is not considered. Research effort will be continued to study particle deposition with particle-particle interactions, altered contact geometry by particle attachment, and the electrostatic force.

6. Conclusions

Numerical simulations have been performed to study the effect of surface topography on particle attachment in a two-dimensional channel flow. The ribs on the surface can significantly enhance the shear rates. The shear rate enhancement can be attributed to the wavy flows over the ribbed surface and the weak vortices between adjacent ribs. For arc-shaped ribs of identical height, varying pitch-to-height ratios, λ/H, can alter the amplitude of the wavy flow and the angle of attack of the fluid on the ribs. As a result, the rib geometry with λ/H = 2 demonstrates the greatest shear rate near the rib apex. As the wall-induced lift force is nonlinearly dependent on γ, this surface geometry yields the lowest fraction of particle attachment. However, the ribbed surfaces show negligible effects in two cases. One is the particle attachment from channel flow at low velocity, such as 3 cm/s, and the other is small particle diameter such as 10 micron particles. Analysis of forces acting on the particles identifies a threshold shear rate to reduce the particle attachment. Non-flat surface geometries lead to non-uniform distribution of particles, and the non-uniformity is more pronounced for larger particles and higher flow velocities. Understanding of the effect of surface topography on particle attachment will benefit design of surface textures for mitigating particulate fouling.