Numerical Study of a Liquid Metal Oscillating inside a Pore in the Presence of Lorentz and Capillary Forces
Abstract
1. Introduction
2. Materials and Methods
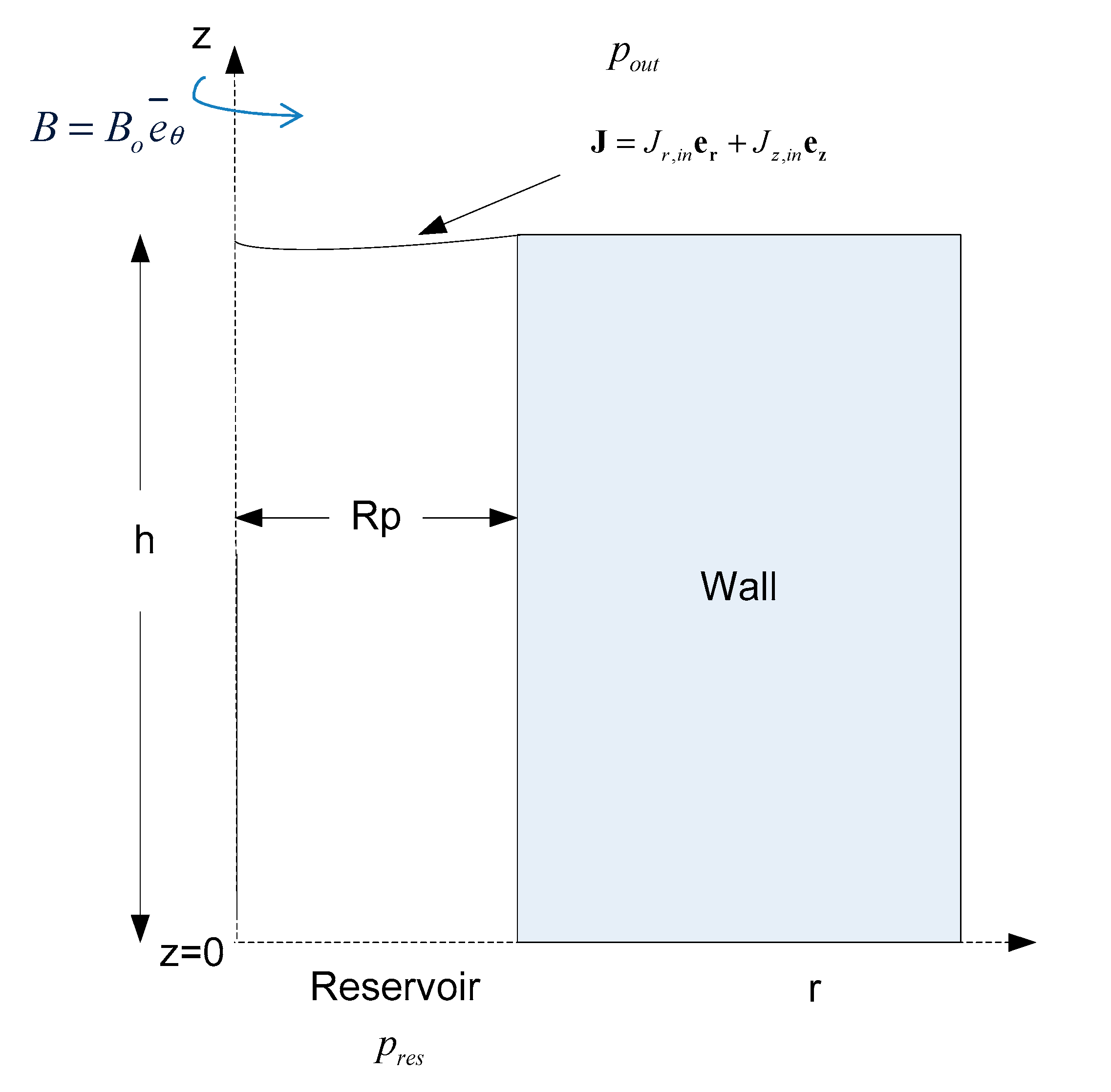
2.1. Problem Formulation
2.2. Numerical
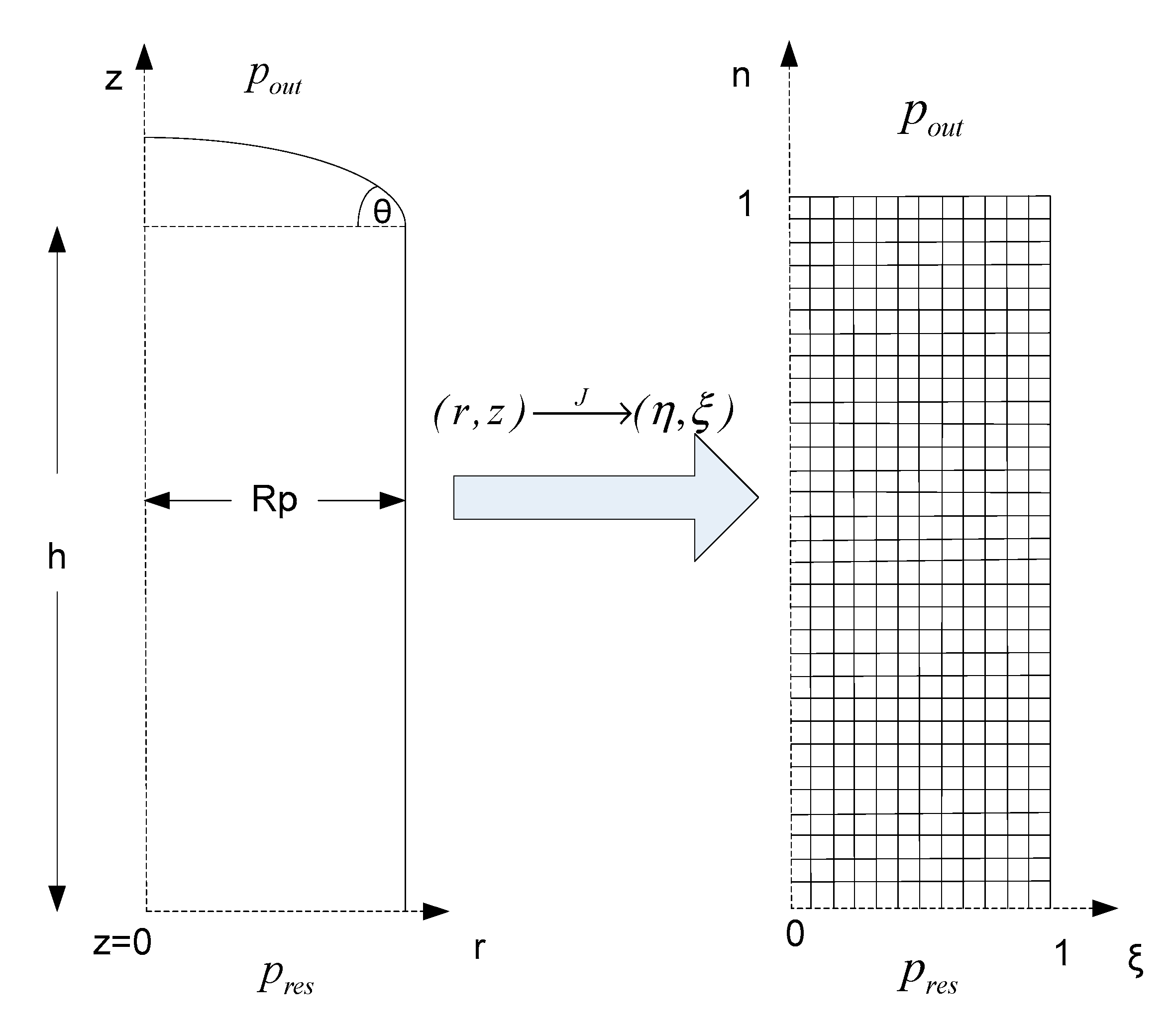
2.2.1. Numerical Method
2.2.2. Grid Construction
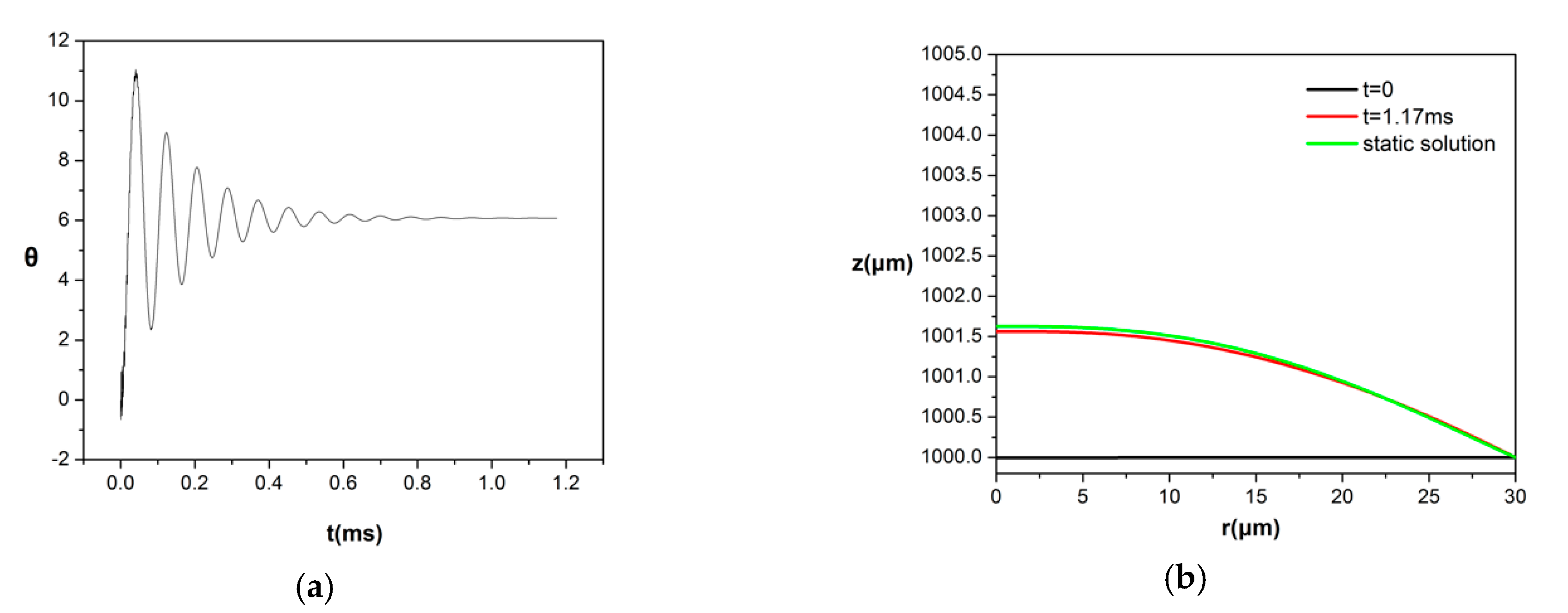
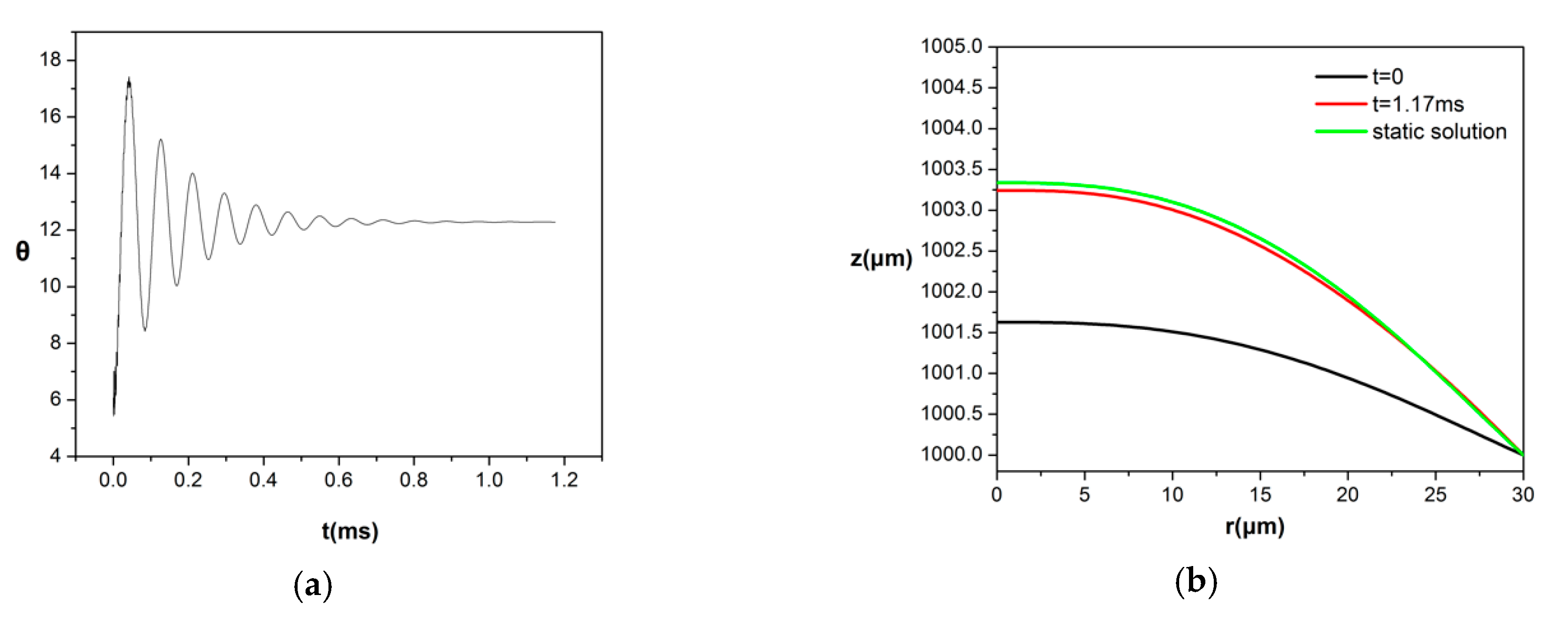
2.2.3. Benchmark Simulations and Code Validation
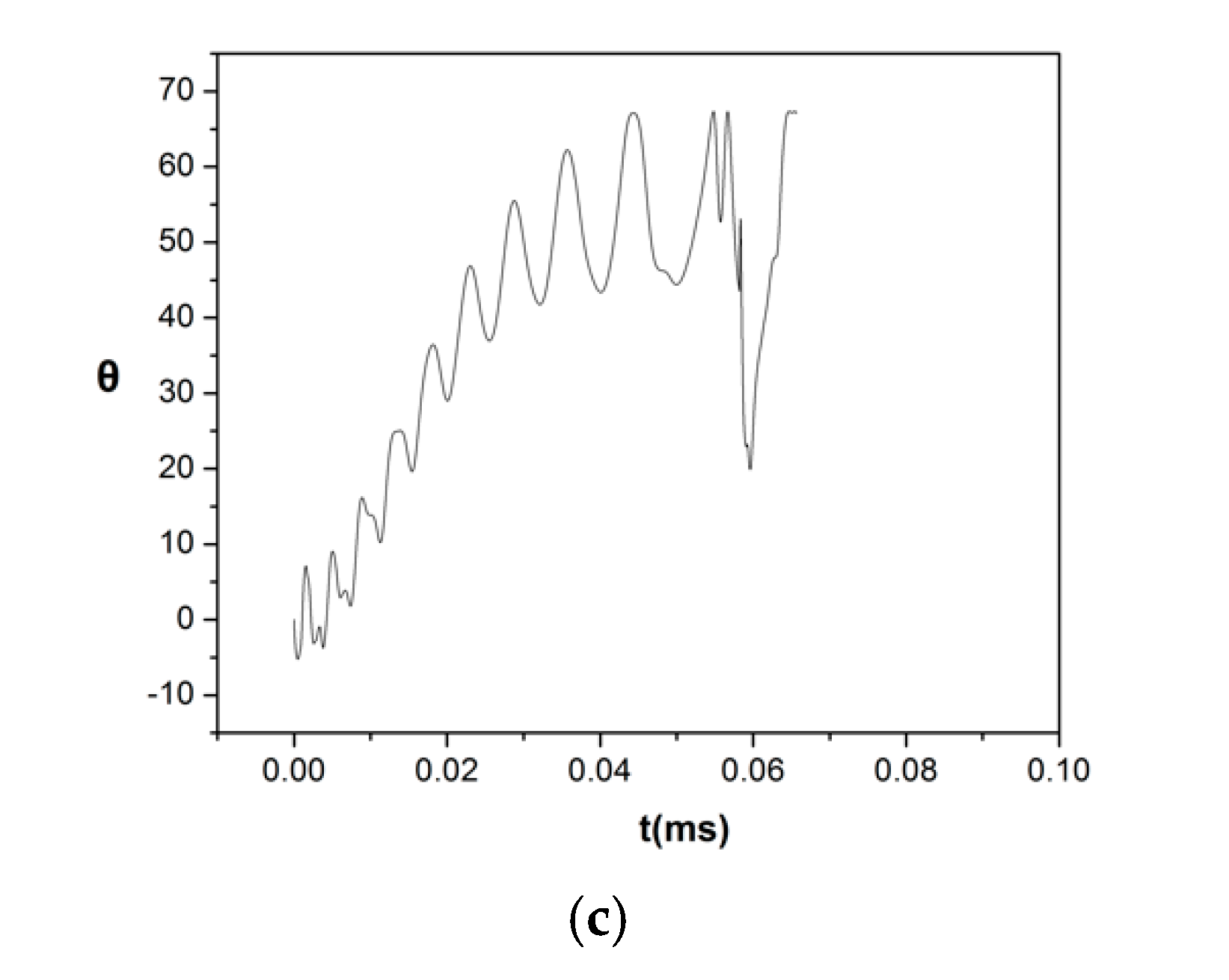
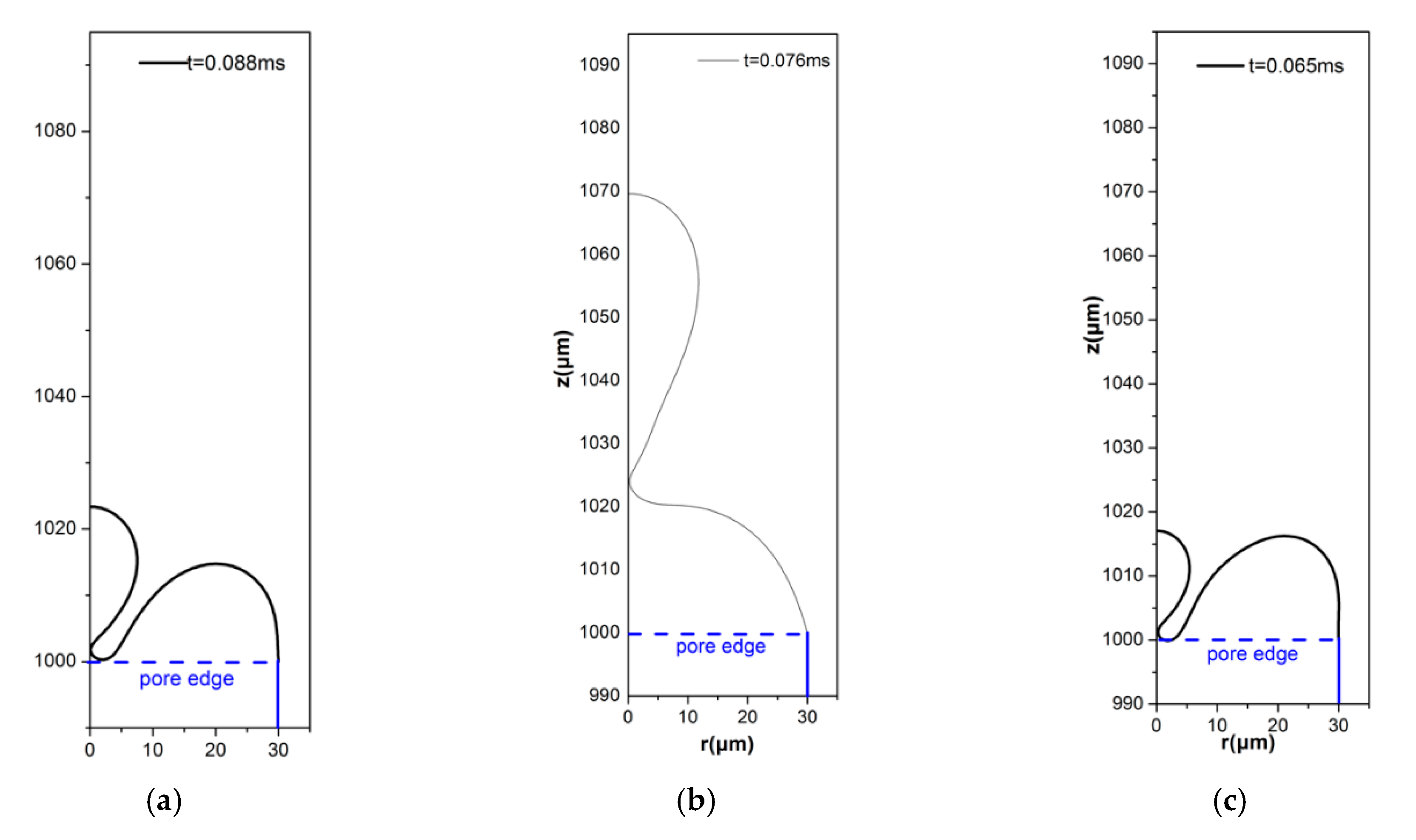
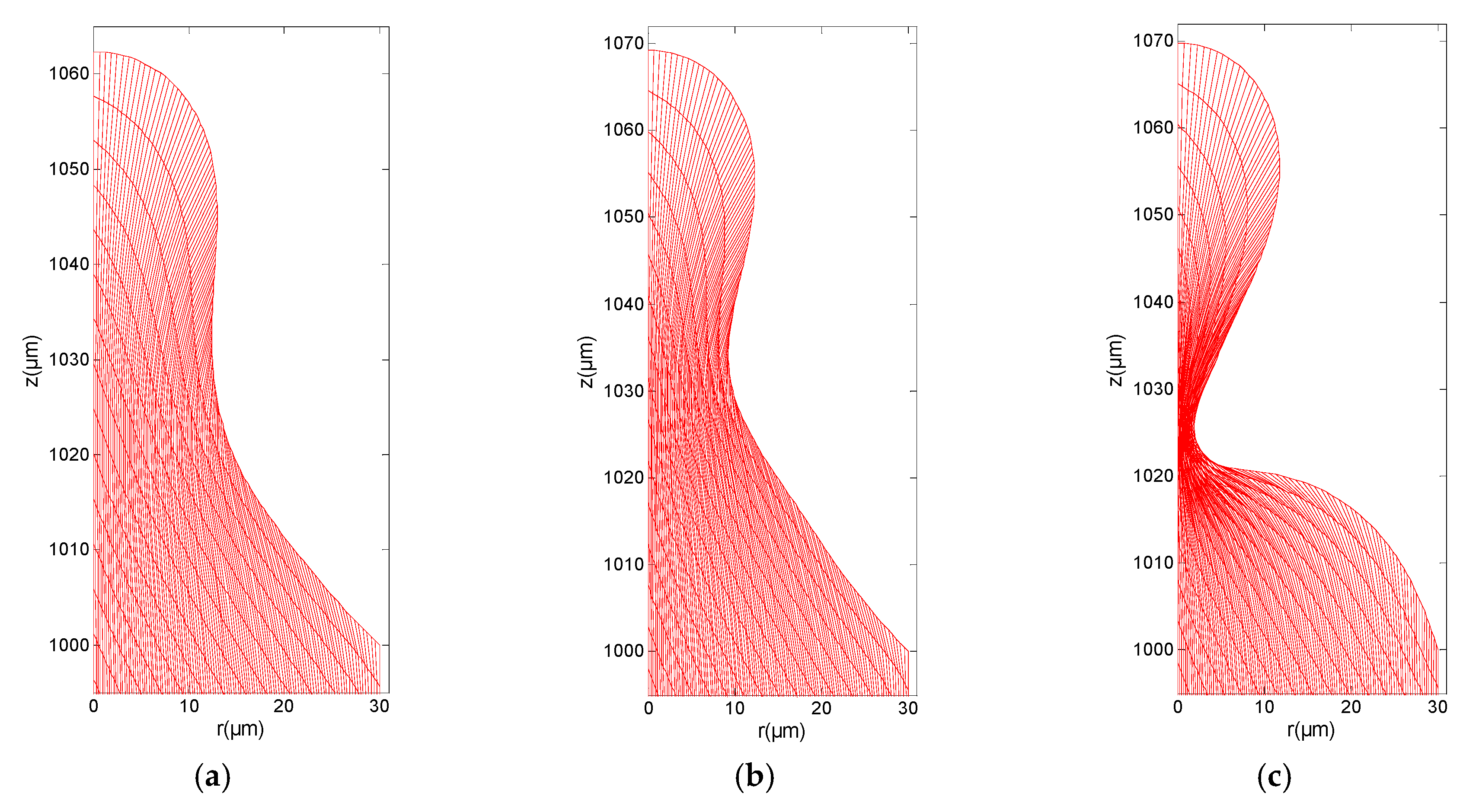
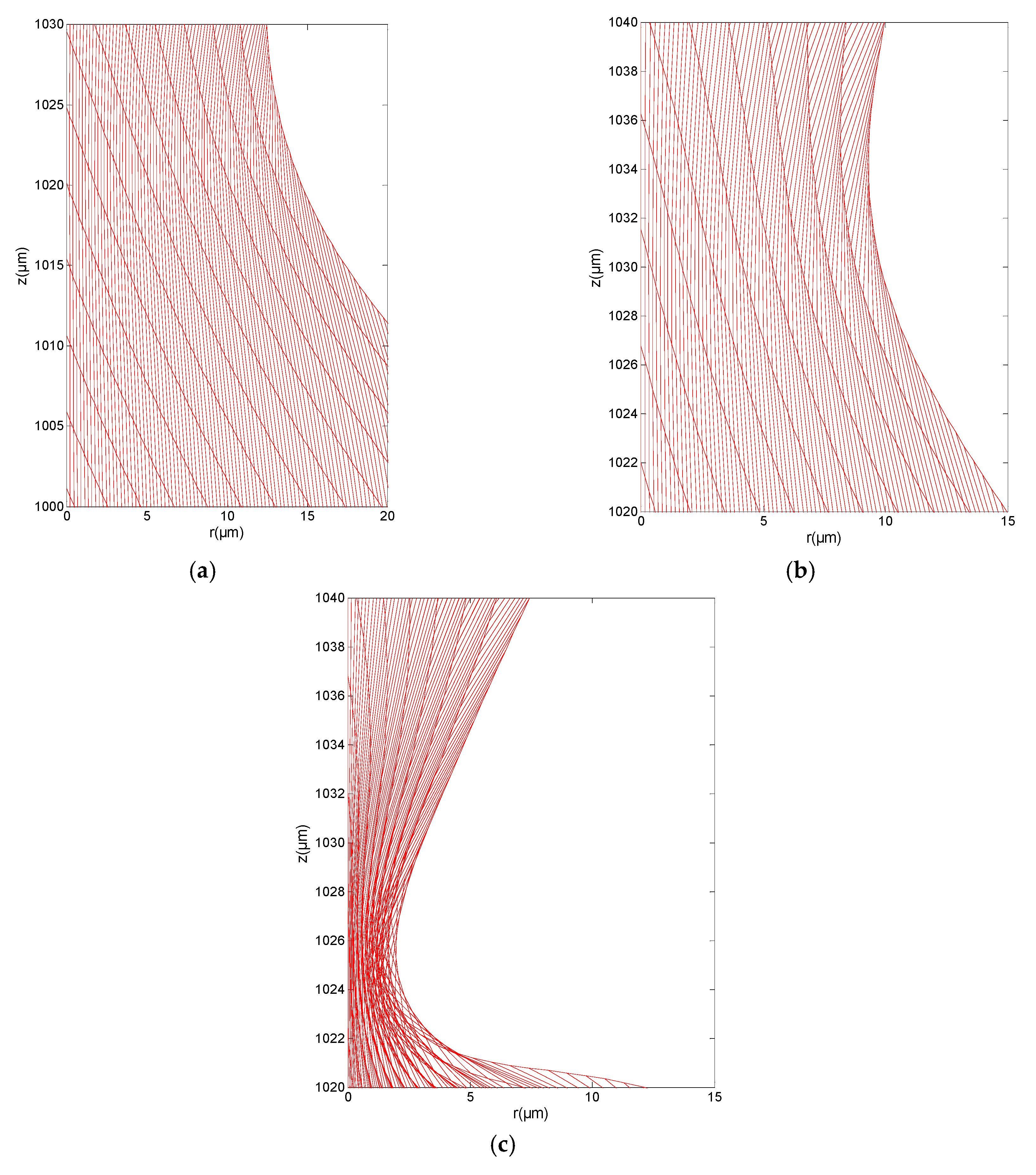
3. Results
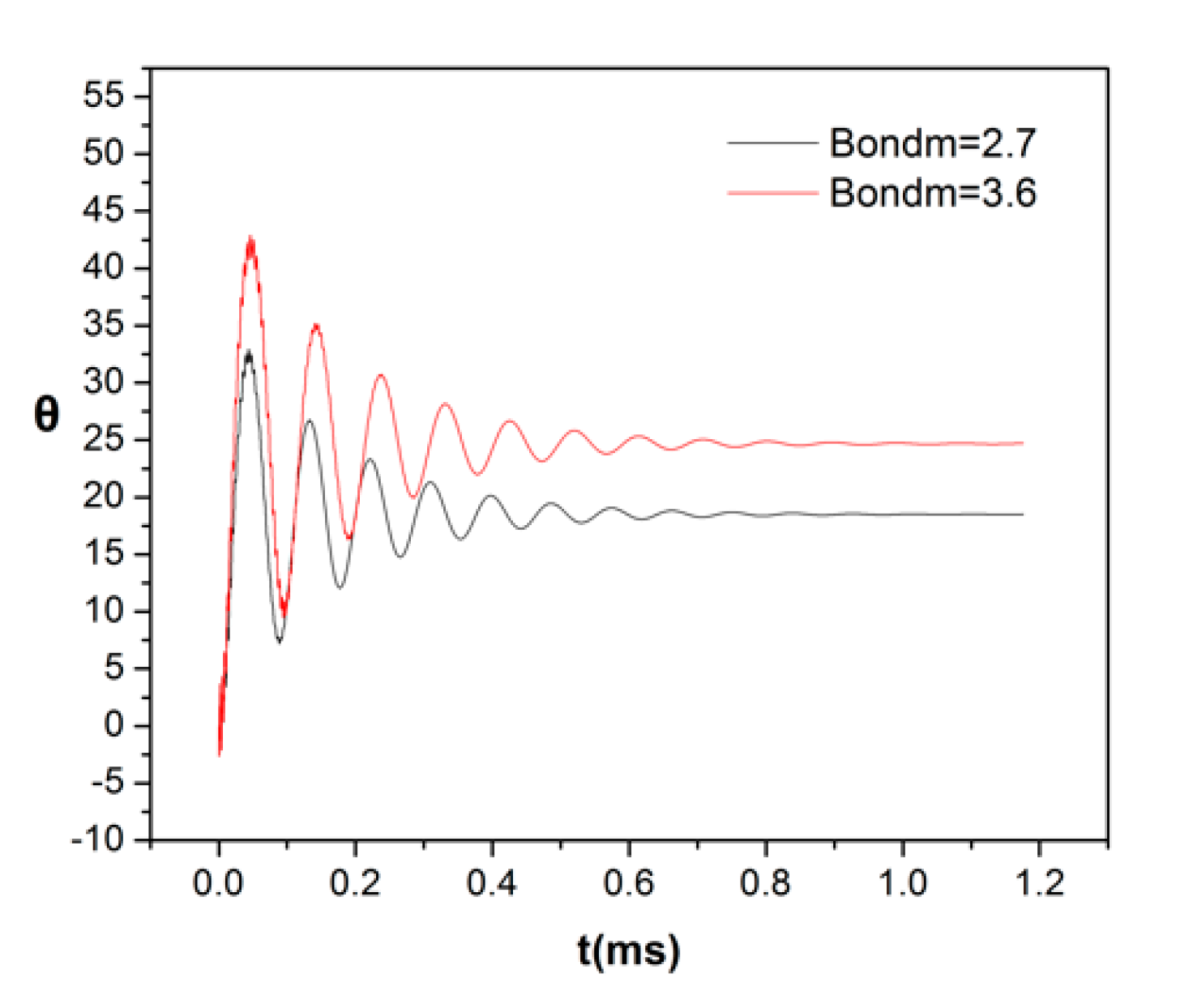
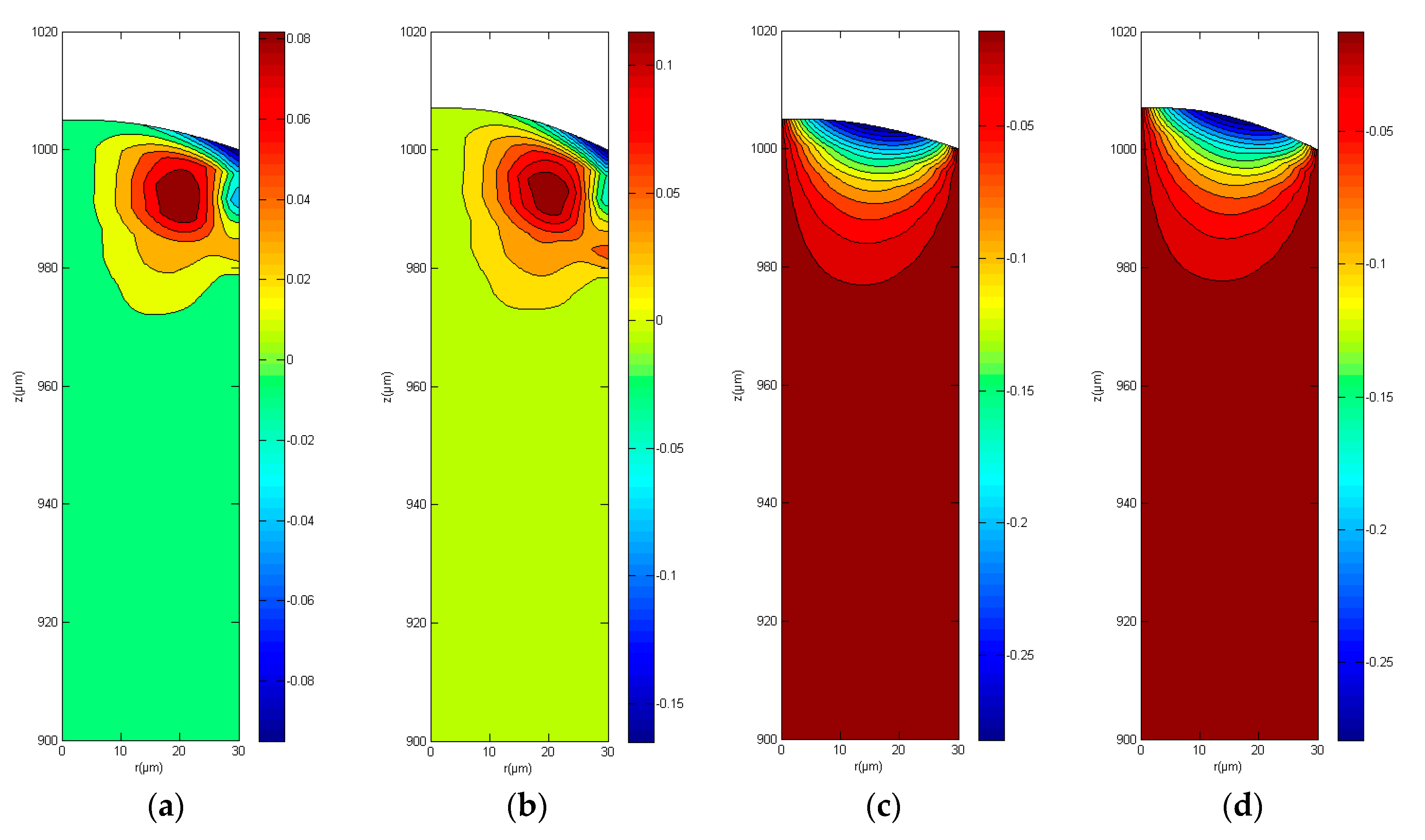
3.1. Effect of Increasing Bondm
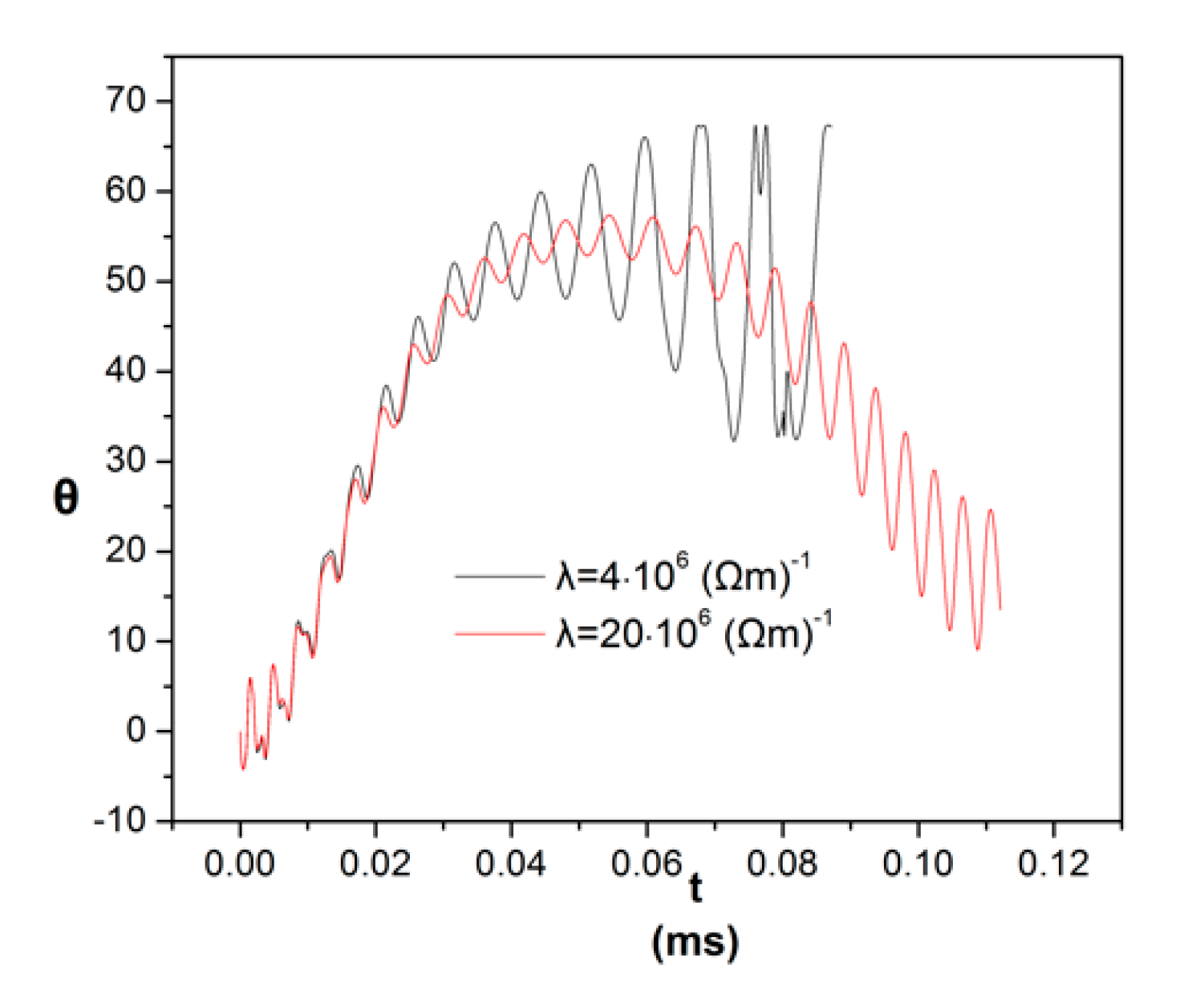
3.2. Effect of Electric Conductivity
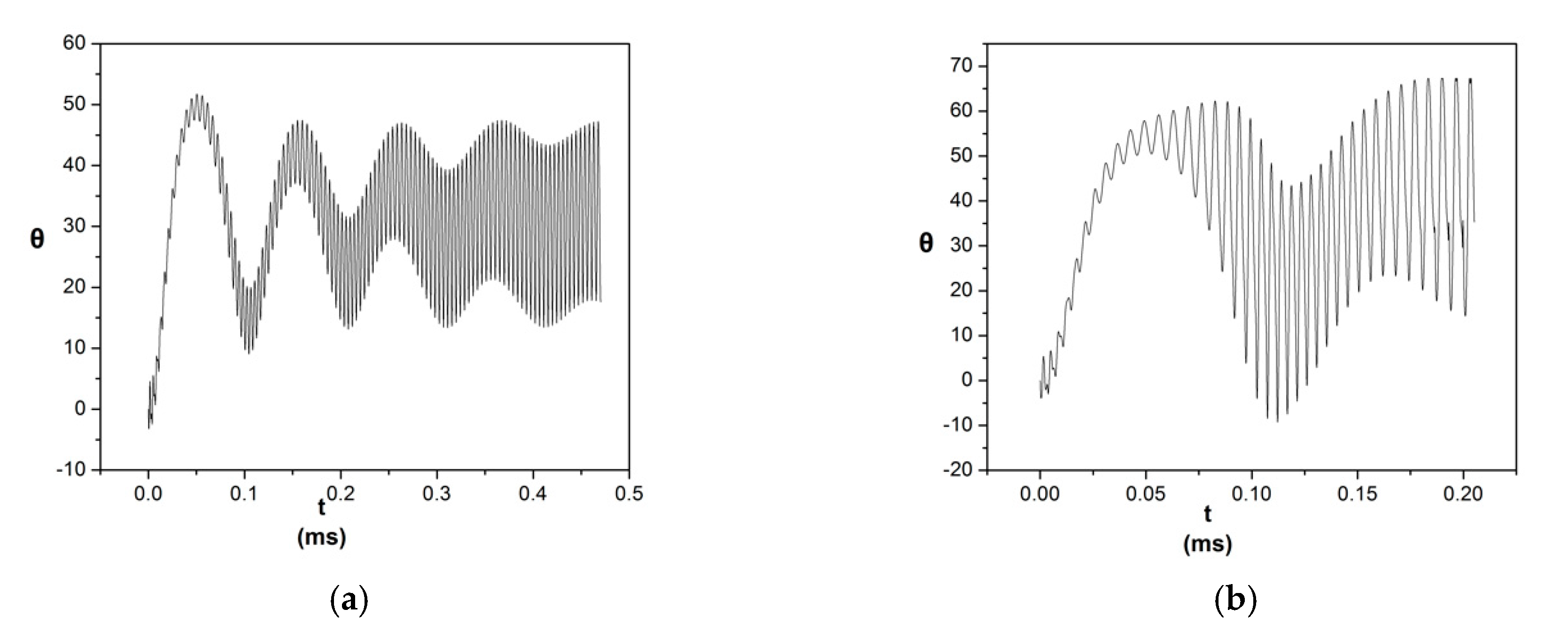
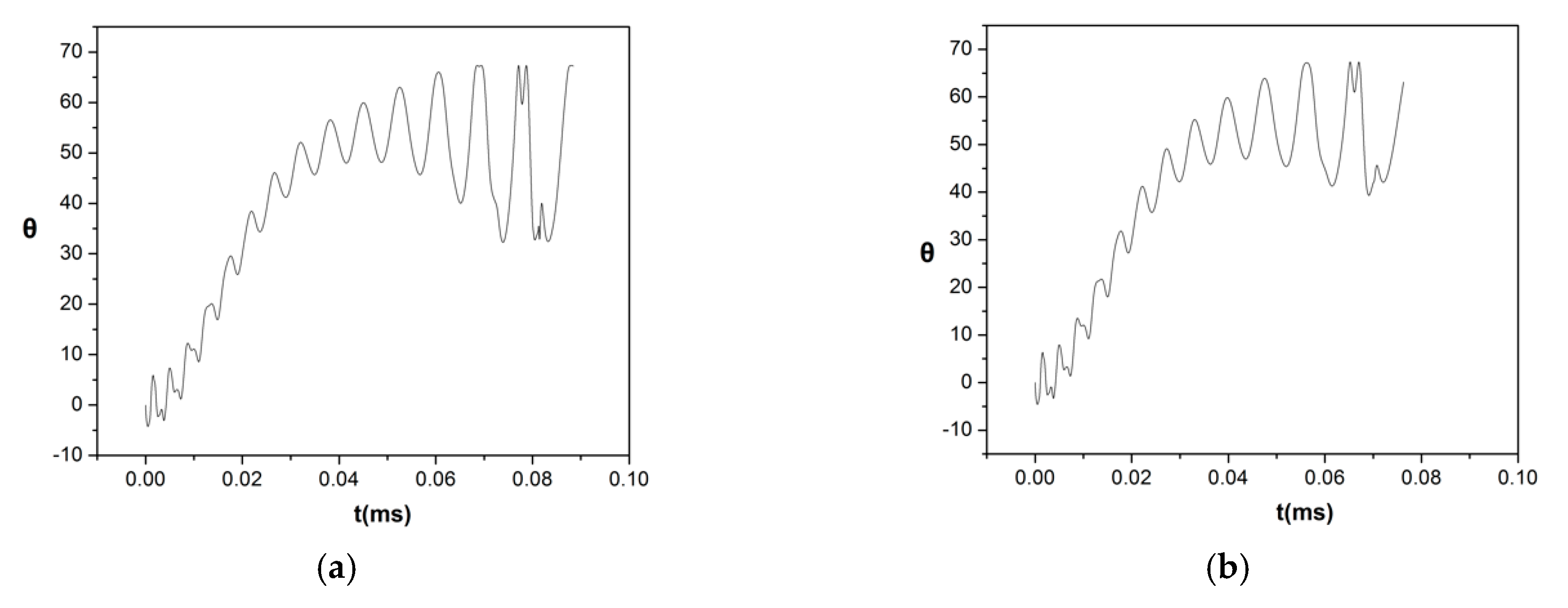
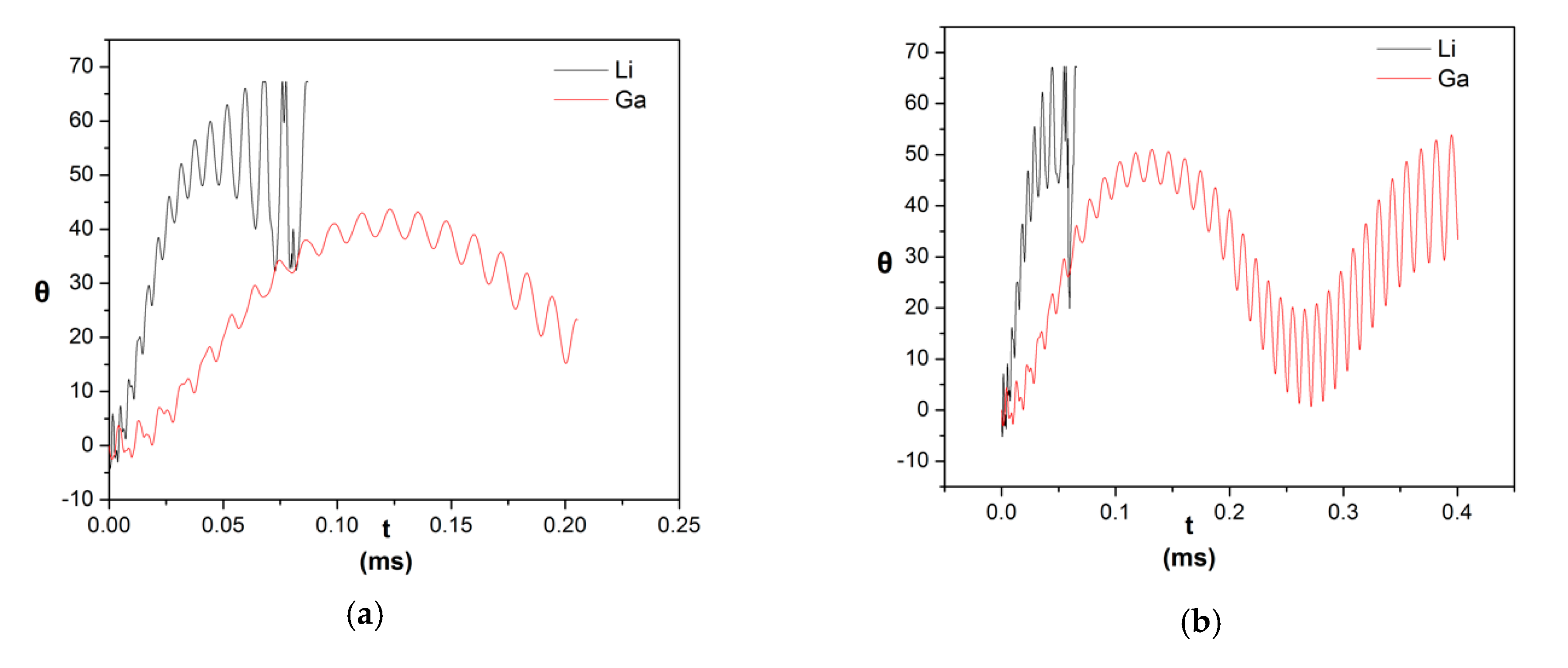
3.3. The Case of Liquid Gallium (Ga)
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Holdren, J.P.; Berwald, D.H.; Budnitz, R.J.; Crocker, J.G.; Delene, J.G.; Endicott, R.D.; Kazimi, M.S.; Krakowski, R.A.; Logan, B.G.; Schultz, K.R. Summary of the Report of the Senior Committee on Environmental, Safety, and Economic Aspects of Magnetic Fusion Energy; Technical Report; Lawrence Livermore National Laboratory: Livermore, CA, USA, 1987. [Google Scholar]
- Ryzhkov, S.V. Low radioactive and hybrid fusion. Sustain. Cities Soc. 2015, 14, 313–315. [Google Scholar] [CrossRef]
- Hirooka, Y.; Mazzitelli, G.; Mirnov, S.; Ono, M.; Shimada, M.; Tabarés, F.L. A review of the present status and future prospects of the application of liquid metals for Plasma-Facing Components in magnetic fusion devices. Fusion Sci. Technol. 2015, 68, 477–483. [Google Scholar] [CrossRef]
- Christofilos, N.C. Design for a high power-density Astron reactor. Fusion Energy 1989, 8, 97–105. [Google Scholar] [CrossRef]
- Tabarés, F.L. Present status of liquid metal research for a fusion reactor. Plasma Phys. Control. Fusion 2015, 58, 014014. [Google Scholar] [CrossRef]
- Mirnov, S.V.; Azizov, E.A.; Evtikhin, V.A.; Lazarev, V.B.; Lyublinski, I.E.; Vertokv, A.V.; Prokhorov, D.Y. Experiments with lithium limiter on T-11M tokamak and applications of the lithium capillary-pore system in future fusion reactor devices. Plasma Phys. Control. Fusion 2006, 48, 821–837. [Google Scholar] [CrossRef]
- Coenen, J.W.; De Temmerman, G.; Federici, G.; Philipps, V.; Sergienko, G.; Stohmayer, G.; Terra, A.; Unterberg, B.; Wegener, T.; Van den Bekerom, D.C.M. Liquid metals as alternative solution for the power exhaust of fusion devices: Status and perspective. Phys. Scr. 2014, 2014, T159. [Google Scholar] [CrossRef]
- Evtikhin, V.A.; Lyublinski, I.E.; Vertkov, A.V.; Mirnov, S.V.; Lazarev, V.B. Technological aspects of lithium capillary-pore systems application in tokamak device. Fusion Eng. Des. 2001, 56–57, 363–367. [Google Scholar] [CrossRef]
- Mirnov, S.V.; Lazarev, V.B. Li experiments at the tokamak T-11 M field of steady state PFC investigations. Nucl. Mater. 2011, 415, S417–S420. [Google Scholar] [CrossRef]
- Golubchikov, L.G.; Evtkhin, V.A.; Lyublinski, I.E.; Pistunovich, V.I.; Potapov, I.N.; Chumanov, A.N. Development of a liquid-metal fusion reactor divertor wih a capillary-pore system. J. Nucl. Mater. 1996, 233–237, 667–672. [Google Scholar] [CrossRef]
- Whyte, D.G.; Evans, T.E.; Wong, C.P.C.; West, W.P.; Bastasz, R.; Allain, J.P.; Brooks, J.N. Experimental observations of lithium as a plasma-facing surface in the DIII-D tokamak divertor. Fusion Eng. Des. 2004, 72, 133–147. [Google Scholar] [CrossRef]
- Zuo, G.Z.; Ren, J.; Hu, J.S.; Sun, Z.; Yang, Q.X.; Li, J.G.; Zakharov, L.E.; Ruzic, D.N.; The HT-7 Team. Liquid lithium surface control and its effect on plasma performance in the HT-7 tokamak. Fusion Eng. Des. 2014, 89, 2845–2852. [Google Scholar] [CrossRef]
- Evtikhin, V.A.; Lyublinski, I.E.; Vertkov, A.V.; Yezhov, N.I.; Khripunov, B.I.; Sotnikov, S.M.; Mirnov, S.V.; Petrov, V.B. Energy removal and MHD performance of lithium capillary-pore system for divertor target application. Fusion Eng. Des. 2000, 49–50, 195–200. [Google Scholar] [CrossRef]
- Apicella, M.L.; Apruzzese, G.; Mazzitelli, G.; Pericoli Ridolfini, V.; Alekseyev, A.G.; Lazarev, V.B.; Mirnov, S.V.; Zagorski, R. Lithization of the FTU tokamak with a critical amount of lithium injection. Plasma Phys. Control. Fusion 2012, 54, 035001. [Google Scholar] [CrossRef]
- Jaworski, M.A.; Abrams, T.; Allain, J.P.; Bell, M.G.; Bell, R.E.; Diallo, A.; Gray, T.K.; Gerhardt, S.P.; Kaita, R.; Kugel, H.W.; et al. Liquid lithium divertor characteristics and plasma-material interactions in NSTX high performance plasmas. Nucl. Fusion 2013, 53, 083032. [Google Scholar] [CrossRef]
- Evtikhin, V.A.; Vertkov, A.V.; Luyblinski, I.E.; Khripunov, B.I.; Petrov, V.B.; Mirnov, S.V. Research of lithium capillary-pore systems for fusion reactor plasma facing components. Nucl. Mater. 2002, 307–311, 1664–1669. [Google Scholar] [CrossRef]
- Jaworski, M.A.; Gerhardt, S.P.; Morley, N.B.; Abrams, T.; Kaita, R.; Kallman, J.; Kugel, H.; Majeski, R.; Ruzik, D.N. Macroscopic motion of liquid metal plasma facing components in a diverted plasma. J. Nucl. Mater. 2011, 415, S985–S988. [Google Scholar] [CrossRef]
- Jaworski, M.A.; Morley, N.B.; Ruzic, D.N. Thermocapillary and thermoelectric effects in liquid lithium plasma facing components. J. Nucl. Mater. 2009, 390–391, 1055–1058. [Google Scholar] [CrossRef]
- Pelekasis, N.; Benos, L. Static arrangement of a capillary porous system (CPS): Modelling. Fusion Eng. Des. 2017, 117, 180–187. [Google Scholar] [CrossRef]
- Benos, L. First Principles Study of the Static Arrangement of a Plasma Facing Component in the Form of a Capillary Porous System (CPS). Ph.D. Thesis, Mechanical Engineering, University of Thessaly, Thessaly, Greece, 2017. [Google Scholar]
- Israelachvili, J.N. Intermolecular and Surface Forces, 3rd ed.; Academic Press, Elsevier: Cambridge, MA, USA, 2011. [Google Scholar]
- Davidson, P.A. An Introduction to Magnetohydrodynamics; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Gao, D.; Morley, N.B. Equilibrium and initial linear stability analysis of liquid metal falling film flows in a varying spanwise magnetic field. Magnetohydrodynamics 2002, 38, 359–375. [Google Scholar]
- Morley, N.B.; Smolentsev, S.; Gao, D. Modeling infinite/axisymmetric liquid metal magnetohydrodynamic free surface flows. Fusion Eng. Des. 2002, 63–64, 343–351. [Google Scholar] [CrossRef]
- Saad, Y.; Schultz, M.H. GMRES: A generalized minimal residual algorithm for solving non-symmetric linear systems. SIAM J. Sci. Stat. Comput. 1986, 7, 856–869. [Google Scholar] [CrossRef]
- Saad, Y. Iterative Methods for Sparse Linear Systems; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1996. [Google Scholar]
- Christodoulou, K.N.; Scriven, L.E. Discretization of free surface flows and other moving boundary problems. J. Comput. Phys. 1992, 99, 39–55. [Google Scholar] [CrossRef]
- Tsiveriotis, K.; Brown, R.A. Boundary-conforming mapping applied to computations of highly deformed solidification interfaces. Int. J. Numer. Methods Fluids 1992, 14, 981–1003. [Google Scholar] [CrossRef]
- Dimakopoulos, Y.; Tsamopoulos, J. A quasi-elliptic transformation for moving boundary problems with large anisotropic deformations. J. Comp. Phys. 2003, 192, 494–522. [Google Scholar] [CrossRef]
- Vlachomitrou, M.; Pelekasis, N. Dynamic simulation of a coated microbubble in an unbounded flow: Response to a step change in pressure. J. Fluid Mech. 2017, 882, 717–761. [Google Scholar] [CrossRef]
- Zoueshtiagh, F.; Amiroudine, S.; Narayanan, R. Experimental and numerical study of miscible Faraday instability. J. Fluid Mech. 2009, 628, 43–55. [Google Scholar] [CrossRef]
- Reznik, S.N.; Yarin, A.L.; Theron, A.; Zussman, E. Transient and steady shapes of droplets attached to a surface in a strong electric field. J. Fluid Mech. 2004, 516, 349–377. [Google Scholar] [CrossRef]
- Tsiglifis, K.; Pelekasis, N. Non-Linear Oscillations and Collapse of Elongated Bubbles Subject to Weak Viscous Effects: Effect of Internal Overpressure. Phys. Fluids 2007, 19, 072106. [Google Scholar] [CrossRef]
- Drazin, P.G.; Reid, W.H. Hydrodynamic Stability, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Chandrasekhar, S. Hydrodynamic and Hydromagnetic Stability; Oxford University Press: Oxford, UK, 1961. [Google Scholar]
- Morgan, T.W.; Van den Bekerom, G.; De Temmerman, G. Interaction of a tin-based capillary porous structure with ITER/DEMO relevant plasma conditions. Nucl. Mater. 2015, 463, 1256–1259. [Google Scholar] [CrossRef]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vlachomitrou, M.; Pelekasis, N. Numerical Study of a Liquid Metal Oscillating inside a Pore in the Presence of Lorentz and Capillary Forces. Fluids 2020, 5, 12. https://doi.org/10.3390/fluids5010012
Vlachomitrou M, Pelekasis N. Numerical Study of a Liquid Metal Oscillating inside a Pore in the Presence of Lorentz and Capillary Forces. Fluids. 2020; 5(1):12. https://doi.org/10.3390/fluids5010012
Chicago/Turabian StyleVlachomitrou, Maria, and Nikos Pelekasis. 2020. "Numerical Study of a Liquid Metal Oscillating inside a Pore in the Presence of Lorentz and Capillary Forces" Fluids 5, no. 1: 12. https://doi.org/10.3390/fluids5010012
APA StyleVlachomitrou, M., & Pelekasis, N. (2020). Numerical Study of a Liquid Metal Oscillating inside a Pore in the Presence of Lorentz and Capillary Forces. Fluids, 5(1), 12. https://doi.org/10.3390/fluids5010012




