Full-Span Flying Wing Wind Tunnel Test: A Body Freedom Flutter Study
Abstract
1. Introduction
2. Theory of Aeroelastic Modeling
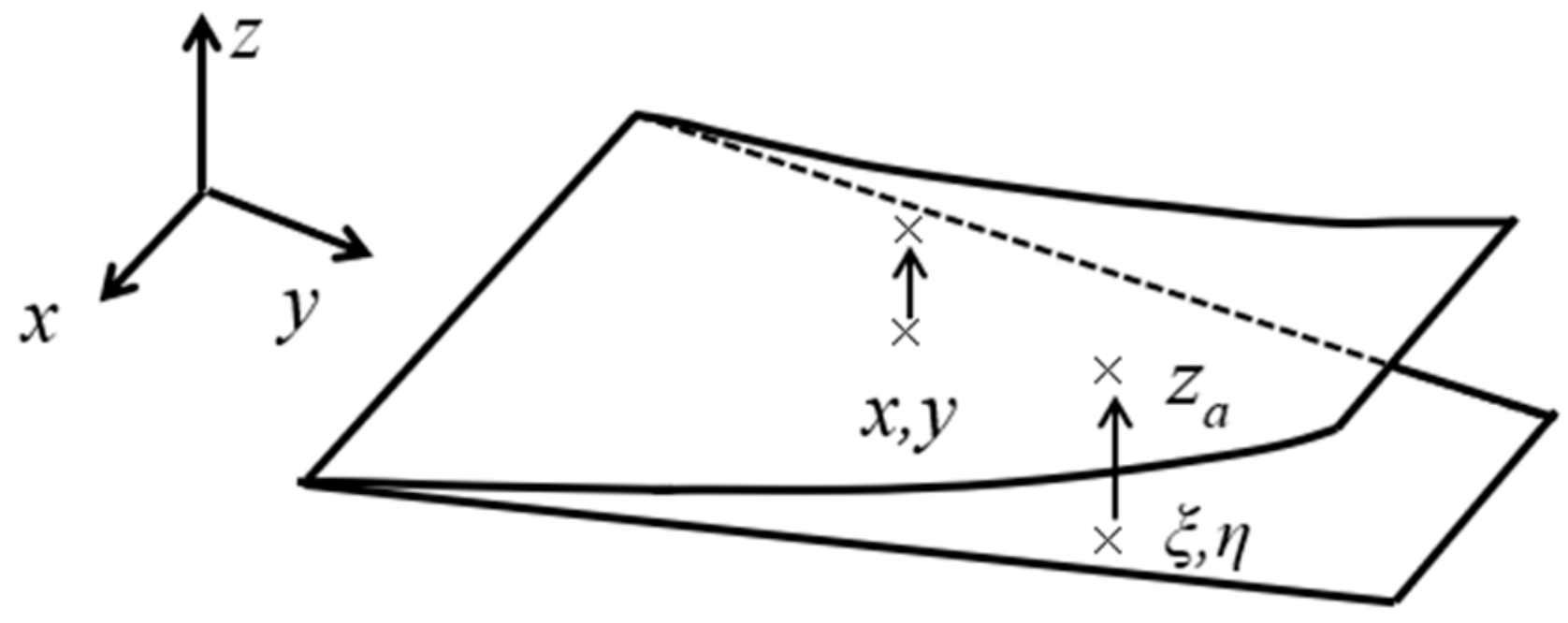
2.1. Structural Dynamics
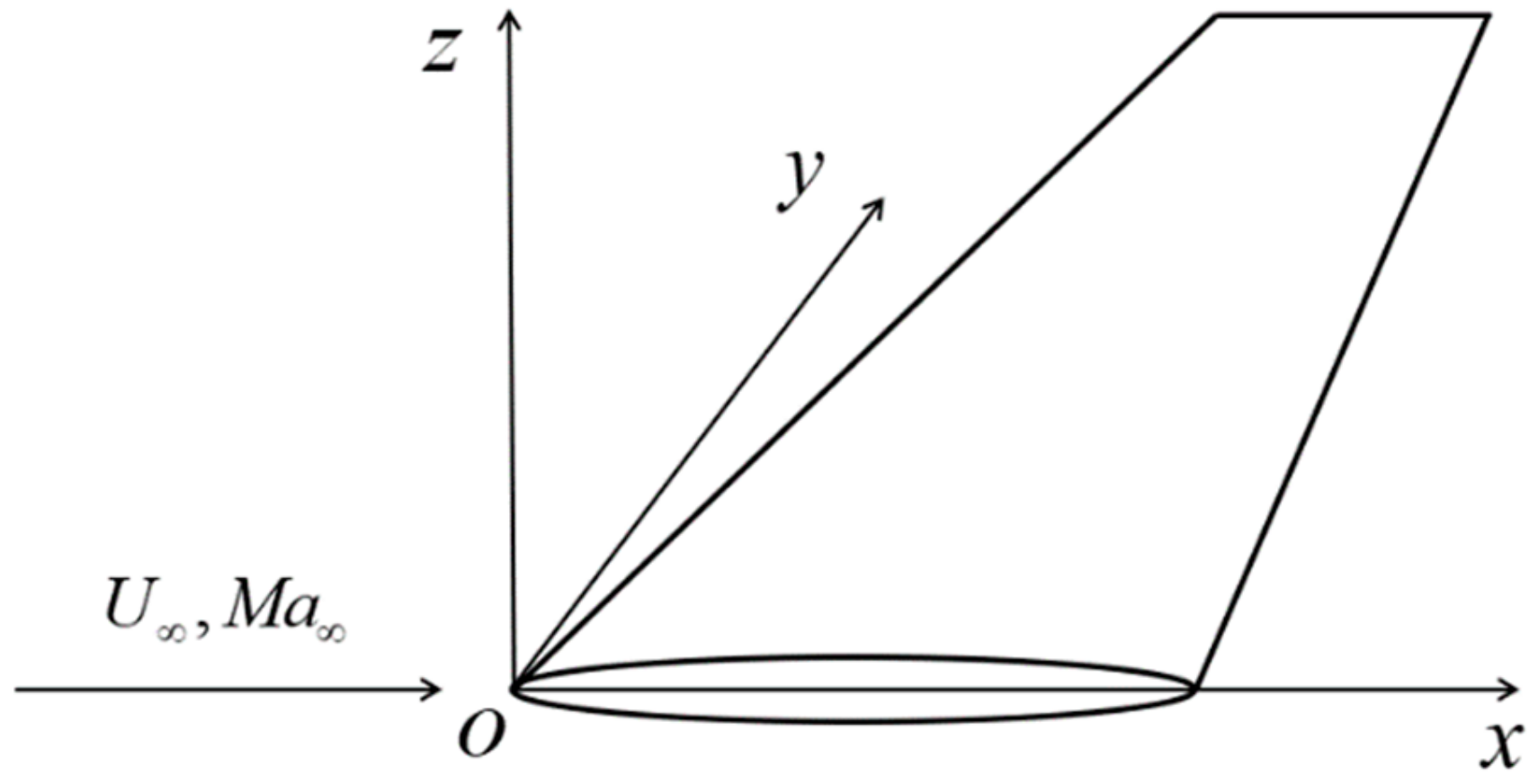
2.2. Doublet Lattice Method (DLM) for Unsteady Aerodynamics
- —The downwash at the 3/4 chord length point of the ith grid
- —The pressure coefficient on the jth grid, has the following relationship with the pressure difference :
- —Mid section length of the jth grid
- —Length at 1/4 chord of the jth grid
- —the sweepback angle at 1/4 chord of the jth grid
- —Aerodynamic kernel function
- is pressure distribution vector at the point of pressure action
- is the downwash vector at the downwash control point
- is the aerodynamic influence coefficient matrix
3. Preliminary Modeling and Analysis of BFF Wind Tunnel Test UAV
3.1. Modeling and Analysis of Structural Dynamics
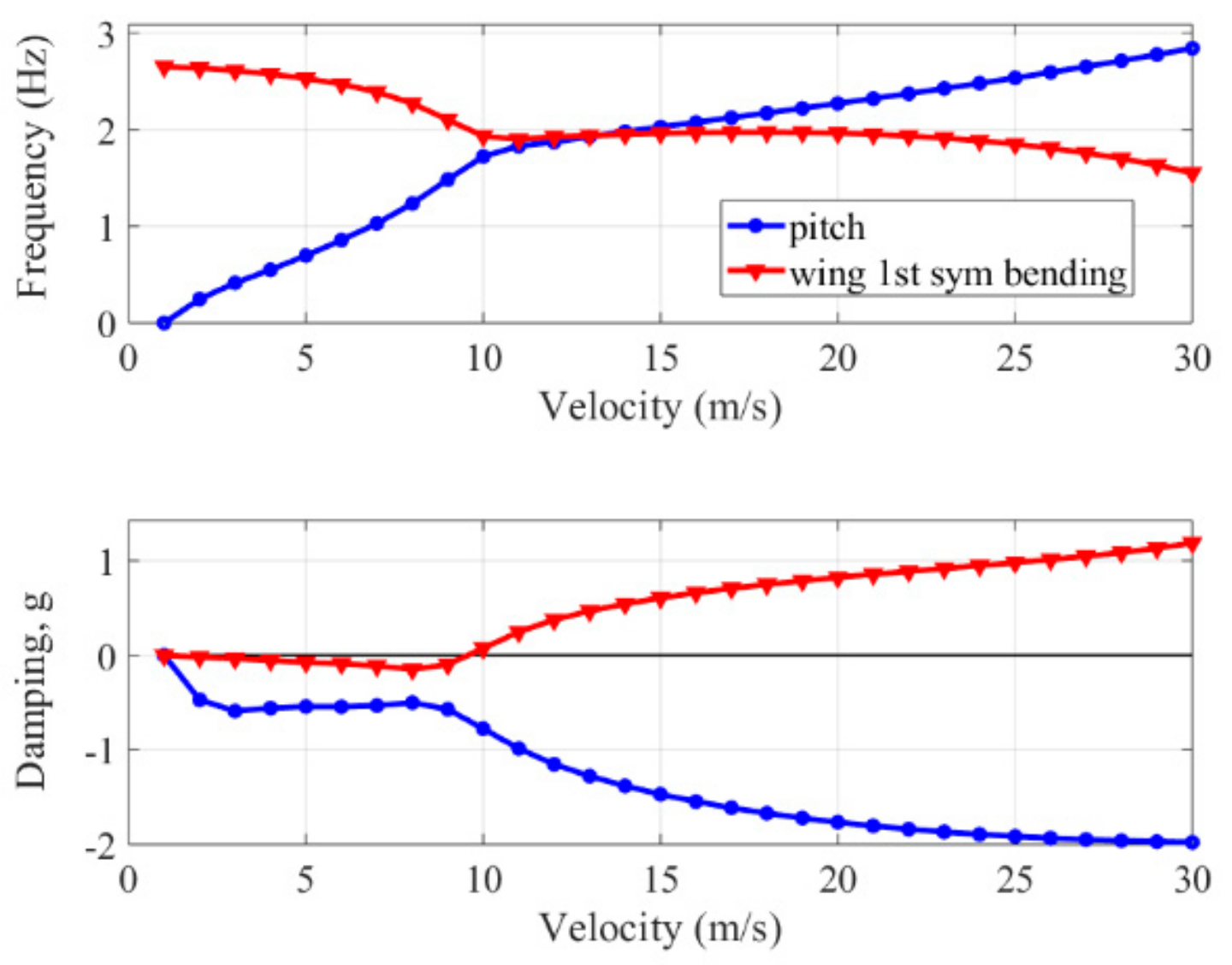
3.2. Aeroelastic Modelling and Analysis
4. Ground Vibration Test and Model Updating
4.1. Design and Manufacture of the BFF Wind Tunnel Test UAV
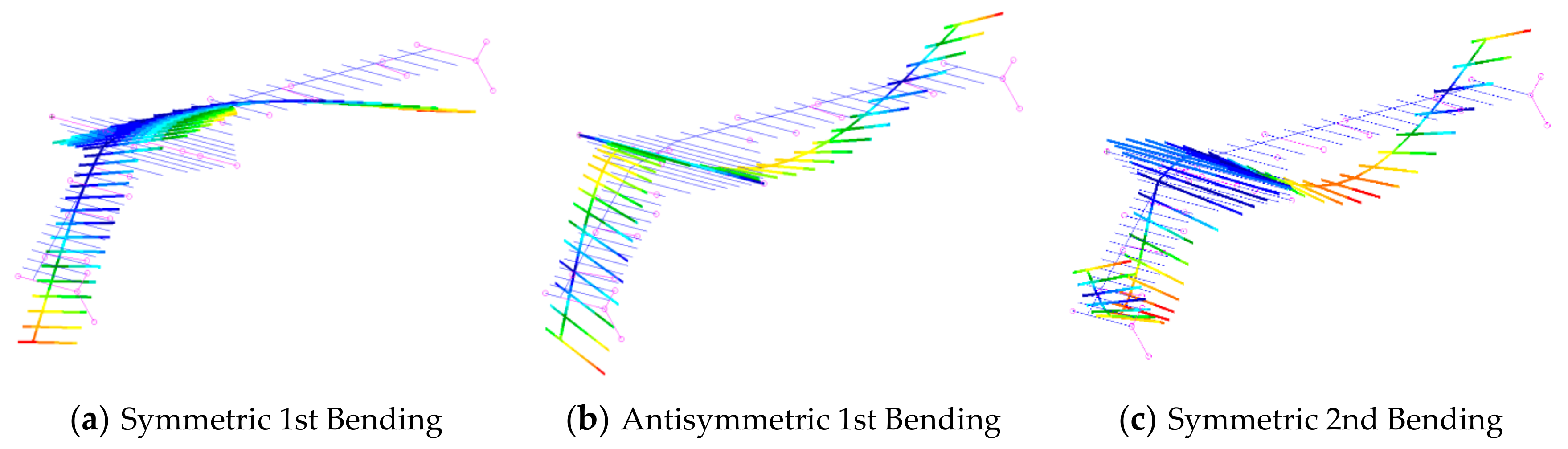
4.2. Ground Vibration Test
4.3. Theoretical Analysis Model Updating
5. Body Freedom Flutter Wind Tunnel Test
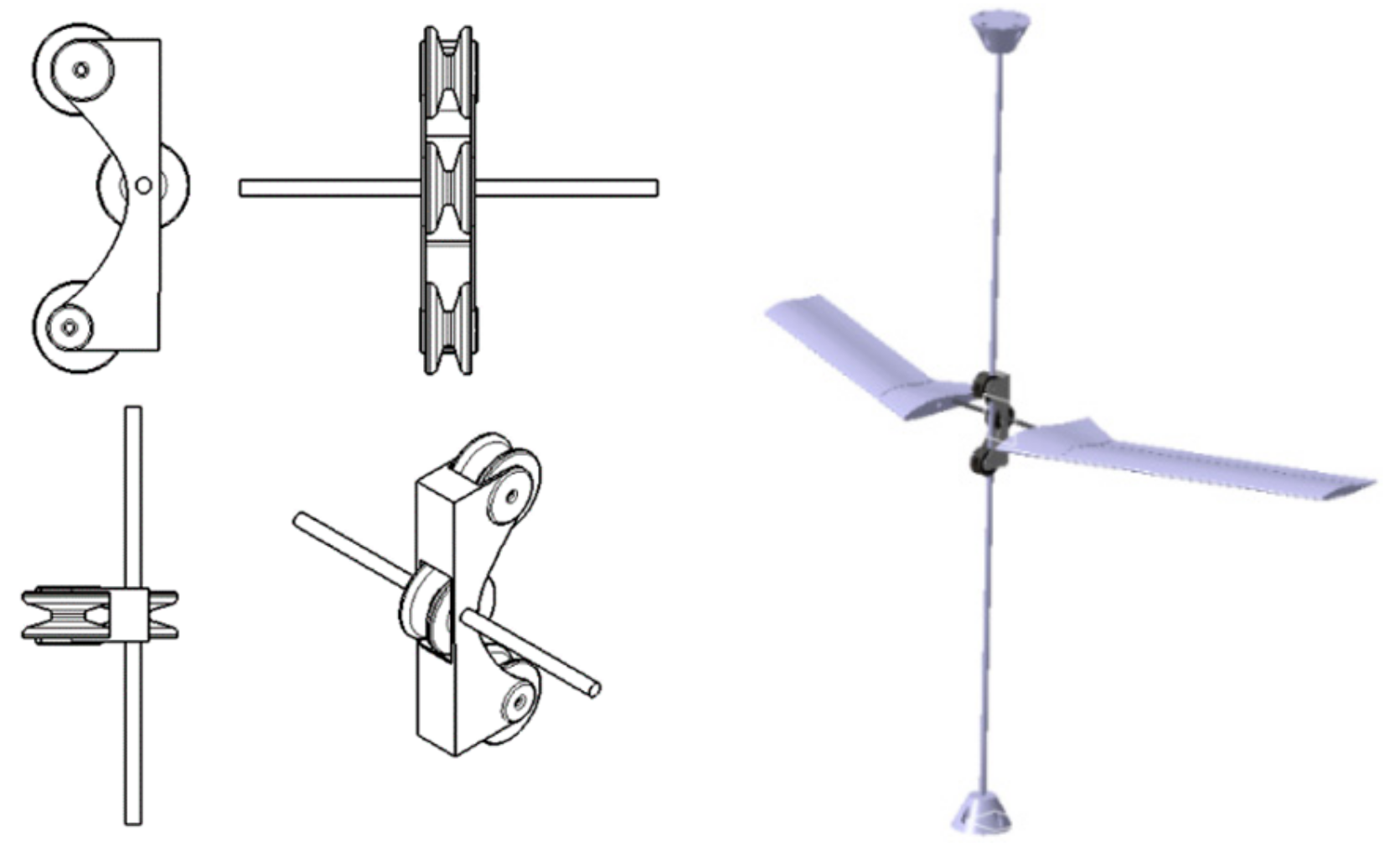
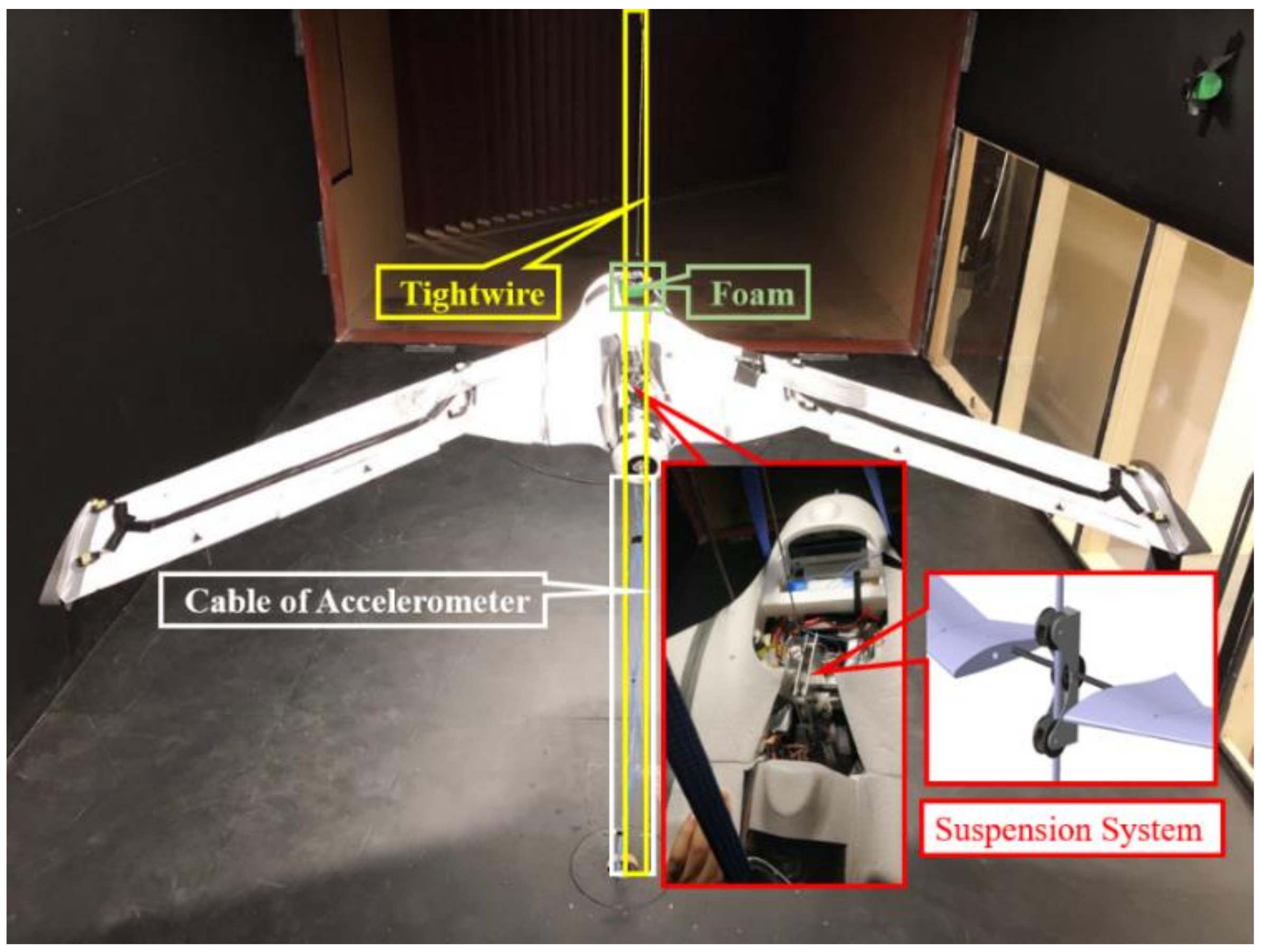
5.1. Suspension System Design
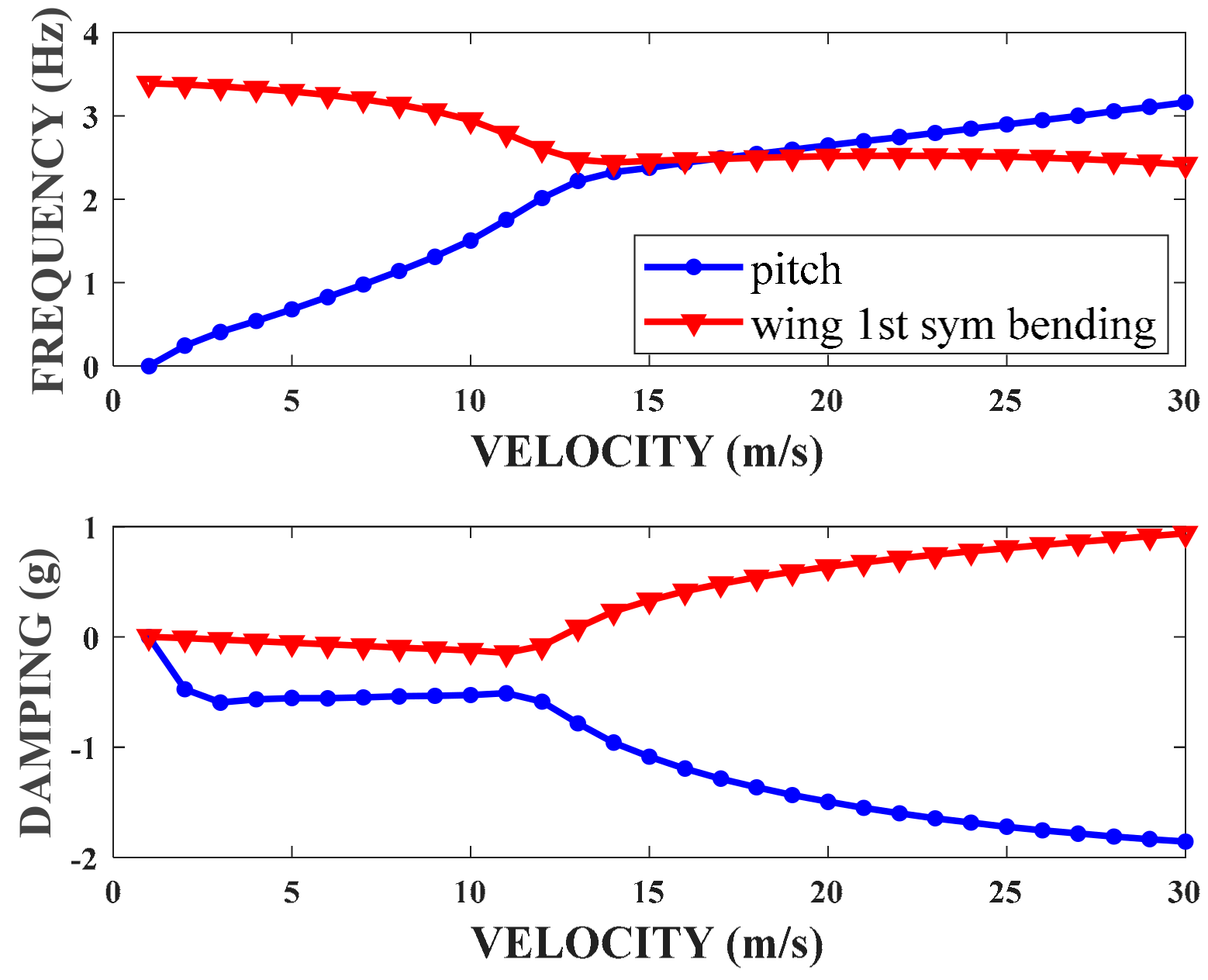
5.2. Body Freedom Flutter Wind Tunnel Test
5.3. Effect of Mass Balance at Nose on Characteristics of BFF
6. Conclusions
- (1)
- The theoretical analysis results show that the BFF wind tunnel test UAV can encounter BFF at low airspeed, which is suitable for performing BFF wind tunnel test.
- (2)
- The modal characteristics of updated FEM agree well with the ground vibration test results, indicating that the revised theoretical analysis model can accurately reflect the structural dynamic characteristics of the UAV.
- (3)
- Comparison of the wind tunnel test and theoretical analysis results shows that they agree well, indicating that the designed quasi-free-flying suspension system can effectively guarantee the test accuracy in wind tunnel BFF test.
- (4)
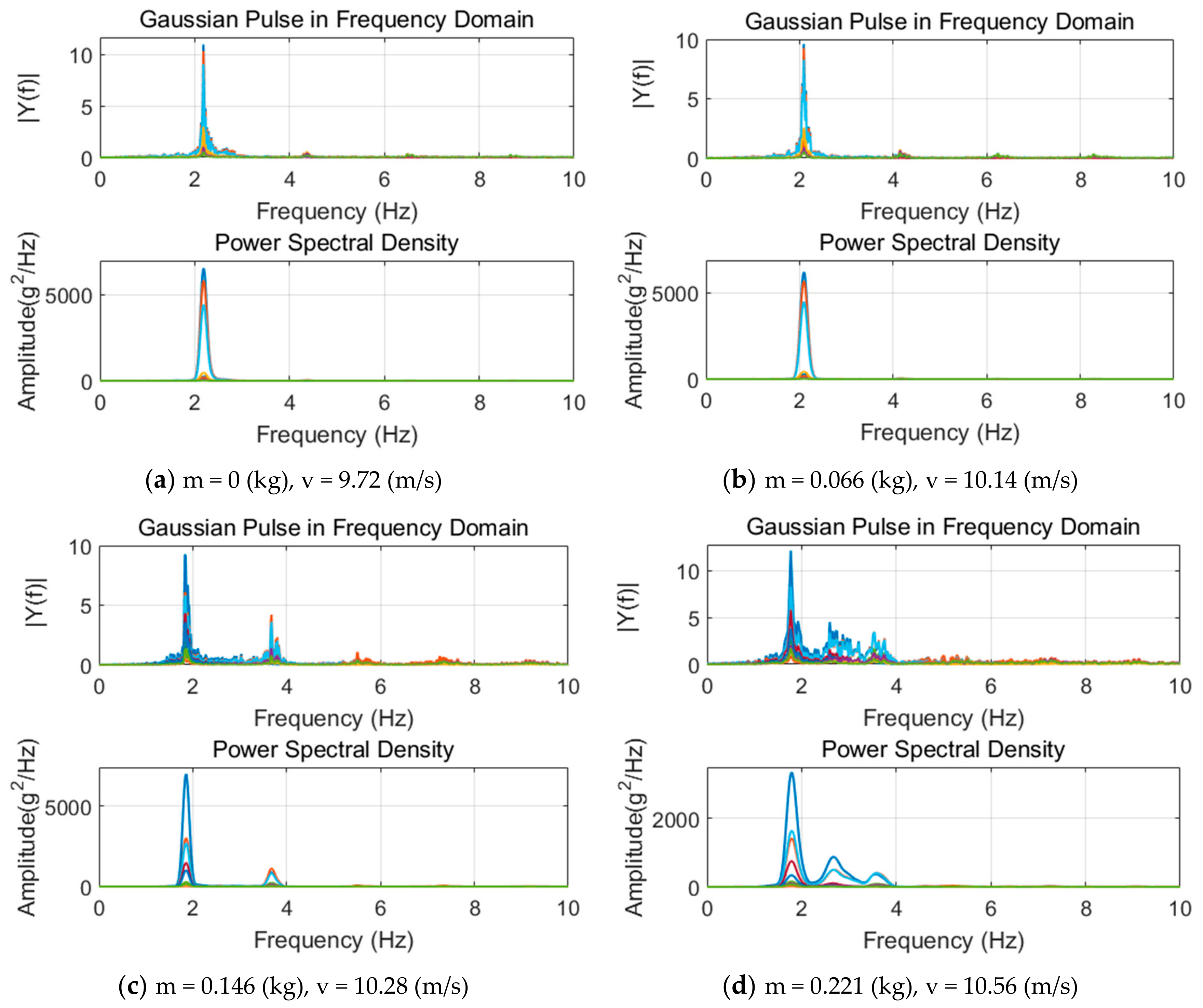
- Increasing the mass balance at nose of the flying wing leads to an increase in the pitch moment of inertia, which in turn increases the BFF boundary.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Banerjee, J.R. Flutter characteristics of high aspect ratio tailess aircraft. J. Aircr. 1984, 21, 733–736. [Google Scholar] [CrossRef]
- Moreno, C.P.; Seiler, P.J.; Balas, G.J. Model Reduction for Aeroservoelastic Systems. J. Aircr. 2014, 51, 280–290. [Google Scholar] [CrossRef]
- Iannelli, A.; Marcos, A.; Lowenberg, M. Study of Flexible Aircraft Body Freedom Flutter with Robustness Tools. J. Guid. Control Dyn. 2018, 41, 1083–1094. [Google Scholar] [CrossRef]
- Saltari, F.; Riso, C.; Matteis, G.D.; Mastroddi, F. Finite-Element-Based Modeling for Flight Dynamics and Aeroelasticity of Flexible Aircraft. J. Aircr. 2017, 54, 2350–2366. [Google Scholar] [CrossRef]
- Riso, C.; Mastroddi, F.; Cesnik, C.E.S. Coupled flight dynamics and aeroelasticity of very flexible aircraft based on commercial finite element solvers. In Proceedings of the AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar]
- Ouellette, J.A. Aeroservoelastic Modeling of Body Freedom Flutter for Control System Design. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, Denver, CO, USA, 5 June 2017. [Google Scholar]
- Reasor, D.A.; Bhamidipati, K.K.; Chin, A.W. X-56A Aeroelastic Flight Test Predictions. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016. [Google Scholar]
- Gupta, R.; Love, N.J.; Kapania, R.K.; Schmidt, D.K. Development of a flight dynamics analysis framework for inclusion into the MDAO process. In Proceedings of the 19th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Atlanta, GA, USA, 25–29 June 2018. [Google Scholar]
- Regan, C.D. mAEWing2: Conceptual Design and System Test. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar]
- Beranek, J.; Nicolai, L.; Buonanno, M.; Burnett, E.; Atkinson, C.; Holm-Hansen, B.; Flick, P. Conceptual design of a multi-utility aeroelastic demonstrator. In Proceedings of the 13th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference (MAO), Fort Worth, TX, USA, 13–15 September 2010. [Google Scholar]
- Gupta, A.; Moreno, C.P.; Pfifer, H.; Taylor, B.; Balas, G.J. Updating a finite element based structural model of a small flexible aircraft. In Proceedings of the AIAA Modeling and Simulation Technologies Conference, Dallas, TX, USA, 22–26 June 2015. [Google Scholar]
- Liu, J.; Gu, Y.; Xie, K.; Shi, P. Flutter Modeling, Analysis and Test for Blended-Wing-Body Flying Wing. In Proceedings of the 2018 Asia-Pacific International Symposium on Aerospace Technology, Chengdu, Sichuan, China, 16–18 October 2018. [Google Scholar]
- Schmidt, D.K.; Zhao, W.; Kapania, R.K. Flight-dynamics and flutter modeling and analysis of a flexible flying-wing drone. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, San Diego, CA, USA, 4–8 January 2016. [Google Scholar]
- Schmidt, D.K. MATLAB-Based Flight-Dynamics and Flutter Modeling of a Flexible Flying-Wing Research Drone. J. Aircr. 2016, 53, 1045–1055. [Google Scholar] [CrossRef]
- Theis, J.; Pfifer, H.; Seiler, P.J. Robust Control Design for Active Flutter Suppression. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, San Diego, CA, USA, 4–8 January 2016. [Google Scholar]
- Danowsky, B.P.; Schmidt, D.K.; Pfifer, H. Control-Oriented System and Parameter Identification of a Small Flexible Flying-Wing Aircraft. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar]
- Kotikalpudi, A.; Danowsky, B.P.; Schmidt, D.; Theis, J.; Seiler, P. Flutter Suppression Control Design for a Small, Flexible Flying-Wing Aircraft. In Proceedings of the 2018 Multidisciplinary Analysis and Optimization Conference, Atlanta, GA, USA, 25–29 June 2018. [Google Scholar]
- Schmidt, D.K. Stability augmentation and active flutter suppression of a flexible flying-wing drone. J. Guid. Control Dyn. 2016, 39, 409–422. [Google Scholar] [CrossRef]
- Danowsky, B.P.; Kotikalpudi, A.; Schmidt, D.; Regan, C.; Seiler, P. Flight Testing Flutter Suppression on a Small Flexible Flying-Wing Aircraft. In Proceedings of the 2018 Multidisciplinary Analysis and Optimization Conference, Atlanta, GA, USA, 25–29 June 2018. [Google Scholar]
- Danowsky, B.P. Flutter Suppression of a Small Flexible Aircraft using MIDAAS. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar]
- Hong, Z.Y.; Zhang, P.F.; Xu, Z.H. Optimal Design of a Hydraulic Suspension Mechanism of Aircraft Recovery Vehicle. Appl. Mech. Mater. 2014, 670–671, 886–891. [Google Scholar] [CrossRef]
- Ocokolji, G.; Rauo, B.; Kozi, M. Supporting system interference on aerodynamic characteristics of an aircraft model in a low-speed wind tunnel. Aerosp. Sci. Technol. 2017, 64, 133–146. [Google Scholar] [CrossRef]
- Fan, L.T.; Duan, X.F.; Xue, W. Advances in test techniques based on multifunctional sting support system for 8m6m wind tunnel. In Proceedings of the 2013 2nd International Conference on Measurement, Instrumentation and Automation (ICMIA) 2013, Harbin, Heilongjiang, China, 23–24 April 2013; Volume 336–338, pp. 880–884. [Google Scholar]
- Lafourcade, P.; Libre, M.; Reboulet, C. Design of a parallel wire-driven manipulator for wind tunnels. In Proceedings of the Workshop on Fundamental Issues and Future Directions for Parallel Mechanisms and Manipulators, Quebec, QC, Canada, 3–4 October 2002; pp. 187–219. [Google Scholar]
- Wang, X.; Peng, M.; Hu, Z.; Chen, Y.; Lin, Q. Feasibility investigation of large-scale model suspended by cable-driven parallel robot in hypersonic wind tunnel test. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2017, 231, 2375–2383. [Google Scholar] [CrossRef]
- Zheng, Y.; Lin, Q.; Xiongwei, L.; Mitrouchev, P. On Wire-Driven Parallel Suspension Systems for Static and Dynamic Derivatives of the Aircraft in Low-Speed Wind Tunnels. J. Eng. Res. 2009, 7, 1549–1554. [Google Scholar]
- Scott, R.C.; Vetter, T.K.; Penning, K.B.; Coulson, D.A.; Heeg, J. Aeroservoelastic Testing of A Sidewall Mounted Free Flying Wind-Tunnel Model. In Proceedings of the 26th AIAA Applied Aerodynamics Conference (AIAA 2008-7186), Honolulu, HI, USA, 18–21 August 2008. [Google Scholar]
- Huang, C.; Wu, Z.; Yang, C.; Dai, Y. Flutter Boundary Prediction for a Flying-Wing Model Exhibiting Body Freedom Flutter. In Proceedings of the 58th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference (AIAA 2017-0415), Grapevine, TX, USA, 9–13 January 2017. [Google Scholar]
- Scott, R.C.; Vetter, T.K.; Penning, K.B.; Coulson, D.A.; Heeg, J. Aeroservoelastic Testing of Free Flying Wind Tunnel Models, Part 2: A Centerline Supported Fullspan Model Tested for Gust Load Alleviation, NASA/TP-2014-218170; NASA Langley Research Center: Hampton, VA, USA, 2014.
- Gu, Y.; Yang, Z.; Marzocca, P.; He, S. Body freedom flutter of a flexible blended wing body like plate—An experimental study. In Proceedings of the 17th International Forum on Aeroelasticity and Structural Dynamics (IFASD), Como, Italy, 25–28 June 2017. [Google Scholar]
- Dowell, E.H.; Clark, R.; Cox, D.; Curtiss, H.C.J.; Edwards, J.W.; Hall, K.C.; Peters, D.A.; Scanlan, R.; Simiu, E.; Sisto, F.; et al. A Modern Course in Aeroelasticity; Springer: Berlin/Heidelberg, Germany; Dordrecht, The Netherlands, 2005. [Google Scholar]
- Albano, E.; Rodden, W.P. A doublet-lattice method for calculating lift distributions on oscillating surfaces in subsonic flows. AIAA J. 1969, 7, 279–285. [Google Scholar] [CrossRef]



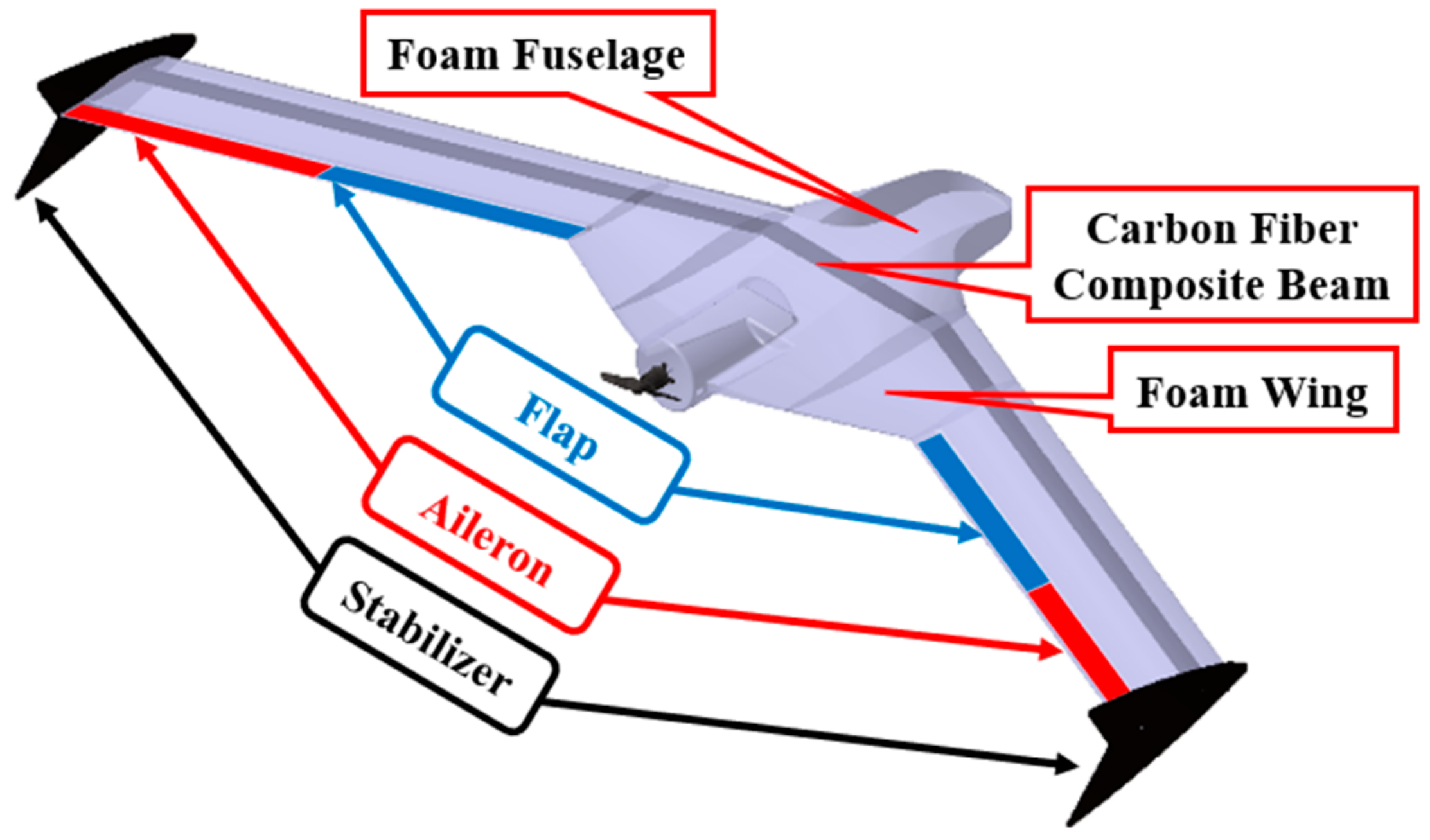





| Items | Value |
|---|---|
| Total weigth (kg) | 2.072 |
| C.G. (from nose, mm) | 385 |
| Wing span (mm) | 2000 |
| Aspect ratio | 10 |
| Taper ratio | 1 |
| Swept-back (degree) | 22.0 |
| Modes | Frequency (Hz) |
|---|---|
| Symmetric 1st bending | 3.40 |
| Antisymmetric 1st bending | 10.70 |
| Symmetric 2nd bending | 16.67 |
| Modes | Frequency (Hz) |
|---|---|
| Symmetric 1st bending | 2.90 |
| Antisymmetric 1st bending | 8.98 |
| Symmetric 2nd bending | 12.89 |
| Modes | Frequency (Hz) | Error (%) | |
|---|---|---|---|
| Tested | Updated | ||
| Symmetric 1st bending | 2.90 | 2.87 | −1.03 |
| Antisymmetric 1st bending | 8.98 | 8.85 | −1.44 |
| Symmetric 2nd bending | 12.89 | 13.79 | 6.07 |
| BFF Characteristic | Analyzed | Tested | Error (%) |
|---|---|---|---|
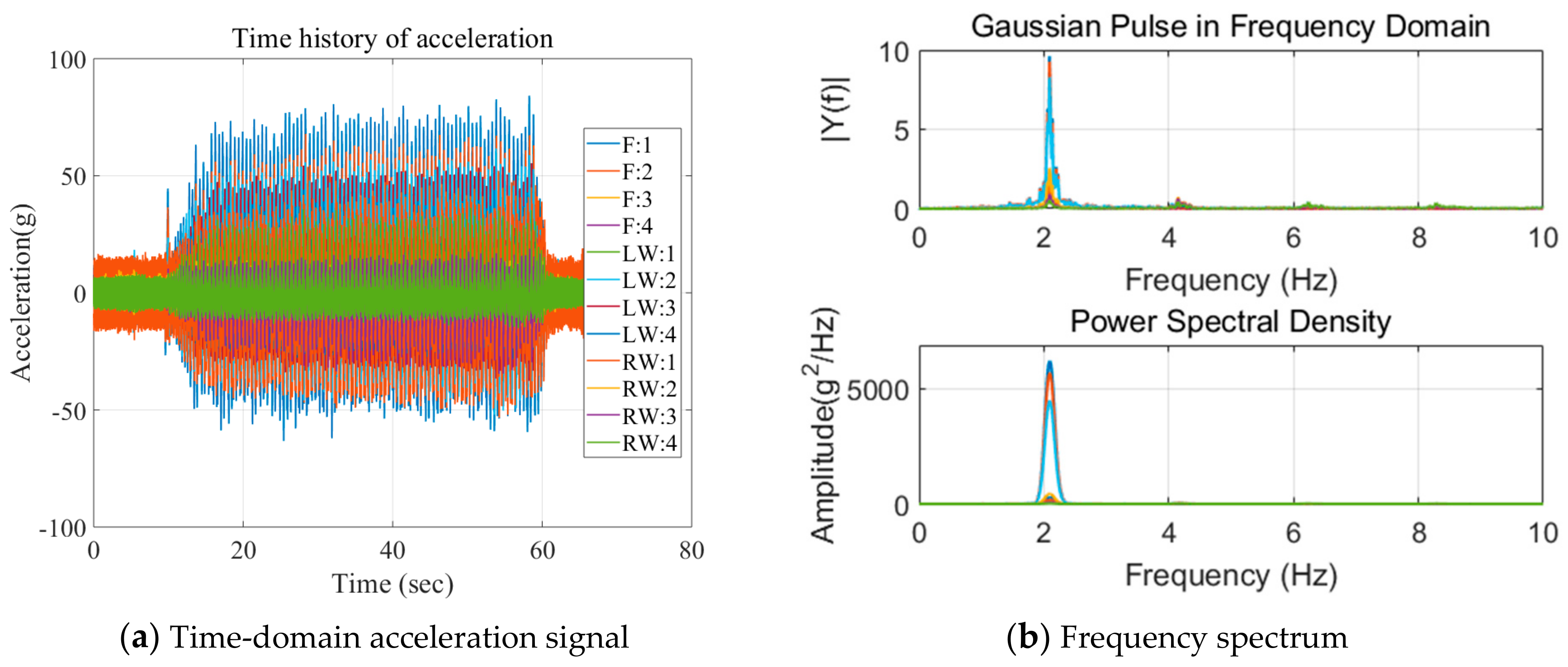
| Flutter speed (m/s) | 9.49 | 9.72 | 2.37 |
| Flutter frequency (Hz) | 2.03 | 2.18 | 6.88 |
| Additional Weight (kg) | Flutter Speed (m/s) | Flutter Frequency (Hz) | ||||
|---|---|---|---|---|---|---|
| Analyzed | Tested | Error (%) | Analyzed | Tested | Error (%) | |
| 0 | 9.49 | 9.72 | −2.37 | 2.03 | 2.18 | −6.88 |
| 0.066 | 9.69 | 10.14 | −4.44 | 2.00 | 2.09 | −4.31 |
| 0.146 | 9.96 | 10.28 | −3.11 | 1.95 | 1.86 | 4.84 |
| 0.221 | 10.23 | 10.56 | −3.13 | 1.92 | 1.80 | 6.67 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, P.; Liu, J.; Gu, Y.; Yang, Z.; Marzocca, P. Full-Span Flying Wing Wind Tunnel Test: A Body Freedom Flutter Study. Fluids 2020, 5, 34. https://doi.org/10.3390/fluids5010034
Shi P, Liu J, Gu Y, Yang Z, Marzocca P. Full-Span Flying Wing Wind Tunnel Test: A Body Freedom Flutter Study. Fluids. 2020; 5(1):34. https://doi.org/10.3390/fluids5010034
Chicago/Turabian StyleShi, Pengtao, Jihai Liu, Yingsong Gu, Zhichun Yang, and Pier Marzocca. 2020. "Full-Span Flying Wing Wind Tunnel Test: A Body Freedom Flutter Study" Fluids 5, no. 1: 34. https://doi.org/10.3390/fluids5010034
APA StyleShi, P., Liu, J., Gu, Y., Yang, Z., & Marzocca, P. (2020). Full-Span Flying Wing Wind Tunnel Test: A Body Freedom Flutter Study. Fluids, 5(1), 34. https://doi.org/10.3390/fluids5010034






