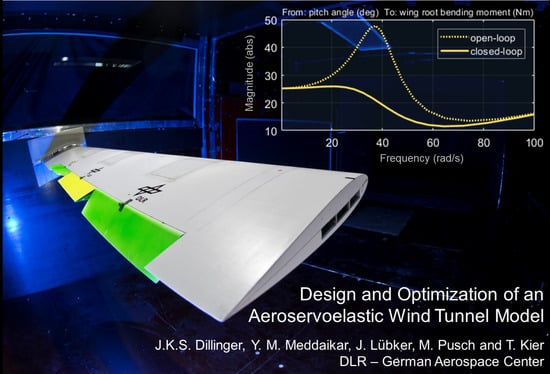
Design and Optimization of an Aeroservoelastic Wind Tunnel Model
Abstract
1. Introduction
2. Model Design
2.1. Previous Campaigns: Lessons Learned
- Aeroelastic experiments combine the uncertainties of structural, aerodynamic, and measurement disciplines;
- Eliminating uncertainties is key to finding realistic explanations for aeroelastic effects and elimination of uncertainties can be achieved by:
- o
- separating the disciplines in pretests where ideally only one discipline at a time is involved which allows for the identification of effects that can only be generated by the discipline investigated;
- o
- keeping disciplines as simple and predictable as possible.
- It is of utmost importance to gather and document as much information on the actual building process of the model as possible which allow for a meaningful update of the simulation models, and thus the elimination of a major source of uncertainties;
- Composite properties have to be determined, ideally, with every new material applied in the model;
- Clamping the model at the root and attaching it to the balance can be a large source for uncertainties which relates to the internal structure of the model itself, as well as the external structure required to transfer loads from the model to the balance.
2.2. Model Specification
2.3. Flap Considerations
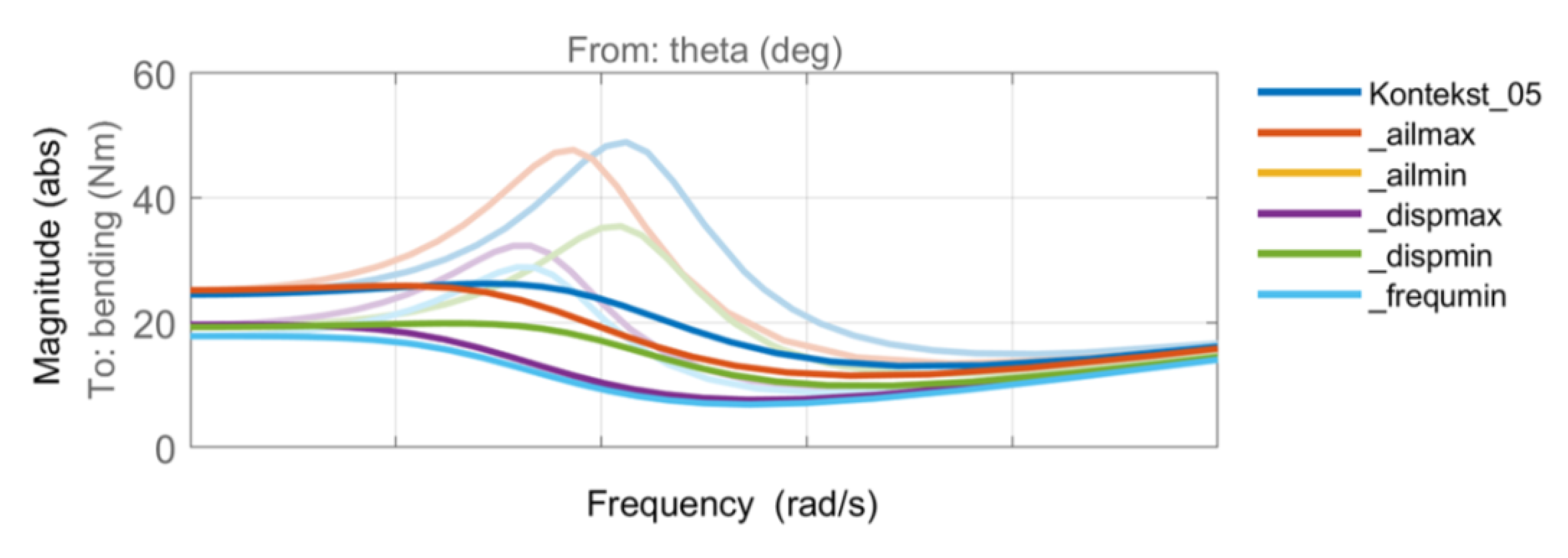
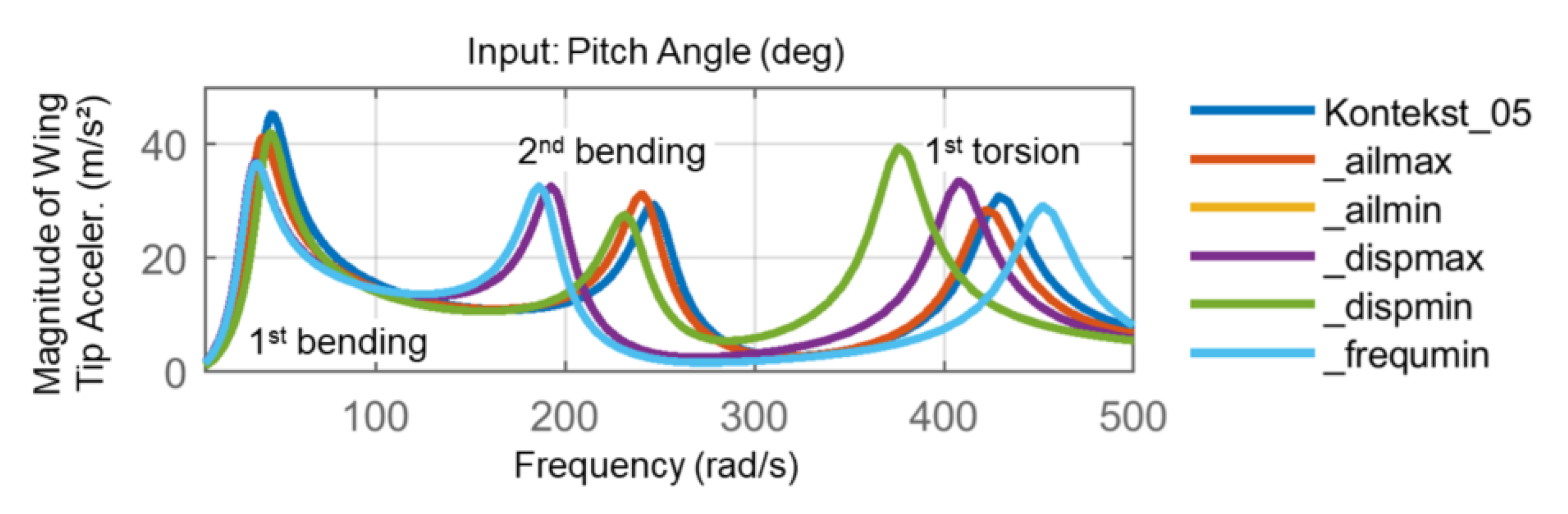
3. Optimization
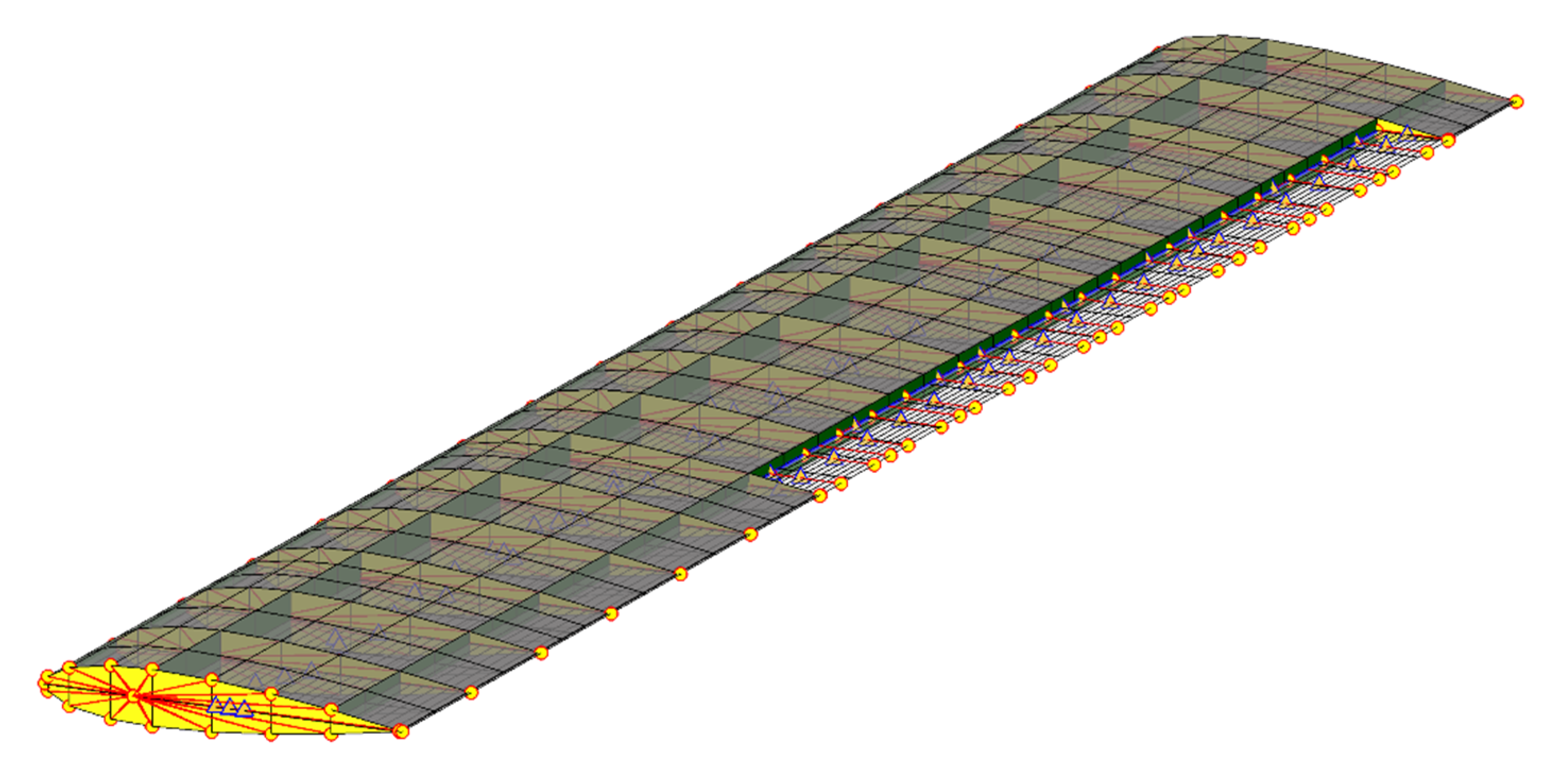
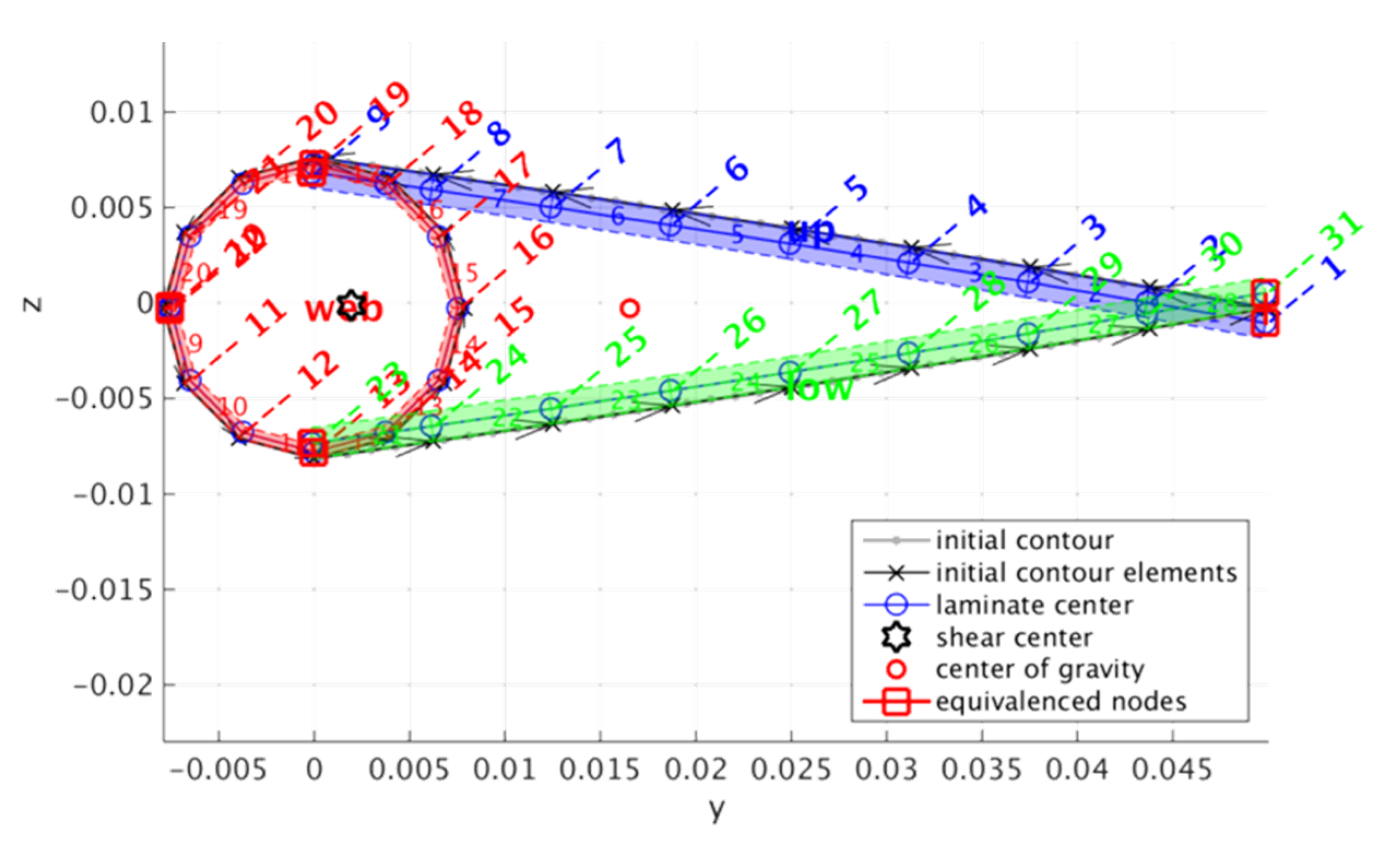
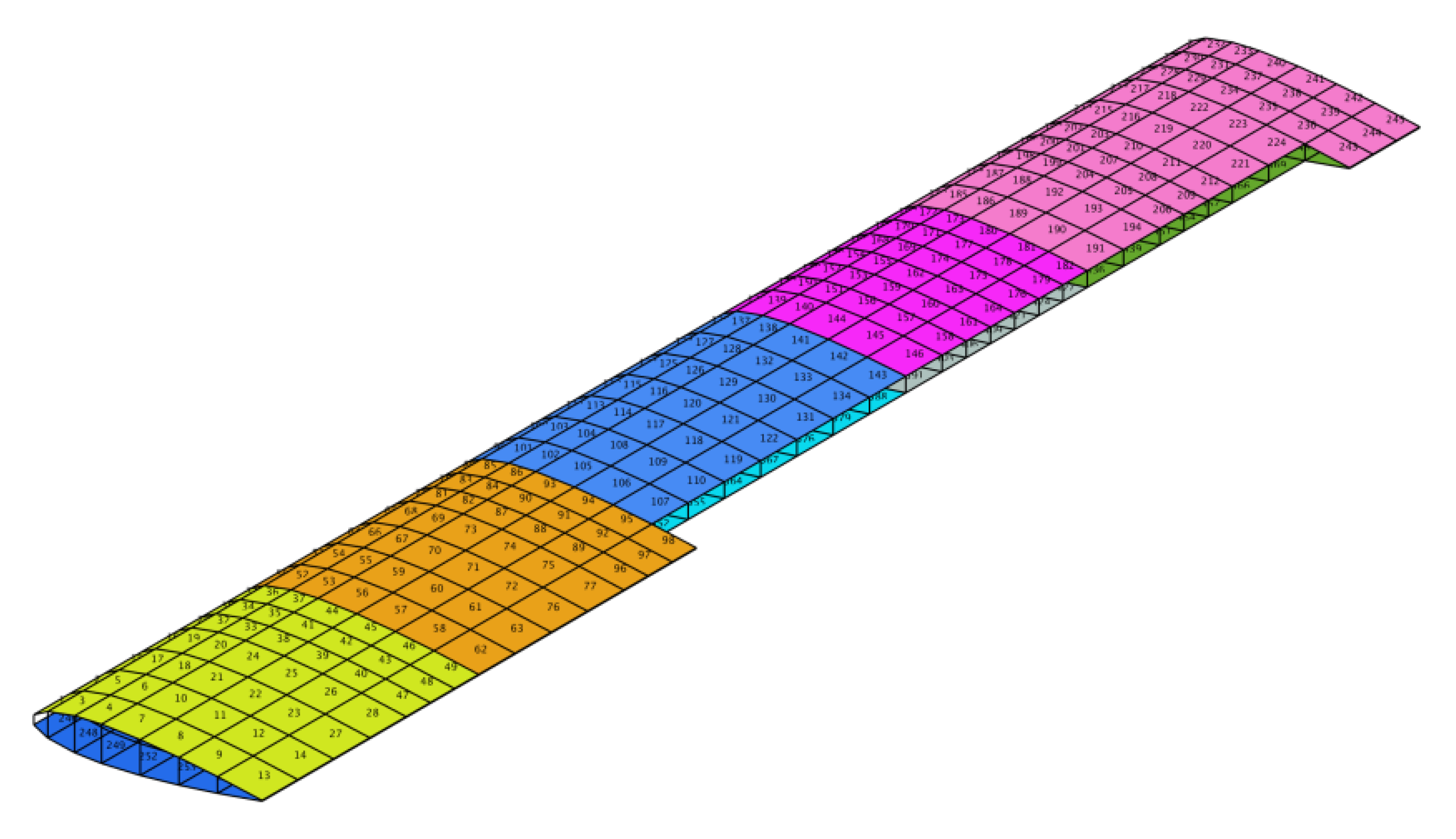
3.1. Analysis Model
3.2. Structural Optimization
- aileron effectiveness maximization, ηmax;
- aileron effectiveness minimization, ηmin;
- tip deflection maximization, dmax;
- tip deflection minimization, dmin;
- 1st bending mode frequency minimization, fmin.
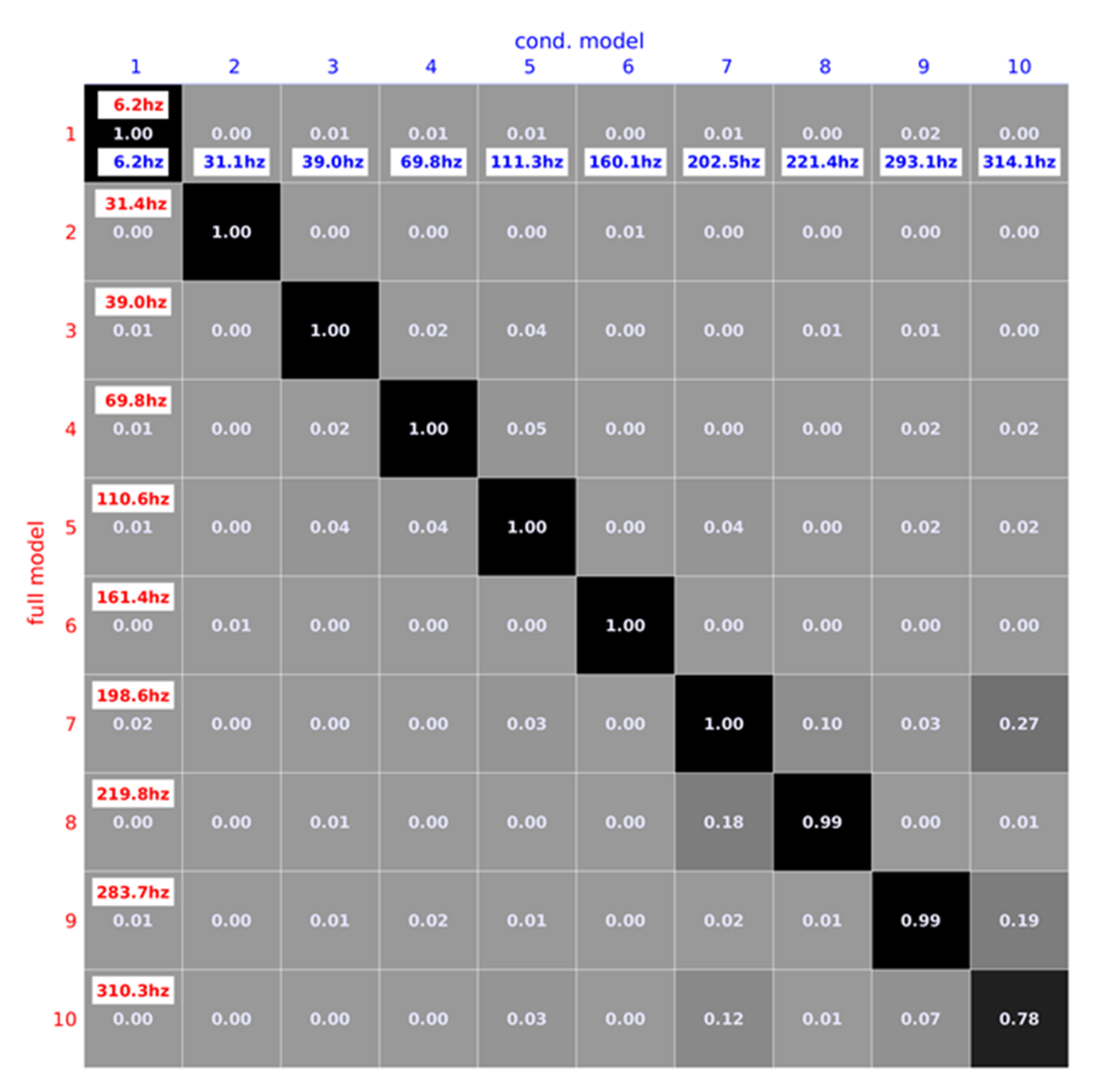
3.3. Controller Design and Model Selection
3.3.1. State Space Modeling and Modal Decomposition
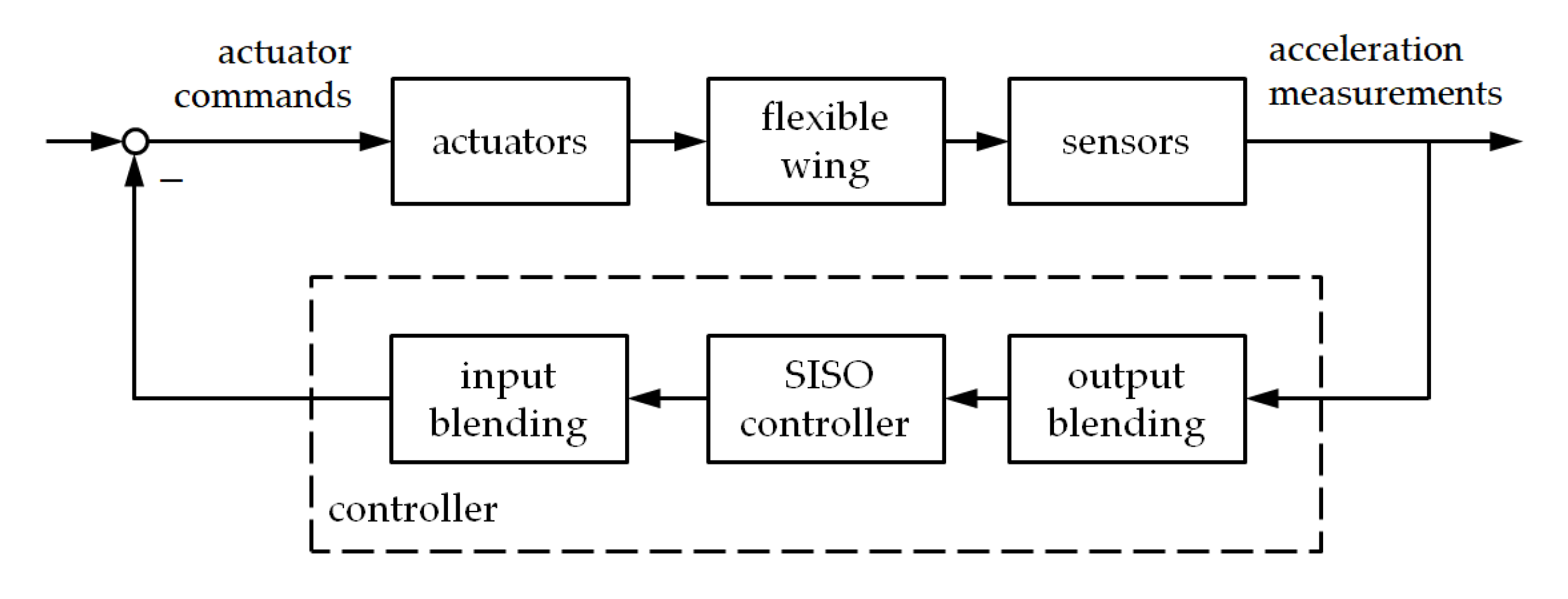
3.3.2. Modal Control Using Blended Inputs and Outputs
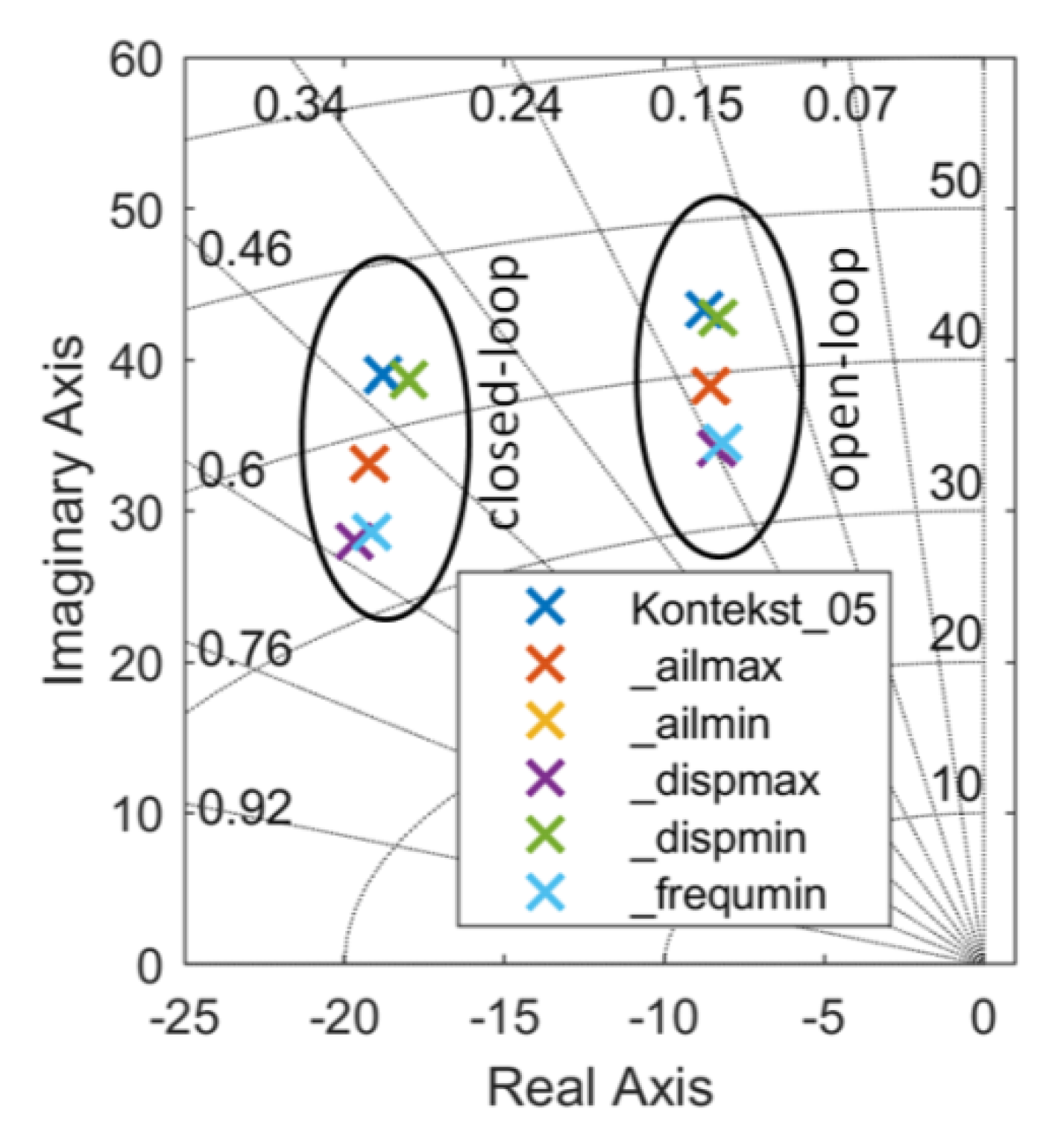
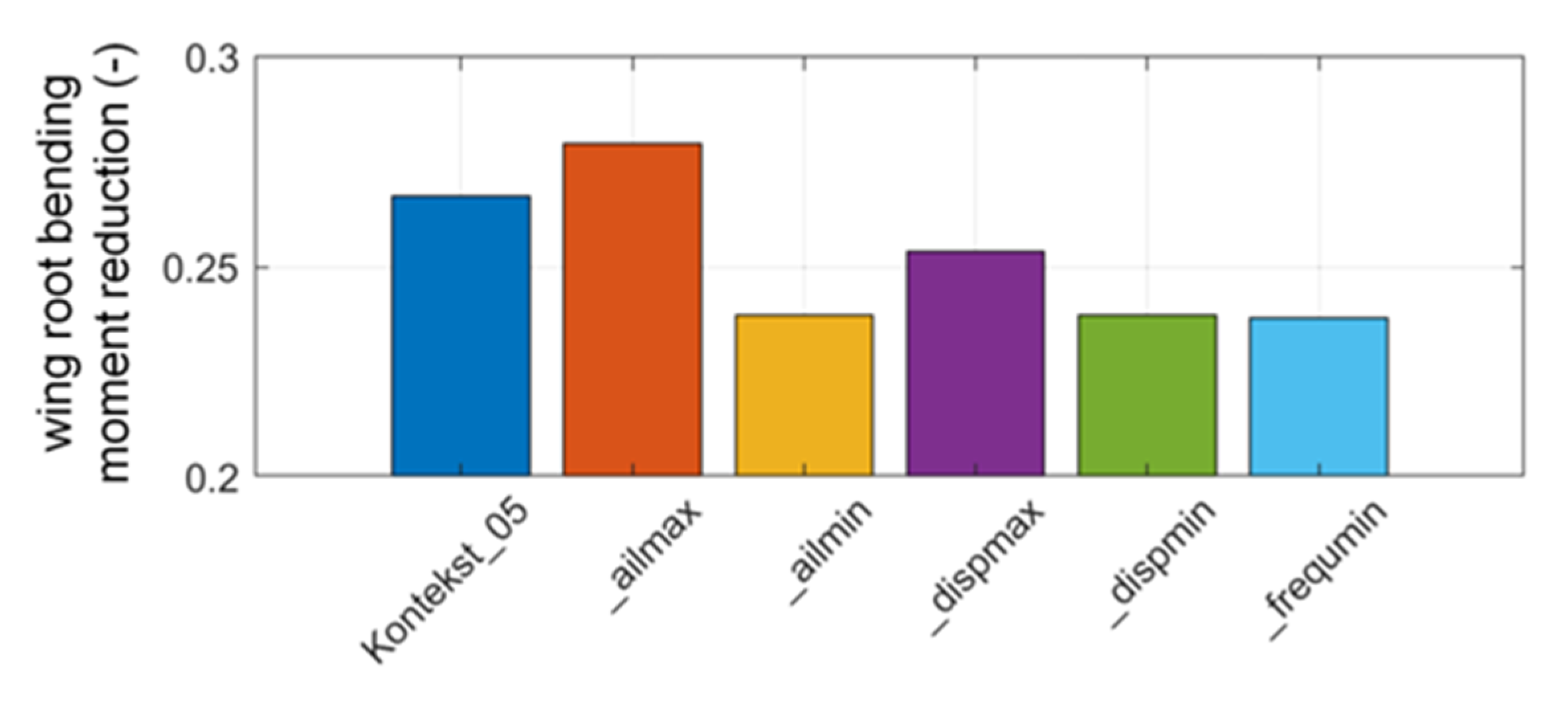
3.3.3. Closed-Loop Evaluation
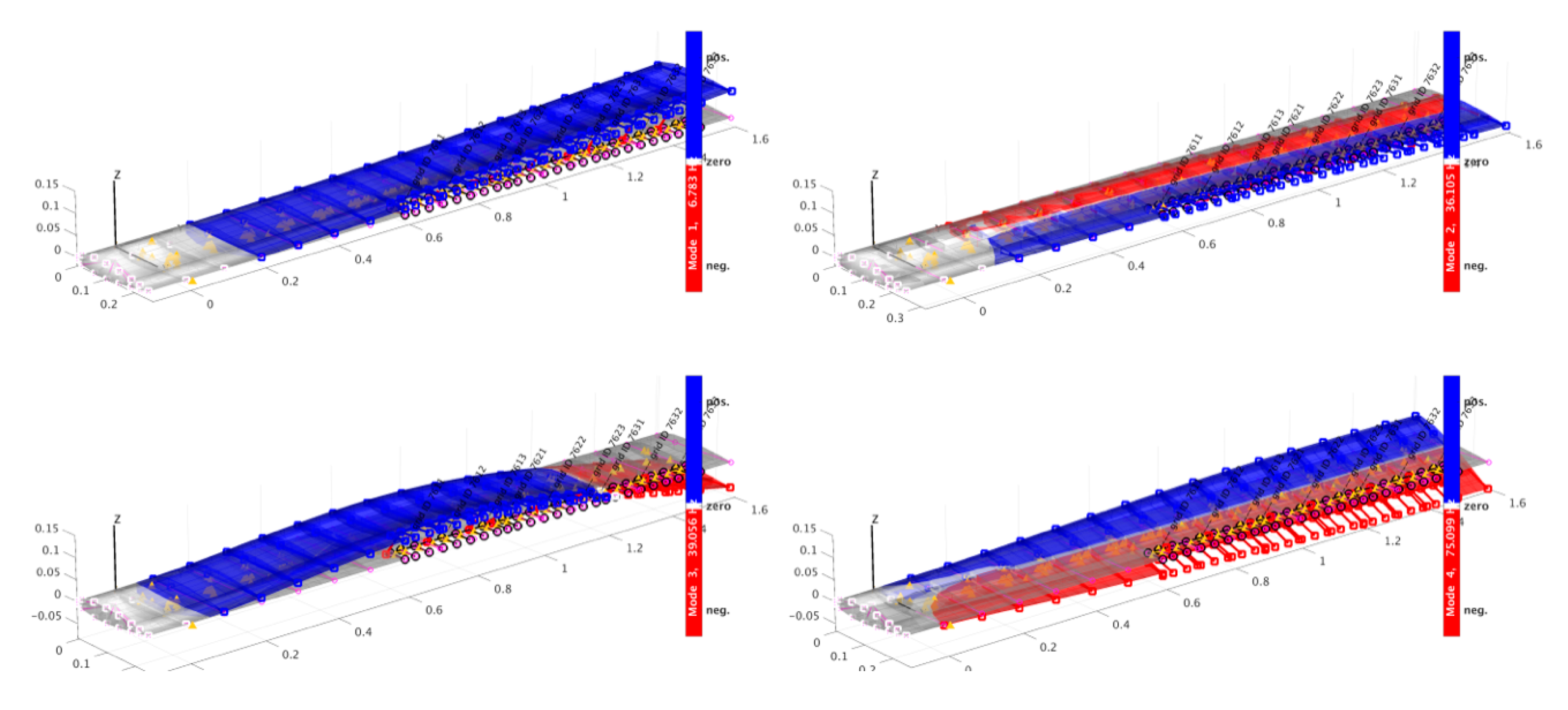
4. Manufacturing and Update
4.1. Model-Building and Sensor Installation
4.2. Model Update
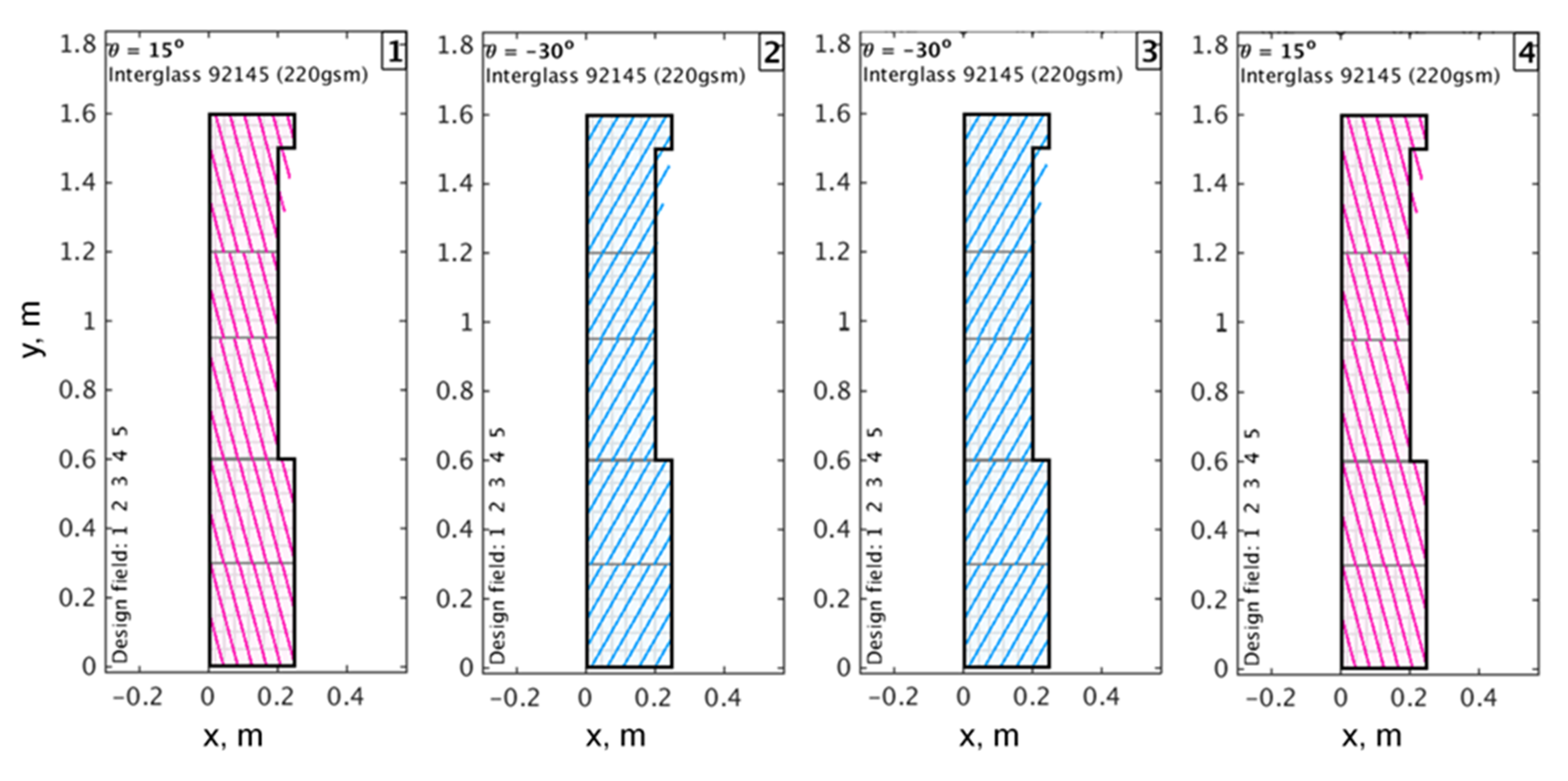
- Between 1° and 2° adaption of the fiber angles in the 15° and −30° wing skin layers (compare Figure 10), owing to uncertainties in the hand lay-up;
- Adaption of a diminution factor accounting for fiber ondulation in the UD glass fiber layer from 0.9 to 1.0 (no ondulation effect);
- Foam core density reduction, resulting from varying declarations by the manufacturer.
5. Conclusions and Outlook
Author Contributions
Funding
Conflicts of Interest
References
- Krüger, W. KonTeKst—Konfigurationen und Technologien für das Emissions- und Lärmarme Kurzstreckenflugzeug, Göttingen. 2015. Available online: https://www.dlr.de/fl/en/desktopdefault.aspx/tabid-1149/1737_read-47235/ (accessed on 16 March 2020).
- Starnes, J.H., Jr.; Haftka, R.T. Preliminary Design of Composite Wings for Buckling, Strength, and Displacement Constraints. J. Aircr. 1979, 16, 564–570. [Google Scholar] [CrossRef]
- Hollowell, S.J.; Dungundji, J. Aeroelastic Flutter and Divergence of Stiffness Coupled, Graphite Epoxy Cantilevered Plates. J. Aircr. 1984, 21, 69–76. [Google Scholar] [CrossRef]
- Green, J.A. Aeroelastic tailoring of aft-swept high-aspect-ratio composite wings. J. Aircr. 1987, 24, 812–819. [Google Scholar] [CrossRef]
- Shirk, M.H.; Hertz, T.J.; Weisshaar, T.A. Aeroelastic tailoring—Theory, practice, and promise. J. Aircr. 1986, 23, 6–18. [Google Scholar] [CrossRef]
- Vanderplaats, G.N.; Weisshaar, T.A. Optimum design of composite structures. Int. J. Numer. Methods Eng. 1989, 27, 437–448. [Google Scholar] [CrossRef]
- Stodieck, O.; Cooper, J.E.; Weaver, P.M. Interpretation of Bending/Torsion Coupling for Swept, Nonhomogenous Wings. J. Aircr. 2016, 53, 892–899. [Google Scholar] [CrossRef][Green Version]
- Stodieck, O.; Cooper, J.E.; Weaver, P.M.; Kealy, P. Aeroelastic Tailoring of a Representative Wing Box Using Tow-Steered Composites. AIAA J. 2017, 55, 1425–1439. [Google Scholar] [CrossRef]
- Stodieck, O.; Cooper, J.E.; Weaver, P.M.; Kealy, P. Improved aeroelastic tailoring using tow-steered composites. Compos. Struct. 2013, 106, 703–715. [Google Scholar] [CrossRef]
- Stanford, B.K.; Jutte, C.V.; Coker, C.A. Aeroelastic Sizing and Layout Design of a Wingbox Through Nested Optimization. AIAA J. 2018, 27, 1–10. [Google Scholar]
- Jutte, C.; Stanford, B.K. Aeroelastic Tailoring of Transport Aircraft Wings: State-of-the-Art and Potential Enabling Technologies; NASA Langley Research Center: Hampton, VA, USA, 2014. [Google Scholar]
- Dillinger, J.K.S.; Klimmek, T.; Abdalla, M.M.; Gürdal, Z. Stiffness Optimization of Composite Wings with Aeroelastic Constraints. J. Aircr. 2013, 50, 1159–1168. [Google Scholar] [CrossRef]
- Dillinger, J. Static Aeroelastic Optimization of Composite Wings with Variable Stiffness Laminates; TU Delft, Delft University of Technology: Delft, The Netherlands, 2014. [Google Scholar]
- Livne, E. Integrated Aeroservoelastic Optimization: Status and Direction. Aiaa J. Aircr. 1999, 36, 122–145. [Google Scholar] [CrossRef]
- Livne, E. Future of airplane aeroelasticity. J. Aircr. 2003, 40, 1066–1092. [Google Scholar] [CrossRef]
- Mukhopadhyay, V. Historical perspective on analysis and control of aeroelastic responses. J. Guid. Control. Dyn. 2003, 26, 673–684. [Google Scholar] [CrossRef]
- Theis, J. Robust and Linear Parameter-Varying Control of Aeroservoelastic Systems; Technische Universität Hamburg-Harburg: Hamburg, Germany, 2018. [Google Scholar]
- Regan, C.D.; Jutte, C.V. Survey of Applications of Active Control Technology for Gust Alleviation and New Challenges for Lighter-Weight Aircraft; NASA: Bellevue, WA, USA, 2012.
- Disney, T.E. The C-5A Active Load Alleviation System. Am. Inst. Aeroenaut. Astronaut. 1977, 14, 81–86. [Google Scholar] [CrossRef]
- Menon, A.N.; Chakravarthy, A.; Gruenwald, B.C.; Yucelen, T.; Steck, J.E. Modeling and Control of Uncertain Hybrid Structure Flexible, Morphing Wings with Stability and Performance Guarantees. In Proceedings of the AIAA Scitech Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar]
- Hashemi, K.E.; Alder, A.; Cramer, N.B.; Nguyen, N.T. Mode-based Sensing and Actuation Techniques for Multi-objective Flexible Aircraft Control. In Proceedings of the AIAA Scitech Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar]
- Sanders, B.; Eastep, F.E.; Forster, E. Aerodynamic and Aeroelastic Characteristics of Wings with Conformal Control Surfaces for Morphing Aircraft. J. Aircr. 2003, 40, 94–99. [Google Scholar] [CrossRef]
- Murua, J.; Palacios, R.; Peiró, J. Camber effects in the dynamic aeroelasticity of compliant airfoils. J. Fluids Struct. 2010, 26, 527–543. [Google Scholar] [CrossRef]
- Arena, M.; Concilio, A.; Pecora, R. Aero-servo-elastic design of a morphing wing trailing edge system for enhanced cruise performance. Aerosp. Sci. Technol. 2019, 86, 215–235. [Google Scholar] [CrossRef]
- Kuzmina, S.; Ishmuratov, F.; Zichenkov, M.; Chedrik, V.; Amiryants, G.A.; Kulesh, V.; Malyutin, V.; Chedrik, A.; Timokhin, V.; Shalaev, S.; et al. Wind Tunnel Testing of Adaptive Wing Structures. Morphing Wing Technol. 2018, 1, 713–755. [Google Scholar]
- Pusch, M.; Knoblach, A. Integrated Optimization of Ailerons for Active Gust Load Alleviation. In Proceedings of the Internetional Forum on Aeroelasticity and Structural Dynamics (IFASD), St. Petersburg, Russia, 28 June–2 July 2015. [Google Scholar]
- Pusch, M. Allocation of Distributed Flaps for Gust Load Alleviation. In Proceedings of the Conference on Control, Technology and Application (CCTA), Kohala Coast, HI, USA, 27–30 August 2017. [Google Scholar]
- Nguyen, N.; Urnes, J. Aeroelastic Modeling of Elastically Shaped Aircraft Conceptual Wing Shaping Control for Drag Reduction. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, Minneapolis, MN, USA, 13–16 August 2012. [Google Scholar]
- Danowsky, B.; Thompson, P.; Lee, D. Modal Isolation and Damping for Adaptive Aeroservoelastic Suppression. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, Boston, MA, USA, 19–22 August 2013. [Google Scholar]
- Pusch, M. Aeroelastic Mode Control using H2-optimal Blends for Inputs and Outputs. In Proceedings of the 2018 AIAA Guidance Conference on Navigation and Control, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar]
- Pusch, M.; Ossmann, D. Blending of inputs and outputs for modal velocity feedback. In Proceedings of the 27th IEEE Mediterranean Conference on Control. and Automation, Akko, Israel, 1–4 July 2019. [Google Scholar]
- Pusch, M.; Ossmann, D. H2-optimal Blending of Inputs and Outputs for Modal Control. IEEE Trans. Control. Syst. Technol. 2019, 27, C3. [Google Scholar] [CrossRef]
- Meddaikar, Y.; Dillinger, J.; Sodja, J.; Mai, H.; de Breuker, R. Optimization, manufacturing and testing of a composite wing with maximized tip deflection. In Proceedings of the 57th AIAA/ASCE/AHS/ASC Structures Structural Dynamics, and Materials Conference, San Diego, CA, USA, 4–8 January 2016. [Google Scholar]
- Meddaikar, M.Y.; Dillinger, J.; Ritter, M.R.; Govers, Y. Optimization & Testing of Aeroelastically-Tailored Forward Swept Wings. In Proceedings of the IFASD 2017—International Forum on Aeroelasticity and Structural Dynamics, Como, Italy, 25–28 June 2017. [Google Scholar]
- Drela, M. XFOIL: An Analysis and Design System for Low Reynolds Number Airfoils. In Low Reynolds Number Aerodynamics; Springer: Berlin, Heidelberg, 1989. [Google Scholar]
- Maskew, B. PROGRAM VSAERO: A Computer Program for Calculating the Non-Linear Aerodynamic Characteristics of Arbitrary Configurations: User’s Manual; NASA: Bellevue, WA, USA, 1982.
- Klimmek, T. Parameterization of topology and geometry for the multidisciplinary optimization of wing structures. In Proceedings of the CEAS 2009—European Air and Space Conference, Manchester, UK, 6–29 October 2009. [Google Scholar]
- Ferede, E.; Abdalla, M. Cross-sectional modelling of thin-walled composite beams. In Proceedings of the 55th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, National Harbor, Maryland, 13–17 January 2014. [Google Scholar]
- Dillinger, J.; Abdalla, M.M.; Meddaikar, Y.M.; Klimmek, T. Static Aeroelastic Stiffness Optimization of a Forward Swept Composite Wing with CFD Corrected Aero Loads. In Proceedings of the International Forum on Aeroelasticity and Structural Dynamics (IFASD 2015), Saint Petersburg, Russia, 28 June–2 July 2015. [Google Scholar]
- Meddaikar, Y.; Irisarri, F.-X.; Abdalla, M. Blended Composite Optimization combining Stacking Sequence Tables and a Modified Shepard’s Method. In Proceedings of the 11th World Congress on Structural and Multidisciplinary Optimization (Submitted), Sydney, Australia, 7–12 June 2015. [Google Scholar]
- Pusch, M.; Ossmann, D.; Kier, T.; Tang, M.; Lübker, J.; Dillinger, J. Aeroelastic Modeling and Control of an Experimental Flexible Wing. In Proceedings of the Guidance, Navigation and Control (GNC), Milano, Italy, 3–5 April 2019. [Google Scholar]
- Albano, E.; Rodden, W. A doublet-lattice method for calculating lift distributions on oscillating surfaces in subsonic flows. Aiaa J. 1969, 7, 279–285. [Google Scholar] [CrossRef]
- Roger, K. Airplane Math Modelling Methods for Active Control Design. In Proceedings of the 44th AGARD Structures and Materials Panel, AGARD-CP-228, Lisbon, Portugal, 21 April 1977; pp. 4.1–4.11. [Google Scholar]

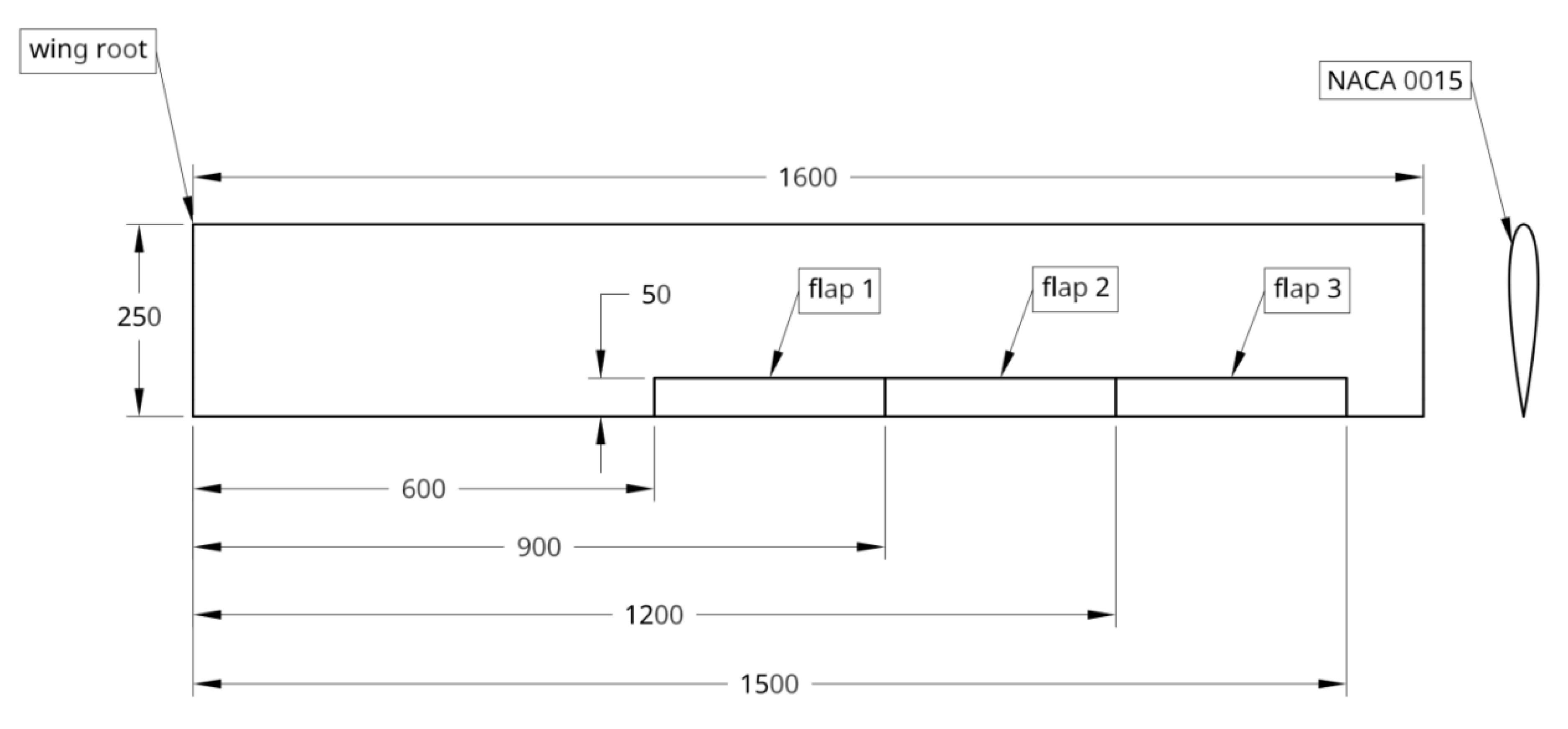

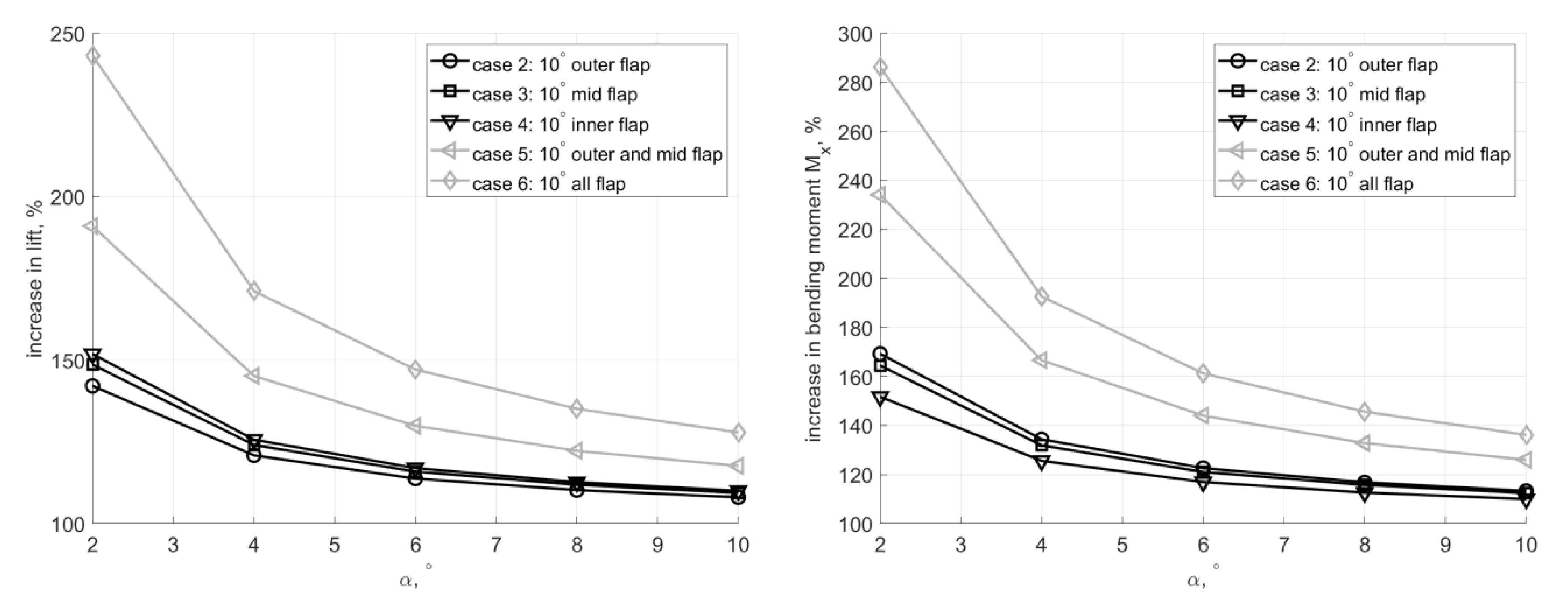




| Flap | Spanwise Boundaries | Case | |||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| 1 | 0.6–0.9 m | 0° | 0° | 0° | 10° | 0° | 10° |
| 2 | 0.9–1.2 m | 0° | 0° | 10° | 0° | 10° | 10° |
| 3 | 1.2–1.5 m | 0° | 10° | 0° | 0° | 10° | 10° |
| Case | Type | α | V | Flap 1 | Flap 2 | Flap 3 |
|---|---|---|---|---|---|---|
| 1001 | αfixed | 5.0° | 50.0 m/s | 0.0° | 0.0° | 0.0° |
| 1002 | αfixed | 10.0° | 50.0 m/s | 0.0° | 0.0° | 0.0° |
| 1003 | αfixed | 15.0° | 60.0 m/s | 0.0° | 0.0° | 0.0° |
| 1004 | αfixed | −5.0° | 50.0 m/s | 0.0° | 0.0° | 0.0° |
| 1005 | αfixed | −10.0° | 50.0 m/s | 0.0° | 0.0° | 0.0° |
| 1006 | αfixed | −15.0° | 60.0 m/s | 0.0° | 0.0° | 0.0° |
| 1007 | divergence | % | % | 0.0° | 0.0° | 0.0° |
| 1008 | eigenfrequency | % | % | 0.0° | 0.0° | 0.0° |
| 1009 | ail. eff. | % | 50.0 m/s | 0.0° | 0.0° | 1.0° |
| 1010 | ail. eff. | % | 50.0 m/s | 0.0° | 1.0° | 0.0° |
| 1011 | ail. eff. | % | 50.0 m/s | 1.0° | 0.0° | 0.0° |
| Type | Position | Output |
|---|---|---|
| accelerometer | 25% chord: x = 62.5 mm y = [300/600/900/1200/1500] mm | acceleration in z |
| - | 60% chord: x = 150.0 mm y = [300/600/900/1200/1500] mm | acceleration in z |
| - | x = 62.5 mm y = [900/1500] mm | acceleration in x |
| 3-axes accelerometer | 25% chord: x = 62.5 mm y = [200/400/600/900/1200/1500] mm | acceleration in xyz |
| strain gauge | upper skin: x = [62.5/150] mm y = [50/50] mm | 3-axes strain rosette |
| - | lower skin: x = [62.5/150/150] mm y = [50/50/600] mm | 3-axes strain rosette |
| strain fiber | 25% and 60% chord: y = [0–1600] mm | strain in fiber direction |
| potentiometer | installed in hinge line of each flap | flap deflection |
| Mode Name | Measurement | Initial FEM | Updated FEM | |||
|---|---|---|---|---|---|---|
| f (Hz) | m (kg) | f (Hz) | m (kg) | f (Hz) | m (kg) | |
| 1st wing bending | 6.9 | 0.83 | 6.2 | 0.77 | 6.8 Hz | 0.81 |
| 1st in-plane | 26.8 | 1.24 | 31.4 | 0.75 | 36.1 Hz | 0.78 |
| 2nd wing bending | 39.0 | 0.90 | 39.0 | 0.61 | 39.1 Hz | 0.77 |
| 1st torsion | 75.2 | 0.29 | 69.8 | 0.90 | 75.1 Hz | 0.82 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dillinger, J.K.S.; Meddaikar, Y.M.; Lübker, J.; Pusch, M.; Kier, T. Design and Optimization of an Aeroservoelastic Wind Tunnel Model. Fluids 2020, 5, 35. https://doi.org/10.3390/fluids5010035
Dillinger JKS, Meddaikar YM, Lübker J, Pusch M, Kier T. Design and Optimization of an Aeroservoelastic Wind Tunnel Model. Fluids. 2020; 5(1):35. https://doi.org/10.3390/fluids5010035
Chicago/Turabian StyleDillinger, Johannes K. S., Yasser M. Meddaikar, Jannis Lübker, Manuel Pusch, and Thiemo Kier. 2020. "Design and Optimization of an Aeroservoelastic Wind Tunnel Model" Fluids 5, no. 1: 35. https://doi.org/10.3390/fluids5010035
APA StyleDillinger, J. K. S., Meddaikar, Y. M., Lübker, J., Pusch, M., & Kier, T. (2020). Design and Optimization of an Aeroservoelastic Wind Tunnel Model. Fluids, 5(1), 35. https://doi.org/10.3390/fluids5010035