Dynamics of Swimmers in Fluids with Resistance
Abstract
1. Introduction
2. Methods
2.1. Fluid Model
2.2. Sperm Representation
2.3. Numerical Methods
3. Results
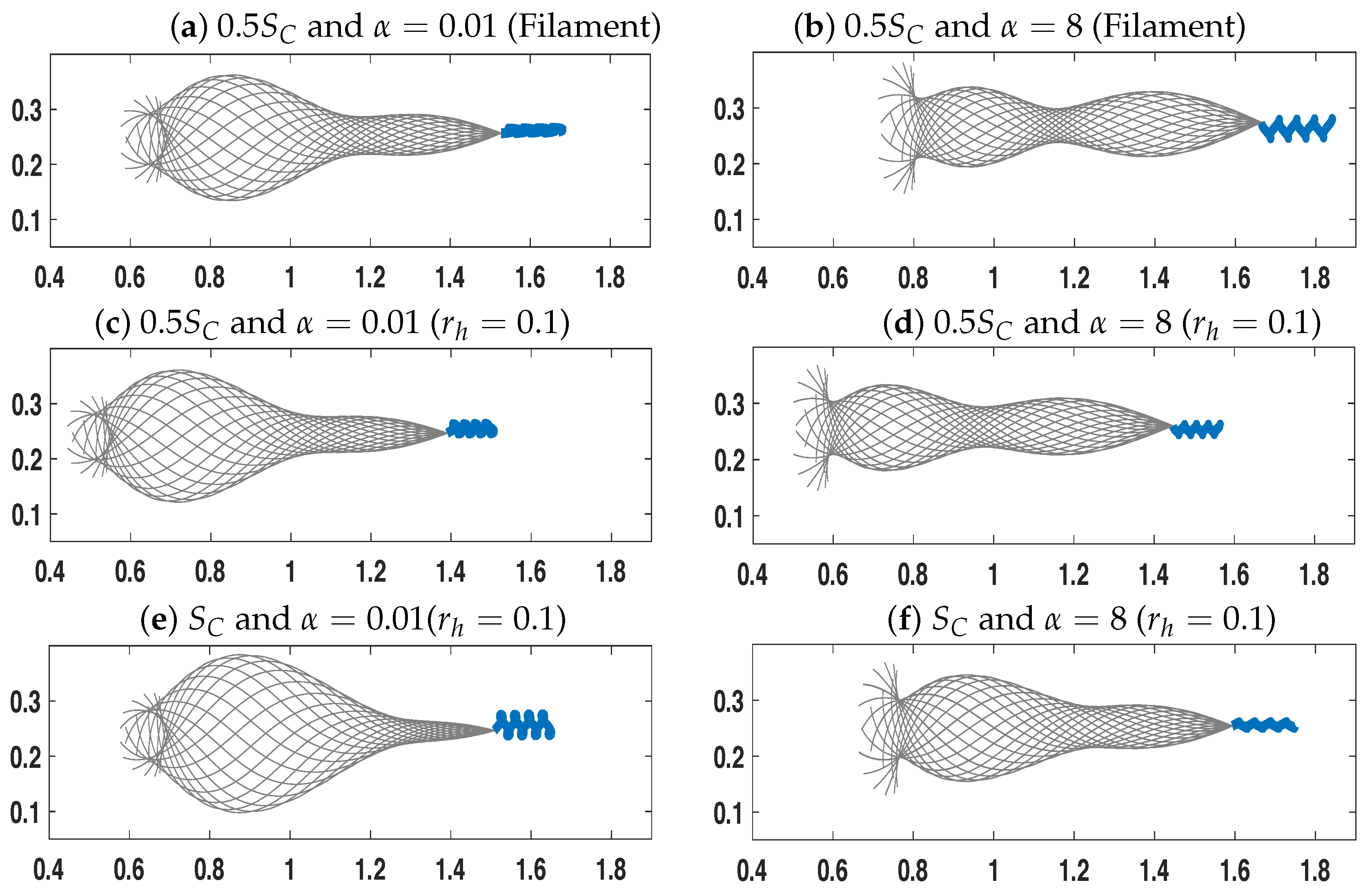
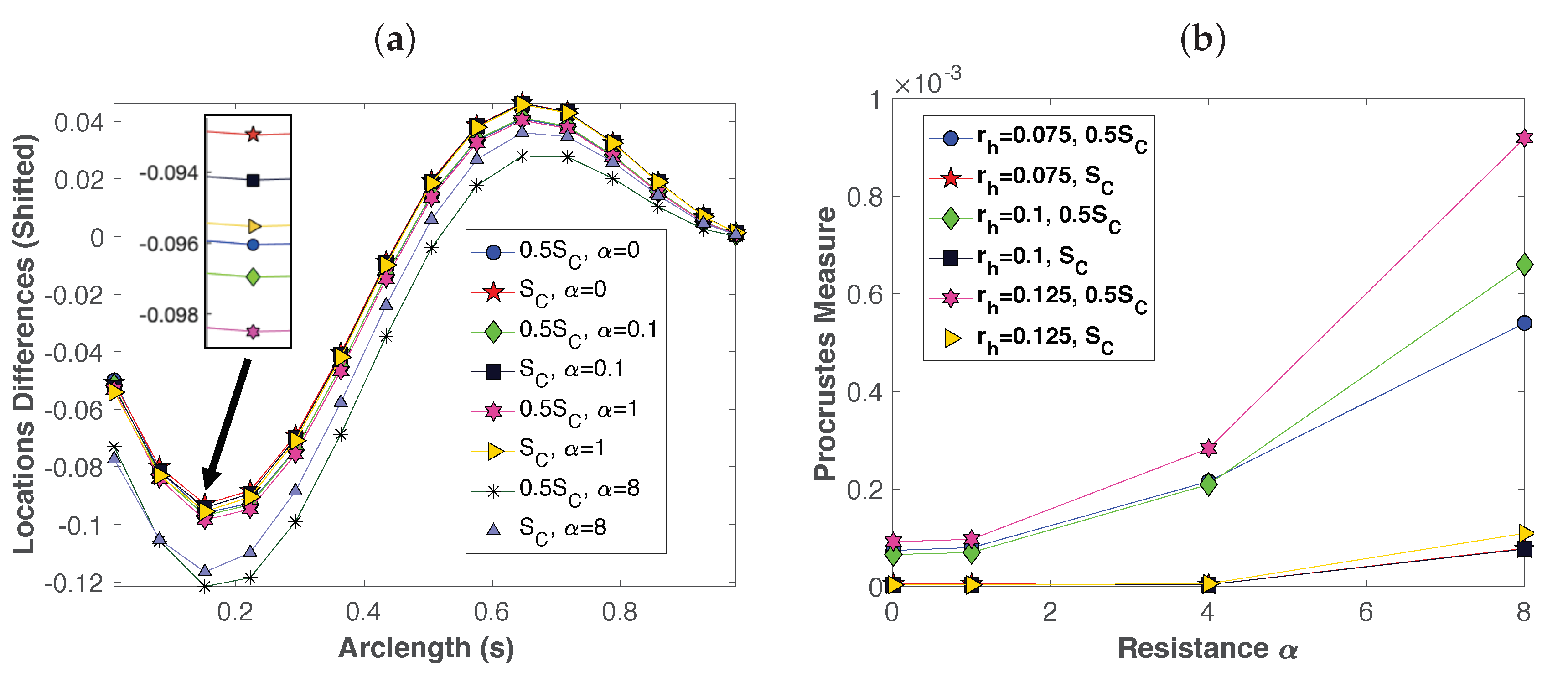
3.1. Dynamics of a Single Swimmer
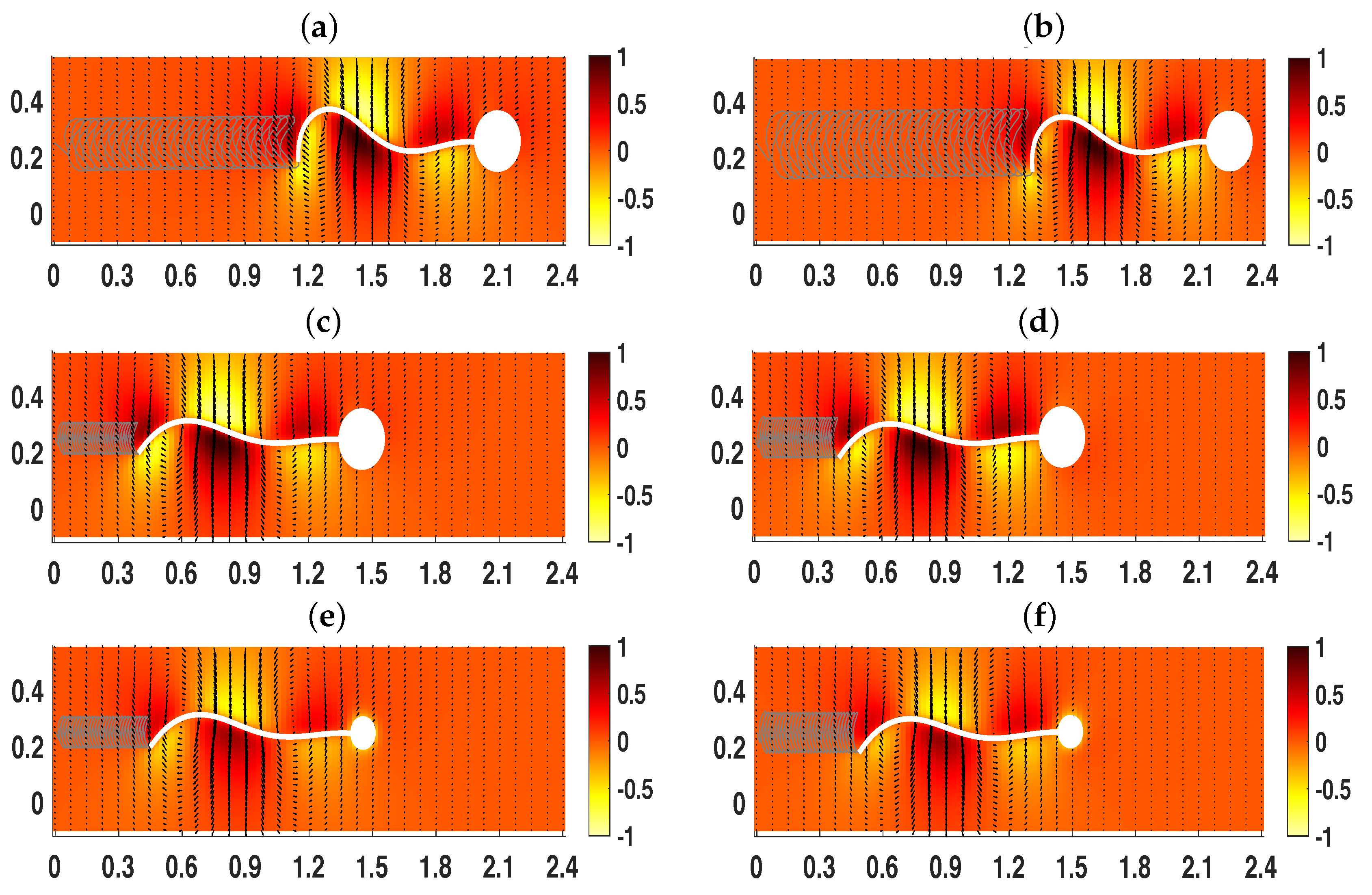
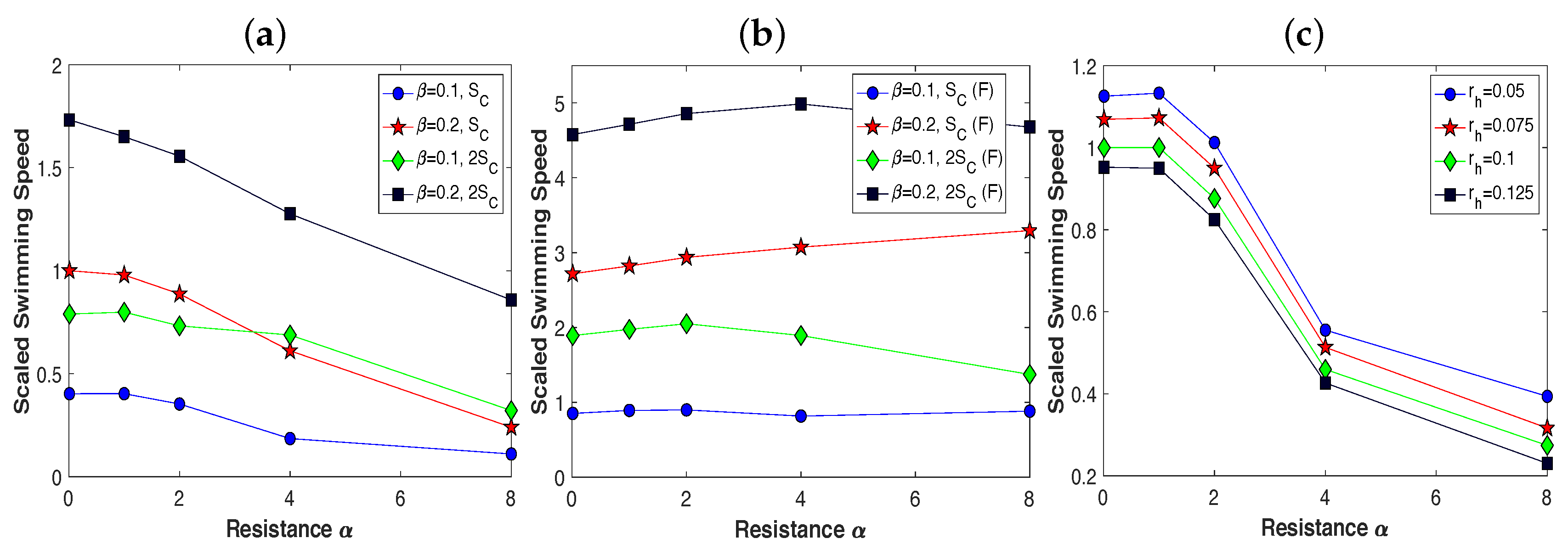
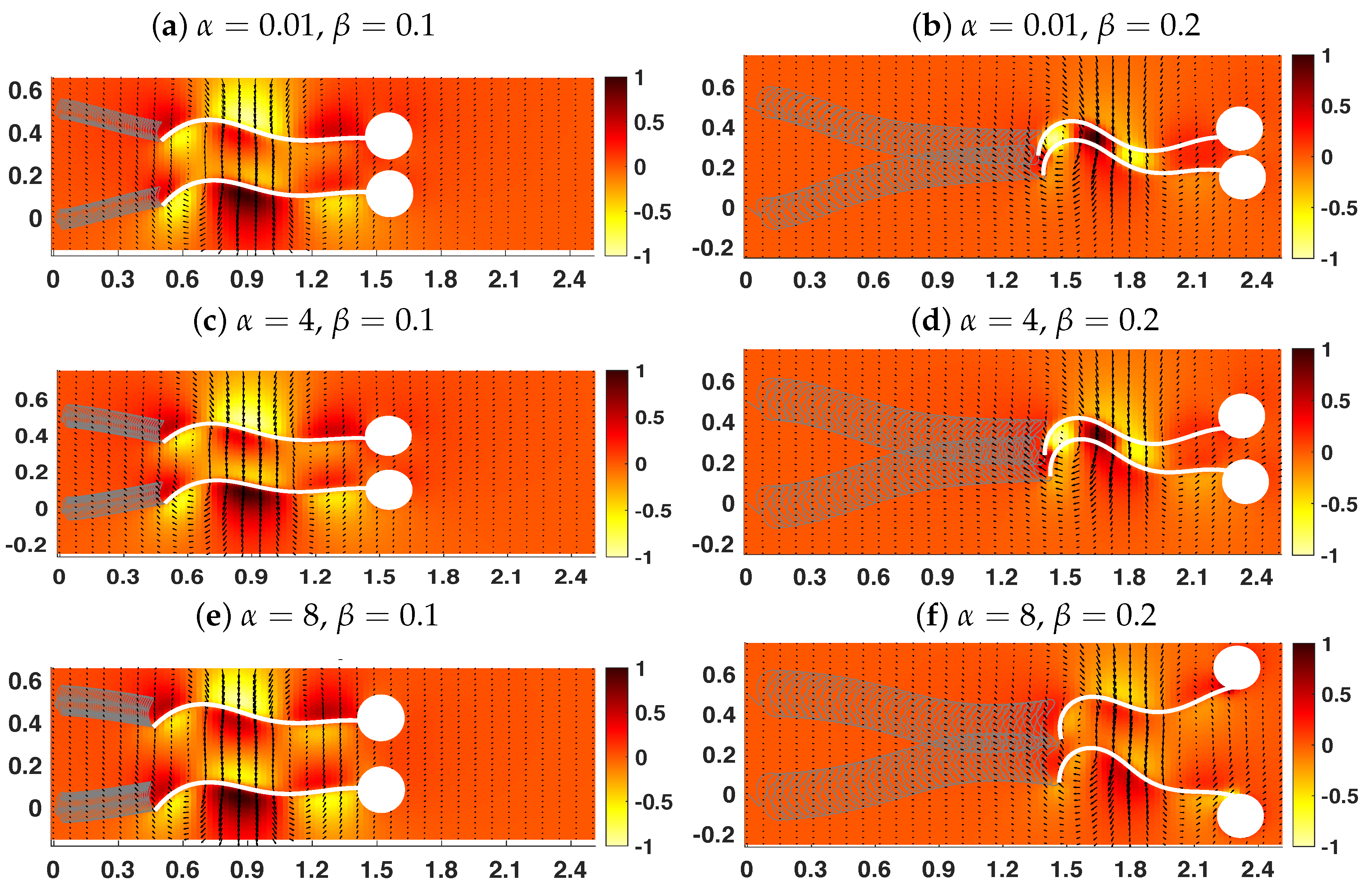
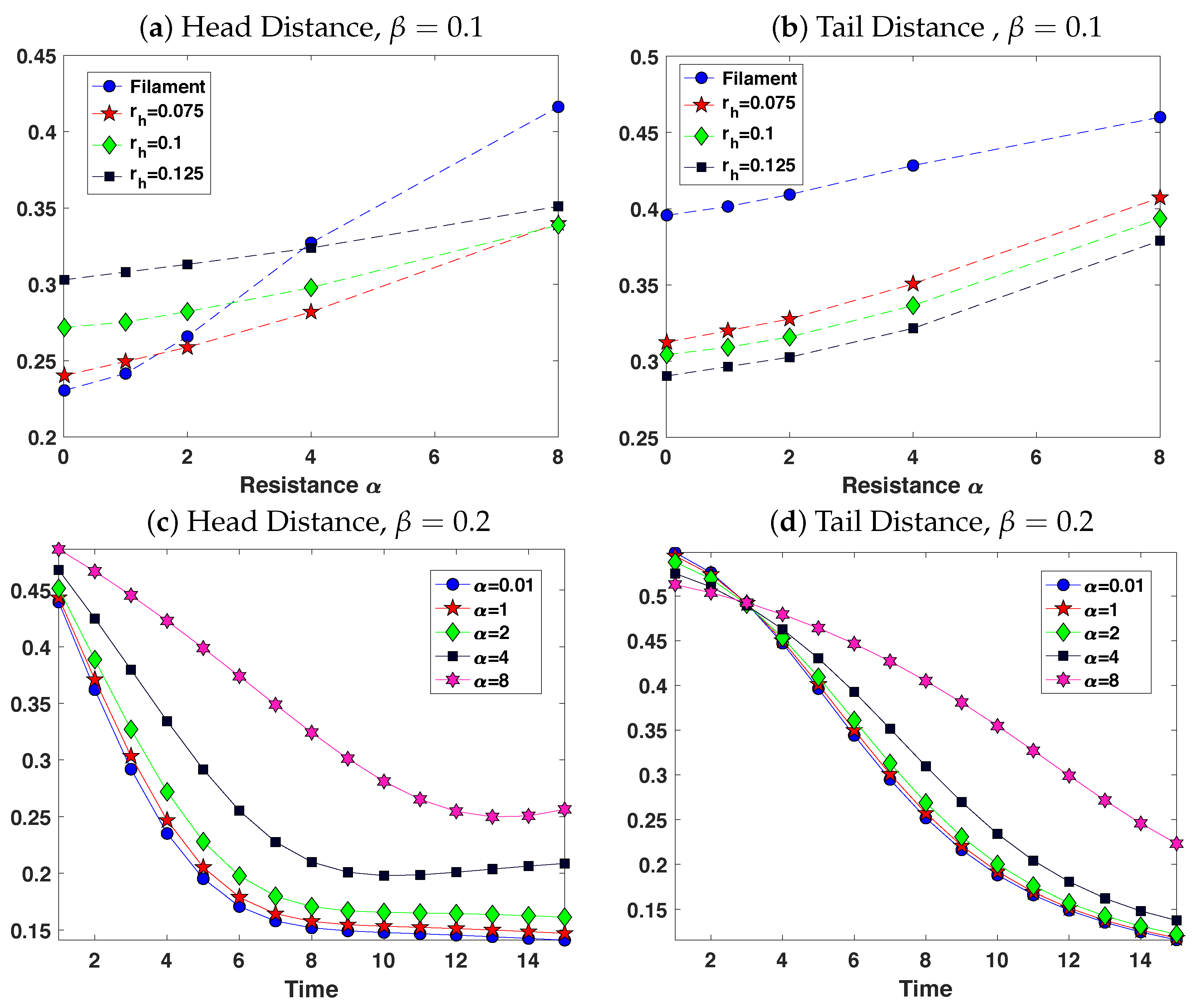
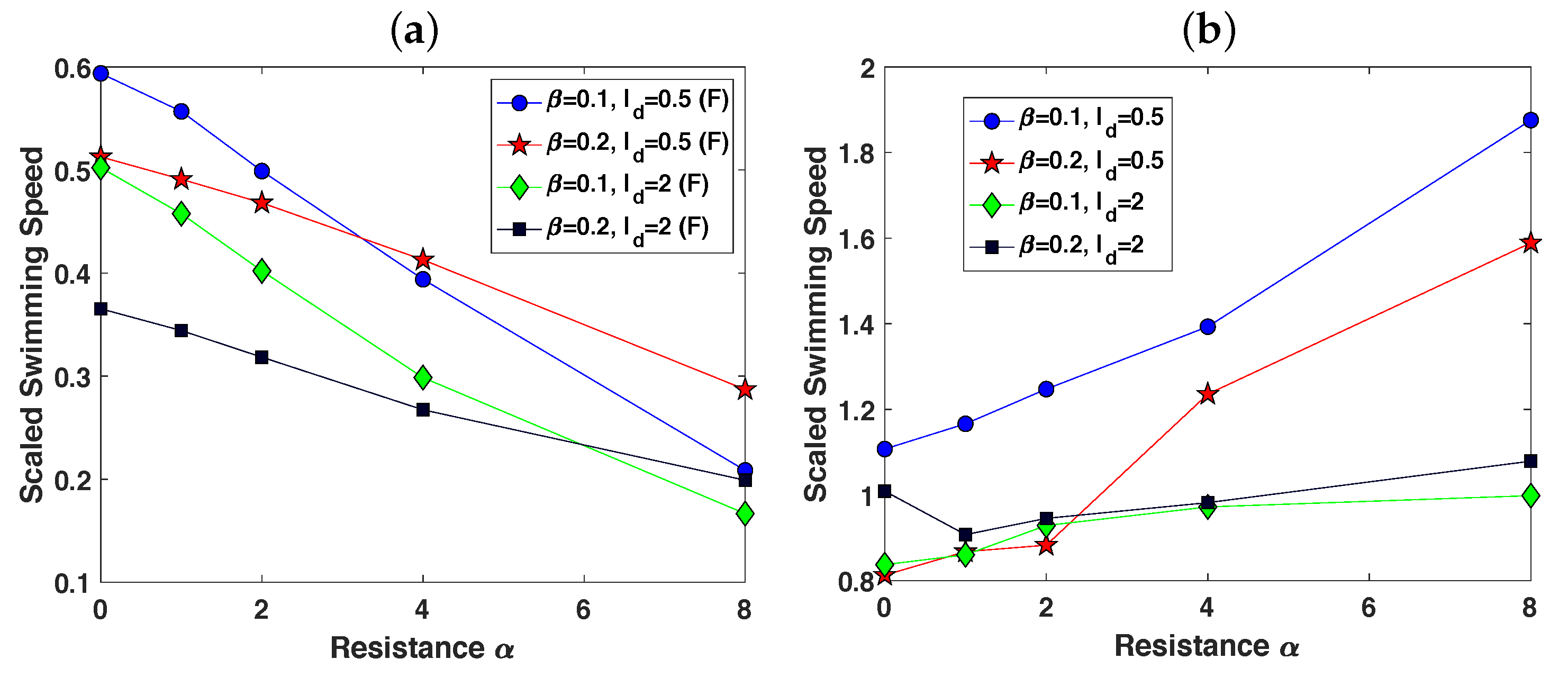
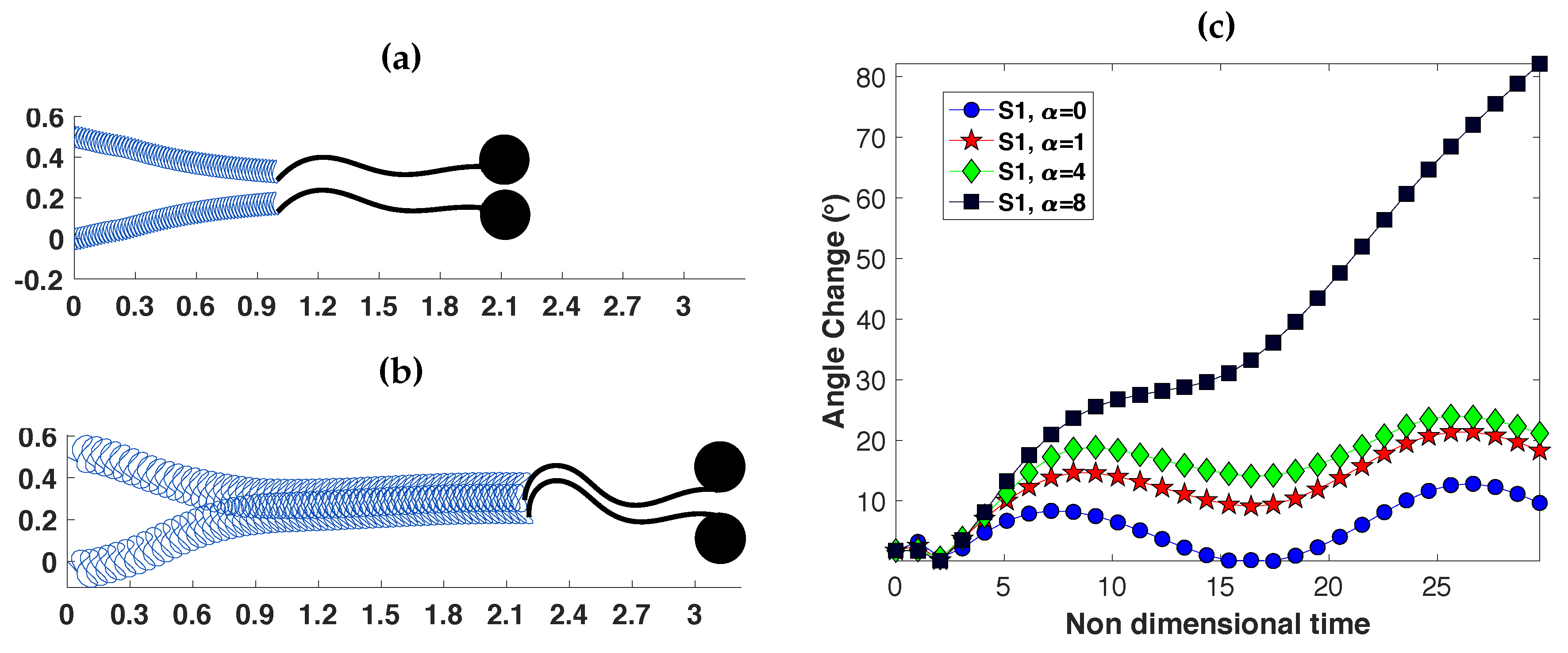
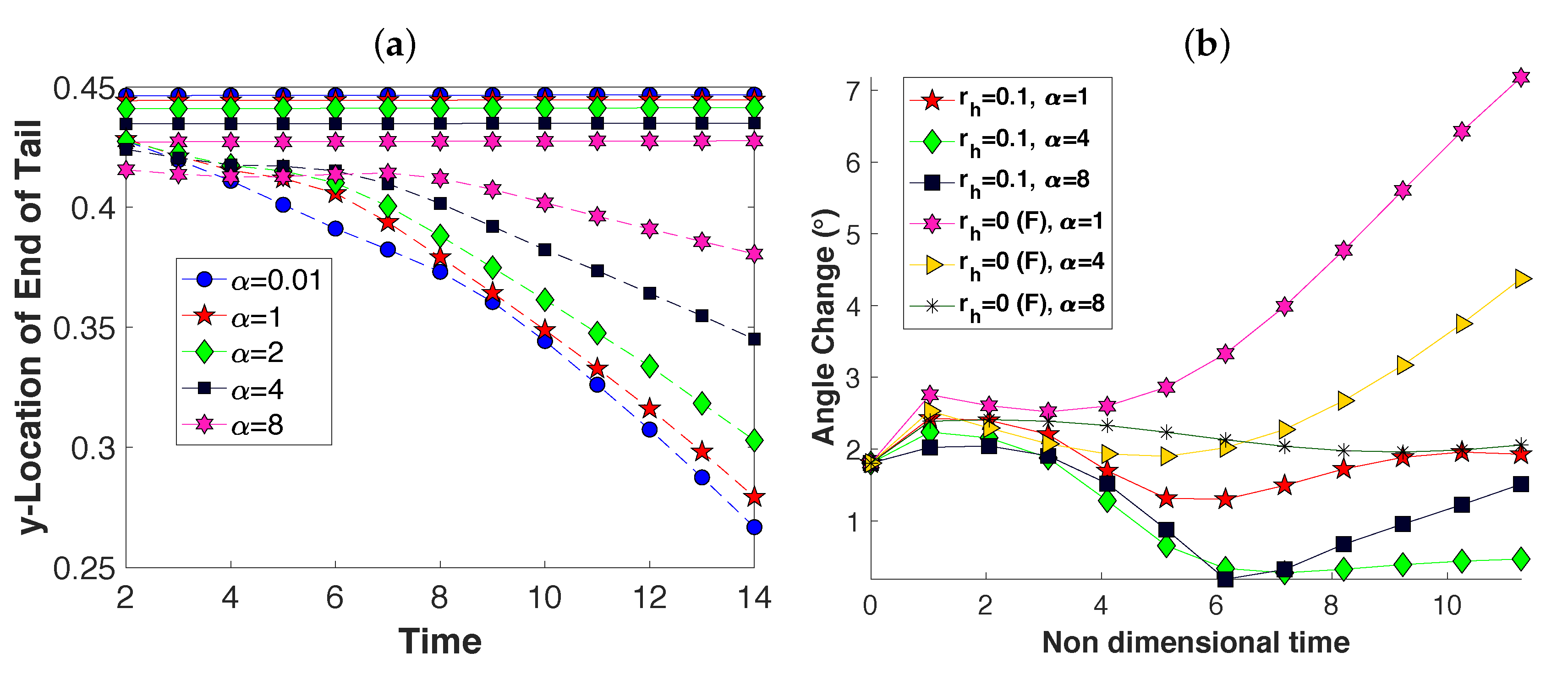
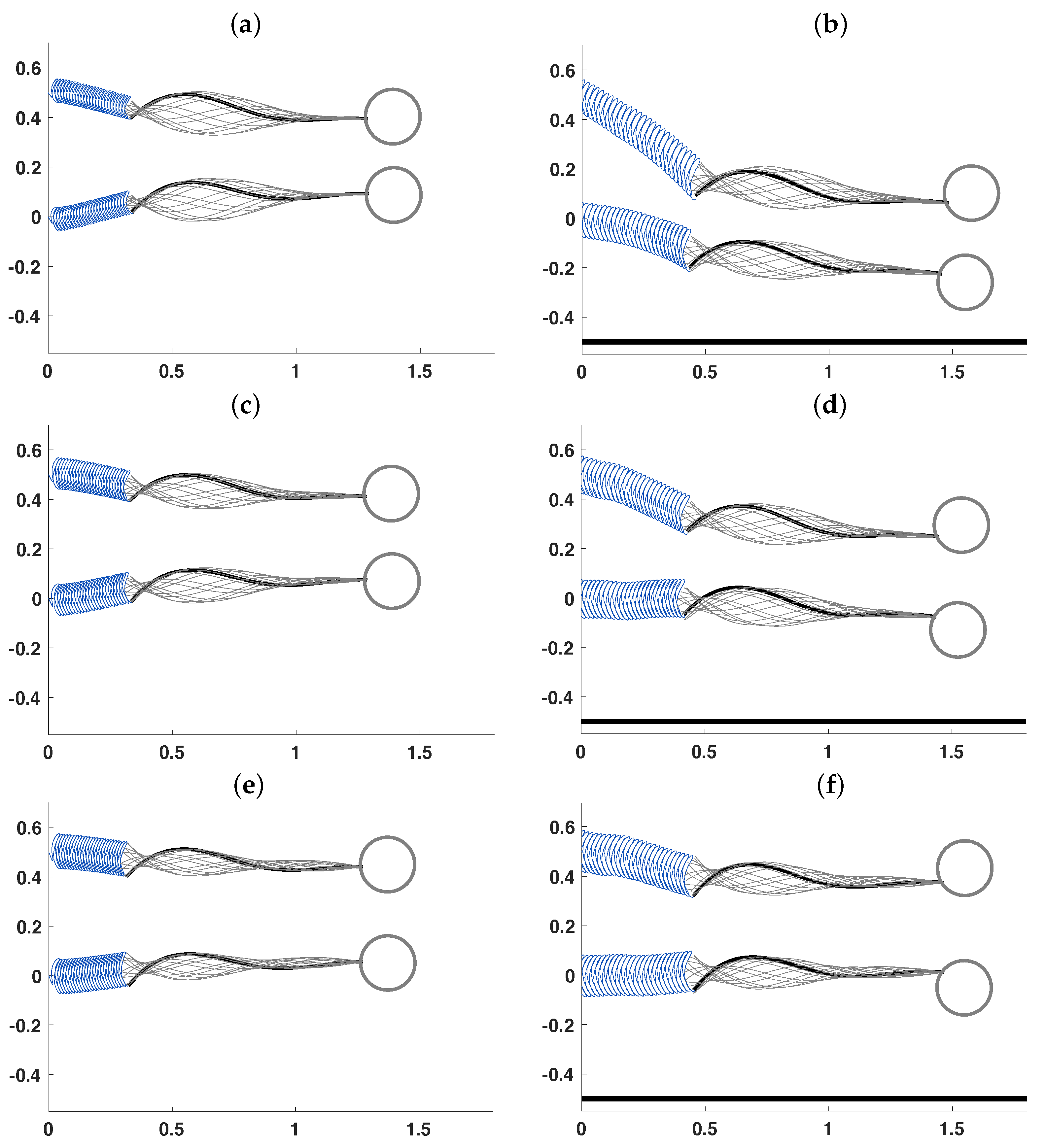
3.2. Pairs of Swimmers
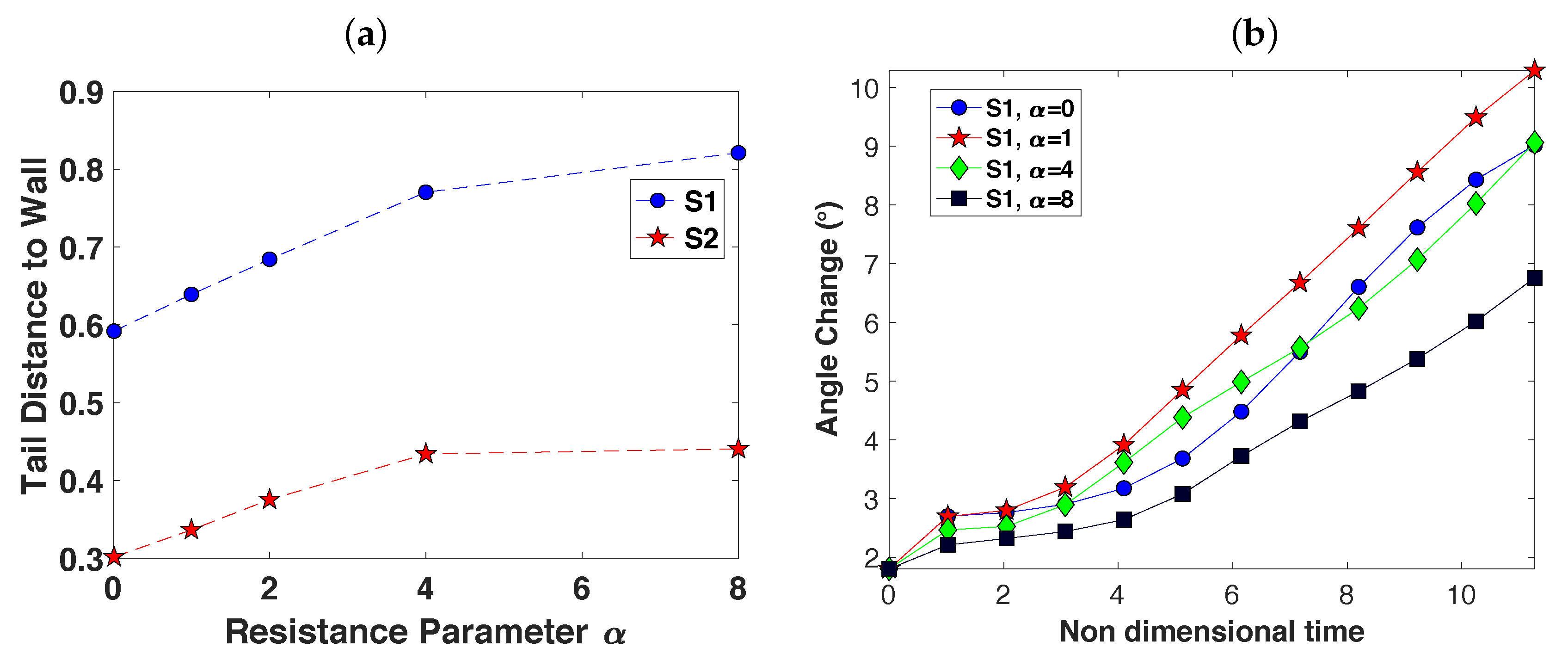
3.3. Wall Interactions
4. Discussions and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lindemann, C.B.; Lesich, K.A. Flagellar and ciliary beating: The proven and the possible. J. Cell Sci. 2010, 123, 519–528. [Google Scholar] [CrossRef]
- Woolley, D. Flagellar oscillation: A commentary on proposed mechanisms. Biol. Rev. 2010, 85, 453–470. [Google Scholar] [CrossRef]
- Gaffney, E.A.; Gadêlha, H.; Smith, D.J.; Blake, J.R.; Kirkman-Brown, J.C. Mammalian sperm motility: Observation and theory. Annu. Rev. Fluid Mech. 2011, 43, 501–528. [Google Scholar] [CrossRef]
- Li, H.; Ding, X.; Guan, H.; Xiong, C. Inhibition of human sperm function and mouse fertilization in vitro by an antibody against cation channel of sperm 1: The contraceptive potential of its transmembrane domains and pore region. Fertil. Steril. 2009, 92, 1141–1146. [Google Scholar] [CrossRef]
- Suarez, S. How do sperm get to the egg? Bioengineering expertise needed! Exp. Mech. 2010, 50, 1267–1274. [Google Scholar] [CrossRef]
- Gao, W.; Wang, J. Synthetic micro/nanomotors in drug delivery. Nanoscale 2014, 6, 10486–10494. [Google Scholar] [CrossRef] [PubMed]
- Sanders, L. Microswimmers make a splash: Tiny travelers take on a viscous world. Sci. News 2009, 176, 22–25. [Google Scholar] [CrossRef]
- Simons, J.; Olson, S.D. Sperm Motility: Models for Dynamic Behavior in Complex Environments. In Cell Movement: Modeling and Applications; Springer International Publishing: Cham, Switzerland, 2018; pp. 169–209. [Google Scholar]
- Rutllant, J.; Lopez-Bejar, M.; Lopez-Gatius, F. Ultrastructural and rheological properties of bovine vaginal fluid and its relation to sperm motility and fertilization: A review. Reprod. Dom. Anim. 2005, 40, 79–86. [Google Scholar] [CrossRef]
- Saltzman, W.M.; Radomsky, M.L.; Whaley, K.J.; Cone, R.A. Antibody diffusion in human cervical mucus. Biophys. J. 1994, 66, 508. [Google Scholar] [CrossRef]
- Brinkman, H.C. A calculation of the viscous force exerted by a flowing fluid on a dense swarm of paticles. Appl. Sci. Res. 1947, 1, 27–34. [Google Scholar] [CrossRef]
- Lauga, E.; Powers, T. The hydrodynamics of swimming microorganisms. Rep. Prog. Phys. 2009, 72, 096601. [Google Scholar] [CrossRef]
- Carichino, L.; Olson, S. Emergent three-dimensional sperm motility: Coupling calcium dynamics and preferred curvature in a kirchhoff rod model. J. Math. Med. Biol. 2018. [Google Scholar] [CrossRef] [PubMed]
- Dillon, R.; Fauci, L.; Yang, X. Sperm motility and multiciliary beating: An integrative mechanical model. Comput. Math. Appl. 2006, 52, 749–758. [Google Scholar] [CrossRef][Green Version]
- Elgeti, J.; Kaupp, U.; Gompper, G. Hydrodynamics of sperm cells near surfaces. Biophys. J. 2010, 99, 1018–1026. [Google Scholar] [CrossRef] [PubMed]
- Elgeti, J.; Winkler, R.; Gompper, G. Physics of Microswimmers- Single Particle Motion and Collective Behavior: A review. Rep. Prog. Phys. 2015, 78, 056601. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Carichino, L.; Olson, S. Hydrodynamic interactions of actuated elastic filaments near a planar wall with applications to sperm motility. J. Coupled. Syst. Multiscale Dyn. 2018, 6, 163–175. [Google Scholar] [CrossRef]
- Ishimoto, K.; Gaffney, E. An elastohydrodynamical simulation study of filament and spermatozoan swimming driven by internal couples. IMA J. Appl. Math. 2018, 83, 655–679. [Google Scholar] [CrossRef]
- Olson, S.; Suarez, S.; Fauci, L. Coupling biochemistry and hydrodynamics captures hyperactivated sperm motility in a simple flagellar model. J. Theor. Biol. 2011, 283, 203–216. [Google Scholar] [CrossRef]
- Schoeller, S.; Keaveny, E. Flagellar undulations to collective motion: Predicting the dynamics of sperm suspensions. J. Roy. Soc. Interface 2018, 15, 20170834. [Google Scholar] [CrossRef]
- Smith, D.; Gaffney, E.; Blake, J.; Kirkman-Brown, J. Human sperm accumulation near surfaces: A simulation study. J. Fluid. Mech. 2009, 621, 289–320. [Google Scholar] [CrossRef]
- Omori, T.; Ishikawa, T. Swimming of Spermatozoa in a Maxwell Fluid. Micromach 2019, 10, 78. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Elgeti, J.; Gompper, G. Cooperation of sperm in two dimensions: Synchronization, attraction, and aggregation through hydrodynamic interactions. Phys. Rev. E 2008, 78, 061903. [Google Scholar] [CrossRef] [PubMed]
- Taylor, G. Analysis of the swimming of microscopic organisms. Proc. Roy. Soc. Lond. Ser. A 1951, 209, 447–461. [Google Scholar]
- Taylor, G. The action of waving cylindrical tails in propelling microscopic organisms. Proc. Roy. Soc. Lond. Ser. A 1952, 211, 225–239. [Google Scholar]
- Ho, N.; Leiderman, K.; Olson, S. Swimming speeds of filaments in viscous fluids with resistance. Phys. Rev. E 2016, 93, 043108. [Google Scholar] [CrossRef]
- Leshansky, A. Enhanced low-Reynolds-number propulsion in heterogenous viscous environments. Phys. Rev. E 2009, 80, 051911. [Google Scholar] [CrossRef]
- Ho, N.; Leiderman, K.; Olson, S. A 3-dimensional model of flagellar swimming in a Brinkman fluid. J. Fluid Mech. 2019, 864, 1088–1124. [Google Scholar] [CrossRef]
- Olson, S.; Leiderman, K. Effect of fluid resistance on symmetric and asymmetric flagellar waveforms. J. Aero Aqua. Bio-Mech. 2015, 4, 12–17. [Google Scholar] [CrossRef]
- Leiderman, K.; Olson, S. Swimming in a two-dimensional Brinkman fluid: Computational modeling and regularized solutions. Phys. Fluids 2016, 28, 021902. [Google Scholar] [CrossRef]
- Cortez, R.; Cummins, B.; Leiderman, K.; Varela, D. Computation of three-dimensional Brinkman flows using regularized methods. J. Comput. Phys. 2010, 229, 7609–7624. [Google Scholar] [CrossRef]
- Auriault, J.L. On the domain of validity of Brinkman’s equation. Trans. Porous Media 2009, 79, 215–223. [Google Scholar] [CrossRef]
- Durlofsky, L.; Brady, J.F. Analysis of the Brinkman equation as a model for flow in porous media. Phys. Fluids 1987, 30, 3329–3341. [Google Scholar] [CrossRef]
- Howells, I.D. Drag due to the motion of a Newtonian fluid through a sparse random array of small fixed rigid objects. J. Fluid Mech. 1974, 64, 449–475. [Google Scholar] [CrossRef]
- Spielman, L.; Goren, S.L. Model for predicting pressure drop and filtration efficiency in fibrous media. Env. Sci. Tech. 1968, 1, 279–287. [Google Scholar] [CrossRef]
- Fu, H.; Shenoy, V.; Powers, T. Low Reynolds number swimming in gels. Europhys. Lett. 2010, 91, 24002. [Google Scholar] [CrossRef]
- Morandotti, M. Self-propelled micro-swimmers in a Brinkman fluid. J. Biol. Dyn. 2012, 6, 88–103. [Google Scholar] [CrossRef]
- Nganguia, H.; Pak, O. Squirming motion in a Brinkman medium. J. Fluid Mech. 2018, 855, 554–573. [Google Scholar] [CrossRef]
- Smith, D.; Gaffney, E.; Gadêlha, H.; Kapur, N.; Kirkman-Brown, J. Bend propagation in the flagella of migrating human sperm, and its modulation by viscosity. Cell Motil. Cytoskel. 2009, 66, 220–236. [Google Scholar] [CrossRef]
- Olson, S.; Fauci, L. Hydrodynamic interactions of sheets vs filaments: Synchronization, attraction, and alignment. Phys. Fluids 2015, 27, 121901. [Google Scholar] [CrossRef]
- Fauci, L.; McDonald, A. Sperm motility in the presence of boundaries. Bull. Math. Biol. 1995, 57, 679–699. [Google Scholar] [CrossRef]
- Peskin, C. The immersed boundary method. Acta Numer. 2002, 11, 459–517. [Google Scholar] [CrossRef]
- Cortez, R. The method of regularized Stokeslets. SIAM J. Sci. Comput. 2001, 23, 1204–1225. [Google Scholar] [CrossRef]
- Leiderman, K.; Olson, S. Erratum: “Swimming in a two-dimensional Brinkman fluid: Computational modeling and regularized solutions”. Phys. Fluids 2017, 29, 029901. [Google Scholar] [CrossRef]
- Woolley, D.; Crockett, R.; Groom, W.; Revell, S. A study of synchronisation between the flagella of bull spermatozoa, with related observations. J. Exp. Biol. 2009, 212, 2215–2223. [Google Scholar] [CrossRef] [PubMed]
- Ishimoto, K.; Gaffney, E. A study of spermatozoan swimming stability near a surface. J. Theor. Biol. 2014, 360, 187–199. [Google Scholar] [CrossRef] [PubMed]
- Suarez, S. Sperm transport and motility in the mouse oviduct: Observations in situ. Biol. Reprod. 1987, 36, 203–210. [Google Scholar] [CrossRef]
- Rothschild. Non-random distribution of bull spermatozoa in a drop of sperm suspension. Nature 1963, 198, 1221. [Google Scholar] [CrossRef]
- Gillies, E.; Cannon, R.; Green, R.; Pacey, A. Hydrodynamic propulsion of human sperm. J. Fluid Mech. 2009, 625, 445–474. [Google Scholar] [CrossRef]
- Ishimoto, K.; Gaffney, E. Mechanical tuning of mammalian sperm behaviour by hyperactivation, rheology and substrate adhesion: A numerical exploration. J. Royal. Soc. Int. 2016, 13, 20160633. [Google Scholar] [CrossRef]
- Simons, J.; Olson, S.; Cortez, R.; Fauci, L. The dynamics of sperm detachment from epithelium in a coupled fluid-biochemical model of hyperactivated motility. J. Theor. Biol. 2014, 354, 81–94. [Google Scholar] [CrossRef]
- Ainley, J.; Durkin, S.; Embid, R.; Boindala, P.; Cortez, R. The method of images for regularized Stokeslets. J. Comp. Phys. 2008, 227, 4600–4616. [Google Scholar] [CrossRef]
- Nguyen, H.; Olson, S.; Leiderman, K. Computation of a regularized Brinkmanlet near a plane wall. J. Eng. Math. 2019, 114, 19–41. [Google Scholar] [CrossRef]
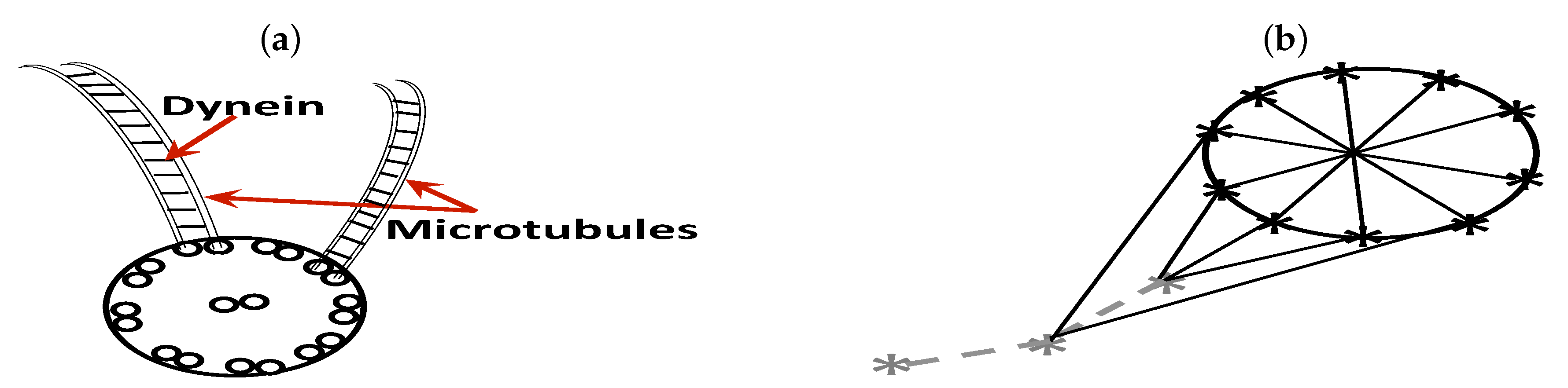


| , characteristic time scale, | 0.05 s (beat frequency 20 Hz) |
| , characteristic length scale | 50 m |
| , characteristic velocity scale | (wavespeed) |
| , viscosity | 0.001 kg m s |
| , characteristic force scale | |
| L, tail length | 1 |
| , head radius | 0.1 |
| , wavenumber | |
| , amplitude | varied [0.1,0.3] |
| , frequency | |
| , curvature stiffness of tail | 8 |
| , tensile stiffness of tail | 10,000 |
| , tensile stiffness of neck | 500 |
| , tensile stiffness of head | 10,000 |
| , curvature stiffness of head | 0.8 |
| , stiffness for tail-head connecting angle | 10,000 |
| Parameters | ||||
|---|---|---|---|---|
| S1, , | 4.1427 | 4.0591 | 3.3784 | 2.6849 |
| S2, , | 2.6702 | 2.5901 | 2.1684 | 1.4504 |
| S1, , | 29.8417 | 10.0230 | 12.0022 | 21.1165 |
| S2, , | 2.7297 | 3.1615 | 6.3438 | 15.9360 |
| S1, , (F) | 8.5972 | 8.3903 | 6.1374 | 3.4372 |
| S2, , (F) | 0.7264 | 0.7264 | 0.4022 | 1.0445 |
| S1, , (F) | 5.3680 | 5.3680 | 6.1029 | 3.6030 |
| S2, , (F) | 1.5309 | 1.2868 | 0.7523 | 0.3240 |
| Parameters | ||||
|---|---|---|---|---|
| W, S1 | 9.9491 | 11.4553 | 10.5367 | 7.9992 |
| W, S2 | 3.2190 | 4.1000 | 1.9124 | 1.9891 |
| S1 | 4.4893 | 4.3786 | 3.5096 | 2.5974 |
| S2 | 2.3740 | 2.3133 | 2.0395 | 1.5294 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeznach, C.; Olson, S.D. Dynamics of Swimmers in Fluids with Resistance. Fluids 2020, 5, 14. https://doi.org/10.3390/fluids5010014
Jeznach C, Olson SD. Dynamics of Swimmers in Fluids with Resistance. Fluids. 2020; 5(1):14. https://doi.org/10.3390/fluids5010014
Chicago/Turabian StyleJeznach, Cole, and Sarah D. Olson. 2020. "Dynamics of Swimmers in Fluids with Resistance" Fluids 5, no. 1: 14. https://doi.org/10.3390/fluids5010014
APA StyleJeznach, C., & Olson, S. D. (2020). Dynamics of Swimmers in Fluids with Resistance. Fluids, 5(1), 14. https://doi.org/10.3390/fluids5010014






