Naut Your Everyday Jellyfish Model: Exploring How Tentacles and Oral Arms Impact Locomotion
Abstract
1. Introduction
2. Mathematical Methods
2.1. Computational Parameters
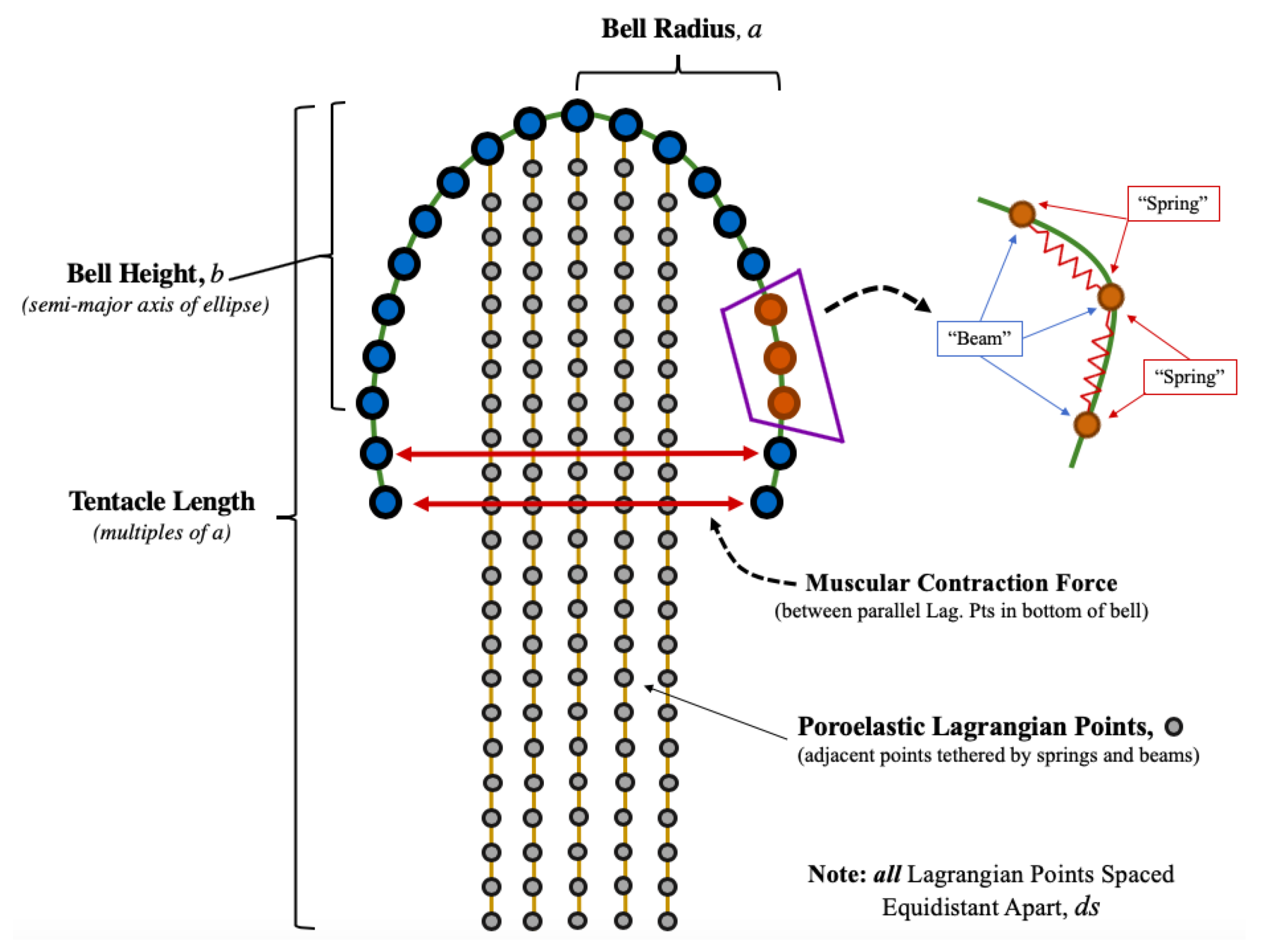
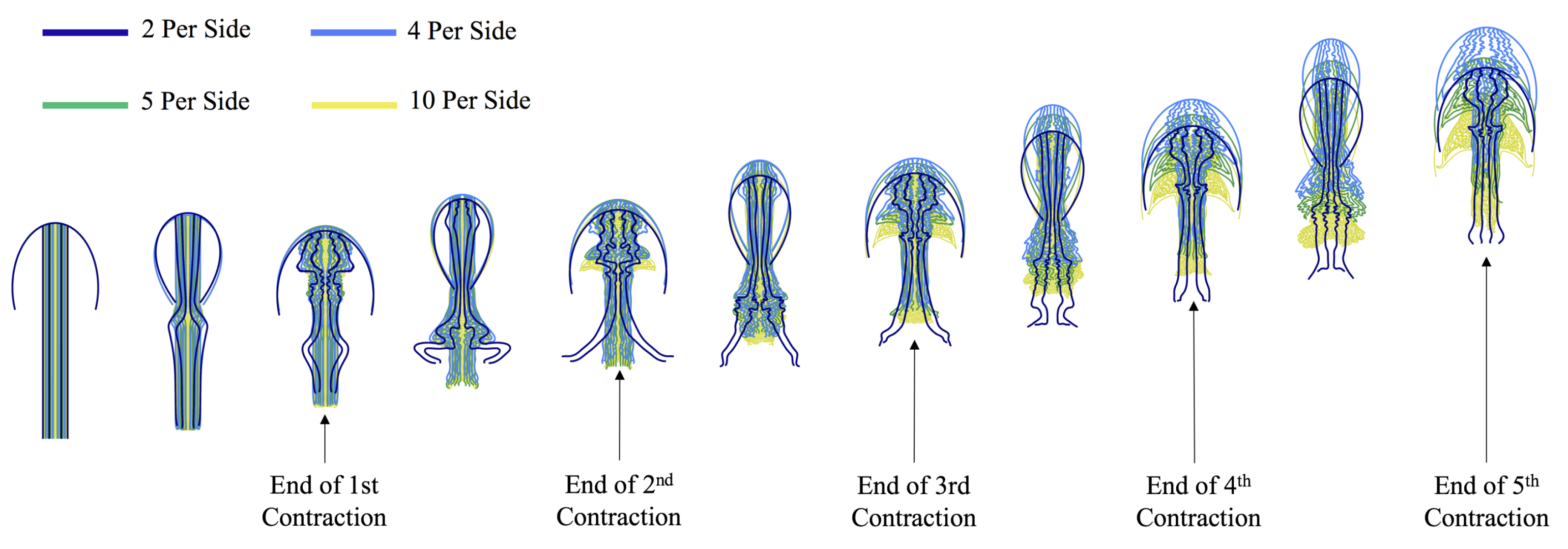
2.2. Jellyfish Computational Model
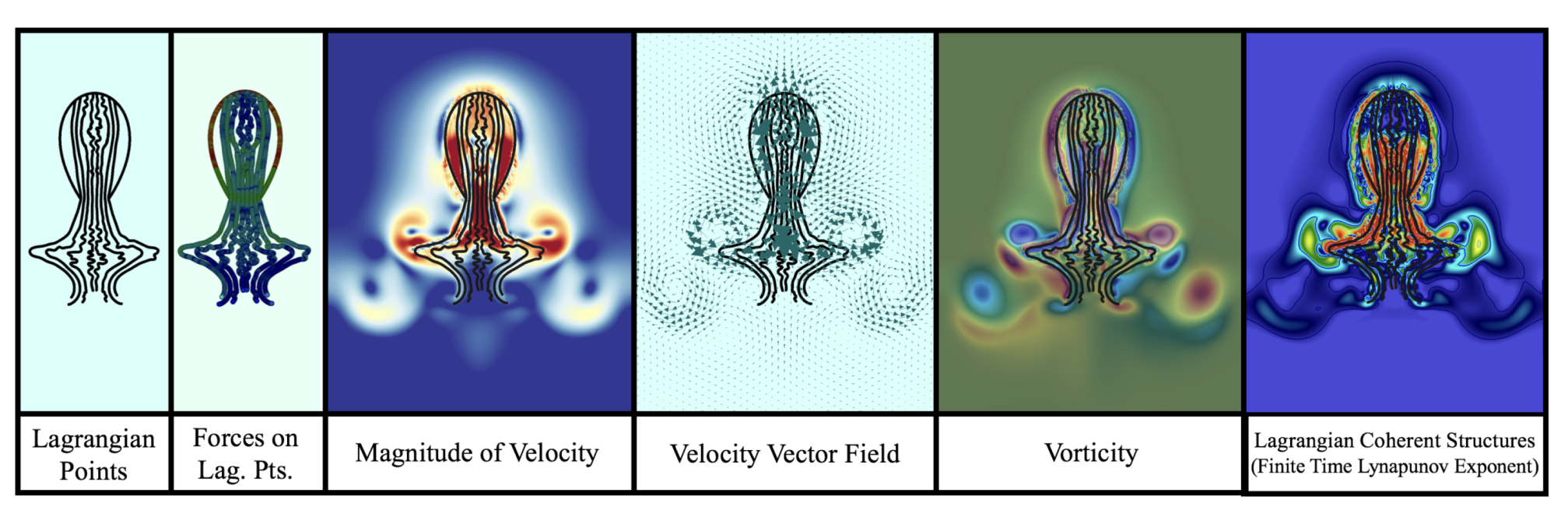
- Position of Lagrangian points.
- Forces on each lagrangian point (horizontal/vertical and normal/tangential forces).
- Fluid velocity.
- Fluid vorticity.
- Forces spread from the Lagrangian mesh onto the Eulerian grid (jellyfish forces onto fluid).
3. Results
- Is it only the outer placed tentacles that affect its swimming?
- How does tentacle density affect its swimming?
- If the placement of interior tentacles is varied, will it affect its swimming?
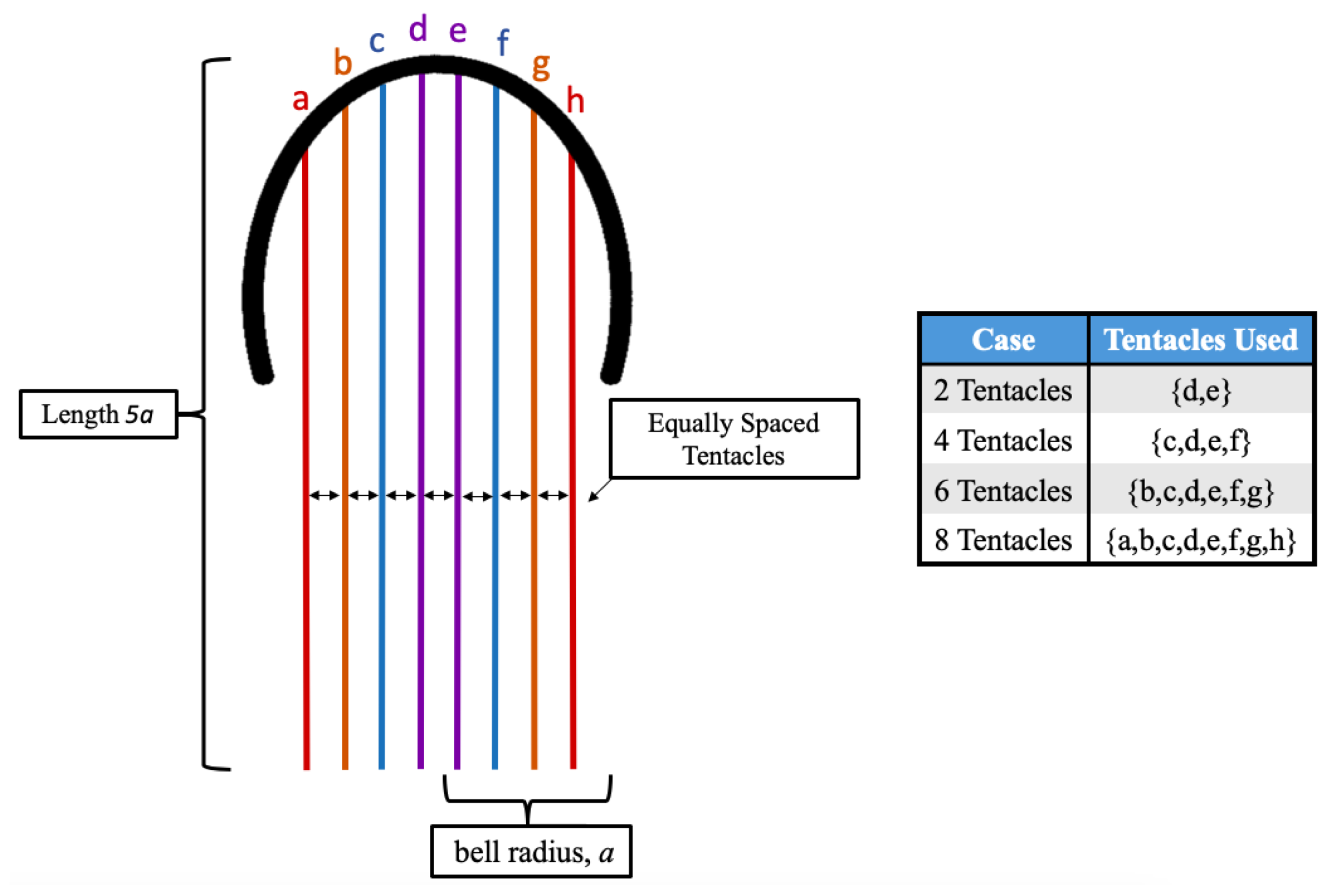
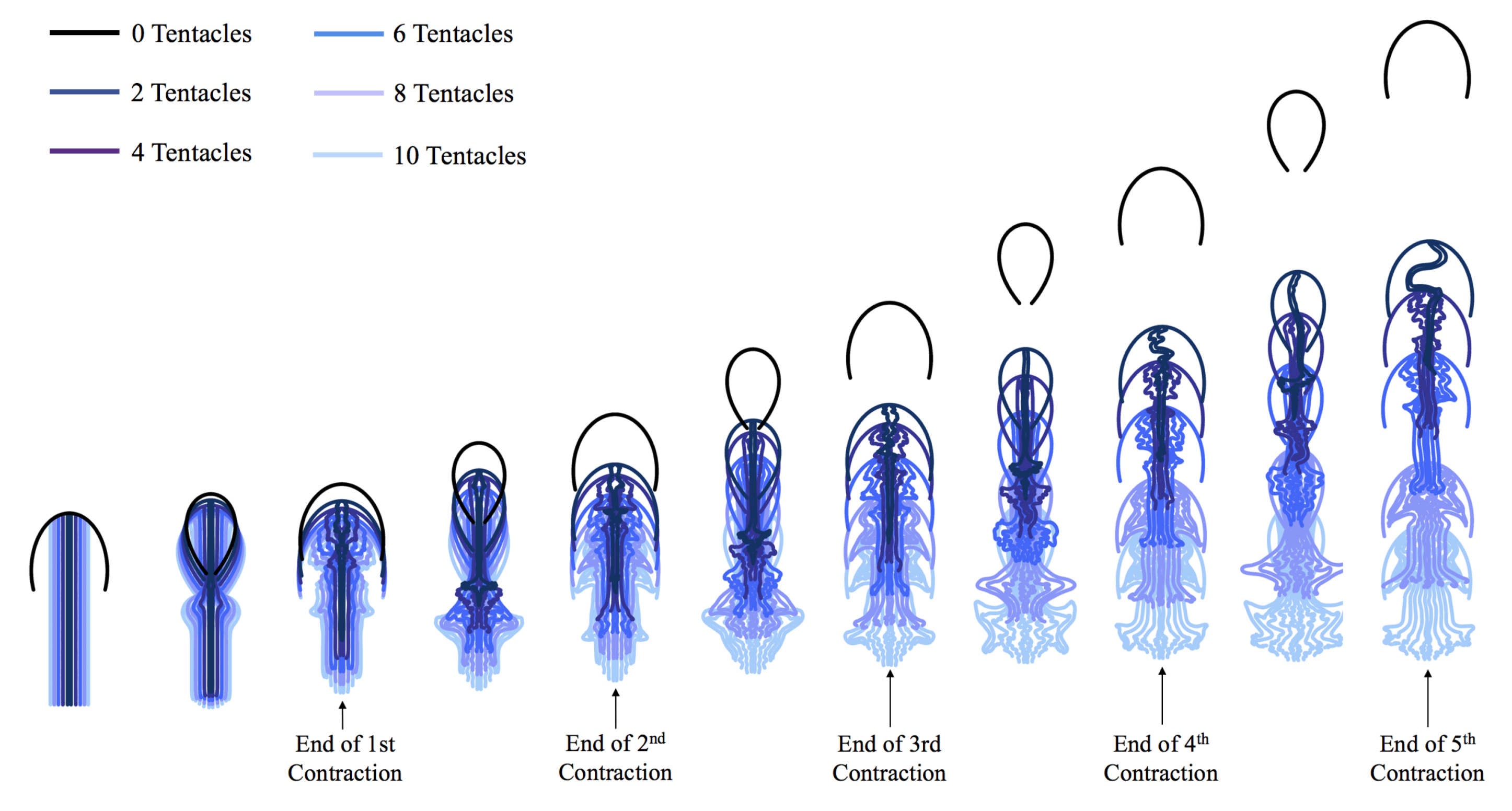
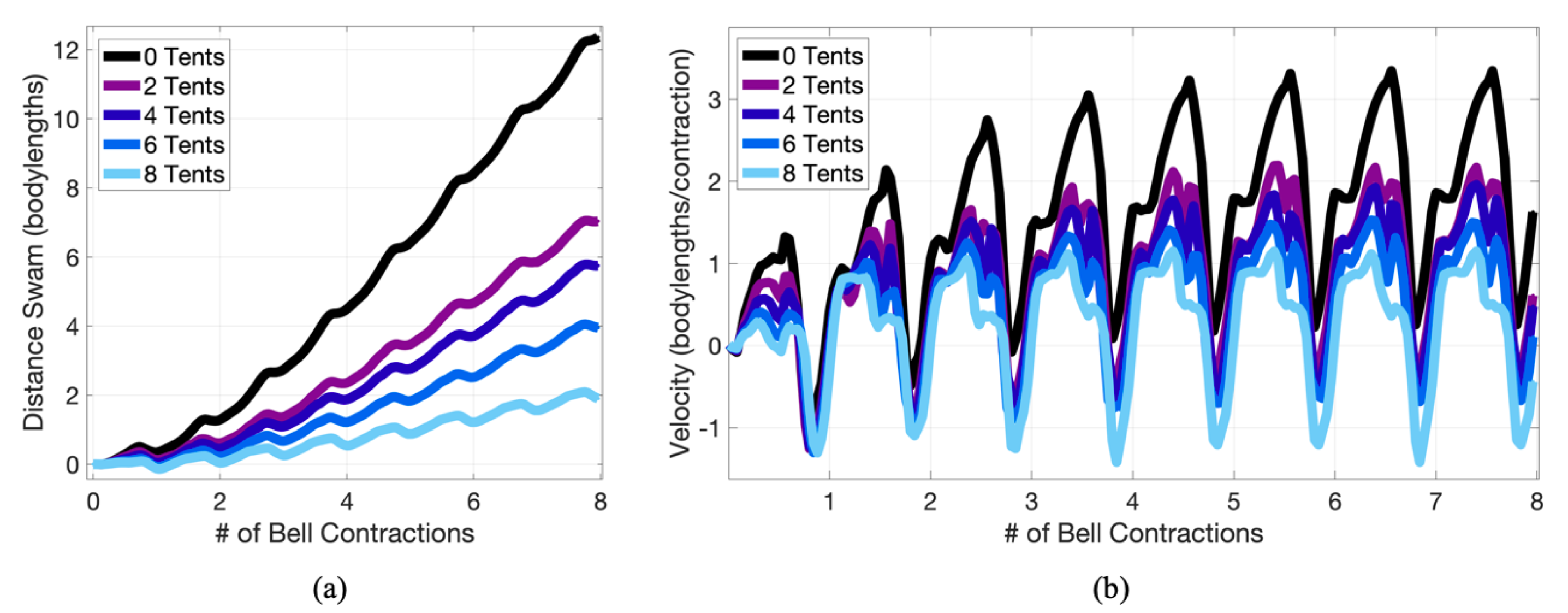
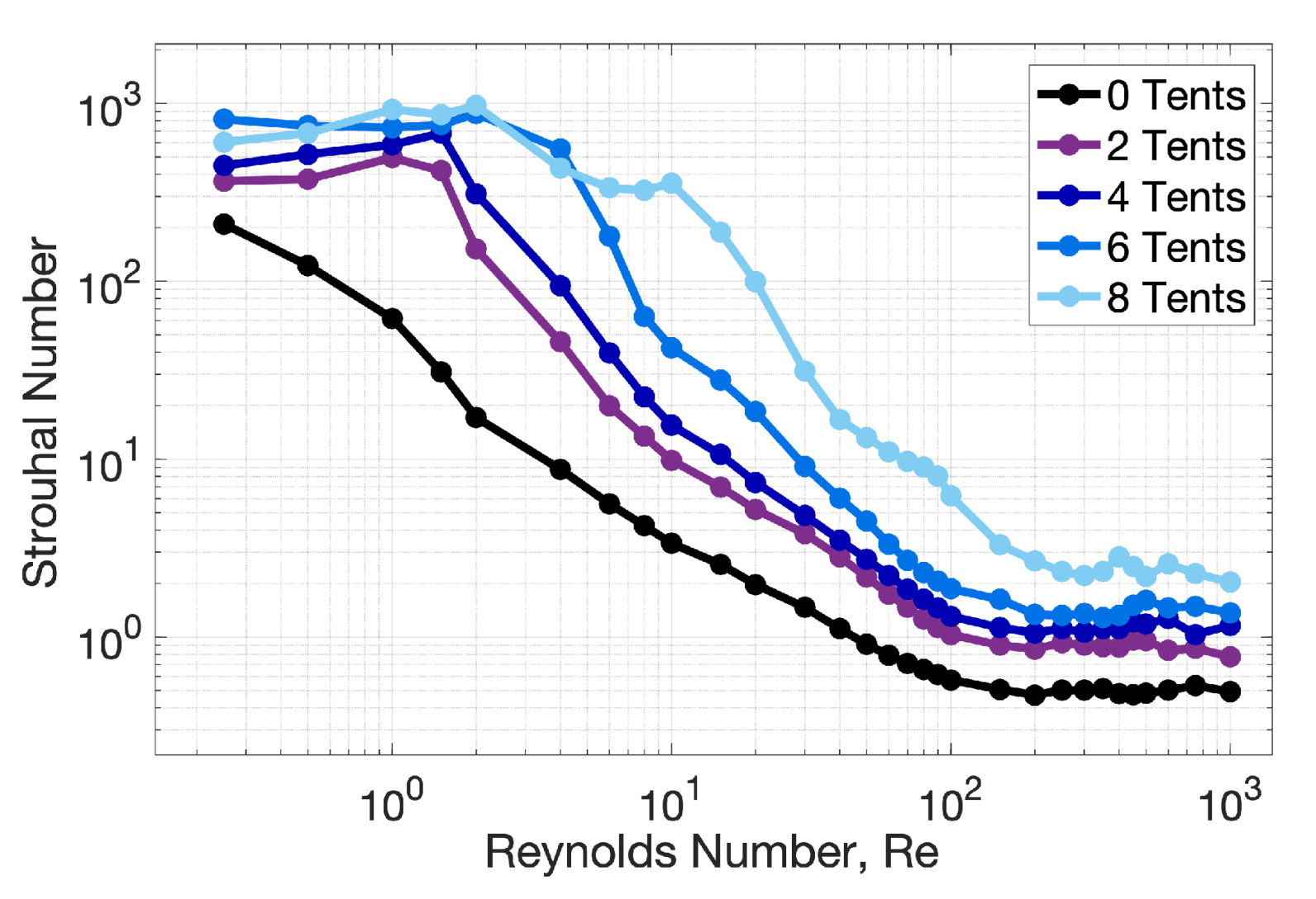
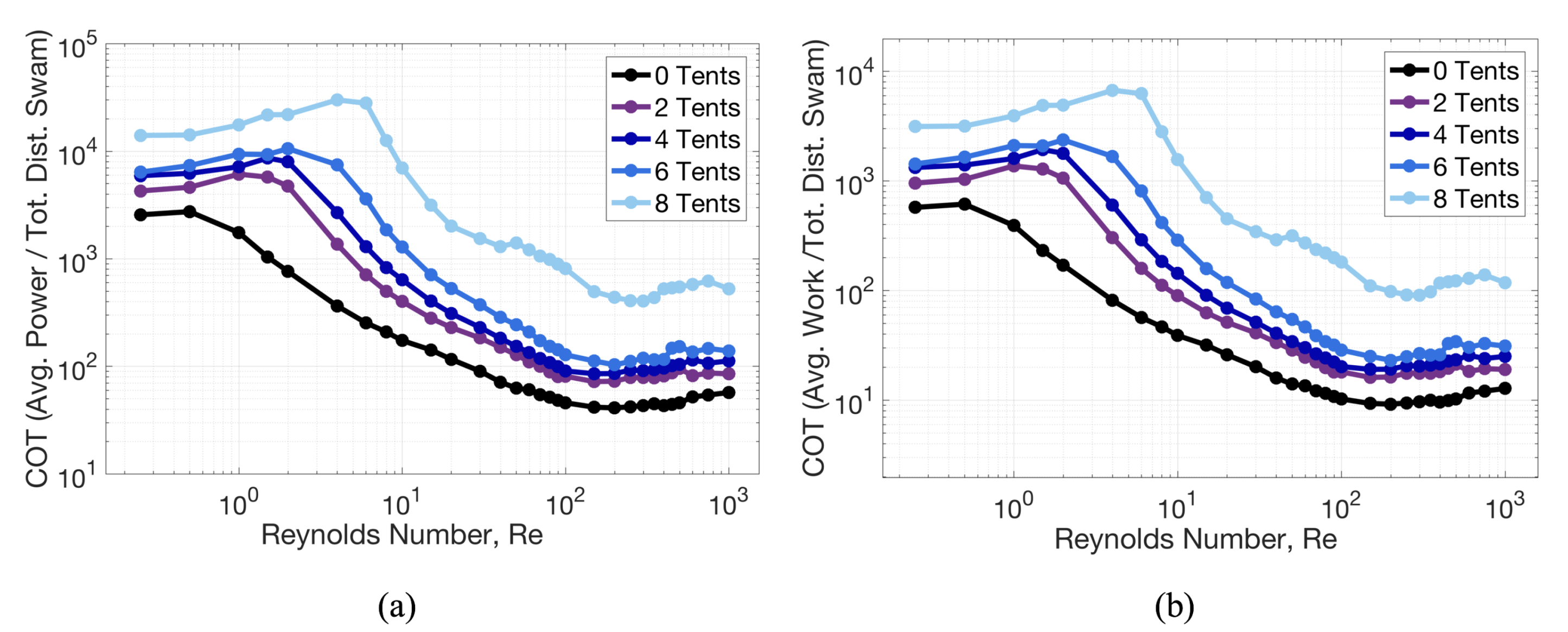
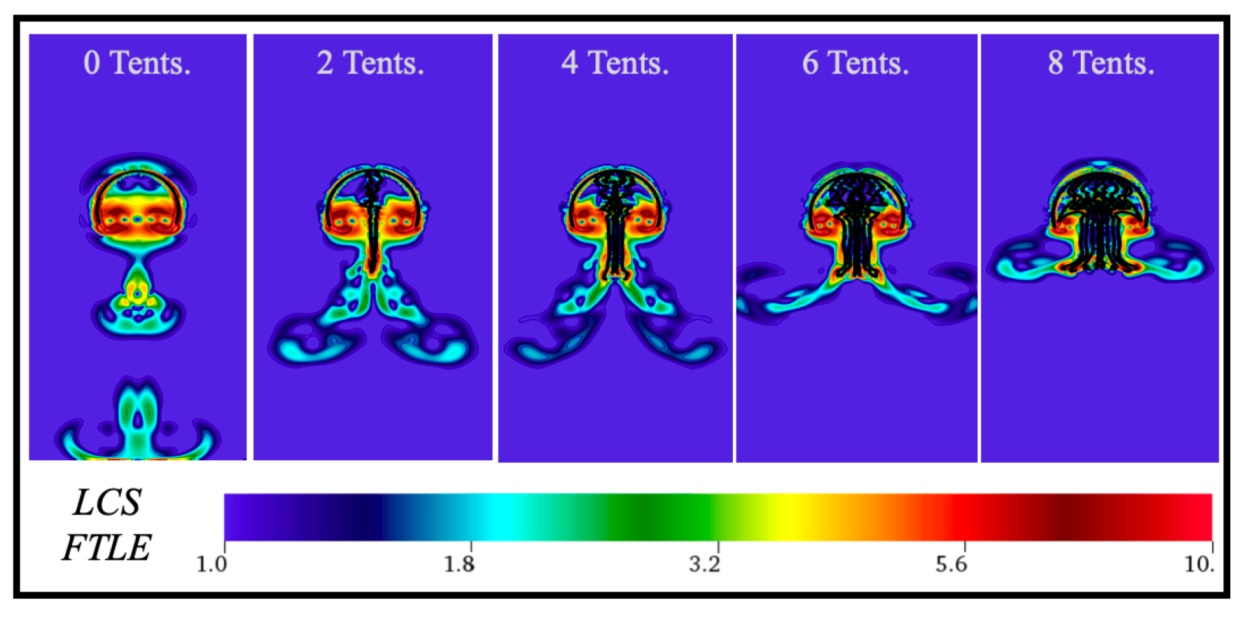
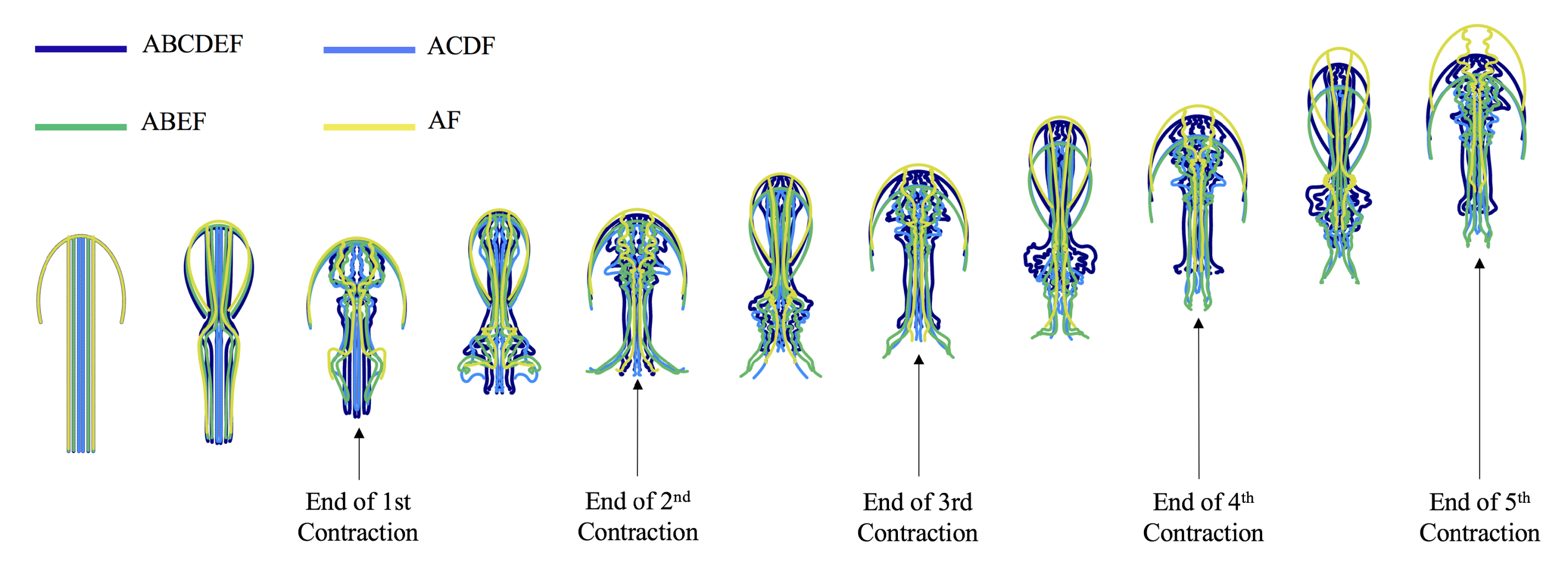
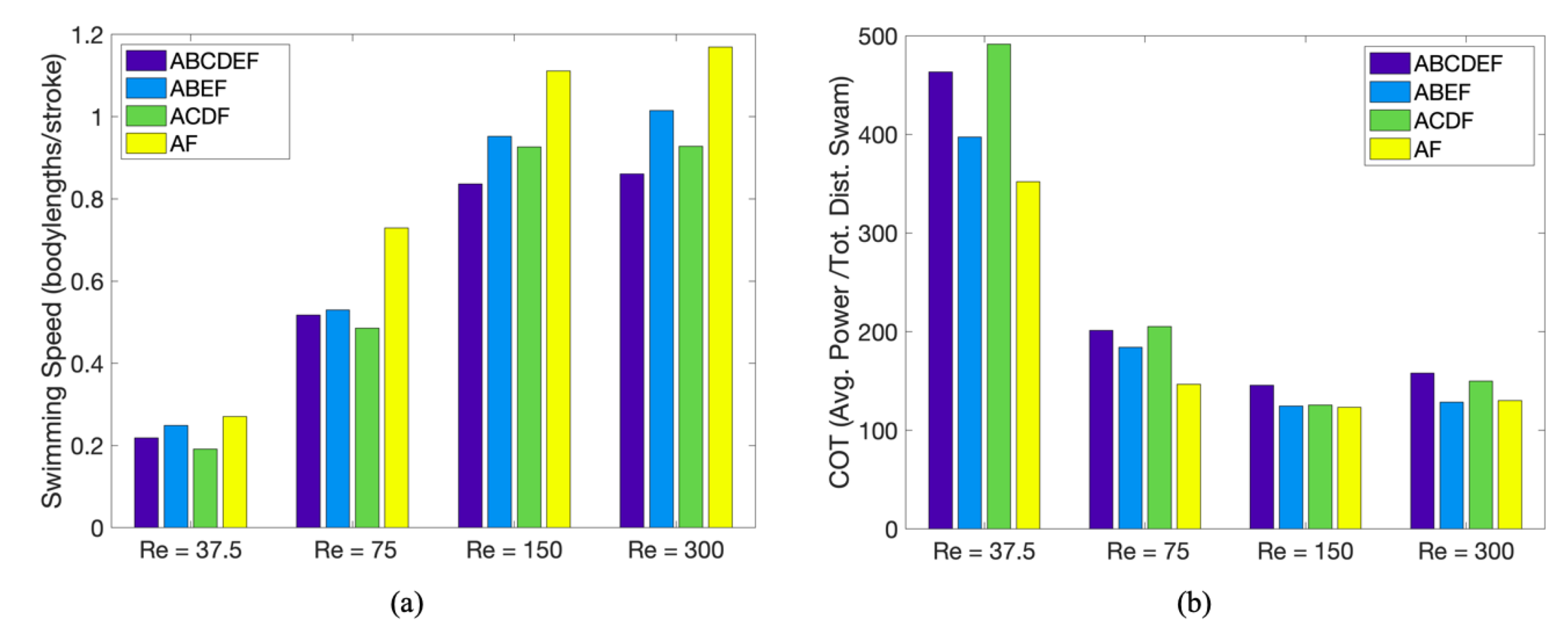
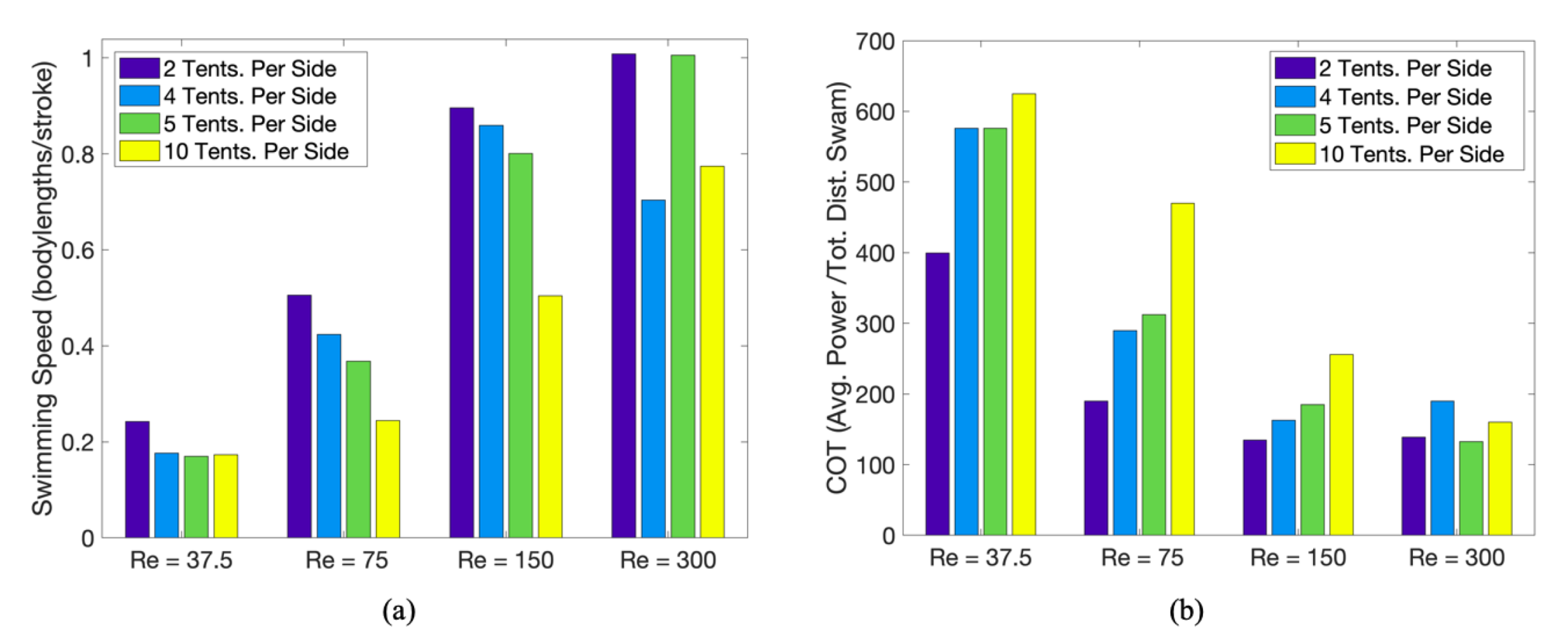
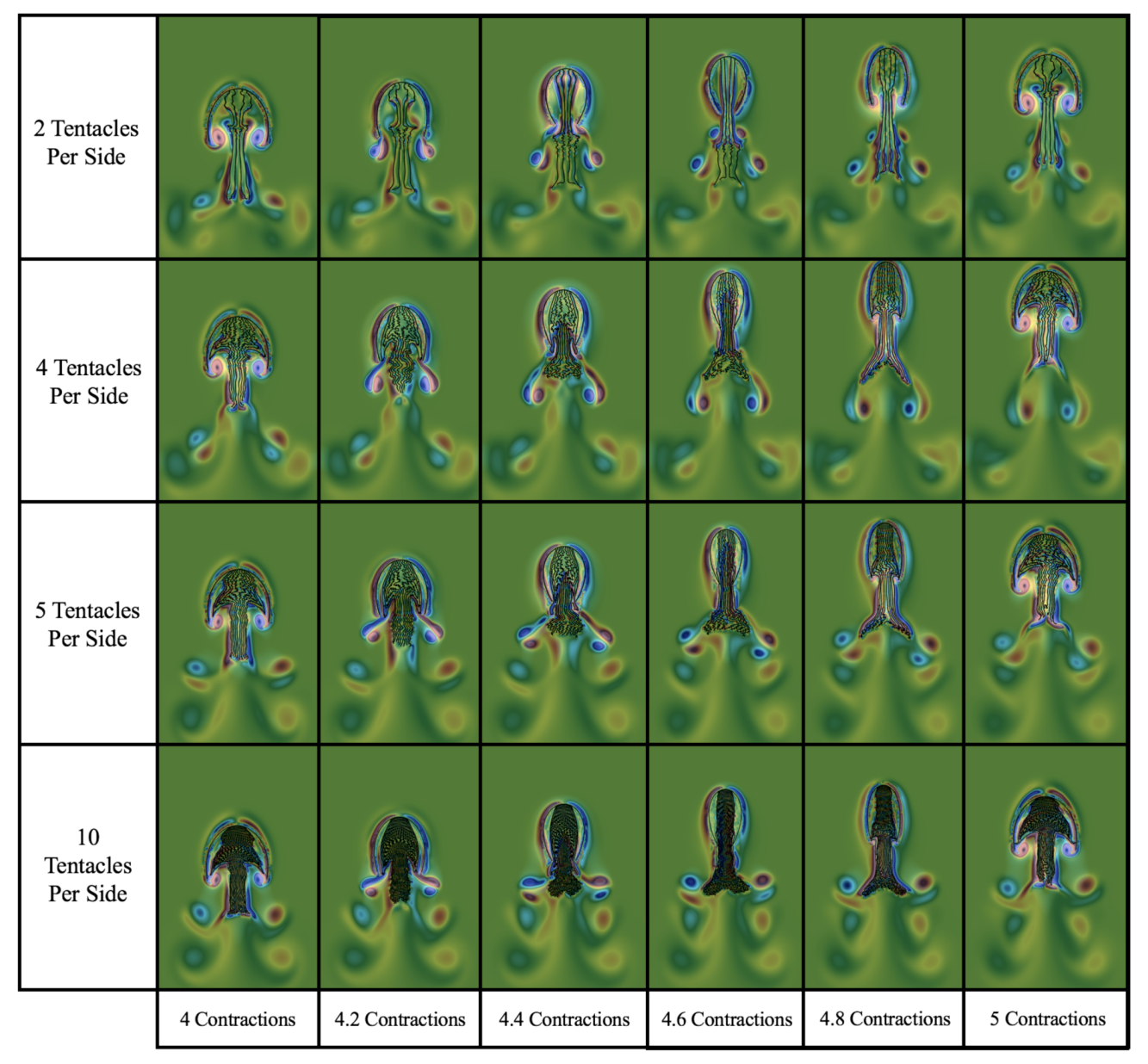
3.1. Results: Varying and Number of Tentacles/Oral Arms
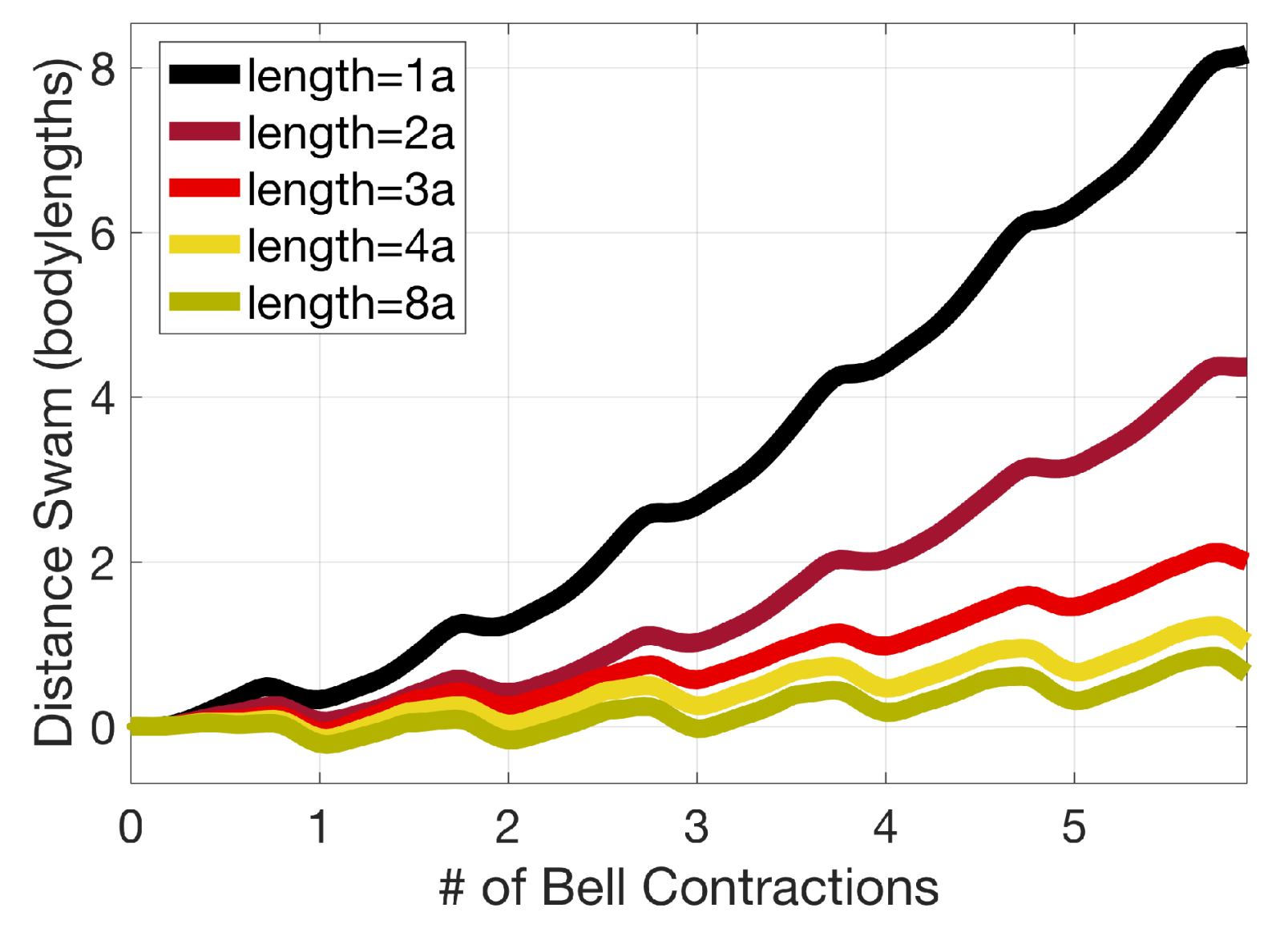
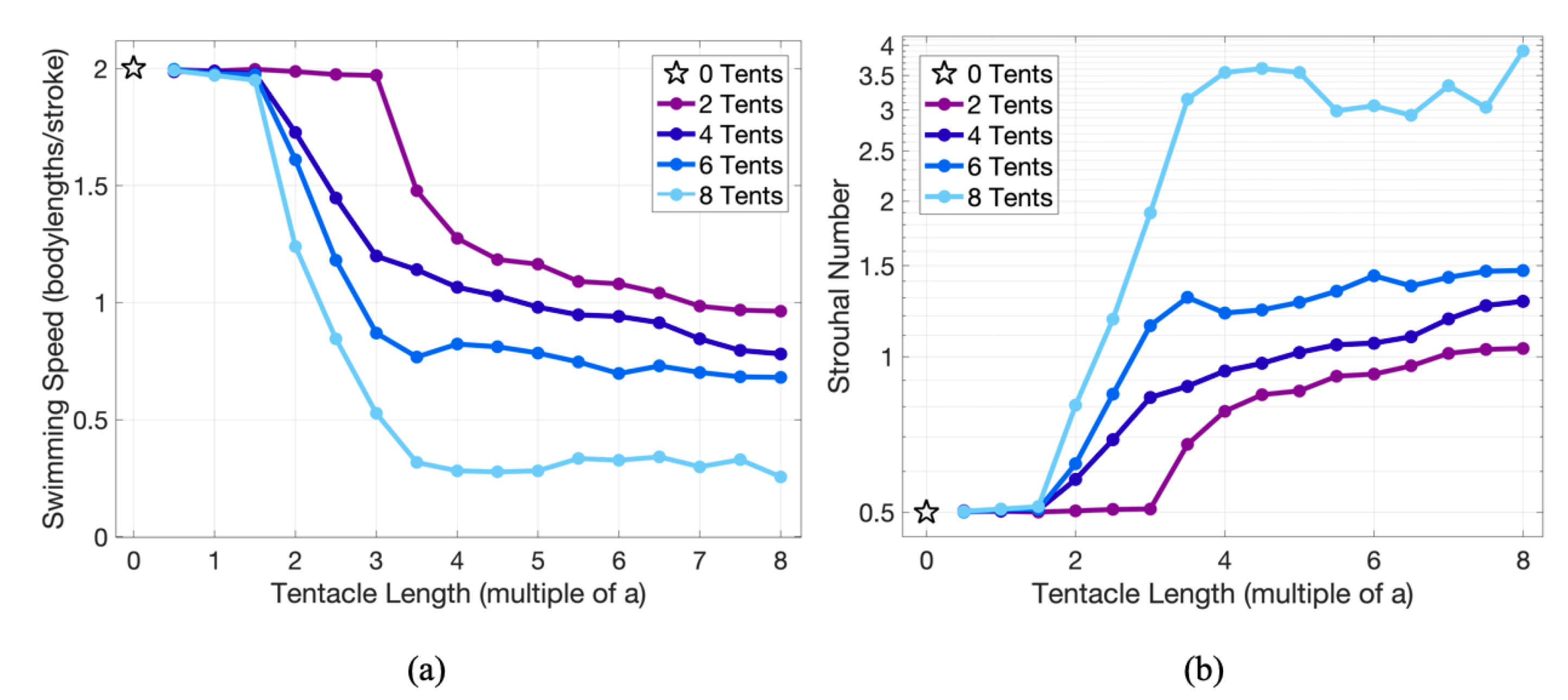
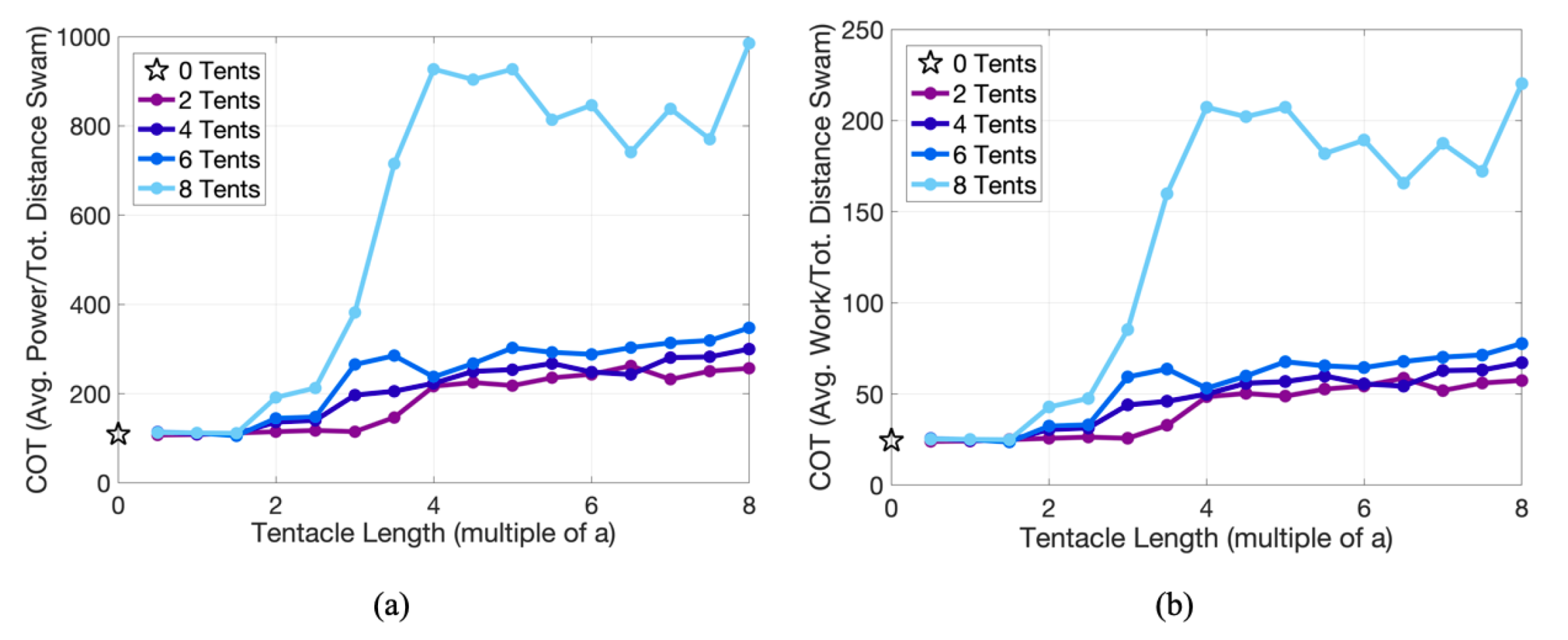
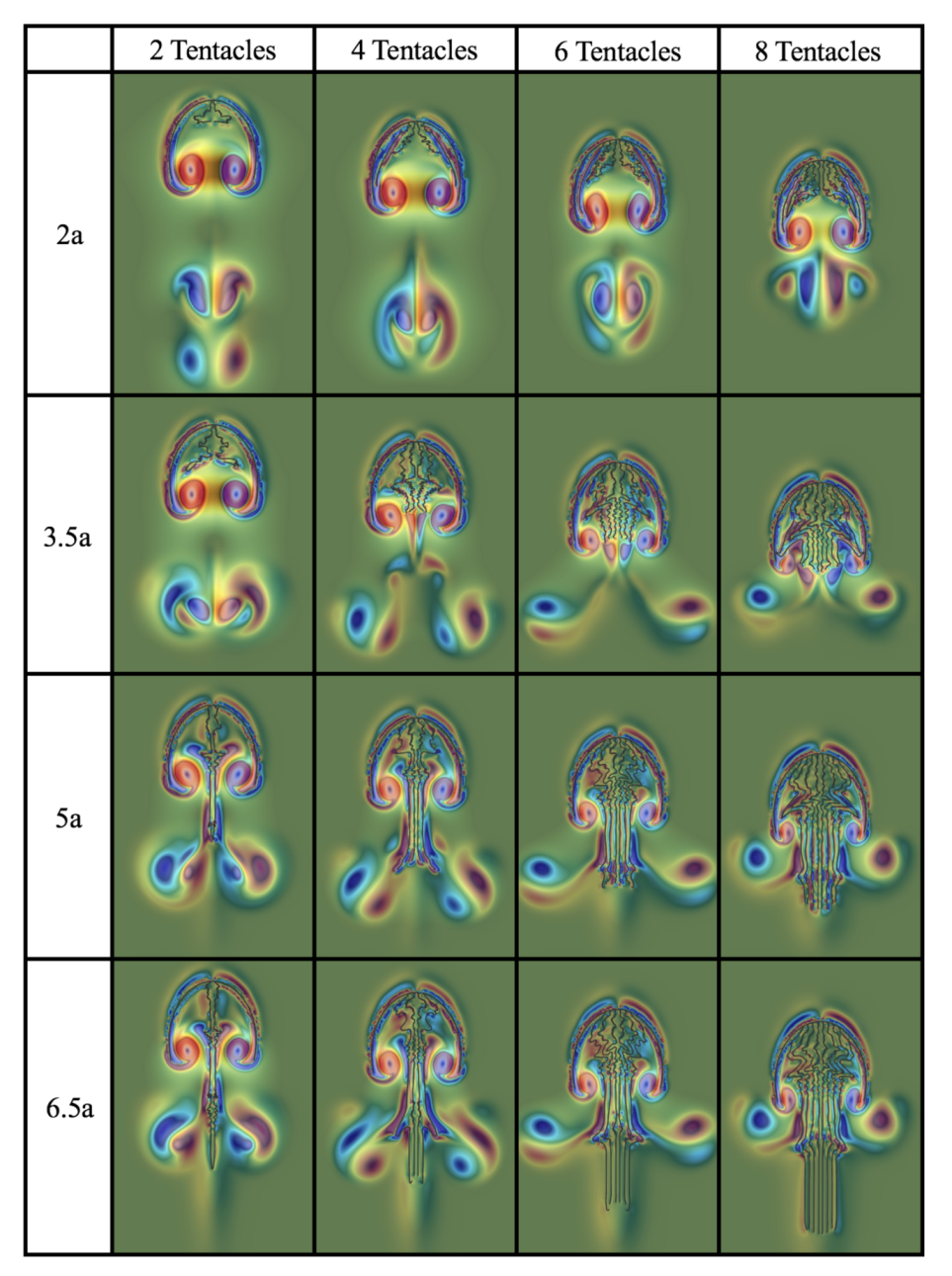
3.2. Results: Varying the Length of Tentacles/Oral Arms
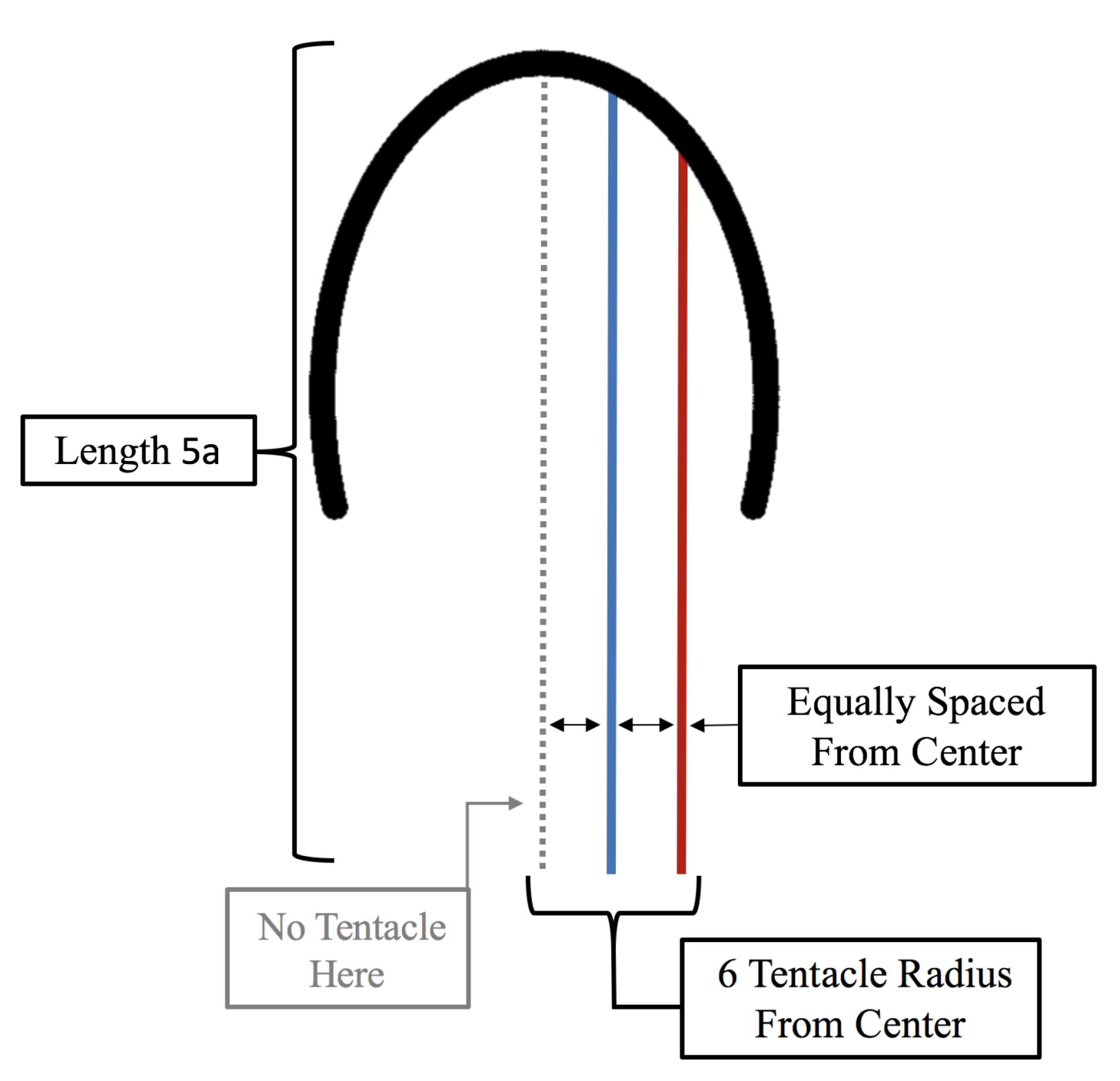
3.3. Results: Tentacle/Oral Arm Placement and Density
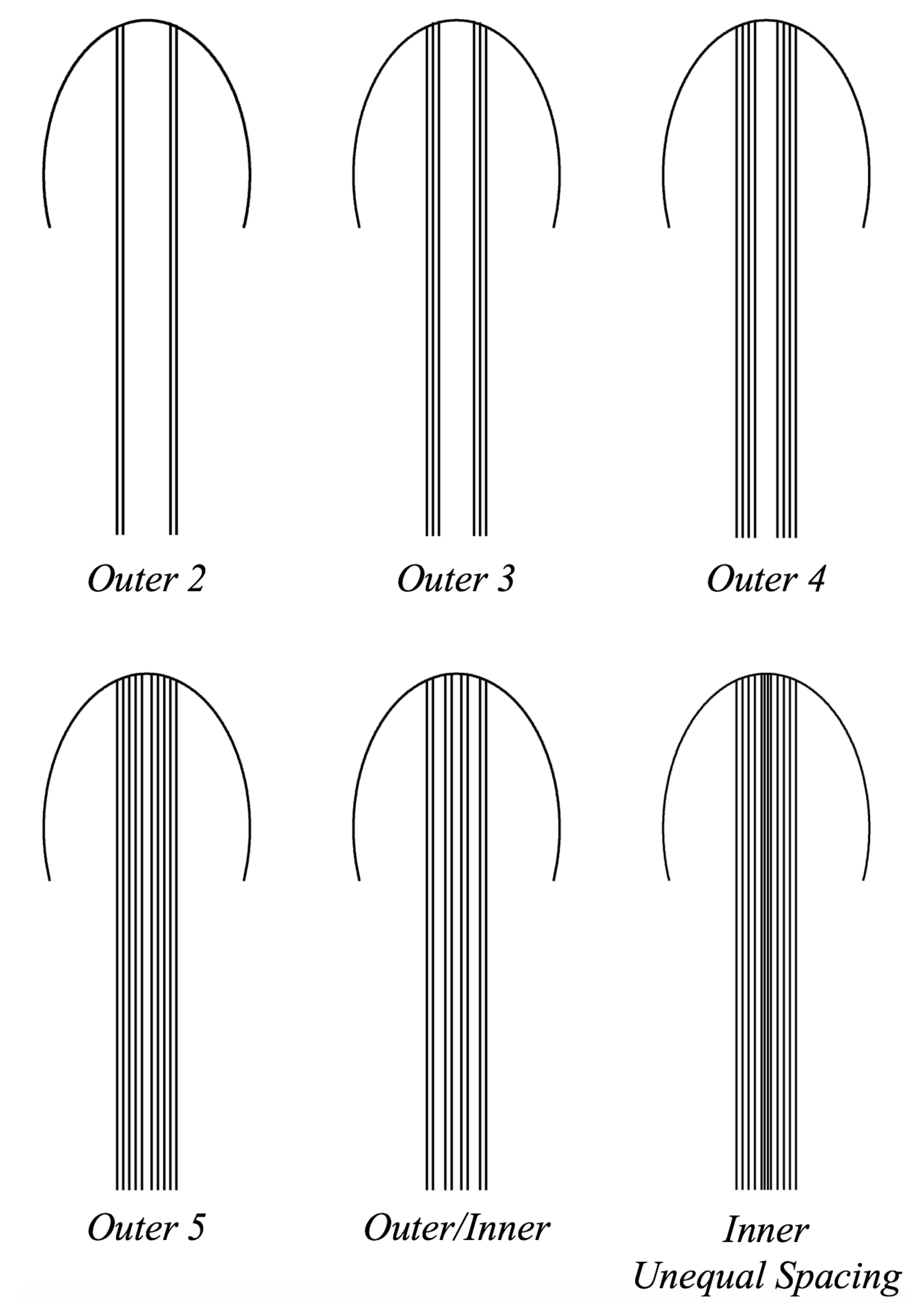
- Is the placement of the outermost tentacles/oral arms what affects swimming performance? We will hold the location of the outermost tentacles/oral arms constant and change the location of the inner tentacles/oral arms, see Figure 19.
- How does density of tentacles affect swimming performance? We will again hold the location of the outermost tentacles/oral arms constant, and vary the amount of other tentacles inside that region; however, in contrast to the question above, the spacing between tentacles/oral arms will change as more or less tentacles/oral arms are considered within that region, see Figure 23.
- How does stacking tentacle/oral arms towards the outermost ones affect swimming performance? We will hold the location of the outermost tentacles constant and place more tentacles towards the outermost tentacles/oral arms and observe how swimming performance is affected. In addition, we will explore if there are clusters of tentacles/oral arms and how they may affect forward swimming performance, see Figure 27.
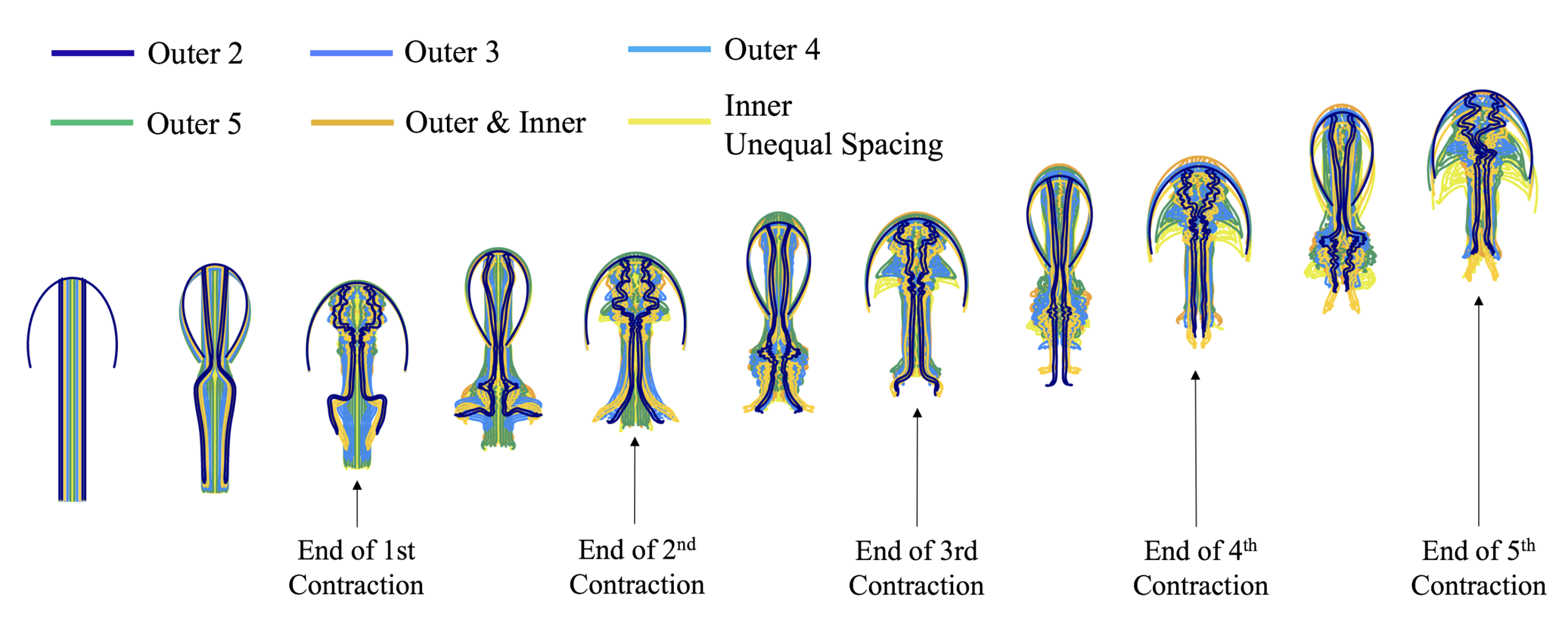
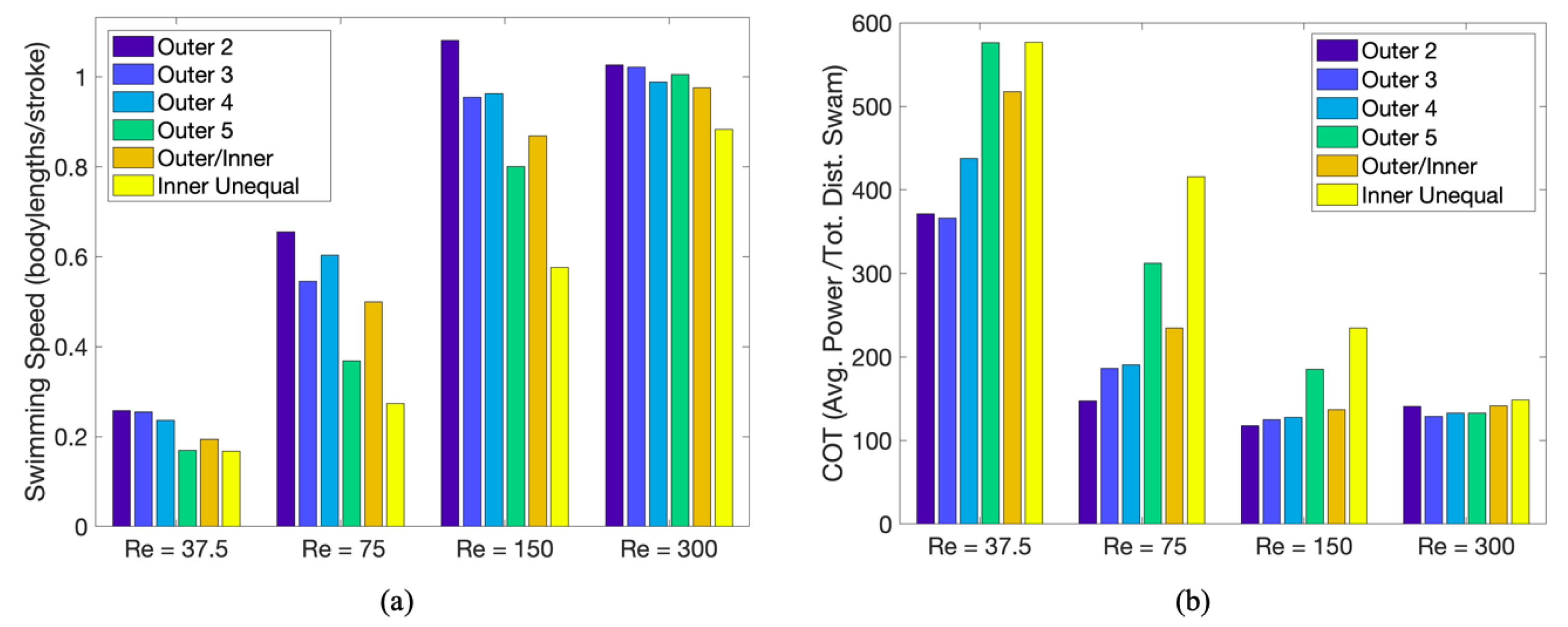
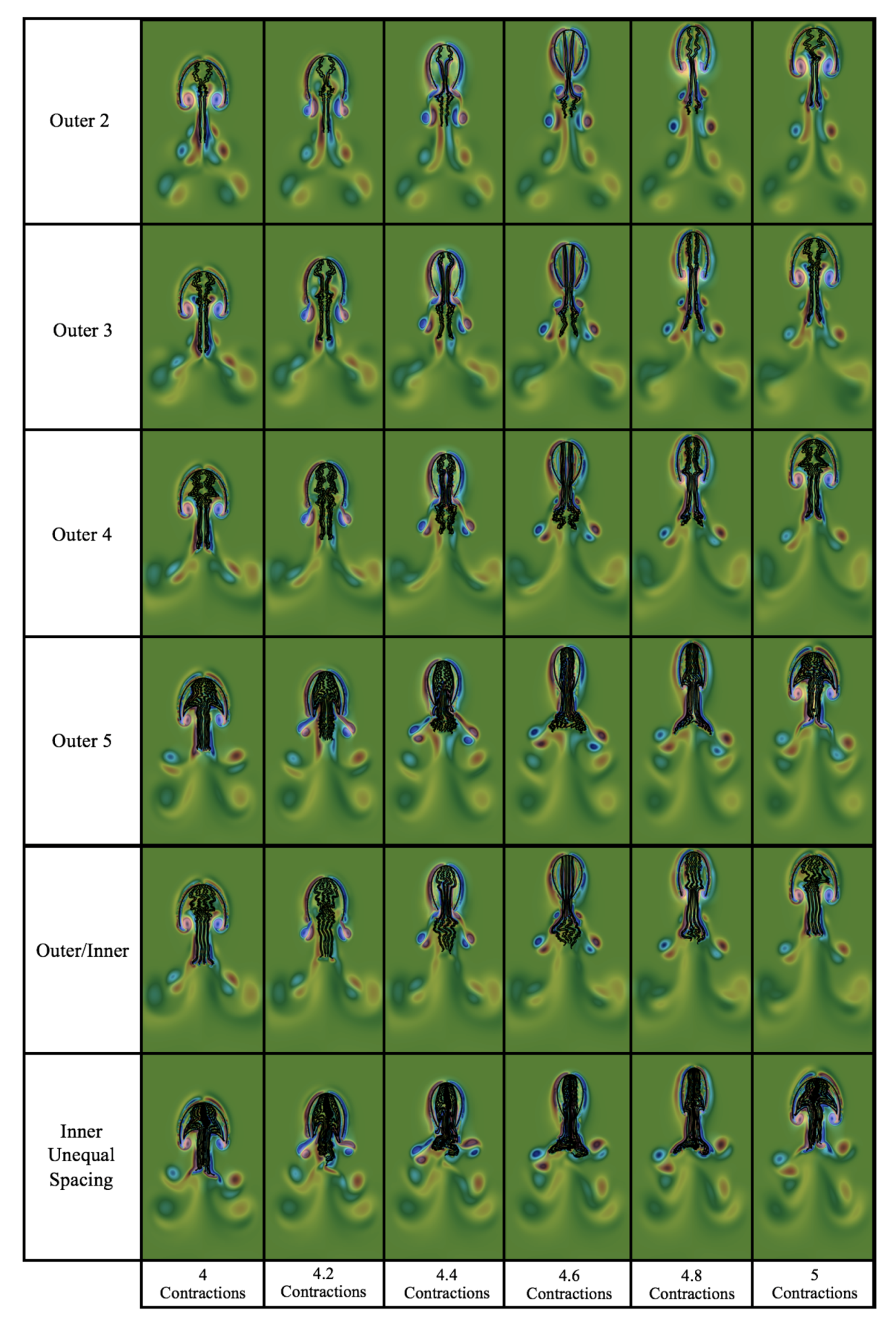
3.3.1. Is the Placement of the Outermost Tentacles/Oral Arms What Affects Swimming Performance?
3.3.2. How Does the Density of Tentacles Affect Swimming Performance?
3.3.3. How Does Stacking Tentacle/Oral Arms towards the Outermost Ones Affect Swimming Performance?
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Reynolds Number | |
| Immersed Boundary Method | |
| Cost of Transport |
Appendix A. Details on IB
Appendix A.1. Governing Equations of IB
Appendix A.2. Numerical Algorithm
Appendix A.3. Running the Simulation in MATLAB & Visualizing in VisIt
- Either clone the IB2d repository or download the IB2d zip file at https://github.com/nickabattista/ib2d to your local machine. Note you can download or clone this repository to any directory on your local machine.
- Open MATLAB and go to the appropriate sub-directory within the IB2d software for the Tentacle_Jelly example. The path to this example is: IB2d → matIB2d → Examples → Example_Jellyfish_Swimming → Tentacle_Jelly
- To run the example as is (case: , 6 tentacles/oral arms, ), type main2d into the MATLAB command window and click enter.
- Wait… it will produce two folders viz_IB2d and hier_IB2d_data containing the simulation data in the form of formatted files. As the simulation runs, it will print more data into these folders. Note that these simulations will take on the order of days.
- Open VisIt
- Open the desired data (Lagrangian Points, Vorticity, Velocity Vectors, etc.)
- To Visualize the Lagrangian Points:
- (a)
- Click Open
- (b)
- Go to the viz_IB2d data folder that the simulation produced
- (c)
- Click on the grouping of lagsPts, click OK
- (d)
- In VisIt, click on Add then Mesh→mesh.
- (e)
- Then click Draw
- (f)
- You can elect to change the color of boundary or size by double clicking on the Mesh in the VisIt data listing window.
- To Visualize the Eulerian scalar data (e.g., Vorticity, Magnitude of Velocity, etc.):
- (a)
- Click Open
- (b)
- Go to the viz_IB2d data folder that the simulation produced
- (c)
- Click on the grouping of the desired Eulerian scalar data, for example, Omega (for Vorticity), click OK
- (d)
- In VisIt, click on Add then Pseudocolor→Omega.
- (e)
- Then click Draw
- (f)
- You can elect to change the colormap and/or colormap scaling by double clicking on Omega in the VisIt data listing window.
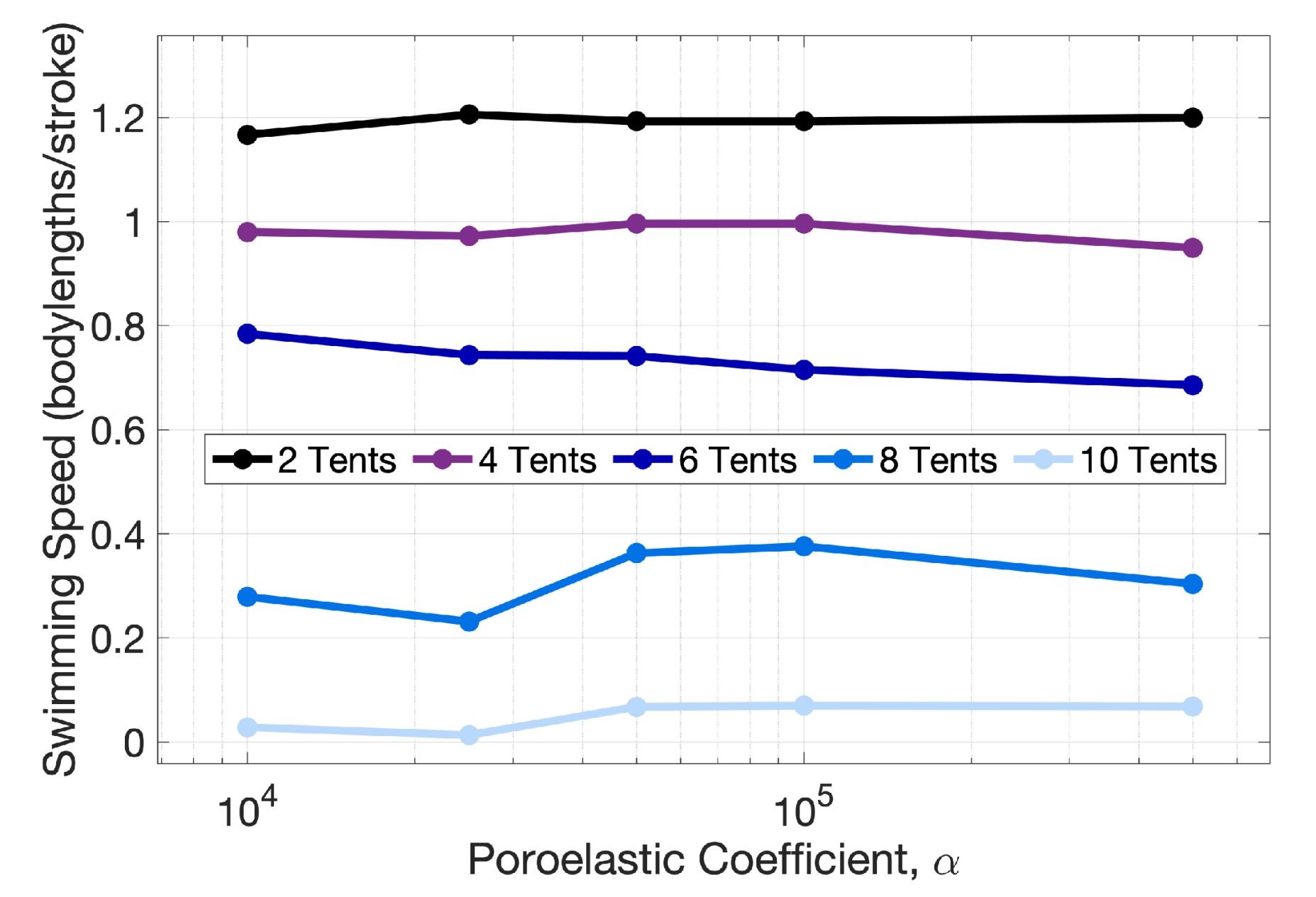
Appendix B. Varying the Poroelastic Coefficient, α
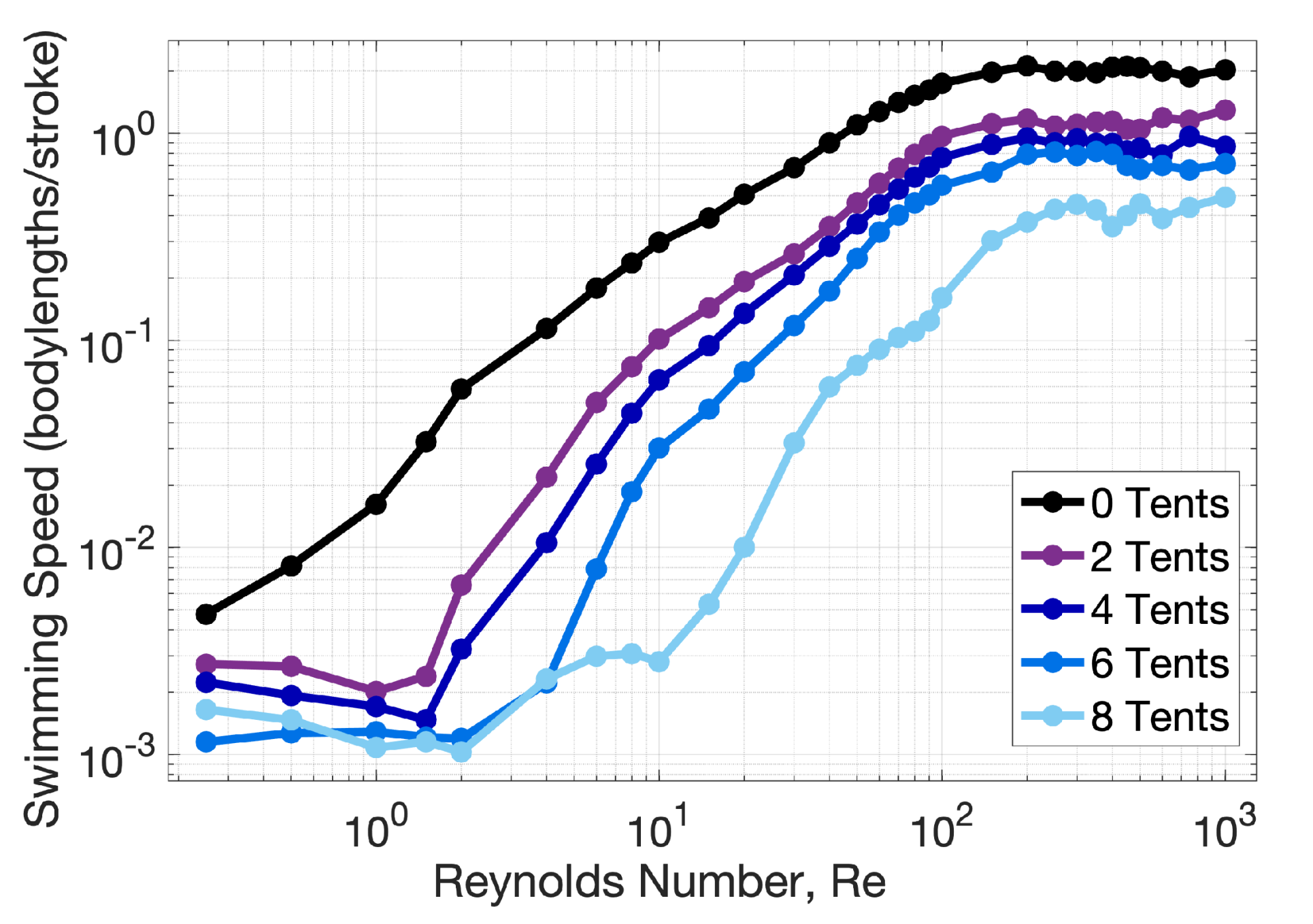
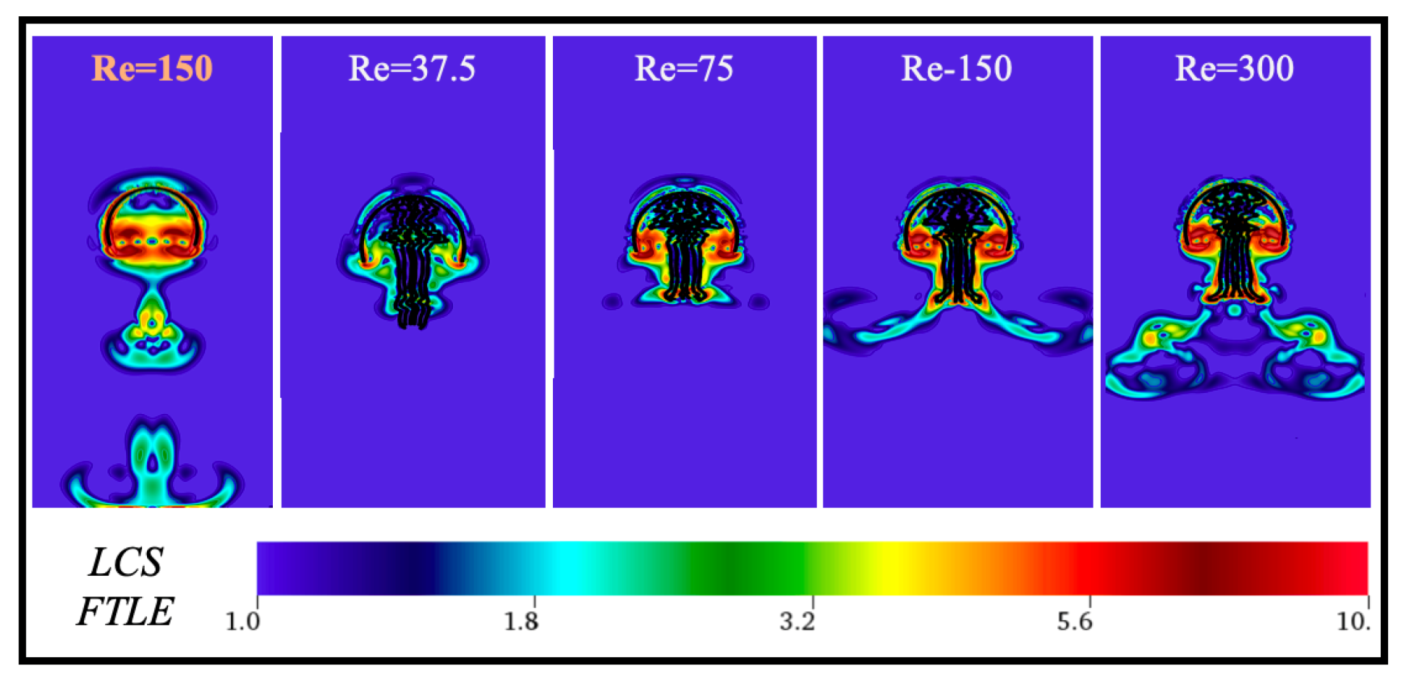
Appendix C. Varying the Reynolds Number, Re
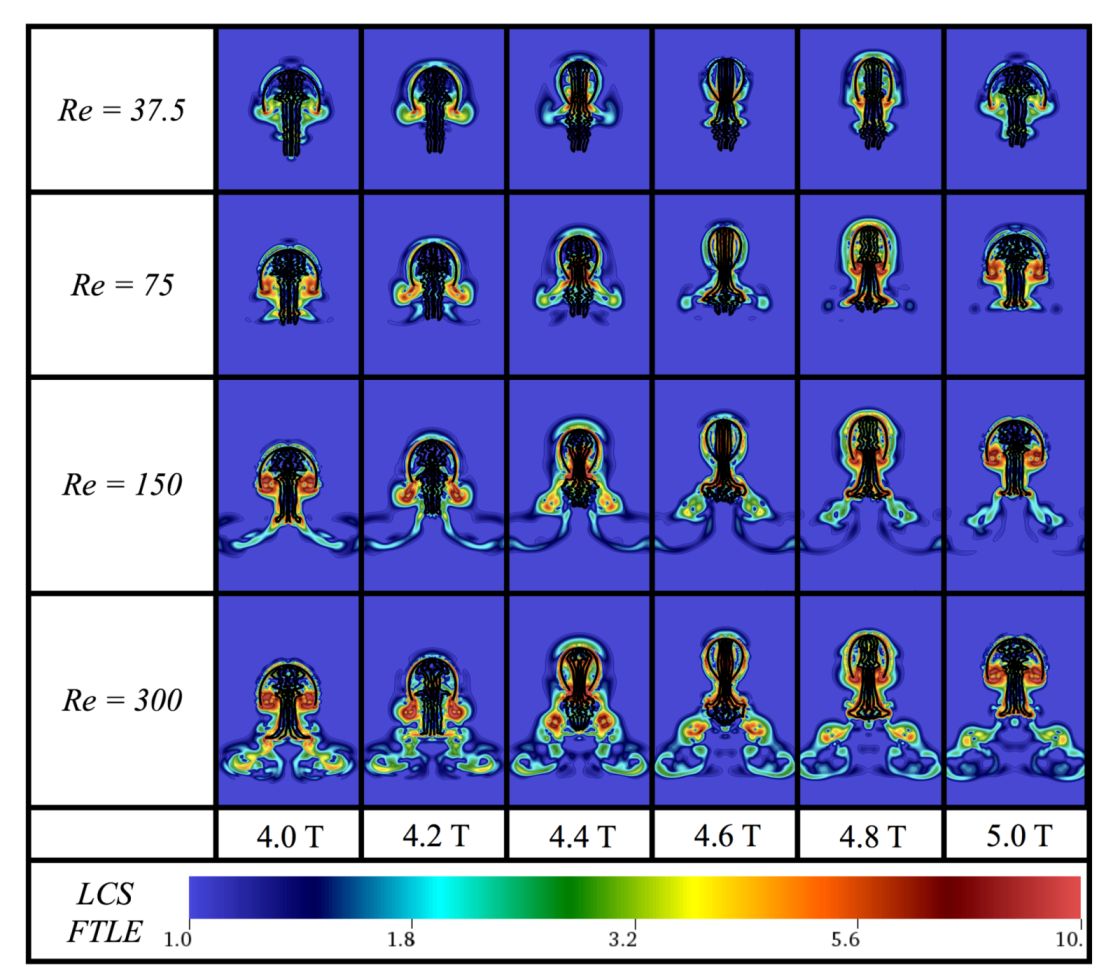
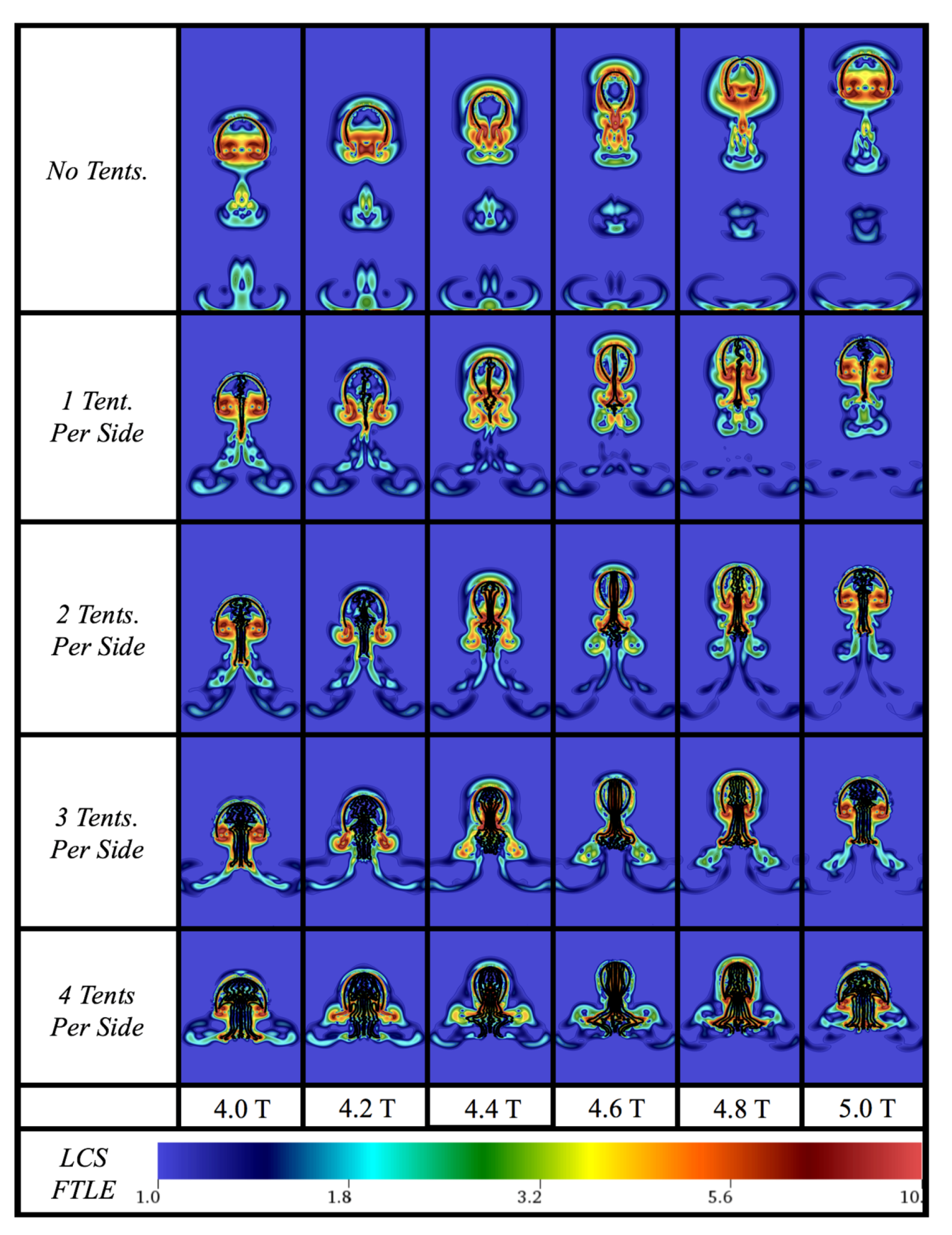
Appendix D. Varying the Tentacle/Oral Arm Length

References
- Higgins, J.E.; Ford, M.D.; Costello, J.H. Transitions in morphology, nematocyst distribution, fluid motions, and prey capture during development of the scyphomedusa Cyanea capillata. Biol. Bull. 2008, 214, 29–41. [Google Scholar] [CrossRef] [PubMed]
- Beckmann, A.; Özbek, S. The nematocyst: A molecular map of the cnidarian stinging organelle. Int. J. Dev. Biol. 2012, 56, 577–582. [Google Scholar] [CrossRef] [PubMed]
- Nüchter, T.; Benoit, M.; Engel, U.; Özbek, S.; Holstein, T.W. Nanosecond-scale kinetics of nematocyst discharge. Curr. Biol. 2006, 16, R316–R318. [Google Scholar] [CrossRef] [PubMed]
- Strychalski, W.; Bryant, S.; Jadamba, B.; Kilikian, E.; Lai, X.; Shahriyari, L.; Segal, R.; Wei, N.; Miller, L.A. Fluid Dynamics of Nematocyst Prey Capture. In Understanding Complex Biological Systems with Mathematics; Radunskaya, A., Segal, R., Shtylla, B., Eds.; Springer: New York, NY, USA, 2018; Chapter 6; pp. 123–144. [Google Scholar]
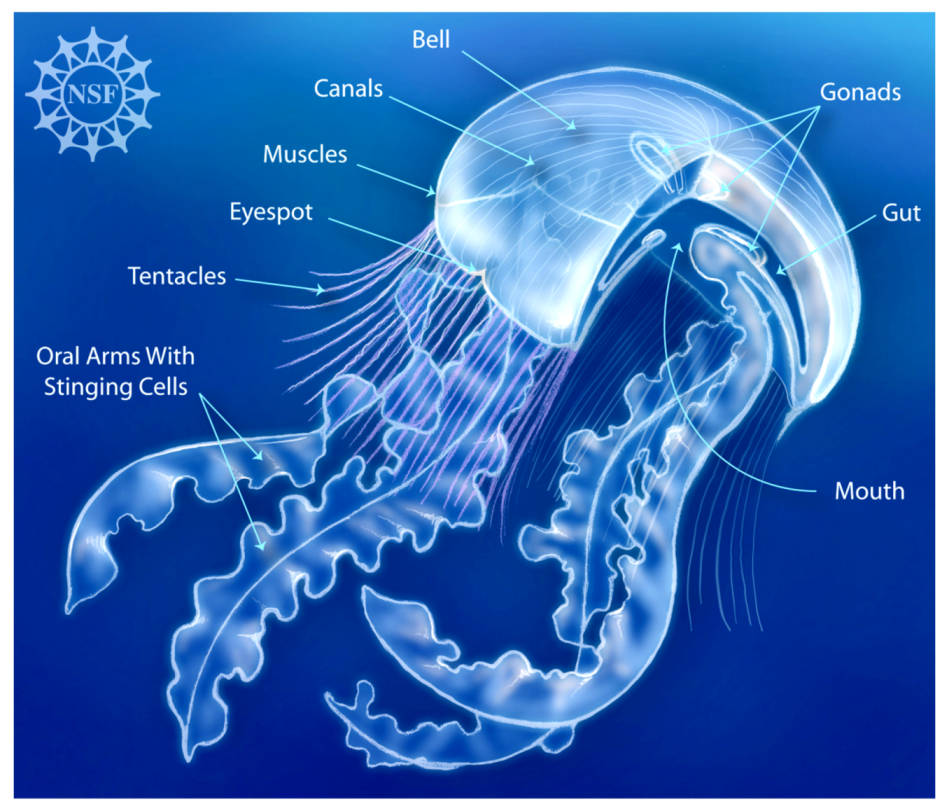
- Deretsky, Z. Jellyfish Anatomy. 2008. Available online: https://www.nsf.gov/news/mmg/mmg_disp.jsp?med_id=65101 (accessed on 29 June 2019).
- Cegolon, L.; Heymann, W.C.; Lange, J.H.; Mastrangelo, G. Jellyfish Stings and Their Management: A Review. Mar. Drugs 2013, 11, 523–550. [Google Scholar] [CrossRef] [PubMed]
- Wrobel, D.; Mills, C. Pacific Coast Pelagic Invertebrates: A Guide to the Common Gelatinous Animals; Sea Challengers: Monterey, CA, USA, 2003. [Google Scholar]
- Katija, K.; Colin, S.P.; Costello, J.H.; Jiang, H. Ontogenetic propulsive transitions by Sarsia tubulosa medusae. J. Exp. Biol. 2015, 218, 2333–2343. [Google Scholar] [CrossRef] [PubMed]
- National Aquarium in Baltimore. Lion’s Mane Jellyfish: Cyanea capillata. 2019. Available online: https://www.aqua.org/Experience/Animal-Index/lions-mane-jellyfish (accessed on 29 June 2019).
- Two Oceans Aquarium. The Jelly Gallery: Moon Jellyfish. 2017. Available online: https://commons.wikimedia.org/wiki/File:Moon_Jellyfish_(Two_Oceans_Aquarium).png (accessed on 2 July 2017).
- Audubon Aquarium of the Americas. The Jelly Gallery: Moon Jellyfish. 2017. Available online: https://commons.wikimedia.org/wiki/File:Moon_Jellyfish_(Audubon_Aquarium).jpg (accessed on 7 January 2017).
- Aquarium of Niagara. Aliens of the Sea: Australian Spotted Jellyfish. 2019. Available online: https://commons.wikimedia.org/wiki/File:Australian_Spotted_Jelly.png and https://commons.wikimedia.org/wiki/File:Australian_Spotted_Jelly2.png (accessed on 21 June 2019).
- Steiger, H. Blue Blubber Jellyfish. 2014. Available online: https://commons.wikimedia.org/w/index.php?curid=42266254 (accessed on 29 June 2019).
- Abbott, B. Flame Jellyfish. 2015. Available online: https://en.wikipedia.org/wiki/Rhopilema_esculentum#/media/File:Rhopilema_esculentum_at_Monterey_Bay_Aquarium.jpg (accessed on 29 June 2019).
- Osaka Aquarium Kaiyukan. Jellyfish: Flame Jellyfish. 2014. Available online: https://commons.wikimedia.org/wiki/File:Adult_Flame_Jellyfish.png (accessed on 30 July 2014).
- National Aquarium In Baltimore. Jellies Invasion: Oceans Out of Balance—Japanese Sea Nettle. 2019. Available online: https://commons.wikimedia.org/wiki/File:Beautiful_Japanese_Sea_Nettle.jpg (accessed on 19 January 2019).
- Key Largo Marine Research Lab. Cassiopea: Upside-Down Jellyfish. 2017. Available online: https://commons.wikimedia.org/wiki/File:Upside_Down_Jelly.png (accessed on 15 March 2018).
- Fredski2013. Spiegeleikwal Voor de Westkust van het. 2015. Available online: https://commons.wikimedia.org/wiki/File:Spiegeleikwal_voor_de_westkust_van_Sardinië.jpg (accessed on 29 June 2019).
- Sontuoso, A. Cassiopea Jellyfish (Cotylorhiza tuberculata). 2008. Available online: https://commons.wikimedia.org/wiki/File:Cassiopea_Jellyfish_(Cotylorhiza_tuberculata)_-_Mar_Jonio,_Italy.jpg (accessed on 29 June 2019).
- National Aquarium in Baltimore. Jellies Invasion: Oceans out of Balance—Cannonball Jellyfish. 2019. Available online: https://commons.wikimedia.org/wiki/File:Expanded_Phase_Cannonball_Jellyfish.png and https://commons.wikimedia.org/wiki/File:Contracted_Phase_Cannonball_Jellyfish.png (accessed on 19 January 2019).
- Hershman, D. A Lion’s Mane Jelly. 2006. Available online: https://commons.wikimedia.org/wiki/File:Largelionsmanejellyfish.jpg (accessed on 29 June 2019).
- Gautsch, G. A box jellyfish (Chironex sp.)—Tiny but Dangerous. 2007. Available online: https://commons.wikimedia.org/wiki/File:Avispa_marina.jpg (accessed on 5 July 2019).
- Spragg, B. Purple-striped jelly. 2007. Available online: https://commons.wikimedia.org/wiki/File:Purple-striped_jelly_(16048869339).jpg (accessed on 1 August 2019).
- Hosia, A. Sarsia tubulosa. 2016. University Museum of Bergen, Natural History Collections. Available online: http://v3.boldsystems.org/index.php/Taxbrowser_Taxonpage?taxid=514041 (accessed on 1 August 2019).
- Monterey Bay Aquarium. Moon Jelly. 2019. Available online: https://www.montereybayaquarium.org/animal-guide/invertebrates/moon-jelly (accessed on 29 June 2019).
- Haddad, M.A.; Júnior, M. Reappearance and seasonality of Phyllorhiza punctata von Lendenfeld (Cnidaria, Scyphozoa, Rhizostomeae) medusae in southern Brazil. Rev. Bras. Zool. 2006, 23, 824–831. [Google Scholar] [CrossRef]
- Boon, L.L. Morphological Characterization of Selected Scyphozoan Jellyfish Species and Geometric Morphometric Analysis of Chrysaora chinensis in Peninsular Malaysia. Master’s Thesis, University of Malaya Kuala Lumpur, Kuala Lumpur, Malaysia, 2017. [Google Scholar]
- Monterey Bay Aquarium. Blue Blubber Jellyfish. 2019. Available online: https://www.montereybayaquarium.org/animal-guide/invertebrates/blubber-jelly (accessed on 29 June 2019).
- Pitt, K.A.; Purcell, J.E. Jellyfish Blooms: Causes, Consequences and Recent Advances; Springer: Gold Coast, Queensland, Australia, 2009; pp. 116–118. [Google Scholar]
- ArcticOceanDiversity. Sea Nettle: Chrysaora melanaster. 2010. Available online: http://www.arcodiv.org/watercolumn/cnidarian/Chrysaora_melanaster.html (accessed on 29 June 2019).
- Georgia Aquarium. Upside down Jellyfish. 2019. Available online: https://www.georgiaaquarium.org/animal/upside-down-jelly/ (accessed on 29 June 2019).
- Kikinger, R. Cotylorhiza tuberculata (Cnidaria: Scyphozoa)—Life History of a Stationary Population. Mar. Ecol. 1992, 13, 333–362. [Google Scholar] [CrossRef]
- Griffin, D.B.; Murphy, T.M. Cannonball Jellyfish: Stomolophus meleagris. 2011. Available online: http://www.dnr.sc.gov/cwcs/pdf/Cannonballjellyfish.pdf (accessed on 30 June 2019).
- McClain, C.R.; Balk, M.A.; Benfield, M.C.; Branch, T.A.; Chen, C.; Cosgrove, J.; Dove, A.D.; Gaskins, L.C.; Helm, R.R.; Hochberg, F.G.; et al. Sizing ocean giants: Patterns of intraspecific size variation in marine megafauna. PeerJ 2015, 3, e715. [Google Scholar] [CrossRef] [PubMed]
- Barnes, J.H. Chironex fleckeri and Chiropsalmus quadrigatus morphological distinctions. North Qld. Nat. 1965, 32, 13–22. [Google Scholar]
- Lewis, C.; Bentlage, B. Clarifying the identity of the Japanese Habu-kurage, Chironex yamaguchii, sp nov (Cnidaria: Cubozoa: Chirodropida). Zootaxa 2009, 32, 59–65. [Google Scholar] [CrossRef]
- Georgia Aquarium. Purple Striped Jellyfish. 2019. Available online: https://www.georgiaaquarium.org/animal/purple-striped-jelly/ (accessed on 29 June 2019).
- Kinsey, B. More Barnes on Box Jellyfish; Sir George Fisher Centre for Tropical Marine Studies, James Cook University of North Queensland: North Queensland, Australia, 1988. [Google Scholar]
- Linnaeus, C. Systema Naturae per regna tria naturae, secundum classes, ordines, genera, species, cum characteribus, differentiis, synonymis, locis. In Editio Decima, Reformata. Laurentius Salvius: Holmiae. ii; Impensis Direct. L. Salvius: Stockholm, Sweden, 1758; p. 824. [Google Scholar]
- Powell, M.D.; Atland, D.A. Acute lion’s mane jellyfish, Cyanea capillata (Cnideria: Scyphozoa), exposure to Atlantic salmon (Salmo salar L.). J. Fish Dis. 2018, 41, 751–759. [Google Scholar] [CrossRef] [PubMed]
- Hamlet, C.; Miller, L.A. Feeding currents of the upside-down jellyfish in the presence of background flow. Bull. Math. Biol. 2012, 74, 2547–2569. [Google Scholar] [CrossRef]
- Santhanakrishnan, A.; Dollinger, M.; Hamlet, C.L.; Colin, S.P.; Miller, L.A. Flow structure and transport characteristics of feeding and exchange currents generated by upside-down Cassiopea jellyfish. J. Exp. Biol. 2011, 215, 2369–2381. [Google Scholar] [CrossRef] [PubMed]
- Bastian, T. The Broad-Scale Distribution and Abundance of Scyphomedusae in Irish Waters. Ph.D. Thesis, University College Cork, Cork, Ireland, 2011. [Google Scholar]
- Bastian, T.; Haberlin, D.; Gallagher, M.C.; Rooney, S.; Hays, G.C.; Doyle, T.K. Tracking the lion’s mane jellyfish: Horizontal and vertical movements of Cyanea capillata (Scyphozoa) in a shallow coastal environment, 2012. In Proceedings of the PISCES 2012 Annual Meeting, Hiroshima, Japan, 12–21 October 2012. [Google Scholar]
- Moriarty, P.E.; Andrews, K.S.; Harvey, C.J.; Kawase, M. Vertical and horizontal movement patterns of scyphozoan jellyfish in a fjord-like estuary. Mar. Ecol. Prog. Ser. 2012, 455, 1–12. [Google Scholar] [CrossRef]
- Costello, J.H.; Klos, E.; Ford, M.D. In situ time budgets of the scyphomedusae Aurelia aurita, Cyanea sp., and Chrysaora quinquecirrha. J. Plankton Res. 1998, 20, 383–391. [Google Scholar] [CrossRef]
- Purell, J.E.; Arai, M.N. Interactions of pelagic cnidarians and ctenophores with fish: A review. Hydrobiologia 2001, 451, 27–44. [Google Scholar] [CrossRef]
- Purell, J.E. Predation on zooplankton by large jellyfish (Aurelia labiata, Cyanea capillata, Aequorea aequorea) in Prince William Sound, Alaska. Mar. Ecol. Prog. Ser. 2003, 246, 137–152. [Google Scholar] [CrossRef]
- Crawford, R.E. Occurrence of a gelatinous predator (Cyanea capillata) may affect the distribution of Boreogadus saida, a key Arctic prey fish species. Polar Biol. 2016, 39, 1049–1055. [Google Scholar] [CrossRef]
- Gordon, M.R.; Seymour, J.E. Quantifying movement of the tropical Australian cubozoan Chironex fleckeri using acoustic telemetry. Hydrobiologia 2009, 616, 87–97. [Google Scholar] [CrossRef]
- Kinsey, B.E. Barnes on Box Jellyfish; James Cook University: North Queensland, Australia, 1986; Unpublished. [Google Scholar]
- Rifkin, J. Jellyfish Mechanisms. In Venomous and Poisonous Marine Animals—A Medical and Biological Handbook; Williamson, J.A., Fenner, P.J., Burnett, J.W., Rifkin, J., Eds.; University of New South Wales Press: Randwick, Australia, 1996. [Google Scholar]
- Bastian, T. Quantifying Ecological Aspects of the Seasonally Abundant Box Jellyfish Chironex fleckeri within Coastal and Estuarine Waters of Far North Queensland. Ph.D. Thesis, James Cook University, North Queensland, Australia, 2014. [Google Scholar]
- Colin, S.P.; Costello, J.H.; Katija, K.; Seymour, J.; Kiefer, K. Propulsion in Cubomedusae: Mechanisms and Utility. PLoS ONE 2013, 8, e56393. [Google Scholar] [CrossRef] [PubMed]
- Shorten, M.; Davenport, J.; Seymour, J.E.; Cross, M.C.; Carrette, T.J.; Woodward, G.; Cross, T.F. Kinematic analysis of swimming in Australian box jellyfish, Chiropsalmus sp. and Chironex fleckeri (Cubozoa, Cnidaria: Chirodropidae). J. Zool. 2005, 267, 371–380. [Google Scholar] [CrossRef]
- Hoover, A.P.; Miller, L.A. A numerical study of the benefits of driving jellyfish bells at their natural frequency. J. Theor. Biol. 2015, 374, 13–25. [Google Scholar] [CrossRef]
- Hoover, A.P.; Griffith, B.E.; Miller, L.A. Quantifying performance in the medusan mechanospace with an actively swimming three-dimensional jellyfish model. J. Fluid Mech. 2017, 813, 1112–1155. [Google Scholar] [CrossRef]
- Courtney, R.; Sachlikidis, N.; Jones, R.; Seymour, J. Prey Capture Ecology of the Cubozoan Carukia barnesi. PLoS ONE 2015, 10, e0124256. [Google Scholar] [CrossRef]
- Garm, A.; Bielecki, J.; Petie, R.; Nilsson, D.E. Hunting in Bioluminescent Light: Vision in the Nocturnal Box Jellyfish Copula sivickisi. Front. Physiol. 2016, 7, 99. [Google Scholar] [CrossRef]
- Grzimek, D. Grzimek’s Animal Ecyclopedia, Vol. 1, Lower Animals; Van Nostrand Reinhold Company: New York, NY, USA, 1972. [Google Scholar]
- Leonard, J.L. Variability of the swimming ‘rhythm’ in a hydromedusa. Am. Zool. 1978, 18, 589. [Google Scholar]
- Leonard, J.L. Temporal organization of swimming activity in Sarsia tubulosa M. Sara (Hydrozoa). J. Comp. Physiol. 1980, 136, 219–335. [Google Scholar] [CrossRef]
- Colin, S.P.; Costello, J.H. Morphology, swimming performance and propulsive mode of six co-occurring hydromedusae. J. Exp. Biol. 2002, 205, 427–437. [Google Scholar]
- Sahin, M.; Mohseni, K.; Colin, S.P. The numerical comparison of flow patterns and propulsive performances for the hydromedusae Sarsia tubulosa and Aequorea victoria. J. Exp. Biol. 2009, 212, 2656–2667. [Google Scholar] [CrossRef]
- Miles, J.G.; Battista, N.A. Don’t be jelly: Exploring effective jellyfish locomotion. arXiv 2019, arXiv:1904.09340. [Google Scholar]
- Dular, J.; Bajcar, T.; Sirok, B. Numerical Investigation of Flow in the Vicinity of a Swimming Jellyfish. Eng. Appl. Comp. Fluid Mech. 2009, 3, 258–270. [Google Scholar] [CrossRef]
- Wilson, M.M.; Peng, J.; Dabiri, J.O.; Eldredge, J.D. Lagrangian coherent structures in low reynolds number swimming. J. Phys. Condens. Matter 2009, 21, 204105. [Google Scholar] [CrossRef] [PubMed]
- Herschlag, G.; Miller, L.A. Reynolds number limits for jet propulsion: A numerical study of simplified jellyfish. J. Theor. Biol. 2011, 285, 84–95. [Google Scholar] [CrossRef] [PubMed]
- Alben, S.; Miller, L.A.; Peng, J. Efficient kinematics for jet-propelled swimming. J. Fluid Mech. 2013, 733, 100–133. [Google Scholar] [CrossRef]
- Yuan, H.; Shu, S.; Niu, X.; Li, M. A Numerical Study of Jet Propulsion of an Oblate Jellyfish Using a Momentum Exchange-Based Immersed Boundary-Lattice Boltzmann Method. Adv. Appl. Math. Mech. 2014, 6, 307–326. [Google Scholar] [CrossRef]
- Hoover, A.P.; Porras, A.J.; Miller, L.A. Pump or coast: The role of resonance and passive energy recapture in medusan swimming performance. J. Fluid. Mech. 2019, 863, 1031–1061. [Google Scholar] [CrossRef]
- PAllasdies, F.; Goedeke, S.; Braun, W.; Memmesheimer, R. From Single Neurons to Behavior in the Jellyfish Aurelia aurita. arXiv 2019, arXiv:1907.05060. [Google Scholar]
- Dabiri, J.O.; Gharib, M.; Colin, S.P.; Costello, J.H. Vortex motion in the ocean: In situ visualization of jellyfish swimming and feeding flows. Phys. Fluids 2005, 17, 091108. [Google Scholar] [CrossRef]
- Dabiri, J.O.; Colin, S.P.; Costello, J.H.; Gharib, M. Flow patterns generated by oblate medusan jellyfish: Field measurements and laboratory analyses. J. Exp. Biol. 2005, 208, 1257–1265. [Google Scholar] [CrossRef]
- Dabiri, J.O.; Colin, S.P.; Costello, J.H. Fast-swimming hydromedusae exploit velar kinematics to form an optimal vortex wake. J. Exp. Biol. 2006, 209, 2025–2033. [Google Scholar] [CrossRef]
- Bajcar, T.; Malacic, V.; Malej, A.; Sirok, B. Kinematic properties of the jellyfish Aurelia sp. In Jellyfish Blooms: Causes, Consequences, and Recent Advances; Pitt, K.A., Purcell, J.E., Eds.; Springer: Dordrecht, The Netherlands, 2008; Volume 206. [Google Scholar]
- Peng, J.; Dabiri, J.O. Transport of inertial particles by lagrangian coherent structures: application to predator- prey interaction in jellyfish feeding. J. Fluid Mech. 2009, 623, 75–84. [Google Scholar] [CrossRef]
- Gemmell, B.; Costello, J.; Colin, S.P.; Stewart, C.; Dabiri, J.; Tafti, D.; Priya, S. Passive energy recapture in jellyfish contributes to propulsive advantage over other metazoans. Proc. Natl. Acad. Sci. USA 2013, 110, 17904–17909. [Google Scholar] [CrossRef] [PubMed]
- Gemmell, B.; Costello, J.; Colin, S.P. Exploring vortex enhancement and manipulation mechanisms in jellyfish that contributes to energetically efficient propulsion. Commun. Integr. Biol. 2014, 7, e29014. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Gemmell, B.; Costello, J.; Colin, S.P.; Dabiri, J. Suction-based propulsion as a basis for efficient animal swimming. Nat. Commun. 2015, 6, 8790. [Google Scholar] [CrossRef] [PubMed]
- Costello, J.H.; Colin, S.P.; Gemmell, B.J.; Dabiri, J.O. Hydrodynamics of Vortex Generation during Bell Contraction by the Hydromedusa Eutonina indicans (Romanes, 1876). Biomimetics 2019, 4, 44. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Chamorro, L.P. Lagrangian description of the unsteady flow induced by a single pulse of a jellyfish. Phys. Rev. Fluids 2019, 4, 064605. [Google Scholar] [CrossRef]
- Katija, K. Morphology Alters Fluid Transport and the Ability of Organisms to Mix Oceanic Waters. Int. Comp. Biol. 2015, 55, 698–705. [Google Scholar] [CrossRef] [PubMed]
- Battista, N.A.; Baird, A.J.; Miller, L.A. A Mathematical Model and MATLAB Code for Muscle-Fluid-Structure Simulations. Integr. Comp. Biol. 2015, 55, 901–911. [Google Scholar] [CrossRef]
- Battista, N.A.; Strickland, W.C.; Miller, L.A. IB2d: A Python and MATLAB implementation of the immersed boundary method. Bioinspir. Biomim. 2017, 12, 036003. [Google Scholar] [CrossRef]
- Battista, N.A.; Strickland, W.C.; Barrett, A.; Miller, L.A. IB2d Reloaded: A more powerful Python and MATLAB implementation of the immersed boundary method. Math. Method Appl. Sci 2018, 41, 8455–8480. [Google Scholar] [CrossRef]
- Smits, A.J. Undulatory and oscillatory swimming. J. Fluid Mech. 2019, 874, P1. [Google Scholar] [CrossRef]
- Floryan, D.; Van Buren, T.; Smits, A.J. Swimmers’ Wakes Are not Reliable Indicators of Swimming Performance. 2019. Available online: https://arxiv.org/abs/1906.10826 (accessed on 27 June 2019).
- Peskin, C. Flow patterns around heart valves: A numerical method. J. Comput. Phys. 1972, 10, 252–271. [Google Scholar] [CrossRef]
- Peskin, C. Numerical analysis of blood flow in the heart. J. Comput. Phys. 1977, 25, 220–252. [Google Scholar] [CrossRef]
- Peskin, C.S. The immersed boundary method. Acta Numer. 2002, 11, 479–517. [Google Scholar] [CrossRef]
- Fauci, L.; Fogelson, A. Truncated Newton methods and the modeling of complex immersed elastic structures. Commun. Pure Appl. Math 1993, 46, 787–818. [Google Scholar] [CrossRef]
- Lai, M.C.; Peskin, C.S. An Immersed Boundary Method with Formal Second-Order Accuracy and Reduced Numerical Viscosity. J. Comp. Phys. 2000, 160, 705–719. [Google Scholar] [CrossRef]
- Cortez, R.; Minion, M. The Blob Projection Method for Immersed Boundary Problems. J. Comp. Phys. 2000, 161, 428. [Google Scholar] [CrossRef]
- Griffith, B.E.; Peskin, C.S. On the order of accuracy of the immersed boundary method: Higher order convergence rates for sufficiently smooth problems. J. Comput. Phys 2005, 208, 75–105. [Google Scholar] [CrossRef]
- Mittal, R.; Iaccarino, C. Immersed boundary methods. Annu. Rev. Fluid Mech. 2005, 37, 239–261. [Google Scholar] [CrossRef]
- Griffith, B.E.; Hornung, R.; McQueen, D.; Peskin, C.S. An adaptive, formally second order accurate version of the immersed boundary method. J. Comput. Phys. 2007, 223, 10–49. [Google Scholar] [CrossRef]
- Griffith, B.E. An Adaptive and Distributed-Memory Parallel Implementation of the Immersed Boundary (IB) Method. 2014. Available online: https://github.com/IBAMR/IBAMR (accessed on 24 January 2019).
- Griffith, B.E.; Luo, X. Hybrid finite difference/finite element version of the immersed boundary method. Int. J. Numer. Meth. Engng. 2012, 33. [Google Scholar] [CrossRef]
- Huang, W.X.; Tian, F.B. Recent trends and progresses in the immersed boundary method. Proc. Inst. Mech. Eng. Part J. Mech. Eng. Sci. 2019. [Google Scholar] [CrossRef]
- Miller, L.A. Fluid Dynamics of Ventricular Filling in the Embryonic Heart. Cell Biochem. Biophys. 2011, 61, 33–45. [Google Scholar] [CrossRef] [PubMed]
- Griffith, B.E. Immersed boundary model of aortic heart valve dynamics with physiological driving and loading conditions. Int. J. Numer. Meth. Biomed. Eng. 2012, 28, 317–345. [Google Scholar] [CrossRef]
- Battista, N.A.; Lane, A.N.; Miller, L.A. On the dynamic suction pumping of blood cells in tubular hearts. In Women in Mathematical Biology: Research Collaboration; Layton, A., Miller, L.A., Eds.; Springer: New York, NY, USA, 2017; Chapter 11; pp. 211–231. [Google Scholar]
- Battista, N.A.; Lane, A.N.; Liu, J.; Miller, L.A. Fluid Dynamics of Heart Development: Effects of Trabeculae and Hematocrit. Math. Med. Biol. 2018, 35, 493–516. [Google Scholar] [CrossRef] [PubMed]
- Battista, N.A. Fluid-Structure Interaction for the Classroom: Interpolation, Hearts, and Swimming! arXiv 2018, arXiv:1808.08122. [Google Scholar]
- Bhalla, A.; Griffith, B.E.; Patankar, N. A forced damped oscillation framework for undulatory swimming provides new insights into how propulsion arises in active and passive swimming. PLOS Comput. Biol. 2013, 9, e1003097. [Google Scholar] [CrossRef] [PubMed]
- Bhalla, A.; Griffith, B.E.; Patankar, N. A unified mathematical frame- work and an adaptive numerical method for fluid–structure interaction with rigid, deforming, and elastic bodies. J. Comput. Phys. 2013, 250, 446–476. [Google Scholar] [CrossRef]
- Hamlet, C.; Fauci, L.J.; Tytell, E.D. The effect of intrinsic muscular nonlinearities on the energetics of locomotion in a computational model of an anguilliform swimmer. J. Theor. Biol. 2015, 385, 119–129. [Google Scholar] [CrossRef]
- Miller, L.A.; Peskin, C.S. When vortices stick: An aerodynamic transition in tiny insect flight. J. Exp. Biol. 2004, 207, 3073–3088. [Google Scholar] [CrossRef]
- Miller, L.A.; Peskin, C.S. A computational fluid dynamics of clap and fling in the smallest insects. J. Exp. Biol. 2009, 208, 3076–3090. [Google Scholar] [CrossRef] [PubMed]
- Jones, S.K.; Laurenza, R.; Hedrick, T.L.; Griffith, B.E.; Miller, L.A. Lift- vs. drag-based for vertical force production in the smallest flying insects. J. Theor. Biol. 2015, 384, 105–120. [Google Scholar] [CrossRef] [PubMed]
- Berger, M.J.; Oliger, J. Adaptive mesh refinement for hyperbolic partial-differential equations. J. Comput. Phys. 1984, 53, 484–512. [Google Scholar] [CrossRef]
- Roma, A.M.; Peskin, C.S.; Berger, M.J. An adaptive version of the immersed boundary method. J. Comp. Phys. 1999, 153, 509–534. [Google Scholar] [CrossRef]
- Battista, N.A.; Mizuhara, M.S. Fluid-Structure Interaction for the Classroom: Speed, Accuracy, Convergence, and Jellyfish! arXiv 2019, arXiv:1902.07615. [Google Scholar]
- Brinkman, H.C. A calculation of the viscous force exerted by a flowing fluid on a dense swarm of particles. Appl. Sci. Res. 1949, 1, 27–34. [Google Scholar] [CrossRef]
- Nield, D.A.; Bejan, A. Convection in Porous Media; Springer: New York, NY, USA, 1992. [Google Scholar]
- Childs, H.; Brugger, E.; Whitlock, B.; Meredith, J.; Ahern, S.; Pugmire, D.; Biagas, K.; Miller, M.; Harrison, C.; Weber, G.H.; et al. VisIt: An End-User Tool For Visualizing and Analyzing Very Large Data. In High Performance Visualization–Enabling Extreme-Scale Scientific Insight; CRC Press: Boca Raton, FL, USA, 2012; pp. 357–372. [Google Scholar]
- Taylor, G.K.; Nudds, R.L.; Thomas, A.L. Flying and swimming animals cruise at a Strouhal number tuned for high power efficiency. Nature 2003, 425, 707–711. [Google Scholar] [CrossRef]
- Schmidt-Nielsen, K. Locomotion: energy cost of swimming, flying, and running. Science 1972, 177, 222–228. [Google Scholar] [CrossRef]
- Bale, R.; Hao, M.; Bhalla, A.; Patankar, N.A. Energy efficiency and allometry of movement of swimming and flying animals. Proc. Natl. Acad. Sci. USA 2014, 111, 7517–7521. [Google Scholar] [CrossRef]
- Haller, G. Finding finite-time invariant manifolds in two-dimensional velocity fields. Chaos 2000, 10, 99–108. [Google Scholar] [CrossRef]
- Shadden, S.C.; Lekien, F.; Marsden, J.E. Definition and properties of Lagrangian coherent structures from finite-time Lyapunov exponents in two-dimensional aperiodic flows. Physica D 2005, 212, 271–304. [Google Scholar] [CrossRef]
- Haller, G. Lagrangian Coherent Structures. Annual Review of Fluid Mechanics 2015, 47, 137–162. [Google Scholar] [CrossRef]
- Sapsis, T.; Peng, J.; Haller, G. Instabilities on prey dynamics in jellyfish feeding. Bull. Math. Biol. 2011, 73, 1841–1856. [Google Scholar] [CrossRef] [PubMed]
- Franco, E.; Pekarek, D.; Peng, J.; Dabiri, J.O. Geometry of unsteady fluid transport during fluid–structure interactions. J. Fluid Mech. 2007, 125–145, 589. [Google Scholar] [CrossRef]
- Zhang, Z.J. Identification of Lagrangian Coherent Structures around Swimming Jellyfish from Experimental Time-series Data. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 2008; pp. 1–30. [Google Scholar]
- Lipinski, D.; Mohseni, K. Flow structures and fluid transport for the hydromedusae Sarsia tubulosa and Aequorea victoria. J. Exp. Biol. 2009, 212, 2436–2447. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Haller, G.; Sapsis, T. Lagrangian coherent structures and the smallest finite-time Lyapunov exponent. Chaos 2011, 21, 023115. [Google Scholar] [CrossRef] [PubMed]
- Taheri, A. Lagrangian Coherent Structure Analysis of Jellyfish Swimming Using Immersed Boundary FSI Simulations. J. Mech. Civ. Eng. 2018, 15, 69–74. [Google Scholar]
- Nudds, R.L.; John, E.L.; Keen, A.N.; Shiels, H.A. Rainbow trout provide the first experimental evidence for adherence to a distinct Strouhal number during animal oscillatory propulsion. J. Exp. Biol. 2014, 217, 2244–2249. [Google Scholar] [CrossRef] [PubMed]
- Costello, J.H.; Colin, S.P.; Dabiri, J.O. Constraints and consequences in medusan evolution. Invert. Biol. 2008, 127, 265–290. [Google Scholar] [CrossRef]
- Piraino, S.; Boero, F.; Aeschbach, B.; Schmid, V. Reversing the Life Cycle: Medusae Transforming into Polyps and Cell Transdifferentiation in Turritopsis nutricula (Cnidaria, Hydrozoa). Biol. Bull. 1996, 190, 302–312. [Google Scholar] [CrossRef]
- Vogel, S. Life in Moving Fluids: The Physical Biology of Flow; Princeton Paperbacks: Princeton, NJ, USA, 1996. [Google Scholar]
- MATLAB. Version 8.5.0 (R2015a); The MathWorks Inc.: Natick, MA, USA, 2015. [Google Scholar]






| Name | Scientific Name | Max. Bell Diameter (cm) | Tentacle/Oral Arm Length (cm) | Range | References |
|---|---|---|---|---|---|
| Moon Jellyfish | Aurelia aurita | 38 | Along the East & West Coast, Europe, Japan, and the Gulf of Mexico | [25] | |
| Australian Spotted Jellyfish | Phyllorhiza punctata | 60 | ≳60 | Western Pacific (From Australia to Japan) | [26,27] |
| Blue Blubber Jellyfish | Catostylus mosaicus | 45 | ∼45 | Along the east and north coasts of Australia | [28] |
| Flame Jellyfish | Rhopilema esculentum | 70 | ≳70 | Warm temperate waters of the Pacific Ocean | [27,29] |
| Japanese Sea Nettle | Chrysaora melanaster | 60 | 300 | Northern Pacific Ocean & adjacent parts of the Arctic Ocean | [30] |
| Upside-Down Jellyfish | Cassiopea | 36 | 36 | Western Atlantic, including the Gulf of Mexico, Bermuda, and the Caribbean | [31] |
| Fried Egg Jellyfish | Cotylorhiza tuberculata | 40 | ≳40 | Mediterranean Sea, coastal lagoons | [32] |
| Cannonball Jellyfish | Stomolophus meleagris | 25 | ≳25 | Pacific Ocean and the mid-west of the Atlantic Ocean | [33] |
| Lion’s Mane Jellyfish | Cyanea capillata | 250 | 3600 | Cold waters of the Arctic, Northern Atlantic, and Northern Pacific | [9,34] |
| Sea Wasp (Box Jellyfish) | Chironex fleckeri | 30 | 300 | Australia and Indo-West Pacific Ocean | [35,36] |
| Purple Striped Jellyfish | Chrysaora colorata | 70 | 800 | Eastern Pacific Ocean primarily off the coast of California | [37] |
| Clapper Hydroid | Sarsia tubulosa | 0.5 | 3–4 | Central California to the Bering Sea | [7,8] |
| Parameter | Variable | Units | Value |
|---|---|---|---|
| Domain Size | m | ||
| Spatial Grid Size | m | ||
| Lagrangian Grid Size | m | ||
| Time Step Size | s | ||
| Total Simulation Time | T | pulses | 8 |
| Fluid Density | kg/m | 1000 | |
| Fluid Dynamic Viscosity | kg/(ms) | varied | |
| Bell Radius | a | m | (and varied) |
| Bell Diameter | D () | m | (and varied) |
| Bell Height | b | m | |
| Contraction Frequency | f | 1/s | |
| Spring Stiffness | kg·m/s | ||
| Beam Stiffness | kg·m/s | ||
| Tentacle Spring Stiffness | kg·m/s | ||
| Tentacle Beam Stiffness | kg·m/s | ||
| Muscle Spring Stiffness | kg·m/s | ||
| Poroelasticity Coefficient | m | varied |
| Total # Tentacles/Oral Arms | ||||
|---|---|---|---|---|
| 2 | −55.9% | −45.5% | −43.6% | −44.3% |
| 4 | −64.3% | −58.3% | −55.1% | −52.7% |
| 6 | −79.5% | −68.0% | −67.0% | −60.7% |
| 8 | −91.8% | −92.7% | −84.6% | −77.3% |
| ABCDEF | −71.1% | −64.1% | −57.4% | −57.6% |
| ABEF | −67.5% | −62.5% | −49.8% | −49.8% |
| ACDF | −74.7% | −65.5% | −51.1% | −52.6% |
| AF | −64.6% | −49.5% | −42.7% | −40.6% |
| 2 Per Side | −69.3% | −65.5% | −54.6% | −49.3% |
| 4 Per Side | −77.6% | −71.0% | −56.4% | −64.6% |
| 5 Per Side | −78.5% | −74.9% | −59.4% | −49.5% |
| 10 Per Side | −78.1% | −83.3% | −74.4% | −61.1% |
| Outer 2 | −67.4% | −55.3% | −45.2% | −48.4% |
| Outer 3 | −67.7% | −62.7% | −51.6% | −48.6% |
| Outer 4 | −70.1% | −58.8% | −51.2% | −50.3% |
| Outer 5 | −78.5% | −74.9% | −59.4% | −49.5% |
| Outer/Inner | −75.4% | −65.9% | −55.9% | −51.0% |
| Inner Unequal | −78.8% | −81.3% | −70.8% | −55.6% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miles, J.G.; Battista, N.A. Naut Your Everyday Jellyfish Model: Exploring How Tentacles and Oral Arms Impact Locomotion. Fluids 2019, 4, 169. https://doi.org/10.3390/fluids4030169
Miles JG, Battista NA. Naut Your Everyday Jellyfish Model: Exploring How Tentacles and Oral Arms Impact Locomotion. Fluids. 2019; 4(3):169. https://doi.org/10.3390/fluids4030169
Chicago/Turabian StyleMiles, Jason G., and Nicholas A. Battista. 2019. "Naut Your Everyday Jellyfish Model: Exploring How Tentacles and Oral Arms Impact Locomotion" Fluids 4, no. 3: 169. https://doi.org/10.3390/fluids4030169
APA StyleMiles, J. G., & Battista, N. A. (2019). Naut Your Everyday Jellyfish Model: Exploring How Tentacles and Oral Arms Impact Locomotion. Fluids, 4(3), 169. https://doi.org/10.3390/fluids4030169






