Temperature Error Reduction of DPD Fluid by Using Partitioned Runge-Kutta Time Integration Scheme
Abstract
1. Introduction
2. Methodology
2.1. Governing Equations
2.2. Time Integration Algorithms
Partitioned Runge-Kutta Scheme
3. Results and Discussion
3.1. Simulation Details
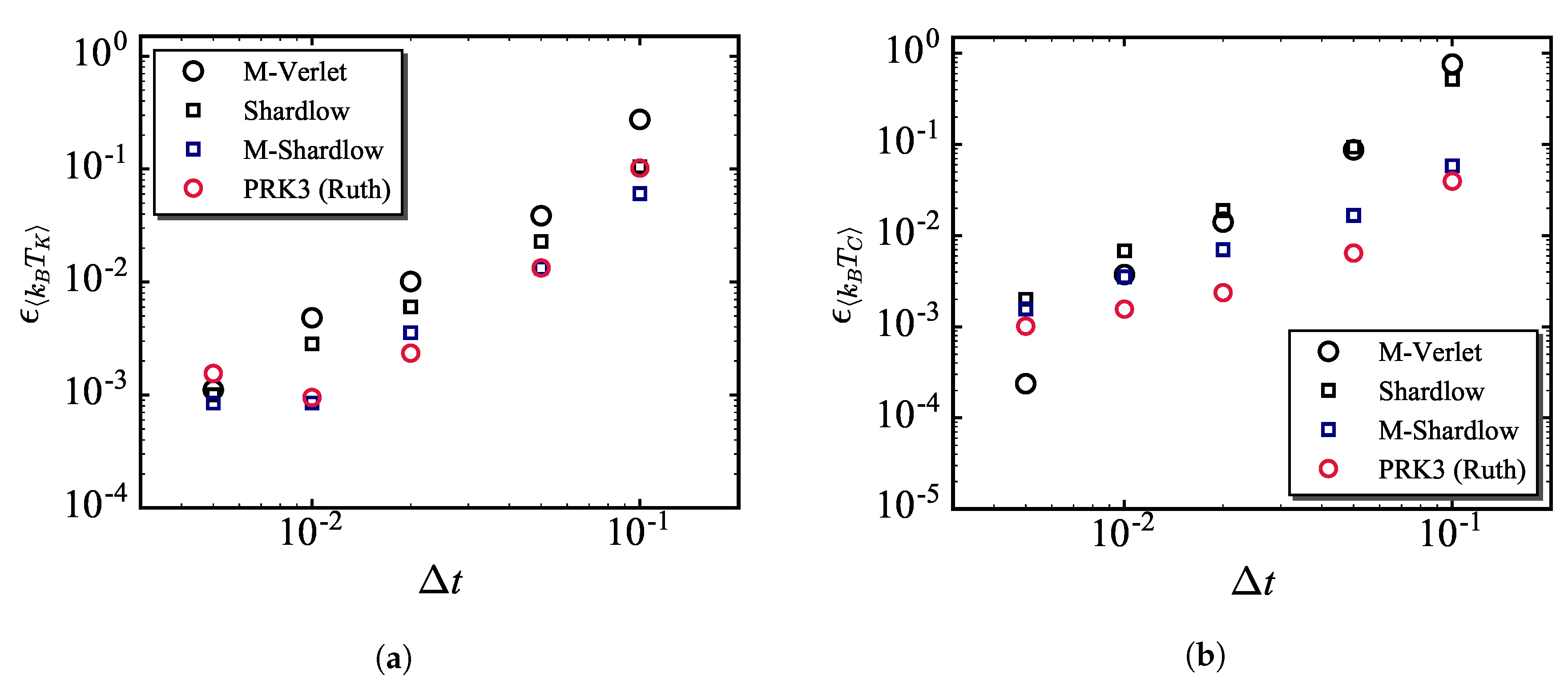
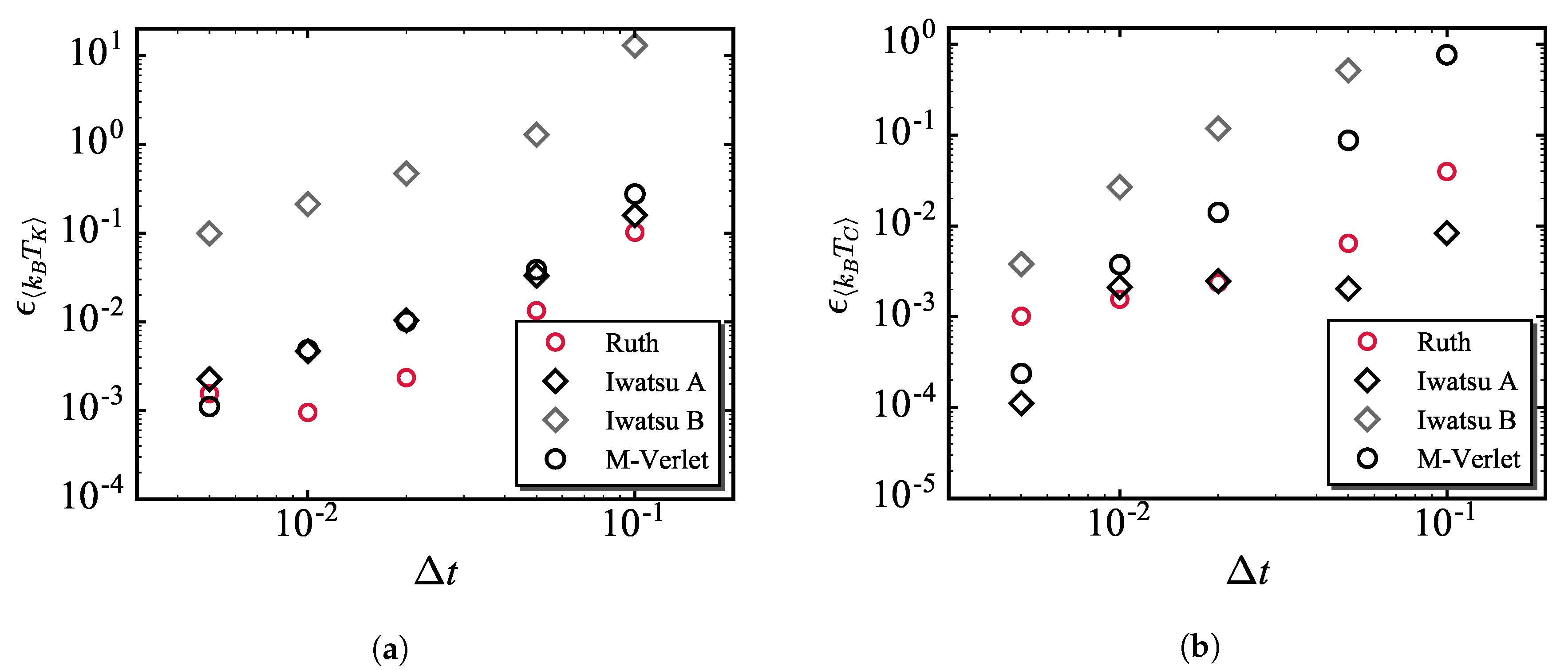
3.2. Temperature Errors on Different Time Integration Schemes
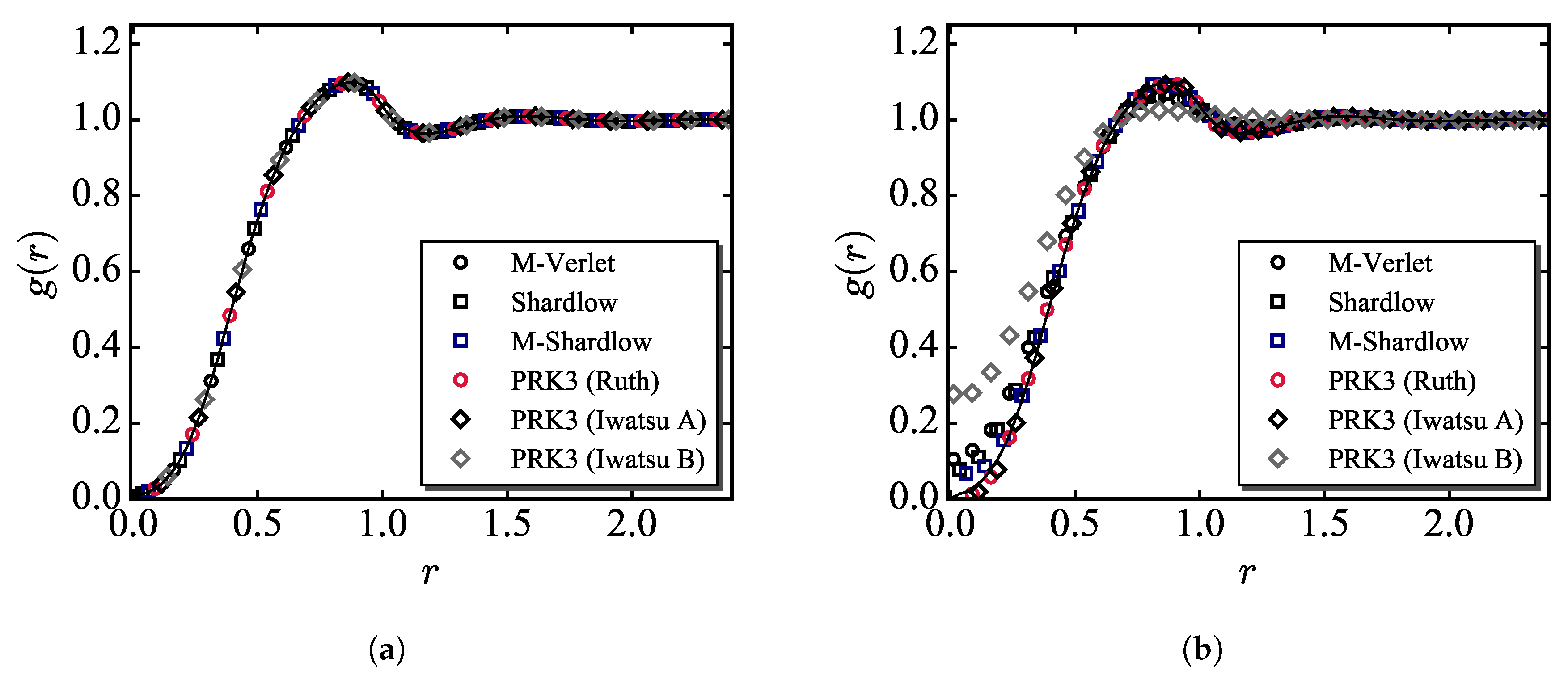
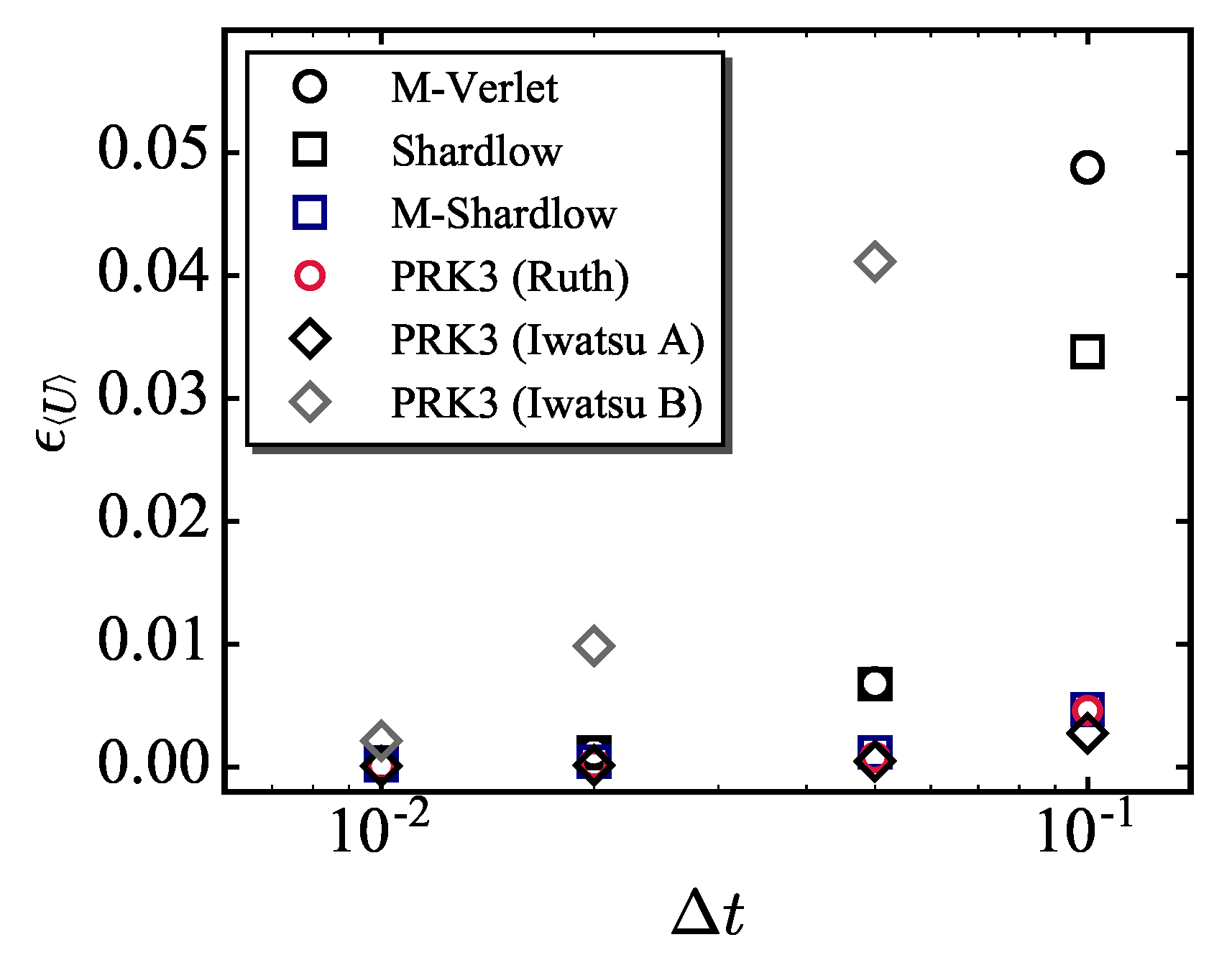
3.3. Errors in Configurational and Dynamic Properties
3.4. Computational Efficiency
4. Conclusions
- The comparison of the temperature errors among three PRK3 schemes showed that the PRK3 (Ruth) scheme can be superior to the existing schemes in both kinetic and configurational temperatures. Whereas the PRK3 (Iwatsu A) scheme has a disadvantage in the kinetic temperature error. Both temperature errors obtained by using the PRK3 (Iwatsu B) scheme were inferior to those by the existing scheme. This series of results are almost ranked in the same order of computational error and degree of dispersibility shown in the previous study though the time integrations of the non-conservative part for these PRK3 schemes differently influence on the error as well as the conservative part. This strongly supports the findings in our previous study that the conservative part of the PSP is significantly influences the time integration in the DPD simulations.
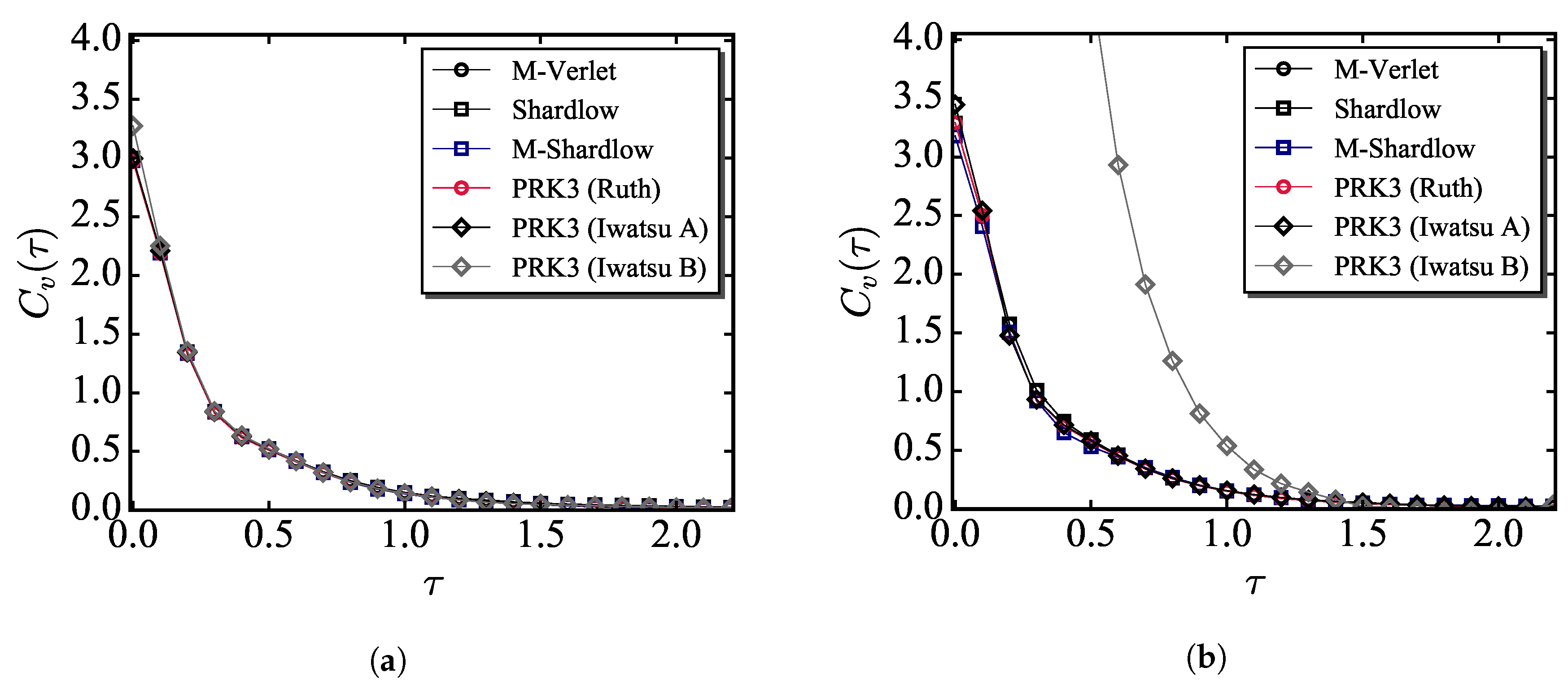
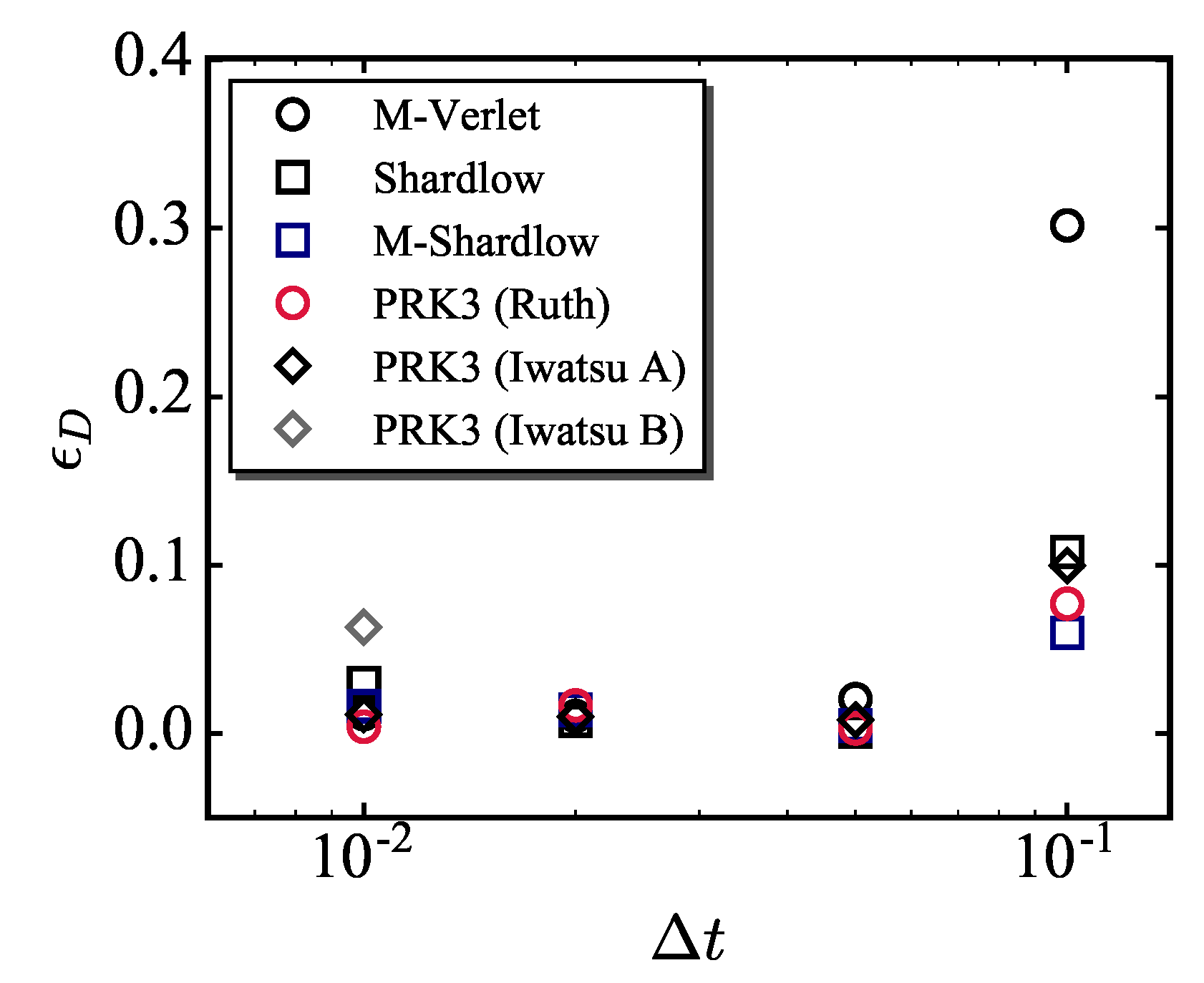
- The radial distribution function and velocity autocorrelation function were estimated for the simulations by using the existing and PRK3 schemes to compare the errors in configurational and kinetic quantities. It was found from this comparison that the PRK3 (Ruth) scheme can be regarded as one of the best scheme among the available schemes.
- Comparison of kinetic/configurational quantities and temperatures showed that the kinetic and configurational temperatures involve errors from different characteristics. Thus, both temperatures are important to scale the computational error in DPD.
- The computational efficiency was finally estimated. The results showed that the PRK3 (Ruth) scheme is more efficient than the existing schemes, and substantially low error can be kept in a wide time increment range.
Author Contributions
Funding
Conflicts of Interest
Appendix A. Numerical Time Integration Schemes
Appendix A.1. M-Verlet Scheme
Appendix A.2. Shardlow and M-Shardlow Schemes
References
- Hoogerbrugge, P.J.; Koelman, J.M.V.A. Simulating microscopic hydrodynamic phenomena with dissipative particle dynamics. Europhys. Lett. 1992, 19, 155–160. [Google Scholar] [CrossRef]
- Petsev, N.D.; Leal, L.G.; Shell, M.S. An integrated boundary approach for colloidal suspensions simulated using smoothed dissipative particle dynamics. Comput. Fluids 2019, 179, 672–686. [Google Scholar] [CrossRef]
- Howard, M.P.; Truskett, T.M.; Nikoubashman, A. Cross-stream migration of a Brownian droplet in a polymer solution under Poiseuille flow. Soft Matter 2019, 15, 3168–3178. [Google Scholar] [CrossRef] [PubMed]
- Sevink, G.; Fraaije, J. Efficient solvent-free dissipative particle dynamics for lipid bilayers. Soft Matter 2014, 10, 5129–5146. [Google Scholar] [CrossRef] [PubMed]
- Waheed, W.; Alazzam, A.; Al-Khateeb, A.N.; Sung, H.J.; Abu-Nada, E. Investigation of DPD transport properties in modeling bioparticle motion under the effect of external forces: Low Reynolds number and high Schmidt scenarios. J. Chem. Phys. 2019, 150, 054901. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Xue, Y.H.; Qian, H.J.; Lu, Z.Y.; Sun, C.C. A practical method to avoid bond crossing in two-dimensional dissipative particle dynamics simulations. J. Chem. Phys. 2008, 129, 024902. [Google Scholar] [CrossRef]
- Araki, Y.; Kobayashi, Y.; Kawaguchi, T.; Kaneko, T.; Arai, N. Water permeation in polymeric membranes: Mechanism and synthetic strategy for water-inhibiting functional polymers. J. Membr. Sci. 2018, 564, 184–192. [Google Scholar] [CrossRef]
- Groot, R.D.; Warren, P.B. Dissipative Particle Dynamics: Bridging the Gap Between Atomistic and Mesoscopic Simulation. J. Chem. Phys. 1997, 107, 4423–4435. [Google Scholar] [CrossRef]
- Shardlow, T. Splitting for dissipative particle dynamics. SIAM J. Sci. Comput. 2003, 24, 1267–1282. [Google Scholar] [CrossRef]
- Pagonabarraga, I.; Hagen, M.H.J.; Frenkel, D. Self-consistent dissipative particle dynamics algorithm. Europhys. Lett. 1998, 42, 377–382. [Google Scholar] [CrossRef]
- Serrano, M.; De Fabritiis, G.; Español, P.; Coveney, P.V. A stochastic Trotter integration scheme for dissipative particle dynamics. Math. Comput. Simul. 2006, 72, 190–194. [Google Scholar] [CrossRef]
- Farago, O.; Grønbech-Jensen, N. On the connection between dissipative particle dynamics and the Itô-Stratonovich dilemma. J. Chem. Phys. 2016, 144, 084102. [Google Scholar] [CrossRef] [PubMed]
- Yamada, T.; Itoh, S.; Morinishi, Y.; Tamano, S. Improving computational accuracy in dissipative particle dynamics via a high order symplectic method. J. Chem. Phys. 2018, 148, 224101. [Google Scholar] [CrossRef] [PubMed]
- Lowe, C.P. An alternative approach to dissipative particle dynamics. Europhys. Lett. 1999, 47, 145–151. [Google Scholar] [CrossRef]
- Leimkuhler, B.; Shang, X. Pairwise adaptive thermostats for improved accuracy and stability in dissipative particle dynamics. J. Comput. Phys. 2016, 324, 174–193. [Google Scholar] [CrossRef]
- Leimkuhler, B.; Shang, X. On the numerical treatment of dissipative particle dynamics and related systems. J. Comput. Phys. 2015, 280, 72–95. [Google Scholar] [CrossRef]
- Moshfegh, A.; Jabbarzadeh, A. Dissipative particle dynamics: Effects of parameterization and thermostating schemes on rheology. Soft Mater. 2015, 13, 106–117. [Google Scholar] [CrossRef]
- Moshfegh, A.; Jabbarzadeh, A. Modified Lees–Edwards boundary condition for dissipative particle dynamics: Hydrodynamics and temperature at high shear rates. Mol. Simul. 2015, 41, 1264–1277. [Google Scholar] [CrossRef]
- Moshfegh, A.; Jabbarzadeh, A. Fully explicit dissipative particle dynamics simulation of electroosmotic flow in nanochannels. Microfluid. Nanofluid. 2016, 20, 67. [Google Scholar] [CrossRef]
- Grønbech-Jensen, N.; Farago, O. A simple and effective Verlet-type algorithm for simulating Langevin dynamics. Mol. Phys. 2013, 111, 983–991. [Google Scholar] [CrossRef]
- Abdulle, A.; Vilmart, G.; Zygalakis, K.C. Long time accuracy of Lie–Trotter splitting methods for Langevin dynamics. SIAM J. Numer. Anal. 2015, 53, 1–16. [Google Scholar] [CrossRef]
- Stoltz, G. Stable schemes for dissipative particle dynamics with conserved energy. J. Comput. Phys. 2017, 340, 451–469. [Google Scholar] [CrossRef]
- Butler, B.D.; Ayton, G.; Jepps, O.G.; Evans, D.J. Configurational Temperature: Verification of Monte Carlo Simulations. J. Chem. Phys. 1998, 109, 6519–6522. [Google Scholar] [CrossRef]
- Ruth, R.D. A canonical integration technique. IEEE Trans. Nucl. Sci. 1983, NS-30, 2669–2671. [Google Scholar] [CrossRef]
- Iwatsu, R. Two new solutions to the third-order symplectic integration method. Phys. Lett. A 2009, 373, 3056–3060. [Google Scholar] [CrossRef]
- Allen, M.P. Configurational temperature in membrane simulations using dissipative particle dynamics. J. Phys. Chem. B 2006, 110, 3823–3830. [Google Scholar] [CrossRef]
- Den Otter, W.K.; Clarke, J.H.R. A new algorithm for dissipative particle dynamics. Europhys. Lett. 2001, 53, 426–431. [Google Scholar] [CrossRef]
- Español, P.; Warren, P. Statistical mechanics of dissipative particle dynamics. Europhys. Lett. 1995, 30, 191–196. [Google Scholar] [CrossRef]
- Fan, X.; Phan-Thien, N.; Chen, S.; Wu, X.; Ng, T.Y. Simulating flow of DNA suspension using dissipative particle dynamics. Phys. Fluids 2006, 18, 063102. [Google Scholar] [CrossRef]
- Li, Z.; Tang, Y.H.; Lei, H.; Caswell, B.; Karniadakis, G.E. Energy-conserving dissipative particle dynamics with temperature-dependent properties. J. Comput. Phys. 2014, 265, 113–127. [Google Scholar] [CrossRef]
- Pan, W.; Caswell, B.; Karniadakis, G.E. Rheology, microstructure and migration in Brownian colloidal suspensions. Langmuir 2009, 26, 133–142. [Google Scholar] [CrossRef]
- Azhar, M.; Greiner, A.; Korvink, J.G.; Kauzlarić, D. Dissipative particle dynamics of diffusion-NMR requires high Schmidt-numbers. J. Chem. Phys. 2016, 144, 244101. [Google Scholar] [CrossRef]
- Morohoshi, K.; Hayashi, T. Modeling and simulation for fuel cell polymer electrolyte membrane. Polymers 2013, 5, 56–76. [Google Scholar] [CrossRef]
- Gavrilov, A.A.; Chertovich, A.V.; Potemkin, I.I. Phase Behavior of Melts of Diblock-Copolymers with One Charged Block. Polymers 2019, 11, 1027. [Google Scholar] [CrossRef]
- Yoshida, H. Construction of higher order symplectic integrators. Phys. Lett. A 1990, 150, 262–268. [Google Scholar] [CrossRef]
| Scheme | 10% TH | 1% TH | ||
|---|---|---|---|---|
| SE | SE | |||
| M-Verlet | 0.05 | 1 | 0.01 | 1 |
| M-Shardlow | 0.1 | 0.39 | 0.02 | 0.40 |
| PRK3 (Ruth) | 0.1 | 1.02 | 0.05 | 2.55 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yamada, T.; Itoh, S.; Morinishi, Y.; Tamano, S. Temperature Error Reduction of DPD Fluid by Using Partitioned Runge-Kutta Time Integration Scheme. Fluids 2019, 4, 156. https://doi.org/10.3390/fluids4030156
Yamada T, Itoh S, Morinishi Y, Tamano S. Temperature Error Reduction of DPD Fluid by Using Partitioned Runge-Kutta Time Integration Scheme. Fluids. 2019; 4(3):156. https://doi.org/10.3390/fluids4030156
Chicago/Turabian StyleYamada, Toru, Shugo Itoh, Yohei Morinishi, and Shinji Tamano. 2019. "Temperature Error Reduction of DPD Fluid by Using Partitioned Runge-Kutta Time Integration Scheme" Fluids 4, no. 3: 156. https://doi.org/10.3390/fluids4030156
APA StyleYamada, T., Itoh, S., Morinishi, Y., & Tamano, S. (2019). Temperature Error Reduction of DPD Fluid by Using Partitioned Runge-Kutta Time Integration Scheme. Fluids, 4(3), 156. https://doi.org/10.3390/fluids4030156





