1. Introduction
It is well known that much can be learned about a physical phenomenon if a mathematical model exists that can mimic and predict its behavior. The world of complex fluids is no different, and, therefore, several models have been proposed over the years for that purpose. These models can be more or less complex, depending on the properties of the fluids that are taken into account.
In this work, we are interested in viscoelastic materials [
1], for which several models have been proposed in the past. One can classify these models as: differential (that make use of the local deformation field only) and integral (that take into account all the past deformation at each instant). Differential models usually allow a faster numerical solution of the differential equations involved, while integral models are computationally expensive and may lead to error propagation. On the other hand, integral models allow a better modelling, since they incorporate the real world fluid memory (the present state is influenced by all past weighted deformations). It is therefore of major importance to improve the fitting capabilities of differential models and reduce the computational effort needed to compute integral models.
In a recent work, Ferrás et al. [
2] proposed an improved differential model based on the model by Nhan Phan-Thien and Roger Tanner (PTT [
3]), derived from the Lodge–Yamamoto type of network theory for polymeric fluids. The constitutive equation proposed by Nhan Phan-Thien and Roger Tanner, for the case of an isothermal flow, is given by:
with
where
is the rate of deformation tensor,
is the stress tensor,
is a relaxation time,
is the polymeric viscosity,
is the trace of the stress tensor,
represents the extensibility parameter and
represents the Gordon–Schowalter derivative defined as
Here,
is the velocity vector,
is the velocity gradient and the parameter
accounts for the slip between the molecular network and the continuous medium (it should be remarked that for the derivation of the analytical solutions we will consider
). Later, Phan-Thien proposed a new model, based on an exponential function form [
4] and showed that this new function would be quite adequate to represent the rate of destruction of junctions, but the parameter
should be of the order 0.01. The function
is given by:
Ferrás et al. [
2] considered a more general function for the rate of destruction of junctions, the Mittag–Leffler function where one or two fitting constants are included, in order to achieve additional fitting flexibility [
2]. The Mittag–Leffler function is defined by,
with
,
real and positive. When
, the Mittag–Leffler [
5] function reduces to the exponential function. When
, the original one-parameter Mittag–Leffler function,
, is obtained. Thus, the new function of the trace of stress tensor (now denoted by
instead of
, to distinguish from the classical cases) describing the network destruction of junctions is written as:
where
is the Gamma function and the normalisation
is used to ensure that
, for all choices of
.
The linear and the exponential model of the Phan-Thien–Tanner has been frequently used in the literature, and in fact Ferrás et al. [
6] considered a new quadratic version of the PTT model, i.e., a second-order expansion of the exponential model given by:
Here, we compare the generalised Phan-Thien–Tanner (gPTT), given by Equation (
6), with the linear, the exponential and the quadratic versions of the PTT (Equations (
2), (
4) and (
7), respectively).
To compare these models, we study the dimensionless material properties in steady shear flow of the three versions of the PTT model and compare them with the new gPTT model, considering different values of and .
The material functions can be obtained considering a steady-state Couette flow in the
x-direction,
, where
is the shear rate. For this flow, considering the parameter
, the constitutive Equation (
1) reduces to:
From the system of Equation (
8),
and applying some algebra in the first two equations, a relationship between the shear stress and the normal stress is found,
We can also obtain the viscometric material functions: the steady shear viscosity,
, the first normal stress difference coefficient,
, and the second normal stress difference coefficient,
, which are given by:
As for other versions of the simplified PTT models for which
, the second normal stress coefficient is null,
, so, we only need to find
and
. Therefore, manipulating the second equation of the system of Equations (
8) we get,
The dimensionless expression for the steady shear viscosity becomes,
and the dimensionless first normal stress coefficient is given by,
In [
6], it was shown that, for the linear PTT, the quadratic PTT and the exponential PTT, the dimensionless material functions depend on the generalised Deborah number,
. We show that the same happens for the gPTT model. To obtain the material function for the gPTT model, we need to solve the non-linear system of equations (Equation (
8)), which can be written in terms of
in the non-linear form:
Giving values to
, we can find
using Equation (
16). Then, the function
is directly calculated, allowing us to obtain the material functions given by Equations (
14) and (
15).
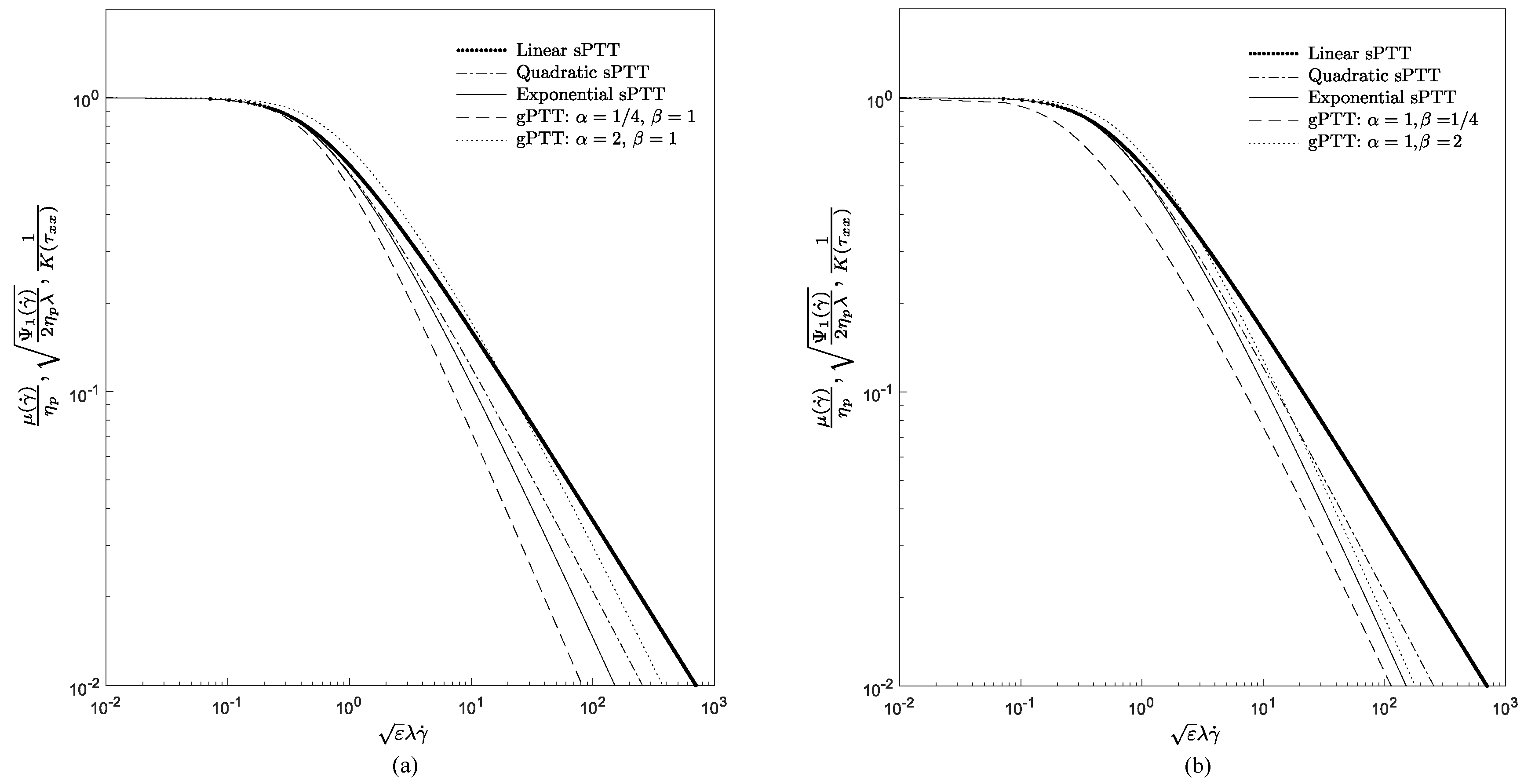
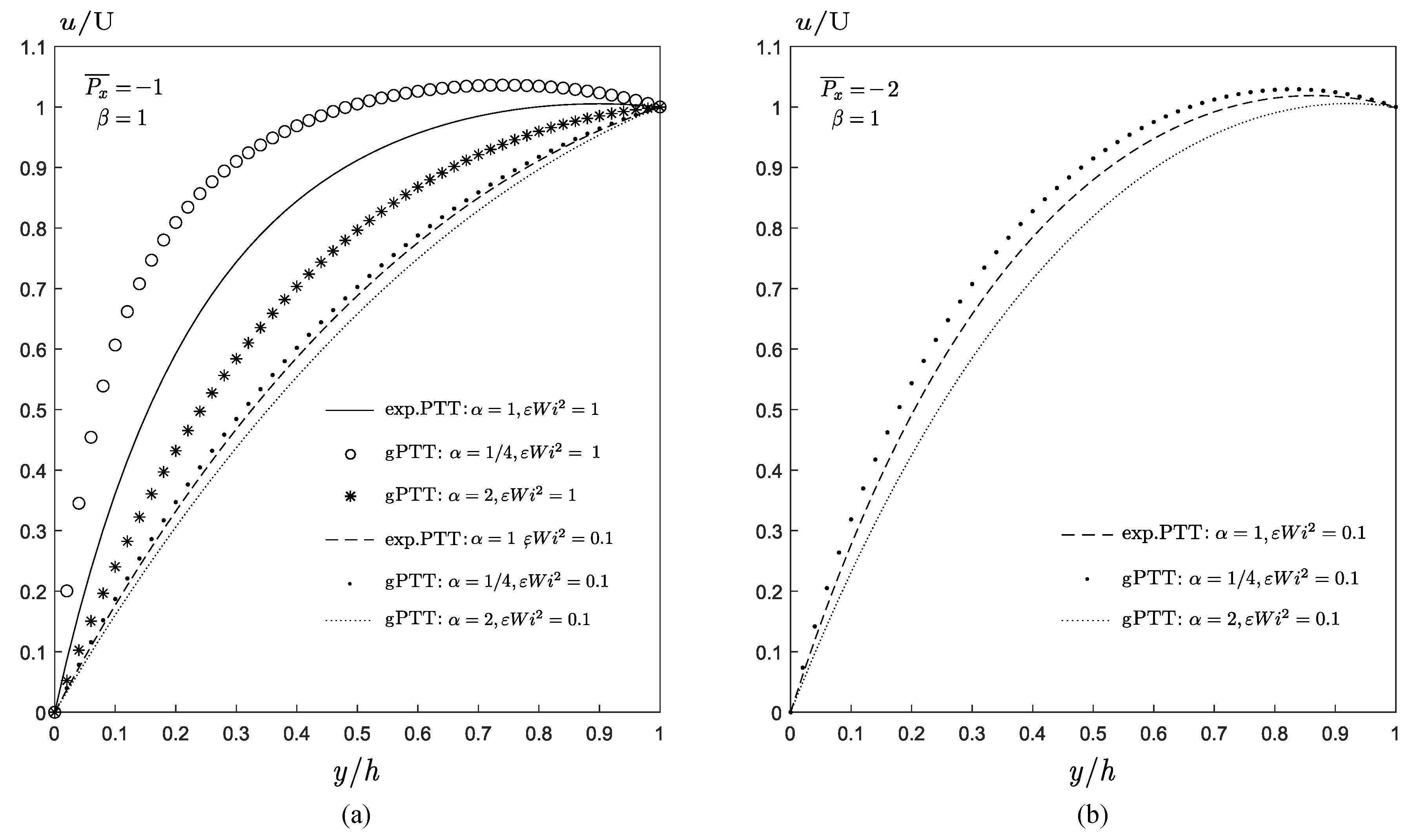
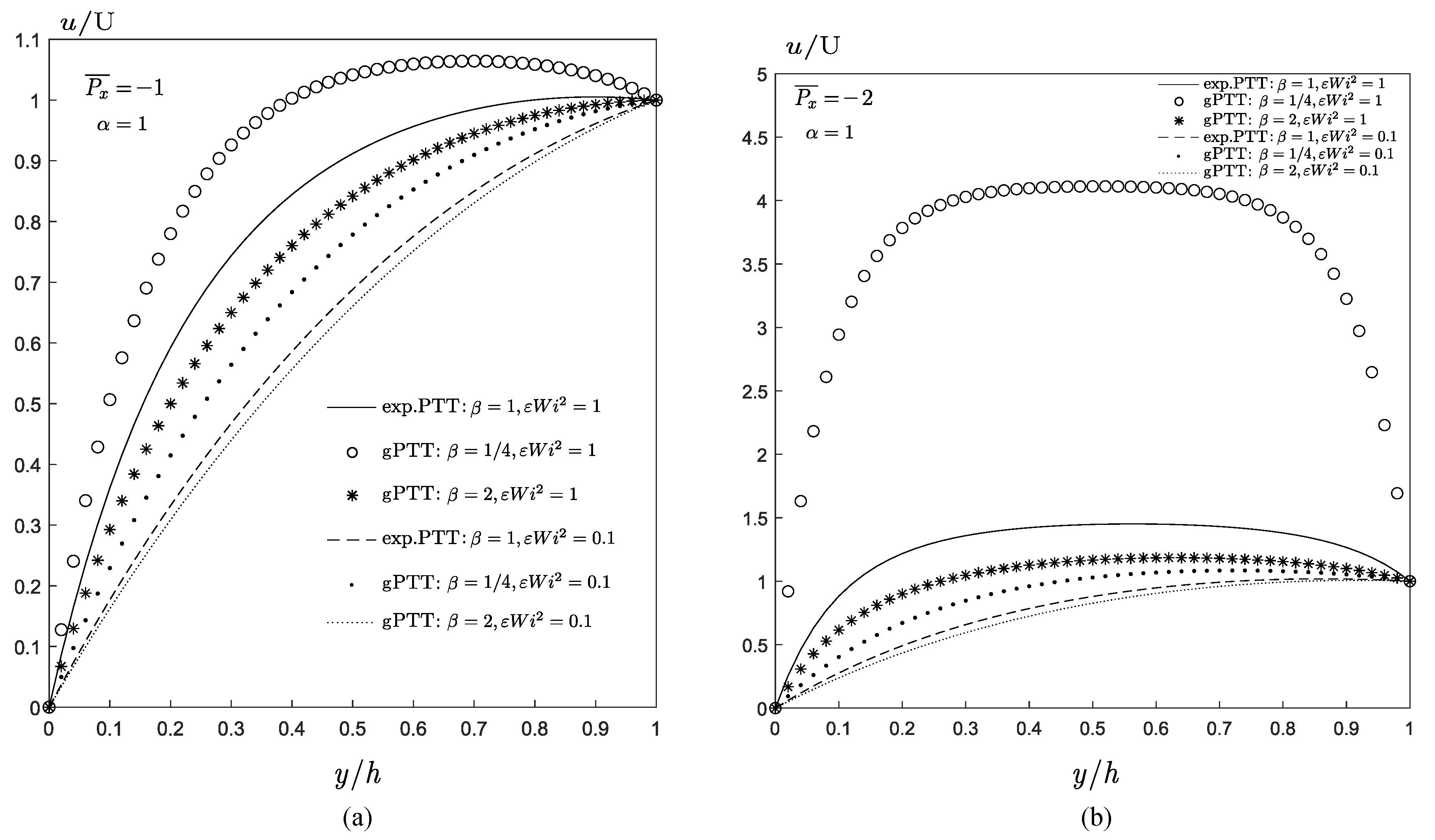
Figure 1 presents the dimensionless material properties for the steady-state Couette flow using three versions of the PTT (linear, quadratic, and exponential) and also the gPTT model. In
Figure 1a, we set
and use different values of
, and, in
Figure 1b, we set
and use different values to
.
We observe that the new generalised function allows a broader description of the thinning properties of the fluid. Both the thinning rate and the onset of the thinning behavior can be controlled by the new model parameters. Therefore, this new model must be further explored for weak flows, such as Couette flows.
This model was extensively studied for strong flows in [
2], where an explanation on the influence of the new model parameters was provided.
Note that the exponential version of the model was developed to take into account the strong destruction of network junctions, which occurs, for example, in strong flows (e.g., extensional flows). Although the exponential model was derived for such strong flows, it was shown in [
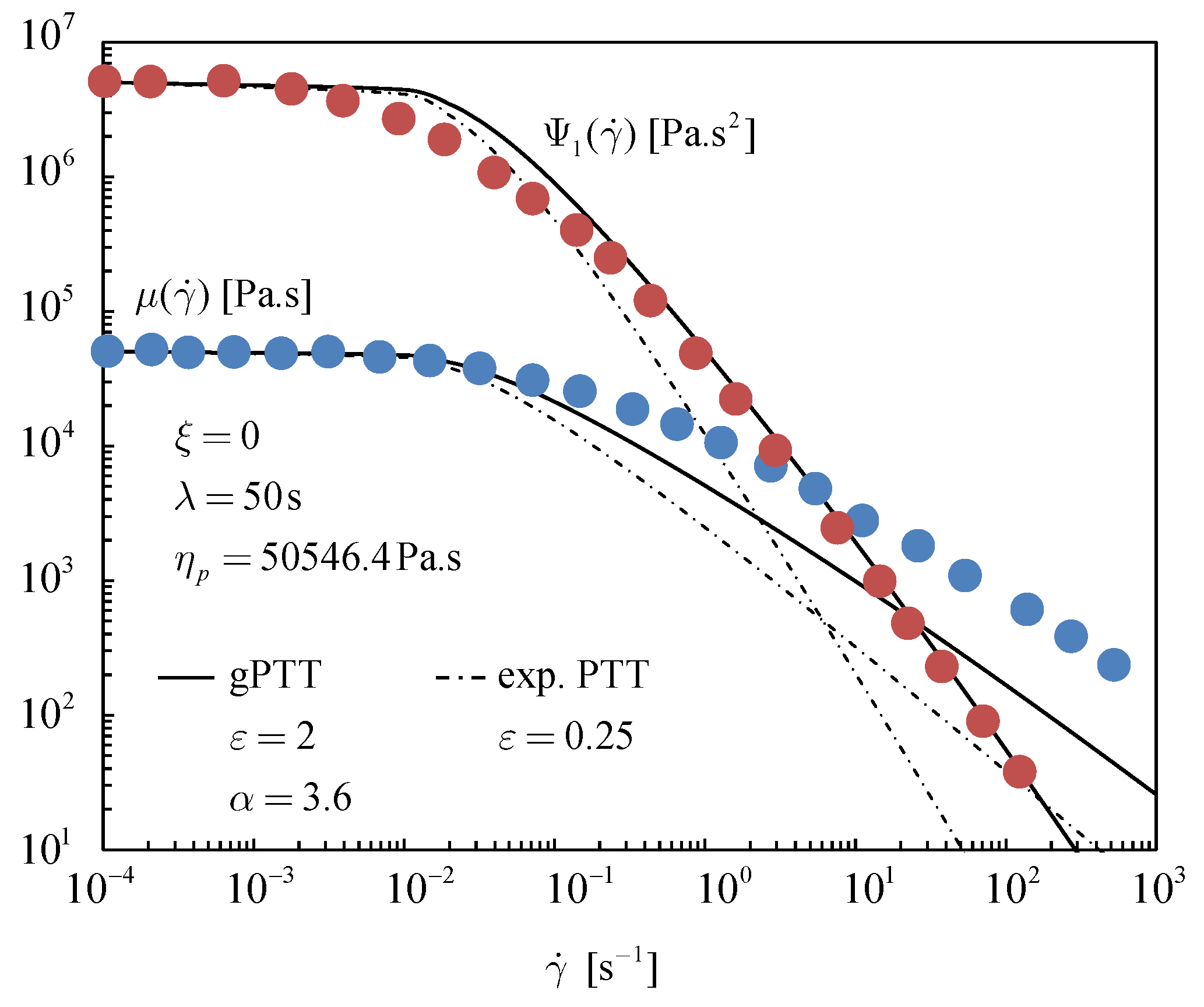
2] that the gPTT model could slightly improve the fitting for shear (weak) flows, considering polymer solutions. Here, we consider polymer melts.
Figure 2 shows that the gPTT model provides a much better fitting to weak flows of polymer melts (low density polyethylene melt [
7]), even when using only one extra parameter (
).
To quantify the error incurred during the fitting process, we used a mean square error given by
with
and
the number of experimental points obtained for
and
, respectively.
A better fit was obtained for the new generalised model when compared to the original exponential PTT model. The total mean square error obtained for the exponential PTT model was , being five times the error obtained for its generalised version (for which a value of was obtained). The new model allows a better fit for low and high shear rates for the first normal stress difference (where the obtained for the exponential PTT model is 20 times higher than the error obtained for the gPTT). For the shear viscosity, the gPTT model predicts a lower value (when compared to experimental data) for high shear rates (although it should be remarked that the is four times smaller when compared to the exponential model).
Based on what is described above, this work presents analytical and semi-analytical solutions for pure Couette and Poiseuille–Couette flows, described by the generalised Phan-Thien–Tanner constitutive equation. It is well known that the rate of destruction of junctions increases for strong flows (e.g., extensional flows), but, in this case, we consider weak flows, and study the capability of this new model to describe them. This is done by performing a parametric study for the influence of the gPTT parameters.
2. Analytical Solution for the gPTT Model in Couette flow
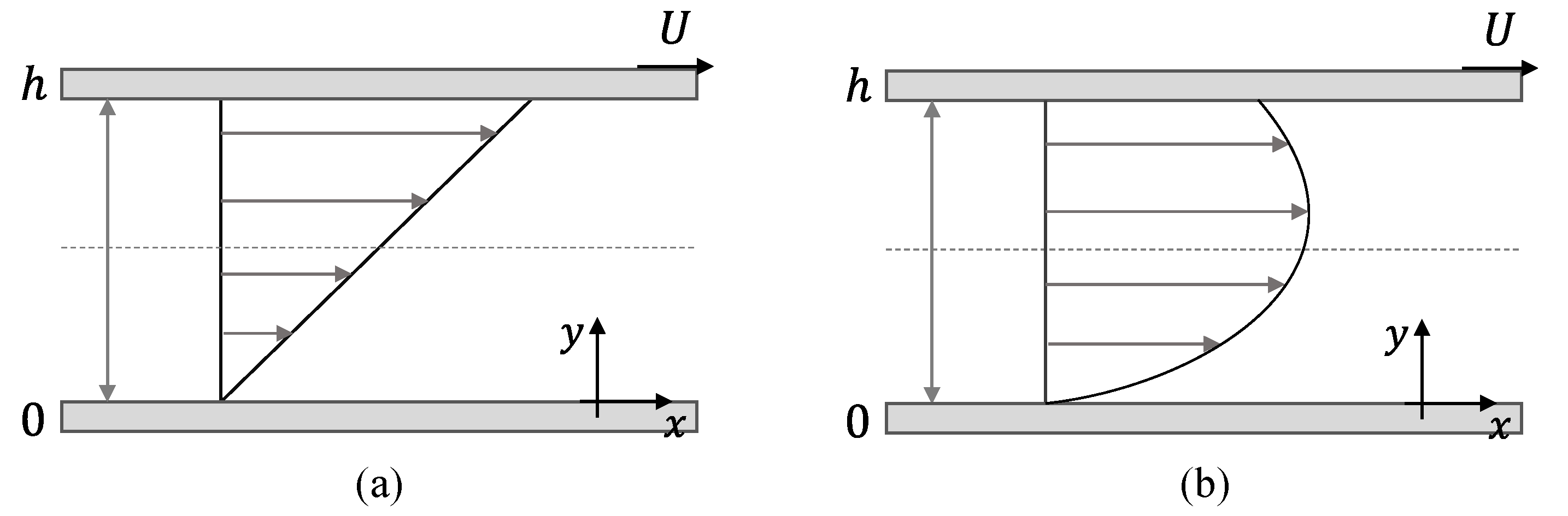
In this section, we derive the analytical solution for the fully developed flow of the gPTT model considering both Couette and Poiseuille–Couette flows (cf.
Figure 3). To obtain closed form analytical solutions, the slip parameter in the Gordon–Schowalter derivative is set to
.
The equations governing the flow of an isothermal incompressible fluid are the continuity,
and the momentum equation,
together with the constitutive equation,
where
is the material derivative,
p is the pressure,
t is the time and
is the fluid density.
We consider a Cartesian coordinate system with
x,
y, and
z being the streamwise, transverse and spanwise directions, respectively. The flow is assumed to be fully-developed and therefore the governing equations can be further simplified since
Therefore, Equation (
21) can be integrated, leading to the following general equation for the shear stress:
where
is the pressure gradient in the
x direction,
is the shear stress and
is a stress constant. This equation is valid regardless of the rheological constitutive equation. The constitutive equations for the generalised PTT model describing this flow can be further simplified leading to:
where the shear rate
is a function of
y (
) and
is the trace of the stress tensor. Assuming
, Equation (
26) implies that
, and the trace of the stress tensor becomes
. Dividing Equation (
25) by Equation (
27),
cancels out, and we get the explicit relationship between the streamwise normal stress and the shear stress given by Equation (
9).
Now, combining Equations (
9), (
24) and (
27), the following shear rate profile is obtained,
The velocity profile can be obtained integrating the shear rate subject to the Couette boundary conditions (null velocity at the immobile wall),
and an imposed constant velocity, U, at the moving wall,
This leads to the following velocity profile:
where
can be obtained by solving numerically the following equation,
Combining Equations (
31) and (
32) leads to the following dimensionless velocity profile:
with
,
,
,
and
the Weissenberg number.
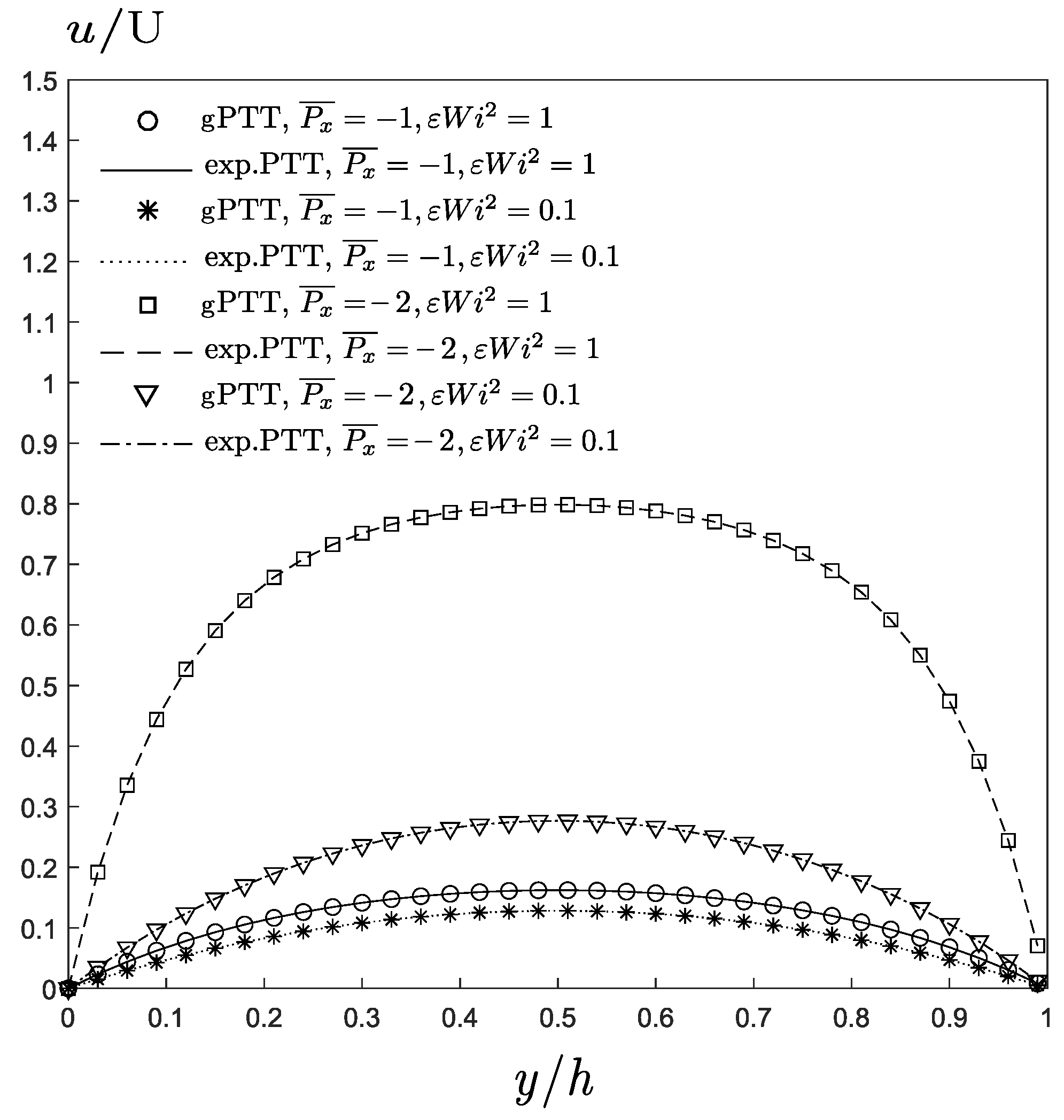
Remark 1. Note that, if , Equation (31) becomes,and Equation (32) leads to , corresponding to Poiseuille flow with no slip boundary conditions. The velocity profile can be written in dimensionless form as: When we consider , this equation reduces to the one presented by Oliveira and Pinho [8] for the planar channel flow of an exponential PTT fluid: Figure 4 shows a comparison between the gPTT model and exponential PTT (Equations (35) and (36)) for different values of . As expected, the results are identical, confirming the solution limit for on the Mittag–Leffler function.