Computational Optimization of Adaptive Hybrid Darrieus Turbine: Part 1
Abstract
1. Introduction
2. State of art of Computational Simulations on VAWT
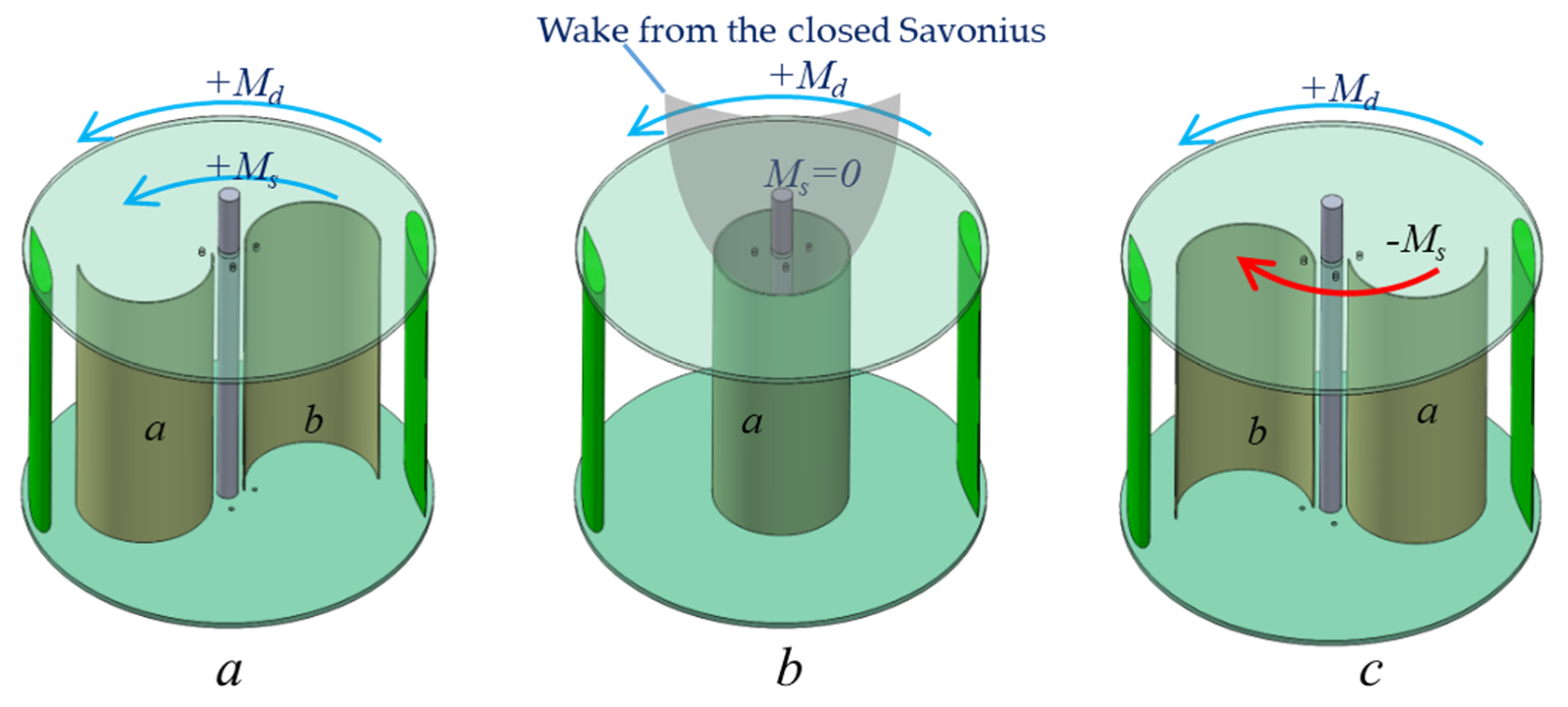
3. Overview of Adaptive Hybrid Darrieus Turbine
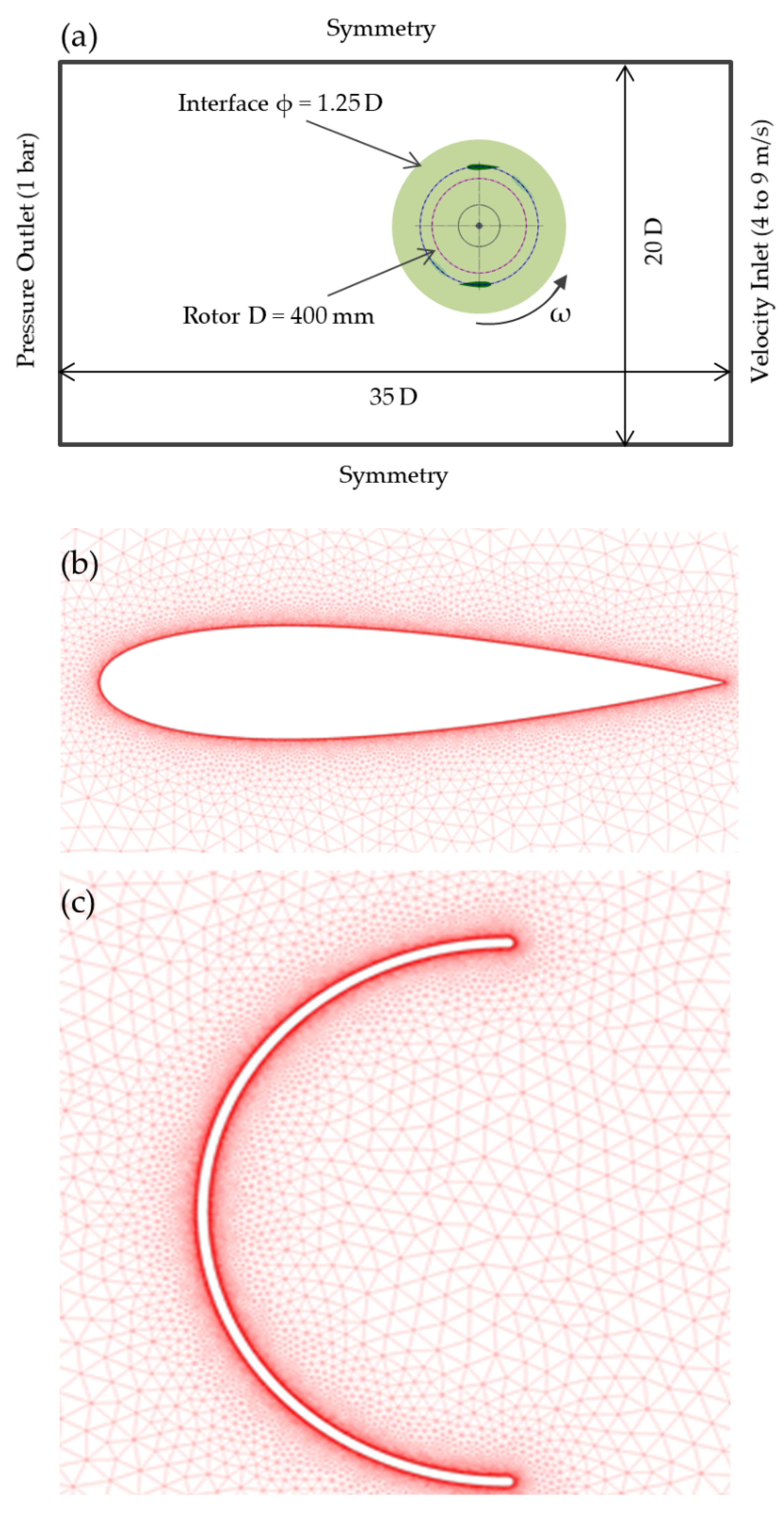
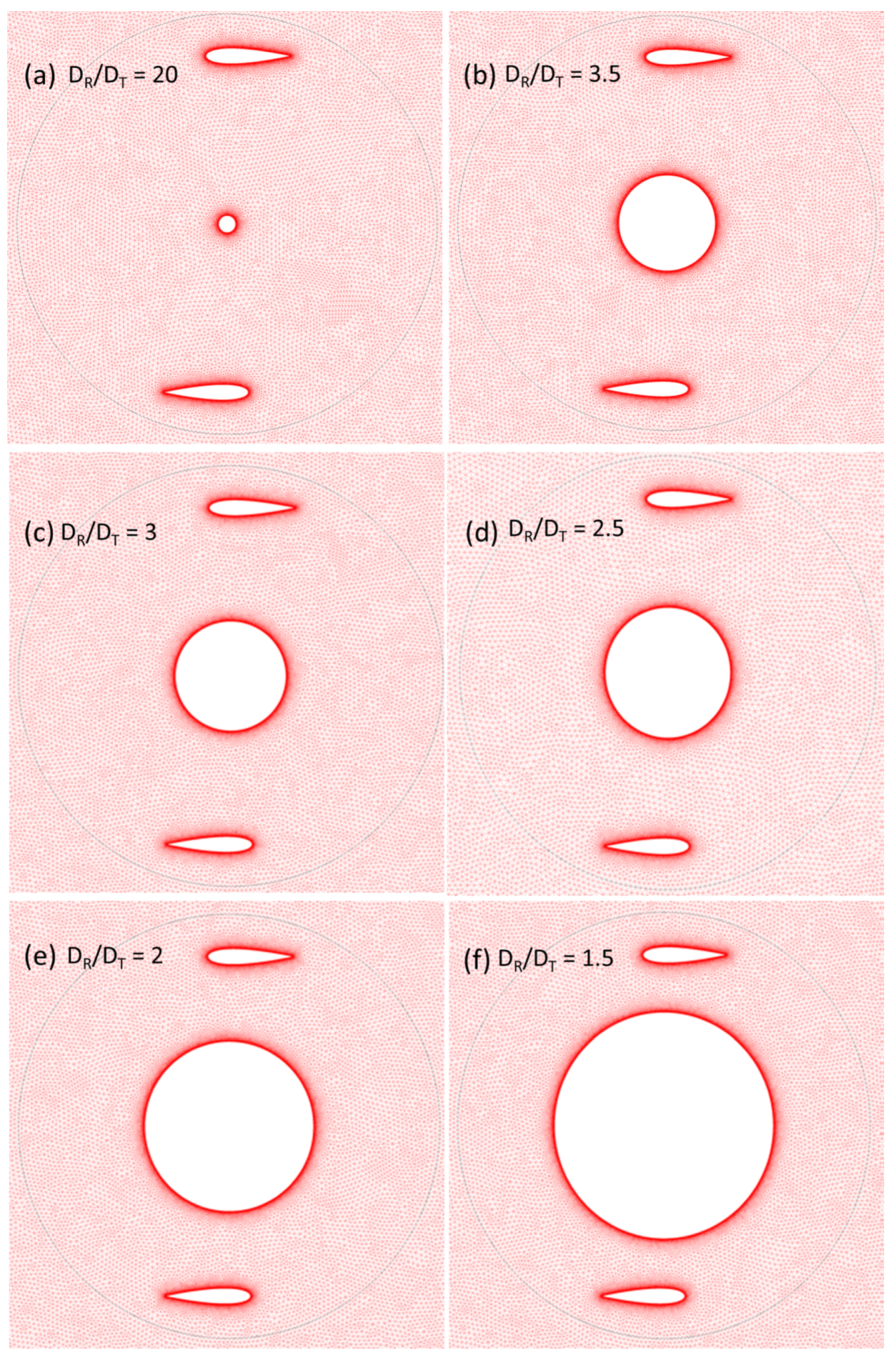
4. Computational Domain and Meshing
5. Convergence Analysis
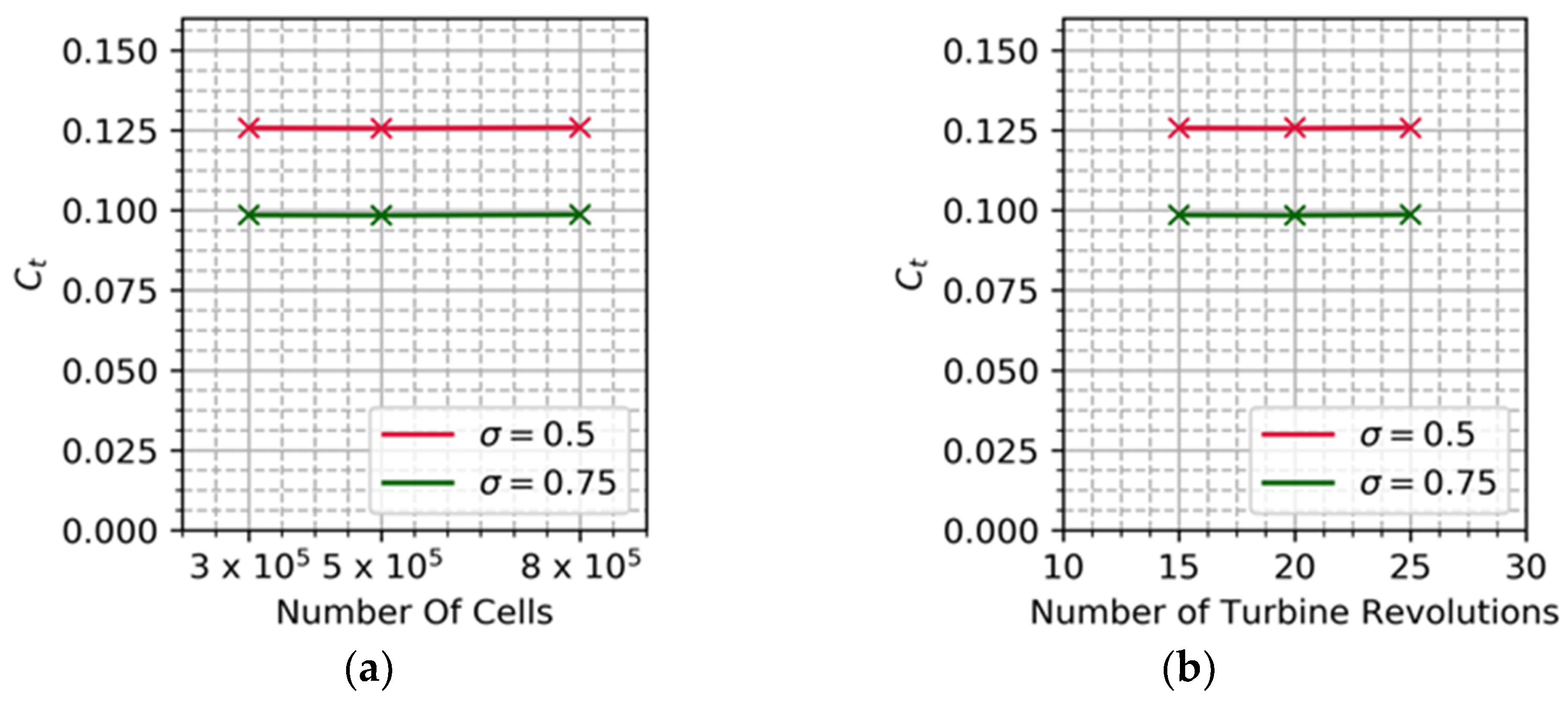
5.1. Grid Convergence Analysis
5.2. Revolution Convergence Analysis
6. Mathematical Methodology
6.1. Reynolds Averaged Navier–Stokes Model
6.2. Turbulence Model
7. Results and Discussion
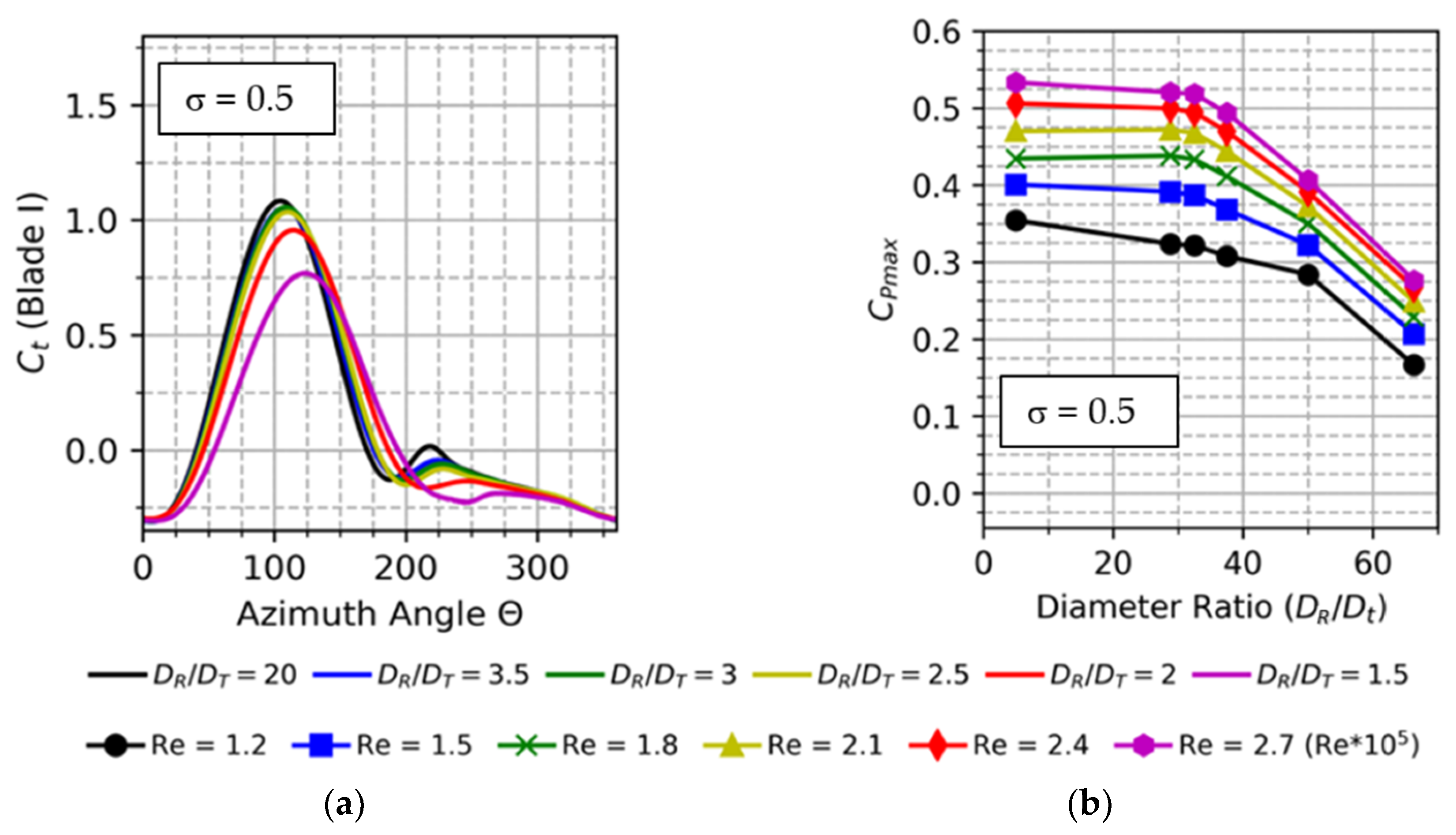
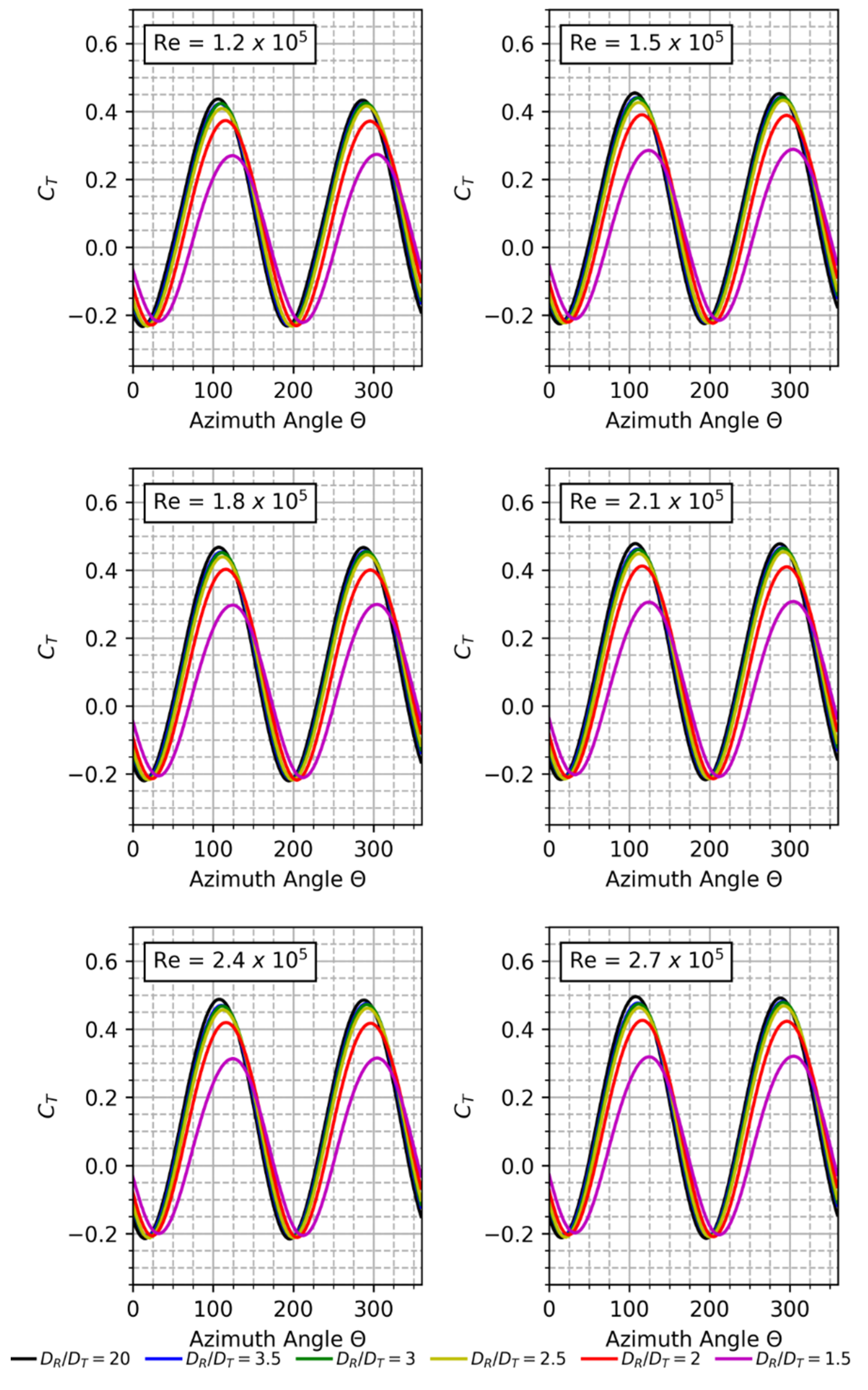
7.1. Torque Coefficient Comparison for Different (DR/DT)
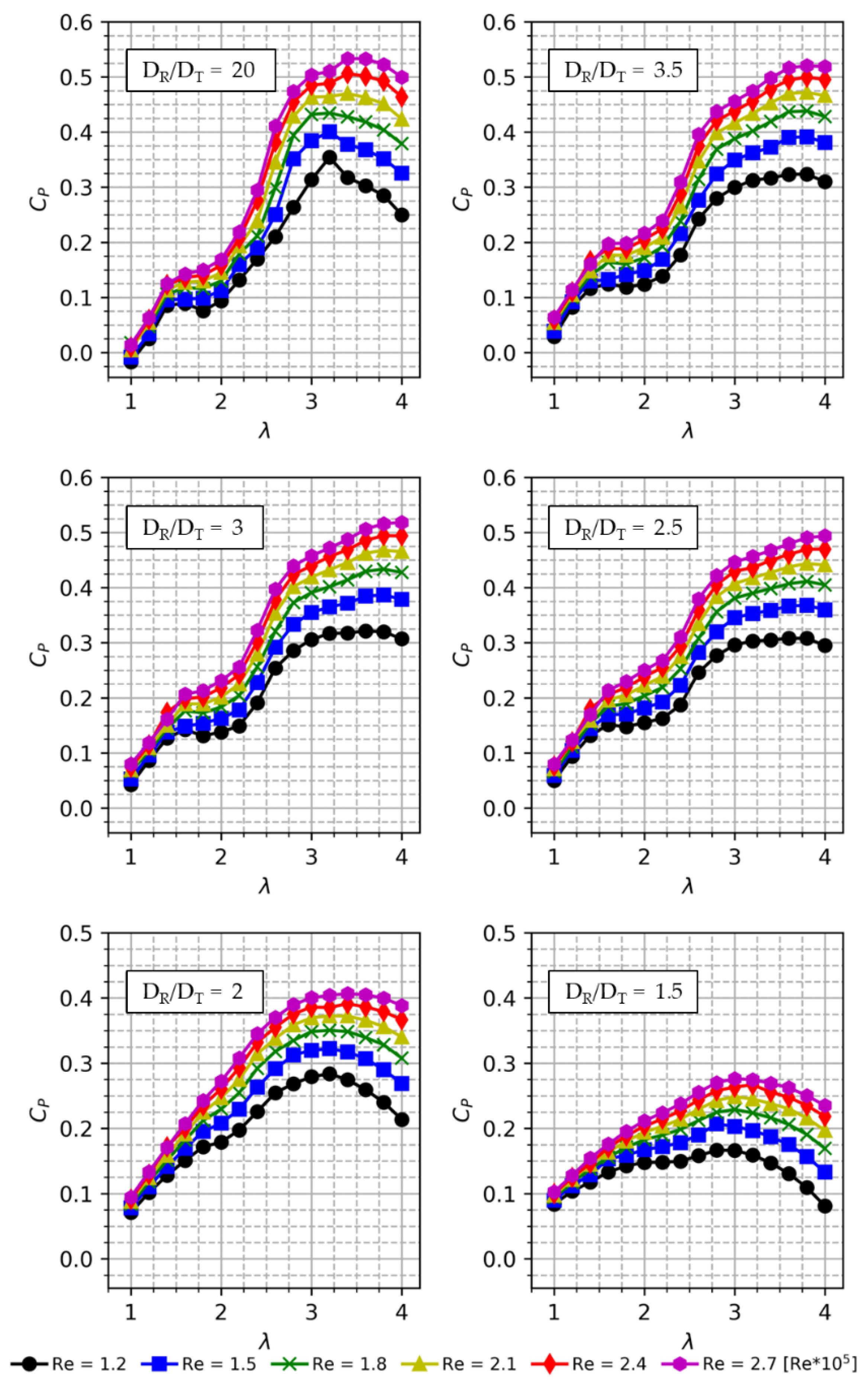
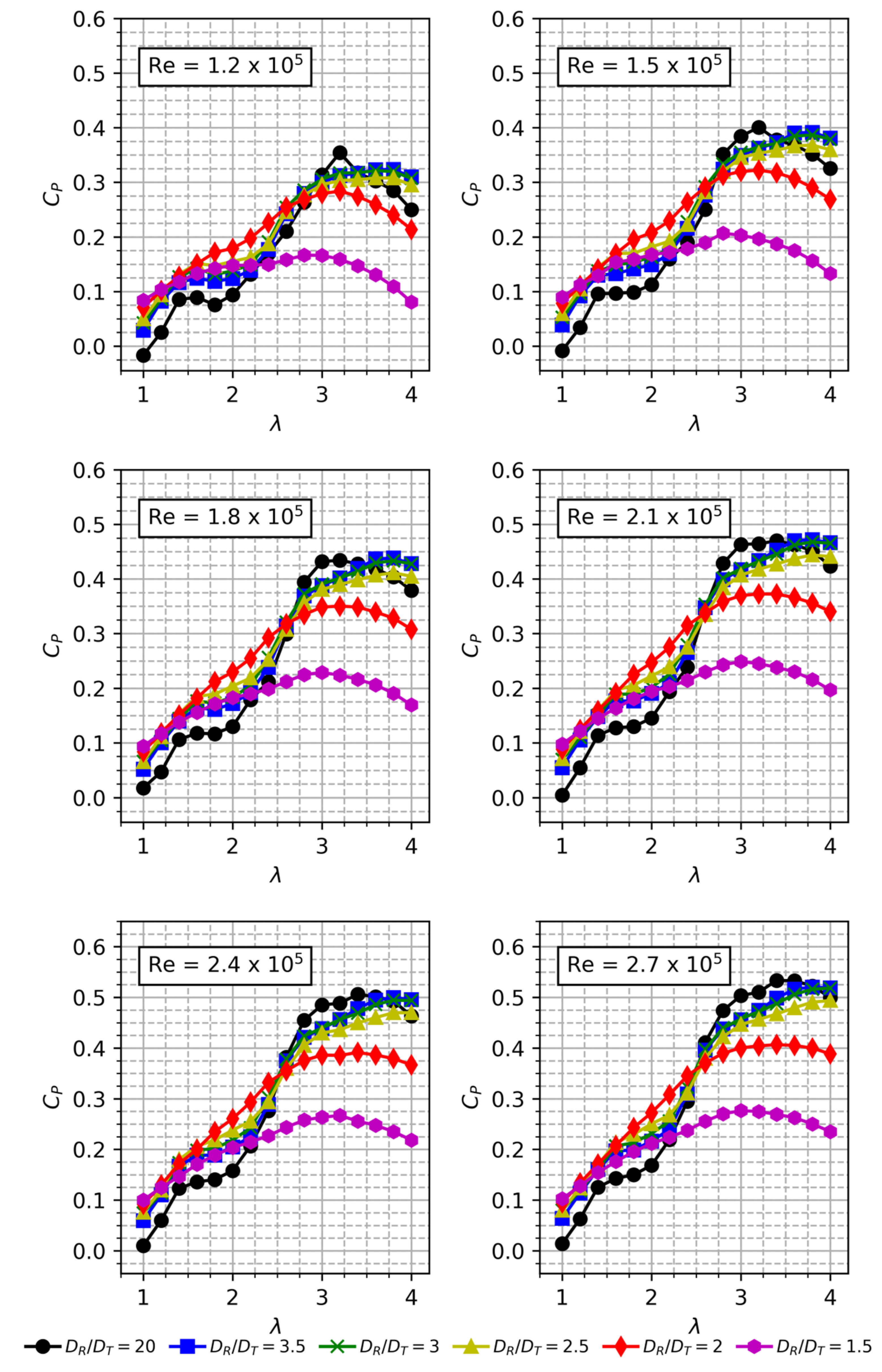
7.2. Power Coefficient Comparison for Different (DR/DT)
7.3. Effect of Re on Cp for Different DR/DT
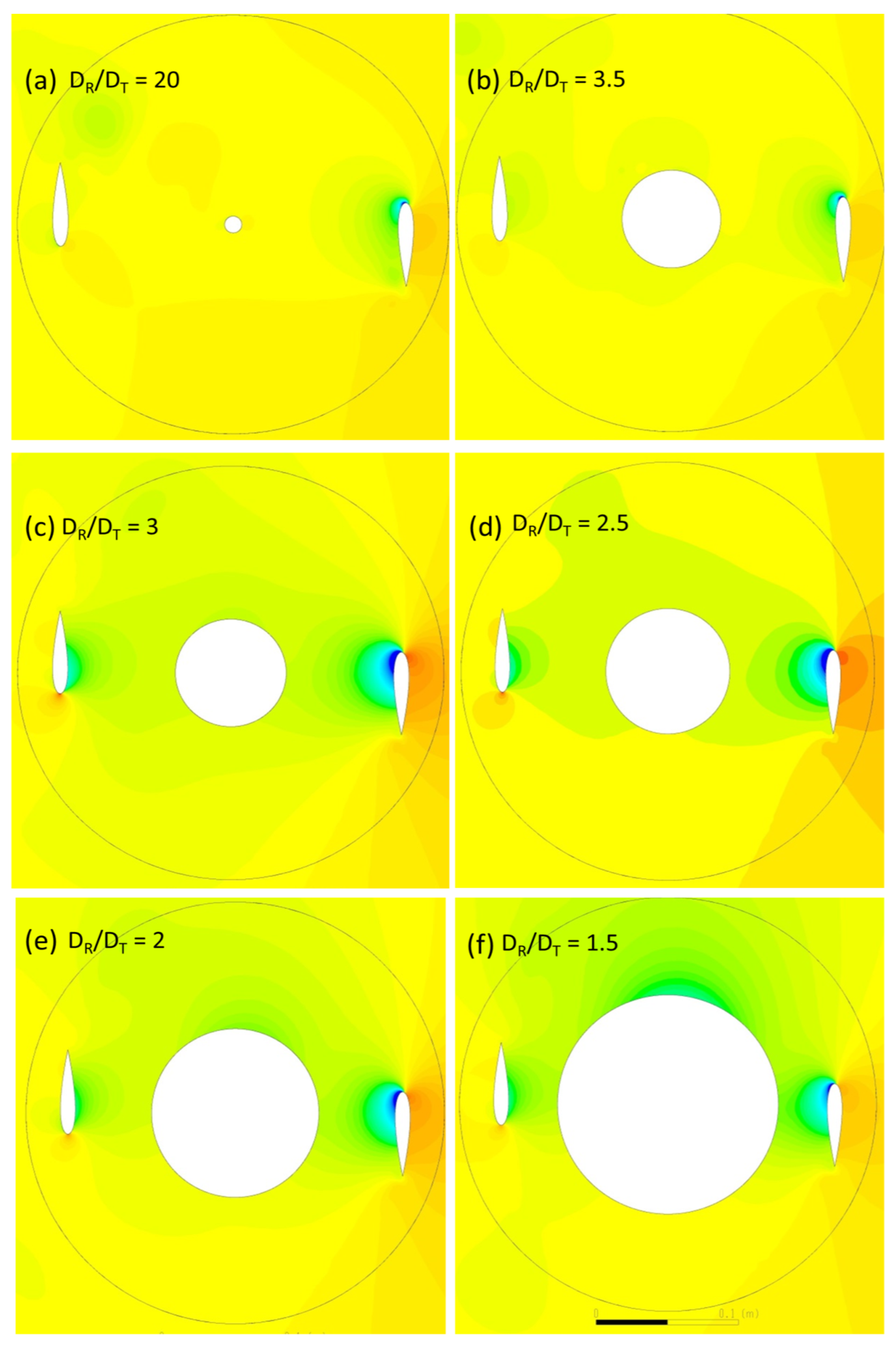
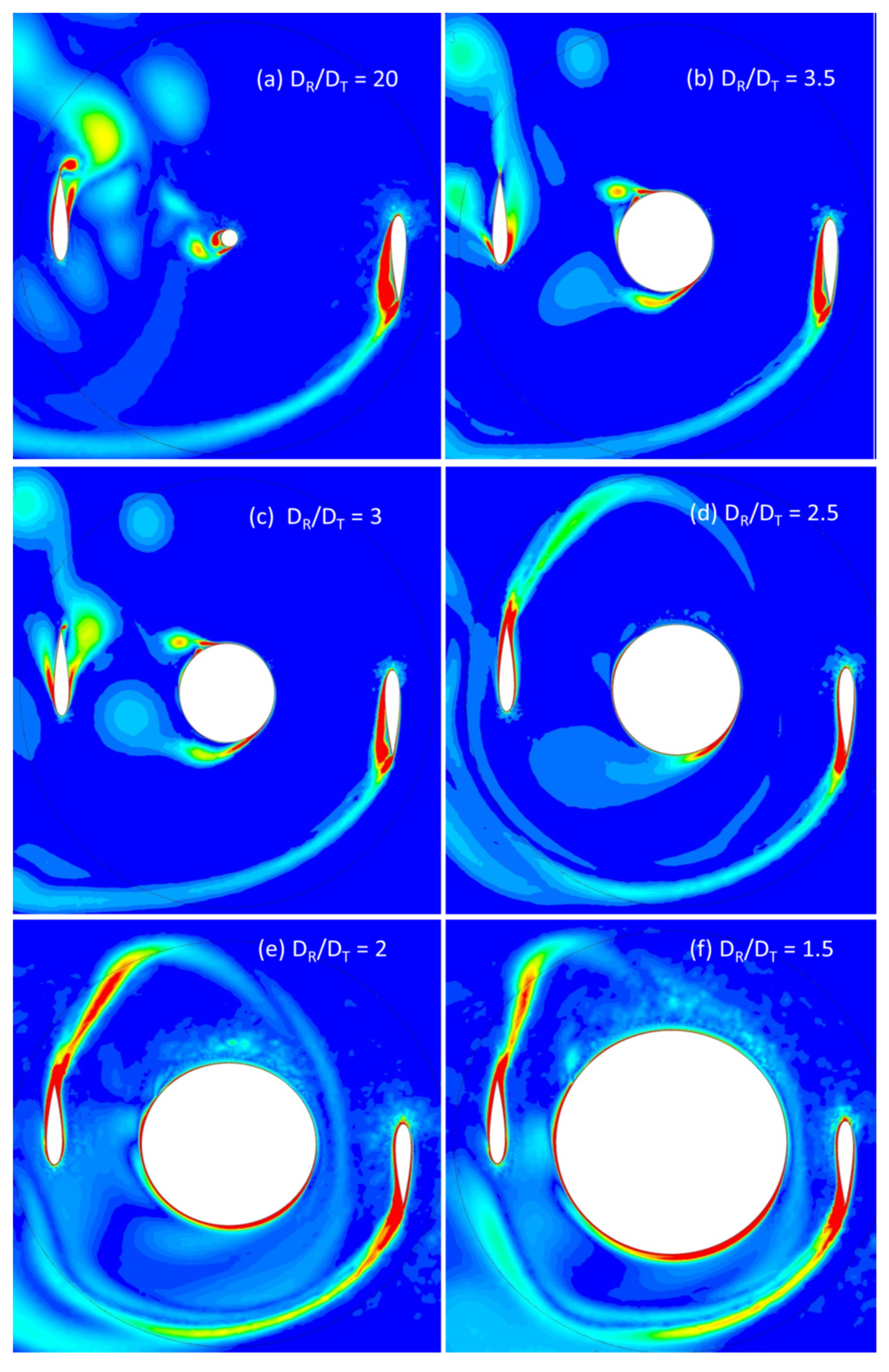
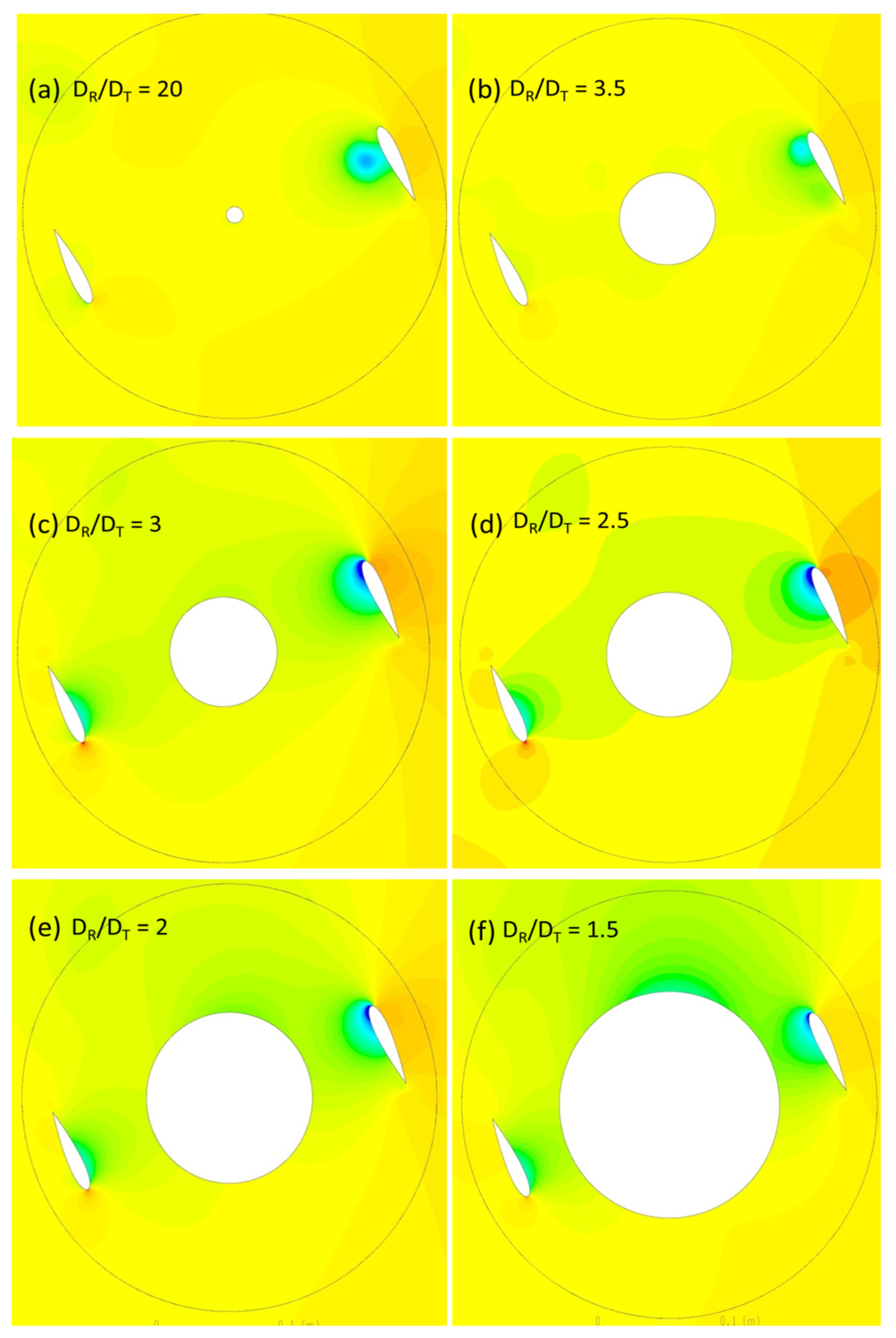
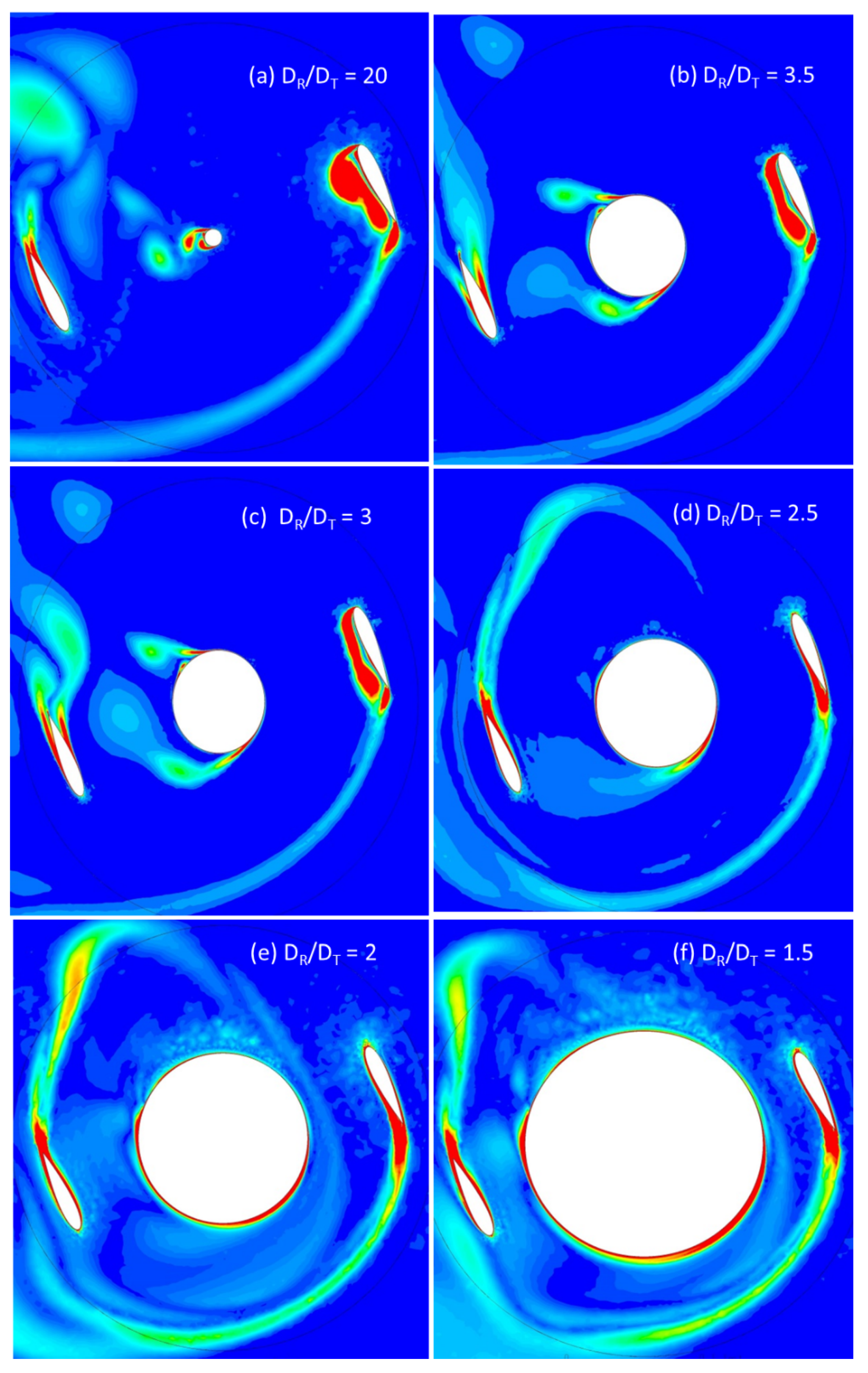
7.4. Discussion of Pressure and Vorticity Contours
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- International Energy Agency. Available online: https://www.iea.org/ (accessed on 4 April 2019).
- Karthikeya, B.; Negi, P.S.; Srikanth, N. Wind resource assessment for urban renewable energy application in Singapore. Renew. Energy 2016, 87, 403–414. [Google Scholar] [CrossRef]
- Shikha; Bhatti, T.S.; Kothari, D.P. Early Development of Modern Vertical and Horizontal Axis Wind Turbines: A Review. Wind Eng. 2005, 29, 287–299. [Google Scholar] [CrossRef]
- IEC 61400-2:2013 Wind Turbines Part 2: Small Wind Turbines. Available online: https://webstore.iec.ch/publication/5433 (accessed on 17 May 2019).
- Golecha, K.; Kamoji, M.A.; Kedare, S.B.; Prabhu, S.V. Review on Savonius Rotor for Harnessing Wind Energy. Wind Eng. 2012, 36, 605–645. [Google Scholar] [CrossRef]
- Mohan Kumar, P.; Surya, M.M.R.; Narasimalu, S.; Lim, T.-C. Experimental and numerical investigation of novel Savonius wind turbine. Wind Eng. 2019, 43, 247–262. [Google Scholar] [CrossRef]
- Kumar, P.M.; Purimitla, S.R.; Shubhra, S.; Srikanth, N. Numerical and analytical study on telescopic savonius turbine blade. In Proceedings of the 2017 3rd International Conference on Power Generation Systems and Renewable Energy Technologies (PGSRET), Johor Bahru, Malaysia, 4–6 April 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 107–112. [Google Scholar]
- Gorlov, A. Development of the Helical Reaction Hydraulic Turbine; Final Technical Report; Northeastern Univ.: Boston, MA, USA, 1998. [Google Scholar]
- Baker, J. Features to aid or enable self starting of fixed pitch low solidity vertical axis wind turbines. J. Wind Eng. Ind. Aerodyn. 1983, 15, 369–380. [Google Scholar] [CrossRef]
- Shiono, M.; Suzuki, K.; Kiho, S. Output characteristics of Darrieus water turbine with helical blades for tidal current generations. In Proceedings of the Twelfth International Offshore and Polar Engineering Conference, Kitakyushu, Japan, 26–31 May 2002; ISOPE: Cupertino, CA, USA, 2002. [Google Scholar]
- Kumar, M.; Surya, M.M.R.; Sin, N.P.; Srikanth, N. Design and experimental investigation of airfoil for extruded blades. Int. J. Adv. Agric. Environ. Eng. 2017, 3, 359–400. [Google Scholar]
- Kumar, P.M.; Surya, M.M.R.; Kethala, R.; Srikanth, N. Experimental investigation of the performance of darrieus wind turbine with trapped vortex airfoil. In Proceedings of the 2017 3rd International Conference on Power Generation Systems and Renewable Energy Technologies (PGSRET), Johor Bahru, Malaysia, 4–6 April 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 130–135. [Google Scholar]
- Kumar, P.M.; Surya, M.M.R.; Srikanth, N. On the improvement of starting torque of darrieus wind turbine with trapped vortex airfoil. In Proceedings of the 2017 IEEE International Conference on Smart Grid and Smart Cities (ICSGSC), Singapore, 23–26 July 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 120–125. [Google Scholar]
- Kumar, P.M.; Ajit, K.R.; Surya, M.R.; Srikanth, N.; Lim, T.-C. On the self starting of darrieus turbine: An experimental investigation with secondary rotor. In Proceedings of the 2017 Asian Conference on Energy, Power and Transportation Electrification (ACEPT), Singapore, 24–26 October 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–7. [Google Scholar]
- Kumar, P.M.; Kulkarni, R.; Srikanth, N.; Lim, T.-C. Performance Assessment of Darrieus Turbine with Modified Trailing Edge Airfoil for Low Wind Speeds. Smart Grid Renew. Energy 2017, 8, 425–439. [Google Scholar] [CrossRef]
- Wakui, T.; Tanzawa, Y.; Hashizume, T.; Nagao, T. Hybrid configuration of Darrieus and Savonius rotors for stand-alone wind turbine-generator systems. Electr. Eng. Jpn. 2005, 150, 13–22. [Google Scholar] [CrossRef]
- Kjellin, J.; Bernhoff, H. Electrical starter system for an H-rotor type VAWT with PM-generator and auxiliary winding. Wind Eng. 2011, 35, 85–92. [Google Scholar] [CrossRef]
- Chougule, P.D.; Nielsen, S.R.K.; Basu, B. Active Blade Pitch Control for Straight Bladed Darrieus Vertical Axis Wind Turbine of New Design. Key Eng. Mater. 2013, 569–570, 668–675. [Google Scholar] [CrossRef]
- Hwang, I.S.; Min, S.Y.; Jeong, I.O.; Lee, Y.H.; Kim, S.J. Efficiency improvement of a new vertical axis wind turbine by individual active control of blade motion. In Proceedings of the SPIE Smart Structures and Materials + Nondestructive Evaluation and Health Monitoring, San Diego, CA, USA, 5 April 2006; SPIE: Bellingham, WA, USA; p. 617311. [Google Scholar]
- Rassoulinejad-Mousavi, S.; Jamil, M.; Layeghi, M. Experimental study of a combined three bucket H-rotor with savonius wind turbine. World Appl. Sci. J. 2013, 28, 205–211. [Google Scholar]
- Gupta, R.; Das, R.; Sharma, K. Experimental study of a Savonius-Darrieus wind machine. In Proceedings of the International Conference on Renewable Energy for Developing Countries, Washington, DC, USA, 6 April 2006. [Google Scholar]
- Gupta, R.; Sharma, K. Flow physics of a combined Darrieus-Savonius rotor using computational fluid dynamics (CFD). Int. Res. J. Eng. Sci. Technol. Innov. 2012, 1, 1–13. [Google Scholar]
- Kyozuka, Y. An experimental study on the Darrieus-Savonius turbine for the tidal current power generation. J. Fluid Sci. Technol. 2008, 3, 439–449. [Google Scholar] [CrossRef]
- Tescione, G.; Ragni, D.; He, C.; Ferreira, C.S.; Van Bussel, G. Near wake flow analysis of a vertical axis wind turbine by stereoscopic particle image velocimetry. Renew. Energy 2014, 70, 47–61. [Google Scholar] [CrossRef]
- Balduzzi, F.; Drofelnik, J.; Bianchini, A.; Ferrara, G.; Ferrari, L.; Campobasso, M.S. Darrieus wind turbine blade unsteady aerodynamics: a three-dimensional Navier-Stokes CFD assessment. Energy 2017, 128, 550–563. [Google Scholar] [CrossRef]
- Ferreira, C.S.; Van Kuik, G.; Van Bussel, G.; Scarano, F. Visualization by PIV of dynamic stall on a vertical axis wind turbine. Exp. Fluids 2009, 46, 97–108. [Google Scholar] [CrossRef]
- Balduzzi, F.; Bianchini, A.; Maleci, R.; Ferrara, G.; Ferrari, L. Blade design criteria to compensate the flow curvature effects in H-Darrieus wind turbines. J. Turbomach. 2015, 137, 011006. [Google Scholar] [CrossRef]
- Rezaeiha, A.; Kalkman, I.; Blocken, B. Effect of pitch angle on power performance and aerodynamics of a vertical axis wind turbine. Appl. Energy 2017, 197, 132–150. [Google Scholar] [CrossRef]
- Kumar, P.M.; Surya, M.M.R.; Srikanth, N. Comparitive CFD analysis of darrieus wind turbine with NTU-20-V and NACA0018 airfoils. In Proceedings of the 2017 IEEE International Conference on Smart Grid and Smart Cities (ICSGSC), Singapore, 23–26 July 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 108–114. [Google Scholar]
- Rezaeiha, A.; Kalkman, I.; Montazeri, H.; Blocken, B. Effect of the shaft on the aerodynamic performance of urban vertical axis wind turbines. Energy Convers. Manag. 2017, 149, 616–630. [Google Scholar] [CrossRef]
- Fujisawa, N.; Gotoh, F. Visualization study of the flow in and around a Savonius rotor. Exp. Fluids 1992, 12, 407–412. [Google Scholar] [CrossRef]
- Kumar, P.M.; Rashmitha, S.R.; Srikanth, N.; Lim, T.-C. Wind Tunnel Validation of Double Multiple Streamtube Model for Vertical Axis Wind Turbine. Smart Grid Renew.Energy 2017, 8, 412–424. [Google Scholar] [CrossRef][Green Version]
- Kumar, P.M.; Ajit, K.R.; Srikanth, N.; Lim, T.-C. On the Mathematical Modelling of Adaptive Darrieus Wind Turbine. J. Power Energy Eng. 2017, 5, 133–158. [Google Scholar] [CrossRef][Green Version]
- Kumar, P.M.; Anbazhagan, S.; Srikanth, N.; Lim, T.-C. Optimization, Design, and Construction of Field Test Prototypes of Adaptive Hybrid Darrieus Turbine. J. Fundam. Renew. Energy Appl. 2017, 7, 245. [Google Scholar]
- Rezaeiha, A.; Kalkman, I.; Blocken, B. CFD simulation of a vertical axis wind turbine operating at a moderate tip speed ratio: guidelines for minimum domain size and azimuthal increment. Renew. Energy 2017, 107, 373–385. [Google Scholar] [CrossRef]
| Re × 105 | DR/DT | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 20 | 3.5 | 3 | 2.5 | 2 | 1.5 | |||||||
| Cp | Δ % | Cp | Δ % | Cp | Δ % | Cp | Δ % | Cp | Δ% | Cp | Δ% | |
| 1.2 | 0.35 | - | 0.32 | - | 0.32 | - | 0.30 | - | 0.24 | - | 0.10 | - |
| 1.5 | 0.40 | 11.7 | 0.39 | 17.1 | 0.38 | 17.3 | 0.36 | 16.3 | 0.29 | 17.2 | 0.15 | 30.6 |
| 1.8 | 0.43 | 18.4 | 0.43 | 26.0 | 0.43 | 26.1 | 0.41 | 25.1 | 0.32 | 26.8 | 0.19 | 42.9 |
| 2.1 | 0.47 | 24.6 | 0.47 | 31.3 | 0.46 | 36.6 | 0.44 | 30.6 | 0.35 | 32.6 | 0.21 | 49.5 |
| 2.4 | 0.50 | 30.0 | 0.49 | 35.1 | 0.49 | 35.2 | 0.47 | 34.5 | 0.36 | 34.6 | 0.23 | 54.2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohan Kumar, P.; Surya, M.R.; Sivalingam, K.; Lim, T.-C.; Ramakrishna, S.; Wei, H. Computational Optimization of Adaptive Hybrid Darrieus Turbine: Part 1. Fluids 2019, 4, 90. https://doi.org/10.3390/fluids4020090
Mohan Kumar P, Surya MR, Sivalingam K, Lim T-C, Ramakrishna S, Wei H. Computational Optimization of Adaptive Hybrid Darrieus Turbine: Part 1. Fluids. 2019; 4(2):90. https://doi.org/10.3390/fluids4020090
Chicago/Turabian StyleMohan Kumar, Palanisamy, Mohan Ram Surya, Krishnamoorthi Sivalingam, Teik-Cheng Lim, Seeram Ramakrishna, and He Wei. 2019. "Computational Optimization of Adaptive Hybrid Darrieus Turbine: Part 1" Fluids 4, no. 2: 90. https://doi.org/10.3390/fluids4020090
APA StyleMohan Kumar, P., Surya, M. R., Sivalingam, K., Lim, T.-C., Ramakrishna, S., & Wei, H. (2019). Computational Optimization of Adaptive Hybrid Darrieus Turbine: Part 1. Fluids, 4(2), 90. https://doi.org/10.3390/fluids4020090







