Time-Reversal Analogy by Nonlinear Acoustic–Gravity Wave Triad Resonance

Abstract

Time reversal of free-surface water (gravity) waves due to a sudden change in the effective gravity has been extensively studied in recent years. Here, we show that an analogy to time-reversal can be obtained using nonlinear acoustic-gravity wave theory. More specifically, we present a mathematical model for the evolution of a time-reversed gravity wave packet from a nonlinear resonant triad perspective. We show that the sudden appearance of an acoustic mode in analogy to a sudden vertical oscillation of the liquid film, can resonate effectively with the original gravity wave packet causing energy pumping into an oppositely propagating (time-reversed) surface gravity wave of an almost identical shape.

1. Introduction

The propagation of an incident surface gravity wave disturbance over a fluid layer that is subject to a sudden vertical movement (oscillation) may excite a second disturbance travelling in an opposite direction. When the excited disturbance has a similar wave packet and frequency compared to that of the incident wave the phenomenon is known as time reversal, e.g., see Refs. [1,2] and references within.

Time reversal has been studied for water waves [3,4], though also for acoustic [5,6], elastic [7] and electromagnetic [8] waves. The so called instantaneous time mirror has been rationalised theoretically by Ref. [1] who modelled the wave celerity by employing a doorstep rectangular function whose limit case, when time tends to zero, is the Dirac delta function. Such setting dictates that once the reversed wave is generated the surface is exclusively governed by the two gravity waves; an assumption which is valid in linear wave theory. However, it is well established now that two gravity waves of opposite direction and identical frequencies [9], or more generally similar frequencies [10,11], will interact nonlinearly, transferring energy to a compression-type wave or a propagating acoustic mode, if the compressibility of the medium is not neglected, and the boundary conditions allow the existence of such mode. Thus, for a rigid bottom the water should be deep enough, otherwise an elastic boundary needs to be considered which allows propagation of the fundamental mode in the water at any depth [12]. Under these settings, not only the evolution of an ‘instantaneous’ wave amplitude is derived, but the contribution of modulated surface amplitude due to energy transfer in the interior of the fluid is assessed. To this end, the main objective of this paper is to demonstrate an analogy for the evolution of a ‘time-reversed’ wave amplitude from a nonlinear acoustic-gravity triad resonance perspective. Specifically, we discuss the amplitude evolution equations for the case of a long-crested acoustic–gravity mode interacting with two gravity waves when the elasticity of the bottom is considered. Since the interaction occurs at the surface, the long-crested mode is effectively causing a vertical oscillation of the liquid layer. To illustrate the analogy to instantaneous time reversal we present a numerical example of an incident gravity wave packet interacting with the long crested acoustic-gravity mode for a very short time. The interaction results in the evolution of a reversed gravity wave. Note that the analogy between the acoustic-gravity mode and the oscillating bath is not only mathematical. An uplift of the elastic bottom would generate a countable infinity of acoustic-gravity modes. Below the critical depth there will be only one frequency peak that would resonate with gravity waves, and thus the rest can be ignored as they cannot interact via the triad mechanism. Therefore, the proposed model considers acoustic-gravity modes about double the frequency. Finally, to illustrate the generality of the interaction mechanism, we discuss two more cases of interaction involving higher propagating modes or when the oscillation is harmonic resulting in the evolution of standing waves of double the frequency, which can arguably describe the evolution of Faraday-type waves.

2. Preliminaries

Part of the analysis in this section is based on Ref. [11]. Acoustic–gravity wave triad resonance depends on a small parameter $\mu =gh/c^2$, $(\mu \ll 1)$ (see Ref. [11] for details) that governs the effects of gravity relative to compressibility, where g is the effective gravitational acceleration, c is the propagation speed of acoustic–gravity waves in water, and h is an effective depth that allows describing the acoustic mode appropriately as discussed below. The water is treated as an inviscid barotropic fluid, and the motion is assumed irrotational.

The acoustic–gravity wave problem is formulated in terms of the velocity potential $\phi (x,z,t)$, where $\mathbf{u}=\nabla \phi$ is the velocity field. Moreover, we shall use dimensionless variables, employing $\mu h$ as lengthscale and $h/c$ as timescale. The governing equation is the two dimensional nonlinear wave equation by combining continuity with the unsteady Bernoulli equation (e.g., see Ref. [9]),

$${\phi }_{tt}-\frac{1}{{\mu }^2}\left({\phi }_{xx}+{\phi }_{zz}\right)+{\phi }_z+{|\nabla \phi |}_t^2+\frac{1}{2}\nabla \phi ·\nabla \left({|\nabla \phi |}^2\right)=0.$$

(1)

On the free surface $z=\eta (x,t)$ the standard kinematic and dynamic conditions apply. Expanding these conditions about $z=0$ correct up to cubic terms in the perturbation, and after expressing $\eta$ in terms of $\phi$ we arrive at the combined free-surface condition,

$$\begin{array}{c}{\phi }_{tt}+{|\nabla \phi |}_t^2+{\phi }_z+\frac{1}{2}\nabla \phi ·\nabla \left({|\nabla \phi |}^2\right)-{\phi }_t{({\phi }_{tt}+{\phi }_z)}_z\hfill \\ -{\left({\phi }_t{|\nabla \phi |}_t^2\right)}_z-\frac{1}{2}{\left[({\phi }_{tt}+{\phi }_z)\left({|\nabla \phi |}^2-{\phi }_t^2\right)\right]}_z=0.\hfill \end{array}$$

(2)

The bottom boundary condition plays a crucial role in the physical problem, as the water depth on a rigid bottom would determine the scales involved. For example, Ref. [11] considers a rigid bottom at $z=-1/\mu$ which reads

$${\phi }_z=0(z=-1/\mu ).$$

(3)

This condition dictates that the physical problem is limited by a critical water depth $h_{cr}$ below which no acoustic–gravity waves can exist. For example, if the gravity waves frequency is in the order of magnitude of a few Hertz the critical depth is of the order of tens of metres, and lower frequencies require much deeper water. To allow propagation at much shallower depths, e.g., wave flume scale the elasticity of the bottom should be considered as found by Ref. [12] who showed that the first acoustic–gravity mode can propagate in the water layer at any depth, regardless to its frequency. Therefore, at the bottom we consider an elastic half-space using dilatational and rotational (velocity) potentials in the solid,

$${\phi }_{s,tt}-\frac{1}{{\mu }_s^2}\left({\phi }_{s,xx}+{\phi }_{s,zz}\right)+{\phi }_{s,z}=0(z\le -1/\mu ),$$

(4)

$${\psi }_{s,tt}-\frac{1}{{\mu }_p^2}\left({\psi }_{s,xx}+{\psi }_{s,zz}\right)+{\psi }_{s,z}=0(z\le -1/\mu ),$$

(5)

with

$${\mu }_p=gh/c_p^2,{\mu }_s=gh/c_s^2,$$

(6)

where $c_p$ and $c_s$ are the pressure and shear wave velocities normalised by c. There are three conditions at the bottom $(z=-1/\mu )$

$${\phi }_z=-\left({\phi }_{s,z}-{\psi }_{z,x}\right);{\sigma }_{zz}=-{\phi }_t;{\sigma }_{xz}=0,$$

(7)

where the axial and shear stresses, ${\sigma }_{zz}$ and ${\sigma }_{xz}$, are given by

$${\sigma }_{zz}=\overline{\lambda }(u_{s,x}+w_{s,z})+2\overline{\mu }{w}_{s,z};{\sigma }_{xz}=\overline{\mu }(w_{s,x}+u_{s,z})$$

(8)

where $\overline{\lambda }$ and $\overline{\mu }$ are the normalised elasticity properties,

$$(\overline{\lambda }+2\overline{\mu })={\rho }_s{c}_p^2;\overline{\mu }={\rho }_s{c}_s^2,$$

(9)

and

$$u_s={\phi }_{s,x}+{\psi }_{s,z}{w}_s={\phi }_{s,z}-{\psi }_{s,x}$$

(10)

Note that the densities in liquid, $\rho =1$, and solid, ${\rho }_s$, are normalised by the density of the liquid.

3. Linear Solution

Uppon applying the separation of variables,

$$\phi ={\mathrm{e}}^{\frac{1}{2}{\mu }^{2}z}f\left(z\right){\mathrm{e}}^{\mathrm{i}(kx-\omega t)},{\phi }_s=C_1{\mathrm{e}}^{\frac{1}{2}{\mu }^{2}z}{\mathrm{e}}^{qz}{\mathrm{e}}^{\mathrm{i}(kx-\omega t)},{\psi }_s=C_2{\mathrm{e}}^{\frac{1}{2}{\mu }^{2}z}{\mathrm{e}}^{sz}{\mathrm{e}}^{\mathrm{i}(kx-\omega t)},$$

(11)

the linearised equations become

$$\frac{{\mathrm{d}}^{2}f}{\mathrm{d}{z}^2}-\left(k^2-{\mu }^2{\omega }^2+\frac{{\mu }^4}{4}\right)f=0(-1/\mu <z<0),$$

(12)

$$\frac{\mathrm{d}f}{\mathrm{d}z}-\left({\omega }^2-\frac{{\mu }^2}{2}\right)f=0(z=0)$$

(13)

$$\frac{\mathrm{d}f}{\mathrm{d}z}+\frac{{\mu }^2}{2}f=-\left(\frac{\mathrm{d}{\phi }_s}{{\phi }_z}-\frac{\mathrm{d}{\psi }_s}{\mathrm{d}x}\right)(z=-1/\mu ).$$

(14)

Rescaling the wavenumber $k=\mu \kappa$, and $Z=\mu z$, the general solution of (12) takes the form

$$f=Acos\Omega (Z+1)+Bsin\Omega (Z+1)+O\left({\mu }^2\right).$$

(15)

where

$${\Omega }^2={\omega }^2-{\kappa }^2-\frac{{\mu }^2}{4}.$$

(16)

Substitution into (13), (14), and the stress conditions at the bottom, and noting that

$$k^2=s^2+c_s^{-2}{\omega }^2-\frac{{\mu }_s^2}{4}=s^2+c_p^{-2}{\omega }^2-\frac{{\mu }_p^2}{4}$$

(17)

the general dispersion relation for acoustic-gravity and gravity modes is derived,

$$cos\Omega +\mu \frac{{\Omega }^2-{\kappa }^2-{\omega }^2{\mathcal{E}}_1/\mu }{2\Omega \left({\omega }^2+\mu {\mathcal{E}}_2/2\right)}sin\Omega =O\left(\mu \right)$$

(18)

where ${\mathcal{E}}_1$ and ${\mathcal{E}}_2$ represent elastic terms that are easily found from the boundary conditions. Solving (18) reveals a countable infinity of modes, $n=0,1,2,\dots$, m that satisfy the general dispersion relations,

$${\omega }^2={\omega }_n^2+{\kappa }^2+\mu \frac{{\omega }_n^2-{\kappa }^2-({\omega }_n^2+{\kappa }^2){\mathcal{E}}_1/\mu }{{\omega }_n^2+{\kappa }^2+\mu {\mathcal{E}}_2/2}+O\left({\mu }^2\right)$$

(19)

where

$${\omega }_n=\left(n+\frac{1}{2}\right)\pi .$$

(20)

Note that in the rigid case limit, ${\mathcal{E}}_1$, ${\mathcal{E}}_2$ are set to zero thus (18) reduces to

$${\omega }^2=-\mu \Omega tan\Omega \left(1-\frac{{\omega }^2}{2{\Omega }^2}+\frac{1}{4}\frac{{\mu }^2}{{\Omega }^2}\right),$$

(21)

whose dimensional form is given in Equation (3.2) of Ref. [10]. On the other hand, (19) reduced to the dispersion relations,

$${\omega }^2={\omega }_n^2+{\kappa }^2+\mu \frac{{\omega }_n^2-{\kappa }^2}{{\omega }_n^2+{\kappa }^2}+O\left({\mu }^2\right)(n=0,1,2,\dots ),$$

(22)

On the other hand, when $\mu \ll 1$ and $k=O\left(1\right)$ the solution to the linearised Equation (12) decays exponentially into the fluid,

$$f={\mathrm{e}}^{\left|k\right|z}+O\left({\mu }^4\right),$$

(23)

and thus from the boundary conditions (13) and (14) we recover the familiar surface gravity wave dispersion relation

$${\omega }^2=\left|k\right|+O\left({\mu }^4\right).$$

(24)

Considering the elasticity of the bottom, Equation (18) predicts that the fundamental acoustic mode has no cut-off frequency and will propagate in the water layer even when the water is very shallow as presented in detail by Ref. [12].

4. Nonlinear Triad Resonance

The exercise undertaken in the previous section demonstrates three important, though somewhat obvious, conclusions: (I) due to elasticity of the bottom a fundamental low frequency acoustic mode can be generated and could propagate under laboratory conditions; (II) The gravity waves are not affected by the elasticity of the bottom as long as the water is deep enough satisfying Equation (24); (III) The bottom elasticity modifies the acoustic triad member via its dispersion relation, though since the nonlinear interaction takes place at the surface only, elasticity can have no direct effect on the amplitude evolution equations under the specific conditions considered in the sequel. Therefore, in principle, elasticity is important when the model is employed to describe a physical problem where the acoustic mode should actually exist, whereas if the acoustic mode is used to mathematically represent the surface oscillation it might be sufficient to consider an effective depth (that allows its existence) with a rigid bottom.

We consider an arbitrary surface gravity wave packet of amplitude $S_{+}$ and wavenumber $k_{+}$ propagating with frequency ${\omega }_{+}$ in the $+x$ direction, over a layer of fluid of depth $1/\mu$. At time $t=0$ we oscillate the fluid layer vertically, say by an acoustic mode. The oscillation can be described by a spectrum of frequencies though only those of frequency near $\omega$ can resonate effectively. The acoustic mode and the surface gravity wave interact nonlinearly generating an opposing surface gravity wave packet of wavenumber $k_{-}$ and frequency ${\omega }_{-}$. The general resonance condition is given by

$$k_{+}+k_{-}=\mu \kappa ;{\omega }_{+}+{\omega }_{-}=\omega +\mu \beta ,$$

(25)

where $\beta =O\left(1\right)$ is a detuning parameter. In the case of pure vertical oscillations $\kappa =0$, and ${\omega }_{\pm }={\omega }^{\prime }=\omega /2$. To study this case we expand the velocity potential for the three modes as follows

$$\begin{array}{c}\hfill \phi =ϵ{\mathrm{e}}^{kz}{S}_{+}\left(T\right){\mathrm{e}}^{\mathrm{i}(kx-{\omega }^{\prime }t)}+\alpha cos\omega (Z+1)A\left(X,T\right){\mathrm{e}}^{\mathrm{i}\beta T}{\mathrm{e}}^{-\mathrm{i}\omega t}+ϵ{\mathrm{e}}^{kz}{S}_{-}\left(T\right){\mathrm{e}}^{-\mathrm{i}(kx+{\omega }^{\prime }t)}\\ \hfill +{ϵ}^3{G}_{+}(z,T){\mathrm{e}}^{\mathrm{i}(kx-{\omega }^{\prime }t)}+{ϵ}^{2}F(Z,T){\mathrm{e}}^{-\mathrm{i}\omega t}+{ϵ}^3{G}_{-}(z,T){\mathrm{e}}^{-\mathrm{i}(kx+{\omega }^{\prime }t)}+\mathrm{c}.\mathrm{c}.+\dots .\end{array}$$

(26)

where the gravity modes are $O\left(ϵ\right)$ and the acoustic mode is $O\left(\alpha \right)$, scaled in the vertical coordinate $Z=\mu z$. The surface wave amplitudes $S_{\pm }$ and the acoustic mode amplitude A depend on the ‘slow’ time $T=\mu t$, where $ϵ=\alpha {\mu }^{1/2}$ with $\alpha =O\left(1\right)$. The general problem of an acoustic mode, $\kappa ={\kappa }_0+O\left(\mu \right)$, propagating in space $X={\mu }^{2}x$ was solved by Ref. [11]. Here, we seek a solution using expansion (26) where the acoustic mode is oscillating in the vertical direction, $\kappa =O\left({\mu }^{1/2}\right)$, and thus the proper scaling $X={\mu }^{3/2}x$ is used instead. The full triad resonance is reached at slow time T, though for the generated gravity wave to be $O\left(ϵ\right)$ requires an interaction duration $\Delta T=O\left({\mu }^{1/2}\right)$. For example, an effective depth of $h\sim 150$ m corresponds to gravity wavelength $\lambda \sim 0.1$ m, and dimensional frequency ${\omega }^{*}\sim 10$ rad/s. Note that during the interaction g presents the effective gravitational acceleration, thus can be tuned as well.

We substitute (26) in the wave Equation (1) and the boundary conditions, and focus on terms proportional to $exp\left\{\mathrm{i}(kx-{\omega }^{\prime }t)\right\}$, $exp\{-\mathrm{i}(kx+{\omega }^{\prime }t)\}$, and $exp\{-\mathrm{i}\omega t\}$ (in the general case the focus is on $exp\left\{\mathrm{i}\right(\mu \kappa x-\omega t\left)\right\}$). These terms cause secular behaviour at higher order in expansion (26) as they have the same spatial and temporal dependence as the three linear propagation modes at the leading order. To overcome this difficulty we impose solvability conditions on the problems governing higher-order corrections to these modes. The correction to the acoustic–gravity mode takes the form ${ϵ}^2\{F(Z,T){\mathrm{e}}^{-\mathrm{i}\omega t}+\mathrm{c}.\mathrm{c}.\}$, which satisfies the inhomogeneous boundary-value problem,

$$\begin{array}{c}\hfill F_{ZZ}+{\omega }_n^{2}F=-\frac{1}{\alpha }\{2\mathrm{i}\omega \frac{\partial A}{\partial T}cos{\omega }_n(Z+1)+2\mathrm{i}\kappa \frac{{\partial }^{2}A}{\partial X^2}cos{\omega }_n(Z+1)\\ \hfill +{\omega }_{n}Asin{\omega }_n(Z+1)\}-4\mathrm{i}\omega k^2{S}_{+}{S}_{-}{\mathrm{e}}^{2kz},(-1<Z<0);\end{array}$$

(27)

$$-{\omega }^{2}F=\frac{1}{\alpha }\left\{{\omega }_n{(-1)}^{n}A+4\mathrm{i}\omega k^2{S}_{+}{S}_{-}\right\},(Z=0);$$

(28)

$$F_Z=0,(Z=-1).$$

(29)

Finally, the solvability is imposed by multiplying both sides of (27) and (28) with the homogeneous solution $cos{\omega }_n(Z+1)$ and integrating over the depth which results in the desired evolution equation for the acoustic–gravity mode,

$$\frac{\partial A}{\partial T}+\frac{\mathrm{i}}{2\omega }\frac{{\partial }^{2}A}{\partial X^2}=-\mathrm{i}\left(\frac{1}{2{\omega }_n}+2\beta \right)A+\frac{{(-1)}^n}{4}{\omega }^2{\omega }_n\alpha S_{+}{S}_{-}.$$

(30)

In the case of $\kappa \ne 0$ not that the spatial scaling is different ($X={\mu }^{2}x$) and thus the collection of terms is different resulting in the acoustic evolution equation which was derived by Ref. [11],

$$\frac{\partial A}{\partial T}+\frac{\kappa }{\omega }\frac{\partial A}{\partial X}=\mathrm{i}\left(\frac{{\kappa }^2-{\omega }_n^2}{2{\omega }^3}-2\beta \right)A+\frac{{(-1)}^n}{4}{\omega }^2{\omega }_n\alpha S_{+}{S}_{-}.$$

(31)

For the gravity wave, a similar programme is carried out with a correction that takes the form ${ϵ}^3\{G(z,T){\mathrm{e}}^{\pm \mathrm{i}(k_{\pm }x\mp \omega t)}+\mathrm{c}.\mathrm{c}.\}$, which satisfies the free-surface condition provided that $O\left({ϵ}^3\right)$ interactions vanish there. This correction leads to the gravity amplitude evolution equations,

$$\frac{\mathrm{d}{S}_{\pm }}{\mathrm{d}T}=-\frac{{(-1)}^n}{8}{\omega }^2{\omega }_n\alpha A{S}_{\mp }^{*}-\frac{\mathrm{i}}{64}{\omega }^7{\alpha }^2\left(S_{\pm }^2{S}_{\pm }^{*}-2{\left|S_{\mp }\right|}^2{S}_{\pm }\right),$$

(32)

where * stands for complex conjugate. Equation (30) is similar to (31) or Equation (5.10) of [11] with the fundamental difference that here the spatial dependancy of A$\propto {\partial }^2/\partial X^2$.

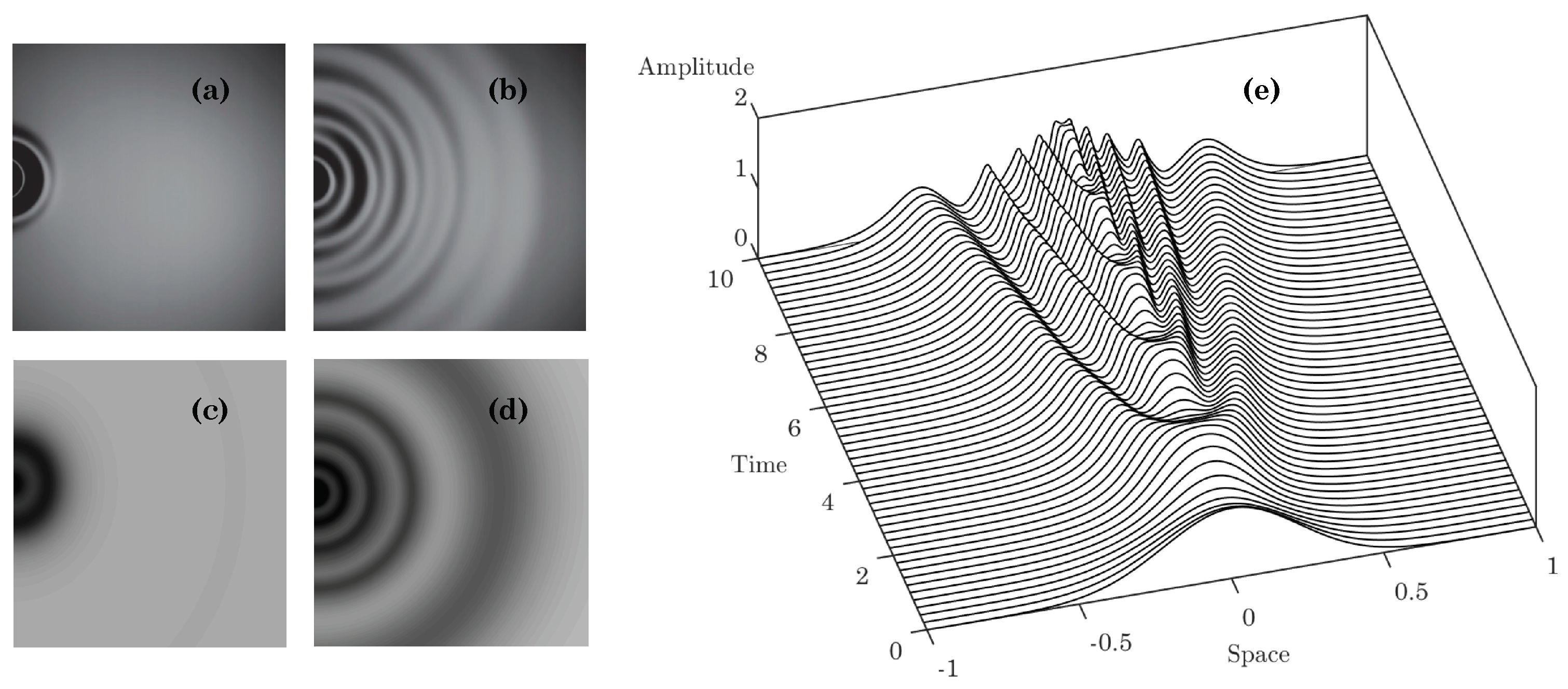
5. Results and Discussion

To gain more insight on the generated gravity wave packet during the vertical oscillation we solved numerically the amplitude Equations (30) and (32) for various wave packets, as demonstrated in Figure 1. For simplicity, we took $\beta =-1/4{\omega }_n$ and focused on vertical oscillations only ($\kappa =0$, and $\omega ={\omega }_n$). At the initial stage ($T=-10$) we consider a gravity wave packet traveling from left to right (see Figure 1a), where $S_{+}=exp(-X^2)sin3Xcos5X$, $S_{-}=0$ and $A=0$ (all at $T=-10$), thus no interaction can occur. At time $T=0$ we oscillate the liquid layer vertically for a large amplitude $A(T=0)=10$ and $\alpha =5$ and very short time $\Delta T=0.01$. During this time the gravity wave packet and the acoustic mode interact generating a reversed gravity wave packet that travels in the opposite direction as depicted in Figure 1b. The two gravity waves continue propagating each in its own direction without triad interaction (Figure 1c,d). A very similar result can be achieved with $\alpha =1$, $A(T=0)=1$, but with a higher effective gravitational acceleration. The shape of the envelope of the reversed gravity wave is similar to that of the original wave. To further study this phenomenon we consider four wave packets that combine Gaussian, Sine and Saw functions as illustrated in Figure 2a–d. Specifically, we compare the original and reversed gravity waves after the two waves have separated, similarly to the situation in Figure 1c. The reversed wave packets are similar to the original regardless to the shape, since the nature of the interaction is orthogonal to the propagation direction, and the interaction duration is not long enough to allow the cubic terms come into play.

During the interaction, and assuming $\beta =-1/4{\omega }_n$, there are four free parameters that can detune the interaction: $\alpha$, $\Delta T$, g, and $A(X,T=0)$. At the initial stage of the evolution, since there exists a single gravity wave packet, only the quadratic terms contribute to the evolution of the second gravity wave packet. Thus, for an interaction time $\Delta T\ll 1$ the amplitude of the second gravity wave packet can be estimated by

$$\frac{S_{-}}{S_{+}^{*}}=-\frac{{\pi }^3}{4}{\left(n+\frac{1}{2}\right)}^3\alpha \Delta TA.$$

(33)

Although, the contributions of A and $\Delta T$ are linear, there is a fundamental difference between the two. The amplitude A dictates the amount of energy transferred in a given time (energy flux), whereas the duration $\Delta T$ dictates how developed the evolution is, i.e., the interaction is in its initial stages when $\Delta T\ll 1$, and fully developed when $\Delta T=O\left(1\right)$, as will be discussed in the last paragraph. It is noted here that the time reversal property is not exclusive to the fundamental mode only, but higher modes may cause a similar effect, as in Equation (33). However, higher modes require an effectively shorter interaction time compared to the fundamental mode, which otherwise would lead to further modulating of the original shape of the wave packet, though both original and generated one are modulated in a similar way (see Figure 3). This behaviour is easily seen in (32) where the cubic contribution is proportional to $n^7$ as opposed to $n^3$ in the case of quadratic terms. In the specific example given in Figure 3, with $n=1$, the interaction duration has to be extremely small to allow generating the second gravity mode without further modulating the wavepackets, as in Figure 3a. It is also noticeable that the reversed wave is more sensitive to the modulation (Figure 3b,c), whereas a sufficiently large interaction time would eventually result in a similar modulation of both wavepackets (Figure 3d). Note that since $n=1$ there is a phase shift in the wavepacket, i.e., see Figure 3a with $n=1$ as opposed to Figure 2a with $n=0$.

The nonlinear triad interaction occurs near the free surface of the liquid layer, which is sufficient to determine the wave field within the water layer, e.g., see [13,14]. Thus, for the gravity wave, the sudden appearance of a vertically oscillating acoustic mode is analogous to a sudden vertical oscillation. The current mathematical model is not only capable to describe the evolution of the time reversed gravity wave packet, but also the original gravity wave and the oscillating surface, see Figure 4. The evolution of the reversed gravity wave is ‘gradual’ and linear, as shown in Figure 4b, and it is in agreement with (33). On the other hand, the original gravity wave remains unchanged, Figure 4a, and most of the energy that transfers to the reversed gravity wave comes from the acoustic mode that experiences evolution in its own amplitude, see Figure 4c. Thus, the presented model predicts the appearance of gentle surface ripples (from the acoustic mode) that propagate independently of the two gravity waves. These are gravity-acoustic waves with amplitudes that can be order of magnitude smaller than that of the surface-gravity waves, which makes their observation a challenge.

Employing acoustic-gravity wave theory is not limited to the vertically oscillating modes ($\kappa =0$) presented above. Employing the full general evolution equations with a propagating acoustic mode ($\kappa \ne 0$) allows asymmetric deformation of the amplitudes. Moreover, the theory is general and is capable in capturing the interaction over a longer timescale which has various implications, such as in the case of the generation of microseisms as in Refs. [9,11], but also for the evolution of Faraday-type standing waves that oscillate at half the driving frequency.

A Note on the Evolution of Faraday-Type Waves

If instead of a sudden oscillation one allows a periodic oscillation, and a longer timescale interaction not $\Delta T\ll 1$ as of the time-reversal but $T=O\left(1\right)$, then a localised disturbance at the surface can evolve into standing waves of half the frequency of the oscillating water layer, and the entire surface reveals the evolution of Faradays-type waves. To gain some insight on this unique evolution, a qualitative comparison between experiments (originally presented in [15]) and calculations from acoustic-gravity wave theory is shown in Figure 5a–e. The experiments describe a wave field generated by a falling steel ball on a vertically oscillating liquid bath at two different times (a,b). The numerical calculations are for $\kappa =0$, as in time reversal though for a continuously oscillating bath interacting with two identical gravity waves of overlapping Gaussian wave packets traveling in opposite directions. Thus, the two gravity wave packets present a standing disturbance in an analogy to a disturbance by the falling steel ball impacting the surface. The detailed evolution of the liquid surface is given in Figure 5e.