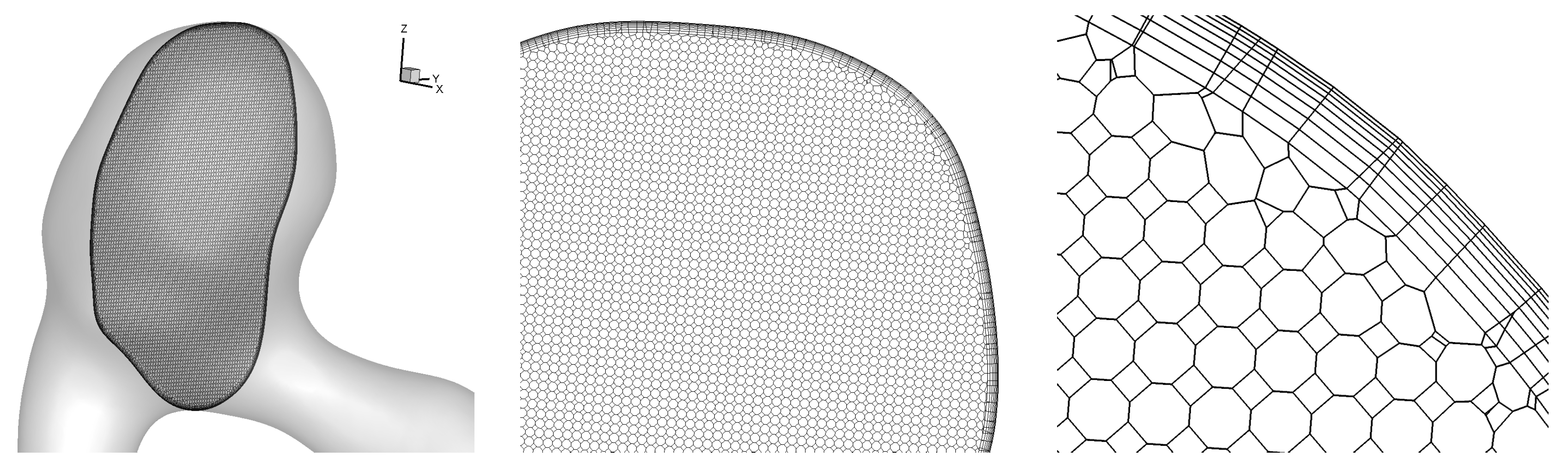
1. Introduction
Biological systems are complex, often involving a multitude of coupled processes occurring at different scales, both spatially and temporally. When events such as diseases form, it is a challenging and daunting task to deconstruct the processes involved in identifying succinctly a relation and cause. The cardiovascular system is responsible for transport and signalling, thus linking cells throughout the body, and acting as a conduit. Cardiovascular diseases have benefited from intense research and the resulting important breakthroughs; however, they remain prevalent and a leading causes of mortality. A pathophysiology which has been the focus of much research is that of aneurysms, especially cerebral and abdominal. Aneurysms are largely asymptomatic, until they rupture, at which stage the risks of mortality or morbidity are very high. The task of unravelling the cause of aneurysm initiation, growth and rupture has developed immensely over recent decades, and while there are still many open questions it is widely accepted that the fluid mechanics plays an important role in all aneurysm stages.
The consensus is that the haemodynamics plays a determining role in cardiovascular diseases in large arteries [
1,
2,
3,
4], and both the mechanical and transport properties have been scrutinised. Simply put, an abnormal flow field, usually described as complex and disturbed (not necessarily turbulent flow), is often related to diseased states. The greatest attention has involved principally the fluid mechanics in the near-wall region, hence the flow field at or near the lumen boundary since it is in this region that the haemodynamics in effect interfaces with the body’s tissues. Measures such as wall shear stress (WSS) and spatial WSS gradients [
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17], aneurysm formation index (AFI) [
18], oscillatory shear index (OSI) [
19], gradient oscillatory number (GON) [
20], transverse wall shear stress [
21], viscous dissipation and kinetic energy [
11], energy loss [
22,
23], helicity and vortical flow [
24,
25,
26], among others [
4,
27], have all been used as correlators to diseases. There have also been efforts in characterising the vessel’s shape, since this is the no-slip boundary condition, together with the resulting fluid mechanics [
22,
28,
29,
30,
31,
32,
33]. Means of recovering the no-slip boundary from flow data have also been proposed [
34,
35]. The fluid-structure interactions and constitutive models of the cerebral tissues have also been investigated [
36,
37], but even with the simpler rigid wall boundary condition one can also show that the spatial gradients of all shear stress would be expected to generate inter-cellular tension and shearing forces in the vessel tissue [
38].
As a result of the many studies, often with limited cohort sizes, overall mean trends have emerged and have spurred various formulations for fluid mechanics correlators to disease [
27]. However, when considering patient-specific studies with personalised results and conclusions, there is evident conflicting information and confusion as to how to post-process and extract meaningful information from the haemodynamic observables [
4,
39]. It is evident that one cannot singularly look at the haemodynamics as a indication of disease, and the mass transport [
40,
41], inflammation process [
42,
43], auto-regulation [
44] and genetic factors [
3], among others, must be ultimately incorporated in any analysis. While the problem is indeed multi-scale and multi-physics, the consensus that the haemodynamics plays a determining role in cardiovascular diseases in large arteries still remains.
In recent years, a novel analysis of the flow field at or near the lumen boundary was undertaken, based on observation from the wall shear stress field, its spatial gradients and temporal evolution. It was shown in [
15] that the flow field at a small distance inside the free-stream domain can be recovered from the wall shear stress and its gradients, leading to further promising developments and interest in the field [
16,
45,
46]. The methodology in effect revolves around a perturbation analysis (which has been previously explored in [
47]) together with the realisation that: (i) the wall shear stress, which is the tangential component of the viscous traction exerted by the flow on the wall, can also be seen as the tangential component of the fluid velocity in the limit of the wall; (ii) the divergence of wall shear stress on the other hand is related to the normal component of the fluid velocity in the limit of the wall [
15]. These works were further extended by considering Lagrangian Coherent Structures (LSC) [
48] of the wall shear stress, and the time evolved partitioning of the flow, as well as investigating the effects of transport and diffusion in the near-wall region [
45,
46,
49].
This is then the setting for the present paper. We do not aim to provide insight into the coupled and complex problem of cardiovascular diseases. Rather, since it is widely accepted that the haemodynamics does play an important role, we focus on providing an accessible means to better understand the fluid mechanics. From this, we can also develop a better appreciation of the lumen-endothelial interface, denoted by the
near-wall region in the present work. In this region, mass transport to/from the blood and tissue, and signalling via mechanotransduction occurs. We will use the analysis proposed in [
15] based on a Taylor expansion of the flow field, together with wall shear stress critical points, which are locations where the wall shear stress is zero, to recover dividing surface shear lines, which provide information about the flow partitioning at an instance in time [
16,
17]. The physical appreciation, as well as the numerical tools developed, are certainly valuable in studying cardiovascular and physiological flows in general, where the near-wall flow field is a defining factor. Additionally, we hope that the greater physical appreciation of the fluid mechanics will avoid the unfortunate disarray of metrics used to correlate fluids measures to disease [
4,
27,
39]. In the present investigation, we apply the methodology to investigate the near-wall haemodynamics in cerebral aneurysms of six patient cases under pulsatile flow conditions.
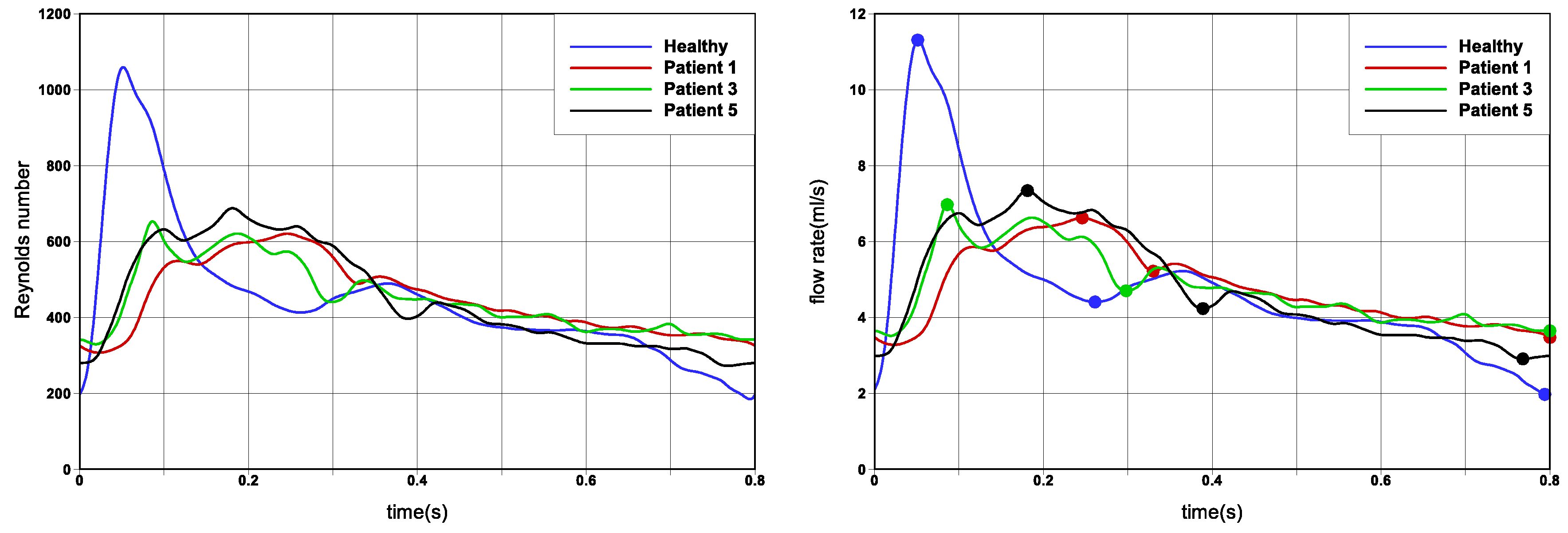
While the patient cohort is limited, to investigate variability and sensitivity to flow conditions and modelling assumptions, we make use of different cardiac flow rate profiles, as well as both Newtonian and non-Newtonian rheological models. These results are tabulated in the
Appendix A.
3. Results and Discussion
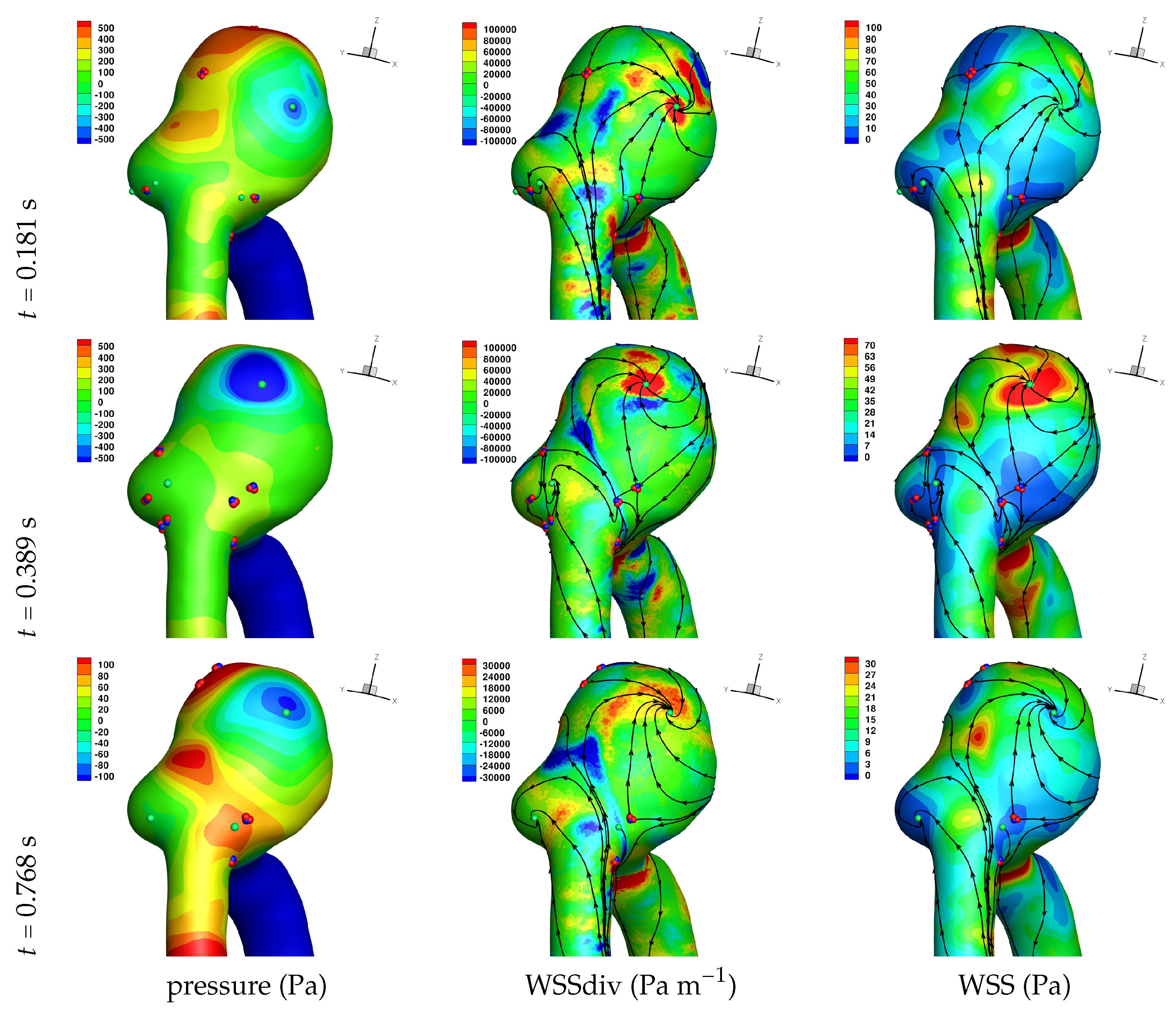
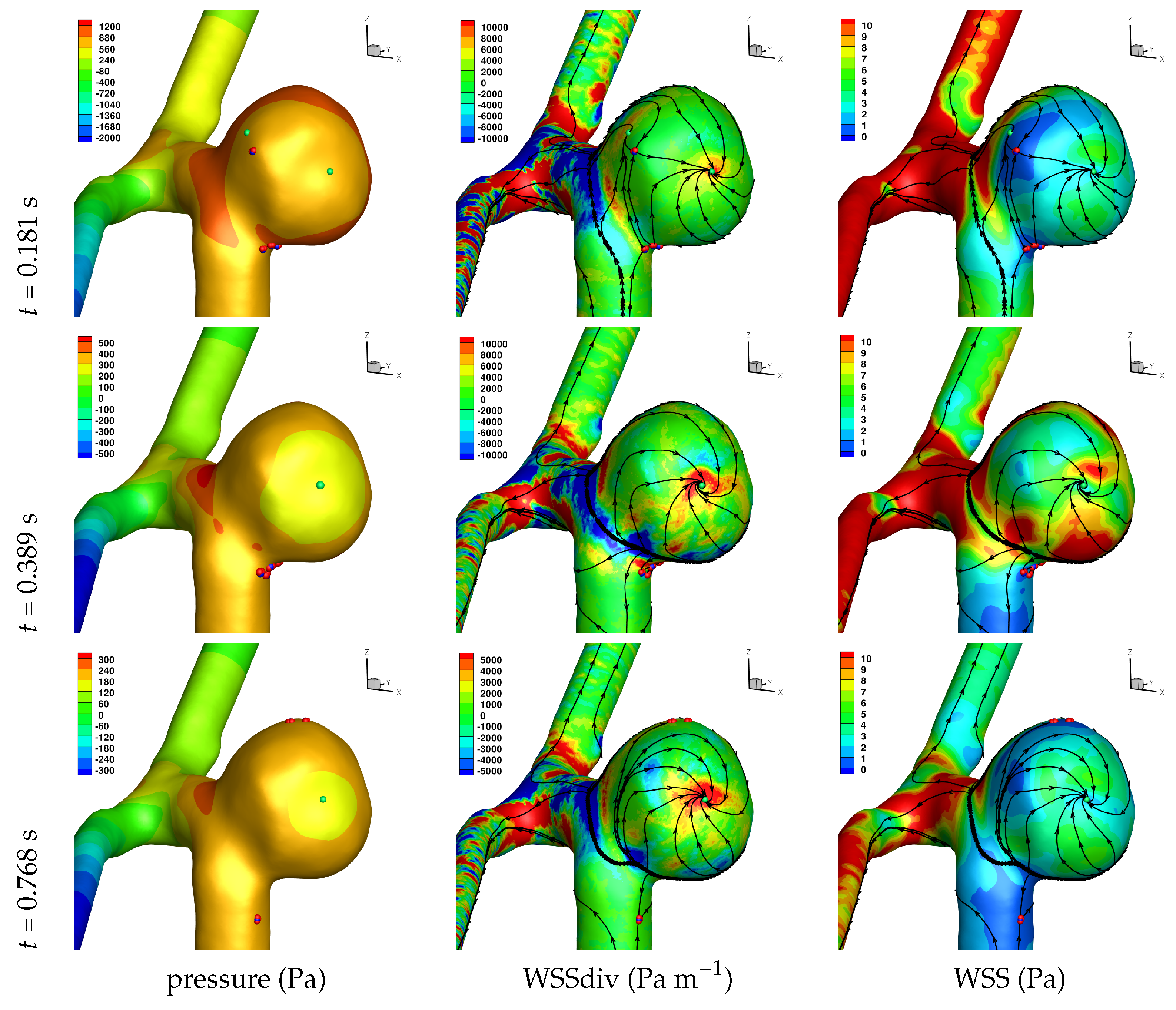
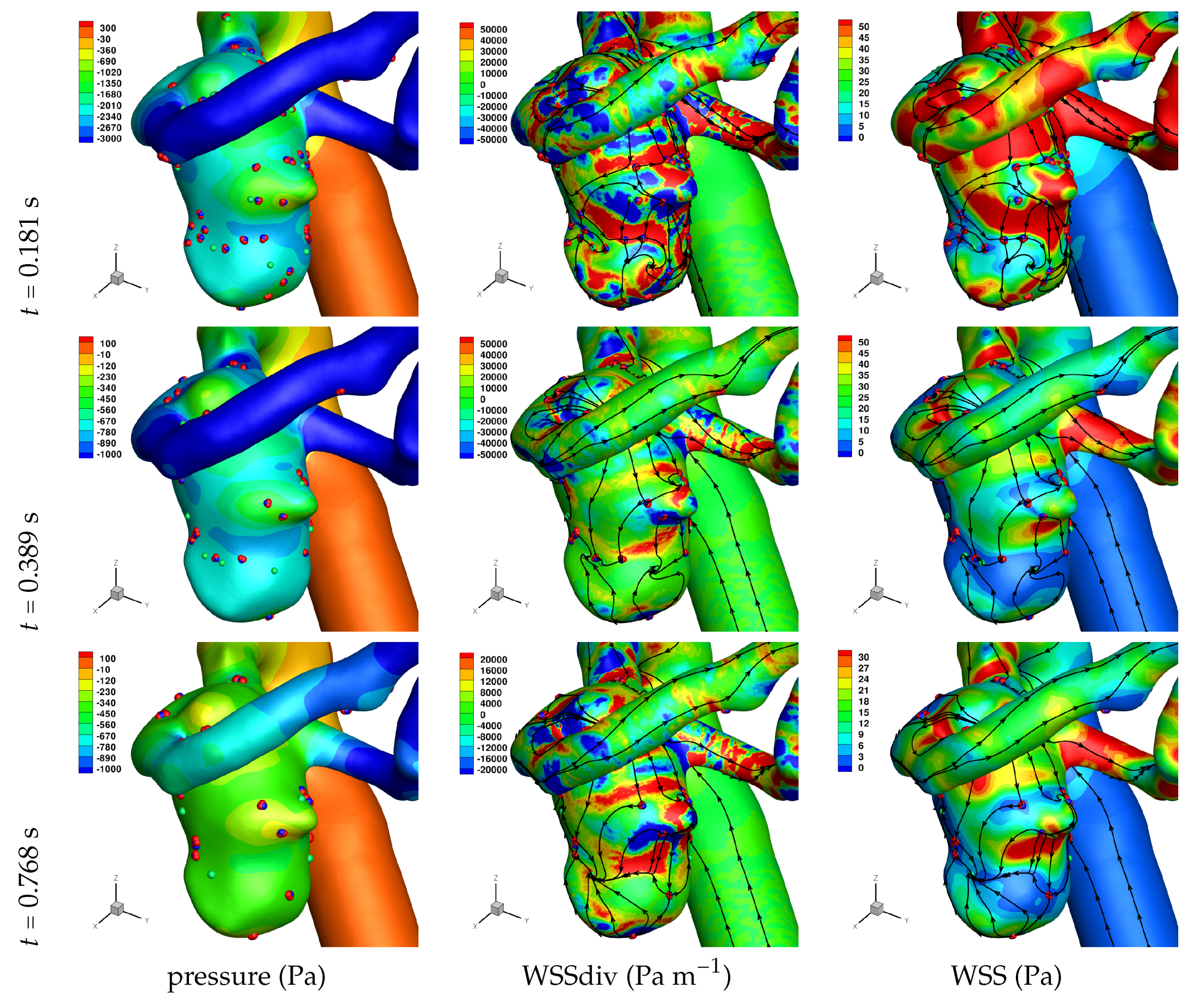
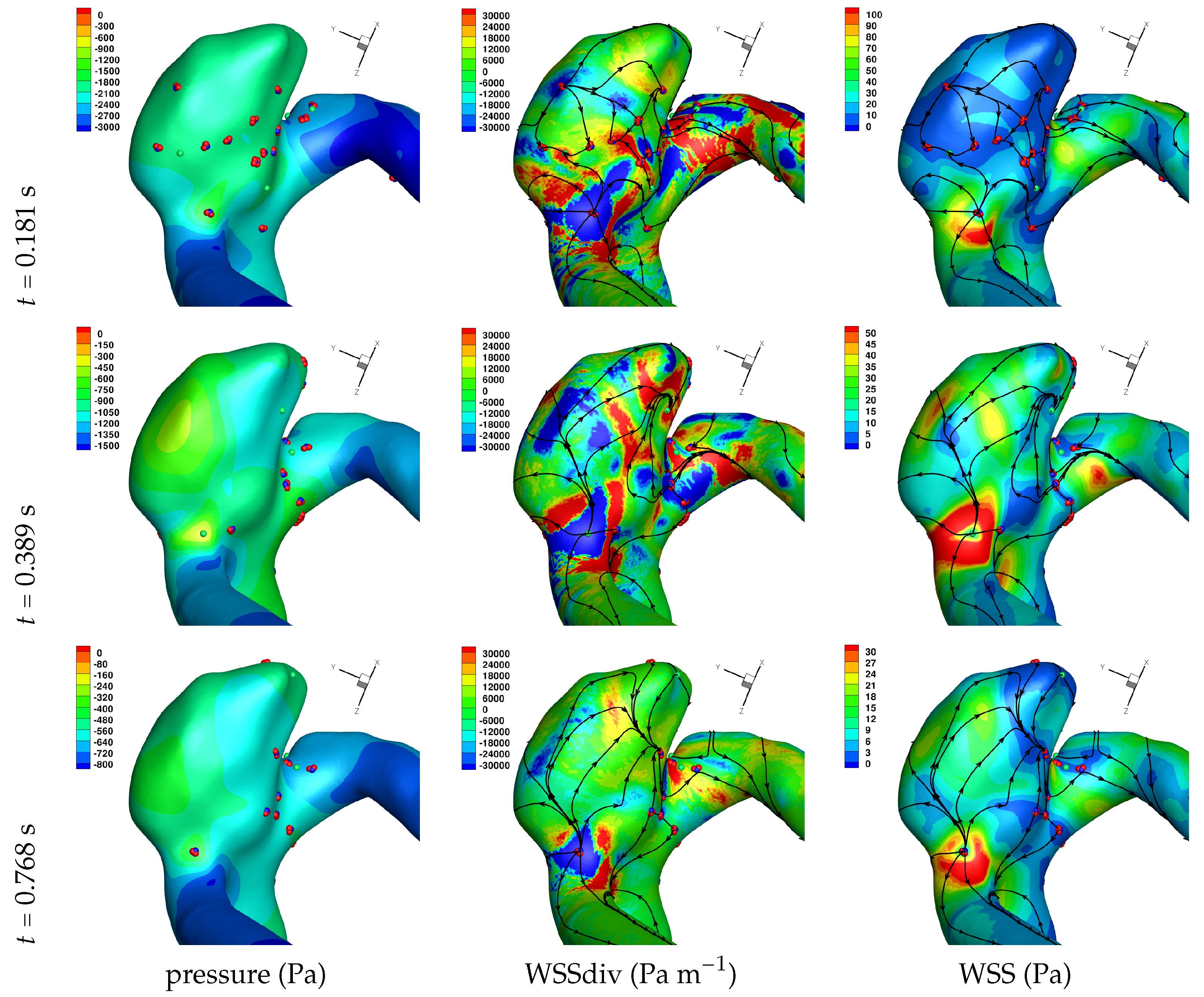
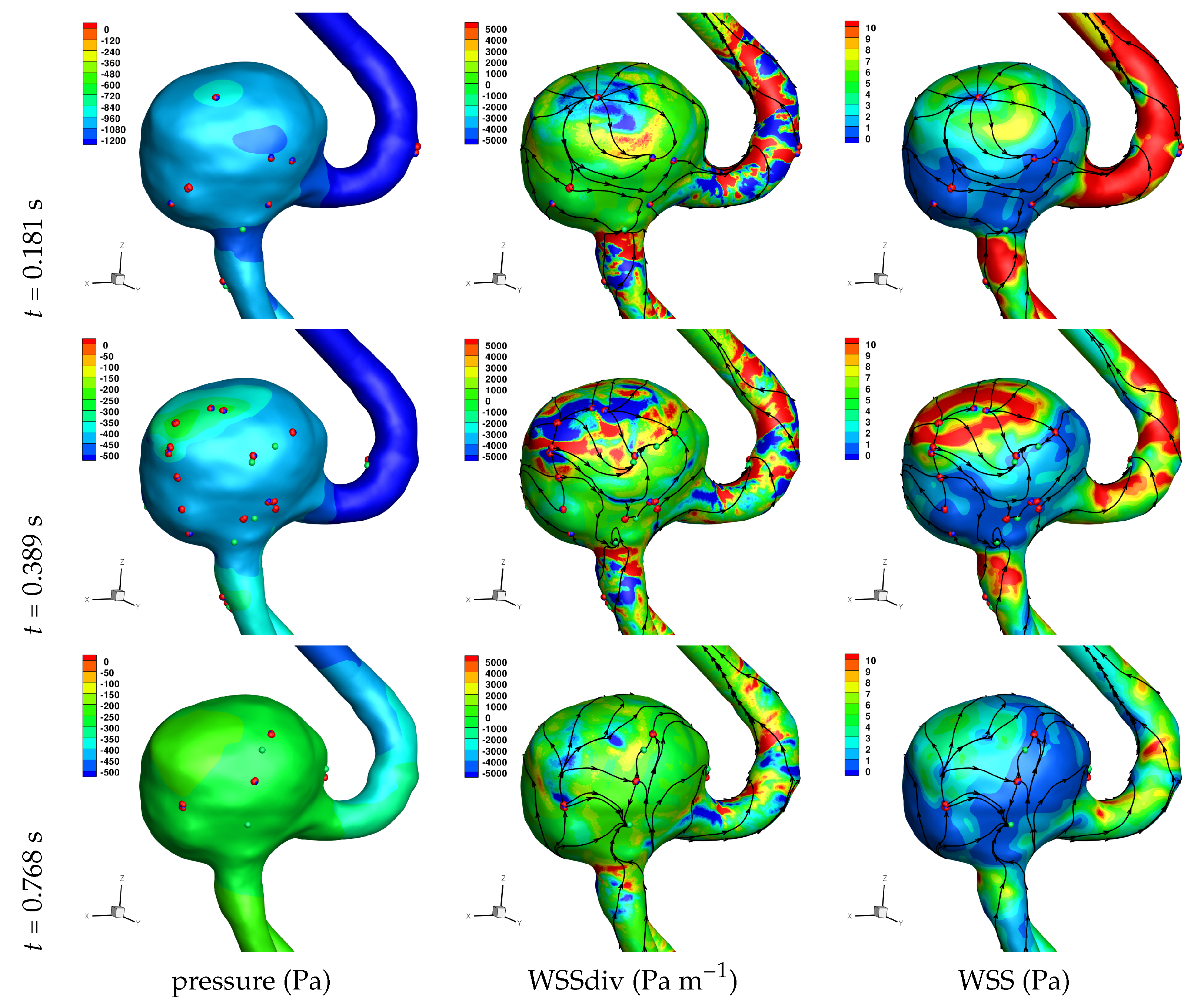
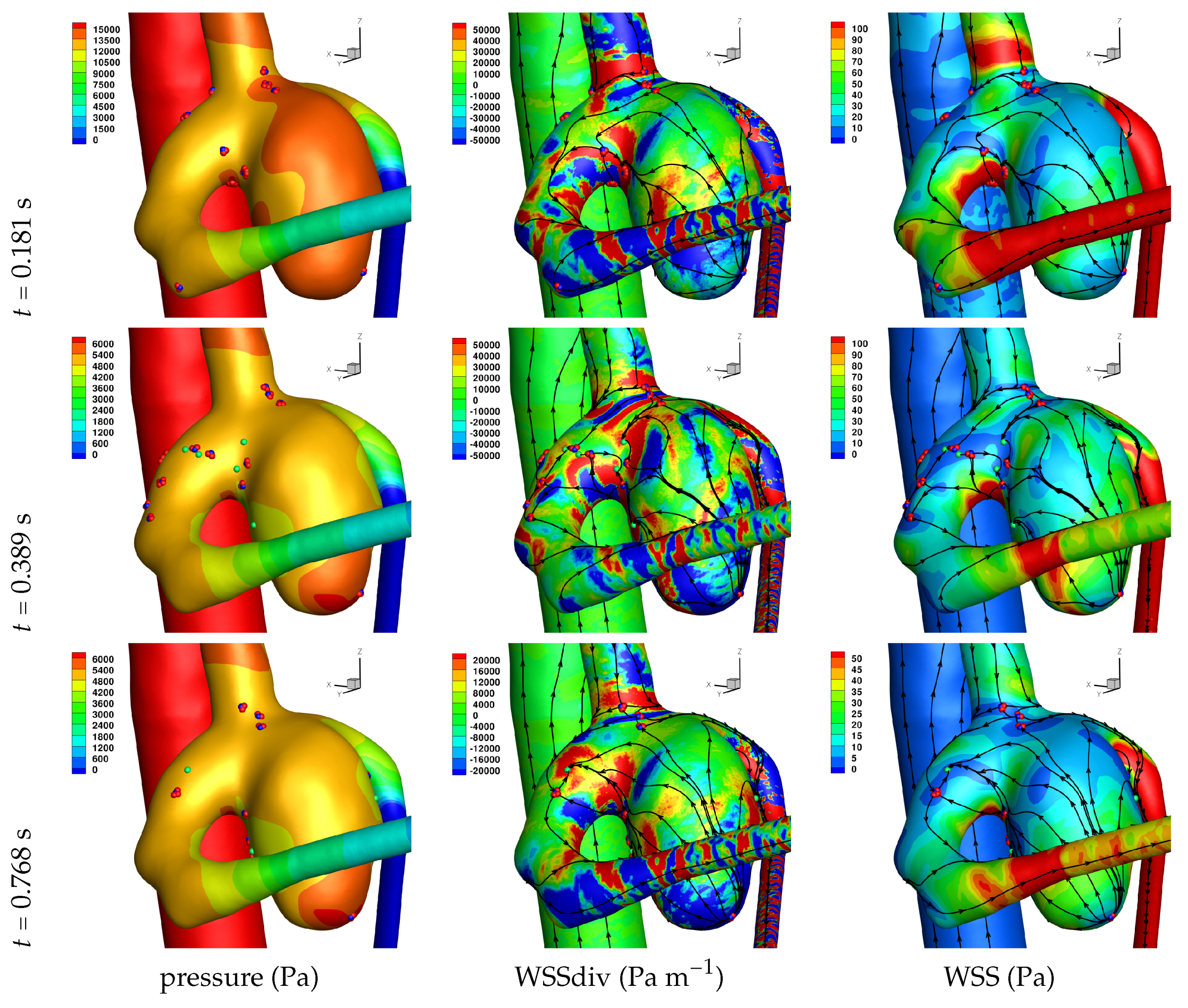
Results of the simulations, with a Newtonian viscosity model and inflow flow rate boundary condition for Patient 5 (see
Figure 2), are presented in
Figure 4,
Figure 5,
Figure 6,
Figure 7,
Figure 8 and
Figure 9 at three instances in the cardiovascular cycle representing
peak systole,
end systole (dicrotic notch) and
end diastole. In these figures, the wall shear stress critical points are marked by coloured dots, such that green indicates a focus, hence complex conjugate pair solution (spiralling motion), blue indicates a saddle or node, hence real solution, and red are locations a small distance along the eigenvectors (hence principal directions of dividing surface shear lines). It is apparent that the near-wall flow field is very complex for all cases, though some particularly so such as Case 3, while others are simpler such as Case 2. We observe that the WSSdiv patterns, which describes the normal component of the velocity, tends to be more stable than the WSS, which describes the horizontal component of the velocity. This was also reported in [
16].
A common feature to most cases is that of a persistent focus, which is present throughout the cardiac cycle. In
Table 2 the strongest persistent focus is reported, based on WSSdiv magnitude, throughout the three instances of the cardiac cycle. When present, these anchored (on the no-slip wall) vortices help stabilise the flow within the aneurysm. For Case 4 there is no evident persistent focus, while for Case 6 (Newtonian rheology) the focus appears only in the decelerating phase of the cardiac cycle. These focii are located in a region of positive WSSdiv, and hence indicate the near-wall flow is moving away from the wall. This is also identifiable by the negative sign of the real component of the complex eigenvalue pair which form the solution (see Equation (
6)), indicating these are
stable focii. Consequently, the flow moves from the near-wall region into the main free-stream flow, along a vortex which is anchored at the wall. If we take as example Case 1, at time 0.181 s, from
Table 2 we have WSSdiv = 420,000 Pa m
and can approximate the normal velocity component at a distance
using Equation (
2): for
m then
m s
, and for
mm then
m s
, highlighting that these vortices are indeed comprised of fast moving flow. The spiralling compactness (
) is also reported in
Table 2, and the observed general trend is a reduction (or negligible change) in spiralling compactness between peak systole and end diastole. For high values of spiralling compactness, there is a rapid motion to the focus centre without many rotations about the centre, while a zero spiralling compactness indicates purely circular motion about the centre with no radial change [
72]. As one would expect from physical principles, we observe similar trends in positive WSSdiv and negative
. The magnitude of the negative
indicates the attractor strength of the stable focus, and since mass in conserved, as the flow approaches the focus it must also move away from the wall with a positive WSSdiv, at a similar rate.
The number of critical points within the aneurysm are also reported in
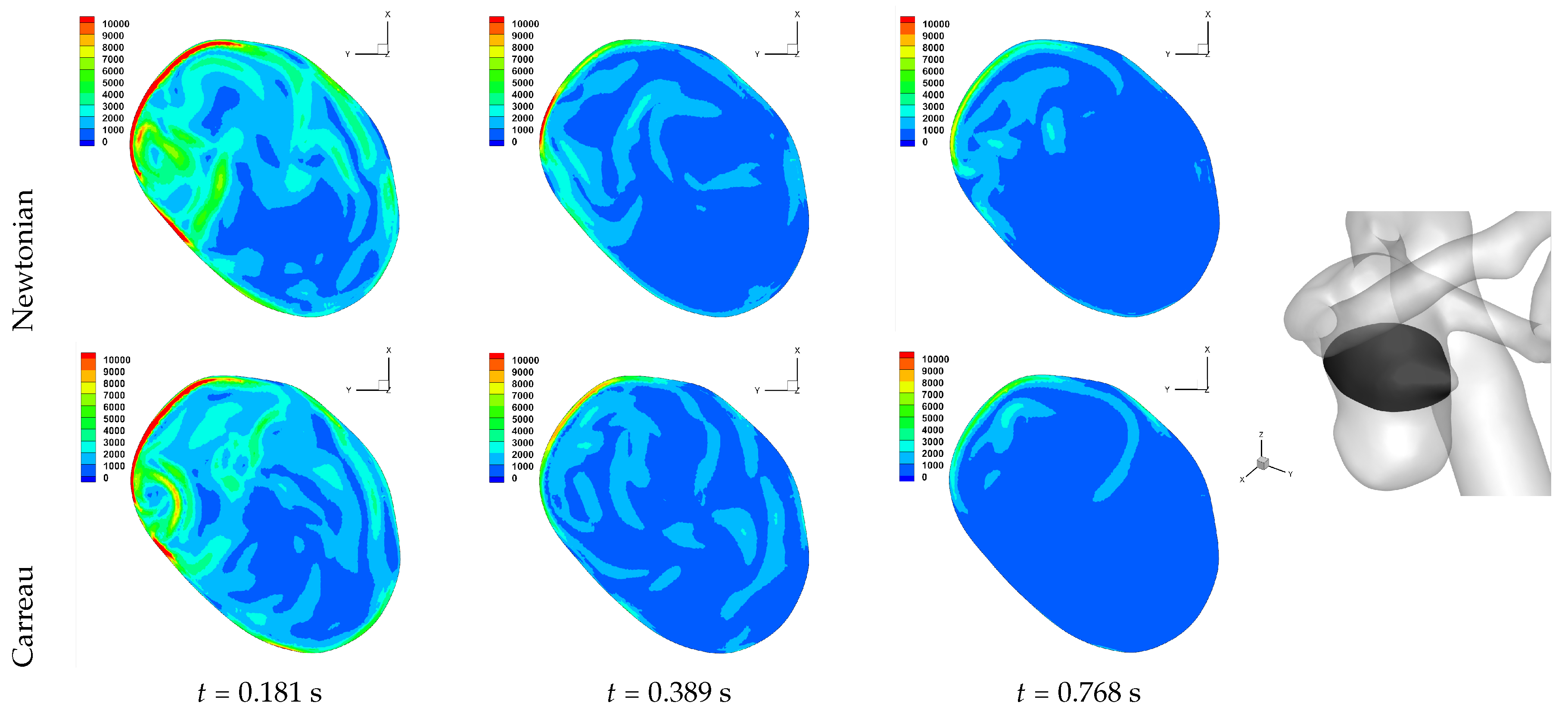
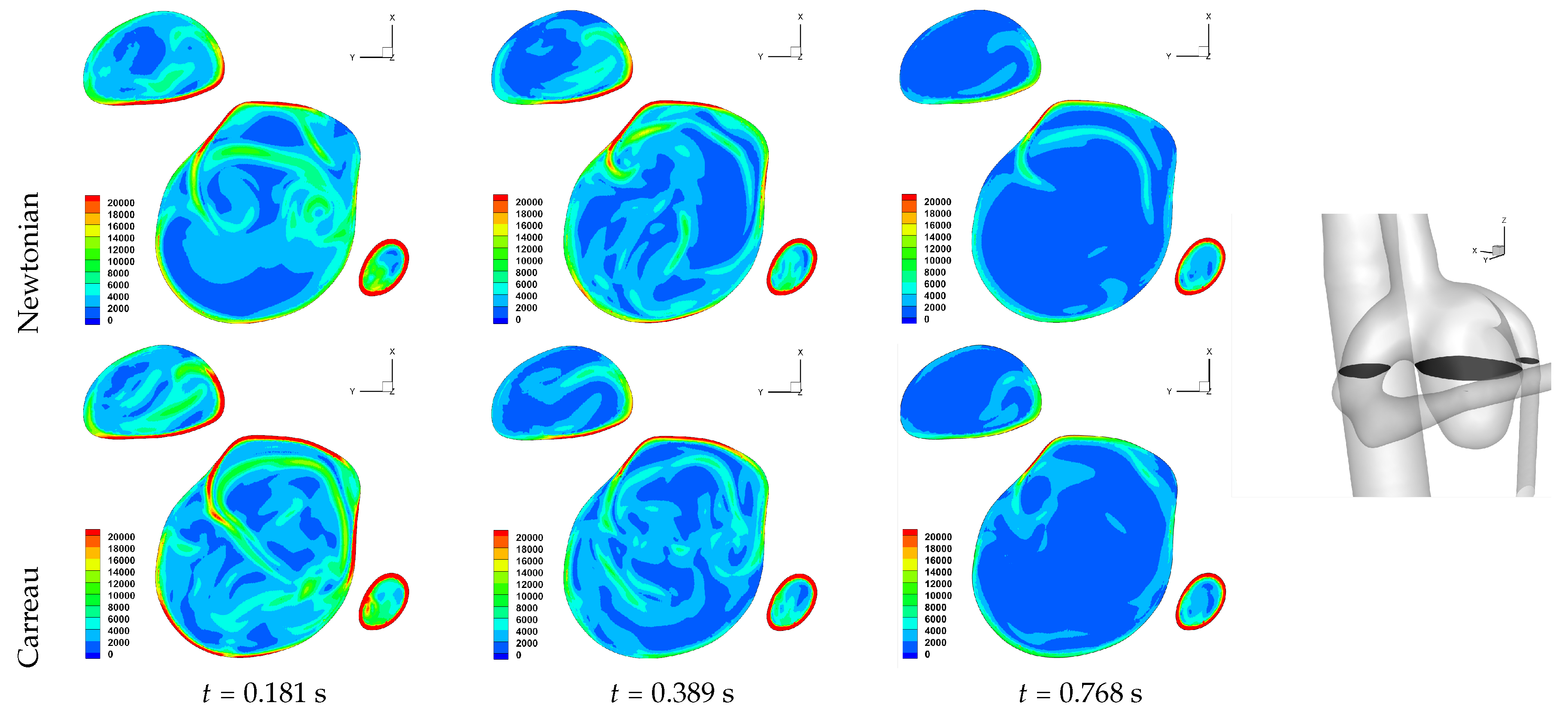
Table 2. We observe an overall trend of a decrease in number, between peak systole and end diastole, however at end systole both an increase and decrease are observed. The reason for this is that at end systole there is a deceleration of the flow, which will require dissipation, and commonly this results in eddy formation. This consequently affects the near-wall flow field as vorticity is generated at the wall and is diffused and transported into the free-stream flow field. While one should not confuse vorticity (hence angular velocity) with eddies, this simplified description of the process is useful here. The question then is at what stage of the overall dissipation due to deceleration does the end systole time instance lie. This will be case dependent, as the aneurysm shape and flow field will affect this. We in fact see that for some cases the number of critical points has increased, which suggests significant eddy motion within the aneurysm is still present at this time, while for other cases there is a decrease in number of critical points, which suggests that the deceleration of the flow has largely already occurred, though there is a further reduction in number of critical points by the end diastole stage. The decrease in spiralling compactness of the strongest persistent focus critical point during the deceleration phase of the cardiac cycle, supports this discussion of increased eddy motion as a dissipation mechanism. It is also interesting to observe the shear rate magnitude (
) through the cardiac cycle, since viscosity diffuses momentum by means of the rate of strain tensor (
D), and results for Case 3 and 6 are shown respectively in
Figure 10 and
Figure 11. From these we observe a decrease in shear rate from peak systole through to end diastole for Case 3, however for Case 6 we observe an increase in shear rate from peak systole to end systole and then a subsequent decrease at end diastole. This trend is similarly seen in the number of critical points from
Table 2.
An aneurysm’s surface area can been partitioned based on the near-wall flow field characteristics, and results are presented in
Table 3. We should first highlight that while partitioning the aneurysm surface by values of WSS and WSSdiv, the values of WSS and WSSdiv at a given point are uncorrelated, as previously reported in [
15]. The reason for the lack of correlation is due to the fact that they describe fluid motion in mutually orthogonal directions. In order to investigate the nature of the near-wall flow field for each aneurysm, we have chosen the threshold values of WSS = 1 Pa and WSSdiv = ±1000 Pa m
based on previous work [
15]. The WSS = 1 Pa threshold is widely used to indicate propensity for disease [
4]. The different near-wall flow regimes covered in
Table 3 are listed here again for clarity, together with the shorthand notation adopted.
WSS < 1 Pa suggests slow tangential flow, (→)
WSS > 1 Pa suggests faster tangential flow, (⇉)
WSSdiv < -1000 Pa m suggests fast perpendicular flow to the wall, (⇊)
WSSdiv > 1000 Pa m suggests fast perpendicular flow from the wall, (⇈)
|WSSdiv| < 1000 Pa m suggests slow perpendicular flow, (⇵)
We observe that a threshold of WSS = 1 Pa biases the results to lie in the WSS > 1 Pa regions, except for Case 5 which is a large scaccular basilar aneurysm. From Equation (
2) we can approximate the tangential velocity component for WSS = 1 Pa, and for
m we have
m s
, and for
mm we have
m s
. Given these approximations of very low near-wall tangential flow, it is worth reconsidering the various WSS thresholds associated with diseases reported in the literature [
4].
While a value of m s at mm is indeed not negligible so close to the wall, the values reported above for the normal component of the velocity for a persistent strong focus at the same distance is m s, which is clearly substantially larger. At the smaller distance of m, the normal and tangential components of velocity for a strong persistent vortex and what is considered to be a slow tangential flow, are now similar. The discrepancy in magnitude of and at larger arises from the approximation of and , from which we can see the influence of the order of . These equations are the leading order terms of a Taylor expansion, and it may be beneficial to include higher order terms to match the order of .
Let us return to
Table 3, and focus on the associated percentage aneurysm area for WSS > 1 and |WSSdiv| > 1000, hence for the more prevalent situations occurring within the aneurysm dome. We observe that for WSSdiv < −1000 the trend is a decrease in percentage area, from peak systole to end systole and then to end diastole. On the other hand we observe that for WSSdiv > 1000 the trend is an increase in percentage area between peak systole and end systole, and then a decrease between end systole and end diastole. The reasons for this are as follows. During the deceleration of the fluid (from peak systole to end diastole), we expect a decrease in magnitude of flow impingement on the wall, hence less observed percentage area for WSSdiv < −1000. Also, during the deceleration phase, we typically have an increase in eddying motion in order to diffuse momentum, and since the focii critical points tend to be of stable type, hence locations of positive WSSdiv, we observe the increase in percentage area with WSSdiv > 1000 from peak systole to end systole. By the time we reach end diastole the flow has further decelerated and diffused much of the momentum, consequently the eddying motion has decreased and so has the number of stable focii, resulting in less percentage area associated with WSSdiv > 1000.
Let us now consider the average values of WSSdiv when WSS < 1 Pa and WSS > 1 Pa, as presented in
Table 4. We note that the average values of negative WSSdiv (near-wall flow moving to the wall) are greater in magnitude than the counterpart positive WSSdiv (near-wall flow moving away from the wall). This is due to the fact that flow moving to the wall will have higher momentum, and hence velocity (we are assuming constant density). This fluid volume will subsequently run along the wall before moving away again, decreasing its momentum by means of the viscous forces during this trajectory. In this table, and from the plots shown in
Figure 4,
Figure 5,
Figure 6,
Figure 7,
Figure 8 and
Figure 9, we observe that some aneurysms exhibit higher WSS and average WSSdiv magnitude, namely Case 1, Case 3 and Case 6, and the reason for this is not apparent based on the geometric characterisations presented in
Table 1, nor from qualitative analysis. One therefore needs to investigate the entire flow field to understand how the fluid is entering the aneurysm, promoting the large near-wall WSSdiv and WSS values observed. For near-wall transport both to and from the wall, the average WSSdiv magnitude drops between peak systole and end diastole due to the flow having decelerated, but it typically increases at end systole, indicating a higher transfer between free-stream and near-wall regions.
We now report on the effects of rheology, between Newtonian and Carreau generalised Newtonian models, for Case 2, Case 3 and Case 6. Overall we do not observe marked changes in patterns of WSS and WSSdiv, indicating that the free-stream flow field is unlikely to have altered considerably also. This has been reported in previous works [
54,
60]; namely that in large artery haemodynamic the non-Newtonian rheological models do not affect the flow field and the wall shear stress field significantly, and variations in boundary conditions (inflow/outflow, no-slip domain) have a greater effect.
In
Table 2 we observe the same trends as discussed above if the Carreau model is adopted. We also observe greater
and WSSdiv for results with the Carreau model in comparison to the Newtonian model, indicating faster flow leaving the wall at the strongest persistent focus critical point, and in general either no significant change or an increase in the number of critical point. These are seen throughout the cardiac cycle.
In
Table 3 we see that there is no pronounced change in the percentage area covered by the WSS and WSSdiv partitions if the Newtonian or the Carreau model is adopted. On closer inspection we do observe a general modest increase in the percentage area covered by WSS > 1 Pa and WSSdiv < −1000 Pa m
(i.e., non-stagnant flow moving to the wall). In fact there is also a general increase in the percentage area covered by WSS > 1 Pa and WSSdiv > 1000 Pa m
(i.e., non-stagnant flow moving from the wall), but to a lesser extent. The Carreau model adopted is a shear thinning model, and since we can in general expect higher shear rates closer to the walls, we would have a lower apparent viscosity close to the no-slip domain. This will lead to smaller boundary layers, hence effectively bringing the far field free-stream flow closer to the no-slip wall. Additionally, as the flow moving to the wall has higher momentum (as indicated in
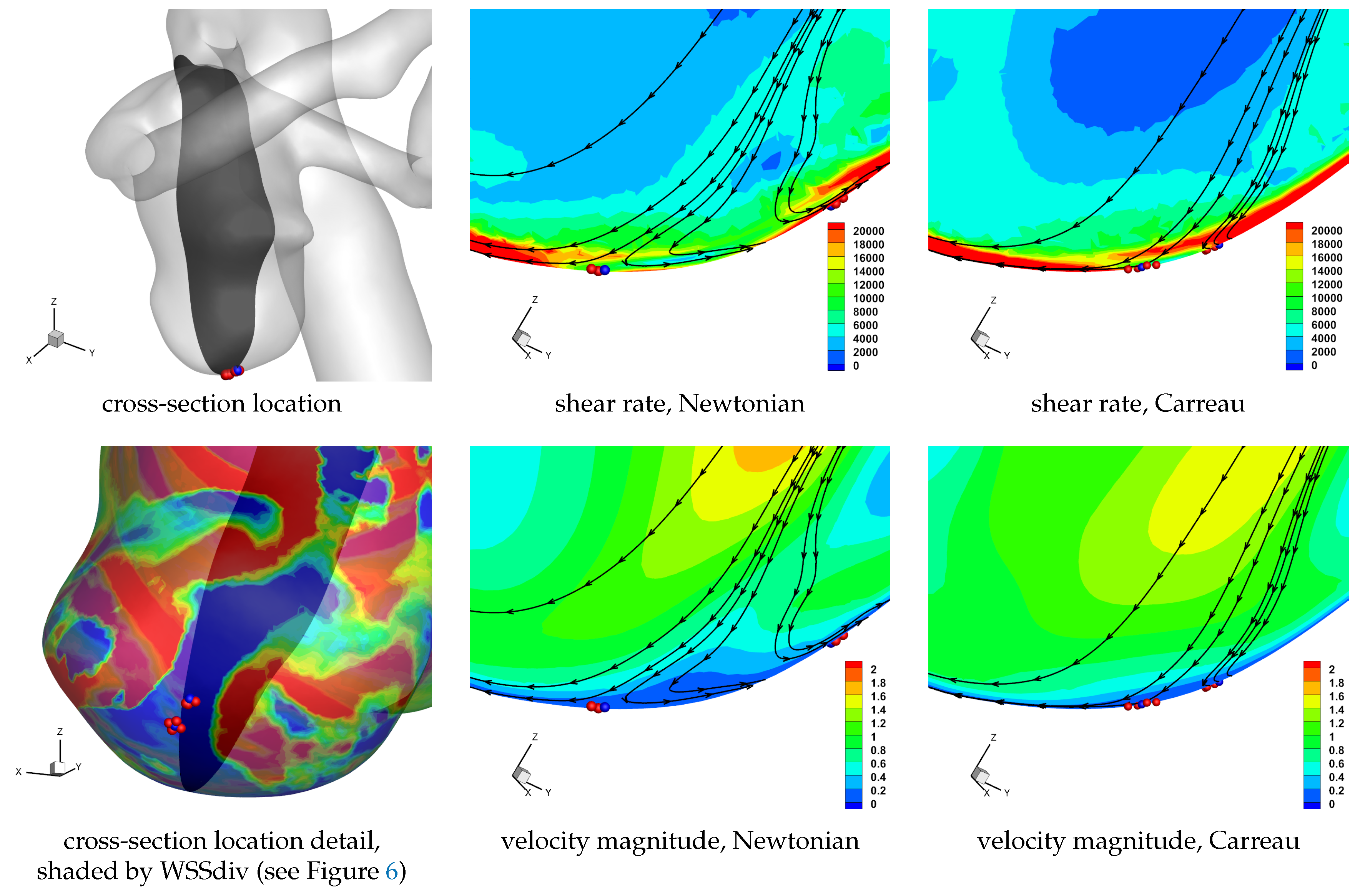
Table 4) since it comes from the faster flowing free-stream domain, as it encounters the rigid wall with no-slip condition the fluid will be subjected to higher strain rates. Now, since the flow moving towards the wall is subjected to higher strain rate it will correspondingly have lower viscosity if the shear-thinning non-Newtonian model is used, and as such it will also flow less inhibited and cover a larger surface area. These may be some of the reason for the modest increase in observed flow moving to the wall, which interestingly occurs throughout the cardiac cycle. Similar reasoning can be applied for the flow moving away from the wall, though the flow has lost some of its momentum by means of viscosity during its near-wall trajectory (involving approaching the wall, moving along it, and finally moving away from it), and will consequently have a lower shear rate magnitude and the apparent viscosity will be more similar to the Newtonian value. Results for a cross-section of the domain near a set of unstable node critical points provide a visual aid in understanding the above discussion, as shown in
Figure 12. We note the higher shear rate magnitude in the non-Newtonian solution, as well as the wider extent of the velocity moving to the wall, as compared to the Newtonian solution.
In
Table 4 we again observe the same trends as discussed above if the Carreau model is adopted. The differences between shear-thinning and constant viscosity models reported in
Table 4 suggest a general reduction (or effectively unaltered) magnitude of average WSSdiv throughout the cardiac cycle. As discussed above, the higher shear rates are expected to occur at the no-slip domain, resulting in a reduced apparent viscosity at the wall for the Carreau model, allowing the fluid to flow more easily. This will allow the flow to align tangentially to the wall more easily, resulting in a lower magnitude of near-wall normal velocity. This is also observed in
Figure 12.
The results presented thus far have considered a limited cohort of six patient cases, a single Reynolds number to define the flow regime, and two rheological models. To generalise the results, allowing for greater robustness of the findings and easier translation to other patient cases, we have also undertaken simulations for different cardiac profiles as shown in
Figure 2 for Case 2, Case 3 and Case 6. The results of these simulations have been tabulated in a similar fashion to the results discussed above, and can be found in the
Appendix A in
Table A1,
Appendix A in
Table A1,
Table A2 and
Table A3. Without providing detailed discussion, we summarise the main findings. On changing the inlet flow rate profiles, the flow field has also noticeably changed and the values reported can be seen to differ considerably from those in
Table 2,
Table 3 and
Table 4. The trends between peak systole, end systole and end diastole however still hold, with the ‘Healthy’ flow rate profile (see
Figure 2) reporting the greatest deviation in trends. The ‘Healthy’ flow rate profile exhibits greater acceleration and deceleration phases, as compared to the ‘Patient’ cases. Please note that since the flow field has changed, the strongest persistent focus critical point reported in
Table A1 will not be the same as in
Table 2, and hence a direct comparison of values is not meaningful.
4. Conclusions
In this paper, we have presented simple, yet effective means to describe the near wall-flow field, as velocity components
tangential to the wall or
perpendicular to it, based on previous work [
15]. These velocity components are effectively proportional to the wall shear stress (WSS) and the divergence of wall shear stress (WSSdiv), respectively. The tangential velocity component (hence WSS) is then further analysed to observe the local instantaneous surface shear lines, including locations of critical points and the principal directions of motion at these points, based on previous work [
16]. This physically meaningful description, the mathematical tool set developed and simple numerical formulations, together provide the means to efficiently deconstruct the near-wall flow field, in a computationally inexpensive manner. These measures are not intended to substitute the existing correlators to disease [
4,
11,
27,
49], but rather they complement those findings and provide a simple and practical means of observing the near-wall flow field.
The analysis of the near-wall flow field was performed on six cerebral aneurysms. Unsteady numerical simulations of the haemodynamics were effected, and the aneurysm wall was partitioned into regions based on the the magnitude and direction of the tangential and perpendicular velocity components. Changes in the percentage surface area covered by the different regions, together with the average WSSdiv within each partition, were reported during the cardiac cycle at peak systole, end systole and end diastole. The WSS critical points were also analysed during the cardiac cycle, with respect to their type, the relative numbers and the persistence of the strongest stable focus. Together these provide extensive detail into the dynamics of the near-wall flow, and overall trends between the six patients cases analysed can be seen, and importantly the outliers also. Flow deceleration during the cardiac cycle promotes the formation of eddies as a momentum dissipation mechanism, and the effects of this are evident in the near-wall flow field, with an increase in WSS critical points, changes in percentage area associated with a flow characteristic and in mean WSS and WSSdiv values.
A comparison of Newtonian versus non-Newtonian rheological models was carried out on three aneurysms. The results indicate a very modest changes in the near-wall velocity field. Higher shear rate magnitude at the wall leads to lower effective viscosities at the near-wall region, resulting in smaller boundary layers, as well as flow aligning more readily to the no-slip wall tangent plane.
Since WSSdiv and WSS are related to orthogonal components of the near-wall velocity, they provide independent forms of information. The current literature on cardiovascular research commonly makes use of WSS and derived measures (such as: time averaged wall shear stress, residence times, oscillatory motion), however this only covers information of the near-wall tangential velocity, and it is certainly worth including WSSdiv in the analysis in order to describe the near-wall perpendicular velocity. This physical understanding of the measures provides greater insight into how to analyse and develop a better understanding of disease occurrence and progression.
In [
45,
46,
49] the analysis of the near-wall flow was incorporated with the analysis method of Lagrangian Coherent Structures (LCS) in the context of cardiovascular flows. This time-evolved partitioning of the flow, together with the effects of transport and diffusion in the near-wall region, does indeed provide additional physically motivated information, important in understanding the near-wall flow field. Interestingly however, it was shown in these works that the near-wall flow LCS in fact showed good correlation to the WSS critical points of a time-averaged WSS field. Therefore, even with the simple methods outlined in this work one can obtain insight into time-evolved results, by simply performing a time average WSS and WSSdiv field to analyse.
A sensitivity analysis was carried out to quantify the error and its propagation through the data analysis. Six patient specific cases were investigated, adopting a Newtonian viscosity model and an inlet flow rate profile (‘Patient 5’,
Figure 2). Additionally, three Cases were selected for further investigation, including using a shear-thinning non-Newtonian model for viscosity and three further flow rate profiles (also shown in
Figure 2). Overall, similar general trends were reported, for three time instances in the cardiac cycle. The difference between Newtonian and non-Newtonian rheological models was not as marked as when changing the flow rate waveform. The ‘Healthy’ flow rate profile reported the greatest difference in computed solution. This sensitivity study provides greater robustness of the findings and easier translation to other patient cases.
We expect the methods outlined in the paper to be directly transferable to other problems where the near-wall region plays an important role, acting effectively as interface domain between wall and free-stream fluid. This is common in biological and physiological flows, where mass transport and signalling are important phenomena.