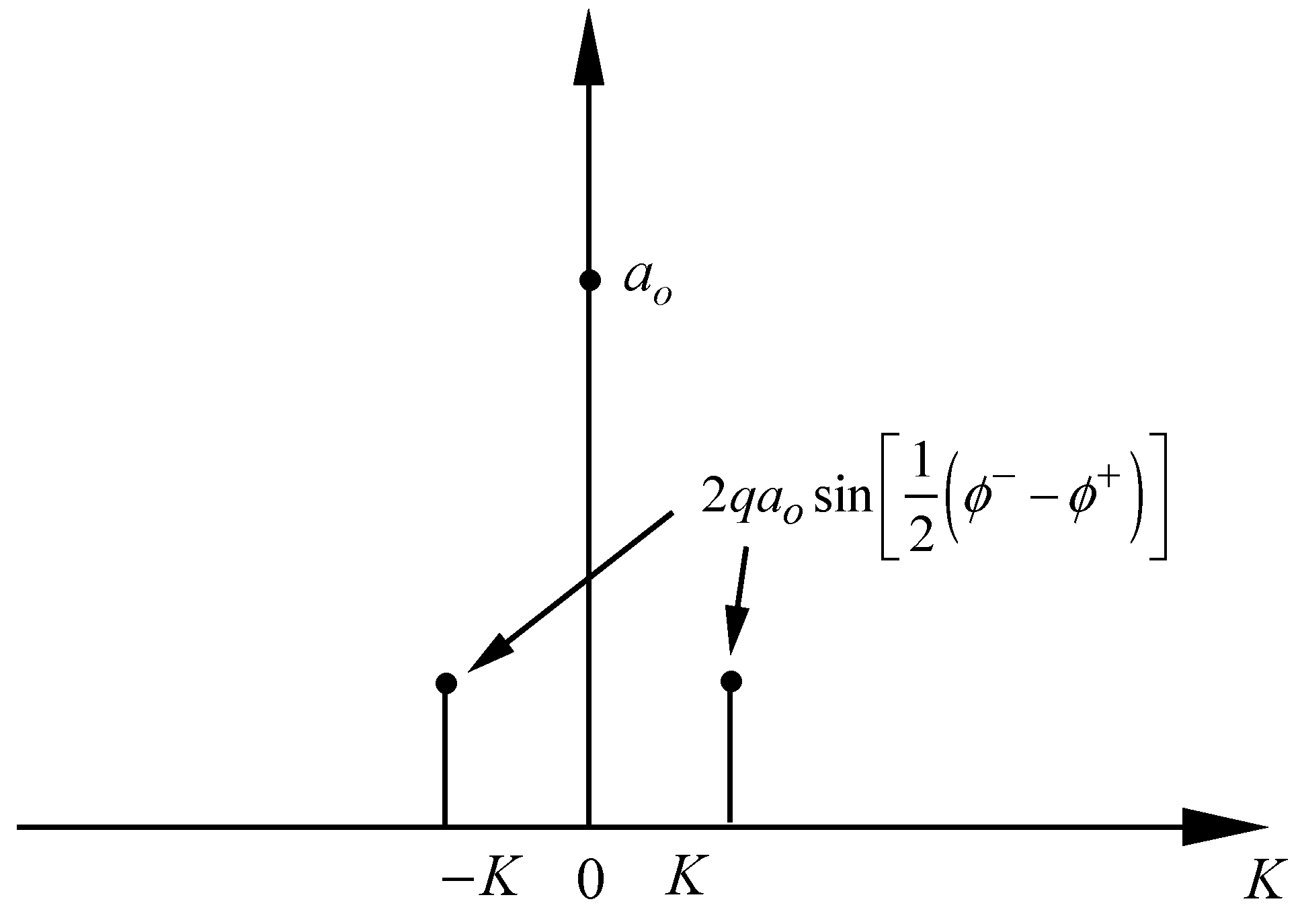1. Introduction
I apply the methods of nonlinear Fourier analysis (NLFA) [
1,
2,
3,
4] to the theoretical and numerical study of ocean waves. NLFA is an approach where
quasiperiodic Fourier series, rather than standard Fourier series, are applied to the study of
nonlinear wave dynamics. The starting place is the study of the classical so-called nonlinear integrable equations of mathematical physics. There are an infinite number of these nonlinear integrable wave equations, many of which have physical applications to water waves. These include the Korteweg-deVries (KdV), the Kadomtsev-Petviashvili (KP) and the nonlinear Schrödinger (NLS) equations. To solve these integrable wave equations, one uses the
inverse scattering transform (IST) for
periodic/quasiperiodic boundary conditions [
5]. The IST theory is also referred to as
finite gap theory (FGT), a terminology used in Russia [
6,
7]. An overview of theoretical and numerical methods for applications of IST to physical oceanography is given in Reference [
3]. The special coherent structure solutions of the nonlinear integrable equations include
solitons,
kinks,
breathers,
superbreathers and
vortices. Thus, the full nonlinear theory of wave motion uses these solutions as
nonlinear basis functions that interact nonlinearly with one another, while standard Fourier analysis uses only sine waves and is therefore unable to characterize the coherent nature of water waves.
Recent papers [
1,
8] analyze surface wave data obtained in Currituck Sound, South Carolina and both
soliton turbulence and
breather turbulence were found. The data analysis methods were those of the periodic IST (also FGT) [
3], which allows for nonlinear spectral decomposition of the data. The importance of these works is to: (1) establish new methods to determine the nonlinear effects at work in measured ocean wave trains and (2) to apply the methods to determine what nonlinear Fourier modes are active in a particular data set. The nonlinear Fourier modes of the NLS equation consist of (1) sine waves, (2) Stokes waves, (3) solitons, (4) breathers, and also (5) superbreathers. This contrasts to traditional Fourier analysis which projects measured data only onto simple sine waves. We now have at our disposal the mathematical methods to project data onto the nonlinear modes and this is therefore an important period in the understanding of the presence of coherent structures in ocean waves. The goal of this paper is to provide closure on a complete theoretical and numerical approach for the U. S. Navy that can be used in real time to assess the actual nonlinear spectrum of measured wind waves by shipboard radar and lidar and by synthetic aperture radar onboard airplanes.
It is important to understand what we mean by the phrase “dense breather turbulence.” This terminology suggests that the breathers in a sea state are crowded together, perhaps even overlapping each other. Such a sea state must
per forza have a large number of
rogue waves, the latter defined to be the central wave in a breather packet at its maximum height during the Fermi-Pasta-Ulam (FPU) cycle time: We call a sea state with dense breathers a “rogue sea.” This concept was born in our analysis of surface wave data taken in Currituck Sound [
1] where about 95% of the FGT spectral components were breather trains. Basically the time series analyzed in this data set were about
T = 1680 s long with a typical number of breathers
(this is the number of “eigenvalue pairs connected by a spine” in the FGT spectrum). The peak period (
, where
is the peak spectral frequency) of the waves is about
s, so this would suggest that there are about 3.36 waves over each 8.4 s breather interval (found from 1680 s/200 breathers). We also determine the FGT spectral properties of breather packets, one of which is the number of waves in a breather packet, that we call here
, thus suggesting considerable overlapping of the breathers in the data because 5.1 waves > 3.36 waves. This means that the breather packets are “dense” in the sense that their tails overlap the adjacent breathers. While our definition of “dense” is somewhat
ad hoc, it does suffice to give the following expression for the density of breathers in the Currituck Sound data [
1]:
The fact that for the Currituck Sound data means that the breather packets are squeezed together, with overlapping tails. One presumes that there are considerable nonlinear interactions among the crowded breather trains in the time series. In the case that D << 1, we have breathers that are few in number and sparsely scattered over the length of the time series. For the case with , the breathers are, on average, fairly evenly scattered over the time series but there is no average overlapping: This is still likely a highly nonlinear case because each breather has its own group velocity, so that some breathers will interact by catching up with slower breathers, while others will fall behind faster moving breathers, resulting in interactions. It is tempting to call the case D > 1, a rogue sea, but we have yet to carry out sufficient numerical simulations to fully understand the effect of this parameter on the intensity of the sea state and on the statistical distribution of wave amplitudes and wave heights.
The theoretical formulation given herein provides a full characterization of the
nonlinear Fourier analysis (NLFA)
spectrum (here the inverse scattering transform or finite gap theory spectrum with periodic/quasiperiodic boundary conditions) based on the exact nonlinear spectral solution of the NLS equation. Future efforts will include extending this work to fully two dimensions and to higher order. The physical description of NLFA spectral solutions of NLS simultaneously consists of nonlinearly interacting
sine waves,
Stokes waves and
breather packets, all of which are viewed as
nonlinear basis functions in NLFA. Because of the coherent nature of Stokes waves and breathers, we have
exact spectral solutions that have remarkably complex nonlinear dynamics that
resemble classical turbulence, i.e., in which one has oscillatory waves and vortices. Furthermore, we find that because of the
highly random nature of complex sea states dominated by breather packets, there is the need for a
stochastic formulation of the motion (see Reference [
4]). To this end, I discuss the
nonlinear random phase approximation for
nonlinear waves and the consequent
breather turbulence and discuss how to apply it to
stochastic properties of the motion and to the data analysis of measured random, nonlinear ocean waves.
However, many other issues need to be addressed, some of which are discussed herein. Why are breather trains important? Because the largest breathers generate the largest waves, many of which are much larger than predicted by the Gaussian or Rayleigh distributions, commonly used for estimating large amplitudes and wave heights in ocean waves. Other important features of the method relate to the space/time dynamics of breathers (and their associated rogue waves) and the stochastic behavior of breather turbulence. This work is important because sea states of this type are “rogue seas”, i.e., those sea states that have large numbers of large rogue waves and therefore place shore facilities, ships, offshore platforms, and undersea pipelines at high risk. Characterization of these sea states is of fundamental importance for future operations in a world ocean where climate change is slowly increasing the size of sea waves and is therefore increasing their nonlinearity and risk level.
To establish what I mean by NLFA, I first give a brief overview comparing standard Fourier series with quasiperiodic Fourier series. Standard Fourier analysis consists of ordinary
trigonometric series:
Here,
Kn are the wavenumbers,
ωn are the frequencies and
are the phases. The expression
is called the
dispersion relation that connects the wavenumbers to the frequencies. The series (1) are the standard tools for the
linear theory of wave motion and for the
numerical analysis and modeling of both linear [
9]
and nonlinear wave motions [
10,
11]. Equation (1) is normally implemented with the fast Fourier transform algorithm. Furthermore, wind/wave models are based upon the
Hasselmann kinetic equation [
12] that describes the four-wave interactions of weakly interacting sine waves driven by the wind in the presence of wave-breaking dissipation [
13,
14,
15].
The modern approach to nonlinear wind waves owes much to Zakharov and coworkers [
16,
17,
18,
19,
20]. The Alber equation provides a modern approach that gives added perspective to the wind wave problem at higher order [
21]. Athanassoulis has also addressed wind waves from the point of view of the Wigner Equation [
22]. An excellent review of rogue waves and their impact on ships and offshore structures is given in Reference [
23]. In very recent and relevant work, Grimshaw modifies the nonlinear Schroedinger equation to include wind; the method actually creates waves groups by the shear layer instability [
24], (see also the Grimshaw paper in this issue of Fluids [
25]).
A whole host of modern work relates to the study of waves in wave tanks [
26,
27,
28] and to experimental measurements and analysis in fiber optics [
28,
29,
30]. One of the most relevant bodies of work is that relating to the study of so-called integrable turbulence done by El and coworkers [
31,
32,
33,
34,
35]. It is hard to overemphasize the importance of these latter studies and their relevance to ocean waves: The contributions are particularly important because they lead to exact kinetic equations for describing the integrable turbulence; this is crucial because they include the coherent structures in their formulations. For those with general interest in extreme and rogue waves in the ocean, see the important books by References [
36,
37].
The field of physical oceanography thinks in terms of the Fourier series (1) in a very pragmatic way. By putting (1) in discrete form (for indeed space/time series are discrete), one finds the inverse Fourier transform occurs simply by changing the sign of the exponential. Then the fast Fourier transform (FFT) allows (1), and its inverse, to be computed rapidly. Random waves are addressed simply by using uniformly distributed random phases in (1), i.e., the so-called random phase approximation. Furthermore, (1) can be used to compute all kinds of wonderful properties of waves. Indeed, one introduces the correlation function, power spectrum, coherence functions, etc. to characterize the stochastic properties of random waves. Then (1) becomes the basis of stochastic kinetic equations to characterize slowly varying sine waves in sea states driven by the wind. One question that the present paper addresses: Is there a similar formulation that can allow us to conveniently determine the full properties of nonlinear coherent waves in the same spirit as (1)? One possibility for carrying out such a plan is Equation (2) below, which I now discuss.
Now we make a bold leap for solving nonlinear wave equations and instead of (1) I use quasiperiodic Fourier series that have the form:
Here
is an
N-dimensional
integer summation vector is an
N-dimensional wavenumber vector so that
and
is an
N-dimensional
frequency vector (As determined by the
nonlinear dispersion relation of a particular wave equation [
4]), and
is an
N-dimensional phase vector
. The “dot” or “
” indicates the
inner or
dot product:
Equation (2) is the basis for the NLFA formulation of nonlinear waves. We see that such a formulation is also linear, but due to the dot product it contains all harmonics to all orders for all of the Fourier components. With these harmonics, one is able to construct all of the coherent waveforms that occur in integrable nonlinear wave equations. These include the Stokes waves, solitons, breathers, superbreathers, vortices, etc. that are the nonlinear Fourier components in the motion of nonlinear waves.
It is worthwhile pointing out that the nonlinear dispersion relation, written symbolically above after Equation (2) (
) indicates that the frequency
is a function of the wavenumbers
. The dot product notation means there are an infinite number of wavenumbers and frequencies that form a
discretuum, i.e., a dense point set that lies between a discrete set and a continuum. Substituting (2) into a particular nonlinear wave equation determines the dispersion relation
so that the dispersion relation also has amplitude-dependent terms (see how this substitution works in
Section 3.4,
Section 3.8 below and Osborne [
4]). From the point of view of finite gap theory, the frequencies
depend on the full set of
spectral parameters that are the branch points of the Riemann surface. Algebraic geometric loop integrals constitute the formulas for the computation of the frequencies (and the period matrix and phases) using finite gap theory, see Kotljarov and Its [
38], Tracy and Chen [
39] and Belokolos et al. [
6]. See Osborne [
3] for additional theoretical and numerical methods.
One goal of the present paper is to address the possibility that (2) can be used to characterize ocean waves to determine their nonlinear properties just as (1) can determine linear properties of waves. For (2), the inverse problem is found by changing the sign of the exponential [
3]. What physical information does (2) have that (1) does not? The answer is that (2) has the coherent structures of water waves automatically included in the formulation: Stokes waves, breathers, superbreathers, kinks, vortices, etc. The random phase approximation can be extended to nonlinear problems by using uniformly distributed random phases in (2). The nonlinear correlation function, power spectrum, coherence function, etc. can all be computed from (2), as I show herein. New methods for dealing with nonlinearity in water waves using quasiperiodic Fourier series are found in this paper and other recent studies of oceanic wave data sets [
1,
2,
4,
8].
The perspective given herein contrasts to finite gap theory, but nevertheless employs it, in that NLFA is symmetric in terms of the direct and inverse problems, as is the standard Fourier series. The standard Fourier approach has a Fourier series (1) as the direct problem and (2) also as the inverse problem (with a sign change in the exponential). Quasiperiodic Fourier series have this same property, i.e., they are symmetric for both the direct and inverse problems, with the same change in sign of the exponential. On the other hand, the FGT is asymmetric: The direct problem is the solution of a Floquet eigenvalue problem and the inverse problem is computed from Riemann theta functions. Therefore, the symmetry of quasiperiodic Fourier series (2) and its inverse may be a welcome change for some. Certainly some aspects of the numerical analysis are also simplified.
One can now ask: How does one establish a quasiperiodic Fourier series solution (2) of a particular nonlinear wave equation? How does one determine what the Stokes waves and breathers are in the spectrum? There are three steps to address these issues:
- (1)
First, one uses quasiperiodic FGT to establish the spectral parameters
, where
is the Riemann matrix of nonlinear Fourier amplitudes,
is the wavenumber vector,
is the frequency vector, and
is the vector of the phases. Here the Riemann matrix
τ contains the amplitudes of the sine waves, Stokes waves and breathers on the diagonal terms and the nonlinear interactions are on the off diagonal terms, while the frequencies
are computed from the nonlinear dispersion relation
, given by particular loop integrals [
1,
3].
- (2)
Second, one uses results from the
Baker-Mumford theorem (see
Appendix A) to establish the
mathematical validity of going from the spectrum
to the quasiperiodic Fourier series (2).
- (3)
Third, one uses a method presented below (
Section 2) to establish the parameters of the quasiperiodic Fourier series
directly from the Riemann parameters
Experimentally, the inverse of the process is important, i.e., to go from the
experimentally determined parameters in (2) to the Riemann (NLFA) parameters of the coherent structure spectrum
In the remainder of this paper, I discuss the
most general quasiperiodic solution of the NLS equation as a ratio of Riemann theta functions (
Section 2). I then address how to determine from the results of
Section 2 the associated
quasiperiodic Fourier series solutions (2) for NLS (
Section 3.1). This result is important because it renders finite gap theory in the form of quasiperiodic Fourier series which have immense applicability from theoretical and numerical points of view, as see in later Sections.
Section 3 also addresses other important properties of these solutions, found by the study of
small amplitude oscillations (
Section 3.2 and
Section 3.3). The
modulational dispersion relation, relating to the
Benjamin-Feir instability, is given in
Section 3.4 in terms of the perspective of quasiperiodic Fourier series. The simple
dnoidal wave solution of the NLS equation, a
stable solution of the equation, is discussed in
Section 3.5. I then give a full overview of the quasiperiodic Fourier series for the
surface wave elevation associated with the NLS equation in
Section 3.6. In
Section 3.7, I discuss how the solution for the surface wave elevation may be viewed in terms of
Stokes waves and their mutual
pair-wise nonlinear interactions.
Phase locking of two Stokes waves gives rise to
breathers, a result discussed in
Section 3.8 using the theta function solution of NLS. The
nonlinear random phase approximation and properties of the associated
stochastic solutions of NLS are discussed in
Section 4.1 for which the
correlation function and
power spectrum (
Section 4.2) are analytically computed. The special case of spatially (or temporally) periodic boundary conditions, important for numerical modeling and space/time series analysis [
3], is discussed in
Section 4.3.
Section 5 gives a discussion and conclusions for applications of the approaches given herein to problems in physical oceanography.
2. The Nonlinear Schrödinger Equation, Its Spectral Solutions and the Surface Elevation
The dimensional nonlinear Schrödinger equation has the well-known form [
16,
40,
41]
Equation (4) describes the complex modulation of a narrow banded wave train. Here
is the linear group speed,
is the coefficient of the dispersion term and
is the coefficient of the cubic nonlinear term. The exact formulation of the coefficients is given in the literature [
3,
42,
43]. Well-known particular homoclinic breather solutions are discussed in the classical papers [
44,
45,
46]. The coefficients for the deep-water case are worth writing here:
The parameters
and
are the
carrier frequency and
wavenumber. For deep water, the dispersion relation has the form
. The
Stokes perturbed frequency Ω’ and
wavenumber are given by taking the plane wave
and using this in (4) we get the
dispersion relation :
Note the
amplitude-dependent correction to the dispersion
, found by Stokes in 1847. Unfortunately, (7) is not completely general because of the modulational instability, which forces a different strategy to determine the
modulational dispersion relation that is valid for the unstable modes of NLS, which I discuss in more detail in
Section 3.4.
The general solution of the NLS equation can be written in terms of FGT for periodic/quasiperiodic boundary conditions [
6,
38,
39]:
Here
and
are Riemann theta functions defined by:
The period matrix
contains amplitude and interaction information for the nonlinear spectrum, including sine waves, Stokes waves and breathers. The two sets of phases
and
are computed from FGT and are distinct for sine waves and Stokes waves, but are
dynamically phase locked for breathers. The Akhmediev, Peregrine and Kuznetsov-Ma breathers occur for particular values of
,
and
, see
Section 3.8 and References [
1,
3]. The general quasiperiodic solution (8) of NLS (4) describes the space/time evolution of the
complex modulation function,
for a
nonlinear spectrum [
,
,
], here for water waves, but generally for the physics described by the NLS equation. In this formulation,
is the
Stokes frequency correction and
is a similar
correction for the wavenumber, but this latter is often taken to be zero
, except in complex data analysis situations [
3,
39].
For many cases, the
surface wave elevation arises from this simple form from the leading order term of the Stokes wave:
One can go on to as high an order that one wants to for (10), say to the Stokes fifth order approximation [
1,
3]. Here
and
are the
carrier wavenumber and
frequency. Insert the above theta function solution (8) of NLS into the expression for the surface elevation (10) and find:
Note that
is the
carrier wave amplitude, here defined to be the average of the modulus of the complex modulation
over space:
This definition is particularly important for ocean waves, which have
near Gaussian time series, see Reference [
1] for a discussion. This observation means that
small amplitude modulations play a subsidiary role in ocean waves where
large amplitude modulations most often dominate [
1,
3,
4].
It is natural to introduce a
complex surface elevation by introducing the
auxiliary surface elevation [
3]:
where
is the Hilbert transform. Then the
complex surface elevation is given by
This leads to the connection between the complex surface elevation and the complex modulational envelope:
It is worth noting that (14) can be interpreted in terms of the
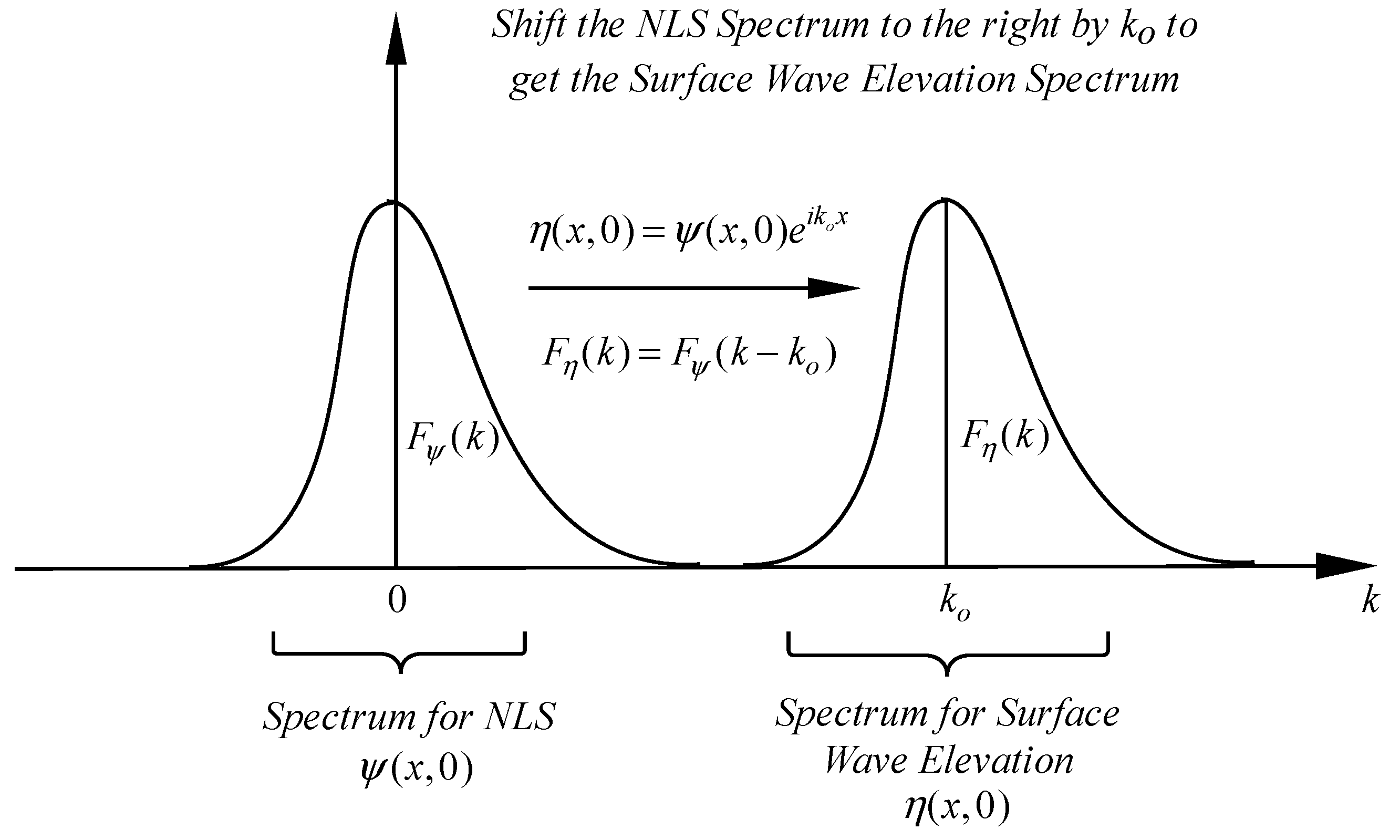
Fourier shifting theorem. The real part of (14) is the measured (in an experimental context) surface wave elevation (11). Let us now see the physics of the shifting theorem. The complex modulation envelope is given by
and its spectrum is centered about zero modulational wavenumber
K =
K’ ≈ 0 and frequency
: Thus the spectrum of
, which we call
, will be centered about the origin (
Figure 1). The complex surface elevation
has Fourier spectrum
that is centered about wavenumber
(and frequency
). Here the surface elevation wavenumber is
and the frequency is
. While we deal with the standard Fourier spectrum in this simple example in
Figure 1, it is important to note that in what follows we will be physically dealing with quasiperiodic Fourier series and their spectrum on a
discretuum of wavenumbers
and frequencies
(the discussion below describes this notation). It follows that perhaps the most important feature of this theoretical formulation is the characterization of the coherent structures by the Riemann spectrum
,
,
] of Stokes waves and breathers, not the sine wave amplitudes of standard Fourier series.
Furthermore, in terms of the theta functions, the quasiperiodic solution of NLS (8) tells us that we are guaranteed to find the Stokes corrections
and
(the algebraic geometric formulas are given in the literature [
3,
39]), so that we have the particular wavenumbers and frequencies
and
for the surface elevation (11). These definitions are made clearer below in terms of
quasiperiodic Fourier series. However, as discussed in Osborne et al. [
1], these parameters can be obtained directly from the time series when analyzing data.
It is worthwhile noting that (8), in the absence of a modulation, has
(the deep water case), and this provides the important plane wave solution of NLS:
The corresponding associated surface wave elevation (10) is
Clearly this is the first term in the Stokes wave expansion, here given with the nonlinear Stokes deep water, amplitude-dependent correction first found in his fundamental paper over 170 years ago [
47].
3. Quasiperiodic Fourier Series Solution of the NLS Equation and other Considerations
3.1. The Quasiperiodic Fourier Series
Consider the FGT solution of NLS (4):
The principle idea given in this paper, consistent with the
Baker-Mumford theorem (see
Appendix A and [
4]) is to convert (8) to a
quasiperiodic Fourier series (2). Once we have the quasiperiodic Fourier series, we can do all the new kinds of wonderful analytical and numerical computations possible with such a series. The Baker-Mumford theorem means that there must exist a quasiperiodic Fourier series for (8) which I write in the following form:
The goal is to find the coefficients
, the frequencies
and phases
to make (16) true. I now carry out this computation, based on an idea of Zygmund [
48].
First, we write the theta functions in terms of their usual definition as a quasiperiodic Fourier series [
49,
50,
51]:
Notice that I have used the
modulational wavenumbers and
modulational frequencies in this expression. This is because the solution of NLS is always in terms of these parameters, i.e., those for the
modulations (for which I use the capital symbols
and
as in Yuen and Lake [
41]), not for the
surface elevation (for which I use
and
). Here,
is the
period matrix that contains the
Riemann spectrum of the
quasiperiodic modulations: This matrix contains
Stokes waves on the diagonal elements and the
breathers consist of two-by-two sub matrices along the diagonal with appropriate dynamical phases (this is essentially the phase locking of two Stokes waves to obtain a breather [
3]). There are two sets of the phases, one for the numerator
and one for the denominator
(see Tracy and Chen [
39] and Osborne [
3] for formulas to compute these parameters).
I now absorb the phases into the coefficients, i.e., rewrite (17) in the following way:
let us compute the ratio
of the two theta functions in (16) as a quasiperiodic Fourier series:
Note that I have suppressed the
in the theta functions for simplicity. The fact that such a result exists is justified by the Baker-Mumford theorem (see
Appendix A), which states (in part) that a single valued, multiperiodic, meromorphic Fourier series can be found from the ratio of two theta functions with different phases. The Baker-Mumford theorem does not give a procedure for determining the quasiperiodic Fourier series. The construction of the right hand series in (19) is a goal of this paper. FGT theory tells us how to connect the parameters of the theta functions (period matrix, frequencies and phases) to a particular Cauchy or boundary value problem [
6,
39]. The solution to the NLS equation then has the form
To compute the series in (19), we first need to compute the inverse series of the denominator, which we define to be
where
are the coefficients of the series (21) which we call an
inverse theta function series. The
are determined by a method of Zygmund [
48] for ordinary Fourier series, but which is here applied to multiperiodic Fourier series. We have
so that
implying a
convolution for the coefficients of the product
so that
Note that the definition of
is:
To be clear, we have from (18) and (21) the quasiperiodic Fourier series with the coefficients
and
:
In matrix-vector notation, we have
for (22). By definition,
is an unknown infinite length column vector and
is an infinite dimensional matrix formed from the known coefficients on the right hand side of the first line of Equation (23):
is a vector we seek in terms of the Riemann spectrum
. This leads to the vector of coefficients
of the inverse series (21). Here,
is an infinite length column vector whose elements are all zero except for that at the central position, that is 1, i.e., for which
. In this way,
is just the unit one,
In component form, we have from (22)
The convergence of the series (16, 17, 21, 23) occurs because of the extraordinary properties of theta functions [
6,
49,
50,
51,
52,
53]. In this way, one is led to the conclusion that the matrix
is invertible (see also Zygmund [
48] for arguments relating to the convergence properties).
Now we have the coefficients we seek from (25a):
which then can be explicitly written
Now we need to complete the computation of (19)
where
Equation (27) implies a convolution of the coefficients given explicitly in terms of the Riemann spectrum (the amplitudes and phases of FGT: ) in (27). Let us now write this convolution.
For the product of two Fourier series
we define:
Then the product is
We use the well-known result [
48]:
Both ways to write this latter expression are equivalent: The first is a convolution, while the second describes three-wave interactions. Finally we have
where
Then
The following are then the results of the convolution:
Or, simplifying the notation:
The latter expressions can also be written in the following form:
These are the coefficients
on the right hand side of the series (20). We have thus found the quasiperiodic Fourier series for the solution of the NLS equation, as originally sought. Notice that Equations (20) retain the same information as the theta function formulation of the solution of the NLS equation as a ratio of Riemann theta functions (20), namely the period matrix
, and phases
describing the Cauchy initial conditions. One can choose which of the three forms of the coefficients (29) is appropriate for a particular application. To help see what I mean, I give a simple example in
Section 3.2.
In summary, the
quasiperiodic solution to the NLS equation then has two equivalent forms: (1) the ratio of two Riemann theta functions with different phases and (2) a quasiperiodic Fourier series.
where the Stokes wave corrections
and
are given in the
Appendix A of Tracy and Chen [
39]. Here, as discussed above, to determine (30), the coefficients are given by
plus any of the equivalent forms of (29).
3.2. An Approximation for a Single Degree of Freedom Solution
I now give some insight about the coefficients in (29) and how to compute them. Here is the matrix we need to invert, that depends on the period matrix
and phase
:
Clearly
and
The full generality and associated computations of the algebra of matrices, whose indices are two infinite-length integer vectors
i and
j, will be explored in a future paper. For now, let us look at the genus 1 case where we have a period matrix
which is 1 × 1, a simple complex number. Then sum from −1, 0, 1 (essentially the first two terms in the Stokes wave) for each of the two indices
i and
j, so that the infinite matrix is reduced to a 3 × 3 case:
One might query at this point why we can deal physically with a 3 × 3 matrix when in reality the matrix is infinitely dimensional. In the present simple case, we assume that
, so the resultant three term Stokes series is defined by
. Then the inverse is
According to (29), we need the central column vector of this latter matrix:
Now evaluate this to order
and use the “plus“ phase
Multiply this result times the
matrix (29c) with the negative phase:
These then are the coefficients of the quasiperiodic Fourier series
Now from (30) we seek the first three terms in the one-degree-of-freedom solution of NLS:
If we use the familiar physical Stokes correction for a single degree of freedom
and further simplify by setting
,
,
and
so that we find (see
Figure 2):
or
where
Notice that if
, then:
This latter result is the case of a
dnoidal wave solution of the NLS equation, which is of course stable (see discussion below in
Section 3.5). Otherwise we are more interested in the general case just derived (35) where the phases are arbitrary so that instabilities can occur and we write (35):
This is the starting place of Yuen and Lake [
41] who derived the modulational dispersion relation by inserting this expression into the NLS equation and linearizing about
and solving the resultant eigenvalue problem for
and
(see
Section 3.4 below for details). The above expression (37), derived here from the quasiperiodic Fourier series solution of the NLS Equation (30), can of course be generalized to arbitrary order and to an arbitrary number of degrees of freedom using the methods just discussed. Likewise, the modulational dispersion relation can be derived to arbitrary order, which is necessary for the analysis of measured time series (see discussion below in
Section 3.4). The spectrum of the small amplitude modulation (37) is given in
Figure 2.
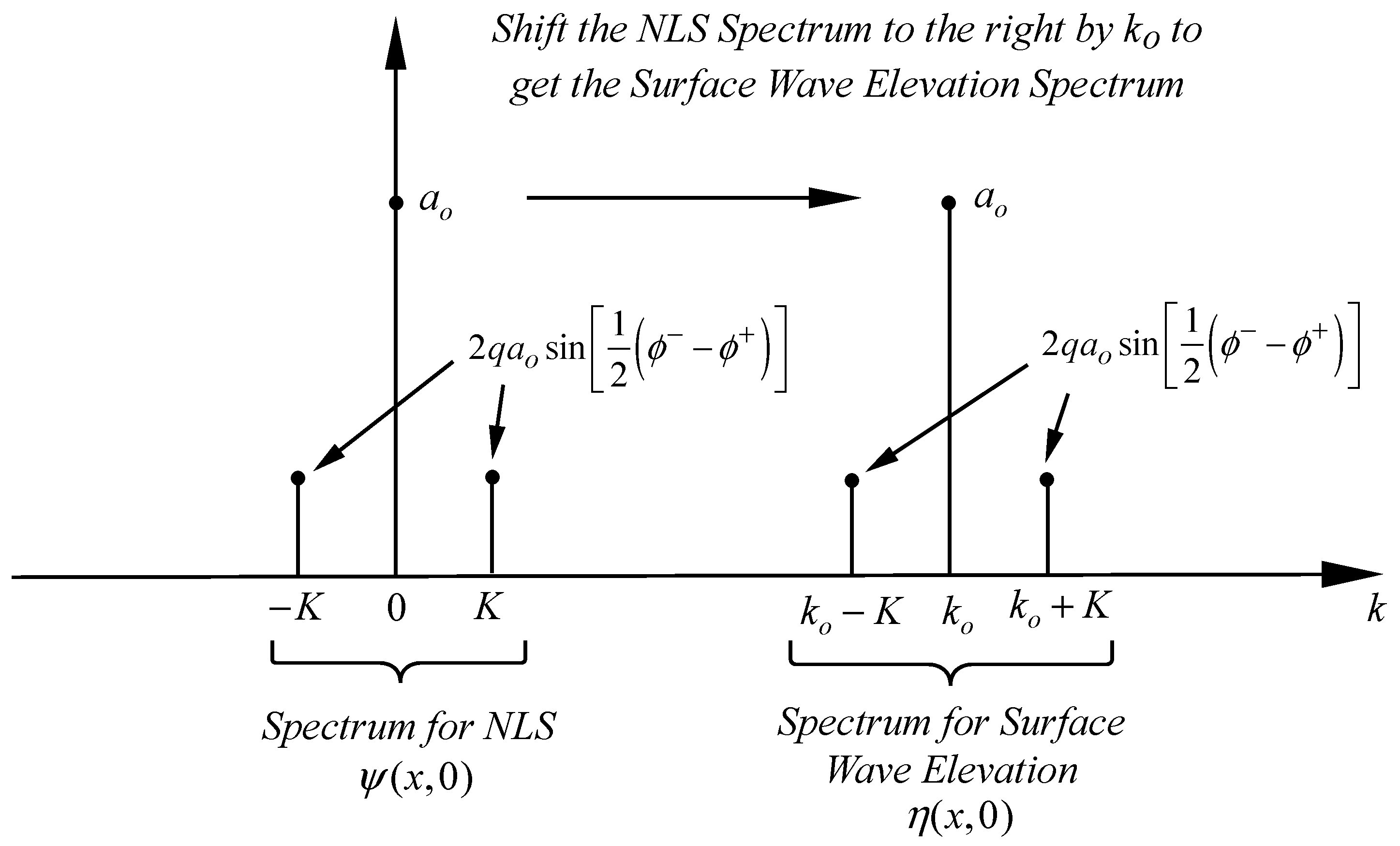
The complex surface elevation associated with (37) is
Taking the real part and simplifying as before (see the associated spectrum in
Figure 3):
Note that the dnoidal wave (
Section 3.5 below) occurs when there is a difference of
between the phases. So the general case has complex phases (see (48) below) and hence distinct epsilons
and therefore we have the generality necessary to obtain the modulational dispersion relation (
Section 3.4).
3.3. Another Approximation for a Single Degree of Freedom Small Amplitude Solution
To approximately evaluate the above theta function solution (8) for the NLS equation for a single Stokes waves (genus 1) solution, let us first find the ratio of two theta functions with different phases out to order
q in the elliptic nome:
where
, for
the single period matrix element. The next order terms are O(
) and are not included at this simple stage of the analysis. This derivation compliments the results of the last
Section 3.2 where the results are much more general. The derivation given here is much simpler, but insufficient for the case of arbitrary genus. We would like to get the leading order Fourier series for this ratio. The power series approximation to order
q has the form:
which leads to the simple expression
This means that the leading order complex modulational solution of the NLS equation is (here I take the standard result
and
, which is the Stokes frequency correction)):
And the surface wave elevation is:
We see that the surface elevation is a simple cosine (with the amplitude-dependent Stokes wave correction to the frequency included) with a small amplitude modulation (since ), which is long (since ) and slowly varying (since ). Note that the amplitude of the modulation depends on the difference of the original phases, and the phase of the modulation depends on the sum of the original phases.
Now we write the above results in a more explicit form to enable us to graph the Fourier transform. Recall the relation:
Use this in the above to find:
for
The final result for the small amplitude solution of the NLS equation is:
where we set
Then we find
Where the complex phase is defined by
so that
The quasiperiodic Fourier series, together with quasiperiodic inverse scattering theory,
generically have phases with real and imaginary parts (see below with regard to breather construction in
Section 3.8). Here the real part is related to the sum of the IST phases and the imaginary part is related to the difference of the phases.
Therefore alternative forms for the epsilons are
where I have used the relation for the
complex phase (47). Note that if we set
,
we get the leading order term in the dnoidal wave solution of the NLS equation (
Section 3.5 below). I will revisit this relation below for the introduction of the
with regard to the
nonlinear random phase approximation (
Section 4.1 below). Because
has real and imaginary parts it has an important extended role in periodic inverse scattering theory with respect to the real phases of standard Fourier series.
As mentioned above, we take
and
. Then we again get the leading order estimate for a small amplitude modulation of the nonlinear Schrödinger equation:
Here we can think of the
modulational dispersion relation as that due to the modulational instability, see
Section 3.4, for more details with regard to quasiperiodic Fourier series. See
Figure 2 for a graph of the Fourier spectrum of
(49).
3.4. The Modulational Dispersion Relation
The modulational dispersion relation was originally derived by Benjamin and Feir [
54]. Other excellent papers in this regard are those of Stuart and DiPrima [
55], Yuen and Lake [
41] and Tracy and Chen [
39]. Indeed, the paper by Stuart and DiPrima discusses that Benjamin-Feir work together with that of Eckhaus [
56], the latter of which develops the instability method for vortical motions in fluids. Vortex dynamics are discussed with regard to finite gap theory in Chapter 27 of Osborne [
3]. Vortex motions have yet to be studied in the context of quasiperiodic Fourier series. This is an exciting area of future work.
Here I derive the modulational dispersion relation with regard to quasiperiodic Fourier series. The plane wave for the NLS Equation (4) is given by:
At this point, we assume that the coefficients
and
in (4) are those of Hasimoto and Ono [
42] (see also Osborne [
3]) and are generally functions of the water depth
h. We would now like to perturb the plane wave (50) by placing a
small oscillatory modulation on it. This is conveniently done by setting the small-time evolution of the nonlinear Schrödinger equation to be (I have modified the notation of (49) slightly for present convenience):
where
As pointed out previously, the expression (51) is a simple leading order to the quasiperiodic Fourier series (2). The * means complex conjugate and we assume . Here is the modulational wavenumber and is the modulational frequency: Both and are viewed as small with respect to and (a narrow banded NLS spectrum) which correspond to the rapid oscillations of the carrier wave, while and are long and slow oscillations of the complex envelope.
Now insert the above small modulation (51) into the NLS equation and expand the result and truncate to
:
This can be rearranged as coefficients of
and
to obtain:
Now take the complex conjugate of this latter equation:
This can be put into matrix form:
One can compute a nontrivial solution to these two linear equations provided that the determinant of the coefficients is zero:
This gives the modulational dispersion relation:
Thus a small modulation of a Stokes wave is unstable if because the frequency will be imaginary. If we turn off the nonlinearity (set ), we have , a stable condition.
Let us rewrite (55) in the following way:
This allows us to identify the general form of the
Benjamin-Feir instability parameter:
Using Equation (5) for deep water, we find the well-known form [
1,
3]:
In shallow water, the sign of
(
) changes with respect to that in deep water and no instability occurs; this is the modulational regime of shallow water KdV and NLS where breathers cannot occur. If the nonlinearity is small
we get:
For small nonlinearity () there are no surprises, i.e., the frequency is real and the solution to NLS is stable: A small-amplitude modulated Stokes wave at time zero will always remain a Stokes wave with small modulation.
For the scaled NLS equation,
and
, so we have for the modulational dispersion relation (for example see Tracy and Chen [
39]):
This is unstable if , since then is imaginary. Otherwise we have stable waves.
For deep-water, we find the modulational dispersion relation in 1D is given by [
41]:
This is unstable if
, since then
is imaginary and
explodes exponentially, i.e., the Stokes wave is unstable in deep water. This is the resonance pointed out by Stuart and DiPrima [
55].
Now it should be clear that the modulational dispersion relation given above is only to first order. The method of derivation given above, actually quite didactical in nature, but with modern notation, is easily extended to higher order. The higher order expression, to be discussed in a future paper, is necessary for the analysis of ocean wave data.
3.5. The Dnoidal Wave Solution of NLS
This section discusses the simple solution of the NLS equation known as the
dnoidal wave. The latter function is one of the Jacobian elliptic functions of classical complex analysis [
57]. The goal is to better understand what role the dnoidal wave plays in FGT. To this end, let us look for
stationary solutions of the NLS Equation (4): These are solutions that move with constant velocity and do not change their shape in space and time. To do this, one carries out a Galilean transformation to a coordinate frame moving at the group speed,
:
and then seeks a stationary solution in this moving frame of reference [
41]:
Here,
is real and
is a to-be-determined constant which corresponds to the Stokes frequency correction to the wave train. Insert this into the
Galilean transformed NLS equation
and find:
This is a second-order ordinary differential equation that can be integrated by multiplying first by the integrating factor
. After integrating the resultant equation, one finds the
Jacobian elliptic function solutions of the second kind referred to as
dnoidal waves:
Here
m is the modulus or parameter that lies between 0 and 1:
. We also find
A useful Fourier series for the dnoidal wave is given by:
This Fourier series is just the Stokes wave expansion of the NLS equation. The function
is the elliptic function of the second kind [
58].
We know that the surface elevation has the form:
Thus, the unmodulated carrier wave is a Stokes wave where the nonlinear dispersion relation is given by:
In the limit
, the dnoidal wave approaches a hyperbolic secant profile and the solution becomes:
This is the
soliton solution of the NLS equation. Generally, for
m not equal to 0 or 1, we have periodic (Stokes like) wave solutions of the NLS equation. These are analogous to the cnoidal wave solution of the KdV equation [
3]. Thus, the goal here is to search for interacting dnoidal wave solutions of the NLS equation as a spectral decomposition of the equation. The
dnoidal waves are then the NLFA components of the NLS equation, i.e., they are the Stokes waves of NLS. This is seen by noting the close connection between
cnoidal waves and
dnoidal waves:
.
The plane wave solution occurs for the limit
in (2.20):
This describes the unmodulated state of the NLS equation. The surface elevation has the form:
We see that this is just the first term in a Stokes series expansion for water waves.
Note that the squared modulus of the NLS dnoidal wave solution has the form:
Here I have used the above-mentioned relation
between dnoidal waves and cnoidal waves [
58]. Those already familiar with the cnoidal wave in the engineering literature will therefore be instantly familiar with dnoidal waves. This last expression says that the squared modulus of the NLS equation has cnoidal wave solutions similar to those of the KdV equation [
40].
Comparing the dnoidal wave solution of the NLS equation to the general solution in terms of theta functions, we notice [
59], eqs. 1052:
This is an important result because it connects the theta functions of FGT with the dnoidal wave solutions of the NLS equation. Generally speaking, the theta functions are related to the Jacobian elliptic functions [
57,
58]. The theta functions are well known to be the starting place for numerical computations. Engineering discussions of cnoidal waves are given in References [
60,
61]. Notice that the phases are given by the simple relations
. This means
and
so that:
Thus, we have the one-degree-of-freedom solution for a single dnoidal wave in terms of theta functions. Since the theta functions are the basis of the full periodic solution of the NLS equation, this is an important step.
Summarizing: The dnoidal wave solution of the NLS equation, written as the ratio of two theta functions, occurs when the phases are simple real values,
and
. This means that the small amplitude expression derived above for the ratio of two single-degree-of-freedom theta functions (49) is however stable. Only by generalizing the phase to complex numbers can we introduce instability in the solutions of the NLS equation. Nevertheless, this exercise is important, because it tells us how to determine the stability/instability of nonlinear Fourier spectral components in the IST of a time series, i.e., by characterizing the actual phases computed in the time series analysis [
3].
3.6. The Surface Wave Elevation
The surface wave elevation arises from the simple expression (10), and the associated complex surface elevation is given by (13), (14). Many of the stochastic computations, including the correlation function, power spectra, triple correlations, bi-spectra, etc., are done more simply with the complex function . One takes the real part of to obtain the results for the real surface elevation: .
Finally, we summarize the main results of this paper in Equations (74)–(83) below.
Insert the theta function solution of NLS (8) into the expression for the complex surface elevation (14) and find:
Note that is the carrier wave amplitude, which physically equals the space and/or time average value of the modulational envelope. Here and below .
The
quasiperiodic Fourier series for the solution to the NLS equation is:
The
quasiperiodic Fourier series for the associated complex surface wave elevation has the form:
Here the
wavenumbers and
frequencies for the surface elevation are
The actual real surface wave elevation is then:
The coefficients of the quasiperiodic Fourier series are:
The
Riemann spectrum (
) is encoded into the formulation as follows:
The quasiperiodic Fourier series (75), (76) and (78) are useful for time series analysis and for the computation of stochastic properties of nonlinear waves. In the above formulation, the Riemann matrix is complex, while the phases of the theta function are also complex. This implies that the composite phase is also complex (47). Thus, the phases supply not only a phase shift for each IST component, but also have an influence on the amplitude of the components as we have seen in the small amplitude computations above (36), (46) and (47).
It is worth noting that I take
for the analysis of time series. The value of the Stokes correction to the frequency
is obtained directly from the time series themselves by a fitting procedure [
1,
3].
3.7. Perspective in Terms of Stokes Waves and Their Interactions
The above multidimensional, quasiperiodic Fourier series for surface elevation can be expressed as:
By construction, as we have seen here and in Reference [
4], the above solution of the NLS equation is a
spectral theory of Stokes waves,
To see this, we note that a single Stokes wave has the form:
The
nth Stokes wave
of (85) has a set of amplitudes
, wavenumbers
, frequencies
, and phases
The dispersion relation is represented by
. Here
is the
frequency shift first identified by Stokes [
47]. The above multidimensional Fourier series can be represented by
N nested sums [
3]. We see that each of these sums, in the absence of the others, is a single Stokes wave, together with the usual Stokes “amplitude-dependent frequency correction,” here computed for the NLS equation. The interactions in (84) are accounted for by pairwise cross terms among the individual Stokes waves, which are not analytically computed here.
We see that the multiperiodic Fourier series have all of the Stokes wave harmonics (i.e., those that “glue” wave components together to make a single Stokes wave), together with all the “cross harmonics” amongst the Stokes waves that create nonlinear interactions between pairs of Stokes waves. The Stokes wave components form the “bound modes” in terms of the index m (phase locked sine waves make up an individual Stokes wave), and the Stokes waves themselves are then the “free modes” that can move relative to one another and undergo pairwise scattering from the others in the nonlinear dynamics.
It is important to realize that the breather solutions are constructed from two phase-locked Stokes waves. This makes the problem one of “genus 2” in the FGT solution of the NLS equation. Such solutions are discussed in the next subsection.
3.8. Modulational Instability and the Construction of Breathers with Theta Functions
Up to now, I have dealt with the exact solution of the NLS Equation (75) and the approximate solution with small amplitude modulations (45). Now I look at the breather solution in terms of the Riemann theta functions.
The breather train discussed here is characterized by a 2 × 2 period matrix,
, which implies that the genus
[
3,
39]. This means the theta function reduces to
There are essentially five spectral parameters in the formulation which describe a single mode:
, where
A is real (the carrier wave in scaled coordinates),
and
(more details and figures are given in Reference [
3]). The spectrum is symmetric about the real axis, so that
is paired by
,
by
and
by
(here “
i” is the imaginary unit, “*” refers to complex conjugate and the subscripts “
” refer to real and imaginary parts). The first parameter in the spectrum,
A, describes the carrier wave amplitude. All other parameters describe the long-wave modulation of the carrier. Physically, the NLS equation describes the space-time dynamics of the nonlinear interaction between the carrier wave and the modulation. Of course in a more complex situation the “carrier” wave consists of “all the other waves in a wave train of high complexity” (see a discussion in Reference [
1] on the “near Gaussian, nonlinear approximation for solutions of the NLS equation). It is this dynamic that leads to the unstable modes and breather wave trains discussed herein. In the present analysis, in order to obtain concrete formulas for these modes, one seeks a singular asymptotic expansion in terms of the parameter
where we assume
; the limit as
tends to zero is singular. The wavenumbers, frequencies, phases, and period matrix are given to order
are found to be [
3,
39]:
Width of Expansion Parameter and Sign of Riemann Sheet Index
Phases
Use of the above formulas in the theta function solution of (86) provides a simple way to compute the unstable modes and breathers for a modulated plane wave carrier. However, because of the generality of the theta function formulation, these solutions describe not only the classical
small-amplitude modulations (the Akhmediev breather, say), but also the
large amplitude modulations (for example the Kuznetsov-Ma breather) as well.
Note that the phase formulation in (93), together with the period matrices (91) and (92), constitute the fundamental information necessary to “glue” together the full Riemann spectrum for the genus 2 case to insure that we have a “structure” in the form of a breather that propagates and “breathes” up and down in space and time in a coherent manner. The entire breather itself will have a separate (presumably random) phase that I have not added to (93), a phase that would be a component in the spectrum, say, of an arbitrary time series. In the nonlinear random phase approximation discussed in the next
Section 4.1, it is this latter phase that would be randomized.
What is a superbreather? Above we have seen that a breather is a genus 2 solution of the NLS equation with a 2 × 2 Riemann matrix. A superbreather is a genus 3 or 4 solution (up to arbitrary genus actually) with a 3 × 3 or 4 × 4 Riemann matrix. On the basis of the analysis of thousands of time series, it would appear that the 4 × 4 case is most likely to occur in the real world, although this observation has not yet been verified from ocean data. The 4 × 4 superbreather case is just the “gluing” of two 2 × 2 breathers together by phase locking. This process can continue up to an arbitrarily high genus, although it is unclear whether large genus solutions actually occur in the ocean.
Additional very fine work with regard to the breather formulation using finite gap theory is given by Grinevich and Santini [
62,
63]. These papers provide important developments beyond the original work of Tracy and Chen [
39]. I have benefited greatly from the original insight of Grinevich and Santini.