1. Introduction
The effect of the Earth’ rotation on the dynamics of nonlinear waves in the oceans was extensively studied in the last decades (see, for example, References [
1,
2,
3,
4,
5,
6,
7,
8] and references therein). As well-know, wave propagation in big lakes can also be affected by the Earth’ rotation [
9,
10,
11,
12,
13]. In particular, the dynamics of solitary waves has been investigated within the framework of the Ostrovsky equation and it was established that they cannot propagate steadily because of the permanent radiation of small-amplitude long waves [
14,
15] (however, they can steadily propagate being supported by a long background wave [
16,
17]). As a result, an initial solitary wave experiences a terminal decay which leads formally to it vanishing in a finite time [
3,
18]. However, the process of solitary wave decay is more complicated in reality and leads eventually to the formation of envelope solitons described by the nonlinear Shrödinger (NLS) equation or its modifications [
19,
20,
21,
22,
23,
24]. In an inhomogeneous medium, the dynamics of solitary waves is determined by the synergetic effects of inhomogeneity and fluid rotation. In particular, at a certain relationship between these two factors, a Korteweg–de Vries (KdV) soliton propagating towards a coast with a gradually decreasing depth can preserve its shape and amplitude, whereas its width and velocity adiabatically changes [
8].
In the real ocean, when a KdV soliton approaches a coastal zone, it can experience a terminal decay in the domain where the depth is constant, so that it can be ultimately transformed into an NLS envelop soliton, and then the envelop soliton can enter into the inhomogeneous domain where an oceanic depth gradually decreases. An NLS soliton can be formed from a rather arbitrary initial perturbation independently on the transformation of a KdV soliton. It is a matter of interest to study the adiabatic dynamics of an NLS envelop soliton when it approaches a shoaling zone. To this end, we consider below different models of NLS-type equations for water waves in a rotating ocean, their solutions in the form of envelop solitons, and the dynamics of such solitons in the ocean with a gradually decreasing depth.
3. The Variable Coefficients NLS Equation
In the coastal zone, where the bottom profile gradually varies with the distance, the NLS equation describing soliton evolution contains the additional “inhomogeneous” term and has the form of the “time-like NLS” (TNLS) equation (cf. References [
25,
26,
27]):
where the coefficients
and
are linked with the coefficients of the Ostrovsky Equation (
1) (cf. Reference [
22]):
The group velocity
as follows from the Ostrovsky Equation (
1) is
Note that in a stationary, but spatially inhomogeneous media, the wavenumber k depends on x, whereas the frequency is maintained.
The dependence of the wavenumber of a carrier wave on the spatial coordinate
x follows from the dispersion relation Equation (
4) where
, and other parameters,
c,
, and
depend on
x.
Using the results obtained in Reference [
22], let us present the soliton solution of the TNLS Equation (
7) assuming that all its coefficients are constants:
where the amplitude
A and speed
V can be considered as the free parameters, whereas soliton duration
,
, and the chirp and gauge respectively are:
In the particular case when
, we obtain
The solution to Equation (
10) is invalid when the dispersion coefficient
p in the TNLS Equation (
7) vanishes. This occurs at the frequency
when the group velocity has a maximum
. In a such case, the generalised NLS equation derived in References [
19,
20] should be used.
If the envelope soliton Equation (
10) enters the region where the coefficients of TNLS Equation (
7) gradually varies with
x, then the adiabatic evolution of the soliton’s main parameters
A and
V can be determined from the balance equations, which follows from the conservation laws for the TNLS equation ([
28,
29], see also Reference [
30]). Alternatively, the rigorous asymptotic theory can be developed, but as has been shown in Reference [
31], the outcome reduces to the first two conservation laws, the conservation of the total flux of “quasi-particles”:
and conservation of quasi-momentum:
Substituting the soliton solution of Equation (
10) into Equation (
13), we obtain after simple manipulations:
Then, from Equation (
14), using Equation (
10) and the result obtained for the soliton amplitude in Equation (
15), we derive for the soliton speed:
After that, we can determine the evolution of the other soliton parameters by means of the relationships (Equation (
11)).
In the particular case, when
, Equation (
17) vanishes, and we have only one Equation (
15) determining the evolution of soliton amplitude.
As mentioned above, the TNLS Equation (
7) becomes invalid when its dispersion coefficient vanishes, then the generalised NLS equation derived in References [
19,
20] should be used. In the next section, we consider this special case.
4. Generalised Variable Coefficients NLS Equation
In the vicinity of the point where the second-order dispersion in the TNLS equation becomes very small or vanishes, i.e., when
, the equation should be generalised by inclusion of additional terms [
19]. For the boundary-value problem, the corresponding equation reads
where
stands for complex-conjugate with respect to function
, and the coefficients
and
are linked with the coefficients of the Ostrovsky Equation (
1) (cf. Reference [
19]):
The soliton solution to Equation (
18) with the constant coefficients has the same form as Equation (
10), but in contrast to the conventional NLS soliton, it is now a one parametric solution with only one independent parameter. If we choose the amplitude as the independent parameter, then other soliton parameters can be presented as follows:
This solution can be reduced to the conventional NLS envelope soliton Equation (
10) if we assume that
,
,
, but such that
.
In another limiting case, when
, the parameters of the soliton solution as the functions of amplitude are
and
remains the same as in Equation (
19).
When a solition propagates in the inhomogeneous medium, its frequency remains constant, but the wavenumber varies in accordance with the formula (cf. Equation (
4)):
As follows from this equation, the critical wavenumber, where the group velocity has a maximum, adiabatically changes in accordance with the variation of parameters. Therefore, if the envelope soliton has been created near the critical point, it will remain further than the corresponding critical point.
According to the numerical results of Reference [
19], envelope solitons emerging from the KdV solitons in the course of long-term evolution have almost zero correction to the group speed (see Figure 9 in Reference [
19]). In our notations this corresponds to
. Such value of speed correction corresponds to a soliton with a fixed amplitude:
The gauge
and parameter
determining the half-width of a soliton are also fixed in this case:
In an inhomogeneous medium, all soliton parameters from Equations (
19)–(
21) vary with
x. The equation governing the parameter variations follows from the conservation of a total flux of “quasi-particles” as per Equation (
13):
Then, using Equations (
19)–(
21), one can determine variation of the parameter
, velocity
, and gauge
, whereas the chirp
varies adiabatically as per Equation (
19) and independently of soliton amplitude.
In the limiting case, when
, all soliton parameters are determined only by the coefficients of the generalised NLS Equation (
18). Then, its amplitude can vary adiabatically with
x only at a very special relationship between the coefficient
and linear wave speed
c such that
.
5. What Is the Most Probable Frequency of Envelope Soliton?
Consider the constant coefficients of NLS Equation (
7). As follows from the analysis of the stability of a uniform wave train with the amplitude amplitude
, the modulation instability occurs when
. In our case, as follows from Equation (
8),
q is always positive, whereas
p becomes positive when
. The maximum growth rate of modulation instability is
(see, e.g., References [
32,
33,
34]). Substituting here
q as per Equation (
8), we obtain
This expression has a maximum at
, where the maximal growth rate for the given amplitude of a wave train is
Thus, one can expect that an envelope soliton will evolve from a quasilinear wave train with the carrier frequency
corresponding to the maximal growth rate of modulation instability. This agrees with the arguments presented in Reference [
24], where it was shown that an envelope soliton cannot emerge at the carrier frequency
, as was assumed in References [
19,
20,
21], but should emerge at a higher carrier frequency. The concrete carrier frequency was not found, but only roughly estimated from the numerical data. As follows from the above theory, the relative frequency shift is fairly significant:
Therefore, one can expect that in the process of evolution of a KdV soliton in a uniform rotating ocean, it eventually transforms into an NLS envelope soliton with the carrier frequency
. If such a soliton enters into a coastal zone with a gradually decreasing depth, it then changes adiabatically, and its basic parameters, amplitude
A and velocity
V, vary with
x in accordance with Equations (
15) and (
17).
6. Estimations for the Real Oceanic Conditions
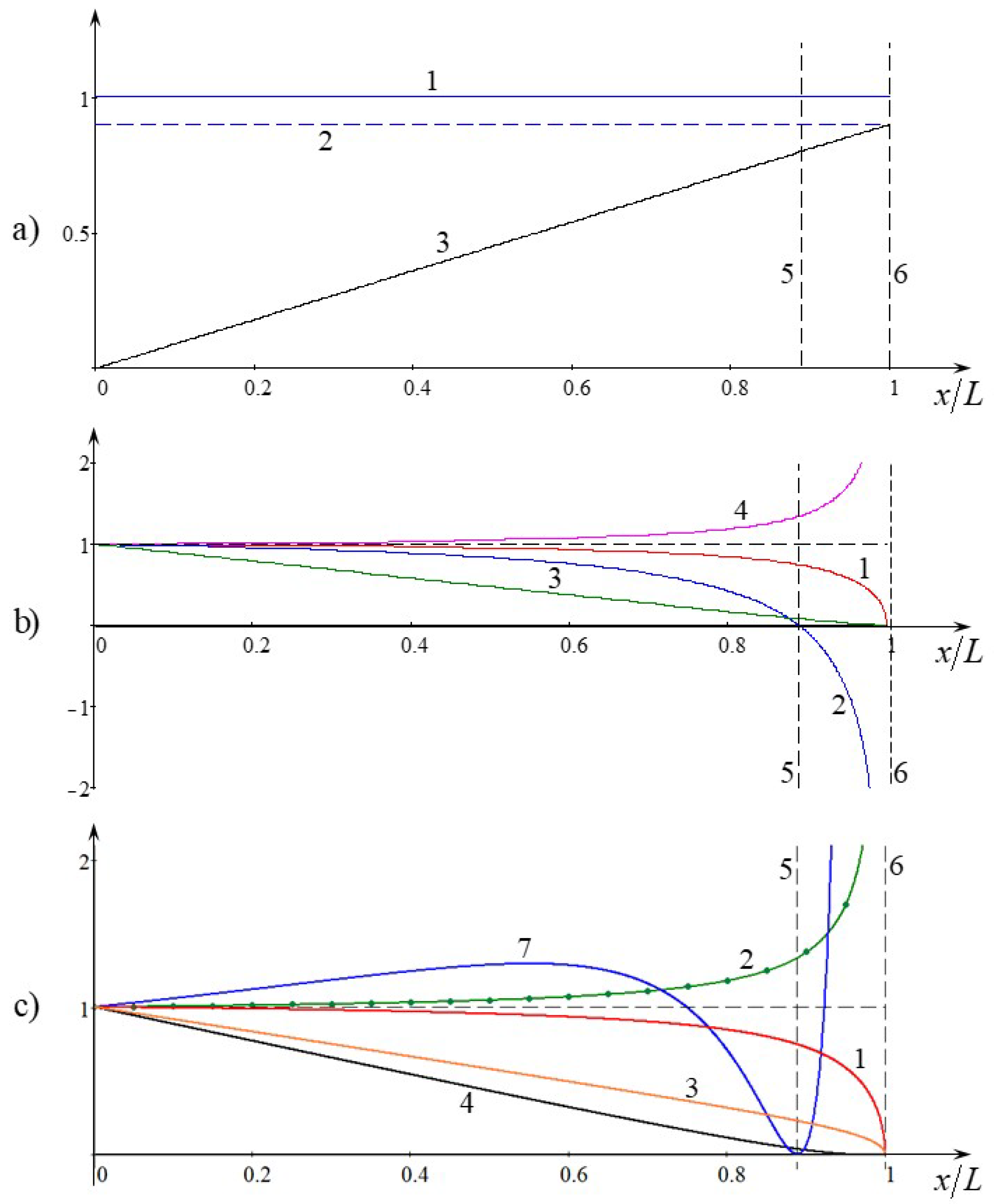
Let us assume that in the coastal zone the bottom profile is a linear function of a distance, so that the depth linearly decreases from
m up to
m at the distance
m, and the pycnocline is located at the depth
m as shown in
Figure 1a. Then, the initial thickness of the lower layer
m; it gradually decreases with the distance
and becomes zero at
. The normalised bottom profile
is shown by line 3 in Frame (a) of
Figure 1. Let us set the Coriolis parameter
1/s, which is a typical value for the moderate latitudes, and
m/s
. With this parameters we obtain for the time-like Ostrovsky Equation (
3) the following values of coefficients:
m/c,
1/s,
m
/s,
1/(m· s).
The dependences of these coefficients on the distance are shown in
Figure 1b. The nonlinear coefficient
vanishes at some distance
, where
becomes equal to
. Then, it changes its sign and becomes positive. This effect is well-known (see, e.g., References [
35,
36] and the references therein). To avoid confusion, it should be kept in mind that the the nonlinear coefficient in this figure is presented in the normalised form
, therefore this ratio is positive when
and becomes negative when
.
Frame (c) demonstrates the dependences of coefficients in the TNLS Equation (
7). Line 1 for the normalised linear speed
in this frame is the same as in Frame (b), and line 3 illustrates the dependence of normalised group speed
as per Equation (
9). Line 2 shows the dependence of the carrier wave number for the envelope soliton Equation (
10) when
. This dependence is practically indistinguishable from the similar dependence plotted for
; the latter one is shown in the same frame by dots on line 2. Line 4 shows the dependence of dispersion coefficient
, and line 7 shows the dependence of nonlinear coefficient
as per Equation (
8).
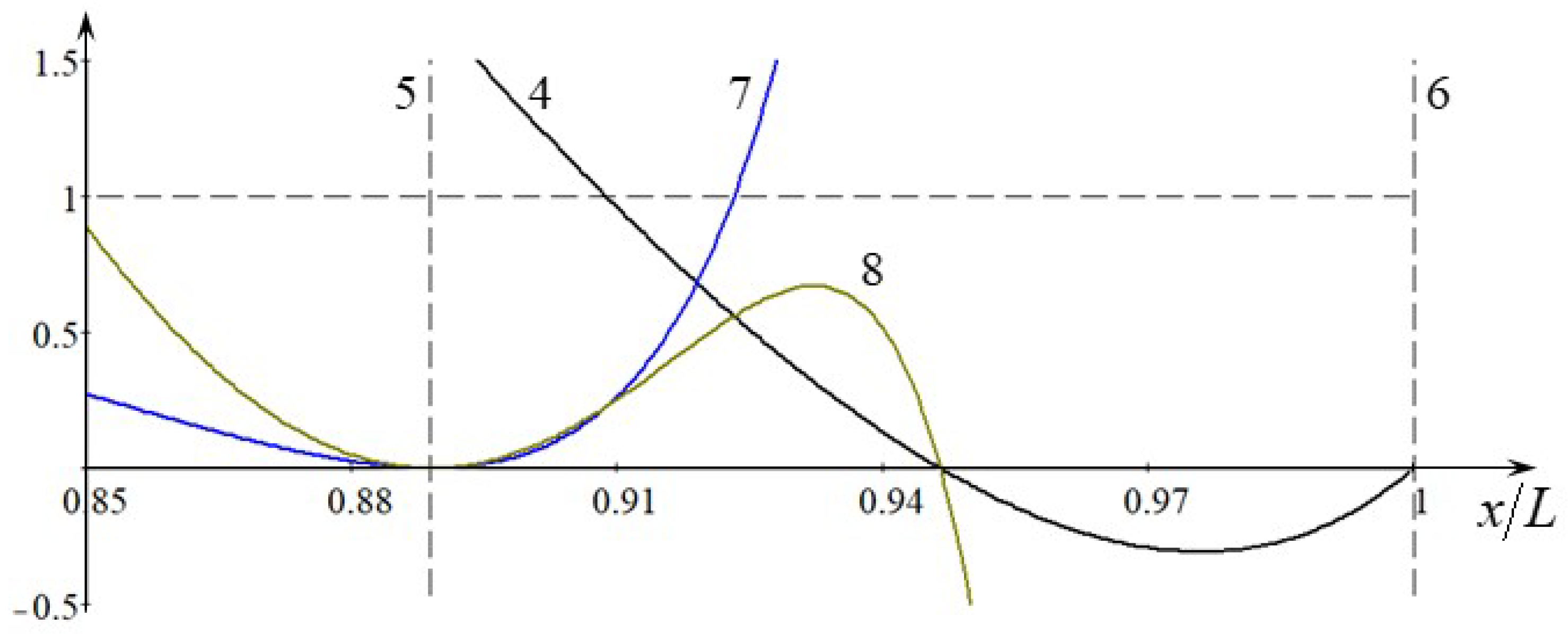
In the vicinity of distance
(see vertical dashed line 5), the dispersion and nonlinear coefficients experience dramatic changes. The nonlinear coefficient
q becomes zero at
, and then quickly increases in absolute value remaining negative for all
. The dispersion coefficient
p becomes zero a bit further along, at
, and then changes its sign from negative to positive; this is shown in details in
Figure 2, where the dispersion coefficient is multiplied by a factor of 50 to make it clearly visible (we remind you again that these coefficients are presented in the normalised forms in
Figure 1 and
Figure 2). Again in the
Figure 2, a normalised product
(see line 8) is also shown, which determines the modulation stability/instability. The instability occurs when this product is positive (see, e.g., References [
32,
33,
34]). In our case, the modulation instability providing the existence of NLS envelop solitons of Equation (
10) occurs when either
or
. In the vicinity of
and
, the TNLS equation is not valid and should be replaced by the generalised NLS Equation (
18).
Now, let us estimate the key parameters of the NLS envelope soliton Equation (
10). A carrier frequency (where the growth rate of modulation instability has a maximum) is
1/s (the corresponding period is
s), and the maximal spatial growth rate of Equation (
32) for the initial amplitude
m is
1/m. The carrier wave number
where the growth rate of modulation instability has a maximum is
1/m (the corresponding wavelength
km), whereas the carrier wave number
, where the group velocity has a maximum is
1/m (
km).
The nonlinear coefficient in the time-like NLS Equation (
7) at
is
1/(m
s), and the dispersion coefficients at the same point is
(m
/s).
If we assume that an NLS soliton of Equation (
10) has the initial amplitude
m and velocity
m/s, then we obtain that its characteristic duration is:
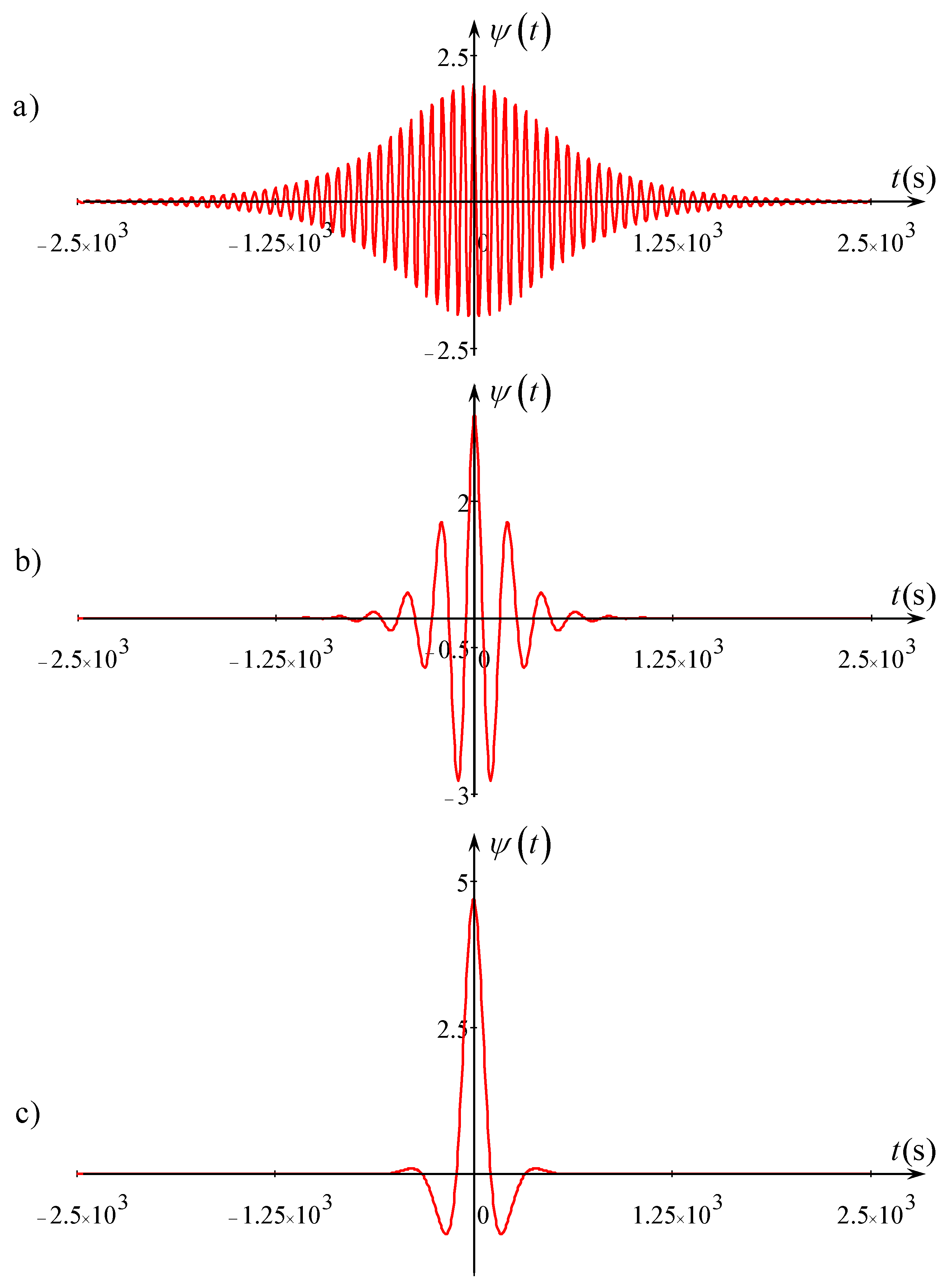
s
min. The soliton chirp Equation (
11) at
is
1/s and the corresponding carrier wave period is
s. This means that there are
carrier wave periods on the half-duration of envelope soliton (see Frame (a) in
Figure 3).
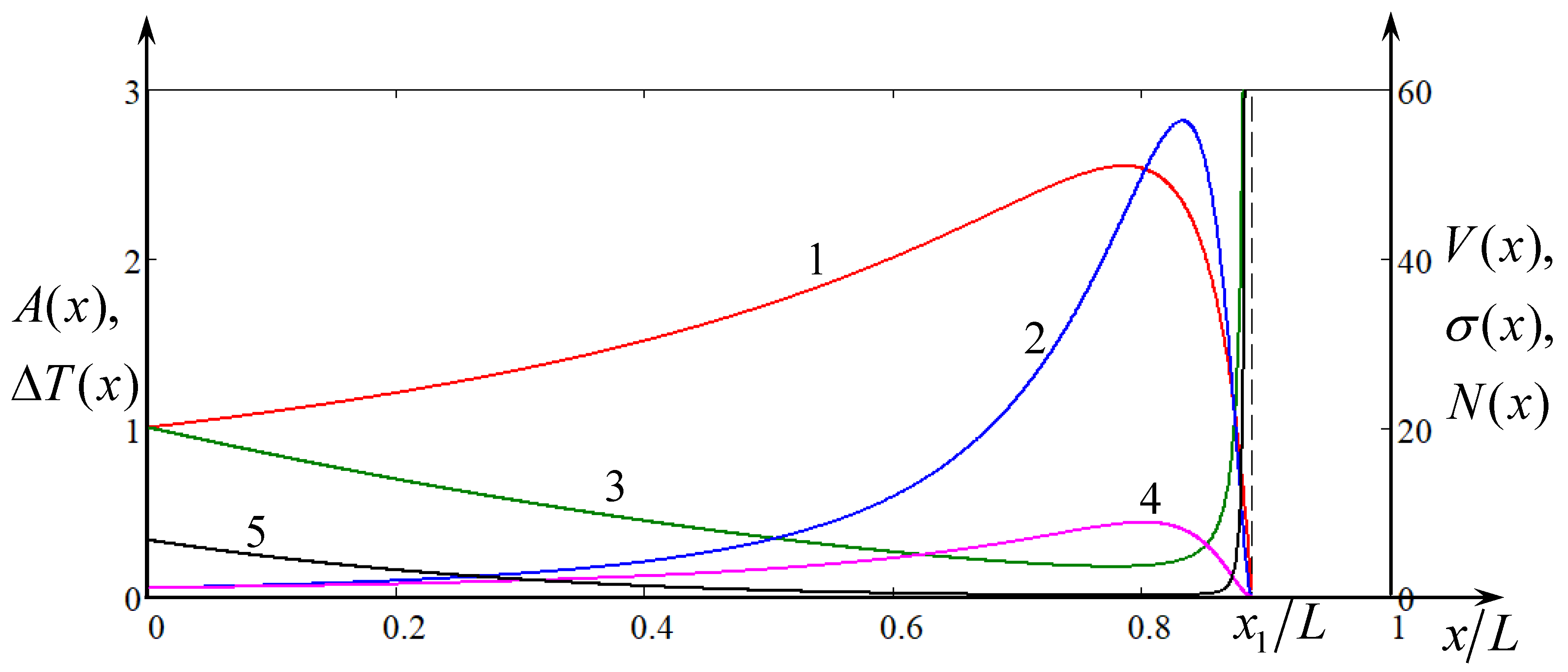
In the process of propagation towards the shoaling, a soliton experiences amplitude enhancement as per Equation (
15) with simultaneous shrinking of its duration; its velocity
V also increases with
x in accordance with Equation (
17). Variation of soliton amplitude, velocity, duration, as well as carrier wave period
are shown in
Figure 4. As one can see from this figure, both the amplitude and velocity increase first and attain the maximal values, but at different distances, after that they quickly decrease when the soliton approaches the distance where the lower and upper layers have equal thicknesses, and the nonlinear coefficient becomes zero (see lines 1 and 2 in
Figure 4). In particular, the maximal soliton amplitude becomes 2.55 times greater than the initial one, whereas the maximal velocity becomes 57 times greater than the initial one. Note that a very similar effect of soliton amplitude decrease (while the duration increases) upon approaching the critical depth where
was revealed in Reference [
25] when a soliton propagates in a non-rotating fluid with a smoothly varying bottom. In both cases (in this paper and in Reference [
25]), the reason of soliton amplitude decrease is the vanishing of the nonlinear coefficients in the NLS equations, even though they vanish at different values of
.
When x becomes greater than , the soliton amplitude and velocity formally increase again and go to infinity when (this is not shown in the plot). However, the adiabatic theory breaks much earlier, when , and the process of wave transformation in the vicinity of this point should be reconsidered more thoroughly, apparently, on the basis of primitive equations.
The soliton duration varies in an inversely proportional manner to the amplitude, therefore it decreases first, but then dramatically increases when
(see line 3 in
Figure 4). In contrast to that, the period of the carrier wave increases first, attains a maximal value and then quickly drops to zero, when
(see line 4 in
Figure 4). In the result of this, the number of carrier wave periods within the soliton half-duration
decreases first to zero and then formally increases again when
(see line 5 in
Figure 4).
The transformation of soliton shape in the process of its propagation towards the coast is illustrated by
Figure 3. The soliton shape half-way to the coast when
is still close to that of the NLS envelope soliton (see Frame (b)). However, at
, where the soliton amplitude becomes close to the maximal value, it looks rather like a solitary wave, but represents a non-stationary formation oscillating in time (see Frame (c)). Such a formation can hardly be described by the TNLS equation which presumes that
.
Thus, in the process of soliton propagation towards the shoaling, it becomes narrower and transforms from the wave train shown in Frame (a) of
Figure 3 to the pulse-type non-stationary solitary wave (a breather) as shown in Frame (c). To a certain extent, this behaviour is opposite to the transformation of the KdV solitary wave into the envelope soliton described, for example, in References [
19,
20,
21,
22].