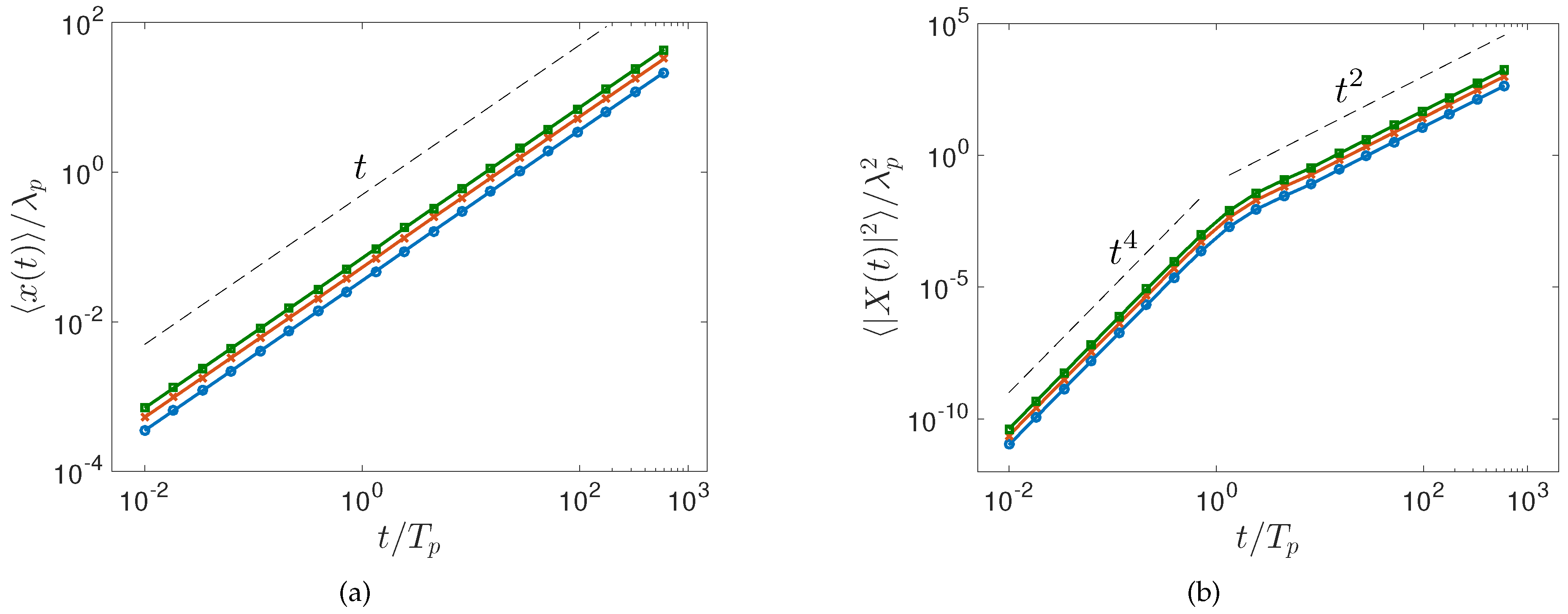1. Introduction
Water waves cause the material transport of fluid particles on the free surface of the fluid. The waves induce a fluid velocity on the free surface which in turn determines the horizontal motion of fluid particles on the free surface. This phenomena has been known since Stokes [
1] who studied the average velocity of fluid parcels transported by a linear monochromatic wave. The resulting displacement is referred to as the Stokes drift.
More specifically, denote the horizontal trajectory of a fluid particle on the free surface by
(or
, for short). For simplicity, we assume that the waves are unidirectional. The map
denotes the horizontal position of a fluid parcel at time
t given its initial position
at time
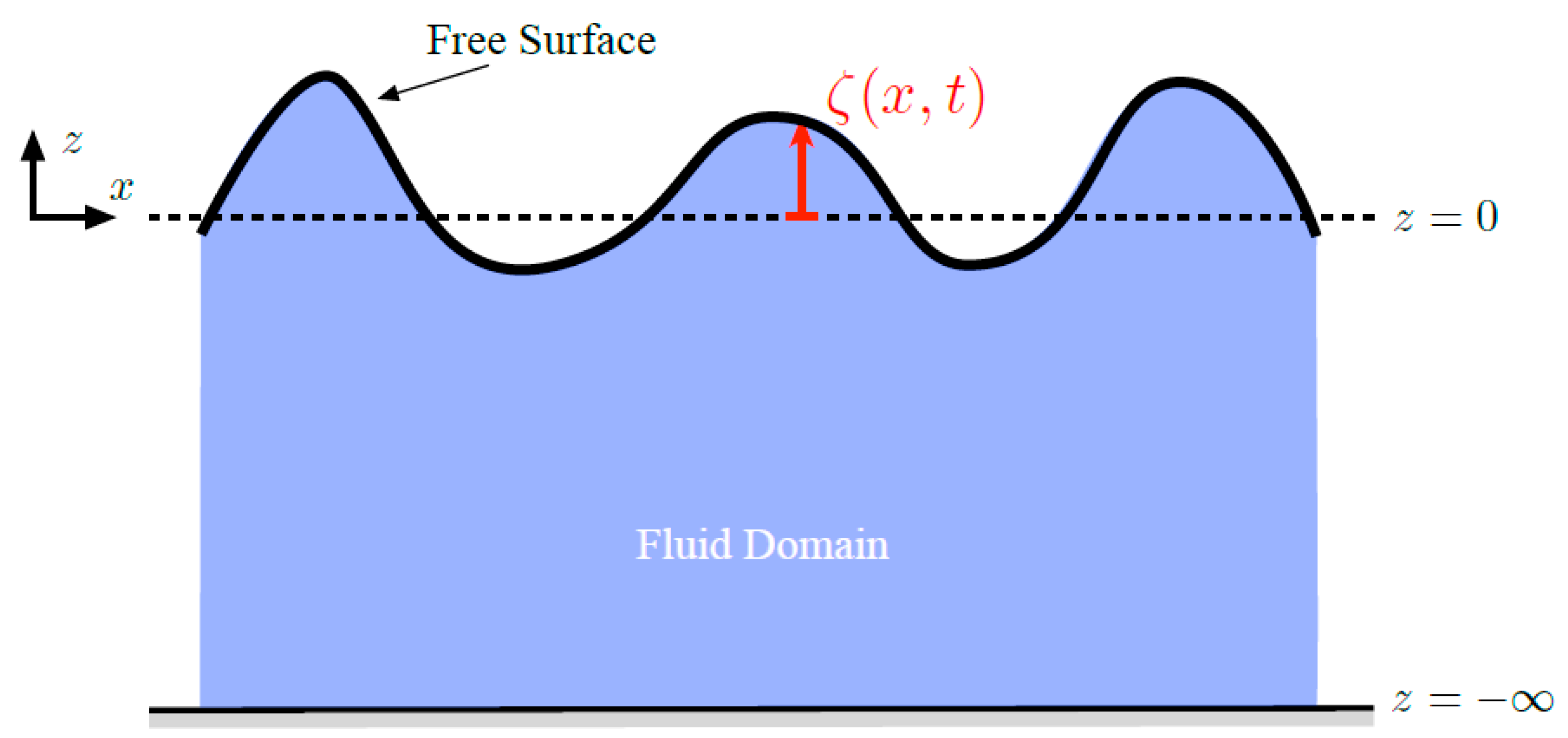
. The surface elevation is assumed to be a graph over the horizontal coordinates and is denoted by
(see
Figure 1). Since the fluid parcels on the free surface are constrained to it, their vertical position of the parcel is given by
. Therefore, knowledge of the horizontal position
of the fluid particles and the free surface elevation
completely determines the position of the particles.
For a fixed initial condition
, Stokes’ theory [
1] seeks to determine the average displacement
of the particles at a later time. Here,
denotes the ensemble average over many realizations of the random surface waves. In other words, the Stokes’ theory is concerned with the first-order statistics of the fluid displacement on the free surface. The main focus of the present work is the second-order statistics of particle dispersion. More precisely, we examine the temporal evolution of the variance
where
denotes the mean-zero displacement of the fluid particles.
1.1. Summary of the Main Results
As we review in
Section 1.2, this second-order statistics has also been studied extensively. However, previous studies either assume the velocity field as a linear superposition of the velocity induced by linear waves or use perturbation theory to approximate the velocity field. Here, however, we obtained the fluid particle trajectories
from an exact model known as the John–Sclavounos (JS) equation (see
Section 3 for a review). This exact nonlinear kinematic model was first derived by John [
2] for unidirectional irrotational water waves. Sclavounos [
3] generalized the equations to two-dimensional waves and removed the irrotationality assumption. Fedele et al. [
4] further analyzed the JS equation discovering its underlying Hamiltonian structure.
Using the JS equation, we compute the temporal evolution of the variance
for fluid particles evolving from a given initial condition
. This puts us in the framework of the single-particle dispersion theory. Single-particle dispersion was first studied by Taylor [
5] in the context of homogeneous, isotropic turbulence (see
Section 2, for a review). Taylor’s dispersion theory predicts that the variance
exhibits a ballistic motion for short times (i.e.,
) and a diffusive motion for large times (i.e.,
), so that the variance follows the scaling laws
These scaling laws are often assumed in the study of fluid particles dispersed by surface waves. The main contribution of the present study is to show that Taylor’s dispersion laws (
1) may be violated for particles advected by free-surface waves. More precisely, our results can be summarized as follows.
The variance
of the particles advected by a surface wave follow the scaling laws
where
denotes the wave period. This is markedly different from the prediction of Taylor’s theory. In particular, the long-term evolution of the variance follows a ballistic motion as opposed to a diffusive motion.
Central to Taylor’s theory of single-particle dispersion is the autocorrelation function
of the Lagrangian fluid velocities (see
Section 2, for a precise definition of
R). To arrive at the scaling laws (
1), Taylor assumes that this autocorrelation function decays to zero rapidly enough so that the integral
exists and its value is finite. We show, however, that for particles dispersed by surface waves, the autocorrelation function decays to
as
. This observation, in turn, explains the unusual scaling (
2).
1.2. Earlier Studies
Previous studies of particle dispersion on the free surface of a fluid can be divided into three general categories: (i) Passive tracers on a flat free surface, (ii) Linear or nonlinear waves with the induced velocity field modeled based on simplifying assumptions, and (iii) Velocity field derived from satellite altimetry data.
The first category is concerned with the Lagrangian motion of fluid particles on the flat free surface of a fluid in a container. Although the three-dimensional flow is incompressible, the velocity field restricted to the surface can be compressible. As a result, the passive tracers can form clusters on a nontrivial subset of the surface. Such no-slip surface flows have been studied experimentally [
6,
7] and numerically [
8,
9,
10,
11] with their main emphasis being on the clustering patterns formed by tracers on the free surface. However, they neglect the effect of waves on the dispersion of the tracers by assuming a flat free surface.
The second category considers the effect of waves on the particle dispersion [
12,
13,
14,
15,
16,
17]. These studies often assume (explicitly or implicitly) that the longterm particle dispersion is diffusive (Taylor’s theory) and aim to approximate the diffusion tensor. However, they use a simplified model for the fluid velocity field on the surface. For instance, Herterich and Hasselmann [
12] assume that the Eulerian velocity field is a linear superposition of the velocities obtained from linear wave theory. Weichman and Glazman [
13] also assume such a linear wave theory for their study of passive tracer advection (also see Refs. [
14,
15]).
Bühler and Holmes–Cerfon [
16] consider dispersion by random waves in the rotating shallow water framework. They go beyond the linear wave theory by using the wave-mean interaction theory to account for second-order corrections to the linear velocity field. Holmes–Cerfon et al. [
17] use a similar approach in the framework of the rotating Boussinesq equation. Although accounting for the second-order nonlinear effects, these studies also assume that the longterm dispersion is diffusive (Taylor’s theory).
The third category derives ocean velocity field from the satellite altimetry data [
18,
19,
20,
21,
22,
23]. These studies are concerned with the large scale mixing in the ocean (on the order of a few kilometers). It is believed that, over such scales, the main contribution to mixing comes from the large ocean eddies with negligible contribution from the wave motion. Nonetheless, the velocity field is derived from the sea surface height measured by altimetry techniques [
24]. In order to relate the sea surface height to the fluid velocity field, one makes the so-called quasi-geostrophic assumption, resulting in an approximation of the true velocity field.
In contrast to previous studies, here we used the John–Sclavounos equation to compute the exact Lagrangian trajectory of fluid parcels on the free surface and thereby examine the validity of the underlying assumptions of Taylor’s single-particle dispersion theory.
Before proceeding further, we also refer to the work on pilot-wave hydrodynamics which concerns the motion of droplets bouncing on the surface of a fluid [
25,
26]. These droplets create a wave when bouncing off the surface which in turn guides the motion of the droplet upon subsequent bounces. Clearly, the pilot-wave phenomena is distinct from the dispersion of fluid parcels that belong to the free surface (as considered here) and the two should not be confused.
1.3. Outline of the Paper
In
Section 2, we review Taylor’s single-particle dispersion theory.
Section 3 reviews the JS equation for the motion of fluid particles on a surface wave. In
Section 4, we describe the set-up of our numerical simulations. Our numerical results are presented in
Section 5. Finally, we present our concluding remarks in
Section 6.
2. Review of Taylor’s Single-Particle Dispersion Theory
In this section, we briefly review the single-particle dispersion theory of Taylor [
5]. This theory is not limited to particle on a free-surface wave and applies more generally to fluid particles advected by turbulent velocity fields which satisfy the simplifying assumptions mentioned below. Fluid particles move according to the ordinary differential equation,
where
denotes the trajectory of a fluid particle starting from the point
at the initial time
. The time-dependent vector field
denotes the Eulerian fluid velocity field.
We also define the Lagrangian velocity
which measures the fluid velocity along the trajectory
. Integrating Equation (
3) in time, we obtain
Taylor [
5] views the Lagrangian velocity
as a stochastic process and seeks to derive the properties of the resulting stochastic process
. In the following, we briefly review Taylor’s argument. For notational convenience, we omit the dependence of the Lagrangian trajectory and velocity on the initial conditions
and simply write
and
.
Taylor [
5] also assumes that the flow is homogeneous and isotropic. These assumptions imply that the flow can be considered as a one-dimensional motion (
). Therefore, we omit the vectorization of the quantities and denote the fluid parcel’s position and velocity by
and
, respectively. We also define the mean-zero position and Lagrangian velocity of the particles,
where
denotes the ensemble average. It is straightforward to show that
Taylor’s theory predicts the scaling (
1) for the variance of the quantity
. Note that this prediction implies that, for short times, the particle dispersion is ballistic while, for long times, the particles diffuse as if they are undergoing Brownian motion. In order to derive expression (
1), we consider the time derivative of the variance of
,
where for the last identity we used the change of variables
and assumed
(without loss of generality). Assuming that
V is a stationary process, the covariance
only depends on
. Therefore, the autocorrelation function
only depends on the delay parameter
. Integrating Equation (
7) in time, we obtain
We note that, for homogeneous and isotropic flows with stationary Lagrangian velocities
, Equation (
8) is exact. In order to arrive at the scaling laws (
1), Taylor [
5] makes further simplifying assumptions. In particular, he assumes that, for small
t, the autocorrelation function is constant. As a result, for small
t, we obtain
(note that the variance
is time-independent since we assumed the Lagrangian velocity is a stationary stochastic process). Furthermore, assume that
and
exist and are finite. Then, for large
t, we have
where
.
To summarize, for the scaling laws (
1) to hold, the stochastic Lagrangian velocities
must be stationary. Furthermore, the autocorrelation function
must decay to zero fast enough so that the integrals
and
are finite. In
Section 5, we show that some of these assumptions do not hold generally for particles advected by random surface waves. Our results were obtained by numerically integrating an exact model of the fluid trajectories on the free surface. We introduce this model in the next section.
3. John–Sclavounos Equation
The John–Sclavounos (JS) [
2,
3] equation describes the horizontal motion of fluid particles on a free surface
. Lets denote the horizontal coordinate by
x and denote the vertical coordinate (corresponding to the depth) by
z. We assume that the free surface is a graph over the horizontal coordinate
x so that on the free surface
(see
Figure 1). The position of the particles on the free surface at time
t is then given by
. The Eulerian velocity field inside the fluid is denoted by
. The fluid velocity
and the free surface
satisfy the water wave equations.
With this notation, the JS equation reads
where
is shorthand notation for the partial derivative
and similarly for partial derivatives with respect to time. Supplying Equation (
9) with the appropriate initial conditions
and integrating in time, the horizontal motion of the particles on the free surface can be computed. The JS equation is quite a remarkable result. It implies that if the surface elevation
is known, then the motion of the particles on the free surface can be deduced without knowing the full fluid velocity field
.
Denoting the horizontal Lagrangian velocity of a fluid parcel by
, we write the JS equation as a set of first-order differential equations
where
Fedele et al. [
4] showed that the JS Equations (
10) have a Hamiltonian structure which in the 1D case is given by
where the Hamiltonian
H reads
and the generalized momentum
p is given by
.
In the time-independent case, where
, the Hamiltonian is a conserved quantity. In other words, the quantity,
is invariant along the trajectories of the JS equation. However, in the realistic situation where the free surface elevation is time-dependent, the energy
H is no longer conserved and complex particle motion is possible.
The derivation of Fedele et al. [
4] also shows that the JS equation holds more generally for any particle constrained on a surface
and moving under the gravitational force. In particular, they show that the JS equation can be derived without making use of the continuity equation.
In the following, we do not leverage the Hamiltonian structure of the JS equation. Instead, for a given surface elevation
, we numerically integrate the JS Equation (
10) and compute the resulting particle dispersion properties. Although here we focused on unidirectional waves, the JS equation is applicable to two-dimensional waves (see Refs. [
3,
4]) and therefore our results can be generalized in a straightforward fashion.
We point out that a model similar to the JS equation was proposed by Herbers and Janssen [
27] (see their Equation (20)). That model however is inaccurate since it neglects the denominator in Equation (
9).
5. Numerical Results
In this section, we present the results obtained from numerically integrating the JS Equation (
10). All results are reported in the non-dimensional variables discussed in
Section 4.3. First, we generate the random wave fields from (
15) with
and the JONSWAP spectrum (
16). The computational domain is
with periodic boundary conditions. The domain is large enough to avoid finite-box effects. The parameter
in the JONSWAP spectrum (
16) is set to
which guarantees that the resulting waves have average steepness
. We report our results for three wave steepness values
,
and
which are below the threshold for breaking waves (Recall that JS equation is not valid for breaking waves).
Figure 2 shows a realization of the random wave field with steepness
.
Given a wave field
, we integrated the JS Equation (
10) with the embedded Runge–Kutta scheme RK5(4) of MATLAB [
30]. The initial conditions were
and
with the initial velocity
discussed in
Section 4.2 (see Equation (
17)). For each steepness
, we generated 50,000 random waves. For each realization of the waves, we computed the particle trajectories and estimated the ensemble averages
from these 50,000 trajectories.
First, we examine the average drift
as shown in
Figure 3a. The average drift grows linearly with time
t which agrees with Stokes’ prediction [
1,
31]. However, the variance
of the particle positions exhibited a surprising behavior. Recall that
is the mean-zero position of the particles.
Figure 3b shows this variance as a function of time. For short times
grows with the power law scaling
. After roughly one wave period, the growth of the variance changes and scales as
. These two regimes result in the scaling law (
2).
Note that this behavior is very different from Taylor dispersion theory (
1) in the absence of waves. Taylor dispersion predicts a scaling
for short times while, in the presence of waves, we observe the scaling
. For large times, Taylor dispersion predicts a Brownian-type diffusion where the variance increases linearly with time while, in the presence of waves, we observe a ballistic dispersion with
.
This super-diffusive asymptotic behavior has been reported in homogeneous, isotropic turbulence where
with
[
32,
33,
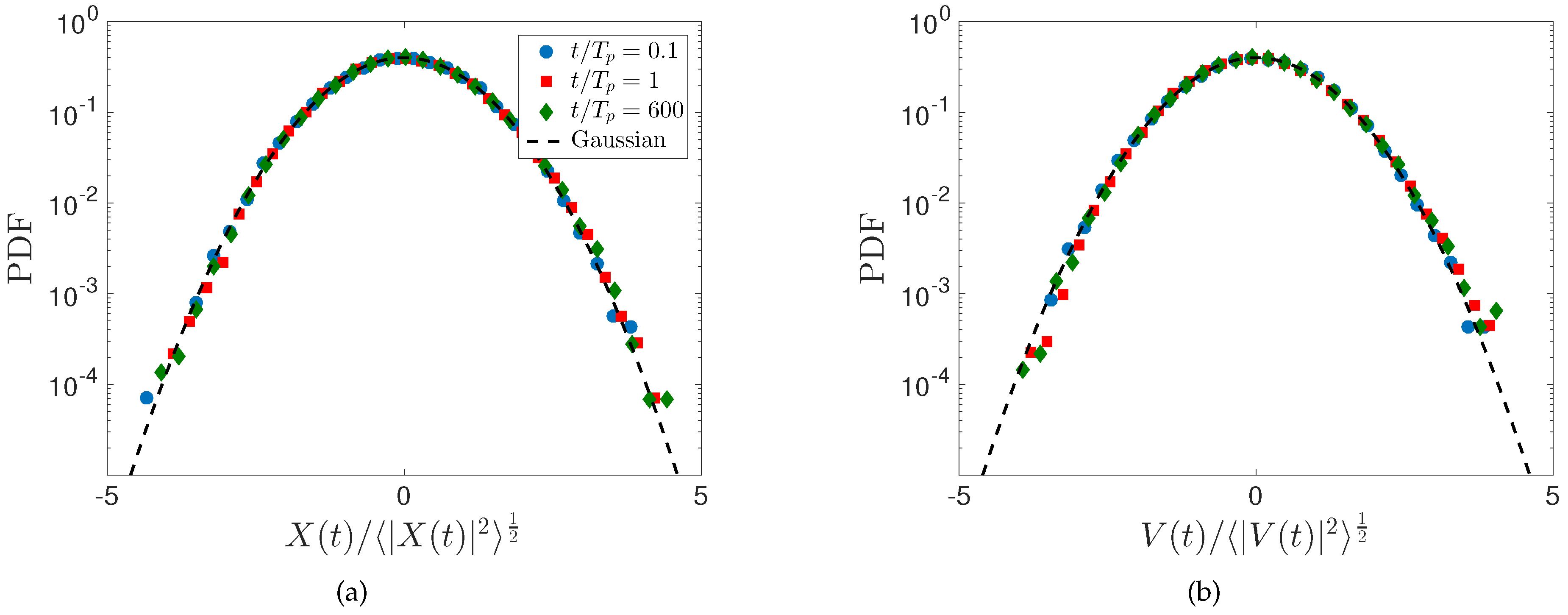
34]. In turbulence, the departure from Taylor dispersion theory is often associated with intermittency which manifests itself as heavy tails in the distributions of the particle positions and velocities. However, for particle dispersion by waves, we do not observe such heavy-tail statistics. In fact, as
Figure 4 shows, the PDF of particle positions and velocities are Gaussian. Note that the initial conditions
are deterministic and therefore their initial distributions are delta functions. However, as shown in
Figure 4, they rapidly converge to a Gaussian for
(e.g., see the circles marking the PDFs at time
). As we show in
Appendix A, these Gaussian distributions can be deduced from the JS equations and a central limit theorem.
The unusual scaling (
2) observed here can be explained by examining the autocorrelation function
. For
t large enough, this function is independent of
t and only depends on the delay
.
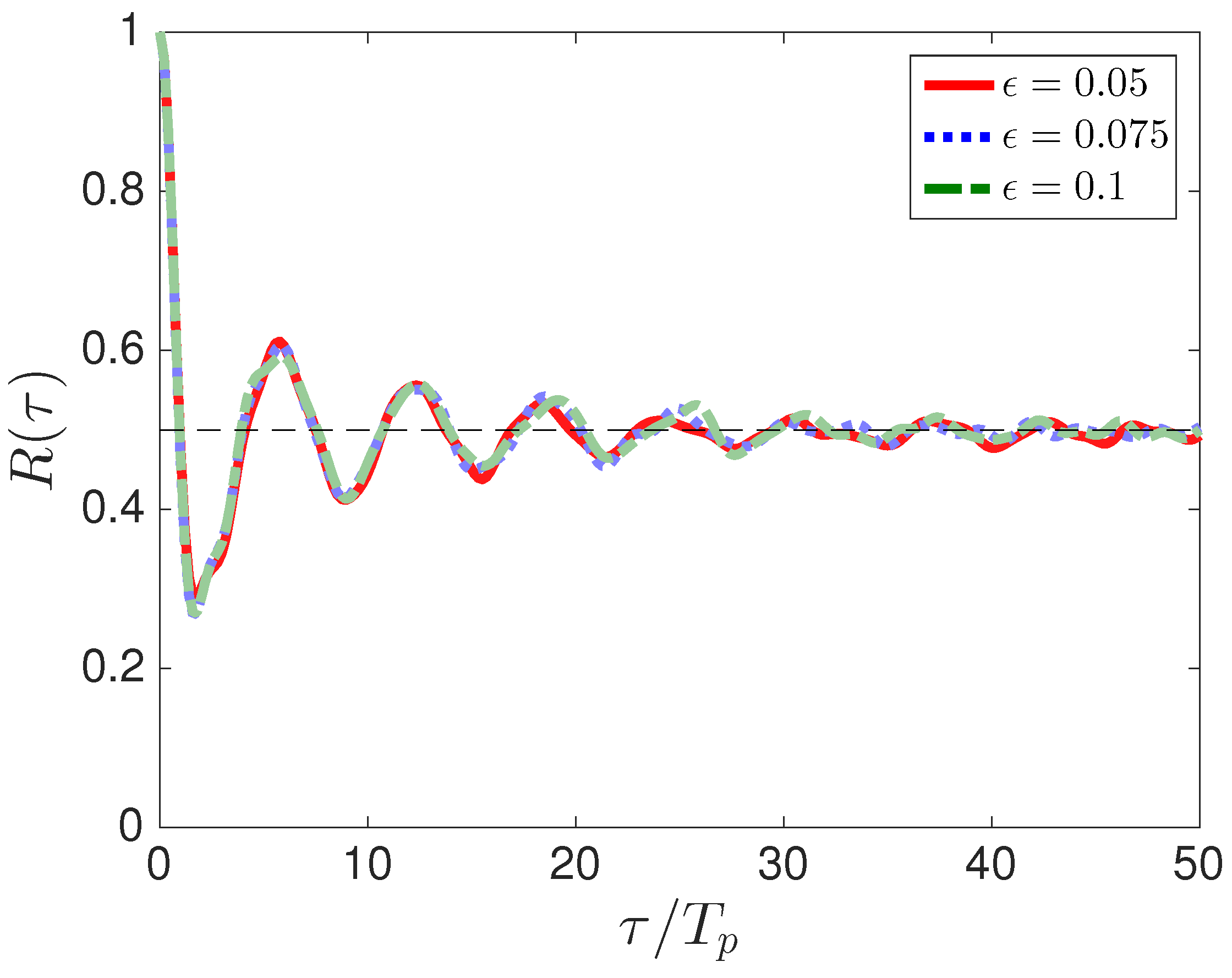
Figure 5 shows
computed for
. One important feature of this autocorrelation function is that it does not decay to zero for large
. Instead, it decays to
, indicating that the Lagrangian particle velocities on the free surface remain correlated indefinitely.
This correlation explains the ballistic motion of particles observed in
Figure 3b for large
t, i.e.,
. Recall Equation (
8) that relates the variance of the particles to the autocorrelation function. For large
, the autocorrelation tends to
and therefore the integral
scales as
as
. Furthermore, the variance
is constant for large
t (see
Figure 6). These numerical observations, together with Equation (
8), imply that
.
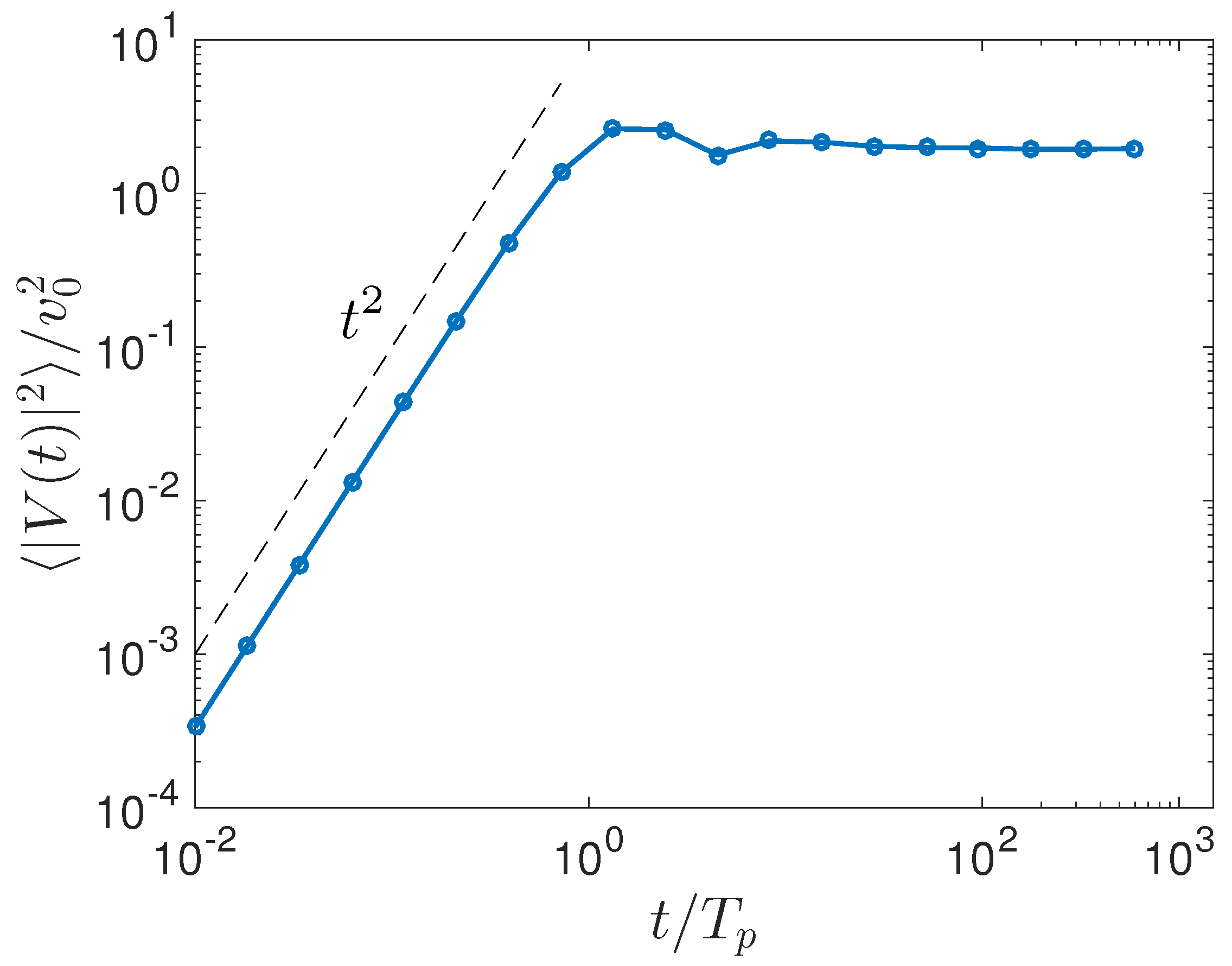
Finally, we turn our attention to the short-term behavior
reported in
Figure 3b.
Figure 6 shows that, for
, the variance
increases quadratically in time. This together with Equation (
8) implies that the variance
of the fluid parcels should in fact increase as
.
6. Conclusions
Here, we investigated the nonlinear dispersion of fluid parcels on the free surface of a random wave in deep ocean. The free surface is assumed to be a superposition of linear waves with random phases and the JONSWAP spectrum. However, the fluid particle trajectories are computed using an exact nonlinear model known as the John–Sclavounos (JS) equation [
2,
3,
4].
Our main finding is the breakdown of Taylor’s dispersion theory [
5]. In particular, for large times, the particles disperse ballistically as opposed to diffusively. More precisely, the variance
of the distribution of the particles increases quadratically in time for large
t so that
. For short times, the variance is proportional to
giving rise to the scaling laws (
2).
We showed that this unusual scaling law is a consequence of longterm correlation of Lagrangian velocities of the fluid particles. This is a clear violation of Taylor’s assumption that these correlations decay to zero asymptotically. Clearly, our results have profound implications for modeling the dispersion of fluid particles (and pollutants) on the ocean surface.
Since the JS equations are valid in two dimensions, extending our results to two-dimensional waves is straightforward and will be presented in future work. Furthermore, future work will investigate the single-particle dispersion on the surface of (weakly) nonlinear waves. This can be accomplished, for instance, by the one-way coupling of the JS equation to an envelop equation for the free surface (e.g., the nonlinear Schrödinger equation).