Constructive Study of Modulational Instability in Higher Order Korteweg-de Vries Equations
Abstract
:1. Introduction
2. Traveling Wave: Phase Plane Analysis
- (a)
- (b)
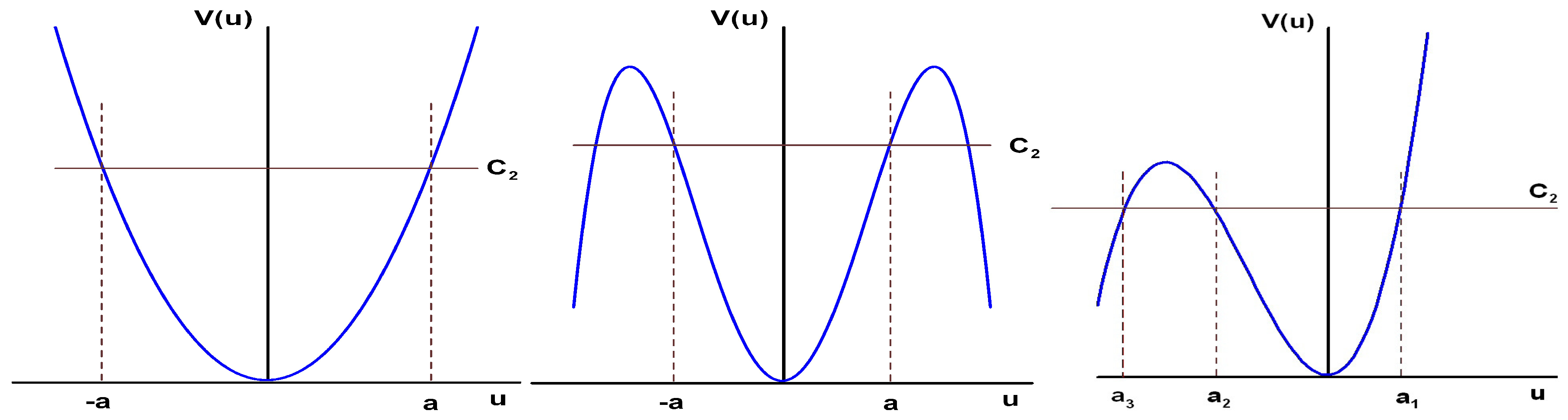
- they are symmetric with respect to horizontal axes for even powers of the nonlinearity, i.e., , and asymmetric for odd powers of the nonlinearity, .
3. Frequency Correction, Symmetric Case
4. Frequency Correction, Asymmetric Case
4.1. Case A: Zero Mean Level
4.2. Case B: Non-Zero Mean Level
4.3. Total Frequency Correction
5. Modified NLS Equations
6. Discussion
- We have deduced the constructive condition for the occurrence of modulational instability in the class of the higher order KdV equations with an arbitrary positive integer p. We demonstrated constructively that for the weakly modulated wave train is described by the high-order NLS equation whose solutions are stable for both even and odd p if . Notice that in the known literature examples of studying stability of solutions to specific equations of this class by other methods, e.g., [25,28], yield results depending on the the sign of a pedestal.It is important to realize that in the frame of the KdV-family of equations, the Fourier mode describes the wave-induced mean flow term. In the symmetric case this fact does not influence the form of the nonlinear frequency correction obtained in Section 3 while in the asymmetric case it will contribute into the nonlinear term in the NLS equation. The influence of the zero harmonic requires a special wave-mean flow analysis which has been explicitly performed in this paper.Some other substantial differences between symmetric and asymmetric cases are demonstrated below.
- For deducing the conditions of the instability, we first computed the nonlinear corrections to the frequency of the Stokes wave and then explored the coefficients of (m)NLS equations obtained, thus deducing explicit expressions for the instability growth rate, maximum of the increment and the boundaries of the instability interval. These results can be used for planning numerical and laboratory experiments similar to [15,16], and for explaining the available data, e.g., [22,23]. An important issue here would be to choose small parameters and initial amplitudes facilitating these results which is not a simple problem. The approximations of a solution of gKdV equations by solutions of gNLS equations are the subject of a few tedious mathematical studies (see e.g., [32] and the bibliography therein), where it is rigorously proven that the quality of approximation depends not only on p and s but also on the parameters of the initial excitation.
- We have shown that conditions of the modulational instability have different forms depending on whether p is an even number (symmetric case) or odd number (asymmetric case) where the words symmetric and asymmetric are used loosely referring to the form of the corresponding solutions, as discussed in Section 2. An interesting mathematical fact is that the properties of the corresponding NLS-family of equations are also different. Namely,
- (a)
- In the symmetric case the nonlinear terms have the same power both in the initial (m)KdV equation and corresponding (m)NLS equation; this means in particularly that (m)NLS equations with an odd power of nonlinearity, for instancecan not appear this way.
- (b)
- in the asymmetric case starting with different higher order KdV equations one can come to the same (m)NLS equation. Further on we call these couples of equations an associate pair. The first trivial associate pair readsand both equations are reduced to the classical NLS equationMore interesting example of a non-trivial associated pair is given by equationsthat can be reduced toAn associated pair consist of one symmetric and one asymmetric (m)KdV equation.
- (c)
- In asymmetric case, each (m)KdV equation belongs to some associated pair.
- (d)
- In symmetric case, there are single (m)KdV equations which do not belong to any associated pair, for example, equationis single and generates (m)NLS of the formAll these properties point indicate an existence of different inner structures of the NLS-families appearing in symmetrical and asymmetrical cases which deserves a special study. The existence of associated pair might also imply a corresponding physical interpretation. These issues are presently under study.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kurkina, O.E.; Kurkin, A.A.; Soomere, T.; Pelinovsky, E.N.; Ruvinskaya, E.A. Higher-order (2+4) Korteweg-de Vries—Like equation for interfacial waves in a symmetric three-layer fluid. Phys. Fluids 2011, 23, 116602. [Google Scholar] [CrossRef]
- Kurkina, O.E.; Kurkin, A.A.; Ruvinshaya, E.A.; Pelinovsky, E.N.; Soomere, T. Dynamics of solitons in a nonintegrable version of the modified Korteweg-de Vries equation. JETP Lett. 2012, 95, 91–95. [Google Scholar] [CrossRef]
- Rudenko, O.V. Modular solitons. Dokl. Math. 2016, 94, 708–711. [Google Scholar] [CrossRef]
- Nazarov, V.E.; Kiyashko, S.B.; Radostin, A.V. Stationary waves in a bimodular rod of finite radius. Wave Motion 2017, 75, 72–76. [Google Scholar] [CrossRef]
- Chatterjee, A. Asymptotic solution for solitary waves in a chain of elastic spheres. Phys. Rev. E 1999, 59, 5912–5919. [Google Scholar] [CrossRef]
- James, G.; Pelinovsky, D.E. Gaussian solitary waves and compactons in Fermi-Pasta-Ulam lattices with Hertzian potentials. Proc. R. Soc. A 2014, 470, 20130465. [Google Scholar] [CrossRef]
- Dumas, E.; Pelinovsky, D.E. Justification of the log-KdV equation in granular chains: The case of precompression. SIAM J. Math. Anal. 2014, 46, 4075–4103. [Google Scholar] [CrossRef]
- Pelinovsky, D.E.; Giniyatullin, A.R.; Panfilova, Y.A.; Shurgalina, E.G.; Rodin, A.A. Analytical approximations of solitary waves in granular crystals. Trans. Nizhni Novgorod State Tech. Univ. R.Y. Alexeev 2013, 100, 55–69. (In Russian) [Google Scholar]
- Martel, Y.; Merle, F. Instability of solitons for the critical generalized Korteweg-de Vries equation. GAFA Geom. Funct. Anal. 2001, 11, 74–123. [Google Scholar] [CrossRef]
- Martel, Y.; Merle, F. Asymptotic stability of solitons of the gKdV equations with general nonlinearity. Math. Ann. 2008, 341, 391–427. [Google Scholar] [CrossRef]
- Klein, C.; Peter, R. Numerical study of blow-up and dispersive shocks in solutions to generalized Korteweg-de Vries equations. Physica D 2015, 304–305, 52–78. [Google Scholar] [CrossRef]
- Zakharov, V.E.; Kuznetsov, E.A. Multi-scale expansions in the theory of systems integrable by the inverse scattering transform. Physica D 1986, 18, 455–463. [Google Scholar] [CrossRef]
- Grimshaw, R.; Pelinovsky, D.; Pelinovsky, E.; Talipova, T. Wave group dynamics in weakly nonlinear long-wave models. Physica D 2001, 159, 35–57. [Google Scholar] [CrossRef]
- Grimshaw, R.; Pelinovsky, E.; Talipova, T.; Ruderman, M.; Erdelyi, R. Short-lived large-amplitude pulses in the nonlinear long-wave model described by the modified Korteweg-de Vries equation. Stud. Appl. Math. 2005, 114, 189–210. [Google Scholar] [CrossRef]
- Ruderman, M.S.; Talipova, T.; Pelinovsky, E. Dynamics of modulationally unstable ion-acoustic wave packets in plasmas with negative ions. J. Plasma Phys. 2008, 74, 639–656. [Google Scholar] [CrossRef]
- Grimshaw, R.; Pelinovsky, E.; Talipova, T.; Sergeeva, A. Rogue internal waves in the ocean: Long wave model. Eur. Phys. J. Spec. Top. 2010, 185, 195–208. [Google Scholar] [CrossRef]
- Chowdury, A.; Ankiewicz, A.; Akhmediev, N. Periodic and rational solutions of modified Korteweg-de Vries equation. Eur. Phys. J. D 2016, 70, 104. [Google Scholar] [CrossRef]
- Kartashova, E. Energy spectra of 2D gravity and capillary waves with narrow frequency band excitation. EPL 2012, 97, 30004. [Google Scholar] [CrossRef]
- Kartashova, E. Energy transport in weakly nonlinear wave systems with narrow frequency band excitation. Phys. Rev. E 2012, 86, 041129. [Google Scholar] [CrossRef]
- Kartashova, E. Time scales and structures of wave interaction exemplified with water waves. EPL 2013, 102, 44005. [Google Scholar] [CrossRef]
- Tobisch, E. Energy spectrum of ensemble of weakly nonlinear gravity-capillary waves on a fluid surface. J. Exp. Theor. Phys. 2014, 119, 359–365. [Google Scholar] [CrossRef]
- Dutykh, D.; Tobisch, E. Direct dynamical energy cascade in the modified KdV equation. Physica D 2015, 297, 76–87. [Google Scholar] [CrossRef]
- Dutykh, D.; Tobisch, E. Observation of the inverse energy cascades in the modified Korteweg-de Vries equation. EPL 2014, 107, 14001. [Google Scholar] [CrossRef]
- Whitham, G.B. Linear and Nonlinear Waves; Wiley Series in Pure and Applied Mathematics; Wiley: Hoboken, NJ, USA, 1999. [Google Scholar]
- Bronski, J.C.; Hur, V.M.; Johnson, M.A. Modulational instability in equations of KdV type. In New Approaches to Nonlinear Waves; Tobish, E., Ed.; Springer: Berlin, Germany, 2015; pp. 79–125. [Google Scholar]
- Minzoni, A.A.; Smyth, N.F. Modulation theory, dispersive shock waves and Gerald Beresford Whitham. Physica D 2016, 333, 6–10. [Google Scholar] [CrossRef]
- El, G.E.; Hoefer, M.A. Dispersive shock waves and modulational theory. Physica D 2016, 333, 11–65. [Google Scholar] [CrossRef]
- Tobisch, E.; Pelinovsky, E.N. Conditions for modulation instability in higher order Korteweg- de Vries equations. Appl. Math. Lett. 2018, 88, 28–32. [Google Scholar] [CrossRef]
- Johnson, E.R.; Pelinovsky, D.E. Orbital stability of periodic waves in the class of reduced Ostrovsky equations. J. Diff. Equ. 2016, 261, 3268–3304. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M.; Geronimus, Y.V.; Tseytlin, M.Y. Table of Integrals, Series, and Products; Academic Press: Cambridge, MA, USA, 1980. [Google Scholar]
- Kartashova, E. Nonlinear Resonance Analysis: Theory, Computation, Applications; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Masaki, S.; Segata, J. Existence of a minimal non-scattering solution to the mass-subcritical generalized Korteweg-de Vries equation. Annales de l’Institut Henri Poincaré C Analyse non LinéAire 2018, 35, 283–326. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tobisch, E.; Pelinovsky, E. Constructive Study of Modulational Instability in Higher Order Korteweg-de Vries Equations. Fluids 2019, 4, 54. https://doi.org/10.3390/fluids4010054
Tobisch E, Pelinovsky E. Constructive Study of Modulational Instability in Higher Order Korteweg-de Vries Equations. Fluids. 2019; 4(1):54. https://doi.org/10.3390/fluids4010054
Chicago/Turabian StyleTobisch, Elena, and Efim Pelinovsky. 2019. "Constructive Study of Modulational Instability in Higher Order Korteweg-de Vries Equations" Fluids 4, no. 1: 54. https://doi.org/10.3390/fluids4010054
APA StyleTobisch, E., & Pelinovsky, E. (2019). Constructive Study of Modulational Instability in Higher Order Korteweg-de Vries Equations. Fluids, 4(1), 54. https://doi.org/10.3390/fluids4010054





