1. Introduction
In the Deuterium-Tritium phase, ITER is expected to operate in the so-called High-confinement (H) mode. The H-mode regime, in opposition to the Low-confinement mode (L), is characterized by a visible steepening of the profiles of plasma density in the edge region that leads ultimately to a higher plasma pressure at the magnetic axis. This phenomenon is associated with a reduction in turbulent transport, which is the dominant particle and heat transport mechanism in the edge plasma. More specifically, in H-mode conditions, the fluctuation level is strongly reduced in a region of the edge plasma radially localized near the separatrix: this partial turbulence suppression in a localized region is also called “transport barrier”. The transition from L to H-mode is experimentally obtained when the power injected into the plasma exceeds a certain threshold. This power threshold depends on the device characteristics and on the plasma conditions [
1]. When the threshold is exceeded, the dynamic system exhibits a bifurcation, the level of fluctuation is drastically reduced, and large relaxation events as edge localized modes (ELMs) are usually observed. The magnetohydrodynamic (MHD) stability and the transport processes in the region affected by the transport barrier are extensively studied in the so-called pedestal physics [
2].
Even if the L-H transition is experimentally reproducible, theory cannot yet completely explain this process, making difficult the extrapolation of the existing scaling laws to new devices. Up to now, it seems clear that the suppression of turbulent structures is due to the shear of the plasma velocity in the poloidal direction, which is perpendicular both to the magnetic field and to the direction perpendicular to flux surfaces [
3]. However, the cause of this shear is still unclear, and several mechanisms have been pointed out. Indeed, the
poloidal velocity derives from the radial profile of the electric field, which tends to balance the radial pressure gradient. Turbulence itself is a potential source of poloidal flows, uniform on a flux surface but with a finite radial wavenumber: these are also called Zonal Flows (ZF). As well-explained in [
4], small turbulence scales can, in fact, provide energy to large scale flows in an inverse cascade process, in particular through the mechanism of the Reynolds stress. Therefore small-scale turbulence, which is affected by the
shear, contributes to the formation of the shear itself. The problem is complicated by the fact that the characteristics of turbulence depend on the background plasma equilibrium. In fact, the energy available for interchange turbulence depends on the average pressure gradient in the plasma. Also, there are some turbulence saturation mechanisms, which depend on the background gradients [
5]. Turbulence is the main transport mechanism and therefore affects, in turn, the global equilibrium.
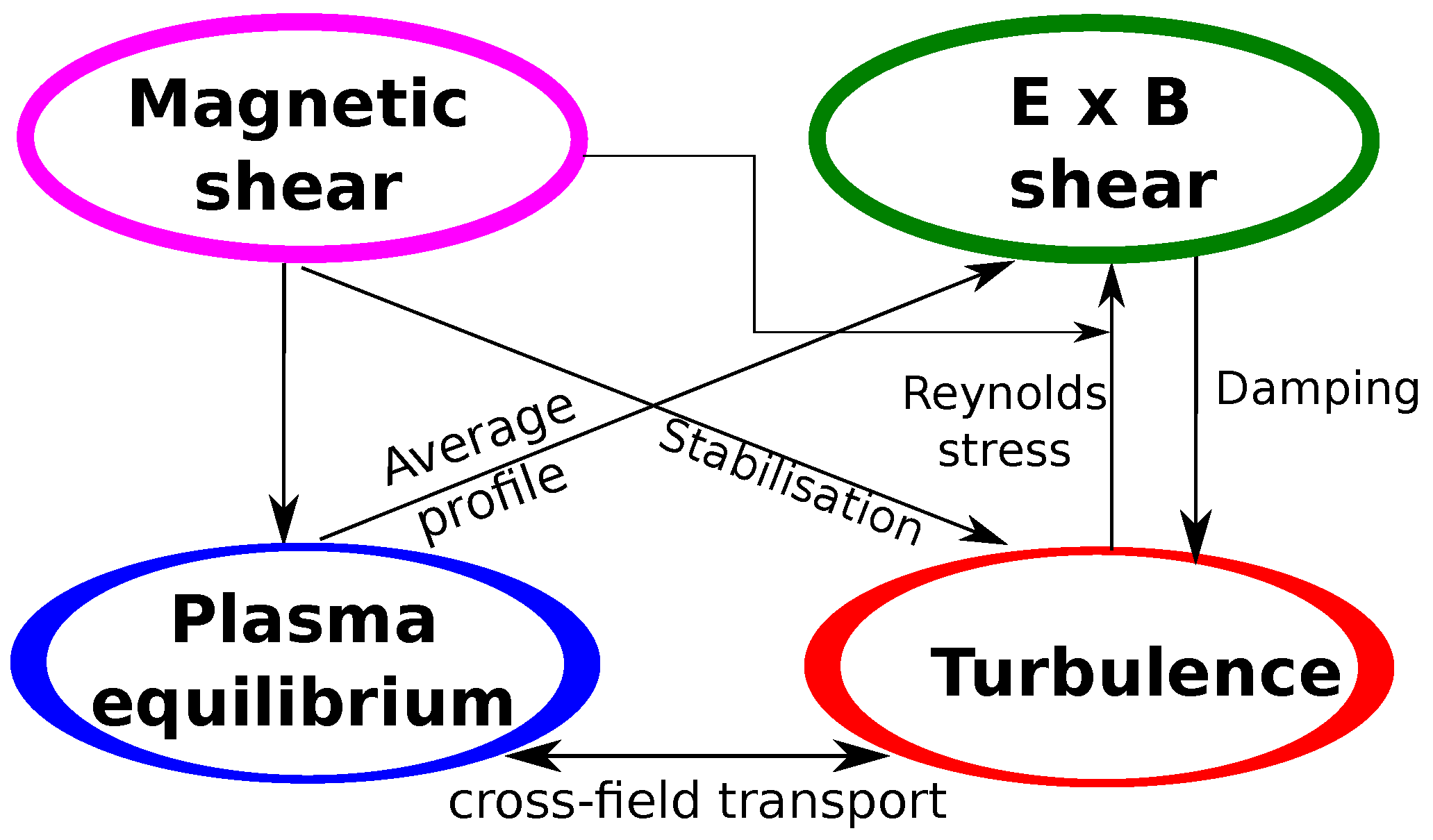
Figure 1 shows schematically the complex interplay between turbulence and the background conditions.
Another element which is affecting turbulence and, in turn, the overall equilibrium, is the magnetic shear, namely the variation of the field line pitch angle in the cross-field direction. In past works, it has been proven that interchange turbulence growth rate is maximum for a certain value of the shear in circular geometries: this can be proven analytically [
6] and numerically with linear and non-linear gyrokinetic simulations [
7]. Recently, it has been pointed out that the magnetic shear can induce an
shear [
8]: this synergy further complicates the identification of the primary causes of the build-up of a transport barrier.
The complex problem of the transport barriers calls for an investigation with global turbulence simulations, which are presently able to include all the mentioned aspects of the edge plasma physics. During the years, fluid turbulence codes have addressed the transport barriers problem in various ways. On one hand, transport barriers were forced by regulating some physical parameters in 2D turbulence codes (see e.g., [
9,
10]), then assessing the effect of barriers on turbulence properties. On the other hand, some anisothermal 2D turbulence codes have reproduced transport barriers by varying the energy source value, in some cases (see e.g., [
5,
11]) leading to a dynamics in the system behavior coherent with an L-H transition. In 3D global edge turbulence fluid simulations, instead, macroscopic transport barriers have never been highlighted, to our knowledge. An enhancement of radial pressure gradient was observed in Global Braginskii Solver (GBS) simulations in the first open flux surfaces [
12], however not associated with a lowering of turbulence levels. It is worth noting that the XGC1 gyrokinetic code [
13], simulating an edge plasma with realistic magnetic geometry and physical parameters, has reproduced a bifurcative dynamics associable to the L-H transition. However, in XGC1 simulations, the initial background profiles are artificially imposed, and the system evolves for a small time with respect to the confinement time. Therefore, simulations run on longer time scales are required to better interpret the outcome of these simulations. In this context, 3D fluid turbulence codes can play an important role, giving an insight on global mechanisms as the formation of edge transport barriers.
It is to be noted that the H-mode has been first achieved in the Axially Symmetric Divertor Experiment (ASDEX) [
14], when a divertor magnetic configuration was first introduced. Even though several examples of improved confinement exist also in limiter configuration (e.g., [
15]), the H-mode is routinely achieved only in divertor configuration. This fact suggests that the particular geometry of the magnetic field in the vicinity of the X-point, can somehow affect the global behavior of turbulence in the edge plasma. In this work, we will exploit the ability of the TOKAM3X code to perform global simulations in divertor configuration [
16], to study the effects of the magnetic geometry introduced by the X-point on the turbulence local and global behavior, including the formation of transport barriers. In order to limit the computational cost of simulations we solve, in this work, the isothermal version of the TOKAM3X model. Although the isothermal assumption clearly represents a strong limitation in the description of the edge plasma, first TOKAM3X simulations with the anisothermal model have shown that turbulence nature and statistical properties are qualitatively similar to the isothermal case [
17]. Therefore, we expect the general conclusions of this paper to be qualitatively valid also in an anisothermal framework.
In
Section 2 we briefly describe TOKAM3X, and the setup of the divertor simulations. In
Section 3 we describe the results of the simulations, including the local effect of the X-point on fluctuations shape and amplitude, and the characteristics of the observed transport barrier. We also investigate the physical mechanism underneath the formation of the transport barrier. In
Section 4 we isolate the role of the Reynolds stress in driving the poloidal flows. This publication can be seen as complementary of [
18], where we described the macroscopic behavior of the background plasma in the same divertor configuration.
2. The TOKAM3X Code
TOKAM3X solves a two-fluid, electrostatic model for electrons and ions. The physical system is obtained by calculating the successive moments of the Boltzmann equation for the two species. The relatively low temperature of the edge plasma, and thus the high collisionality, allows to adopt the so-called Braginskii closure [
19]. The large anisotropy of magnetized plasmas is conveniently described by separating the dynamics parallel to the magnetic field to the one perpendicular to it. In particular, equations are drift-reduced, assuming that the characteristic turbulence frequencies are slow compared to the ion cyclotronic frequency. The motion of the fluid in the cross-field direction is given, at the first order, by the drift velocities:
where
s denotes the specie,
the electric charge of the specie,
E the electric field,
T the temperature, and
B the magnetic field. The first term on the right hand side (RHS) is the
drift, which we rename
, while the second is the
drift, which we call
. The ions polarization drift, being of second order, is retained only when it is in a divergence operator, since its divergence is of the same order of the other drifts’ one. The centrifugal drift here is omitted: this hypothesis is justified by the fact that parallel velocity is large only in a small region of the domain, in the vicinity of the targets, thus the associated drift is not expected to change the overall behavior of the system. An ordering procedure is carried out basing on the ordering parameter
, namely the ratio of the characteristic frequency of each term with respect to the ion cyclotronic frequency
. The edge plasma is modelled as quasi-neutral, since the considered characteristic lengths are much larger than the typical Debye length. Moreover, the magnetic field is fixed in space and time, thus neglecting the feedback actions of currents on it: this hypothesis is usually satisfied for L-mode, sufficiently low-
plasmas, as the ones that we are considering in this work. Under this hypothesis, one obtains the system of equations:
In this system, Equation (
2) represents the electrons particle balance, (3) the ion momentum balance, (4) the electric charge balance and (5) the so-called Ohm’s law. The system is thus solved for the electron density
N, the ion parallel momentum
, the electric potential
and the parallel current density
. In these equations, the vorticity
W is calculated with a Boussinesq-like approximation [
20], so it can be defined as:
We point the reader to the publication [
16] for more details on the derivation of the equations. In this work, the code is run in isothermal mode, with a constant temperature for both species,
, where
is the reference temperature. In the normalized equations, by consequence, temperature has a constant unitary value. As shown in [
16], the correct implementation and solution of the physical isothermal model in TOKAM3X has been verified by means of the Method of Manufactured Solutions.
The parallel resistivity
is an independent parameter in TOKAM3X model, and, in SI units, it is expressed as:
where
is Coulomb logarithm,
is a constant, derived from the Braginskii theory, and all the quantities are expressed in SI units, apart from
, expressed in
. In the simulations presented here, the normalized parallel resistivity is set to
. This value can be obtained, for example, by choosing
,
and
. These values are comparable with the ones measurable in the edge plasma of a small tokamak as COMPASS [
21].
In Equations (
2)–(4), diffusive terms can be considered as representative of a collisional transport, and they roughly account for the dynamics of the scales smaller than the grid spacing. The amplitude of the diffusive terms is regulated by the parameters
and
. Their weight is kept low (
in this work), so that non-linear terms have a dominant role in determining the turbulent transport. Considering the reference values for density and temperature mentioned before, one would obtain diffusivities of ∼0.075 m
/s, a value close to the typical ones of neoclassical transport. Since in the version used in this code, TOKAM3X does not deal with the neutral dynamics, ionization sources are not calculated self-consistently. Instead, a particle source is imposed at the inner boundary of the geometrical domain, in the closed flux surfaces region, to mimic an ionization source. The behavior of the system is therefore closer to a sheath-limited regime, where the main particle source for the scrape-off layer (SOL) is given by the outflow from the edge region, than to an high-recycling regime, in which the ionization source would be mainly localized close to the divertor targets [
22]. The imposed particle source has a Gaussian shape in the radial direction, with a half-width of about
, where
a is the minor radius. The particle source is constant in time and along the poloidal and toroidal directions. Choosing the above-mentioned reference parameters, one would obtain a particle source of ∼4 × 10
s
, which is a value somewhat realistic for a discharge in small-size devices as COMPASS.
Bohm’s boundary conditions are imposed in the parallel direction at the targets. A logical condition on parallel Mach number is imposed such that
where
in the isothermal framework. We combine the Ohm’s law to the Bohm’s boundary condition on the parallel current, to obtain the condition on the electrostatic potential
where
is the electric potential drop at a floating surface, and a linearization has been performed in the limit
. The conditions
and
are also needed at the targets. Neumann conditions of null flux are imposed in the radial direction on the inner boundary of the domain, and on the open flux surfaces outer boundary. The TOKAM3X grid cells size is of the order of the main normalization length, which is the ionic Larmor radius
. The minor radius of the simulated tokamak measures 256
.
We choose to simulate a COMPASS-like diverted magnetic equilibrium. This particular shape has been chosen envisaging a future comparison with experimental results, which would be allowed by the relatively small size of the device.
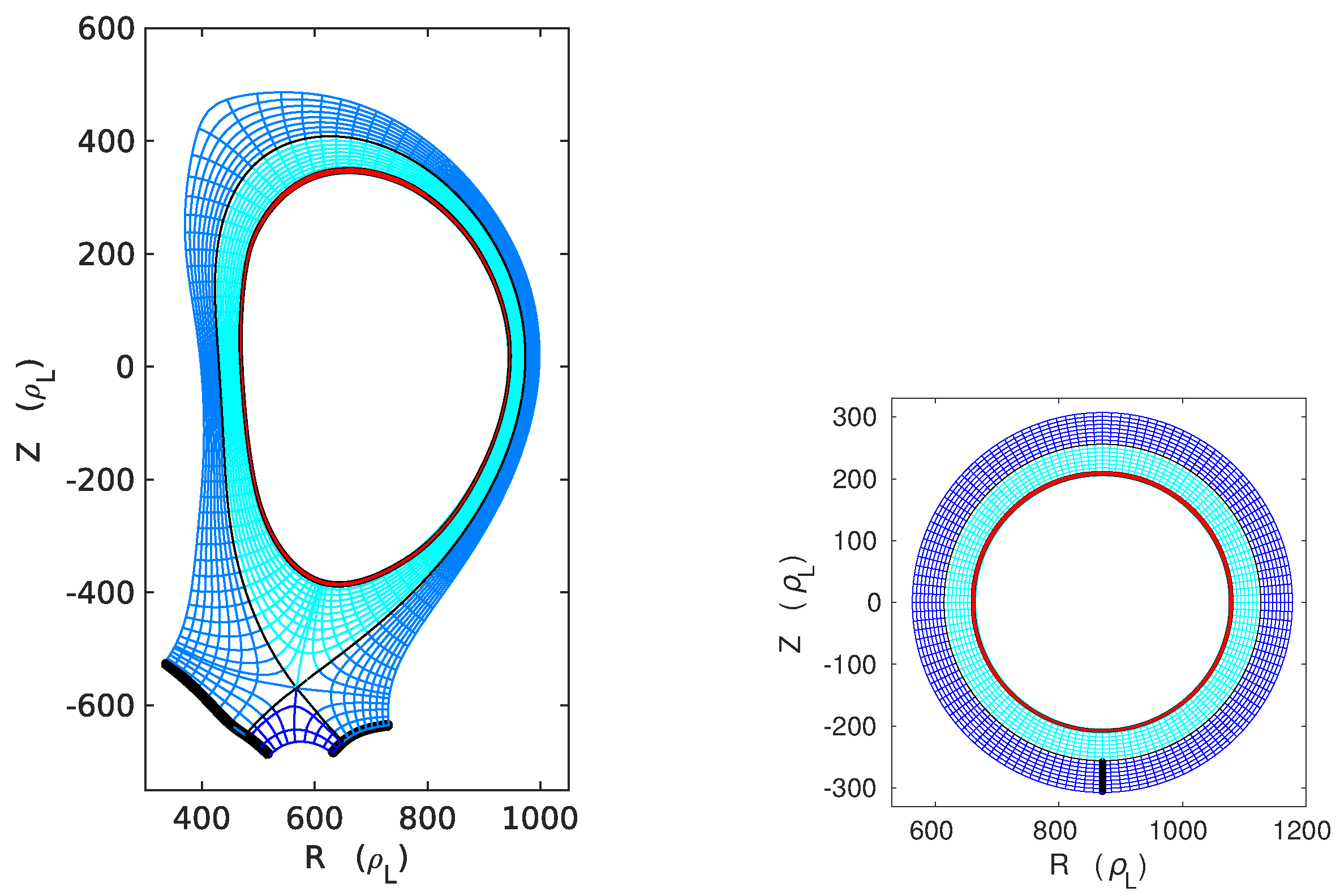
Figure 2 shows the mesh grid used for TOKAM3X divertor simulations. We will sometimes compare, throughout the work, the divertor simulations with a limiter simulation with circular geometry, run with the same physical parameters. The grid of the limiter simulations is shown on the right.
TOKAM3X is based on a flux-surface aligned coordinate system,
, where
labels flux surfaces,
is a curvilinear abscissa along the magnetic flux surface in the poloidal plane, and
is the toroidal direction. The grid resolution in the
space is
in the divertor simulation (plus
for the region below the X-point), and
in the limiter one. The geometrical domain is subdivided in several subdomains, rectangular in the
plane, connected to each other in the radial or in the poloidal direction. This division in subdomains allows the treatment of arbitrary axisymmetric magnetic topologies, including the single-null divertor configuration. In this case, by a proper choice of the domain subdivision [
16], the X-point is a corner point, common to several subdomains communicating with each other. Since the magnetic field is calculated in the center of cells, the singularity in flux-aligned coordinates is by-passed.
TOKAM3X adopts a flux-driven approach: this means that no scale separation is assumed, and the background plasma is evolved together with the small-scale fluctuations. Initially, an artificial average profile is imposed (where all the normalized fields are set to 0, apart from T which is set to 1), then we let the system evolve freely. Gradients form thanks to the imposed particle source, and the plasma becomes turbulent when a critical value of the gradient is reached. Simulations are run for times longer than the characteristic confinement time (∼10) until the quantities N, and W, integrated over the whole domain, show small temporal variation () over a sufficiently long period of time.
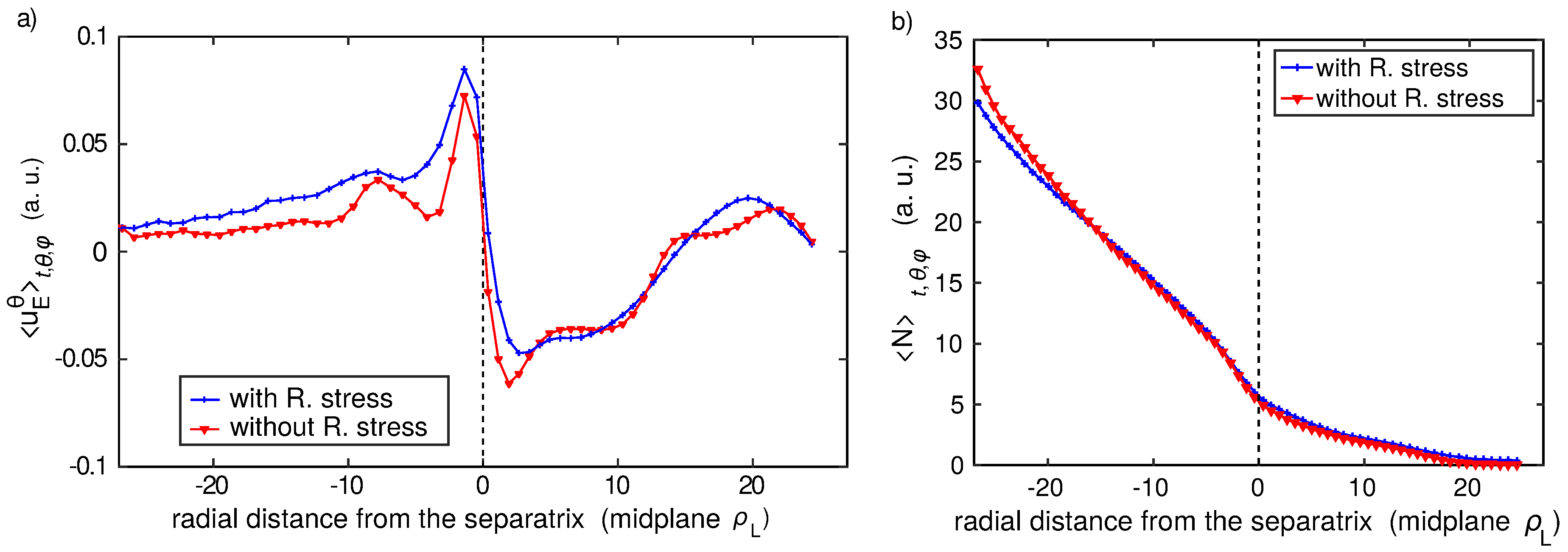
4. Discussion: The Role of Reynolds Stress in Generating Poloidal Fluxes
The radial profile of the
poloidal velocity, and thus of the electrostatic potential, is determined by the vorticity balance (4). This balance equation contains the information about the conservation of the poloidal momentum. As described in [
4], turbulence can drive ZF, by means of the Reynolds stress. This mechanism can be described, in the simplest way and in a simplified Cartesian geometry, by the equation:
where the coordinate
x identifies the radial direction,
y the poloidal one, and
is the so-called Reynolds stress.
In TOKAM3X model, the radial derivative of the Reynolds stress is contained in the
advection term in vorticity equation. The other terms, however, contribute as well to determine the equilibrium profile of the
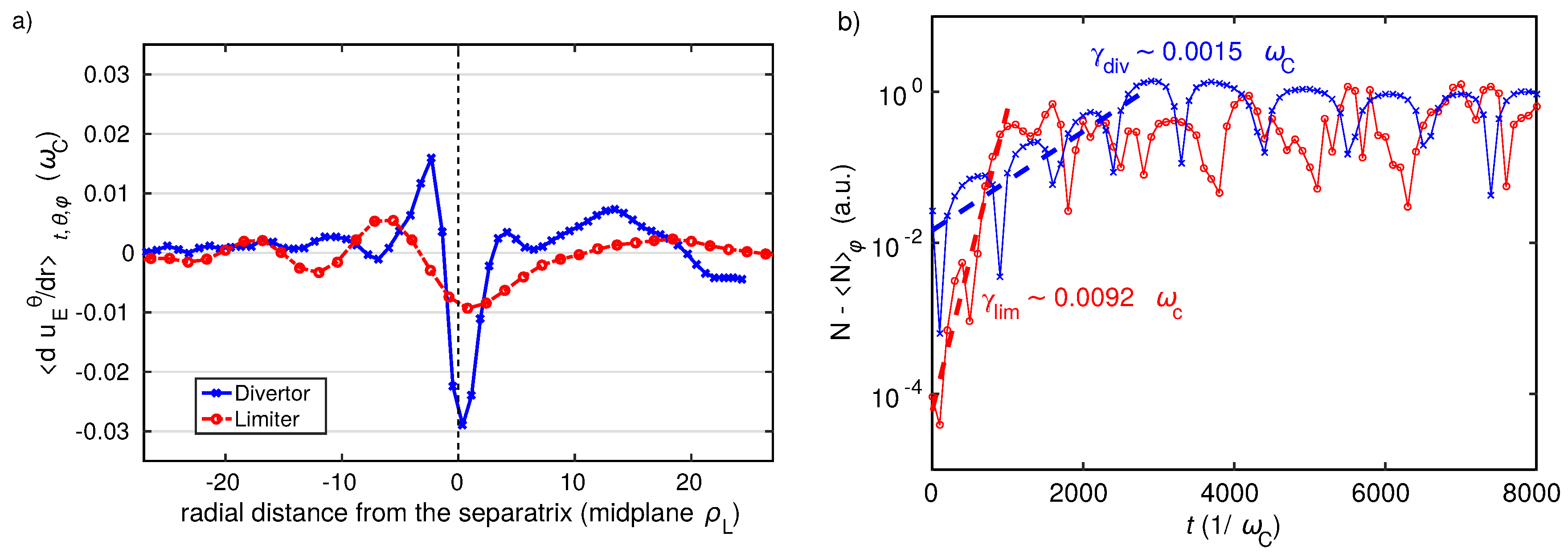
velocity. To investigate the impact of the Reynolds stress mechanism on the formation of the transport barrier, we run a divertor simulation with the same physical and geometrical parameters as the previously described one, and we artificially suppress the Reynolds stress term in the vorticity equation. The resulting profile of
poloidal velocity is represented in
Figure 9a.
One can notice in
Figure 9a that the poloidal
velocity is slightly reduced in magnitude, in the case without Reynolds stress driving, and its radial derivative is weakly impacted. The amplitude of the transport barrier and the global equilibrium, are not affected, as shown in
Figure 9b, by the absence of the
advection term in the vorticity equation. This analysis suggests that the radial profile of the average
poloidal velocity is mainly dominated by the linear terms in Equation (4): in particular, the average electric field tends to equilibrate the radial pressure gradient.
We have thus excluded the turbulence-driven ZF from the causes of the transport barrier build-up in our simulations. In order to identify, between the
and the magnetic shear, the mechanism leading to the formation of the observed transport barrier, further simulations have been setup, in which an artificial magnetic shear is introduced in a simplified circular geometry: this is the subject of the work [
35]. The results show, more clearly than in divertor simulations, that in isothermal cases, the
shear plays a minor role in damping turbulent fluctuations, with respect to the magnetic shear, essentially confirming the central role of the magnetic shear in creating the transport barrier observed in this work.
5. Conclusions
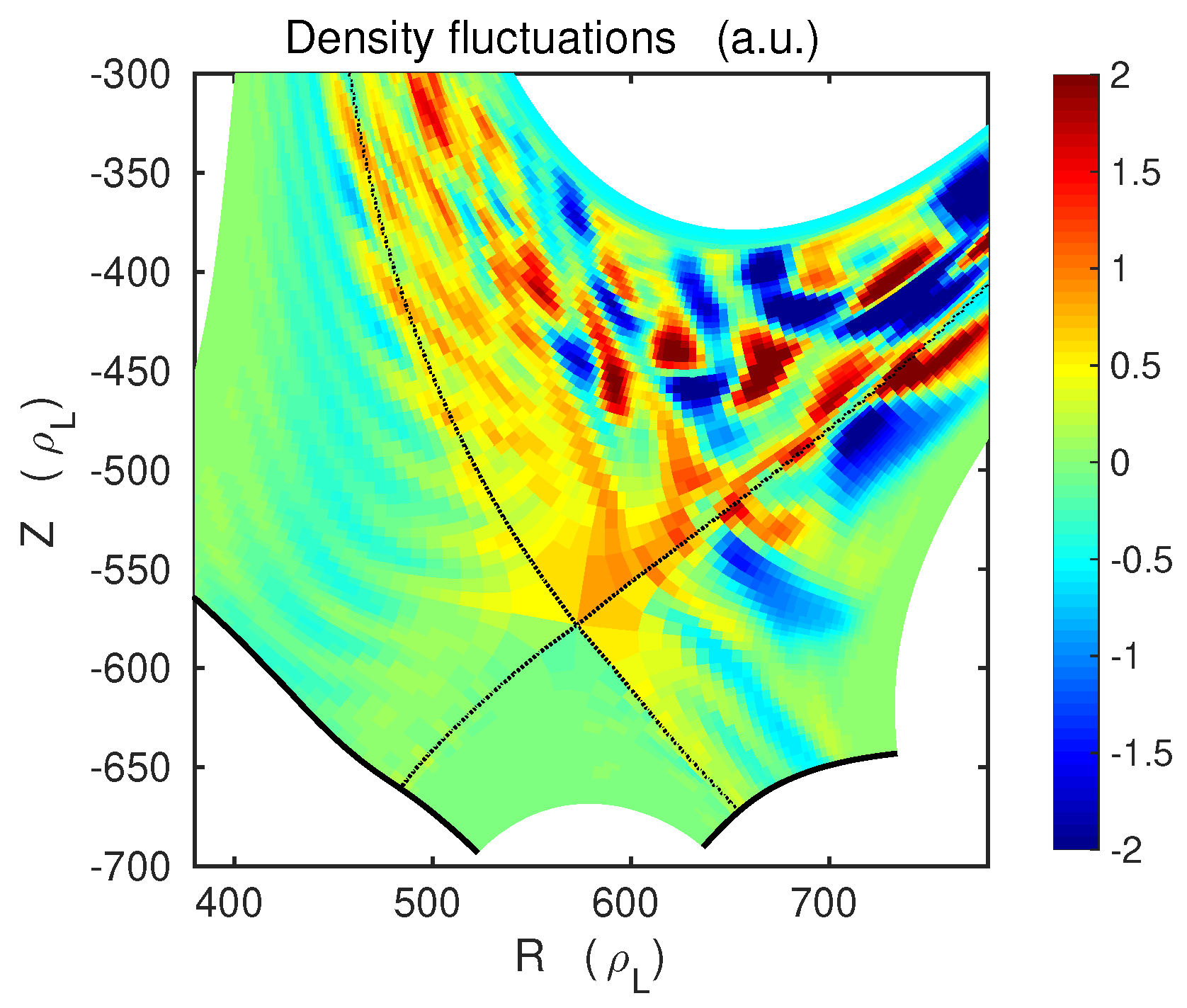
TOKAM3X global simulations of electrostatic turbulence in tokamak edge plasma have been run in realistic divertor geometry. As previously found theoretically and experimentally, filaments get strongly elongated and poloidally thin in the X-point region, because of the large flux expansion.
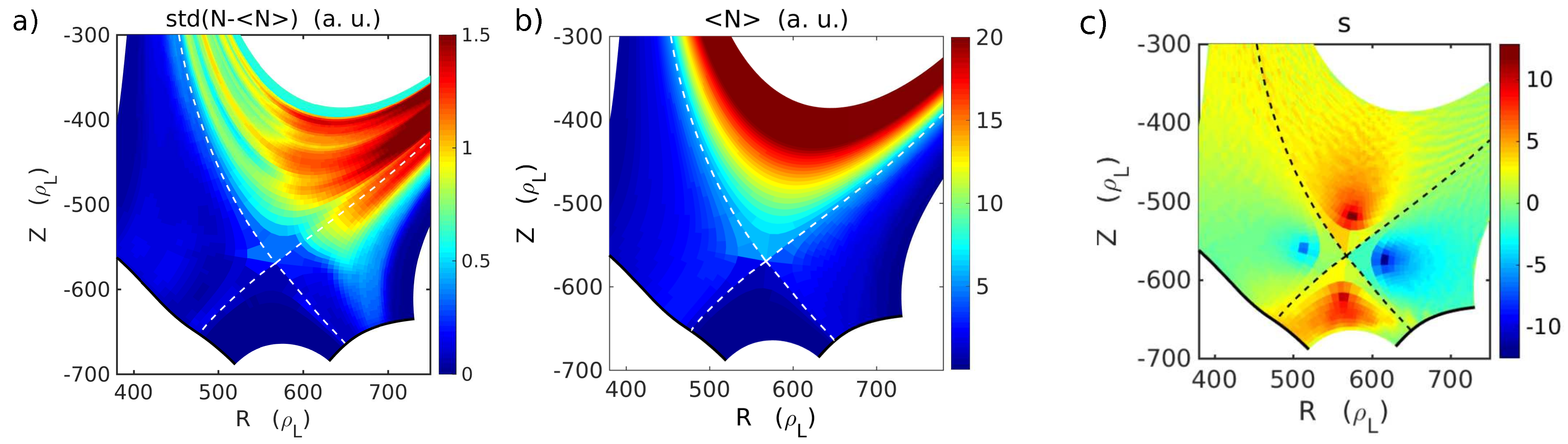
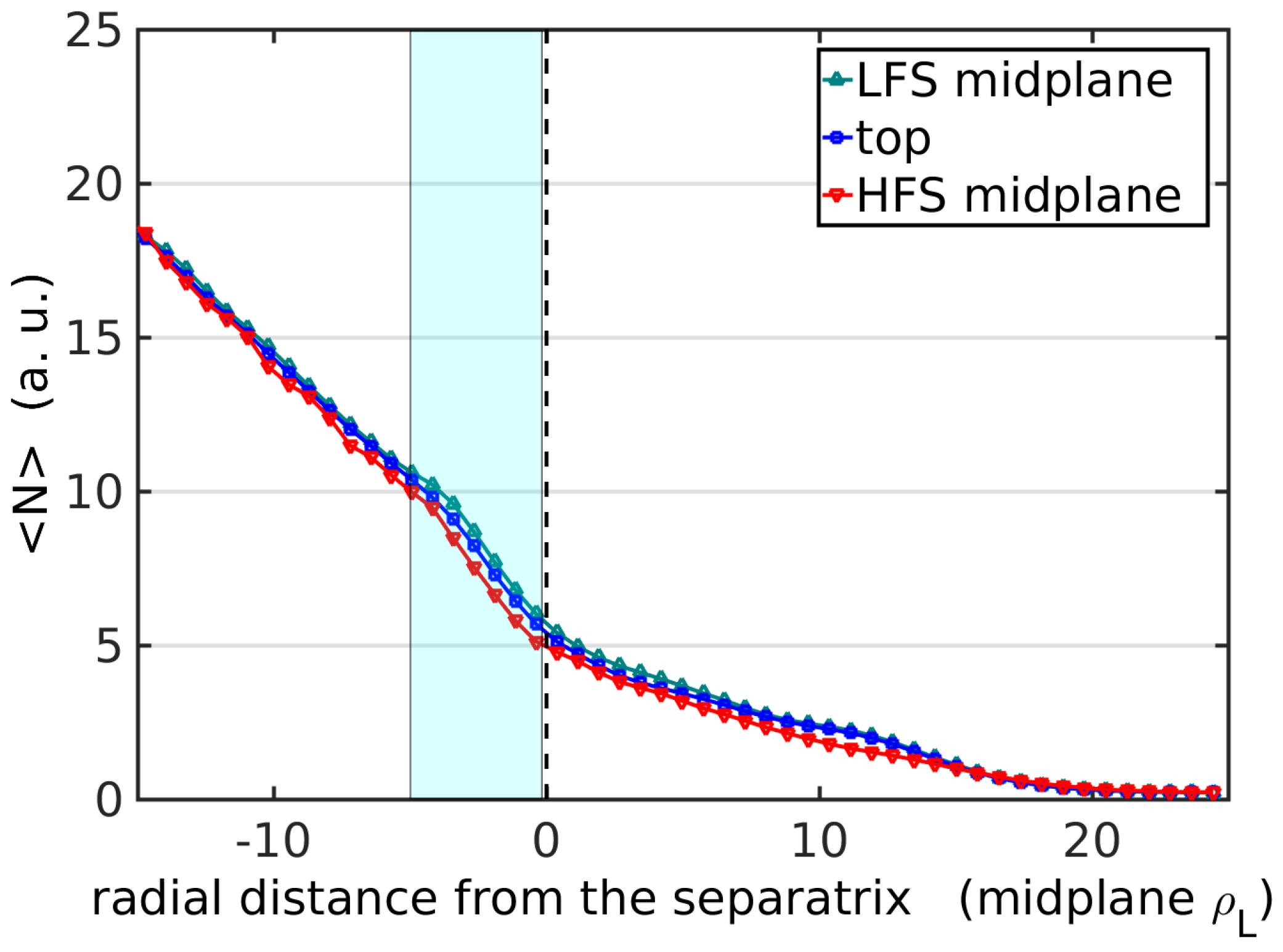
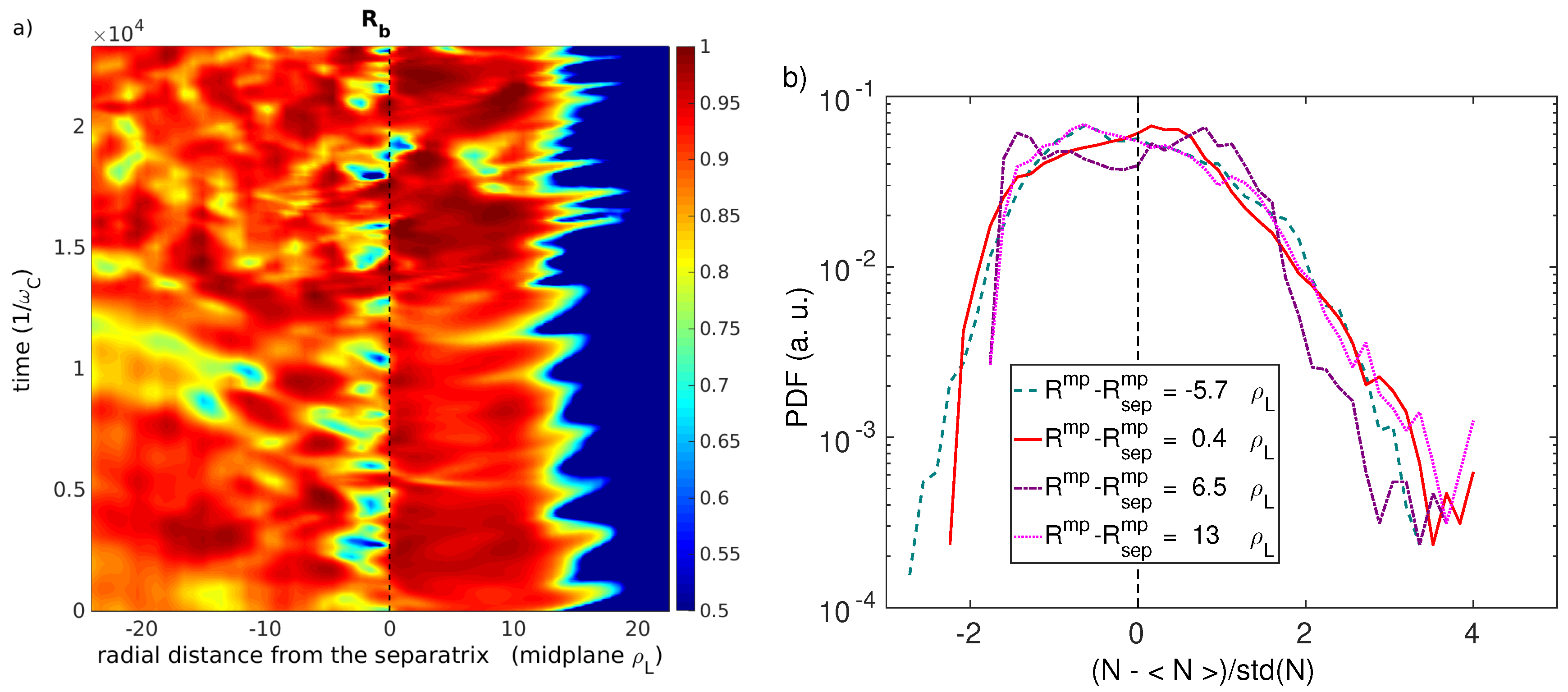
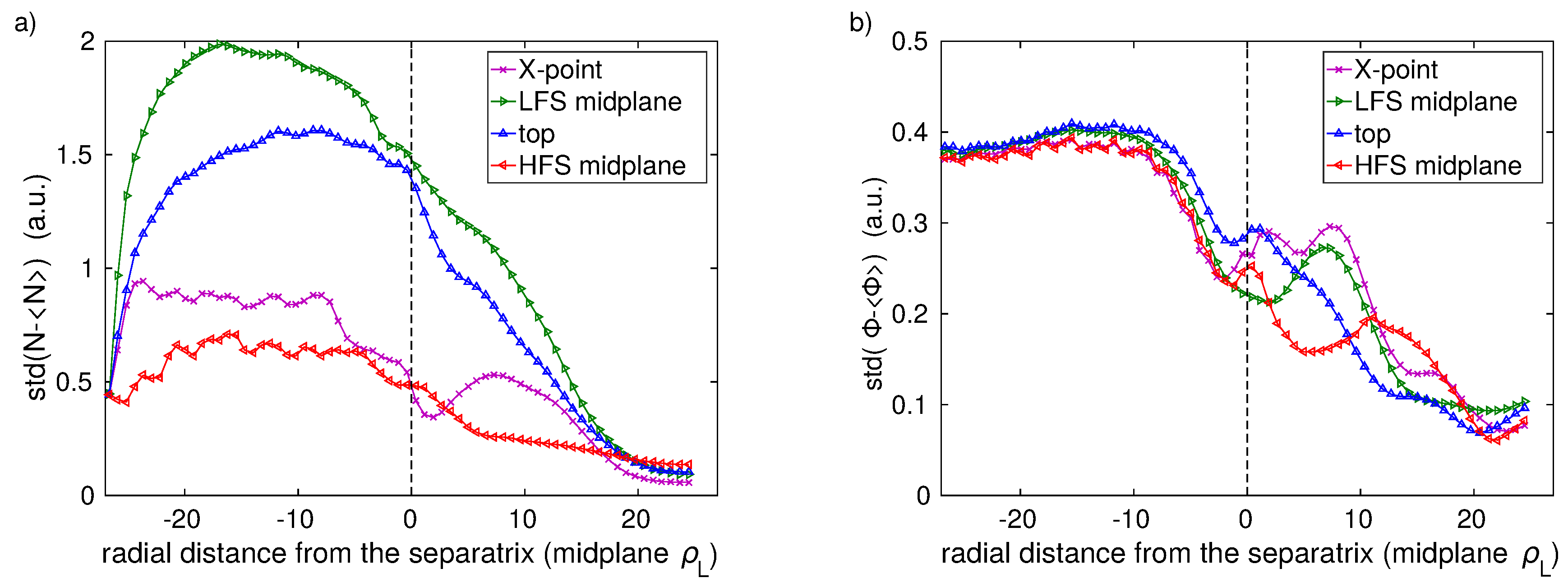
A quiescent region, where the fluctuation level is drastically reduced, similar to the one observed in recent experiments, is found in the divertor SOL, close to the separatrix. The magnetic shear introduced by the X-point is pointed out as the possible cause for this damping. Indeed, the low poloidal field leads to large
values around the X-point, so that dissipation processes tend to damp turbulent structures. More non-linear simulations, spanning different values of the magnetic shear, are needed to clarify this point. In the interpretation of the results here presented, one must consider the effects of the finite size of the grid cells. Near the X-point, in fact, turbulent structures can reach, in the poloidal direction, sizes comparable to the grid cell. This process is likely to introduce a cut-off in the possible range of scales describable by the code. Also, a strong numerical diffusion could intervene, smoothing the sharp gradients from one cell to the adjacent. The weight of the numerical diffusion in TOKAM3X simulations with divertor configuration, is currently being evaluated by means of the PoPe method [
41], and the first results seem to show that numerical diffusion is of the same order of magnitude as the imposed physical one. Nevertheless, even if the nature of the dissipation of turbulent fluctuations around the X-point is still uncertain, this characteristic reproduces qualitatively well the experimental observations.
It is important to notice that in TOKAM3X divertor simulations, this local mechanism probably leads to a non-local effect, namely the reduction of the fluctuation amplitude over the last closed flux surfaces. Simulations have shown indeed the spontaneous formation of a transport barrier, namely not forced by any physical parameter, which increases the pressure gradient in the outermost zone of the confined plasma. This gradient steepening is associated with a reduction in fluctuation amplitude, which could be due to the magnetic shear at the X-point, or to the
shear along the flux surface. The
shear indeed appears to be strong near the separatrix, and comparable with the linear growth rate of the instability. The simulations carried out in absence of Reynolds stress seem to indicate that at least for the considered plasma parameters, the poloidal flows driven by turbulence have a little effect on the total poloidal velocity, and thus also on the formation of the transport barrier. Nevertheless, the fact that turbulence is mainly damped near the X-point region, and the slight misalignment of the location of the maximum
shear with respect to the location of the transport barrier, seem to indicate the magnetic shear as the main cause of the transport barrier in the simulations. A further confirmation of this view has been recently given by the simulations carried out in [
35], where an artificial magnetic shear is introduced in a simplified circular geometry.
Even if the observed transport barrier is mild, and does not lead to a bifurcation in the dynamical behavior of the system as in the L-H transition, it has characteristics in common with the experimentally observed edge transport barriers, as the localization near the separatrix and its narrow radial extension. The behavior of the dynamical system could potentially change significantly with the inclusion of the energy transport [
17], and of self-consistent plasma-neutrals interactions [
42]. Although the nature of the instability is not expected to change, in anisothermal simulations with divertor geometry we might observe higher potential background gradients in open and closed field lines, leading to higher
shear values near the separatrix. This could potentially lead to stronger transport barriers, and consequently to steeper characteristics gradients, in a bifurcative dynamics. The capability of TOKAM3X, as well as of other codes of the same kind (e.g., [
43,
44]) to perform simulations with such complex models and realistic divertor geometries, will hopefully shed more light on the L-H transition dynamics. Nevertheless, the geometric effects of the X-point on turbulence here described might be an important element in the formation of the edge transport barriers, which seems to be linked both to plasma and magnetic field characteristics. The simulations here described will help, in the interpretation of more complete, and complex, simulations, and they are part of the necessary step-by-step process for the understanding of the edge transport barriers formation. Moreover, investigating the interaction between turbulent fluctuations and the magnetic X-point also contributes to the understanding of particles and heat flux deposition on targets. Indeed, the radial extent of the SOL region carrying most of the heat flux is comparable with the one of the observed quiescent regions. This aspect will be further studied in anisothermal simulations with divertor configuration.