On the Fractional Diffusion-Advection Equation for Fluids and Plasmas
Abstract
:1. Introduction
2. The Fractional Diffusion–Advection Equation
3. Steady-State Solutions of Fractional Diffusion–Advection Equations
3.1. Solutions with the Left Contribution Only
3.2. Solutions with the Right Contribution Only
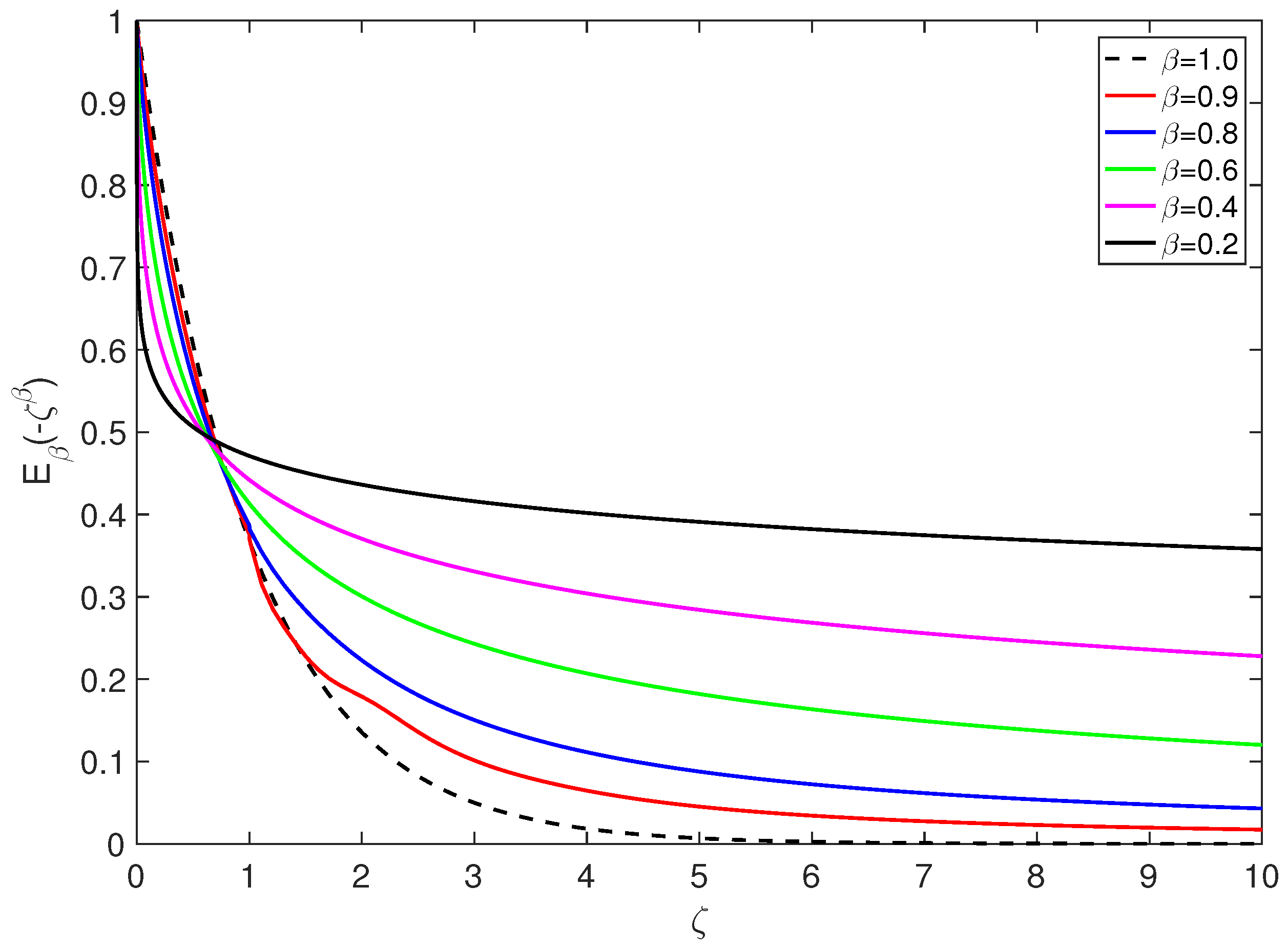
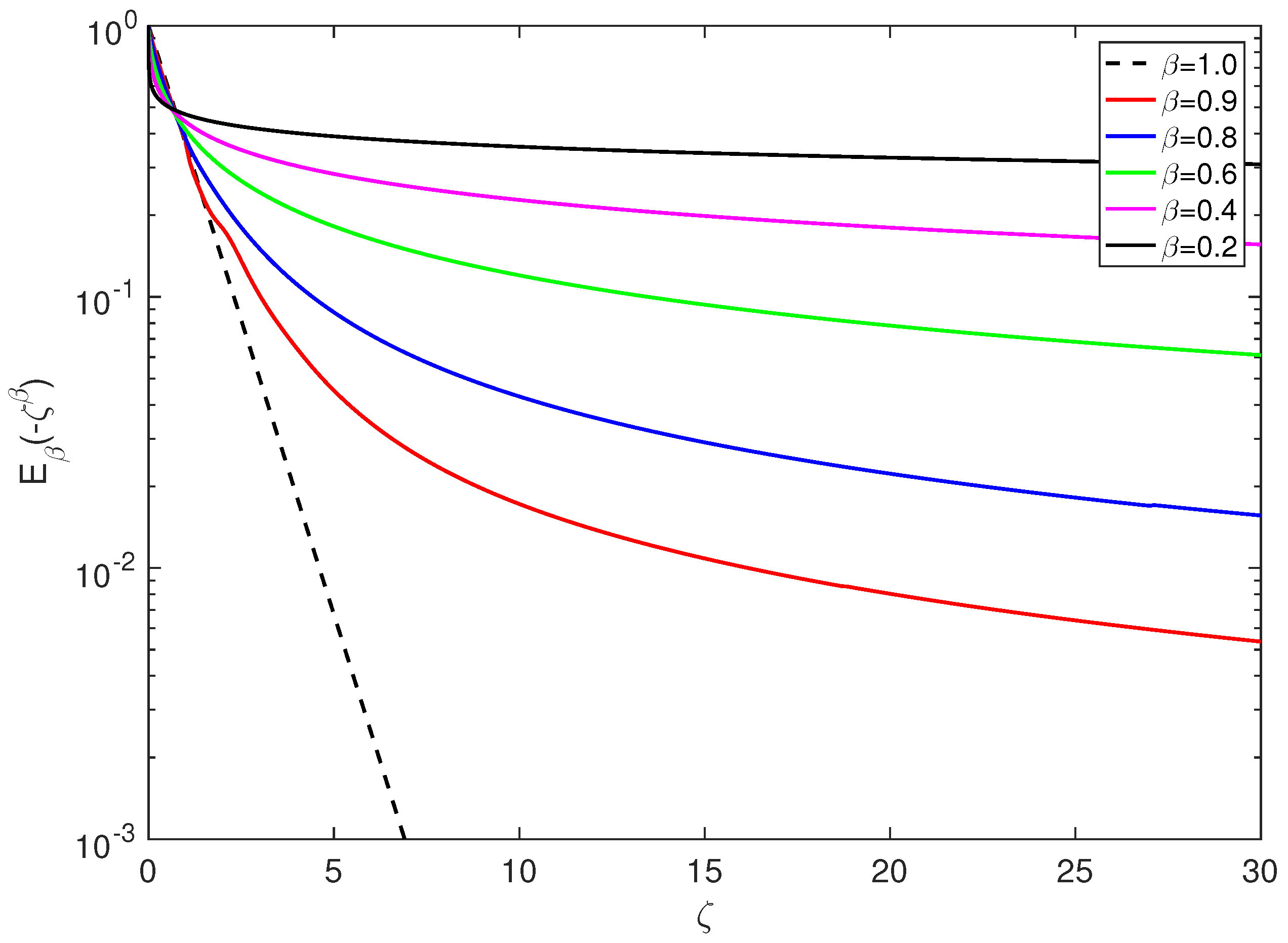
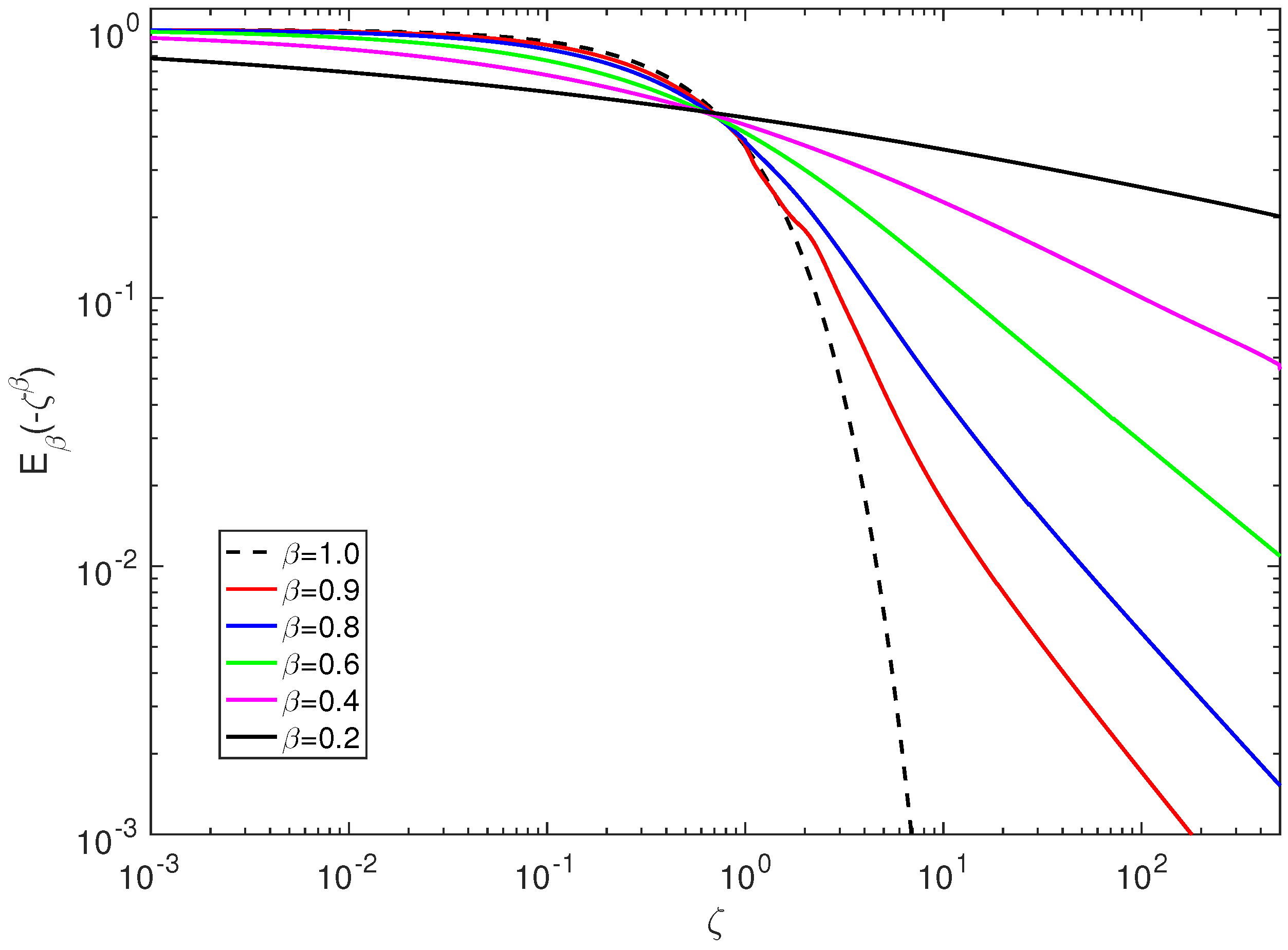
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Perrone, D.; Dendy, R.O.; Furno, I.; Sanchez, R.; Zimbardo, G.; Bovet, A.; Fasoli, A.; Gustafson, K.; Perri, S.; Ricci, P.; et al. Nonclassical transport and particle-field coupling: From laboratory plasmas to the solar wind. Space Sci. Rev. 2013, 178, 233–270. [Google Scholar] [CrossRef]
- Yamanaka, K.; Narumi, T.; Hashiguchi, M.; Okabe, H.; Hara, K.; Hidaka, Y. Time-Dependent Diffusion Coefficients for Chaotic Advection due to Fluctuations of Convective Rolls. Fluids 2018, 3, 99. [Google Scholar] [CrossRef]
- Zimbardo, G.; Amato, E.; Bovet, A.; Effenberger, F.; Fasoli, A.; Fichtner, H.; Furno, I.; Gustafson, K.; Ricci, P.; Perri, S. Superdiffusive transport in laboratory and astrophysical plasmas. J. Plasma Phys. 2015, 81, 495810601. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The restaurant at the end of the random walk: Recent developments in the description of anomalous transport by fractional dynamics. J. Phys. A Math. Gen. 2004, 37, R161. [Google Scholar] [CrossRef]
- Zaburdaev, V.; Denisov, S.; Klafter, J. Lévy walks. Rev. Mod. Phys. 2015, 87, 483–530. [Google Scholar] [CrossRef]
- Bovet, A.; Fasoli, A.; Ricci, P.; Furno, I.; Gustafson, K. Nondiffusive transport regimes for suprathermal ions in turbulent plasmas. Phys. Rev. E 2015, 91, 041101(R). [Google Scholar] [CrossRef] [PubMed]
- Carreras, B.A.; Lynch, V.E.; Zaslavsky, G.M. Anomalous diffusion and exit time distribution of particle tracers in plasma turbulence model. Phys. Plasmas 2001, 8, 5096–5103. [Google Scholar] [CrossRef]
- del-Castillo-Negrete, D.; Carreras, B.A.; Lynch, V.E. Fractional diffusion in plasma turbulence. Phys. Plasmas 2004, 11, 3854–3864. [Google Scholar] [CrossRef]
- Furno, I.; Bovet, A.; Fasoli, A.; Gauthey, C.; Gustafson, K.; Ricci, P.; van Milligen, B.P. Non-diffusive transport of suprathermal ions by intermittent turbulent structures. Plasma Phys. Control. Fusion 2016, 58, 014023. [Google Scholar] [CrossRef]
- Mier, J.A.; Sanchez, R.; Garcıa, L.; Carreras, B.A.; Newman, D.E. Characterization of Nondiffusive Transport in Plasma Turbulence via a Novel Lagrangian Method. Phys. Rev. Lett. 2008, 101, 165001. [Google Scholar] [CrossRef] [PubMed]
- Perri, S.; Zimbardo, G. Evidence of superdiffusive transport of electrons accelerated at interplanetary shocks. Astrophys. J. Lett. 2007, 671, 177. [Google Scholar] [CrossRef]
- Perri, S.; Zimbardo, G. Superdiffusive transport of electrons accelerated at corotating interaction regions. J. Geophys. Res. 2008, 113, A03107. [Google Scholar] [CrossRef]
- Klafter, J.; Sokolov, I.M. Anomalous diffusion spreads its wings. Phys. World 2005, 18, 29. [Google Scholar] [CrossRef]
- Isliker, H.; Vlahos, L.; Constantinescu, D. Fractional Transport in Strongly Turbulent Plasmas. Phys. Rev. Lett. 2017, 119, 045101. [Google Scholar] [CrossRef]
- Isliker, H.; Pisokas, T.; Vlahos, L.; Anastasiadis, A. Particle Acceleration and Fractional Transport in Turbulent Reconnection. Astrophys. J. 2017, 849, 35. [Google Scholar] [CrossRef]
- Klafter, J.; Blumen, A.; Shlesinger, M.F. Stochastic pathway to anomalous diffusion. Phys. Rev. A 1987, 35, 3081–3085. [Google Scholar] [CrossRef]
- Lazarian, A.; Yan, H. Superdiffusion of cosmic rays: Implications for cosmic ray acceleration. Astrophys. J. 2014, 784, 38. [Google Scholar] [CrossRef]
- Shlesinger, M.F.; West, B.J.; Klafter, J. Lévy dynamics of enhanced diffusion: Application to turbulence. Phys. Rev. Lett. 1987, 58, 1100. [Google Scholar] [CrossRef]
- Zimbardo, G. Anomalous particle diffusion and Lévy random walk of magnetic field lines in three-dimensional solar wind turbulence. Plasma Phys. Control. Fusion 2005, 47, B755–B767. [Google Scholar] [CrossRef]
- Perri, S.; Zimbardo, G. Magnetic variances and pitch-angle scattering times upstream of interplanetary shocks. Astrophys. J. 2012, 754, 8. [Google Scholar] [CrossRef]
- Perri, S.; Pucci, F.; Malara, F.; Zimbardo, G. On the power-law distribution of pitch angle scattering times in solar wind turbulence. Sol. Phys. 2019, 294, 34. [Google Scholar] [CrossRef]
- Pucci, F.; Malara, F.; Perri, S.; Zimbardo, G.; Sorriso-Valvo, L.; Valentini, F. Energetic particle transport in the presence of magnetic turbulence: Influence of spectral extension and intermittency. MNRAS 2016, 459, 3395–3406. [Google Scholar] [CrossRef]
- Gustafson, K.; Ricci, P.; Furno, I.; Fasoli, A. Nondiffusive Suprathermal Ion Transport in Simple Magnetized Toroidal Plasmas. Phys. Rev. Lett. 2012, 108, 035006. [Google Scholar] [CrossRef] [PubMed]
- Walkden, N.R.; Wynn, A.; Militello, F.; Lipschultz, B.; Matthews, G.; Guillemaut, C.; Harrison, J.; Moulton, D.; Contributors, J.E. Interpretation of scrape-off layer profile evolution and first-wall ion flux statistics on JET using a stochastic framework based on fillamentary motion. Plasma Phys. Control. Fusion 2017, 59, 085009. [Google Scholar] [CrossRef]
- Callen, J.D.; Kissick, M.W. Evidence and concepts for non-local transport. Plasma Phys. Control. Fusion 1997, 39, B173. [Google Scholar] [CrossRef]
- Lin, R.P. Non-relativistic solar electrons. Space Sci. Rev. 1974, 16, 189–256. [Google Scholar] [CrossRef]
- Reames, D.V. Particle acceleration at the Sun and in the heliosphere. Space Sci. Rev. 1999, 90, 413–491. [Google Scholar] [CrossRef]
- Giacalone, J. Cosmic-Ray Transport and Interaction with Shocks. Space Sci. Rev. 2013, 176, 73–88. [Google Scholar] [CrossRef]
- Ida, K.; Shi, Z.; Sun, H.J.; Inagaki, S.; Kamiya, K.; Rice, J.E.; Tamura, N.; Diamond, P.H.; Dif-Pradalier, G.; Zou, X.L.; et al. Towards an emerging understanding of non-locality phenomena and non-local transport. Nucl. Fusion 2015, 55, 013022. [Google Scholar] [CrossRef]
- Sanchez, R.; Newman, D.E. Self-organized criticality and the dynamics of near-marginal turbulent transport in magnetically confined fusion plasmas. Plasma Phys. Control. Fusion 2015, 57, 123002. [Google Scholar] [CrossRef]
- Beresnyak, A. Asymmetric Diffusion of Magnetic Field Lines. Astrophys. J. Lett. 2013, 767, L39. [Google Scholar] [CrossRef]
- Perri, S.; Zimbardo, G.; Effenberger, F.; Fichtner, H. Parameter estimation of superdiffusive motion of energetic particles upstream of heliospheric shocks. Astron. Astrophys. 2015, 578, A2. [Google Scholar] [CrossRef]
- Zimbardo, G.; Perri, S. From Lévy walks to superdiffusive shock acceleration. Astrophys. J. 2013, 778, 35. [Google Scholar] [CrossRef]
- Sokolov, I.M.; Klafter, J.; Blumen, A. Fractional Kinetics. Phys. Today 2002, 55, 48. [Google Scholar] [CrossRef]
- Zaslavsky, G.M. Chaos, fractional kinetics, and anomalous transport. Phys. Rep. 2002, 371, 461. [Google Scholar] [CrossRef]
- Calvo, I.; Sanchez, R.; Carreras, B.A.; van Milligen, B.P. Fractional Generalization of Fick’s Law: A Microscopic Approach. Phys. Rev. Lett. 2007, 99, 230603. [Google Scholar] [CrossRef]
- del-Castillo-Negrete, D.; Carreras, B.A.; Lynch, V.E. Nondiffusive Transport in Plasma Turbulence: A Fractional Diffusion Approach. Phys. Rev. Lett. 2005, 94, 065003. [Google Scholar] [CrossRef]
- Litvinenko, Y.; Effenberger, F. Analytical Solutions of a Fractional Diffusion-advection Equation for Solar Cosmic-Ray Transport. Astrophys. J. 2014, 796, 125. [Google Scholar] [CrossRef]
- de Oliveira, E.C.; Machado, J.A.T. A Review of Definitions for Fractional Derivatives and Integral. Math. Probl. Eng. 2014, 2014, 238459. [Google Scholar] [CrossRef]
- Ricci, P.; Halpern, F.D.; Jolliet, S.; Loizu, J.; Mosetto, A.; Fasoli, A.; Furno, I.; Theiler, C. Simulation of plasma turbulence in scrape-off layer conditions: The GBS code, simulation results and code validation. Plasma Phys. Control. Fusion 2012, 54, 124047. [Google Scholar] [CrossRef]
- del-Castillo-Negrete, D. Fractional diffusion models of nonlocal transport. Phys. Plasmas 2006, 13, 082308. [Google Scholar] [CrossRef]
- Zimbardo, G.; Perri, S.; Effenberger, F.; Fichtner, H. Fractional Parker equation for the transport of cosmic rays: Steady-state solutions. Astron. Astrophys. 2017, 607, A7. [Google Scholar] [CrossRef]
- Gosling, J.T.; Thomsen, M.F.; Bame, S.J.; Feldman, W.C.; Paschmann, G.; Sckopke, N. Evidence for specularly reflected ions upstream from the quasi-parallel bow shock. Geophys. Res. Lett. 1982, 9, 1333. [Google Scholar] [CrossRef]
- Perri, S.; Zimbardo, G. Ion superdiffusion at the solar wind termination shock. Astrophys. J. Lett. 2009, 693, 118. [Google Scholar] [CrossRef]
- Toyokuni, S.; Ikehara, Y.; Kikkawa, F.; Hori, M. (Eds.) Plasma Medical Science; Academic Press: Cambridge, MA, USA, 2018; ISBN 9780128150047. [Google Scholar]
- Perri, S.; Zimbardo, G. Short Acceleration Times from Superdiffusive Shock Acceleration in the Heliosphere. Astrophys. J. 2015, 815, 75. [Google Scholar] [CrossRef]
- Chaves, A.S. A fractional diffusion equation to describe Lévy flights. Phys. Lett. A 1998, 239, 13–16. [Google Scholar] [CrossRef]
- Paradisi, P.; Cesari, R.; Mainardi, F.; Tampieri, F. The fractional Fick’s law for non-local transport processes. Phys. A Stat. Mech. Appl. 2001, 293, 130–142. [Google Scholar] [CrossRef]
- Mainardi, F. On some properties of the Mittag-Leffler function Eα (-tα), completely monotone for t > 0 with 0 < α < 1. Discret. Contin. Dyn. Syst. Ser. B 2014, 19, 2267–2278. [Google Scholar] [CrossRef]
- Prete, G.; Perri, S.; Zimbardo, G. Influence of the transport regime on the energetic particle density profiles upstream and downstream of interplanetary shocks. Adv. Space Res. 2019, 63, 2659–2671. [Google Scholar] [CrossRef]
- Gorenflo, R.; De Fabritiis, G.; Mainardi, F. Discrete random walk models for symmetric Lévy-Feller diffusion processes. Phys. A 1999, 269, 79. [Google Scholar] [CrossRef]
- Gorenflo, R.; Mainardi, F. Fractals and Fractional Calculus in Continuum Mechanics; Carpinteri, A., Mainardi, F., Eds.; Springer Verlag: Wien, Austria, 1997; pp. 223–276. [Google Scholar]
- Mittag-Leffler, M.G. Sur la nouvelle fonction Eα(x). C. R. Acad. Sci. Paris 1903, 137, 554–558. [Google Scholar]
- Zimbardo, G.; Perri, S.; Pommois, P.; Veltri, P. Anomalous particle transport in the heliosphere. Adv. Space Res. 2012, 49, 1633–1642. [Google Scholar] [CrossRef]
- Perri, S. Superdiffusion of relativistic electrons at supernova remnant shocks. Plasma Phys. Control. Fusion 2018, 60, 014005. [Google Scholar] [CrossRef]
- Perri, S.; Amato, E.; Zimbardo, G. Transport of relativistic electrons at shocks in shell-type supernova remnants: Diffusive and superdiffusive regimes. Astron. Astrophys. 2016, 596, A34. [Google Scholar] [CrossRef]
- Allen, R.C.; Livi, S.A.; Goldstein, J. Variations of oxygen charge state abundances in the global magnetosphere, as observed by Polar. J. Geophys. Res. Space Phys. 2016, 121, 1091–1113. [Google Scholar] [CrossRef]
- Angelopoulos, V.; Runov, A.; Zhou, X.Z.; Turner, D.L.; Kiehas, S.A.; Li, S.S.; Shinohara, I. Electromagnetic energy conversion at reconnection fronts. Science 2013, 341, 1478–1482. [Google Scholar] [CrossRef]
- Panov, E.V.; Nakamura, R.; Baumjohann, W.; Angelopoulos, V.; Petrukovich, A.A.; Retinò, A.; Volwerk, M.; Takada, T.; Glassmeier, K.H.; McFadden, J.P.; et al. Multiple overshoot and rebound of a bursty bulk flow. Geophys. Res. Lett. 2010, 37, L08103. [Google Scholar] [CrossRef]
- Zimbardo, G.; Greco, A.; Sorriso-Valvo, L.; Perri, S.; Vörös, Z.; Aburjania, G.; Chargazia, K.; Alexandrova, O. Magnetic turbulence in the geospace environment. Space Sci. Rev. 2010. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zimbardo, G.; Perri, S. On the Fractional Diffusion-Advection Equation for Fluids and Plasmas. Fluids 2019, 4, 62. https://doi.org/10.3390/fluids4020062
Zimbardo G, Perri S. On the Fractional Diffusion-Advection Equation for Fluids and Plasmas. Fluids. 2019; 4(2):62. https://doi.org/10.3390/fluids4020062
Chicago/Turabian StyleZimbardo, Gaetano, and Silvia Perri. 2019. "On the Fractional Diffusion-Advection Equation for Fluids and Plasmas" Fluids 4, no. 2: 62. https://doi.org/10.3390/fluids4020062
APA StyleZimbardo, G., & Perri, S. (2019). On the Fractional Diffusion-Advection Equation for Fluids and Plasmas. Fluids, 4(2), 62. https://doi.org/10.3390/fluids4020062





