Using a Dynamic and Constant Mesh in Numerical Simulation of the Free-Rising Bubble
Abstract
:1. Introduction
2. Numerical Model
2.1. Governing Equations
- continuity
- momentum transportwhere α is the liquid volume fraction, ui is the velocity vector, p is the pressure, σij is the stress tensor due to the molecular viscosity, gi is the gravity acceleration vector, σ is the surface tension coefficient and κ is the gas–liquid interface curvature. Equation (1) and Equation (2) are connected through material properties. The mixture density ρ and mixture dynamic viscosity μ are determined by the following equations:where ρl and ρg are the liquid and gas density, whereas μl and μg are liquid and gas dynamic viscosity. The system of Equations (1)–(4) was solved within the OpenFOAM [19,20] toolkit, which has proven to be an effective tool for solving such problems [21].
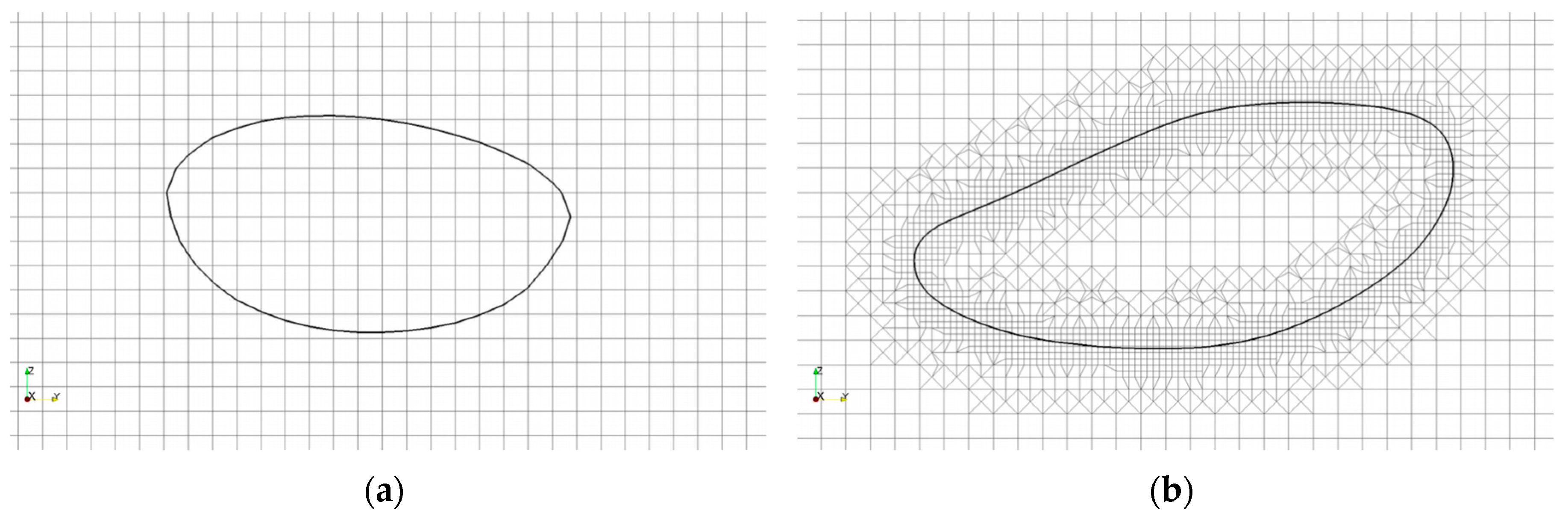
2.2. Discrete Model
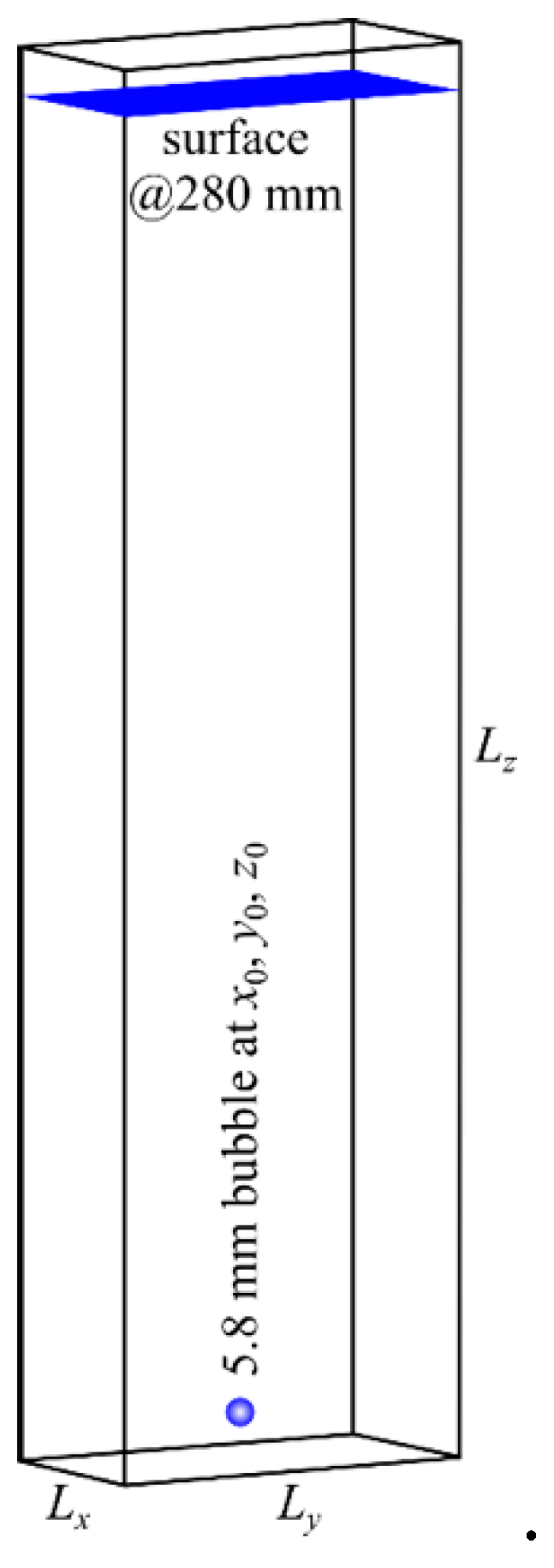
3. Numerical Simulation
- Euler explicit for the time derivative,
- Gauss linear for the gradient operator,
- Gauss upwind for the divergence operator
- Gauss linear corrected for the Laplacian operator.
- The division of computational cells increases the number of equations considerably.
- The Δt decreases due to the small cells and consequently increases the number of time steps.
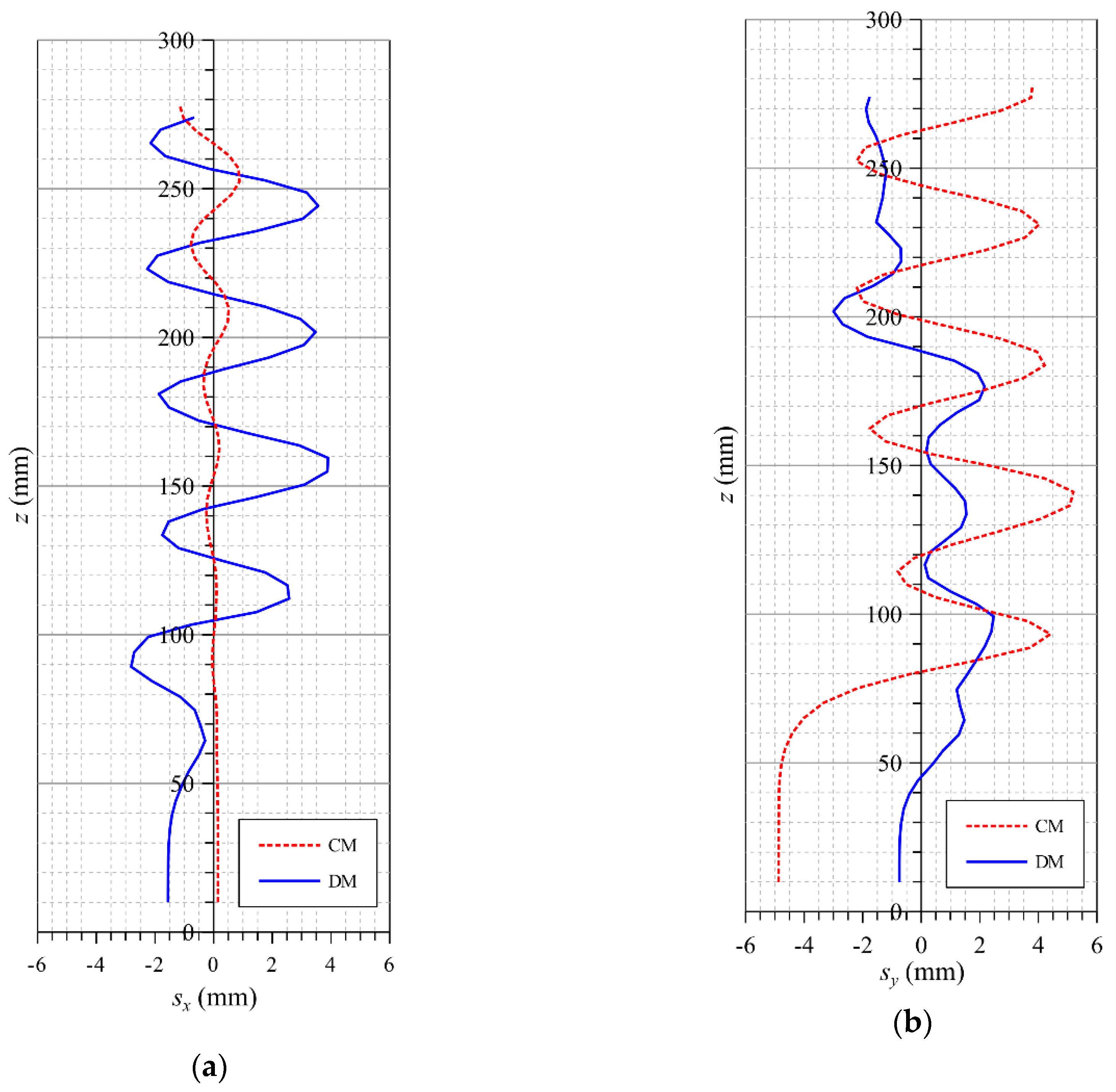
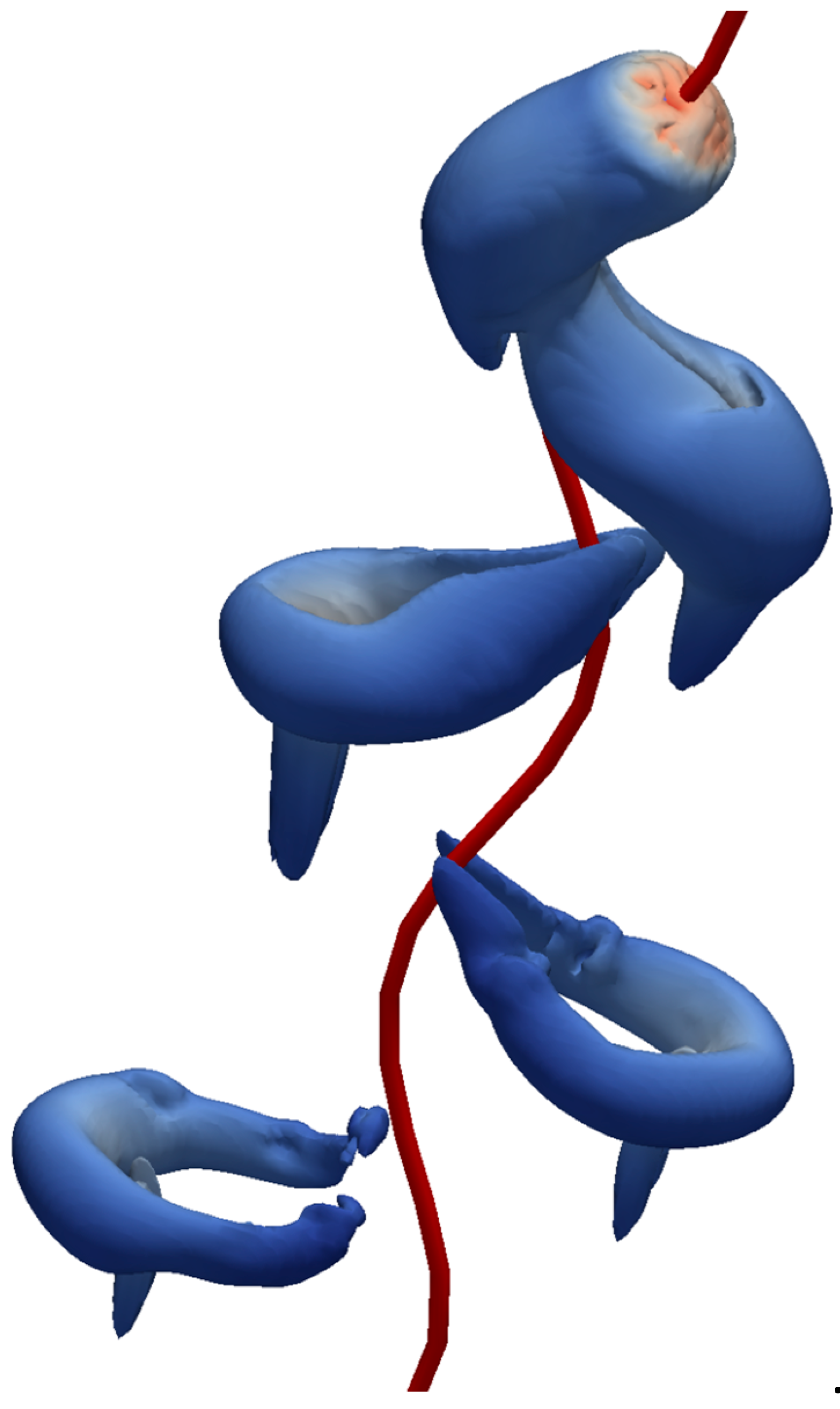
4. Results and Discussion
5. Conclusions
Funding
Conflicts of Interest
References
- Bombač, A.; Žun, I. Individual impeller flooding in aerated vessel stirred by multiple-Rushton impellers. Chem. Eng. J. 2006, 116, 85–95. [Google Scholar] [CrossRef]
- Hibiki, T.; Ishii, M. Interfacial area concentration in steady fully-developed bubbly flow. Int. J. Heat Mass Transf. 2001, 44, 3443–3461. [Google Scholar] [CrossRef]
- Fletcher, D.F.; McClure, D.D.; Kavanagh, J.M.; Barton, G.W. CFD simulation of industrial bubble columns: Numerical challenges and model validation successes. Appl. Math. Model. 2017, 44, 25–42. [Google Scholar] [CrossRef]
- Talvy, S.; Cockx, A.; Line, A. Modeling of oxygen mass transfer in a gas-liquid airlift, reactor. AIChE J. 2007, 53, 316–326. [Google Scholar] [CrossRef]
- Zun, I.; Perpar, M.; Gregorc, J.; Hayashi, K.; Tomiyama, A. Mixing of thermally stratified water layer by a free rising wobbling air bubble. Chem. Eng. Sci. 2012, 72, 155–171. [Google Scholar] [CrossRef]
- O’Reilly Meehan, R.; Donnelly, B.; Nolan, K.; Persoons, T.; Murray, D.B. Flow structures and dynamics in the wakes of sliding bubbles. Int. J. Multiph. Flow 2016, 84, 145–154. [Google Scholar] [CrossRef]
- Ohta, M.; Imura, T.; Yoshida, Y.; Sussman, M. A computational study of the effect of initial bubble conditions on the motion of a gas bubble rising in viscous liquids. Int. J. Multiph. Flow 2005, 31, 223–237. [Google Scholar] [CrossRef]
- Cano-Lozano, J.C.; Bolaños-Jiménez, R.; Gutiérrez-Montes, C.; Martínez-Bazán, C. The use of Volume of Fluid technique to analyze multiphase flows: Specific case of bubble rising in still liquids. Appl. Math. Model. 2015, 39, 3290–3305. [Google Scholar] [CrossRef]
- Gaudlitz, D.; Adams, N.A. Numerical investigation of rising bubble wake and shape variations. Phys. Fluids 2009, 21, 122102. [Google Scholar] [CrossRef]
- Floryan, J.M.; Rasmussen, H. Numerical Methods for Viscous Flows With Moving Boundaries. Appl. Mech. Rev. 1989, 42, 323–341. [Google Scholar] [CrossRef]
- Osher, S.; Fedkiw, R.P. Level Set Methods: An Overview and Some Recent Results. J. Comput. Phys. 2001, 502, 463–502. [Google Scholar] [CrossRef]
- Sussman, M.; Smereka, P.; Osher, S. A Level Set Approach for Computing Solutions to Incompressible Two-Phase Flow. J. Comput. Phys. 1994, 114, 146–159. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–255. [Google Scholar] [CrossRef]
- Rider, W.J.; Kothe, D.B. Reconstructing Volume Tracking. J. Comput. Phys. 1998, 141, 112–152. [Google Scholar] [CrossRef] [Green Version]
- Tomiyama, A.; Shimada, N. A Numerical Method for Bubbly Flow Simulation Based on a Multi-Fluid Model. J. Press. Vessel Technol. 2001, 23, 510–516. [Google Scholar] [CrossRef]
- Besagni, G.; Di Pasquali, A.; Gallazzini, L.; Gottardi, E.; Colombo, L.P.M.; Inzoli, F. The effect of aspect ratio in counter-current gas-liquid bubble columns: Experimental results and gas holdup correlations. Int. J. Multiph. Flow 2017, 94, 53–78. [Google Scholar] [CrossRef]
- Fuster, D.; Agbaglah, G.; Josserand, C.; Popinet, S.; Zaleski, S. Numerical simulation of droplets, bubbles and waves: State of the art. Fluid Dyn. Res. 2009, 41, 065001. [Google Scholar] [CrossRef]
- Brackbil, J.; Kothe, D.B.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- OpenFOAM. The Open Source CFD Toolbox: User Guide; OpenFOAM Foundation: London, UK, 2014. [Google Scholar]
- Marić, T.; Höpken, J.; Mooney, K. The OpenFOAM Technology Primer; Sourceflux: Duisburg, Germany, 2014. [Google Scholar]
- Rek, Z.; Gregorc, J.; Bouaifi, M.; Daniel, C. Numerical simulation of gas jet in liquid crossflow with high mean jet to crossflow velocity ratio. Chem. Eng. Sci. 2017, 172, 667–676. [Google Scholar] [CrossRef]
- Tomiyama, A. Some Attempts for the Improvement of Computational Bubble Dynamics. In Proceedings of the 10th Workshop on Two-Phase Flow Predictions, Merseburg, Germany, 9–12 April 2002; pp. 125–136. [Google Scholar]
- OpenFOAM. The OpenSource CFD Toolbox: Programmer’s Guide; OpenFOAM Foundation: London, UK, 2014. [Google Scholar]
- Fric, T.F.; Roshko, A. Vortical structure in the wake of a transverse jet. J. Fluid Mech. 1994, 279, 1–47. [Google Scholar] [CrossRef]
- Zun, I.; Groselj, J. The structure of bubble non-equilibrium movement in free-rise and agitated-rise conditions. Nucl. Eng. Des. 1996, 163, 99–115. [Google Scholar] [CrossRef]
- Clift, R.; Grace, J.R.; Weber, M.E.; Weber, M.F. Bubbles, Drops and Particles; Academic Press: Cambridge, MA, USA, 1978; ISBN1 012176950X. ISBN2 9780121769505. [Google Scholar]
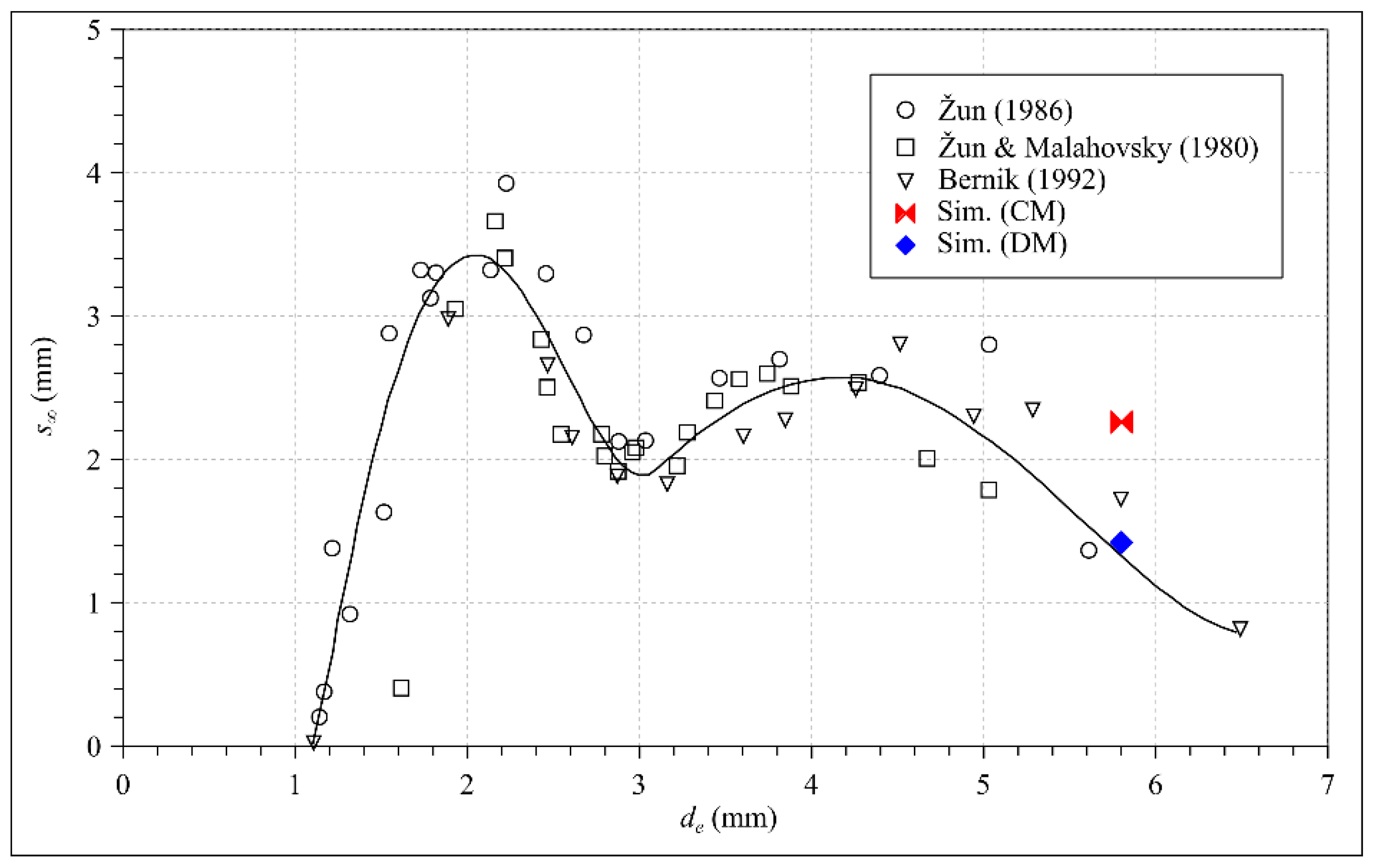
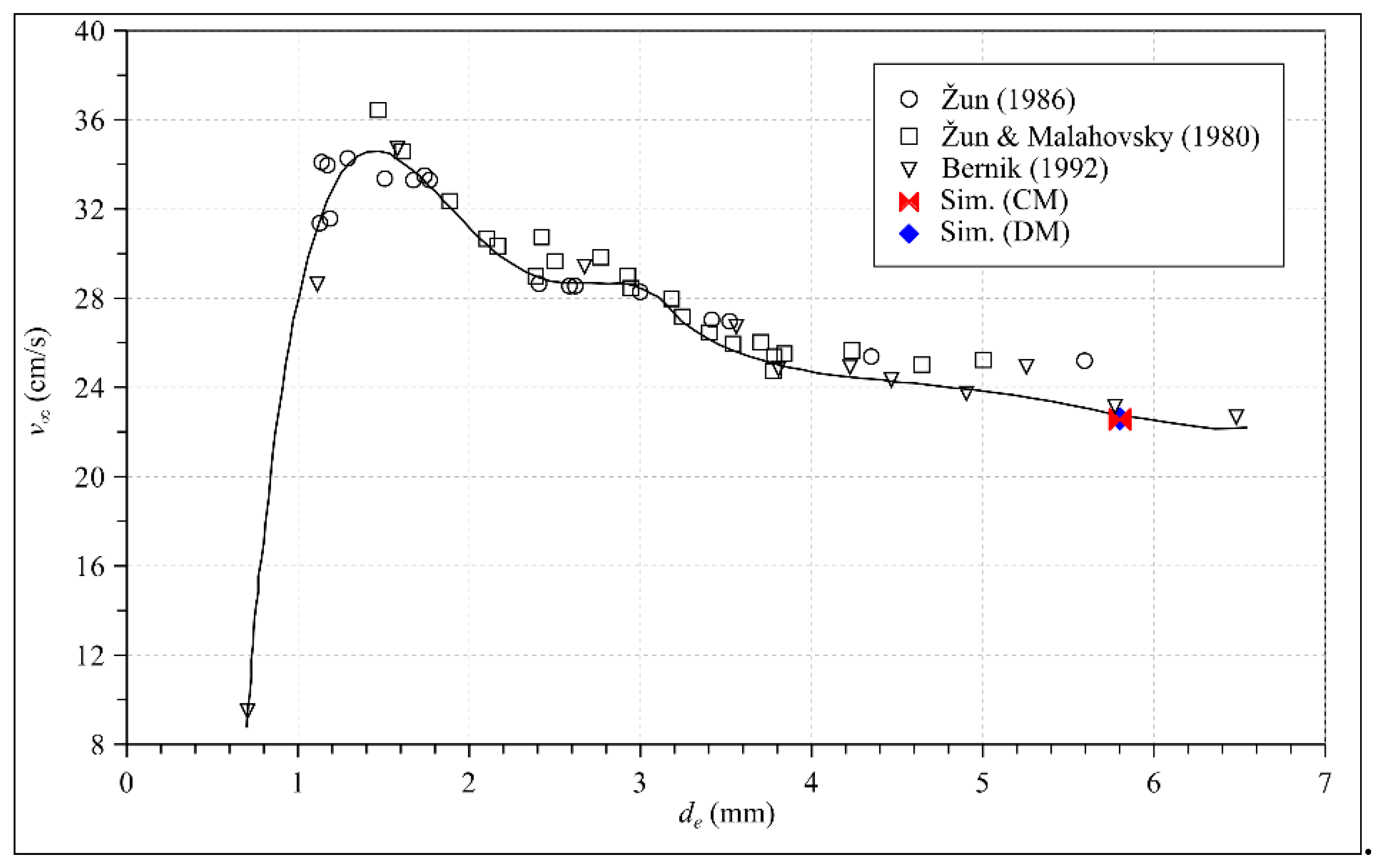
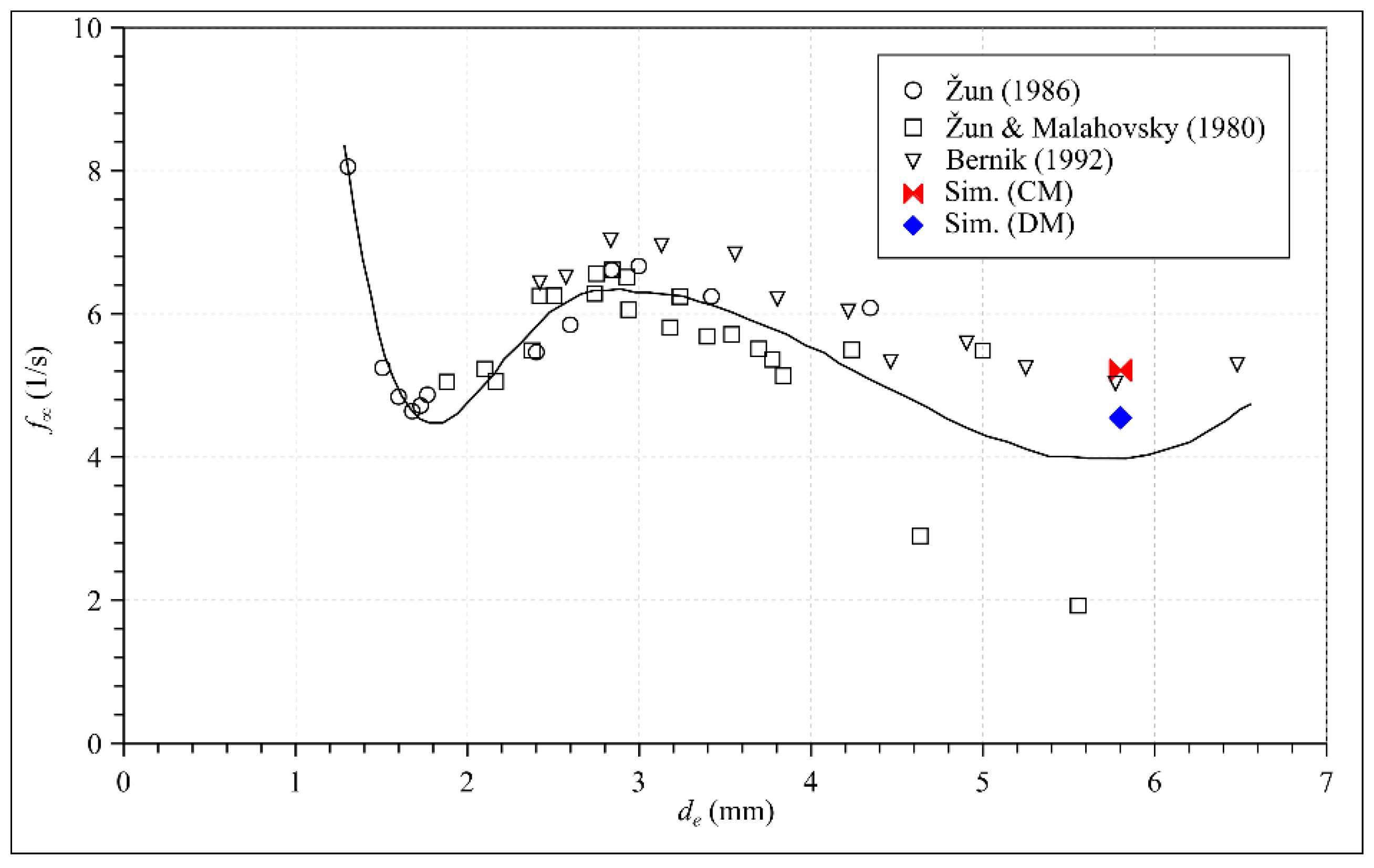
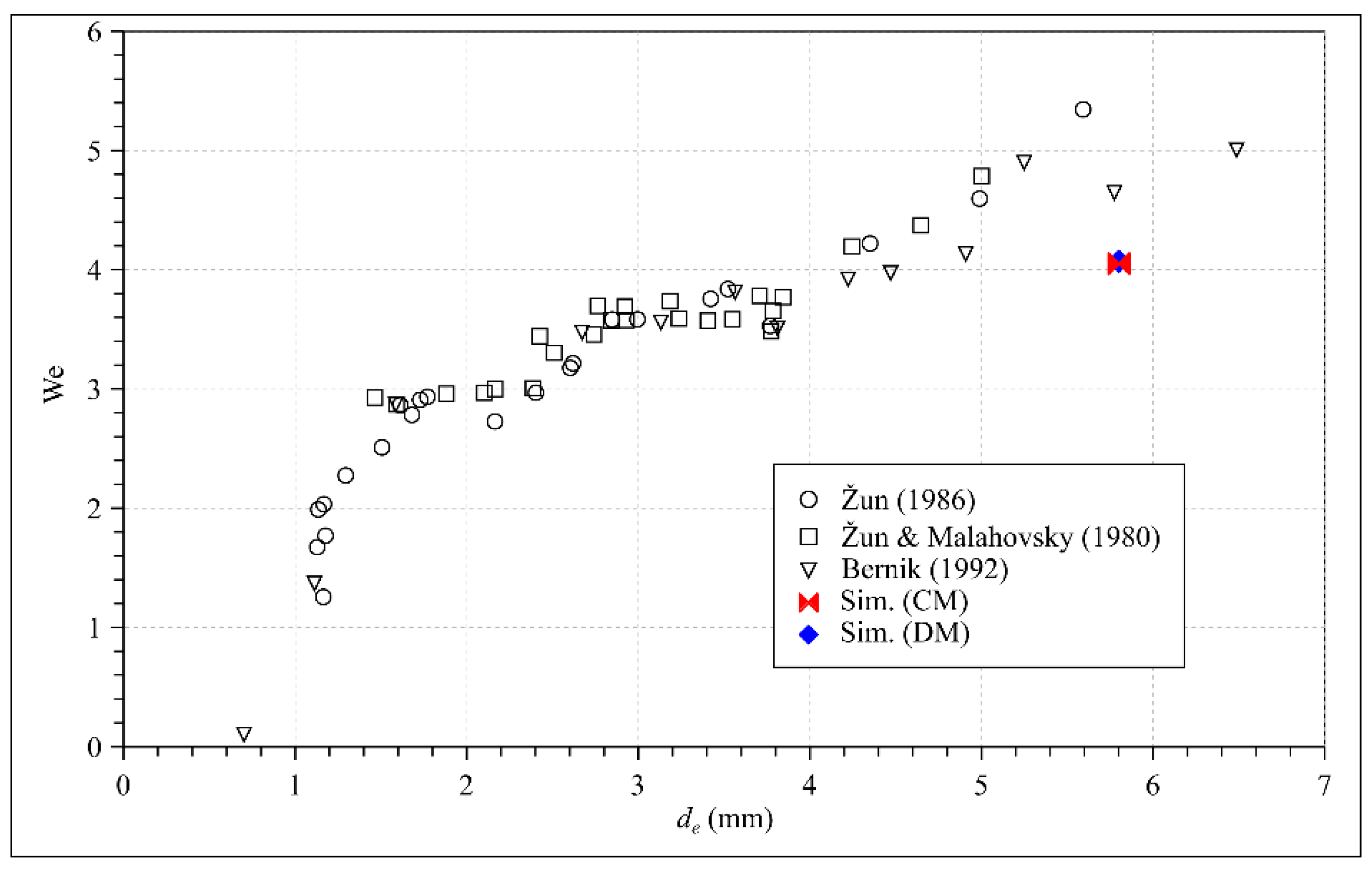

| ρ (kg/m3) | μ (Pas) | σ (N/m) | |
|---|---|---|---|
| water | 998.2 | 1.003 × 10−3 | 0.072 |
| air | 1.225 | 1.790 × 10−5 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rek, Z. Using a Dynamic and Constant Mesh in Numerical Simulation of the Free-Rising Bubble. Fluids 2019, 4, 38. https://doi.org/10.3390/fluids4010038
Rek Z. Using a Dynamic and Constant Mesh in Numerical Simulation of the Free-Rising Bubble. Fluids. 2019; 4(1):38. https://doi.org/10.3390/fluids4010038
Chicago/Turabian StyleRek, Zlatko. 2019. "Using a Dynamic and Constant Mesh in Numerical Simulation of the Free-Rising Bubble" Fluids 4, no. 1: 38. https://doi.org/10.3390/fluids4010038
APA StyleRek, Z. (2019). Using a Dynamic and Constant Mesh in Numerical Simulation of the Free-Rising Bubble. Fluids, 4(1), 38. https://doi.org/10.3390/fluids4010038





