A Continuum Model for Complex Flows of Shear Thickening Colloidal Solutions
Abstract
1. Introduction
2. Materials and Methods
SPPC Model
3. Results
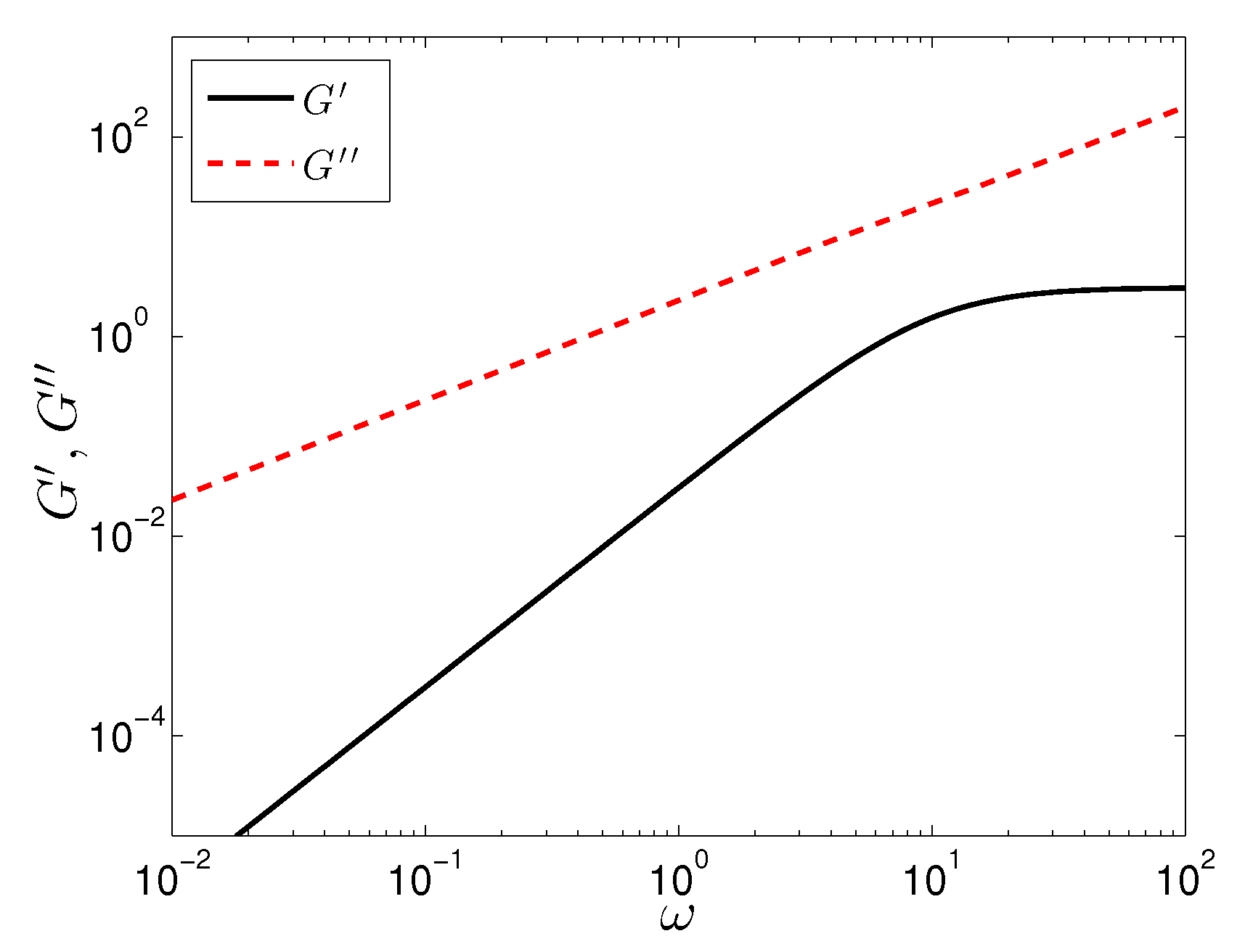
3.1. SAOS
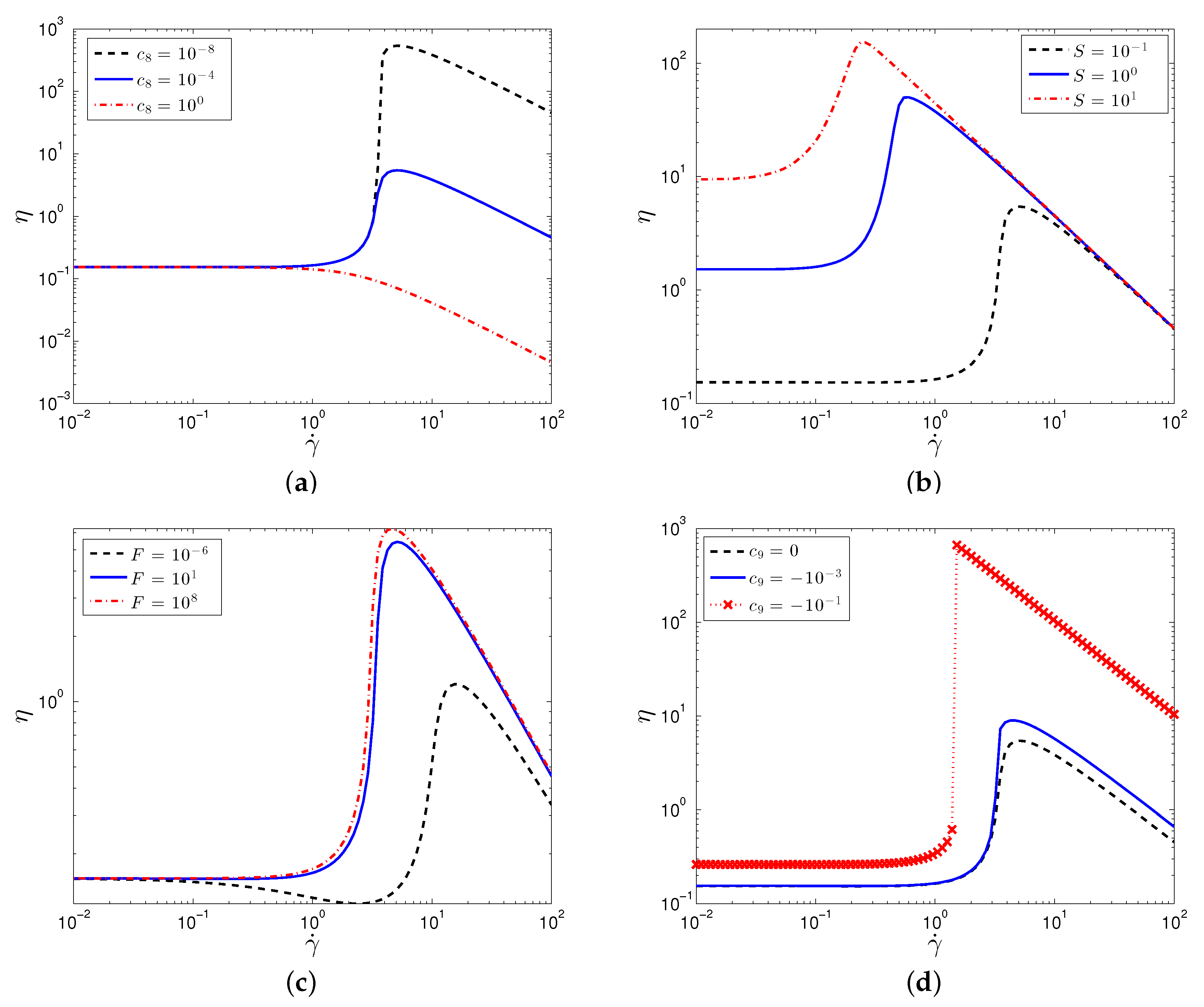
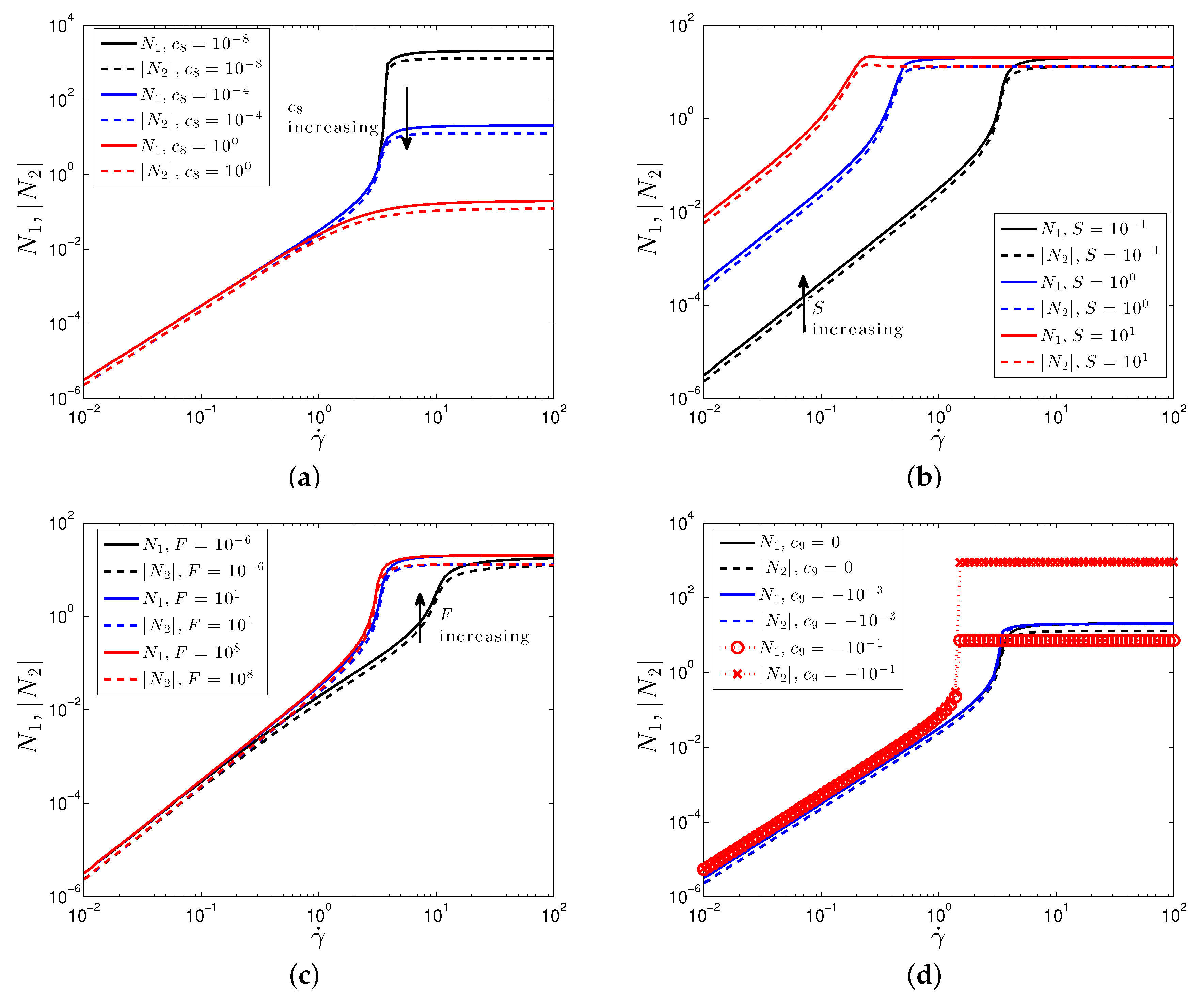
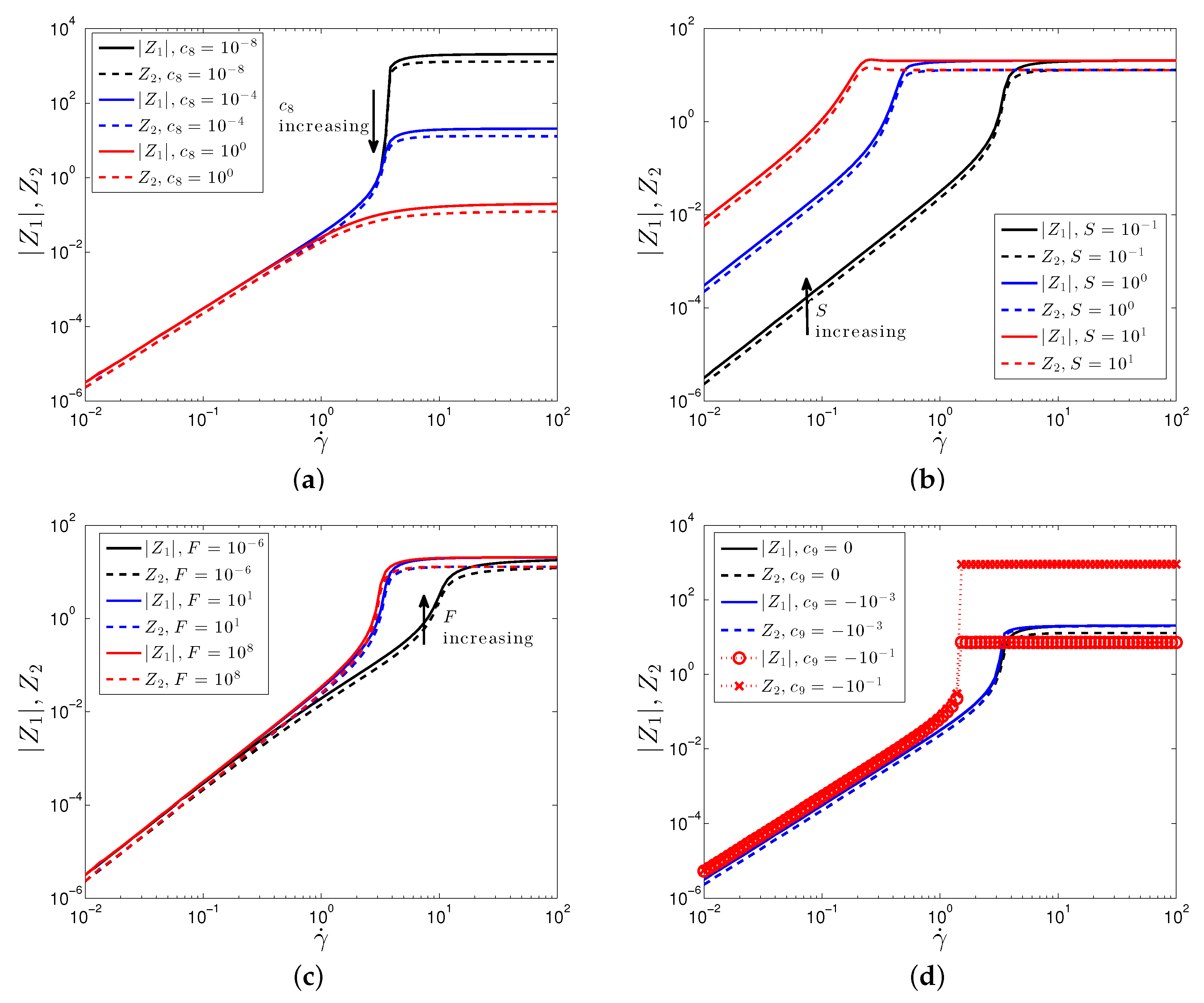
3.2. Non-Linear Rheology
3.2.1. Simple Shear Flow
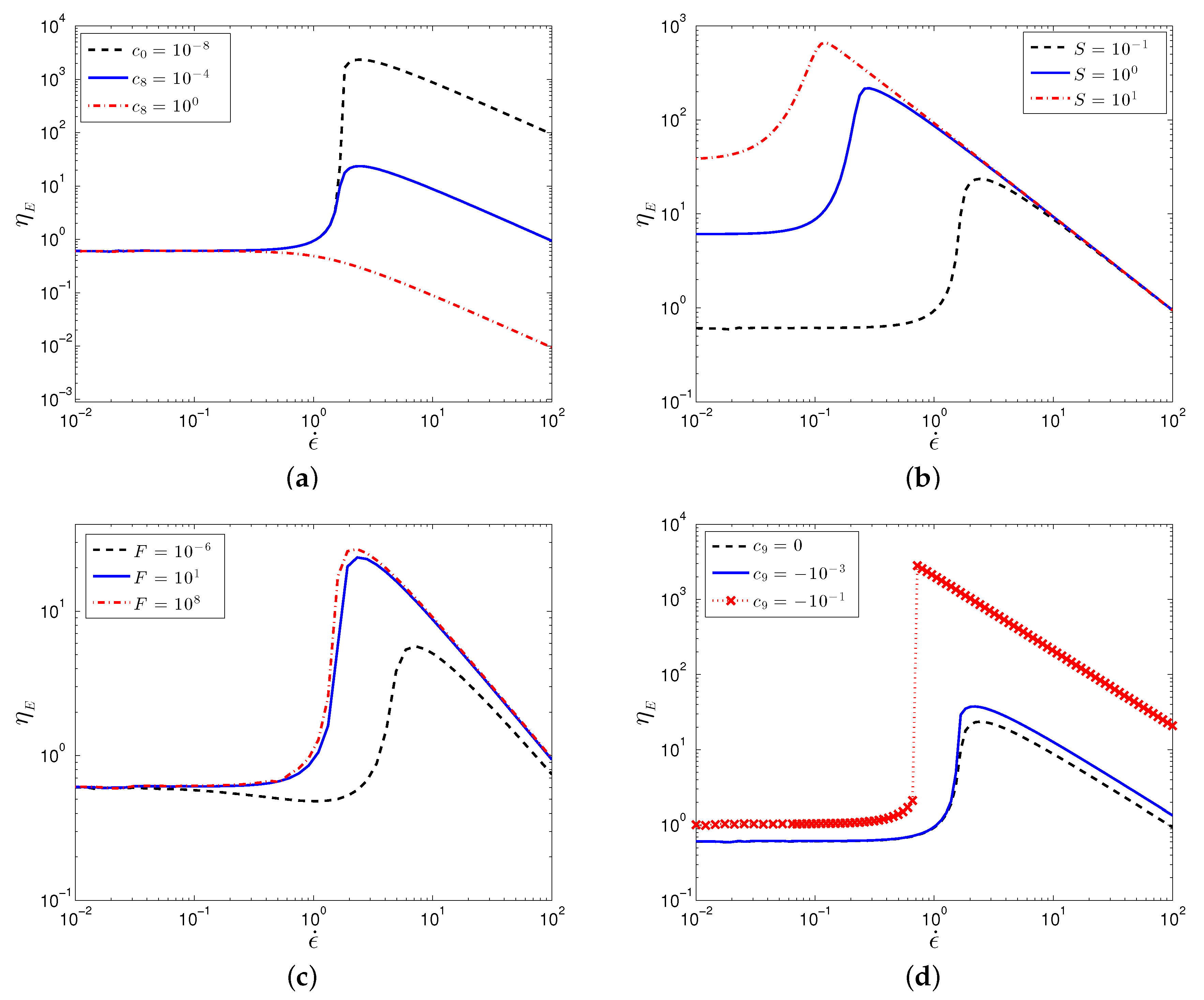
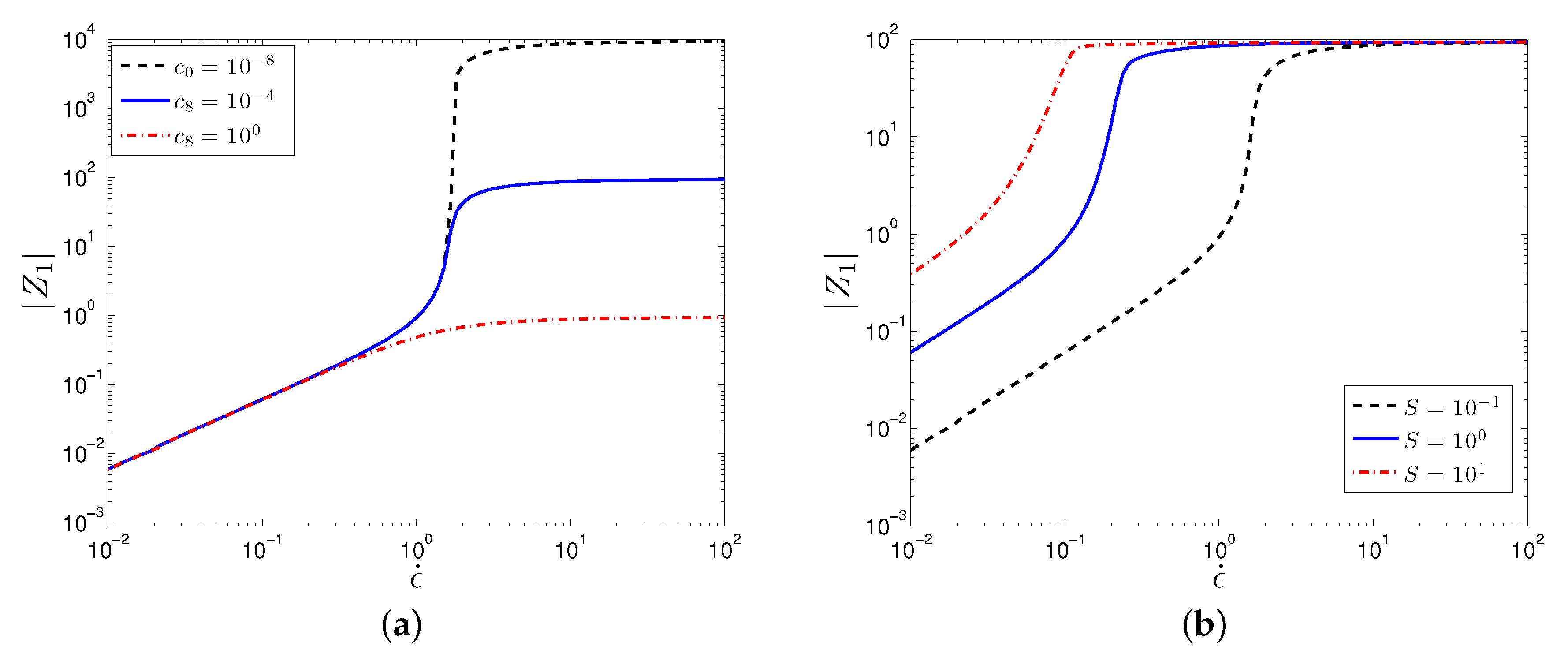
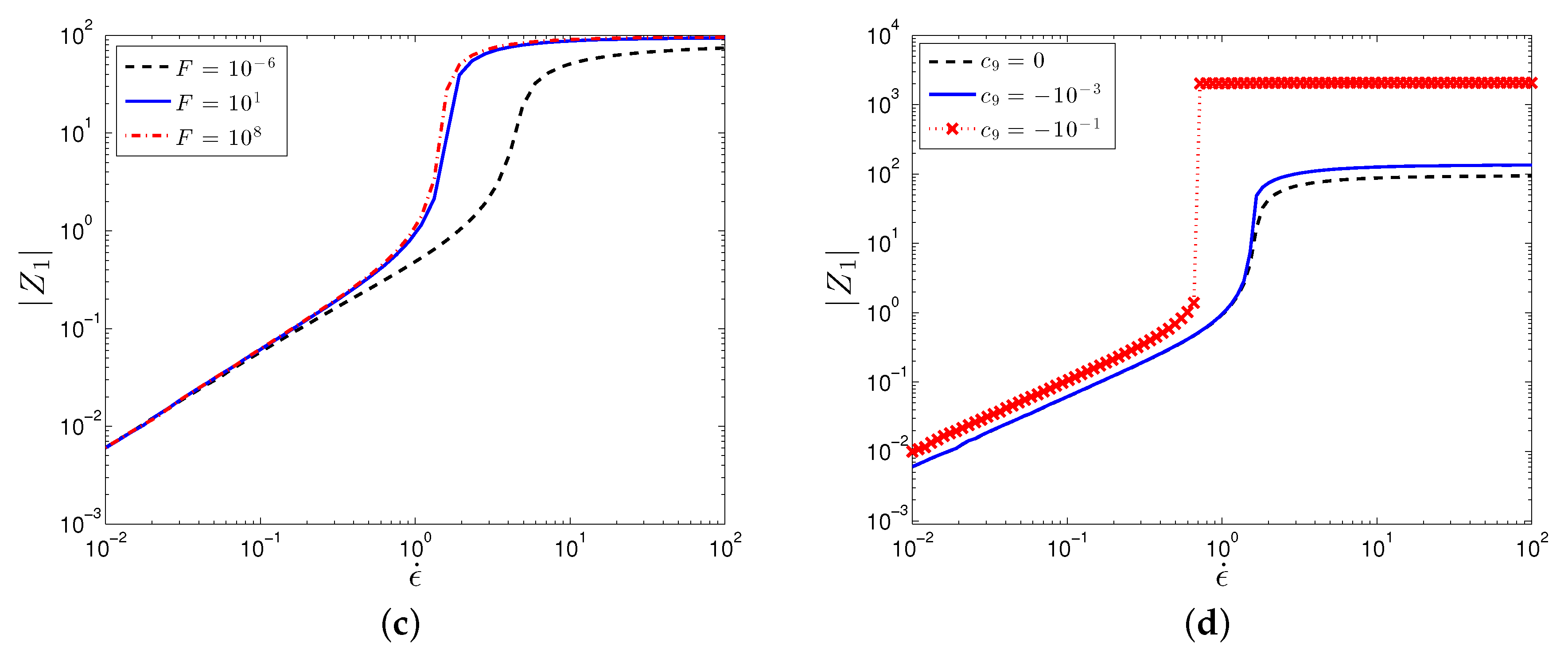
3.2.2. Planar Extensional Flow
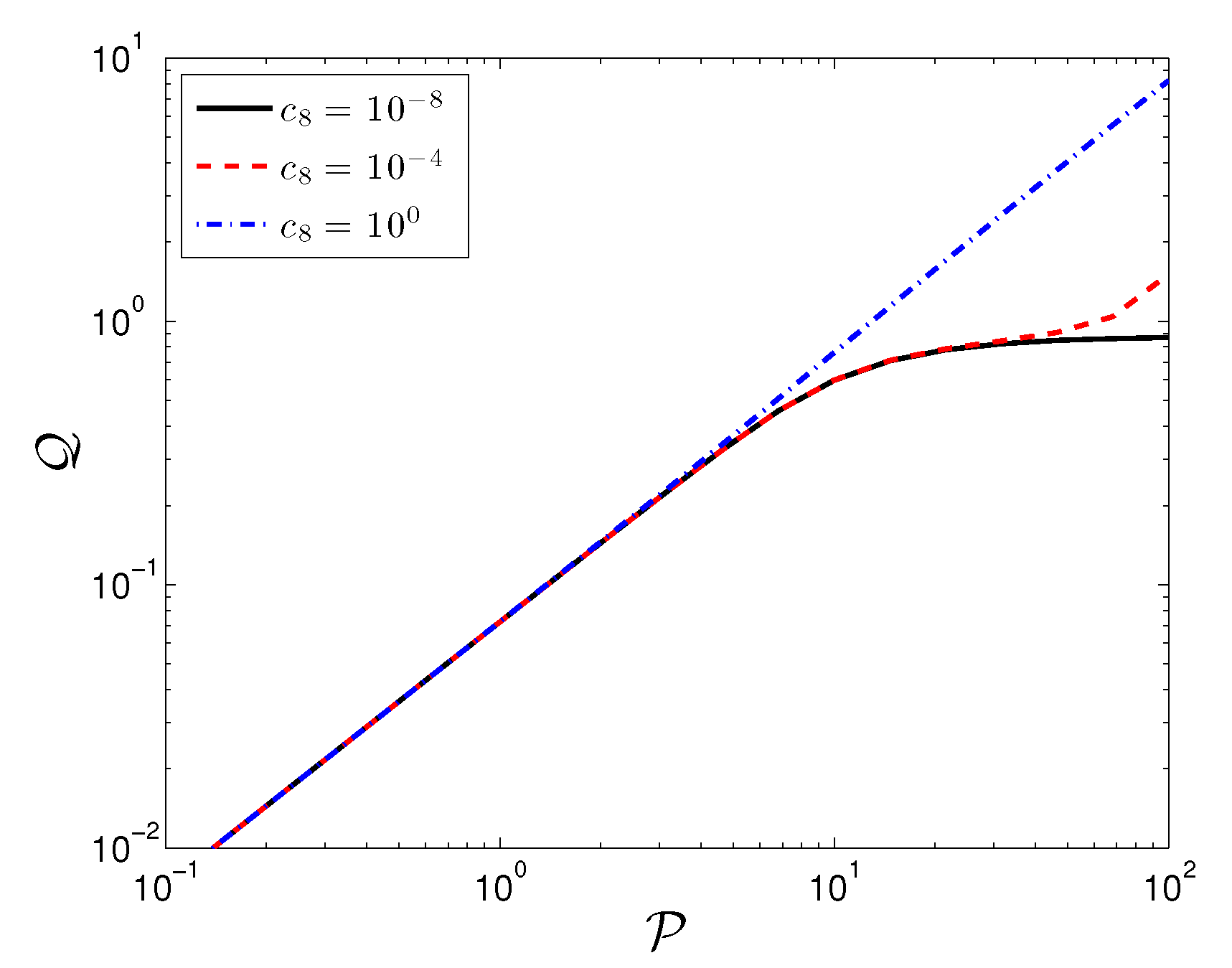
3.3. Results for Steady Poiseuille Flow
3.3.1. One-Dimensional
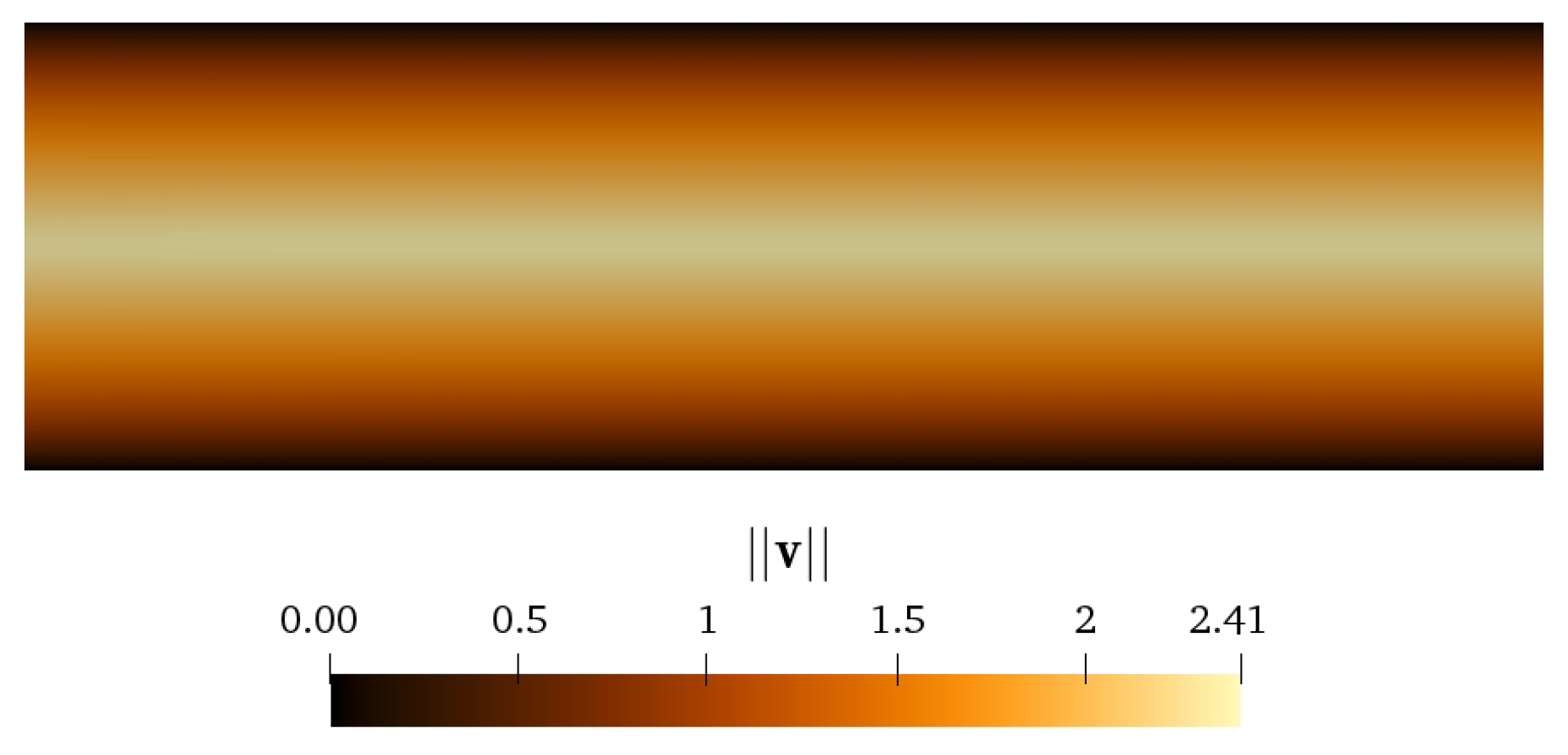
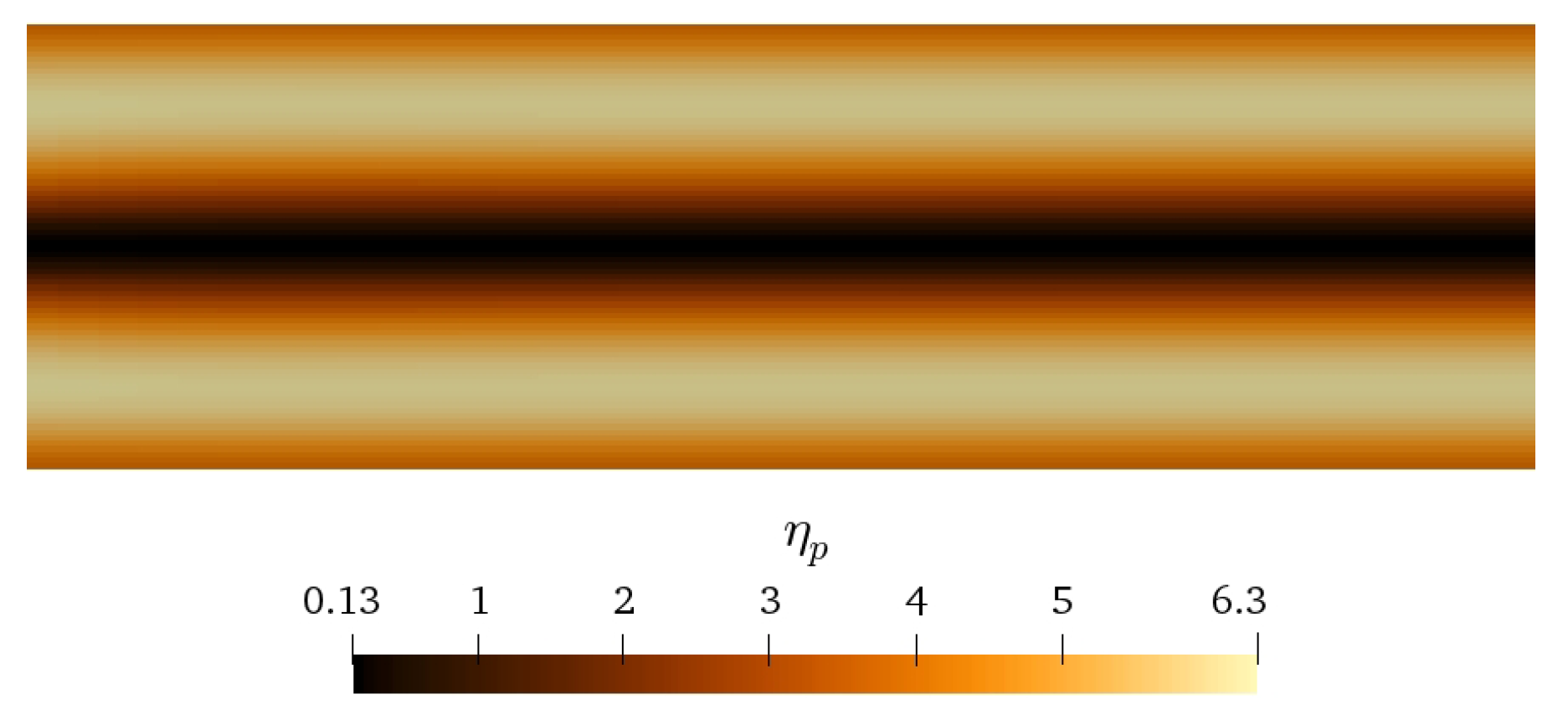
3.3.2. Two-Dimensional
4. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Ding, J.; Li, W.; Shen, S.Z. Research and applications of shear thickening fluids. Recent Pat. Mater. Sci. 2011, 4, 43–49. [Google Scholar] [CrossRef]
- Lee, Y.S.; Wetzel, E.D.; Wagner, N.J. The ballistic impact characteristics of Kevlar® woven fabrics impregnated with a colloidal shear thickening fluid. J. Mater. Sci. 2003, 38, 2825–2833. [Google Scholar] [CrossRef]
- Decker, M.J.; Halbach, C.J.; Nam, C.H.; Wagner, N.J.; Wetzel, E.D. Stab resistance of shear thickening fluid (STF)-treated fabrics. Compos. Sci. Technol. 2007, 67, 565–578. [Google Scholar] [CrossRef]
- Wagner, N.J.; Brady, J.F. Shear thickening in colloidal dispersions. Phys. Today 2009, 62, 27–32. [Google Scholar] [CrossRef]
- Nilsson, M.A.; Kulkarni, R.; Gerberich, L.; Hammond, R.; Singh, R.; Baumhoff, E.; Rothstein, J.P. Effect of fluid rheology on enhanced oil recovery in a microfluidic sandstone device. J. Non-Newton. Fluid Mech. 2013, 202, 112–119. [Google Scholar] [CrossRef]
- Chellamuthu, M.; Arndt, E.M.; Rothstein, J.P. Extensional rheology of shear-thickening nanoparticle suspensions. Soft Matter 2009, 5, 2117–2124. [Google Scholar] [CrossRef]
- White, E.E.B.; Chellamuthu, M.; Rothstein, J.P. Extensional rheology of a shear-thickening cornstarch and water suspension. Rheol. Acta 2010, 49, 119–129. [Google Scholar] [CrossRef]
- Smith, M.I.; Besseling, R.; Cates, M.E.; Bertola, V. Dilatancy in the flow and fracture of stretched colloidal suspensions. Nat. Commun. 2010, 1, 114. [Google Scholar] [CrossRef]
- Roché, M.; Kellay, H.; Stone, H.A. Heterogeneity and the role of normal stresses during the extensional thinning of non-Brownian shear-thickening fluids. Phys. Rev. Lett. 2011, 107, 134503. [Google Scholar] [CrossRef]
- Zimoch, P.J.; McKinley, G.H.; Hosoi, A.E. Capillary breakup of discontinuously rate thickening suspensions. Phys. Rev. Lett. 2013, 111, 036001. [Google Scholar] [CrossRef]
- Majumdar, S.; Peters, I.R.; Han, E.; Jaeger, H.M. Dynamic shear jamming in dense granular suspensions under extension. Phys. Rev. E 2017, 95, 012603. [Google Scholar] [CrossRef]
- Wyart, M.; Cates, M.E. Discontinuous shear thickening without inertia in dense non-Brownian suspensions. Phys. Rev. Lett. 2014, 112, 098302. [Google Scholar] [CrossRef]
- Mari, R.; Seto, R.; Morris, J.F.; Denn, M.M. Shear thickening, frictionless and frictional rheologies in non-Brownian suspensions. J. Rheol. 2014, 58, 1693–1724. [Google Scholar] [CrossRef]
- Seto, R.; Giusteri, G.G.; Martiniello, A. Microstructure and thickening of dense suspensions under extensional and shear flows. J. Fluid Mech. 2017, 825, R3. [Google Scholar] [CrossRef]
- Ouriev, B.; Windhab, E.J. Novel ultrasound based time averaged flow mapping method for die entry visualization in flow of highly concentrated shear-thinning and shear-thickening suspensions. Meas. Sci. Technol. 2003, 14, 140–147. [Google Scholar]
- Von Kann, S.; Snoeijer, J.H.; Lohse, D.; van der Meer, D. Nonmonotonic settling of a sphere in a cornstarch suspension. Phys. Rev. E 2011, 84, 060401. [Google Scholar] [CrossRef] [PubMed]
- Hasanzadeh, M.; Mottaghitalab, V. The role of shear-thickening fluids (STFs) in ballistic and stab-resistance improvement of flexible armor. J. Mater. Eng. Perform. 2014, 23, 1182–1196. [Google Scholar] [CrossRef]
- Brady, J.F.; Bossis, G. Stokesian dynamics. Ann. Rev. Fluid Mech. 1988, 20, 111–157. [Google Scholar] [CrossRef]
- Foss, D.R.; Brady, J.F. Structure, diffusion and rheology of Brownian suspensions by Stokesian Dynamics simulation. J. Fluid Mech. 2000, 407, 167–200. [Google Scholar] [CrossRef]
- Picano, F.; Breugem, W.P.; Mitra, D.; Brandt, L. Shear thickening in non-Brownian suspensions: An excluded volume effect. Phys. Rev. Lett. 2013, 111, 098302. [Google Scholar] [CrossRef] [PubMed]
- Seto, R.; Mari, R.; Morris, J.F.; Denn, M.M. Discontinuous Shear Thickening of Frictional Hard-Sphere Suspensions. Phys. Rev. Lett. 2013, 111, 218301. [Google Scholar] [CrossRef] [PubMed]
- Mari, R.; Seto, R.; Morris, J.F.; Denn, M.M. Discontinuous shear thickening in Brownian suspensions by dynamic simulation. Proc. Nat. Acad. Sci. USA 2015, 112, 15326–15330. [Google Scholar] [CrossRef] [PubMed]
- Boromand, A.; Jamali, S.; Grove, B.; Maia, J.M. A generalized frictional and hydrodynamic model of the dynamics and structure of dense colloidal suspensions. J. Rheol. 2018, 62, 905–918. [Google Scholar] [CrossRef]
- Wilson, H.J. ‘Shear thickening’ in non-shear flows: The effect of microstructure. J. Fluid Mech. 2018, 836, 1–4. [Google Scholar] [CrossRef]
- Phan-Thien, N. Constitutive equation for concentrated suspensions in Newtonian liquids. J. Rheol. 1995, 39, 679–695. [Google Scholar] [CrossRef]
- Phan-Thien, N.; Fan, X.-J.; Khoo, B.C. A new constitutive model for monodispersed suspensions of spheres at high concentrations. Rheol. Acta 1999, 38, 297–304. [Google Scholar] [CrossRef]
- Stickel, J.J.; Phillips, R.J.; Powell, R.L. A constitutive model for microstructure and total stress in particulate suspensions. J. Rheol. 2006, 50, 379–413. [Google Scholar] [CrossRef]
- Goddard, J. A dissipative anisotropic fluid model for non-colloidal particle dispersions. J. Fluid Mech. 2006, 568, 1–17. [Google Scholar] [CrossRef]
- Morris, J.F. A review of microstructure in concentrated suspensions and its implications for rheology and bulk flow. Rheol. Acta 2009, 48, 909–923. [Google Scholar] [CrossRef]
- Miller, R.M.; Singh, J.P.; Morris, J.F. Suspension flow modeling for general geometries. Chem. Eng. Sci. 2009, 64, 4597–4610. [Google Scholar] [CrossRef]
- Ozenda, O.; Saramito, P.; Chambon, G. A new rate-independent tensorial model for suspensions of noncolloidal rigid particles in Newtonian fluids. J. Rheol. 2018, 62, 889–903. [Google Scholar] [CrossRef]
- Singh, A.; Mari, R.; Denn, M.M.; Morris, J.F. A constitutive model for simple shear of dense frictional suspensions. J. Rheol. 2018, 62, 457–468. [Google Scholar] [CrossRef]
- Gillissen, J.J.J.; Wilson, H.J. Modeling sphere suspension microstructure and stress. Phys. Rev. E 2018, 98, 033119. [Google Scholar] [CrossRef]
- II, G.G.L.; Denn, M.M.; Hur, D.U.; Boger, D.V. The flow of fiber suspensions in complex geometries. J. Non-Newton. Fluid Mech. 1988, 26, 297–325. [Google Scholar]
- Hand, G.L. A theory of anisotropic fluids. J. Fluid Mech. 1962, 13, 33–46. [Google Scholar] [CrossRef]
- Barthés-Biesel, D.; Acrivos, A. The rheology of suspensions and its relation to phenomenological theories for non-Newtonian fluids. Int. J. Multiph. Flow 1973, 1, 1–24. [Google Scholar] [CrossRef]
- Stickel, J.J.; Phillips, R.J.; Powell, R.L. Application of a constitutive model for particulate suspensions: Time-dependent viscometric flows. J. Rheol. 2007, 51, 1271–1302. [Google Scholar] [CrossRef]
- Yapici, K.; Powell, R.L.; Phillips, R.J. Particle migration and suspension structure in steady and oscillatory pipe flow. Phys. Fluids 2009, 21, 053302. [Google Scholar] [CrossRef]
- Chacko, R.N.; Mari, R.; Fielding, S.M.; Cates, M.E. Shear reversal in dense suspensions: The challenge to fabric evolution models from simulation data. J. Fluid Mech. 2018, 847, 700–734. [Google Scholar] [CrossRef]
- Nott, P.R.; Brady, J.F. Pressure-driven flow of suspensions: Simulation and theory. J. Fluid Mech. 1994, 275, 157–199. [Google Scholar] [CrossRef]
- Morris, J.F.; Boulay, F. Curvilinear flows of noncolloidal suspensions: The role of normal stresses. J. Rheol. 1999, 43, 1213–1237. [Google Scholar] [CrossRef]
- Frank, M.; Anderson, D.; Weeks, E.R.; Morris, J.F. Particle migration in pressure-driven flow of a Brownian suspension. J. Fluid Mech. 2003, 493, 363–378. [Google Scholar] [CrossRef]
- Truesdell, C.; Noll, W. The non-linear field theories of mechanics. In The Non-Linear Field Theories of Mechanics; Springer: Berlin/Heidelberg, Germany, 2004; pp. 1–579. [Google Scholar]
- Passey, P.; Mehta, R.G. Study of Pre-Shearing Protocol and Rheological Parameters of Shear Thickening Fluids Containing Nano Particles. Ph.D. Thesis, Thapar University, Patiala, India, 2016. [Google Scholar]
- Mewis, J.; Wagner, N.J. Colloidal Suspension Rheology; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Maranzano, B.J.; Wagner, N.J. Flow-small angle neutron scattering measurements of colloidal dispersion microstructure evolution through the shear thickening transition. J. Chem. Phys. 2002, 117, 10291–10302. [Google Scholar] [CrossRef]
- Royer, J.R.; Blair, D.L.; Hudson, S.D. Rheological signature of frictional interactions in shear thickening suspensions. Phys. Rev. Lett. 2016, 116, 188301. [Google Scholar] [CrossRef] [PubMed]
- Kawasaki, T.; Ikeda, A.; Berthier, L. Thinning or thickening? Multiple rheological regimes in dense suspensions of soft particles. Europhys. Lett. 2014, 107, 28009. [Google Scholar] [CrossRef]
- Brady, J.F.; Morris, J.F. Microstructure of strongly sheared suspensions and its impact on rheology and diffusion. J. Fluid Mech. 1997, 348, 103–139. [Google Scholar] [CrossRef]
- Sierou, A.; Brady, J.F. Rheology and microstructure in concentrated noncolloidal suspensions. J. Rheol. 2002, 46, 1031–1056. [Google Scholar] [CrossRef]
- Ouriev, B.; Windhab, E.J. Rheological study of concentrated suspensions in pressure-driven shear flow using a novel in-line ultrasound Doppler method. Exp. Fluids 2002, 32, 204–211. [Google Scholar]
- Favero, J.L.; Secchi, A.R.; Cardozo, N.S.M.; Jasak, H. Viscoelastic flow analysis using the software OpenFOAM and differential constitutive equations. J. Non-Newton. Fluid Mech. 2010, 165, 1625–1636. [Google Scholar] [CrossRef]
- Sweby, P.K. High resolution schemes using flux limiters for hyperbolic conservation laws. SIAM J. Numer. Anal. 1984, 21, 995–1011. [Google Scholar] [CrossRef]
- Issa, R.I. Solution of the implicitly discretised fluid flow equations by operator-splitting. J. Comput. Phys. 1986, 62, 40–65. [Google Scholar] [CrossRef]
- Fernandes, C.; Araujo, M.S.B.; Ferrás, L.L.; Nóbrega, J.M. Improved both sides diffusion (iBSD): A new and straightforward stabilization approach for viscoelastic fluid flows. J. Non-Newton. Fluid Mech. 2017, 249, 63–78. [Google Scholar] [CrossRef]
- Lim, A.S.; Lopatnikov, S.L.; Wagner, N.J.; Gillespie, J.W., Jr. Investigating the transient response of a shear thickening fluid using the split Hopkinson pressure bar technique. Rheol. Acta 2010, 49, 879–890. [Google Scholar] [CrossRef]
- Lomakin, E.V.; Mossakovsky, P.A.; Bragov, A.M.; Lomunov, A.K.; Konstantinov, A.Y.; Kolotnikov, M.E.; Antonov, F.K.; Vakshtein, M.S. Investigation of impact resistance of multilayered woven composite barrier impregnated with the shear thickening fluid. Arch. Appl. Mech. 2011, 81, 2007–2020. [Google Scholar] [CrossRef]
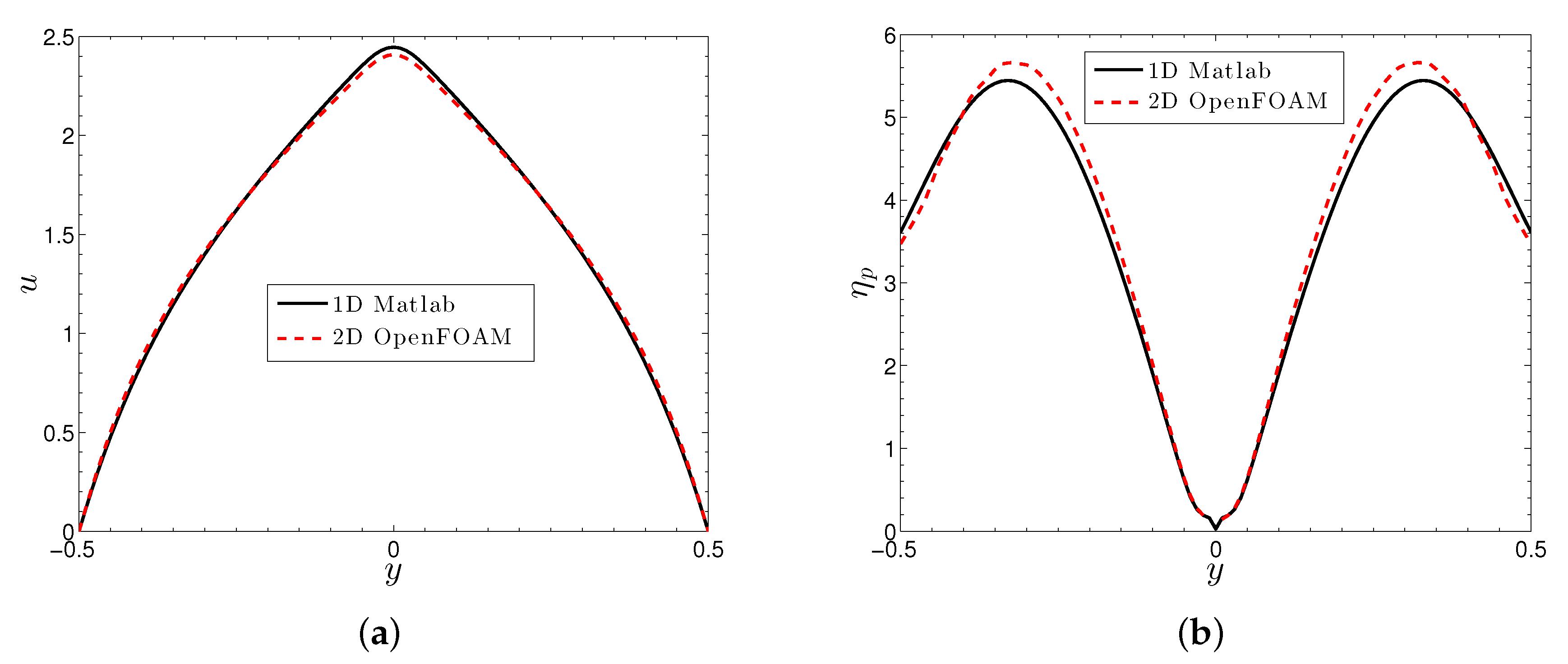
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Green, J.A.; Ryckman, D.J.; Cromer, M. A Continuum Model for Complex Flows of Shear Thickening Colloidal Solutions. Fluids 2019, 4, 21. https://doi.org/10.3390/fluids4010021
Green JA, Ryckman DJ, Cromer M. A Continuum Model for Complex Flows of Shear Thickening Colloidal Solutions. Fluids. 2019; 4(1):21. https://doi.org/10.3390/fluids4010021
Chicago/Turabian StyleGreen, Joseph A., Daniel J. Ryckman, and Michael Cromer. 2019. "A Continuum Model for Complex Flows of Shear Thickening Colloidal Solutions" Fluids 4, no. 1: 21. https://doi.org/10.3390/fluids4010021
APA StyleGreen, J. A., Ryckman, D. J., & Cromer, M. (2019). A Continuum Model for Complex Flows of Shear Thickening Colloidal Solutions. Fluids, 4(1), 21. https://doi.org/10.3390/fluids4010021



