Vortex Interactions Subjected to Deformation Flows: A Review
Abstract
1. Introduction
2. Problem Formulation
2.1. Quasi-Geostrophic Potential Vorticity Equations
2.2. External Deformation Flow
2.3. Singular Vortices
2.4. Uniformly Distributed Vortex Models: Elliptic (Kida Vortex), Ellipsoidal Vortices in Deformation Flows
3. Regular and Chaotic Dynamics in the Systems of Singular Vortices
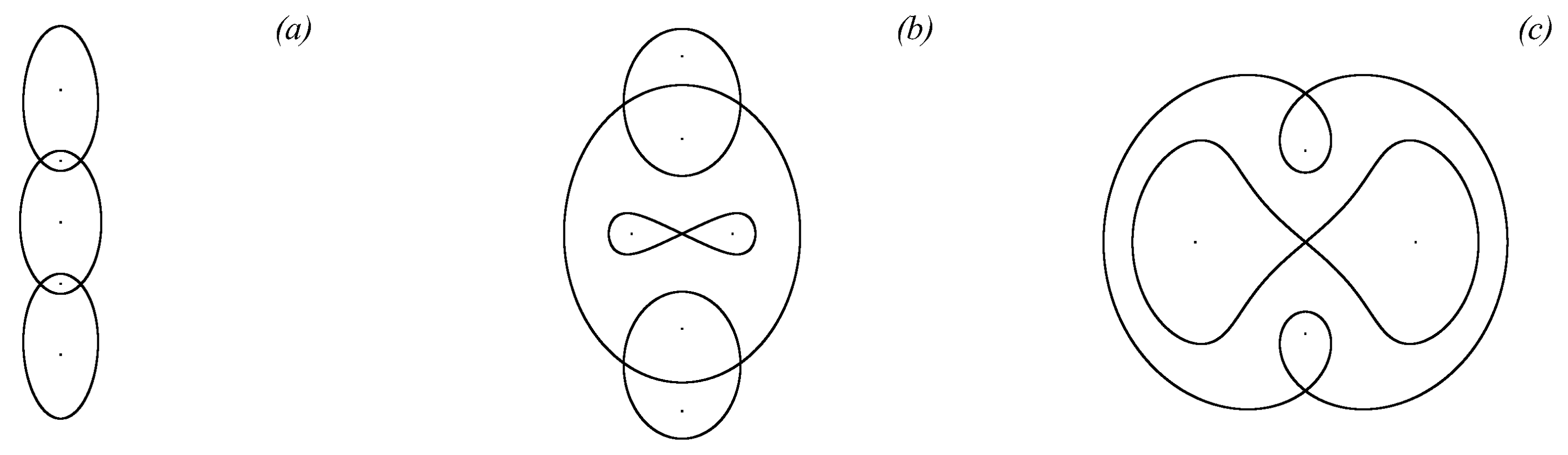
3.1. Vorticity Centre Motion in Non-Stationary Deformation Flows
3.2. Regular Behaviour of Relative Motion of Two Singular Vortices
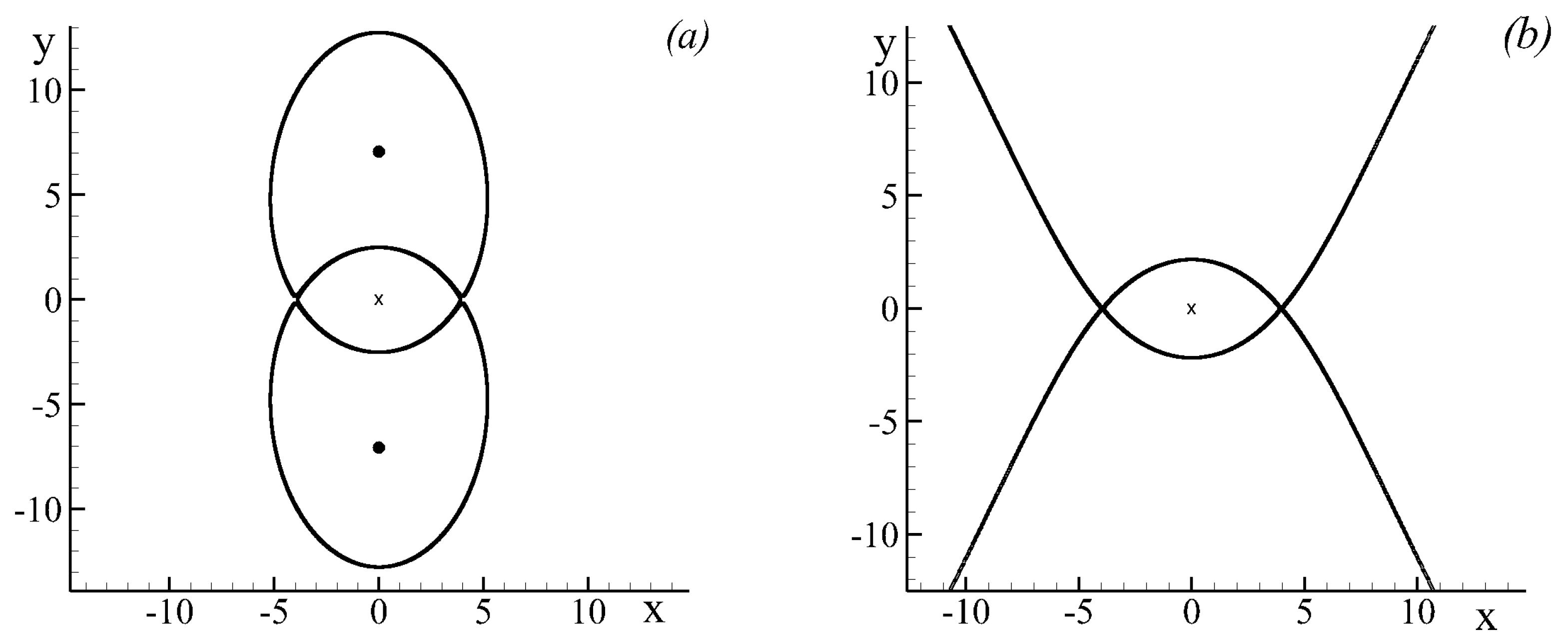
3.2.1. Two Singular Vortices in An Alternating Deformation Flow
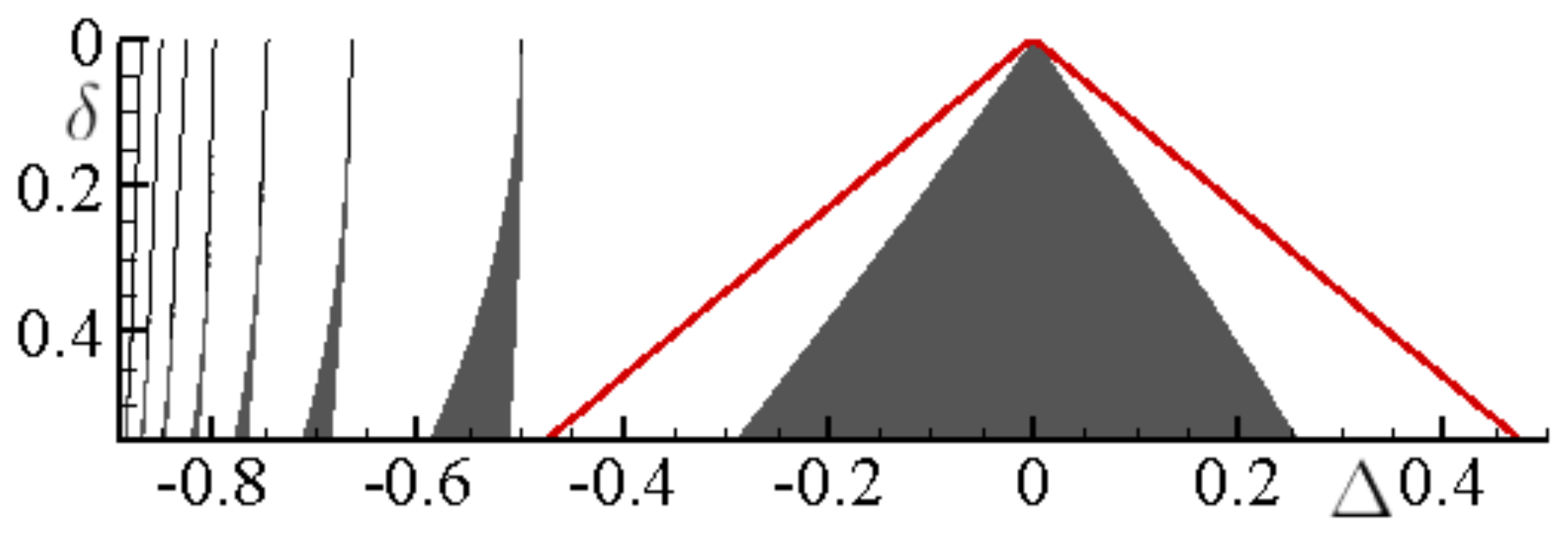
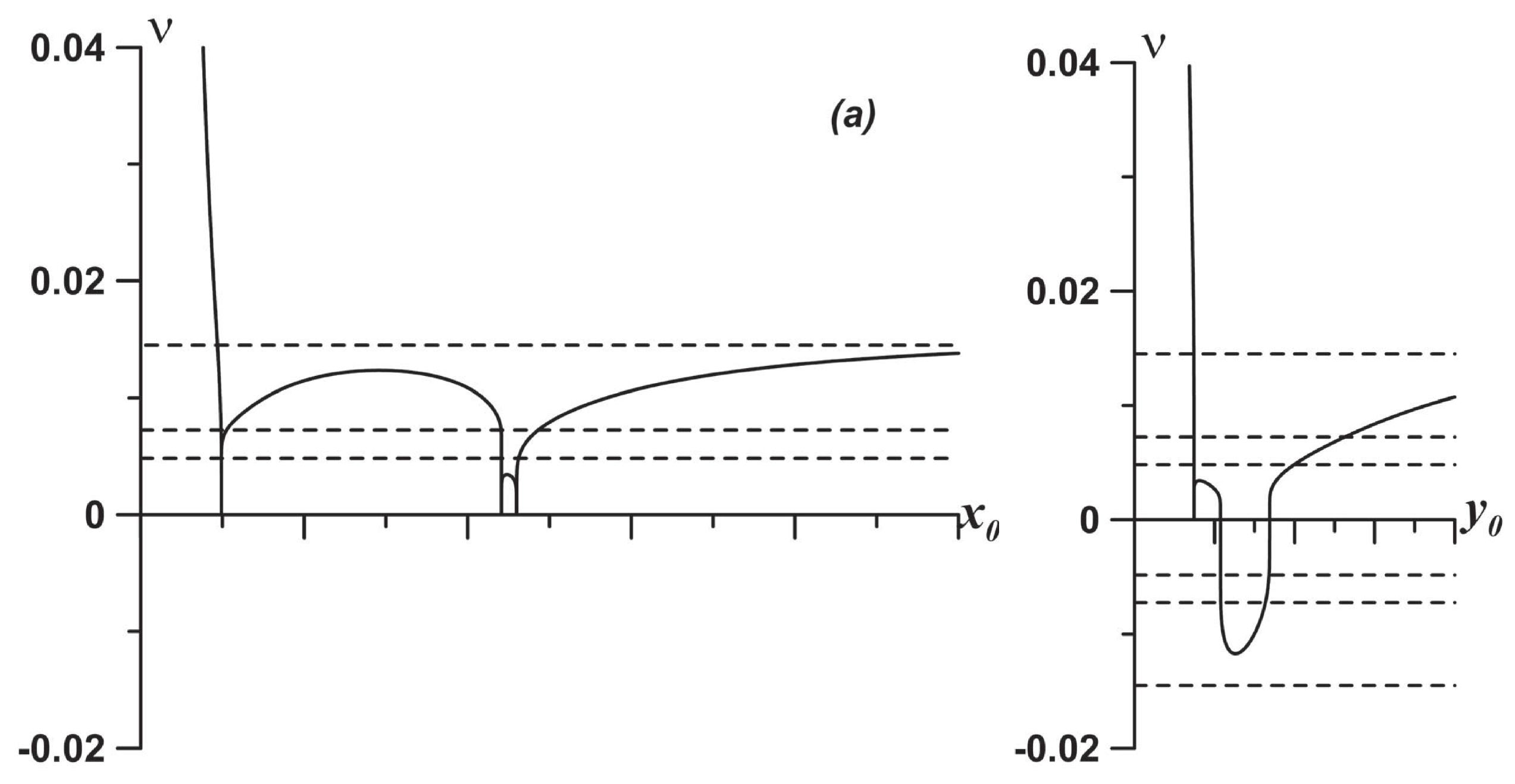
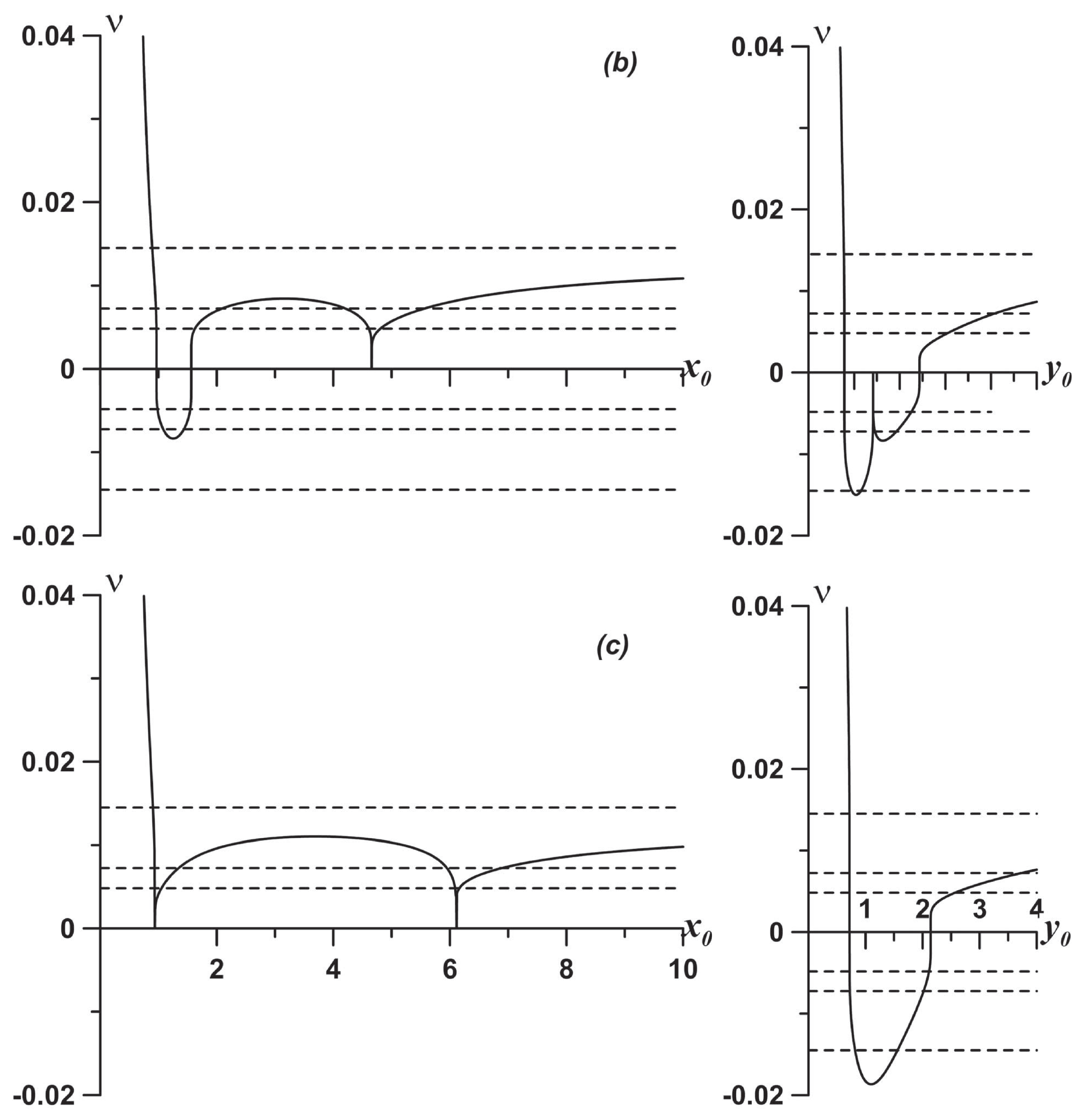
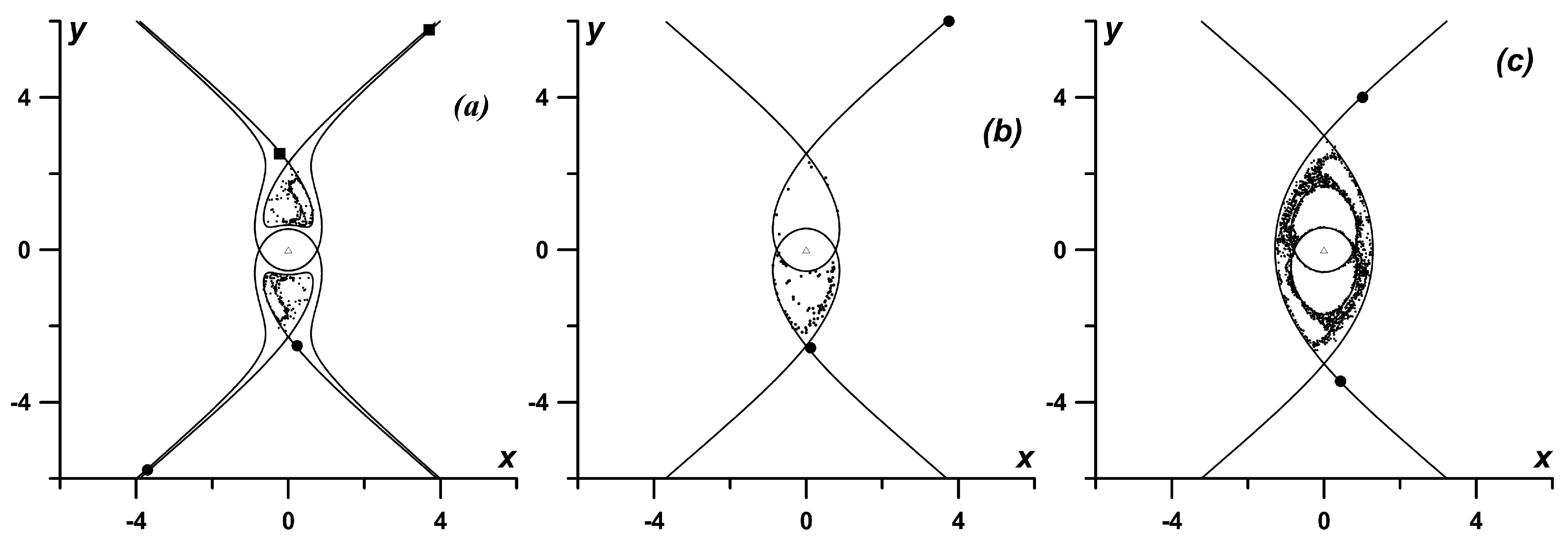
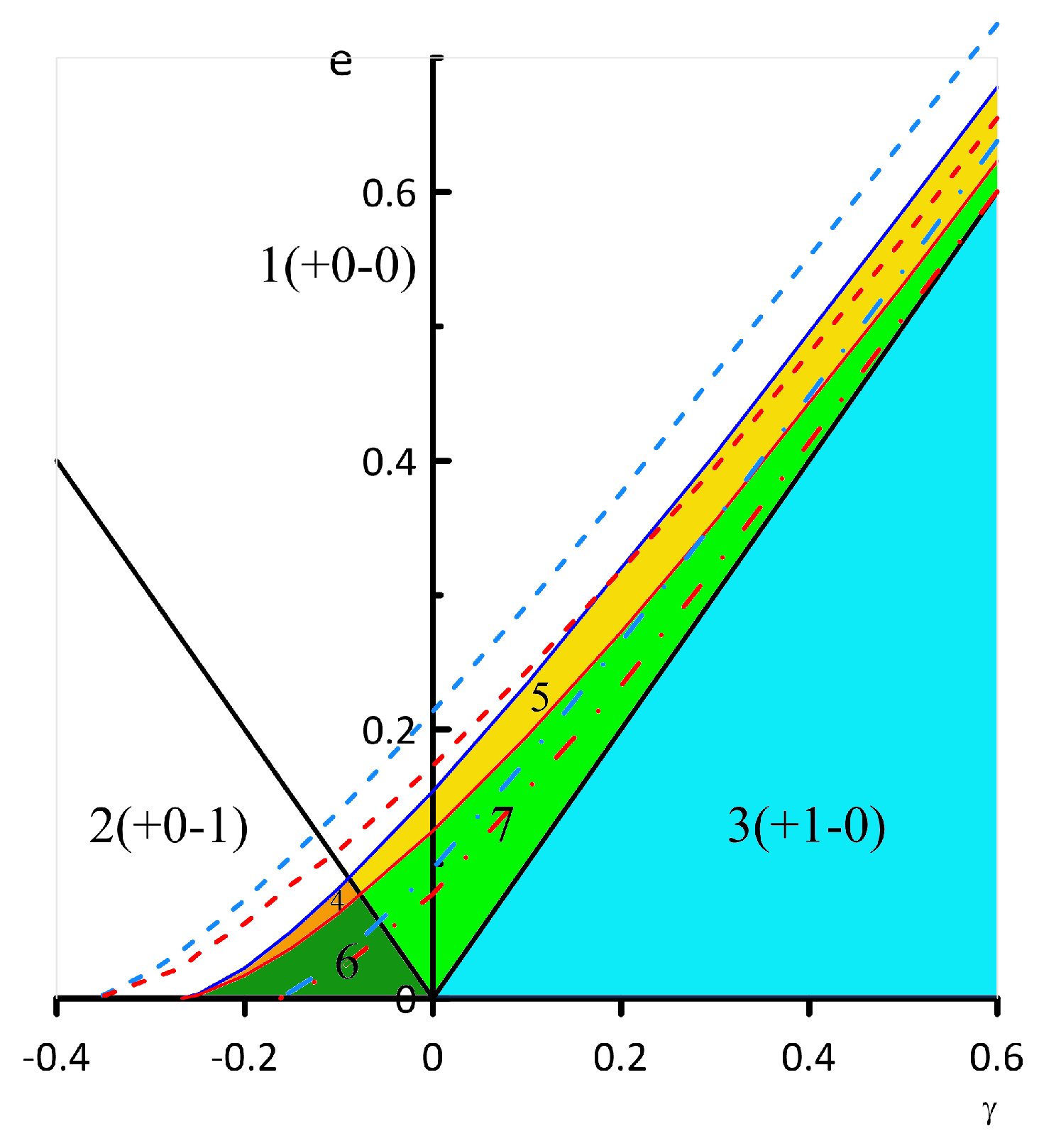
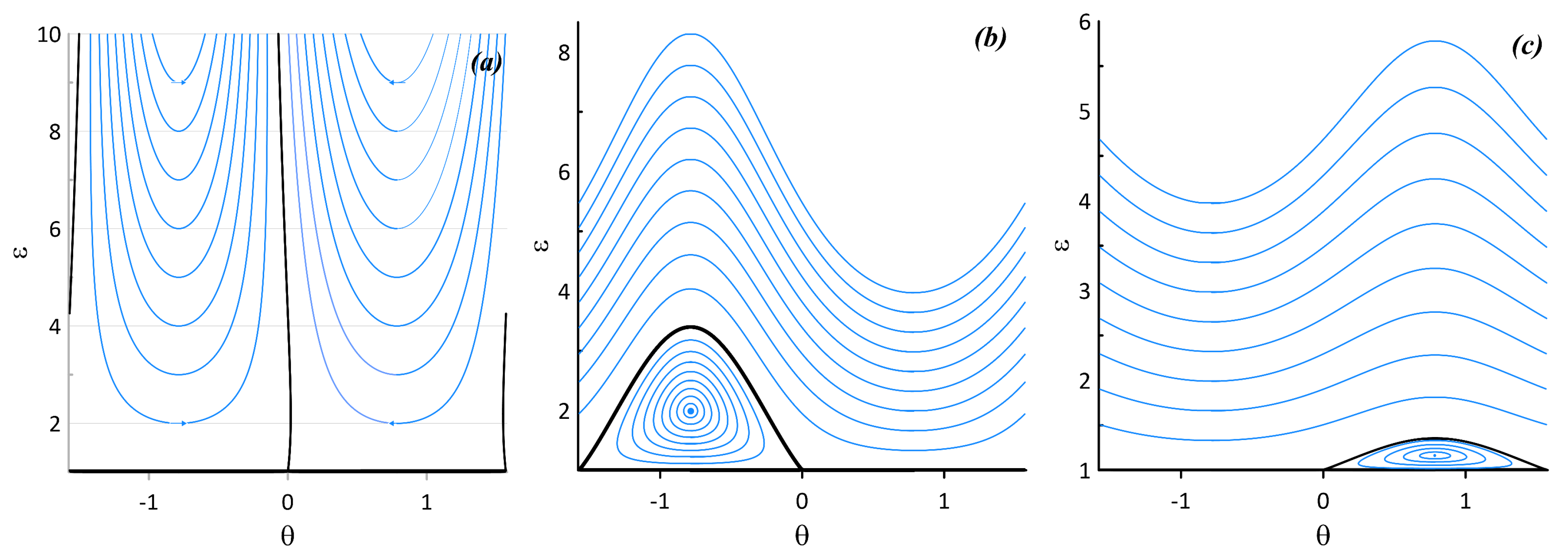
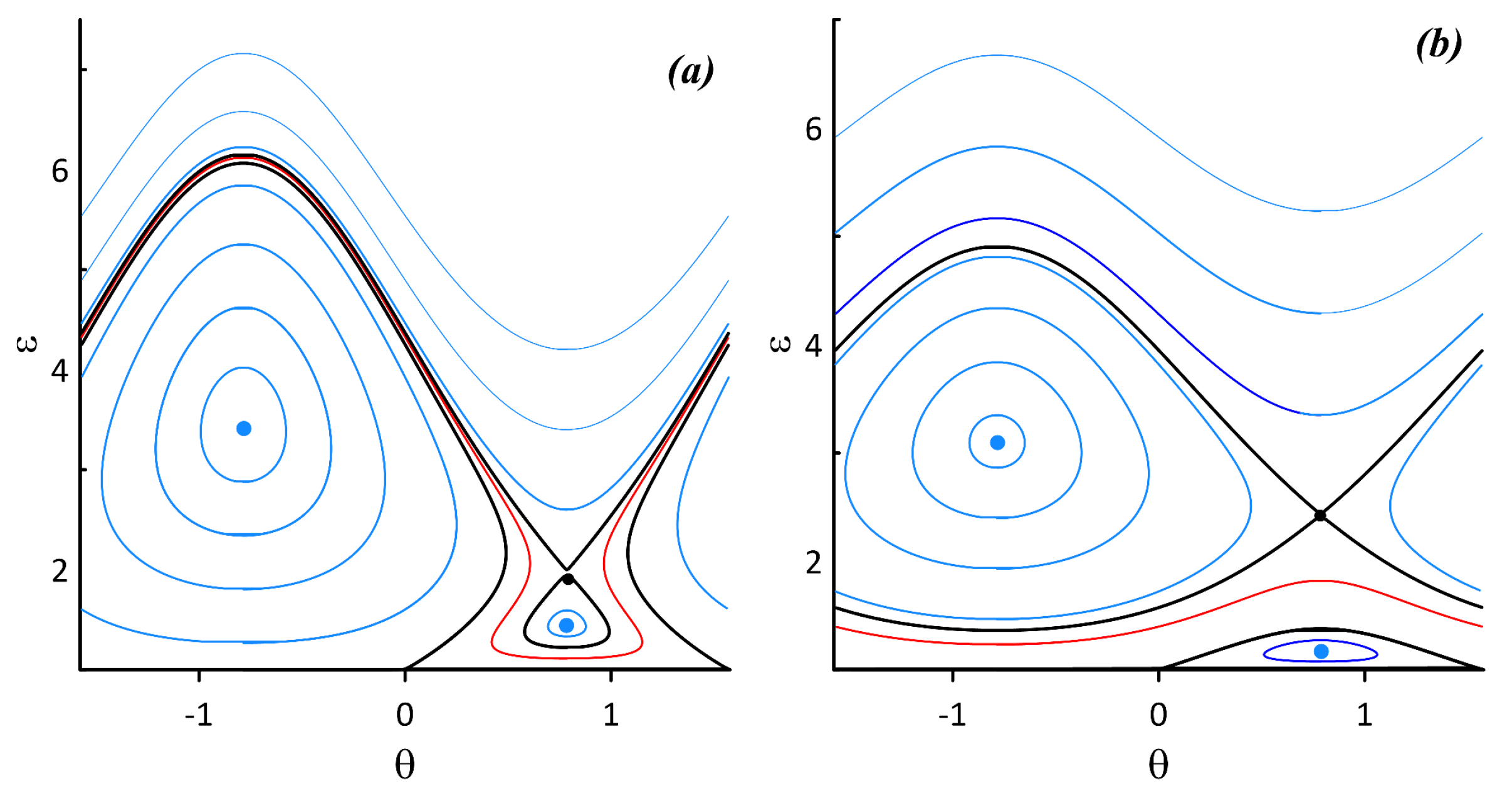
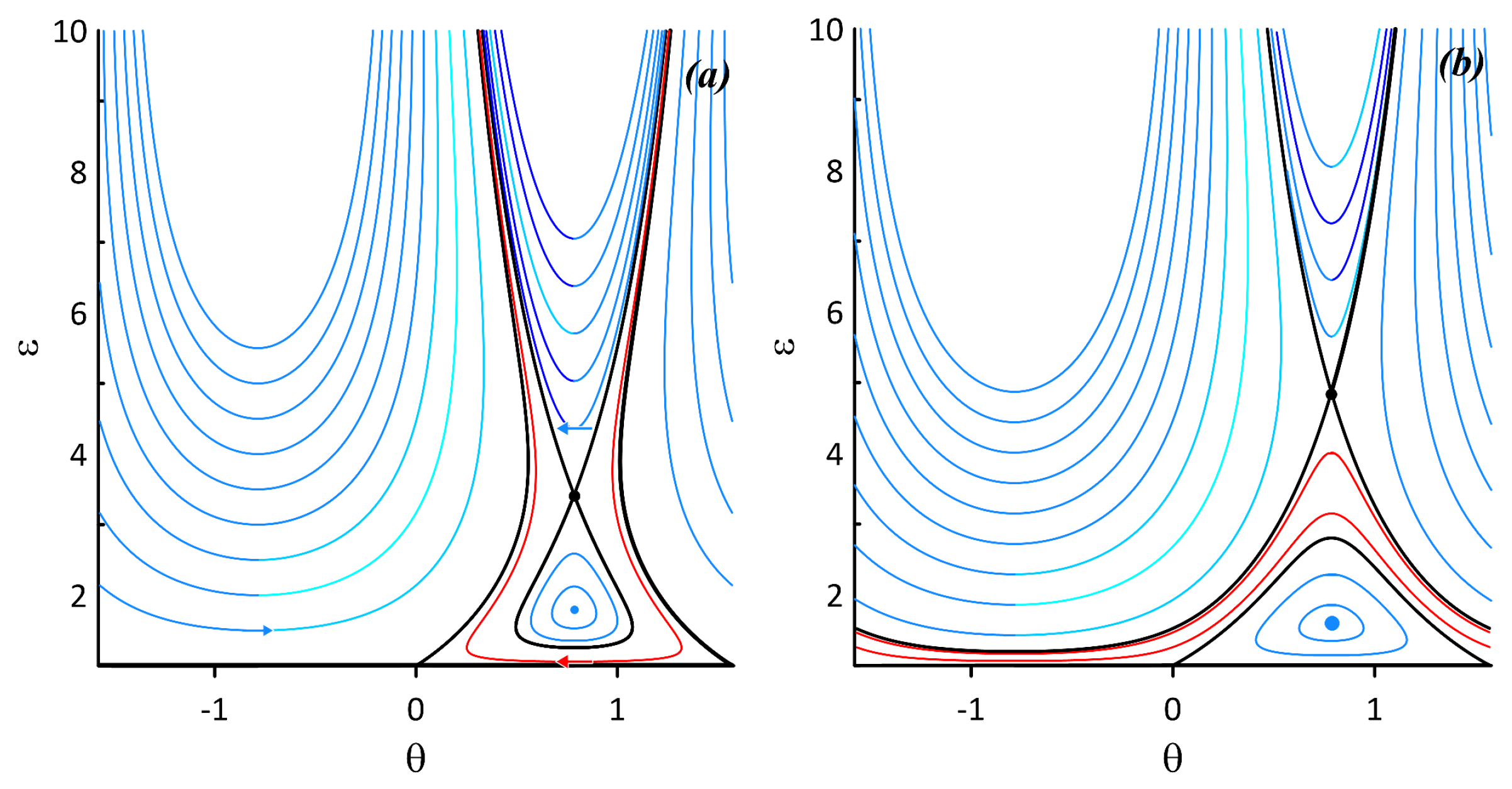
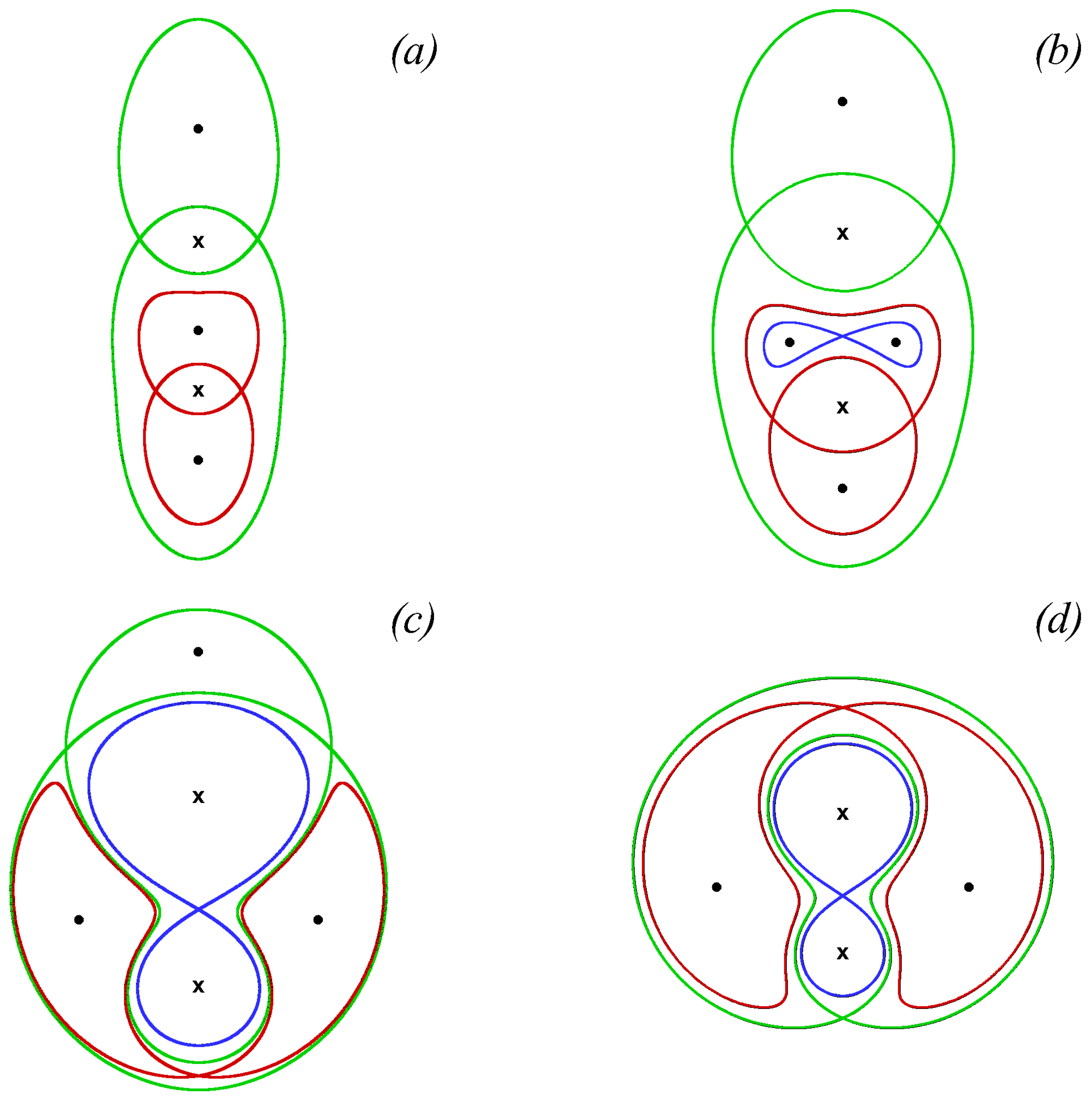
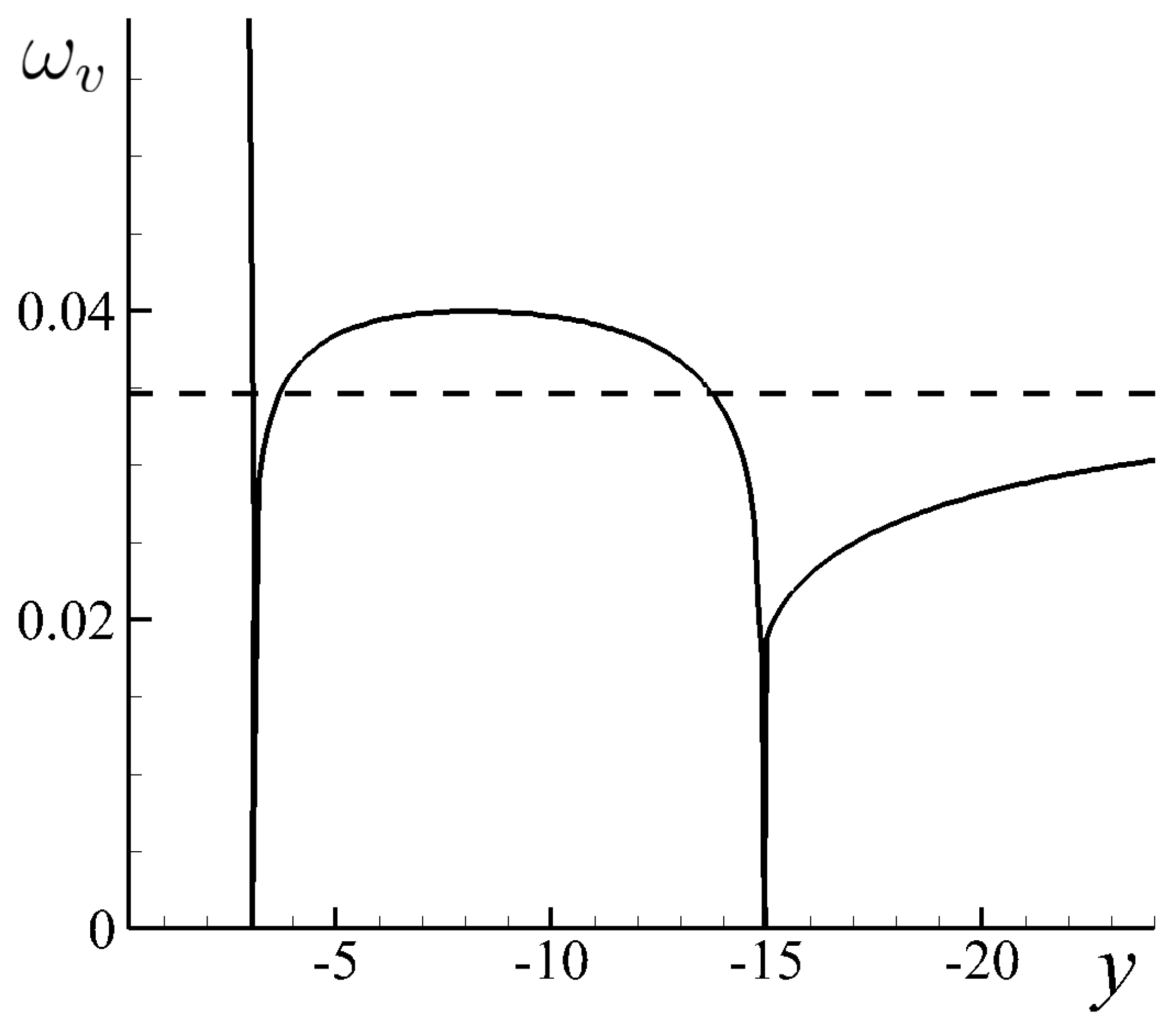
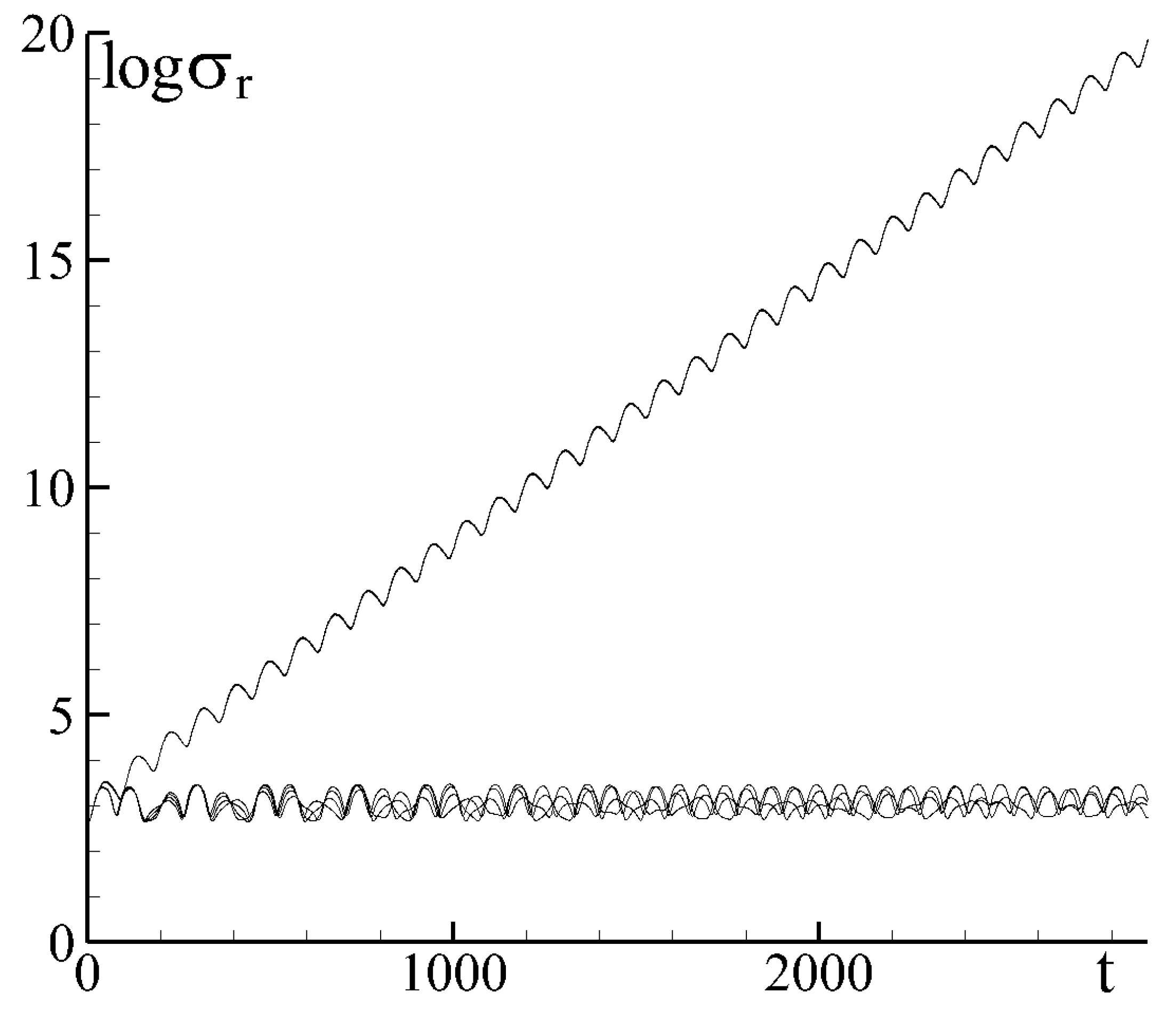
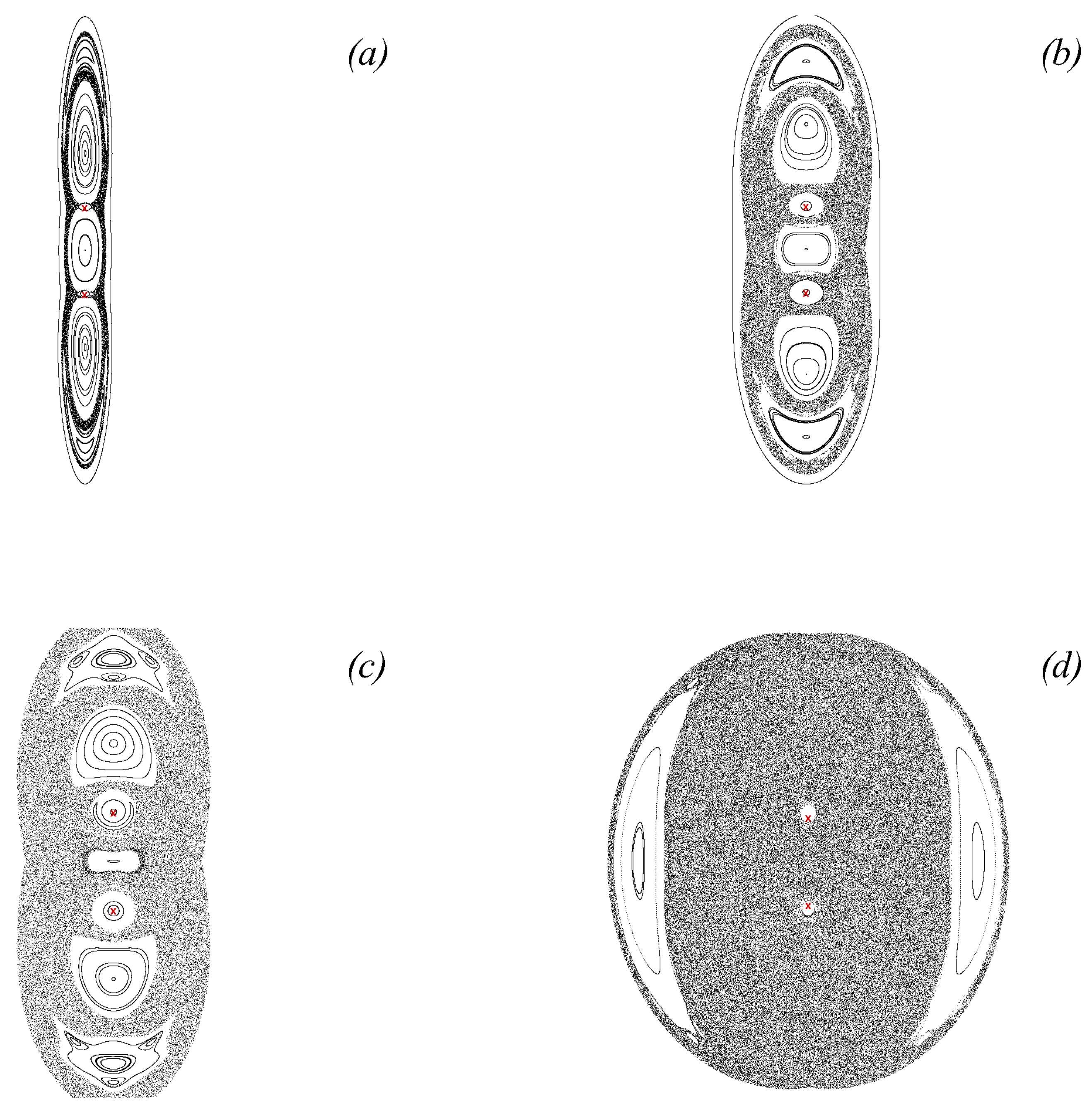
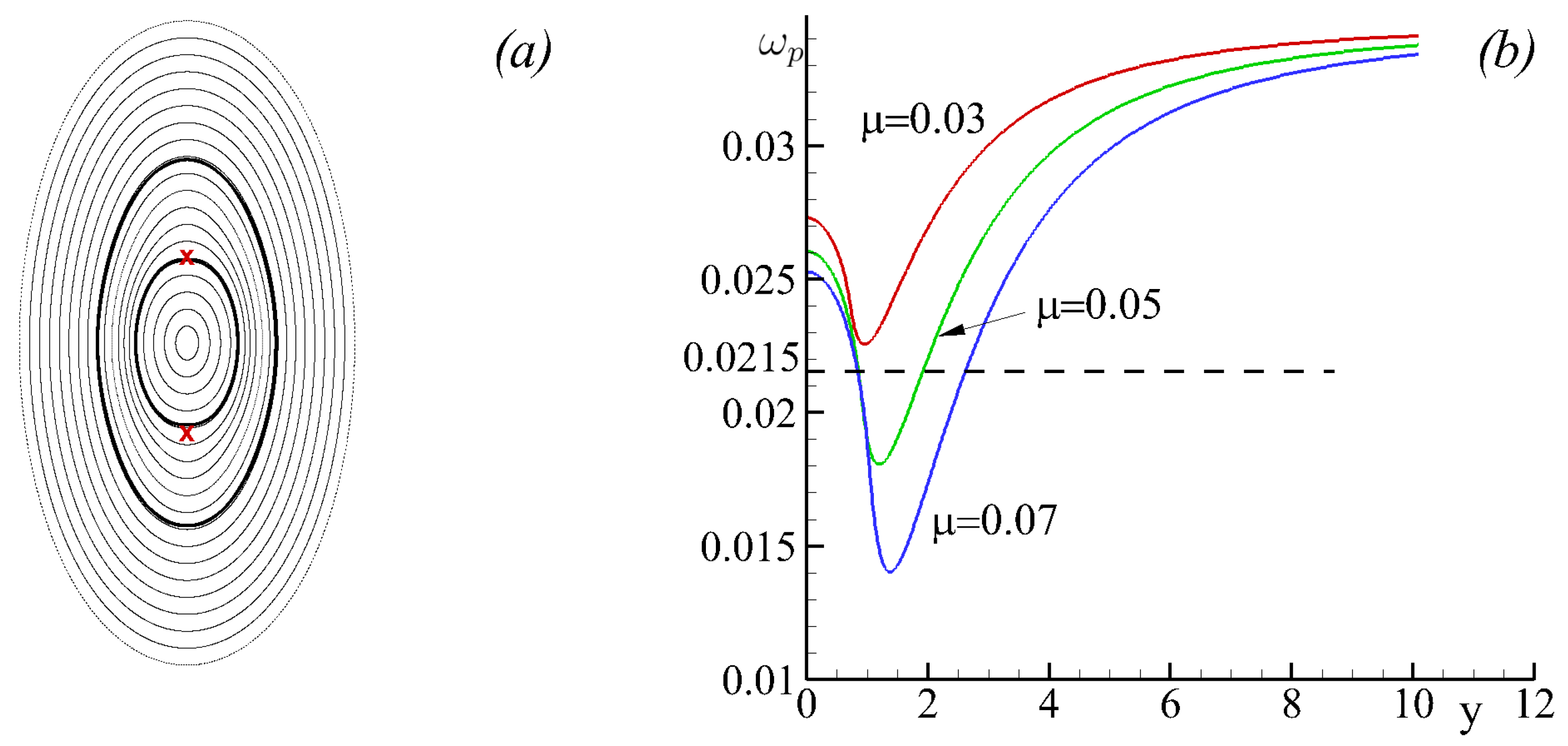
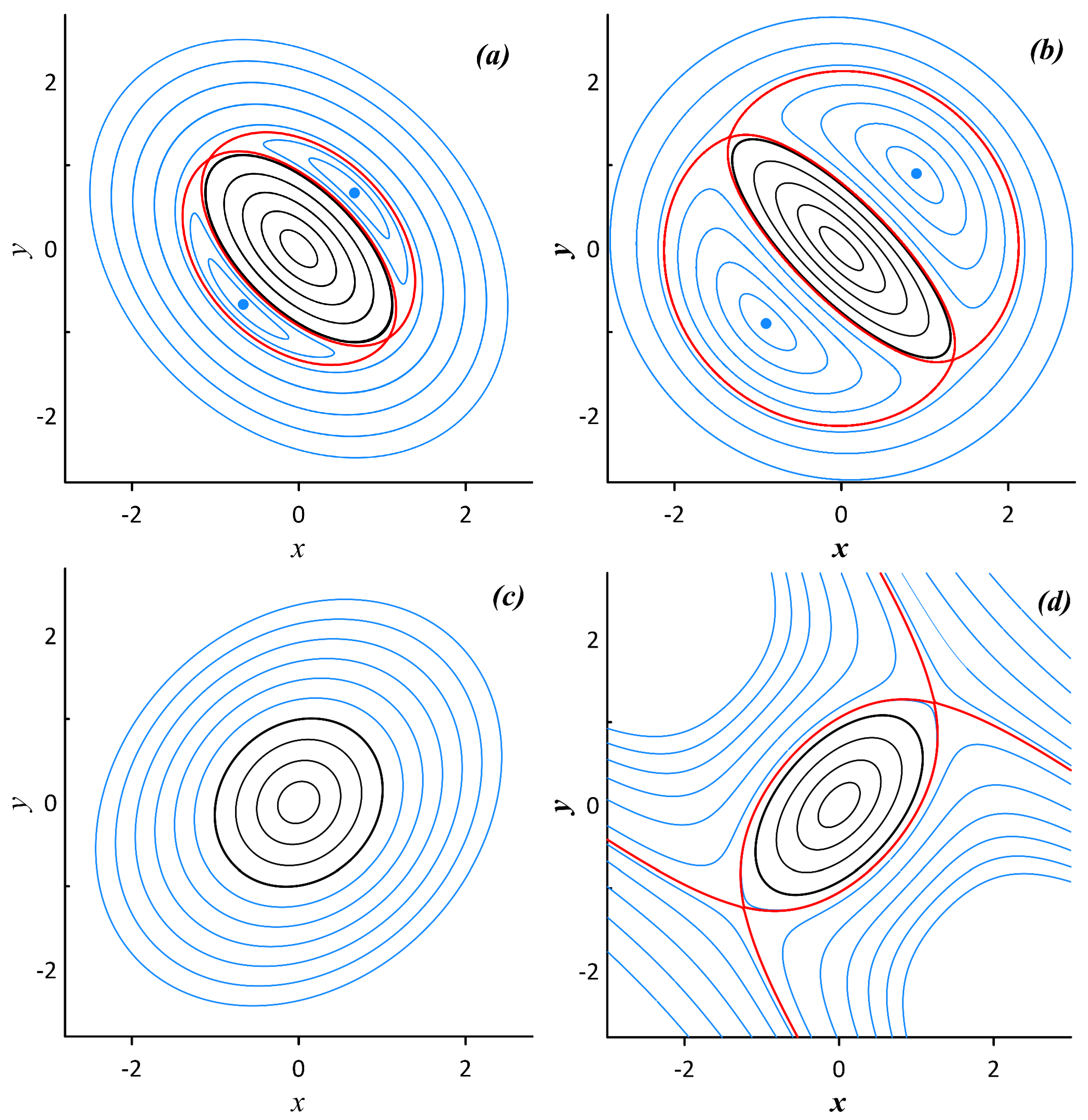
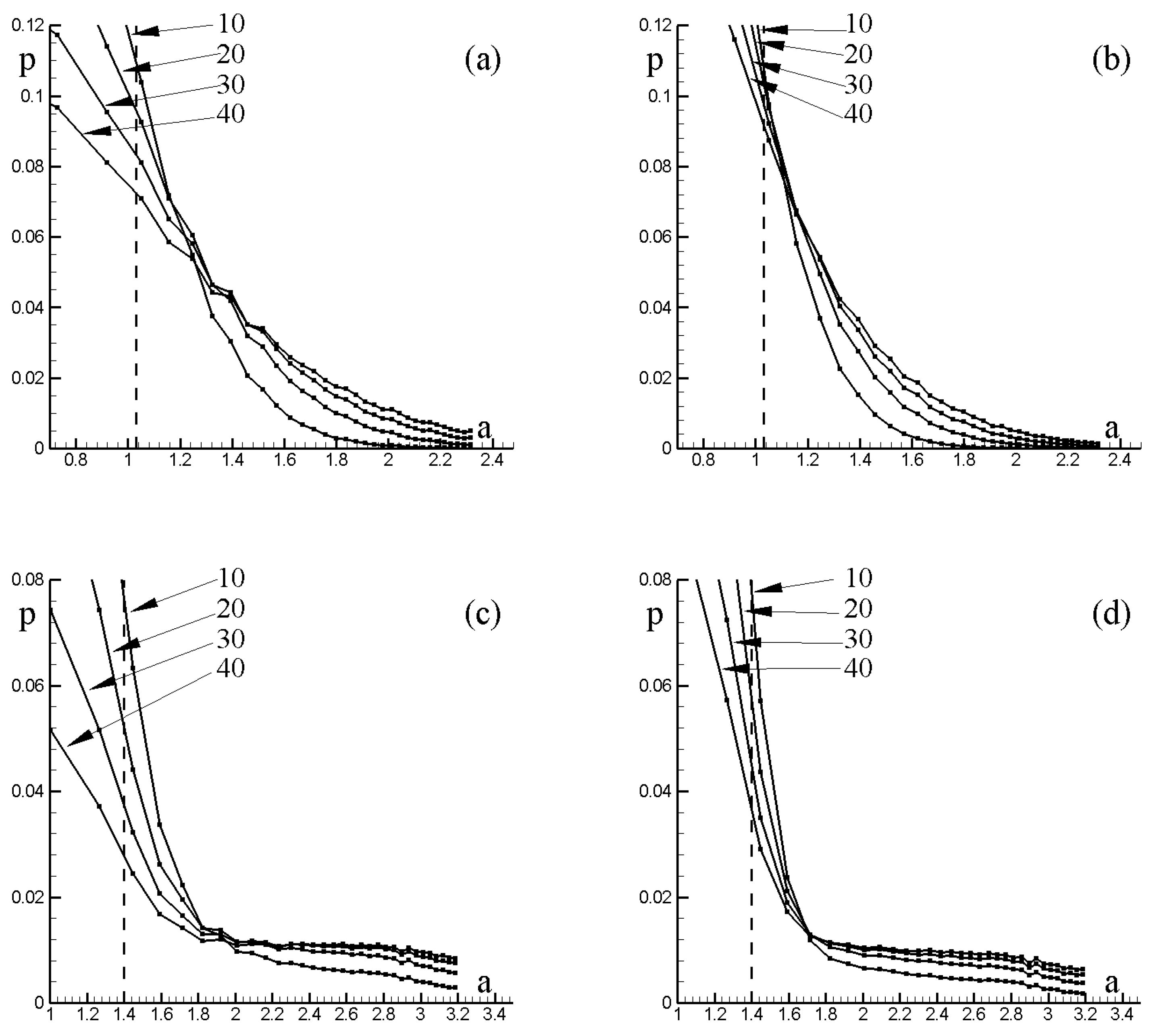
3.2.2. Parametric Instability of the Relative Vortex Motion Near Elliptic Fixed Points
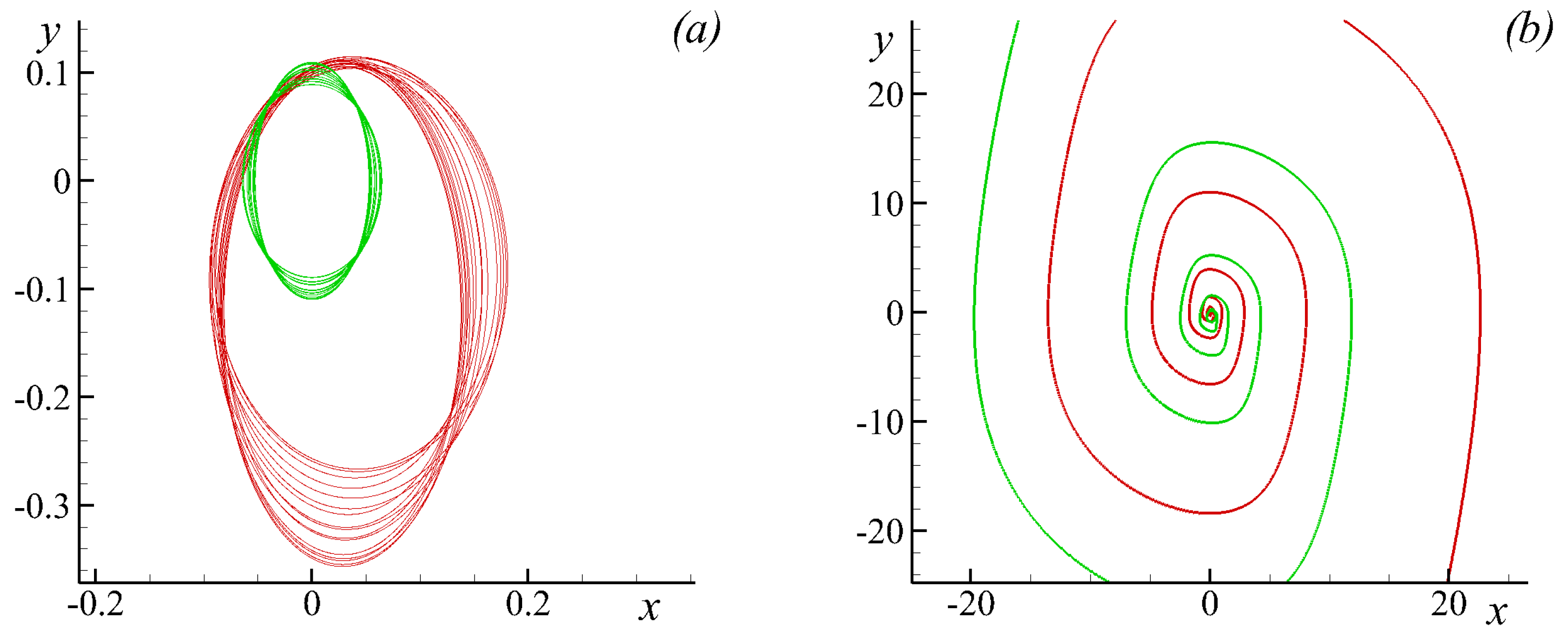
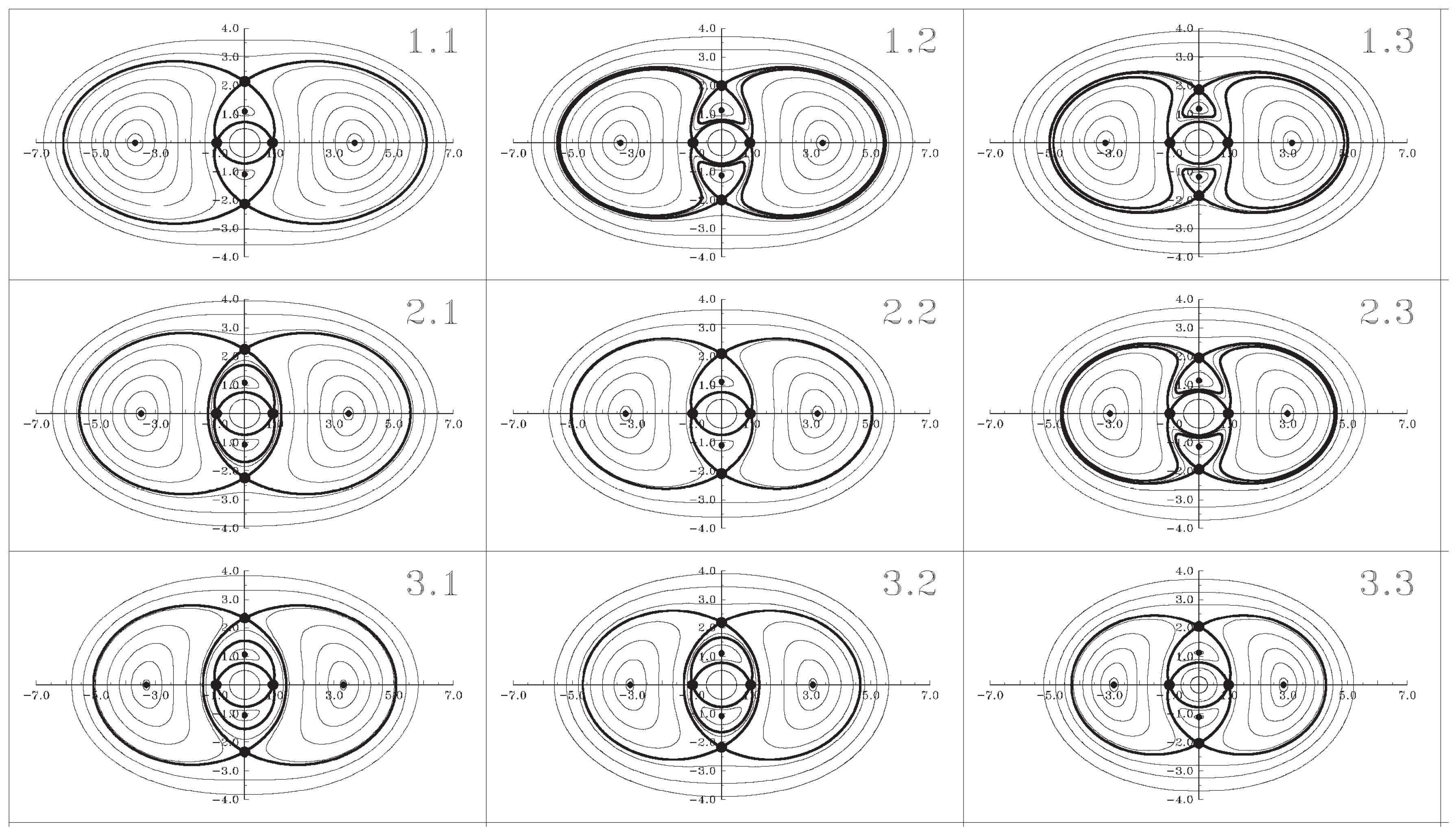
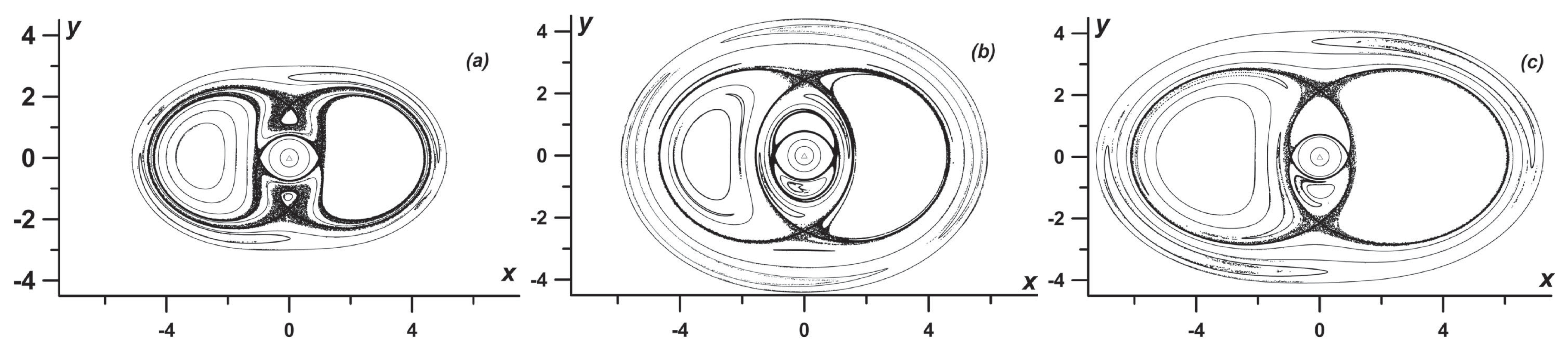
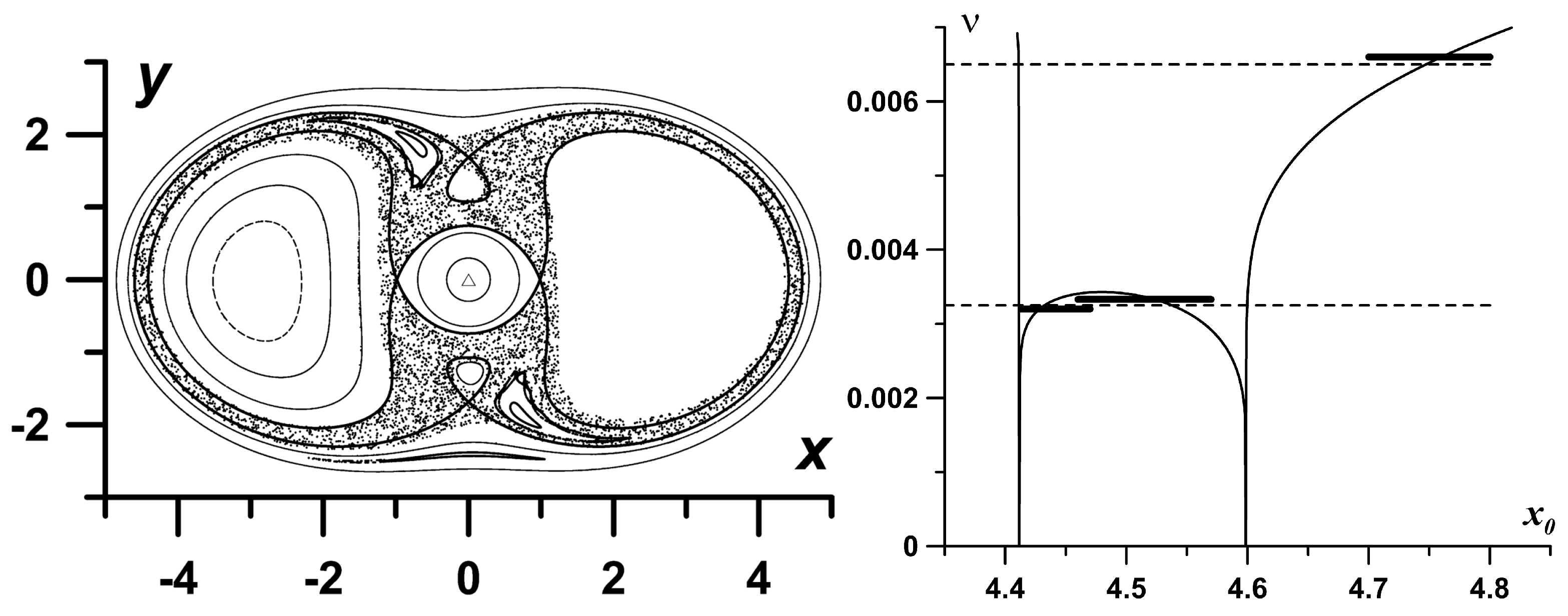
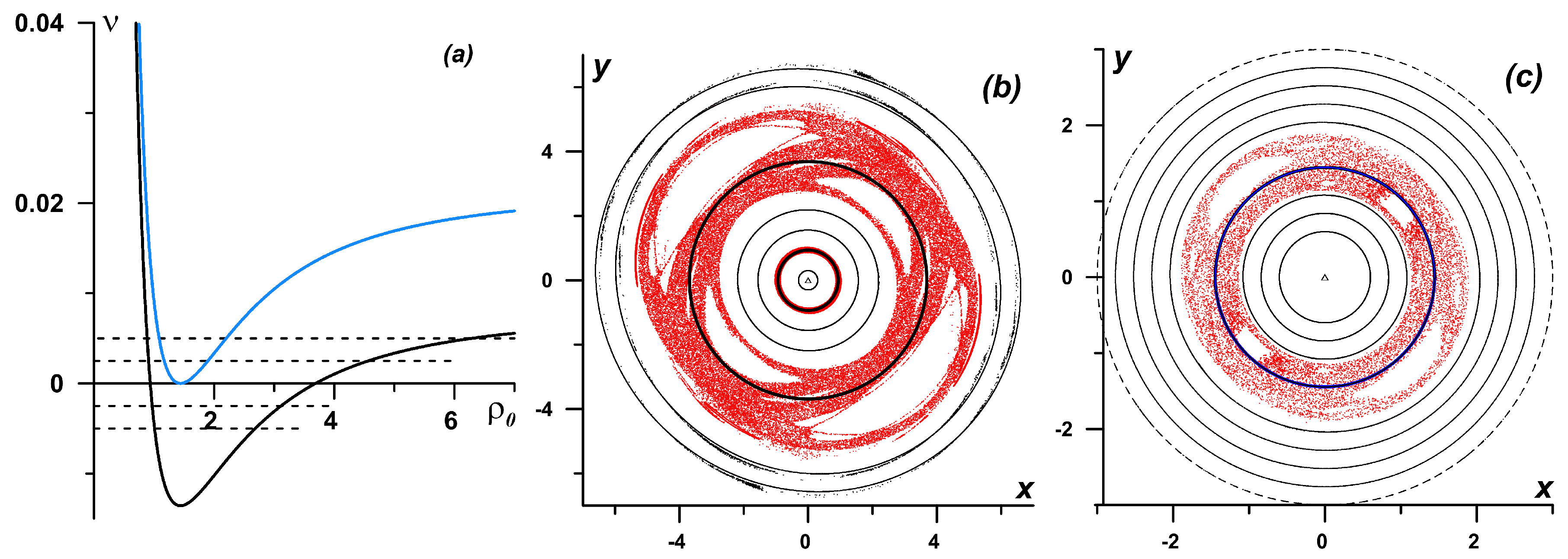
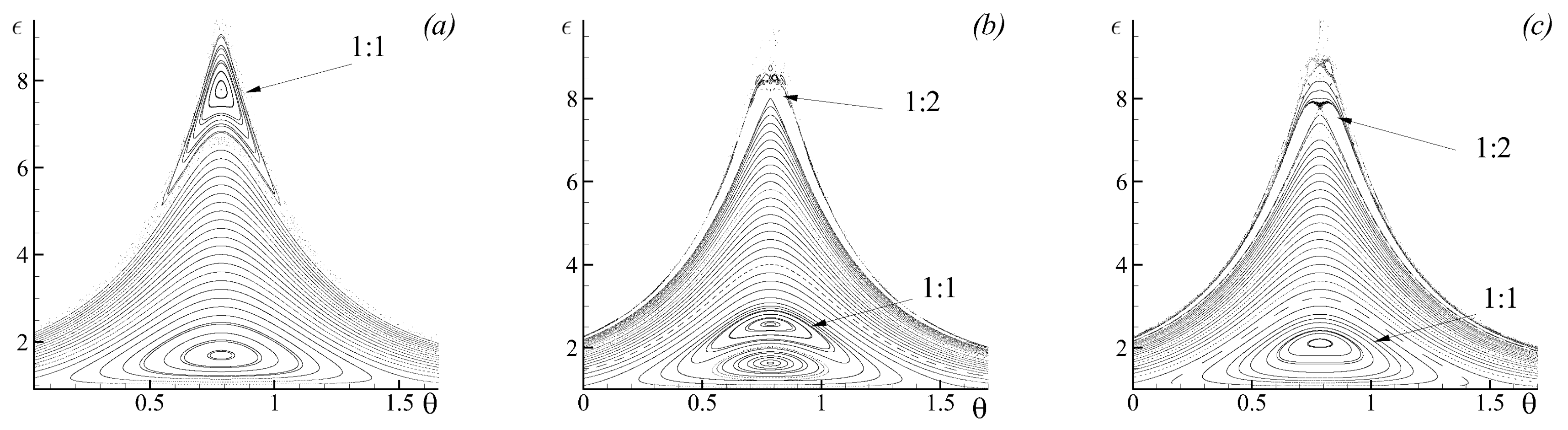
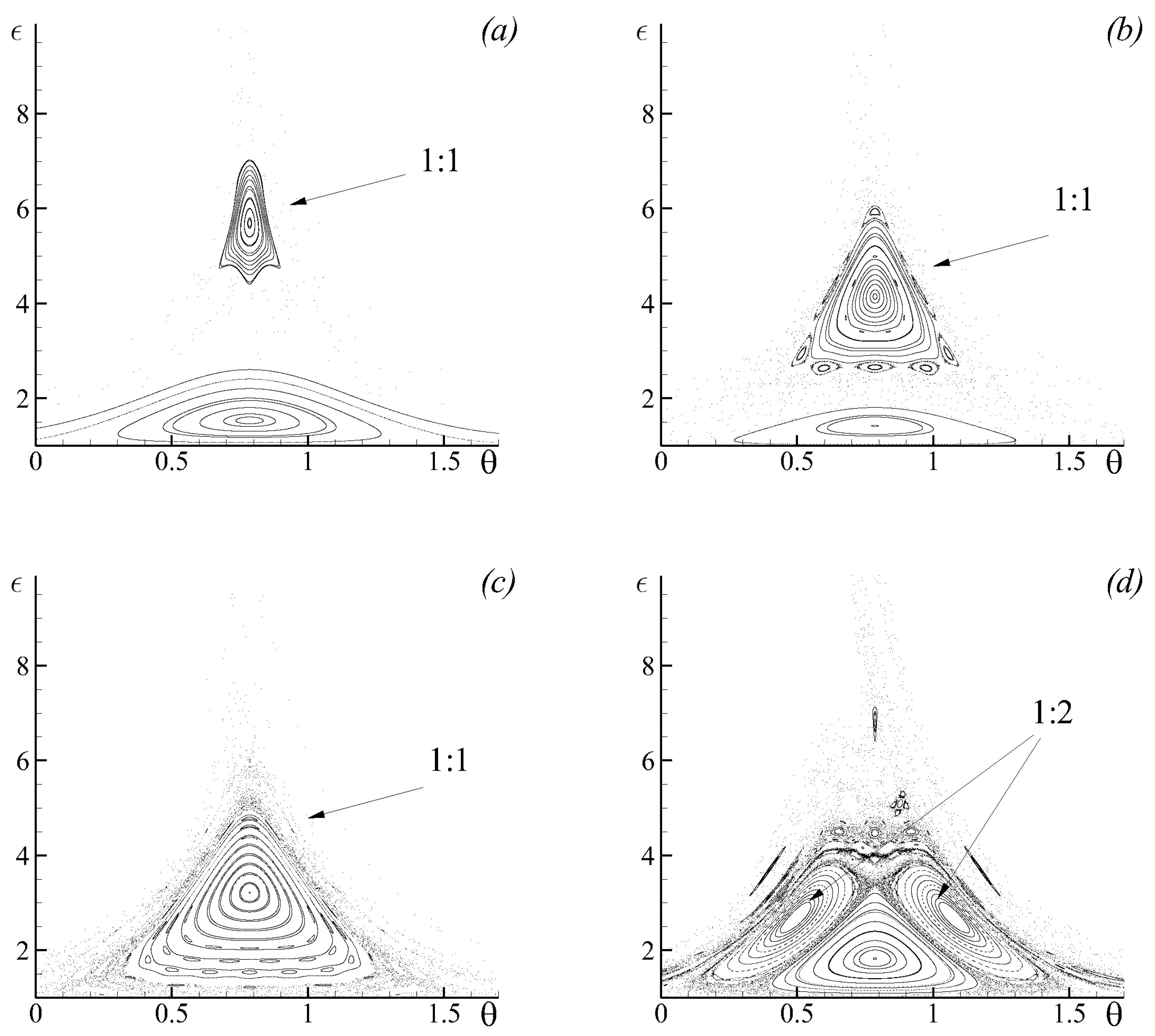
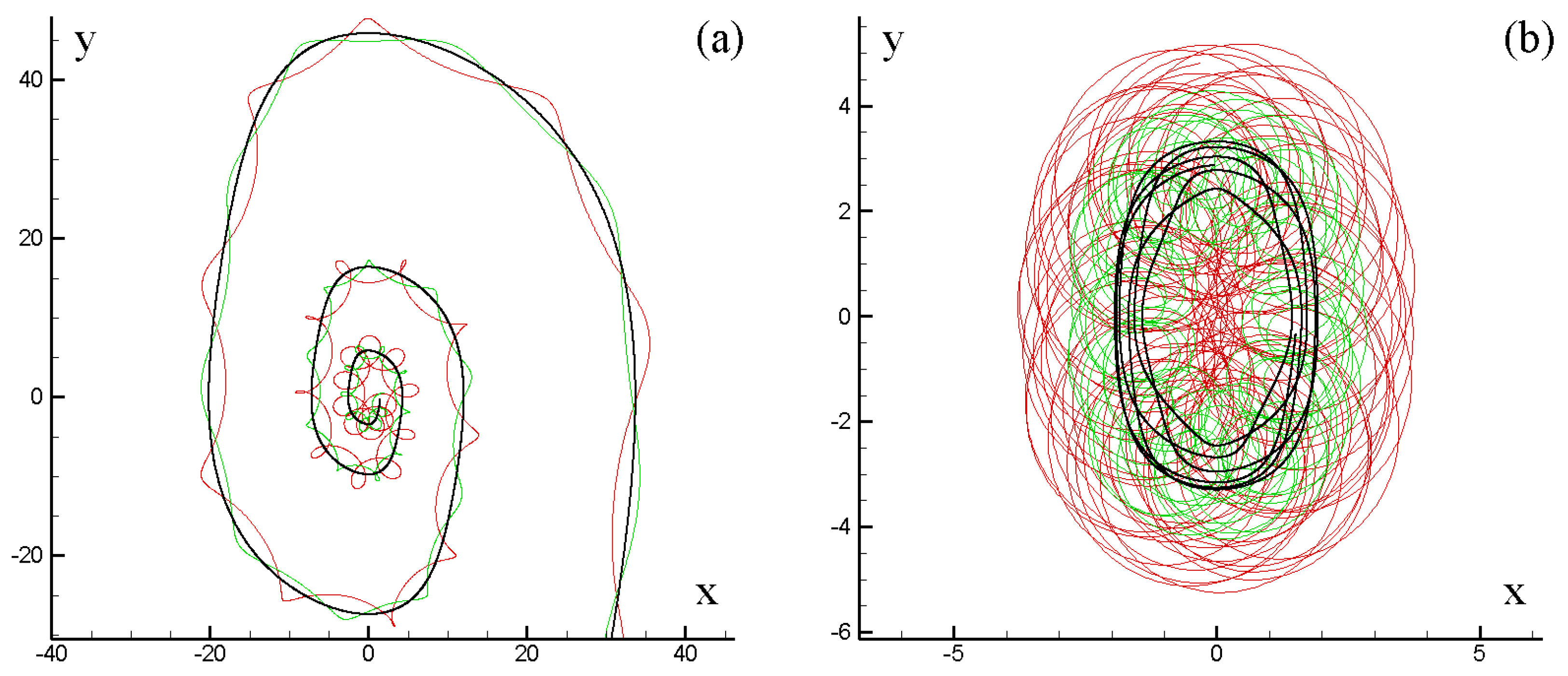
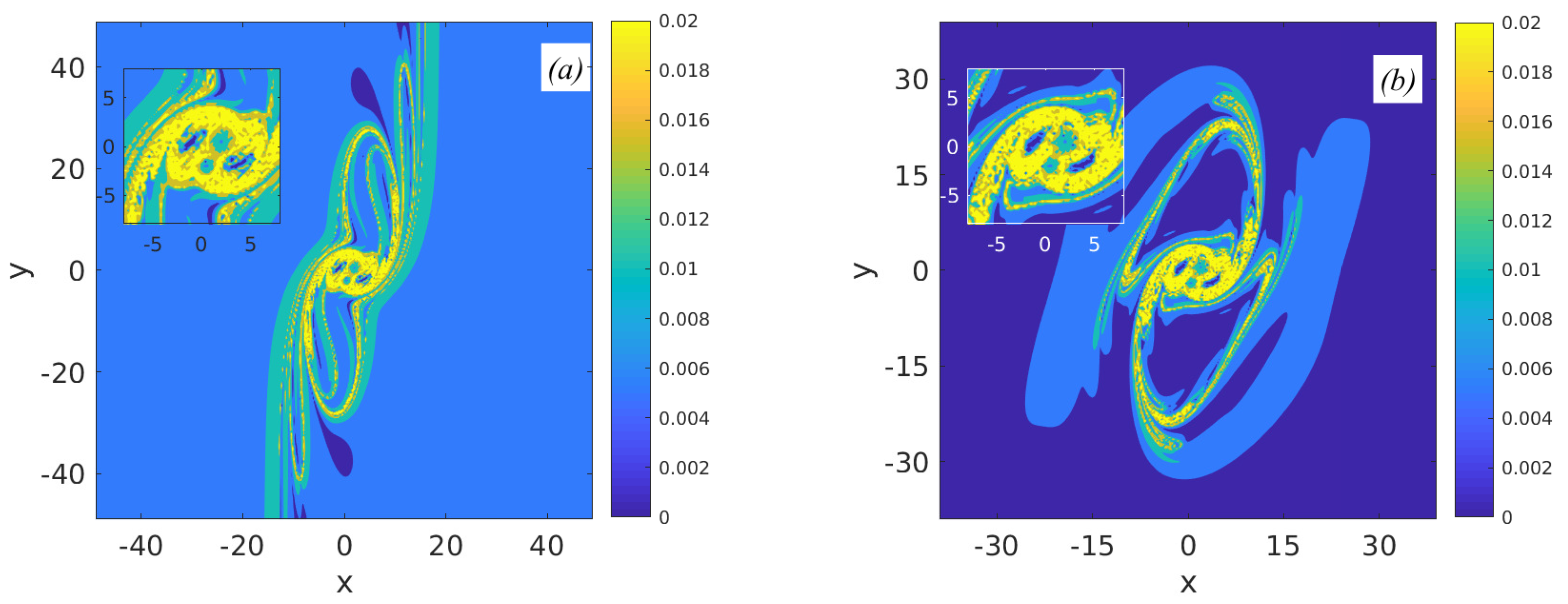
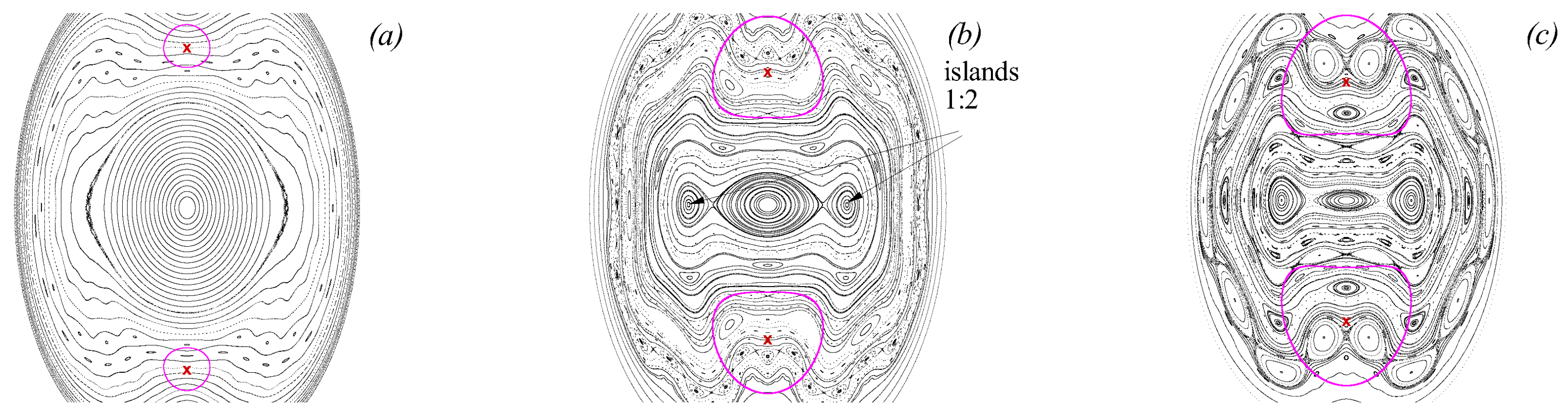
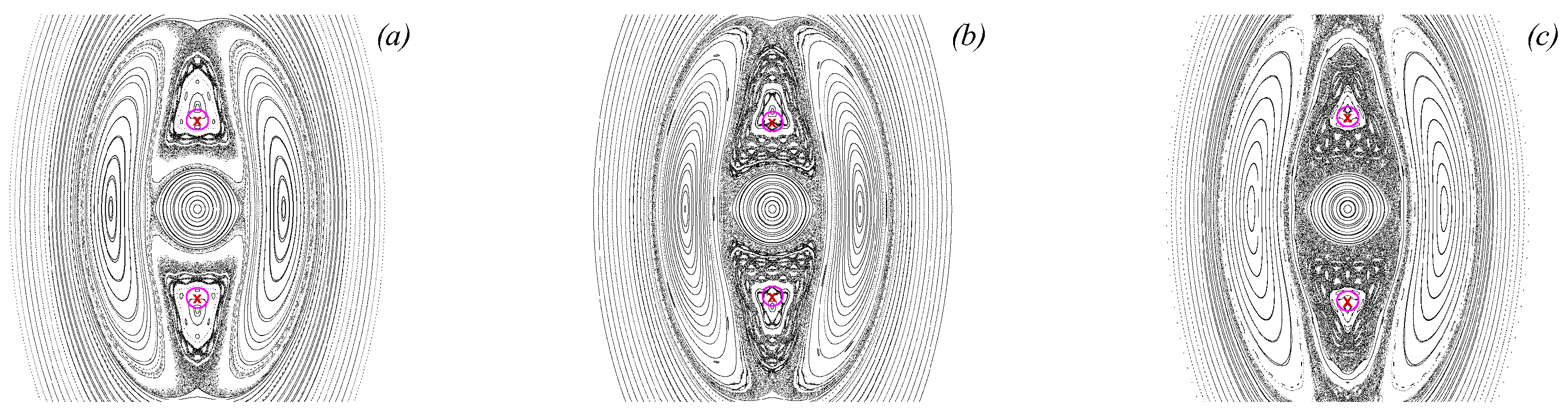
3.3. Chaotic Dynamics of Singular Vortices
3.4. Regular and Chaotic Motion of a Reduced Two-Layer Three-Vortex Problem in a Non-Stationary Deformation Flow
4. Regular and Chaotic Dynamics in the Systems of Distributed Vortices (Elliptical and Ellipsoidal)
4.1. Regular Dynamics of an Ellipsoidal Vortex
Parametric Instability of the Relative Motion of an Elliptic Vortex
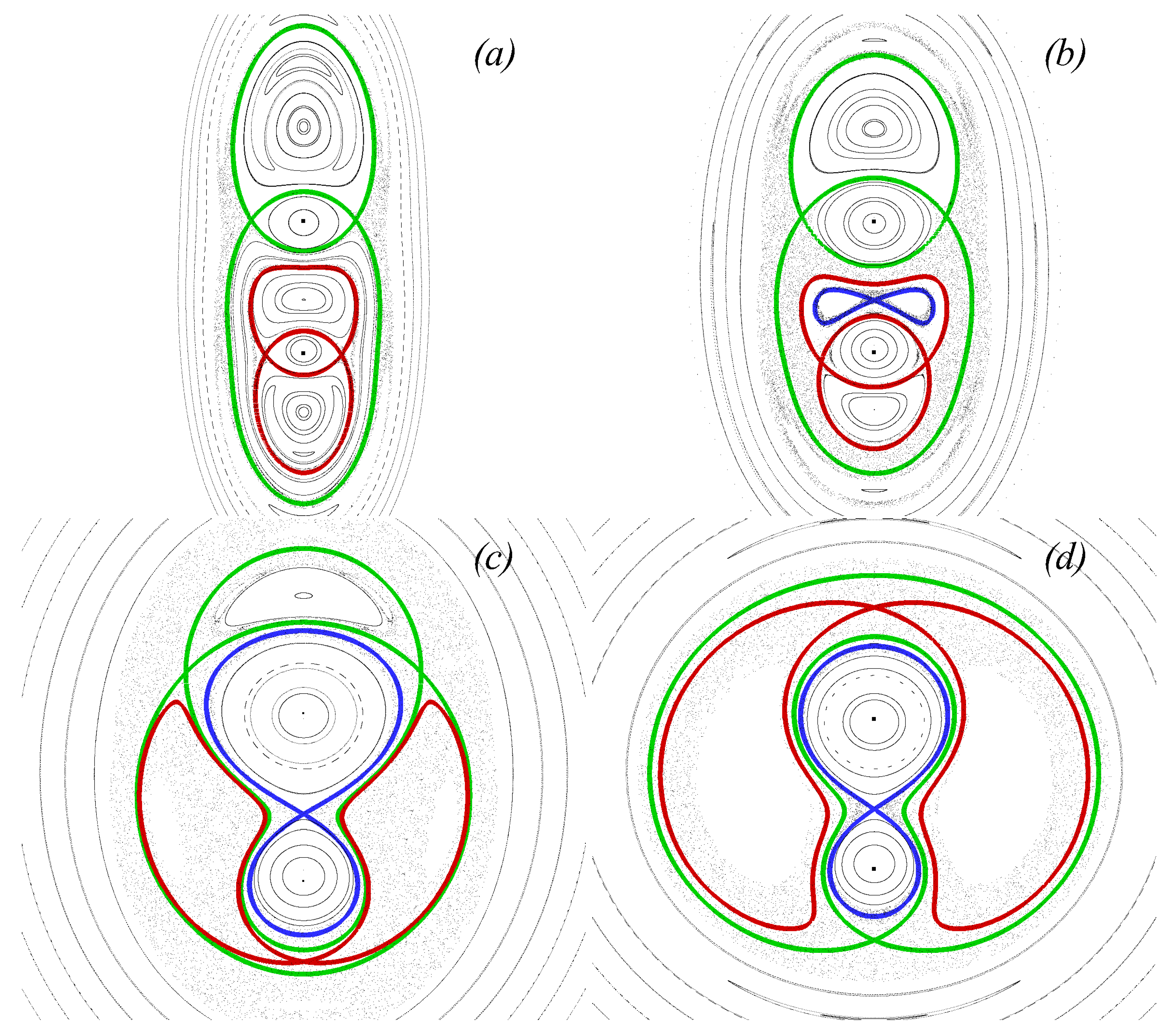
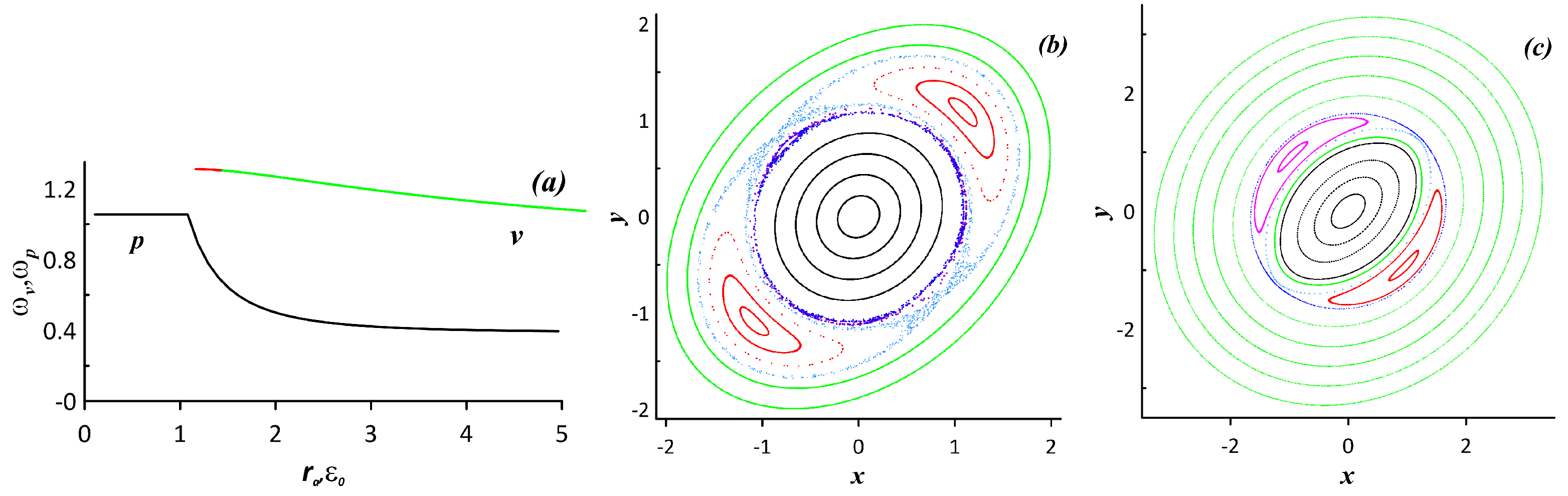
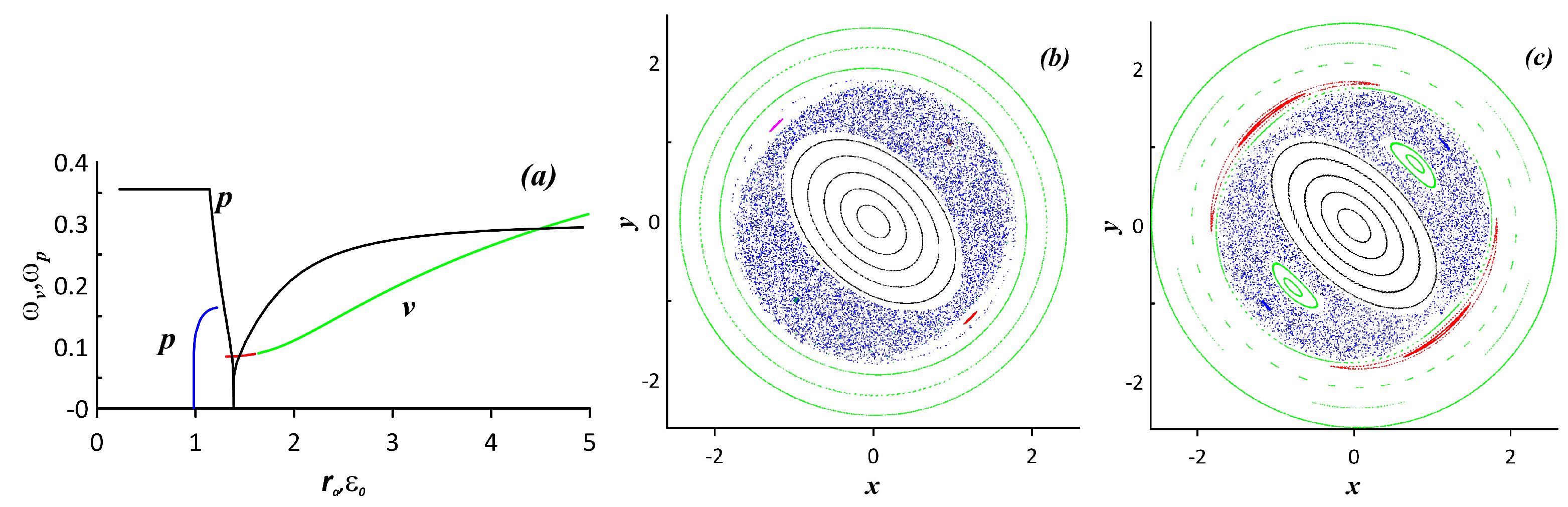
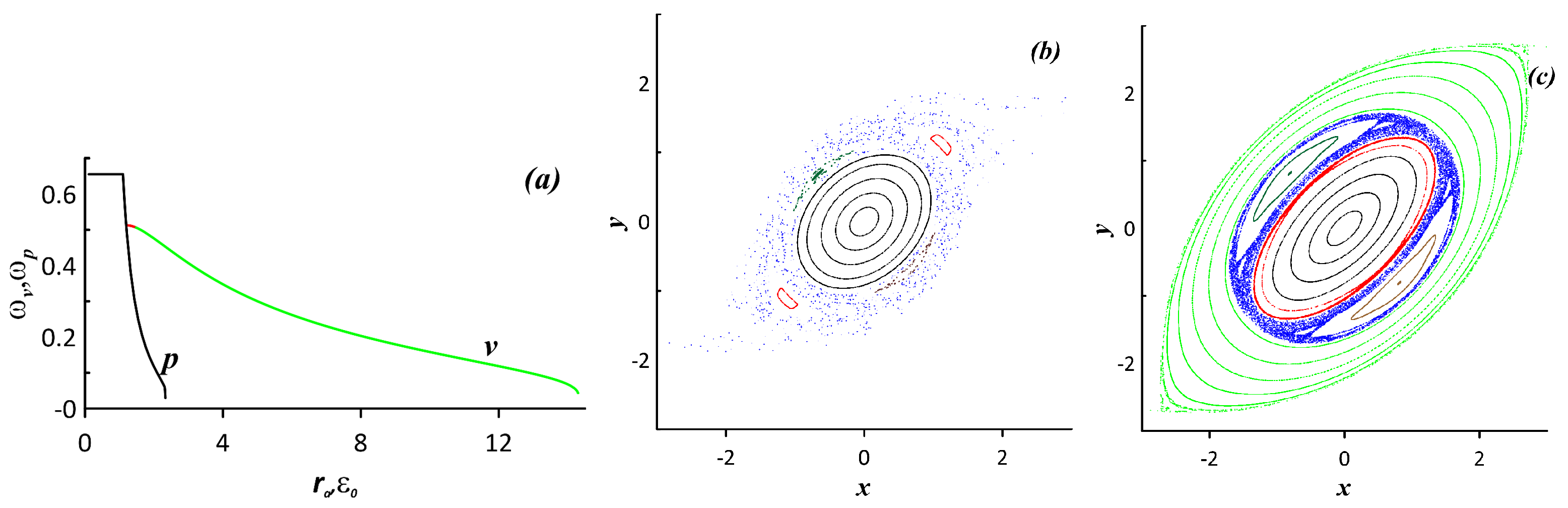
4.2. Chaotic Dynamics of an Elliptic Vorticity Patch Subject to an Alternating Deformation Flow
5. Regular and Chaotic Advection of Scalars Induced by Point Vortex Systems Subjected to Deformation Flows
5.1. Barotropic Flow with Two Singular Vortices Subject to Deformation Flow
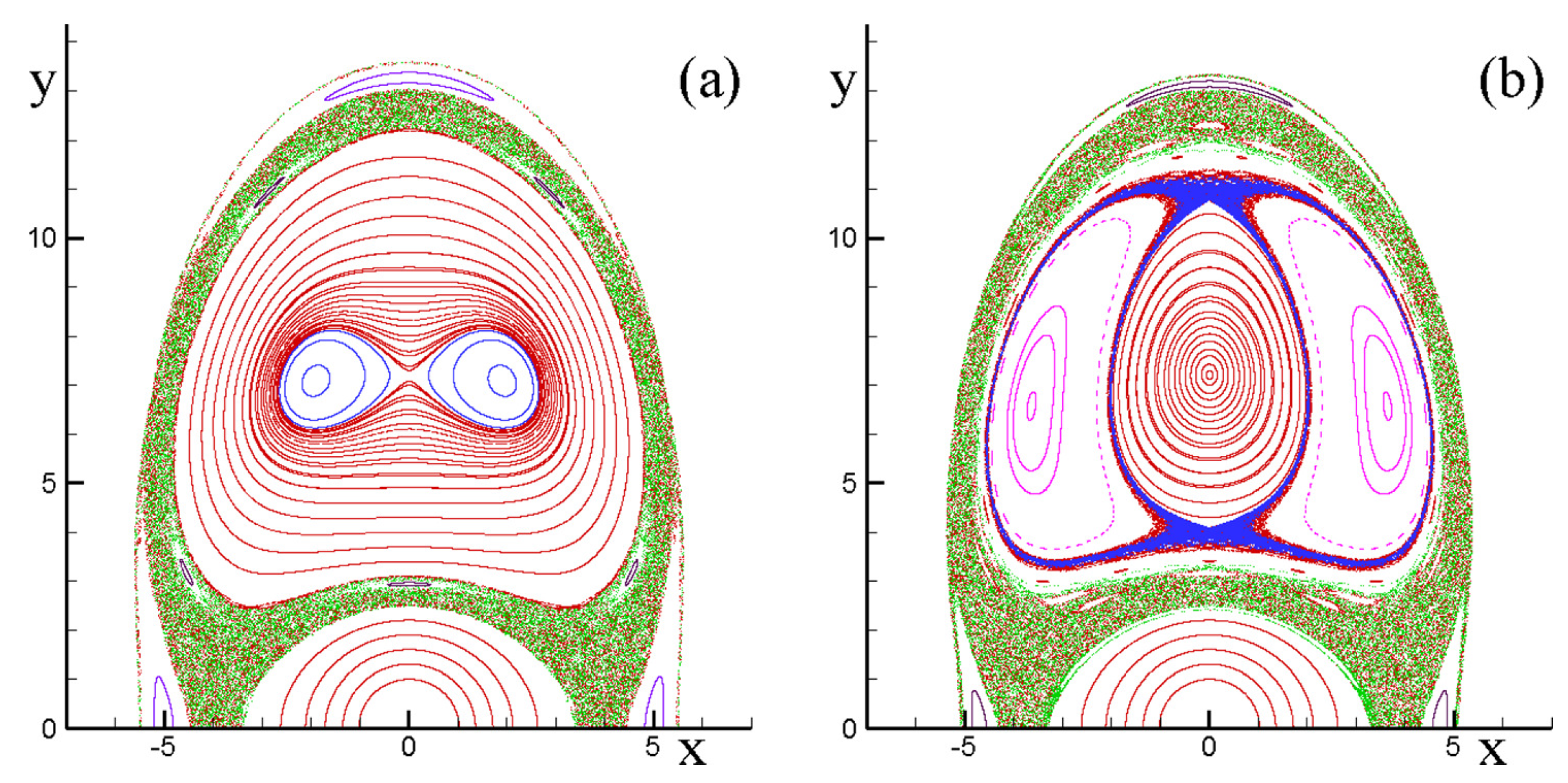
5.2. Fluid Particle Advection in the System Subject to an Alternating Deformation Flow in the Parametric Instability Regime
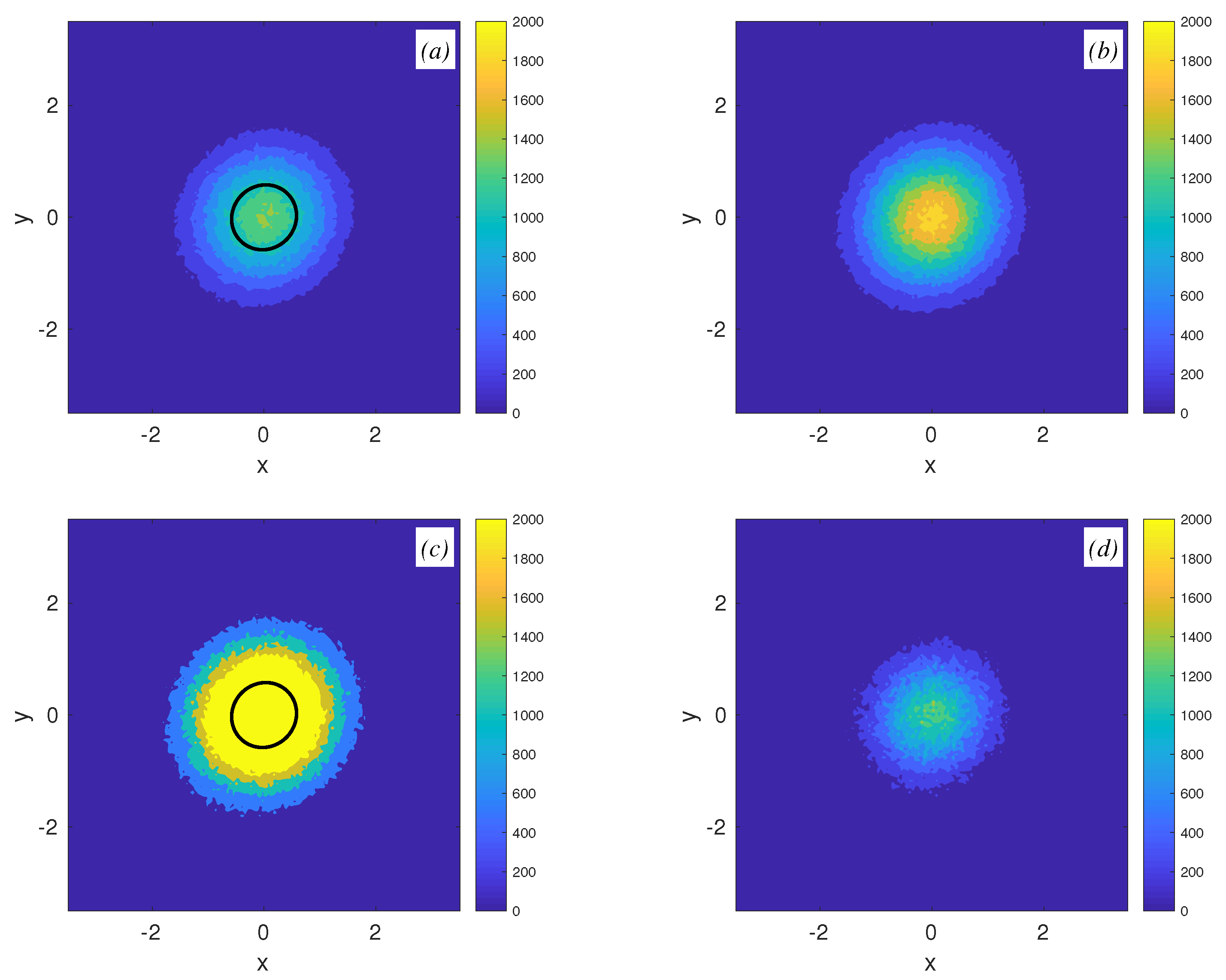
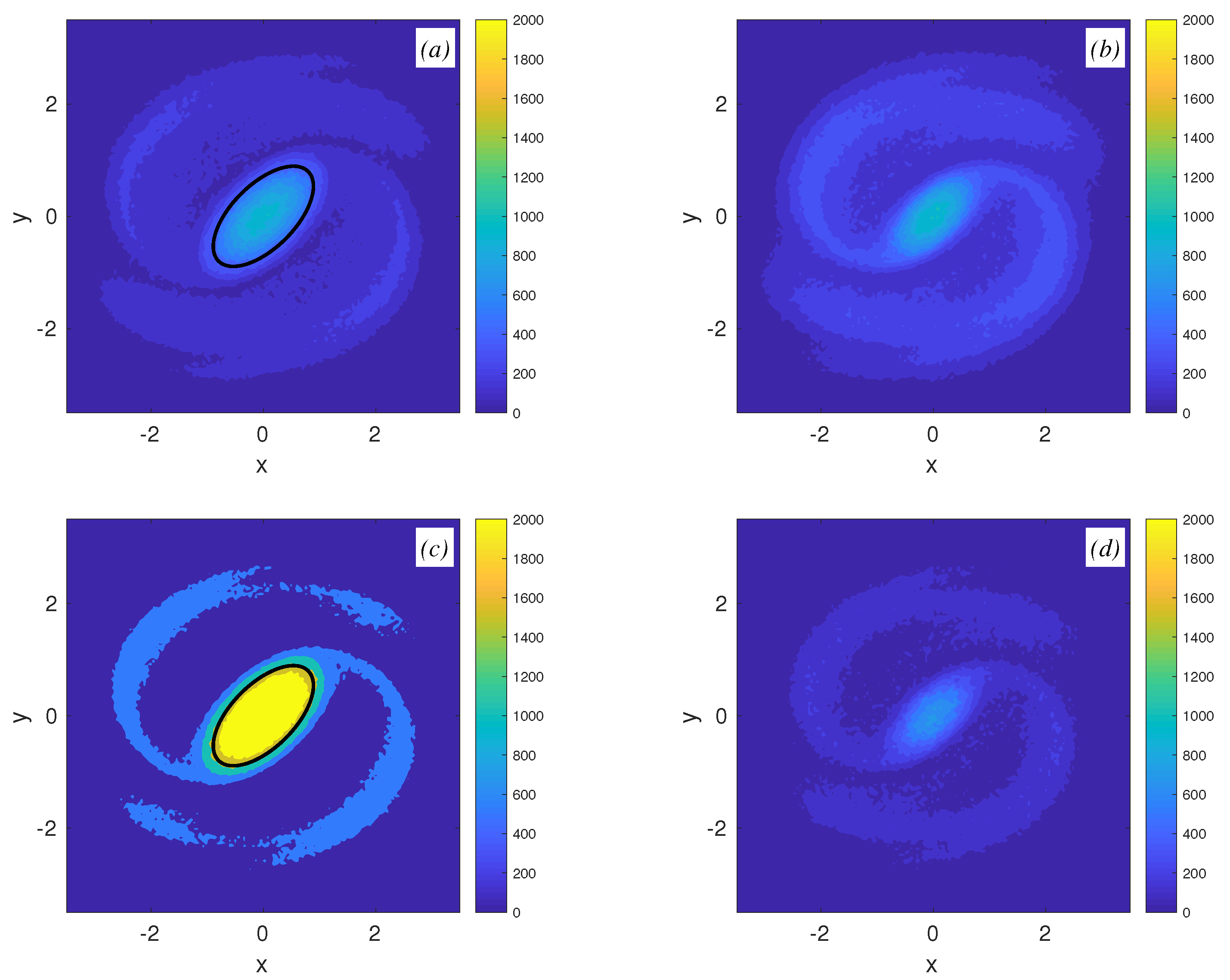
5.3. Fluid Particle Advection in Singular Vortex Systems in Layered Flows
5.4. Regular and Chaotic Dynamics of Passive Scalars Close to an Ellipsoid Vortex
5.5. Diffusion-Affected Leakage of an Ellipsoidal Vortex
6. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Determination of the Resonant Frequencies by Averaging Over Fast Oscillations
References
- Carton, X. Hydrodynamical modeling of oceanic vortices. Surv. Geophys. 2001, 22, 179–263. [Google Scholar] [CrossRef]
- Chelton, D.B.; Schlax, M.G.; Samelson, R.M.; de Szoeke, R.A. Global observations of large oceanic eddies. Geophys. Res. Lett. 2007, 34, L15606. [Google Scholar] [CrossRef]
- Chelton, D.B.; Schlax, M.G.; Samelson, R.M. Global observations of nonlinear mesoscale eddies. Prog. Oceanogr. 2011, 91, 167–216. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, W.; Qiu, B. Oceanic Mass Transport by Mesoscale Eddies. Science 2014, 345, 322–324. [Google Scholar] [CrossRef] [PubMed]
- Samelson, R.M. Lagrangian Motion, Coherent Structures, and Lines of Persistent Material Strain. Annu. Rev. Mar. Sci. 2013, 5, 137–163. [Google Scholar] [CrossRef] [PubMed]
- Barbosa Aguiar, A.C.; Peliz, A.; Carton, X. A census of Meddies in a long-term high-resolution simulation. Prog. Oceanogr. 2013, 116, 80–94. [Google Scholar] [CrossRef]
- Dong, C.; McWilliams, J.C.; Liu, Y.; Chen, D. Global heat and salt transports by eddy movement. Nat. Commun. 2014, 5, 3294. [Google Scholar] [CrossRef]
- Abernathey, R.; Haller, G. Transport by Lagrangian Vortices in the Eastern Pacific. J. Phys. Oceanogr. 2018, 48, 667–685. [Google Scholar] [CrossRef]
- Sokolovskiy, M.A.; Verron, J. Dynamics of Vortex Structures in a Stratified Rotating Fluid; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Haller, G. An objective definition of a vortex. J. Fluid Mech. 2005, 525, 1–26. [Google Scholar] [CrossRef]
- Peacock, T.; Froyland, G.; Haller, G. Introduction to Focus Issue: Objective Detection of Coherent Structures. Chaos 2015, 25, 087201. [Google Scholar] [CrossRef]
- Hadjighasem, A.; Farazmand, M.; Blazevski, D.; Froyland, G.; Haller, G. A critical comparison of Lagrangian methods for coherent structure detection. Chaos 2017, 27, 053104. [Google Scholar] [CrossRef] [PubMed]
- Stepanov, D.V. Mesoscale eddies and baroclinic instability over the eastern Sakhalin shelf of the Sea of Okhotsk: a model-based analysis. Ocean Dyn. 2018, 68, 1353–1370. [Google Scholar] [CrossRef]
- Stepanov, D.V.; Diansky, N.A.; Fomin, V.V. Eddy energy sources and mesoscale eddies in the Sea of Okhotsk. Ocean Dyn. 2018, 68, 825–845. [Google Scholar] [CrossRef]
- Stern, M.E.; Flierl, G.R. On the Interaction of a Vortex With a Shear Flow. J. Geophys. Res. 1987, 92, 10733–10744. [Google Scholar] [CrossRef]
- Nazarenko, S.V.; Zakharov, V.E. Kinetic equation for point vortices in a shear flow. Physica D 1992, 56, 381–388. [Google Scholar] [CrossRef]
- Samelson, R.M. Fluid exchange across a meandering jet. J. Phys. Oceanogr. 1992, 22, 431–440. [Google Scholar] [CrossRef]
- Del-Castillo-Negrete, D.; Morrison, P. Chaotic transport by Rossby waves in shear flow. Phys. Fluids 1993, 5, 948–965. [Google Scholar] [CrossRef]
- Schecter, D.A.; Dubin, D.H.E. Vortex Motion Driven by a Background Vorticity Gradient. Phys. Rev. Lett. 1999, 83, 2191–2194. [Google Scholar] [CrossRef]
- Finn, J.M.; del-Castillo-Negrete, D. Lagrangian chaos and Eulerian chaos in shear flow dynamics. Chaos 2001, 11, 816. [Google Scholar] [CrossRef]
- Budyansky, M.V.; Uleysky, M.Y.; Prants, S.V. Detection of barriers to cross-jet Lagrangian transport and its destruction in a meandering flow. Phys. Rev. E 2009, 79, 056215. [Google Scholar] [CrossRef]
- Uleysky, M.Y.; Budyansky, M.V.; Prants, S.V. Mechanism of destruction of transport barriers in geophysical jets with Rossby waves. Phys. Rev. E 2010, 81, 017202. [Google Scholar] [CrossRef] [PubMed]
- Balasuriya, S. Meridional and Zonal Wavenumber Dependence in Tracer Flux in Rossby Waves. Fluids 2016, 1, 30. [Google Scholar] [CrossRef]
- Reinaud, J.N.; Dritschel, D.G.; Carton, X. Interaction between a surface quasi-geostrophic buoyancy filament and an internal vortex. Geophys. Astrophys. Fluid Dyn. 2016, 110, 461–490. [Google Scholar] [CrossRef]
- Reinaud, J.N.; Carton, X.; Dritschel, D.G. Interaction between a Quasi-Geostrophic Buoyancy Filament and a Heton. Fluids 2017, 2, 37. [Google Scholar] [CrossRef]
- Le Dizès, S.; Eloy, C. Short-wavelength instability of a vortex in a multipolar strain field. Phys. Fluids 1999, 11, 500–502. [Google Scholar] [CrossRef]
- Eloy, C.; Le Dizès, S. Stability of the Rankine vortex in a multipolar strain field. Phys. Fluids 2001, 13, 660. [Google Scholar] [CrossRef]
- Helmholtz, H. On Integrals of the hydrodynamical equations, which express vortex-motion. Philos. Mag. Ser. 4 1867, 33, 485–512. [Google Scholar] [CrossRef]
- Kirchhoff, G. Vorlesungen uber mathematische Physik. Mechanik; B. G. Teubner: Leipzig, Germany, 1876; p. 255. [Google Scholar]
- Middelkamp, S.; Torres, P.; Kevrekidis, P.; Frantzeskakis, D.; Carretero-Gonzalez, R.; Schmelcher, P.; Freilich, D.V.; Hall, D. Guiding-center dynamics of vortex dipoles in Bose-Einstein condensates. Phys. Rev. A 2011, 84, 011605. [Google Scholar] [CrossRef]
- Torres, P.J.; Kevrekidis, P.G.; Frantzeskakis, D.J.; Carretero-Gonzalez, R.; Schmelcher, P.; Hall, D.S. Dynamics of vortex dipoles in confined Bose-Einstein condensates. Phys. Lett. A 2011, 375, 3044–3050. [Google Scholar] [CrossRef]
- Torres, P. Mathematical Models with Singularities: A Zoo of Singular Creatures; Atlantis Press: Paris, France, 2015. [Google Scholar]
- Bannikova, E.Y.; Kontorovich, V.M.; Reznik, G.M. Dynamics of a vortex pair in radial flow. J. Exp. Theor. Phys. 2007, 105, 542–548. [Google Scholar] [CrossRef]
- Hogg, N.G.; Stommel, H.M. The Heton, an Elementary Interaction Between Discrete Baroclinic Geostrophic Vortices, and Its Implications Concerning Eddy Heat-Flow. Proc. R. Soc. Lond. A 1985, 397, 1–20. [Google Scholar] [CrossRef]
- Hogg, N.; Stommel, H. Hetonic explosions: the break-up and spread of warm pools as explained by baroclinic point vortices. J. Atmos. Sci. 1985, 42, 1465–1476. [Google Scholar] [CrossRef]
- Gryanik, V.M. Dynamics of singular geostrophical vortices in a 2-level model of the atmosphere (ocean). Izv. Atmos. Ocean. Phys. 1983, 19, 227–240. [Google Scholar]
- Gryanik, V.M.; Tevs, M.V. Dynamics of singular geostrophical vortices in a N-level model of the atmosphere (ocean). Izv. Atmos. Ocean. Phys. 1989, 25, 179–188. [Google Scholar]
- Reznik, G.M. Dynamics of singular vortices on a beta-plane. J. Fluid Mech. 1992, 240, 405–432. [Google Scholar] [CrossRef]
- Sokolovskiy, M.A.; Verron, J. Four-vortex motion in the two layer approximation: Integrable case. Regul. Chaotic Dyn. 2000, 5, 413–436. [Google Scholar] [CrossRef]
- Legg, S.; Marshall, J. A heton model of the spreading phase of open-ocean deep convection. J. Phys. Oceanogr. 1993, 23, 1040–1056. [Google Scholar] [CrossRef]
- Legg, S.Y.; Jones, H.; Visbeck, M. A heton perspective of baroclinic eddy transfer in localized open ocean convection. J. Phys. Oceanogr. 1996, 26, 2251–2266. [Google Scholar] [CrossRef]
- Gryanik, V.M.; Doronina, T.N.; Olbers, D.J.; Warncke, T.H. The theory of three-dimensional hetons and vortex-dominated spreading in localized turbulent convection in a fast rotating stratified fluid. J. Fluid Mech. 2000, 423, 71–125. [Google Scholar] [CrossRef]
- Gryanik, V.M.; Sokolovskiy, M.A.; Verron, J. Dynamics of heton-like vortices. Regul. Chaotic Dyn. 2006, 11, 383–434. [Google Scholar] [CrossRef]
- Reznik, G.; Kizner, Z. Two-layer quasi-geostrophic singular vortices embedded in a regular flow. Part 1. Invariants of motion and stability of vortex pairs. J. Fluid Mech. 2007, 584, 185–202. [Google Scholar] [CrossRef]
- Reznik, G.; Kizner, Z. Two-layer quasi-geostrophic singular vortices embedded in a regular flow. Part 2. Steady and unsteady drift of individual vortices on a beta-plane. J. Fluid Mech. 2007, 584, 185–202. [Google Scholar] [CrossRef]
- Reznik, G.M. Dynamics of Localized Vortices on the Beta Plane. Izv. Atmos. Ocean. Phys. 2010, 46, 784–797. [Google Scholar] [CrossRef]
- Kunnen, R.; Trieling, R.; van Heijst, G.J. Vortices in time-periodic shear flow. Theor. Comput. Fluid Dyn. 2010, 24, 315–322. [Google Scholar] [CrossRef]
- Koshel, K.V.; Reinaud, J.N.; Riccardi, G.; Ryzhov, E.A. Dynamics of a vortex pair interacting with a fixed point vortex revisited. Part I: Point vortices. Phys. Fluids 2018, 30, 096603. [Google Scholar] [CrossRef]
- Newton, P.K. The N-Vortex Problem: Analytical Techniques; Springer: Berlin, Germany, 2001. [Google Scholar]
- Kurakin, L.G. On nonlinear stability of the regular vortex systems on a sphere. Chaos 2004, 14, 592. [Google Scholar] [CrossRef] [PubMed]
- Newton, P.K. The N-vortex problem on a sphere: geophysical mechanisms that break integrability. Theor. Comput. Fluid Dyn. 2010, 24, 137–149. [Google Scholar] [CrossRef]
- Kurakin, L.G.; Ostrovskaya, I.V. Nonlinear Stability Analysis of a Regular Vortex Pentagon Outside a Circle. Regul. Chaotic Dyn. 2012, 17, 385–396. [Google Scholar] [CrossRef]
- Kurakin, L.G. Influence of annular boundaries on Thomson’s vortex polygon stability. Chaos 2014, 24, 023105. [Google Scholar] [CrossRef]
- Kida, S. Motion of an elliptic vortex in a uniform shear flow. J. Phys. Soc. Jpn. 1981, 50, 3517–3520. [Google Scholar] [CrossRef]
- Zhmur, V.V. Localized eddy formation in a shear-flow. Oceanology 1988, 28, 536–538. [Google Scholar]
- Zhmur, V.V. Subsurface mesoscale eddy structures in a stratificated ocean. Oceanology 1989, 29, 28–32. [Google Scholar]
- Zhmur, V.V.; Pankratov, K.K. The dynamics of the semi-ellipsoid subsurface vortex in the non-uniform flow. Oceanology 1989, 29, 205–211. [Google Scholar]
- Zhmur, V.V.; Pankratov, K.K. Dynamics of mesoscale eddy formation in the field currents of large intensive vortex. Okeanologia 1990, 30, 124–129. [Google Scholar]
- Meacham, S.P.; Flierl, G.R.; Send, U. Vortices in shear. Dyn. Atmos. Oceans 1989, 14, 333–386. [Google Scholar] [CrossRef]
- Meacham, S.P. Quasigeostrophic, ellipsoidal vortices in stratified fluid. Dyn. Atmos. Oceans 1992, 16, 189–223. [Google Scholar] [CrossRef]
- Meacham, S.P.; Pankratov, K.K.; Shchepetkin, A.F.; Zhmur, V.V. The interaction of ellipsoidal vortices with background shear flows in a stratified fluid. Dyn. Atmos. Oceans 1994, 21, 167–212. [Google Scholar] [CrossRef]
- D’Ovidio, F.; Isern-Fontanet, J.; López, C.; Hernández-García, E.; García-Ladona, E. Comparison between Eulerian diagnostics and finite-size Lyapunov exponents computed from altimetry in the Algerian basin. Deep Sea Res. 2009, 56, 15–31. [Google Scholar] [CrossRef]
- Dritschel, D.G.; Legras, B. The elliptical model of two-dimensional vortex dynamics. II: Disturbance equations. Phys. Fluids A 1991, 3, 855. [Google Scholar] [CrossRef]
- Dhanak, M.R.; Marshall, M.P. Motion of an elliptic vortex under applied periodic strain. Phys. Fluids 1993, 5, 1224–1230. [Google Scholar] [CrossRef]
- Ide, K.; Wiggins, S. The dynamics of elliptically shaped regions of uniform vorticity in time-periodic, linear external velocity fields. Fluid Dyn. Res. 1995, 15, 205–235. [Google Scholar] [CrossRef]
- Bayly, B.J.; Holm, D.D.; Lifschitz, A. Three-dimensional stability of elliptical vortex columns in external strain flows. Philos. Trans. R. Soc. Lond. A 1996, 354, 895–926. [Google Scholar] [CrossRef]
- Ngan, K.; Meacham, S.P.; Morrison, P.J. Elliptical vortices in shear: Hamiltonian moment formulation and Melnikov analysis. Phys. Fluids 1996, 8, 896–913. [Google Scholar] [CrossRef]
- Riccardi, G.; Piva, R. Motion of an elliptical vortex under rotating strain: conditions for asymmetric merging. Fluid Dyn. Res. 1998, 23, 63–88. [Google Scholar] [CrossRef]
- Riccardi, G.; Piva, R. The interaction of an elliptical patch with a point vortex. Fluid Dyn. Res. 2000, 27, 269–289. [Google Scholar] [CrossRef]
- McKiver, W.J.; Dritschel, D.G. The stability of a quasi-geostrophic ellipsoidal vortex in a background shear flow. J. Fluid Mech. 2006, 560, 1–17. [Google Scholar] [CrossRef]
- Polvani, L.M.; Wisdom, J. Chaotic Lagrangian trajectories around an elliptical vortex patch embedded in a constant and uniform background shear flow. Phys. Fluids A 1990, 2, 123–126. [Google Scholar] [CrossRef]
- Dahleh, M.D. Exterior flow of the Kida ellipse. Phys. Fluids A 1992, 4, 1979–1985. [Google Scholar] [CrossRef]
- Kawakami, A.; Funakoshi, M. Chaotic motion of fluid particles around a rotating elliptic vortex in a linear shear flow. Fluid Dyn. Res. 1999, 25, 168–193. [Google Scholar] [CrossRef]
- Kuznetsov, L.; Zaslavsky, G.M. Regular and chaotic advection in the flow field of a three-vortex system. Phys. Rev. E 1998, 58, 7330–7349. [Google Scholar] [CrossRef]
- Kuznetsov, L.; Zaslavsky, G.M. Passive particle transport in three-vortex flow. Phys. Rev. E 2000, 61, 3777–3792. [Google Scholar] [CrossRef]
- Kozlov, V.F.; Koshel, K.V.; Stepanov, D.V. Influence of the boundary on chaotic advection in the simplest model of a topographic vortex. Izv. Atmos. Ocean. Phys. 2005, 41, 217–227. [Google Scholar]
- Koshel, K.V.; Prants, S.V. Chaotic advection in the ocean. Physics-Uspekhi 2006, 49, 1151–1178. [Google Scholar] [CrossRef]
- Kozlov, V. Models of the Topographic Vortices in Ocean; Nauka: Moscow, Russia, 1984. [Google Scholar]
- Pedlosky, J. Geophysical Fluid Dynamics, 2 ed.; Springer: New York, NY, USA, 1987. [Google Scholar]
- Monin, A. Theoretical Geophysical Fluid Dynamics; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1990. [Google Scholar]
- Pedlosky, J. Ocean Circulation Theory; Springer: New York, NY, USA, 1996. [Google Scholar]
- McWilliams, J. Fundamentals of Geophysical Fluid Dynamics; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Cushman-Roisin, B.; Beckers, J.M. Introduction to Geophysical Fluid Dynamics. Physical and Numerical Aspects, 2nd ed.; Academic Press; Elsevier Inc.: New York, NY, USA, 2011. [Google Scholar]
- Zhmur. Mezoscale Ocean Eddies; GEOS: Moscow, Russia, 2011. (In Russian) [Google Scholar]
- Vallis, G.K. Atmospheric and Oceanic Fluid Dynamics; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Gryanik, V.M.; Doronina, T.N. Advective transport of passive mixture by localized (point) geostrophic vortices in the atmosphere (ocean). Izv. Atmos. Ocean. Phys. 1990, 26, 1011–1026. [Google Scholar]
- Kozlov, V.F. Background currents in geophysical hydrodynamics. Izv. Atmos. Ocean. Phys. 1995, 31, 245–250. [Google Scholar]
- Mckiver, W.J.; Dritschel, D.G. Balance in non-hydrostatic rotating stratified turbulence. J. Fluid Mech. 2008, 596, 201–219. [Google Scholar] [CrossRef]
- Zhmur, V.V.; Ryzhov, E.A.; Koshel, K.V. Ellipsoidal vortex in a nonuniform flow: Dynamics and chaotic advections. J. Mar. Res. 2011, 69, 435–461. [Google Scholar] [CrossRef]
- Bretherton, F.P. Critical layer instability in baroclinic flows. Q. J. R. Meteorol. Soc. 1966, 92, 325–334. [Google Scholar] [CrossRef]
- Walsh, D. A model of a mesoscale lens in large scale shear. Part I. Linear Calculations. J. Phys. Oceanogr. 1995, 25, 735–746. [Google Scholar] [CrossRef]
- Walsh, D.; Pratt, L.J. The interaction of a pair of point potential vortices in uniform shear. Dyn. Atmos. Oceans 1995, 22, 135–160. [Google Scholar] [CrossRef]
- Walsh, P.L.; Richarson, J.L. Observation of tilting meddies. J. Phys. Oceanogr. 1996, 26, 1023–1039. [Google Scholar] [CrossRef]
- Maze, G.; Carton, X.; Lapeyre, G. Dynamics of a 2D vortex doublet under external deformation. Regul. Chaotic Dyn. 2004, 9, 477–497. [Google Scholar] [CrossRef]
- Perrot, X.; Carton, X. Point-vortex Interaction in an oscillatory deformation field: Hamiltonian dynamics, harmonic resonance and transition to chaos. Discrete Cont. Dyn. B 2009, 11, 971–995. [Google Scholar] [CrossRef]
- Sokolovskiy, M.A.; Koshel, K.V.; Carton, X. Baroclinic multipole evolution in shear and strain. Geophys. Astrophys. Fluid Dyn. 2011, 105, 506–535. [Google Scholar] [CrossRef]
- McKiver, W.J. The Ellipsoidal Vortex: A Novel Approach to Geophysical Turbulence. Adv. Math. Phys. 2015, 2015, 613683. [Google Scholar] [CrossRef]
- Reinaud, J.N.; Sokolovkiy, M.A.; Carton, X. Hetonic quartets in a two-layer quasi-geostrophic flow: V–states and stability. Phys. Fluids 2018, 30, 056602. [Google Scholar] [CrossRef]
- Novikov, E. Dynamics and statistics of a system of vortices. Sov. Phys. JETP 1975, 68, 1868–1882. [Google Scholar]
- Sutyrin, G.G.; Perrot, X.; Carton, X. Integrable motion of a vortex dipole in an axisymmetric flow. Phys. Lett. A 2008, 372, 5452–5457. [Google Scholar] [CrossRef]
- Sokolovskiy, M.; Koshel, K.; Verron, J. Three-vortex quasi-geostrophic dynamics in a two-layer fluid. Part 1. Analysis of relative and absolute motions. J. Fluid Mech. 2013, 717, 232–254. [Google Scholar] [CrossRef]
- Newton, P. Point vortex dynamics in the post-Aref era. Fluid Dyn. Res. 2014, 46, 031401. [Google Scholar] [CrossRef]
- Aref, H. Integrable, chaotic, and turbulent vortex motion in two-dimensional flows. Annu. Rev. Fluid Mech. 1983, 15, 345–389. [Google Scholar] [CrossRef]
- Legras, B.; Dritschel, D. The elliptical model of two-dimensional vortex dynamics. I: The basic state. Phys. Fluids 1991, 3, 845–854. [Google Scholar] [CrossRef]
- McKiver, W.J.; Dritschel, D.G. The motion of a fluid ellipsoid in a general linear background flow. J. Fluid Mech. 2003, 474, 147–173. [Google Scholar] [CrossRef]
- Dritschel, D.G.; Reinaud, J.N.; McKiver, W.J. The quasi-geostrophic ellipsoidal vortex model. J. Fluid Mech. 2004, 505, 201–223. [Google Scholar] [CrossRef]
- Lilly, J.M. Kinematics of a Fluid Ellipse in a Linear Flow. Fluids 2018, 3, 16. [Google Scholar] [CrossRef]
- Lamb, H. Hydrodynamics, 6th ed.; Cambridge University Press: Cambridge, UK, 1932. [Google Scholar]
- Koshel, K.V.; Ryzhov, E.A. Parametric resonance with a point-vortex pair in a nonstationary deformation flow. Phys. Lett. A 2012, 376, 744–747. [Google Scholar] [CrossRef]
- Ryzhov, E.A.; Koshel, K.V. Resonance phenomena in a two-layer two-vortex shear flow. Chaos 2016, 26, 113116. [Google Scholar] [CrossRef]
- Koshel, K.V.; Ryzhov, E.A. Parametric resonance in the dynamics of an elliptic vortex in a periodically strained environment. Nonlinear Processes Geophys. 2017, 24, 1–8. [Google Scholar] [CrossRef]
- Ryzhov, E.A.; Koshel, K.V. Parametric instability of a many point-vortex system in a multi-layer flow under linear deformation. Regul. Chaotic Dyn. 2016, 21, 254–266. [Google Scholar] [CrossRef]
- Ryzhov, E.A.; Koshel, K.V. The effects of chaotic advection in a three-layer ocean model. Izv. Atmos. Ocean. Phys. 2011, 47, 241–251. [Google Scholar] [CrossRef]
- Magnus, W.; Winkler, S. Hill’s Equation; Interscience-Wiley: New York, NY, USA, 1966; p. 135. [Google Scholar]
- Klyatskin, V.I.; Koshel, K.V. Numerical modeling of wave propagation in periodic media. J. Exp. Theor. Phys. 1983, 84, 2092–2098. [Google Scholar]
- Ryzhov, E.A.; Koshel, K.V.; Carton, X.J. Passive scalar advection in the vicinity of two point vortices in a deformation flow. Eur. J. Mech. B Fluid 2012, 34, 121–130. [Google Scholar] [CrossRef]
- Sokolovskiy, M.A.; Verron, J. Finite-core hetons: stability and interactions. J. Fluid Mech. 2000, 423, 127–154. [Google Scholar] [CrossRef]
- Ryzhov, E.A.; Koshel, K.V. Two-point-vortex evolution in an oscillatory shear flow with rotation. Europhys. Lett. 2014, 108, 24002. [Google Scholar] [CrossRef]
- Koshel, K.V.; Ryzhov, E.A. Local parametric instability near elliptic points in vortex flows under shear deformation. Chaos 2016, 26, 083111. [Google Scholar] [CrossRef] [PubMed]
- Zaslavsky, G.M.; Chirikov, B.V. Stochastic instability of nonlinear oscillations. Soviet Physics Uspekhi 1972, 14, 549–672. [Google Scholar] [CrossRef]
- Chirikov, B.V. A universal instability of many-dimensional oscillator systems. Phys. Rep. 1979, 52, 263–379. [Google Scholar] [CrossRef]
- Lichtenberg, A.; Lieberman, M. Regular and Stochastic Motion; Springer: New York, NY, USA, 1983. [Google Scholar]
- Zaslavsky, G.M. Physics of Chaos in Hamiltonian Dynamics; Imperial College Press: London, UK, 1998. [Google Scholar]
- Rom-Kedar, V.; Leonard, A.; Wiggins, A. An analytical study of transport, mixing and chaos in an unsteady vortical flow. J. Fluid Mech. 1990, 214, 347–394. [Google Scholar] [CrossRef]
- Neishtadt, A.I. Probability phenomena due to separatrix crossing. Chaos 1991, 1, 42–48. [Google Scholar] [CrossRef]
- Wiggins, S. Chaotic Transport in Dynamical Systems; Springer: New York, NY, USA, 1992. [Google Scholar]
- Koshel, K.V.; Sokolovskiy, M.A.; Davies, P.A. Chaotic advection and nonlinear resonances in an oceanic flow above submerged obstacle. Fluid Dyn. Res. 2008, 40, 695–736. [Google Scholar] [CrossRef]
- Zavodney, L.; Nayfeh, A.; Sanchez, N. Bifurcations and Chaos in Parametrically Excited Single-Degree-of-Freedom Systems. Nonlinear Dyn. 1990, 1, 1–21. [Google Scholar] [CrossRef]
- Jeon, D.; Bai, M.; Chu, C.; Kang, X.; Lee, S.; Riabko, A.; Zhao, X. Role of parametric resonances in global chaos. Phys. Rev. E 1996, 54, 4192–4201. [Google Scholar] [CrossRef]
- Prants, S.; Konkov, L. Parametric instability and Hamiltonian chaos in cavity semiclassical electrodynamics. J. Exp. Theor. Phys. 1999, 88, 406–414. [Google Scholar] [CrossRef]
- Kandrup, H.E.; Vass, I.M.; Sideris, I.V. Transient chaos and resonant phase mixing in violent relaxation. Mon. Not. R. Astron. Soc. 2003, 341, 927–936. [Google Scholar] [CrossRef]
- Kecik, K.; Warminski, J. Chaos in mechanical pendulum-like system near main parametric resonance. Procedia IUTAM 2012, 5, 249–258. [Google Scholar] [CrossRef]
- Khomeriki, G. Parametric resonance induced chaos in magnetic damped driven pendulum. Phys. Lett. A 2016, 380, 2382–2385. [Google Scholar] [CrossRef]
- Gluhovsky, A.; Klyatskin, V. On dynamics of flipover phenomena in simple hydrodynamic models. Dokl. Earth Sci. Sec. 1977, 237, 18–20. [Google Scholar]
- Klyatskin, V. Stochastic Equations. Theory and Its Applications to the Acoustics, Fluid Dynamics, and Radiophysics; Fizmatlit: Moscow, Russia, 2008; Volume 1–2. [Google Scholar]
- Perrot, X.; Carton, X. 2D vortex interaction in a non-uniform flow. Theor. Comput. Fluid Dyn. 2010, 24, 95–100. [Google Scholar] [CrossRef]
- Perrot, X.; Carton, X.; Guillou, A. Geostrophic vortex alignment in external shear or strain. IUTAM Symposium on Turbulence in the Atmosphere and Oceans. In IUTAM Bookseries; Springer: Berlin, Germany, 2010; Volume 28, pp. 217–228. [Google Scholar]
- Perrot, X.; Reinaud, J.N.; Carton, X.; Dritschel, D.G. Homostrophic Vortex Interaction under External Strain, in a Coupled QG-SQG Model. Regul. Chaotic Dyn. 2010, 15, 66–83. [Google Scholar] [CrossRef]
- Koshel, K.V.; Stepanov, D.V. Some specific features of chaotization and transport in pulsating barotropic flow over a topographic point vortex near boundary. Regul. Chaotic Dyn. 2004, 9, 439–449. [Google Scholar] [CrossRef]
- Izrailsky, Y.G.; Koshel, K.V.; Stepanov, D.V. Determination of optimal excitation frequency range in background flows. Chaos 2008, 18, 013107. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Xu, Y. Penetration depth of diapycnal mixing generated by wind stress and flow over topography in the northwestern Pacific. J. Geophys. Res. 2014, 119, 5501–5514. [Google Scholar] [CrossRef]
- Liu, Z.; Roebber, P.J. Vortex-Driven Sensitivity in Deformation Flow. J. Phys. Oceanogr. 2008, 65, 3819–3839. [Google Scholar] [CrossRef]
- Ryzhov, E.A.; Koshel, K.V. Chaotic transport and mixing of a passive admixture by vortex flows behind obstacles. Izv. Atmos. Ocean. Phys. 2010, 46, 184–191. [Google Scholar] [CrossRef]
- Koshel, K.V.; Ryzhov, E.A.; Zhmur, V.V. Diffusion-affected passive scalar transport in an ellipsoidal vortex in a shear flow. Nonlinear Process. Geophys. 2013, 20, 437–444. [Google Scholar] [CrossRef]
- Ryzhov, E.A.; Koshel, K.V. Interaction of a monopole vortex with an isolated topographic feature in a three-layer geophysical flow. Nonlinear Process. Geophys. 2013, 20, 107–119. [Google Scholar] [CrossRef]
- Southwick, O.R.; Johnson, E.R.; McDonald, N.R. A point vortex model for the formation of ocean eddies by flow separation. Phys. Fluids 2015, 27, 016604. [Google Scholar] [CrossRef]
- Haller, G.; Poje, A. Finite time transport in aperiodic flows. Physica D 1998, 119, 352–380. [Google Scholar] [CrossRef]
- Haller, G.; Yuan, G. Lagrangian coherent structures and mixing in two-dimensional turbulence. Physica D 2000, 147, 352–370. [Google Scholar] [CrossRef]
- Prants, S.V. Dynamical systems theory methods to study mixing and transport in the ocean. Phys. Scr. 2013, 87, 038115. [Google Scholar] [CrossRef]
- Haller, G. Lagrangian coherent structures. Annu. Rev. Fluid Mech. 2015, 47, 137–162. [Google Scholar] [CrossRef]
- Aurell, E.; Boffetta, G.; Crisanti, A.; Paladin, G.; Vulpiani, A. Predictability in the large: An extension of the concept of Lyapunov exponent. J. Phys. A Math. Gen. 1997, 30, 1–26. [Google Scholar] [CrossRef]
- Rypina, I.I.; Scott, S.E.; Pratt, L.J.; Brown, M.G. Investigating the connection between complexity of isolated trajectories and Lagrangian coherent structures. Nonlinear Process. Geophys. 2011, 18, 977–987. [Google Scholar] [CrossRef]
- Mendoza, C.; Mancho, A. Hidden geometry of ocean flows. Phys. Rev. Lett. 2010, 105, 038501. [Google Scholar] [CrossRef] [PubMed]
- Ryzhov, E.A.; Koshel, K.V. Estimating the size of the regular region of a topographically trapped vortex. Geophys. Astrophys. Fluid Dyn. 2011, 105, 536–551. [Google Scholar] [CrossRef]
- Tychensky, A.; Carton, X. Hydrological and dynamical characterization of Meddies in the Azores region: A paradigm for baroclinic vortex dynamics. J. Geophys. Res. 1998, 103, 25061–25079. [Google Scholar] [CrossRef]
- Richardson, P.L.; Bower, A.S.; Zenk, W. A census of Meddies tracked by floats. Prog. Oceanogr. 2000, 45, 209–250. [Google Scholar] [CrossRef]
- Viudez, A. Vertical Splitting of Vortices in Geophysical Dipoles. J. Phys. Oceanogr. 2010, 40, 2170–2179. [Google Scholar] [CrossRef]
- LaCasce, J.H.; Wang, J. Estimating Subsurface Velocities from Surface Fields with Idealized Stratification. J. Phys. Oceanogr. 2015, 45, 2424–2435. [Google Scholar] [CrossRef]
- Ryzhov, E.A.; Koshel, K.V. Global chaotization of fluid particle trajectories in a sheared two-layer two-vortex flow. Chaos 2015, 25, 103108. [Google Scholar] [CrossRef]
- Assassi, C.; Morel, Y.; Vandermeirsch, F.; Chaigneau, A.; Pegliasco, C.; Morrow, R.; Colas, F.; Fleury, S.; Carton, X.; Klein, P.; et al. An index to distinguish surface and subsurface intensified vortices from surface observations. J. Phys. Oceanogr. 2016, 46, 2529–2552. [Google Scholar] [CrossRef]
- Ciani, D.; Carton, X.; Verron, J. On the merger of subsurface isolated vortices. Geophys. Astrophys. Fluid Dyn. 2016, 110, 23–49. [Google Scholar] [CrossRef]
- Sokolovskiy, M.A.; Carton, X.J.; Filyushkin, B.N.; Yakovenko, O.I. Interaction between a surface jet and subsurface vortices in a three-layer quasi-geostrophic model. Geophys. Astrophys. Fluid Dyn. 2016, 110, 201–223. [Google Scholar] [CrossRef]
- Brown, M.G.; Samelson, R.M. Particle motion in vorticity-conserving, 2-dimensional incompressible flows. Phys. Fluids 1994, 6, 2875–2876. [Google Scholar] [CrossRef]
- Klyatskin, V.I. Statistical description of the diffusion of a passive tracer in a random velocity field. Physics-Uspekhi 1994, 37, 501–513. [Google Scholar] [CrossRef]
- Koshel, K.V.; Alexandrova, O.V. Some results of a numerical modeling of the diffusion of passive tracers in a random field of velocities. Izv. Atmos. Ocean. Phys. 1999, 35, 578–588. [Google Scholar]
- Klyatskin, V.I.; Koshel, K.V. The simplest example of the development of a cluster-structured passive tracer field in random flows. Physics-Uspekhi 2000, 170, 771–778. [Google Scholar]
- Klyatskin, V.I. Stochastic Equations through the Eyes of the Physicist (Basic Concepts, Exact Results, and Asymptotic Approximations); Elsevier Science: Amsterdam, The Netherlands, 2005; p. 556. [Google Scholar]
- Koshel, K.V.; Ryzhov, E.A.; Zhmur, V.V. Effect of the vertical component of diffusion on passive scalar transport in an isolated vortex model. Phys. Rev. E 2015, 92, 053021. [Google Scholar] [CrossRef]
- Monin, A.S.; Ozmidov, R.V. Turbulence in the Ocean; Reidel: Dordrecht, The Netherlands, 1985; p. 247. [Google Scholar]
- Polvani, L.M.; Wisdom, J.; DeJong, E.; Ingersoll, A.P. Simple Dynamical Models of Neptune’s Great Dark Spot. Science 1990, 249, 1393–1398. [Google Scholar] [CrossRef]
- McWilliams, J. Geostrophic Vortices. In Nonlinear Topics in Ocean Physics: Proceedings of the International School of Physics “Enrico Fermi”, Course 109; Osborne, A., Ed.; North-Holland, Elsevier Science Publishers B.V.: Amsterdam, The Netherlands, 1991; pp. 5–50. [Google Scholar]
- Ince, E.L. Ordinary Differential Equations; Courier Dover Publications: New York, NY, USA, 1956. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koshel, K.V.; Ryzhov, E.A.; Carton, X.J. Vortex Interactions Subjected to Deformation Flows: A Review. Fluids 2019, 4, 14. https://doi.org/10.3390/fluids4010014
Koshel KV, Ryzhov EA, Carton XJ. Vortex Interactions Subjected to Deformation Flows: A Review. Fluids. 2019; 4(1):14. https://doi.org/10.3390/fluids4010014
Chicago/Turabian StyleKoshel, Konstantin V., Eugene A. Ryzhov, and Xavier J. Carton. 2019. "Vortex Interactions Subjected to Deformation Flows: A Review" Fluids 4, no. 1: 14. https://doi.org/10.3390/fluids4010014
APA StyleKoshel, K. V., Ryzhov, E. A., & Carton, X. J. (2019). Vortex Interactions Subjected to Deformation Flows: A Review. Fluids, 4(1), 14. https://doi.org/10.3390/fluids4010014





