The Effect of a Variable Background Density Stratification and Current on Oceanic Internal Solitary Waves
Abstract
1. Introduction
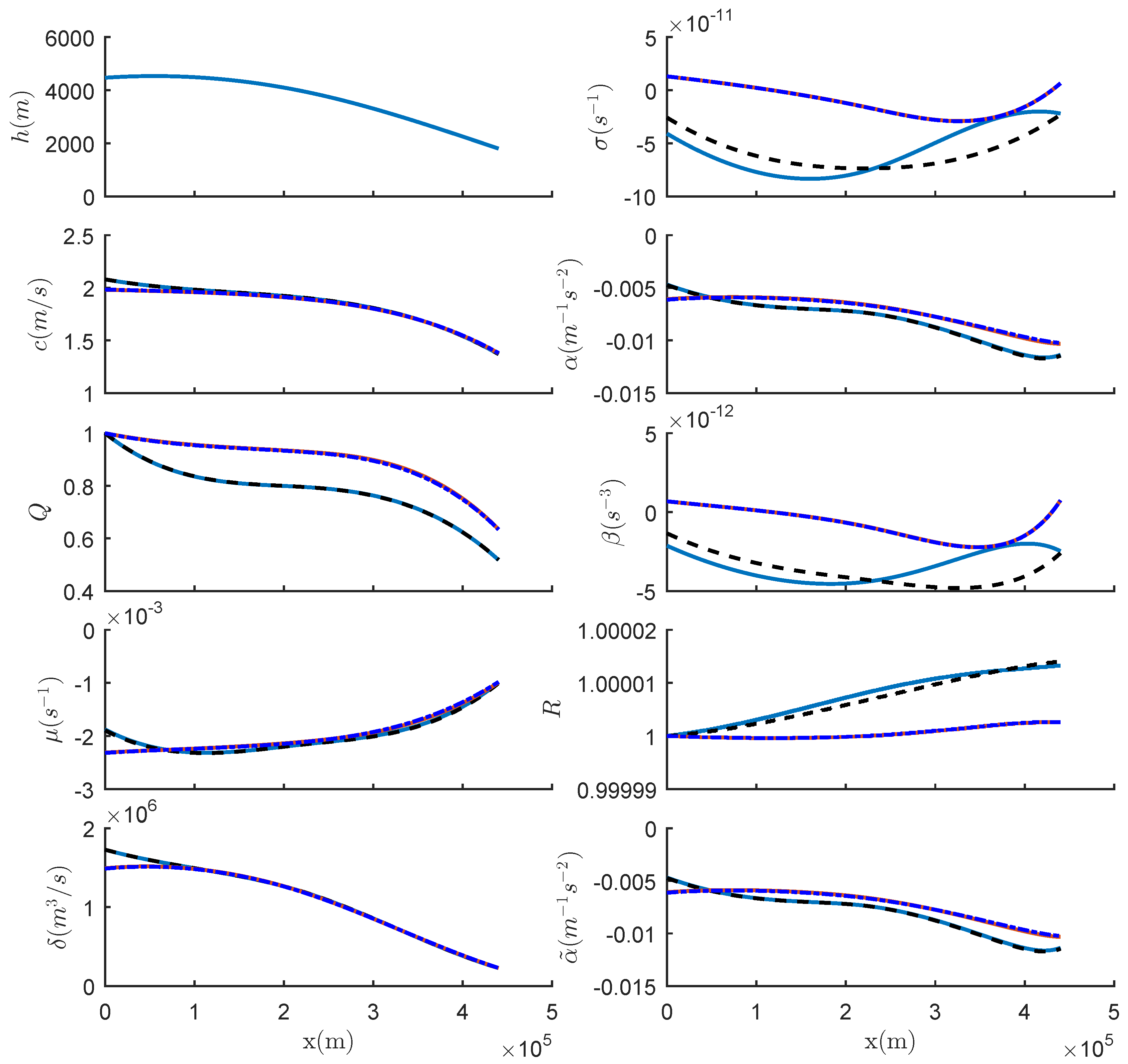
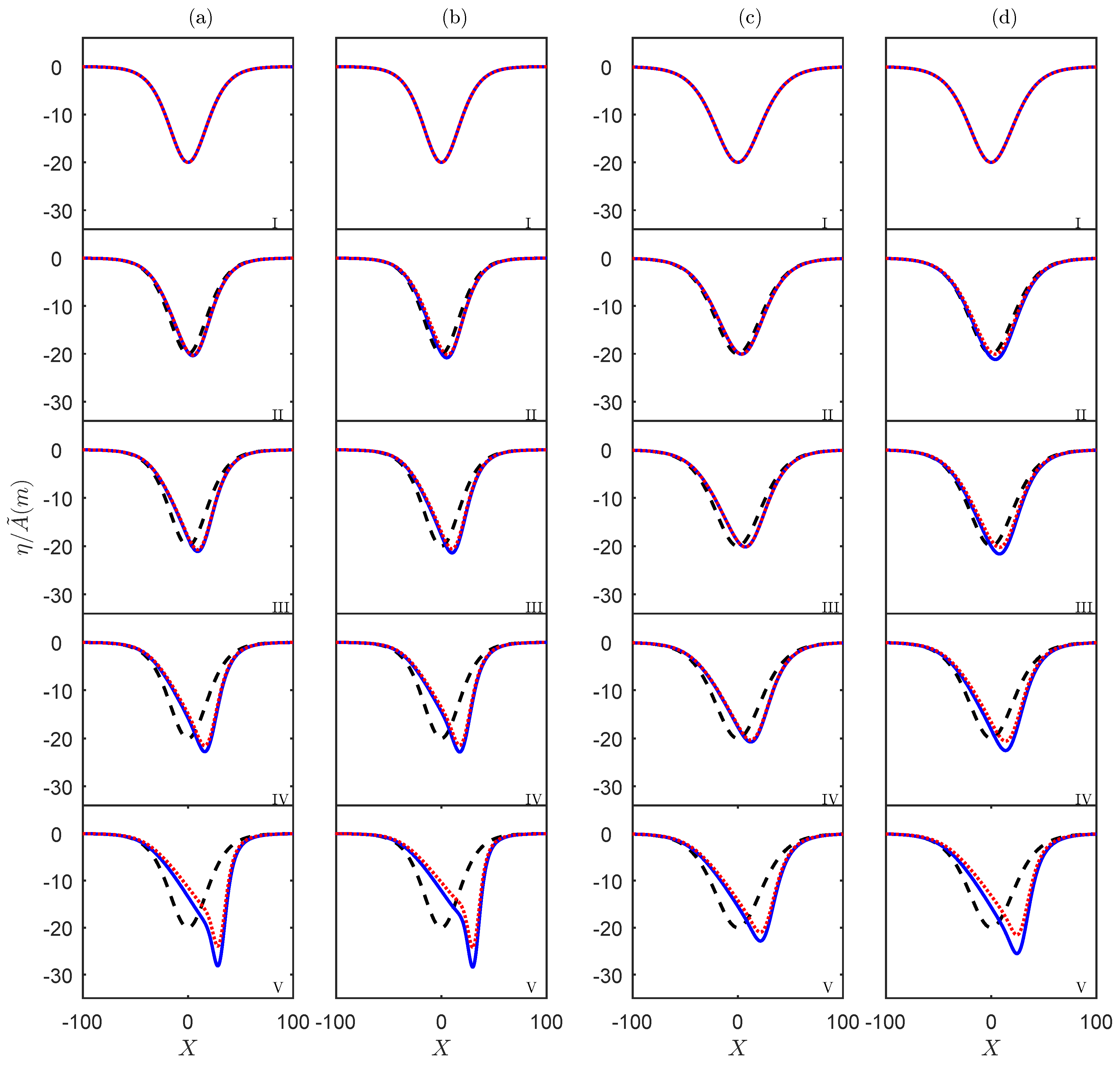
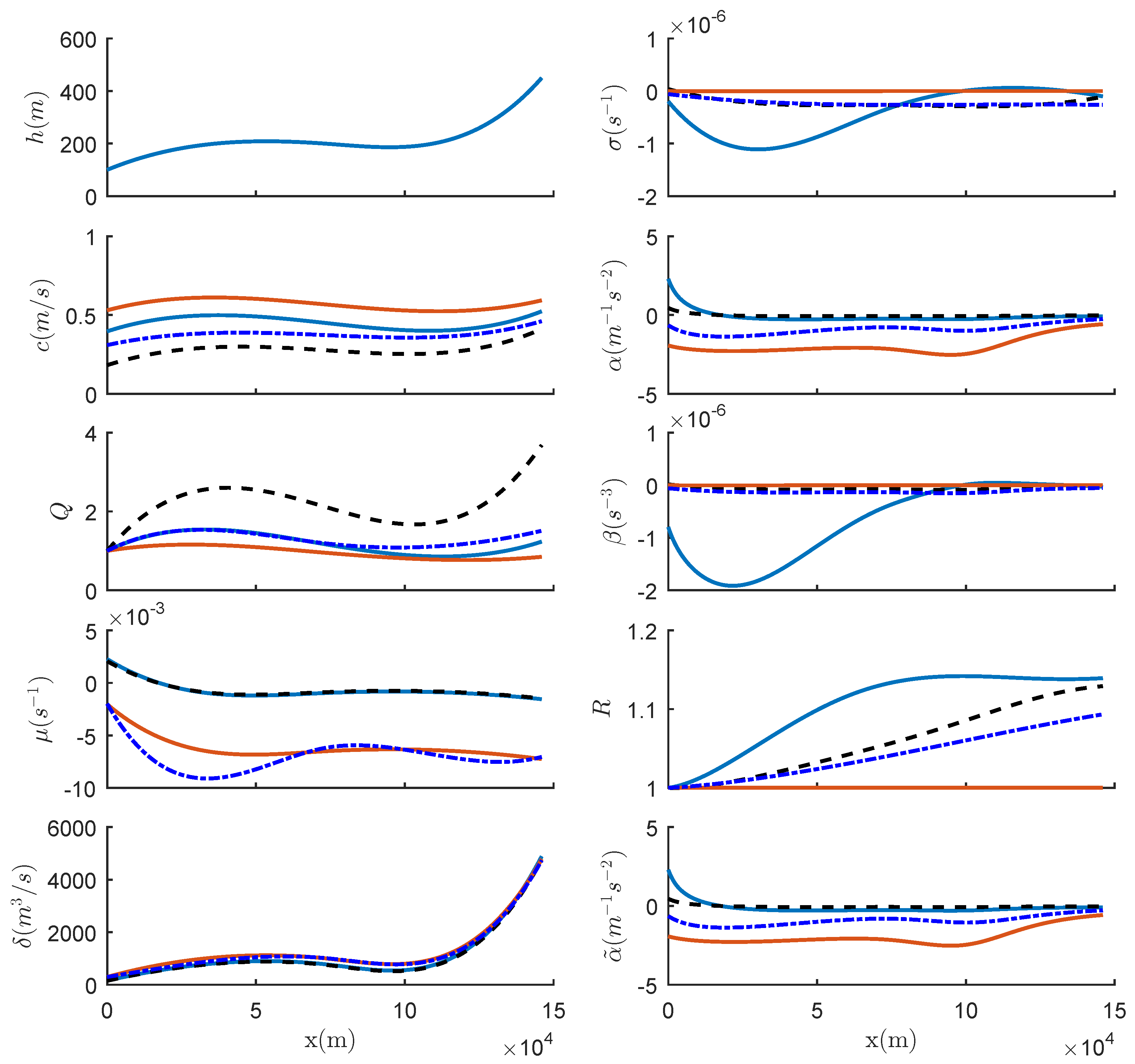
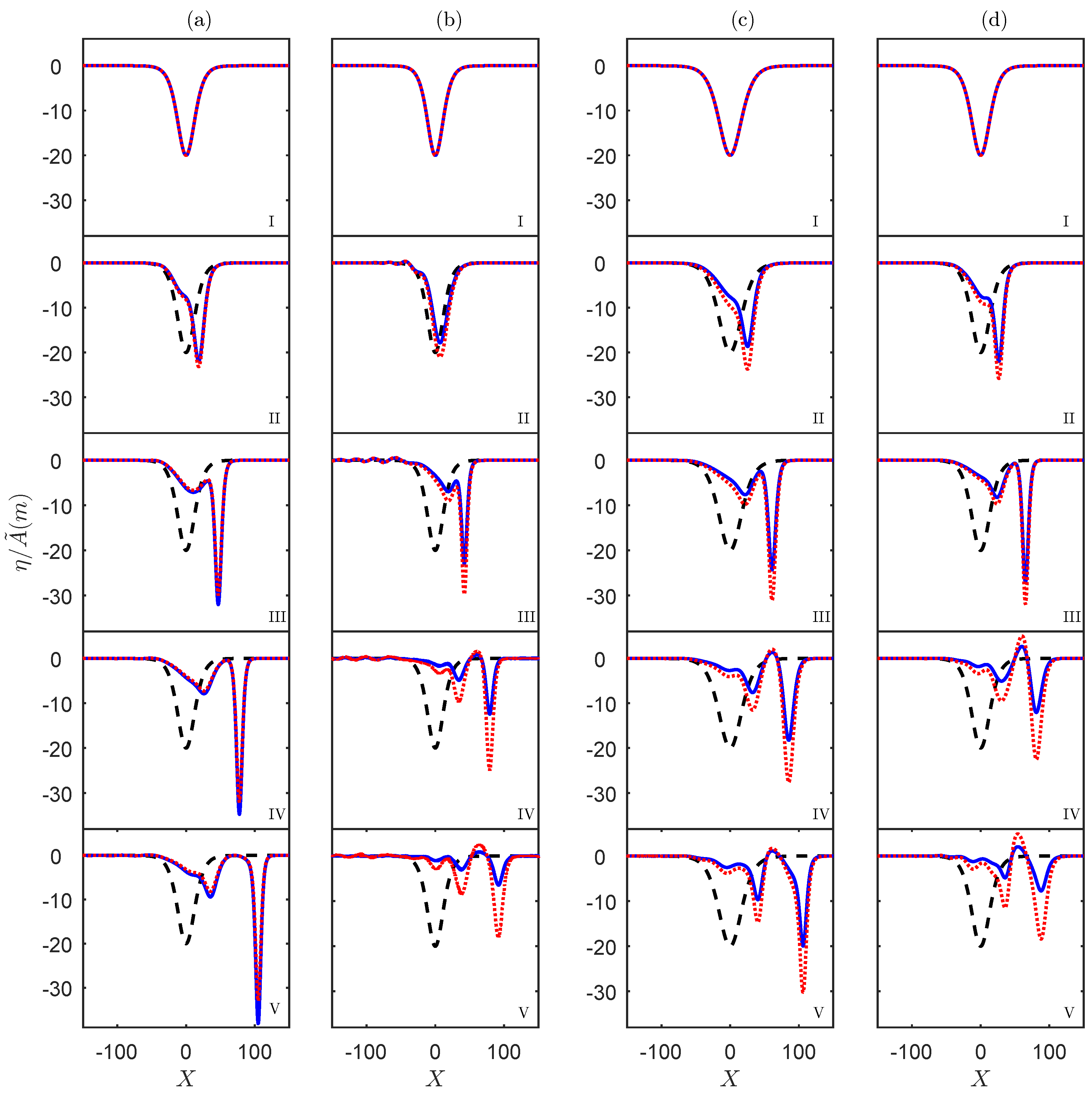
2. Variable-Coefficient Korteweg–De Vries Equation
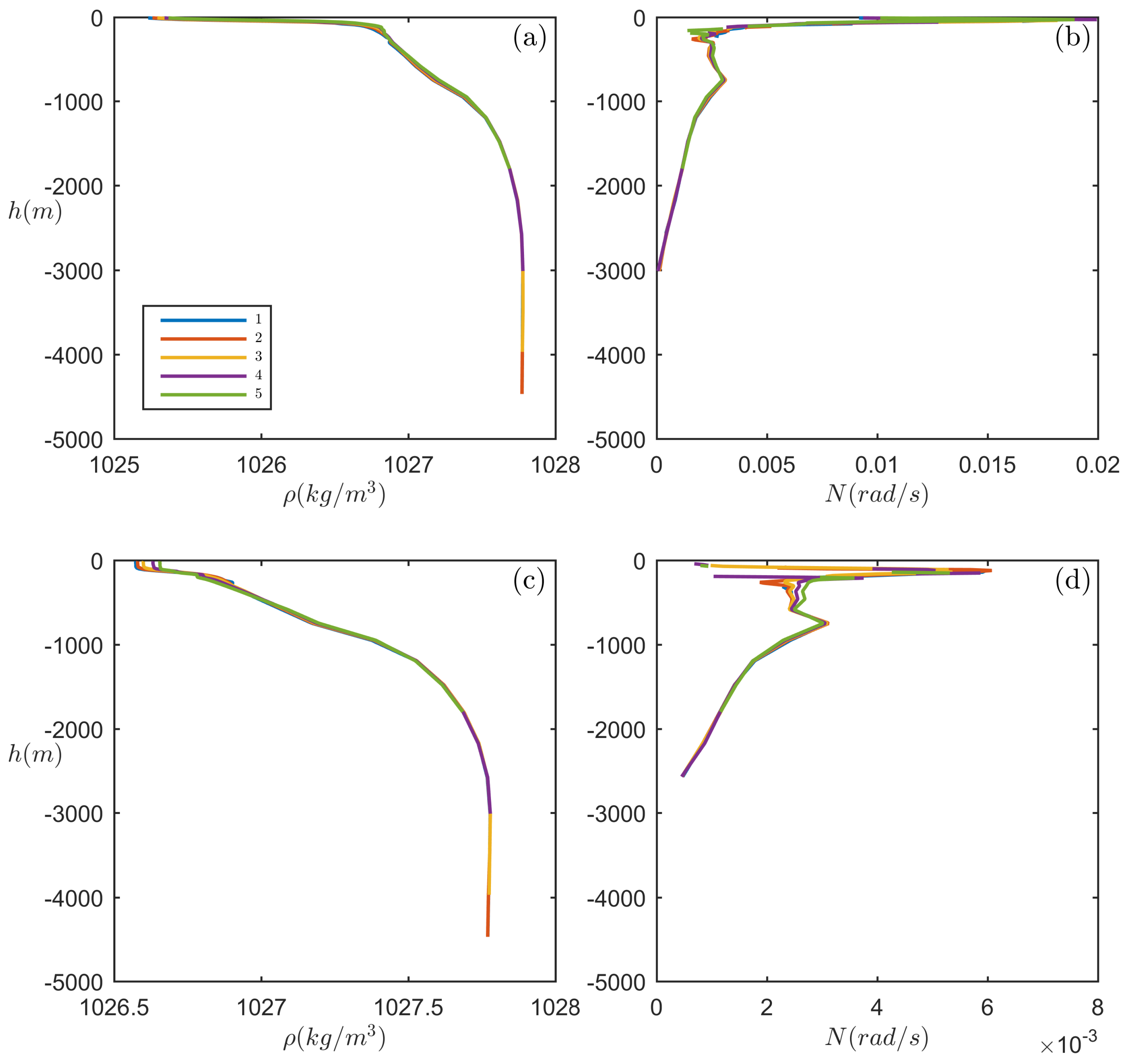
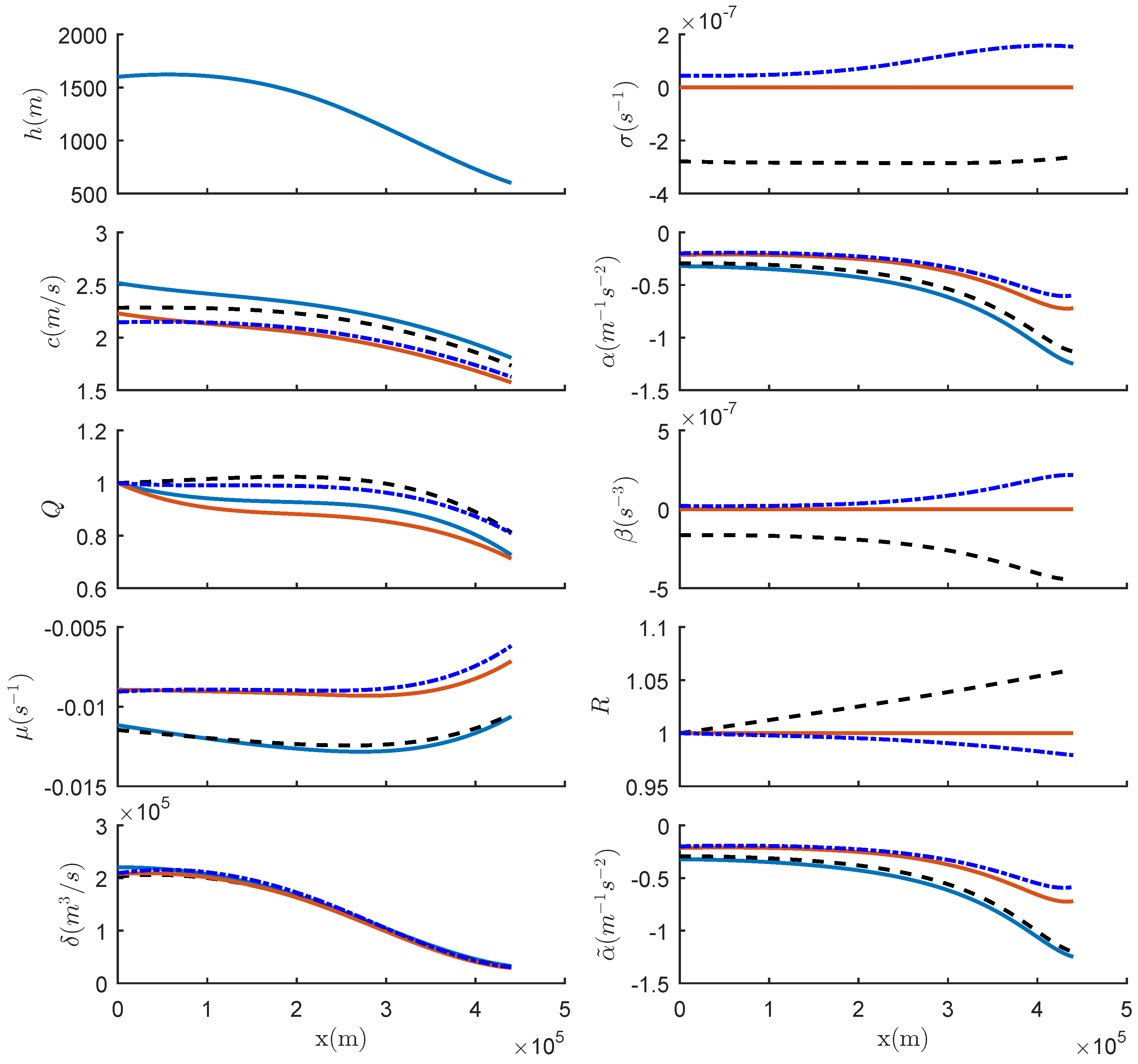
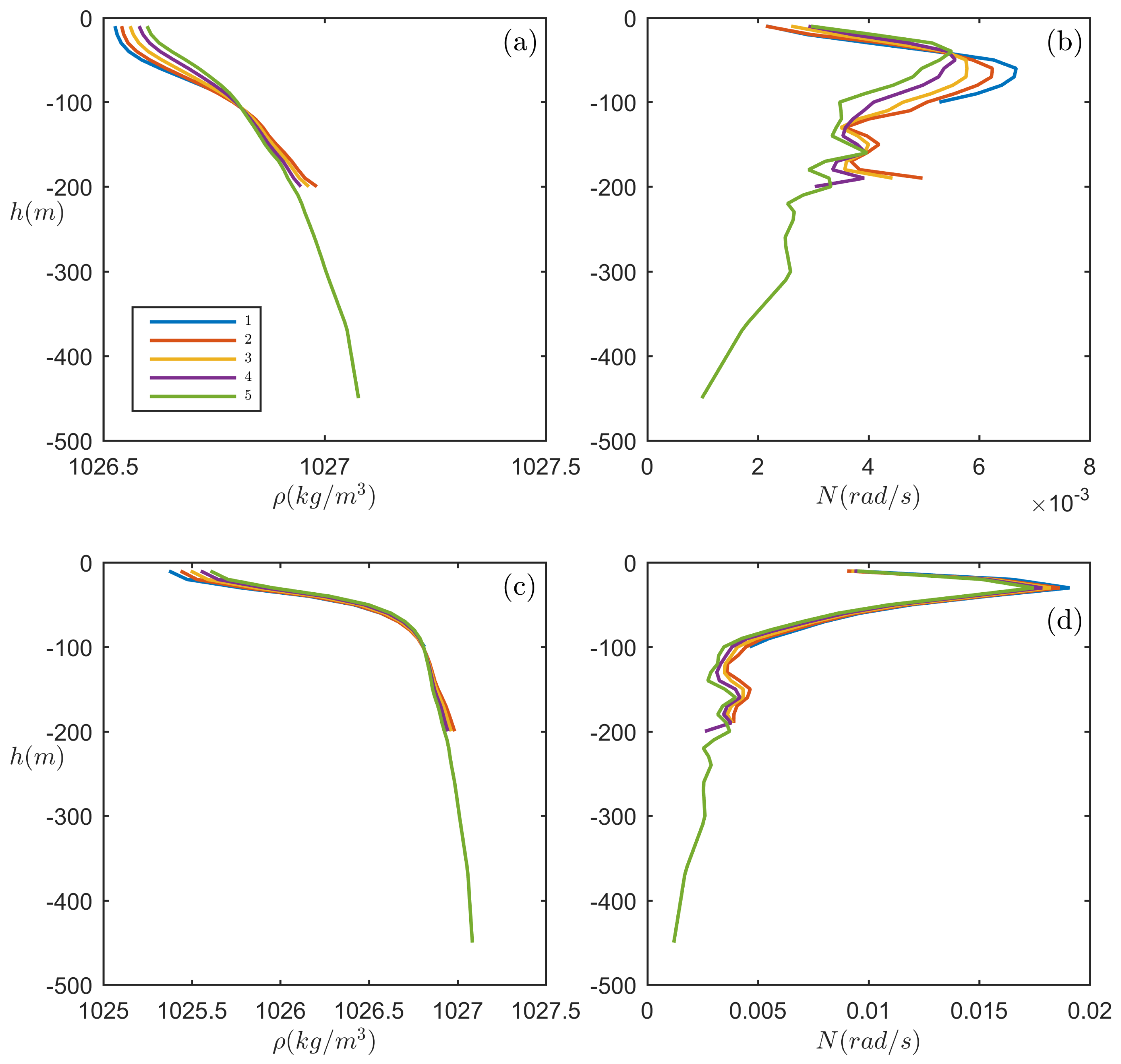
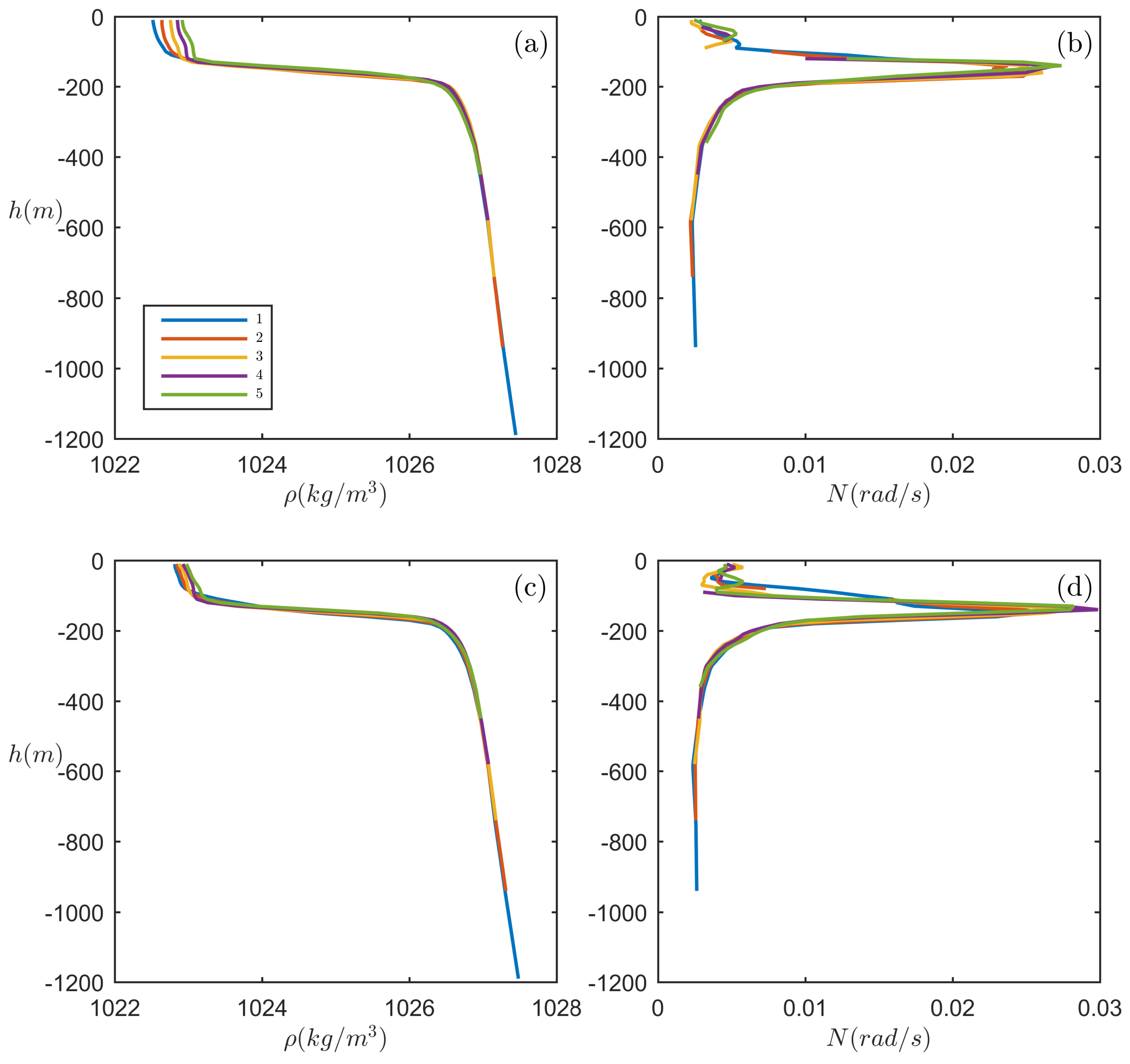
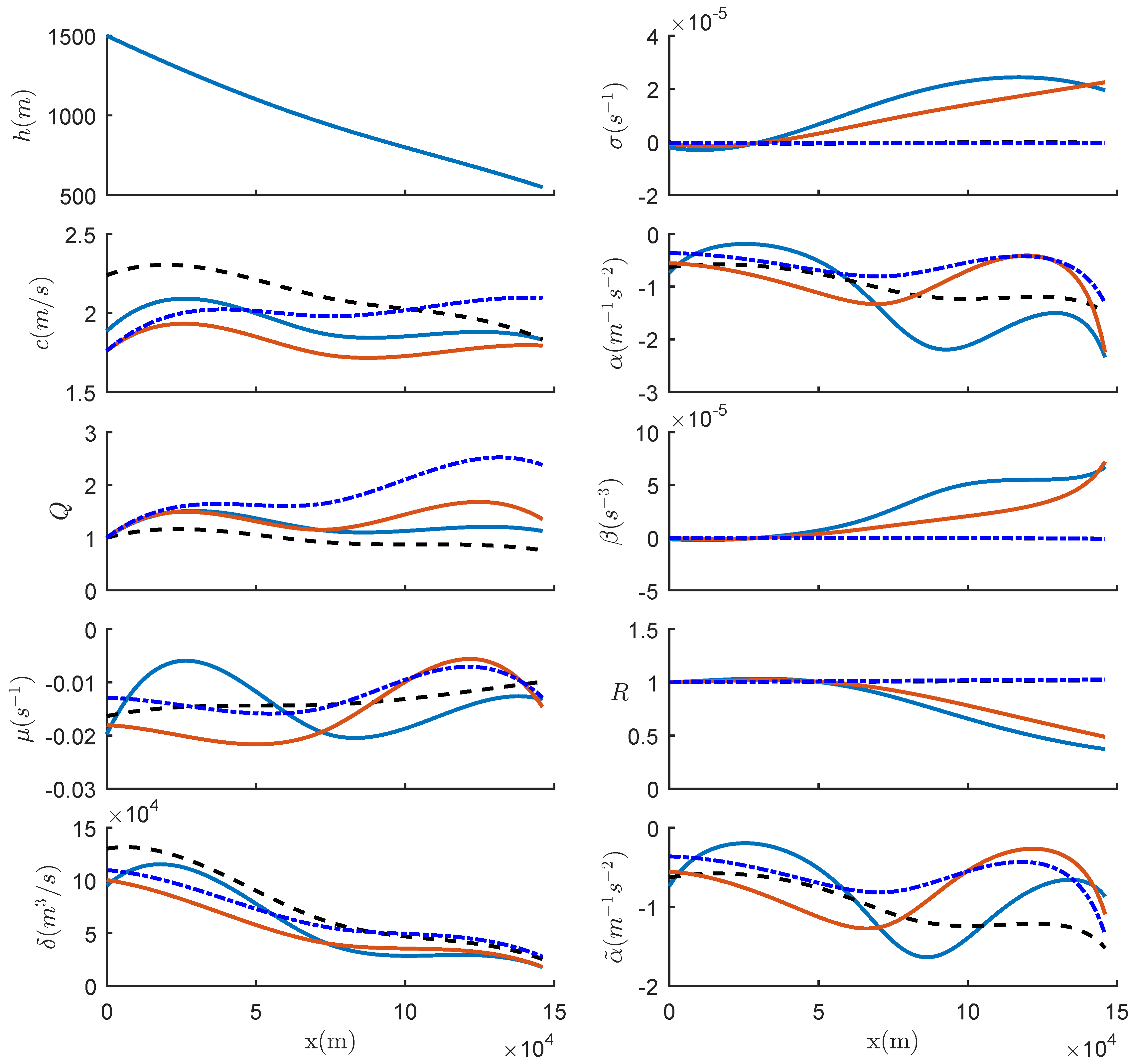
3. Estimation of the Non-Conservative Term from Oceanic Data
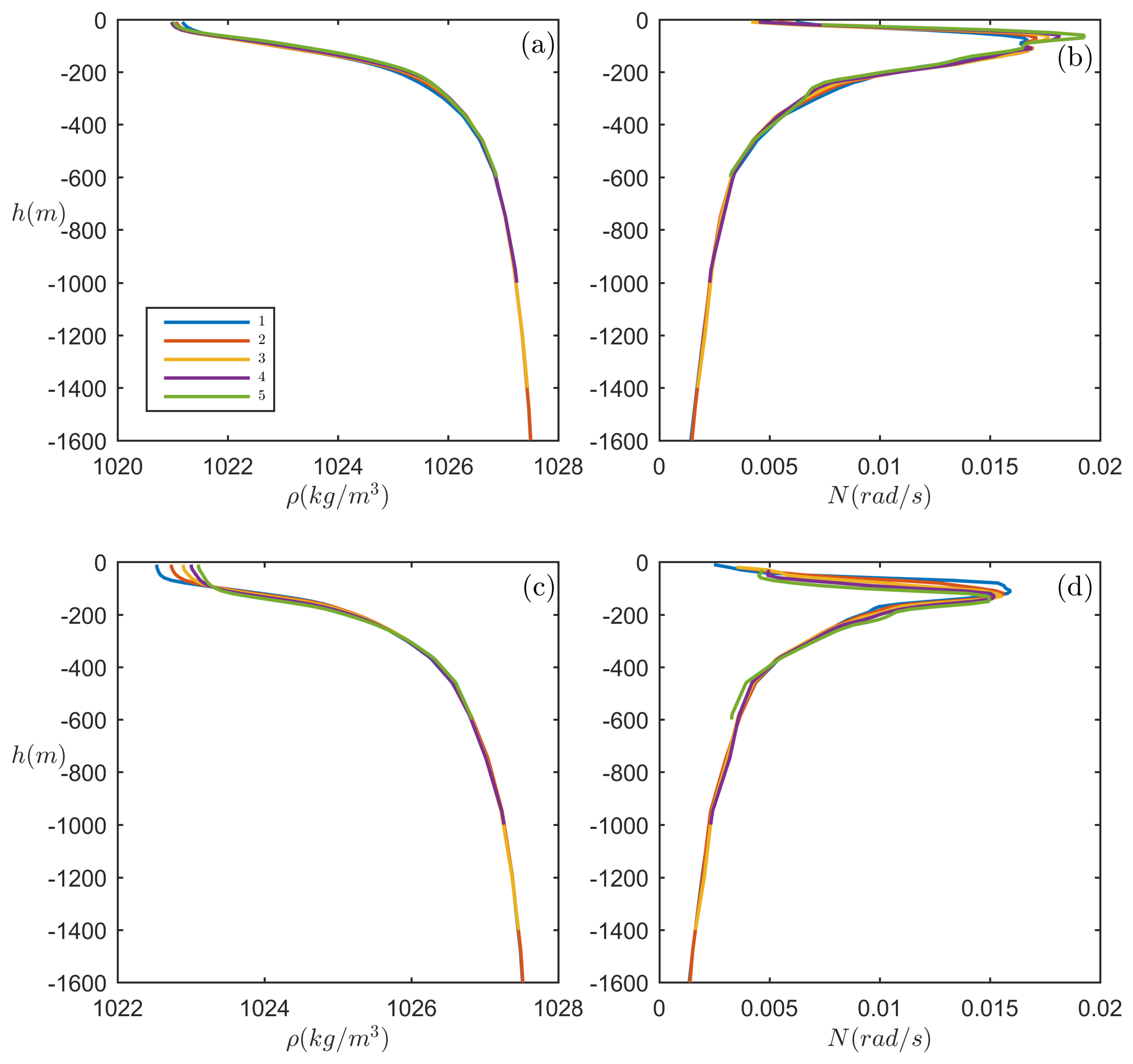
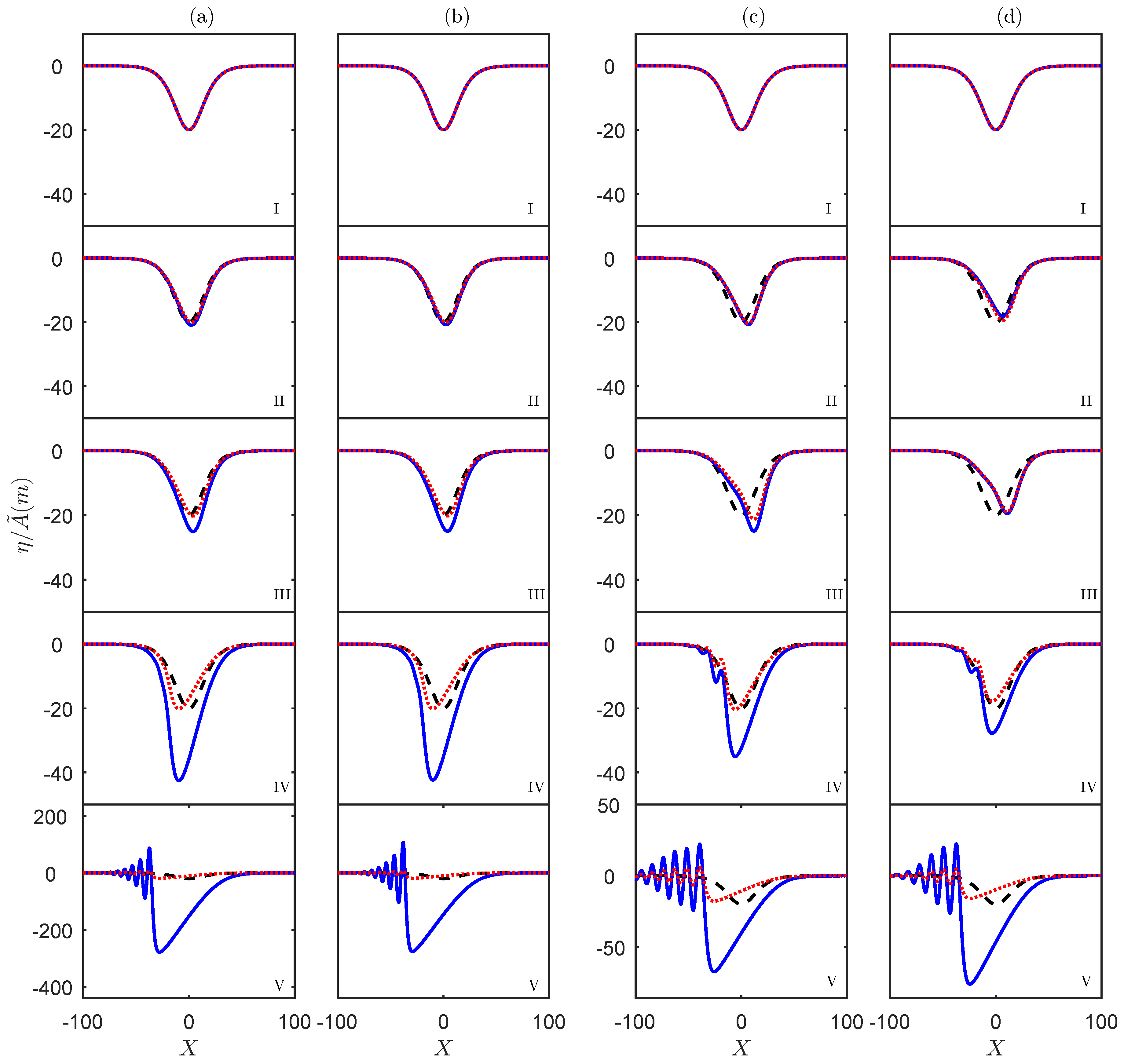
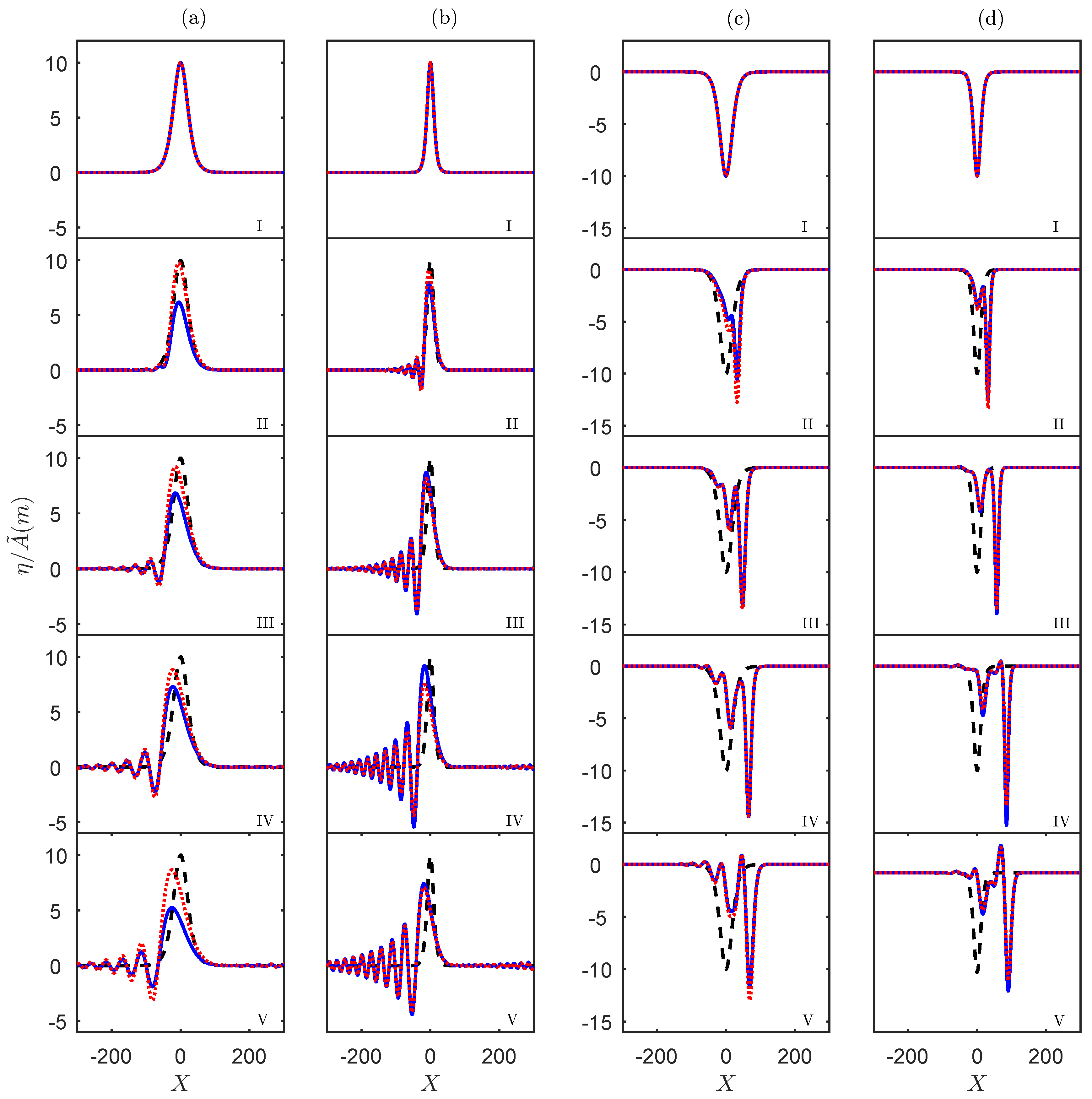
3.1. Cases Where the Horizontal Density Stratification Is the Major Effect
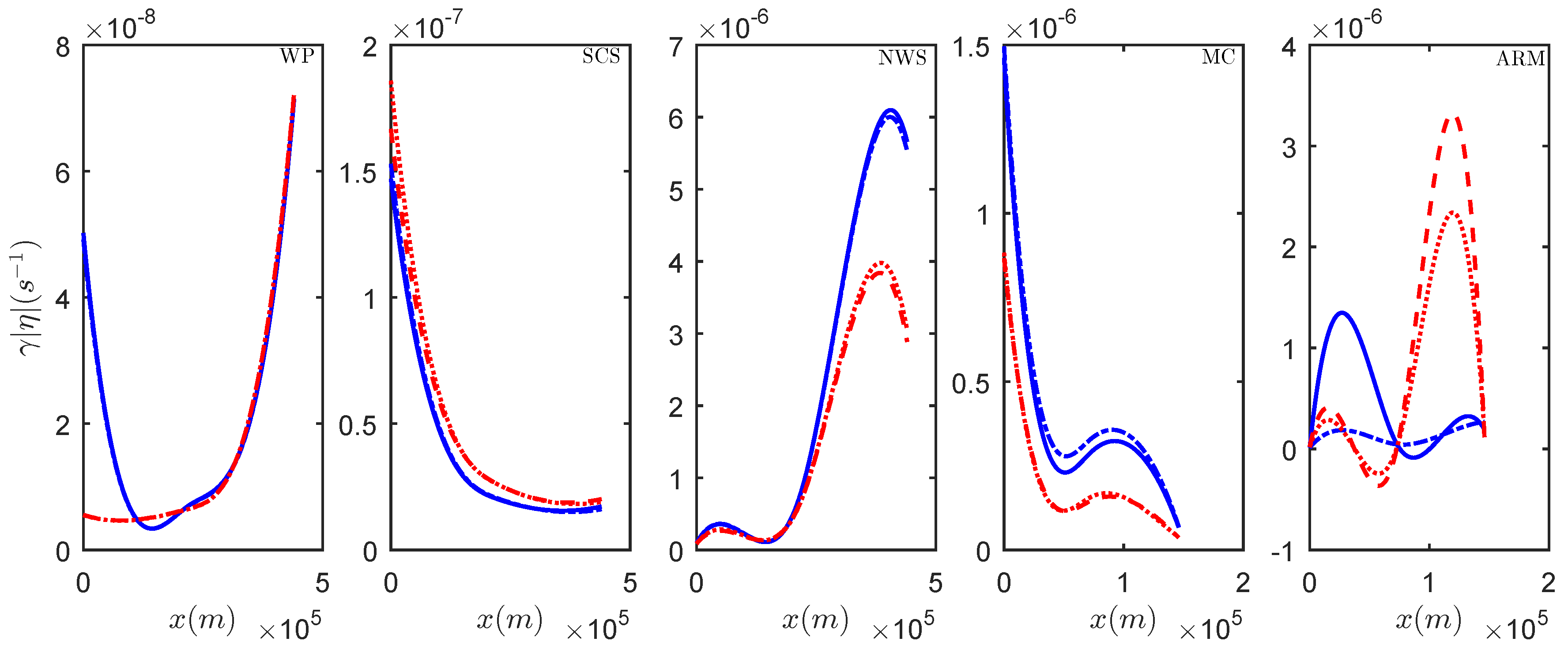
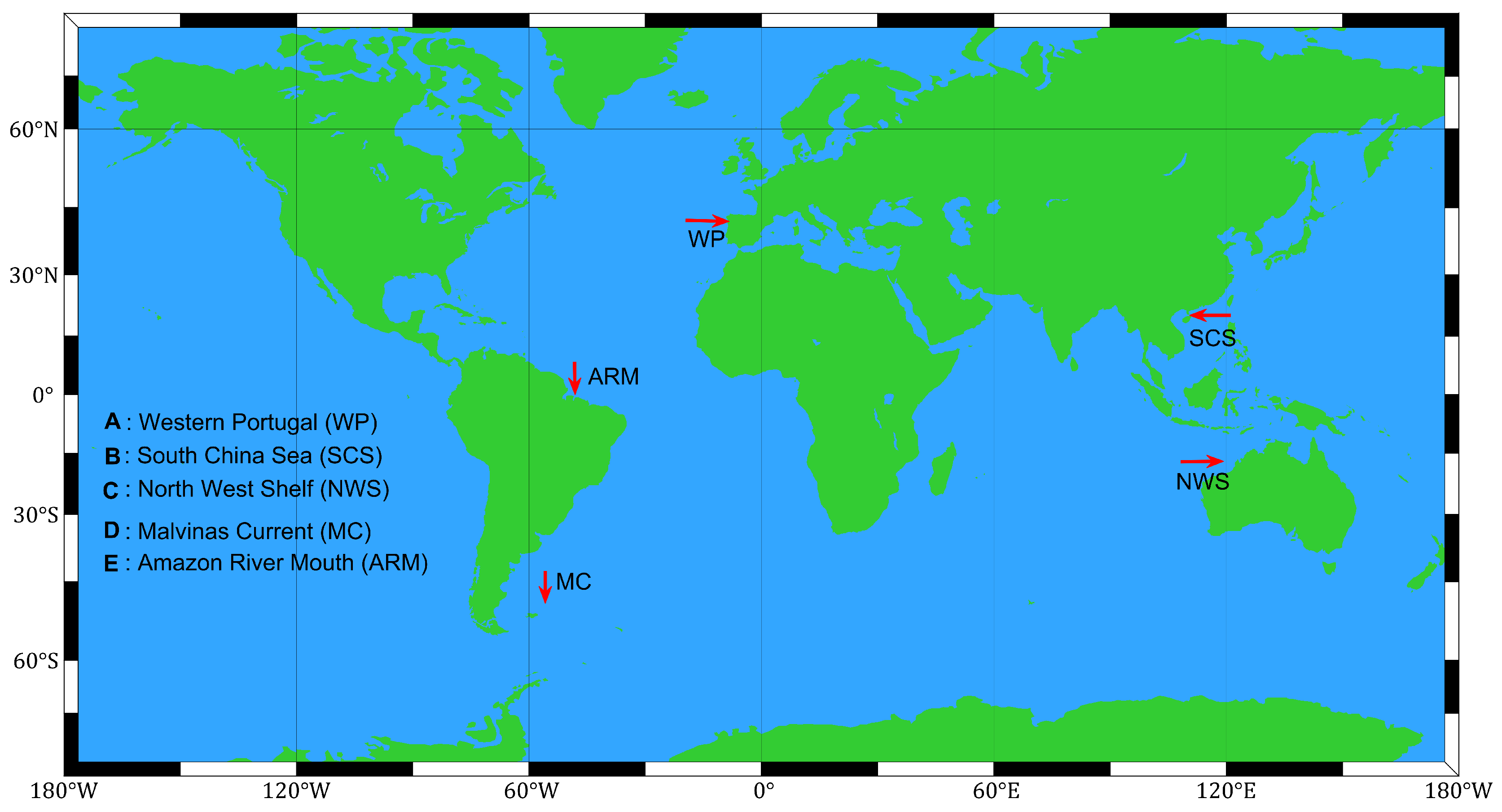
3.1.1. A: Western Portugal
3.1.2. B: South China Sea
3.1.3. C: North West Shelf
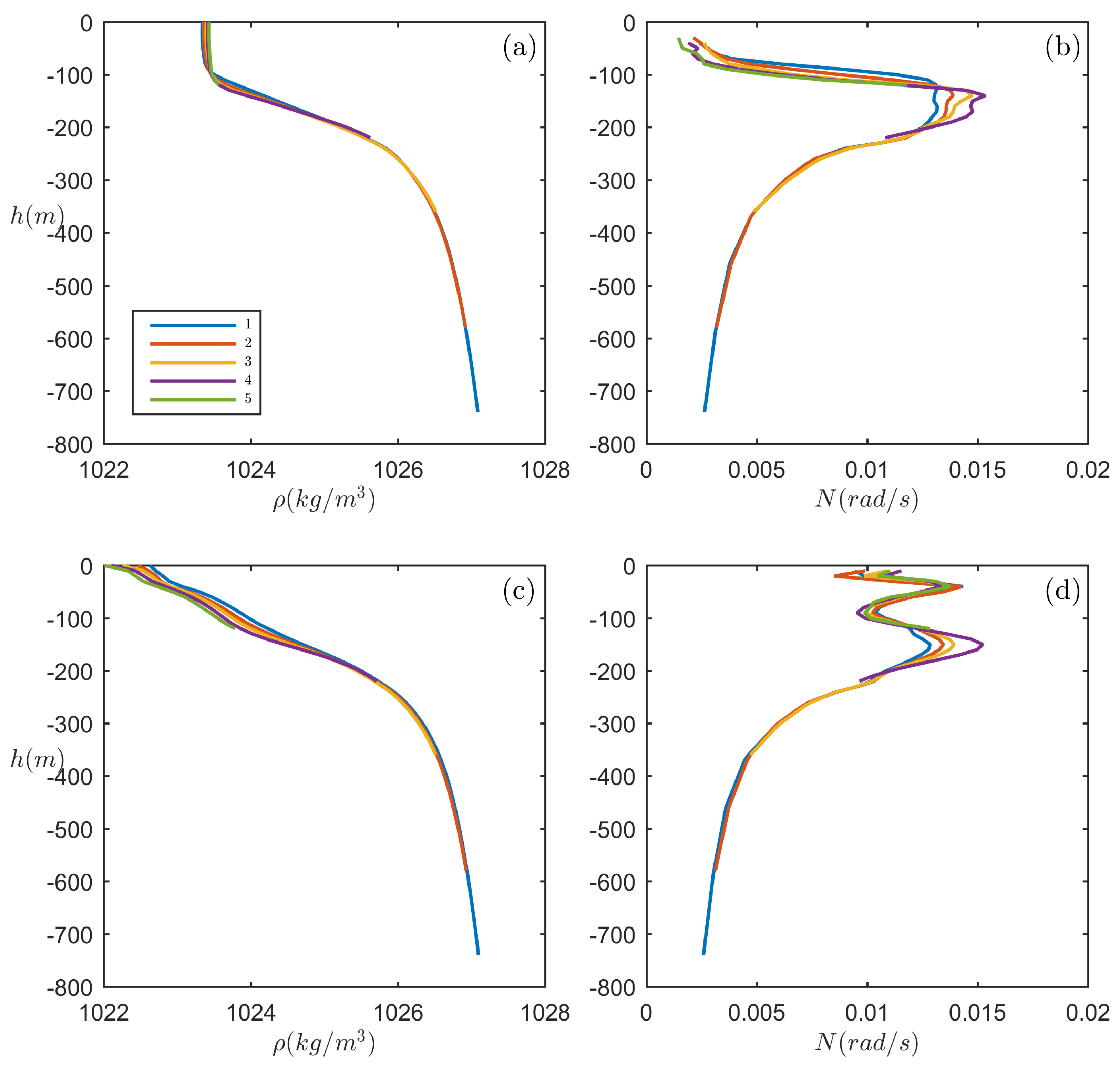
3.2. Cases Where the Horizontal Current Variation Is Significant
3.2.1. D: Malvinas Current
3.2.2. E: Amazon River Mouth
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Bottom Friction
Appendix B. Rotational Effects
| Case | A | B | C | D | E | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Season | S | W | S | W | S | W | S | W | S | W |
| Os | 0.44 | 0.71 | 74 | 42 | 126 | 136 | 18 | 14 | 10,579 | 6106 |
| (day) | 0.4 | 0.4 | 6.0 | 5.0 | 9.0 | 9.0 | 1.5 | 1.8 | 407.4 | 309.6 |
| (day) | 2.8 | 2.8 | 2.3 | 2.6 | 5.8 | 4.9 | 3.8 | 3.0 | 0.9 | 1.0 |
References
- Grimshaw, R. Internal solitary waves. In Environmental Stratified Flows; Grimshaw, R., Ed.; Kluwer: Boston, MA, USA, 2001; pp. 1–27. [Google Scholar]
- Holloway, P.; Pelinovsky, E.; Talipova, T. Internal tide transformation and oceanic internal solitary waves. In Environmental Stratified Flows; Grimshaw, R., Ed.; Kluwer: Boston, MA, USA, 2001; pp. 31–60. [Google Scholar]
- Ostrovsky, L.A.; Stepanyants, Y.A. Internal solitons in laboratory experiments: Comparison with theoretical models. Chaos 2005, 28, 037111. [Google Scholar] [CrossRef] [PubMed]
- Helfrich, K.R.; Melville, W.K. Long nonlinear internal waves. Ann. Rev. Fluid Mech. 2006, 38, 395–425. [Google Scholar] [CrossRef]
- Grimshaw, R. Internal solitary waves in a variable medium. Ges. Angew. Math. 2007, 30, 96–109. [Google Scholar] [CrossRef]
- Grimshaw, R.; Pelinovsky, E.; Talipova, T.; Kurkina, A. Internal solitary waves: Propagation, deformation and disintegration. Nonlinear Process. Geophys. 2010, 17, 633–649. [Google Scholar] [CrossRef]
- Vlasenko, V.I.; Stashchuk, N.M.; Hutter, K. Baroclinic Tides: Theoretical Modelling and Observational Evidence; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Benney, D.J. Long non-linear waves in fluid flows. J. Math. Phys. 1966, 45, 52–63. [Google Scholar] [CrossRef]
- Benjamin, T.B. Internal waves of finite amplitude and permanent form. J. Fluid Mech. 1966, 25, 241–270. [Google Scholar] [CrossRef]
- Grimshaw, R. Evolution equations for long nonlinear internal waves in stratified shear flows. Stud. Appl. Math. 1981, 65, 159–188. [Google Scholar] [CrossRef]
- Zhou, X.; Grimshaw, R. The effect of variable currents on internal solitary waves. Dyn. Atmos. Oceans 1989, 14, 17–39. [Google Scholar] [CrossRef]
- Liu, Z.; Grimshaw, R.; Johnson, E. Internal solitary waves propagating through variable background hydrology and currents. Ocean Model. 2017, 116, 134–145. [Google Scholar] [CrossRef]
- Andrews, D.G.; McIntyre, M.E. On wave-action and its relatives. J. Fluid Mech. 1978, 89, 647–664. [Google Scholar] [CrossRef]
- Grimshaw, R. Wave action and wave-mean flow interaction, with application to stratified shear flows. Ann. Rev. Fluid Mech. 1984, 16, 11–44. [Google Scholar] [CrossRef]
- Grimshaw, R.; Pelinovsky, E.; Talipova, T.; Kurkin, A. Simulation of the transformation of internal solitary waves on oceanic shelves. J. Phys. Ocean 2004, 34, 2774–2779. [Google Scholar] [CrossRef]
- Grimshaw, R.; Pelinovsky, E.; Stepanyants, Y.; Talipova, T. Modelling internal solitary waves on the Australian North West shelf. Mar. Freshw. Res. 2006, 57, 265. [Google Scholar] [CrossRef]
- Magalhaes, J.M.; da Silva, J.C. Internal Waves Along the Malvinas Current: Evidence of Transcritical Generation in Satellite Imagery. Oceanography 2017, 30, 110–119. [Google Scholar] [CrossRef]
- Lentini, C.A.; Magalhaes, J.M.; da Silva, J.C.; Lorenzzetti, J.A. Transcritical Flow and Generation of Internal Solitary Waves off the Amazon River: Synthetic Aperture Radar Observations and Interpretation. Oceanography 2016, 29, 187–195. [Google Scholar] [CrossRef]
- Johns, W.E.; Lee, T.N.; Beardsley, R.C.; Candela, J.; Limeburner, R.; Castro, B. Annual Cycle and Variability of the North Brazil Current. J. Phys. Oceanogr. 1998, 28, 103–128. [Google Scholar] [CrossRef]
- Ostrovsky, L. Nonlinear internal waves in a rotating ocean. Oceanology 1978, 18, 119–125. [Google Scholar]
- Grimshaw, R. Evolution equations for weakly nonlinear, long internal waves in a rotating fluid. Stud. Appl. Math. 1985, 73, 1–33. [Google Scholar] [CrossRef]
- Grimshaw, R.; Helfrich, K.R. Long-time solutions of the Ostrovsky equation. Stud. Appl. Math. 2008, 121, 71–88. [Google Scholar] [CrossRef]
- Grimshaw, R.; da Silva, J.C.B.; Magalhaes, J.M. Modelling and observations of oceanic nonlinear internal wave packets affected by the Earth’s rotation. Ocean Model. 2017, 116, 146–158. [Google Scholar] [CrossRef]
- Grimshaw, R. Models for nonlinear long internal waves in a rotating fluid. Fundam. Appl. Hydrophys. 2013, 6, 4–13. [Google Scholar]
- Grimshaw, R.; Helfrich, K.; Johnson, E. The reduced Ostrovsky equation: Integrability and breaking. Stud. Appl. Math. 2012, 129, 414–436. [Google Scholar] [CrossRef]
- Farmer, D.; Li, Q.; Park, J. Internal wave observations in the South China Sea: The role of rotation and non-linearity. Atmosphere-Ocean 2009, 47, 267–280. [Google Scholar] [CrossRef]
- Li, Q.; Farmer, D.M. The generation and evolution of nonlinear internal waves in the deep basin of the South China Sea. J. Phys. Ocean. 2011, 41, 1345–1363. [Google Scholar] [CrossRef]


| Case | A | B | C | D | E | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Season | S | W | S | W | S | W | S | W | S | W |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Grimshaw, R.; Johnson, E. The Effect of a Variable Background Density Stratification and Current on Oceanic Internal Solitary Waves. Fluids 2018, 3, 96. https://doi.org/10.3390/fluids3040096
Liu Z, Grimshaw R, Johnson E. The Effect of a Variable Background Density Stratification and Current on Oceanic Internal Solitary Waves. Fluids. 2018; 3(4):96. https://doi.org/10.3390/fluids3040096
Chicago/Turabian StyleLiu, Zihua, Roger Grimshaw, and Edward Johnson. 2018. "The Effect of a Variable Background Density Stratification and Current on Oceanic Internal Solitary Waves" Fluids 3, no. 4: 96. https://doi.org/10.3390/fluids3040096
APA StyleLiu, Z., Grimshaw, R., & Johnson, E. (2018). The Effect of a Variable Background Density Stratification and Current on Oceanic Internal Solitary Waves. Fluids, 3(4), 96. https://doi.org/10.3390/fluids3040096





