Extreme Learning Machines as Encoders for Sparse Reconstruction
Abstract
1. Introduction
2. The Sparse Reconstruction Problem
2.1. Sparse Reconstruction Theory
2.2. Data-Driven Sparse Basis Computation Using POD
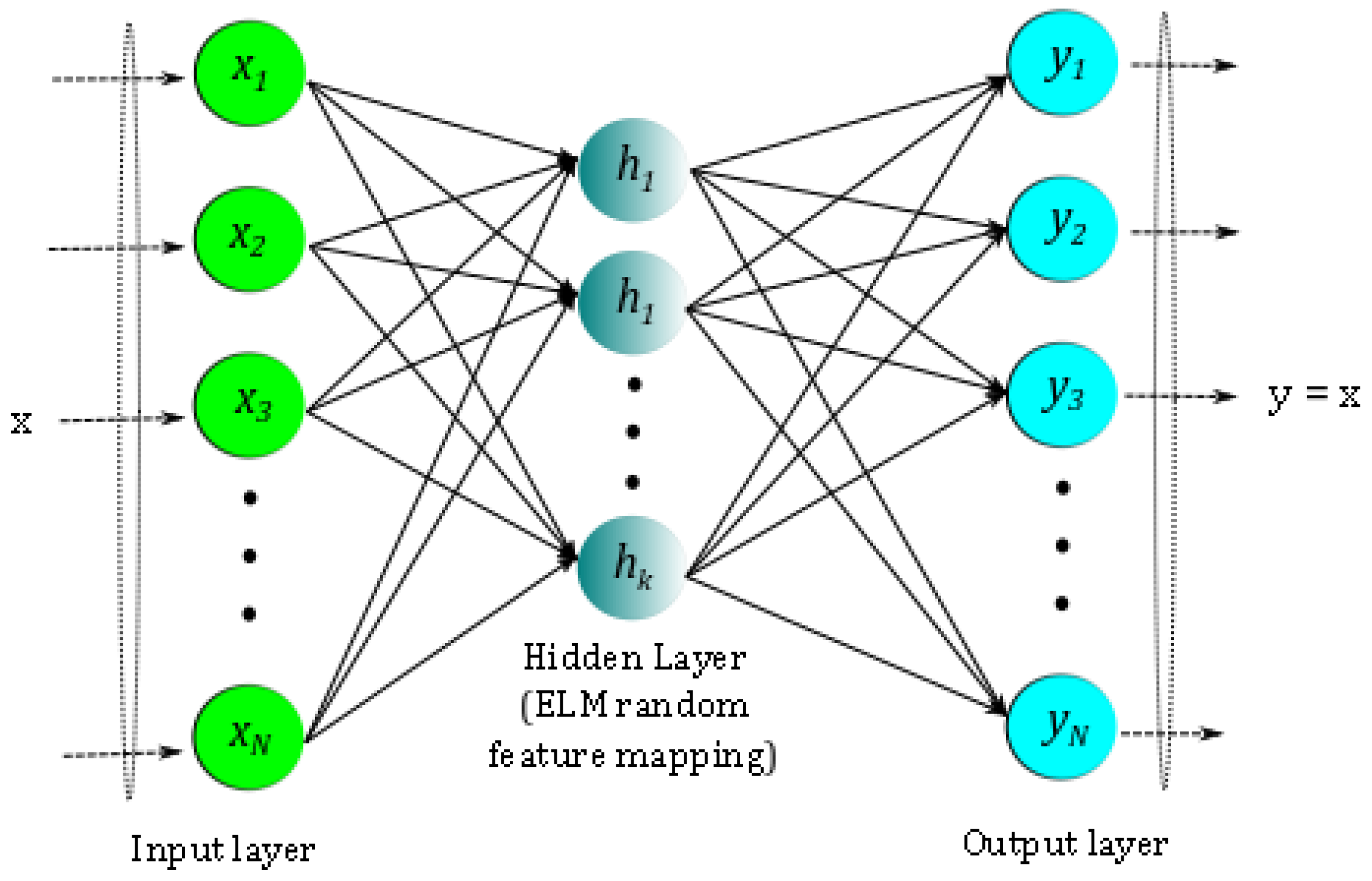
2.3. Data-Driven Sparse Basis Computation Using an ELM Autoencoder
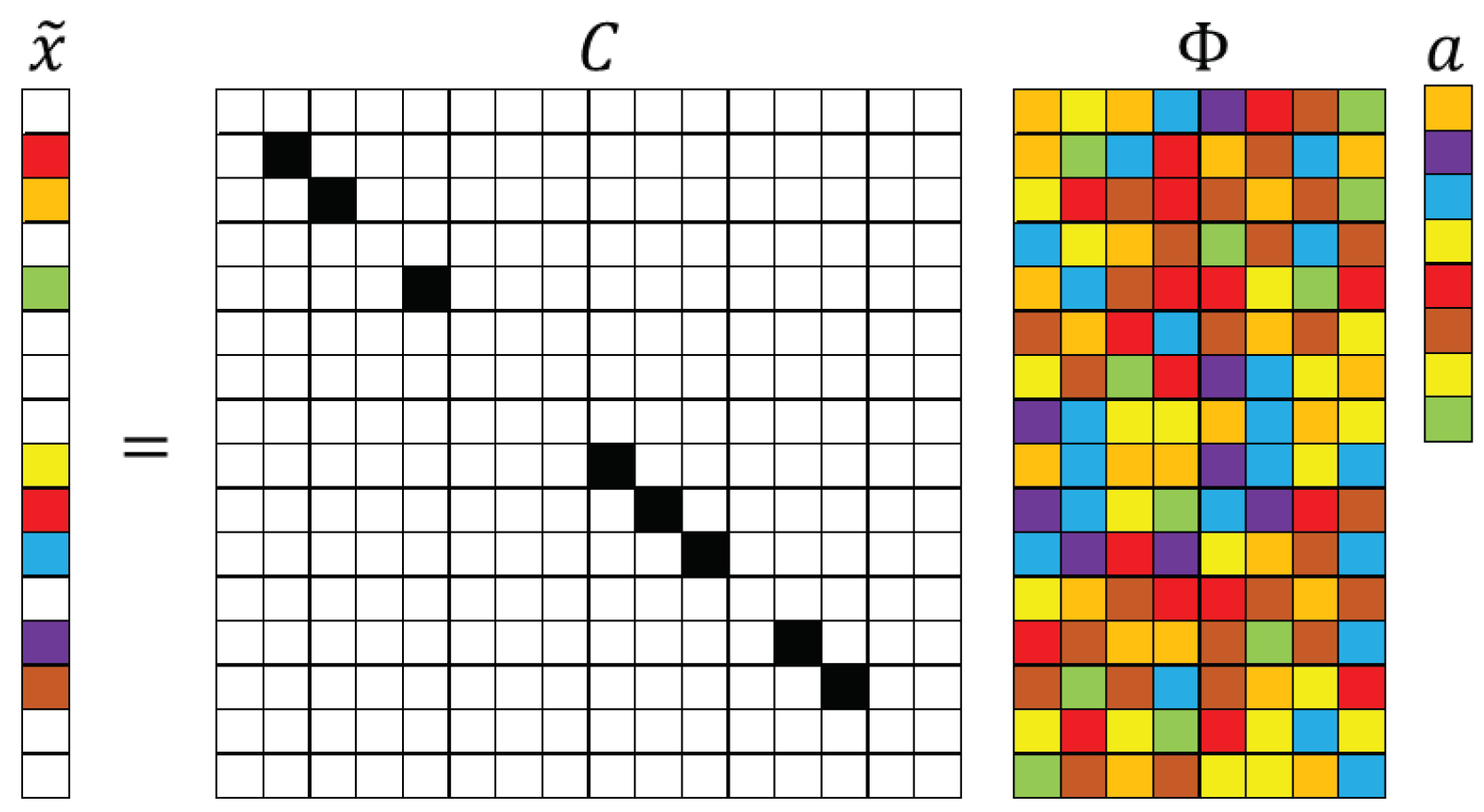
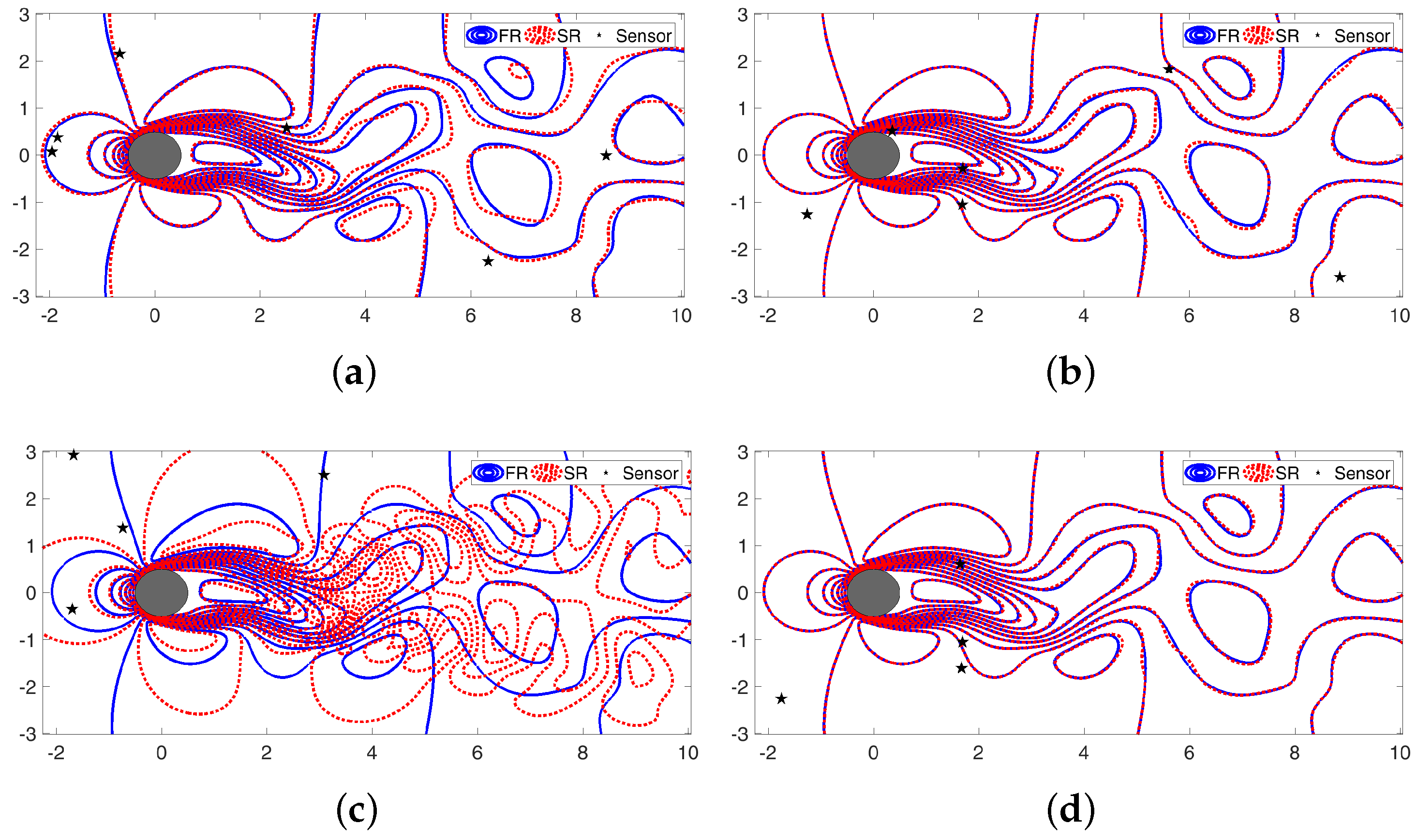
2.4. Measurement Locations, Data Basis, and Incoherence
2.5. Sparse Recovery Framework
| Algorithm 1:-based algorithm: Sparse reconstruction with known basis, . |
 |
2.6. Algorithmic Complexity
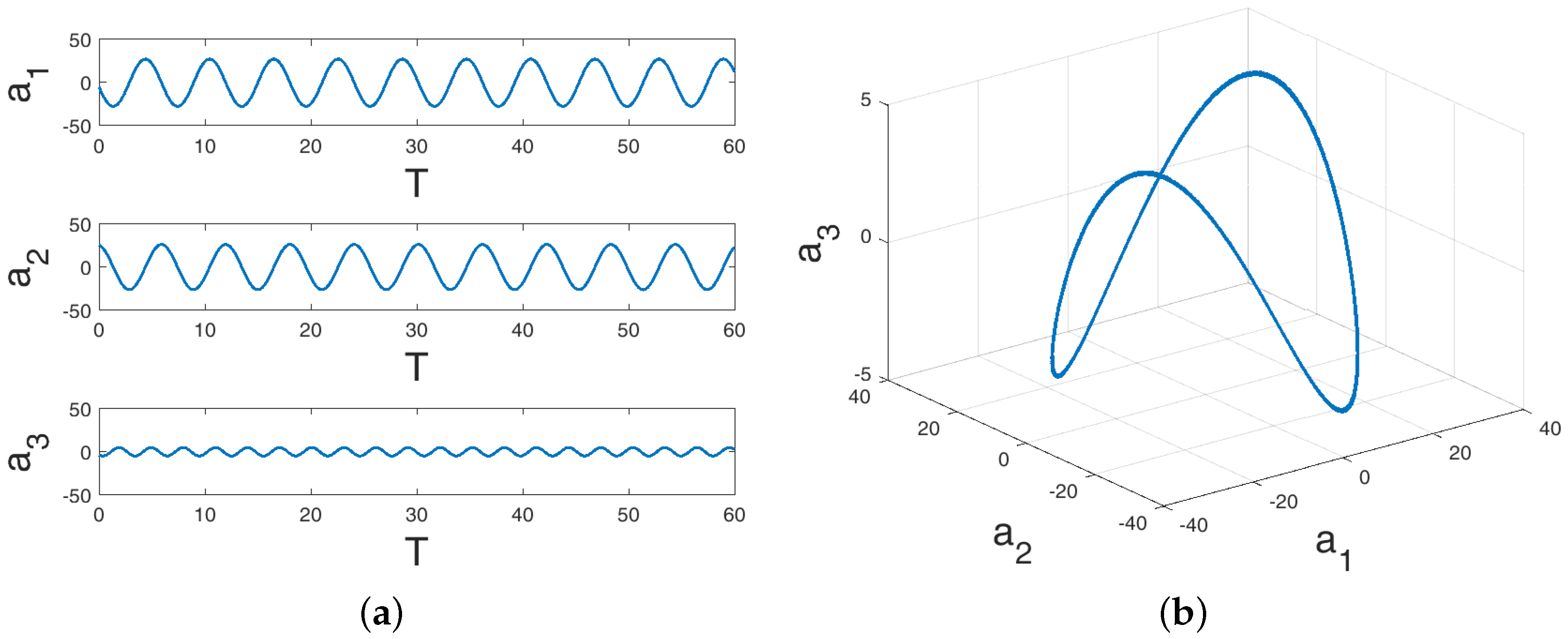
3. Data Generation for Canonical Cylinder Wake
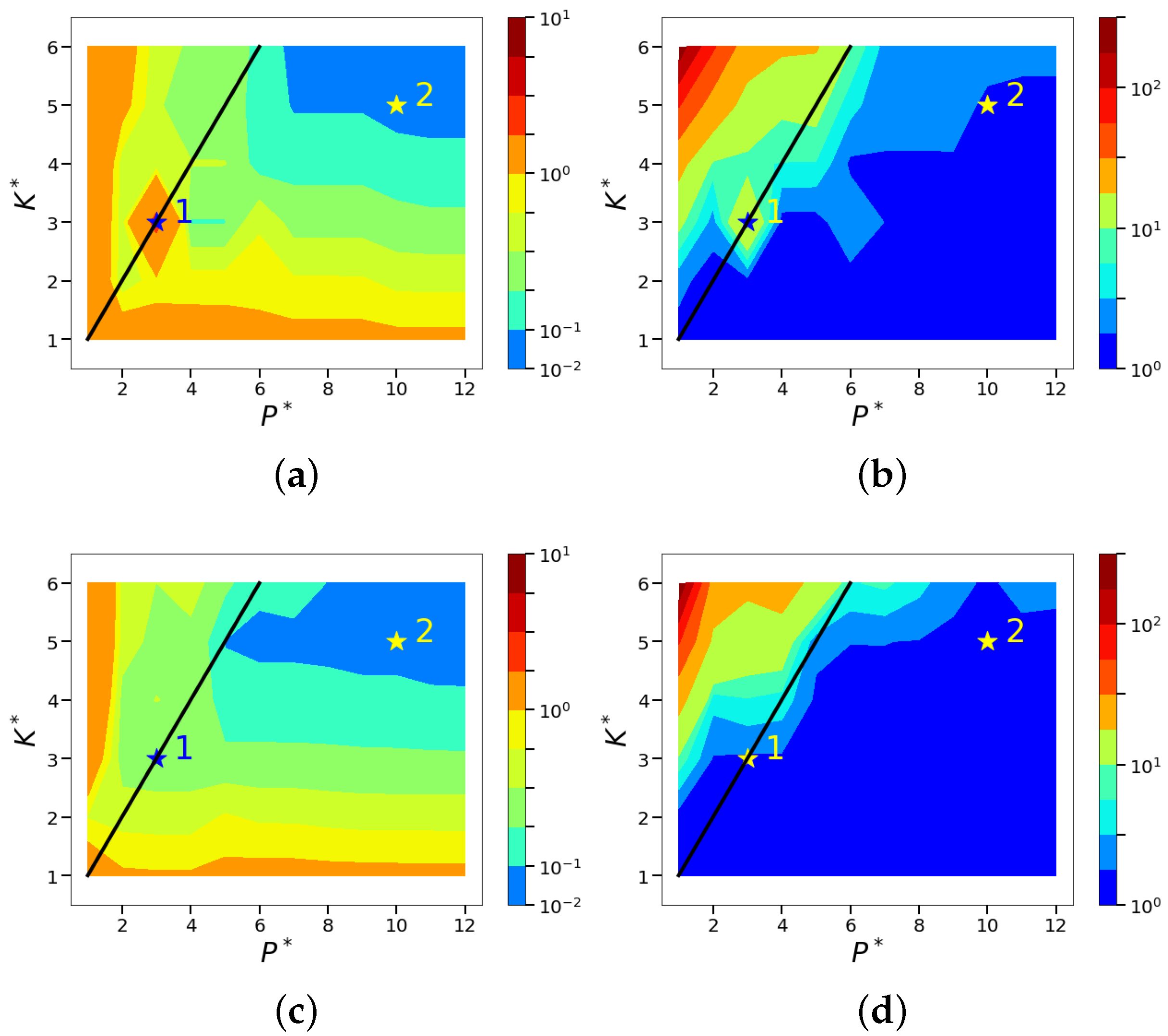
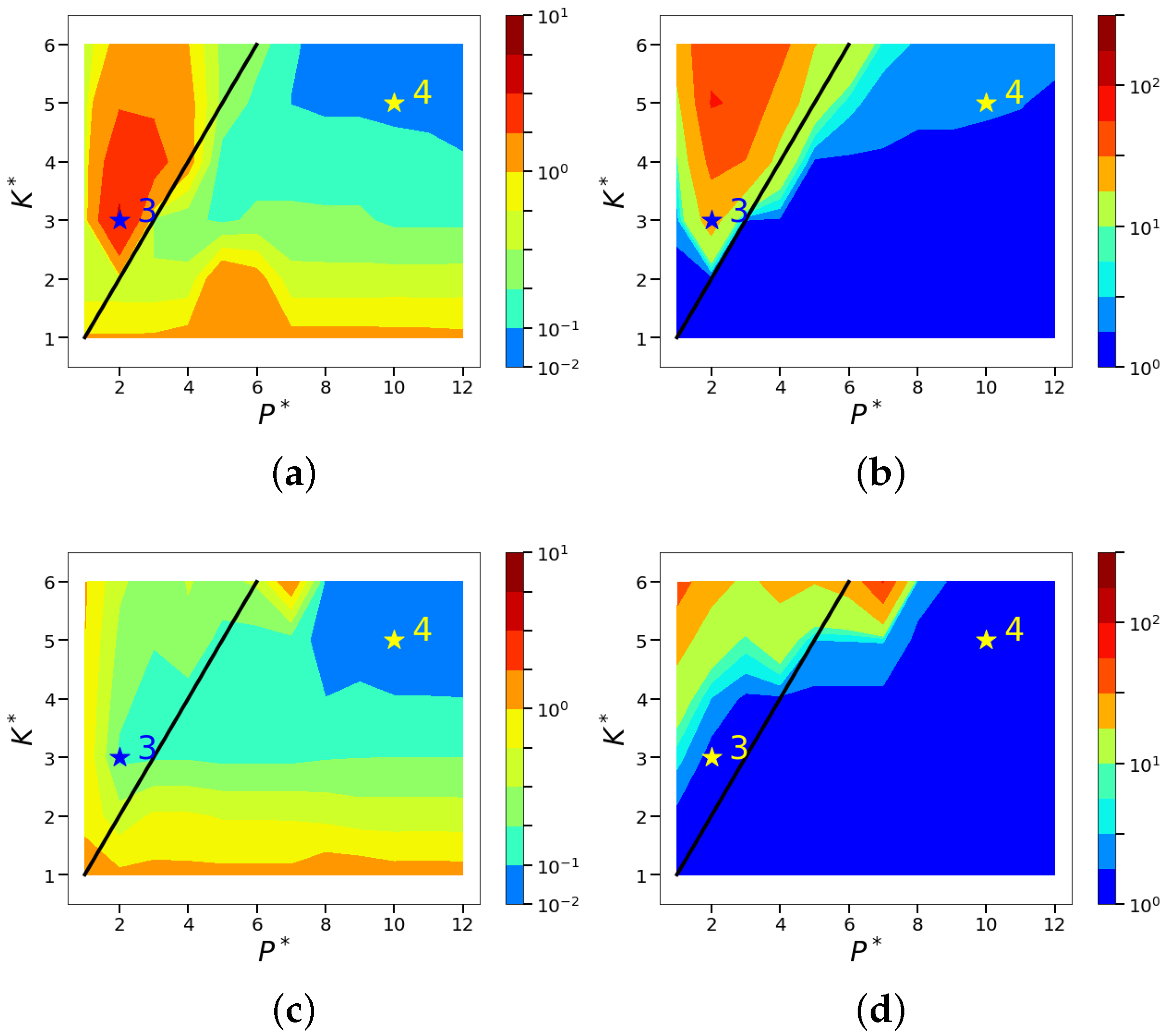
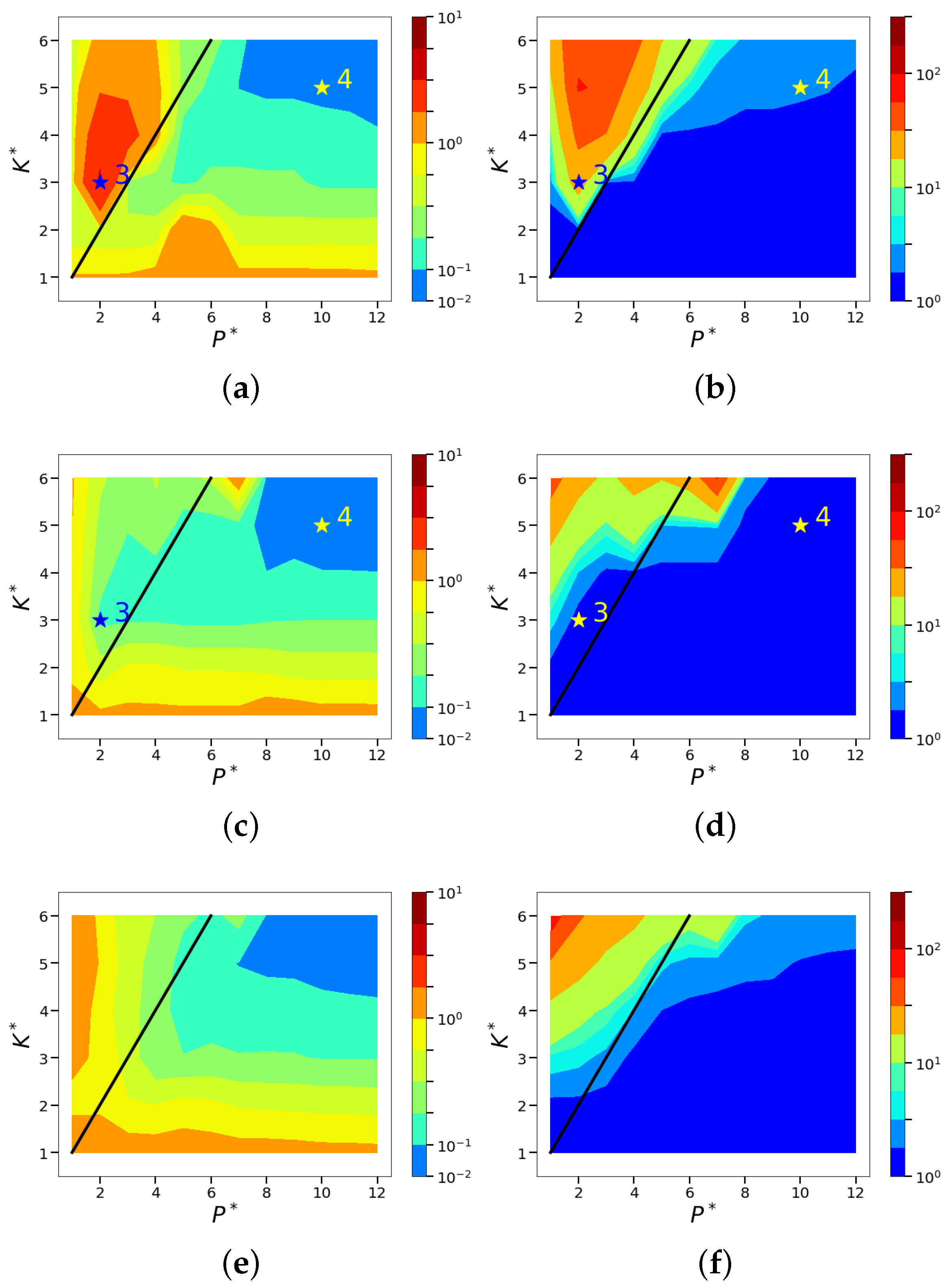
4. Sparse Reconstruction of Cylinder Wake Limit-Cycle Dynamics
4.1. Sparse Reconstruction Experiments and Analysis
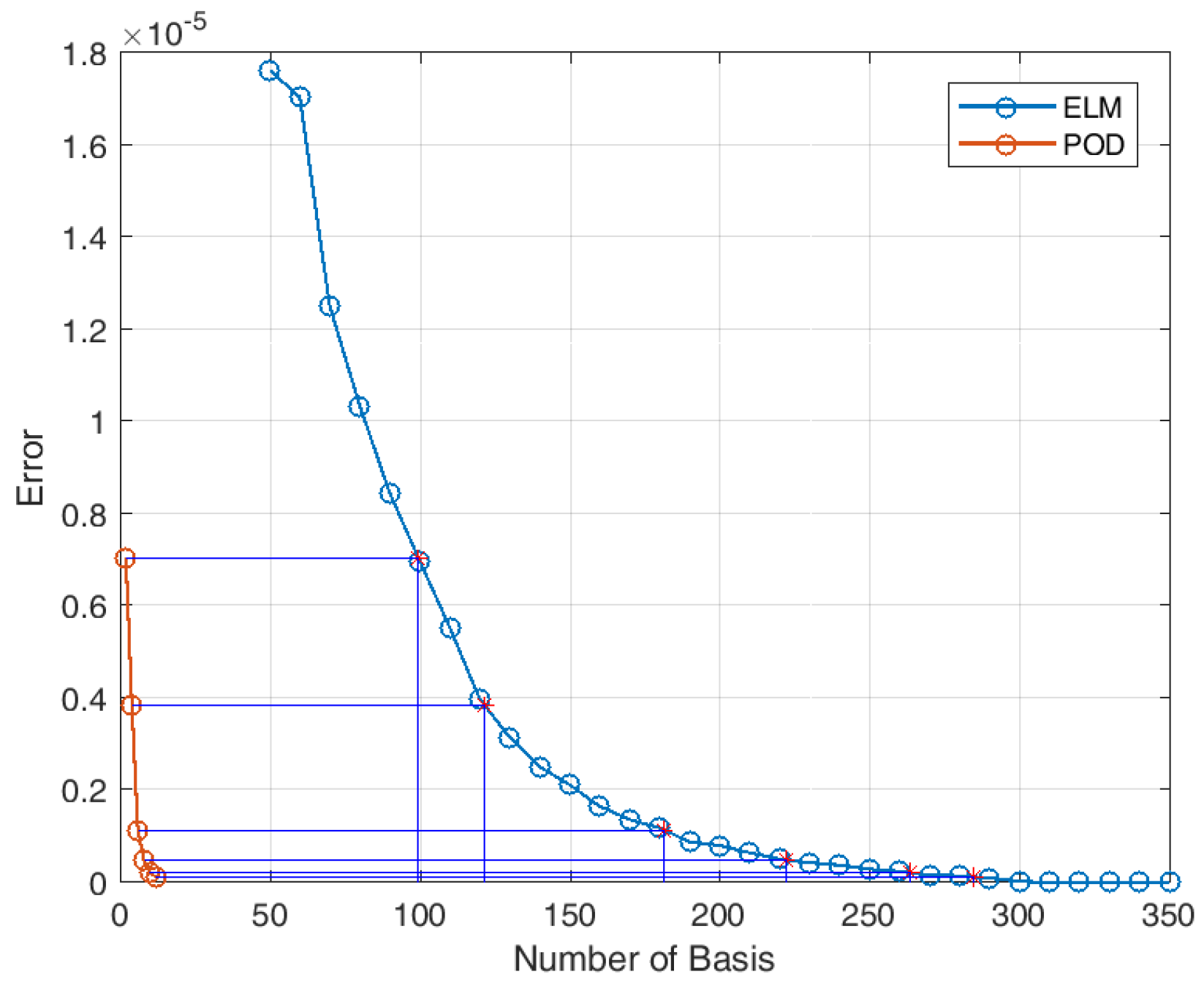
4.2. Sparsity and Energy Metrics
4.3. Sparse Reconstruction of Limit-Cycle Dynamics in Cylinder Wakes Using the POD Basis
4.4. Sparse Reconstruction Using the ELM Basis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Comparison of Predicted ELM Features and Snapshot Reconstruction
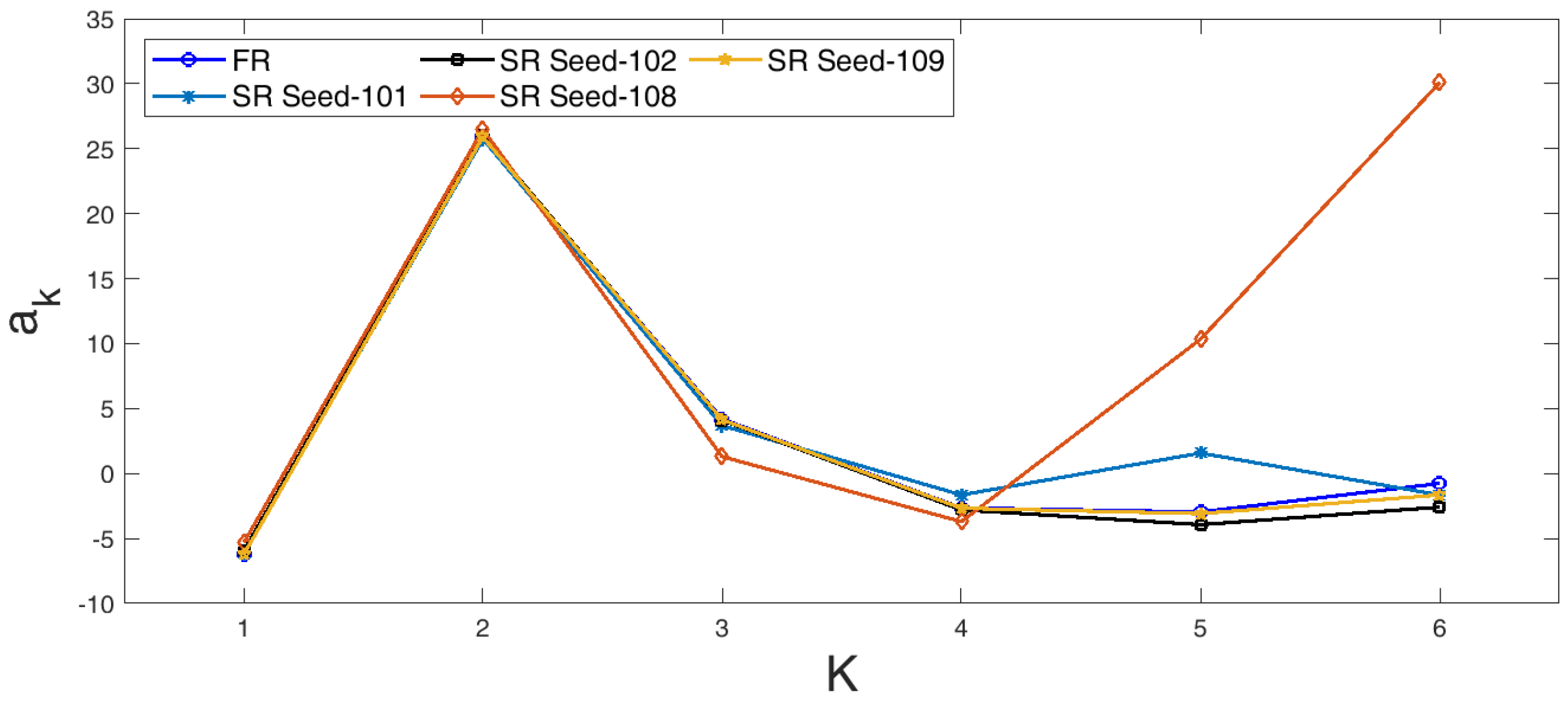
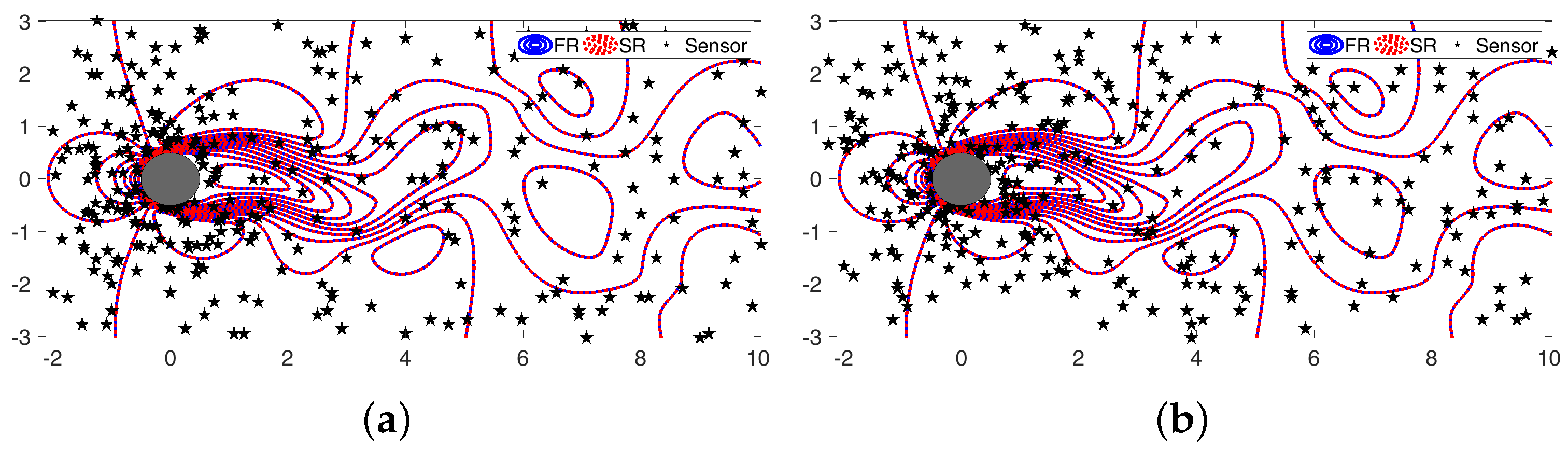
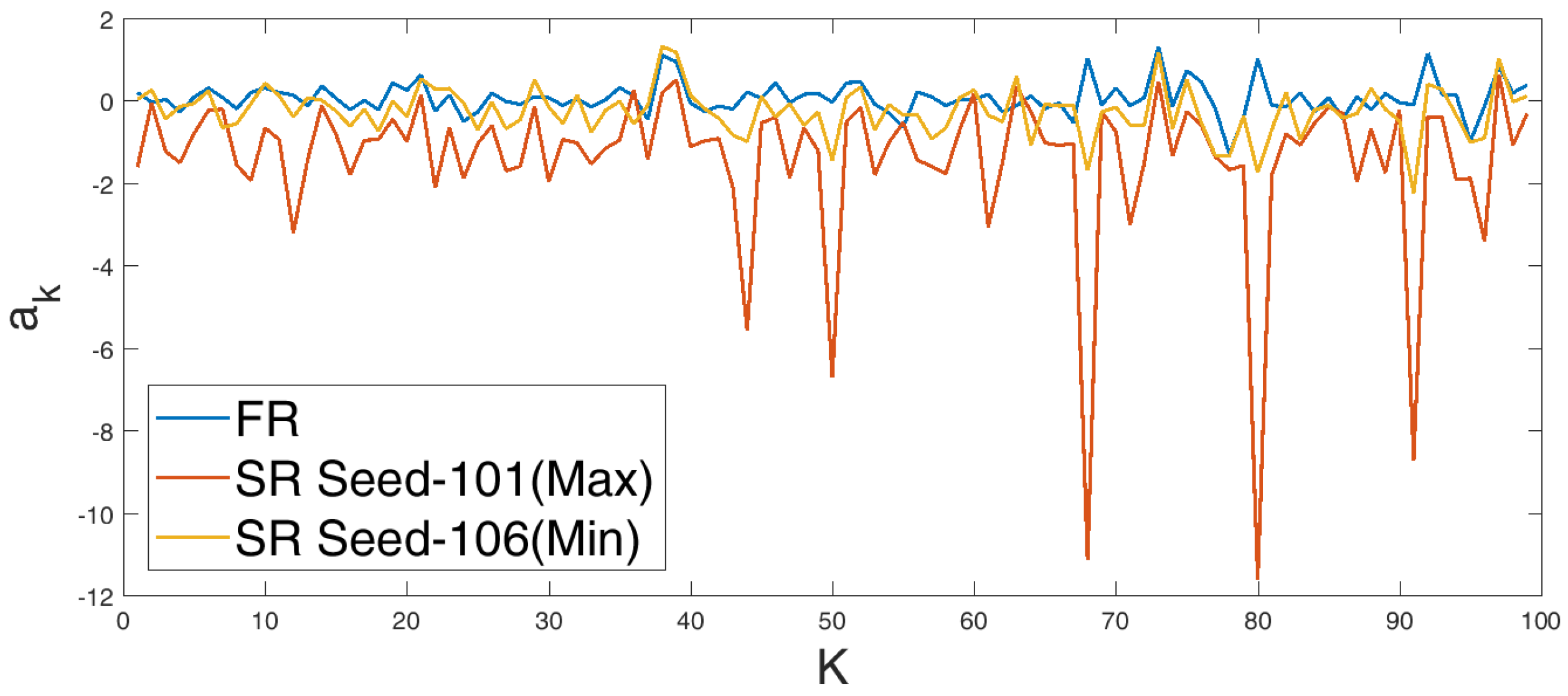
Appendix B. Impact of Retaining the Data Mean for Sparse Reconstruction
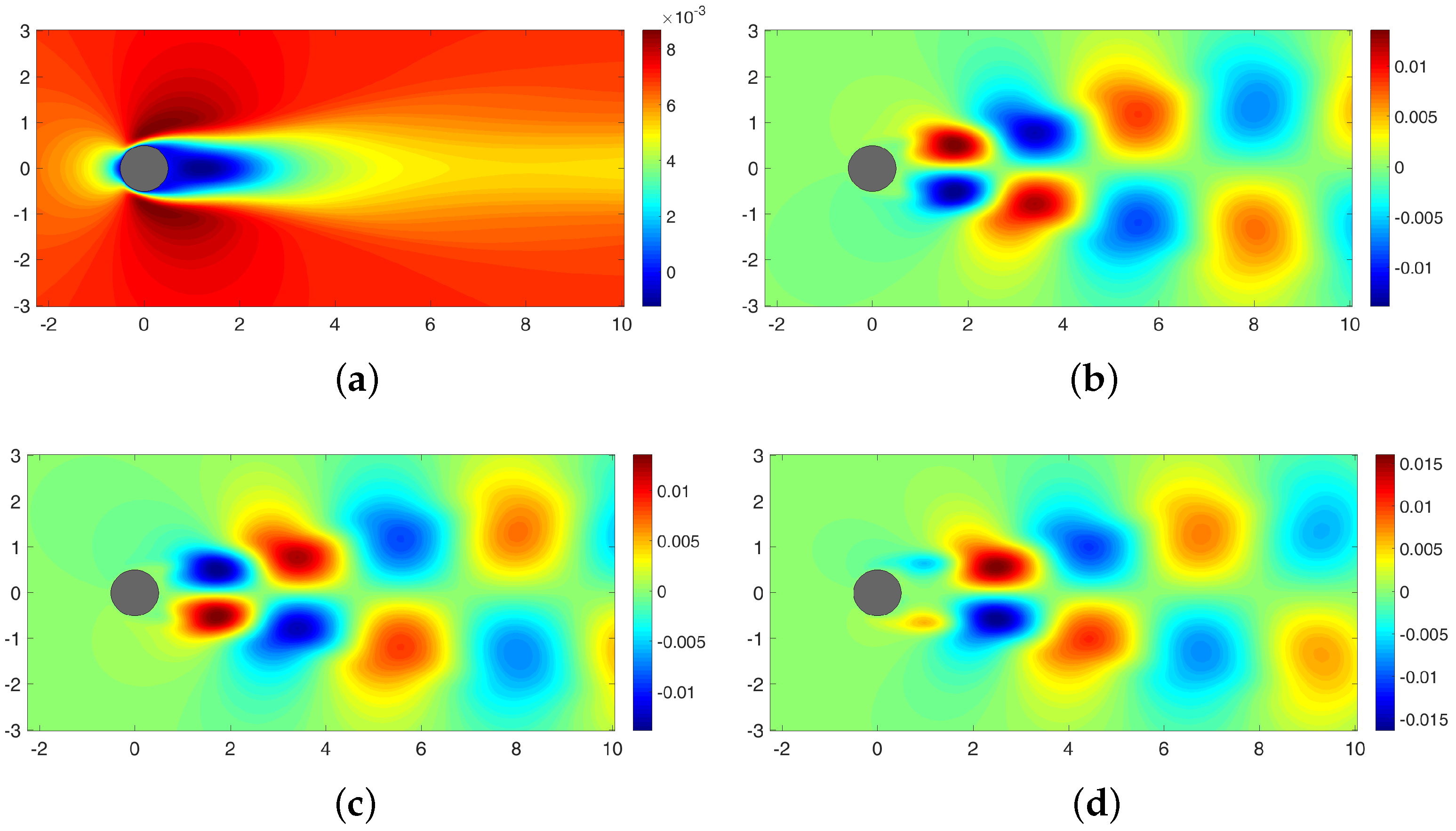
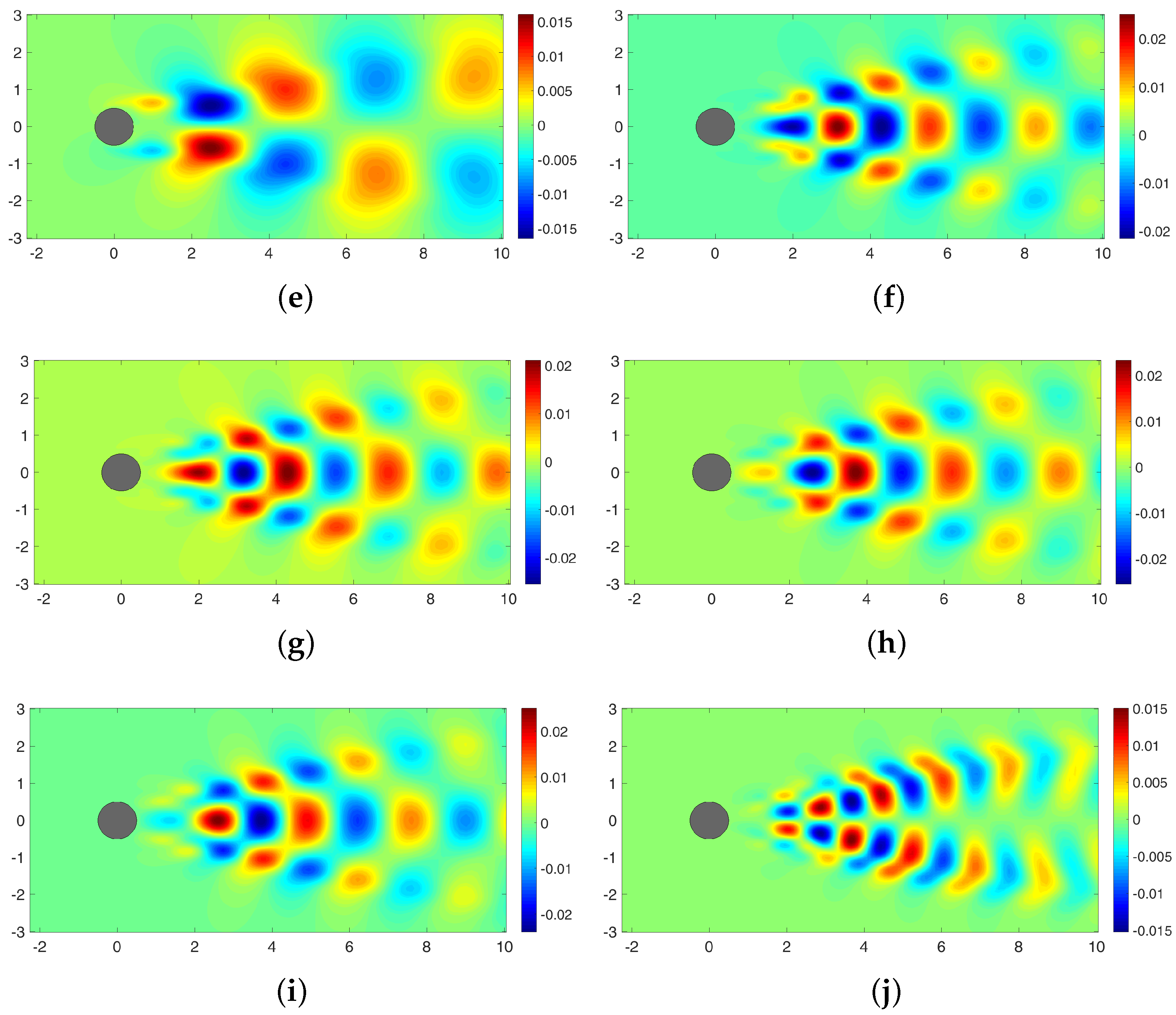
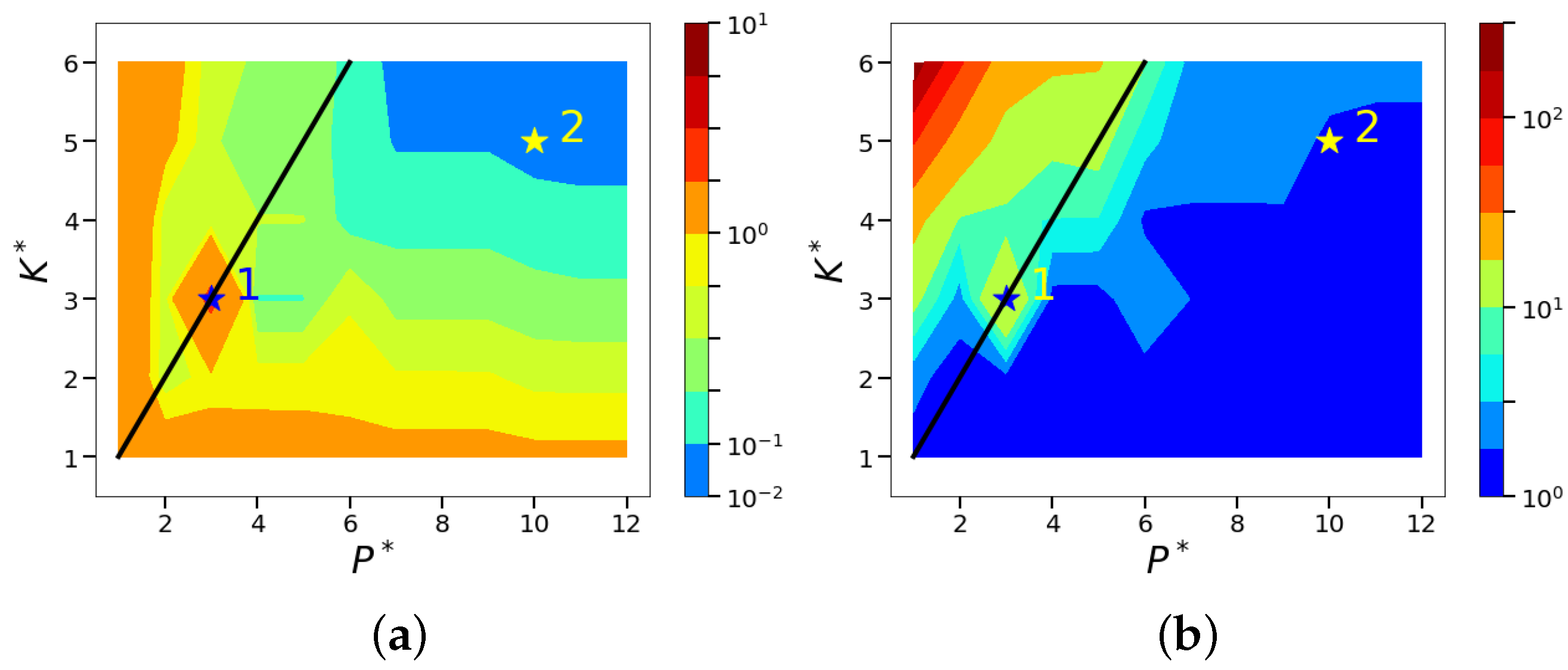

Appendix C. POD-Based Sparse Reconstruction for Cylinder Wake with Re = 800
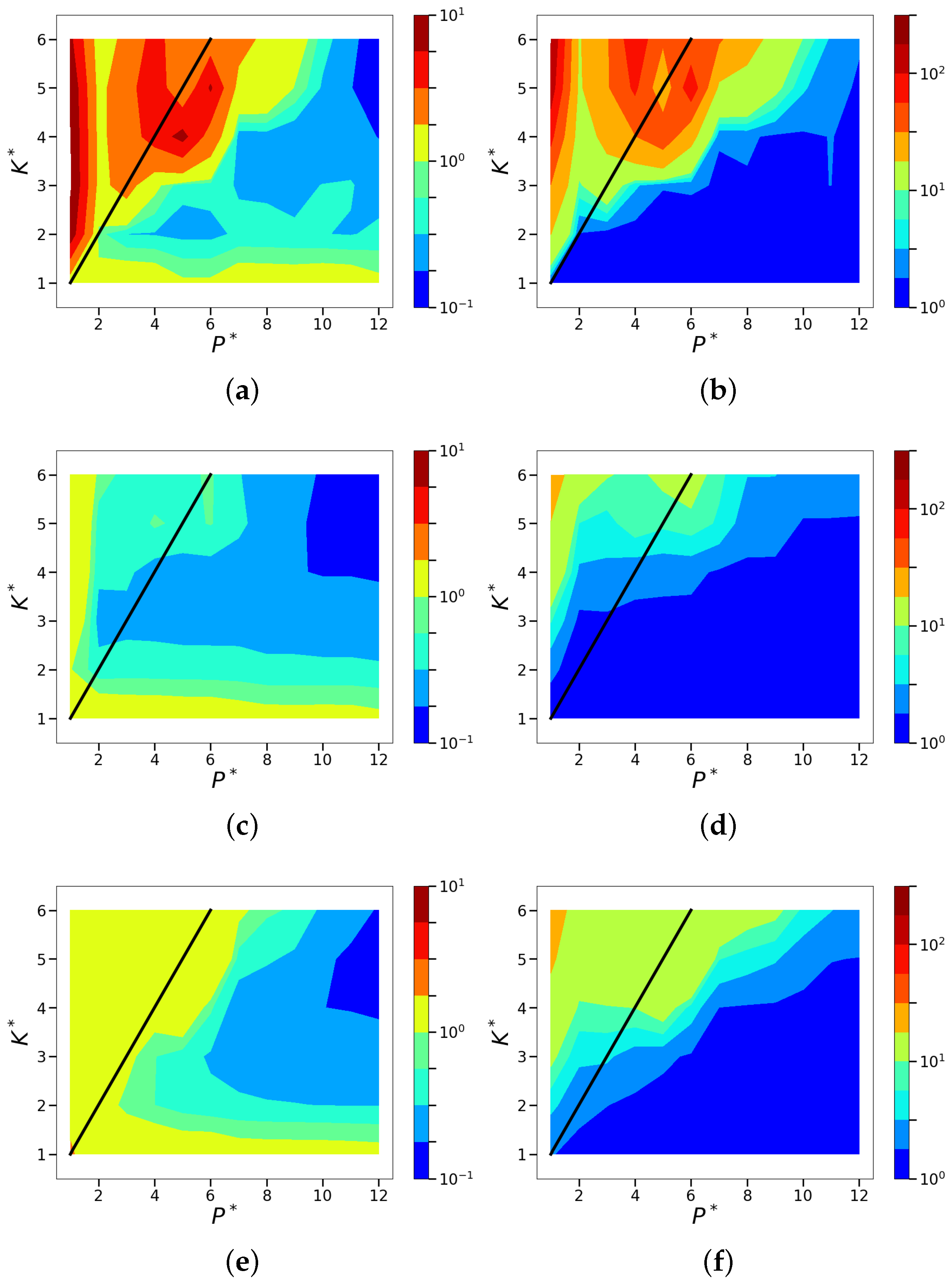
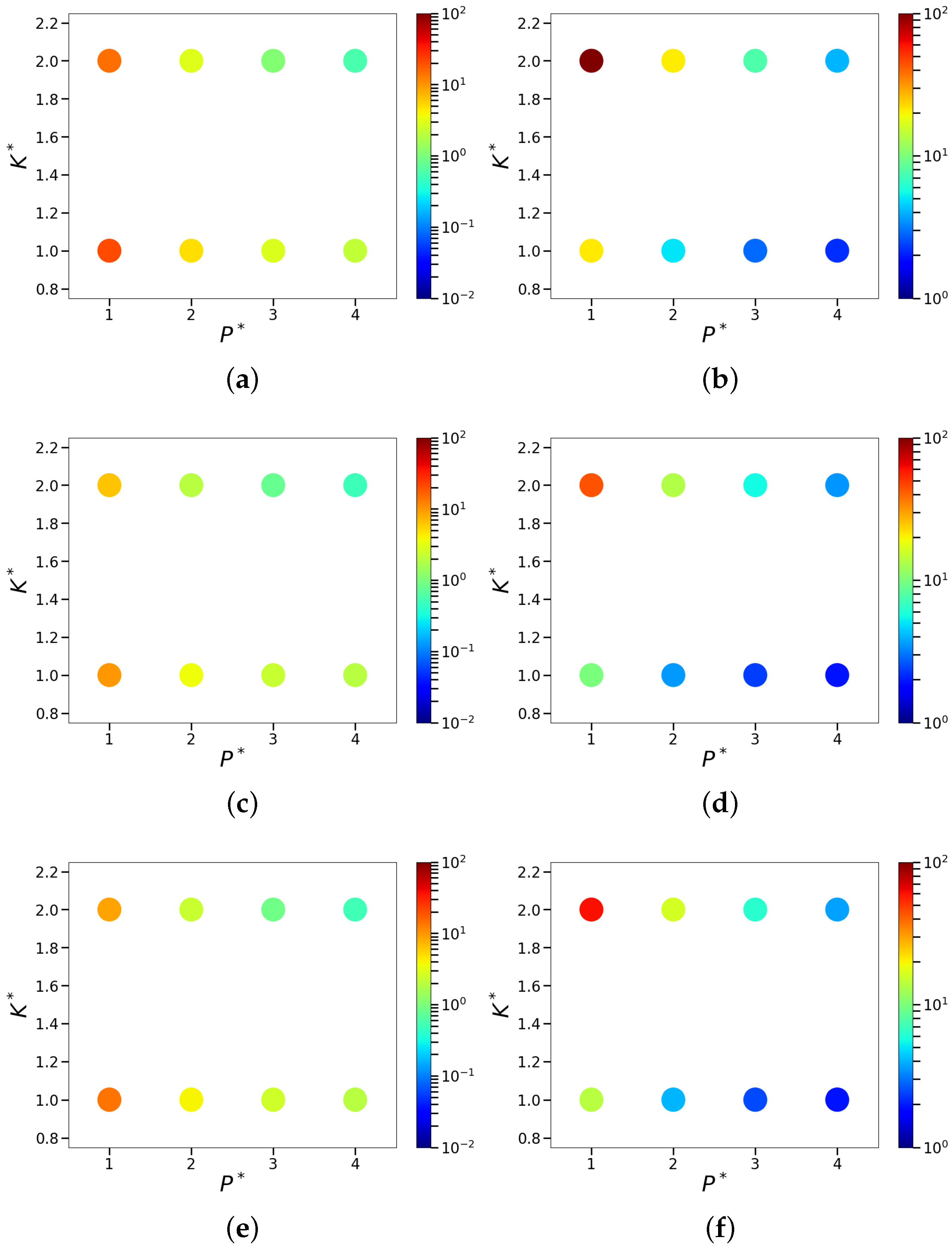

References
- Friedman, J.; Hastie, T.; Tibshirani, R. The Elements of Statistical Learning; Springer Series in Statistics: New York, NY, USA, 2001; Volume 1. [Google Scholar]
- Holmes, P. Turbulence, Coherent Structures, Dynamical Systems and Symmetry; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Berkooz, G.; Holmes, P.; Lumley, J.L. The proper orthogonal decomposition in the analysis of turbulent flows. Annu. Rev. Fluid Mech. 1993, 25, 539–575. [Google Scholar] [CrossRef]
- Taira, K.; Brunton, S.L.; Dawson, S.; Rowley, C.W.; Colonius, T.; McKeon, B.J.; Schmidt, O.T.; Gordeyev, S.; Theofilis, V.; Ukeiley, L.S. Modal analysis of fluid flows: An overview. AIAA J. 2017, 55, 4013–4041. [Google Scholar] [CrossRef]
- Jayaraman, B.; Lu, C.; Whitman, J.; Chowdhary, G. Sparse convolution-based markov models for nonlinear fluid flows. arXiv, 2018; arXiv:1803.08222. [Google Scholar]
- Bai, Z.; Wimalajeewa, T.; Berger, Z.; Wang, G.; Glauser, M.; Varshney, P.K. Low-dimensional approach for reconstruction of airfoil data via compressive sensing. AIAA J. 2014, 53, 920–933. [Google Scholar] [CrossRef]
- Bright, I.; Lin, G.; Kutz, J.N. Compressive sensing based machine learning strategy for characterizing the flow around a cylinder with limited pressure measurements. Phys. Fluids 2013, 25, 127102. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436. [Google Scholar] [CrossRef] [PubMed]
- Brunton, S.L.; Proctor, J.L.; Kutz, J.N. Compressive sampling and dynamic mode decomposition. arXiv, 2013; arXiv:1312.5186. [Google Scholar]
- Candès, E.J. Compressive sampling. In Proceedings of the International Congress of Mathematicians, Madrid, Spain, 22–30 August 2006; Volume 3, pp. 1433–1452. [Google Scholar]
- Tropp, J.A.; Gilbert, A.C. Signal recovery from random measurements via orthogonal matching pursuit. IEEE Trans. Inf. Theory 2007, 53, 4655–4666. [Google Scholar] [CrossRef]
- Candès, E.J.; Wakin, M.B. An introduction to compressive sampling. IEEE Signal Process. Mag. 2008, 25, 21–30. [Google Scholar] [CrossRef]
- Needell, D.; Tropp, J.A. Cosamp: Iterative signal recovery from incomplete and inaccurate samples. Appl. Comput. Harmon. Anal. 2009, 26, 301–321. [Google Scholar] [CrossRef]
- Bui-Thanh, T.; Damodaran, M.; Willcox, K. Aerodynamic data reconstruction and inverse design using proper orthogonal decomposition. AIAA J. 2004, 42, 1505–1516. [Google Scholar] [CrossRef]
- Willcox, K. Unsteady flow sensing and estimation via the gappy proper orthogonal decomposition. Comput. Fluids 2006, 35, 208–226. [Google Scholar] [CrossRef]
- Venturi, D.; Karniadakis, G.E. Gappy data and reconstruction procedures for flow past a cylinder. J. Fluid Mech. 2004, 519, 315–336. [Google Scholar] [CrossRef]
- Gunes, H.; Sirisup, S.; Karniadakis, G.E. Gappy data: To krig or not to krig? J. Comput. Phys. 2006, 212, 358–382. [Google Scholar] [CrossRef]
- Gunes, H.; Rist, U. On the use of kriging for enhanced data reconstruction in a separated transitional flat-plate boundary layer. Phys. Fluids 2008, 20, 104109. [Google Scholar] [CrossRef]
- Huang, G.-B.; Zhu, Q.-Y.; Siew, C.-K. Extreme learning machine: theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Huang, G.-B.; Wang, D.-H.; Lan, Y. Extreme learning machines: A survey. Int. J. Mach. Learn. Cybern. 2011, 2, 107–122. [Google Scholar] [CrossRef]
- Kasun, L.L.C.; Zhou, H.; Huang, G.-B.; Vong, C.M. Representational learning with extreme learning machine for big data. IEEE Intell. Syst. 2013, 28, 31–34. [Google Scholar]
- Zhou, H.; Soh, Y.C.; Jiang, C.; Wu, X. Compressed representation learning for fluid field reconstruction from sparse sensor observations. In Proceedings of the 2015 International Joint Conference on Neural Networks (IJCNN), Killarney, Ireland, 12–17 July 2015; pp. 1–6. [Google Scholar]
- Zhou, H.; Huang, G.-B.; Lin, Z.; Wang, H.; Soh, Y.C. Stacked extreme learning machines. IEEE Trans. Cybern. 2015, 45, 2013–2025. [Google Scholar] [CrossRef] [PubMed]
- Romberg, J. Imaging via compressive sampling. IEEE Signal Process. Mag. 2008, 25, 14–20. [Google Scholar] [CrossRef]
- Everson, R.; Sirovich, L. Karhunen—Loeve procedure for gappy data. JOSA A 1995, 12, 1657–1664. [Google Scholar] [CrossRef]
- Saini, P.; Arndt, C.M.; Steinberg, A.M. Development and evaluation of gappy-pod as a data reconstruction technique for noisy piv measurements in gas turbine combustors. Exp. Fluids 2016, 57, 1–15. [Google Scholar] [CrossRef]
- Mallet, S. A Wavelet Tour of Signal Processing; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Brunton, S.L.; Tu, J.H.; Bright, I.; Kutz, J.N. Compressive sensing and low-rank libraries for classification of bifurcation regimes in nonlinear dynamical systems. SIAM J. Appl. Dyn. Syst. 2014, 13, 1716–1732. [Google Scholar] [CrossRef]
- Bai, Z.; Brunton, S.L.; Brunton, B.W.; Kutz, J.N.; Kaiser, E.; Spohn, A.; Noack, B.R. Data-driven methods in fluid dynamics: Sparse classification from experimental data. In Whither Turbulence and Big Data in the 21st Century? Springer: New York, NY, USA, 2017; pp. 323–342. [Google Scholar]
- Kramer, B.; Grover, P.; Boufounos, P.; Nabi, S.; Benosman, M. Sparse sensing and dmd-based identification of flow regimes and bifurcations in complex flows. SIAM J. Appl. Dyn. Syst. 2017, 16, 1164–1196. [Google Scholar] [CrossRef]
- Schmid, P.J. Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 2010, 656, 5–28. [Google Scholar] [CrossRef]
- Tu, J.H.; Rowley, C.W.; Luchtenburg, D.M.; Brunton, S.L.; Kutz, J.N. On dynamic mode decomposition: Theory and applications. arXiv, 2013; arXiv:1312.0041. [Google Scholar]
- Rowley, C.W.; Dawson, S.T.M. Model reduction for flow analysis and control. Annu. Rev. Fluid Mech. 2017, 49, 387–417. [Google Scholar] [CrossRef]
- Wu, H.; Noé, F. Variational approach for learning markov processes from time series data. arXiv, 2017; 17, arXiv:1707.04659. [Google Scholar]
- Lu, C.; Jayaraman, B. Interplay of sensor quantity, placement and system dimensionality on energy sparse reconstruction of fluid flows. arXiv, 2018; arXiv:1806.08428. [Google Scholar]
- Tarantola, A. Inverse Problem Theory and Methods for Model Parameter Estimation; SIAM: Philadelphia, PA, USA, 2005; Volume 89. [Google Scholar]
- Arridge, S.R.; Schotland, J.C. Optical tomography: Forward and inverse problems. Inverse Probl. 2009, 25, 123010. [Google Scholar] [CrossRef]
- Tarantola, A.; Valette, B. Generalized nonlinear inverse problems solved using the least squares criterion. Rev. Geophys. 1982, 20, 219–232. [Google Scholar] [CrossRef]
- Neelamani, R. Inverse Problems in Image Processing. Ph.D. Thesis, Rice University, Houston, TX, USA, 2004. [Google Scholar]
- Khemka, A. Inverse Problems in Image Processing. Ph.D. Thesis, Purdue University, West Lafayette, IN, USA, 2009. [Google Scholar]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Baraniuk, R.G. Compressive sensing [lecture notes]. IEEE Signal Process. Mag. 2007, 24, 118–121. [Google Scholar] [CrossRef]
- Baraniuk, R.G.; Cevher, V.; Duarte, M.F.; Hegde, C. Model-based compressive sensing. IEEE Trans. Inf. Theory 2010, 56, 1982–2001. [Google Scholar] [CrossRef]
- Sarvotham, S.; Baron, D.; Wakin, M.; Duarte, M.F.; Baraniuk, R.G. Distributed compressed sensing of jointly sparse signals. In Proceedings of the Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 30 October–2 November 2005; pp. 1537–1541. [Google Scholar]
- Candès, E.J.; Romberg, J.; Tao, T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar] [CrossRef]
- Candes, E.J.; Romberg, J.K.; Tao, T. Stable signal recovery from incomplete and inaccurate measurements. Commun. Pure Appl. Math. 2006, 59, 1207–1223. [Google Scholar] [CrossRef]
- Candes, E.J.; Tao, T. Near-optimal signal recovery from random projections: Universal encoding strategies? IEEE Trans. Inf. Theory 2006, 52, 5406–5425. [Google Scholar] [CrossRef]
- Candes, E.J.; Romberg, J.K. Signal recovery from random projections. In Proceedings of the Computational Imaging III, San Jose, CA, USA, 16–20 January 2005; Volume 5674, pp. 76–87. [Google Scholar]
- Chen, S.S.; Donoho, D.L.; Saunders, M.A. Atomic decomposition by basis pursuit. SIAM Rev. 2001, 43, 129–159. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B Methodol. 1996, 58, 267–288. [Google Scholar]
- Candes, E.J.; Wakin, M.B.; Boyd, S.P. Enhancing sparsity by reweighted ℓ 1 minimization. J. Fourier Anal. Appl. 2008, 14, 877–905. [Google Scholar] [CrossRef]
- Kim, S.-J.; Koh, K.; Lustig, M.; Boyd, S.; Gorinevsky, D. An interior-point method for large-scale l1 regularized least squares. IEEE J. Sel. Top. Signal Process. 2007, 1, 606–617. [Google Scholar] [CrossRef]
- Brunton, S.L.; Proctor, J.L.; Kutz, J.N. Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proc. Natl. Acad. Sci. USA 2016, 201517384. [Google Scholar] [CrossRef] [PubMed]
- Lumley, J.L. Stochastic Tools in Turbulence; Academic: New York, NY, USA, 1970. [Google Scholar]
- Sirovich, L. Turbulence and the dynamics of coherent structures. I. coherent structures. Q. Appl. Math. 1987, 45, 561–571. [Google Scholar] [CrossRef]
- Astrid, P.; Weiland, S.; Willcox, K.; Backx, T. Missing point estimation in models described by proper orthogonal decomposition. In Proceedings of the 43rd IEEE Conference on Decision and Control, Nassau, Bahamas, 14–17 December 2004; Volume 2, pp. 1767–1772. [Google Scholar]
- Bui-Thanh, T.; Damodaran, M.; Willcox, K. Proper orthogonal decomposition extensions for parametric applications in compressible aerodynamics. In Proceedings of the 21st AIAA Applied Aerodynamics Conference, Orlando, FL, USA, 23–26 June 2003; p. 4213. [Google Scholar]
- Brunton, S.L.; Rowley, C.W.; Williams, D.R. Reduced-order unsteady aerodynamic models at low reynolds numbers. J. Fluid Mech. 2013, 724, 203–233. [Google Scholar] [CrossRef]
- Candes, E.; Romberg, J. Sparsity and incoherence in compressive sampling. Inverse Probl. 2007, 23, 969. [Google Scholar] [CrossRef]
- Csató, L.; Opper, M. Sparse on-line gaussian processes. Neural Comput. 2002, 14, 641–668. [Google Scholar] [CrossRef] [PubMed]
- Cohen, K.; Siegel, S.; McLaughlin, T. Sensor placement based on proper orthogonal decomposition modeling of a cylinder wake. In Proceedings of the 33rd AIAA Fluid Dynamics Conference and Exhibit, Orlando, FL, USA, 23–26 June 2003; p. 4259. [Google Scholar]
- Kubrusly, C.S.; Malebranche, H. Sensors and controllers location in distributed systems—A survey. Automatica 1985, 21, 117–128. [Google Scholar] [CrossRef]
- Roshko, A. On the Development of Turbulent Wakes from Vortex Streets; NACA: Kitty Hawk, NC, USA, 1954. [Google Scholar]
- Williamson, C.H.K. Oblique and parallel modes of vortex shedding in the wake of a circular cylinder at low reynolds numbers. J. Fluid Mech. 1989, 206, 579–627. [Google Scholar] [CrossRef]
- Noack, B.R.; Afanasiev, K.; Morzynski, M.; Tadmor, G.; Thiele, F. A hierarchy of low-dimensional models for the transient and post-transient cylinder wake. J. Fluid Mech. 2003, 497, 335–363. [Google Scholar] [CrossRef]
- Cantwell, C.D.; Moxey, D.; Comerford, A.; Bolis, A.; Rocco, G.; Mengaldo, G.; de Grazia, D.; Yakovlev, S.; Lombard, J.-E.; Ekelschot, D.; et al. Nektar++: An open-source spectral/hp element framework. Comput. Phys. Commun. 2015, 192, 205–219. [Google Scholar] [CrossRef]
- Chaturantabut, S.; Sorensen, D.C. Nonlinear model reduction via discrete empirical interpolation. SIAM J. Sci. Comput. 2010, 32, 2737–2764. [Google Scholar] [CrossRef]
- Zimmermann, R.; Willcox, K. An accelerated greedy missing point estimation procedure. SIAM J. Sci. Comput. 2016, 38, A2827–A2850. [Google Scholar] [CrossRef]
- Dimitriu, G.; Stefanescu, R.; Navon, I.M. Comparative numerical analysis using reduced-order modeling strategies for nonlinear large-scale systems. J. Comput. Appl. Math. 2017, 310, 32–43. [Google Scholar] [CrossRef]
- Beck, A.; Teboulle, M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imaging Sci. 2009, 2, 183–202. [Google Scholar] [CrossRef]

| (a) | (b) |


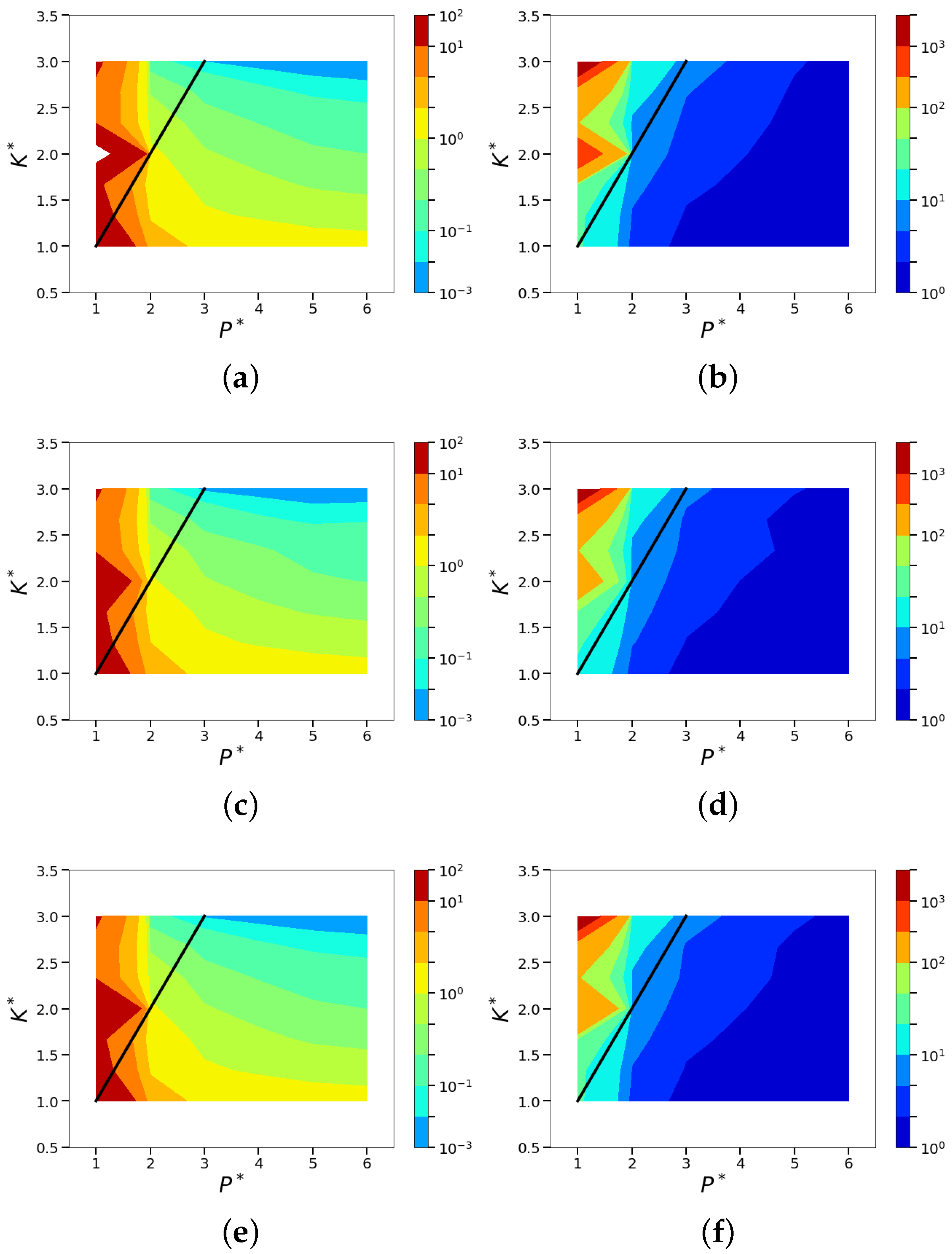
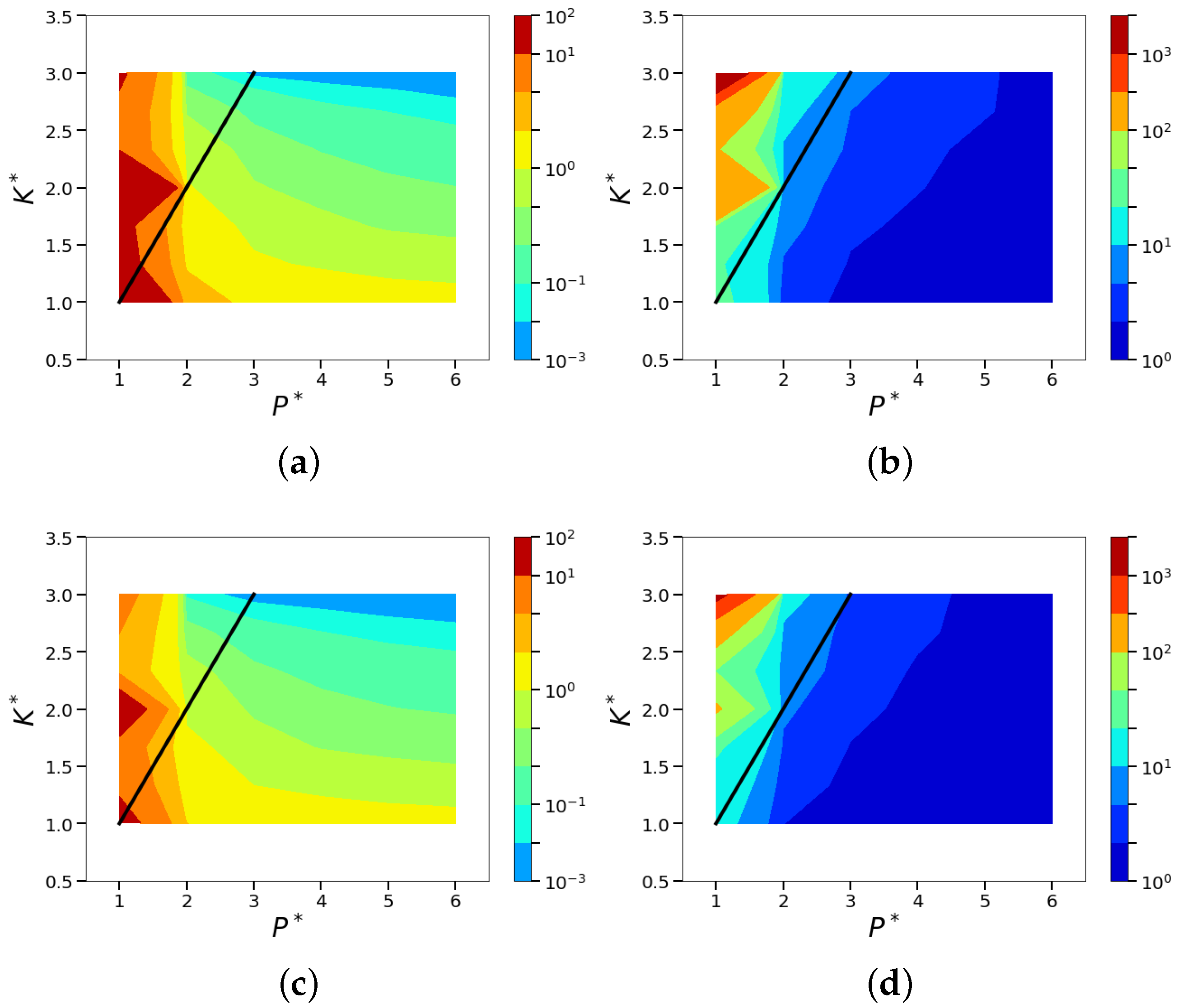
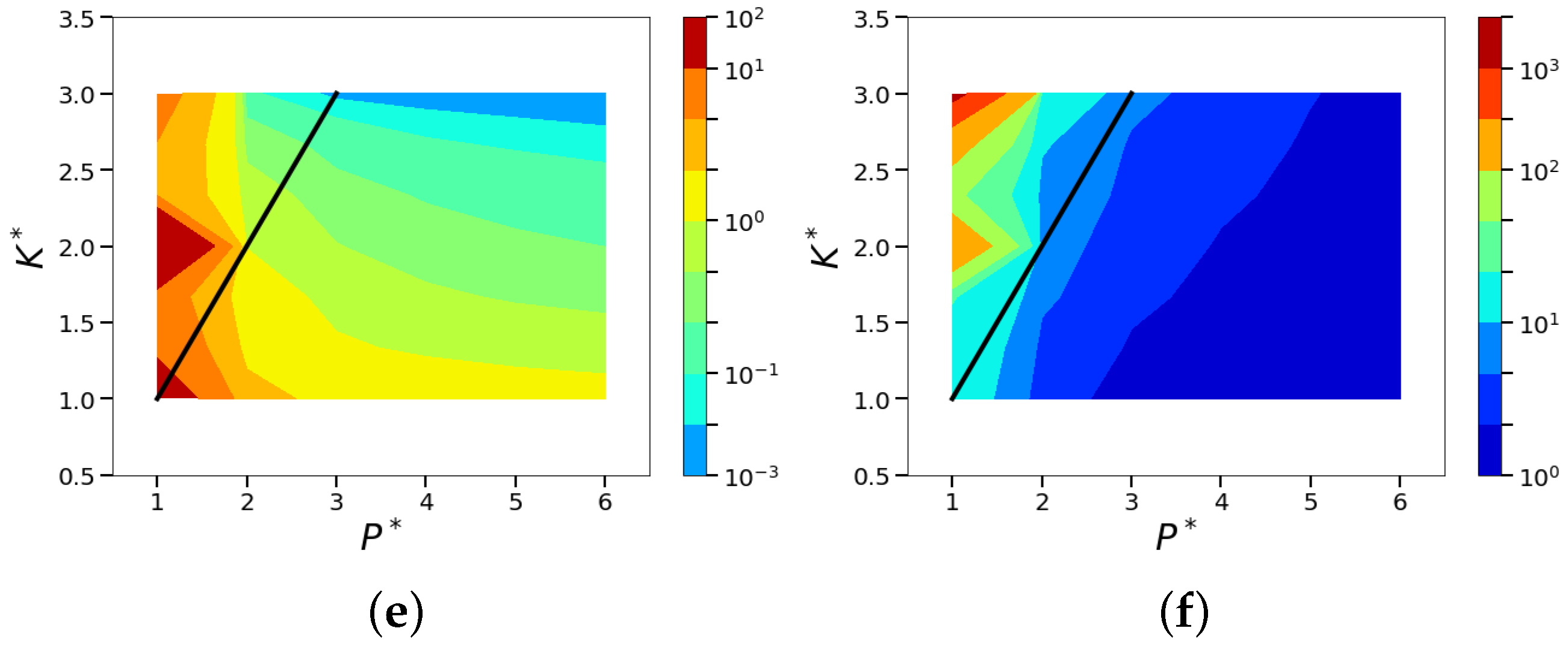
| Case | Relationship | Relationship | Algorithm | Reconstructed Dimension |
|---|---|---|---|---|
| 1 | K | |||
| 2 | P | |||
| 3 | P | |||
| 4 | K or P | |||
| 5 | K or |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al Mamun, S.M.A.; Lu, C.; Jayaraman, B. Extreme Learning Machines as Encoders for Sparse Reconstruction. Fluids 2018, 3, 88. https://doi.org/10.3390/fluids3040088
Al Mamun SMA, Lu C, Jayaraman B. Extreme Learning Machines as Encoders for Sparse Reconstruction. Fluids. 2018; 3(4):88. https://doi.org/10.3390/fluids3040088
Chicago/Turabian StyleAl Mamun, S M Abdullah, Chen Lu, and Balaji Jayaraman. 2018. "Extreme Learning Machines as Encoders for Sparse Reconstruction" Fluids 3, no. 4: 88. https://doi.org/10.3390/fluids3040088
APA StyleAl Mamun, S. M. A., Lu, C., & Jayaraman, B. (2018). Extreme Learning Machines as Encoders for Sparse Reconstruction. Fluids, 3(4), 88. https://doi.org/10.3390/fluids3040088





