Evolve Filter Stabilization Reduced-Order Model for Stochastic Burgers Equation
Abstract
1. Introduction
2. Stochastic Burgers Equation (SBE)
2.1. Numerical Discretization of SBE
3. Reduced Order Modeling
3.1. Proper Orthogonal Decomposition
3.2. Galerkin Projection ROM (G-ROM)
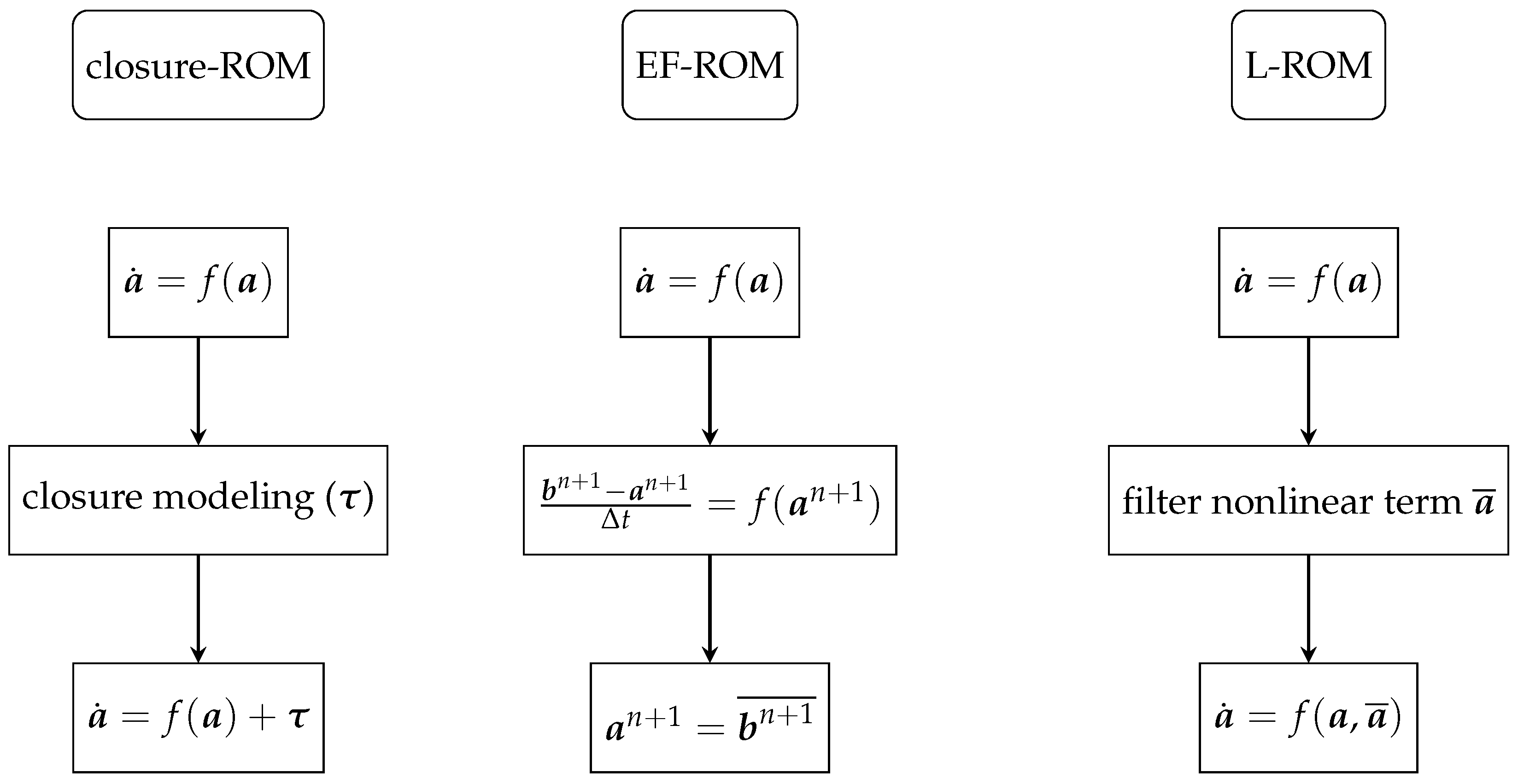
4. Evolve-Then-Filter Regularized ROM
4.1. POD Differential Filter
4.2. EF-ROM for SBE
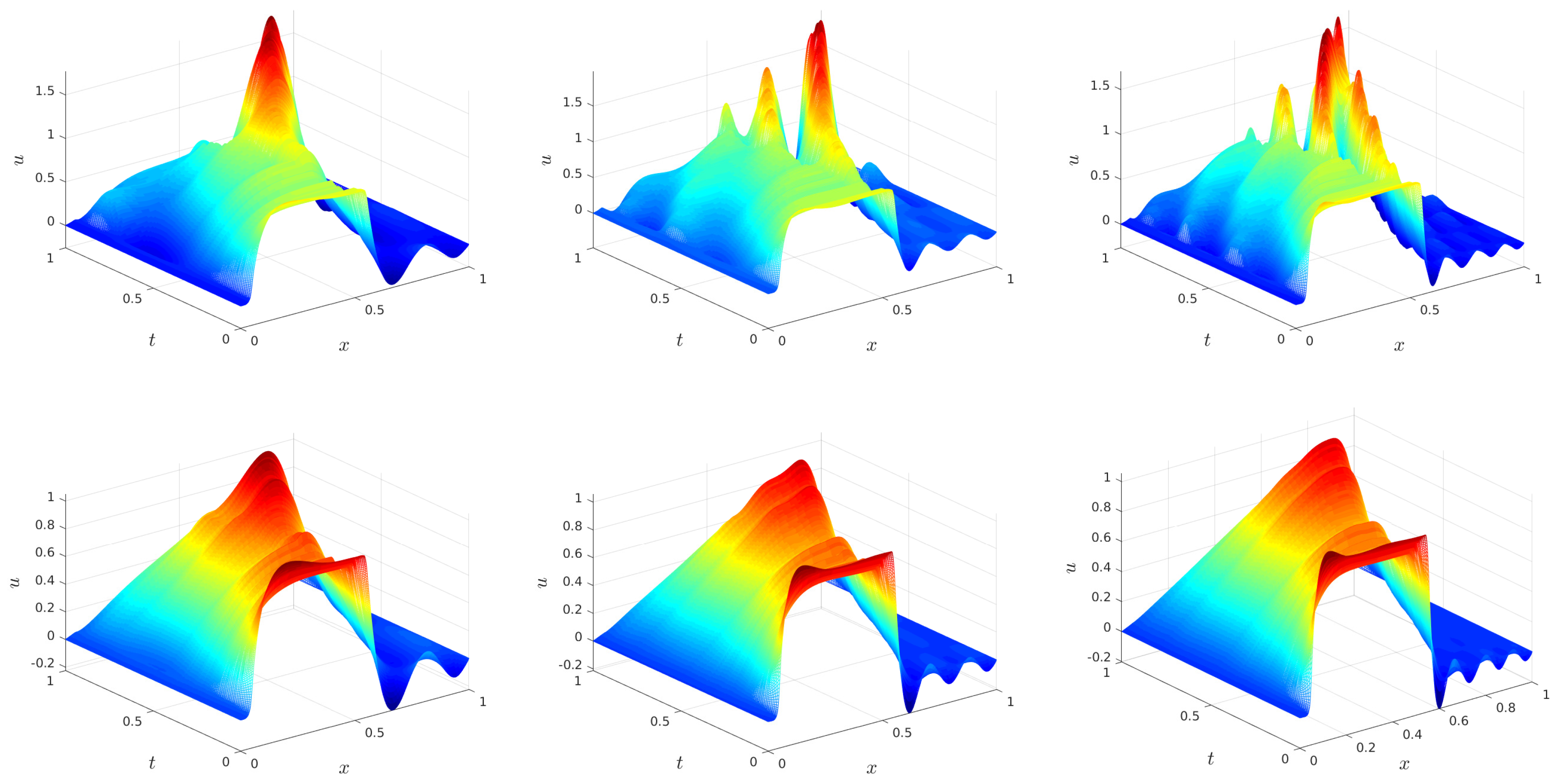
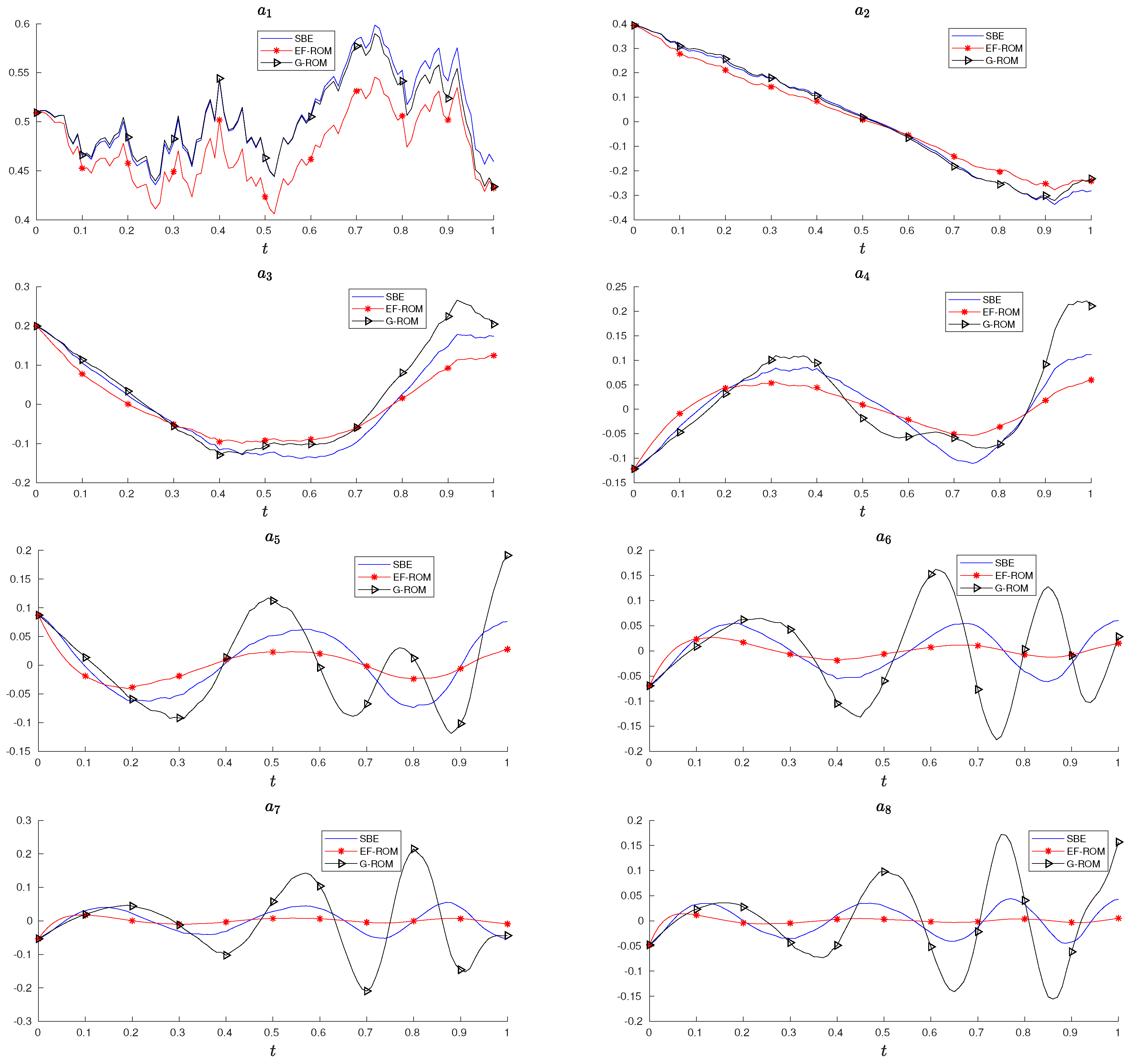
5. Numerical Results
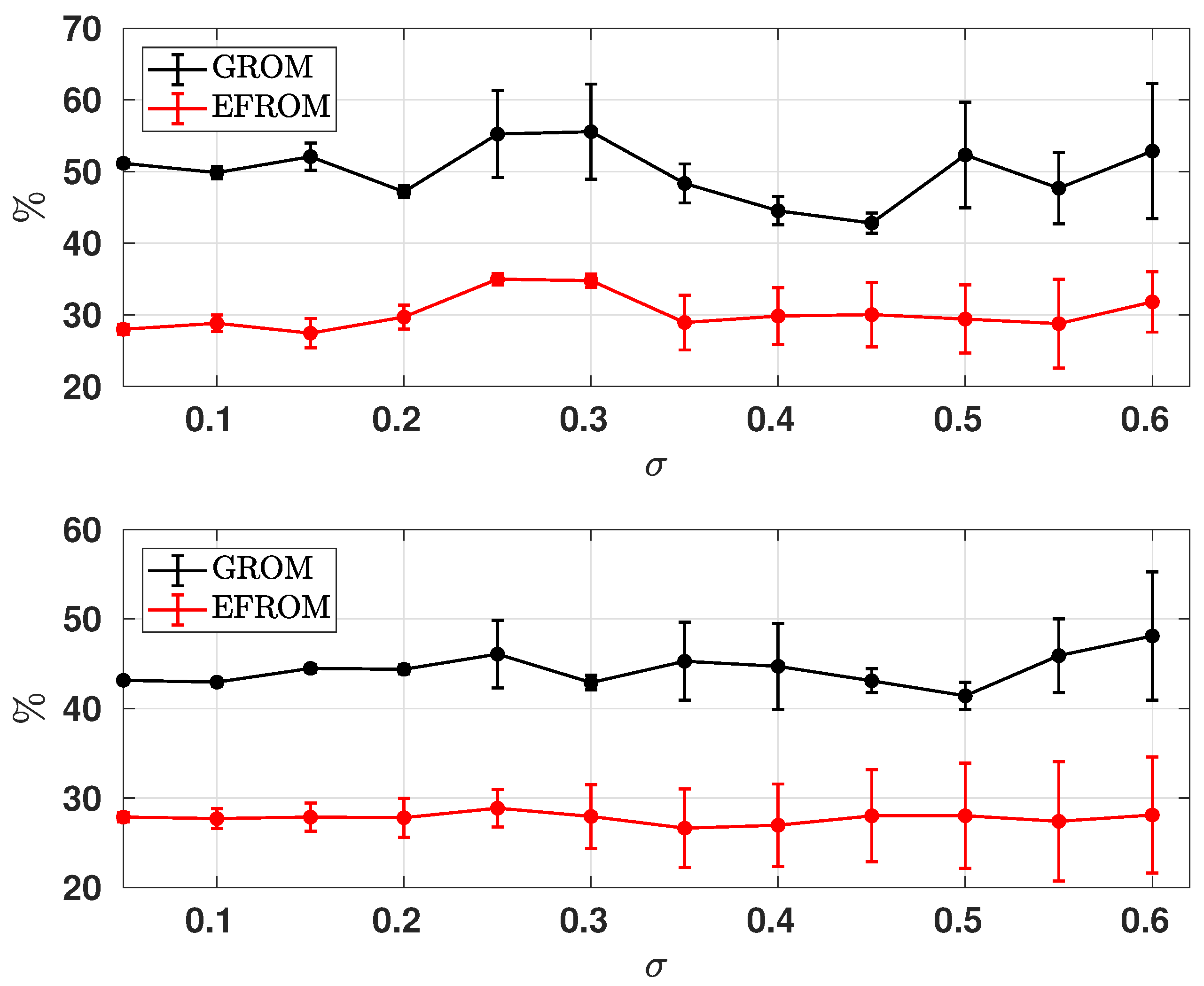
Robustness of EF-ROM
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ROM | Reduced order modeling |
| EF-ROM | Evolve then filter reduced order model |
| L-ROM | Leray reduced order model |
| G-ROM | Galerkin reduced order model |
| POD | Proper orthogonal decomposition |
| DF | Differential filter |
| SBE | Stochastic Burgers equation |
| SDE | Stochastic differential equation |
| SPDE | Stochastic partial differential equation |
References
- Noack, B.R.; Morzynski, M.; Tadmor, G. Reduced-Order Modelling for Flow Control; Springer: Berlin/Humberger, Germany, 2011. [Google Scholar]
- Rempfer, D. On low-dimensional Galerkin models for fluid flow. Theor. Comput. Fluid Dyn. 2000, 14, 75–88. [Google Scholar] [CrossRef]
- Carlberg, K.; Farhat, C.; Cortial, J.; Amsallem, D. The GNAT method for nonlinear model reduction: effective implementation and application to computational fluid dynamics and turbulent flows. J. Comput. Phys. 2013, 242, 623–647. [Google Scholar] [CrossRef]
- Noack, B.R.; Stankiewicz, W.; Morzyński, M.; Schmid, P.J. Recursive dynamic mode decomposition of transient and post-transient wake flows. J. Fluid Mech. 2016, 809, 843–872. [Google Scholar] [CrossRef]
- Noack, B.R.; Papas, P.; Monkewitz, P.A. The need for a pressure-term representation in empirical Galerkin models of incompressible shear flows. J. Fluid Mech. 2005, 523, 339–365. [Google Scholar] [CrossRef]
- Loiseau, J.C.; Noack, B.R.; Brunton, S.L. Sparse reduced-order modelling: sensor-based dynamics to full-state estimation. J. Fluid Mech. 2018, 844, 459–490. [Google Scholar] [CrossRef]
- Amsallem, D.; Farhat, C. Stabilization of projection-based reduced-order models. Int. J. Numer. Methods Eng. 2012, 91, 358–377. [Google Scholar] [CrossRef]
- Barone, M.F.; Kalashnikova, I.; Segalman, D.J.; Thornquist, H.K. Stable Galerkin reduced order models for linearized compressible flow. J. Comput. Phys. 2009, 228, 1932–1946. [Google Scholar] [CrossRef]
- Giere, S.; Iliescu, T.; John, V.; Wells, D. SUPG Reduced Order Models for Convection-Dominated Convection-Diffusion-Reaction Equations. Comput. Methods Appl. Mech. Eng. 2015, 289, 454–474. [Google Scholar] [CrossRef]
- Kalashnikova, I.; Barone, M.F. On the stability and convergence of a Galerkin reduced order model (ROM) of compressible flow with solid wall and far-field boundary treatment. Int. J. Numer. Methods Eng. 2010, 83, 1345–1375. [Google Scholar] [CrossRef]
- Pacciarini, P.; Rozza, G. Stabilized reduced basis method for parametrized advection–diffusion PDEs. Comput. Meth. Appl. Mech. Eng. 2014, 274, 1–18. [Google Scholar] [CrossRef]
- Wang, Z.; Akhtar, I.; Borggaard, J.; Iliescu, T. Proper orthogonal decomposition closure models for turbulent flows: A numerical comparison. Comput. Methods Appl. Mech. Eng. 2012, 237-240, 10–26. [Google Scholar] [CrossRef]
- Balajewicz, M.J.; Dowell, E.H.; Noack, B.R. Low-dimensional modelling of high-Reynolds-number shear flows incorporating constraints from the Navier–Stokes equation. J. Fluid Mech. 2013, 729, 285–308. [Google Scholar] [CrossRef]
- Ballarin, F.; Manzoni, A.; Quarteroni, A.; Rozza, G. Supremizer stabilization of POD–Galerkin approximation of parametrized steady incompressible Navier–Stokes equations. Int. J. Numer. Methods Eng. 2015, 102, 1136–1161. [Google Scholar] [CrossRef]
- San, O.; Maulik, R. Neural network closures for nonlinear model order reduction. Adv. Comput. Math. 2018, 1–34. [Google Scholar] [CrossRef]
- San, O.; Maulik, R. Machine learning closures for model order reduction of thermal fluids. Appl. Math. Model. 2018, 60, 681–710. [Google Scholar] [CrossRef]
- Xie, X.; Wells, D.; Wang, Z.; Iliescu, T. Approximate deconvolution reduced order modeling. Comput. Methods Appl. Mech. Eng. 2017, 313, 512–534. [Google Scholar] [CrossRef]
- Sabetghadam, F.; Jafarpour, A. α regularization of the POD-Galerkin dynamical systems of the Kuramoto–Sivashinsky equation. Appl. Math. Comput. 2012, 218, 6012–6026. [Google Scholar] [CrossRef]
- Wells, D.; Wang, Z.; Xie, X.; Iliescu, T. An evolve-then-filter regularized reduced order model for convection-dominated flows. Int. J. Numer. Methods Fluids 2017, 84, 598–615. [Google Scholar] [CrossRef]
- Galbally, D.; Fidkowski, K.; Willcox, K.; Ghattas, O. Non-linear model reduction for uncertainty quantification in large-scale inverse problems. Int. J. Numer. Methods Eng. 2010, 81, 1581–1608. [Google Scholar] [CrossRef]
- Lassila, T.; Manzoni, A.; Quarteroni, A.; Rozza, G. A reduced computational and geometrical framework for inverse problems in hemodynamics. Int. J. Numer. Methods Biomed. Eng. 2013, 29, 741–776. [Google Scholar] [CrossRef] [PubMed]
- Boyaval, S.; Le Bris, C.; Lelièvre, T.; Maday, Y.; Nguyen, N.C.; Patera, A.T. Reduced basis techniques for stochastic problems. Arch. Comput. Methods Eng. 2010, 17, 435–454. [Google Scholar] [CrossRef]
- Chen, P.; Quarteroni, A.; Rozza, G. A weighted reduced basis method for elliptic partial differential equations with random input data. SIAM J. Numer. Anal. 2013, 51, 3163–3185. [Google Scholar] [CrossRef]
- Haasdonk, B.; Urban, K.; Wieland, B. Reduced Basis Methods for Parameterized Partial Differential Equations with Stochastic Influences Using the Karhunen–Loéve Expansion. SIAM/ASA J. Uncertain. Quantif. 2013, 1, 79–105. [Google Scholar] [CrossRef]
- Torlo, D. Stabilized Reduced Basis Method for Transport PDEs with Random Inputs. Master’s Thesis, SISSA International School, Università degli Studi di Trieste, Trieste, Italy, 2016. [Google Scholar]
- Burkardt, J.; Gunzburger, M.; Webster, C. Reduced order modeling of some nonlinear stochastic partial differential equations. Int. J. Numer. Anal. Model. 2007, 4, 368–391. [Google Scholar]
- Chekroun, M.D.; Liu, H.; Wang, S. Parameterizing Manifolds and Non-Markovian Reduced Equations: Stochastic Manifolds for Nonlinear SPDEs II; SpringerBriefs in Mathematics; Springer: New York, NY, USA, 2015. [Google Scholar]
- Iliescu, T.; Liu, H.; Xie, X. Regularized reduced order models for a stochastic Burgers equation. arXiv, 2017; arXiv:1701.01155. [Google Scholar]
- Blömker, D. Amplitude Equations for Stochastic Partial Differential Equations; World Scientific Publishing Co. Pte. Ltd.: Hackensack, NJ, USA, 2007; Volume 3, p. x+126. [Google Scholar]
- Birnir, B. The Kolmogorov-Obukhov Theory of Turbulence: A Mathematical Theory of Turbulence; Springer Briefs in Mathematics; Springer: New York, NY, USA, 2013. [Google Scholar]
- Cross, M.C.; Hohenberg, P.C. Pattern formation outside of equilibrium. Rev. Mod. Phys. 1993, 65, 851–1112. [Google Scholar] [CrossRef]
- Muñoz, M.A. Multiplicative noise in non-equilibrium phase transitions: A tutorial. In Advances in Condensed Matter and Statistical Physics; Nova Science Publishers, Inc.: Hauppauge, NY, USA, 2004; pp. 37–68. [Google Scholar]
- Øksendal, B. Stochastic Differential Equations: An Introduction with Applications, 6th ed.; Springer: Berlin, Germany, 2003; p. xxiv+360. [Google Scholar]
- Alabert, A.; Gyöngy, I. On numerical approximation of stochastic Burgers’ equation. In From Stochastic Calculus to Mathematical Finance; Springer: Berlin, Germany, 2006; pp. 1–15. [Google Scholar]
- Blömker, D.; Jentzen, A. Galerkin approximations for the stochastic Burgers equation. SIAM J. Numer. Anal. 2013, 51, 694–715. [Google Scholar] [CrossRef]
- Hou, T.Y.; Luo, W.; Rozovskii, B.; Zhou, H.M. Wiener chaos expansions and numerical solutions of randomly forced equations of fluid mechanics. J. Comput. Phys. 2006, 216, 687–706. [Google Scholar] [CrossRef]
- Jentzen, A.; Kloeden, P.E. Taylor Approximations for Stochastic Partial Differential Equations; CBMS-NSF Regional Conference Series in Applied Mathematics; SIAM: Philadelphia, PA, USA, 2011; Volume 83. [Google Scholar]
- Lord, G.J.; Rougemont, J. A numerical scheme for stochastic PDEs with Gevrey regularity. IMA J. Numer. Anal. 2004, 24, 587–604. [Google Scholar] [CrossRef]
- Brunton, S.L.; Proctor, J.L.; Kutz, J.N. Compressive sampling and dynamic mode decomposition. arXiv, 2013; arXiv:1312.5186. [Google Scholar]
- Brunton, S.L.; Proctor, J.L.; Kutz, J.N. Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proc. Natl. Acad. Sci. USA 2016. [Google Scholar] [CrossRef] [PubMed]
- Schmid, P.J. Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 2010, 656, 5–28. [Google Scholar] [CrossRef]
- Holmes, P.; Lumley, J.L.; Berkooz, G. Turbulence, Coherent Structures, Dynamical Systems and Symmetry; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Kunisch, K.; Volkwein, S. Galerkin proper orthogonal decomposition methods for parabolic problems. Numer. Math. 2001, 90, 117–148. [Google Scholar] [CrossRef]
- Kloeden, P.E.; Platen, E. Numerical Solution of Stochastic Differential Equations; Applications of Mathematics; Springer: Berlin, Germany, 1992; p. xxxvi+632. [Google Scholar]
- Germano, M. Differential filters for the large eddy numerical simulation of turbulent flows. Phys. Fluids 1986, 29, 1755–1757. [Google Scholar] [CrossRef]
- Germano, M. Differential filters of elliptic type. Phys. Fluids 1986, 29, 1757–1758. [Google Scholar] [CrossRef]
- Geurts, B.J.; Holm, D.D. Regularization modeling for large-eddy simulation. Phys. Fluids 2003, 15, L13–L16. [Google Scholar] [CrossRef]
- Layton, W.J.; Rebholz, L.G. Approximate Deconvolution Models of Turbulence: Analysis, Phenomenology and Numerical Analysis; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Cordier, L.; Abou El Majd, B.; Favier, J. Calibration of POD reduced-order models using Tikhonov regularization. Int. J. Numer. Methods Fluids 2010, 63, 269–296. [Google Scholar] [CrossRef]
- Quarteroni, A.; Rozza, G.; Manzoni, A. Certified reduced basis approximation for parametrized partial differential equations and applications. J. Math. Ind. 2011, 1, 1–49. [Google Scholar] [CrossRef]
- Ervin, V.J.; Layton, W.J.; Neda, M. Numerical analysis of filter-based stabilization for evolution equations. SIAM J. Numer. Anal. 2012, 50, 2307–2335. [Google Scholar] [CrossRef]
- Xie, X.; Wells, D.; Wang, Z.; Iliescu, T. Numerical analysis of the Leray reduced order model. J. Comput. Appl. Math. 2018, 328, 12–29. [Google Scholar] [CrossRef]
- Bourgeois, J.; Noack, B.; Martinuzzi, R. Generalized phase average with applications to sensor-based flow estimation of the wall-mounted square cylinder wake. J. Fluid Mech. 2013, 736, 316–350. [Google Scholar] [CrossRef]
- Peherstorfer, B.; Willcox, K. Data-driven operator inference for nonintrusive projection-based model reduction. Comput. Methods Appl. Mech. Eng. 2016, 306, 196–215. [Google Scholar] [CrossRef]
- Xie, X.; Mohebujjaman, M.; Rebholz, L.; Iliescu, T. Data-driven filtered reduced order modeling of fluid flows. SIAM J. Sci. Comput. 2018, 40, B834–B857. [Google Scholar] [CrossRef]
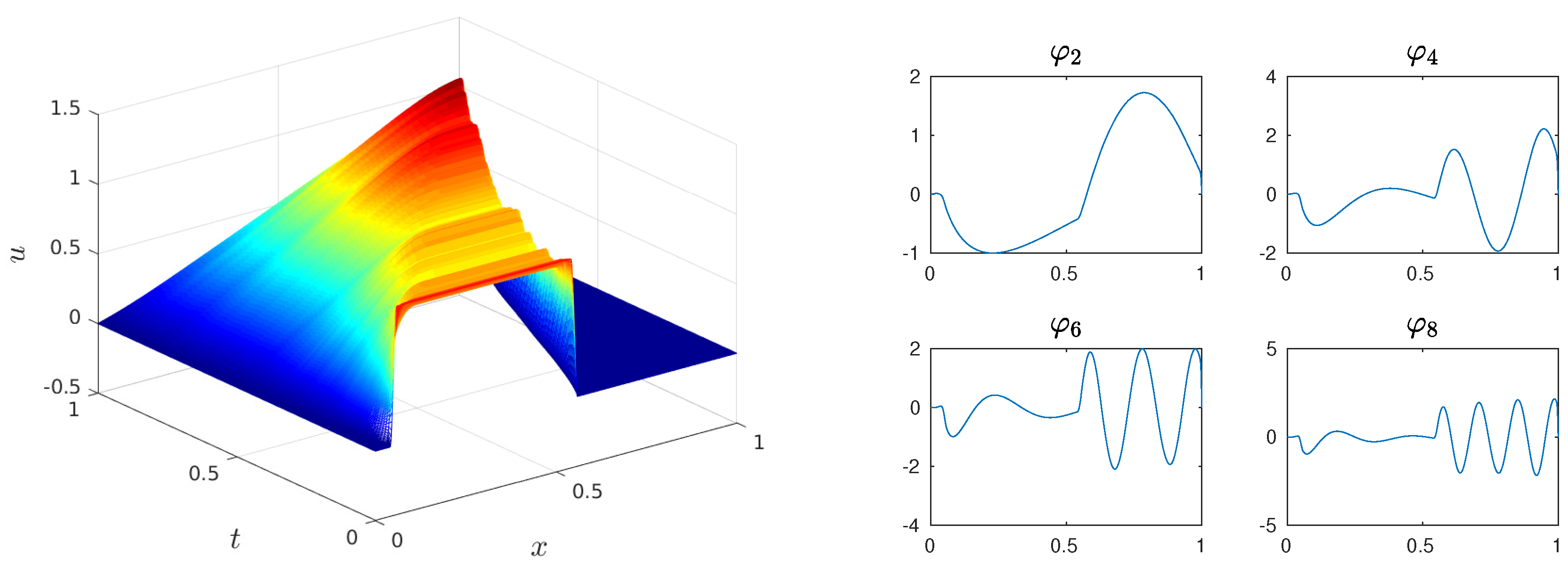
| No. of Basis | Energy |
|---|---|
| 2 | 91.38% |
| 4 | 97.20% |
| 6 | 98.46% |
| 8 | 99.02% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, X.; Bao, F.; Webster, C.G. Evolve Filter Stabilization Reduced-Order Model for Stochastic Burgers Equation. Fluids 2018, 3, 84. https://doi.org/10.3390/fluids3040084
Xie X, Bao F, Webster CG. Evolve Filter Stabilization Reduced-Order Model for Stochastic Burgers Equation. Fluids. 2018; 3(4):84. https://doi.org/10.3390/fluids3040084
Chicago/Turabian StyleXie, Xuping, Feng Bao, and Clayton G. Webster. 2018. "Evolve Filter Stabilization Reduced-Order Model for Stochastic Burgers Equation" Fluids 3, no. 4: 84. https://doi.org/10.3390/fluids3040084
APA StyleXie, X., Bao, F., & Webster, C. G. (2018). Evolve Filter Stabilization Reduced-Order Model for Stochastic Burgers Equation. Fluids, 3(4), 84. https://doi.org/10.3390/fluids3040084




