Investigation of the Turbulent Near Wall Flame Behavior for a Sidewall Quenching Burner by Means of a Large Eddy Simulation and Tabulated Chemistry
Abstract
1. Introduction
2. Methods
2.1. Numerical Description
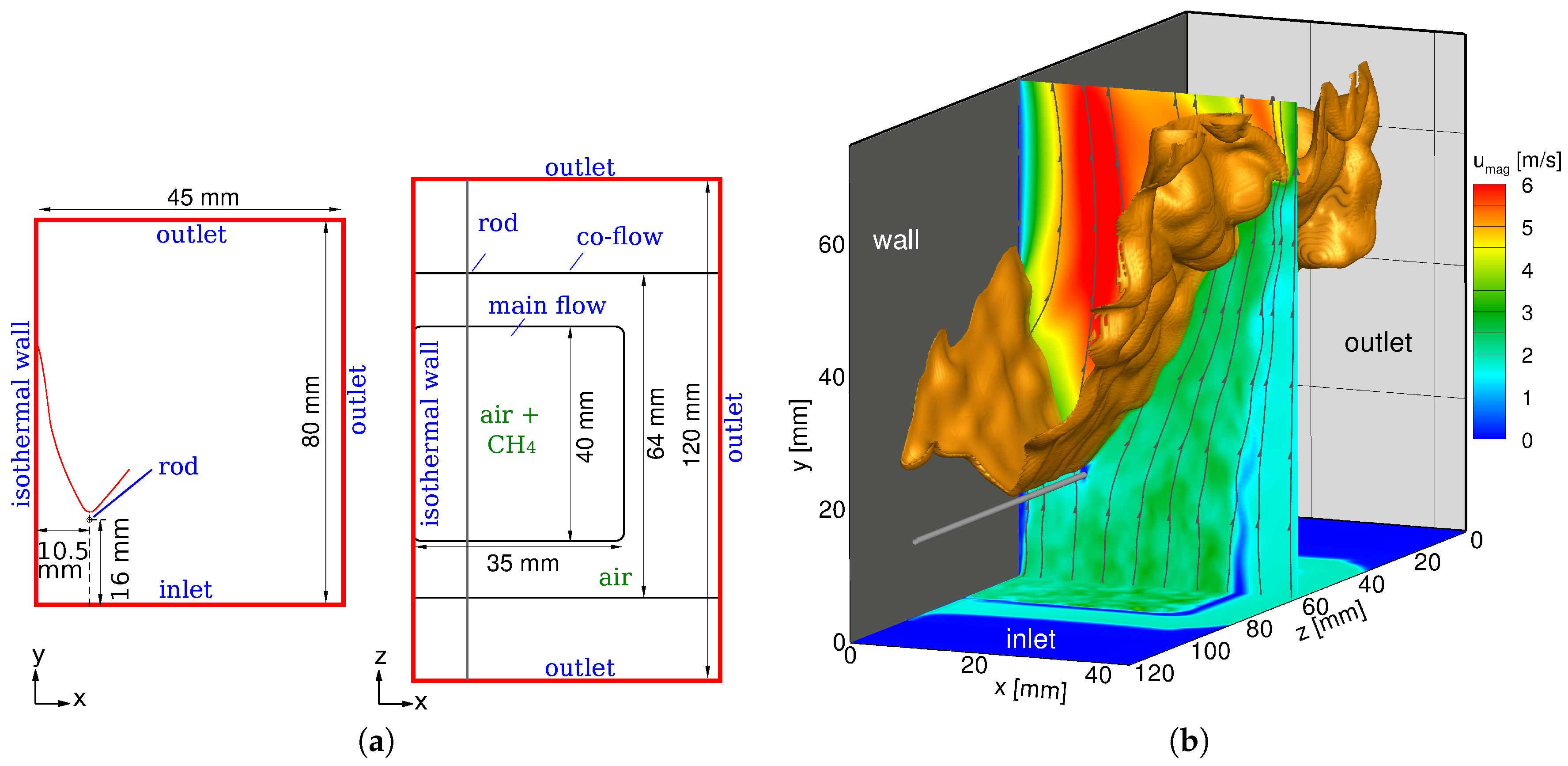
2.2. Numerical Domain
2.3. Chemistry Treatment
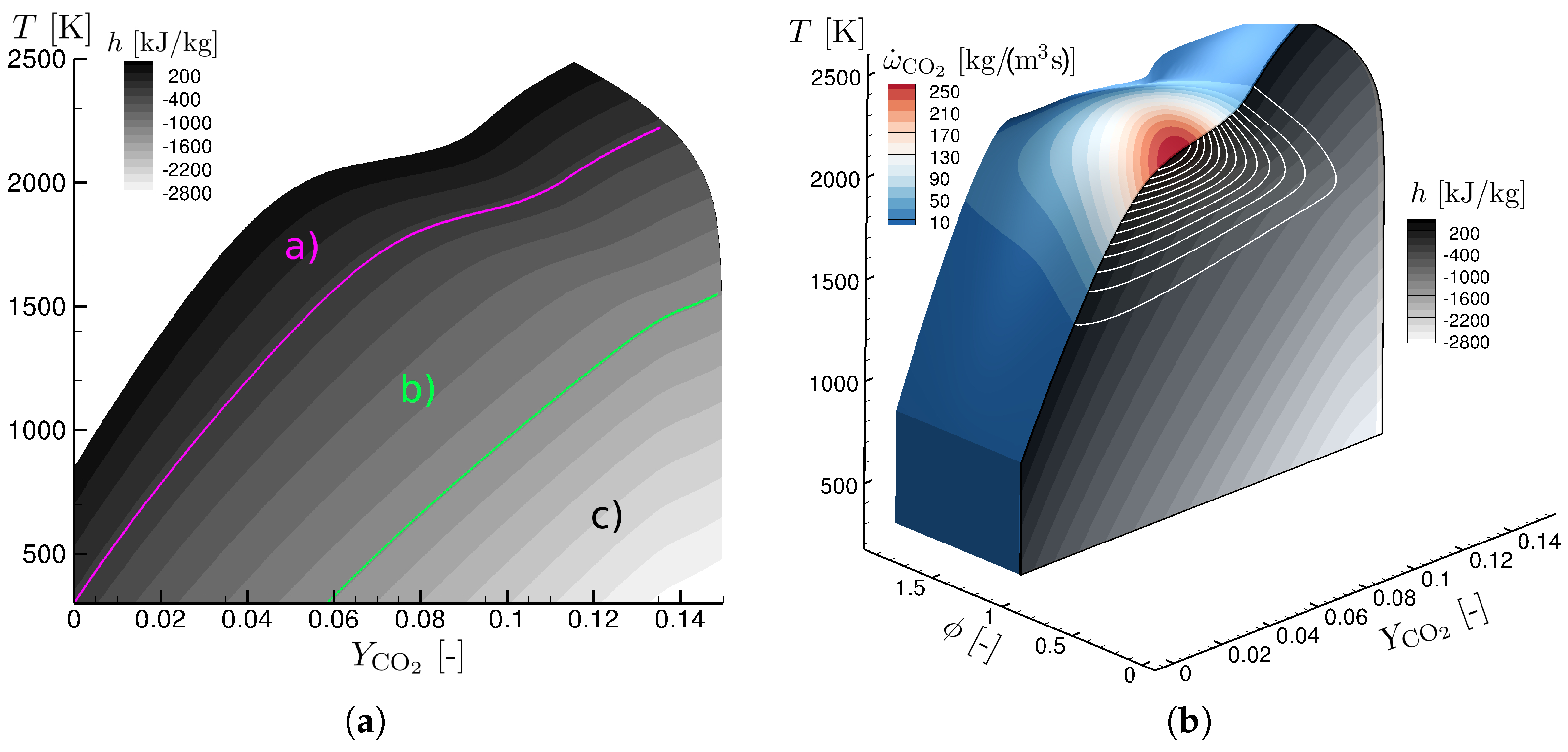
2.3.1. Construction of the FGM Table
2.3.2. Evaluation of Simplifying Assumptions for FWI Application
2.3.3. Treatment in the Turbulent FWI Flow
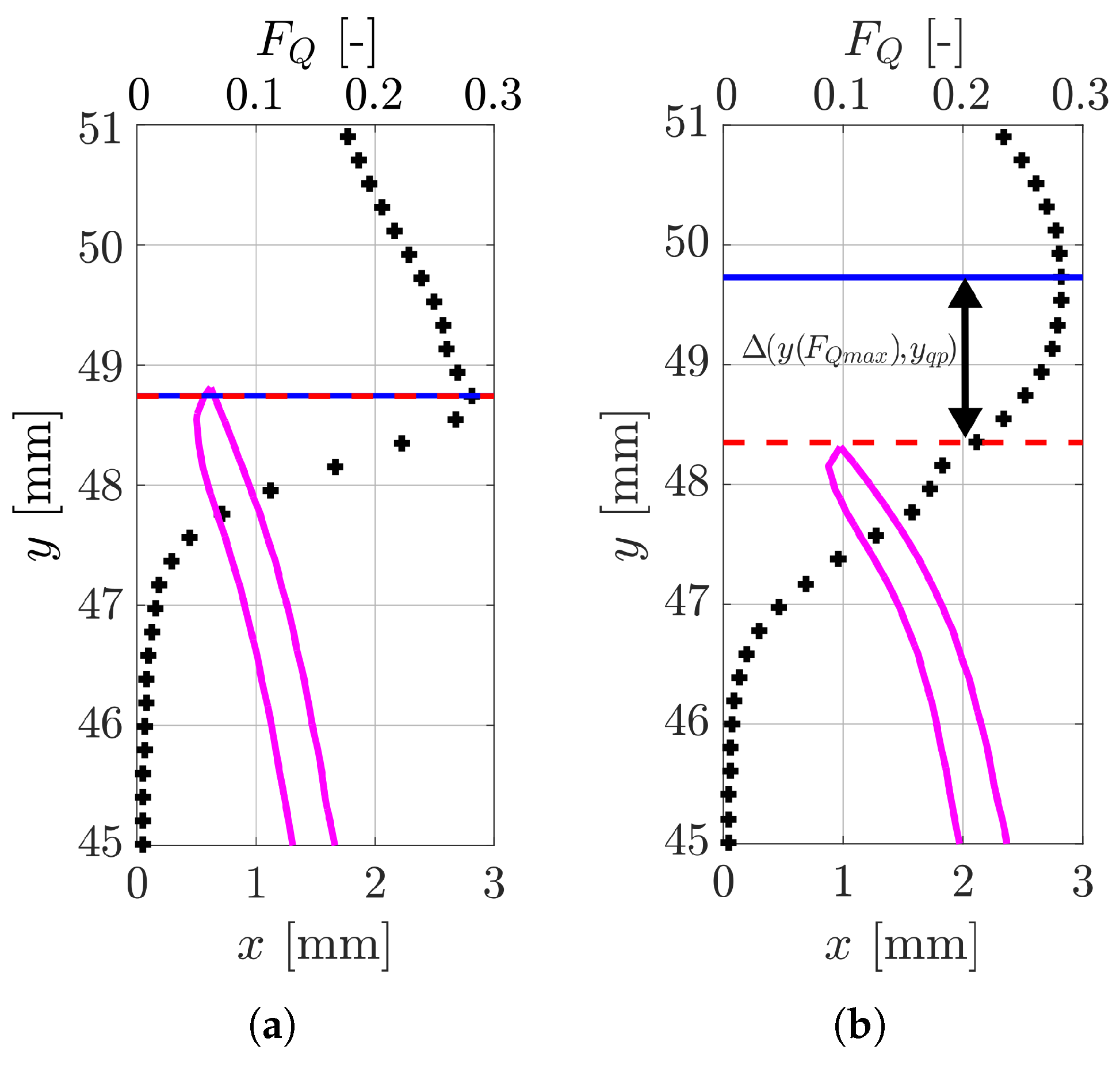
2.4. Determination of the Quenching Point
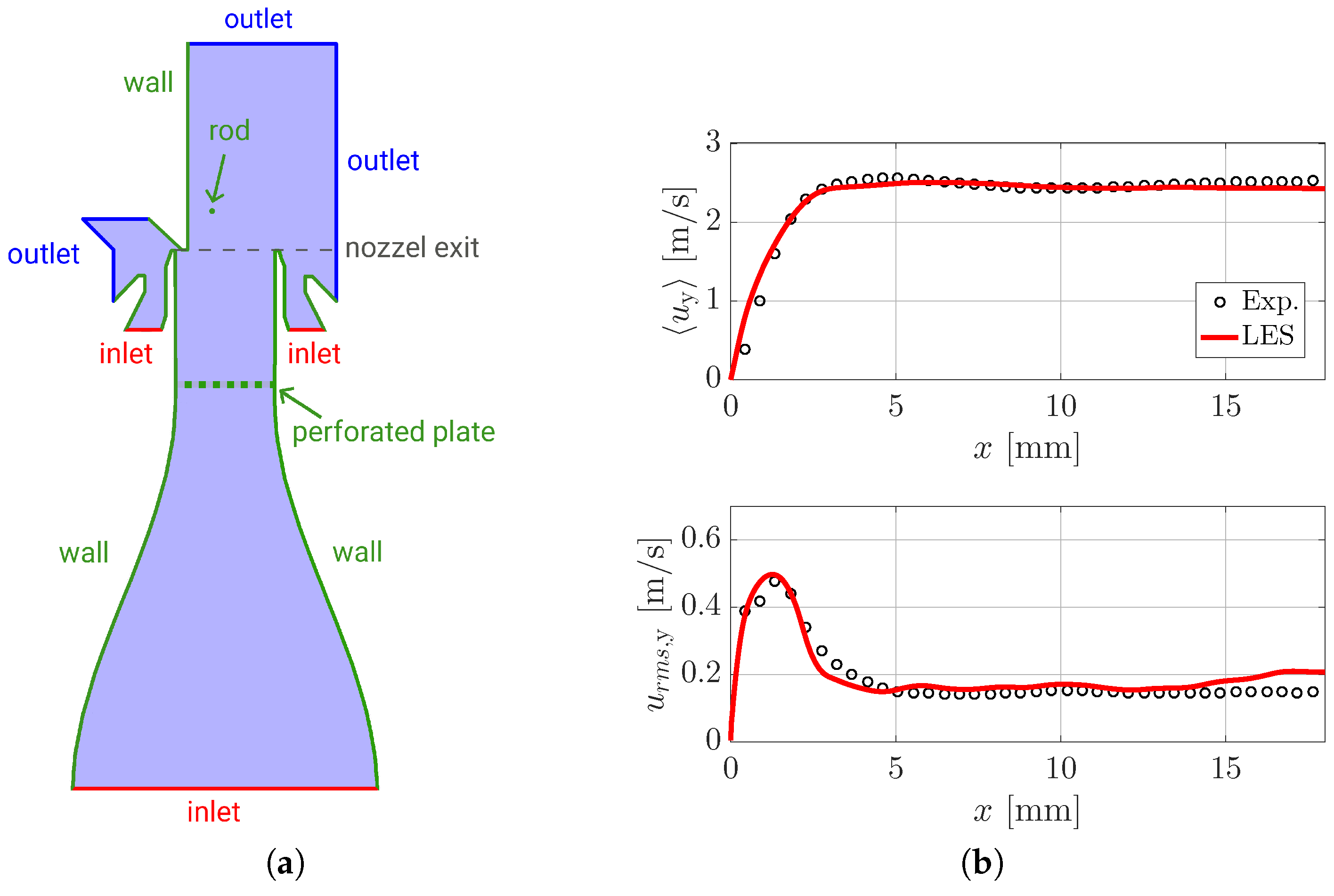
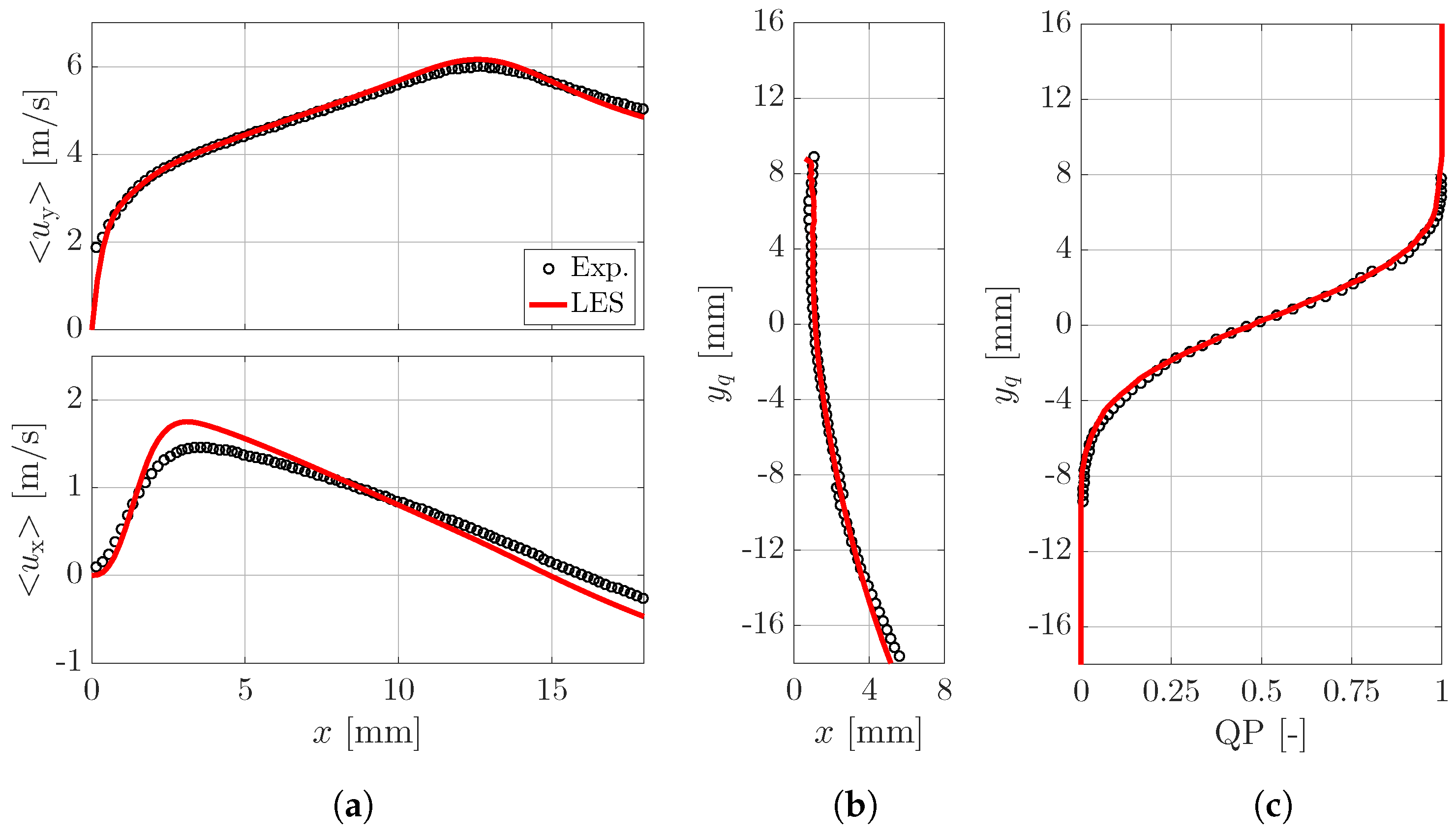
2.5. Comparison with Experimental Data
2.6. Dimensionless Parameters
3. Results
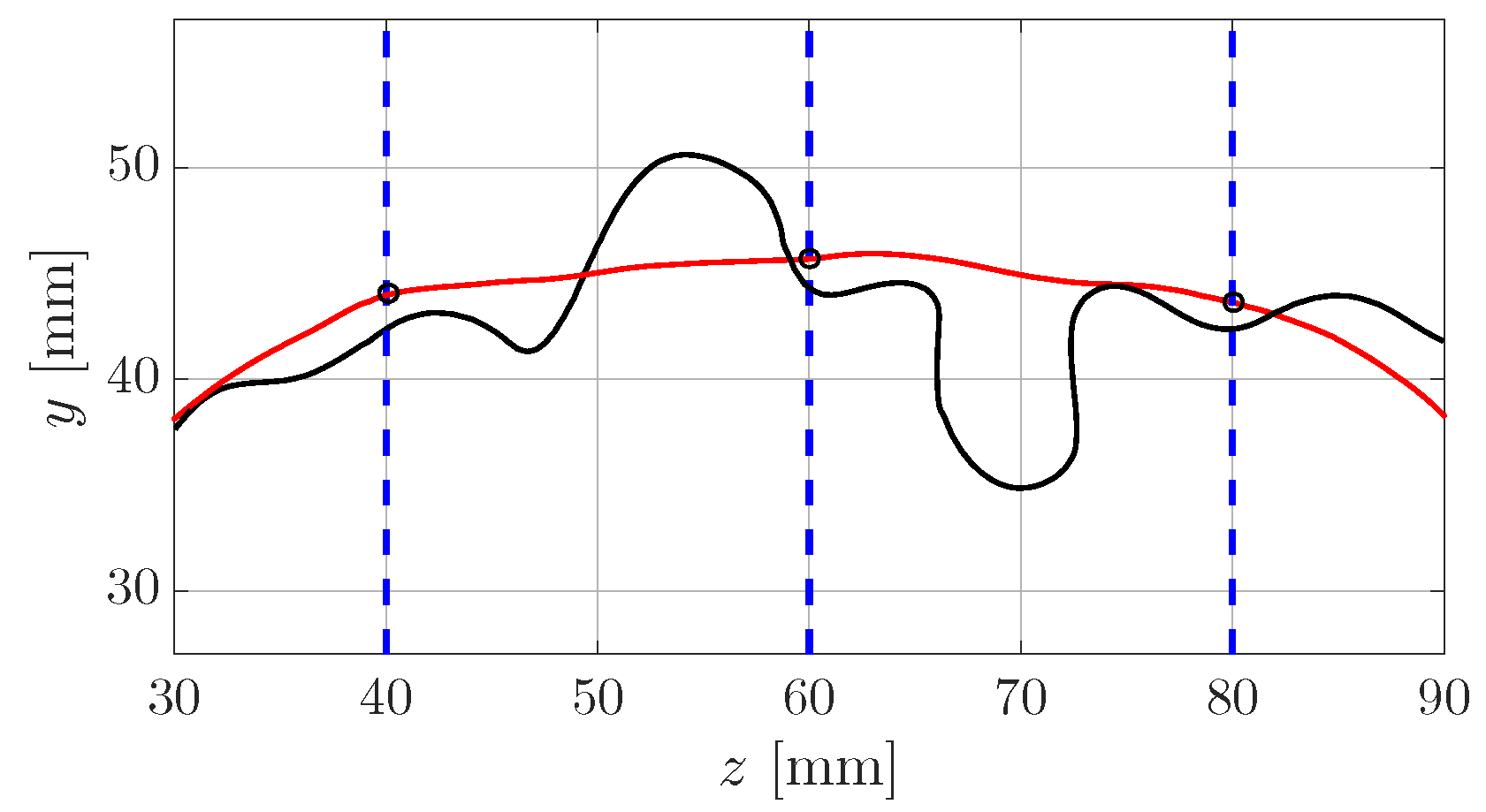
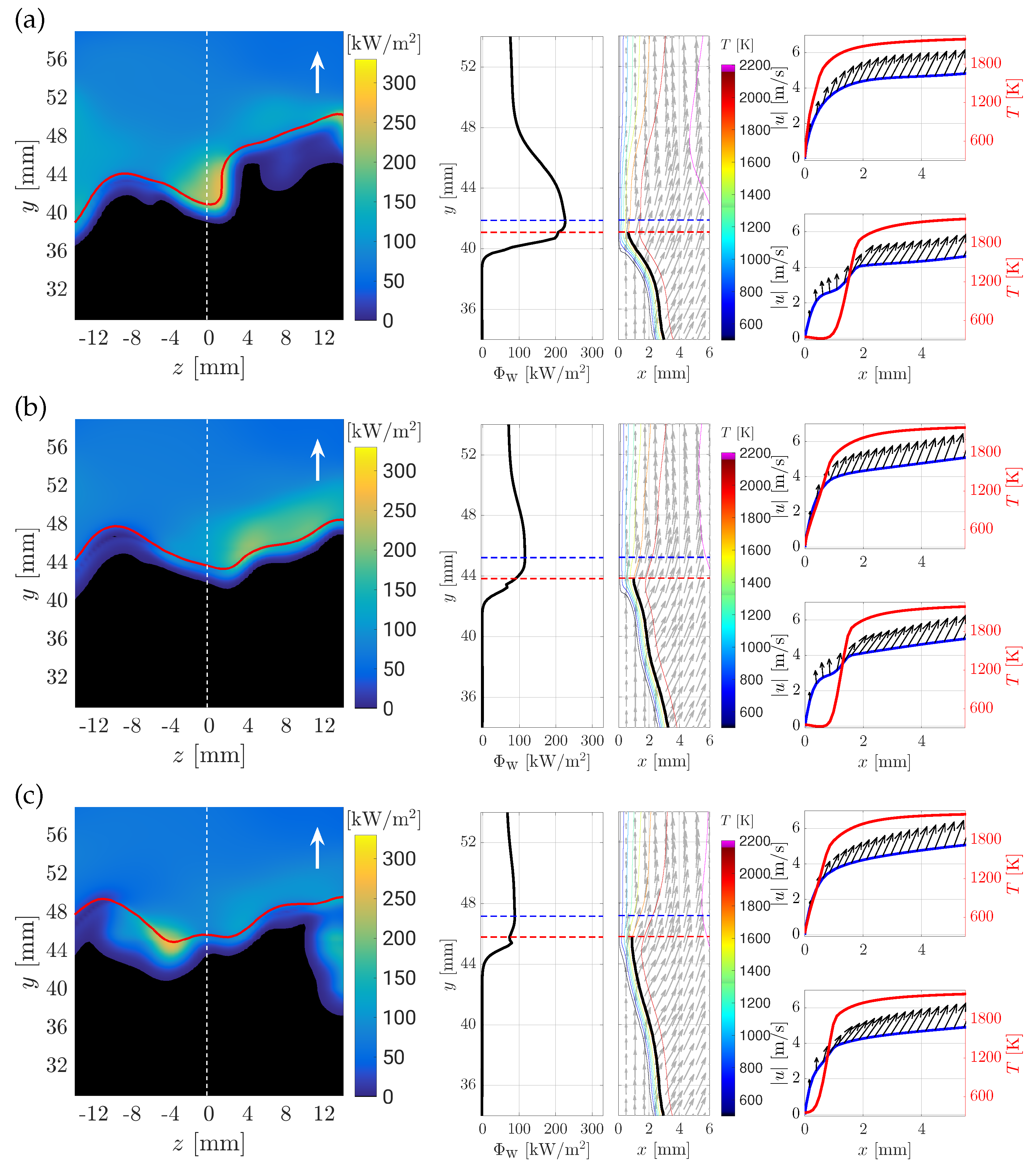
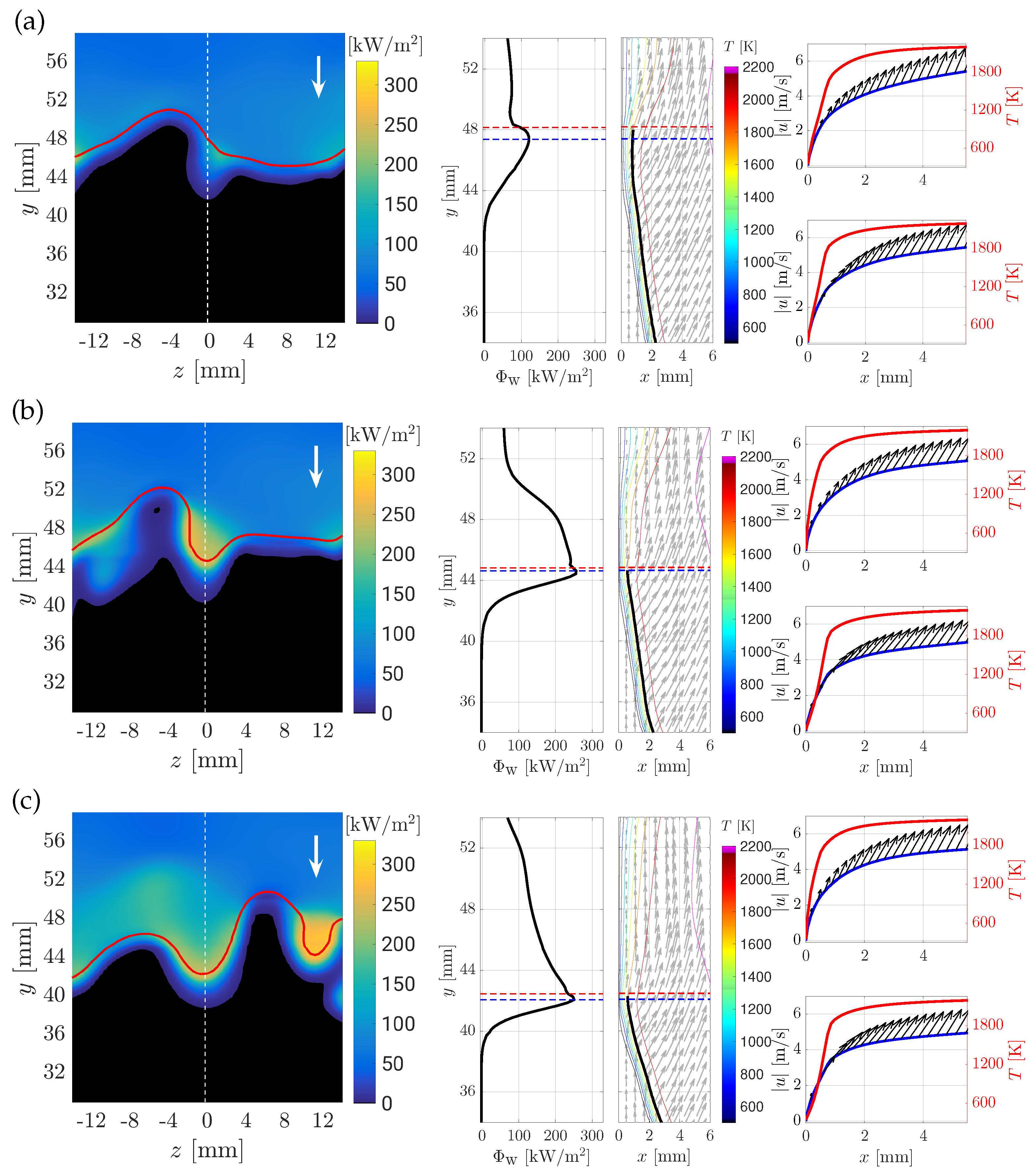
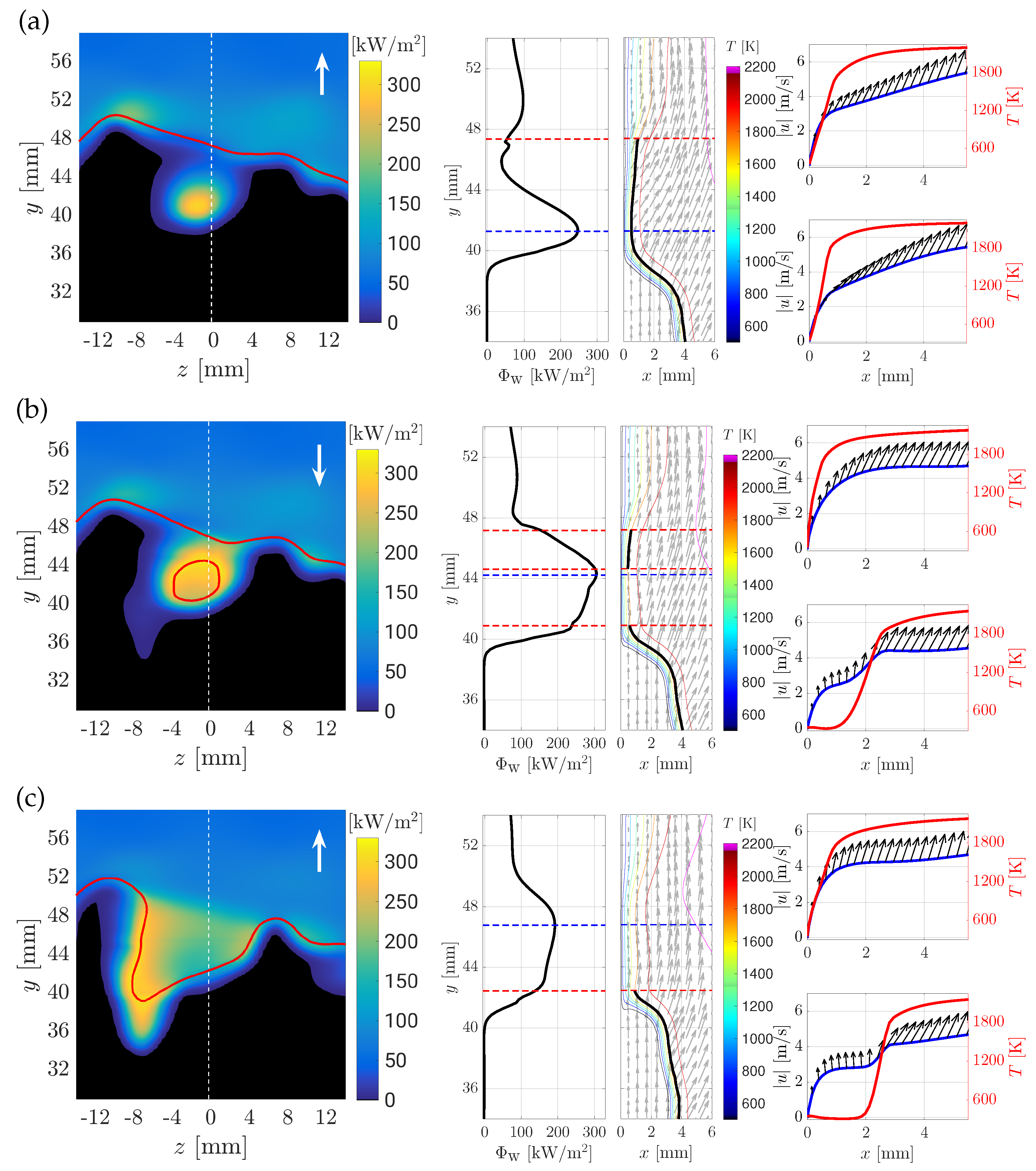
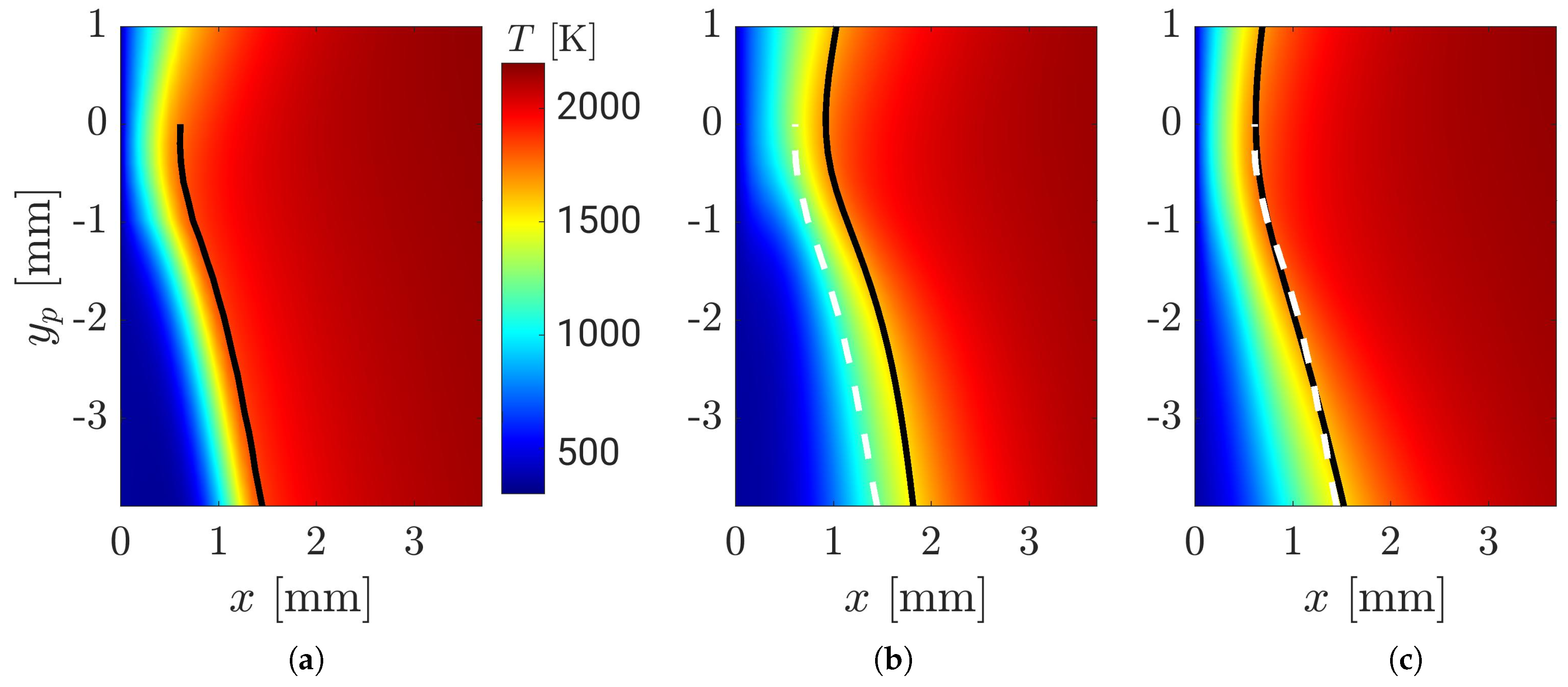
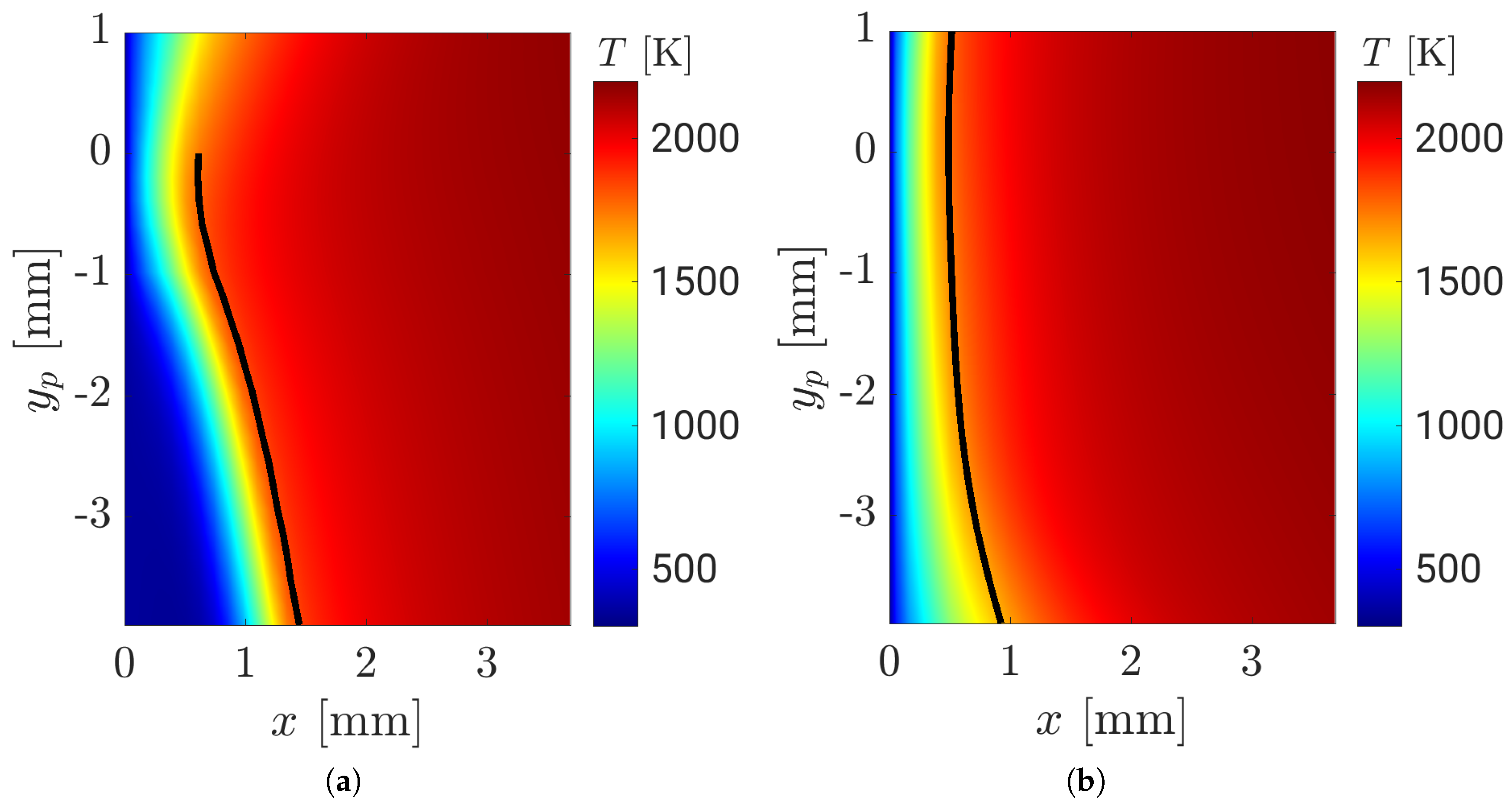
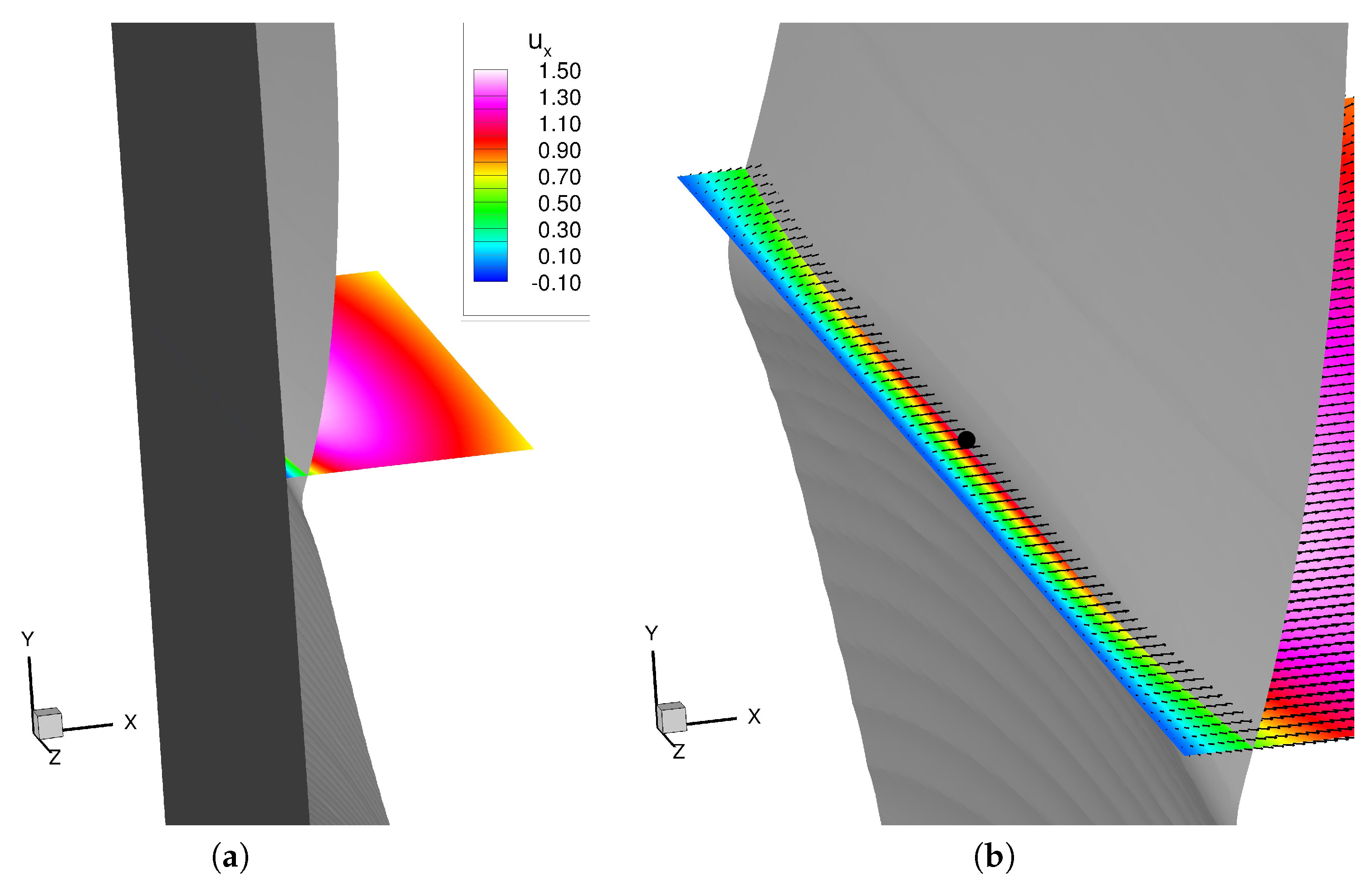
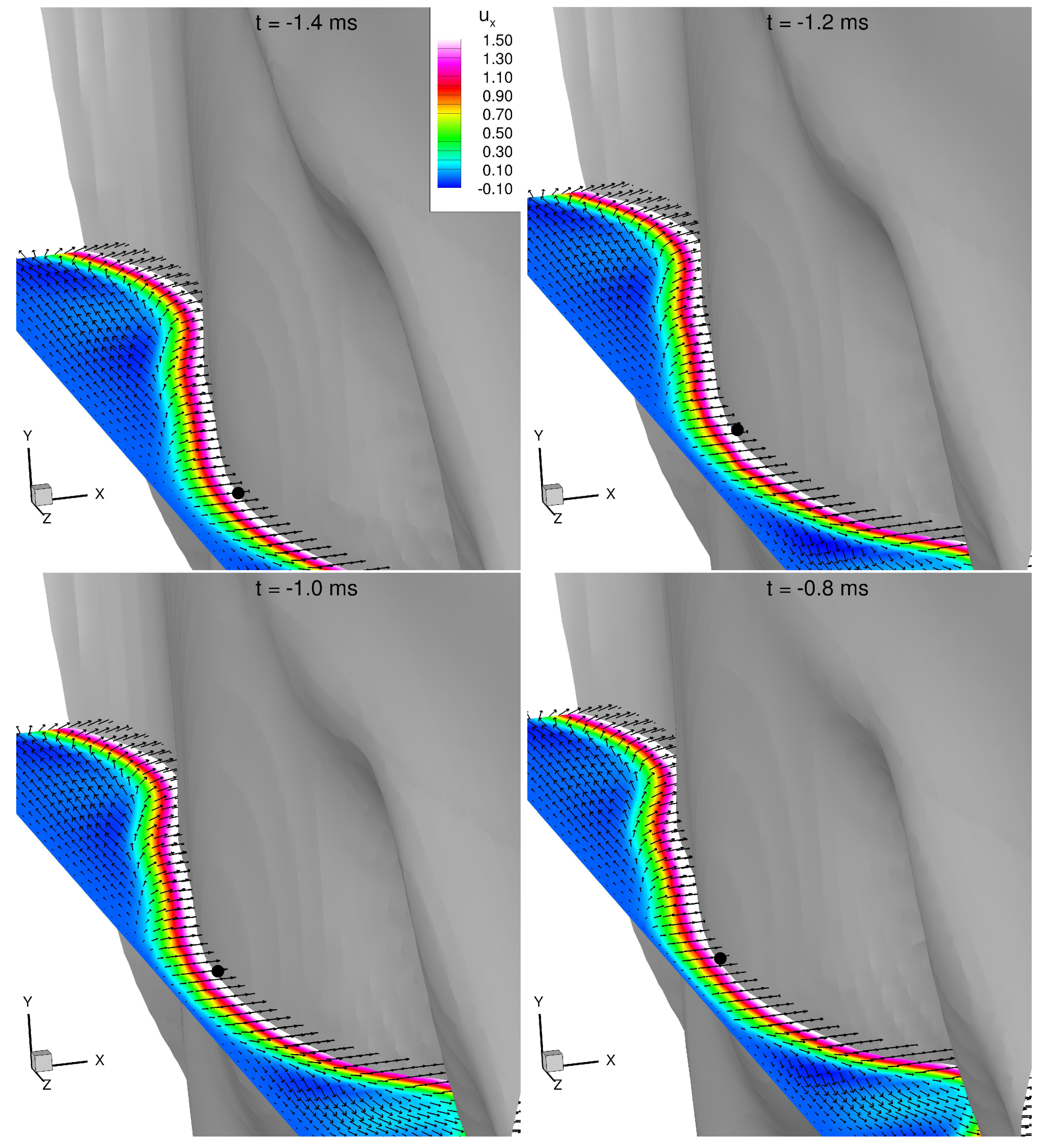
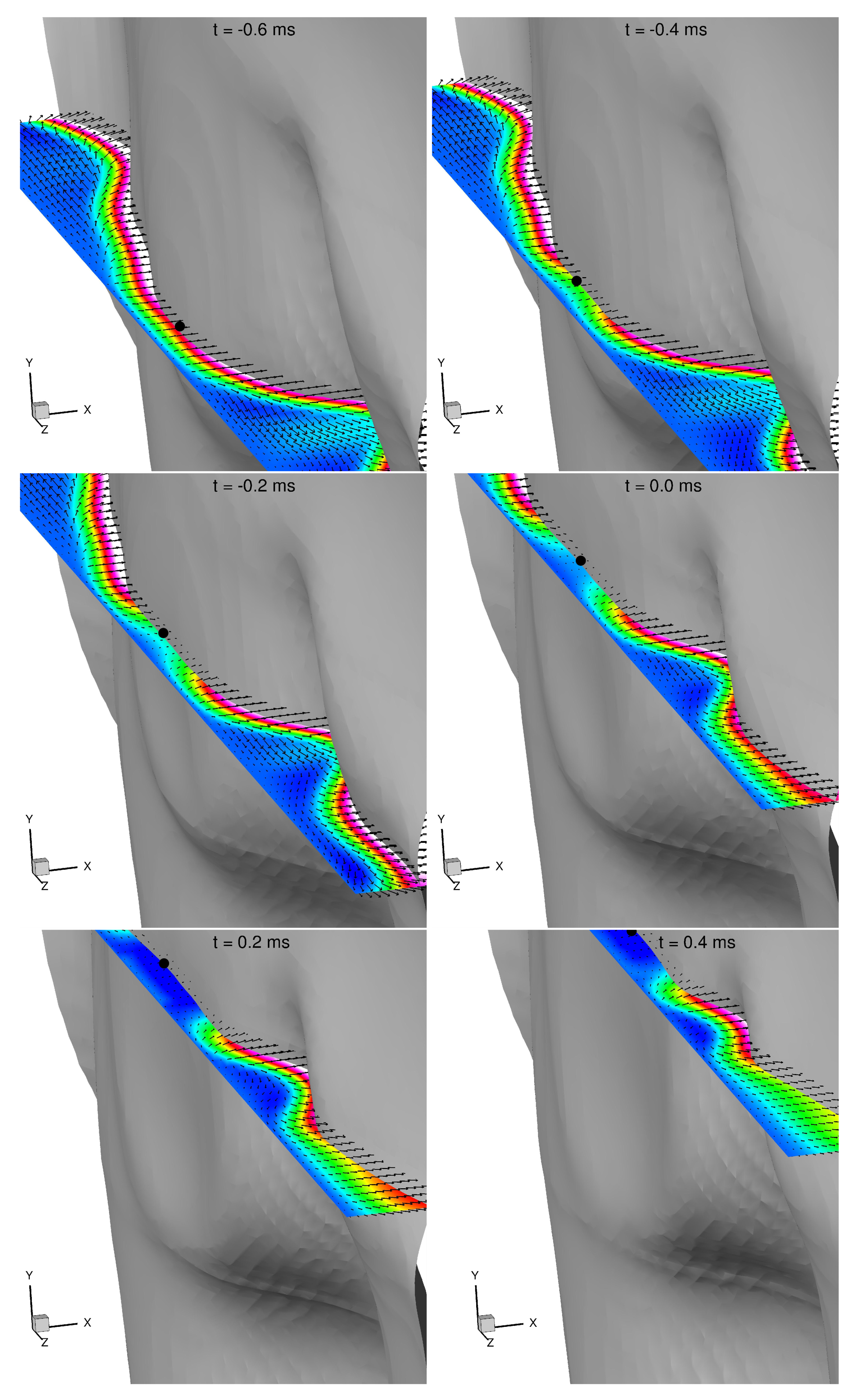
3.1. Description of the Quenching Point Movement
- (A)
- A downstream movement,
- (B)
- A moderate upstream movement,
- (C)
- A jump-like upstream movement with multiple quenching points.
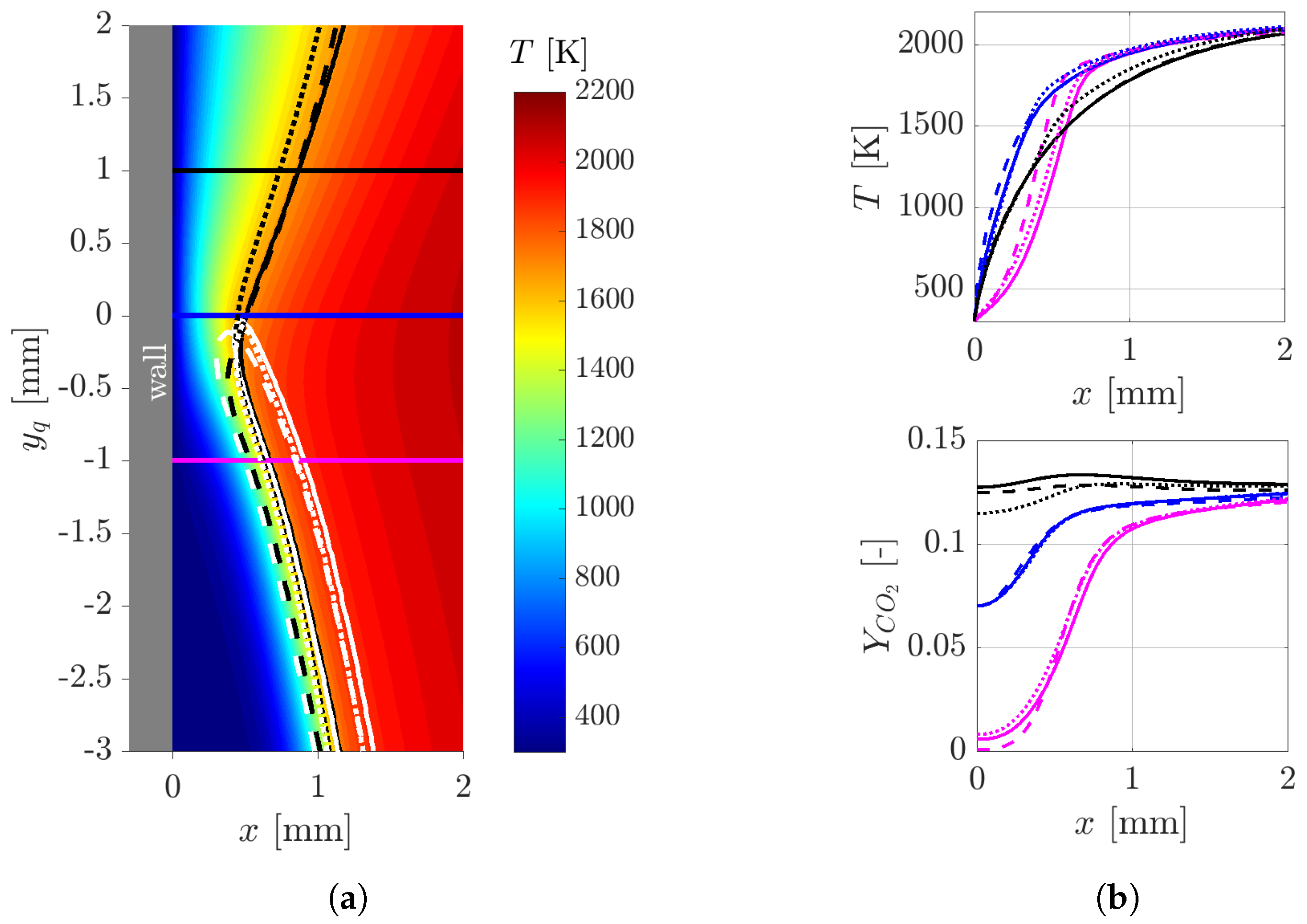
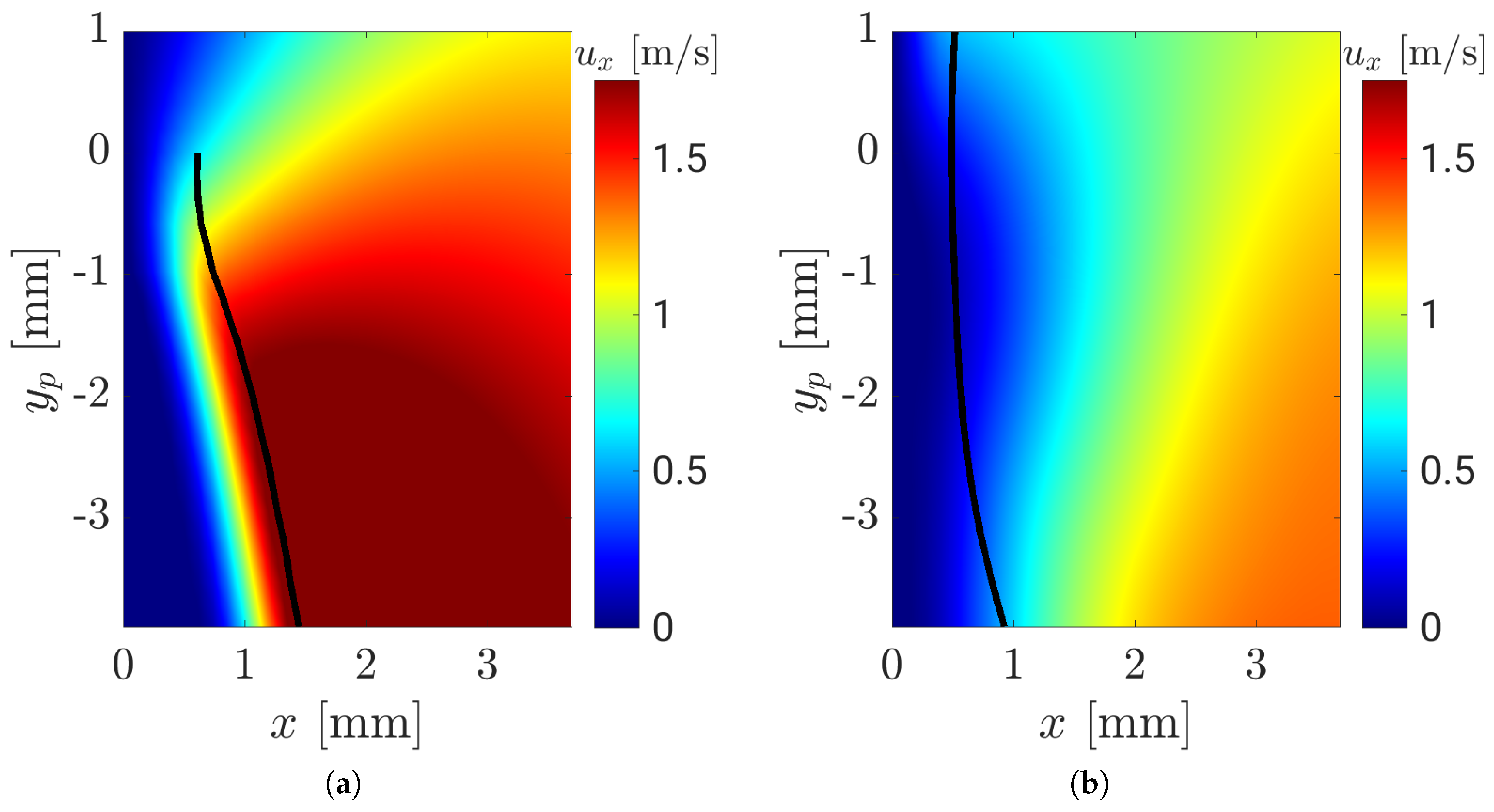
- two-dimensional contour plot of the wall heat flux together with the quenching line (red line), the position of the extracted profiles (z = 0 mm, white line) and the moving direction of the flame tip (white arrow)
- along the wall at z = 0 mm, including the position of the maximum wall heat flux point (blue dashed line) and (red dashed line),
- a 2D slice (x-y-plane) with temperature isolines at z = 0 mm with the flame position (black line) overlaid with the velocity vectors and (blue dashed line) and (red dashed line),
- the temperature field including the magnitude of the velocity and its vector for two positions at z = 0 mm (one at , one at , where is the thermal thickness of the flame).
(Scenario A)
(Scenario B)
(Scenario C)
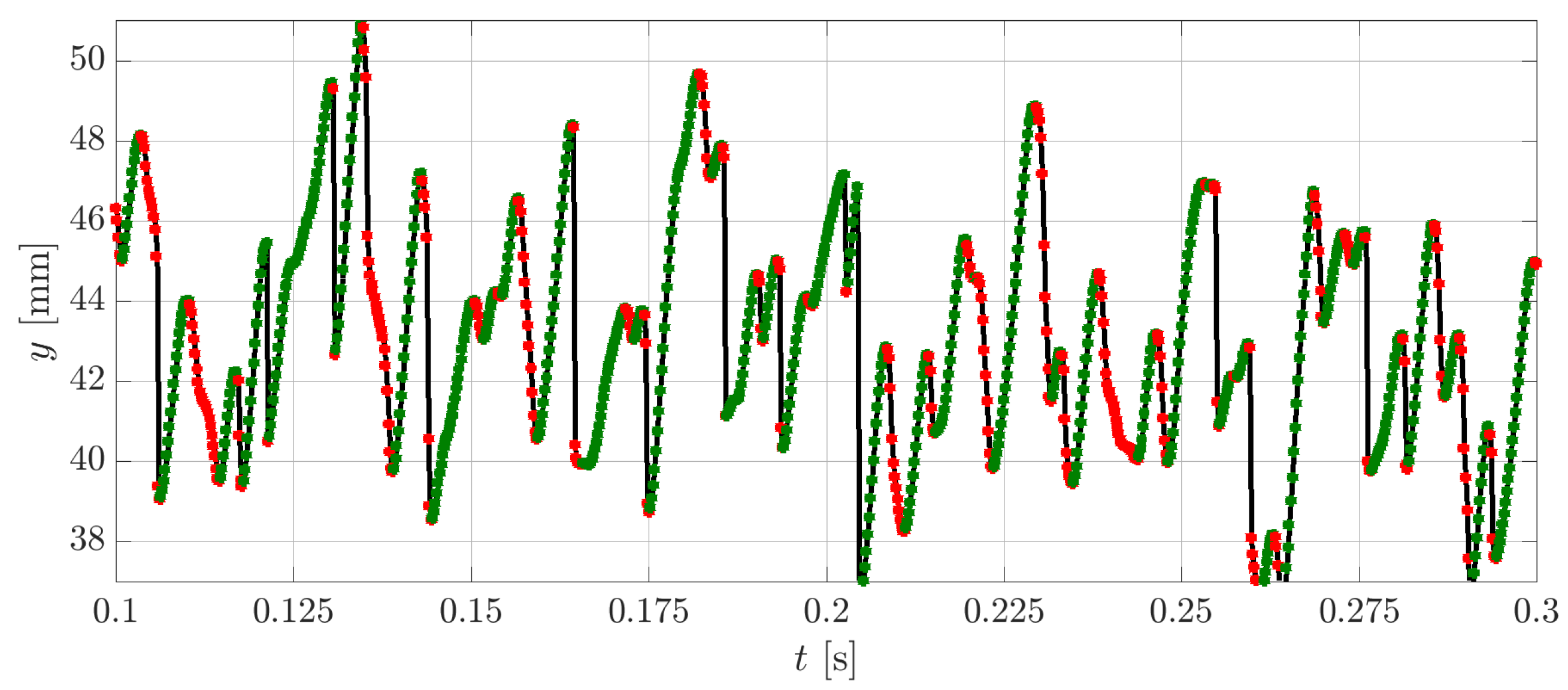
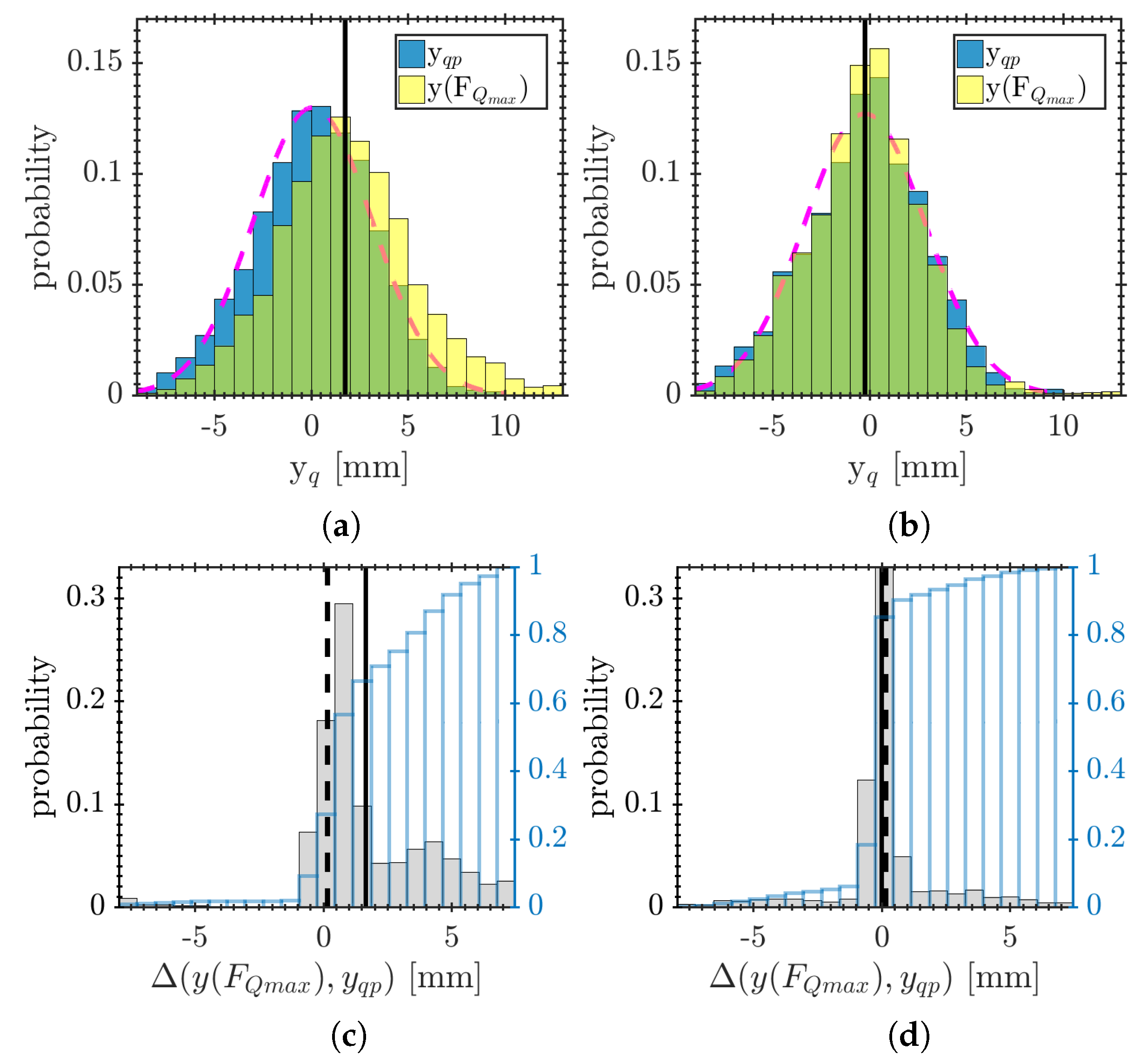
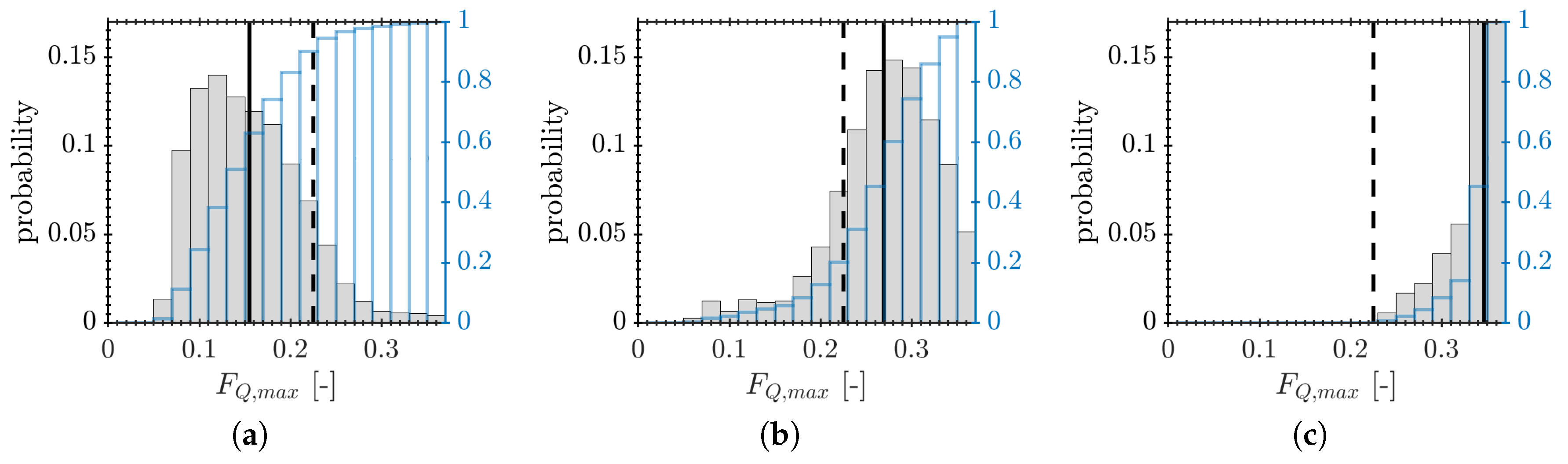
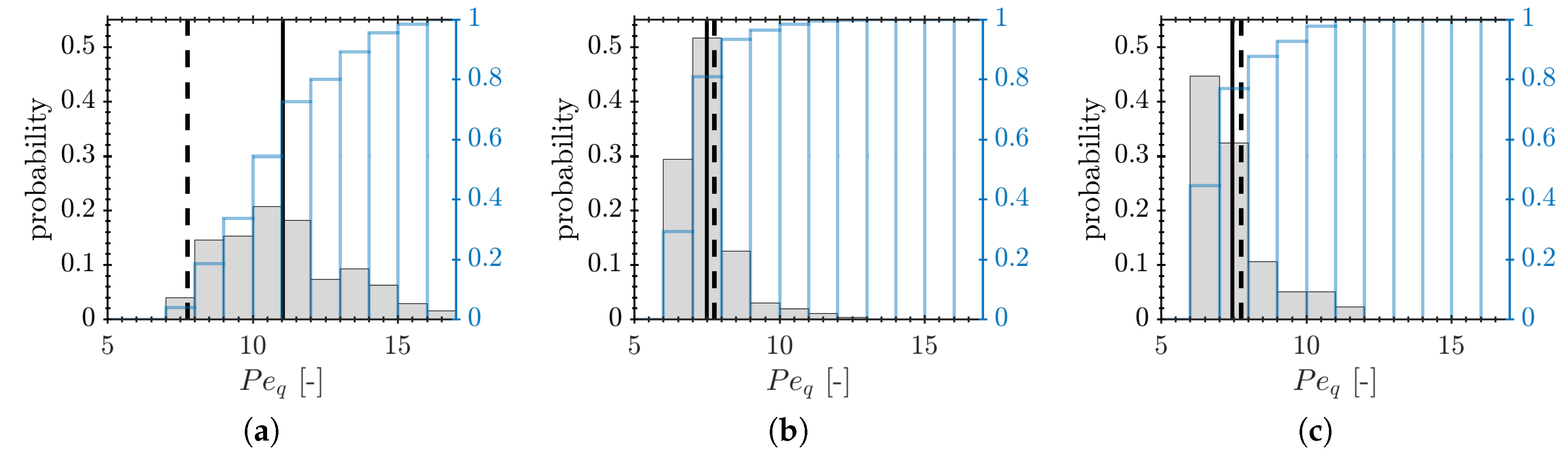
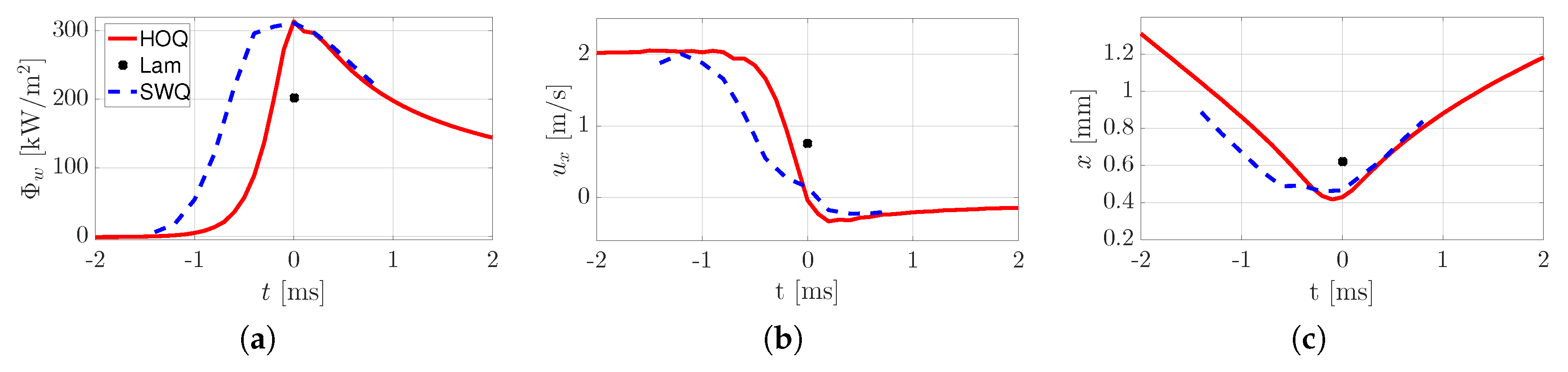
3.2. Statistics of the Axial Quenching Position and the Maximum Wall Heat Flux
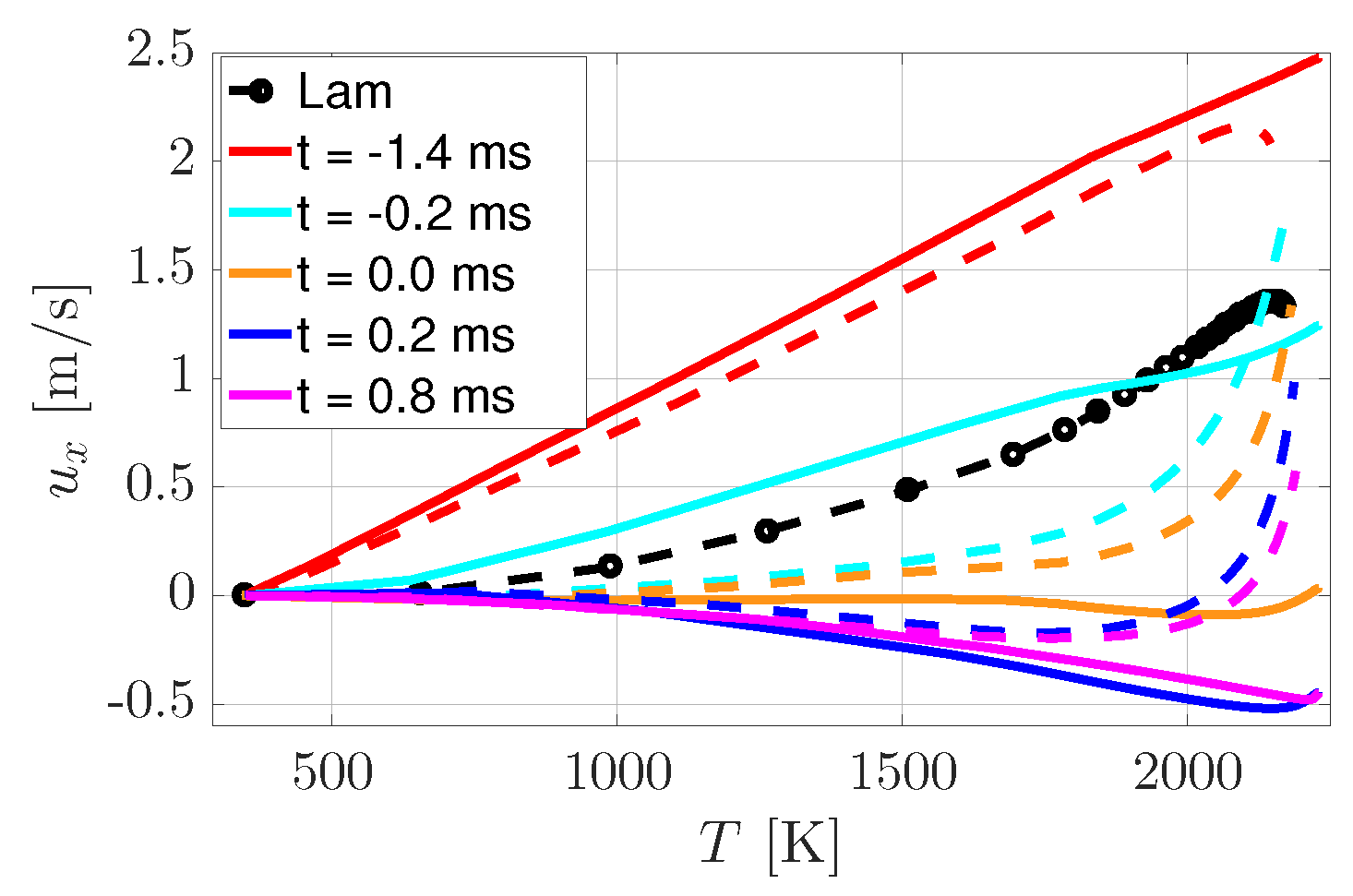
3.3. Physical Mechanism Governing the FWTI
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- International Energy Agency (IEA). World Energy Outlook; IEA: Paris, France, 2017. [Google Scholar]
- BP. Statistical Review of World Energy; BP: London, UK, 2018. [Google Scholar]
- Lazik, W.W.; Doerr, T.; Bake, S.S.; vd Bank, R.R.; Rackwitz, L.L. Development of Lean-Burn Low-NOx Combustion Technology at Rolls-Royce Deutschland. In ASME Turbo Expo: Power for Land, Sea, and Air; Volume 3: Combustion, Fuels and Emissions, Parts A and B; American Society of Mechanical Engineers (ASME): New York, NY, USA, 2008; pp. 797–807. [Google Scholar] [CrossRef]
- Dreizler, A.; Böhm, B. Advanced laser diagnostics for an improved understanding of premixed flame–wall interactions. Proc. Combust. Inst. 2015, 35, 37–64. [Google Scholar] [CrossRef]
- Poinsot, T.; Veynante, D. Theoretical and Numerical Combustion, 3rd ed.; Thierry Poinsot and Denis Veynante; Institut de Mécanique des Fluides de Toulouse: Toulouse, France, 2012. [Google Scholar]
- Cheng, R.; Bill, R.; Robben, F. Experimental study of combustion in a turbulent boundary layer. Symp. (Int.) Combust. 1981, 18, 1021–1029. [Google Scholar] [CrossRef]
- Gruber, A.; Sankaran, R.; Hawkes, E.R.; Chen, J.H. Turbulent flame–wall interaction: A direct numerical simulation study. J. Fluid Mech. 2010, 658, 5–32. [Google Scholar] [CrossRef]
- Saffman, M. Parametric studies of a side wall quench layer. Combust. Flame 1984, 55, 141–159. [Google Scholar] [CrossRef]
- Lu, J.; Ezekoye, O.; Greif, R.; Sawyer, R. Unsteady heat transfer during side wall quenching of a laminar flame. Symp. (Int.) Combust. 1991, 23, 441–446. [Google Scholar] [CrossRef]
- Ezekoye, O.; Greif, R.; Sawyer, R. Increased surface temperature effects on wall heat transfer during unsteady flame quenching. Symp. (Int.) Combust. 1992, 24, 1465–1472. [Google Scholar] [CrossRef]
- Boust, B.; Sotton, J.; Labuda, S.; Bellenoue, M. A thermal formulation for single-wall quenching of transient laminar flames. Combust. Flame 2007, 149, 286–294. [Google Scholar] [CrossRef]
- Alshaalan, T.M.; Rutland, C.J. Turbulence, scalar transport, and reaction rates in flame–wall interaction. Symp. (Int.) Combust. 1998, 27, 793–799. [Google Scholar] [CrossRef]
- Alshaalan, T.M.; Rutland, C.J. Wall heat flux in turbulent premixed reacting flow. Combust. Sci. Technol. 2002, 174, 135–165. [Google Scholar] [CrossRef]
- Jainski, C.; Rißmann, M.; Böhm, B.; Dreizler, A. Experimental investigation of flame surface density and mean reaction rate during flame–wall interaction. Proc. Combust. Inst. 2016, 36, 1827–1834. [Google Scholar] [CrossRef]
- Jainski, C.; Rißmann, M.; Böhm, B.; Janicka, J.; Dreizler, A. Sidewall quenching of atmospheric laminar premixed flames studied by laser-based diagnostics. Combust. Flame 2017, 183, 271–282. [Google Scholar] [CrossRef]
- Heinrich, A.; Ganter, S.; Kuenne, G.; Jainski, C.; Dreizler, A.; Janicka, J. 3D Numerical Simulation of a Laminar Experimental SWQ Burner with Tabulated Chemistry. Flow Turbul. Combust. 2017, 100, 535–559. [Google Scholar] [CrossRef]
- Heinrich, A.; Ries, F.; Kuenne, G.; Ganter, S.; Hasse, C.; Sadiki, A.; Janicka, J. Large Eddy Simulation with tabulated chemistry of an experimental sidewall quenching burner. Int. J. Heat Fluid Flow 2018, 71, 95–110. [Google Scholar] [CrossRef]
- Lehnhäuser, T.; Schäfer, M. Improved linear interpolation practice for finite-volume schemes on complex grids. Int. J. Numer. Methods Fluids 2002, 38, 625–645. [Google Scholar] [CrossRef]
- Smagorinsky, J. General Circulation Experiments with the Primitive Equations, 1. the basic experiment. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Germano, M.; Piomelli, U.; Moin, P.; Cabot, W.H. A dynamic subgrid-scale eddy viscosity model. Phys. Fluids A Fluid Dyn. 1991, 3, 1760–1765. [Google Scholar] [CrossRef]
- Lilly, D.K. A proposed modification of the Germano subgrid-scale closure method. Phys. Fluids A Fluid Dyn. 1992, 4, 633–635. [Google Scholar] [CrossRef]
- Zhou, G.; Davidson, L.; Olsson, E. Transonic inviscid/turbulent airfoil flow simulations using a pressure based method with high order schemes. In Proceedings of the Fourteenth International Conference on Numerical Methods in Fluid Dynamics, Bangalore, India, 11–15 July 1994; Deshpande, S.M., Desai, S.S., Narasimha, R., Eds.; Springer: Berlin/Heidelberg, Germany, 1995; pp. 372–378. [Google Scholar]
- Van Oijen, J.A.; de Goey, L.P.H. Modelling of Premixed Laminar Flames using Flamelet-Generated Manifolds. Combust. Sci. Technol. 2000, 161, 113–137. [Google Scholar] [CrossRef]
- Smith, G.P.; Golden, D.M.; Frenklach, M.; Moriarty, N.W.; Eiteneer, B.; Goldenberg, M.; Bowman, C.T.; Hanson, R.K.; Song, S.; Gardiner, W.C., Jr.; et al. GRI-Mech 3.0, 1999. Available online: http://combustion.berkeley.edu/gri-mech/ (accessed on 1 September 2018).
- Chem1D. A One-Dimensional Laminar Flame Code, Developed at Eindhoven University of Technology. Available online: https://www.tue.nl/en/university/departments/mechanical-engineering/research/research-groups/multiphase-and-reactive-flows/our-expertise/chem1d/ (accessed on 1 September 2018).
- Van Oijen, J.A.; Lammers, F.A.; de Goey, L.P.H. Modeling of complex premixed burner systems by using flamelet-generated manifolds. Combust. Flame 2001, 127, 2124–2134. [Google Scholar] [CrossRef]
- Ketelheun, A.; Kuenne, G.; Janicka, J. Heat Transfer Modeling in the Context of Large Eddy Simulation of Premixed Combustion with Tabulated Chemistry. Flow Turbul. Combust. 2013, 91, 867–893. [Google Scholar] [CrossRef]
- Kuenne, G.; Euler, M.; Ketelheun, A.; Avdić, A.; Dreizler, A.; Janicka, J. A Numerical Study of the Flame Stabilization Mechanism Being Determined by Chemical Reaction Rates Submitted to Heat Transfer Processes. Zeitschrift für Physikalische Chemie 2014, 229, 643–662. [Google Scholar] [CrossRef]
- Avdić, A.; Kuenne, G.; Janicka, J. Flow Physics of a Bluff-Body Swirl Stabilized Flame and their Prediction by Means of a Joint Eulerian Stochastic Field and Tabulated Chemistry Approach. Flow Turbul. Combust. 2016, 97, 1185–1210. [Google Scholar] [CrossRef]
- Avdić, A.; Kuenne, G.; di Mare, F.; Janicka, J. LES combustion modeling using the Eulerian stochastic field method coupled with tabulated chemistry. Combust. Flame 2017, 175, 201–219. [Google Scholar] [CrossRef]
- Meier, T.; Kuenne, G.; Ketelheun, A.; Janicka, J. Numerische Abbildung von Verbrennungsprozessen mit Hilfe detaillierter und tabellierter Chemie. In VDI Berichte; Number 2162; VDI Verlag GmbH: Duisburg, Germany, 2013; pp. 643–652. [Google Scholar]
- Ganter, S.; Heinrich, A.; Meier, T.; Kuenne, G.; Jainski, C.; Rißmann, M.C.; Dreizler, A.; Janicka, J. Numerical analysis of laminar methane–air side-wall-quenching. Combust. Flame 2017, 186, 299–310. [Google Scholar] [CrossRef]
- Ganter, S.; Straßacker, C.; Kuenne, G.; Meier, T.; Heinrich, A.; Maas, U.; Janicka, J. Laminar near-wall combustion: Analysis of tabulated chemistry simulations by means of detailed kinetics. Int. J. Heat Fluid Flow 2018, 70, 259–270. [Google Scholar] [CrossRef]
- Williams, F.A. Combustion Theory: The Fundamental Theory of Chemically Reacting Flow Systems; Addison/Wesley Pub. Co.: Boston, MA, USA, 1985; p. 680. [Google Scholar]
- Colin, O.; Ducros, F.; Veynante, D.; Poinsot, T. A thickened flame model for large eddy simulations of turbulent premixed combustion. Phys. Fluids 2000, 12, 1843–1863. [Google Scholar] [CrossRef]
- Butler, T.; O’Rourke, P. A numerical method for two dimensional unsteady reacting flows. Symp. (Int.) Combust. 1977, 16, 1503–1515. [Google Scholar] [CrossRef]
- Durand, L.; Polifke, W. Implementation of the Thickened Flame Model for Large Eddy Simulation of Turbulent Premixed Combustion in a Commercial Solver. In ASME Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers (ASME): New York, NY, USA, 2007; Volume 2, pp. 869–878. [Google Scholar] [CrossRef]
- Kuenne, G.; Ketelheun, A.; Janicka, J. LES modeling of premixed combustion using a thickened flame approach coupled with FGM tabulated chemistry. Combust. Flame 2011, 158, 1750–1767. [Google Scholar] [CrossRef]
- Charlette, F.; Meneveau, C.; Veynante, D. A power-law flame wrinkling model for LES of premixed turbulent combustion Part I: Non-dynamic formulation and initial tests. Combust. Flame 2002, 131, 159–180. [Google Scholar] [CrossRef]
- Peters, N. Laminar flamelet concepts in turbulent combustion. Symp. (Int.) Combust. 1986, 21, 1231–1250. [Google Scholar] [CrossRef]
- Van Oijen, J.; Bastiaans, R.; de Goey, L. Low-dimensional manifolds in direct numerical simulations of premixed turbulent flames. Proc. Combust. Inst. 2007, 31, 1377–1384. [Google Scholar] [CrossRef]
- Van Oijen, J.; Groot, G.; Bastiaans, R.; de Goey, L. A flamelet analysis of the burning velocity of premixed turbulent expanding flames. Proc. Combust. Inst. 2005, 30, 657–664. [Google Scholar] [CrossRef]
| 300 K | 2286 K | 37.1 cm/s | 1077 J/(K kg) | 1.123 kg/m | 0.0283 W/(m K) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heinrich, A.; Kuenne, G.; Ganter, S.; Hasse, C.; Janicka, J. Investigation of the Turbulent Near Wall Flame Behavior for a Sidewall Quenching Burner by Means of a Large Eddy Simulation and Tabulated Chemistry. Fluids 2018, 3, 65. https://doi.org/10.3390/fluids3030065
Heinrich A, Kuenne G, Ganter S, Hasse C, Janicka J. Investigation of the Turbulent Near Wall Flame Behavior for a Sidewall Quenching Burner by Means of a Large Eddy Simulation and Tabulated Chemistry. Fluids. 2018; 3(3):65. https://doi.org/10.3390/fluids3030065
Chicago/Turabian StyleHeinrich, Arne, Guido Kuenne, Sebastian Ganter, Christian Hasse, and Johannes Janicka. 2018. "Investigation of the Turbulent Near Wall Flame Behavior for a Sidewall Quenching Burner by Means of a Large Eddy Simulation and Tabulated Chemistry" Fluids 3, no. 3: 65. https://doi.org/10.3390/fluids3030065
APA StyleHeinrich, A., Kuenne, G., Ganter, S., Hasse, C., & Janicka, J. (2018). Investigation of the Turbulent Near Wall Flame Behavior for a Sidewall Quenching Burner by Means of a Large Eddy Simulation and Tabulated Chemistry. Fluids, 3(3), 65. https://doi.org/10.3390/fluids3030065





