Quality Measures of Mixing in Turbulent Flow and Effects of Molecular Diffusivity
Abstract
1. Introduction
2. Materials and Methods
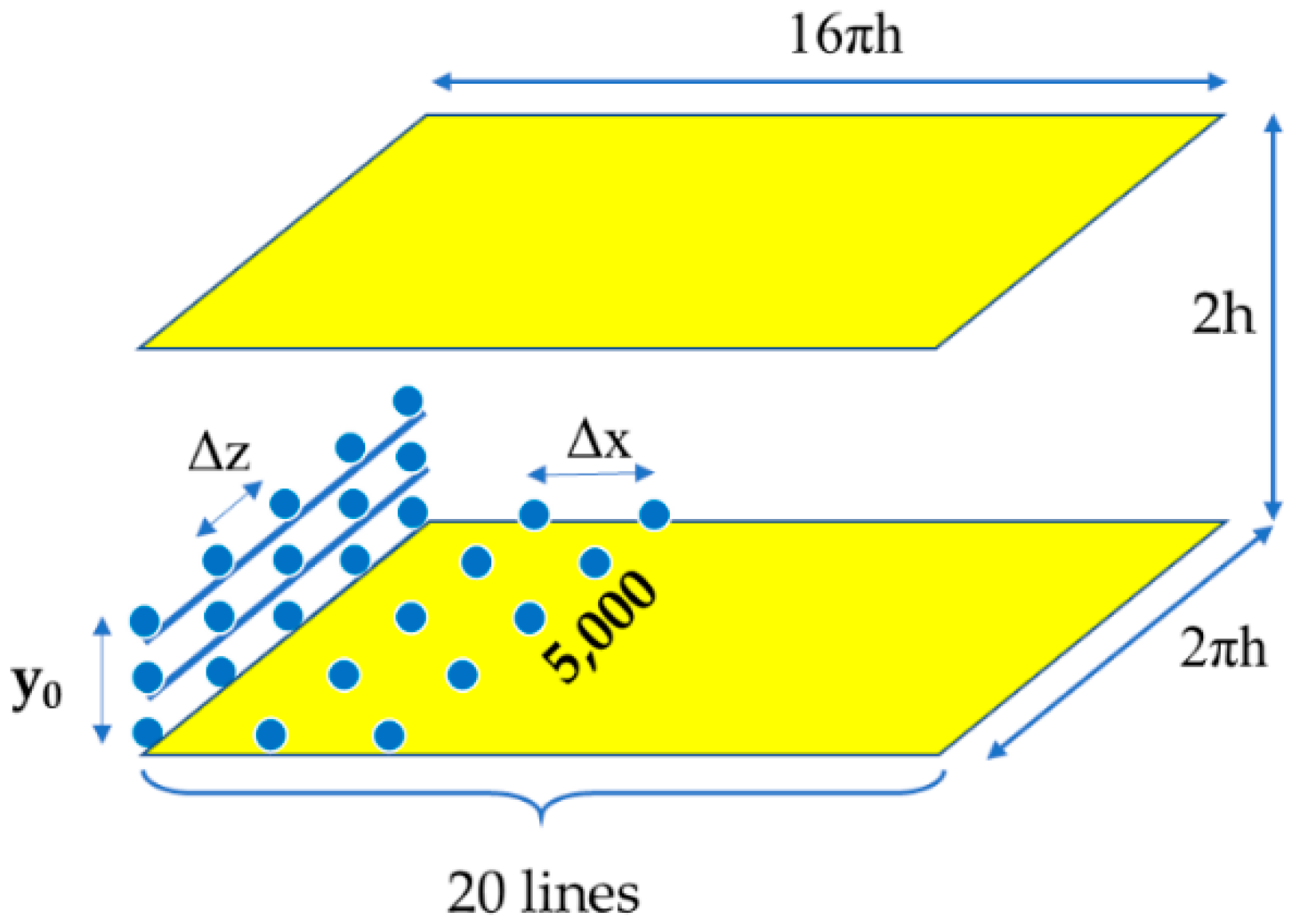
2.1. Flow Field Simulation and Lagrangian Scalar Tracking Approach
2.2. Mixing Calculations
3. Results
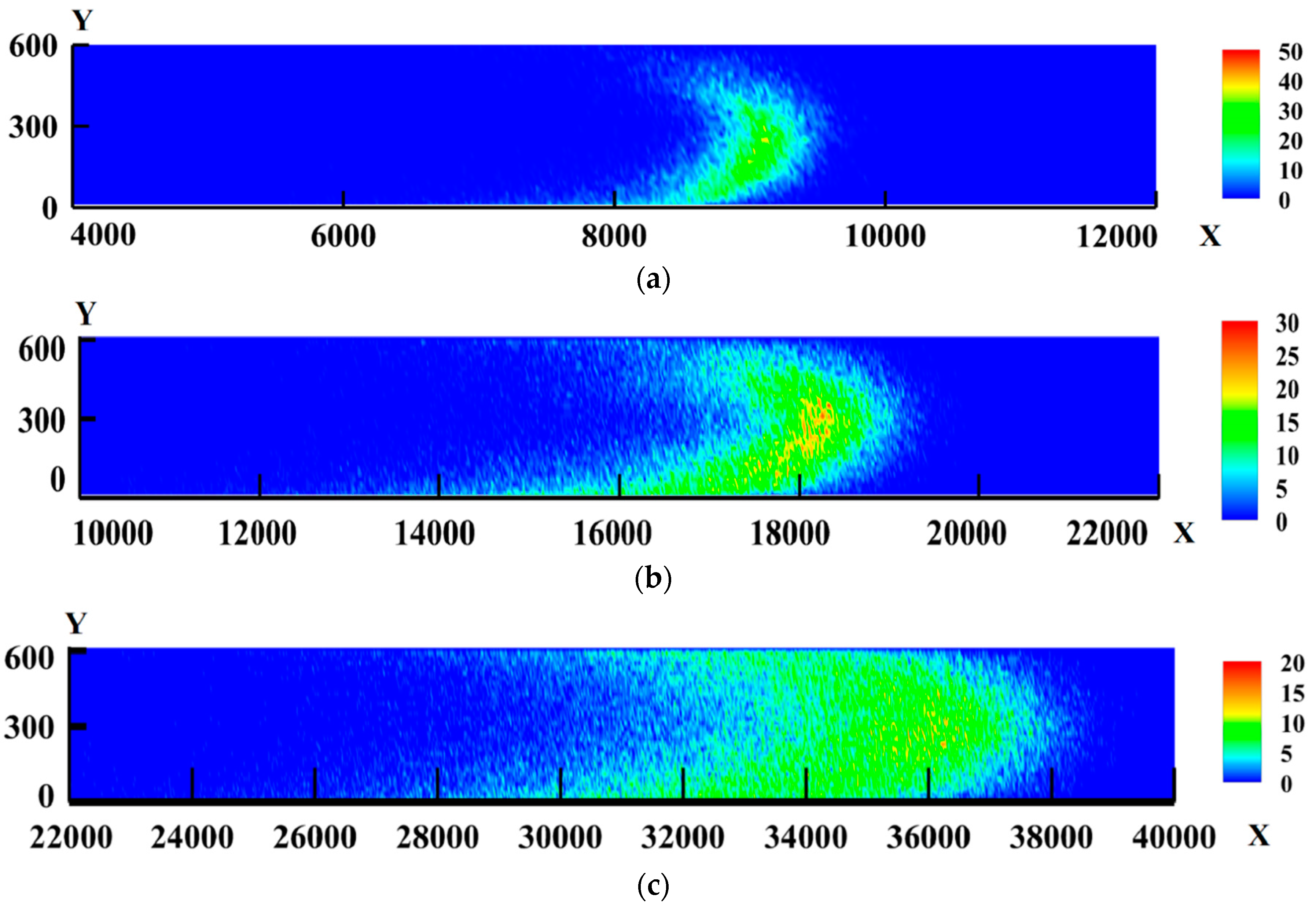
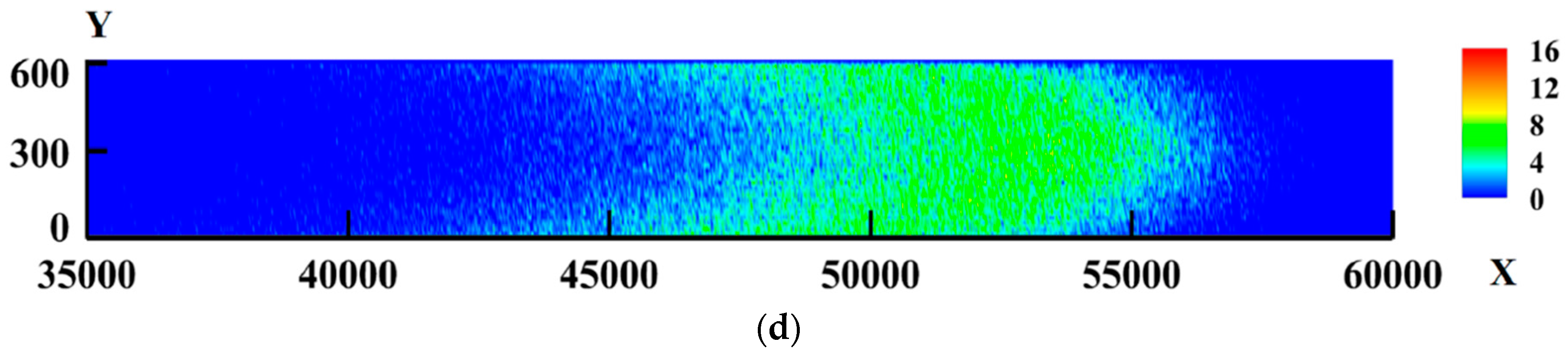
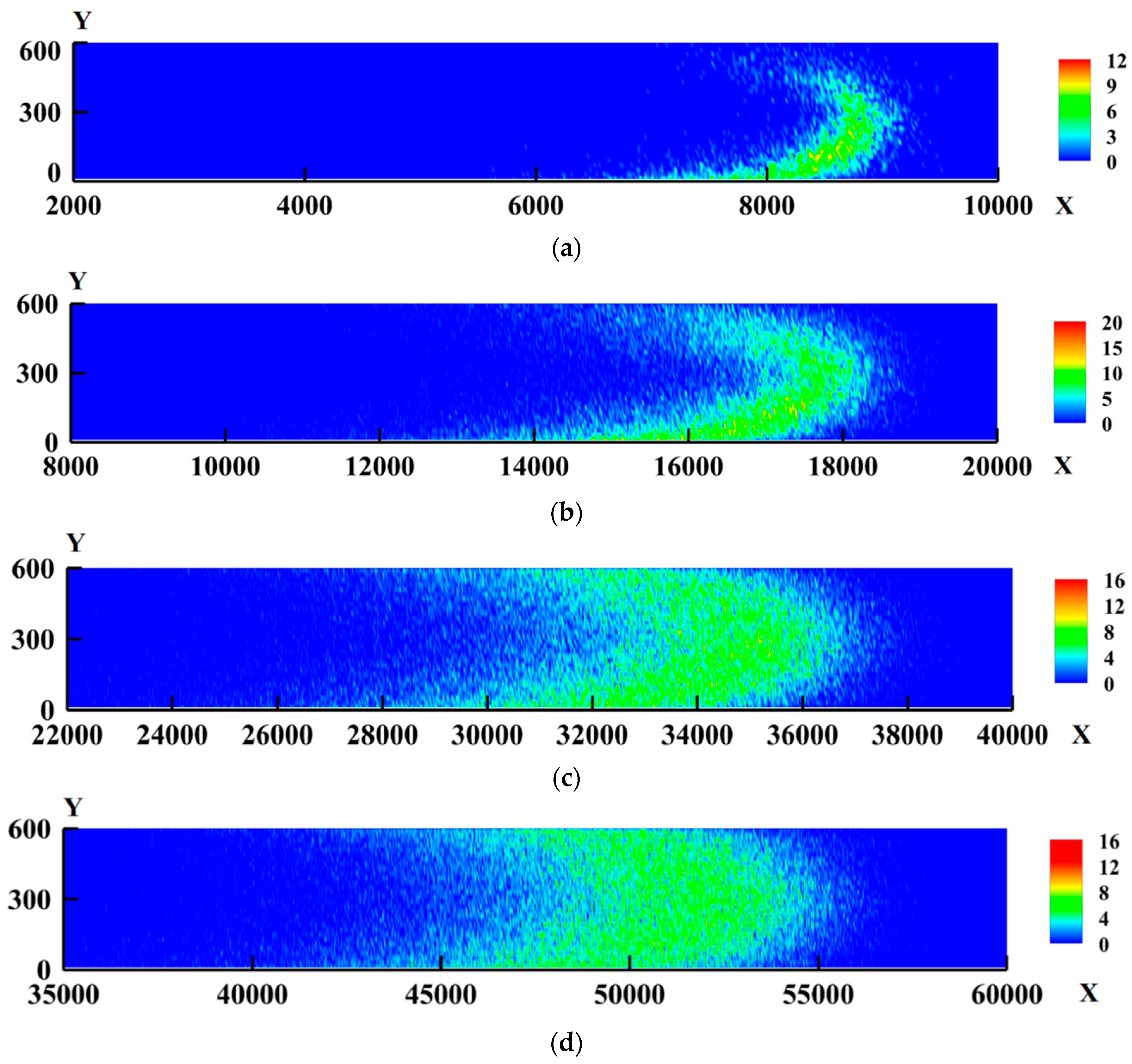
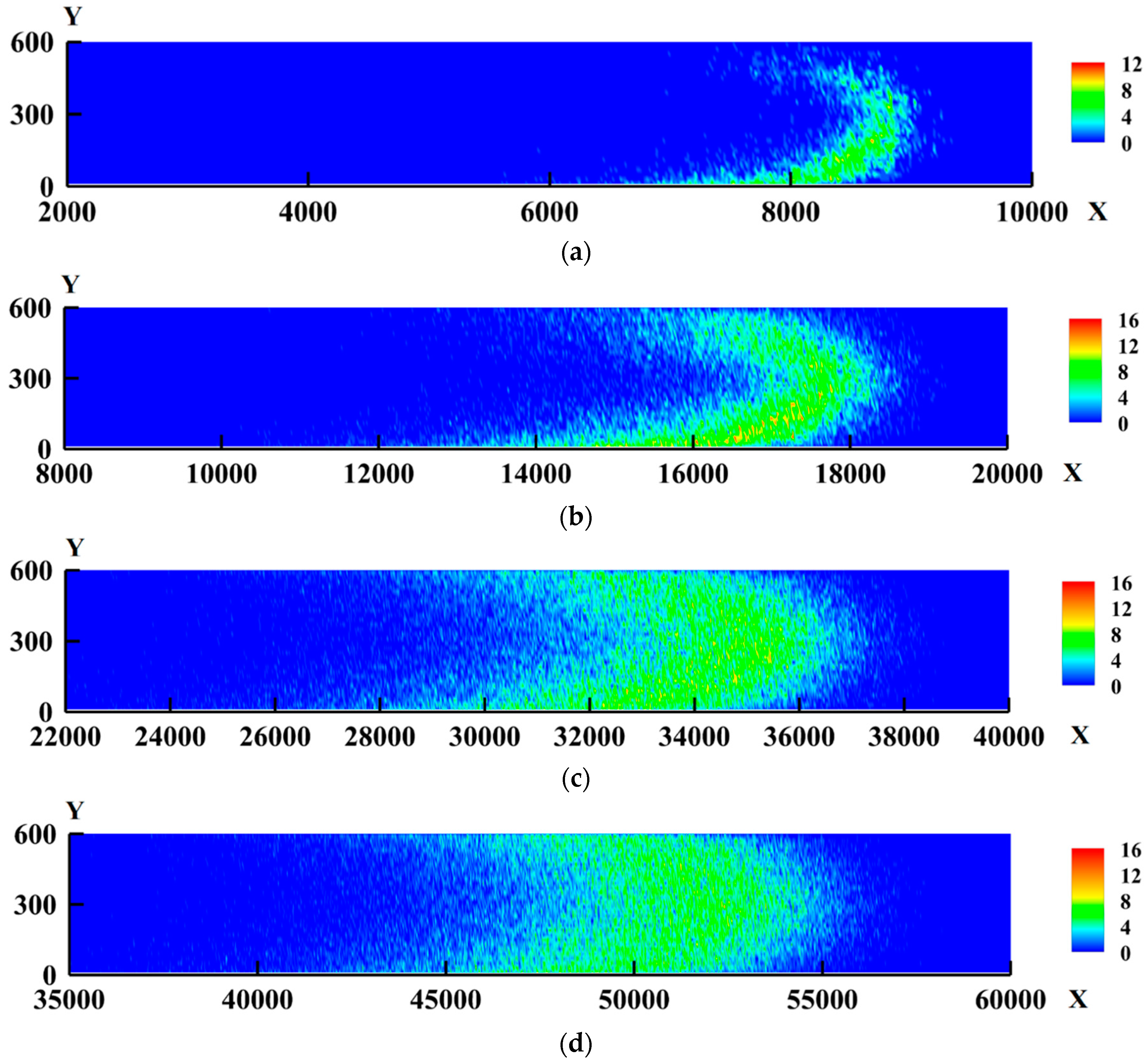
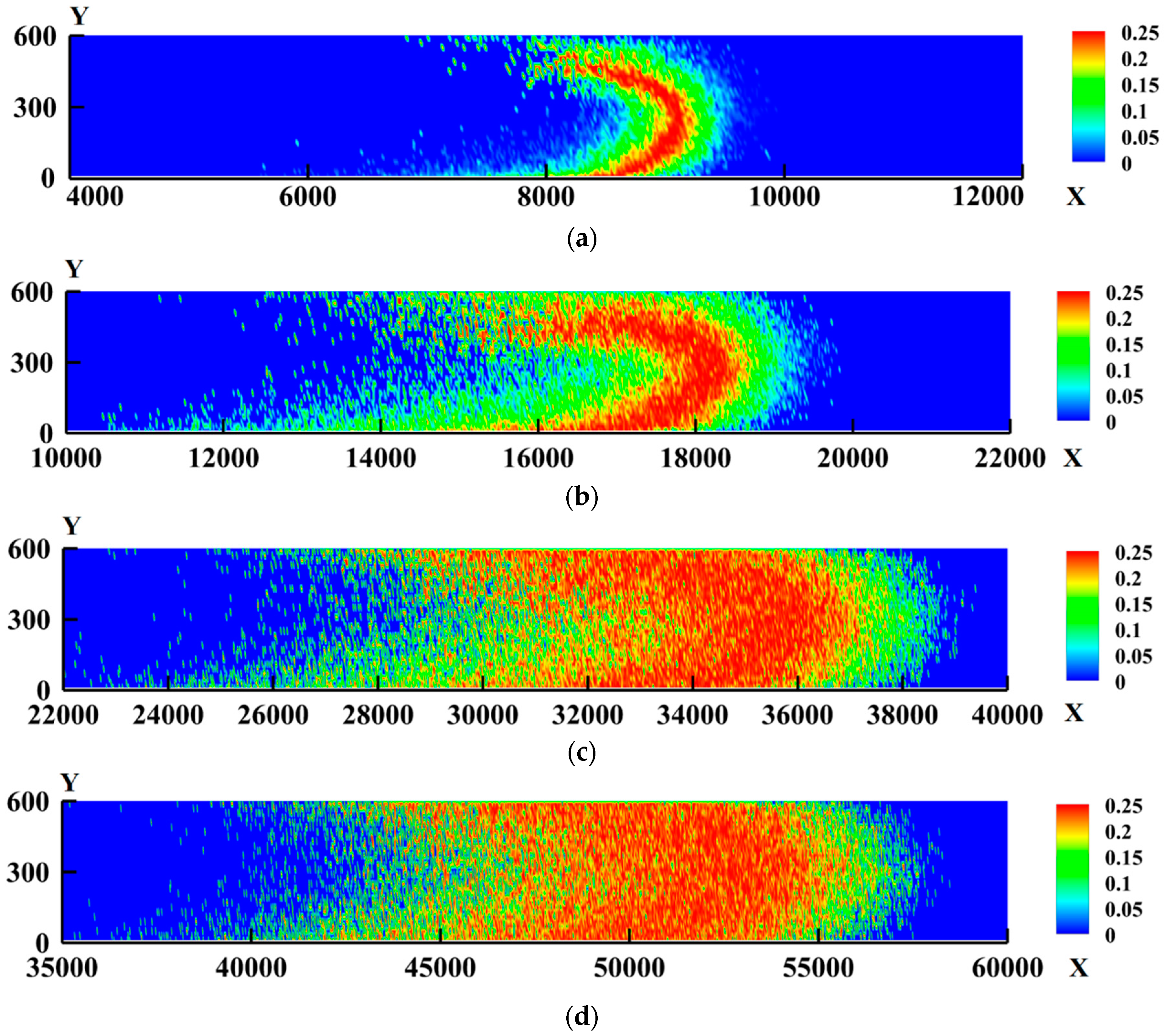
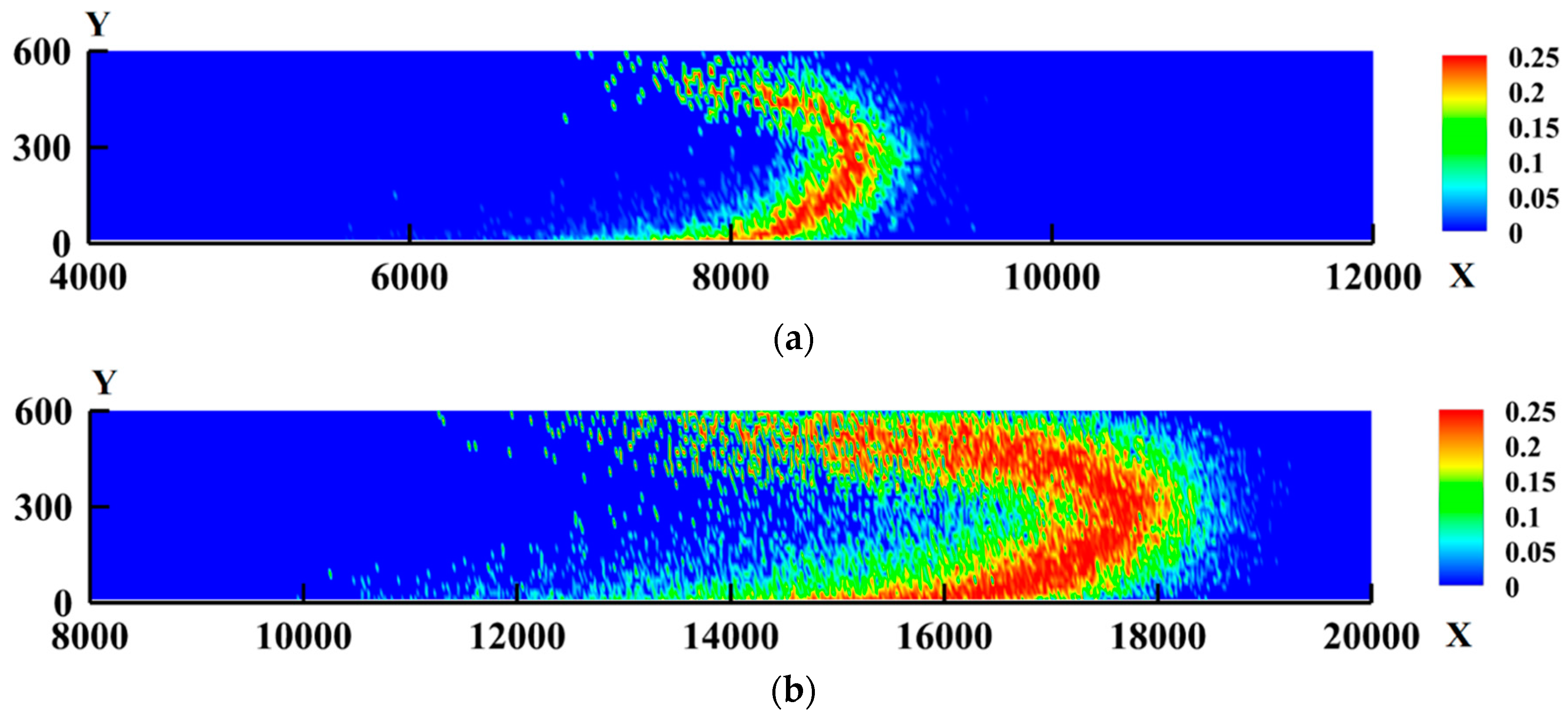
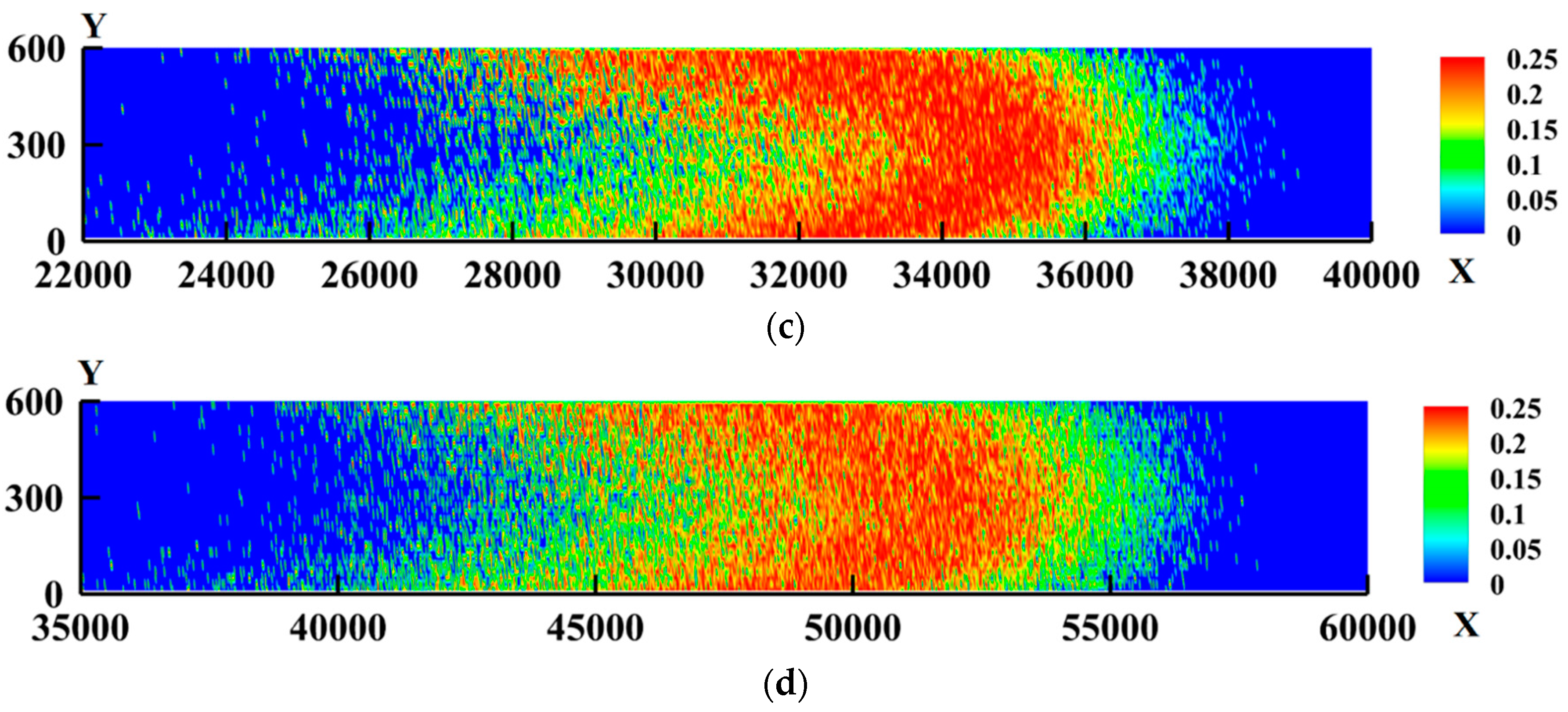
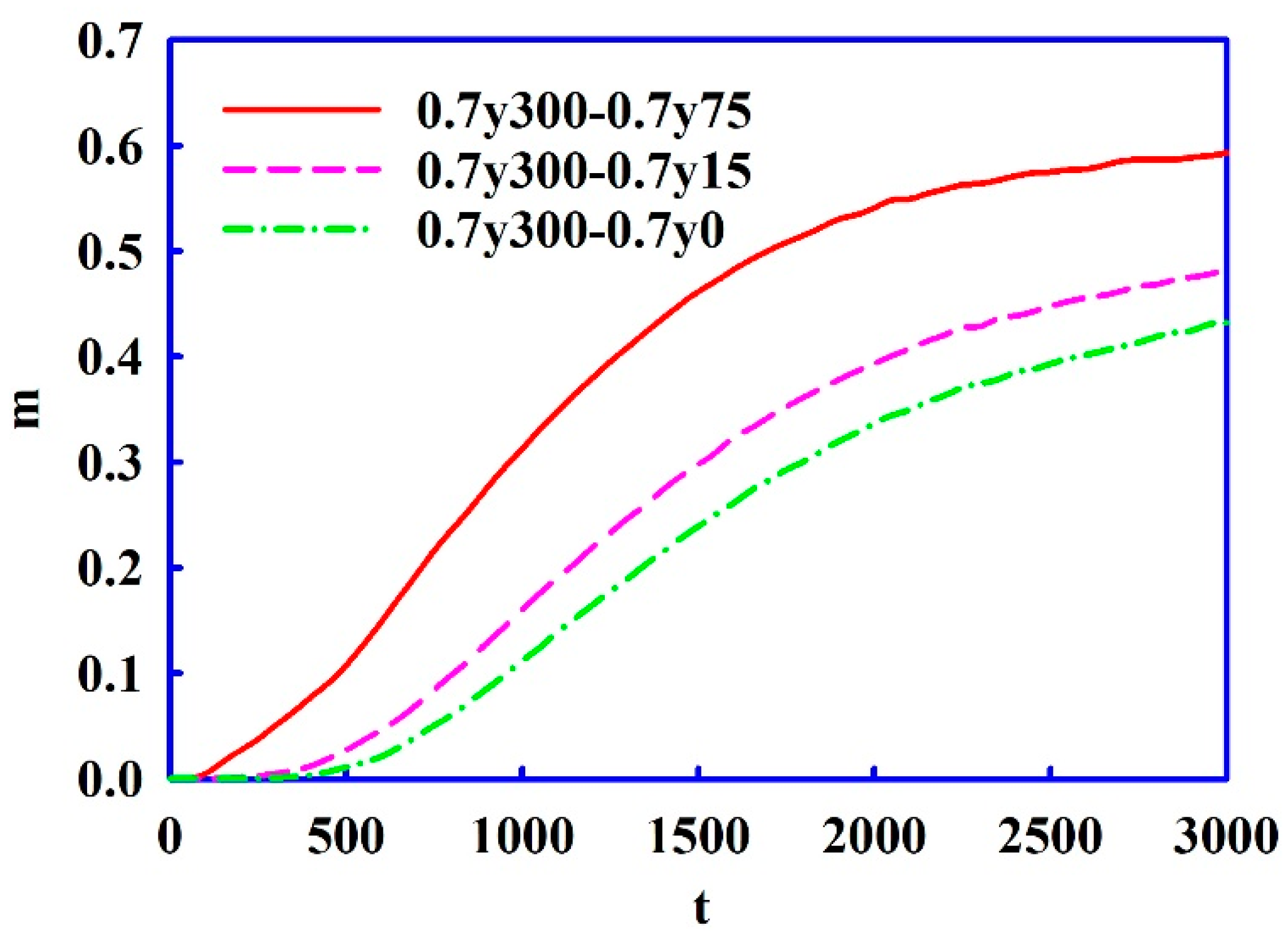
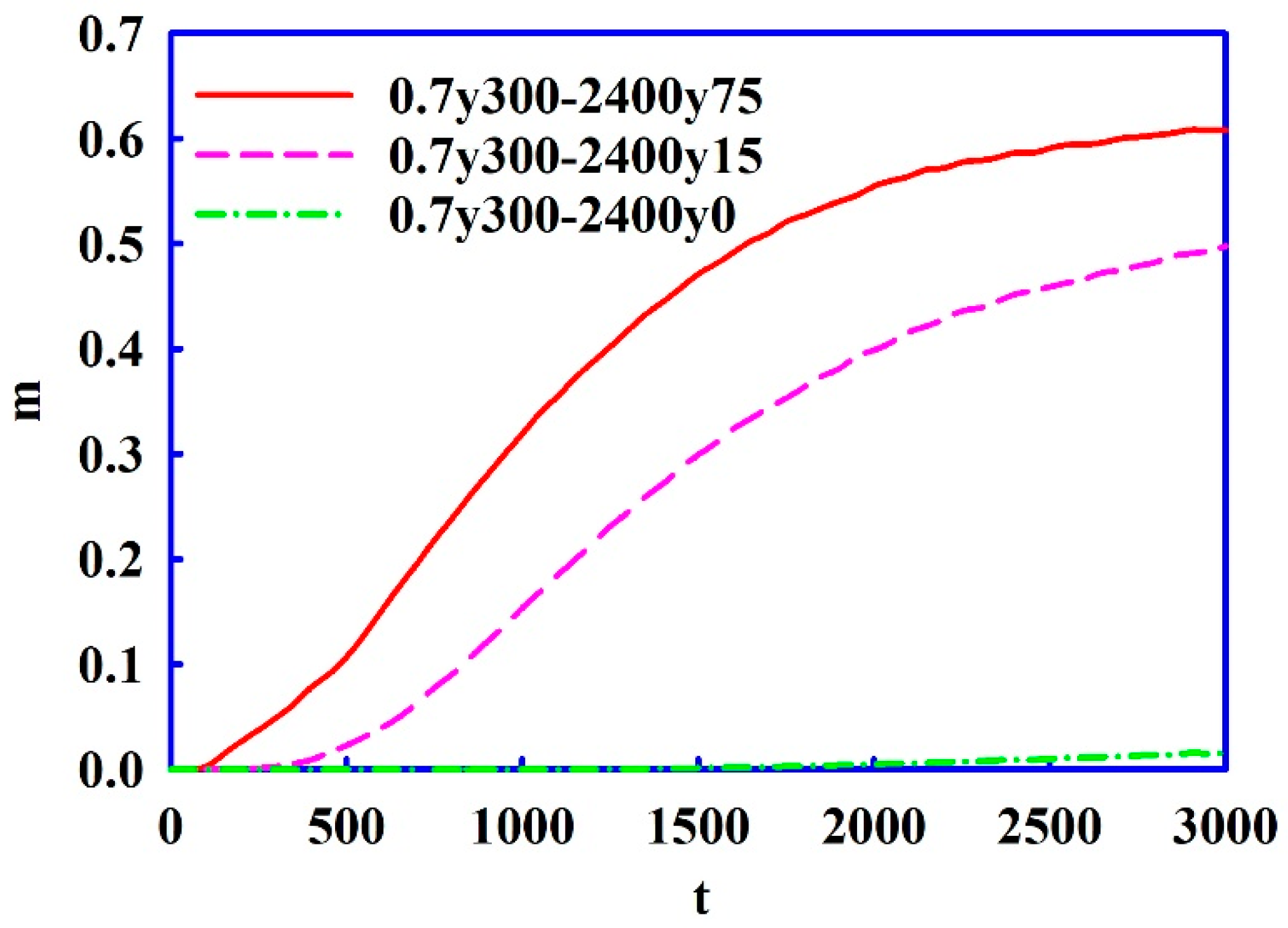
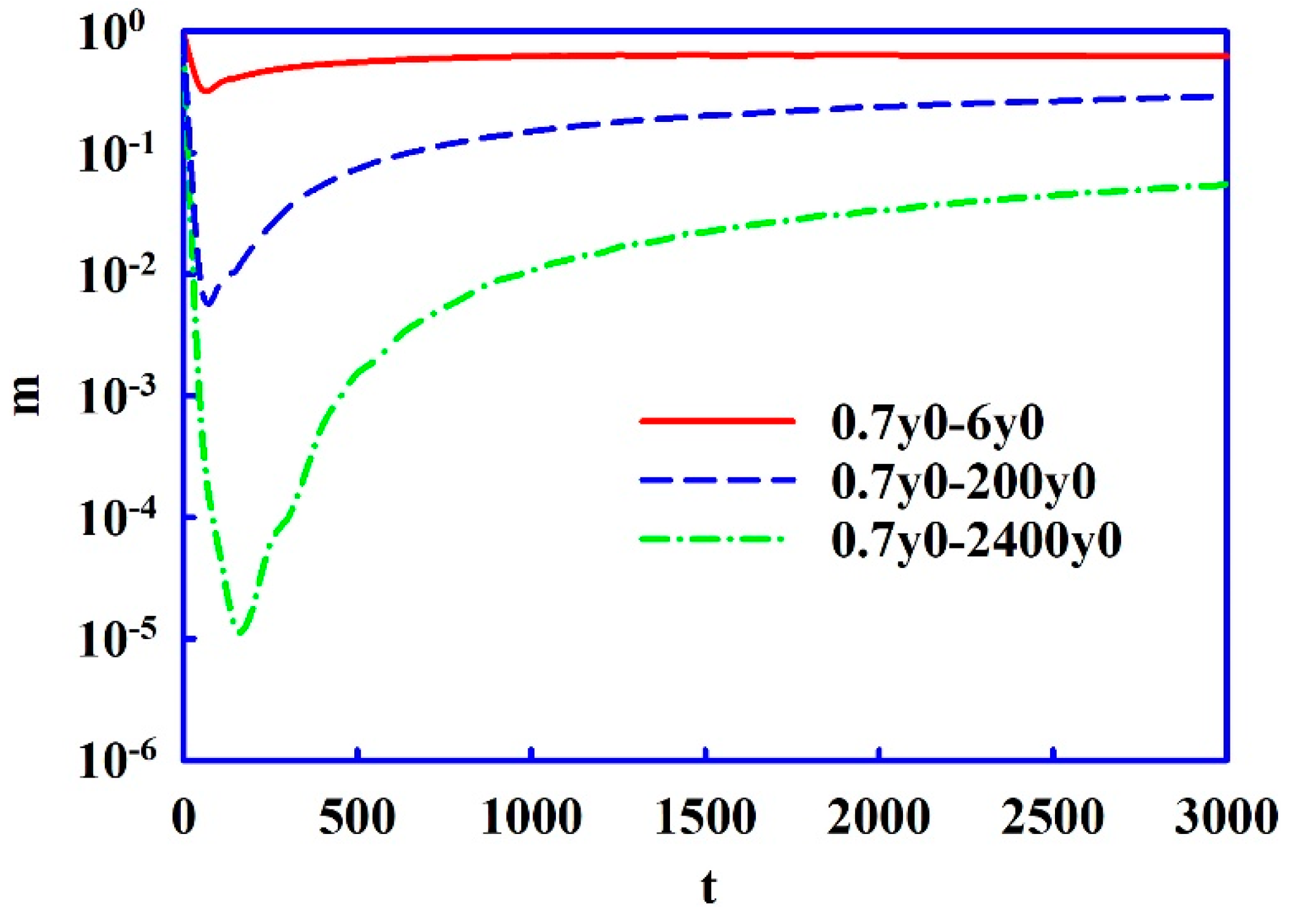
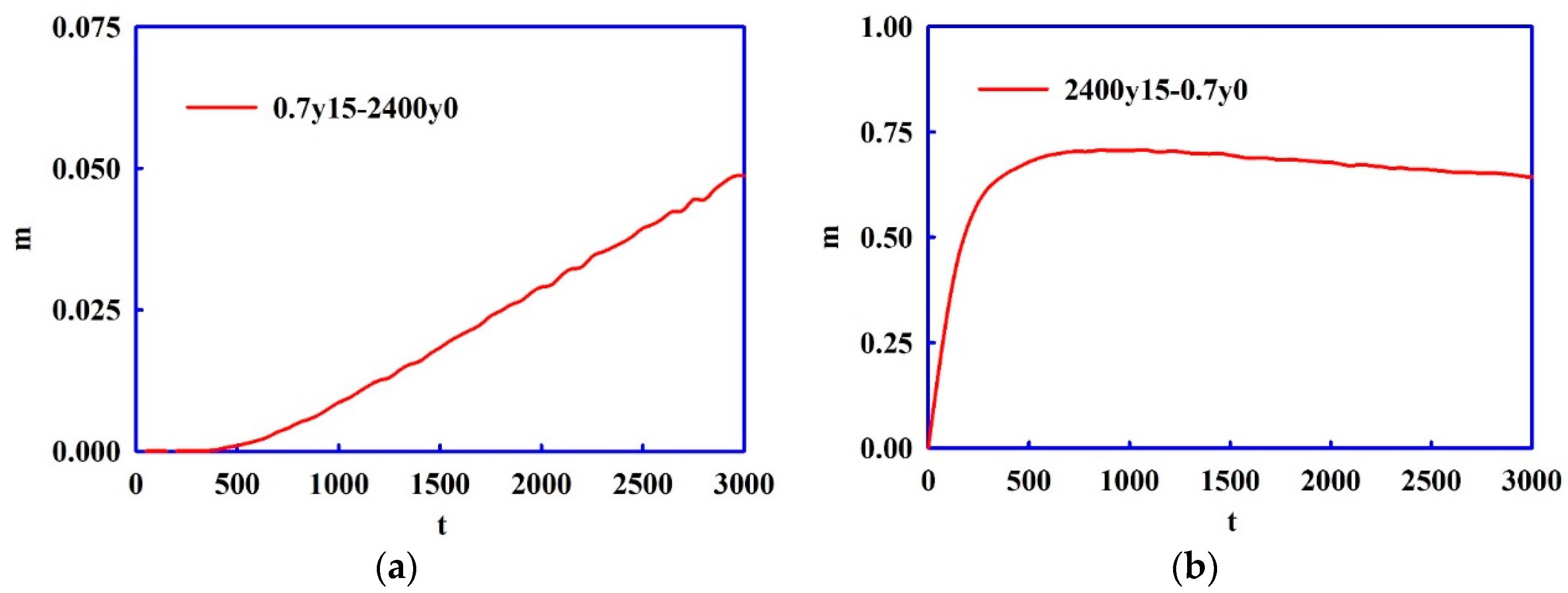
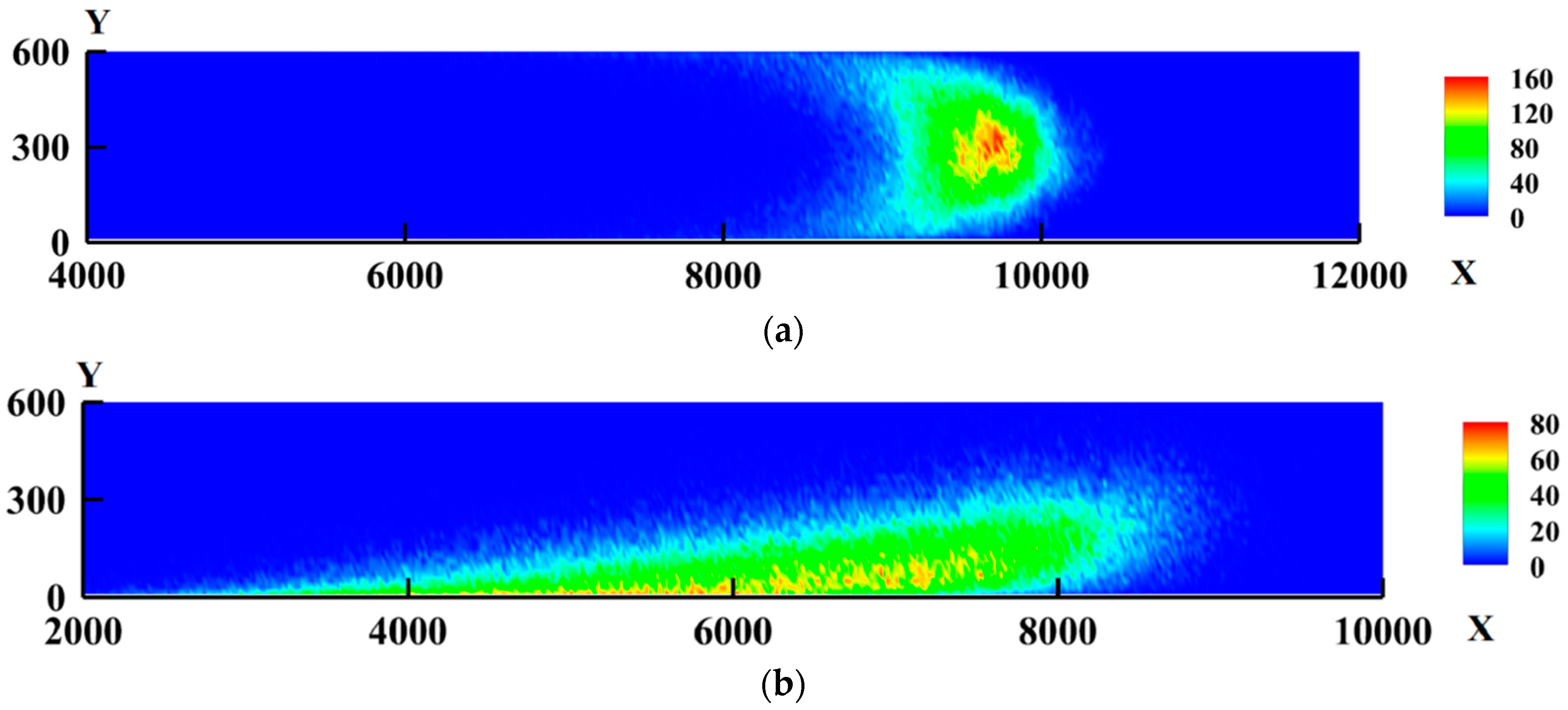
3.1. Development of Mixing Region with Time
3.2. Quality of Mixing
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tennekes, H.; Lumley, J.L. A First Course in Turbulence; MIT Press: Boston, MA, USA, 1972. [Google Scholar]
- Dimotakis, P.E. Turbulent Mixing. Annu. Rev. Fluid Mech. 2005, 37, 329–356. [Google Scholar] [CrossRef]
- Fox, R.O. Computational Models for Turbulent Reacting Flows; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Curl, R.L. Dispersed phase mixing: I. Theory and effects in simple reactors. AlChE J. 1963, 9, 175–181. [Google Scholar] [CrossRef]
- Subramaniam, S.; Pope, S.B. A mixing model for turbulent reactive flows based on Euclidean minimum spanning trees. Combust. Flame 1998, 115, 487–514. [Google Scholar] [CrossRef]
- Oldshue, J.W. Fluid Mixing Techology; McGraw Hill: New York, NY, USA, 1983. [Google Scholar]
- Paul, E.L.; Atiemo-Obeng, V.A.; Kresta, M.S. Handbook of Industrial Mixing: Science and Practice; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Mylne, K.R.; Mason, P.J. Concentration fluctuation measurements in a dispersing plume at a range of up to 1000 m. QJRMS 1991, 117, 177–206. [Google Scholar] [CrossRef]
- Pasquill, F.; Smith, F.B. Atmospheric Diffusion; Horwood, E., Ed.; John Wiley & Sons: Hoboken, NJ, USA, 1983; p. 437. [Google Scholar]
- Ottino, J.M. The Kinematics of Mixing: Stretching, Chaos, and Transport; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
- Kukukova, A.; Aubin, J.; Kresta, S.M. A new definition of mixing and segregation: Three dimensions of a key process variable. Chem. Eng. Res. Des. 2009, 87, 633–647. [Google Scholar] [CrossRef]
- Calzavarini, E.; Cencini, M.; Lohse, D.; Toschi, F. Quantifying Turbulence-Induced Segregation of Inertial Particles. Phys. Rev. Lett. 2008, 101, 084504. [Google Scholar] [CrossRef] [PubMed]
- Green, D.W.; Perry, R.H. Perry’s Chemical Engineers’ Handbook, 8th ed.; McGraw Hill: New York, NY, USA, 2007. [Google Scholar]
- Papavassiliou, D.V. Turbulent transport from continuous sources at the wall of a channel. Int. J. Heat Mass Transf. 2002, 45, 3571–3583. [Google Scholar] [CrossRef]
- Hanratty, T.J. Heat transfer through a homogeneous isotropic turbulent field. AlChE J. 1956, 2, 42–45. [Google Scholar] [CrossRef]
- Papavassiliou, D.V.; Hanratty, T.J. Transport of a passive scalar in a turbulent channel flow. Int. J. Heat Mass Transf. 1997, 40, 1303–1311. [Google Scholar] [CrossRef]
- Mitrovic, B.M.; Le, P.M.; Papavassiliou, D.V. On the Prandtl or Schmidt number dependence of the turbulent heat or mass transfer coefficient. Chem. Eng. Sci. 2004, 59, 543–555. [Google Scholar] [CrossRef]
- Incropera, F.P.; Kerby, J.S.; Moffatt, D.F.; Ramadhyani, S. Convection heat transfer from discrete heat sources in a rectangular channel. Int. J. Heat Mass Transf. 1986, 29, 1051–1058. [Google Scholar] [CrossRef]
- Raupach, M.R.; Legg, B.J. Turbulent dispersion from an elevated line source—Measurements of wind concentration moments and budgets. J. Fluid Mech. 1983, 136, 111–137. [Google Scholar] [CrossRef]
- Poreh, M.; Cermak, J.E. Study of diffusion from a line source in a turbulent boundary layer. Int. J. Heat Mass Transf. 1964, 7, 1083–1095. [Google Scholar] [CrossRef]
- Fackrell, J.E.; Robins, A.G. Concentration fluctuations and fluxes in plumes from point sources in a turbulent boundary layer. J. Fluid Mech. 1982, 117, 1–26. [Google Scholar] [CrossRef]
- Shlien, D.J.; Corrsin, S. Dispersion measurements in a turbulent boundary layer. Int. J. Heat Mass Transf. 1976, 19, 285–295. [Google Scholar]
- Beguier, C.; Dekeyser, I.; Launder, B.E. Ratio of scalar and velocity dissipation time scales in shear flow turbulence. Phys. Fluids 1978, 21, 307–310. [Google Scholar] [CrossRef]
- Ma, B.K.; Warhaft, Z. Some aspects of the thermal mixing layer in grid turbulence. Phys. Fluids 1986, 29, 3114–3120. [Google Scholar] [CrossRef]
- Dahm, W.J.A.; Dimotakis, P.E. Mixing at large Schmidt number in the self-similar far field of turbulent jets. J. Fluid Mech. 1990, 217, 299–330. [Google Scholar] [CrossRef]
- Yeung, P.K.; Xu, S. Schmidt number effects on turbulent transport with uniform mean scalar gradient. Phys. Fluids 2002, 14, 4178–4191. [Google Scholar] [CrossRef]
- Borgas, M.S.; Sawford, B.L.; Xu, S.; Donzis, D.A.; Yeung, P.K. High Schmidt number scalars in turbulence: Structure functions and Lagrangian theory. Phys. Fluids 2004, 16, 3888–3899. [Google Scholar] [CrossRef]
- Buaria, D.; Yeung, P.K.; Sawford, B.L. A Lagrangian study of turbulent mixing: Forward and backward dispersion of molecular trajectories in isotropic turbulence. J. Fluid Mech. 2016, 799, 352–382. [Google Scholar] [CrossRef]
- Yeung, P.K.; Donzis, D.A. High-Reynolds-number simulation of turbulent mixing. Phys. Fluids 2005, 17, 081703. [Google Scholar] [CrossRef]
- Sawford, B.L. Lagrangian modeling of scalar statistics in a double scalar mixing layer. Phys. Fluids 2006, 18, 085108. [Google Scholar] [CrossRef]
- Sawford, B.L.; Kops, S.M.D.B. Direct numerical simulation and Lagrangian modeling of joint scalar statistics in ternary mixing. Phys. Fluids 2008, 20, 095106. [Google Scholar] [CrossRef]
- Brethouwer, G.; Hunt, J.C.R.; Nieuwstadt, F.T.M. Micro-structure and Lagrangian statistics of the scalar field with a mean gradient in isotropic turbulence. J. Fluid Mech. 2003, 474, 193–225. [Google Scholar] [CrossRef]
- Yeung, P.K.; Xu, S.; Donzis, D.A.; Sreenivasan, K.R. Simulations of three-dimensional turbulent mixing for Schmidt numbers of the order 1000. Flow Turbul. Combust. 2004, 72, 333–347. [Google Scholar] [CrossRef]
- Srinivasan, C.; Papavassiliou, D.V. Heat Transfer Scaling Close to the Wall for Turbulent Channel Flows. Appl. Mech. Rev. 2013, 65. [Google Scholar] [CrossRef]
- Srinivasan, C.; Papavassiliou, D.V. Prediction of the turbulent Prandtl number in wall flows with Lagrangian simulations. Ind. Eng. Chem. Res. 2011, 50, 8881–8891. [Google Scholar] [CrossRef]
- Srinivasan, C.; Papavassiliou, D.V. Comparison of backwards and forwards scalar relative dispersion in turbulent shear flow. Int. J. Heat Mass Transf. 2012, 55, 5650–5664. [Google Scholar] [CrossRef]
- Hasegawa, Y.; Kasagi, N. Low-pass filtering effects of viscous sublayer on high Schmidt number mass transfer close to a solid wall. Int. J. Heat Fluid Flow 2009, 30, 525–533. [Google Scholar] [CrossRef]
- Mito, Y.; Hanratty, T.J. Lagrangian stochastic simulation of turbulent dispersion of heat markers in a channel flow. Int. J. Heat Mass Transf. 2003, 46, 1063–1073. [Google Scholar] [CrossRef]
- Koumoutsakos, P. Multiscale flow simulations using particles. Annu. Rev. Fluid Mech. 2005, 37, 457–487. [Google Scholar] [CrossRef]
- Moin, P.; Mahesh, K. Direct numerical simulation: A tool in turbulence research. Annu. Rev. Fluid Mech. 1998, 30, 539–578. [Google Scholar] [CrossRef]
- Lee, M.; Moser, R.D. Direct numerical simulation of turbulent channel flow up to Re-tau approximate to 5200. J. Fluid Mech. 2015, 774, 395–415. [Google Scholar] [CrossRef]
- Lyons, S.L.; Hanratty, T.J.; McLaughlin, J.B. Direct numerical simulation of passive heat transfer in a turbulent channel flow. Int. J. Heat Mass Transf. 1991, 34, 1149–1161. [Google Scholar] [CrossRef]
- Alfonsi, G. On Direct Numerical Simulation of Turbulent Flows. Appl. Mech. Rev. 2011, 64, 64. [Google Scholar] [CrossRef]
- Nguyen, Q.; Feher, S.E.; Papavassiliou, D.V. Lagrangian Modeling of Turbulent Dispersion from Instantaneous Point Sources at the Center of a Turbulent Flow Channel. Fluids 2017, 2. [Google Scholar] [CrossRef]
- Nguyen, Q.; Papavassiliou, D.V. Scalar mixing in anisotropic turbulent flow. AlChE J. 2018. [Google Scholar] [CrossRef]
- Lyons, S.L.; Hanratty, T.J.; McLaughlin, J.B. Large-scale computer simulation of fully developed turbulent channel flow with heat transfer. Int. J. Numer. Methods Fluids 1991, 13, 999–1028. [Google Scholar] [CrossRef]
- Gunther, A.; Papavassiliou, D.V.; Warholic, M.D.; Hanratty, T.J. Turbulent flow in a channel at a low Reynolds number. Exp. Fluids 1998, 25, 503–511. [Google Scholar] [CrossRef]
- Kontomaris, K.; Hanratty, T.J.; McLaughlin, J.B. An algorithm for tracking fluid particles in a spectral simulation of turbulent channel flow. J. Comput. Phys. 1992, 103, 231–242. [Google Scholar] [CrossRef]
- Mitrovic, B.M.; Papavassiliou, D.V. Transport properties for turbulent dispersion from wall sources. AlChE J. 2003, 49, 1095–1108. [Google Scholar] [CrossRef]
- Na, Y.; Papavassiliou, D.V.; Hanratty, T.J. Use of direct numerical simulation to study the effect of Prandtl number on temperature fields. Int. J. Heat Fluid Flow 1999, 20, 187–195. [Google Scholar] [CrossRef]
- Orszag, S.A.; Kells, L.C. Transition to turbulence in plane Poiseuille and plane Couette flow. J. Fluid Mech. 1980, 96, 159–205. [Google Scholar] [CrossRef]
- Marcus, P.S. Simulation of Taylor-Couette flow. 1. Numerical methods and comparison with experiment. J. Fluid Mech. 1984, 146, 45–64. [Google Scholar] [CrossRef]
- Einstein, A. Uber die von der molekular-kinetischen Theorie der Warme geforderte Bewegung von in ruhenden Flussigkeiten suspendierten Teilchen. Ann. Phys. 1905, 17, 549. [Google Scholar] [CrossRef]
- Papavassiliou, D.V.; Hanratty, T.J. The use of Lagrangian-methods to describe turbulent transport of heat from a wall. Ind. Eng. Chem. Res. 1995, 34, 3359–3367. [Google Scholar] [CrossRef]
- Saffman, P.G. On the effect of the molecular diffusivity in turbulent diffusion. J. Fluid Mech. 1960, 8, 273–283. [Google Scholar] [CrossRef]
- Le, P.M.; Papavassiliou, D.V. Turbulent Dispersion from Elevated Line Sources in Channel and Couette Flow. AlChE J. 2005, 51, 2402–2414. [Google Scholar] [CrossRef]
- Thornber, B.; Drikakis, D.; Youngs, D.L.; Williams, R.J.R. The influence of initial conditions on turbulent mixing due to Richtmyer-Meshkov instability. J. Fluid Mech. 2010, 654, 99–139. [Google Scholar] [CrossRef]
- Nguyen, Q.; Srinivasan, C.; Papavassiliou, D.V. Flow-induced separation in wall turbulence. Phys. Rev. E 2015, 91, 033019. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, Q.; Papavassiliou, D.V. A statistical model to predict streamwise turbulent dispersion from the wall at small times. Phys. Fluids 2016, 28, 125103. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, Q.; Papavassiliou, D.V. Quality Measures of Mixing in Turbulent Flow and Effects of Molecular Diffusivity. Fluids 2018, 3, 53. https://doi.org/10.3390/fluids3030053
Nguyen Q, Papavassiliou DV. Quality Measures of Mixing in Turbulent Flow and Effects of Molecular Diffusivity. Fluids. 2018; 3(3):53. https://doi.org/10.3390/fluids3030053
Chicago/Turabian StyleNguyen, Quoc, and Dimitrios V. Papavassiliou. 2018. "Quality Measures of Mixing in Turbulent Flow and Effects of Molecular Diffusivity" Fluids 3, no. 3: 53. https://doi.org/10.3390/fluids3030053
APA StyleNguyen, Q., & Papavassiliou, D. V. (2018). Quality Measures of Mixing in Turbulent Flow and Effects of Molecular Diffusivity. Fluids, 3(3), 53. https://doi.org/10.3390/fluids3030053





