Experimental Measurement of Dolphin Thrust Generated during a Tail Stand Using DPIV

Abstract

Estimation of force generated by dolphins has long been debated. The problem was that indirect estimates of force production for dolphins resulted in low values that could not be validated. Bubble digital particle image velocimetry (DPIV) measured hydrodynamic force production for swimming dolphins and demonstrated high force production. To validate the bubble DPIV and reconcile force production measurements, two bottlenose dolphins (Tursiops truncatus) performing tail stands were measured with bubble DPIV. Microbubbles were generated from a finely porous hose and compressed air source. Displacement of the bubbles by the propulsive motions of the dolphin was tracked with a high-speed video camera. Oscillations of the dolphin flukes generated strong vortices and a downward directed jet flow into the wake. Application of the Kutta–Joukowski theorem measuring vortex circulations yielded forces up to 997.3 N. Another video camera recorded body height above the water surface to determine the mass-force of the dolphin above the water surface. For the dolphin to hold its position above the water surface, the mass-force approximately balanced the vertical hydrodynamic force from the flukes. The results demonstrated the fluke motions generate high sustained forces roughly equal to the dolphin’s weight out of the water. Bubble DPIV validated high forces measured previously for thrust generated in swimming by animals and demonstrated a more accurate technique compared to standard aerodynamic analysis.

1. Introduction

Swimming by animals requires the transfer of momentum from the organism to the water. The rate of change of momentum generates the propulsive thrust that is indistinguishable from the resistive drag on the actively swimming body [1]. The momentum imparted to the water by a propulsor is visualized in a thrust-type (reverse von Kármán street) wake with a central momentum jet, which is directed through the center of a staggered array of vortex rings [2,3,4,5,6,7]. This exchange of momentum and its measurement have been at the core of examinations of forces and energetics of swimming by animals [8]. To this end, various studies have sought to visualize the wake [9,10,11,12,13,14,15]. The movement of fluid within the wake represents the physical manifestation of the momentum transfer.

Digital particle image velocimetry (DPIV) has been used as an effective technique to quantify the wake and determine hydrodynamic forces. DPIV has been used to examine flow patterns associated with feeding currents and to measure the thrust and lift forces associated with the propulsion of aquatic animals, including fish, squid, and crustaceans [9,10,11,12,13,14,15]. Typically, in using DPIV, microscopic reflective particles are illuminated with a laser sheet. The deflections of the particles in the plane of the laser sheet are recorded with a high-speed digital video camera. Sequential images of the particles within given areas are cross-correlated to determine the velocity field and vorticity, which can be used to compute the forces generated about an organism. A variant of standard DPIV was used to measure the hydrodynamic force production for dolphins during free swimming [7]. As dolphins could not be exposed experimentally to lasers and reflective particles, animals swam along a sheet of microbubbles in natural light (i.e., bubble DPIV). The results of the experiment demonstrated high force production for actively swimming dolphins.

DPIV has been used widely by engineers on static systems that can be independently validated with experimental data from standardized rigid shapes [16]. However, similar validations have not been applied to DPIV results on actively swimming animals. The problem is that there is no proper control or reference value that can be compared with the drag or thrust values of actively swimming animals. The drag is higher for an actively swimming animal compared to a static, rigid body or reference flat plate [17,18]. The dynamic self-propulsion of swimming animals modifies the time-dependent flow compared to that of a rigid body [1]. The problem in estimating the thrust produced by self-propelled animals is that the motions of the body produce drag and thrust simultaneously, which cannot be separated and thus momentum losses and gains are co-mingled [1]. Unlike analysis of a ship traveling at a constant velocity, the drag on the rigid ship’s hull can be separated from the thrust produced by the propeller. For the ship, the propulsive and resistive forces sum to zero.

To validate previous results of DPIV studies on live animals and reconcile force production measurements, bottlenose dolphins performing tail stands were measured with bubble DPIV. Tail stands are defined as a behavior in which a vertically oriented dolphin lifts half or more of its body out of the water. It was expected that the thrust determined from bubble DPIV would match the weight of the dolphin supported above the water surface. For the dolphin to hold its position above the water surface, the mass-force would approximately balance the vertical hydrodynamic force generated by the oscillating flukes. The results of the bubble DPIV were also compared to measurements calculated from lifting wing theory.

2. Materials and Methods

2.1. Experimental Animals and Microbubbles

Experiments were conducted on two adult male bottlenose dolphins (Tursiops truncatus Montagu) (

Table 1. Morphometrics of dolphins (Tursiops truncatus) tested.

Dolphin	Length (m)	Mass (kg)	Fluke Span (m)	Fluke Chord (m)	Fluke Area (m2)
Primo	2.41	181.5	0.67	0.21	0.094
Puka	2.46	205.5	0.68	0.23	0.110

), which were maintained at the Long Marine Laboratory at the University of California Santa Cruz. The animals were measured for their body mass, length, fluke span, fluke chord, and fluke area. Measurements of the flukes were determined from scaled planar photographs of the flukes. The fluke chord was measured at the base of the flukes as the linear distance from leading to trailing edge. The dolphins were held in a large, outdoor, marine pool (15.2 m × 9.1 m × 4.0 m). There were four underwater viewing windows (1.4 m × 1.2 m) along one side of the pool.

Dolphins were trained to perform a tail stand within a sheet of microbubbles. As previously explained [7], microbubbles were generated from a compressed air source (i.e., SCUBA tank) that was forced into a finely porous hose. The hose was located at the bottom of the pool, about 1 m from the pool wall. The hose was held within a metal guide, which weighted the hose and kept it straight. The microbubbles were initially less than 1 mm in diameter, though there was some coalescence as they rose to the surface. The bubble sheet was oriented parallel to an underwater viewing window. The bubble sheet extended from the bottom of the pool to the surface with a length of 6.2 m and a thickness of 2 cm.

Under trainer control, each dolphin executed a series of tail stands. The dolphin aligned itself in the bubble sheet so that its dorsoventral tail motions remained in line with the sheet. The height of the tail stand was controlled by the trainer. The dolphin would raise itself up to a float target at the end of a pole that was held above the dolphin’s rostral tip (Figure 1). The height out of the water was at or above the position of the center of mass (CM), which was located at the anterior insertion of the dorsal fin, about 41% of body length [18]. The dolphin held its position above the surface of the water without a noticeable change in height for a period of 2 s. The height above the water was measured using the eye as a marker, as the tip of the rostrum was not always oriented vertically.

2.2. Bubble DPIV

The size and density of the microbubble sheet provided sufficient resolution for DPIV relative to the dimensions and speed of movements of the dolphins [7,19,20]. A Redlake MotionPro X3 high-speed video camera recorded the movements of the microbubbles through the underwater viewing window as the microbubbles were displaced by strokes of the dolphin’s flukes. The camera had nominally 1000 × 1000 pixel resolution and could frame at rates up to 1000 frames per second at full resolution. The 2D velocity fields, due to the displacements of the microbubbles, were computed with DPIV software. This is a technique in which tracer images—microbubbles in this case—are tracked from one video frame to the next using standard cross-correlation techniques applied to an array of small, square interrogation windows. In-house software was used in this study and a previous study [7] as described by Hsu and Hsu et al. [21,22].

The microbubbles generated in this study were slightly positively buoyant. This resulted in a small, uniform upward velocity component in the flow measurements due to the bubble rise velocity. This was essentially a constant “dc” velocity superimposed on the true flow velocity. By taking data without the dolphins present, this mean rise velocity was measured and subtracted from the dolphin swimming measurements. Because the rise velocity was uniform and constant across the entire field of view, there was no artificial circulation (see following paragraph) added to the measurements.

Using the underwater, high-speed video, the stroke cycle frequency (f, Hz) and the amplitude of heave (A, m) were measured. The frequency was the inverse of the period of a stroke cycle. The amplitude of heave was the horizontal distance traversed by the trailing edge of the flukes for one half-stroke cycle. For comparison between the two test dolphins and with data from other studies, a length-specific amplitude was calculated as A/L, where L is the body length of the dolphin.

2.3. Thrust Calculations

For the tail stand, the motion of the flukes is similar to an oscillating finite wing canted at an angle of attack. The flukes generate lift that is in-line to the longitudinal axis of the body. The anterior body of the dolphin is held out of the water by the lift force, which equals the weight not supported by buoyancy.

Oscillations of hydrofoils like the dolphin’s flukes produced pairs of counter-rotating vortices in a reverse Karman vortex street, as determined by the direction of motion of the flukes [3]. By defining and integrating around a closed contour around the core of each vortex, the circulation, Γ, which is proportional to the lift, was calculated:

Γ = ∫V • ds,

(1)

where V are the velocities around the contour and ds are the corresponding differential tangent vectors on the contour. Circulation at a vector location was calculated by summing the calculated vorticity, ∂u/∂y − ∂v/∂x, at that location multiplied by the differential area of the grid element; this is a standard application of Stoke’s theorem covered in an introductory fluid mechanics text. The total circulation of a vortex was calculated by summing the individual circulations over a rectangular region containing the vortex. The height and width of the grid were varied to ensure that the largest circulation value was found; increasing or decreasing the area would result in a lower circulation value. For ease of calculation, a square contour aligned with the coordinate directions was chosen to simplify the integration. The size of the contour was chosen to be small enough to capture the vortex core—that is, excluding the outer region of the vortex where diffusion and dissipation of vorticity would yield a reduced vortex strength—yet large enough to ensure accurate integration. A sensitivity analysis of size and placement of the contour is provided in Legac [23].

The average V_tail was determined by measuring the maximum distance traveled by the flukes during each half stroke multiplied by the number of half strokes in each direction divided by the total time for those strokes. The V_max was the maximum speed of the flukes moving across the axis of the body in 0.5–0.10 s. For these measurements, a non-zero value of Γ implied the existence of a thrust-producing vortex.

Thrust production was determined from the vortex strength for small-amplitude swimming [7]. Making the first-order approximation that the flukes were simple two-dimensional hydrofoils, the Kutta–Joukowski theorem related Γ and thrust, T, produced by the dolphin:

T = ρΓV_tailb,

(2)

where V_tail is the dorsoventral velocity of the tail, perpendicular to the longitudinal axis of the body, ρ is the fluid density (1024 kg·m⁻³ for seawater), and b is the span of the dolphin’s flukes. To avoid errors in momentum estimation due to the use of PIV, analysis was performed on sequences in which the vortex ring cross-sections were circular [24].

Instantaneous thrust was computed using circulation and V_max. This is the thrust generated for one stroke. The average thrust was computed using circulation and average V_tail. This is better thought of as the instantaneous thrust scaled by the fraction of time the dolphin’s tail is acting as a hydrofoil.

T was also computed using aerodynamic theory according the equation:

T = 0.5ρAC_LV_tail²,

(3)

where A is the planar surface area of the flukes and C_L is the lift coefficient. C_L was based on the cross-sectional geometry of the flukes of a T. truncatus with respect to the angle of attack and was obtained from Fish et al. [25]. It should be noted here that the term lift coefficient, C_L, in this context is actually a thrust coefficient. As discussed in Fish et al. [7], the “lift” generated by the lateral motion of the tail is along the axis of the dolphin’s body (i.e., in the thrust direction). Because C_L is the commonly accepted designation for wings, it is used here. The angle of attack was measured from video images taken during mid-stroke as the angle between the fluke chord and the horizontal.

A Sony Digital 8 Handycam (HDR SR11; 10.2 megapixel resolution, Sony, Tokyo, Japan) camera was used to collect video on the height above the water attained by the dolphin during a tail stand. The camera was positioned on the far side of the pool, approximately 9 m from the dolphin.

To maintain vertical position during a tail stand (Figure 2), all the forces of the system must sum to zero as:

T + F_b − W = 0,

(4)

where F_b is the buoyant upward force and W is the weight of the dolphin. In this configuration, the thrust, T, generated by the tail movements balances the proportion of the dolphin’s weight that is above the water surface and thus the weight minus the buoyant force, F_b:

T = W − F_b.

(5)

F_b is equal to the mass of water displaced by the submerged portion of the body (m_sub) times the acceleration due to gravity (g; 9.8 m·s⁻²):

F_b = m_sub·g.

(6)

The proportion of the dolphin’s weight that is above the surface of the water, and therefore the thrust, required to maintain height is:

T = h/L·W,

(7)

in which h is the height of the rostral tip above the surface of the water (Figure 2). As h increases, T will increase linearly and F_b will decrease (Figure 2). When fully submerged (h < 0), F_b will approximate the weight of the dolphin, whereas if dolphin can hold its body out of the water h ≈ L, the thrust from the flukes will nearly equal the weight of the animal.

2.4. Statistical Analysis

Variation about means was expressed as ± one standard deviation (SD). All least-squares regressions and correlation coefficients, r, were calculated using KaleidaGraph software (version 4.03, Synergy Software, Reading, PA, USA). Correlation coefficients were determined to be statistically significant at a level of p < 0.05.

3. Results

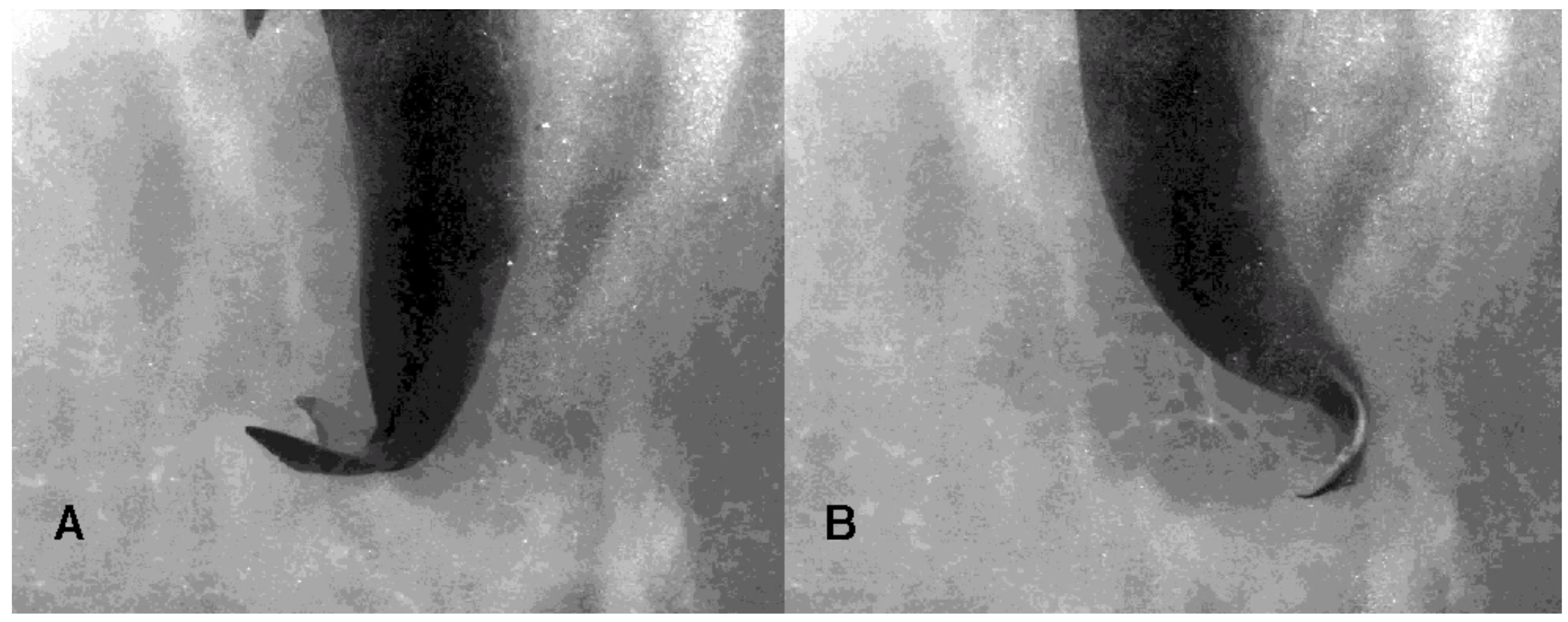
3.1. Tail Stand

A total of 51 separate trials were made by the two dolphins (28 and 23 trials for Primo and Puka, respectively), with morphometrics of the two dolphins are provided in Table 1. Relative to the vertical position of the eye above the surface of the water, the dolphins performed tail stands with the position of the eye at 0.74 ± 0.16 m above the surface of the water. The mean proportion of body mass of the dolphins supported above the water during the tail stands was 0.5 ± 0.1, which is equivalent to a weight of 906.7 ± 214.8 N. For the six trials that were examined with bubble DPIV and aerodynamic analysis, the mean weight supported above the surface of the water was 882.2 ± 165.7 N.

The majority of trials were discarded because the dolphin did not center itself on the bubble sheet, maintain a vertical position, or have the fluke stroke perpendicular to the camera. Only six trials were considered acceptable. In these trials, the flukes oscillated dorsoventrally in a sculling motion. On the downstroke, the ventral side of the flukes faced downward and was canted at a slight positive angle to the horizontal, whereas on the upstroke, the flukes were flipped so that the dorsal side of the flukes faced downward and was canted with a slight positive angle to the horizontal. Considerable spanwise bending of the flukes was observed as the flukes moved through the stroke across the axis of the body, whereas chordwise bending was noted at the transitions in direction change (Figure 2). The mean f was 2.70 ± 0.12 Hz. The mean A was 0.82 ± 0.04 m, which gave an A/L of 0.34 ± 0.02.

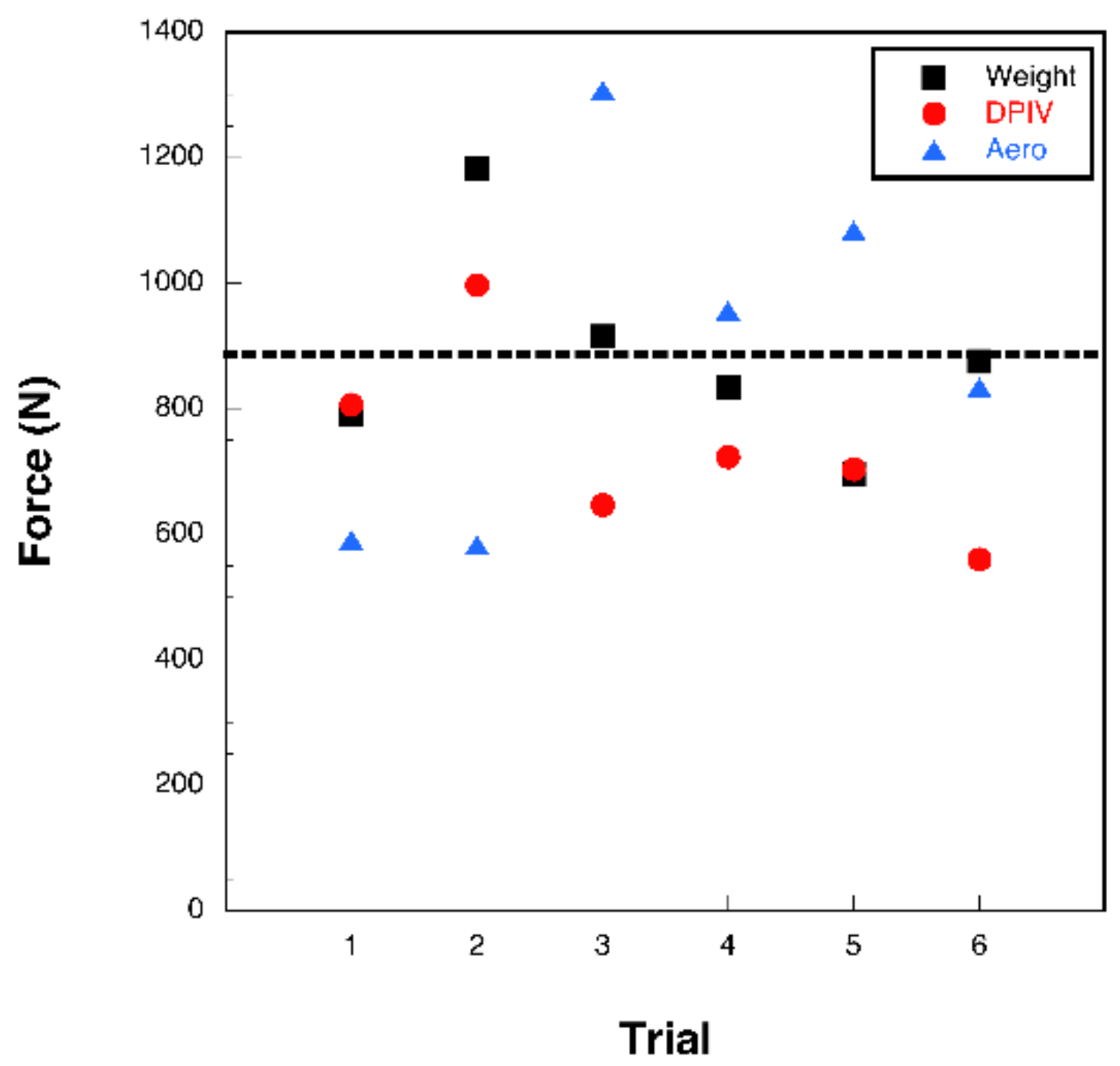
3.2. Bubble DPIV

The oscillatory motions of the flukes produced pairs of counter-rotating vortices with a jet flow that were ejected downward into the wake throughout each propulsive cycle. One vortex was generated at the end of each half stroke as the flukes reversed direction. The vortex was shed from the trailing edge of the flukes (Figure 3).

The mean values for the average (V_tail) and maximum (V_max) velocities of the flukes were 3.03 ± 0.47 m·s⁻¹ and 4.16 ± 0.52 m·s⁻¹, respectively. The mean circulation in the vortices generated by the flukes was 0.370 ± 0.136 m²·s⁻¹, as computed from Equation (1).

Application of the Kutta–Joukowski theorem on measured vortex circulations yielded average thrust varying from 560.0 to 997.3 N with a mean value of 739.7 ± 137.8 N. The percent difference between the computed thrust of the individual trails compared to the weight supported out of the water varied from 1.3% to 36.0% with an average of 16%. In two cases, the difference between the weight supported out of the water and thrust estimated varied only by 1.3% and 1.8%.

The calculated thrust increased linearly with increasing weight supported above the water surface (Figure 4) according to the regression equation:

T = 242.94 + 0.56 W.

(8)

The r value for the regression equation was 0.62.

The average thrust-to-weight ratio was 0.4. The range of thrust values corresponded to mechanical power outputs of 1555.0–2616.5 W. As the percentage of adult body mass comprising the locomotor muscles of dolphins was found to be 25.7% [26], the maximum mass-specific muscle power output then was 27.5–52.4 W·kg⁻¹. These values were within the range of power outputs for vertebrate muscle [27,28] and were consistent with the values measured by bubble DPIV for freely swimming dolphins [7].

3.3. Aerodynamic Analysis

As the flukes were swept through the stroke cycle, the angle of attack varied from 12.0° to 17.0° with a mean of 14.7 ± 1.8°. Such high angles of attack without stall are possible for oscillating foils until the angle exceeds 30° [29]. Using V_tail with Equation (3), the average thrust varied from 582.3 to 1306.6 N with a mean value of 892.1 ± 283.8 N. The thrust based on aerodynamic analysis was 20.6% higher than the average thrust computed from bubble DPIV (Figure 5). Comparisons of the thrust calculated from the aerodynamic analysis for individual trials differed on average from the associated weight supported during tail stands by 32.4% (Figure 5).

4. Discussion

Cetaceans (whales, dolphins, porpoises) are extremely energetic, powerful, and fast swimmers [7,30,31]. The mechanics of swimming by cetaceans entails propulsive lift-based oscillatory movements of the caudal flukes [7,32,33]. The flukes are lateral extensions from the tail of cetaceans with a wing-like planform and symmetrical cross-sectional profile. Estimation of force generated by the motion of the flukes for swimming dolphins has long been debated. The problem has been that early indirect estimates of force production for dolphins resulted in low values that could not be validated [7,34,35].

A simple computational approach led to the erroneous “Gray’s Paradox” [34,35]. The paradox resulted from a miscalculation in which the drag power (i.e., thrust power) for a dolphin to swim at high speed was considered to be higher than the maximum power output from the available propulsive muscle mass [34]. The only resolution to the paradox was to consider the boundary layer to be laminar, producing a low frictional drag. This conclusion was asserted despite a high Reynolds number for the dolphin indicating turbulent flow. Review of the assertions that were the basis for Gray’s Paradox demonstrated that high muscle power output and high thrust power were possible for swimming dolphins [35].

Early experiments undertaken by Rosen [9] to visualize the flow around a dolphin included photographs of vortices in the spray of a leaping dolphin, attaching a dye patch on the head, having the dolphin swim through a two-dimensional screen of negatively buoyant plastic particles, and having the dolphin swim along a screen of bubbles. The latter experiment did not provide satisfactory results, as the bubble were too buoyant due to their size (≤3.0 mm). The rate of rise by the bubbles (0.3–0.5 m/s) could not be subtracted at the time from the flow induced by the dolphin.

The use of the direct method of bubble DPIV has inherent interest as a technique to resolve controversies regarding the swimming performance of dolphins. A study by Fish et al. [7] using bubble DPIV indicated high thrust production for free-swimming dolphins. However, the technique had not been fully validated in a controlled experiment. Examination of the tail stand with bubble DPIV provided a unique set of circumstances to measure the effectiveness of the technique. For the tail stand, the oscillatory motion of the flukes is analogous to a finite wing moving back and forth horizontally in the water at an angle of attack. With each transit, the flukes (or wing) generates lift. The motion of the flukes is perpendicular to the axis of the body, and the “lift” vector (thrust) generated by the flukes therefore points along the body axis toward the head. This lift force, in turn, holds the dolphin up out of the water.

On average, bubble DPIV slightly underestimated the thrust necessary to support the weight of a dolphin performing a tail stand. However, some estimates of thrust corresponded tightly with the weight of the dolphin above the waterline. In comparison to estimates of thrust production based on the aerodynamic analysis, the bubble DPIV demonstrated greater accuracy. However, potential observational errors may have occurred to limit the accuracy of the technique. The cameras were not synchronized. Therefore, the exact video frames for measurement of thrust and the height of the dolphin above the surface of the water may not have exactly coincided. However, the data for both thrust and height were obtained when the animal had reached its maximum height. In addition, measurement of the exact height of the dolphin may have been affected by the motions of the dolphin in producing small waves, which would limit an exact measurement of the distance between the eye and the surface of the water. Another potential error was in the estimation of the center of mass of the specific dolphins examined in this study. The center of mass was determined from published results as a proportion of body length [18]. Lastly, the dolphins had to maintain an exact position and orientation in the bubble curtain to capture the vorticity for thrust calculations. This error was limited by choosing only those trials in which the dolphin maintained the proper position above the bubble curtain. This requirement reduced the number of suitable tests for examination to approximately 12% of all trials. The orientation within the bubble curtain was important in limiting three-dimensional effects. Such three-dimensional considerations may be dealt with in future tests with the application of volumetric DPIV as used to study swimming by fish and squid [36,37,38].

The use of thrust estimates from the aerodynamic analysis has more severe potential errors. The aerodynamic analysis was quasi-steady. The angle of attack of the flukes was determined from still images as the flukes crossed the longitudinal axis. Through the stroke cycle, the angle of attack would change particularly at transitions from upstroke to downstroke and vice versa. Such changes would affect the lift coefficient. The lift coefficient itself was based on a flat, rigid fluke with a symmetrical foil section. Throughout the stroke, the flukes demonstrated flexibility. Cambering by the flukes [25] and changes in the projected planar area were not incorporated into the aerodynamic calculations. As the bubble DPIV only examines the wake and magnitude of the circulation, changes in angle of attack, cambering, and planar area are already incorporated in the calculations of thrust.

The measurement of f was in the range of values obtained from free-swimming dolphins. Using the regression equation from Fish [33], f for the tail stand was equivalent to a bottlenose dolphin swimming at 5.76 m/s, which is within the range of swimming speeds for dolphins [31]. However, A and A/L were larger than values for steady-swimming bottlenose dolphins [7,33]. Dolphins swimming steadily typically have an A/L of 0.15–0.2, whereas the A/L for the tail stand was 70–127% larger. However, A/L of the tail stand was within the range of 0.20–0.50 for large-amplitude strokes [39]. These large-amplitude strokes are associated with accelerations at the start of horizontal swims and at the beginning of the descent and ascent phases of dives. It is evident that the kinematics of the tail stand are similar to the stroke used for accelerations as an unsteady form of locomotion.

A surprising result of the examination of hydrodynamic tail stand of dolphins is the similarity with the hovering flight of hummingbirds. In both cases, the propulsive movements of both the wings and flukes direct a downward jet flow and associated vorticity. In both cases, the downward momentum developed from the kinematics of the propulsor must be given to the fluid at a rate equal to the supported weight of the animal [40]. In hovering flight, with the body oriented vertically in a head-up position, the hummingbird beats its wings horizontally [41,42]. In the downstroke, the wings move through the air at a positive angle of attack with the dorsum of the wing oriented upward. On the upstroke, the wing rotates along its length at the wrist so that the ventral surface is directed upward as it is reciprocated in the opposite horizontal direction with a positive or near-zero angle of attack [41,42,43]. These movements were similar to the actions of the dolphin flukes, which were flipped as the flukes were transitioned between the up- and downstrokes.

Despite the similarity of tail stands in water by dolphins and hovering in air by hummingbirds, flow visualization indicates differences in the mechanics of support within the respective fluids. The vorticity shed by the oscillations of the flukes is generated as a reverse Kármán (thrust-type) vortex street [3]. The vortex street is produced as bound vortices are shed from the oscillating flukes at each half stroke as the direction of the flukes is reversed. The vortices are convected downward producing a staggered array of vortices with opposite spin with a downward jet flow centered within the vortex street. This pattern represents a symmetrical generation of thrust (i.e., lift) between the upstroke and downstroke. On the other hand, the thrust (i.e., lift) for hovering hummingbirds is asymmetrically generated. The stopping vortex at the end of the upstroke and starting vortex at the beginning of the downstroke merge into one [44]. The downstroke was determined to be stronger than the upstroke and to support 66–75% of the weight of the bird [45,46]. This asymmetry produced a pulsed vortex wake that is composed of a single merged vortex ring or bilateral vortex loop [44,45,46]. The difference in the wake structure between hovering hummingbirds and tail stands in dolphins reflects differences in the forces being developed by each species [47].

5. Conclusions

The results of bubble DPIV demonstrated that the fluke motions generated high levels of sustained force, which was roughly equal to the dolphin’s weight supported above the surface of the water during a tail stand. Bubble DPIV, therefore, validated high forces measured previously from bubble PIV for thrust generated in free swimming. This technique can be used in aquarium settings and potentially in the field to visualize flow fields and calculate thrust production for large swimming animals. Furthermore, the physics of high-energy maneuvers, such as the tail stand, has engineering application for understanding ballistic performance across the air/water interface.