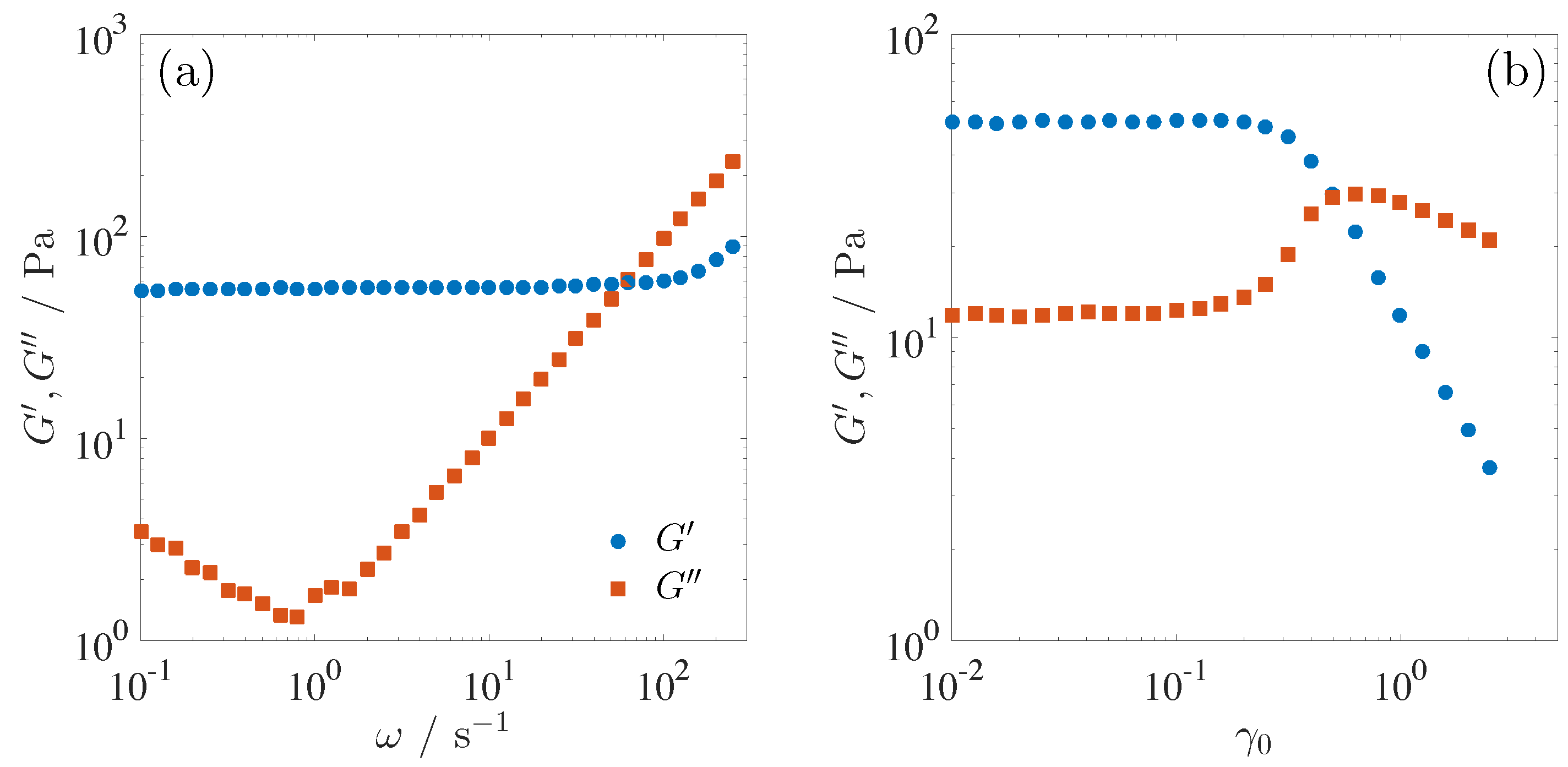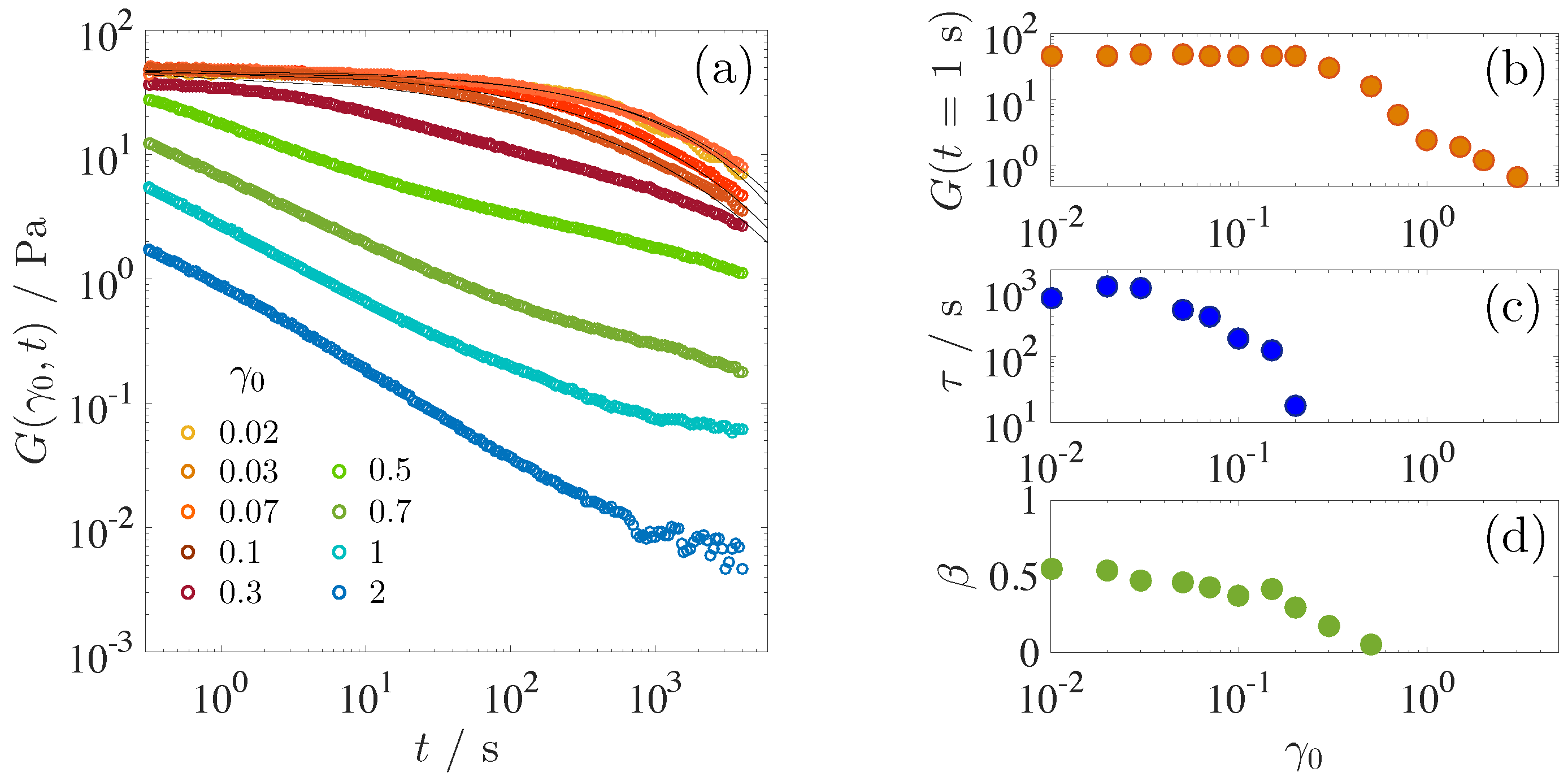2.1. Phase Behavior
Cholesteryl oleyl carbonate (COC) is known to have BPIII between chiral nematic and isotropic phase. Here, we confirm the existence of BPIII and identify the transition temperature in COC.
Figure 1 shows the temperature dependence of the viscosity at
= 1 s
. Shear viscosity obtained during cooling and heating process are shown. During cooling process, the viscosity increases at
T = 35.9
C and shows a peak at 34.8
C. On the other hand, during heating process, the viscosity steeply increases at
T = 34.8
C and shows the peak at 35.1
C. After the increase, the viscosity decreases and coincides with that during the cooling process. Similar viscosity curve for COC was presented by some researchers [
30,
31]. The steep increase in the viscosity during cooling and heating process is attributed to the formation of BPs [
14,
15]. As Henrich et al. presented in their numerical simulation, the viscous stress response of BPs is significantly affected by the deformation of the disclination lines in BPs [
18]. The increase in the viscosity is therefore a characteristic feature of the formation of BPs with disclination networks. It is expected that not only BPIII but also BPI and BPII show the increase of the viscosity when they are formed from isotropic and chiral nematic phases [
14,
15].
Polarized microscope images at different temperatures show dark images at
T = 35.9
C. As temperature decreases, the uniform dark texture becomes gradually brighter, as Taushanoff et al. also observed in their BPIII system [
32]. When the temperature is lowered below
T = 34.8
C, oily streaks which are a typical defect line for the cholesteric phase appears. In general, BPIII shows no platelet texture, which is often observed in many BPI and BPII systems with ordered alignment of DTCs, and it is considered BPIII shows a dark blue texture. However, absence of the platelet texture and dark blue texture do not always indicate the formation of BPIII, as Kim and Chien presented [
22]. Chien et al. provided an accurate method to distinguish BPIII from other BPs by observing optical activity [
21,
24,
25].
Figure 2 shows polarized microscope image at
T = 35.1
C. Image in the center was taken under crossed polarizers, while images on left and right sides were taken at deviation angle between the analyzer and polarizer of
= ±4
by following the method established by Chien’s group [
21,
24]. Under crossed polarizers, the dark blue image is observed as other BPIII system shows [
33]. Deviation of the angle results in the observation of different color due to the optical activity of BP [
21,
22]. The color becomes greenish blue and brownish for positive and negative
, which is similar to the observation of BPIII by Kim and Chien [
22]. Appearance of the optical activity is a sign of the formation of BP. In
Figure 1, the brightness of the polarized microscope image suddenly increases at
T = 34.8
C, which might correspond to a transition into BPII or BPI. Actually, Kim et al. also observed BPI without the platelet texture. To identify the phase exactly, it is necessary to perform a measurement of the reflection spectra, as Kim et al. established [
22]. It seems that the dark image with the optical activity shown in
Figure 2 indicates the formation of BPIII in the temperature range of 35.0
C <
T < 35.9
C. In the following, all experiments were carried out at
T = 35.1
C.
2.2. Linear Rheology
Here, we show that BPIII is an elastic phase and its viscoelasticity resembles soft solid-like materials. We first present the dynamic shear moduli measurement in the linear range ( = 0.03). In addition, we show the strain amplitude dependence of the dynamic moduli as a fundamental property of the nonlinear viscoelasticity.
Figure 3a shows the linear dynamic shear moduli as a function of the angular frequency
measured under small amplitude oscillatory shear (
= 0.03) at
T = 35.1
C. Strain amplitude dependence of the dynamic shear moduli at
= 10 s
is shown in
Figure 3b. The storage shear modulus
shows a plateau modulus
= 54 Pa and is larger than the loss shear modulus
in a wide range of
. Another feature is an increase in
at low
, indicating the existence of a certain relaxation mode below
= 0.1 s
. However, we could not detect the terminal relaxation time within the experimental window of the frequency. Similar viscoelastic properties, the existence of the plateau modulus and slow relaxation have been reported for soft solid-like materials such as concentrated emulsion, silica suspensions and biopolymer network systems [
34,
35,
36]. Soft solid-like behavior has been similarly reported for BPI [
14,
15].
Reminiscent behavior of the soft solid-like materials is also seen in the strain amplitude
dependence of the shear moduli [
34,
35,
36,
37,
38,
39]. At low
, the shear moduli are independent of
, indicating the linear viscoelasticity. As the
increases, however, the loss modulus
shows a strain hardening above
= 0.2 followed by a strain thinning, while the storage modulus
shows a strain thinning behavior. Hyun et al. and Sim et al. qualitatively explained the strain amplitude dependence of the dynamic moduli using a network model composed of segments and junctions [
40,
41]. In the network model, a segment can be regarded as a macromolecular chain or a microstructure connecting junctions. Junctions are nodes where intermolecular interactions are localized such as a crosslinking point. The network model qualitatively predicts that the strain hardening of
is derived from the dynamic balance between the destruction and creation of the network junctions. In the case of the BPIII, the disclination line and their connection at nodal points play a role of the segment and junction in the network model. Under the oscillatory shear deformation, disclination network of the BPIII will be repeatedly broken and created, depending on their destruction and creation rates as Henrich et al. numerically presented for BPI [
18]. Although the structural cause of the strain hardening behavior of
depends on the type of the soft matter and their microstructure, the strain amplitude dependence of the dynamic moduli is closely related to the structural rearrangement as qualitatively predicted by the network model. Raghavan et al. reported that the strain hardening behavior of the flocculated suspensions of a fumed silica occurs when a destruction of the network linkage and resultant change in the flock size appear [
42]. Parthasarathy et al. also explained the strain hardening of an electrorheological fluid in terms of a flow-induced microstructural rearrangement [
43]. They suggested that the hardening of
is originated from a viscous dissipation due to slight rearrangement of unstable cluster. Increase in the strain amplitude causes large scale rearrangement which results in the visco-plastic behavior, i.e., decrease of
.
In analogy with these qualitative explanations for the overshoot of
, nonlinear viscoelasticity of the BPIII in
Figure 3b also arises from the flow-induced structural rearrangement through the fracture of the disclination networks. The overshoot of
in the BPIII is related to the increase of the viscous dissipation produced by the breakage of the disclination networks.
2.3. Nonlinear Dynamic Behavior
As the strain hardening behavior of suggests, nonlinear viscoelasticity of the BPIII is mediated by the rearrangement of the disclination networks. In this section, we present nonlinear viscoelastic behavior under large amplitude oscillatory shear (LAOS) and classify them into two regimes: weak and strong nonlinear regimes. Here, we evaluate the nonlinearity only with the complex shear modulus instead of and , because the phase lag cannot be defined in the nonlinear regime.
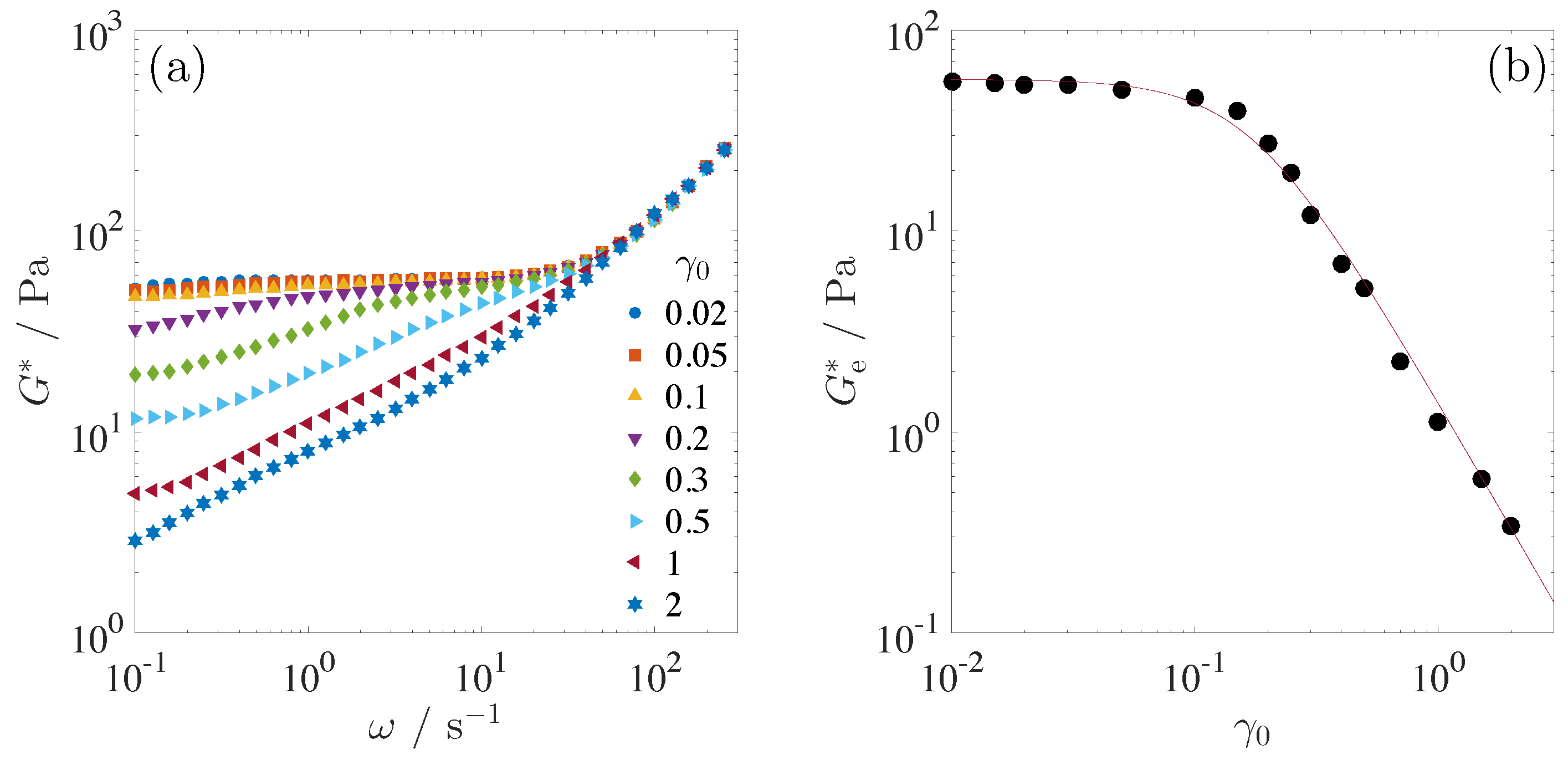
Figure 4a shows angular frequency dependence of the complex shear modulus
measured under LAOS at
T = 35.1
C. For small strain amplitudes,
0.1,
is insensitive to the strain amplitude
and approximately collapses onto the same curve. Viscoelasticity is therefore in the linear regime at low
, as shown in
Figure 3b. Beyond the strain amplitude
= 0.2,
in low
region decreases with
. Despite the occurrence of the nonlinearity,
has a second plateau modulus at around
0.1 s
, suggesting that some elastic feature remains even under LAOS. This second plateau modulus at low
might be a reminiscent of the elastic structure of the BPIII in the quiescent state. Further increase in
decreases the second plateau modulus, and eventually above
= 2, the second plateau modulus disappears, indicating the loss of the elastic structure.
at
= 0.1 s
is utilized as a nonlinear shear modulus
under LAOS. In the
dependence of
(
Figure 4b),
remains independent of
at
0.1 but decreases at
0.2. In the comparison with the shear moduli shown in
Figure 3b, the nonlinear behavior appears at almost the same strain amplitude.
Based on above results, nonlinear viscoelasticity of the BPIII can thus be classified into two regimes: a weak nonlinear regime in the strain amplitude range of 0.2
1 where some elastic structure remains even under LAOS, and a strong nonlinear regime at
2 where the elastic structure is broken up. The threshold strain amplitude
between the weak and strong nonlinear regions is
2.0, and the plateau modulus at the threshold strain amplitude is approximately
3 Pa. Following a simple argument for the isotropic materials such as entangled polymers [
5], it can be shown that the shear modulus scales as
, where
l is a characteristic length scale of disclination networks. Using
3 Pa at
0.1 s
, this leads to an estimate of
110 nm. Under the oscillatory shear, it is expected that the disclination network breaks up and reconnects between nearest neighbors. Therefore, this characteristic length
110 nm might be considered as an average mesh size of the disclination networks that can be reconnected under the oscillatory shear. In other words, the disclination networks destructed under the oscillatory shear can partly recombine in the weak nonlinear regime, while it is difficult to keep the network structure in the strong nonlinear regime. A softening of the BPIII under LAOS suggests that the fracture of the disclination network leads the nonlinearity.
2.4. Nonlinear Relaxation Modulus
In this section, we summarize experimental results on the step shear experiments, which provide insights into a stress relaxation mechanism of the BPIII. We show that the increase of the step strain amplitude changes the stress relaxation behavior. We consider the origin of the nonlinearity from the view point of the fracture of the disclination networks.
A series of the relaxation moduli measured under various step strains in the range 0.02
2.0 are shown in
Figure 5a. Solid curves are the best fit to stretched exponential function;
with a pre-factor
, relaxation time
and exponent
. Relaxation moduli at low strains
0.1 are well fitted with the stretched exponential function as shown in
Figure 5a. However, the stretched exponential function is not applicable to the data at large strain
> 0.1. As
increases, the functional form of the relaxation modulus deviates from the exponential-like function and gradually changes to the power law-like decay in which a characteristic time is not defined. At
= 2.0, the relaxation modulus exhibits the power law decay. The power law decay is generally indicative of the poly-dispersity of the relaxation time. It should be noticed that nonlinear shear modulus
at
= 2.0 has no plateau modulus in the whole frequency region (
Figure 4a). Absence of the elastic components under LAOS at
= 2.0 is attributed to the fractured disclination networks. Power law decay therefore indicates that the disclination networks are fractured into many domains with different sizes.
Figure 5b–d shows values of the relaxation modulus at
t = 1 s, the fitted results for the relaxation time
and the stretched exponent
, respectively. Similar to the strain amplitude dependence of
(
Figure 4b), the relaxation modulus at
t = 1 s is constant at low
but decreases above
= 0.2, which is the same as the threshold strain amplitude in LAOS. On the contrary, the relaxation time
decreases with
even in the linear viscoelastic regime before the nonlinearity appears above
= 0.2. Stretched exponent
, a measure of the relaxation time distribution, also decreases with
, reflecting a broadening of the relaxation time. These results indicate that the step strain induces structural realignment even in the linear viscoelastic regime.
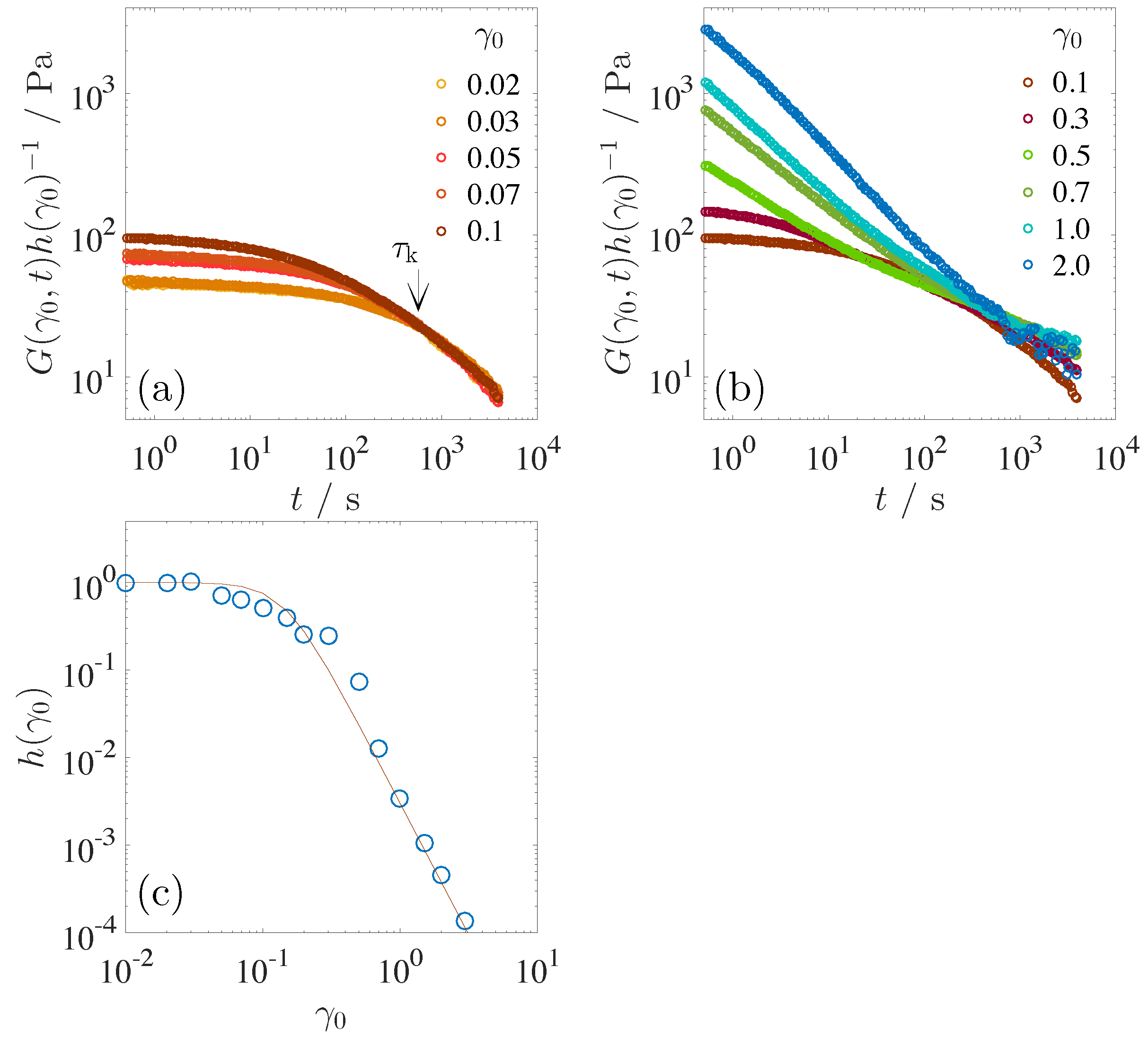
Figure 6a,b shows the relaxation modulus reduced by a damping function
. The damping function is defined as
=
. Here,
is a linear relaxation modulus. At lower step strains
0.1, the relaxation curves at long time region after time
630 s collapse to a single curve, independent of the applied step strain, as shown in
Figure 6a. Superposition of the relaxation modulus curves by a vertical shift indicates that time–strain separability holds in a relaxation process after
[
5]. Before
, on the other hand, the time–strain separability is not satisfied. According to the vertical shift of the relaxation modulus in the time domain of
t >
, the damping function
is introduced as a shift factor. Contrary to the relaxation moduli at lower step strains, the relaxation moduli under large step strain are not collapsed to the single curve even after the reduction with
(
Figure 6b). As mentioned before, the functional form of the relaxation modulus changes from the stretched exponential to the power law decay with
because of the fracture of the disclination networks. The variation of the functional form with
violates the time–strain separability over a broad time range.
The corresponding damping function
is shown in
Figure 6c. BPIII shows a linear response up to
= 0.03, since
is constant. In the step strain range of 0.03 <
< 0.3,
decreases even though this step strain range belongs to the linear viscoelastic regime, as shown in
Figure 5b. Formation of the master curve after
indicates that the disclination networks are not yet fractured in this strain region but significantly deformed. We should mention that the damping function obtained in
Figure 6c is imperfect because of the violation of the time–strain separability at large strain.
Step shear deformation orients the disclination networks, resulting in a finite stress from the resistance of line tension of the disclinations. At small enough strain amplitude where it is assumed that the disclination networks undergo an affine deformation and are not expected to breakup, it will retain a finite amount of stress. The stress relaxes when the disclination networks return to its equilibrium state on the relaxation time scale ∼
. Thus, the macroscopic stress in the linear viscoelastic regime is originated from the orientation of the disclination networks. Decrease of
and
suggests that the deformation of the disclination networks is non-affine. In entangled polymer systems,
is a measure of the local chain contraction. Time–strain separability, the formation of single master curve after
, is confirmed to hold even for a high step strain above
= 10 [
44]. It should be noticed that the violation of the time–strain separability over the whole time range does not occur in the entangled polymer system. The violation is unique phenomenon in the BPIII.
in the BPIII might also be considered as a characteristic time for the contraction of the oriented disclination networks. Steep decrease of
above
= 0.3 indicates the softening of the BPIII, which is the fracture. As presented in the previous section, the weak nonlinearity induced by local fracture of the disclination networks initiates at
0.2.
These experimental findings under large step strain; the broadening of the relaxation time produced by breaking up of the structure, the variation of the functional form of the relaxation modulus, and the violation of the time–strain separability, are plausibly accounted for by the fracture of the disclination networks.
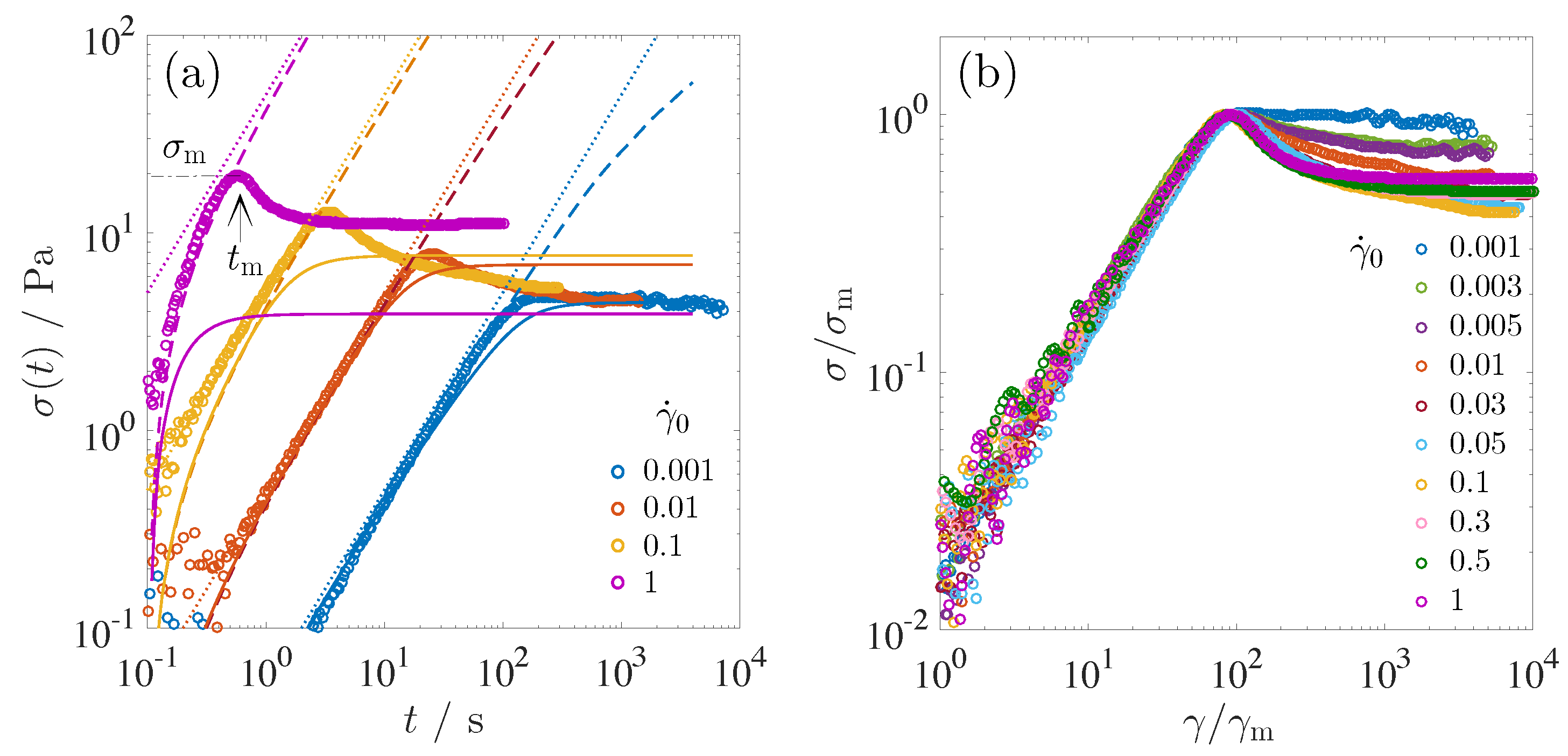
2.5. Stress Growth Behavior
Transient response under step strain deformation shows linear and nonlinear response depending on the step strain amplitude. Not only the step shear deformation but also a continuous accumulation of the shear strain induces the structural deformation and break up. In particular, the orientation and fracture of the disclination networks continuously appears during the accumulation of the shear strain. In this section, we present the stress growth behavior under a constant shear rate and explore the fracture behavior.
Stress growth experiments are performed by applying a constant shear rate at time
t = 0.
Figure 7a shows representative stress growth behavior at
= 0.001, 0.01, 0.1 and 1 s
. In the transient behavior at the lowest shear rate
= 0.001 s
,
increases linearly with time toward a steady state. As the shear rate is increased, the stress growth behavior is characterized by a stress overshoot with a maximum value
at
t =
. It is known that such stress overshoot often occurs when the imposed shear rate exceeds over a terminal relaxation time [
5]. It should be noted that the stress overshoot is observed when the applied shear rate exceeds over the reciprocal of
,
≃ 0.0016 s
. As mentioned in the previous section,
would correspond to the contraction time of the oriented disclination lines. If so, the separability time
in the BPIII can be a criterion for the appearance of the stress overshoot. Beyond the shear rate faster than
, the disclination networks in the BPIII will undergo excessive orientation before it adapts to the shear flow. The appearance of the stress overshoot at
>
supports that
is a characteristic time for the orientation relaxation of the disclination networks.
As shown by dotted lines, the initial linear growth behavior at
= 0.001, 0.01 and 0.1 s
is given by
, where
is the plateau modulus (=54 Pa) shown in
Figure 3. However, at
= 1 s
, the initial stress growth obviously deviates from the linear viscoelasticity behavior
. We explain the viscoelastic stress response using a K-BKZ formulation [
45,
46]:
In the linear viscoleasticity regime where
= 1, the stress can be found analytically as
where the relaxation modulus with the stretched exponential functional form (Equation (
1)) is substituted into Equation (
3). Equation (
3) (dashed lines) well describes the experimental data at
= 1 s
without any fitting parameters. Therefore the BPIII initially undergoes a purely elastic deformation. We also try to describe the whole viscoelastic stress response including nonlinear behavior using K-BKZ equation (Equation (
2)). Here, substituting the damping function
fitted to the experimental data in
Figure 6c into Equation (
2) and integrating numerically, we obtain the solid lines in
Figure 7a. Stress response at
= 0.001 s
is well described by K-BKZ equation, and the steady state value of the stress is also consistent with the experimental data. At
= 0.01 s
, K-BKZ equation coincides with the experimental data only in the elastic deformation region. K-BKZ equation deviates from
before the stress overshoot. As the shear rate further increases, disagreement of K-BKZ equation with the stress growth curves becomes larger. Failure of the prediction is attributed to the variation of the functional form of the relaxation modulus, which drastically changes with the step strain (
Figure 6a,b).
The corresponding normalized stress responses
are shown as a function of the normalized strain
in
Figure 7b.
collapse onto a single master curve only in the elastic deformation regime. As mentioned previously, BPIII undergoes purely elastic deformation in the initial linear growth. Deviation of each curve at
is thus associated with the rearrangement and fracture of the disclination networks.
This stress overshoot phenomenon is resembles the yield behavior of soft glassy materials such as emulsions, microgels, and colloidal suspensions [
34,
37,
39]. The soft glassy materials show the soft solid-like property at rest, and they turn liquid-like above the yield stress. In these materials, the stress overshoot is a sign of the yield stress. The soft glassy materials are characterized by jammed state of microstructures which are in structurally disordered arrangement. In the case of the BPIII, the disclination networks first show the elastic response in the initial linear growth of the stress. As the shear strain is accumulated, the disclination network undergoes the orientation. Eventually, the oriented network will break up at the stress maximum and reach to the steady state by flowing. It would be interesting to investigate if phase transition from BPII to more fluid liquid crystal occurs in the future.
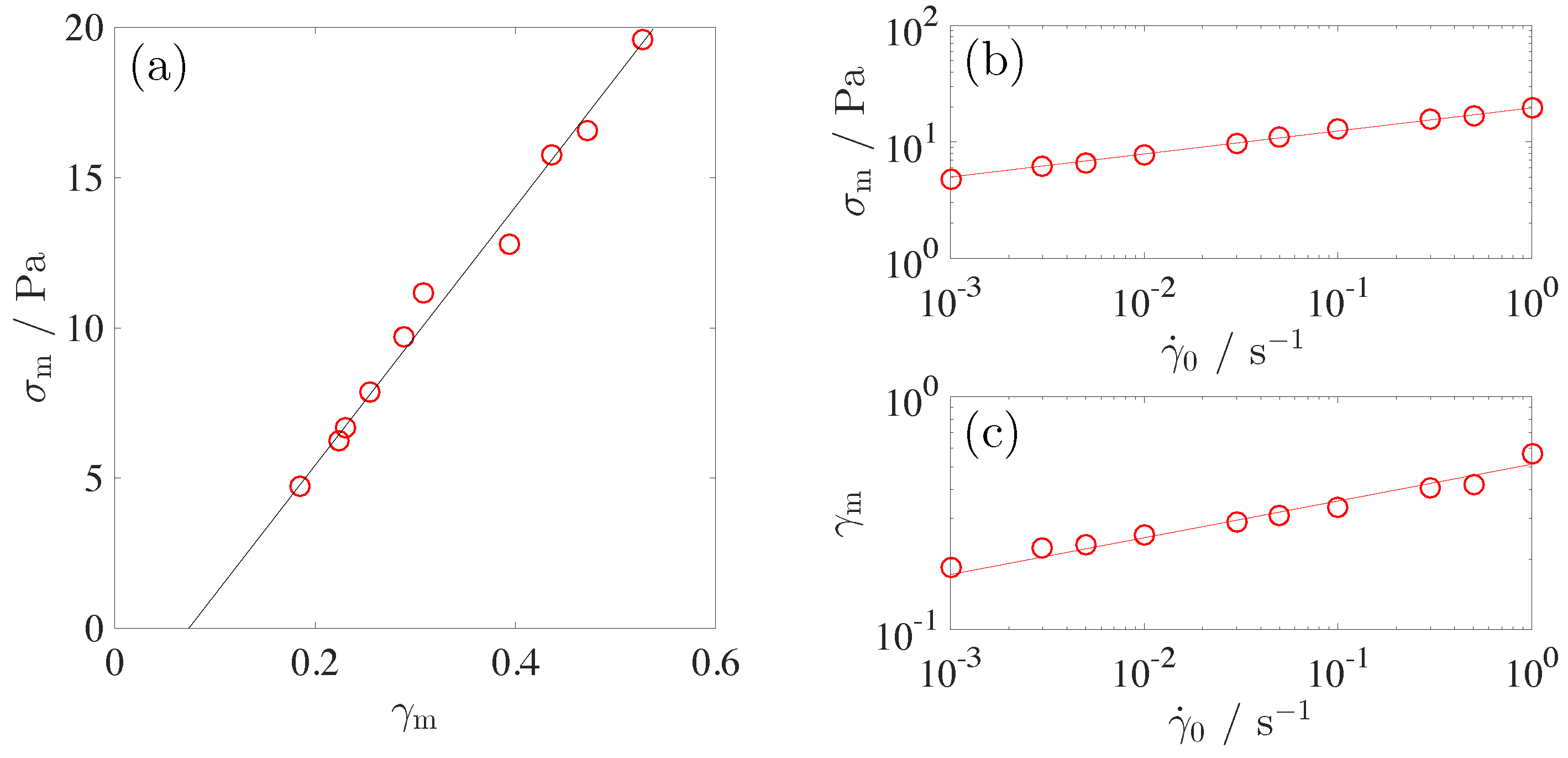
Figure 8 shows that
is a linear function of the strain
=
at the maximum. The slope corresponding to the effective modulus,
=
, is estimated to be
42 Pa, which is softer than its initial state in the linear viscoelasticity regime,
= 54 Pa. The elastic modulus at the yield point
is regarded as a limit value beyond which the disclination networks bearing an external shear deformation begin to break.
Figure 8b,c shows the failure criterion of
and
as a function of the applied shear rate. The stress at the yield point
increases as a weak power law,
= 19.6
. Strain
also shows a power law increase as
= 0.513
. Power law relation suggests that the fracture of the disclination networks delays with
.
Similar scaling behavior of
and
with
has been reported for some colloidal particle systems [
34,
37,
38,
47]. Observed power law exponent varies from system to system. One of the models describing the failure of brittle material such as elastomer and glasses is a fiber-bundle model (FBM) [
48]. Physical origin of the fracture in this model is the accumulation of local failure events. Failure events proceeds with two steps; the first process is immediate breaking which occurs when the stress exceeds the mechanical strength of the fibers, and the second one is a delayed fracture dominated by the rate of damage accumulation. Scaling behavior of
and
with
is presumably explained by assuming the power law dependence of the rate of damage accumulation on the stress.
Upon deformation, each disclination network first suffers an orientation. A strained disclination segment would resist the deformation with the form of a recovery force. The recovery force originates from the elastic resistance of the disclination lines against deformation and increases with accumulated strain. In this simple view of the disclination-mediated rheology, the elastic linear growth of the stress in
Figure 7 reflects the resistance of all disclination segments arisen in response to the shear deformation. However, this simple picture does not explain the shear rate dependences of
and
because the viscoelastic effect is not considered. Deformation of the blue phases is achieved simultaneously by rearrangement of the disclination lines and by realigning the double twist cylinders, which are a viscoelastic matrix with organized structure. Under the continuous deformation, therefore, the viscous force exerted on the disclination lines is produced in the matrix. In other words, the orientation of the disclination lines is supported by the viscous force. In contrast to the recovery force which increases with the orientation of the disclinations, the viscous force decays down as the matrix realigns along the shear flow. A retardation due to the viscous relaxation would lead to the delay effect on the stress overshoot.
If the delayed fracture due to the viscous relaxation is the origin of the power law dependence, creep compliance measurements will provide more detailed fracture behavior. The creep compliance measurement is possible with the use of the stress-controlled rheometer. The delayed fracture behavior with the use of the creep compliance measurement will be the next topic to elucidate the nonlinear viscoelasticity of the BPIII.