Hyperbolic Covariant Coherent Structures in Two Dimensional Flows
Abstract
1. Introduction
2. Covariant Lyapunov Vectors
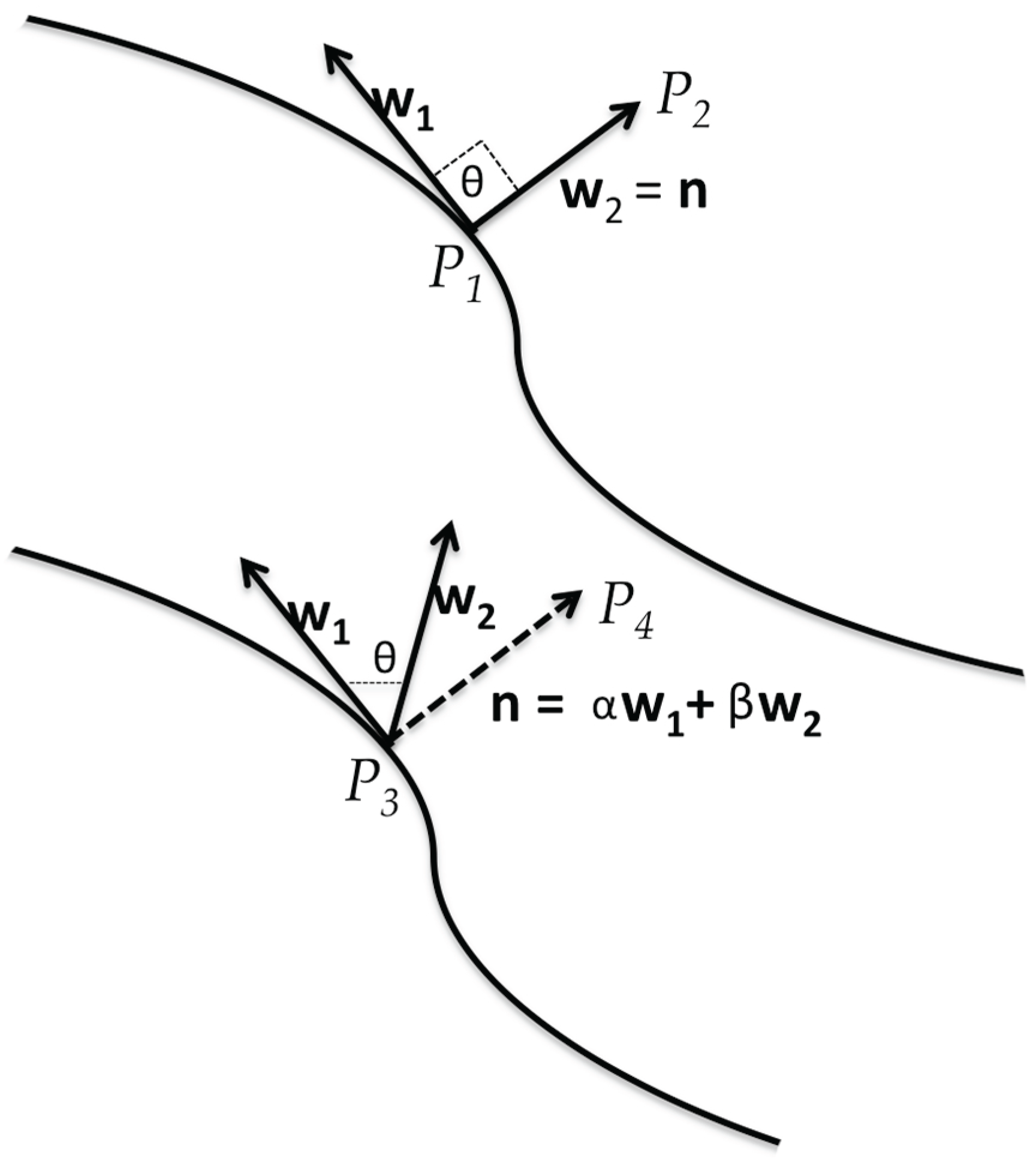
Hyperbolic Covariant Coherent Structures
3. Numerical Examples
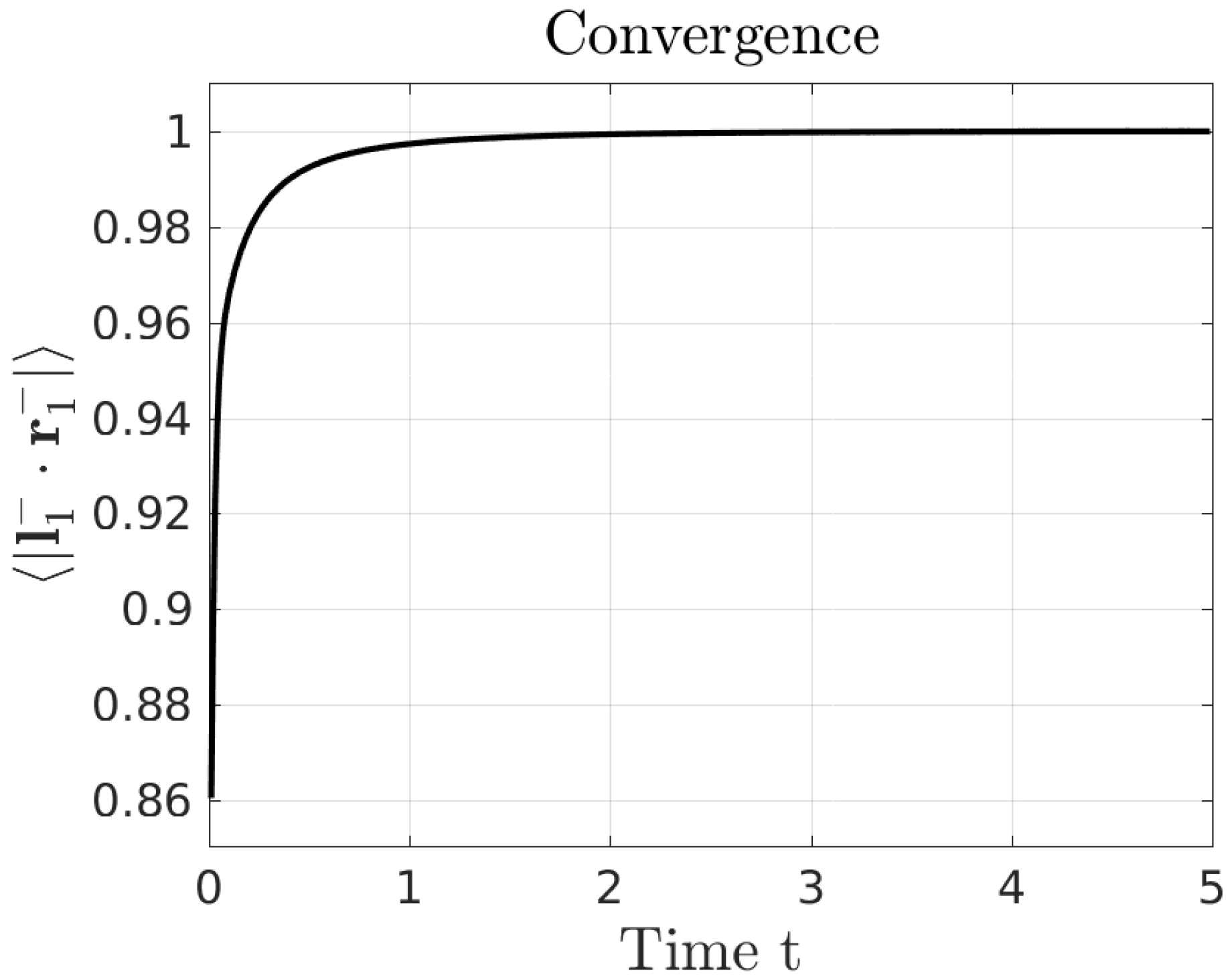
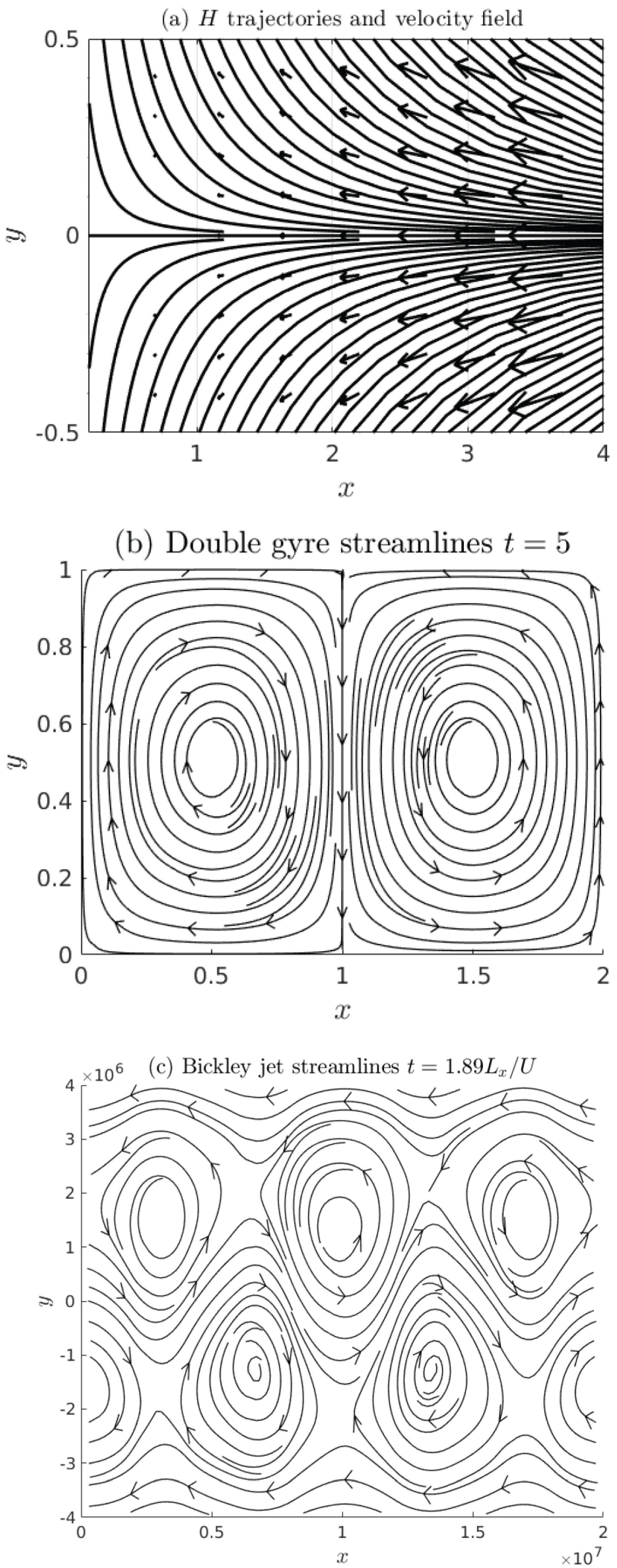
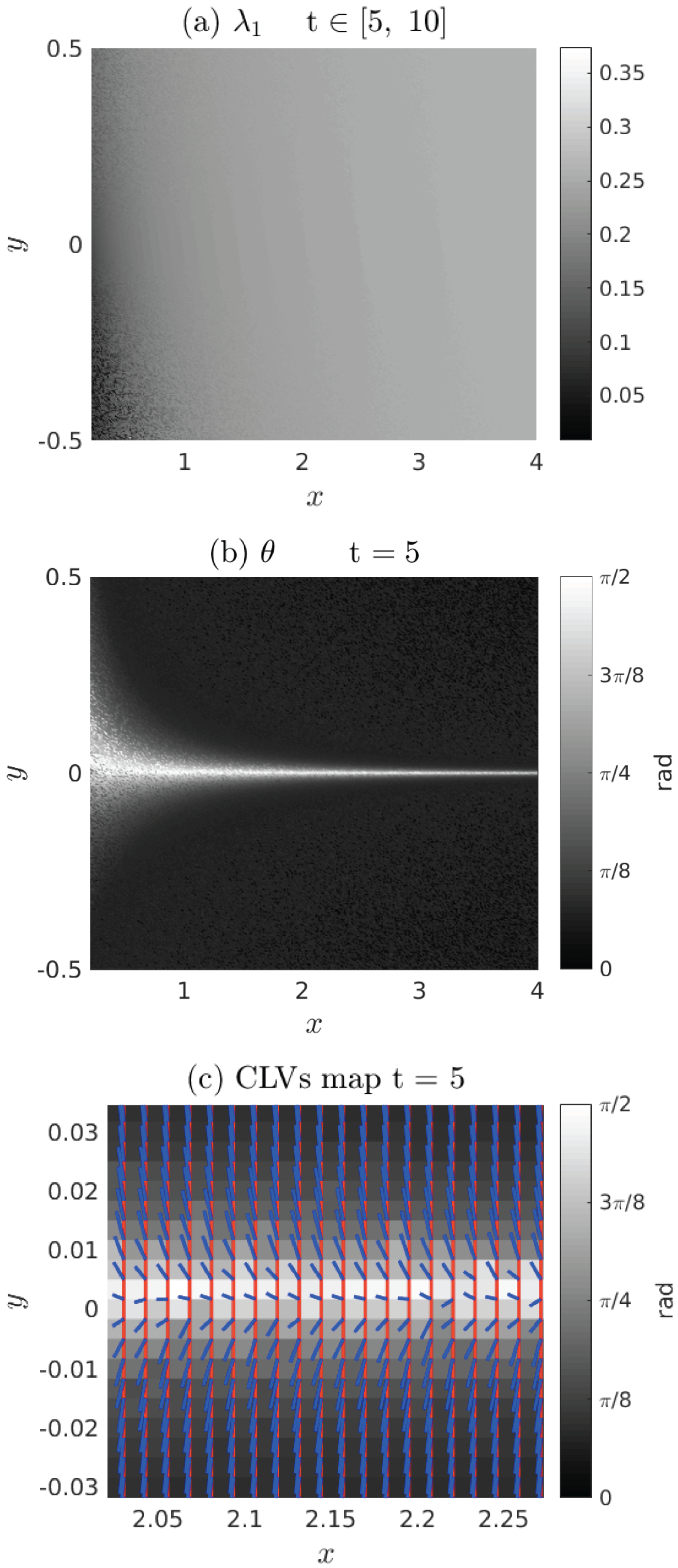
3.1. A Simple Autonomous Hamiltonian System
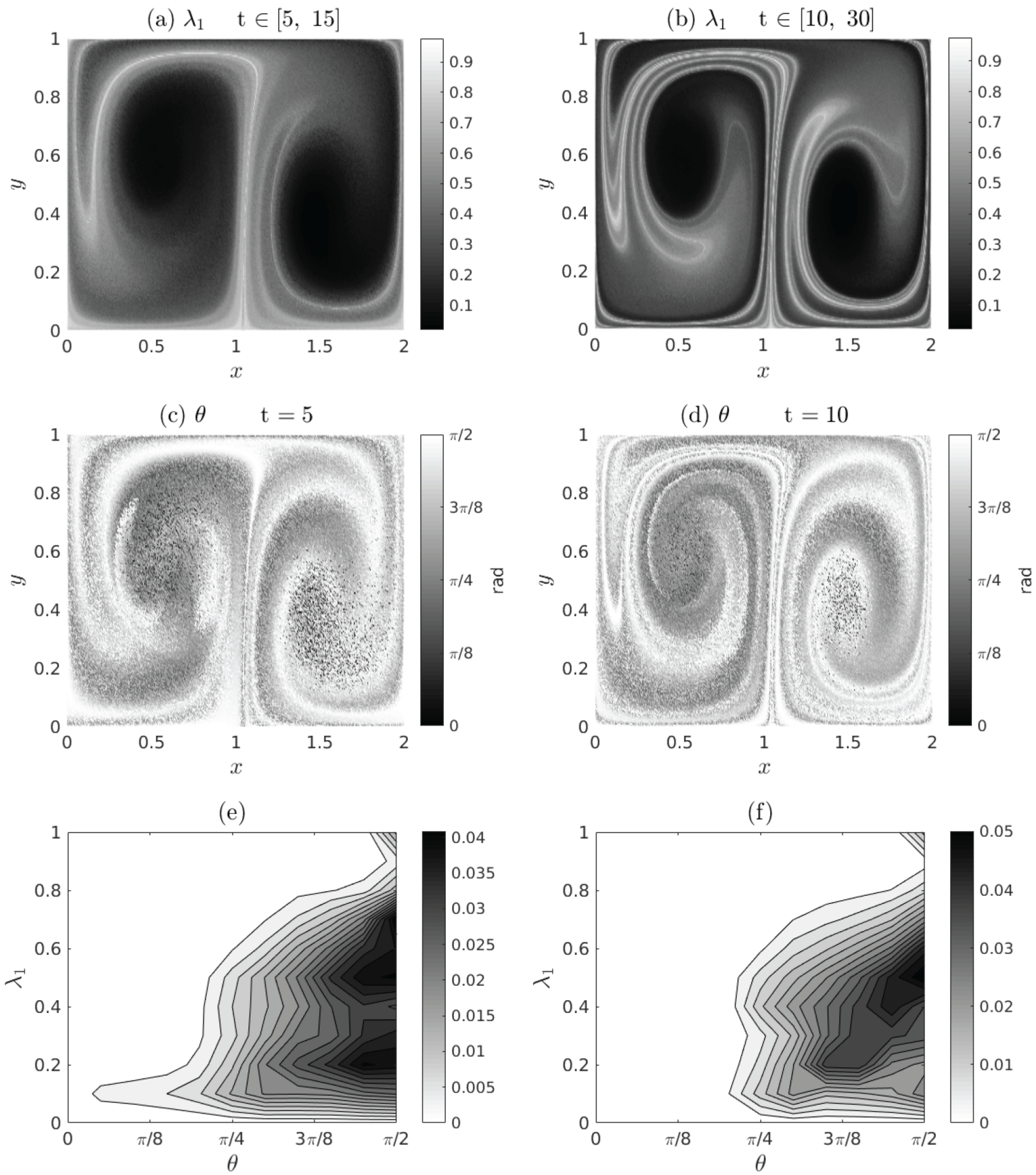
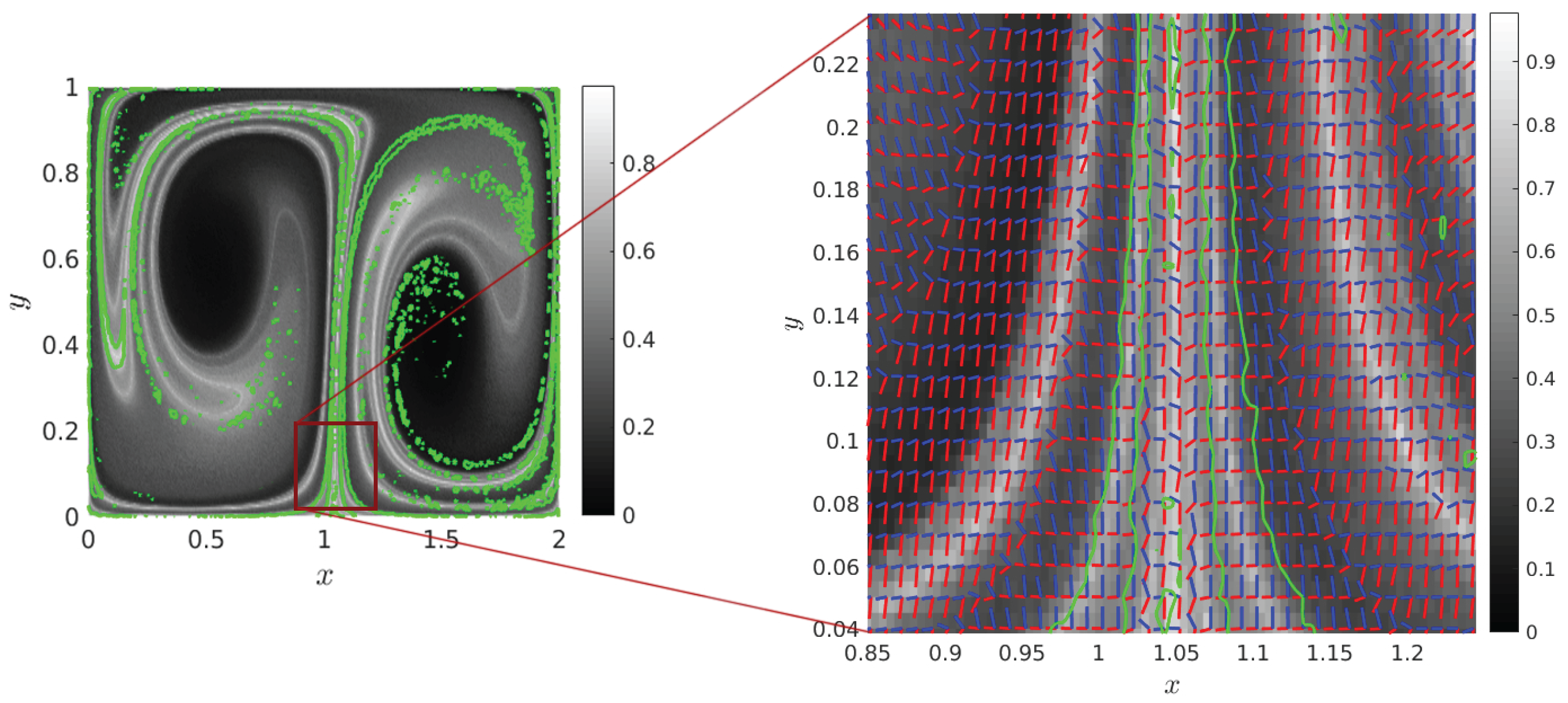
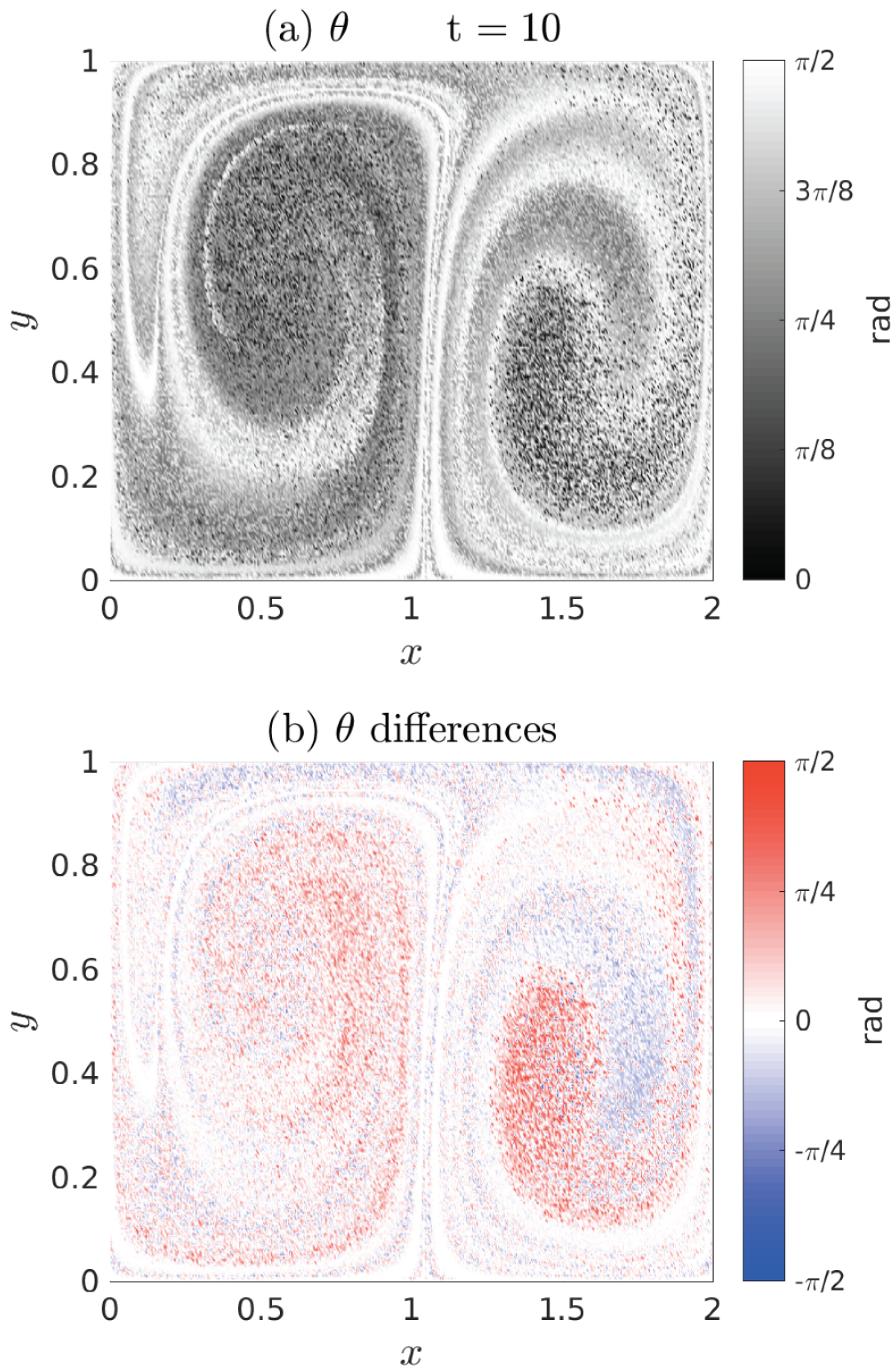
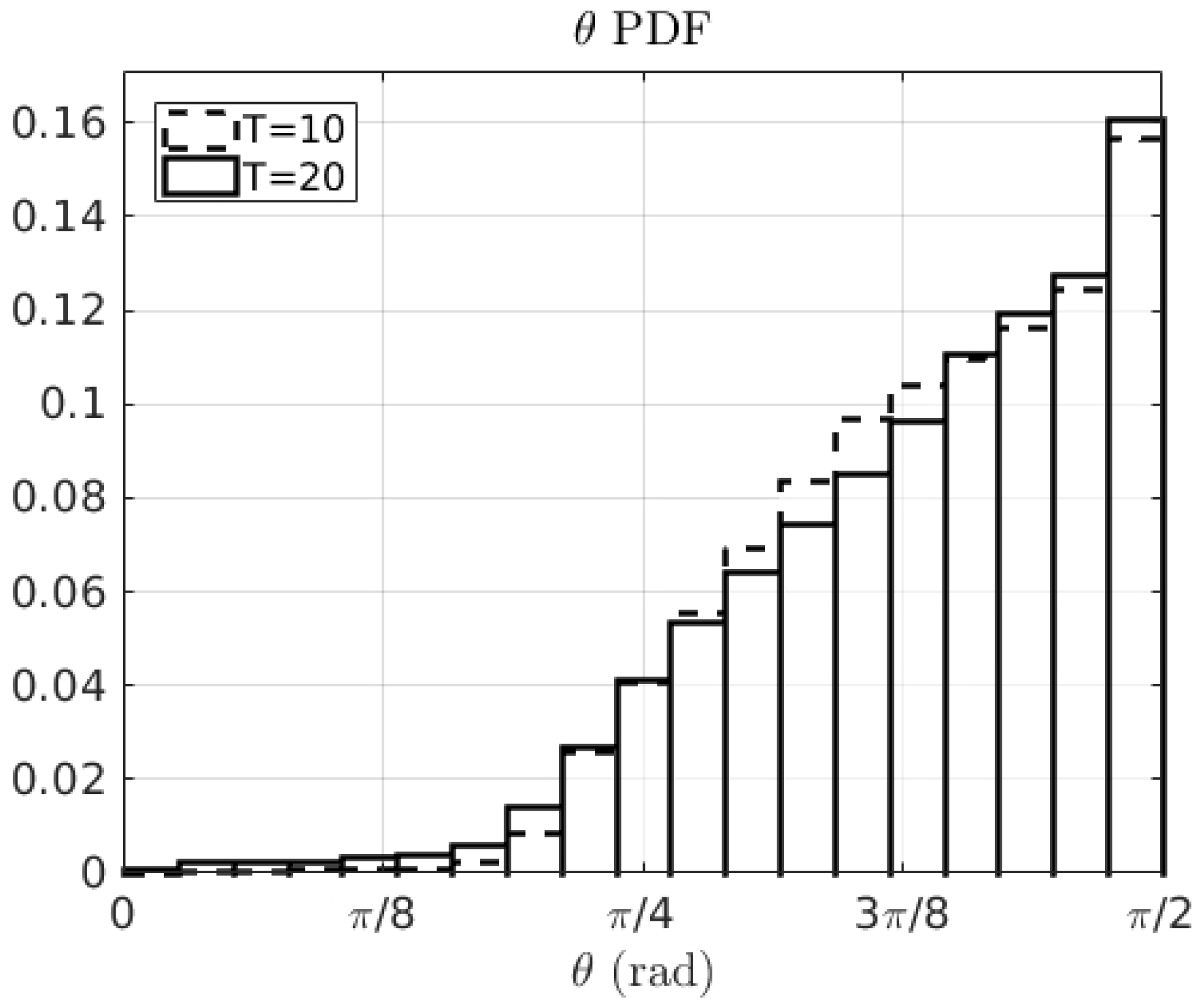
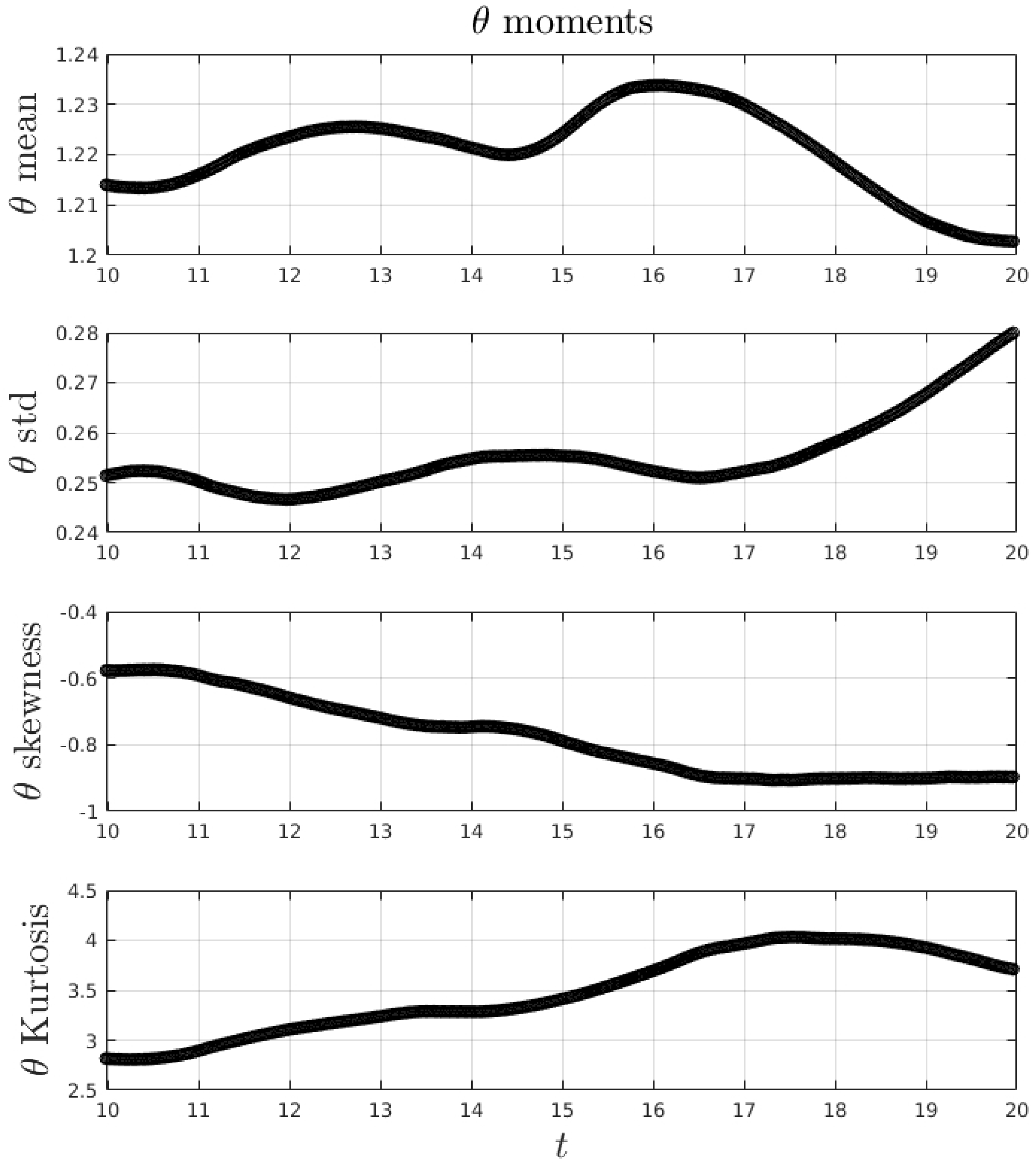
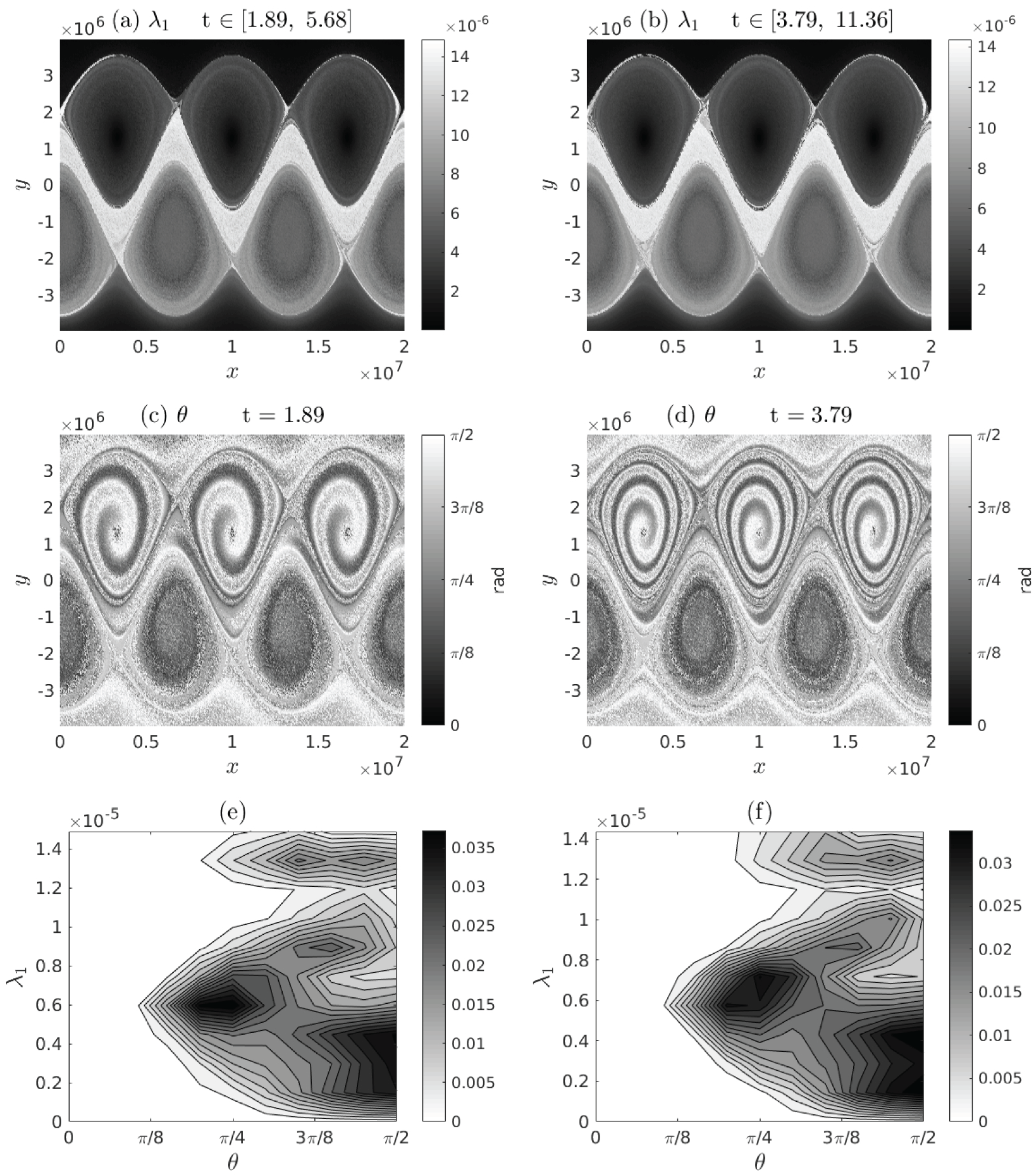
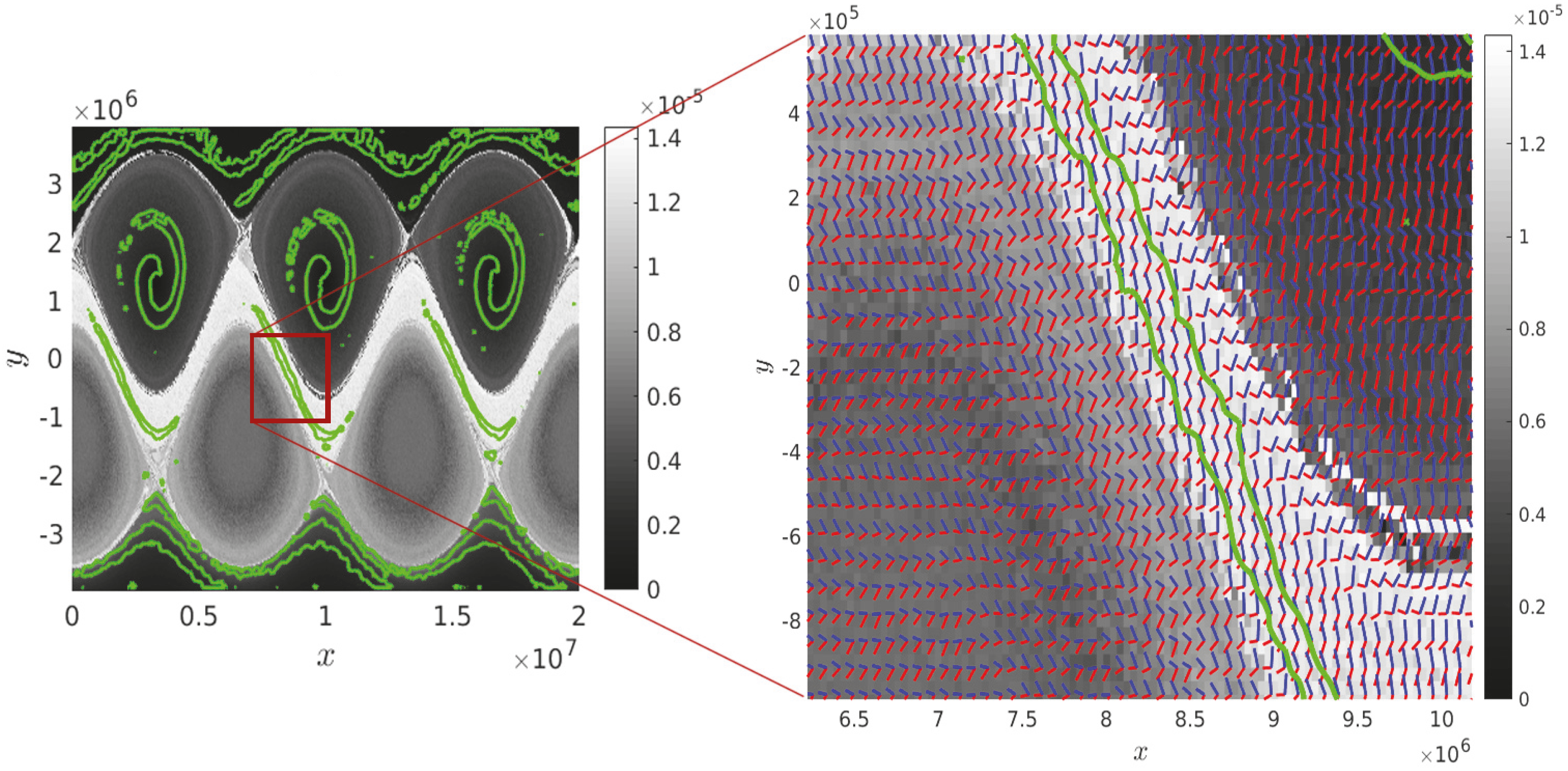
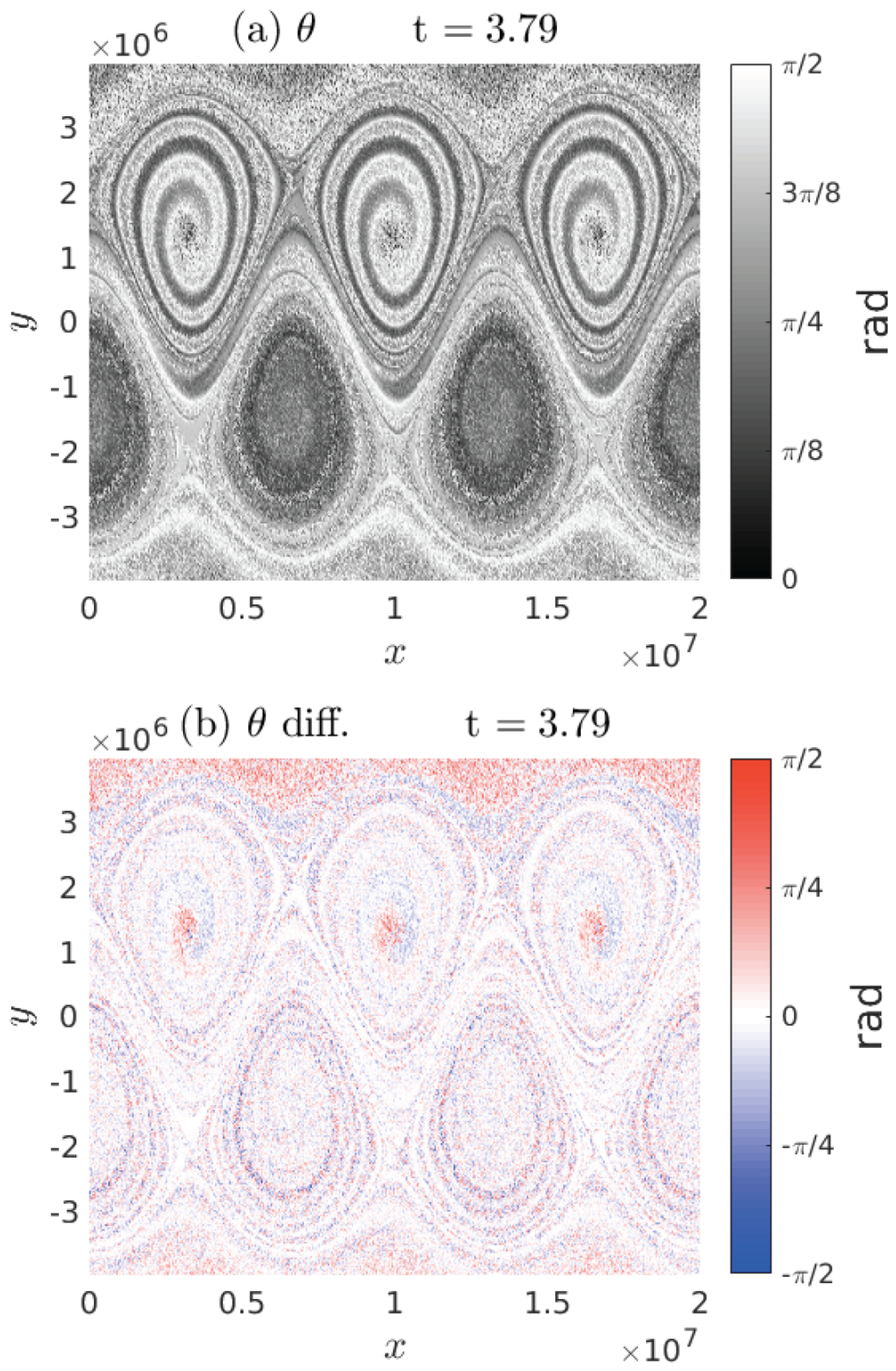
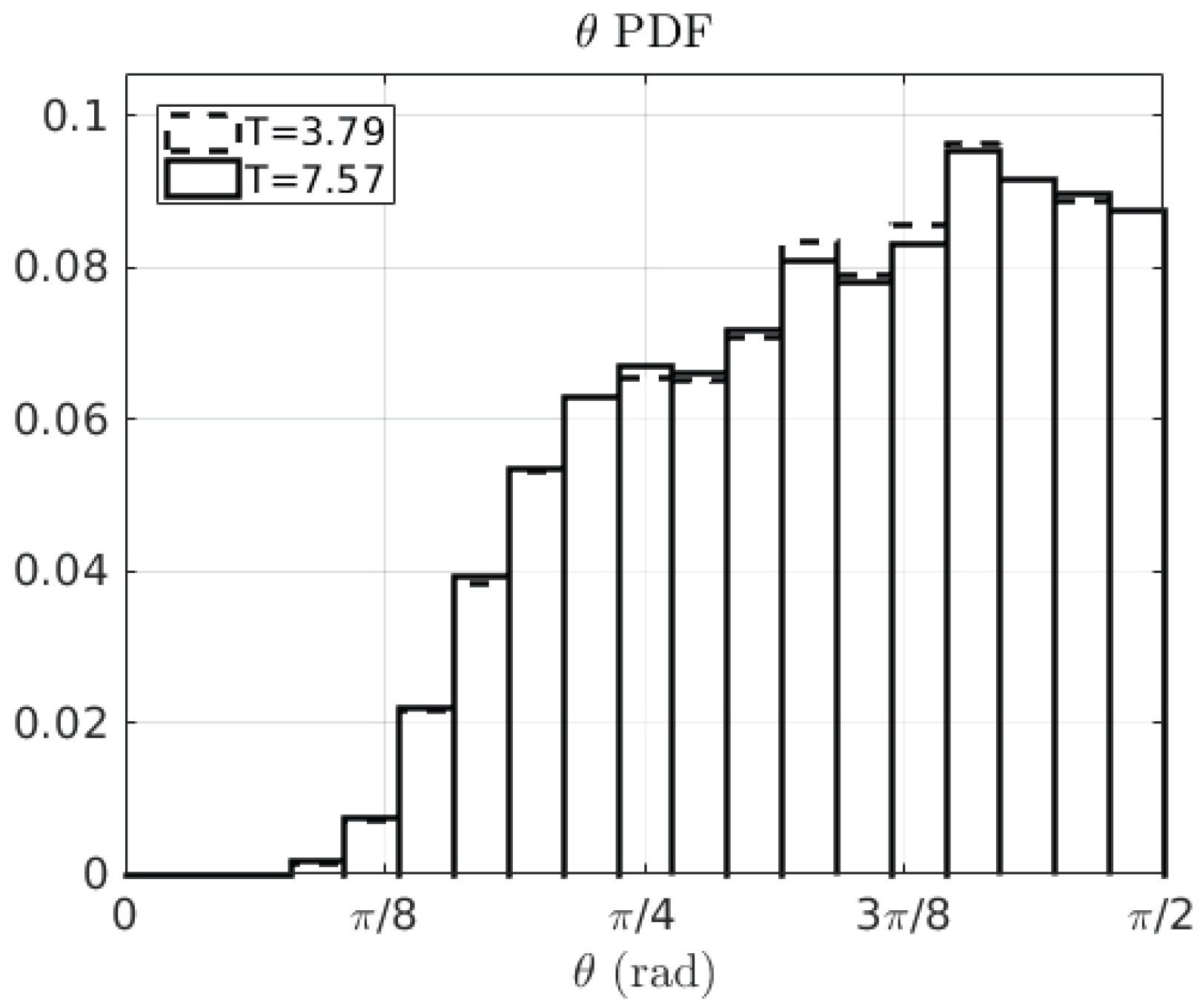
3.2. Double Gyre
3.3. Bickley Jet
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Description of the Algorithm
- Initialization (T1): This preliminary step is used to find the initial backward Lyapunov vector bases for a whole set of initial conditions [73]. A set of initial conditions and two sets of initial orthonormal random bases are defined in the tangent spaces at every point at time . The second set is necessary to check the convergence to the backward Lyapunov vector bases. The initial conditions and the random bases are evolved respectively with Equations (1) and (6) until the convergence of the two bases is reached with the desired accuracy. The convergence toward the Lyapunov vectors is typically exponential in time [51,74]. At every time step, for every initial condition, the evolved vectors are stored as a column of a matrix that is decomposed with a QRdecomposition. The last passage is implemented in order to find the new orthogonal basis at every time step and the upper triangular matrix containing the coefficients that allow one to express the old basis in terms of the new one.
- Forward transition (T2): The backward Lyapunov bases are evolved from time t to . The evolution is done with the help of Equations (1) and (6) and the decomposition for every evolution step. We indicate with the matrix for which columns contain the new bases at time and with the correspondent upper triangular matrix. During this step, both the local Lyapunov bases and upper triangular matrices are stored. The diagonal elements of the upper triangular matrices give information about the local growth rates of the basis vectors at a given time , and they are used to compute the FTLEs as a time average:where N time steps are considered between t and . If the LEs exist, Equation (A1) will converge to them for a sufficiently long evolution. It is worth noting that sometimes the FTLEs are computed using a different method, that is using the so-called Cauchy–Green Tensor (CGT) defined as:This operator is also known as the deformation tensor, whose eigenvalues and eigenvectors satisfy:From a geometric point of view, a set of initial conditions corresponding to the unit sphere is mapped by the dynamics into an ellipsoid, with the principal axis aligned in the direction of the eigenvectors of the CGT and with length determined by the correspondent eigenvalues. The eigenvalues of the CGT determine the FTLEs as:where the dependence to the starting position has here been suppressed. This second method for the computation of the FTLEs exhibits some problems; for example, if just one finite local growth rate is taken into account considering a large time interval, Equation (A4) tends to zero and not to the LEs. The first method should be preferred.
- Forward dynamics (T3): In this step, the trajectories and the bases are further evolved from time to time using Equations (1) and (6). This time interval should grant convergence, during the backward dynamic, to the CLVs. During this step, only the upper triangular matrices are stored and are used to continue the computation of the FTLEs using Equation (A4).
- Backward transition (T4): In this step, random upper triangular matrices are generated for every point of the grid, . These matrices contain the expansion coefficients of a set of two generic vectors (expressed as the column of a matrix) in terms of the bases. Using the stored matrices of Step 3, these matrices are evolved backward in time, until time , using the following relation:where and being the time step between and . This method uses all of the information contained in and not just the diagonal part of the matrix. The diagonal matrices contain the column norm of . Using Equation (A5), it is possible to show [51] that the generic vectors chosen will be aligned with the CLVs. Note that when a trajectory passes close to the tangency of an invariant manifold, the matrices C can be ill-defined, and so, a small amount of noise on the diagonal element of these matrices or an average on the diagonal elements of the neighbor matrices is used to correct the problem.
- Backward dynamics (T5): In this final part of the algorithm, Equation (A5) is used with the matrices of Step 2 to evolve backward the upper triangular matrices , from time to time t. In this phase, the backward Lyapunov bases stored can be used to write the CLVs. The matrix containing in each column the different CLVs at a given point in space and time, , can thus be written as:For a two-dimensional system, the algorithm could be optimized making use of (18). One can follow the first step (T1) of the previous algorithm to find the convergence toward the backward Lyapunov bases in the time interval . After this first step, it is possible to carry out the evolution of the vectors, as in the second step (T2) during the time interval , without saving the triangular matrices. In the same way, it is possible to repeat the step (T1), but for a backward evolution during the time interval to find the forward Lyapunov bases and then continue the backward evolution as in the step (T2) during the time interval . At this stage, it is possible to consider directly the first backward Lyapunov vectors and the second forward Lyapunov vectors in the time interval as the CLVs. In this algorithm, there are just four steps and not five as in the one presented above, but for two times, one has to consider the convergence step (T1), which is more time consuming with respect to Step (T4) or (T5). It should be noted that in this algorithm, the forward and the backward evolutions could be done in parallel. The comparison between this algorithm and the one used for this study is left for future studies.
Appendix B. Technical Details of the Numerical Examples
Appendix B.1. Hamiltonian System
Appendix B.2. Double Gyre
| T1 | T2 | T3 | T4 | T5 | |
|---|---|---|---|---|---|
| DV1 | |||||
| DV2 |
Appendix B.3. Bickley Jet
| T1 | T2 | T3 | T4 | T5 | |
|---|---|---|---|---|---|
| BJ1 | |||||
| BJ2 |
References
- Dombre, T.; Frisch, U.; Greene, J.M.; Hénon, M.; Mehr, A.; Soward, A.M. Chaotic streamlines in the ABC flows. J. Fluid Mech. 1986, 167, 353–391. [Google Scholar] [CrossRef]
- Haller, G. Lagrangian coherent structures. Ann. Rev. Fluid Mech. 2015, 47, 137–162. [Google Scholar] [CrossRef]
- Kelley, D.H.; Allshouse, M.R.; Ouellette, N.T. Lagrangian coherent structures separate dynamically distinct regions in fluid flows. Phys. Rev. E 2013, 88. [Google Scholar] [CrossRef] [PubMed]
- Chian, A.C.L.; Rempel, E.L.; Aulanier, G.; Schmieder, B.; Shadden, S.C.; Welsch, B.T.; Yeates, A.R. Detection of coherent structures in photospheric turbulent flows. Astrophys. J. 2014, 786. [Google Scholar] [CrossRef]
- Pierrehumbert, R.T.; Yang, H. Global chaotic mixing on isentropic surfaces. J. Atmos. Sci. 1993, 50, 2462–2480. [Google Scholar] [CrossRef]
- Doerner, R.; Hübinger, B.; Martienssen, W.; Grossmann, S.; Thomae, S. Stable manifolds and predictability of dynamical systems. Chaos Solitons Fractals 1999, 10, 1759–1782. [Google Scholar]
- Haller, G.; Yuan, G. Lagrangian coherent structures and mixing in two-dimensional turbulence. Phys. D 2000, 147, 352–370. [Google Scholar] [CrossRef]
- Haller, G. Distinguished material surfaces and coherent structures in three-dimensional fluid flows. Phys. D 2001, 149, 248–277. [Google Scholar] [CrossRef]
- Lapeyre, G. Characterization of finite-time Lyapunov exponents and vectors in two-dimensional turbulence. Chaos 2002, 12, 688–698. [Google Scholar] [CrossRef] [PubMed]
- Shadden, S.C.; Lekien, F.; Marsden, J.E. Definition and properties of Lagrangian coherent structures from finite-time Lyapunov exponents in two-dimensional aperiodic flows. Phys. D 2005, 212, 271–304. [Google Scholar] [CrossRef]
- Lekien, F.; Shadden, S.C.; Marsden, J.E. Lagrangian coherent structures in n-dimensional systems. J. Math. Phys. 2007, 48. [Google Scholar] [CrossRef]
- Sulman, M.H.M.; Huntley, H.S.; Lipphardt, B.L., Jr.; kirwan, A.D., Jr. Leaving flatland: Diagnostics for Lagrangian coherent structures in three-dimensional flows. Phys. D 2013, 258, 77–92. [Google Scholar] [CrossRef]
- Rypina, I.I.; Brown, M.G.; Beron-Vera, F.J.; Koçak, H.; Olascoaga, M.J.; Udovydchenkov, I.A. On the Lagrangian dynamics of atmospheric zonal jets and the permeability of the stratospheric Polar Vortex. J. Atmos. Sci. 2007, 64, 3595–3610. [Google Scholar] [CrossRef]
- Rypina, I.I.; Pratt, L.J.; Pullen, J.; Levin, J.; Gordon, A.L. Chaotic Advection in an archipelago. J. Phys. Oceanogr. 2010, 40, 1988–2006. [Google Scholar] [CrossRef]
- Beron-Vera, F.J.; Olascoaga, M.J.; Goni, G.J. Oceanic mesoscale eddies as revealed by Lagrangian coherent structures. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Waugh, D.W.; Abraham, E.R. Stirring in the global surface ocean. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Bettencourt, J.H.; López, C.; Hernández-García, E. Oceanic three-dimensional Lagrangian coherent structures: A study of a mesoscale eddy in the Benguela upwelling region. Ocean Model. 2012, 51, 73–83. [Google Scholar] [CrossRef]
- Harrison, C.S.; Glatzmaier, G.A. Lagrangian coherent structures in the California Current System, sensitivities and limitations. Geophys. Astrophys. Fluid Dyn. 2012, 106, 22–44. [Google Scholar] [CrossRef]
- Waugh, D.W.; Keating, S.R.; Chen, M.L. Diagnosing ocean stirring: comparison of relative dispersion and finite-time Lyapunov exponents. J. Phys. Oceanogr. 2012, 42, 1173–1185. [Google Scholar] [CrossRef]
- Mukiibi, D.; Badin, G.; Serra, N. Three-dimensional chaotic advection by mixed layer baroclinic instabilities. J. Phys. Oceanogr. 2016, 46, 1509–1529. [Google Scholar] [CrossRef]
- Joseph, B.; Legras, B. Relation between kinematic boundaries, stirring, and barriers for the Antarctic polar vortex. J. Atmos. Sci. 2002, 59, 1198–1212. [Google Scholar] [CrossRef]
- D’Ovidio, F.; Fernández, V.; Hernández-García, E.; López, C. Mixing structures in the Mediterranean Sea from finite-size Lyapunov exponents. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Cencini, M.; Vulpiani, A. Finite size Lyapunov exponent: Review on applications. J. Phys. A 2013, 46. [Google Scholar] [CrossRef]
- Karrasch, D.; Haller, G. Do finite-size Lyapunov exponents detect coherent structures? Chaos 2013, 23. [Google Scholar] [CrossRef] [PubMed]
- Karrasch, D. Attracting Lagrangian coherent structures on Riemannian manifolds. Chaos 2015, 25. [Google Scholar] [CrossRef] [PubMed]
- Mancho, A.M.; Wiggins, S.; Curbelo, J.; Mendoza, C. Lagrangian descriptors: A method for revealing phase space structures of general time dependent dynamical systems. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 3530–3557. [Google Scholar] [CrossRef]
- Lopesino, C.; Balibrea-Iniesta, F.; García-Garrido, V.; Wiggins, S.; Mancho, A. A theoretical framework for Lagrangian descriptors. Int. J. Bifurc. Chaos 2017, 27. [Google Scholar] [CrossRef]
- Vortmeyer-Kley, R.; Gräwe, U.; Feudel, U. Detecting and tracking eddies in oceanic flow fields: A Lagrangian descriptor based on the modulus of vorticity. Nonlin. Process. Geophys. 2016, 23, 159–173. [Google Scholar] [CrossRef]
- Froyland, G.; Lloyd, S.; Santitissadeekorn, N. Coherent sets for nonautonomous dynamical systems. Phys. D 2010, 239, 1527–1541. [Google Scholar] [CrossRef]
- Thiffeault, J.L. Braids of entangled particle trajectories. Chaos 2010, 20. [Google Scholar] [CrossRef] [PubMed]
- Mundel, R.; Fredj, E.; Gildor, H.; Rom-Kedar, V. New Lagrangian diagnostics for characterizing fluid flow mixing. Phys. Fluids 2014, 26. [Google Scholar] [CrossRef]
- Skokos, C.; Bountis, T.; Antonopoulos, C. Geometrical properties of local dynamics in Hamiltonian systems: The Generalized Alignment Index (GALI) method. Phys. D 2007, 231, 30–54. [Google Scholar] [CrossRef]
- Cincotta, P.M.; Simo, C. Simple tools to study global dynamics in non-axisymmetric galactic potentials. Astron. Astrophys. Suppl. 2000, 147, 205–228. [Google Scholar] [CrossRef]
- Szezech, J.; Schelin, A.; Caldas, I.; Lopes, S.; Morrison, P.; Viana, R. Finite-time rotation number: A fast indicator for chaotic dynamical structures. Phys. Lett. A 2013, 377, 452–456. [Google Scholar] [CrossRef]
- Szezech, J.D., Jr.; Caldas, I.L.; Lopes, S.R.; Morrison, P.J.; Viana, R.L. Effective transport barriers in nontwist systems. Phys. Rev. E 2012, 86. [Google Scholar] [CrossRef] [PubMed]
- Szezech, J.D., Jr.; Caldas, I.L.; Lopes, S.R.; Viana, R.L.; Morrison, P.J. Transport properties in nontwist area-preserving maps. Chaos 2009, 19. [Google Scholar] [CrossRef] [PubMed]
- Haller, G. A variational theory of hyperbolic Lagrangian Coherent Structures. Phys. D 2011, 240, 574–598. [Google Scholar] [CrossRef]
- Farazmand, M.; Haller, G. Erratum and addendum to A variational theory of hyperbolic Lagrangian coherent structures [Phys. D 240 (2011) 574–598]. Phys. D 2012, 241, 439–441. [Google Scholar] [CrossRef]
- Karrasch, D. Comment on A variational theory of hyperbolic Lagrangian coherent structures [Phys. D 240 (2011) 574–598]. Phys. D 2012, 241, 1470–1473. [Google Scholar] [CrossRef]
- Farazmand, M.; Haller, G. Computing Lagrangian coherent structures from their variational theory. Chaos 2012, 22. [Google Scholar] [CrossRef] [PubMed]
- Farazmand, M.; Haller, G. Attracting and repelling Lagrangian coherent structures from a single computation. Chaos 2013, 23. [Google Scholar] [CrossRef] [PubMed]
- Blazevski, D.; Haller, G. Hyperbolic and elliptic transport barriers in three-dimensional unsteady flows. Phys. D 2014, 273–274, 46–62. [Google Scholar] [CrossRef]
- Haller, G.; Beron-Vera, F.J. Geodesic theory of transport barriers in two-dimensional flows. Phys. D 2012, 241, 1680–1702. [Google Scholar] [CrossRef]
- Farazmand, M.; Blazevski, D.; Haller, G. Shearless transport barriers in unsteady two-dimensional flows and maps. Phys. D 2014, 278–279, 44–57. [Google Scholar] [CrossRef]
- Serra, M.; Haller, G. Objective Eulerian coherent structures. Chaos 2016, 26. [Google Scholar] [CrossRef] [PubMed]
- Serra, M.; Haller, G. Forecasting long-lived Lagrangian vortices from their objective Eulerian footprints. J. Fluid Mech. 2017, 813, 436–457. [Google Scholar] [CrossRef]
- Serra, M.; Haller, G. Efficient computation of null geodesics with applications to coherent vortex detection. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 2017, 473. [Google Scholar] [CrossRef]
- Oseledec, V.I. A multiplicative ergodic theorem: Lyapunov characteristic numbers for dynamical systems. Trans. Mosc. Math. Soc. 1968, 19, 197–231. [Google Scholar]
- Ruelle, D. Ergodic theory of differentiable dynamical systems. Publ. Math. IHES 1979, 50, 27–58. [Google Scholar] [CrossRef]
- Wolfe, C.L.; Roger M., S. An efficient method for recovering Lyapunov vectors from singular vectors. Tellus A 2007, 59, 355–366. [Google Scholar] [CrossRef]
- Ginelli, F.; Poggi, P.; Turchi, A.; Chaté, H.; Livi, R.; Politi, A. Characterizing dynamics with covariant Lyapunov vectors. Phys. Rev. Lett. 2007, 99. [Google Scholar] [CrossRef] [PubMed]
- Froyland, G.; Hüls, T.; Morriss, G.P.; Watson, T.M. Computing covariant Lyapunov vectors, Oseledets vectors, and dichotomy projectors: A comparative numerical study. Phys. D 2013, 247, 18–39. [Google Scholar] [CrossRef]
- Bosetti, H.; Posch, H.A. Covariant Lyapunov vectors for rigid disk systems. Chem. Phys. 2010, 375, 296–308. [Google Scholar] [CrossRef] [PubMed]
- Xu, M.; Paul, M.R. Covariant Lyapunov vectors of chaotic Rayleigh-Bénard convection. Phys. Rev. E 2016, 93. [Google Scholar] [CrossRef] [PubMed]
- Wolfe, C.L.; Samelson, R.M. Singular vectors and time-dependent normal modes of a baroclinic wave-mean oscillation. J. Atmos. Sci. 2008, 65, 875–894. [Google Scholar] [CrossRef]
- Schubert, S.; Lucarini, V. Covariant Lyapunov vectors of a quasi-geostrophic baroclinic model: Analysis of instabilities and feedbacks. Q. J. R. Meteor. Soc. 2015, 141, 3040–3055. [Google Scholar] [CrossRef]
- Schubert, S.; Lucarini, V. Dynamical analysis of blocking events: spatial and temporal fluctuations of covariant Lyapunov vectors. Q. J. R. Meteor. Soc. 2016, 142, 2143–2158. [Google Scholar] [CrossRef]
- Vannitsem, S.; Lucarini, V. Statistical and dynamical properties of covariant Lyapunov vectors in a coupled atmosphere-ocean model-multiscale effects, geometric degeneracy, and error dynamics. J. Phys. A 2015, 49. [Google Scholar] [CrossRef]
- Yang, H.L.; Radons, G. When can one observe good hydrodynamic Lyapunov modes? Phys. Rev. Lett. 2008, 100. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.L.; Radons, G. Comparison between covariant and orthogonal Lyapunov vectors. Phys. Rev. E 2010, 82. [Google Scholar] [CrossRef] [PubMed]
- Kuptsov, P.V.; Parlitz, U. Theory and computation of covariant Lyapunov vectors. J. Nonlinear Sci. 2012, 22, 727–762. [Google Scholar] [CrossRef]
- Sala, M.; Manchein, C.; Artuso, R. Estimating hyperbolicity of chaotic bidimensional maps. Int. J. Bifurc. Chaos 2012, 22. [Google Scholar] [CrossRef]
- Ginelli, F.; Chate, H.; Livi, R.; Politi, A. Covariant Lyapunov vectors. J. Phys. A 2013, 46. [Google Scholar] [CrossRef]
- D’Ovidio, F.; Shuckburgh, E.; Legras, B. Local mixing events in the upper troposphere and lower stratosphere. Part I: Detection with the Lyapunov Diffusivity. J. Atmos. Sci. 2009, 66, 3678–3694. [Google Scholar] [CrossRef]
- Eckmann, J.P.; Ruelle, D. Ergodic theory of chaos and strange attractors. Rev. Mod. Phys. 1985, 57, 617–656. [Google Scholar] [CrossRef]
- Onu, K.; Huhn, F.; Haller, G. LCS Tool: A computational platform for Lagrangian coherent structures. J. Comput. Sci. 2015, 7, 26–36. [Google Scholar] [CrossRef]
- Del Castillo-Negrete, D.; Morrison, P.J. Chaotic transport by Rossby waves in shear flow. Phys. Fluids A 1993, 5, 948–965. [Google Scholar] [CrossRef]
- Beron-Vera, F.J.; Olascoaga, M.J.; Brown, M.G.; Koçak, H.; Rypina, I.I. Invariant-tori-like Lagrangian coherent structures in geophysical flows. Chaos 2010, 20. [Google Scholar] [CrossRef] [PubMed]
- Badin, G.; Tandon, A.; Mahadevan, A. Lateral mixing in the pycnocline by baroclinic mixed layer eddies. J. Phys. Oceanogr. 2011, 41, 2080–2101. [Google Scholar] [CrossRef]
- Badin, G. On the role of non-uniform stratification and short-wave instabilities in three-layer quasi-geostrophic turbulence. Phys. Fluids 2014, 26. [Google Scholar] [CrossRef]
- Badin, G. Surface semi-geostrophic dynamics in the ocean. Geophys. Astro. Fluid Dyn. 2013, 107, 526–540. [Google Scholar] [CrossRef]
- Ragone, F.; Badin, G. A study of surface semi-geostrophic turbulence: Freely decaying dynamics. J. Fluid Mech. 2016, 792, 740–774. [Google Scholar] [CrossRef]
- Benettin, G.; Galgani, L.; Giorgilli, A.; Strelcyn, J.M. Lyapunov Characteristic Exponents for smooth dynamical systems and for hamiltonian systems; A method for computing all of them. Part 2: Numerical application. Meccanica 1980, 15, 21–30. [Google Scholar] [CrossRef]
- Goldhirsch, I.; Sulem, P.L.; Orszag, S.A. Stability and Lyapunov stability of dynamical systems: A differential approach and a numerical method. Phys. D 1987, 27, 311–337. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Conti, G.; Badin, G. Hyperbolic Covariant Coherent Structures in Two Dimensional Flows. Fluids 2017, 2, 50. https://doi.org/10.3390/fluids2040050
Conti G, Badin G. Hyperbolic Covariant Coherent Structures in Two Dimensional Flows. Fluids. 2017; 2(4):50. https://doi.org/10.3390/fluids2040050
Chicago/Turabian StyleConti, Giovanni, and Gualtiero Badin. 2017. "Hyperbolic Covariant Coherent Structures in Two Dimensional Flows" Fluids 2, no. 4: 50. https://doi.org/10.3390/fluids2040050
APA StyleConti, G., & Badin, G. (2017). Hyperbolic Covariant Coherent Structures in Two Dimensional Flows. Fluids, 2(4), 50. https://doi.org/10.3390/fluids2040050





