The Eddy Diffusivity in Barotropic β-Plane Turbulence

Abstract

Geostrophic turbulent eddies play a crucial role in the oceans, mixing properties such as heat, salt, and geochemical tracers. A useful reduced model for geostrophic turbulence is barotropic (2D) turbulence. The focus of this study is on 2D $\beta$-plane turbulence with quadratic drag, which, although arguably the most realistic barotropic model of ocean turbulence, has remained unexplored thus far. We first review and test classical scaling arguments for the eddy diffusivity in three regimes: the strong friction limit, the weak friction/strong $\beta$ limit, and a transition regime. We then develop a generalized theory by parameterizing the nonlinear eddy–eddy interactions as a stochastic process, which leads to an analytical solution for the eddy diffusivity spectrum, whose integral yields a “bulk” diffusivity. The theory successfully predicts the smooth transition of diffusivity across the three regimes, and echoes with the recent argument that eddy phase propagation relative to the mean flow suppresses the eddy diffusivity. Moreover, the generalized theory reduces to the classical scaling arguments in both the strong friction and strong $\beta$ limits, which has not been clear from the previous work on diffusivity suppression by flow-relative phase propagation.

1. Introduction

Geostrophic turbulent eddies are crucial in geophysical fluids for the transport and mixing of properties. However, in the earth’s oceans, they cannot be fully resolved by current global climate models, due to their relatively small size [1]. Therefore, their representation has to rely on adequate eddy parameterization schemes [2,3,4]. A common practice to parameterize sub-grid scale turbulence is to employ a diffusive closure, which assumes that unresolved eddy fluxes can be related to the large scale mean gradient via an eddy diffusivity. The eddy parameterization problem then comes down to expressing the eddy diffusivity based on resolvable large scale quantities. This paper aims to improve parameterizations for the eddy diffusivity by studying 2D turbulence as a reduced model for geostrophic turbulence.

2D turbulence is characterized by an inverse energy cascade. Once kinetic energy (KE) is created by forcing at small scales, it will be transferred to larger scales via nonlinear eddy–eddy interactions, which will become increasingly slow as the scale increases. If large scale friction is present, a steady state can be achieved when the nonlinear interaction becomes as slow as the energy dissipation rate by friction, and the cascade will be arrested at the so-called halting scale, where most of the energy will be found [5].

The simplest case to study this phenomenon is f-plane turbulence with linear drag and forcing [6,7]. However, the f-plane approximation (i.e., the assumption of constant background vorticity) excludes dynamics that are crucial to large-scale geophysical fluids, such as the formation of Rossby waves. This limitation is overcome by the use of a $\beta$-plane approximation, which accounts for the importance of the planetary vorticity gradient. Including $\beta$ significantly complicates the problem by adding a non-dimensional parameter. Moreover, the introduction of $\beta$ can lead to anisotropy, where eddy kinetic energy (EKE) is channeled into zonal modes, creating strong zonal flows or jets [6,8,9,10] and suppressing meridional mixing.

While a linear drag is mathematically convenient, turbulent dissipation in the ocean’s bottom boundary layer is arguably better described by a quadratic drag [7,11]. In fact, presently a quadratic drag is prevalently implemented in numerical ocean models [12,13,14]. An important distinction lies in the dimensions: while a linear drag coefficient r provides a time scale (the inverse of the damping rate), a quadratic drag coefficient $C_D$ has a dimension of inverse length in a barotropic model. (The effective quadratic drag coefficient for a barotropic flow is related to the standard non-dimensional $C_D^{*}$ as $C_D=C_D^{*}/H$, where H is the depth of the flow.) As pointed out by [7], the quadratic drag coefficient by itself provides the halting scale in f-plane turbulence, which differs significantly from the linear drag case. The more realistic case of $\beta$-plane turbulence with quadratic drag has remained unexplored thus far and will be the focus of this work.

The two limit cases where either friction or $\beta$ dominates can likely be understood from the existing work. Assuming that $\beta$ is unimportant in the strong friction limit, the conclusions drawn from f-plane turbulence are expected to hold, such that the problem reduces to that studied by [7]. In this case, the halting scale solely depends on $C_D$. The turbulent flow in this regime is fully isotropic, which implies the dominance of EKE over zonal mean KE, enabling the use of total KE as a good approximation to EKE. Total KE in turn can readily be estimated from a balance between forcing and frictional dissipation. Finally, the eddy diffusivity can be formulated based on mixing length theory [15]. Alternatively, the scaling relationship for the eddy diffusivity can be derived directly from dimensional considerations, if we assume that $\beta$ does not enter. In the strong $\beta$ limit, on the other hand, we may assume that friction only affects the zonal jets such that a characteristic turbulent eddy velocity can be determined dimensionally based only on the energy cascade rate and $\beta$. Meanwhile, a characteristic length scale is given by the so-called $\beta$ scale, which again follows directly from dimensional arguments, and is interpreted as the largest scale that is reached by the isotropic KE cascade. The product of the thus obtained velocity and length scales provides a scaling for the eddy diffusivity, which has been found to provide a useful approximation in simulations with large $\beta$ and weak linear friction [6,9].

The regime where both friction and $\beta$ matter (a transition regime) remains poorly understood, despite its relevance to Earth’s ocean. Jansen et al. [14] investigate the diffusivity for baroclinic turbulence in such an ocean-like transition regime and find that mixing is significantly suppressed by the presence of $\beta$, even as the total KE remains dominated by the eddies.

A separate line of recent work has attempted to derive an expression for the eddy diffusivity analytically by linearizing the equation of motion for a single wavenumber, $\kappa$, representing the energy containing scale ([16], hereafter FN10; [17], hereafter NGFP; [18,19], hereafter KA14; [20], hereafter SY14). The resulting expression highlights the importance of mixing suppression by the relative propagation of eddies to the mean flow (hereafter “propagation-suppression argument”). Focusing on idealized barotropic flows, SY14 points out that it is in fact the intrinsic Rossby wave phase speed, arising from the meridional gradient of vorticity, that suppresses the eddy diffusivity. While all theories thus point towards the suppression of mixing for large $\beta$, it is not obvious how exactly the expression of FN10/NGFP/SY14 relates to the classical $\beta$-plane turbulence scaling arguments. We will show below that this connection can only be recovered by noting that mixing in reality is not necessarily dominated by the most energetic eddies. Adopting the linearization technique used in FN10, we have developed a generalized theory for the full diffusivity spectrum in barotropic turbulence, whose integral yields a “bulk” diffusivity that agrees with simulations across all three regimes. This generalized theory is shown to reduce to the classical scaling relations for barotropic turbulence in the limit cases of strong $\beta$ and strong friction.

The idea of considering the full spectrum for the diffusivity is not new. Holloway and Kristmannsson ([21], hereafter HK84) consider the full spectrum of eddy tracer flux for $\beta$-plane 2D turbulence. Their result highlights the importance of $\beta$ in affecting the eddy flux spectrum both by creating anisotropy and by introducing a competition between turbulence and wave propagation, which yields a suppression factor similar to that discussed by FN10. While providing great insight into how Rossby wave propagation acts to suppress the eddy diffusivity, HK84 do not give a predictive expression for the eddy diffusivity, as the results depend on unknown nonlinear transfer timescales as well as an anisotropy parameter. Chen et al. [22] propose a related way to estimate the eddy diffusivity taking into account the multi-scale nature of eddy and mean flow velocities. However, their formulation requires detailed knowledge of the flow field, and therefore remains a highly diagnostic theory. Our work aims to provide a prognostic expression for the eddy diffusivity based solely on external parameters.

This study has four main goals: (1) document the results of a numerical exploration of barotropic turbulence on a $\beta$-plane with quadratic drag; (2) test previously proposed scaling arguments for the eddy diffusivity in the friction regime [7], in the $\beta$ regime [9], and in the transition regime [14]; (3) develop a generalized theory for the eddy diffusivity based on the propagation-suppression argument of FN10; and (4) clarify the connection between the propagation-suppression theory and the classical scaling arguments for the eddy diffusivity in $\beta$-plane turbulence.

This paper is organized as follows. Section 2 introduces the equations of motion and the numerical model used to solve them. Section 3 discusses and tests the classical scaling arguments for 2D turbulence and mixing. In Section 4, we derive a generalized theory for the eddy diffusivity, building on the propagation-suppression argument of FN10. Section 5 discusses the connections between the generalized theory and classical scaling arguments, and Section 6 provides conclusions.

2. Equations of Motion and Numerical Model

We want to study the turbulent flow on a $\beta$-plane, described by the barotropic vorticity equation

$$\frac{\partial q}{\partial t}+J(\psi ,q)+\beta \frac{\partial \psi }{\partial x}=F-C_D\left[\frac{\partial \left(\right|\mathbf{u}\left|v\right)}{\partial x}-\frac{\partial \left(\right|\mathbf{u}\left|u\right)}{\partial y}\right]$$

(1)

where $q={\nabla }^2\psi$ is the vorticity, $\psi$ is the stream function, $J(\psi ,q)\equiv {\partial }_x\psi {\partial }_{y}q-{\partial }_y\psi {\partial }_{x}q$ is the Jacobian operator, $\beta$ is the background vorticity gradient, F is a small scale forcing that crudely represents the generation of eddies by baroclinic instability, $C_D$ is a quadratic drag coefficient, and $\mathbf{u}\equiv (u,v)=(-{\partial }_y\psi ,{\partial }_x\psi )$ is the velocity. A spectral filter (not explicitly included in Equation (1)) removes enstrophy near the grid scale (see Appendix A).

To study turbulent transport, we consider a passive tracer advected by the turbulent flow, which stirs up a constant meridional gradient g:

$$\frac{\partial c}{\partial t}+J(\psi ,c)+g\frac{\partial \psi }{\partial x}=0$$

(2)

where c is tracer concentration. Grid-scale variance is again removed using the same spectral filter as for vorticity. The eddy diffusivity D is computed as

$$D=-\frac{\overline{〈v^{\prime }{c}^{\prime }〉}}{g}$$

(3)

where the overbar denotes a time mean and angle brackets indicate a domain average.

The numerical model used to solve Equations (1) and (2) uses a pseudo-spectral barotropic solver in a doubly-periodic domain with size $2\pi \times 2\pi$ and a real space resolution of $512\times 512$ grid points. The forcing is located at total wavenumber 140 or 80 (differing between simulations), and is formulated as a Markovian forcing, following [23]. Details of forcing, filter, and integration scheme are documented in Appendix A. The model is integrated from a state of rest until a statistical equilibrium is reached. The quantities $\beta$, $C_D$, and the forcing amplitude are varied across a wide range of experiments.

3. General Results and Scaling Arguments

In this section, we discuss scaling arguments for the eddy diffusivity based on classical $\beta$-plane turbulence theory. We first discuss the qualitative role of $\beta$ in affecting the inverse energy cascade and turbulent mixing. Then, the scaling relations for mixing scale, eddy velocity, and eddy diffusivity are reviewed, and tested against a series of numerical simulations. Notice that our discussion does not explicitly distinguish between “stirring” and “mixing”, but assumes that down-gradient eddy fluxes (which may more adequately be considered a result of “stirring”) generally lead to irreversible mixing at the micro-scale [24,25].

The characteristic scales for quantities appearing in Equation (1) are

$$\left|\mathbf{u}\right|\sim u\sim v\sim U,x\sim y\sim L,q\sim \frac{U}{L},\psi \sim UL,F\psi \sim ϵ$$

(4)

where the last term $ϵ$ is the energy cascade rate that describes how fast KE is created by F at small scales and then inversely cascaded upscale (see Appendix A for more details). Ignoring the size of the domain, and the forcing scale, the only external parameters in this system are $C_D$, $\beta$, and $ϵ$. Noting that we have two independent dimensions (length and time), Buckingham $\pi$ theorem implies the existence of one non-dimensional number, which we call $\mu$:

$$\mu \equiv {ϵ}^{-1/5}{\beta }^{3/5}{C}_D^{-1}$$

(5)

$\mu$ describes the importance of $\beta$ relative to $C_D$ and is the only factor controlling the transition between different regimes. We shall point out that we have carefully chosen the range of parameters in our simulations such that the energy containing scale and the scales most relevant for eddy fluxes are significantly larger than the forcing scale, but smaller than the domain size, such that neither should interfere much with the scaling expressions presented hereafter.

3.1. General Results

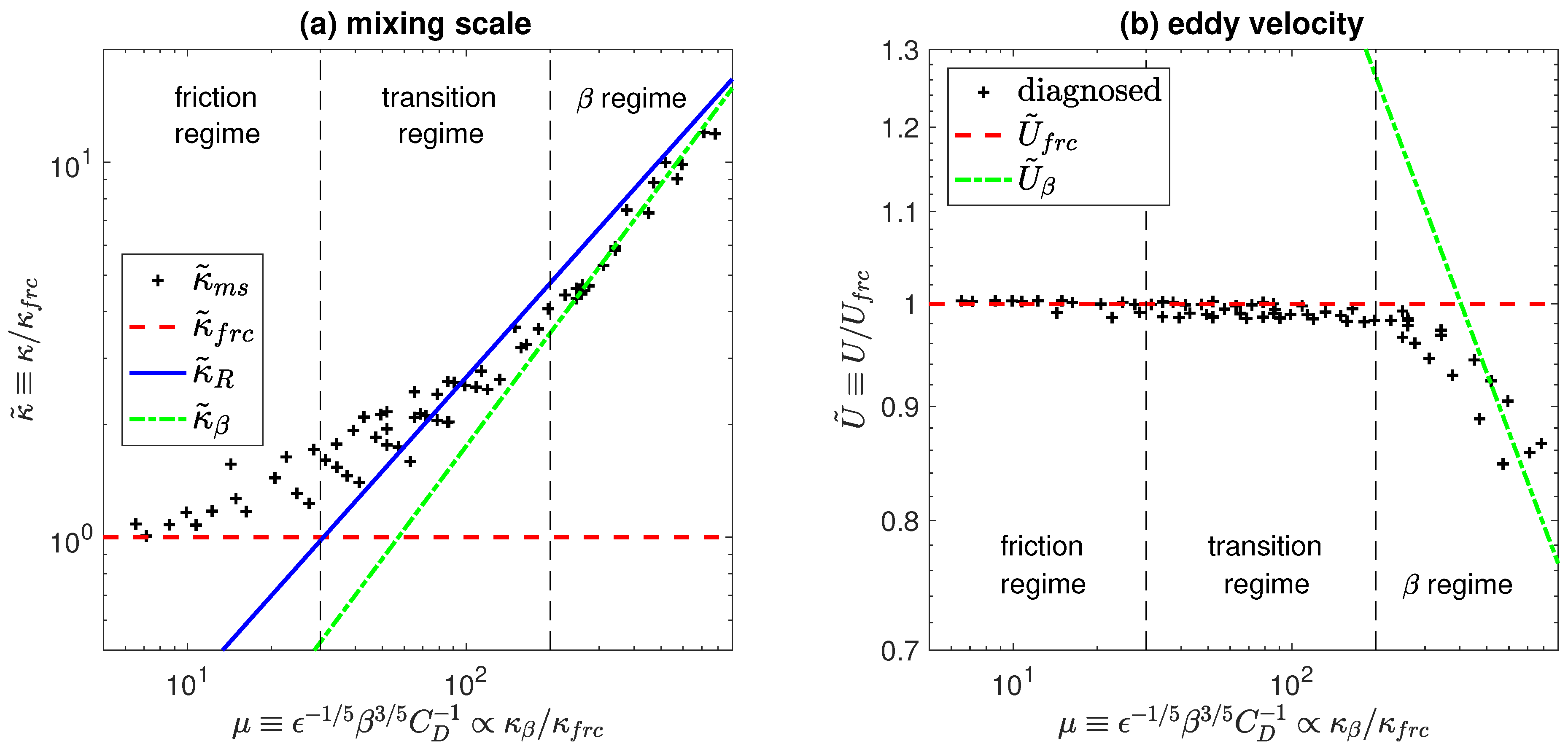
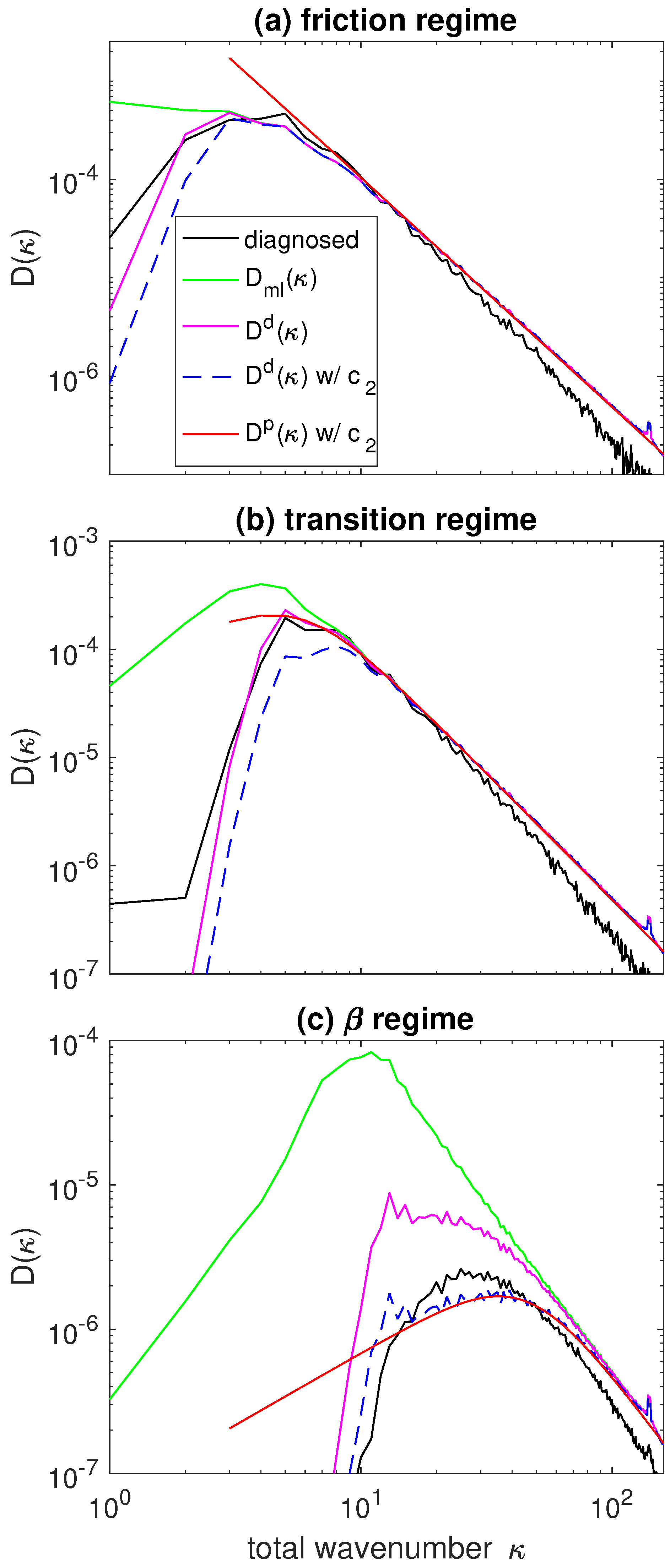
We start by looking at three typical simulations from the three regimes discussed in the introduction (Figure 1). The three rows in Figure 1 show simulations with $\mu =14.3,98.8,$ and $782.9$, which puts them into the friction, transition, and $\beta$ regime, respectively. In addition to KE, we show spectra of eddy diffusivity, defined as the ratio of the eddy tracer flux cross spectrum to the background mean gradient of the passive tracer, g:

$$D\left(\kappa \right)\equiv \sum _{k^2+l^2={\kappa }^2}D(k,l),\mathrm{where}D(k,l)=-\frac{\mathrm{Re}\left(\overline{{\widehat{v}}_{k,l}·{\widehat{c}}_{k,l}^{*}}\right)}{g}$$

(6)

where the hat denotes Fourier transforms, ${}^{*}$ denotes the complex conjugate, and $(k,l,\kappa )$ are zonal, meridional, and total wavenumbers, respectively. The summation amounts to a (discretized) integration in wavenumber space along circles with fixed total wavenumber. The diffusivity spectrum shows at which scale most of the eddy transport occurs. In the following, we will refer to this scale as the “mixing scale”, ${\kappa }_{ml}$. Quantitatively, we define the mixing scale based on the inverse centroid of the diagnosed diffusivity spectrum:

$${\kappa }_{ms}\equiv \frac{{\int }_0^{\infty }D\left(\kappa \right)\mathrm{d}\kappa }{{\int }_0^{\infty }\frac{D\left(\kappa \right)}{\kappa }\mathrm{d}\kappa }$$

(7)

where the inverse centroid is chosen over the centroid because it better captures the peak of the spectrum.

Figure 1 contains rich information about the flow and eddy transport in each regime. The flow in the upper panel is in the friction regime so the energy spectrum is similar to f-plane turbulence, with a relatively smooth energy peak and nearly complete overlap between EKE and total KE, as the flow is highly isotropic (see also right panels). The mixing scale is larger than the energy containing scale by roughly a factor of 2, due to the dependence of the diffusivity on the KE spectrum and on the wavenumber itself, as previously suggested by HK84. Mixing length theory [15] suggests that the diffusivity spectrum can be estimated as

$$D_{ml}\left(\kappa \right)\sim E{\left(\kappa \right)}^{1/2}{\kappa }^{-3/2}$$

(8)

where the subscript “ml” stands for “mixing length” theory. Equation (8) shows that a shift of the peak in the eddy diffusivity spectrum, as compared to the EKE spectrum, results directly from the inverse wavenumber dependency of the eddy diffusivity (given a smooth peak in the spectrum). A quantitative test and modification of this argument will be discussed in Section 4.

As $\mu$ increases, the flow enters the transition regime (middle panel). In this case, $\beta$ starts to suppress mixing, as reflected by the reduction in the eddy diffusivity at large scales. Nevertheless, EKE remains the primary component of total KE, as can be seen from the similarity between the EKE and total KE spectrum in the left panel, as well as by noting that the flow field shown in the right panel remains largely isotropic.

Finally, in the $\beta$ regime, the flow properties change significantly due to the dominant importance of $\beta$. The EKE spectrum significantly deviates from the total KE spectrum near the energy containing scale and at larger scales, reflecting the channeling of KE into zonal jets. This is also illustrated in the right panel, which clearly shows alternating zonal jets. Moreover, the eddy diffusivity is substantially reduced, and the peak in the diffusivity spectrum is now at smaller scales than the peak of the EKE spectrum, consistent with the results of HK84.

3.2. Regime-Based Diffusivity Scaling Expressions

In this section, scaling relations for the eddy velocity, mixing scale, and eddy diffusivity are presented using both physical and dimensional arguments. The results from the scaling relations are compared to the numerical simulations.

3.2.1. Friction Regime

The friction regime emerges at small $\mu$, where $\beta$ can be neglected, and the flow essentially behaves like f-plane turbulence. In this case, the mixing scale is expected to scale with the energy containing scale (although it is typically slightly larger), which, in turn, is given directly by the quadratic drag coefficient $C_D$, as documented in [7]:

$$L\sim \frac{1}{C_D},{\kappa }_{frc}\sim \frac{1}{L}\sim C_D$$

(9)

${\kappa }_{frc}$ is shown in Figure 2a, which compares the diagnosed mixing scale with various scales from the scaling arguments. Notice that the scaling arguments only predict the slope of the various lines in Figure 2. Non-dimensional factors have been chose to match the data, and absorbed into the definition of ${\kappa }_{frc}$ and $U_{frc}$ (see below). The frictional scaling adequately predicts a flattening of the dependence of the mixing scale on $\mu$ at small $\mu$. However, total independence of $\mu$ (and thus $\beta$) is arguably never obtained over the considered parameter range.

The characteristic eddy velocity is determined based on the EKE budget, which in the friction regime is well approximated by the total KE budget. The KE budget can be derived by multiplying Equation (1) by $-\psi$ and integrating over the whole domain:

$$\frac{\partial \mathrm{EKE}}{\partial t}\approx \frac{\partial \mathrm{KE}}{\partial t}=-\int \psi \frac{\partial q}{\partial t}\mathrm{dA}=-\int \psi F\mathrm{dA}+C_D\int \psi \left[\frac{\partial \left(\right|\mathbf{u}\left|v\right)}{\partial x}-\frac{\partial \left(\right|\mathbf{u}\left|u\right)}{\partial y}\right]\mathrm{dA}$$

(10)

In steady state, the time derivative term in Equation (10) drops out, and using Equation (4) we find a scaling relationship between the energy cascade rate, the bottom drag, and the eddy velocity as

$$U_{frc}\sim {\left(\frac{ϵ}{C_D}\right)}^{1/3}$$

(11)

which is shown in Figure 2b. $U_{frc}$ provides an accurate prediction of eddy velocity in the friction regime. Combing Equations (9) and (11), we recover the scaling expression for the eddy diffusivity in the friction regime by [7]:

$$D_{frc}\sim \frac{U_{frc}}{{\kappa }_{frc}}\sim \frac{{ϵ}^{1/3}}{C_D^{4/3}}$$

(12)

Notice that Equation (12) can also be derived based on purely dimensional analysis: since $\beta$ is assumed to be negligible in the friction regime, it shall not appear in the scaling for the eddy diffusivity, in which case the only dimensionally feasible way to express $D_{frc}$ is Equation (12).

The scaling relation predicted by Equation (12) is shown in Figure 3 (red solid line), where eddy diffusivities have been non-dimensionalized using $C_D$ and $ϵ$. The non-dimensional expression for the predicted eddy diffusivity in the friction regime then becomes

$${\tilde{D}}_{frc}\sim 1={\mu }^0$$

(13)

which captures the distribution of the eddy diffusivity in the friction regime reasonably well. A slight overestimation of the diffusivity near the right boundary of the friction regime arises from the overestimate of the mixing scale as shown in Figure 2a. Notice again that the scaling relationship only predicts the slope of the lines in Figure 3, while absolute values were chosen to match the simulations. Also notice that the non-dimensional parameter, $\mu$, captures most, but not all of the spread among different simulations. The remaining spread between simulations is likely explained by the role of the forcing scale and domain size, whose relevance cannot be completely eliminated due to numerical constraints on the resolution and domain size.

3.2.2. $\beta$ Regime

If $\mu$ is very large, the flow enters the $\beta$ regime. While friction necessarily remains important to dissipate KE, it has been argued that the bulk of the dissipation occurs in zonal jets, while the properties of the turbulent eddy field become independent of friction [9]. If $C_D$ shall not appear in the scaling expression, the only dimensionally feasible way to express a length scale is

$$L\sim {ϵ}^{1/5}{\beta }^{-3/5},{\kappa }_{\beta }\sim \frac{1}{L}\sim {ϵ}^{-1/5}{\beta }^{3/5}$$

(14)

which is called the $\beta$ scale. ${\kappa }_{\beta }$ is generally interpreted as the crossover scale between isotropic and anisotropic (wave-)turbulence. For scales smaller than the $\beta$ scale, the $\beta$ effect remains negligible and the flow is isotropic. For scales larger than the $\beta$ scale, however, the Rossby wave frequency becomes higher than the eddy turnover rate (defined as the ratio of the eddy velocity to eddy scale), leading to anisotropic flows, where wave-like disturbances co-exist with zonal jets [6,9,26]. Since linear waves and jets are not expected to contribute significantly to mixing, ${\kappa }_{\beta }$ provides an obvious candidate for the mixing scale.

The idea that the $\beta$ scale provides the mixing scale in $\beta$-plane turbulence has been documented and tested in previous studies [6,9], albeit using a linear rather than a quadratic drag. If eddy properties indeed become independent of friction, we may expect the results to apply similarly in the case of quadratic drag, which is confirmed by our simulations. As shown in Figure 2a, ${\kappa }_{\beta }$ provides an accurate prediction for the mixing scale in the $\beta$ regime.

The characteristic eddy velocity at the $\beta$ scale can be determined from the Kolmogorov –5/3 spectrum (hereafter “Kolmogorov spectrum”), which applies in the inertial range of isotropic turbulence and thus at scales up to ${\kappa }_{\beta }$:

$$E\left(\kappa \right)=K{ϵ}^{2/3}{\kappa }^{-5/3}$$

(15)

where $K=8$ is the non-dimensional Kolmogorov constant. $U_{\beta }$ can therefore be estimated as

$$U_{\beta }\sim \sqrt{E\left({\kappa }_{\beta }\right){\kappa }_{\beta }}\sim {ϵ}^{2/5}{\beta }^{-1/5}$$

(16)

Notice that $U_{\beta }$ is not necessarily the full root mean square eddy velocity but rather the characteristic velocity at ${\kappa }_{\beta }$, where energy is thought to be converted into both waves (that do not contribute to mixing, but do contribute to EKE) and jets (that do not contribute to either mixing or EKE). Nevertheless, Equation (16) qualitatively predicts the reduction of EKE at large $\beta$ (as shown by the dash-dotted green line in Figure 2b).

Combining Equations (14) and (16), we obtain a relationship for the eddy diffusivity as:

$$D_{\beta }\sim \frac{U_{\beta }}{{\kappa }_{\beta }}\sim \frac{{ϵ}^{3/5}}{{\beta }^{4/5}}$$

(17)

Again, Equation (17) can also be retrieved directly from dimensional considerations by assuming that $D_{\beta }$ is independent of $C_D$, but the derivation presented above highlights that the suppression of eddy diffusivity in the $\beta$ regime arises from the role of $\beta$ in suppressing mixing at wavenumbers smaller than ${\kappa }_{\beta }$.

Using the non-dimensional formulation, $D_{\beta }$ becomes:

$${\tilde{D}}_{\beta }\sim {ϵ}^{4/15}{\beta }^{-4/5}{C}_D^{4/3}={\mu }^{-4/3}$$

(18)

which successfully captures the distribution of the eddy diffusivity (green dash-dotted line in Figure 3).

Notice that our non-dimensional parameter, $\mu$, can be related to the friction and $\beta$ scale as

$$\mu \equiv {ϵ}^{-1/5}{\beta }^{3/5}{C}_D^{-1}\sim \frac{{\kappa }_{\beta }}{{\kappa }_{frc}}$$

(19)

which makes its physical meaning clearer: while a small $\mu$ suggests the inverse cascade is arrested at ${\kappa }_{frc}$, a large $\mu$ indicates the termination of the isotropic cascade at ${\kappa }_{\beta }$. However, notice that the absolute value of $\mu$ has to be handled with care when identifying regime transitions, as the relevant non-dimensional factors can easily be $O\left(10\right)$ or larger. In particular, we note that the frictional halting scale is in fact well approximated as ${\kappa }_{frc}=40C_D$ (roughly consistent with the results of [7]).

3.2.3. Transition Regime

The most realistic scenario for Earth’s ocean is one where both friction and $\beta$ are important — a transition regime between the strong $\beta$ and strong friction limits. Analyzing idealized simulations of baroclinic turbulence in a parameter regime thought to be crudely representative of the Southern Ocean, Jansen et al. [14] find that EKE remains controlled by bottom friction, similar to the friction regime, while mixing is nevertheless suppressed significantly by the presence of $\beta$. The notion that EKE remains controlled by bottom friction throughout most of the transition regime is supported by the results in Figure 2b, which shows that the diagnosed eddy velocity is well approximated by $U_{frc}$ throughout most of the transition regime. The important role that $\beta$ plays in suppressing eddy fluxes in the transition regime is also qualitatively consistent with the results in Figure 2a and Figure 3.

Quantitatively, Ref. [14] suggests that a useful estimate of the eddy diffusivity is given by the product of the root mean square eddy velocity and the Rhines scale:

$${\kappa }_R\sim \sqrt{\frac{\beta }{U}}\approx \sqrt{\frac{\beta }{U_{frc}}}$$

(20)

which yields:

$$D_{tr}\sim \frac{U_{frc}}{{\kappa }_R}\sim \frac{{ϵ}^{1/2}}{{\beta }^{1/2}{C}_D^{1/2}}$$

(21)

The non-dimensional form of $D_{tr}$ is again shown in Figure 3:

$${\tilde{D}}_{tr}\sim {ϵ}^{1/6}{\beta }^{-1/2}{C}_D^{5/6}={\mu }^{-5/6}$$

(22)

Equation (22) captures the first order distribution of the eddy diffusivity in the transition regime. Nevertheless, notice that the eddy diffusivity in the transition regime is actually smoothly distributed along a curve, rather than following a straight line, indicating the limitations of using a single power-law scaling relation to represent the eddy diffusivity in this regime.

4. A Generalized Theory for the Eddy Diffusivity

The scaling arguments above are a useful starting point but fail to capture the smooth transition of diffusivity between regimes, thus relying on a somewhat arbitrary specification of regime boundaries. The scaling argument is particularly unsatisfying in the (oceanographically relevant) transition regime where the eddy diffusivity does not follow a power law (Figure 3). This motivates us to develop a more general expression for the diffusivity, which captures the behavior across all regimes.

In this section, we adopt the linearization method in FN10 to derive a generalized expression for the eddy diffusivity in barotropic turbulence and compare it with the scaling arguments discussed above. In addition to providing a generalized expression for the eddy diffusivity, the result helps to reconcile the propagation–suppression argument of FN10 with the classical scaling arguments for the eddy diffusivity in the friction and $\beta$ regimes.

4.1. A Stochastic Model for Nonlinear Eddy–Eddy Interactions

In FN10, the authors obtain an analytical solution for eddy diffusivity in a surface quasi-geostrophic model for a single wavenumber, which is interpreted as the energy containing scale. Their method is to linearize the nonlinear eddy–eddy interaction as a combination of a stochastic white noise forcing and a linear damping process. Here, we want to use this parameterization not only for a single wavenumber but at every wavenumber pair $(k,l)$. In spectral space, the Jacobian term thus becomes

$$\widehat{J}(\psi ,q)=-Q\sqrt{\gamma }·r_1\left(t\right)+\gamma \widehat{q}$$

(23)

where the hat denotes the Fourier transform, Q is the amplitude of the stochastic forcing and has the same dimensions as $\widehat{q}$, $\gamma$ is a linear damping rate that describes the decorrelation due to nonlinear eddy–eddy interactions, and $r_1\left(t\right)$ is a white noise process. Q and $\gamma$ in general can also be functions of k and l. Physically, the forcing term represents how enstrophy is transferred into the respective wavenumber by nonlinear eddy–eddy interactions, while the damping represents transfer to other wavenumbers. The factor $\sqrt{\gamma }$ in the forcing term in Equation (23) is included such that Q gives the amplitude of the generated vorticity perturbation.

Similarly, we parameterize the Jacobian term in Equation (2) as

$$\widehat{J}(\psi ,c)=-C\sqrt{\eta }·r_2\left(t\right)+\eta \widehat{c}$$

(24)

where C is the forcing amplitude, $\eta$ is the tracer’s linear damping rate, and $r_2\left(t\right)$ is again a white noise process, assumed to be independent of $r_1\left(t\right)$. $\eta$ may or may not be the same as $\gamma$ (see also discussions in HK84 and SY14). Notice that FN10 does not consider forcing and damping in the tracer equation, arguably consistent with the assumption that stirring is dominated by a single most energetic wave.

With these parameterizations, Equations (1) and (2) can be formulated in spectral space as

$$\frac{\partial \widehat{q}}{\partial t}+ik\beta \widehat{\psi }=Q\sqrt{\gamma }·r_1\left(t\right)-\gamma \widehat{q}$$

(25)

$$\frac{\partial \widehat{c}}{\partial t}+ikg\widehat{\psi }=C\sqrt{\eta }·r_2\left(t\right)-\eta \widehat{c}$$

(26)

The forcing term $\widehat{F}$ that appears originally on the right-hand side of Equation (25) has been dropped as we are here only interested in scales larger than the forcing scale. The quadratic drag term is also ignored because its amplitude turns out to be negligible at scales near or smaller than the mixing scale.

Solving Equation (25) yields the stream function (see also Appendix B):

$$\widehat{\psi }\left(t\right)=-\frac{Q\sqrt{\gamma }}{{\kappa }^2}{\int }_0^{\infty }{r}_1(t-t_1)exp[(\frac{ik\beta }{{\kappa }^2}-\gamma )t_1]{\mathrm{dt}}_1$$

(27)

The EKE at wavenumber $(k,l)$ can then be computed as (see Appendix C)

$$E(k,l)=\frac{1}{2}\overline{|\kappa \widehat{\psi }{|}^2}=\frac{Q^2}{4{\kappa }^2}$$

(28)

Using Equations (2) and (27), we can solve for the tracer concentration:

$$\widehat{c}\left(t\right)=C{\int }_0^{\infty }{r}_2(t-t_2){\mathrm{e}}^{-\eta t_2}{\mathrm{dt}}_2+\frac{ikgQ\sqrt{\gamma }}{{\kappa }^2}{\int }_0^{\infty }{\int }_0^{\infty }{r}_1(t-t_3-t_4)exp\left[(\frac{ik\beta }{{\kappa }^2}-\gamma )t_4-\eta t_3\right]{\mathrm{dt}}_3{\mathrm{dt}}_4$$

(29)

Together with Equation (27), the mean meridional eddy tracer flux at wavenumber $(k,l)$ can be computed as (see Appendix C)

$$\mathrm{Re}\left(\overline{\widehat{v}·{\widehat{c}}^{*}}\right)=-\frac{k^2{Q}^{2}g}{2{\kappa }^4}·\frac{(\gamma +\eta )}{{(\gamma +\eta )}^2+\frac{k^2{\beta }^2}{{\kappa }^4}}$$

(30)

Consequently, the eddy diffusivity spectrum at wavenumber $(k,l)$ can be written as

$$D_{k,l}\equiv -\frac{\mathrm{Re}\left(\overline{\widehat{v}·{\widehat{c}}^{*}}\right)}{g}=\frac{2k^2}{{\kappa }^2}·\frac{1}{1+\frac{k^2{\beta }^2}{{\kappa }^4}·\frac{1}{{(\gamma +\eta )}^2}}·\frac{E(k,l)}{\gamma +\eta }$$

(31)

Equation (31) is similar to Equation (20) in HK84 (after dividing their equation by the meridional tracer gradient).

The last factor on the right-hand side of Equation (31), $E(k,l)/(\gamma +\eta )$, gives the “unsuppressed” eddy diffusivity spectrum, with the decorrelation rate given by the combined nonlinear eddy damping rate of the vorticity and tracer variance. The first factor, $2k^2/{\kappa }^2$, accounts for the anisotropy of turbulence. The suppression is given by the central factor, which describes the reduction of the effective decorrelation timescale below the nonlinear eddy damping timescale ${(\gamma +\eta )}^{-1}$, due to the effect of the intrinsic Rossby wave frequency $\omega =k\beta /{\kappa }^2$ (see also [18]). Equation (31) shows that eddy phase propagation relative to the mean flow (which controls the wave frequency) will suppress the diffusivity, as pointed out by HK84, FN10, NGFP, and SY14.

In its present form, Equation (31) requires knowledge of the full two-dimensional EKE spectrum, which makes it not very useful for practical purposes. As a first step to simplify the expression to a more useful relationship, we want to reduce it to an equation for the one-dimensional diffusivity spectrum $D\left(\kappa \right)$:

$$D\left(\kappa \right)=\frac{1}{1+\frac{{\beta }^2}{2{\kappa }^2{(\gamma +\eta )}^2}}·\frac{E\left(\kappa \right)}{\gamma +\eta }$$

(32)

where we have made the simplifying substitution that $k^2/{\kappa }^2=1/2$, following FN10. This formally implies the assumption that the EKE is located along the diagonals with $\left|k\right|=\left|l\right|$ in wavenumber space, which is not realistic. A somewhat more realistic assumption would be to assume that EKE is isotropic in wavenumber space, a case that has been discussed by HK84 and SY14. However, in practice, we find that the difference between the solutions arising from the two assumptions is small. We therefore proceed with the assumption of FN10, which simplifies the algebra considerably.

4.2. Relating Eddy Diffusivity to the Eddy Kinetic Energy (EKE) Spectrum

Following FN10, the nonlinear eddy damping rate $\gamma$ can be interpreted as the eddy turnover rate, which scales as

$$\gamma \sim E{\left(\kappa \right)}^{1/2}{\kappa }^{3/2}$$

(33)

We will similarly assume that $\eta$ scales with the eddy turnover rate, which allows us to combine the two as

$$\gamma +\eta =c_{1}E{\left(\kappa \right)}^{1/2}{\kappa }^{3/2}$$

(34)

where $c_1$ is a non-dimensional constant of proportionality. We here simply set $c_1=1$, which provides a reasonably good fit to the results of the numerical simulations in the strong friction limit, where the suppression factor is less important. However, since this is not a priori clear, we will include the parameter $c_1$ in all following equations for generality.

Substituting Equation (34) into Equation (32) gives

$$D^d\left(\kappa \right)=\frac{1}{c_1}·\frac{E{\left(\kappa \right)}^{1/2}{\kappa }^{-3/2}}{1+\frac{{\beta }^2}{2c_1^{2}E\left(\kappa \right){\kappa }^5}}\equiv \frac{1}{1+\frac{{\beta }^2}{2c_1^{2}E\left(\kappa \right){\kappa }^5}}·D_{ml}\left(\kappa \right)$$

(35)

where the superscript d indicates that the diagnosed EKE spectrum, $E\left(\kappa \right)$, is used.

Figure 4 shows $D^d\left(\kappa \right)$ for the same three simulations as previously discussed in Figure 1. The generalized theory provides a useful prediction for the diffusivity spectrum, giving a considerably better fit than the unsuppressed mixing length theory, $D_{ml}\left(\kappa \right)$, in the transition and (especially) $\beta$ regime. However, $D^d\left(\kappa \right)$ still overestimates the eddy diffusivity in the $\beta$ regime, i.e., when $\mu$ is large.

The reasons for this overestimation remain unclear to the authors. The role of the anisotropy does not appear to explain the misfit: no significant improvement is found when using the equation for the full 2D diffusivity spectrum $D(k,l)$ with the diagnosed 2D EKE spectrum (not shown). Another potential candidate is the vorticity gradient associated with the jets. However, over the parameter regime considered here, this gradient remains relatively small compared to $\beta$, suggesting that this effect is unlikely to explain the observed discrepancy. Another possible cause for discrepancy lies in the spatial inhomogeneity. As pointed out by Nakamura [25], significant variations in the meridional gradient of zonal mean vorticity can create large differences between the arithmetic and the harmonic meridional mean of the diffusivity, with the latter arguably being more relevant. However, this is only able to explain up to about $20\%$ of the difference between the diagnosed and predicted diffusivity, hence leaving it as a minor factor.

We speculate that one possible explanation for the misfit is that the nonlinear decorrelation rate $\gamma$ itself needs to be altered as the eddies become more wave-like. Additionally, the meridional shear of the zonal velocity, created by the formation of jets, may suppress the eddy diffusivity when $\mu$ is large: we find that the shear at the flanks of the jets is comparable to the eddy turnover rate $\gamma$ (not shown). Unfortunately, we did not find a way to quantitatively incorporate these factors into our theory, without making the model overly complicated. SY14 include the suppression of mixing by a constant background shear in their linearized model, but even with the simplifying assumption of a given constant background shear, the expressions become highly involved.

In practice, we find that an improved fit can be obtained by including an empirical factor, $c_2=5.5$, in front of the ${\beta }^2$ term in Equation (31), which is shown by the dashed curves in Figure 4. $c_2$ has been chosen to provide a reasonable fit to the magnitude of the diffusivity in the $\beta$ regime. Equation (35) then becomes

$$D^{d\prime }\left(\kappa \right)=\frac{1}{c_1}·\frac{E{\left(\kappa \right)}^{1/2}{\kappa }^{-3/2}}{1+\frac{c_2{\beta }^2}{2c_1^{2}E\left(\kappa \right){\kappa }^5}}$$

(36)

It is worth noting that FN10, albeit not explicitly discussing this issue, effectively include a similar factor to enhance the suppression effect in their Equation (21) (From footnote 2 in FN10 and the text below their Equation (17), one gets $d_2=4{\alpha }^2{d}_1^2$, where their $d_1$ and $d_2$ are proportional to our $c_1^{-1}$ and $c_2/c_1^2$, respectively. $\alpha$ here represents the ratio of the eddy phase speed to the surface current velocity. In the Southern Ocean, we generally find $0<\alpha <1$, which leads to $d_2<4d_1^2$. However, combining their Equations (19) and (21), one retrieves $d_1=0.32$ and $d_2=4$, implying that $d_2$, which governs the strength of the suppression, is chosen much larger than what is suggested by the theory. The adopted values for $d_1$ and $d_2$ therefore reflect the same need to enhance the suppression effect, which in the current work is achieved by introducing the empirical factor $c_2$.) Throughout the rest of this manuscript, we will include this empirical factor, but for readability we will drop the prime sign in the diffusivity.

For practical purposes, we may be more interested in the total “bulk” diffusivity, as opposed to the full diffusivity spectrum. The bulk diffusivity can be obtained by integrating Equation (35):

$$D^d={\int }_0^{\infty }{D}^d\left(\kappa \right)\mathrm{d}\kappa =\frac{1}{c_1}{\int }_0^{\infty }\frac{E{\left(\kappa \right)}^{1/2}{\kappa }^{-3/2}}{1+\frac{c_2{\beta }^2}{2c_1^{2}E\left(\kappa \right){\kappa }^5}}\mathrm{d}\kappa$$

(37)

Equation (37) is compared against the numerical simulations in Figure 5: $D^d$ successfully reproduces the eddy diffusivity across all regimes, although it somewhat underestimates the diffusivity in the transition regime. As a comparison, the prediction made by mixing length theory without the suppression factor ($D_{ml}$) is also plotted in Figure 5, which strongly underestimates the suppression of the eddy diffusivity as $\mu$ becomes large.

While providing a single bulk diffusivity, the prediction in Equation (37) is based on the entire energy spectrum, which is the key aspect that distinguishes it from the approach of FN10/NGFP/KA14, who focus on a single wavenumber representing the scale of the most energetic eddies. To demonstrate the difference quantitatively, we compare our results to those obtained by evaluating Equation (31) for a single wavenumber taken as the diagnosed energy containing scale ${\kappa }_0$. ${\kappa }_0$ is computed based on the inverse centroid of the diagnosed EKE spectrum, similar to the way the mixing scale is calculated (see Equation (7)):

$${\kappa }_0\equiv \frac{{\int }_0^{\infty }E\left(\kappa \right)\mathrm{d}\kappa }{{\int }_0^{\infty }\frac{E\left(\kappa \right)}{\kappa }\mathrm{d}\kappa }$$

(38)

$E\left(\kappa \right)$ is replaced by the diagnosed total EKE, and $\gamma +\eta =c_1\sqrt{{\kappa }^2\mathrm{EKE}}$. Consistent with FN10 and KA14, we still assume $\left|k\right|=\left|l\right|$. Including again the empirical factor $c_2$, we obtain

$$D_{sw}=\frac{1}{c_1}·\frac{1}{1+\frac{c_2{\beta }^2}{2c_1^2{\kappa }^4\mathrm{EKE}}}·\frac{{\mathrm{EKE}}^{1/2}}{\kappa }$$

(39)

where the subscript “sw” denotes the “single wavenumber” approximation. The results from Equation (39) are also shown in Figure 5. The single wavenumber theory captures the distribution of the diffusivity in the friction and transition regimes reasonably well. However, $D_{sw}$ significantly underestimates the diffusivity when $\mu$ gets large. This misfit can readily be understood by noting that mixing is no longer dominated by the energy containing scale at large $\mu$ (see, e.g., the bottom row of Figure 1). As the eddy diffusivity becomes strongly suppressed at the energy containing scale, smaller-scale eddies, which are ignored in the single wavenumber approximation, maintain the bulk of the mixing.

Figure 5 may also explain some of the discrepancy between the theory and observations found in KA14. Figure 6 in KA14 suggests that the theory accurately predicts the eddy diffusivity only in the Southern Ocean; at most other latitudes, the diffusivity is systematically underestimated. Meanwhile, FN10 only focus on a sector in the Southern Ocean. It is plausible that the Southern Ocean falls within a regime where the single wavenumber theory remains appropriate. In less energetic regions and at lower latitudes, $\mu$ instead may be larger, causing the single wavenumber theory to overestimate the mixing suppression.

4.3. Towards a Predictive Theory

Despite its success, $D^d$ is not able to predict the diffusivity without the knowledge of $E\left(\kappa \right)$. We seek to close this problem by assuming that $E\left(\kappa \right)$ can be approximated by the Kolmogorov spectrum (Equation (15)) for $\kappa ⪆{\kappa }_{frc}$, while dropping rapidly to zero for $\kappa <{\kappa }_{frc}$. Generally, we may not expect the Kolmogorov spectrum to extend all the way to ${\kappa }_{frc}$ when $\beta$ is large. However, since mixing at large scales is strongly suppressed in this limit, the results are expected to depend only weakly on the choice of the cut-off wavenumber. For the sake of simplicity, we therefore refrain from introducing another halting scale for the energy spectrum. Combining Equations (15) and (35), we get:

$$D^p\left(\kappa \right)=\frac{\sqrt{K}}{c_1}·\frac{{ϵ}^{1/3}{\kappa }^{-7/3}}{1+\frac{1}{2K{c}_1^2}·\frac{c_2{\beta }^2}{{ϵ}^{2/3}{\kappa }^{10/3}}}$$

(40)

where the superscript p indicates the use of the prognostic relation for $E\left(\kappa \right)$. Equation (40) is assumed to hold for $\kappa ⪆{\kappa }_{frc}$, while $D^p\left(\kappa \right)=0$ is assumed for $\kappa <{\kappa }_{frc}$.

$D^p\left(\kappa \right)$ is included in Figure 4, where it is denoted by red curves. Generally speaking, it is able to capture the basic features of the diffusivity spectra, albeit with some caveats. First, $D^p$ is unable to predict the detailed shape of the spectrum near the mixing scale, which is unsurprising as the Kolmogorov spectrum is not applicable outside of the inertial range. Second, as $\mu$ becomes large, $D^p$ overestimates the diffusivity at scales larger than the mixing scale. This “over-reaching” to large scales results directly from the use of the Kolmogorov spectrum all the way to ${\kappa }_{frc}$.

The bulk diffusivity can again be computed by integrating $D^p\left(\kappa \right)$:

$$D^p\approx {\int }_{{\kappa }_{frc}}^{\infty }{D}^p\left(\kappa \right)\mathrm{d}\kappa =\frac{\sqrt{K}}{c_1}{\int }_{{\kappa }_{frc}}^{\infty }\frac{{ϵ}^{1/3}{\kappa }^{-7/3}}{1+\frac{1}{2K{c}_1^2}·\frac{c_2{\beta }^2}{{ϵ}^{2/3}{\kappa }^{10/3}}}\mathrm{d}\kappa$$

(41)

The non-dimensional form of $D^p$ plotted in Figure 6 is:

$${\tilde{D}}^p=\frac{\sqrt{K}}{c_1}{\int }_{c_0}^{\infty }\frac{{\tilde{\kappa }}^{-7/3}}{1+\frac{c_2}{2K{c}_1^2}·{(\frac{\mu }{\tilde{\kappa }})}^{10/3}}\mathrm{d}\tilde{\kappa }$$

(42)

where $c_0\equiv {\kappa }_{frc}/C_D=40$ and $\tilde{\kappa }\equiv \kappa /C_D$. $c_0$ was chosen so as to provide a good fit to both the diagnosed eddy diffusivity (Figure 6) and the mixing scale (Figure 2) in the limit of strong friction.

${\tilde{D}}^p$ is shown in Figure 6 and successfully reproduces the smooth transition of the diffusivity across regimes. The diffusivity is slightly overestimated in the transition regime, which is contrary to the result in Figure 5. The overestimate in the transition regime appears to be a result of the overestimate of the large-scale EKE by the Kolmogorov spectrum, and is thus not unexpected. One could attempt to include the effect of $\beta$ in the formulation of the energy spectrum, but this would introduce at least one additional free parameter. Considering the overall success of Equation (41), the benefit of such further complications is questionable.

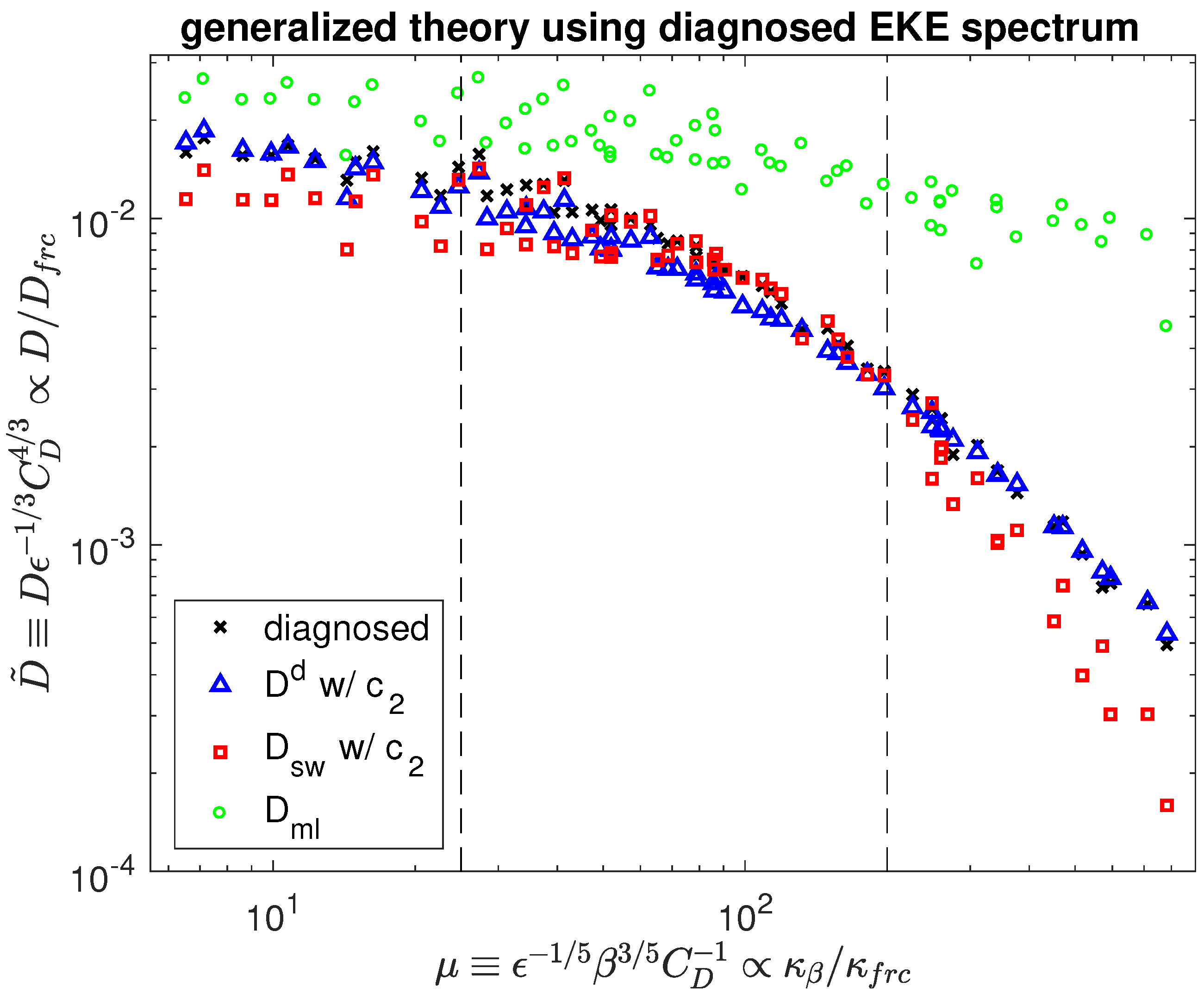
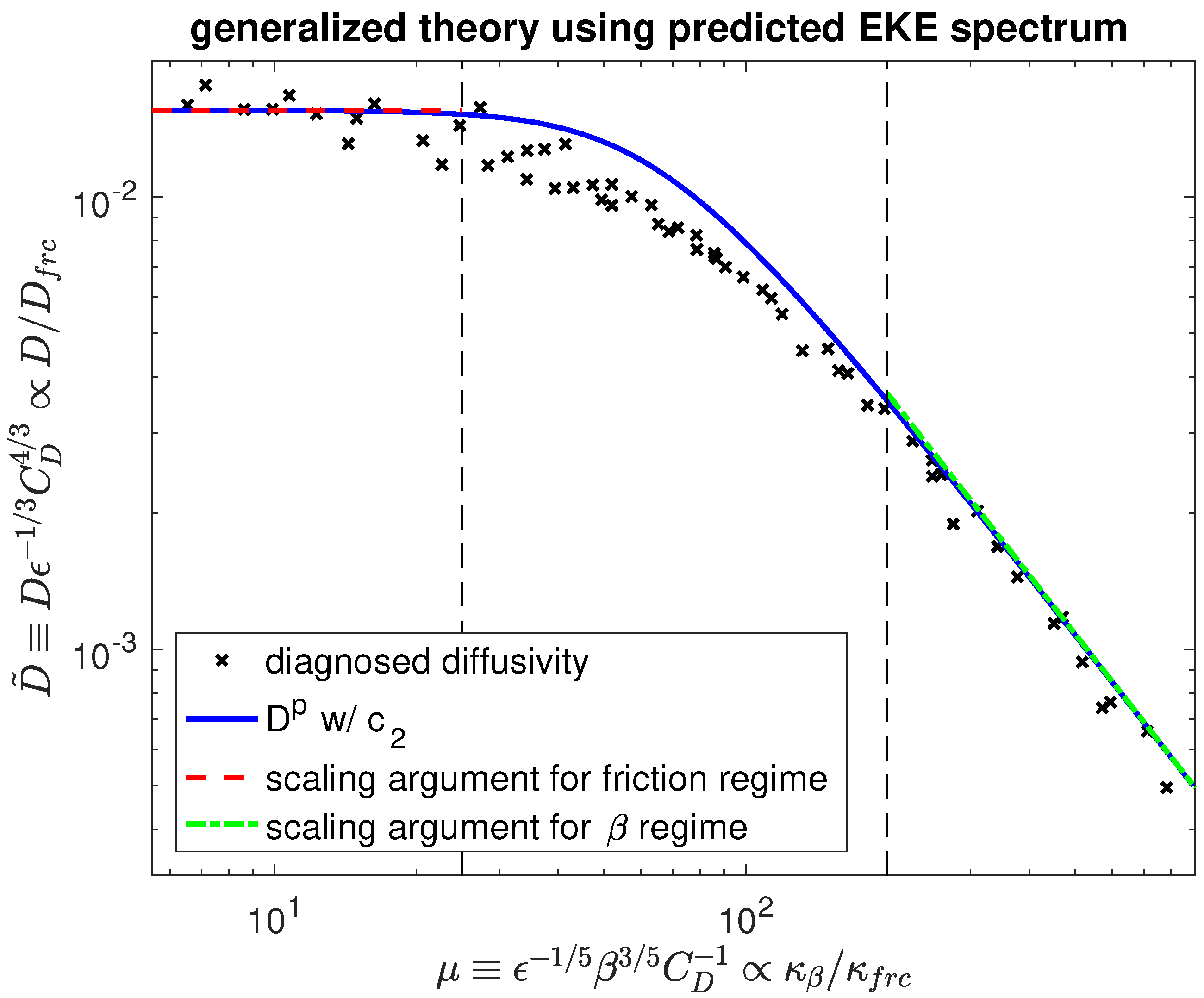
5. Connecting the Generalized Theory to Scaling Arguments

In this section, we will discuss the relationship between the generalized theory for the eddy diffusivity, discussed in Section 4, and the scaling arguments discussed in Section 3. In particular, it will be shown that the generalized theory reduces to the scaling arguments in the limits of strong friction and strong $\beta$.

In the strong friction limit, $\mu$ is small, so that the second term in the denominator of the integrand in Equation (42) can be neglected, and we obtain the same scaling as Equation (12):

$$\underset{\mu \to 0}{lim}D\approx \frac{3\sqrt{K}}{4c_1{c}_0^{4/3}}·\frac{{ϵ}^{1/3}}{C_D^{4/3}}\propto D_{frc}$$

(43)

In this limit, the suppression has no effect, and the EKE spectrum (by assumption) peaks at ${\kappa }_{frc}$. As a result, the generalized theory reduces to the mixing length theory.

On the other hand, when $\mu$ is large, the scaling relation in the $\beta$ regime is most easily retrieved by normalizing $\kappa$ such that $\mathring{\kappa }\equiv \kappa {ϵ}^{1/5}{\beta }^{-3/5}\propto \kappa /{\kappa }_{\beta }$, in which case Equation (41) becomes

$$D^p=\frac{\sqrt{K}{ϵ}^{3/5}}{c_1{\beta }^{4/5}}{\int }_{c_0/\mu }^{\infty }\frac{{\mathring{\kappa }}^{-7/3}}{1+\frac{c_2}{2K{c}_1^2{\mathring{\kappa }}^{10/3}}}\mathrm{d}\mathring{\kappa }$$

(44)

Taking the limit of large $\mu$, we arrive at

$$\underset{\mu \to \infty }{lim}D=\frac{\sqrt{K}{ϵ}^{3/5}}{c_1{\beta }^{4/5}}{\int }_0^{\infty }\frac{\mathrm{d}\mathring{\kappa }}{{\mathring{\kappa }}^{7/3}+\frac{c_2}{2K{c}_1^2\mathring{\kappa }}}\propto \frac{{ϵ}^{3/5}}{{\beta }^{4/5}}\propto D_{\beta }$$

(45)

The physical connection between the two theories in this limit can be seen by noting that the integrand of Equation (45) (or the dimensional form in Equation (41) for that matter) maximizes when the two terms in the denominator become equal, which yields

$$\mathring{\kappa }={(\frac{c_2}{2K{c}_1^2})}^{3/10}\approx 0.73$$

(46)

That is, the major contributions to the eddy diffusivity come from the eddies near the $\beta$ scale, while mixing is strongly suppressed at larger scales. In fact, the physical reasoning is essentially the same as in the classical scaling theory, highlighting the importance of the wave-turbulence crossover wavenumber, below which the Rossby wave frequency exceeds the eddy turnover rate, thus rendering mixing inefficient.

The two limits have been included in Figure 6 as the colored straight lines at both ends of the generalized theory. Taking the limits of the generalized theory therefore provides an alternative way to determine the non-dimensional constants in the scaling arguments for the friction and $\beta$ regimes, relating them back to the Kolmogorov constant K, the non-dimensional factor $c_0$ in the frictional halting scale, the decorrelation constant $c_1$ (here taken to be 1), and (unfortunately) our empirical factor $c_2$. Notice that the connection between the generalized theory and the scaling argument in the transition regime instead is not obvious, as the generalized theory predicts a smooth transition from the friction to the $\beta$ limit, rather than an independent intermediate power law regime.

6. Conclusions

This work set out to investigate the eddy diffusivity in barotropic turbulence on a $\beta$-plane with quadratic drag. Specifically, we use a series of numerical simulations to test previously proposed scaling arguments for the eddy diffusivity in the friction regime, in the $\beta$ regime, and in the transition regime. We then develop a generalized theory for the eddy diffusivity based on the propagation-suppression argument proposed by FN10. Finally, we show that the scaling arguments and the generalized theory are connected in the two limits of strong friction and strong $\beta$.

The scaling arguments, which for the first time are applied to $\beta$-plane turbulence with quadratic drag, identify three regimes depending on the relative importance of $C_D$ and $\beta$. The scaling relations for the characteristic eddy velocity, mixing scale, and eddy diffusivity are formulated for each regime. In the strong friction limit, the role of $\beta$ can be neglected, and the eddy velocity is determined from a balance between the forcing and the energy dissipation by quadratic drag, while the mixing scale is set by the frictional halting scale. In the strong $\beta$ limit, on the other hand, it is the drag that is not important such that both the turbulent eddy velocity and mixing scale follow from dimensional arguments. In a transitional regime, both drag and $\beta$ are important: while the eddy velocity remains controlled by bottom drag, the mixing scale and diffusivity are significantly reduced by the presence of $\beta$. The scaling arguments are tested against diagnosed diffusivities from high-resolution eddy-resolving numerical simulations, and found to successfully predict the eddy diffusivity in the respective regimes.

The generalized theory is motivated by an argument about the suppression of mixing by flow-relative eddy propagation, proposed by FN10. Their approach is here extended to the full diffusivity spectrum. The integral of the diffusivity spectrum then yields a bulk diffusivity, which generally differs from the single-wavenumber theory proposed by FN10, who only apply the argument to the energy containing wavenumber. Assuming that the nonlinear decorrelation rate is identical to the eddy turnover rate, and that the EKE spectrum can be approximated by the Kolmogorov spectrum, we obtain a prognostic equation for the eddy diffusivity that is verified against the numerical simulations, and adequately captures the smooth transition across all parameter regimes.

The generalized theory highlights the importance of considering the entire energy spectrum. At least in the context of barotropic turbulence, the single-wavenumber approximation used by FN10 and KA14 breaks down once the suppression becomes sufficiently strong, at which point eddy transport is no longer dominated by the energy containing scale. An estimate of the suppressed diffusivity considering only the energy containing scale is then likely to overestimate the suppression effect and thus underestimate the eddy diffusivity.

This work helps to clarify the connection between classical scaling theories for $\beta$-plane turbulence and the recently proposed propagation–suppression argument. Classical $\beta$-plane turbulence theory shows that $\beta$ will suppress the eddy diffusivity via decreasing turbulent eddy velocity and mixing scale. Turbulent EKE is reduced due to the channeling of energy into Rossby waves and zonal jets. Similarly, the mixing scale is reduced by the transition from isotropic turbulence to waves and jets at the $\beta$ scale. Since the inverse energy cascade nevertheless proceeds to larger scales, this transition leads to the divergence between the energy containing scale and mixing scale. Meanwhile, the generalized diffusivity theory highlights the propagation of eddies relative to the mean flow as responsible for the suppression of the diffusivity. Noting that the flow-relative phase propagation is related to the intrinsic Rossby wave phase speed, it is readily seen that the flow-relative suppression argument similarly predicts strong suppression of eddy transport at scales beyond the wave-turbulence crossover scale. Indeed, the generalized theory is shown to reduce to the classical scaling arguments in the strong friction and strong $\beta$ limits.

The presented work can provide a foundation for the development of eddy parameterizations in numerical ocean models. We have shown that the mixing suppression formulation has the potential to predict eddy diffusivity over a wide range of parameters, as long as the entire energy spectrum is considered. To apply the closure to meso-scale eddy fluxes in Earth’s ocean, we need to predict the energy spectrum, as well as the wave dispersion relationship, which is complicated by the effects of a baroclinic background flow and bottom topography [27,28,29]. However, it is evident that flow-relative propagation of waves and eddies strongly affects mixing in the ocean (e.g., KA14). Improvements in the representation of eddy transport in coarse resolution ocean circulation models will therefore rely crucially on an adequate incorporation of these propagation effects.