1. Introduction
Thermal convection in a rotating porous medium is an active topic of research since it has many applications including geophysics, chemical engineering, food process industry, binary alloy solidification, cooling of electronics equipment, solidification and centrifugal casting of metals and rotating machinery (see e.g., Vadasz [
1], Vadasz [
2], Vadasz and Govender [
3], Govender [
4] Nield and Bejan [
5], Ingham and Pop [
6], and the references therein). Indeed, thermal convection involving the rotation of the layer of saturated porous medium is a subject receiving attention and is being studied extensively by many researchers, such as Vadasz [
1,
7,
8,
9]. In particular, he investigated the effect of the Coriolis force on thermal convection when the Darcy model is extended by including the time-derivative term in the momentum equation [
9]. A comprehensive review of thermal convection in a rotating porous medium are given by Vadasz [
10]. Palm and Tyvand [
11] showed that the results of thermal instability in a rotating porous layer are equivalent to those of non-rotating anisotropic porous media. Vadasz and Govender [
3] also considered the influence of gravity and centrifugal forces on the onset of convection in a rotating porous layer. Straughan [
12] presented an analysis of the nonlinear stability problem for convection in a rotating isotropic porous medium. He showed that the global nonlinear stability boundary is exactly the same as the linear instability.
It is important to note that the above-mentioned studies considered assumed saturated that the porous medium is isotropic. However, the effect of anisotropy combined with the rotation effect on thermal instability has been the contribution of Alex and Patil [
18], who investigated thermal instability subject to the centrifugal acceleration and the anisotropy effect as in the case of both the Darcy and Brinkman models. Govender [
4] considered the Vadasz paper 1994 [
7] but included the anisotropy effects for both permeability and thermal diffusivity. Later, Malashetty and Swamy [
19] also performed linear instability and weakly nonlinear theory to investigate the anisotropy effects on the onset of convection in a rotating porous medium. They found that increasing an anisotropy parameter for both permeability and thermal diffusivity leads to advancing oscillatory convection. The same authors in [
20] employed linear instability theory to investigate the effect of both thermal modulation and rotation on the onset of the stationary convection. Govender and Vadasz [
21] also deal with the effect that thermal diffusivity and permeability anisotropy have on the thermal convection in a rotating porous medium with a thermal non-equilibrium model.
Recently, Vanishree and Siddheshwar [
22] performed linear instability for an anisotropic porous medium with a temperature dependent viscosity. They also found that the onset of convection in a rotating porous medium is qualitatively similar to that in a non-rotating one. Additionally, the linear instability and nonlinear stability in an anisotropic porous medium were adopted by Kumar and Bhadauria [
23] who considered viscoelastic fluid in a rotating anisotropic porous medium. Saravanan and Brindha [
24] deal with the onset of centrifugal convection in the Brinkman model, and Gaikwad and Begum [
25] considered the onset of double-diffusive reaction convection in an anisotropic porous medium.
In this article, we consider that the system of equations is essentially the same as that given in Vadasz [
9], but we allow for the symmetric permeability tensor to be anisotropic. In particular, we consider the case where the permeability in the vertical direction is different to that in the horizontal plane. In fact, we consider the case of the inverse of the permeability tensor
. The goal of this article is to investigate the effect of anisotropy with rotation on the stability thresholds using linear instability and nonlinear stability methods. Here, we will ignore the inertia term in the momentum equation. More precisely, we consider cases where the values of Vadasz number tend to be large [
9]. We show that the critical Rayleigh number of the linear theory is the same as the critical Rayleigh number of the nonlinear theory. We observe that energy methods are very much in vogue in the current hydrodynamical stability literature cf. Rionero [
13], Capone and Rionero [
14], Hill and Carr [
15,
16], and Hill and Malashetty [
17].
2. Governing Equations
Consider a layer of porous medium heated from below and bounded by two horizontal planes and , with gravity acting in the vertical direction of the z-axis. We assume that an incompressible Newtonian fluid saturates the porous layer and occupies the spatial domain . Furthermore, we suppose that the layer rotates about the z-axis. The Boussineq approximation is assumed to be valid.
The governing equations incorporating fluid inertia for thermal convection in an anisotropic rotating porous media of Darcy type may be written as, cf. Malashetty, and Swamy [
19],
Here, , t, p, T are the velocity field, time, pressure, and temperature, respectively, and , , g, , , are dynamic viscosity, thermal diffusivity, gravity, thermal expansion coefficient of the fluid, constant density coefficient, and porosity, respectively, and is the angular velocity vector with , is an inertia coefficient, is constant and is porosity. Standard indicial notation is employed throughout.
The inverse of the permeability tensor is assumed to be of the form
where
,
are constants. The boundary conditions for the problem are
where
,
are constants with
, and
is the unit outward normal to the boundary, so
on
and
on
.
When no motion occurs and the temperature gradient is constant throughout the layer, the basic steady state solution
whose stability is under investigation is
with
is the pressure at the surface
,
Letting
,
,
, the nonlinear perturbation equations arising from Equations (1)–(3), are
where
.
The perturbation equations are non-dimensionalised with the following scalings as follows:
where
is the Rayleigh number,
is the Taylor number,
is the Vadasz number, and
is the Prandtl number, with
being the Darcy number.
Omitting all stars, the nonlinear non-dimensional perturbation equations are
Here, , where is the anisotropy parameter.
The corresponding boundary conditions are
with
satisfying a plane tiling periodicity in
.
3. The Principle of Exchange of Stabilities Ignoring Inertia Term
As stated in the Vadasz paper [
9], the values of Vadasz for many porous media applications in a real life are large. To this end, we let
in the Equation (7) be
We now take curl of Equation (9a) and curlcurl of the same equation to find
and
where
is the horizontal Laplacian operator, and
is the vorticity.
Upon taking the third component of the foregoing equations, we obtain
We now consider the linearised Equation of (12) by removing the nonlinear term of Equation (12c), and therefore we seek for solutions of the form
By substituting into Equation (12) and removal of exponential parts, we have to solve the system
The corresponding boundary conditions are
In order to show that
, and that the principle of exchange of stabilities holds, we consider a three-dimensional periodic cell
V for solution to Equation (13) and assume momentarily that
,
, and
are complex. Then, we multiply Equation (13a) by
(the complex conjugate of
w)and integrate over
V to obtain
since
, so one may rewrite the first term in Equation (15) as shown below
Recalling
, we have
Making use of Equation (13b)
Furthermore, we now make use of vorticity equation
and so
Then, we form the combination of Equations (17) and (19) to find
After differentiating Equation (20) with respect to
z and expressing
, we employ the results and Equation (16) into Equation (15) to obtain
and hence we arrive at
where
,
and
denote the inner product and norm on the complex Hilbert space
.
By applying the horizontal Laplacian operator
to Equation (13c), multiplying by
(the complex conjugate of
) and again integrating, we find
Next, the addition of Equations (21) and (22) yields
Since
, the equating the imaginary parts of Equation (23) yields
Thus, and so , which implies that the linearized Equation (13) satisfy the strong principle of exchange of stabilities. As such, the instability set in as stationary convection.
4. Linear Instability Analysis
In this section, we seek to find the critical Rayleigh number of linear theory and we follow the work of Chandrasekhar [
26]. To this end, we set
into Equation (13). We further employ Equation (16), and the governing system can be reduced to
where Equation (20) has been differentiated with respect to
z.
We now eliminate
from Equation (24a,b), and therefore system (24) can be written as follows:
To proceed, we assume a normal mode representation for
w, and
of the form
where
is the horizontal planform that satisfies
,
a being a wave number. With
, we arrive at the following system
The corresponding boundary conditions are
The variable
is eliminated from Equation (26) to yield the fourth order differential equation
In view of the boundary conditions (27) and from Equation (26a), we obtain
Applying these boundary conditions to Equation (28), it turns out that
Further differentiation of Equation (28) yields
Thus, we may select
for
. Upon substituting in Equation (28), we have
which leads to
where
. Minimizing over
n yields
. Then, differentiating
with respect to
yields the stationary convection boundary
and the corresponding critical wave number
is given by
It is worth observing that as
, and
, we recover the result for the isotropic problem [
27]
5. Nonlinear Stability Analysis
In this section, we commence with the derivation of further boundary conditions that will be used to continue with the nonlinear stability analysis. To obtain these, we observe from Equations (10) and (18),
One may then deduce from the boundary conditions (14),
In addition, from Equation (18), we also find on the boundaries
One may then deduce from Equations (34) and (35),
and hence
Furthermore, we find from Equations (19) and (20) that
It follows from Equation (36) that
Since
on
, we obtain from Equation (9c)
Then differentiating Equation (9c)
times with respect to
z, we find
where we have used the General Leibniz Rule.
Furthermore, we may rewrite the foregoing equation as shown below:
Now, upon setting
, we have
Thus, employing Equations (14), (36), (39) and (40) yields
We next differentiate Equation (33), an even number of times with respect to
z, to find
In addition, we also differentiate Equation (35) an even number of times with respect to
z, we have
Therefore, from Equations (43) and (44), we obtain
By further differentiation of Equation (38) an even number of times with respect to
z, we find
The above process may be repeated to derive the general boundary conditions
which hold for the solution of the nonlinear problem.
We aim now to study nonlinear energy stability and find a stability threshold. Again, we let
V be a periodic cell for a disturbance to Equation (9), and let
and
be the norm and inner product on
. The energy identities are derived by multiplying the vertical component of Equation (11) by
w, upon use of Equations (16) and (20) with
, and also use some integrations by parts, with the aid of boundary conditions, one may show that
Next, multiply Equation (9c) by
and integrate over
V to find
By adding
(48) to (49), for
a parameter to be chosen, we may derive an energy identity of form
where
Define
by
where
is the space of admissible functions given by
are periodic in .
Therefore, from Equation (50), we deduce
Then, from the Poincaré’s inequality on
D, we have
Provided
, put
and then, from Equation (55), we have
Thus, tends to 0 as at least exponentially. Therefore, at least exponentially.
To obtain the decay of
, we multiply Equation (9) by
and integrate over
V to obtain
We may observe that
where
From Equation (56), it now follows that
and then with use of the arithmetic geometric mean inequality, one shows
for
to be chosen.
If we now pick
, then we show
which implies
must also decay at least exponentially. Hence, the global nonlinear stability criterion is determined by Equation (54).
In order to determine
, we have to derive the Euler–Lagrange equations and maximise in the coupling parameter
. To do this, we must find the stationary point of
, by using the calculus of the variations technique, the Euler–Lagrange equations arising from Equation (54) are determined from
for all
, and
. We have that
and
where we have included the constraint
by way of a Lagrange multiplier
, and
is a positive constant.
Furthermore, after some integrations by parts and using the boundary conditions, we find that
Since
and
were chosen arbitrary functions, from Equation (57), we obtain the Euler–Lagrange equations
where
is now a Lagrange multiplier. Applying the horizontal Laplacian operator to Equation (58), we obtain
We again use a normal mode representation, as for the linear stability analysis,
,
. This leaves us to solve the eigenvalue problem
This system would have to be solved for
subject to the boundary conditions Equation (27). Furthermore, we observe that
W and
satisfy the boundary conditions
By eliminating
, we obtain a fourth order equation in
W,
Hence,
may be written in the form
After some calculations, following the method in
Section 4, one may find
For any fixed wave number
, the minimum with respect to
of
is obtained for
. Then,
Let us now select
, and then
This is exactly the same Equation (30) with
for linear instability problem. This is, in a sense, the best possible threshold for the onset of linear unconditional stability. Thus, the minimum of
with respect to
is identical to the minimum of
with respect to
, and hence no subcritical instabilities can arise. This result is undoubtedly due to the fact that the operator attached to the linear theory is symmetric in this case (see Straughan [
27] and Falsaperla et al. [
28]).
6. Numerical Results
The aim of this paper was to investigate how the inclusion of the Taylor number
affects the thermal instability threshold in an anisotropic porous medium. The results of different values of the anisotropy parameter
and the Taylor number
are presented in
Table 1 and
Table 2, and are presented graphically in
Figure 1,
Figure 2 and
Figure 3.
Table 1 and
Figure 1 present the values of
, the critical Rayleigh number for both the onset of linear instability and for the nonlinear stability. This shows that the effect of increasing the Taylor number
always results in an increase in the critical Rayleigh number
, so that rotation stabilizes the system. Furthermore, the effect of increasing the anisotropy parameter
is seen also to increase the critical Rayleigh number
. This means that, when the rate of rotation and
increase, the stability becomes more pronounced, i.e.,
increases. For example, for
and
, we see from
Table 1 that the critical Rayleigh number is
, whereas, when
and
the critical Rayleigh number is
.
From
Figure 3, it is evident that, when there is no rotation,
, the instability curve starts at
when
and increases when rotation is included. Note that the critical Rayleigh number
became significantly higher at
, which leads to stabilize the system. One can see that, when
increases to
in case
, the instability curve starts at
. This means that the effect of increasing the anisotropy parameter is to delay the onset of convection in a fluid layer. Again, we observe that increasing the Taylor number
leads to an increase in the critical Rayleigh number
. Thus, an increase in the anisotropy parameter
in the vertical direction with an increase in the Taylor number
has the effect of stabilizing the system. We can, therefore, conclude that the effect of rotation is to enhance the stability of the system. In addition, these results are reinforcing the fact that the linear instability analysis is accurately capturing the physics of the onset of convection.
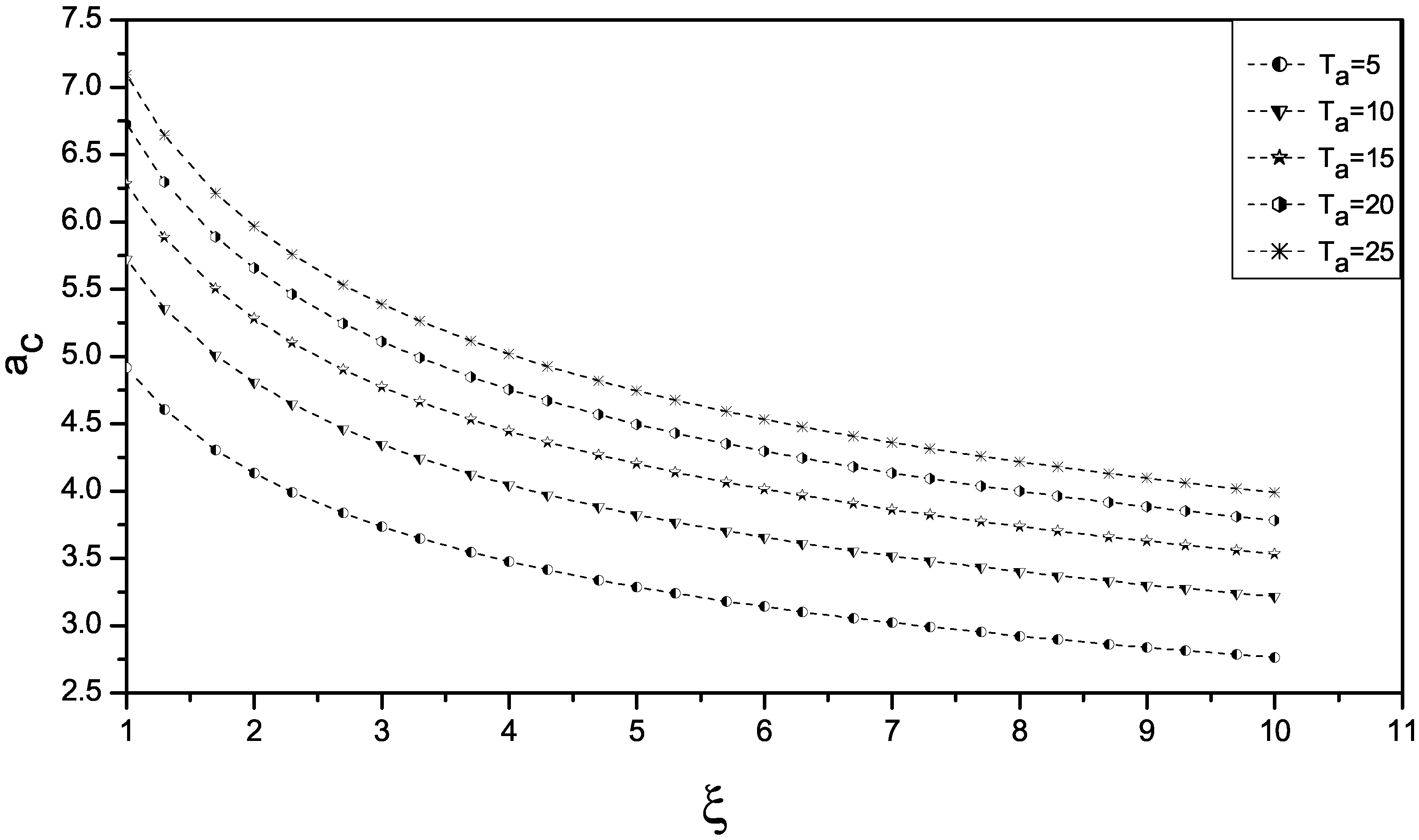
Table 2 and
Figure 2 present the values of
, the critical wave number for both the onset of linear instability and for the nonlinear stability. It can be observed that, for a fixed value of the anisotropy parameter
, the effect of increasing the Taylor number
is to increase the wave number. For example, for
and
, we see from
Table 2 that the critical wave number is
, whereas, when
for the same anisotropy parameter
, the critical wave number is
. It is also observed that increasing the anisotropy parameter
had the effect of decreasing the value of the wave number. However, as soon as the value of the Taylor number
increases, one can observe the critical wave number also increases, which corresponds to the narrower convection cells. These results indicate the effect of incorporating rotation in an anisotropic porous medium.