Abstract
We analyze the thermal convection thresholds and linear characteristics of the primary and secondary instabilities for viscoelastic fluids saturating a porous horizontal layer heated from below by a constant flux. The Galerkin method is used to solve the eigenvalue problem by taking into account the elasticity of the fluid, the ratio between the viscosity of the solvent and the total viscosity of the fluid and the lateral confinement of the medium. For the primary instability, we found out that depending on the rheological parameters, two types of convective structures may appear when the basic conductive solution loses its stability: stationary long wavelength instability as for Newtonian fluids and oscillatory convection. The effect of the lateral confinement of the porous medium by adiabatic walls is to stabilize the oblique and longitudinal rolls and therefore selects transverse rolls at the onset of convection. In the range of the rheological parameters where stationary long wave instability develops first, we use a parallel flow approximation to determine analytically the velocity and temperature fields associated with the monocellular convective flow. The linear stability analysis of the monocellular flow is performed, and the critical conditions above which the flow becomes unstable are determined. The combined influence of the viscoelastic parameters and the lateral confinement on the characteristics of the secondary instability is quantified. The major new findings concerning the secondary instabilities may be summarized as follows: (i) For concentrated viscoelastic fluids, computations showed that the most amplified mode of convection corresponds to oscillatory transverse rolls, which appears via a Hopf bifurcation. This pattern selection is independent of both the fluid elasticity and the lateral confinement of the porous medium; (ii) For diluted viscoelastic fluids, the preferred mode of convection is found to be oscillatory transverse rolls for a very laterally-confined medium. Otherwise, stationary or oscillatory longitudinal rolls may develop depending on the fluid elasticity. Results also showed the destabilizing effect of the relaxation fluid elasticity and the stabilizing effect of the viscosity ratio for the onset of both primary and secondary instabilities.
1. Introduction
The study of viscoelastic fluids has applications in a number of processes that occur in industry, such as the extrusion of polymer fluids, solidification of liquid crystals, suspension solutions and petroleum activities. In contrast to the case of Newtonian fluids, the study of the thermal convection of viscoelastic fluids in porous media is limited. In rheology, one crucial problem is the formulation of the constitutive equations regarding viscoelastic fluid flows in porous media. Recently, a modified Darcy’s law was employed to study the stability of a viscoelastic fluid in a horizontal porous layer using linear and nonlinear stability theory [1,2,3,4,5,6,7,8,9]. Kim et al. [1] and Yoon et al. [2] performed a linear stability analysis and showed that in viscoelastic fluids, such as polymeric liquids, a Hopf bifurcation, as well as a stationary bifurcation may occur depending on the magnitude of the viscoelastic parameter. From the nonlinear point of view, Kim et al. [1] carried out a nonlinear stability analysis by assuming a densely-packed porous layer and found that both stationary and Hopf bifurcations are supercritical relative to the critical heating rate. The question of whether standing or traveling waves are preferred at onset has been fully addressed by Hirata et al. [4]. The three-dimensional convective and absolute instabilities of a viscoelastic fluid in the presence of a horizontal pressure gradient have been analyzed by Hirata and Ouarzazi [5]. Alves et al. [6] studied the effect of viscous dissipation of viscoelastic fluids at the onset of convection. In addition to its theoretical interest, Delenda et al. [7] have shown that viscoelastic convection in porous media may be useful for industrial applications for the separation of species of viscoelastic solutions. The introduction of a porous packing allows one to control the average vertical convective velocity and to generate a homogeneous convection current, improving the separation of species. Fu et al. [8] performed direct numerical simulations on two-dimensional thermal convection of a viscoelastic fluid saturating a porous square cavity. Their numerical experiments revealed the existence of a second transition from oscillatory convection to a stationary one followed by a third transition to oscillatory convection for some combinations of rheological parameters, while these successive transitions never occur for other combinations of viscoelastic parameters. Taleb et al. [9] used both theoretical and numerical approaches and obtained a global picture and bifurcations diagrams on possible successive bifurcations of convection patterns in a square porous cavity saturated by a viscoelastic fluid.
All of the above investigations considered conventional boundary conditions, namely impermeable isothermal horizontal plates, commonly known as Horton–Rogers–Lapwood convection. With a configuration of an isothermal upper wall and impermeable adiabatic side walls, Niu et al. [10] were the first to introduce at the bottom plate a general variable heat flux boundary condition expressed in terms of the Biot number (). They proved by a linear stability analysis that when , the thermal convection properties of a viscoelastic fluid of an Oldroyd fluid type approach that subject to uniform heat flux heating. On the other hand, when , linear properties of convection coincide with those corresponding to isothermal heating. Therefore, convection with different thermal boundary conditions may be analyzed by adjusting the Biot number. However, to the best of our knowledge, no results have been published for thermal convection of viscoelastic fluids in situations more commonly met in engineering applications, namely when the porous medium is subjected, both in the upper and lower walls, to a general variable heat flux boundary condition. Therefore, the objective of this work is to fill a part of this gap by investigating the onset of three-dimensional primary and secondary instabilities of a viscoelastic fluids under the assumption that the upper and lower horizontal walls are kept at a constant flux as a limiting case of a more general variable heat flux boundary condition.
For Newtonian fluids, the stability of an infinite porous layer with different boundary conditions was studied by Nield [11] and is well documented in Section of the book by Nield and Bejan [12]. For the case of a porous medium heated from the bottom and cooled from the top by a constant heat flux, Nield [11] found that the critical Rayleigh number at the onset of convection is approximately 12 with a vanishing critical wavenumber. Mamou et al. [13] extended the work of Nield [11] by taking into account the effect of the anisotropy of the porous medium. Mojtabi and Rees [14] studied the case where the impermeable boundary walls have a finite thickness. They analyzed the combined influence on the onset of convection of the ratio between the thermal conductivity of the horizontal walls and the thermal conductivity of the porous medium, as well as the ratio between the thickness of the horizontal walls and the thickness of the porous layer. The problem of thermal convection in a rotating horizontal layer of a porous medium was analyzed by Falsaperla et al. [15] for a single fluid and by Falsaperla et al. [16] in the case of a binary fluid mixture. In both papers, the authors examined the effects on the linear properties of the convection of boundary conditions for the temperature of the Newton–Robin type with heat flux prescribed as a limiting case.
Kimura et al. [17] investigated secondary instabilities for a Newtonian fluid saturating a porous medium heated from below by a constant flux. For a Rayleigh number larger than its critical value 12 above which the conduction state looses its stability against long wave instability, these authors used the parallel flow approximation and obtained a nonlinear solution, which corresponds to a monocellular flow. Two-dimensional numerical results were also presented to test the validity of the approximated nonlinear solution. In addition, they analyzed its stability against three-dimensional disturbances and showed that the monocellular flow is linearly stable to transverse disturbances for Rayleigh number as high as 506, at which point, a Hopf bifurcation sets in. However, further analysis indicated that an exchange of stability due to longitudinal disturbances will occur much sooner at a Rayleigh number equal to .
This contribution aims to understand how the viscoelastic character of the fluid influences the properties of convection at the onset of primary and secondary instabilities, when the porous layer is heated from below by a constant flux. Therefore, this work may be viewed as an extension to viscoelastic fluids of the work done by Kimura et al. [17].
The paper is organized as follows. After presenting the governing equations in Section 2, the stability of the conductive state is studied in Section 3 by considering steady, as well as oscillatory three-dimensional perturbations. Section 4 is devoted to the discussion of the combined effects of the viscoelastic parameters and the lateral aspect ratio of the porous medium on the pattern selection at the onset of secondary instabilities. Finally, in Section 5, the main conclusions of the present study are presented.
2. Mathematical Formulation
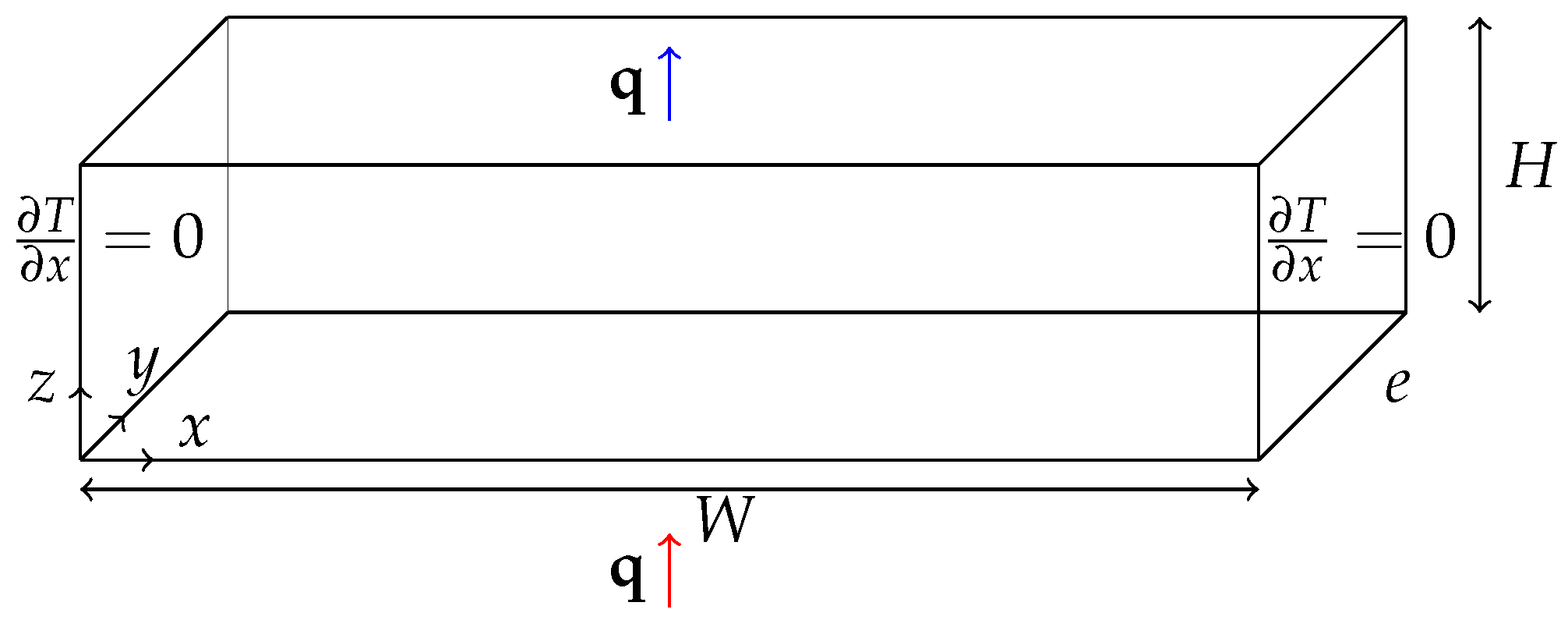
Let us consider an isotropic and homogeneous porous cavity of thickness e, height H and width W (see Figure 1). The porous medium is saturated by an Oldroyd-B fluid, and we assume that the solid matrix is in local thermal equilibrium with the fluid. The upper and lower horizontal walls are kept at constant flux, while the lateral vertical walls are considered adiabatic. The solid walls of the domain are considered impermeable. We assume that the Oberbeck–Boussinesq approximation holds.
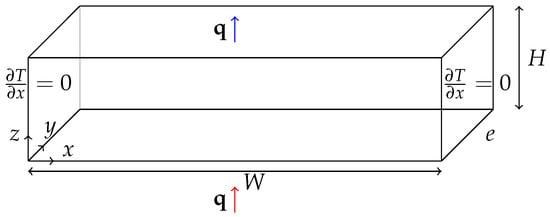
Figure 1.
The porous rectangular cavity heated from below by a constant flux.
There are several ways to obtain macroscopic laws for polymeric flows in a porous medium: by direct numerical simulations of viscoelastic flows in a specific pore geometry model (a good review of these studies can be found in [18]) or by analytical means. In general, the former is the most commonly-used method for the derivation of macroscopic laws. It can be divided in two techniques: the REV method (representative elementary volume method) and the homogenization theory. The starting point for the two techniques is a local description in a pore scale. The pore space is assumed to be saturated by an incompressible viscoelastic fluid. For slow flows, the momentum balance equation can be linearized:
where is the fluid velocity field, is the pressure, is the stress tensor and is the gravity field.
In Newtonian incompressible fluids, the constitutive relation between stress tensor and strain tensor is the Newtonian law , where is the dynamic viscosity, and, in this case, the relation is obtained.
The simplest rheological model useful for describing dilute viscoelastic solutions at high rates of deformation is the Oldroyd-B model. In this model, and for viscoelastic fluids composed of a Newtonian solvent and a polymeric solute of “Newtonian” viscosity and “elastic viscosity” [19], respectively, are given by:
with:
and:
where represents the relaxation time. Then, by combining (2)–(4), we obtain the constitutive equation:
where the dynamic viscosity and the retardation time are related to and by:
An Oldroyd-B fluid may thus be characterized by three parameters: the dynamic viscosity , the relaxation and the retardation times. The relation may also be used instead of .
In order to derive a macroscopic filtration law based on the Oldroyd constitutive equation, we have to introduce, in a fashion similar to that done in the derivation of the classical Darcy law for Newtonian fluids, the superficial velocity defined by:
where is a representative elementary volume (REV) of the medium, incorporating both solid and fluid. Using the REV method by averaging Equation (1) and taking into account Equation (6) leads to:
where K is the permeability.
Under the assumption of low Reynolds number based on the pore dimension, the generalized Darcy’s law (7) is also derived by [20] using a homogenization theory.
The fluid density obeys the state law:
where is the fluid density at temperature , which is chosen here as the temperature at the geometric center of the cavity, and is the thermal expansion coefficient.
Assuming thermal equilibrium between the solid and the fluid phases and neglecting the viscous dissipation effects, energy and continuity equations can then be written as [1,2,3,4,5,6,7,8,9,10]:
The boundary conditions at the impermeable horizontal walls kept at a constant flux q and the impermeable insulated vertical walls are:
Here, (, , , , are respectively the heat capacity per unit volume, the dynamic and kinematic viscosity of the fluid, the effective thermal conductivity and the effective thermal diffusivity. Subscript sf refers to an effective quantity, while f refers to the fluid alone.
We choose H, , , and as reference quantities for the length, velocity, time, pressure and temperature difference (). With this scaling, the following set of dimensionless equations is obtained:
The dimensionless boundary conditions are:
The dimensionless parameters are: the filtration Rayleigh number:
the horizontal and lateral aspect ratios:
the relaxation time:
and the ratio that varies in the interval :
This model reduces to the Maxwell model in the limit and to the Newtonian model in the limit .
In the following, we will examine the stability of the conductive state (the primary instability), as well as the stability of the monocellular flow (the secondary instability).
3. Primary Stationary and Oscillatory Instabilities
In the conductive regime, the basic solution is a motionless state with a vertical thermal stratification .
The aim of this section is to perform a temporal stability analysis of the conductive state with respect to both stationary and oscillatory disturbances.
3.1. Infinite Aspect Ratios
To investigate the stability of the basic solution, infinitesimal three-dimensional perturbations are super-imposed onto the basic solution:
We first assume very large aspect ratios and . The three-dimensional disturbance quantities are expressed as:
where k and l are the wave numbers in the x and y directions, respectively, and the temporal growth rate of unstable perturbations is given by the imaginary part of the complex frequency . Therefore, the neutral temporal stability curve is obtained for , which selects dominant modes at the onset of convection.
Substituting Equations (20), (21) into (12)–(15), linearizing the equations and applying the curl twice to the momentum balance equation, one can obtain:
where and . The corresponding boundary conditions take the form:
The number M of modes is chosen so that the quantitative convergence is secured.
We first examine the single-term Galerkin expansion, or single-term truncation, for the present problem. It allows the generation of analytical expressions that can guide future laboratory experiments, owing to its simplicity. Even when their error in quantitative predictions was high, their qualitative behavior prediction was accurate enough to guide additional numerical efforts. Setting in (25), (26), an algebraic dispersion relation is obtained:
As the viscoelastic parameters appear only in front of a time derivative in the momentum Equation (13) and in front of in the approximated dispersion Equation (27), the elasticity of the fluid cannot influence the properties of a stationary instability. Consequently, the characteristics of the stationary instability are the same as for Newtonian fluids. For such fluids, linear instability analysis has been considered by Nield [11] and has provided quantitative information on the stability condition when the porous layer is supposed infinite in the x and y directions.
On evaluating the minimum of the Rayleigh number defined by (27), we obtain the critical values for the onset of stationarity.
The critical value obtained with a single-term truncation is only percent higher than the exact critical found in [11].
By setting in (27) and minimizing with respect to , we obtain a Hopf bifurcation giving rise to an oscillatory convection if the Rayleigh number exceeds the critical value:
The corresponding critical wave number and critical frequency for oscillatory mode are:
and
As is real, the system exhibits oscillatory convection only if . This condition is satisfied if:
On the other hand, the bifurcation to oscillatory convection precedes the bifurcation to steady convection, i.e., the critical Rayleigh number for oscillatory instability is less than its value for stationary instability if:
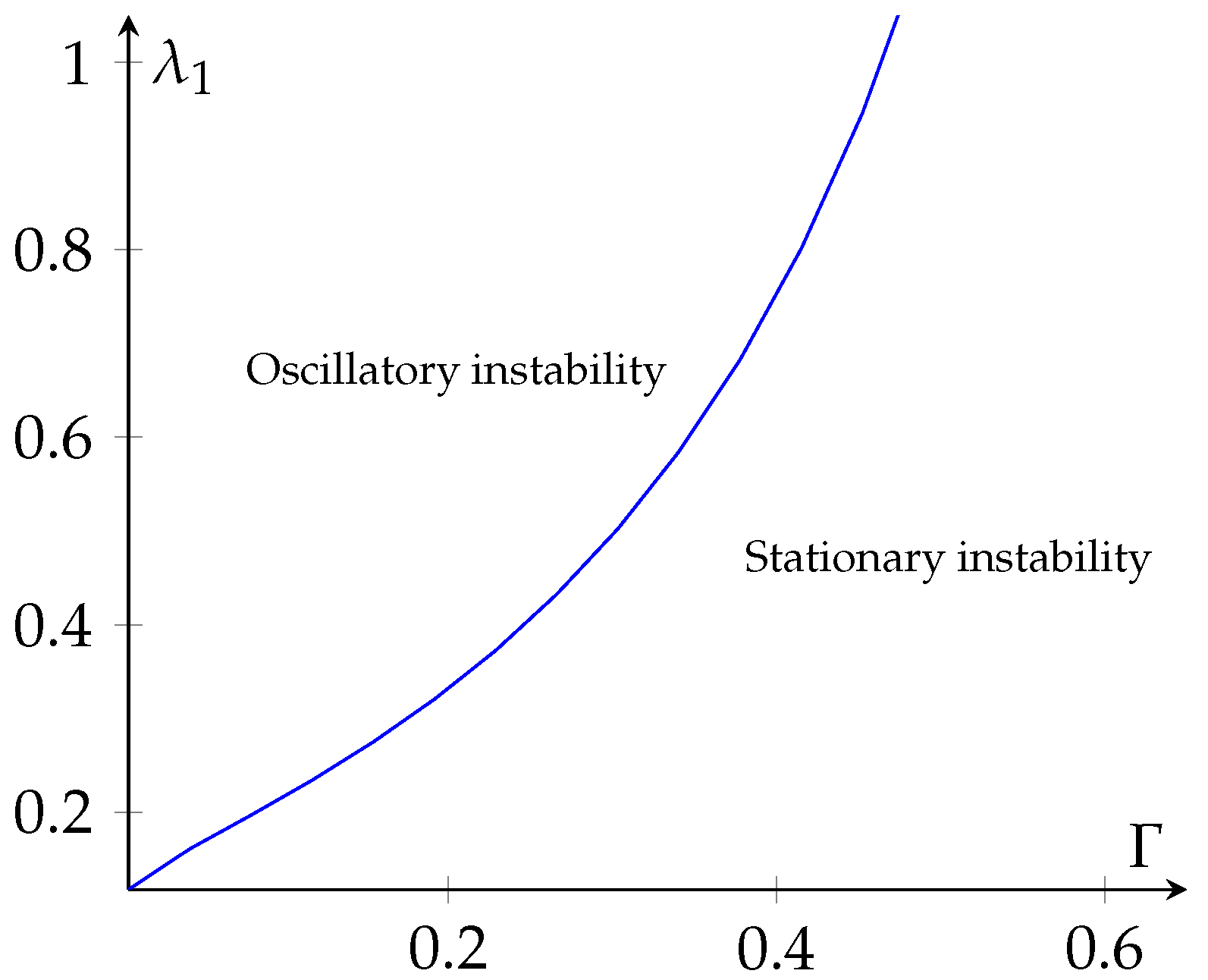
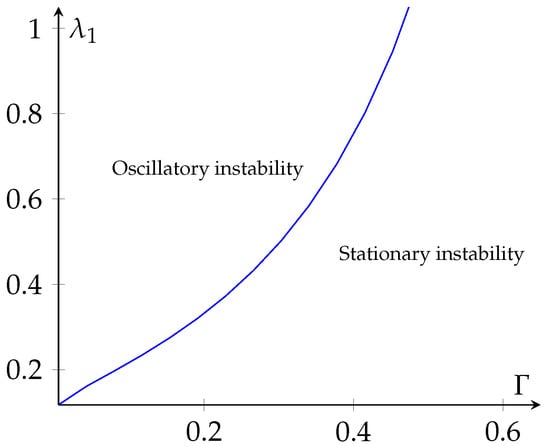
As computations showed that , we concluded that the system selects oscillatory convection as a first instability if . The border separating stationary and oscillatory instabilities is given by the curve , as is shown in the plane (, ) of Figure 2.
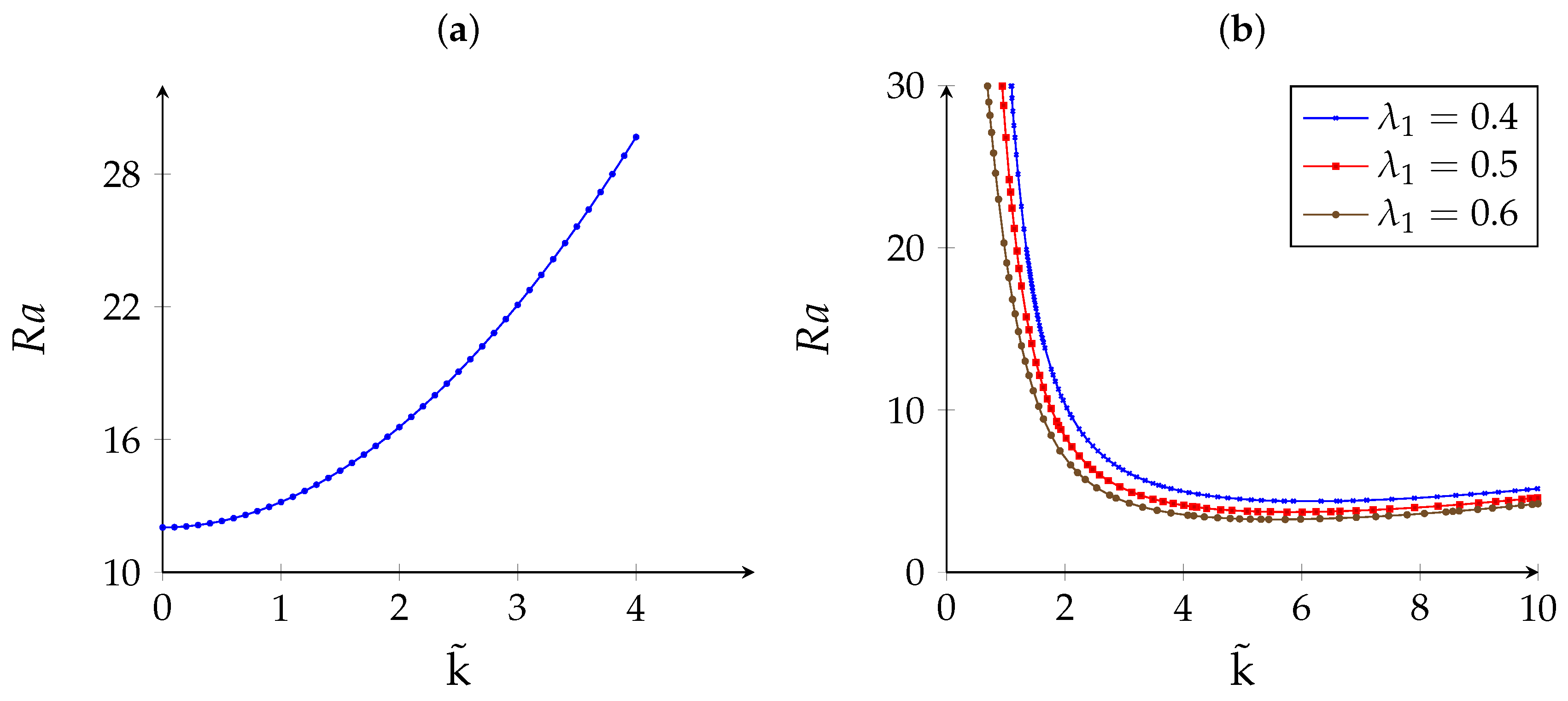
The single-term Galerkin truncation does not present accurate results over the entire range of parameters under consideration, and higher-order truncation becomes necessary. Having used the Galerkin expansion (25) and (26) with , we obtain results with a very good agreement with those obtained in [11] in the case of stationary instability. Figure 3a represents the marginal stability curve in the (, Ra) plane and shows that a long wave instability (i.e., the critical wave number ) may develop if the Darcy–Rayleigh number exceeds the critical value in accordance with the critical value found in [11].
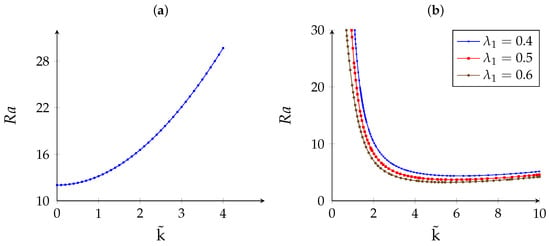
Figure 3.
Neutral stability curves: (a) stationary instability, which exists independently of viscoelastic parameters; (b) oscillatory instability, which may develop first depending on viscoelastic parameters.
In Figure 3b, we plot the curve of neutral stability for oscillatory mode of convection in the plane for and different values of the elasticity number . It can be seen from this figure that the minimum value of the Rayleigh number is lower than the critical Rayleigh number needed to trigger steady long wave instability. Therefore, oscillatory instability may set up as a first convective pattern instead of steady long wave instability.
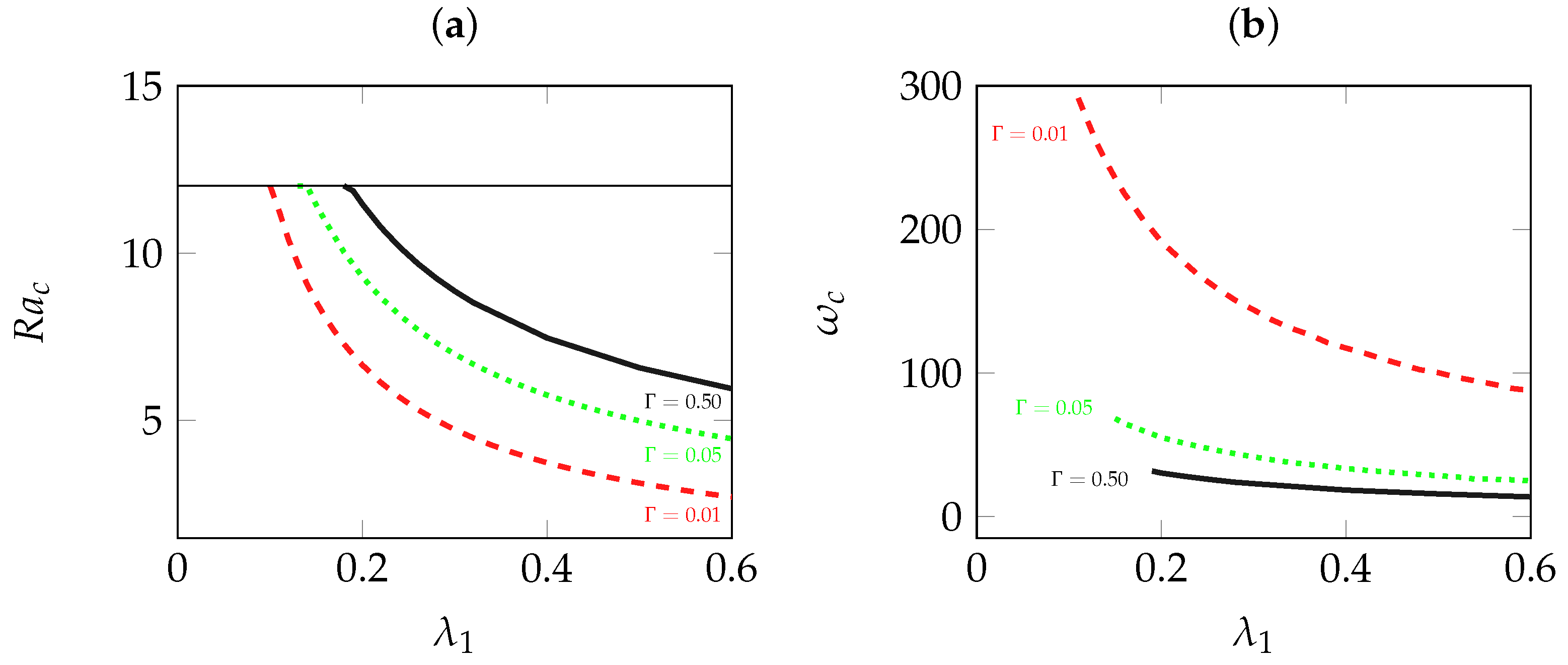
The dependence of the critical Rayleigh number and the critical frequency at the onset of oscillatory convection on the elasticity number for fixed values of is numerically determined, and the results are plotted in Figure 4a,b respectively.
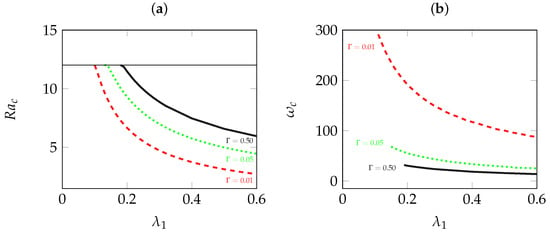
Figure 4.
(a) Critical Rayleigh number and (b) critical frequency at the onset of oscillatory convection as a function of for different values of . The line in (a) corresponds to the critical Rayleigh number at the onset of stationary convection.
It is clear from Figure 4a that an increase in leads to flow destabilization, i.e., to a reduction in the respective critical Rayleigh number. Figure 4a also shows the stabilizing effect of the ratio . Moreover, as is seen in Figure 4a, for a fixed value of , there exists a particular value of where the critical Rayleigh numbers for the onsets of both oscillatory and stationary convection coincide, and therefore, a codimension two bifurcation occurs. For , Figure 4b shows that the critical frequency decreases with the decrease of the fluid elasticity or the increase of the viscosity ratio.
3.2. Effect of Lateral Confinement on Pattern Selection
This section is devoted to investigating the effect of the lateral confinement of the porous cavity by assuming a very large aspect ratio and finite lateral aspect ratio a. The three-dimensional disturbance quantities respecting the boundary conditions (15) are expressed as:
The governing equations are still the system (40) and (41), except with l now replaced by where the integer L is the number of rolls in the y direction.
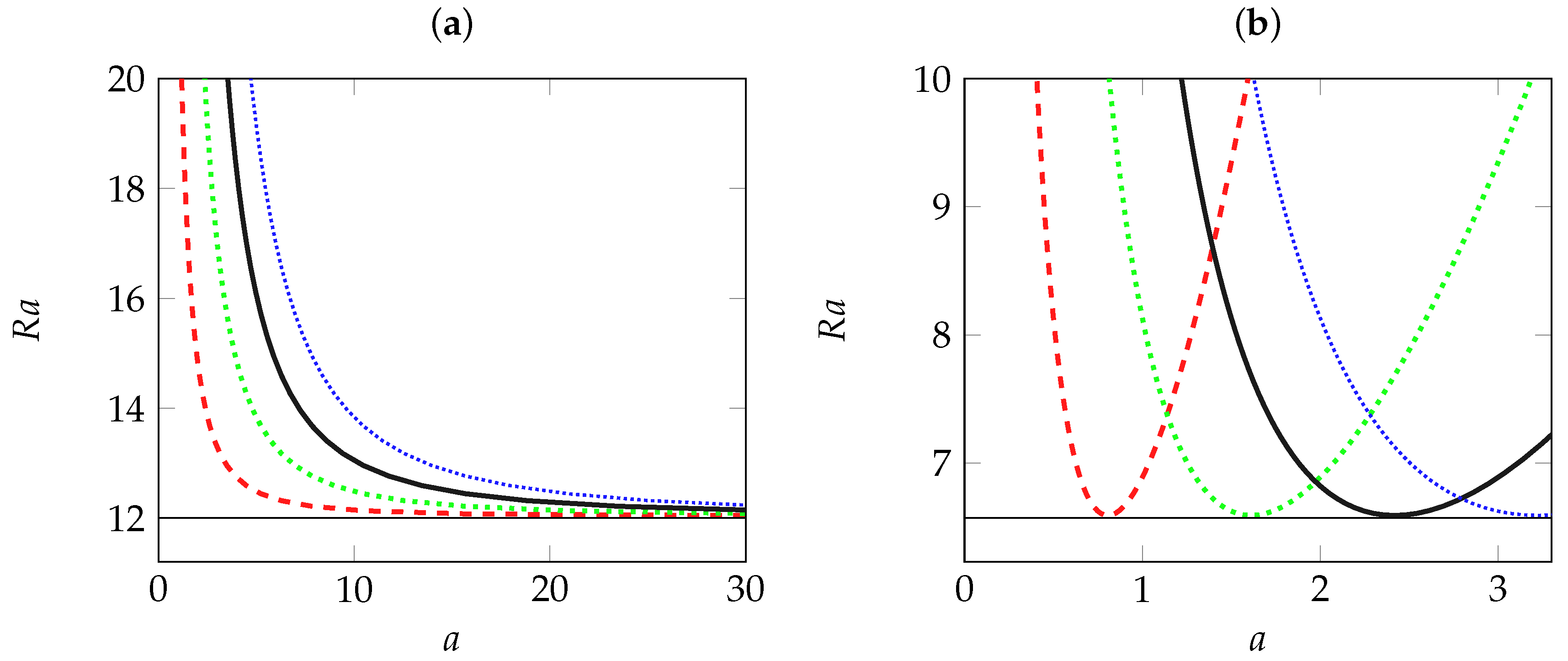
We begin the study by considering the stability of the conductive state against stationary rolls with axes parallel to the x direction, called longitudinal rolls (LRs). Steady longitudinal rolls are characterized by , and . The dependence of the critical Rayleigh number at the onset of LRs on the lateral aspect ratio a for different numbers L of rolls is displayed in Figure 5a. For comparison, we also represent in the same figure the threshold of the steady long wave instability. The threshold of steady three-dimensional patterns in the form of oblique rolls (i.e., , and ) is bounded by the thresholds of the two limiting cases: the steady long wave instability and steady LRs.
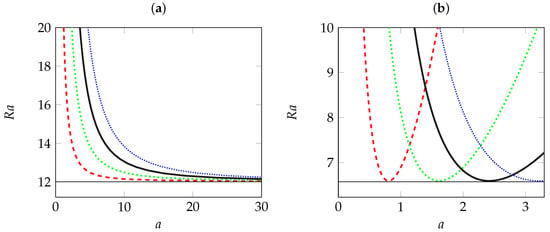
Figure 5.
Critical Rayleigh number against the lateral aspect ratio with different numbers of rolls (: red dashed curve; : green dotted curve; : black dash dotted curve; and : blue densely-dotted curve): (a) steady longitudinal rolls that exist independently of viscoelastic parameters; (b) oscillatory longitudinal rolls for and . In both figures, the horizontal lines indicate the corresponding critical Rayleigh number for transverse rolls.
We remark that the mode is the most unstable mode for LRs. As is expected, we note that the critical Rayleigh number increases as a decreases, meaning that the lateral confinement stabilizes the conductive state against longitudinal rolls. We also note that as , the limiting value of is reached monotonically, and an infinity of modes may be simultaneously unstable in this limit. Consequently, a relatively moderate lateral confinement is necessary to select the long wave instability, which corresponds in real experiments to a monocellular flow in the x direction.
Now, we consider the effect of the lateral confinement on the stability of the conductive state against oscillatory LRs defined by , and . Numerical results for neutral stability curves of oscillatory LRs with , , and are shown in Figure 5b as functions of the lateral aspect ratio a. These curves have a parabolic shape and intersect at some particular values of a, indicating that the true critical Rayleigh number strongly depends on both a and L for fixed rheological parameters. The destabilizing oscillatory LR mode changes in the intersection points of neural curves from a mono-cellular flow to a two-cellular flow, and so on, as the lateral aspect ratio a increases. In addition, the behavior of the critical Rayleigh number is non-monotonic as a increases. We also note that the maximum of critical Rayleigh number decreases as a increases and tends asymptotically to the critical threshold found in the unbounded case (). The results are therefore in contrast to the case of stationary LRs where the dominant mode corresponds to independently of the lateral confinement.
In Figure 5b, the critical Rayleigh number at the onset of oscillatory transverse rolls (TRs) characterized by , and is indicated by the horizontal line. As can be seen from this figure, finite values of a stabilize oscillatory LRs and may select oscillatory TRs as a dominant mode of convection.
4. Secondary Instabilities
4.1. Nonlinear Solution and Formulation of Its Linear Stability
According to the above linear stability analysis, we found that a stationary bifurcation occurs giving rise to a convective pattern in the form of a long wave instability in the x direction provided that the elasticity number does not exceed a particular value , which depends on the viscosity ratio . In that case, the viscoelastic fluid behaves like a Newtonian fluid. Consequently, the nonlinear solution in the regime of steady long wave convection is the same regardless of weather or not the fluid is viscoelastic.
By assuming a shallow cavity and by using the parallel flow approximation [21,22,23], Kimura et al. [17] found that the analytical solution for the monocellular flow consists of: a horizontal asymmetric velocity with a zero mean along any vertical section,
and a vertical, as well as a horizontal stratification of the temperature,
with:
and:
where C is negative or positive according to whether the flow is clockwise or counter-clockwise, and both solutions are possible depending on the initial conditions.
From Equation (39), it is seen that no motion may be induced inside the cavity for . For the case of a porous medium heated from the bottom and cooled from the top by a constant heat flux, a critical Rayleigh number of for the onset of convection was predicted by Nield [11]. This result is in agreement with the prediction of Equation (39).
For finite aspect ratio, Kimura et al. [17] performed two-dimensional numerical simulations of the full problem. Their numerical results show that the conductive state is stable when the Rayleigh number is smaller than 12. Computations carried out for Ra in excess of 12 were found to agree with analytical solutions (36)–(38).
The equations governing the linear stability of the monocellular flow are obtained by the same previous approach used for the stability of the conductive basic solution. By assuming very large aspect ratios and , the following system is obtained:
where we substitute and by their explicit expressions (36)–(38).
The corresponding boundary conditions take the form:
4.2. Results for Newtonian Fluids
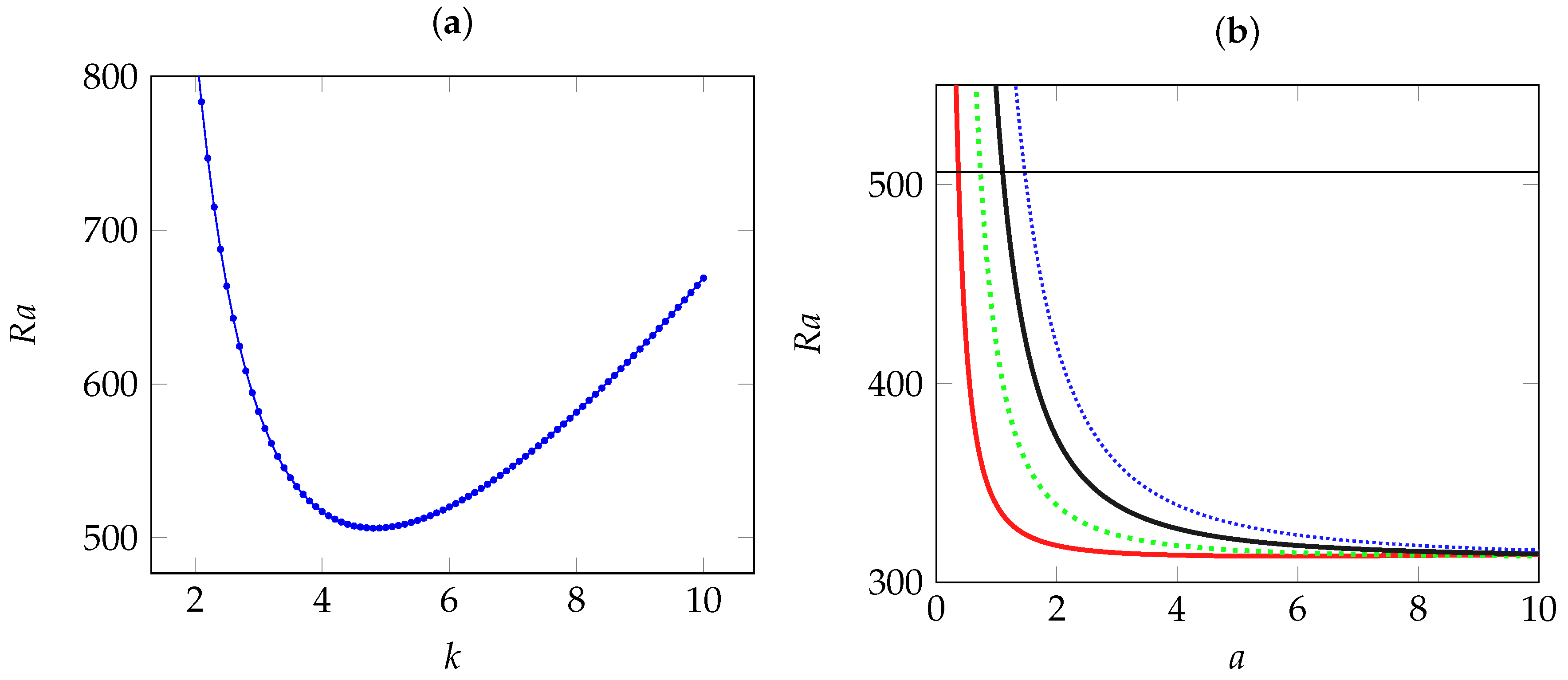
To verify the accuracy of our numerical results based on the Galerkin expansion to the order , we perform a test for the limiting case of a Newtonian fluid and compare the results with those obtained by Kimura et al. [17]. In the first instance, two-dimensional disturbances, corresponding to , were considered. We found out that for the Newtonian fluid, the base velocity and temperature profiles (36)–(38) are stable for values of less than as shown by the neutral stability curve represented in Figure 6a. At this critical Rayleigh number occurs an instability via a Hopf bifurcation to oscillatory TRs with a critical frequency and a critical wave number . These results are in a good agreement with those obtained in [17] by using a shooting method, namely , and .
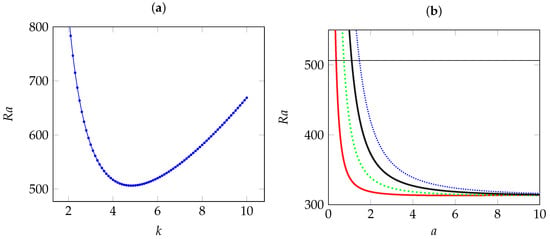
Figure 6.
Newtonian fluids: (a) neutral stability curve at the onset of oscillatory transverse rolls; (b) critical Rayleigh number at the onset of steady longitudinal rolls against the lateral aspect ratio with different numbers of rolls (: red dashed curve; : green dotted curve; : black dash dotted curve; and : blue densely-dotted curve). The horizontal line corresponds to the threshold of oscillatory transverse rolls.
On the other hand, Kimura et al. [17] considered three-dimensional disturbances with the value of the y-wave number l being gradually increased from zero. For , the stability analysis indicates that the monocellular flow will be destabilized not by a Hopf bifurcation, but by an exchange of stability for which the x-wave number k vanishes. In that case the threshold of the appearance of steady longitudinal rolls as a secondary instability is found to be . Since this critical Rayleigh number is much lower than any of those for the Hopf bifurcations obtained when , Kimura et al. [17] concluded that the monocellular flow will in fact be destabilized by longitudinal, rather than transverse, disturbances.
In the second instance, three-dimensional disturbances, corresponding to and , were considered in this study. Numerical results performed by assuming infinite aspects ratios A and a indicated that the most unstable mode corresponds to and . The corresponding critical Rayleigh number above which this most unstable mode is in the form of steady LRs is . Once again, this critical value agrees very well with obtained in [17].
In the third instance, the effect of the confinement of the porous medium in the y direction is explored. We plot in Figure 6b the critical Rayleigh number against the aspect ratio for several of the leading modes, from which it is clear that remains the destabilizing mode, ahead of the other modes , and that the order of these modes, in the sense that , is preserved as a increases. In particular, we also note that as , the limiting value of is approached monotonically. Figure 6b also shows that the curve corresponding to steady longitudinal mode with intersects the line at a particular value of the lateral aspect ratio . This means that perturbations promote the appearance of oscillatory TRs provided that or stationary LRs otherwise.
4.3. Results for Viscoelastic Fluids
4.3.1. Hopf Bifurcation to Transverse Rolls
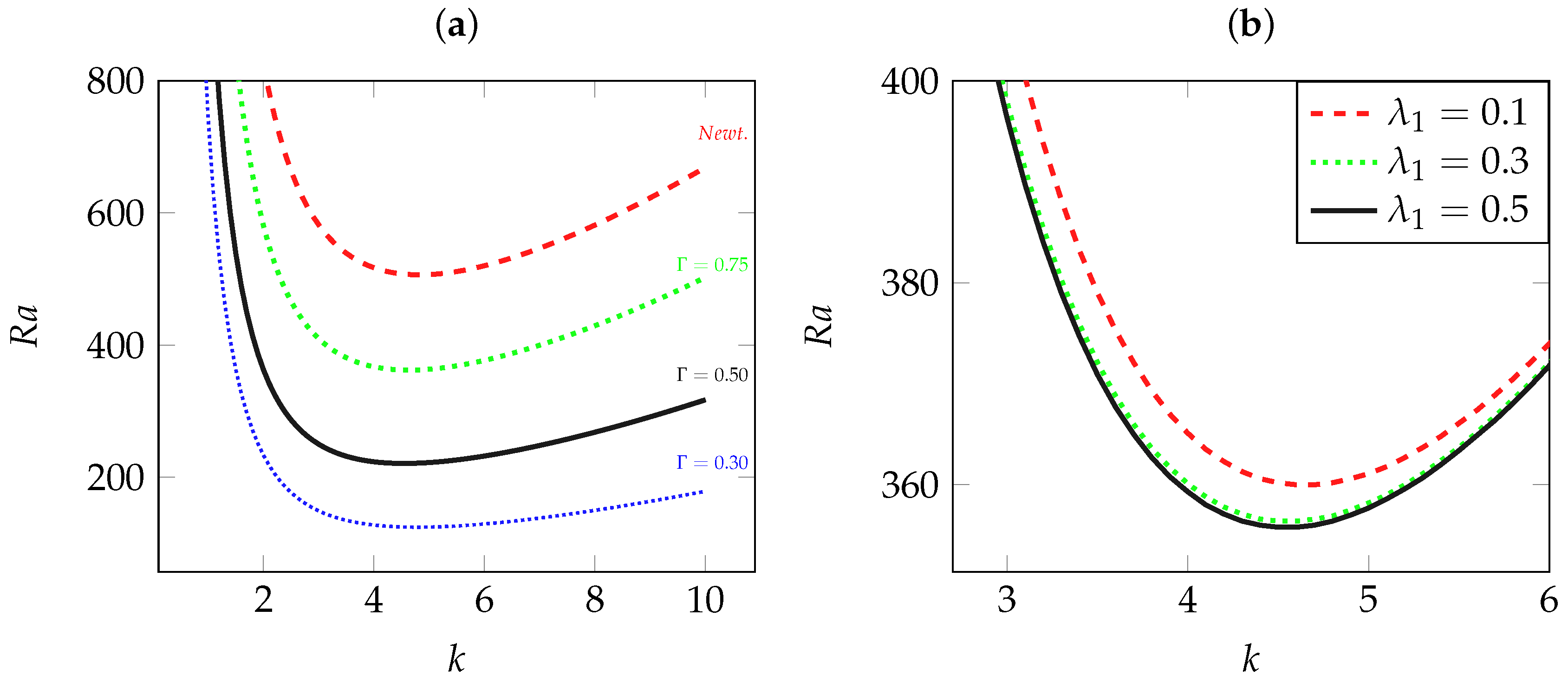
In order to study the influence of viscoelastic parameters on the secondary instability, we first computed the bifurcation line from a stationary monocellular convective pattern to oscillatory TRs for either a fixed value of the elasticity number with varying values of the viscosity ratio or a fixed value of with varying values of . With regard to the question of the influence of the viscosity ratio for a viscoelastic fluid with a relaxation time on the onset of a secondary instability in the form of oscillatory TRs, Figure 7a illustrates the behavior of neutral stability curves in the plane for , and . For a comparison, the Newtonian case is also represented on Figure 7a.
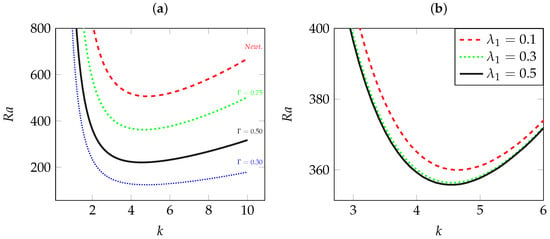
Figure 7.
Critical Rayleigh number for the destabilization of fully-developed flow against the wave number k with for Newtonian fluids (Newt) and for viscoelastic solutions with: (a) and ; (b) and .
We note in this figure that the minimum of neutral stability curves increases when is augmented to reach the critical value for Newtonian fluids in the limit of . Physically, this result means that concentrated polymeric solutions with a small viscosity ratio favor the appearance of oscillatory multicellular flow convection as a secondary instability. On the other hand, for diluted viscoelastic solutions, more heating is needed to trigger the secondary instability.
We report in Table 1 the computed results of critical Rayleigh number , critical frequency and critical wave number at the onset of the secondary instability organized as oscillatory TRs for and different values of . Table 1 shows a strong stabilizing effect of the viscosity ratio. The values of the critical oscillatory frequency decrease with decreasing . This implies that emerging transversal convection rolls have a larger time-period and move with a larger phase velocity when the polymer concentration is high.

Table 1.
Critical Rayleigh number , frequency and wave number at the onset of moving transverse rolls as a secondary instability for and different values of .
We now present results corresponding to the influence of the fluid elasticity by considering the properties of the emerging oscillatory TRs at different values of for a fixed value of . Figure 7b presents neutral stability curves for , a typical viscosity ratio value for Boger fluids and different values of the relaxation time , and . We note from this figure that the neural stability curves are nearly superposed when is increased, meaning that beyond , the increase in the fluid elasticity has little influence on the critical Rayleigh number at the onset of oscillatory TRs. Table 2 gathers the results for seven values of . It can be observed from Table 2 that critical Rayleigh number , critical frequency and critical wave number at the onset of the secondary instability are weakly dependent on the elasticity number number . We conclude that the preponderant effect on the properties of the emerging oscillatory TRs is mainly linked to the variations in the viscosity ratio, while the effect of the elasticity remains very weak.

Table 2.
Critical Rayleigh number , frequency and wave number at the onset of moving transverse rolls as a secondary instability for and different values of .
4.3.2. Bifurcation to Steady or Oscillatory Longitudinal Rolls
Finally, we present in the second part of this section the secondary instability results in the case where disturbances are assumed in the form of longitudinal rolls LRs. We mention that as for the primary instability, the onset of stationary LRs convection is not affected by the two viscoelastic parameters. Consequently, the critical Rayleigh number above which stationary LRs convection develops as a secondary instability is the same as that found for Newtonian fluids, namely . However, the computations indicate Hopf bifurcation from steady unicellular flow to oscillatory LRs convection. We emphasize that the Hopf bifurcation to oscillatory LRs is not observed for Newtonian fluids and is due solely to the viscoelastic character of the fluids. The effects of the two viscoelastic parameters on the linear properties of the oscillatory LRs convection are examined in the remainder of this subsection. In order to evaluate the effect of elasticity alone, the , and cases are investigated for a fixed . On the other hand, the effect of viscosity ratio alone is studied by fixing and investigating the , , and cases. The computed results for the six different cases are reported in Table 3, which indicates the critical Rayleigh number, wave number and oscillatory frequency at the onset of oscillatory LRs’ secondary instability. As has already been highlighted in the previous sections considering the primary instability and the TRs’ secondary instability, we recognize the destabilizing effect of the elasticity number and the stabilizing effect of the viscosity ratio . Moreover, a comparison of Table 1, Table 2 and Table 3 attests that the frequencies of oscillatory LRs are much smaller than those corresponding to oscillatory TRs.

Table 3.
Critical Rayleigh number , frequency and wave number at the onset of oscillatory longitudinal rolls as the secondary instability for different values of and .
An additional remark about Table 3 is necessary. For comparison purposes, we also indicate in this table the threshold of both stationary and oscillatory LRs. It is clear that the true critical Rayleigh number depends on the combination of the rheological parameters. The least stable mode of convection is the one with smallest critical Rayleigh number and is identified in Table 3 with a bold character. For instance, we consider diluted viscoelastic solutions with with different elasticity number . For the combination of the rheological parameters (, ), the true critical Rayleigh number is , indicating that the secondary instability pattern is in the form of steady LRs. In that case, polymeric solutions are almost inelastic and evolve as a Newtonian fluid. In contrast, for the combination (, ), the least stable mode of convection changes from steady LRs to oscillatory LRs, meaning that elastic effects become the most important ones in this range. In the same way, the preferred pattern as a secondary instability depends on the viscosity ratio . Table 3 shows that by keeping and decreasing gradually from (diluted solutions) to (concentrated solutions), the most amplified mode of convection evolves from steady LRs to oscillatory LRs and eventually to oscillatory TRs.
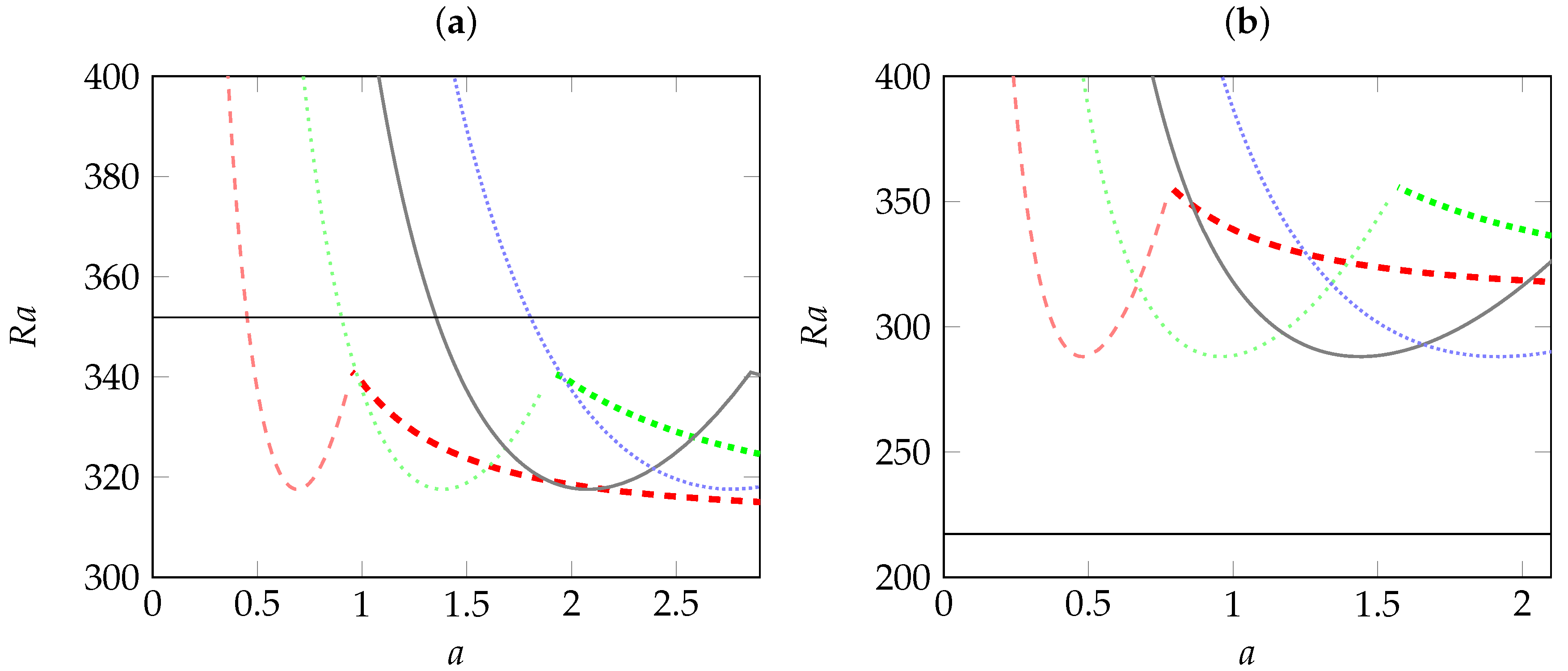
All of the results stated in the Section 4.3 are obtained by assuming infinite aspects ratios in the x and y directions. For the sake of brevity, we exemplify the effect of the lateral aspect ratio a on the pattern selection for two combinations of rheological parameters (, ) and (, ). We plot in Figure 8a,b the variation of the critical Rayleigh number for both stationary LRs and oscillatory LRs as a function of the lateral aspect ratio a in the cases (, ) and (, ), respectively. Computations showed that there is a competition between the two patterns in the sense that depending on the magnitude of lateral confinement, the system may select either stationary LRs or oscillatory LRs. For a fixed value of L and by increasing a, the following behavior is observed for the curves representing the critical Rayleigh number for LRs and all values of rheological parameters (see Figure 8a,b): (i) the curve associated with the critical Rayleigh number of oscillatory LRs decreases to reach a minimum equal to its value for infinite a. This minimum point moves to the right in the (a, ) plane when the number of rolls L is increased; (ii) then, the same curve increases to intersect another branch corresponding to the critical Rayleigh number of steady LRs at a particular value of a; (iii) finally, when a exceeds this particular value, the curve associated with the critical Rayleigh number of steady LRs becomes the lower curve, decreases monotonically and tends asymptotically to the critical Rayleigh number of steady LRs found in the case of infinite a.
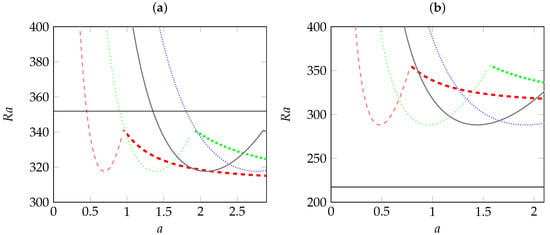
Figure 8.
Critical Rayleigh number for the onset of steady (ultra thick curves) and oscillatory (thick curves) longitudinal rolls as a function of aspect ratio a for different numbers L of rolls (: red dashed curve; : green dotted curve; : black dash-dotted curve; : blue densely-dotted curve). (a) and ; (b) and . The horizontal line corresponds to the threshold of oscillatory transverse rolls.
For the particular combination (, ) and in the limit of infinite a, the critical Rayleigh number of steady LRs is less than the critical Rayleigh number of oscillatory LRs. Consequently, the decreasing curve of the critical Rayleigh number of steady LRs (ultra thick curve) with crosses the absolute minimum of oscillatory LRs at a particular value ( as shown in Figure 8a). This means that for all values of a larger than , the dominant mode of convection is a steady monocellular LRs. Otherwise, the system may select oscillatory LRs or steady monocellular LRs depending on a. It is important to note that Figure 8a also shows that the curve corresponding to oscillatory longitudinal mode (thick curve) with intersects the horizontal line representing the critical Rayleigh number of oscillatory TRs at a particular value of the lateral aspect ratio . This means that perturbations promote the appearance of oscillatory TRs if , oscillatory LRs or a steady monocellular LRs if and stationary LRs if .
In the case of the combination (, ), this behavior is not observed, since as can be seen from Figure 8b, the critical Rayleigh number of oscillatory TRs is much smaller than the critical Rayleigh number for both stationary and oscillatory LRs. For this particular combination, the system selects oscillatory TRs independently of the lateral confinement.
5. Conclusions
In the present paper, the Galerkin method was used to investigate the primary and secondary instabilities of viscoelastic fluids saturating a porous layer heated from below by a constant flux. The modified Darcy’s law based on the Oldroyd-B model was used for modeling the momentum equation. In addition to the Darcy–Rayleigh number , two viscoelastic parameters play a key role when characterizing the temporal behavior of the instability, namely the relaxation time , which measures the elasticity of the fluid and the ratio between the viscosity of the solvent and the total viscosity of the fluid. In the first part of the paper, three-dimensional disturbances were considered in order to study the stability of the basic motionless solution. For sufficiently elastic fluids, we found that the primary instability is oscillatory. Otherwise, the primary bifurcation gives rise to stationary long wave instability. Results indicated that the lateral confinement of the porous layer by isolated side walls eliminates oblique or longitudinal rolls in favor of two-dimensional transverse rolls. Based on a fully-developed parallel flow assumption, a nonlinear analytical solution for the velocity and temperature fields was developed in the range of the rheological parameters where stationary long wave instability develops first. In the second part of the paper, we reported findings on the linear stability analysis of the monocellular flow, which is performed with special attention given to the interplay between the viscoelastic parameters and the lateral aspect ratio a of the porous layer. For weakly-elastic fluids, we determined a second critical value of Rayleigh number above which the system exhibits a Hopf bifurcation from steady monocellular flow to oscillatory transverse rolls convection. The well-known limit of for Newtonian fluids is recovered, and the fluid elasticity effect is found to delay the onset of the Hopf bifurcation.
Three-dimensional analysis showed that for the diluted solutions, as the Boger fluid type (i.e., ), the monocellular flow is more unstable for either stationary longitudinal disturbances for weakly-elastic fluids () or for oscillatory longitudinal rolls for strongly-elastic fluids (). This pattern selection holds if the lateral walls are pushed to infinity. When a finite lateral confinement is taken into account, there exist particular values and of the lateral aspect ratio a such that perturbations promote the appearance of oscillatory transverse rolls if , stationary or oscillatory longitudinal rolls if and stationary longitudinal rolls if . Computations proved that the interval is enlarged by increasing the fluid elasticity.
For concentrated viscoelastic fluids (, and ), it is found that oscillatory transverse rolls are the preferred mode of convection even for weakly-elastic fluids and independently of the lateral confinement of the porous medium.
Author Contributions
Abdoulaye Gueye undertook this research as part of his Ph.D. studies. Mohamed Najib Ouarzazi supervised the work and assisted with the preparation of the manuscript. Silvia Hirata and Haikel Ben Hamed assisted with numerical tools.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kim, M.C.; Lee, S.B.; Kim, S.; Chung, B.J. Thermal instability of viscoelastic fluids in porous media. Int. J. Heat Mass Transf. 2003, 46, 5065–5072. [Google Scholar] [CrossRef]
- Yoon, D.; Kim, M.C.; Choi, C.K. The onset of oscillatory convection in a horizontal porous layer saturated with viscoelastic liquid. Transp. Porous Media 2004, 55, 275–284. [Google Scholar] [CrossRef]
- Bertola, V.; Cafaro, E. Thermal instability of viscoelastic fluids in horizontal porous layers as initial value problem. Int. J. Heat Mass Transf. 2006, 49, 4003–4012. [Google Scholar] [CrossRef]
- Hirata, S.C.; Ella Eny, G.; Ouarzazi, M.N. Nonlinear pattern selection and heat transfer in thermal convection of a viscoelastic fluid saturating a porous medium. Int. J. Therm. Sci. 2015, 95, 136–146. [Google Scholar] [CrossRef]
- Hirata, S.C.; Ouarzazi, M.N. Three-dimensional absolute and convective instabilities in mixed convection of a viscoelastic fluid through a porous medium. Phys. Lett. A 2010, 374, 2661–2666. [Google Scholar] [CrossRef]
- Alves, L.S.B.; Barletta, A.; Hirata, S.; Ouarzazi, M.N. Effects of viscous dissipation on the convective instability of viscoelastic mixed convection flows in porous media. Int. J. Heat Mass Transf. 2014, 70, 586–598. [Google Scholar] [CrossRef]
- Delenda, N.; Hirata, S.C.; Ouarzazi, M.N. Primary and secondary instabilities of viscoelastic mixtures saturating a porous medium: Application to separation of species. J. Non-Newton. Fluid Mech. 2012, 181, 11–21. [Google Scholar] [CrossRef]
- Fu, C.J.; Zhang, Z.Y.; Tan, W.C. Numerical simulation of thermal convection of a viscoelastic fluid in a porous square box heated from below. Phys. Fluids 2007, 19, 104107. [Google Scholar] [CrossRef]
- Taleb, A.; Ben Hamed, H.; Ouarzazi, M.N.; Beji, H. Analytical and numerical analysis of bifurcations in thermal convection of viscoelastic fluids saturating a porous square box. Phys. Fluids 2016, 28, 053106. [Google Scholar] [CrossRef]
- Niu, J.; Fu, C.J.; Tan, W.C. Stability of thermal convection of an Oldroyd-B fluid in a porous medium with Newtonian heating. Phys. Lett. A 2010, 374, 4607–4613. [Google Scholar] [CrossRef]
- Nield, D.A. Onset of thermohaline convection in a porous medium. Water Resour. Res. 1968, 4, 553–560. [Google Scholar] [CrossRef]
- Nield, D.A.; Bejan, A. Convection in Porous Media; Springer: New York, NY, USA, 2006. [Google Scholar]
- Mamou, M.; Mahidjiba, A.; Vasseur, P.; Robillard, L. Onset of convection in an anisotropic porous medium heated from below by a constant heat flux. Int. Commun. Heat Mass Trans. 1998, 25, 799–808. [Google Scholar] [CrossRef]
- Mojtabi, A.; Rees, D.A.S. The effect of conducting bounding plates on the onset of Horton-Rogers-Lapwood convection. Int. J. Heat Mass Trans. 2011, 54, 293–301. [Google Scholar] [CrossRef]
- Falsaperla, P.; Mulone, G.; Straughan, B. Rotating porous convection with prescribed heat flux. Int. J. Eng. Sci. 2010, 48, 685–692. [Google Scholar] [CrossRef]
- Falsaperla, P.; Giacobbe, A.; Mulone, G. Double diffusion in rotating porous media under general boundary conditions. Int. J. Heat Mass Trans. 2012, 55, 2412–2419. [Google Scholar] [CrossRef]
- Kimura, S.; Vynnycky, M.; Alavyoon, F. Unicellular natural circulation in a shallow horizontal porous layer heated from below by a constant flux. J. Fluid Mech. 1995, 294, 231–257. [Google Scholar] [CrossRef]
- Skartsis, L.; Khomami, B.; Kardos, J.L. Polymeric flow through fibrous media. J. Rheol. 1992, 36, 589–620. [Google Scholar] [CrossRef]
- Joseph, D.D. Fluid Dynamics of Viscoelastic Liquids; Springer: New York, NY, USA, 1990. [Google Scholar]
- Khuzhayorov, B.; Auriault, J.L.; Royer, P. Derivation of macroscopic filtration law for transient linear viscoelastic fluid flow in porous media. Int. J. Eng. Sci. 2000, 38, 487–504. [Google Scholar] [CrossRef]
- Bejan, A. The boundary layer regime in a porous layer with uniform heat flux from the side. Int. J. Heat Mass Transf. 1983, 26, 1339–1346. [Google Scholar] [CrossRef]
- Vasseur, P.; Satish, M.G.; Robillard, L. Natural convection in a thin, inclined, porous layer exposed to a constant heat flux. Int. J. Heat Mass Transf. 1987, 30, 537–549. [Google Scholar] [CrossRef]
- Sen, M.; Vasseur, P.; Robillard, L. Multiple steady states for unicellular natural convection in an inclined porous layer. Int. J. Heat Mass Transf. 1987, 30, 2097–2113. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).