Abstract
There is no theoretical underpinning that successfully explains how turbulent mixing is fed by wave breaking associated with nonlinear wave-wave interactions in the background oceanic internal wavefield. We address this conundrum using one-dimensional ray tracing simulations to investigate interactions between high frequency internal waves and inertial oscillations in the extreme scale separated limit known as “Induced Diffusion”. Here, estimates of phase locking are used to define a resonant process (a resonant well) and a non-resonant process that results in stochastic jumps. The small amplitude limit consists of jumps that are small compared to the scale of the resonant well. The ray tracing simulations are used to estimate the first and second moments of a wave packet’s vertical wavenumber as it evolves from an initial condition. These moments are compared with predictions obtained from the diffusive approximation to a self-consistent kinetic equation derived in the ‘Direct Interaction Approximation’. Results indicate that the first and second moments of the two systems evolve in a nearly identical manner when the inertial field has amplitudes an order of magnitude smaller than oceanic values. At realistic (oceanic) amplitudes, though, the second moment estimated from the ray tracing simulations is inhibited. The transition is explained by the stochastic jumps obtaining the characteristic size of the resonant well. We interpret this transition as an adiabatic ‘saturation’ process which changes the nominal background wavefield from supporting no mixing to the point where that background wavefield defines the normalization for oceanic mixing models.
1. Introduction
One of the stories that gets told in Physical Oceanography is that, at the turn of the preceding century, there was one major unsolved problem in Physics, turbulence, and some niggling questions concerning an ultraviolet catastrophe. Physics then went off and did the easier problem, resulting in Quantum Mechanics. While we do have some understanding of turbulence in a homogeneous setting deriving from Kolmogorov [1], we remain generally ignorant about the relation of turbulence to the various species of waves that support turbulence through a spatially inhomogeneous and temporally intermittent breaking process. In short, the difficult problem of developing an understanding of strongly interacting waves that leads to wave breaking and turbulence remains.
The ultraviolet catastrophe is a prediction, assuming an equipartition of energy in the harmonic oscillator modes of a system in thermal equilibrium, that an ideal black body will emit an infinite amount of radiation. There are two aspects to the oceanic ultraviolet catastrophe. Both are both based upon a theory of nonlinear transfers of energy between internal waves formulated as a system of coupled harmonic oscillators [2,3,4]. This theory ultimately results in a Fokker-Planck, or generalized diffusion, equation with the following properties. First, energy in the internal wavefield will typically be transferred from large vertical scales to small at constant horizontal wavenumber and consequently from high frequency to low [5]. With such transfer, a source of internal wave energy at high frequency is required for a stationary balance. A recent systematic review of the nonlinear transfers and possible energy sources of the oceanic internal wavefield [6] strongly suggests that the required energy source at high frequency does not exist. Yet that same theory makes a prediction for the spectral power laws of statistically stationary states that are in good agreement with observed oceanic spectra, Figure 1. The second aspect to the oceanic catastrophe is that the Garrett and Munk 1976 (GM76) version of the oceanic spectrum, which was given “universal” status in [7], is not just a stationary state in the coupled oscillator paradigm: Having no gradients of action in vertical wavenumber, GM76 is a no flux solution of the Fokker-Planck equation, which means no transport of energy to smaller scales. Again, it is highly unlikely that this prediction can be observationally sustained.
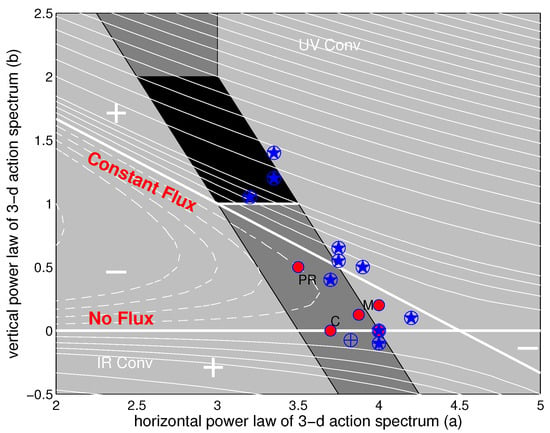
Figure 1.
Estimates of frequency and vertical wavenumber power laws cast in terms of a three dimensional action spectrum with horizontal wavenumber magnitude and vertical wavenumber m and overlain on a theoretical paradigm map. Blue symbols represent power law fits to ocean observations. See [6] (their Figure 36) for the identification of the field programs. Filled circles represent scale-invariant stationary states identified by [8] (PR), a convergent numerical solution determined in [9] (C), the GM76 spectrum at and curve fits to two possible dynamic balances identified in [5] (M). Thin white contours are proportional to the action tendency in the Fokker–Plank with symbols denoting the sign. The [5] states lie in a part of parameter space with decreasing spectral amplitude, which then requires an unidentified source to remain in a steady state. Overlain as thick white lines are the induced diffusion stationary states with the constant flux solution trending diagonally and the no-flux solution lying horizontal along . Adapted from [6], their Figure 37.
The glaring nature of this tension is exposed with the use of finescale parameterizations that seek to characterize the interaction of high frequency waves with near-inertial shear leading to a net downscale transport of energy, turbulent production and mixing. The finescale parameterization was originally set [10] as a high wavenumber gate beyond which wave breaking effects would balance a downscale flux, with no theoretical underpinning for that flux. The finescale parameterization was generalized in [11,12] as an energy (not wave action) cascade process in order to permit its application at larger vertical scales. This generalization is a heuristically motivated advective (not diffusive) closure underpinned by empirical evidence [11,13] that demands spectral transports in horizontal wavenumber similar to those in vertical wavenumber, to the effect that transports in the frequency domain are minimal. In that work the GM76 spectrum is special only in that it serves as a normalization for a finite downscale energy transport.
To date there is no theoretical justification for this finescale parameterization. Yet it has seen wide application in the field (see [13] for a recent review) with the only parameterization vs. data discrepancies arising from wave-mean interactions and from double-diffusive contributions to dissipation.
The first inconsistency could be resolved by recognizing that the historical characterization of the coupled oscillator paradigm is incomplete. Polzin and Lvov [6] present evidence that the coupled oscillator paradigm contains transfers in horizontal wavenumber, which in turn imply transports in frequency that could offset those implied by transfers in vertical wavenumber. These horizontal interactions appear as ‘unclassified triads’ in evaluations of resonant kinetic equations [14,15] and appear to be ‘local’ in the spectral domain [6]. While the presence of unclassified triads is acknowledged in the early literature, they did not fit into the prevailing paradigm of extreme scale separated interactions [14] and lacked interpretation.
The advective nature of the finescale parameterization was motivated in part by ray-tracing results that suggested a non-diffusive behavior of high frequency internal waves in inertial shear [16]. The interpretation is ambiguous as those ray tracing results are compared with a resonant model of diffusion, so that the identification of non-diffusive behavior could simply be a broadened version of a diffusive closure. Providing the wherewithal to make this judgement, though, requires digging deep into the toolbox of Wave Turbulence.
Wave Turbulence is a collection of general techniques for examining nonlinear interactions within many wave systems, with an emphasis on the coupled oscillator paradigm. A perfect introduction and good reference is provided in [17]. Wave Turbulence in its application to high frequency internal waves has important nonlocal elements. In other words, the statistics of internal waves are determined, in large, by nonlinear interactions between internal waves with a significant scale separation between interacting wave vectors. Nonlocal wave turbulence appears in other well known and intensively studied contexts such as Rossby waves and Magneto Hydro Dynamics (MHD) of the solar wind [18]. Ray tracing [19] provides an alternate description of nonlocal interactions and, while it may seem intuitively obvious [20,21] that one might arrive at a diffusive characterization for ray tracing, the first investigation of the general connection between a diffusive approximation to the kinetic equation and ray tracing of which we are aware is contained in [22]. The sticking point is that the diffusion coefficient for ray tracing defies a first principals closure. We will be making judgements about behavior at finite amplitude and thus will require a broadened kinetic equation [23].
Given that both ray tracing and kinetic equations can be rigorously derived from Hamiltonian formulations [24], our tack here is to define a model of high frequency internal wave interactions with inertial shear that minimizes the algebraic infrastructure and permits us to obtain rigorous analytic results from a broadened kinetic equation that can compared with results from ray tracing simulations. At small amplitude, our ray tracing results are consistent with metrics of diffusive behavior derived from the kinetic equation. These ray tracing simulations reveal a transition to a non-diffusive behavior at oceanic amplitudes. Analysis of the corresponding kinetic equation returns an amplitude dependent change in the scaling of the resonant bandwidth, as conjectured by [25,26], but this change in scaling is independent of the breakdown in the diffusive behavior of the ray tracing simulations.
To rationalize the difference we make a distinction between the basis functions used to describe the nonlinear interactions that is grounded in the notion that a signal
has a instantaneous frequency and an instantaneous bandwidth [27], which, in the mean, implies the bandwidth B has variance
and mean frequency . At finite amplitude, kinetic equations are set up as a system of coupled oscillators with wave frequency and wave number obeying a well defined dispersion relation. Wave amplitudes are a function of time:
This defines an amplitude modulated (AM) process. Associated with this amplitude modulation is a bandwidth , a corresponding equation for that bandwidth and an assumption that:
This is the basic inequality that defines a weakly nonlinear system in the coupled oscillator paradigm.
On the other hand, ray tracing considers the localization of a wave packet on spatial scales and time scales that are large relative to the spatial scales corresponding to wavenumber :
If is interpreted as the action spectral density, action density is conserved along ray trajectories so that the bandwidth associated with the nonlinearity appears as the modulation of the phase associated with variations in the Doppler shift as the wave packet refracts in a background velocity profile . The bandwidth in the ray tracing paradigm is thus related to a phase modulation, an FM process. The ray tracing approach is limited by the lack of a systematic theory for assessing spectral transports. However, it comes with no explicit assumption of weak nonlinearity as in (3).
Ray tracing simulations reported here document a dynamical transition in behavior at oceanic amplitude. The coupled oscillator theory does not. It is within this milieu of wave/particle, coupled oscillator/wave packet, AM/FM distinctions that we seek a theoretical answer for the oceanic ultraviolet catastrophe.
Our results concern basic concepts about the migration and dispersion of wave packets in the spectral domain as well as more mathematically sophisticated manipulations of kinetic equations. Section 2.1 introduces the oceanic internal wave spectrum; Section 2.2 describes the fundamentals of ray tracing and Section 2.3 provides the basic diagnostics used to identify diffusive behavior. Ray tracing results for both low and high dimensional systems are presented in Section 3.1 and Section 3.2, respectively. Section 4 presents the internal wave kinetic equation and analytic approximations that result in a Fokker-Planck (a generalized diffusion) equation. Section 5 summarizes and places the results in a more general context.
2. Materials and Methods
2.1. The Empirical Spectrum
Gravity acts as a restoring force in a continuously stratified fluid, much as it does at the ocean’s surface. The restoring forces associated with continuous stratification, though, are much smaller than at the air-sea interface, with the buoyancy frequency,
representing the maximum rate of oscillation of a fluid parcel displaced in the vertical. The rotation of the earth becomes increasingly important as wave frequency decreases, providing a lower bound of f. The dispersion relation,
in which k and l are the horizontal components of the wavevector and , conveys both these frequency bounds for freely propagating waves and that a wave’s aspect ratio depends only on frequency.
For specific calculations a slightly modified version of the Garrett and Munk (GM76) vertical wavenumber spectrum [6] will be used. The expression for energy density is:
with m s, cph and [m] is equivalent to mode-4 in a m deep (buoyancy scaled) ocean. The one-sided spectrum of vertical shear, equal to with kinetic energy density , asymptotes to [m].
Ray tracing simulations reported here use significantly smaller values of the bandwidth parameter than GM76 so that the shear spectral density is independent of vertical wavenumber over a much broader range of vertical scales. The use of lower bandwidth parameters renders the interaction between test wave and background to be scale invariant for test waves within the hydrostatic and non-rotating limits. We report background amplitude variability in the asymptotic shear spectral density as the ratio rather than the more proper notation .
The corresponding vertical wavenumber / horizontal wavenumber magnitude action spectrum is:
Integration over horizontal wavenumber magnitude further provides:
where there is a factor of two difference between wavenumber magnitude and signed wavenumber spectra. We will employ the model spectrum
with given by (5). The definitions here are in depth coordinates. Definitions in the isopycnal coordinate system used by the kinetic equation differ by a factor of .
2.2. Ray Tracing
One begins by assuming a plane-wave solution modulated over large space and time scales:
After transferring into a mixed spatial/temporal/spectral domain, the action balance
expresses conservation of phase along trajectories
and
in which Eulerian frequency and wavenumber are related to the intrinsic frequency :
and thence to a dispersion relation. See [24] for a comprehensive derivation. What has been dropped here are nonlinear terms local in wavenumber and the interaction of the wave packet with the secondary circulation associated with the packet envelope.
Ray tracing results described below will utilize a one dimensional model with
and dispersion relation that assumes constant stratification
2.3. Metrics of Diffusion
Extreme scale separated Hamiltonian systems often admit to a diffusive characterization. There are several generic tools that we utilize.
2.3.1. The Moment Method
In this work ray-tracing results are analyzed by comparison with the time evolution of moments associated with a Fokker-Planck (diffusion) equation with diffusivity :
This application of the moment method consists of multiplying (14) by vertical wavenumber raised to the power j, , invoking the chain rule, then integrating over vertical wavenumber to discard boundary terms at . See, for example, [28]. The high wavenumber asymptote of the GM76 spectrum provides a resonant prescription for D [14],
which remains valid at finite amplitude, Section 4.6. This provides the where-with-all to define the spectral moments:
with associated solutions
in which represents the jth moment at time . These, nominally AM solutions, will be over plotted on the FM metrics estimated from ray tracing in Section 3.
2.3.2. Diffusion in the Spectral Domain
A Lagrangian identity for ray tracing is provided by [29]. For a Lagrangian parcel with coordinate ‘x’:
If the integral converges, one has diffusion with diffusivity
It is a simple step to substitute for x and obtain a quantitative approach for discussing the migration and dispersion of wave packets in the spectral domain. In one dimension, (17) becomes:
The actual derivation [22] of this relation in the context of the action balance (10) requires considerably more effort. Upon recognizing that the integral in (18) represents a lagged autocorrelation function, so that , an obvious ansatz is to assert ergodicity and invoke the Weiner-Khinchin theorem relating the lagged auto-correlation function to the cosine transform of the spectrum :
with encounter frequency s. The power spectrum is available to us as the Fourier transform in time of vertical shear along a ray. Spectra estimated as ensemble averages over many background realizations in Section 4 are bandwidth limited and white.
This produces several nontrivial insights:
The first insight is that the diffusivity is determined as the product of the shear variance and a decorrelation time scale. Since the shear spectrum is essentially a bandwidth limited white spectrum, the bandwidth determines the decorrelation time scale . Thus a very narrow bandwidth, resonant response results in the same diffusivity as a non-resonant process having much larger bandwidth.
The second is that there are initial transients in the development of the second moment. This can seen by making an ad hoc assumption about the algebraic representation of and doing the indicated math. If one were to assume that , the diffusivity would be . Non-parametric estimates of are available as the difference between first and second passage statistics presented in Section 3.
We anticipate our interpretation by stating that it appears to be the interaction of a short time scale non-resonant process with a longer time scale resonant process, both of which are characterized by diffusive behavior, that gives rise to non-diffusive behavior.
3. Results: Ray Tracing
Our investigations are limited to representing the background as a sum of inertial oscillations:
This problem is especially simple. With only vertical gradients and no vertical velocity, a sum of randomly phased inertial oscillations represents an exact solution of the nonlinear equations of motion. Thus the results are not clouded by the disregard of amplitude dependent nonlinearities in the background fields.
Assuming that the test wave is initially oriented along the x axis, the evolution of the wave vector in a field of inertial oscillations reduces to
3.1. Low Dimensional Systems
We start by examining the simple case of a single wave background that demonstrates resonance as a bound wave phenomena. In this example, test waves have initial wave numbers m () approximately 12.5 (11.5) times the background at m, initial frequency of () and background velocity amplitudes of and . The initial conditions are at the nominal ID resonances [ and ), Figure 2]. The small differences in background amplitude are sufficient to make the difference between an off-resonant and resonant behavior, Figure 3. At the smaller background amplitude, the test waves sample all phases of the background. At the larger background amplitude, the test waves transit the resonance condition and occupy the same domain in wave number-frequency space. The test waves no longer sample all the phases of the background wave, which is evident in the time series of background velocity following the wave. This bound wave behavior becomes more exaggerated as the background amplitude increases.
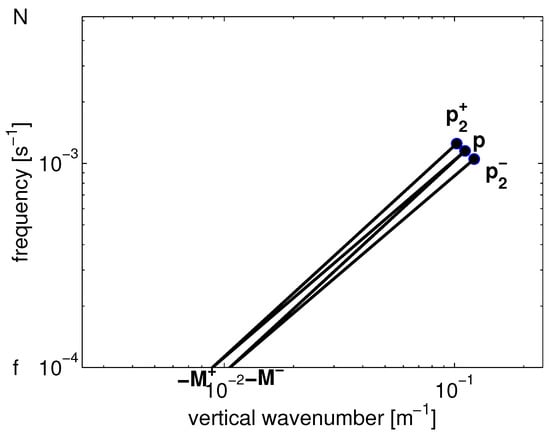
Figure 2.
Resonant configuration of the two triads completing the balance for , [, , ] and [, , ]. The two are distinguished with superscripts of ± according to the sign of . The wavenumber for in the reduced model under discussion, and is denoted as at resonance. The low dimensional example in Section 3.1 employs one of these triads.
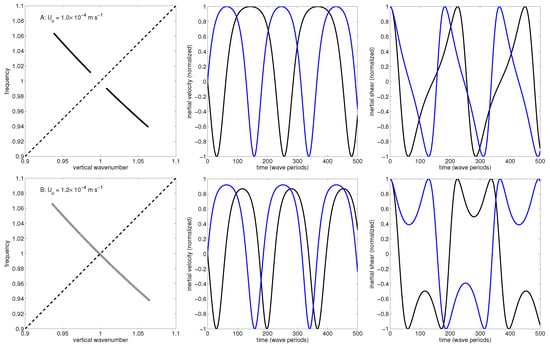
Figure 3.
Solutions for the two high frequency members of the triad. Upper panels: m s. Lower panels: m s. Left panels: vertical wavenumber vs. frequency. In the high amplitude cases the two wave trajectories can not be distinguished and the lower frequency of that duo is over plotted as a thinner white line. Normalization of vertical wavenumber and frequency is provided by dividing the wavenumber-frequency pairs by the mean values for the two triads at . The dashed line represents the resonance curve. Middle Panels: black and blue traces represent the inertial velocity following the ray path, normalized by U. Right Panels: Similarly, black and blue traces represent the inertial shear following the ray path, normalized by . In the low(er) amplitude case all phases of the background are sampled by the test wave. The high(er) amplitude case represents a resonant bound wave phenomena.
The amplitude of the test-wave response can be estimated from the eikonal relation:
In the off-resonant case, ray trajectories are perturbed by only small amounts from straight lines. Thus and integration of (22) provides
This obviously fails at resonance, for which .
‘Near’ resonance we consider the happy state in which and perturbations in vertical wavenumber sufficiently small as to expand the group velocity in a Taylor series:
We recognize the implication for the next iterate is one of growth until the argument of the cosine function attains a value of ,
so that the root-mean-square deviation can be estimated as the product of the amplitude and this time scale:
which provides an effective stepping stone to define the resonance bandwidth in the higher dimensional problems.
Finally, we note that the above characterization of ray tracing results is at odds with that presented in [30]. We have found that simulations using deterministic backgrounds are prone to a numerical instability that results in the test wave running off to very low wavenumber. We have reduced the time step to eliminate this behavior. This tendency was reported in [30,31] and interpreted as a physical result.
3.2. High Dimensional Systems
Here problems are considered using a background (20) having a uniform shear spectral density of
and is varied in order of magnitude steps.
The models (20) and (21) is subject to a number of constraints. First, a scale separation criterion requires the background to simply have larger spatial scales than that of the test wave: . Second, the intent is to maintain fidelity with the scale invariant dynamics associated with a uniform shear spectral density and test waves with group velocity . Thus the analysis is limited to times in which the high and low frequency tails of the test wave spectral distribution are effectively contained within . Third, in trying to mimic a continuous background spectrum, the background is comprised of thousands to tens of thousands of randomly phased inertial oscillations. Fourth, and finally, the test waves are initially uncorrelated with the background but it is our intent to assess the phase locking between test wave and background. We therefore wait a time to start compiling estimates of phase correlations. Estimates of the evolving first and second moments start with a test wave being inserted at a lower wavenumber and higher frequency than the nominal initial condition. Statistics are then accumulated with time starting at the first and second passage past the initial condition of
The first passage statistics have the test wave going to smaller vertical scale. Second passage statistics have the test wave going to larger vertical scales. Their difference (Figure 4) serendipitously permits an estimate of the decorrelation time scale , Section 2.3.2. Consistent with that discussion, altering the scale separation criteria does not significantly impact the asymptotic diffusivity, either. See the Appendix A for background parameters.
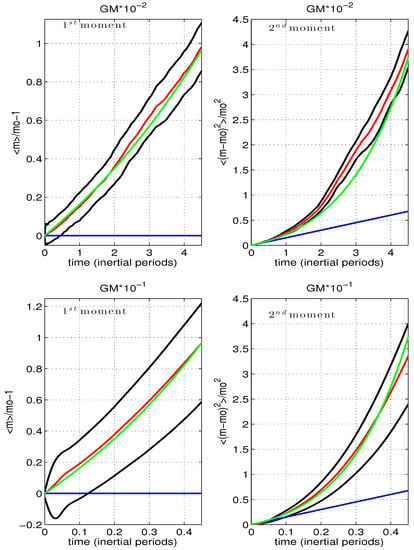
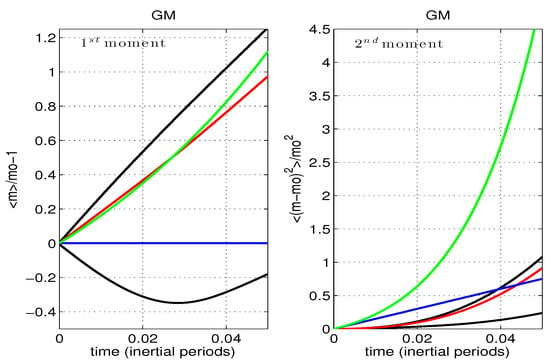
Figure 4.
First and second moments vs time for the high dimensional system (red and black) with prediction based upon the coupled oscillator paradigm (46) (green). The red line represents the ensemble average of the moments. The black lines are ensemble averages conditioned on the sign of the wavenumber tendency (velocity in wavenumber space) at . The blue line represents a constant diffusivity model. Upper left (upper right, lower left) panels are (, ). Left hand panels are the first moment. Right hand panels are the second moment. Differences in the conditioned moments (black lines) reflect a decorrelation time scale from which one can infer a “jump” time scale, Section 3.2.4 and Figure 9.
3.2.1. Analysis via the Moment Method
The diagnostic ability of the resonant closure (15) is investigated by simply over plotting test wave ensemble estimates of the first and second moments with predictions from the Fokker-Planck Equation (17). Following the discussion above, first passage, second passage and ensemble estimates are all displayed in Figure 4. The analysis uses a value for D that is 10% larger than (15). Both ray tracing and analysis code have been closely scrutinized in search of a reason without success.
Both first and second moments are nicely captured by the resonant closure (15) for . Ray tracing derived first moments are consistent with the resonant prediction at oceanic amplitude, , but the second moment is significantly lower than the resonant prediction.
The difference between first (with ) and second (with ) passage estimates of the first moment clearly reveals the decorrelation time scale of approximately 1/25 of an inertial period, corresponding to 1/2 a wave period. Shear spectra in the low amplitude case provide consistent information, Figure 5.
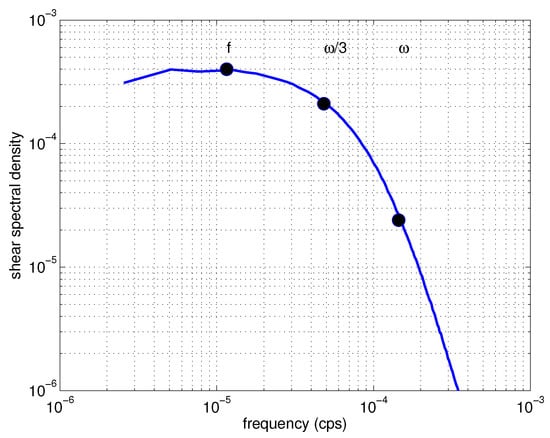
Figure 5.
Example of a frequency spectrum of vertical shear following a ray path for a background with . These frequency spectra are band-width limited and white. Note that the vertical wavenumber spectrum is white and the bandwidth inferred from the frequency spectrum leads to a short decorrelation time scale, approximately 1/2 a wave period.
The time integration at oceanic amplitudes is limited by test waves reaching the boundaries of the spectral domain, but even so, one should be able to appreciate that the second moment shows little sign of rebounding to the prediction ensconced in the time dependent Taylor Formula (19). This inference is supported by ray tracing simulations (not reported) that use a higher stratification N which, in turn, permits increased integration times.
The question becomes why the diffusive paradigm shows signs of breaking down. To answer this we examine the structure of the resonant well relative to the response to non-resonant forcing.
3.2.2. Phase Correlations
Kinetic equations assume a zeroth order description in which wave phases are uncorrelated and then predict action transfer associated with phase locking at first order. The inference of phase locking is indirect as one is closing out a hierarchy of moments.
In ray tracing, phase locking can be much more directly assessed (Figure 6). In this high dimensional system, the probability density of background phase (20) is estimated as a function of background wavenumber :
when the test wave has the value ,
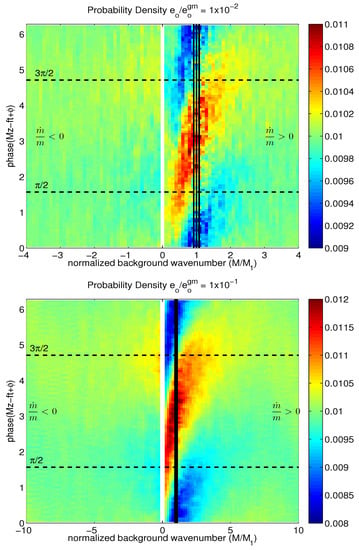
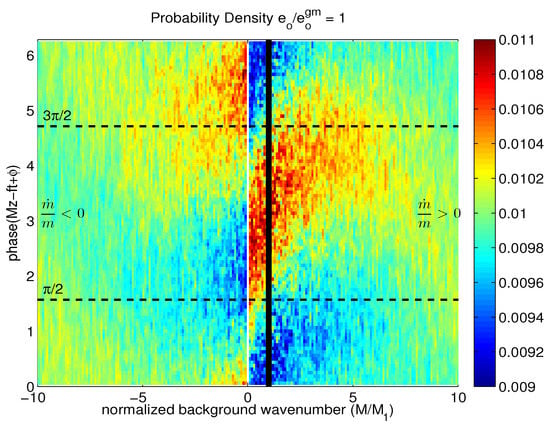
Figure 6.
Probability density of a test wave with vertical wavenumber residing in the background phase as a function of background wavenumber . The three vertical black lines denote the approximate resonance condition and the inertial members of the two triads that participates in. Upper, middle, lower panels are (, ).
Since the background velocity is specified as a sum of sine waves (20), a probability density maximum centered on either or implies a bound wave behavior in which the test wave preferentially occupies a background crest or trough. A probability maximum centered on implies a non-zero average shear and drift to either larger or small scales. We focus on the two behaviors by estimating and , Figure 7. The cosine weighting is proportional to the energy exchanged between test wave and background. The resonance is dominated by the cosine weighting, indicating a net drift of test waves to smaller scales. The shoulders of the resonance appear more representative of a bound wave behavior with lower wavenumber background waves tending to overtake the test wave and higher wavenumber background waves having smaller phase speeds being overtaken.
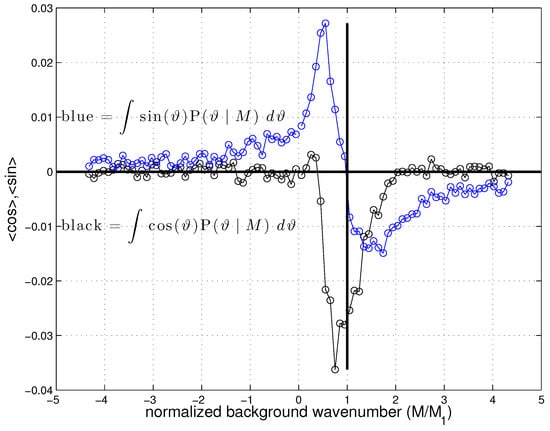
Figure 7.
Drift and bound pieces of the phase locking distributions for . The drift terms implies a mean transport of higher vertical wavenumber and energy exchange between test wave and background. The background wavenumber is normalized by the nominal resonant value.
3.2.3. The Resonant Response and a Resonant Well
A quantitative measure of the resonance bandwidth is provided by a half-width at half-maximum estimate to the magnitude of the probability distribution, Figure 8:
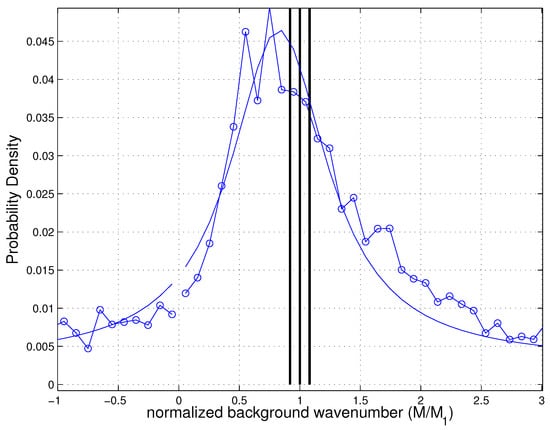
Figure 8.
An example of a resonance half-width estimate for . Circles represent (26). The background wavenumber is normalized by the nominal resonant value.
These probability distributions are neither peaked at the nominal resonance () nor are the distributions precisely symmetric about the peak. However, the half-widths are well predicted by casting the deterministic response (25) as a bandwidth , noting that this projects onto the background as a bandwidth using the resonance criteria, and replacing the background shear of a single wave with the shear associated with the resonance :
The comparison between half-width estimates via fits to (26) and analytic Formula (27) appears in Figure 9.
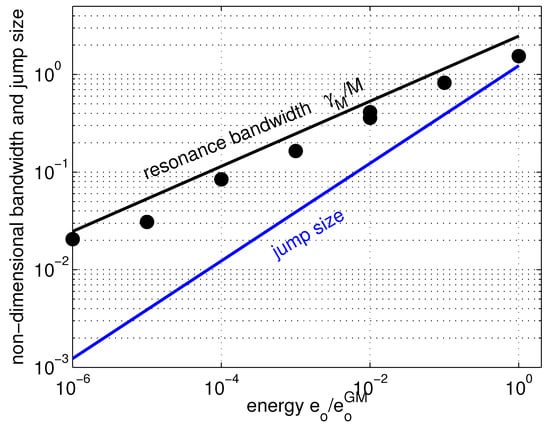
Figure 9.
Ray tracing estimates of the half width of the resonant well, black line and symbols; non resonant jump sizes (28), blue line, versus spectral amplitude. Black dots are fits to the phase locking distributions in Section 3.2.2. The resonant bandwidth (27) is rendered as the black line. Jump size and bandwidths have been nondimensionalized by the resonant wavenumber M. The jump size approaches the size of the resonant well at oceanic amplitudes, , signifying a breakdown of the diffusive characterization.
Most notably, the scaling of the resonant well differs from both small and large amplitude limits of the coupled oscillator, and , as discussed in Section 4.
3.2.4. The Non-Resonant Response and Jump Size
While the phase distributions (Figure 6) depict the structure of a resonant well, a white frequency spectrum (Figure 5) implies substantial forcing which is not translated into that resonant response. With a decorrelation time scale , we characterize this non-resonant response as a random jump on a short time scale. If the non-resonant forcing dominates, movement through the potential well at each jump is times the rms displacement in test wave vertical wavenumber over the decorrelation time scale:
The projection of the jump onto the background wavenumber (28) is approximately equal to the bandwidth (27) at oceanic amplitudes, Figure 9, and suggests that the inhibition of the second moment is related to the wave packet no longer executing many independent jumps within the resonant well. Apparently, what is left is the mean drift articulated by the first moment, Figure 4.
3.3. Summary
In summary, the ray tracing results contain, crudely, two processes: a resonant one with an interaction time scale giving rise to the ‘resonant well’ concept that is made apparent by the phase locking distributions, and off resonant, stochastic jumps at a shorter time scale which are apparent as differences in the first and second passage estimates of the first moment (Figure 4) and as approximate half-power points of the Lagrangian shear spectra. The decorrelation time scales are shorter than that associated with the resonant well; by itself this is too short to explain the inhibition of the second moment at oceanic amplitudes. However, the shear variance associated with the off resonant forcing exceeds that of the resonant forcing. This distinction underlies our interpretation that the diffusive characterization breaks down when the size of the off-resonant jump exceeds the size of the resonant well.
4. Results: Kinetic Equations
4.1. Background
Here we present a necessarily brief summary of equations for the time evolution of the wave action spectrum, , in which action is energy density divided by frequency , with the intent of divining whether a breakdown in diffusion can be inferred from a self-consistent kinetic equation at finite amplitude. Such equations are built around perturbations to plane wave solutions of having wavenumber and Eulerian frequency related by the dispersion relation (4) and thus represent the coupled oscillator paradigm. See [32] for a sketch of the derivation.
Our investigation seeks to understand a qualitative change in behavior of a system of small amplitude internal waves interacting with a much larger amplitude background having much larger spatial scales that occurs as the amplitude of that background crosses a threshold. In particular, what we are looking at is an extreme scale separated system in which nonlinear interactions can occur in triads, or three wave combinations, in which frequencies and wavenumber sum to zero:
We have taken a subscript of 1 to denote the low frequency, large scale member of the triad and it is assumed that wavenumber and frequency are connected by a dispersion relation. Many wave systems (e.g., internal waves, Rossby waves, acoustic waves, capillary-gravity waves) have dispersion relations that permit triadic interactions, so our findings may well be generally applicable. Interactions in this particular internal wave system are dominated by extreme scale separations such that the kinetic equation does not converge unless a lower bound in vertical wavenumber is inserted, which is accomplished by including rotation [9].
As a matter of convention we take wave frequency to be positive in this problem, permit wavenumber to be signed, and there is a third triad
that is not characterized by the extreme scale separation conditions of concern here.
The kinetic equation is a statistical representation for the long time scale evolution of the spectral density for a many wave assembly. A rigorous definition for this long time scale is not obvious without direct calculation: The simple Fourier principal that growth/decay in amplitude leads to a finite bandwidth needs to be accounted for in an internally consistent theory, but prior work on the problem is limited to theories having zero bandwidth (a strictly resonant representation) being interpreted as implying very large bandwidths [21,25,26]. Construction of a proper self-consistent theory is highly nontrivial and requires two key ingredients. The first is that the scattering cross-sections defining the nonlinear coupling need to be defined off the resonant manifold. Much of the work on kinetic equations projects the resonant triad onto the nonlinearity in order to obtain the cross-sections. This method can produce extremely large cross-sectional variability in the neighborhood of the resonant manifold, which is our [32] experience using cross sections defined in [33]. The second is that variational formulations (i.e., one that utilizes either Hamilton’s equation or Lagrange’s equation to define an evolution equation for wave amplitude) require the use of canonical coordinates and this, in turn, can require a coordinate transformation whose radius of convergence is ambiguous. This coordinate transformation can introduce an unknown small amplitude limitation to a broadened theory. The isopycnal Hamiltonian approach used here is free from both these limitations. These ingredients were not available to the investigations reviewed in [21].
Lvov et al. [23] use diagrammatic techniques to derive corrections to the linear frequency resulting from nonlinear wave-wave interactions. In the terminology of diagrammatics, their expression (4.18):
where
represents a single pole, one loop approximation for the mass operator . The mass operator is a complex valued variable in which the real part represents a frequency shift () and imaginary part represents resonance broadening in response to nonlinearity. The single pole nature of the formula can be directly appreciated from the functional dependence of the denominator. The single pole representation assumes that waves are not too far from being linear, so that the Green’s function of the waves are close to the linear Green’s function with renormalized frequency. The diagrammatic technique is in essence a graphical representation of the infinite perturbation theory. The first step of diagrammatic technique is to write graphical representations of the infinite perturbation series for the equation of motion for the field variables . Such graphical representations look like trees, with branching by the three wave vertices representing interactions of wave numbers. To derive statistical quantities such as a correlator, two field variables need to be multiplied and averaged. Graphically this consists of “gluing” together various trees. Branches of glued trees form loops. The one loop approximation takes into account only the lowest nonzero contributions to the double correlator. The reader who is interested is directed to [23] for specific details and [34] for a tutorial. The one loop approximation is self consistent for weakly interacting waves. Its formal validity may be verified by calculating higher order, i.e., two loop approximations, as it was done in [23] for acoustic turbulence. Formal verification of self-consistency of this approximation for internal waves is left for future publication.
4.2. The DIA Equations
The time evolution of the action spectrum is given by (The astute reader may have noted that the prefactors in (31) differ from the those adopted in this section. This is a matter of definitions. We have also taken to writing out the equivalent of (31) rather than assuming the reader understands (31) needs to be parsed for the intended symmetries. Our Equations (33) and (34) correct sign errors in [32]):
with Laurencian
containing the sum of bandwidths along each resonant surface and distance from the resonant surface , etc. which includes the shifts; and an associated equation for the nonlinear frequency bandwidth:
The scattering cross-sections [32,35] are complicated algebraic expressions of the three wavenumbers and completing the triad:
in which for horizontal wavenumber and .
Having provided these formal definitions, we find the shift to be small (see below) and hence consider .
In order to address the ray tracing model we reduce these equations to consider the two triads relevant to the ID process, in which the spectral balance at high wavenumber is defined by transfers between with and with :
and
The approximation in (37) discards terms of . In the limit that and consequently , these contributions are vanishingly small. Specifying as a field of inertial oscillations (8) ensures this. The two members are labeled with additional superscripts, i.e., and which correspond to and in the resonant limit.
Noting that and using the momentum delta function (with it provides and ) allows us to arrive at:
Inserting the GM76 based model (8), and executing the delta function in :
4.3. The Small Amplitude Limit
As a first step we take the limit that on the right-hand-side of (39). In this limit the Laurencians become delta functions, . Also utilizing :
Remembering that and canceling the distinction between isopycnal and depth coordinates (the factor)
The zeros of are . Evaluation of (41) in the high vertical wavenumber power law regime of the GM vertical wavenumber spectrum returns:
and
This broadening is 2/3 the buoyancy normalized shear content times at resonance. The shear spectral density of the background is independent of vertical wavenumber, and an normalized shear content defines the nominal 10 m vertical wavelength transition into the wave breaking regime. Even though the small amplitude limit returns resonance broadening at oceanic amplitudes that is large () at oceanic amplitudes. Inference of this time scale (but not its direct calculation as ) led to extensive commentary in the literature [25,26].
4.4. Broadening at Finite Amplitude
The integral equation for , (36), is potentially subject to a change in scaling at finite amplitude. Numerical evaluation of (39) returns (42) in the small amplitude limit, Figure 10. At amplitudes as small as , though, one obtains a change in scaling from being proportional to to being proportional to . The broadening further evaluates as being , the Doppler shift. [25,26] points to this possibility on the basis of DIA applications to turbulence. That it appears here in a problem with a well defined dispersion relation is by no means a trivial result.
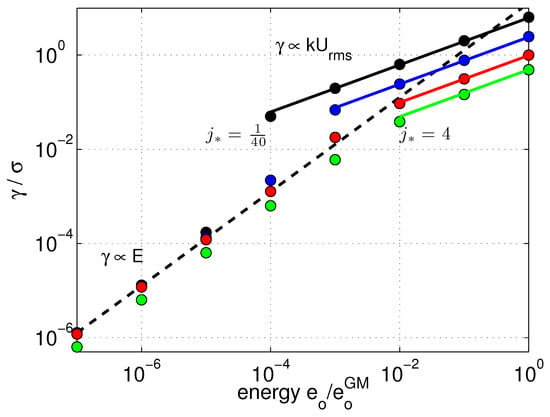
Figure 10.
Bandwidth estimates versus spectral level, normalized by frequency . The dashed black line is the small amplitude limit of (42). Colors differentiate estimates using different values of the GM76 bandwidth parameter = [1/40 1/6 1 4] m as [black blue red green]. The background spectra differ in total kinetic energy and Doppler shift but have the same asymptotic shear spectral density at high vertical wavenumber. The dots indicate numerical estimates using (42). The green dots lie below the others as the GM value of m challenges the assumption of a constant shear spectral density. The scaling regime of is indicated by the solid lines connecting the numerical estimates. The ray tracing results reported here use a background with . The transition in bandwidth scaling for the DIA equations happens at far smaller amplitudes () than the transition noted in the ray-tracing results ().
4.5. The Frequency Shift
The frequency shift corresponding to the broadening (34) can be obtained by noting that . The frequency shift is proportional to the real part:
This equation is reduced using the same arguments as in the previous subsection, obtaining:
in which and . We integrate the resulting expression for the frequency shift numerically using the finite amplitude estimates of in Figure 10. Numerical evaluation of (44) returns shifts that are much smaller than the corresponding bandwidth () estimates. The relative size is a product of cancellation between the two terms, whereas they sum in the equation. In the finite amplitude limit the integrand is dominated by low wavenumber contributions. Here they have opposite signs, which can be seen by noting the sign differences between and when is small. The shifting of the poles in (44) T is given by the difference , which is smaller than .
Thus the shifts are insufficient to delay to onset of the finite amplitude scaling regime for . Frequency shifts do not appear to be involved in a dynamical transition that might explain a breakdown in the diffusive characterization.
4.6. A Fokker-Planck Equation
While the identity of the fast time scale [14] as the relevant metric for resonance broadening and the transition to a Doppler shift scaling were the point of speculation in the early literature, that literature does not address how that resonance broadening impacts a diffusive closure to the kinetic equation. We do so here.
The ID limit of the resonant kinetic equation admits to a diffusive representation, generically referred to as a Fokker-Planck equation [28], as a result of assuming a smooth spectral representation and invoking Taylor series expansions [20]. Derivation from the kinetic Equation (33) starts by integrating over , discarding spectral amplitudes consistent with ; representing differences in the high frequency spectral amplitudes as a truncated Taylor series expansion, and , and then inserting the leading order expression for scattering cross sections :
A Taylor series expansion of the Laurencian’s argument locates the poles at , in which the inertial phase speed equals the high frequency vertical group velocity, and a final Taylor series expansion of the integral provides:
in which the shear content at inertial frequency is evaluated at the approximate resonance condition. Since the GM76 vertical wavenumber shear spectrum is white, i.e., independent of in the limit that , the integral in (47) further reduces to
and thus D is independent of the specification for ! Given the minimal shifts in the pole positions () neither transitions in, nor redefinitions of, are going to show up in either D or associated metrics such as the spectral moments.
4.7. Summary
We’ve investigated the DIA approximation for a self-consistent kinetic equation to the point that we understand a one-pole, single loop formulation returns two scaling regimes for the bandwidth and a diffusive closure. This approach is mathematically sophisticated, linked to first principles and, in one word, dense. We have yet to understand how this model can be manipulated to mimic a departure from a diffusive closure documented by the ray tracing simulations in the previous section. If this DIA system does not admit to a dynamical transition it implies a fundamental difference between waves in fluids as plane waves and waves described as particles via ray tracing. This dualistic tendency finds some articulation in the distinction between AM and FM signals.
5. Discussion
In the Introduction we raised the notion of an oceanic ultraviolet catastrophe. This catastrophe arises as theoretical predictions based upon a one-dimensional Fokker-Planck (generalized diffusion) equation that (i) internal wave energy is transferred from high frequency to low and that (ii) the Garret and Munk spectrum should support a substantially reduced amount of diapycnal mixing compared to other spectral distributions in vertical wavenumber and frequency. Neither prediction is supported by three decades of observational efforts.
We also noted a distinction between describing interactions between waves as a system of coupled oscillators, in which one solves for time dependent amplitudes of plane wave solutions, and that associated with wave-packets (ray tracing), in which one allows for space-time dependent phases with space-time invariant spectral amplitude. The former is supported by a well developed theoretical apparatus which has as its central focus the amplitude modulated bandwidth. No such systematic theory for assessing spectral transports exists for ray tracing. However, we managed to estimate bandwidths for the frequency modulation associated with ray tracing which differ from both the small and finite amplitude limits of the coupled oscillator theory. Thus there is an underlying dualism to describing wave-wave interactions.
We endeavored to understand whether this dualistic tendency could resolve the oceanic ultraviolet catastrophe by comparing ray tracing results and diagnostics based upon the coupled oscillator’s Fokker-Planck (generalized diffusion) equation. These diagnostics concern the evolution of the first and second moments of a high frequency wave packet’s vertical wavenumber (m) with time. At spectral levels 1 to 2 orders of magnitude smaller than GM76, both first and second moments are nicely captured by the diffusive prediction. At oceanic amplitude, the first moment agrees with the diffusive prediction but the second moment is significantly lower than the prediction. We pursued finite amplitude versions of the coupled oscillator theory in the context of the Direct Interaction Approximation, determined that frequency shifts are small and found that predictions for the moments are consequently insensitive to changes in amplitude dependent bandwidth. The noted inhibition of the second moment in the ray tracing results at oceanic amplitude might be taken as implying a threshold for a weakly nonlinear (though finite amplitude) theory that does not exist in the coupled oscillator paradigm.
Our current understanding is that the non-resonant response represents jumps within a resonant well and that agreement with the diffusive diagnostics breaks down when the jumps take on the characteristic size of the resonant well, Figure 9. This change in behavior happens at oceanic amplitudes.
We understand these results as having broader consequences. In a ground breaking study of the coupled oscillator paradigm applied to a nonlinear Schrödinger equation, [36] find that finite amplitude effects include changes in the sign of energy cascades resulting from wave-wave interactions. That amplitude dependent transition is the subject of ongoing research, but [37] identifies the transition as being related to the appearance of solitary waves. This work points to a possible middle ground: solitary waves are associated with spectrally local nonlinearity that is discarded in developing the ray tracing approach [24]. Curiously, the ray theory assumes extreme scale separations, but our estimates of the decorrelation time scales are small, sufficiently small as to lead us to speculate that a solitary wave like basis function could be a more natural description.
One could view this exercise not in terms of nonlinear interactions, but rather wave propagation in a time dependent, spatially inhomogeneous background. Wave propagation in temporally stationary, spatially inhomogeneous media is know to exhibit similar transitions. Specific examples include low energy electrons in a crystal lattice [38], lasers in [39]. In these instances, increasing disorder leads to greater diffusion, until a transition point is reached and the medium becomes an insulator. If our background vertical wavenumber spectrum were other than white, increasing the background amplitude would likely lead to amplitude dependent diffusivity in both wave and particle paradigms. The dynamical transition in the ray-tracing results is one that promotes increasing transports to high wavenumber, with the internal wave dispersion relation demanding a vastly inhibited vertical propagation. Thus our analysis tools and the self-consistent theoretical paradigm have distinct parallels within Solid State Physics.
This work corresponds to a suggestion by [7] that the near-universal character of the oceanic internal wavefield implies some sort of saturation mechanism. That suggestion was investigated in the context of hydrodynamic instabilities and wave breaking. The dynamical transition described here seems a more likely candidate. See [6] for documentation of oceanic variability.
Acknowledgments
Kurt L. Polzin gratefully acknowledges support from Woods Hole Oceanographic Institution’s Investment in Science Program (WHOI’s ISP) program and engaging conversations with Jonathan Lilly and Baylor Fox-Kemper concerning the content of this manuscript. Sources of inspiration for the required mathematical reductionism comes from course work at MIT with Alar Toomre and William R. Young. The authors gratefully acknowledge support from a collaborative National Science Foundation grant, award Nos. 1634644 (KP) and 1635866 (YVL).
Author Contributions
Kurt L. Polzin and Yuri V. Lvov synergistically designed the experiments, developed tools to analyze the numerical output and contributed to the intellectual content. Kurt L. Polzin conceived the one-dimensional model and wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Ray-Tracing Set-Up Parameters
When examining issues of phase correlations (Section 3.2.2) we use a relatively broad background spectrum, Table A1, and implement a scale separation criteria that . Here our concern is to estimate the correlations at with sufficiently small as to provide resolution of the triad configuration.

Table A1.
Run summary for estimating phase correlations (Figure 6). We create an ensemble of test wave time series by creating multiple realizations () of the randomly phased inertial field having constituents uniformly distributed between and . The length of the simulations are denoted by number of time steps ts at the indicated time difference.
Table A1.
Run summary for estimating phase correlations (Figure 6). We create an ensemble of test wave time series by creating multiple realizations () of the randomly phased inertial field having constituents uniformly distributed between and . The length of the simulations are denoted by number of time steps ts at the indicated time difference.
| Name | |||||||
|---|---|---|---|---|---|---|---|
| 12.19.0c | 2500 | 30,000 | 2401 | 0.025 | 160 | ||
| 11.7.1a | 1000 | 30,000 | 2401 | 0.025 | 1600 | ||
| 11.7.1b | 1000 | 30,000 | 2401 | 0.025 | 1600 | ||
| 10.23.2a | 10,000 | 3000 | 24,001 | 0.5 | 1600 | ||
| 10.23.2b | 3000 | 24,001 | 0.5 | 1600 | |||
| 11.13.20 | 1200 | 40,000 | 2001 | 0.25 | 32 | ||
| 11.13.30 | 5000 | 10,000 | 2001 | 0.25 | 32 | ||
| 11.13.40 | 5000 | 10,000 | 5001 | 0.5 | 16 | ||
| 11.13.50 | 10,000 | 10,000 | 6001 | 3.2 | 4.8 | ||
| 7.3.6abcdefghij | 50,000 | 1200 | 24,001 | 3.2 | 4.8 |
When estimating evolution of the spectral moments (Section 3.2.1 and Table A2), our concerns are about the global evolution of the distribution with time. Our intent is to maintain fidelity with the internal dynamics and not have the boundaries of the spectral domain influence the results. In addition to the scale separation described above, we limit our analysis to times in which the high and low frequency tails of the spectral distribution are effectively contained within .

Table A2.
Run summary for estimating the spectral moments that appear in Figure 4. We create an ensemble of test wave time series by creating multiple realizations () of the randomly phased inertial field having constituents.
Table A2.
Run summary for estimating the spectral moments that appear in Figure 4. We create an ensemble of test wave time series by creating multiple realizations () of the randomly phased inertial field having constituents.
| Name | |||||||
|---|---|---|---|---|---|---|---|
| 12.19.0c | 30,000 | 2401 | 0.025 | 160 | |||
| 11.7.1a | 1000 | 30,000 | 2401 | 0.025 | 1600 | ||
| 10.23.2a | 5000 | 3000 | 24,001 | 0.025 | 1600 | ||
| 12.6.2 | 5000 | 3000 | 24,001 | 0.025 | 1600 | ||
| 12.7.3 | 20,000 | 1500 | 24,001 | 0.5 | 16 | ||
| 7.3.6abcdefghij | 50,000 | 1200 | 24,001 | 3.2 | 4.8 | ||
| 12.19.0g | 30,000 | 4801 | 0.025 | 640 | |||
| 11.7.1c.v7.3 | 30,000 | 4801 | 0.025 | 640 |
References
- Kolmogorv, A.N. The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Proc. USSR Acad. Sci. 1941, 30, 299–303. [Google Scholar] [CrossRef]
- Hasselmann, K. On the nonlinear energy transfer in a gravity wave spectrum. Part I. General theory. J. Fluid Mech. 1962, 12, 481–500. [Google Scholar] [CrossRef]
- Hasselmann, K. On the nonlinear energy transfer in a gravity wave spectrum. Part II. Conservation theorems, wave-particle analogy, irreversibility. J. Fluid Mech. 1963, 15, 385–398. [Google Scholar] [CrossRef]
- Zakharov, V.E.; Lvov, V.S.; Falkovich, G. Kolmogorov Spectra of Turbulence; Springer: Berlin, Germany, 1992. [Google Scholar]
- McComas, C.H.; Müller, P. The dynamic balance of internal waves. J. Phys. Oceanogr. 1981, 11, 970–986. [Google Scholar] [CrossRef]
- Polzin, K.L.; Lvov, Y.S. Toward regional characterizations of the oceanic internal wave spectrum. Rev. Geophys. 2011, 49. [Google Scholar] [CrossRef]
- Munk, W. Internal waves and small-scale processes. In Evolution of Physical Oceanography; Warren, B.A., Wunsch, C., Eds.; The MIT Press: Cambridge, MA, USA, 1981; pp. 264–291. [Google Scholar]
- Pelinovskii, E.N.; Raevsky, M.A. Weak turbulence of internal ocean waves. In Izvestiya Akademii Nauk SSSR, Fizika Atmosfery i Okeana, translated in Izvestiya Academy of Sciences USSR, Atmospheric and Oceanic Physics; American Geophysical Union: Washington, DC, USA, 1977; Volume 13, pp. 187–193. [Google Scholar]
- Lvov, Y.V.; Polzin, K.L.; Tabak, E.G.; Yokoyama, N. Oceanic internal wavefield: Theory of scale-invariant spectra. J. Phys. Oceanogr. 2010, 40, 2605–2623. [Google Scholar] [CrossRef]
- Gregg, M.C. Scaling turbulent dissipation in the thermocline. J. Geophys. Res. 1989, 94, 9686–9698. [Google Scholar] [CrossRef]
- Polzin, K.L. A heuristic description of internal wave dynamics. J. Phys. Oceanogr. 2004, 34, 214–230. [Google Scholar] [CrossRef]
- Polzin, K.L.; Toole, J.M.; Schmitt, R.W. Finescale parameterizations of turbulent dissipation. J. Phys. Oceanogr. 1995, 25, 306–328. [Google Scholar] [CrossRef]
- Polzin, K.L.; Naveira Garabato, A.C.; Sloyan, B.M.; Huussen, T.; Waterman, S.N. Finescale Parameterizations of Turbulent Dissipation. J. Geophys. Res. 2014, 119, 1383–1419. [Google Scholar] [CrossRef]
- McComas, C.H.; Müller, P. Timescales of resonant interactions among oceanic internal waves. J. Phys. Oceanogr. 1981, 11, 139–147. [Google Scholar] [CrossRef]
- Pomphrey, N.; Meiss, J.D.; Watson, K.M. Description of nonlinear internal wave interactions using Langevin methods. J. Geophys. Res. 1980, 85, 1085–1094. [Google Scholar] [CrossRef]
- Henyey, F.S.; Pomphrey, N. Eikonal description of internal wave interactions: A non-diffusive picture of “induced diffusion”. Dyn. Atmos. Oceans 1983, 7, 189–208. [Google Scholar] [CrossRef]
- Nazarenko, S. Wave Turbulence; Springer: Berlin, Germany, 2011; ISBN 978-3642159411. [Google Scholar]
- Connaughton, C.; Nazarenko, S.; Quinn, B. Rossby and drift wave turbulence and zonal flows: The Charney? Hasegawa? Mima model and its extensions. Phys. Rep. 2015, 604, 1–71. [Google Scholar] [CrossRef]
- Whitham, G.B. Linear and Nonlinear Waves; Wiley-Interscience: New York, NY, USA, 1974; p. 636. [Google Scholar]
- McComas, C.H.; Bretherton, F.P. Resonant interaction of oceanic internal waves. J. Geophys. Res. 1977, 83, 1397–1412. [Google Scholar] [CrossRef]
- Müller, P.; Holloway, G.; Henyey, F.; Pomphrey, N. Nonlinear interactions among internal gravity waves. Rev. Geophys. 1986, 24, 493–536. [Google Scholar] [CrossRef]
- Nazarenko, S.V.; Newell, A.C.; Galtier, S. Non-local MHD turbulence. Physica D 2001, 152, 646–652. [Google Scholar] [CrossRef]
- Lvov, V.S.; Lvov, Y.V.; Newell, A.C.; Zakharov, V.E. Statistical description of acoustic turbulence. Phys. Rev. E 1977, 56, 390–405. [Google Scholar] [CrossRef]
- Gershgorin, B.; Lvov, Y.V.; Nazarenko, S. Canonical Hamiltonians for waves in inhomogeneous media. J. Math. Phys. 2009, 50, 013527. [Google Scholar] [CrossRef]
- Holloway, G. Oceanic internal waves are not weak waves. J. Phys. Oceanogr. 1980, 10, 906–914. [Google Scholar] [CrossRef]
- Holloway, G. On interaction timescales of oceanic internal waves. J. Phys. Oceanogr. 1982, 12, 293–296. [Google Scholar] [CrossRef]
- Cohen, L.; Lee, C. Instantaneous bandwidth for signals and spectrogram. In Proceedings of the IEEE International Conference Acoustics Speech Signal Processing, Albuquerque, NM, USA, 3–6 April 1990; pp. 2451–2454. [Google Scholar]
- Gardiner, C.W. Handbook of Stochastic Methods; Springer: New York, NY, USA, 2004; p. 415. [Google Scholar]
- Taylor, G.I. Diffusion by continuous movements. Proc. Lond. Math. Soc. 1921, 2, 196–211. [Google Scholar] [CrossRef]
- Broutman, D.; Rottman, J.W.; Eckermann, S.D. Ray methods for internal waves in the atmosphere and ocean. Annu. Rev. Fluid Mech. 2004, 36, 233–253. [Google Scholar] [CrossRef]
- Sun, H.; Kunze, E. Internal wave–wave interactions. Part II: Spectral energy transfer and turbulent production. J. Phys. Oceanogr. 1999, 29, 2905–2919. [Google Scholar] [CrossRef]
- Lvov, Y.V.; Polzin, K.L.; Yokoyama, N. Wave-wave interactions in stratified fluids: A comparison of approaches. J. Phys. Oceanogr. 2012, 42, 669–691. [Google Scholar] [CrossRef]
- Müller, P.; Olbers, D.J. On the dynamics of internal waves in the deep ocean. J. Geophys. Res. 1975, 80, 3848–3860. [Google Scholar] [CrossRef]
- Lvov, V.S.; Procaccia, I. Exact Resummation in the Theory of Hydrodynamic Turbulence. 0. Line-Resummed Diagrammatic Perturbation Approach. In Lecture Notes of the Les Houches 1994 Summer School “Fluctuating Geometries in Statistical Mechanics and Field Theory”; David, F., Ginsparg, P., Eds.; North-Holland: Amsterdam, The Netherlands, 1995; pp. 1027–1075. [Google Scholar]
- Lvov, Y.V.; Tabak, E.G. A Hamiltonian Formulation for Long Internal Waves. Physica D 2004, 195, 106–122. [Google Scholar] [CrossRef]
- Majda, A.J.; McLaughlin, D.W.; Tabak, E.G. A one-dimensional model for dispersive wave turbulence. J. Nonlinear Sci. 1997, 6, 9–44. [Google Scholar] [CrossRef]
- Rumpf, B.; Newell, A.C.; Zakharov, V.E. Turbulent transfer of energy by radiating pulses. Phys. Rev. Lett. 2009, 103, 074502. [Google Scholar] [CrossRef] [PubMed]
- Anderson, P.W. Absence of Diffusion in Certain Random Lattices. Phys. Rev. 1958, 109, 1492–1505. [Google Scholar] [CrossRef]
- Lahini, Y.; Avidan, A.; Pozzi, F.; Sorel, M.; Morandotti, R.; Christodoulides, D.N.; Silberberg, Y. Anderson localization and nonlinearity in one dimensional disordered photonic lattices. Phys. Rev. Lett. 2008, 100, 013906. [Google Scholar] [CrossRef] [PubMed]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).