Linear Stability Analysis of Penetrative Convection via Internal Heating in a Ferrofluid Saturated Porous Layer
Abstract
:1. Introduction
2. Formulation
3. The Steady Solution
4. The Linear Stability Problem
5. Method of Solution
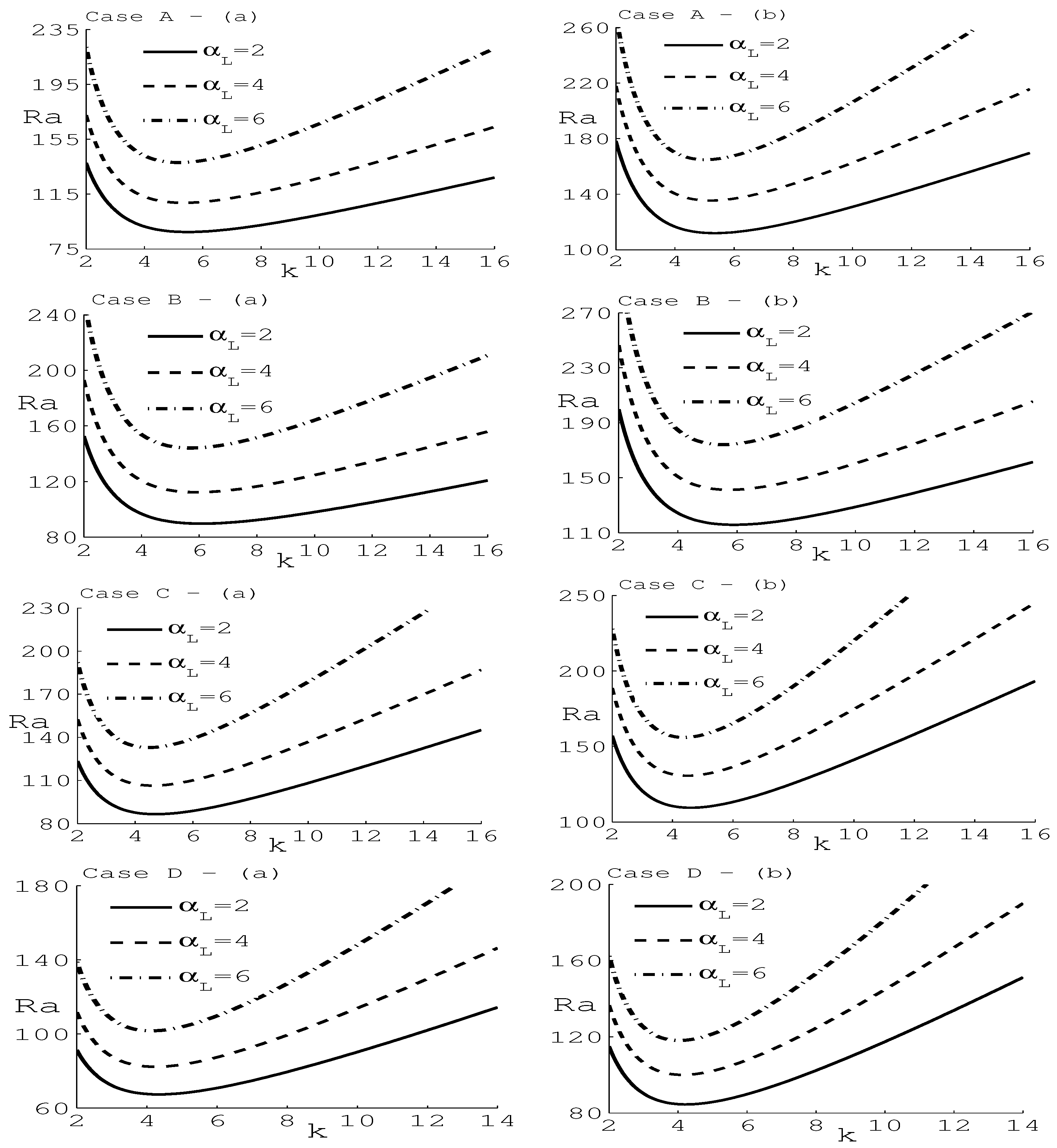
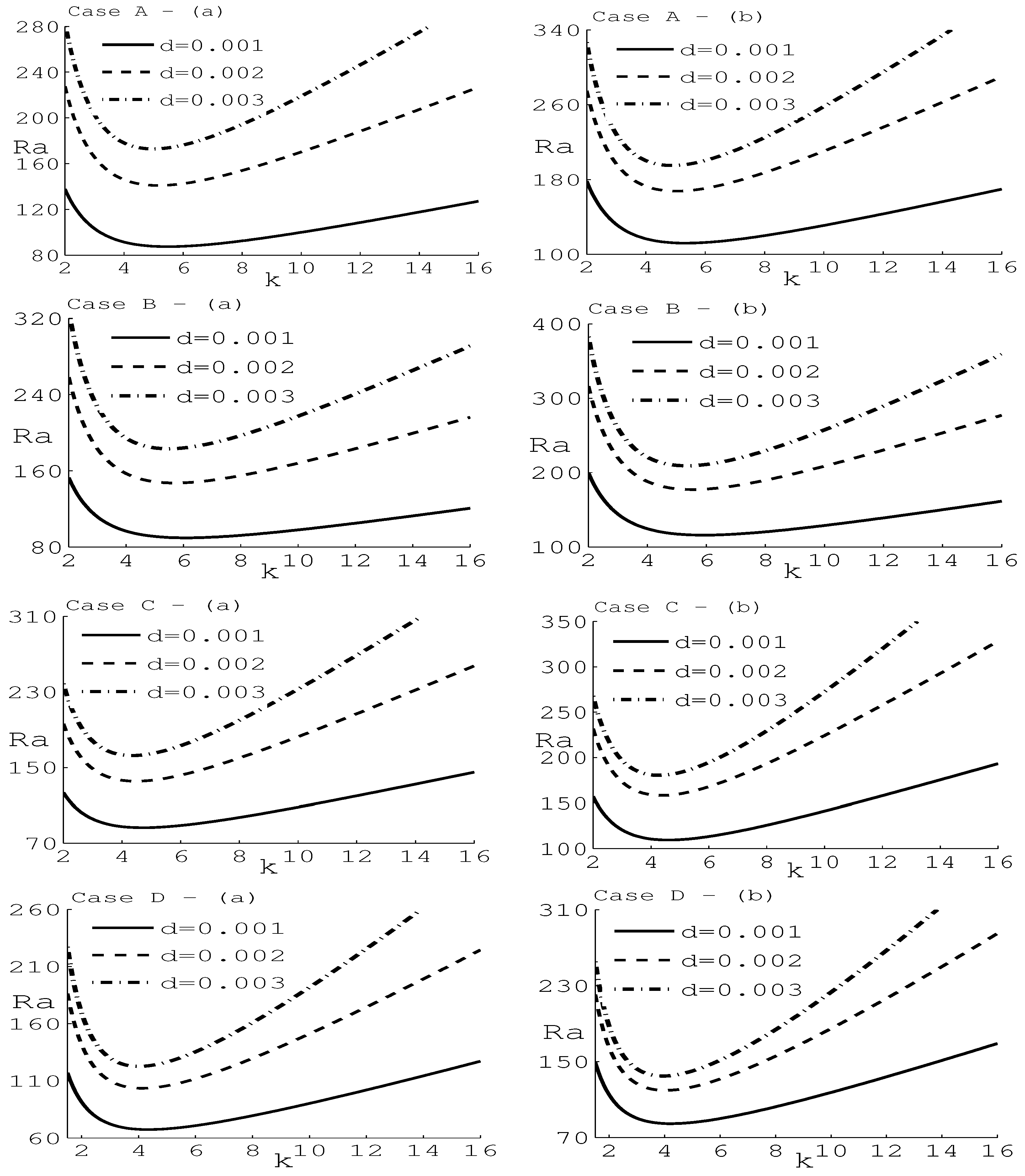
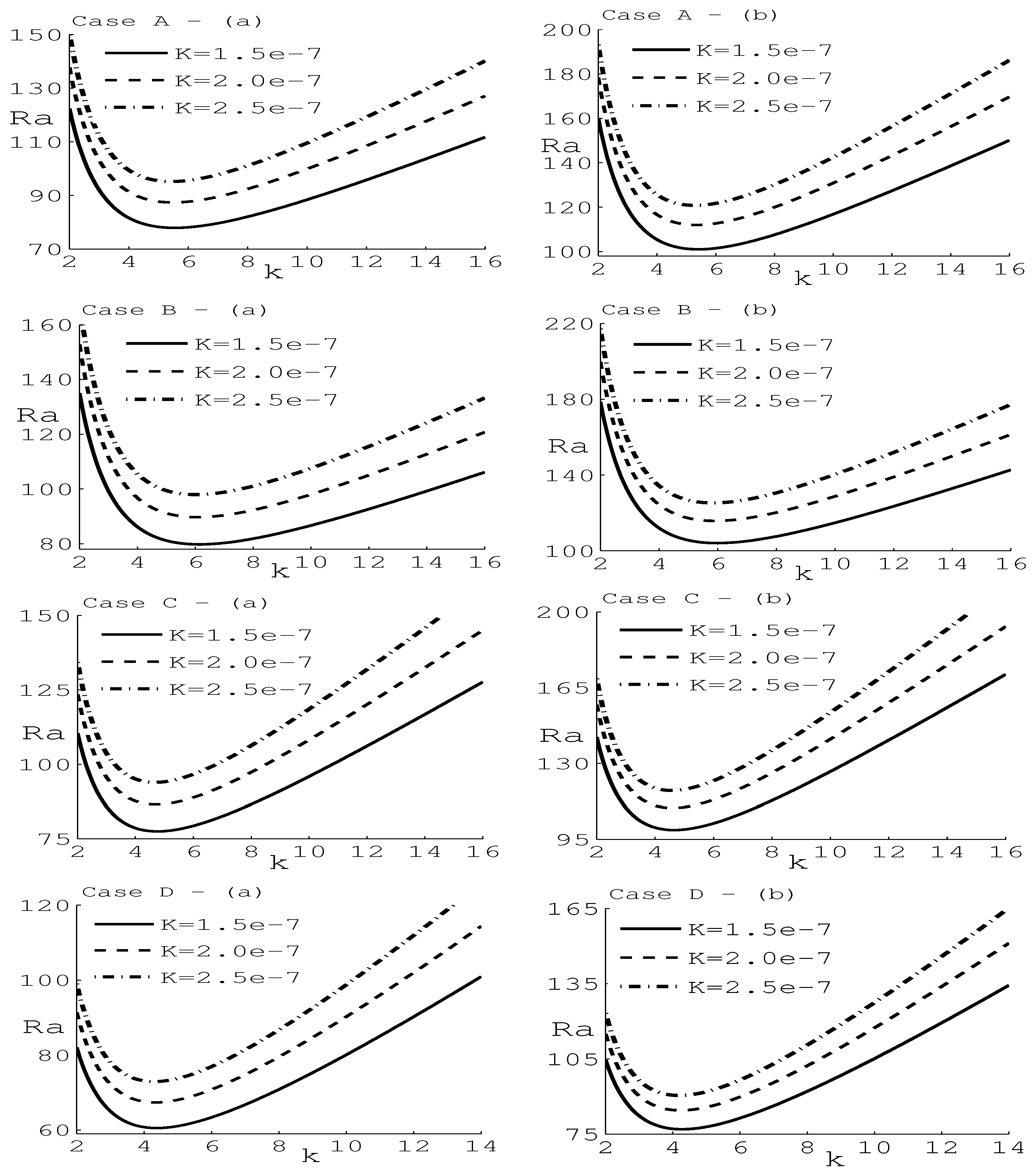
6. Numerical Results and Discussion
7. Conclusions
- The effect of is to stabilize the system, while the parameter has a destabilizing effect on the system.
- The system is most stable for IMP & CON boundary condition, while it is least stable for IMP, CON & CHF boundary condition.
- The water-based ferrofluids are less stable than the ester-based ferrofluids.
- The value of is higher in the case when the heat supply function is increasing, while it is the least in the case when the heat supply function heats and cools the layer in a non-uniform way.
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| d | Thickness of the ferrofluid layer (m) |
| g | Acceleration due to gravity (m/s) |
| H | Magnetic field (T) |
| Unit vector in the z-direction | |
| Thermal conductivity (W/m K) | |
| K | Permeability of porous medium (m) |
| Magnetization (Amp/m) | |
| Magnetic saturation | |
| Boltzmann’s constant | |
| p | Pressure (Pa) |
| Q | Volumetric heat source of strength (W/m) |
| t | Time (s) |
| T | Temperature (K ) |
| Temperature at the lower and upper surfaces (K) | |
| Filtration velocity of the ferrofluid (m/s) | |
| Prandtl number | |
| Darcy number | |
| Vadasz number | |
| Internal Rayleigh number | |
| , | Magnetic parameters |
| Nonlinearity of magnetization | |
| Greek symbols | |
| Coefficient of thermal expansion (1/K) | |
| Langevin parameter | |
| Thermal diffusivity (m/s) | |
| Viscosity of ferrofluid (kg/ms) | |
| Magnetic permeability of vacuum (H/m) | |
| Density (kg/m) | |
| The perturbation in temperature (K) | |
| Tangent magnetization susceptibility | |
| Chord magnetization susceptibility | |
| Porosity | |
| Operators | |
| ∇ | |
References
- Ivanov, A.O.; Kuznetsova, O.B. Magnetic properties of dense ferrofluids: An influence of interparticle correlations. Phys. Rev. E 2001, 64, 041405. [Google Scholar] [CrossRef] [PubMed]
- Nkurikiyimfura, I.; Wang, Y.; Pan, Z. Heat transfer enhancement by magnetic nanofluids—A review. Renew. Sustain. Energy Rev. 2013, 21, 548–561. [Google Scholar] [CrossRef]
- Bahiraei, M.; Hangi, M. Flow and heat transfer characteristics of magnetic nanofluids: A review. J. Magn. Magn. Mater. 2015, 374, 125–138. [Google Scholar] [CrossRef]
- Raj, K.; Moskowitz, R. Commercial applications of ferrofluids. J. Magn. Magn. Mater. 1990, 85, 233–245. [Google Scholar] [CrossRef]
- Finlayson, B. Convective instability of ferromagnetic fluids. J. Fluid Mech. 1970, 40, 753–767. [Google Scholar] [CrossRef]
- Lalas, D.; Carmi, S. Thermoconvective stability of ferrofluids. Phys. Fluids 1971, 14, 436–438. [Google Scholar] [CrossRef]
- Shliomis, M. Magnetic fluids. Sov. Phys. Usp. 1974, 17, 153–169. [Google Scholar] [CrossRef]
- Stiles, P.J.; Kagan, M. Thermoconvective instability of a ferrofluid in a strong magnetic field. J. Colloid Interface Sci. 1990, 134, 435–448. [Google Scholar] [CrossRef]
- Venkatasubramanian, S.; Kaloni, P. Effects of rotation on the thermoconvective instability of a horizontal layer of ferrofluids. Int. J. Eng. Sci. 1994, 32, 237–256. [Google Scholar] [CrossRef]
- Sunil; Mahajan, A. A nonlinear stability analysis for magnetized ferrofluid heated from below. Proc. R. Soc. A 2008, 464, 83–98. [Google Scholar] [CrossRef]
- Borglin, S.E.; Moridis, G.J.; Oldenburg, C.M. Experimental studies of the flow of ferrofluid in porous media. Transp. Porous Media 2000, 41, 61–80. [Google Scholar] [CrossRef]
- Vaidyanathan, G.; Sekar, R.; Balasubramanian, R. Ferroconvective instability of fluids saturating a porous medium. Int. J. Eng. Sci. 1991, 29, 1259–1267. [Google Scholar] [CrossRef]
- Postelnicu, A. Influence of a magnetic field on heat and mass transfer by natural convection from vertical surfaces in porous media considering Soret and Dufour effects. Int. J. Heat Mass Transf. 2004, 47, 1467–1472. [Google Scholar] [CrossRef]
- Ramambason, D.S.R.; Vasseur, P. Influence of a magnetic field on natural convection in a shallow porous enclosure saturated with a binary fluid. Acta Mech. 2007, 191, 21–35. [Google Scholar] [CrossRef]
- Mahdy, A.; Mohamed, R.; Hady, F. Influence of magnetic field on natural convection flow near a wavy cone in porous media. Lat. Am. Appl. Res. 2008, 38, 155–160. [Google Scholar]
- Sunil; Mahajan, A. A nonlinear stability analysis for thermoconvective magnetized ferrofluid saturating a porous medium. Transp. Porous Media 2009, 76, 327–343. [Google Scholar] [CrossRef]
- Antar, B.N. Penetrative double-diffusive convection. Phys. Fluids 1987, 30, 322–330. [Google Scholar] [CrossRef]
- Goluskin, D. Internally Heated Convection and Rayleigh-Bénard Convection; Springer International Publishing AG: Cham, Switzerland, 2015. [Google Scholar]
- Crepeau, J.; Clarksean, R. Similarity solutions of natural convection with internal heat generation. Trans.-Am. Soc. Mech. Eng. J. Heat Transf. 1997, 119, 183–184. [Google Scholar] [CrossRef]
- Gasser, R.; Kazimi, M. Onset of convection in a porous medium with internal heat generation. ASME J. Heat Transf. 1976, 98, 49–54. [Google Scholar] [CrossRef]
- Ames, K.; Cobb, S.S. Penetrative convection in a porous medium with internal heat sources. Int. J. Eng. Sci. 1994, 32, 95–105. [Google Scholar] [CrossRef]
- Straughan, B. The Energy Method, Stability, and Nonlinear Convection; Springer: New York, NY, USA, 2004. [Google Scholar]
- Nandal, R.; Mahajan, A. Linear and nonlinear stability analysis of a Horton–Rogers–Lapwood problem with an internal heat source and Brinkman effects. Transp. Porous Media 2017, 117, 261–280. [Google Scholar] [CrossRef]
- Kulacki, F.; Ramchandani, R. Hydrodynamic instability in a porous layer saturated with a heat generating fluid. Wärme Stoffübertrag. 1975, 8, 179–185. [Google Scholar] [CrossRef]
- Qin, Y.; Guo, J.; Kaloni, P. Double diffusive penetrative convection in porous media. Int. J. Eng. Sci. 1995, 33, 303–312. [Google Scholar] [CrossRef]
- Carr, M.; de Putter, S. Penetrative convection in a horizontally isotropic porous layer. Contin. Mech. Thermodyn. 2003, 15, 33–43. [Google Scholar] [CrossRef]
- Carr, M.; Straughan, B. Penetrative convection in a fluid overlying a porous layer. Adv. Water Resour. 2003, 26, 263–276. [Google Scholar] [CrossRef]
- Straughan, B. Resonant porous penetrative convection. Proc. R. Soc. A 2004, 460, 2913–2927. [Google Scholar] [CrossRef]
- Capone, F.; Gentile, M.; Hill, A.A. Penetrative convection in a fluid layer with throughflow. Ric. Mat. 2008, 57, 251. [Google Scholar] [CrossRef]
- Ferdows, M.; Liu, D.; Ramachandran, B. Boundary layer slip and heat transfer in stagnation point flow over a steady stretching surface embedded in a porous medium with heat sources. Br. J. Math. Comput. Sci. 2016, 18, 1–8. [Google Scholar] [CrossRef]
- Ferdows, M.; Liu, D. Similarity solutions on mixed convection heat transfer from a horizontal surface saturated in a porous medium with internal heat generation. Int. J. Appl. Mech. Eng. 2017, 22, 253–258. [Google Scholar] [CrossRef]
- Nield, D.; Kuznetsov, A. The onset of convection in a horizontal porous layer with spatially non-uniform internal heating. Transp. Porous Media 2016, 111, 541–553. [Google Scholar] [CrossRef]
- Kuznetsov, A.; Nield, D. The effect of spatially nonuniform internal heating on the onset of convection in a horizontal fluid layer. J. Heat Transf. 2016, 138, 062503. [Google Scholar] [CrossRef]
- Sekhar, G.; Rudraiah, N. Convection in magnetic fluids with internal heat generation. Trans. ASME J. Heat Trans. 1991, 113, 122–127. [Google Scholar]
- Nanjundappa, C.; Shivakumara, I.; Srikumar, K. On the penetrative Benard–Marangoni convection in a ferromagnetic fluid layer. Aerosp. Sci. Technol. 2013, 27, 57–66. [Google Scholar] [CrossRef]
- Nanjundappa, C.; Ravisha, M.; Lee, J.; Shivakumara, I. Penetrative ferroconvection in a porous layer. Acta Mech. 2011, 216, 243–257. [Google Scholar] [CrossRef]
- Nanjundappa, C.; Shivakumara, I.; Arunkumar, R. Onset of Bénard-Marangoni ferroconvection with internal heat generation. Microgravity Sci. Technol. 2011, 23, 29–39. [Google Scholar] [CrossRef]
- Nanjundappa, C.; Shivakumara, I.; Lee, J.; Ravisha, M. Effect of internal heat generation on the onset of Brinkman–Bénard convection in a ferrofluid saturated porous layer. Int. J. Therm. Sci. 2011, 50, 160–168. [Google Scholar] [CrossRef]
- Nanjundappa, C.; Shivakumara, I.; Prakash, H. Penetrative ferroconvection via internal heating in a saturated porous layer with constant heat flux at the lower boundary. J. Magn. Magn. Mater. 2012, 324, 1670–1678. [Google Scholar] [CrossRef]
- Yadav, D.; Bhargava, R.; Agrawal, G. Boundary and internal heat source effects on the onset of Darcy–Brinkman convection in a porous layer saturated by nanofluid. Int. J. Therm. Sci. 2012, 60, 244–254. [Google Scholar] [CrossRef]
- Yadav, D.; Kim, C.; Lee, J.; Cho, H.H. Influence of magnetic field on the onset of nanofluid convection induced by purely internal heating. Comput. Fluids 2015, 121, 26–36. [Google Scholar] [CrossRef]
- Yadav, D.; Lee, J.; Cho, H.H. Brinkman convection induced by purely internal heating in a rotating porous medium layer saturated by a nanofluid. Powder Technol. 2015, 286, 592–601. [Google Scholar] [CrossRef]
- Yadav, D. Numerical solution of the onset of natural convection in a rotating nanofluid layer induced by purely internal heating. Int. J. Appl. Comput. Math. 2017, 1–19. [Google Scholar] [CrossRef]
- Nield, D.A.; Bejan, A. Convection in Porous Media; Springer: New York, NY, USA, 2006. [Google Scholar]
- Rosensweig, R.E. Ferrohydrodynamics; Courier Dover Corporation: New York, NY, USA, 1972. [Google Scholar]
- Kaloni, P.; Lou, J. Convective instability of magnetic fluids. Phys. Rev. E 2004, 70, 026313. [Google Scholar] [CrossRef] [PubMed]
- Canuto, C.; Hussaini, M.Y.; Quarteroni, A.M.; Thomas, Z.A., Jr. Spectral Methods in Fluid Dynamics; Springer: New York, NY, USA, 2012. [Google Scholar]
- Mahajan, A.; Sharma, M.K. Penetrative convection in magnetic nanofluids via internal heating. Phys. Fluids 2017, 29, 034101. [Google Scholar] [CrossRef]
- Nouri-Borujerdi, A.; Noghrehabadi, A.R.; Rees, D.A.S. Onset of convection in a horizontal porous channel with uniform heat generation using a thermal nonequilibrium model. Transp. Porous Media 2007, 69, 343–358. [Google Scholar] [CrossRef]

| IMP & CON | |||||
|---|---|---|---|---|---|
| Nouri-Borujerdi et al. [49] | Nield and Kuznetsov [32] | Present Study | |||
| 4.67519 | 471.3787 | 4.67519 | 471.3847 | 4.67518 | 471.3846 |
| IMP & CON | IMP, CON & FRE | IMP, CON & CHF | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Water | Ester | Water | Ester | Water | Ester | ||||||||
| Case A | 1 | 5.37 | 107.90 | 5.21 | 134.62 | 3.11 | 67.83 | 3.01 | 81.23 | 2.98 | 63.95 | 2.92 | 77.41 |
| 2 | 5.48 | 87.39 | 5.34 | 111.96 | 3.20 | 56.48 | 3.09 | 69.89 | 3.04 | 53.06 | 2.97 | 66.21 | |
| 4 | 5.35 | 108.67 | 5.19 | 135.43 | 3.10 | 68.07 | 3.00 | 81.45 | 2.98 | 64.66 | 2.92 | 78.11 | |
| 6 | 5.17 | 138.03 | 5.03 | 164.86 | 3.00 | 82.63 | 2.91 | 94.34 | 2.92 | 79.39 | 2.87 | 91.59 | |
| 8 | 5.05 | 160.66 | 4.92 | 185.04 | 2.93 | 92.60 | 2.86 | 102.08 | 2.87 | 89.77 | 2.83 | 99.95 | |
| 10 | 4.96 | 177.21 | 4.85 | 198.37 | 2.88 | 99.17 | 2.83 | 106.69 | 2.85 | 96.80 | 2.81 | 105.05 | |
| Case B | 1 | 5.94 | 111.45 | 5.75 | 140.36 | 3.37 | 69.67 | 3.26 | 84.28 | 3.21 | 65.47 | 3.14 | 80.03 |
| 2 | 6.08 | 89.70 | 5.90 | 115.79 | 3.47 | 57.58 | 3.35 | 71.89 | 3.27 | 53.94 | 3.20 | 67.89 | |
| 4 | 5.92 | 112.27 | 5.73 | 141.24 | 3.36 | 69.92 | 3.25 | 84.52 | 3.21 | 66.23 | 3.14 | 80.80 | |
| 6 | 5.71 | 144.10 | 5.53 | 174.07 | 3.24 | 85.84 | 3.14 | 99.06 | 3.14 | 82.22 | 3.07 | 95.88 | |
| 8 | 5.55 | 169.31 | 5.39 | 197.34 | 3.16 | 97.06 | 3.08 | 108.07 | 3.09 | 93.81 | 3.04 | 105.53 | |
| 10 | 5.44 | 188.22 | 5.30 | 213.12 | 3.11 | 104.65 | 3.05 | 113.56 | 3.06 | 101.86 | 3.02 | 111.57 | |
| Case C | 1 | 4.62 | 105.71 | 4.50 | 129.92 | 2.81 | 67.65 | 2.73 | 79.79 | 2.71 | 64.15 | 2.67 | 76.51 |
| 2 | 4.71 | 86.51 | 4.60 | 109.45 | 2.87 | 56.97 | 2.79 | 69.55 | 2.76 | 53.79 | 2.71 | 66.26 | |
| 4 | 4.60 | 106.43 | 4.49 | 130.63 | 2.80 | 67.87 | 2.72 | 79.99 | 2.71 | 64.80 | 2.67 | 77.12 | |
| 6 | 4.48 | 132.94 | 4.37 | 156.03 | 2.71 | 81.04 | 2.65 | 91.12 | 2.66 | 78.26 | 2.62 | 88.88 | |
| 8 | 4.39 | 152.49 | 4.30 | 172.57 | 2.66 | 89.66 | 2.62 | 97.50 | 2.63 | 87.33 | 2.60 | 95.83 | |
| 10 | 4.33 | 166.24 | 4.26 | 183.06 | 2.63 | 95.13 | 2.59 | 101.18 | 2.61 | 93.24 | 2.58 | 99.94 | |
| Case D | 1 | 4.25 | 81.73 | 4.15 | 99.47 | 2.66 | 55.72 | 2.59 | 65.02 | 2.58 | 53.04 | 2.54 | 62.58 |
| 2 | 4.33 | 67.36 | 4.23 | 84.50 | 2.72 | 47.32 | 2.65 | 57.21 | 2.61 | 44.82 | 2.57 | 54.68 | |
| 4 | 4.24 | 82.27 | 4.14 | 100.00 | 2.65 | 55.92 | 2.59 | 65.20 | 2.58 | 53.53 | 2.54 | 63.03 | |
| 6 | 4.12 | 101.67 | 4.03 | 118.06 | 2.58 | 65.99 | 2.53 | 73.43 | 2.53 | 63.89 | 2.50 | 71.79 | |
| 8 | 4.05 | 115.59 | 3.97 | 129.46 | 2.54 | 72.36 | 2.50 | 78.00 | 2.51 | 70.65 | 2.48 | 76.81 | |
| 10 | 3.99 | 125.14 | 3.93 | 136.51 | 2.51 | 76.32 | 2.49 | 80.58 | 2.49 | 74.95 | 2.47 | 79.70 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahajan, A.; Sunil; Sharma, M.K. Linear Stability Analysis of Penetrative Convection via Internal Heating in a Ferrofluid Saturated Porous Layer. Fluids 2017, 2, 22. https://doi.org/10.3390/fluids2020022
Mahajan A, Sunil, Sharma MK. Linear Stability Analysis of Penetrative Convection via Internal Heating in a Ferrofluid Saturated Porous Layer. Fluids. 2017; 2(2):22. https://doi.org/10.3390/fluids2020022
Chicago/Turabian StyleMahajan, Amit, Sunil, and Mahesh Kumar Sharma. 2017. "Linear Stability Analysis of Penetrative Convection via Internal Heating in a Ferrofluid Saturated Porous Layer" Fluids 2, no. 2: 22. https://doi.org/10.3390/fluids2020022
APA StyleMahajan, A., Sunil, & Sharma, M. K. (2017). Linear Stability Analysis of Penetrative Convection via Internal Heating in a Ferrofluid Saturated Porous Layer. Fluids, 2(2), 22. https://doi.org/10.3390/fluids2020022






