Abstract
A review of the research on the instability of steady porous media convection leading to chaos, and the possibility of controlling the transition from steady convection to chaos is presented. The governing equations consisting of the continuity, the extended Darcy, and the energy equations subject to the assumption of local thermal equilibrium and the Boussinesq approximation are converted into a set of three nonlinear ordinary differential equations by assuming two-dimensional convection and expansion of the dependent variables into a truncated spectrum of modes. Analytical (weak nonlinear), computational (Adomian decomposition) as well as numerical (Runge-Kutta-Verner) solutions to the resulting set of equations are presented and compared to each other. The analytical solution for the transition point to chaos is identical to the computational and numerical solutions in the neighborhood of a convective fixed point and deviates from the accurate computational and numerical solutions as the initial conditions deviate from the neighborhood of a convective fixed point. The control of this transition is also discussed.
1. Introduction
A review is presented focusing on the instability of steady convection in porous media leading to chaos, and including the possibility of controlling the transition from steady convection to chaos. The governing equations are converted into a set of three nonlinear ordinary differential equations by assuming two-dimensional convection and expansion of the dependent variables into a truncated spectrum of modes. Analytical, computational as well as numerical solutions to the resulting set of equations are presented and compared to each other. The analytical solutions include a linear stability analysis and a weak nonlinear analysis. The “computational” solution refers in this review to the solution obtained via Adomian’s decomposition method [1,2], while the numerical solution of the set of ordinary differential equations refers to the solution based on using the fifth and sixth order Runge-Kutta-Verner method from the IMSL Library [3].
Nield and Bejan [4], Diersch and Kolditz [5], and Masuoka et al. [6] presented reviews on natural convection in porous media. Theoretical results demonstrating that the transition from steady to chaotic (weak turbulent) convection in saturated porous media subject to local thermal equilibrium yields a set of equations that is equivalent to the Lorenz system (Lorenz [7]) were presented Vadasz and Olek [8,9,10,11], Vadasz [12,13,14,15,16,17,18,19], and Jawdat and Hashim [20]. Vadasz [21] presented a review focusing on the analytical capturing of the transition point to weak turbulence. Similar results for the corresponding problem of convection in pure fluids were presented by Vadasz [22,23], and for centrifugally induced convection in a rotating porous layer by Vadasz and Olek [24] (see also Vadasz [25]; Straughan [26]). The instabilities related to this problem have been studied among others by Straughan [27,28], Govender [29,30,31], Vanishree and Siddheshwar [32], Mohammad et al. [33], Ahmad and Ress [34], Noghrehabadi et al. [35], and Rees and Mojtabi [36], and for thermo-solutal (double-diffusive) convection by Lombardo et al. [37], Lombardo and Mulone [38], Schoofs and Spera [39], Mulone and Straughan [40], and Govender [41].
Linear stability analysis of the Lorenz equations around the nontrivial stationary points yields a critical value of the controlling parameter, the scaled Rayleigh number, , representing the transition from steady solutions to chaos, where is the other critical Rayleigh number for the transition from a motionless solution (trivial stationary point) to steady convection (nontrivial stationary point). Numerical, computational (Vadasz [12,13,14,15,16,17,18,19,22,23]; Vadasz and Olek [8,9,10,11]), as well as experimental results (Wang et al. [42], Yuen and Bau [43]) show that the transition from steady convection to chaos occurs at subcritical values of Rayleigh number, i.e., at . Sparrow [44] shows that for the Lorenz system analyzed around the origin, the transition to chaos occurs via a homoclinic explosion and that the homoclinic orbit, which exists just at the point where the solution orbiting around one non-trivial steady solution turns towards the other nontrivial steady solution, belongs to the subcritical Hopf bifurcation obtained at (or ).
Magyari [45] showed that the Lorenz-type model can be transformed into the governing equations of a damped nonlinear oscillator, modulated by a linear degenerated overdamped oscillator (relaxator), which in turn is coupled to a former one by a nonlinear cross-force. The benefit of this mechanical analogy was to produce an intuitive picture of the regular and chaotic dynamics described by Vadasz and Olek [8,9,10,11]. Mahmud and Hashim [46] suggested a feedback control system (Bau [47]) to be applied to the porous media convection based on the porous media feedback control presented by Tang and Bau [48], and Zhao and Bau [49]. Magyari [50] demonstrated that the structure of the feedback control system proposed by Mahmud and Hashim [46] does not change the original uncontrolled system and the only effect that the feedback control has, is in altering the initial conditions of the system. As it is experimentally impossible in practice to know precisely, let alone control the initial conditions, especially when they are treated as small perturbations around the basic stationary convection state, the feedback control system suggested by Mahmud and Hashim [46] can be used to provide an equivalent means of control of the initial conditions as indicated by Magyari [50]. Such a control can then be applied to promote or suppress chaos within some specified domain of the scaled Rayleigh number [51]. Reviewing analytical, computational and numerical results explaining the subcritical transition point and the use of the controller to promote or suppress it forms one of the objectives of the present paper. The other objective is to present the accuracy of the different methods of solution used.
2. Problem Formulation
A narrow () rectangular fluid-saturated porous domain subject to gravity and heated from below, as presented in Figure 1, is considered.
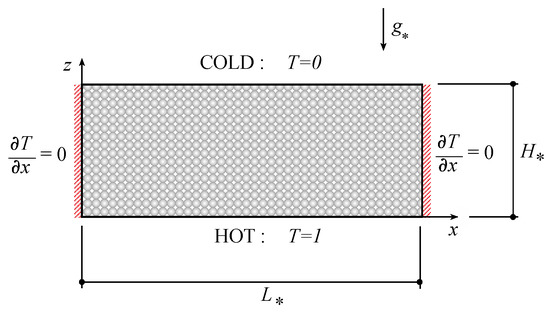
Figure 1.
A rectangular fluid-saturated porous domain heated from below [8,10,14]. (Reproduced with permissions from Peter Vadasz, Shmuel Olek, Transport in Porous Media; published by Springer, 1999, 2000. Peter Vadasz, Journal of Heat Transfer; published by ASME, 2001.)
A Cartesian co-ordinate system is used such that the vertical axis is collinear with gravity, i.e., . The time derivative term is not neglected in Darcy’s equation, a condition that was well discussed and substantiated by Vadasz and Olek [8], and Vadasz [12,25]. Other than that Darcy’s law is assumed to govern the fluid flow and local thermal equilibrium is assumed to govern the heat transfer, while the Boussinesq approximation is applied for the effects of density variations. Subject to these conditions the following dimensionless set of governing equations is obtained
The values , and are used to scale the filtration velocity components (), pressure (), and temperature variations (), respectively, where is the effective thermal diffusivity, is fluid viscosity, and is the permeability of the porous matrix. The height of the layer was used for scaling the variables , and for scaling the time . Accordingly, and and . In Equation (2) is the gravity-related Rayleigh number in porous media defined in the form . The time derivative term was included in Darcy’s Equation (2), where is a dimensionless group including the porosity, the Prandtl, and Darcy numbers that Straughan [26] named the Vadasz number, or alternatively Vadasz coefficient Straughan [52] (see also Sheu [53]). Vadasz and Olek [8,10] have shown that when investigating wave phenomena, such as the present case, the time derivative in Equation (2) needs to be included irrespective of how large the value of is. Without including this term the possibility of oscillatory convection is wiped out, and subsequently the transition to weak turbulence by using the present model becomes impossible. Including the time derivative term in Equation (2) is equivalent to maintaining the highest derivative in an equation in order to satisfy all boundary (or initial) conditions.
As all the boundaries are rigid the solution must follow the impermeability conditions there, i.e., on the boundaries, where is a unit vector normal to the boundary. The temperature boundary conditions are: on all other walls representing the insulation condition on these walls. For convective rolls having axes parallel to the shorter dimension (i.e., ) , and the governing equations can be presented in terms of a stream function defined by and , which upon applying the curl () operator on Equation (2) yields the following system of partial differential equations from Equations (1)–(3)
where the boundary conditions for the stream function are on all solid boundaries.
The set of partial differential Equations (4) and (5) form a non-linear coupled system, which together with the corresponding boundary conditions accepts a basic motionless conduction solution. To obtain the complete solution to the non-linear coupled system of partial differential Equations (4) and (5) we represent the stream function and temperature in the form consistent with the wave number corresponding to the convection threshold (as Lorenz [7] adopted in the equivalent problem for pure fluids)
Equations (6) and (7) are equivalent to a Galerkin expansion of the solution in both and directions, truncated when , where is the Galerkin summation index in the direction and is the Galerkin summation index in the direction. Substituting (6) and (7) into the Equations (4) and (5), multiplying the equations by the orthogonal eigenfunctions corresponding to (6) and (7), and integrating them over the domain, i.e., , yields a set of three ordinary differential equations for the time evolution of the amplitudes (see Vadasz and Olek [10], Vadasz [22]). By rescaling the time , and introducing the following notation
yields the following set of equations
In Equation (8) represents the critical Rayleigh number for the transition from a motionless solution (trivial stationary point) to steady convection (non-trivial stationary point) and a value of corresponding to is the one used in the following calculations.
The fixed (i.e., stationary) points of the system (9)–(11) are obtained by setting all the time derivatives equal to zero and solving the resulting algebraic equations. They yield the following solutions representing the motionless conduction solution, and
representing the steady convection solutions. The behavior of these fixed points as the value of changes is presented graphically on the bifurcation diagrams in Figure 2 by the black curves. One can observe a pitchfork bifurcation at as the transition from a conduction motionless solution towards a steady convection solution occurs. The fixed point associated with the conduction motionless solution loses stability at the bifurcation point where the two fixed points associated with steady convection do appear and are stable, as will be demonstrated analytically in the next section. The latter represent convection cells moving clockwise or counter-clockwise, hence the two fixed points. The red/gray curves represent the envelope of an unsteady limit cycle that evolves as an inverse Hopf bifurcation at another bifurcation point, where the steady convective solutions (12)–(14) lose stability in the linear sense, a result that will be presented later. The following analysis and solution are substantially simplified by rescaling the dependent variables with respect to their fixed points in the form
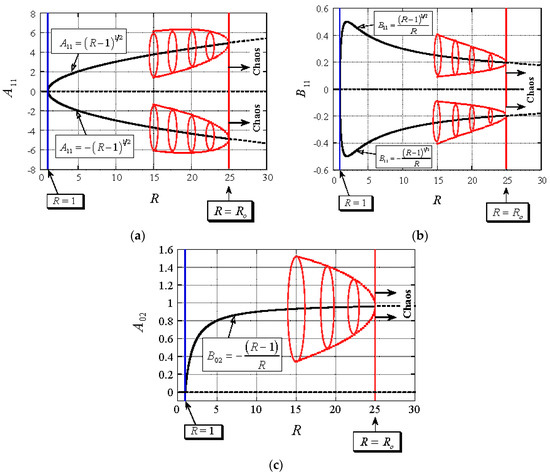
Figure 2.
Graphical description of the solutions (a) ; (b) ; and (c) , as a function of on bifurcation diagrams [21]. (Reproduced with permission from Peter Vadasz, Journal of Porous Media; published by Begell House, 2015.)
The Expansions (6) and (7) are then expressed in terms of the rescaled variables in the form
where and are time dependent convection amplitudes. As a result of this rescaling Equations (9)–(11) take the form
where the dots denote time derivatives .
Mahmud and Hashim [46] suggested a feedback control system (Bau [47]) to be applied to the porous media convection based on the porous media feedback control presented by Tang and Bau [48], Zhao and Bau [50]. Repeating the same procedure as applied above for this feedback control system one obtains a set of three ordinary differential equations, which represents the temporal dynamics of the amplitudes , , , corresponding to the lower order convection modes (Vadasz and Olek [8,10], Vadasz [12]) that in addition include feedback control as proposed by Mahmud and Hashim [46], as follows
The symbol represents the scalar gain controller introduced by Mahmud and Hashim [46]. Equations (21)–(23) are the scaled Lorenz equations (Lorenz [7], and Sparrow [44]) subject to feedback control, and their solution is subject to the initial conditions , and at . Magyari [50] showed that the controlled system (21)–(23) could be converted into the uncontrolled one via the simple transformation
Substituting Magyari’s transformation (24) into Equations (21–(23) yields the uncontrolled system (18)–(20). Equations (21)–(23) can be presented in the vector form where the vector is defined by and representing the right hand side of Equations (21)–(23) has the form , where , , . The fixed points of the system (21)–(23) are obtained by setting the time derivative to be zero leading to , and producing the trivial fixed point and the non-trivial fixed points , and . The former represents the motionless conduction solution, while the latter represent steady state solutions consisting of convection cells moving clockwise or counter-clockwise. The Jacobian matrix associated with this system is defined by and evaluating it at any one of the fixed points yields the original system linearized around the selected fixed point, i.e.
needed for evaluating the eigenvalues and eigenvectors of the linear system around any selected fixed point.
3. Linear Stability Analysis
By deriving the determinant of the Jacobian matrix evaluated around any fixed point yields an equation for the eigenvalues of the original system of ordinary differential equations linearized around the selected fixed point. Evaluating the determinant of the Jacobian matrix for system (21)–(23) around the trivial fixed point produces the following algebraic equation for the eigenvalues
It may be observed that despite the fact that the gain controller appeared explicitly in the Jacobian matrix, its effect disappeared (cancelled out) from its determinant and is not reflected in the eigenvalues equation. Equation (26) has three real roots (for ) as follows
The last two roots and are always real and negative because . The first root, , provides the stability condition for the motionless solution (trivial fixed points) in the form
At the motionless solution (trivial fixed point) loses stability becoming a saddle point, and the convective fixed points take over. As established numerically later (and in [9]) an unstable homoclinic orbit appears at a value of (the large number of digits are needed computationally to guarantee the homoclinic orbit completing one full cycle before the solution is repelled towards one of the stable convective fixed points).
Evaluating the determinant of the Jacobian matrix around the convection (non-trivial) fixed points , and yields the eigenvalues equation in the form
It may be observed again that despite the fact that the gain controller appeared explicitly in the Jacobian matrix, its effect disappeared (cancelled out) from its determinant and is not reflected in the eigenvalue equation. Furthermore, Equation (29) is identical to the one obtained for the uncontrolled Lorenz system (corresponding to ) as presented by Vadasz and Olek [8,11]. The eigenvalues are therefore identical to the ones obtained from the uncontrolled system. Equation (29) yields three eigenvalues. Substituting the general form of an eigenvalue as , where and are the real and imaginary components, respectively, into Equation (29) and separating real and imaginary parts yields two equations for the real and imaginary components of the eigenvalues in the form
The smallest eigenvalue is always real and negative over the whole range of parameters’ values. The other two are real and negative at slightly supercritical values of , therefore the convection fixed points are stable, i.e., simple nodes, as presented in Figure 3. As the value of increases these two roots move on the real axis towards the origin (where ), the smaller of the two chasing the other one and reducing the distance between them. For these roots become equal at (see Figure 3). From this point these two roots become a pair of complex conjugate eigenvalues , where and are their real and imaginary components, respectively. However they still have negative real parts, therefore the convection fixed points are still stable, i.e., spiral nodes. As the value of increases further, both the imaginary and real parts of these complex conjugate eigenvalues increase. On the complex plane, they cross the imaginary axis (where ), i.e., their real part becomes non-negative at a value of that is obtained by substituting the corresponding to , i.e., into Equations (30) and (31) to yield the following two equations
where the subscript in and stands to indicate that these are values associated with . Solving Equations (32) and (33) for and yields
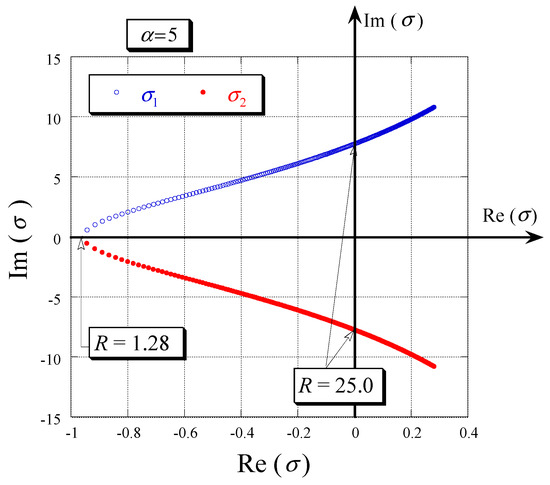
Figure 3.
Variation of the eigenvalues as the value of increases [8,21]. (Reproduced with permissions from Peter Vadasz, Shmuel Olek, Transport in Porous Media; published by Springer, 1999. Peter Vadasz, Journal of Porous Media; published by Begell House, 2015.)
Therefore, the convective fixed points lose stability in the linear sense at a value of the scaled Rayleigh number ( for ) and the basic frequency of the oscillations at marginal stability is . Their values are presented in Equation (34). For the convective fixed points are stable (spiral nodes) and the solution will produce steady convection. At the saddle limit cycle presented in Figure 2 collides with these steady convective fixed points and is annihilated by this collision. For the fixed points are not stable and another type of solution (chaotic) is anticipated. Note that in order to obtain finite positive values for and from (34) their denominator must be positive, implying .
4. Numerical, Computational, and Weak Nonlinear Analytical Solutions
The “computational” solution of the set of ordinary differential Equations (18)–(20) or Equations (21)–(23) refers here to the solution obtained via Adomian’s decomposition method [1,2], while the numerical solution refers to the solution based on using the fifth and sixth order Runge-Kutta-Verner method from the IMSL Library [3]. Using the transformed system following Magyari’s transformation (24) into Equations (21)–(23) yields the original uncontrolled system (18)–(20). Therefore, as Magyari [50] concluded, the main effect that the feedback control suggested by Mahmud and Hashim [46] has is in altering the initial conditions of the system in the form provided by Magyari’s transformation (24), i.e.,
where and are the initial conditions in the uncontrolled and controlled Lorenz system, respectively.
The system (18)–(20) was solved numerically to double precision by using the fifth and sixth order Runge-Kutta-Verner method from the IMSL Library (DIVPRK) (1991) up to a desired tolerance for error control specified by the parameter . The results are presented at two values of , the first at just before the transition to chaos occurs, and the second just after the transition at (note that for ). The results for these two values of in the time domain are presented in Figure 4 for as a function of t. The decay of the solution corresponding to towards the steady state value of is clearly identified in Figure 4a by the envelope of the solution, while Figure 4b shows the details of the solution in the time domain . On the other hand, for , Figure 4c shows a typical chaotic result, while Figure 4d shows the details of the solution in the time domain . It is worth emphasizing the fact that the numerical results show a transition to chaos at a sub-critical value of (the critical value is ). A comparison between Figure 4a,c at a common transient time domain shows that the envelope of the function converges for (Figure 4a) and diverges for (Figure 4c). This suggests that somewhere in-between and the envelope of the function will neither converge nor diverge, producing a typical limit cycle. Looking for this limit cycle provides the result presented in Figure 4e, where it is evident that the envelope of the function does not converge nor diverge, and the inset presented in Figure 4f demonstrates the periodic behavior of the solution. The same numerical results are presented graphically as a trajectory on phase diagrams in Figure 5 as projection of the solution data points on the planes (), (), and ().
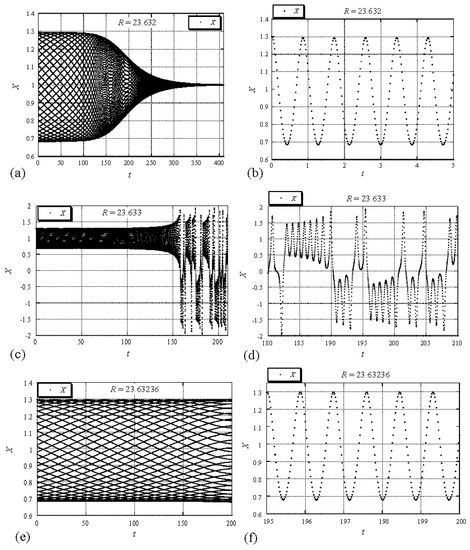
Figure 4.
Numerical results of versus time for different values of around the transition from steady convection to weak turbulence. (a) R = 23.632; (b) R = 23.632 inset; (c) R = 23.633; (d) R = 23.633 inset; (e) R = 23.63236; (f) R = 23.63236 inset [21]. (Reproduced with permission from Peter Vadasz, Journal of Porous Media; published by Begell House, 2015.)
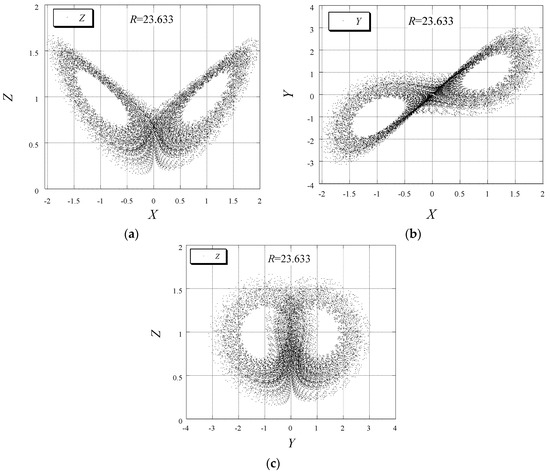
Figure 5.
Phase diagrams as projection of the solution data points on the planes (a) (); (b) (); and (c) () [21]. (Reproduced with permission from Peter Vadasz, Journal of Porous Media; published by Begell House, 2015.)
The computational solution was obtained by using Adomian’s decomposition method [1,2] as described in detail in [8,10]. The method provides in principle an analytical solution in the form of an infinite power series for each dependent variable. The practical need to evaluate numerical values from the infinite power series suggests the use of the decomposition method as an algorithm for the approximation of the dynamical response in a sequence of time intervals. A comparison between the numerical and computational solutions is presented in a later section of this review.
The analytical solution to the problem (18)–(20) was evaluated via a weak non-linear analysis by using an expansion around the point where the non-trivial stationary solutions lose stability in the linear sense, i.e., around ( for ). The stationary (fixed) points of the system (18)–(20) are the convection (non-trivial) solutions , and the trivial solution . The expansion around the trivial stationary solution yields the familiar results of a pitchfork bifurcation from a motionless state to convection at . We expand the dependent variables around the non-trivial stationary points in the form
We also expand in a finite series of the form which now defines the small expansion parameter as , where is the value of where the stationary non-trivial solutions lose their stability in the linear sense as presented in Equation (34) (see also Vadasz and Olek [8,10], Vadasz [18]). Therefore the present weak non-linear analysis is expected to be restricted to initial conditions sufficiently close to any one, but only one, of the non-trivial fixed points. Introducing a long time scale and replacing the time derivatives in Equations (18)–(20) with yields a hierarchy of ordinary differential equations at the different orders. The values of and the basic frequency were derived via the linear stability analysis and are presented in Equation (34). Based on the linear stability analysis the loss of stability of the non-trivial stationary points occurs at a value of . For the linear stability predicts a solution that converges to one of the stationary points, while for a post-transient chaotic solution is anticipated. In reality, numerical and experimental results show that the transition from the steady solution to chaos occurs at a value of . The solutions to order have the form
where , and are the three eigenvalues of the system (18)–(20) linearized around . At marginal stability, i.e., at , the real part of the complex eigenvalues is zero. Therefore, at order one can set the argument of the exponents in Equations (37)–(39) to and , by substituting .
What typically follows when using the weak non-linear method of solution is the neglect of the decaying term from the solution. Clearly this term does not bring any contribution to the post-transient solution. However, while indeed this term vanishes at the post-transient state, its inclusion in the solution becomes essential in order to provide a relationship between the initial conditions in the present analytical solution and the numerical one. The coefficients and are allowed to vary over the long time scale . By substituting the Solutions (37)–(39) into the linearized form of Equations (18)–(20), that apply at order (see [12], for details), one obtains the following relationships between these coefficients
A solvability condition is obtained at order producing an equation for the complex amplitudes and . The polar coordinates representation of this equation is obtained by presenting the complex amplitude in the form
The amplitude and the frequency correction of the solution at order are then obtained from the solvability condition, transforming the amplitude equation in the form
where and
with , , and as parameters that depend on the value of . For , corresponding to , values consistent with the present study , , , , (see Vadasz [12], for details on how these values are obtained), and the following critical values apply and . Clearly for (sub-critical conditions), for (supercritical conditions), and for (critical conditions). The post-transient solution to Equation (43) yields , which produces a real value of only for . The Hopf bifurcation at is therefore sub-critical and in order to investigate the breakdown of the periodic solution at the derivation of the transient solution to Equation (43) is undertaken. This transient solution is obtained by direct integration of (43) in the form
where the following initial conditions apply: at . The solution (46) is valid at leading to , which can be recovered by substituting in Equation (46). Vadasz [12] has shown that the Solution (46) becomes singular, i.e., its denominator vanishes at a critical value of expressed by the equation
When this critical time exists the solution for the amplitude of steady convection blows up in finite time, which can be interpreted as the divergence of the steady convection solution towards a new non-steady one, in this case chaotic. The existence of this critical time is linked to a condition that the argument of the function in Equation (47) is positive and greater or smaller than 1, depending on whether is negative or positive, respectively. The latter requirement comes to impose a positive value of , otherwise no physical significance can be associated with this critical time. This condition exists only for sub-critical values of , i.e., for (), and is presented in the form leading to , while for supercritical values of , i.e., for () the critical time exists unconditionally. Transforming the condition for this transition to occur, from , to the original physical parameters of the system by substituting the definition of , leads to a value of , say , beyond which the transition occurs, which can be expressed in the form
where the minus sign and the absolute value of appear in order to show explicitly that . If the solution decays, spiraling towards the corresponding fixed point, and at we expect the limit cycle solution. Beyond this transitional value of , i.e., , the solution moves away from this fixed point. Therefore, at the value of we expect to obtain a limit cycle solution and beyond it a chaotic solution. Since we attempt solving the controlled system (21)–(23) originally subject to constant initial conditions for the controlled system variables , , , while varying only the value of the gain controller , we need to transform the results obtained for the uncontrolled system (18)–(20) and express them in terms of , , . First, there are relationships linking the initial conditions expressed in terms of the analytical solution amplitudes , and to the initial conditions in terms of , , (Vadasz [17]) in the form (the subscript applied to , , , or , , and to specifies the initial conditions for these variables)
and the inverse relationships are
where , and . Once the value of is established from Equation (52) one can evaluate the value of by substitution, in the form
Substituting Equation (52) and the expression for from Equation (53) into Equation (49) allows expressing in the form
Equations (52)–(54) represent the inverse compatibility relationships between the analytical weak non-linear solution and any numerical solutions, the latter being naturally expressed in terms of , while the former is expressed in terms of .
By introducing now Magyari’s transformation (Magyari [50]) from Equation (24) into Equations (49)–(51) yields the relationship between and in the form
and a corresponding inverse relationship by using , and , in Equations (52)–(54). For constant initial conditions , and the values to be substituted into (52)–(54) depend on only, which is what we aimed, i.e., to observe the effect of the gain controller alone on the solution and its ability to mimic the alteration of the initial conditions in terms of rendering the transition point forwards or backwards. As for constant initial conditions , depends on only if we can evaluate this dependence and substitute the resulting into Equation (48) to produce the analytical curve of the transition point to chaos .
A special case when is also considered although the latter does not produce constant initial conditions in terms of . When the relationships between the initial conditions are
For any choice of
we obtain
and
Substituting (64) into (48) yields the transition point to chaos for this special case of in the form
For Equation (65) produces a simple quadratic function of in the form
To validate the results of the analytical solution, which are accurate only in the neighborhood of a fixed point, the system (18)–(20) was solved to double precision by using the fifth and sixth order Runge-Kutta-Verner method from the IMSL Library (DIVPRK) [3] up to a desired tolerance for error control specified by the parameter . The accuracy of the analytical solution being only in the neighborhood of a fixed point implies in the present case small values of .
5. Results for the Transition Point from Steady Convection to Chaos
Initially the uncontrolled system analytical solutions were compared to the numerical ones obtained for different initial conditions and the transition value of was established numerically by trial and error, and compared to the one obtained analytically from Equation (48). The computations were divided in three computational sets of results. Computational set 1 corresponds to the particular case when and (presented by Vadasz [12]), computational set 2 corresponds to the particular case when , associated with Equations (49)–(51), while computational set 3 corresponds to arbitrary initial conditions that do not belong to any particular case and are therefore general. The results are presented in Figure 6 where the continuous curve represents the analytical solution expressed by Equation (48) while the different dots represent the computational results corresponding to the different computational sets. The very good agreement between the analytical and numerical solutions in the neighborhood of the convective fixed point (i.e., ) is evident from Figure 6. Actually for the numerical and analytical solutions overlap. When considering the condition of validity of the asymptotic expansion, i.e., , the agreement between the results is well within this anticipated domain.
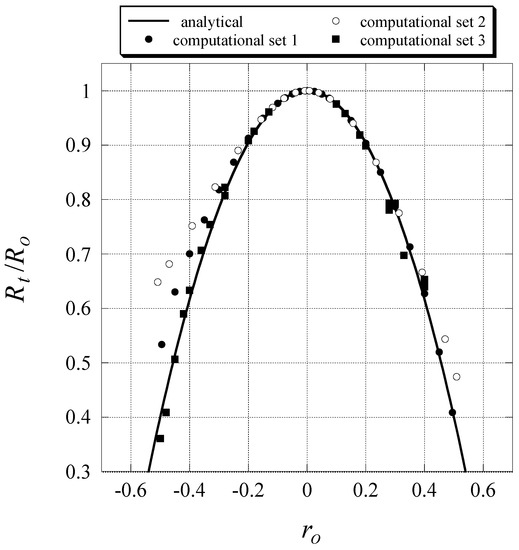
Figure 6.
Transitional subcritical values of the scaled Rayleigh number as a function of the initial conditions corresponding to three computational sets (using Adomian decomposition method) compared to the analytical solution (weak nonlinear) [17,21]. (Reproduced with permissions from Peter Vadasz, International Journal of Non-Linear Mechanics; published by Elsevier, 2001. Peter Vadasz, Journal of Porous Media; published by Begell House, 2015.)
For the controlled system and for constant initial conditions the values corresponding to the uncontrolled system’s convective fixed point were used. As long as the value of is not zero the controlled fixed point does not overlap with . The results for the analytical (weak nonlinear) prediction of the transition point to chaos (65) are compared with the corresponding transition in the numerical (Runge-Kutta-Verner) solutions for different values of the gain controller and are presented in Figure 7. From the figure it can be observed that the analytical (weak nonlinear) and numerical (Runge-Kutta-Verner) results overlap for , which reinforces the anticipation that the analytical results are accurate for small values of . As the value of increases the deviation between the analytical (weak nonlinear) and numerical (Runge-Kutta-Verner) results is evident with a maximum deviation of about 18% at . However, the most important outcome that is evident in this figure is that it is possible to use the gain controller to apparently alter the initial conditions, or actually to promote or suppress the transition to chaos (within a certain range of values of , where is the value of associated with the appearance of the homoclinic orbit). For the special case when the initial conditions are not constant anymore but follow Equations (62) and (63). We used here and Equation (66) to evaluate the analytical (weak nonlinear) curve and compare it to the numerical (Runge-Kutta-Verner) results providing the transition point as presented in Figure 8. From the figure it is evident again that there is wide region of overlap between the analytical prediction and the numerical one. Again, the results show that it is possible to control the transition to chaos via the feedback control system proposed by Mahmud and Hashim [46] and modified by Magyari [50]. This implies that by varying the gain controller , weak turbulence (chaos) can be either promoted or suppressed within a certain range of values of , where is the value of associated with the appearance of the homoclinic orbit. In both cases the deviation between the analytical and numerical results is not symmetrical with respect to , a result that is quite anticipated. In the second case, the analytical result expressed by Equation (66) is symmetrical around , as the orbit representing the limit cycle at the transition point is an ellipse when using the analytical (weak nonlinear) solution, however the numerical (Runge-Kutta-Verner) solution shows that the ellipse is a good approximation in the neighborhood of the fixed point, but as the orbit moves away from the fixed point and closer to the homoclinic orbit its shape is by far different from an ellipse.
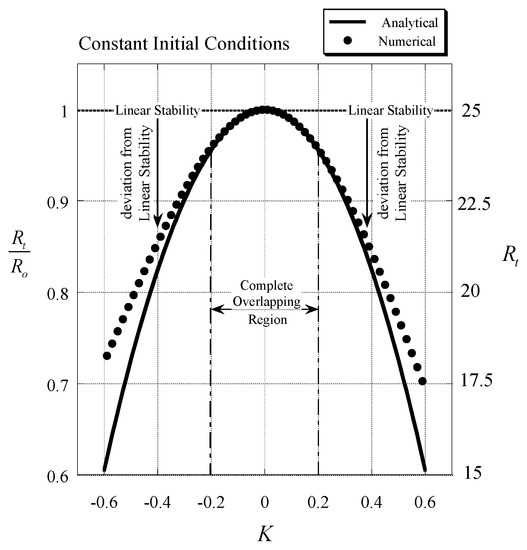
Figure 7.
Transitional subcritical values of the scaled Rayleigh number as a function of the feedback gain controller parameter corresponding to constant initial conditions of [51]. (Reproduced with permission from Peter Vadasz, Transport in Porous Media; published by Springer, 2010.)
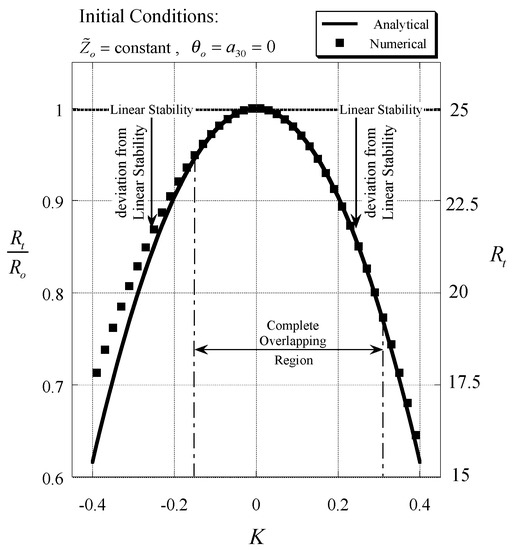
Figure 8.
Transitional subcritical values of the scaled Rayleigh number as a function of the feedback gain controller parameter corresponding to initial conditions of [51]. (Reproduced with permission from Peter Vadasz, Transport in Porous Media; published by Spinger, 2010.)
6. Results for the Comparison between the Computational (Adomian Decomposition) and Numerical (Runge-Kutta-Verner) Solutions
The system (18)–(20) was solved numerically to double precision by using the fifth and sixth order Runge-Kutta-Verner method from the IMSL Library (DIVPRK) [3] up to a desired tolerance for error control specified by the parameter . The numerical solution results (referred thereafter as “the numerical results”) were then compared to the Adomian decomposition results (referred thereafter as “the computational results”) by evaluating the difference between the two solutions at all values of up to , and plotting this difference in the results as projections of the trajectory of differences on the planes ( plane), ( plane) and ( plane), where , and . The indices “” and “” stand for representing the computational (Adomian decomposition) and numerical (Runge-Kutta) results, respectively. However, just before undertaking this comparison the impact of the number of terms in the series solution, and its truncation, on the results was assessed by evaluating the Adomian decomposition results for and with 15 and 150 terms in the series and comparing them. The results of this comparison showed that their numerical values are identical over the whole range of significant digits of the double precision computation. One could therefore conclude that it is sufficiently accurate for the following computations to use 15 terms in the series for the computational solution. The results of the comparison between the computational and numerical solutions corresponding to a value of used in the computational solution, and to a value of the tolerance control parameter used in the numerical solution, and for , are presented in Figure 9a–c. From these figures it is evident that the difference between the computational and numerical solutions is of the order of magnitude . Attempting to increase the accuracy of the numerical solution by decreasing the value of the tolerance control parameter to and keeping the value of unchanged, i.e., , yields the results presented in Figure 9d–f in terms of projections of trajectories data points on the planes , and , where the data points are not connected. It can be observed from these figures that increasing the accuracy of the numerical solution brought the computational and numerical results closer to each other up to an order of magnitude of (for the maximum difference between the two). In addition one can observe by comparing the Figure 9a with Figure 9d, Figure 9b with Figure 9e and Figure 9c with Figure 9f that the shape of the trajectory of differences is kept quite similar under the scale reduction, which resulted from increasing the accuracy of the numerical solution. A further attempt to increase the accuracy of the numerical solution by reducing the tolerance control parameter to (which is the smallest possible value that produces valid results) and evaluating the differences between the numerical and computational solutions yields the results as presented in Figure 10. It is evident that the maximum difference is now of an order of magnitude of , as can be observed from Figure 10a–c. Their corresponding results in the time domain are presented in Figure 10d representing the envelope of the solution , and their details are highlighted as insets in Figure 10e,f. Up to this point the comparison between the computational and numerical results shows that by increasing the accuracy of the numerical solution (i.e., decreasing the value of the tolerance control parameter) brings its results closer to the computational solution up to a maximum difference between the two of an order of magnitude of . These results correspond to steady convection, i.e., subcritical conditions (). Naturally, one cannot expect similar results for supercritical conditions when the solution is chaotic, because then two nearby trajectories diverge (at least one their Lyapunov exponents is positive). In order to compare the results between the numerical and computational solutions and establish the accuracy of Adomian’s decomposition method at supercritical conditions we use the existence of periodic windows within the chaotic regime and evaluate the comparison at values of corresponding to these periodic windows. The first wide periodic window appears around (see Vadasz and Olek [8]).
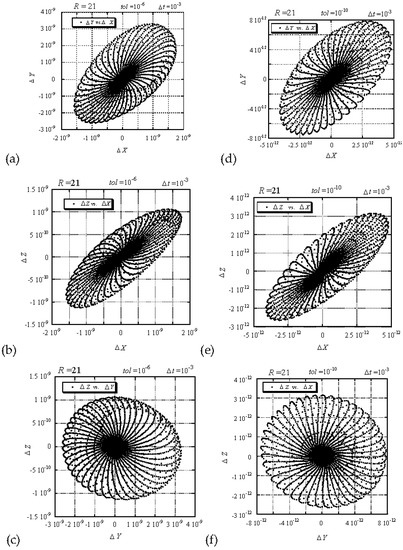
Figure 9.
Trajectory of differences between the computational (Adomian decomposition) and numerical (Runge-Kutta) solutions corresponding to in the computational solution, and . (a) projection of trajectory’s data points on the plane , with in the numerical solution; (b) projection of trajectory’s data points on the plane , with in the numerical solution; (c) projection of trajectory’s data points on the plane , with in the numerical solution; (d) projection of trajectory’s data points on the plane , with in the numerical solution; (e) projection of trajectory’s data points on the plane , with in the numerical solution; (f) projection of trajectory’s data points on the plane , with in the numerical solution. (Data points are not connected) [11]. (Reproduced with permission from Peter Vadasz, Shmuel Olek, International Journal of Heat and Mass Transfer; published by Elsevier, 2000.)
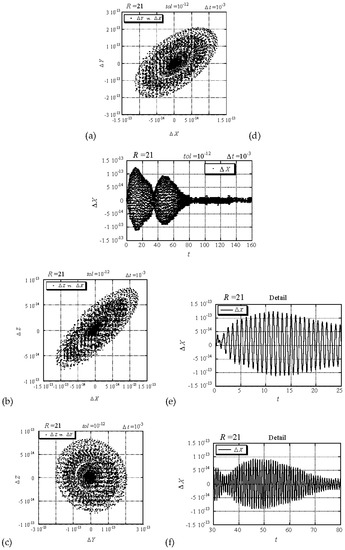
Figure 10.
Trajectory of differences between the computational (Adomian decomposition) and numerical (Runge-Kutta) solutions corresponding to in the computational solution, in the numerical solution, and . (a) projection of trajectory’s data points on the plane ; (b) projection of trajectory’s data points on the plane ; (c) projection of trajectory’s data points on the plane ; (d) the solution of projected on the time domain; (e) inset of the solution projected on the time domain for ; (f) inset of the solution projected on the time domain for . (Except for Figure 10e,f, the data points are not connected) [11]. (Reproduced with permission from Peter Vadasz, Shmuel Olek, International Journal of Heat and Mass Transfer; published by Elsevier, 2000.)
We evaluate therefore the differences between the computational and numerical solutions, and at providing the results presented in Figure 11a–c in terms of projections of trajectories data points on the planes , and , where the data points are not connected. A value of was used in the computational solution, and a value of the tolerance control parameter was used in the numerical solution for the results presented in Figure 11. It can be observed from the figures that the maximum difference between the two solutions is of the order of magnitude of . At this stage we were interested to establish the reason for the greater difference between the solutions as compared with the results obtained at subcritical conditions, i.e., for , and in particular we attempted to establish which one of the solutions, the computational or the numerical is to be “blamed” for increasing the difference between the two from at to at . In order to establish this we evaluated the differences between two consecutive computational solutions corresponding to and , respectively, and two consecutive numerical solutions corresponding to and , respectively. The differences between the two computational solutions showed that the maximum difference in the computational solution is of the order of magnitude while the maximum difference in the numerical solution is of the order of magnitude . We can therefore establish that the computational solution is more accurate in this case (i.e., its level of accuracy is saturated) and the “blame” for the loss of accuracy is to be placed on the numerical solution. Naturally, one can improve the accuracy of the numerical method by adopting a constant rather than variable time step algorithm, which is less efficient computationally, or by choosing a higher order Runge-Kutta scheme. Nevertheless, the comparison offered here is related to a standard library package (IMSL DIVPRK [3]) that is likely to be widely used. In this context, the comparison shows that when the standard library package tolerance parameter is taken to its limit (no more tightening of tolerance is possible beyond ), the computational solution outperforms the numerical one. Furthermore, even when we decrease the number of terms in the series to 10 the computational results remain the same up to the whole range of digits of machine precision. Therefore, the computational results are more accurate than the presently used numerical ones corresponding to their smallest possible tolerance, even with only 10 terms in the series. The reason for the latter is that the accuracy of the computational solution with 10 terms in the series is saturated. Reducing further the number of terms in the series decreases the accuracy of the computational results.
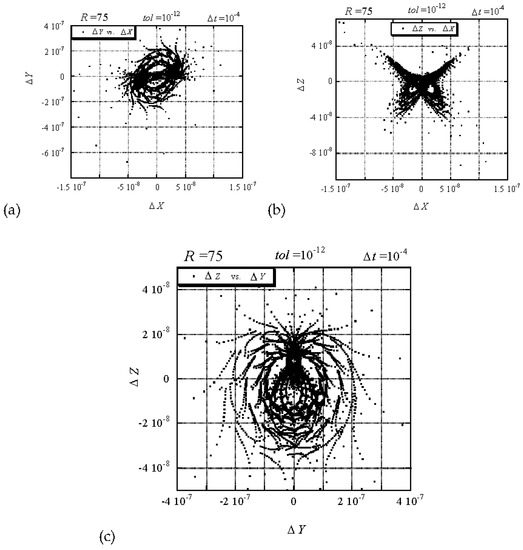
Figure 11.
Trajectory of differences between the computational (Adomian decomposition) and numerical (Runge-Kutta) solutions corresponding to in the computational solution, in the numerical solution, and . (a) projection of trajectory’s data points on the plane ; (b) projection of trajectory’s data points on the plane ; (c) projection of trajectory’s data points on the plane . (Data points are not connected) [11]. (Reproduced with permission from Peter Vadasz, Shmuel Olek, International Journal of Heat and Mass Transfer; published by Elsevier, 2000.)
7. Conclusions
The analytical (weak nonlinear), numerical (Runge-Kutta-Verner) and computational (Adomian decomposition) results confirmed the transition from steady convection to chaos via a saddle limit cycle at a subcritical value of the Rayleigh number. The subcritical transition was explained by investigating the transient amplitude solution obtained via the weak nonlinear theory. The anticipation raised by Magyari’s transformation (Magyari [50]) to the feedback control problem suggested by Mahmud and Hashim [46] as well as Roslan et al. [54] that it might be possible to control weak turbulence in porous media convection was shown to be correct. One may use the gain controller to promote or suppress chaos in porous media convection. It acts as an apparent alteration of the initial conditions, the latter being unpredictable and difficult to measure with the accuracy needed to control weak turbulence directly. Therefore the method presented is an elegant practical way to overcome the latter difficulty. The comparison of the evaluated transition point to chaos via the weak nonlinear solution with the numerical (or computational) solution showed an excellent match in the neighborhood of a convective fixed point in the uncontrolled case and an excellent match for small values of the gain controller . Comparison between the numerical and computational solutions by evaluating the difference between the two solutions showed that the accuracy of the computational solution being saturated was always better than the corresponding numerical solution.
Conflicts of Interest
The author declares no conflict of interest.
References
- Adomian, G. A Review of the Decomposition Method in Applied Mathematics. J. Math. Anal. Appl. 1988, 135, 501–544. [Google Scholar] [CrossRef]
- Adomian, G. Solving Frontier Problems in Physics: The Decomposition Method; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1994. [Google Scholar]
- International Mathematics and Statistics Library (IMSL Library). Fortran Subroutines for Mathematical Applications, Version 2; International Mathematics and Statistics Library: Houston, TX, USA, 1991. [Google Scholar]
- Nield, D.A.; Bejan, A. Convection in Porous Media, 5th ed.; Springer: New York, NY, USA, 2017. [Google Scholar]
- Diersch, H.-J.G.; Kolditz, O. Variable-density flow and transport in porous media: Approaches and challenges. Adv. Water Resour. 2002, 25, 899–944. [Google Scholar] [CrossRef]
- Masuoka, T.; Rudraiah, N.; Siddheshwar, P.G. Nonlinear convection in porous media: A review. J. Porous Media 2003, 6, 1–32. [Google Scholar] [CrossRef]
- Lorenz, E.N. Deterministic non-periodic flows. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Vadasz, P.; Olek, S. Weak turbulence and chaos for low Prandtl number gravity driven convection in porous media. Transp. Porous Media 1999, 37, 69–91. [Google Scholar] [CrossRef]
- Vadasz, P.; Olek, S. Computational recovery of the homoclinic orbit in porous media convection. Int. J. Non Linear Mech. 1999, 34, 89–93. [Google Scholar] [CrossRef]
- Vadasz, P.; Olek, S. Route to chaos for moderate Prandtl number convection in a porous layer heated from below. Transp. Porous Media 2000, 41, 211–239. [Google Scholar] [CrossRef]
- Vadasz, P.; Olek, S. Convergence and accuracy of Adomian’s decomposition method for the solution of Lorenz equations. Int. J. Heat Mass Transf. 2000, 43, 1715–1734. [Google Scholar] [CrossRef]
- Vadasz, P. Local and global transitions to chaos and hysteresis in a porous layer heated from below. Transp. Porous Media 1999, 37, 213–245. [Google Scholar] [CrossRef]
- Vadasz, P. A note and discussion on J.-L. Auriault’s letter: Comments on the paper—Local and global transitions to chaos and hysteresis in a porous layer heated from below. Transp. Porous Media 1999, 37, 251–254. [Google Scholar] [CrossRef]
- Vadasz, P. Heat transfer regimes and hysteresis in porous media convection. J. Heat Transf. 2001, 123, 145–156. [Google Scholar] [CrossRef]
- Vadasz, P. The effect of thermal expansion on porous me- dia convection, Part 1. Thermal expansion solution. Transp. Porous Media 2001, 44, 421–443. [Google Scholar] [CrossRef]
- Vadasz, P. The effect of thermal expansion on porous media convection, Part 2. Thermal convection solution. Transp. Porous Media 2001, 44, 445–463. [Google Scholar] [CrossRef]
- Vadasz, P. Equivalent initial conditions for compatibility between analytical and computational solutions of convection in porous media. Int. J. Non Linear Mech. 2001, 36, 197–208. [Google Scholar] [CrossRef]
- Vadasz, P. Hysteresis and chaos in porous media convection. Trends Heat Mass Momentum Transf.—Res. Trends 2002, 8, 59–102. [Google Scholar]
- Vadasz, P. Analytical prediction of the transition to chaos in Lorenz equations. Appl. Math. Lett. 2010, 23, 503–507. [Google Scholar] [CrossRef]
- Jawdat, J.M.; Hashim, I. Low Prandtl number chaotic convection in porous media with uniform internal heat generation. Int. Commun. Heat Mass Transf. 2010, 37, 629–636. [Google Scholar] [CrossRef]
- Vadasz, P. Capturing analytically the transition to weak turbulence and its control in porous media convection. J. Porous Media 2015, 18, 1075–1089. [Google Scholar] [CrossRef]
- Vadasz, P. Subcritical transitions to chaos and hysteresis in a fluid layer heated from below. Int. J. Heat Mass Transf. 2000, 43, 705–724. [Google Scholar] [CrossRef]
- Vadasz, P. Chaotic dynamics and hysteresis in thermal convection. Proc. IMechE Part C J. Mech. Eng. Sci. 2006, 220, 309–323. [Google Scholar] [CrossRef]
- Vadasz, P.; Olek, S. Transitions and chaos for free convection in a rotating porous layer. Int. J. Heat Mass Transf. 1998, 41, 1417–1435. [Google Scholar] [CrossRef]
- Vadasz, P. Coriolis effect on gravity driven convection in a rotating porous layer heated from below. J. Fluid Mech. 1998, 376, 351–375. [Google Scholar] [CrossRef]
- Straughan, B. A sharp nonlinear stability threshold in rotating porous convection. Proc. R. Soc. Lond. A 2001, 457, 87–93. [Google Scholar] [CrossRef]
- Straughan, B. Resonant porous penetrative convection. Proc. R. Soc. Lond. A 2004, 460, 2913–2927. [Google Scholar] [CrossRef]
- Straughan, B. Global nonlinear stability in porous convection with a thermal non-equilibrium model. Proc. R. Soc. Lond. A 2006, 462, 409–418. [Google Scholar] [CrossRef]
- Govender, S. Coriolis effect on the linear stability of convection in a porous layer placed far away from the axis of rotation. Transp. Porous Media 2003, 51, 315–326. [Google Scholar] [CrossRef]
- Govender, S. Stability of gravity driven convection in a cylindrical porous layer subjected to vibration. Transp. Porous Media 2006, 63, 489–502. [Google Scholar] [CrossRef]
- Govender, S. Vadasz number influence on vibration in a rotating porous layer placed far away from the axis of rotation. J. Heat Transf. 2010, 132, 112601–112605. [Google Scholar] [CrossRef]
- Vanishree, R.K.; Siddheshwar, P.G. Effect of rotation on thermal convection in an anisotropic porous medium with temperature-dependent viscosity. Transp. Porous Media 2010, 81, 73–87. [Google Scholar] [CrossRef]
- Mohammad, A.N.; Rees, D.A.S.; Mojtabi, A. The effect of conducting boundaries on the onset of convection in a porous layer which is heated from below by internal heating. Transp. Porous Media 2017, 117, 189–206. [Google Scholar] [CrossRef]
- Ahmad, S.; Rees, D.A.S. The effect of conducting sidewalls on the onset of convection in a porous cavity. Transp. Porous Media 2016, 111, 287–304. [Google Scholar] [CrossRef]
- Noghrehabadi, A.; Rees, D.A.S.; Bassom, A.P. Linear stability of a developing thermal front induced by a constant heat flux. Transp. Porous Media 2013, 99, 493–513. [Google Scholar] [CrossRef]
- Rees, D.A.S.; Mojtabi, A. The Effect of Conducting Boundaries on Weakly Nonlinear Darcy-Benard Convection. Transp. Porous Media 2011, 88, 45–63. [Google Scholar] [CrossRef]
- Lombardo, S.; Mulone, G.; Straughan, B. Non-linear stability in the Bénard problem for a double-diffusive mixture in a porous medium. Math. Methods Appl. Sci. 2001, 24, 1229–1246. [Google Scholar] [CrossRef]
- Lombardo, S.; Mulone, G. Necessary and sufficient con- ditions of global nonlinear stability for rotating double- diffusive convection in a porous medium. Contin. Mech. Thermodyn. 2002, 14, 527–540. [Google Scholar] [CrossRef]
- Schoofs, S.; Spera, F.J. Transition to chaos and flow dynamics of thermochemical porous medium convection. Transp. Porous Media 2003, 50, 179–195. [Google Scholar] [CrossRef]
- Mulone, G.; Straughan, B. An operative method to obtain necessary and sufficient stability conditions for double diffusive convection in porous media. Z. Angew. Math. Mech.-J. Appl. Math. Mech. 2006, 86, 507–520. [Google Scholar] [CrossRef]
- Govender, S. Effect of Darcy-Prandtl number on the stability of solutal convection in solidifying binary alloys. J. Porous Media 2006, 9, 523–539. [Google Scholar] [CrossRef]
- Wang, Y.; Singer, J.; Bau, H.H. Controlling chaos in a thermal convection loop. J. Fluid Mech. 1992, 237, 479–498. [Google Scholar] [CrossRef]
- Yuen, P.; Bau, H.H. Rendering a subcritical Hopf bifurcation supercritical. J. Fluid Mech. 1996, 317, 91–109. [Google Scholar] [CrossRef]
- Sparrow, C. The Lorenz Equations: Bifurcations, Chaos, and Strange Attractors; Springer: New York, NY, USA, 1982. [Google Scholar]
- Magyari, E. The Vadasz-Olek model regarded as a system of coupled oscillators. Transport Porous Media 2010, 85, 415–435. [Google Scholar] [CrossRef]
- Mahmud, M.N.; Hashim, I. Small and moderate Prandtl number chaotic convection in porous media in the presence of feedback control. Transp. Porous Media 2010, 84, 421–440. [Google Scholar] [CrossRef]
- Bau, H.H. Control of Marangoni-Benard convection. Int. J. Heat Mass Transf. 1999, 42, 1327–1341. [Google Scholar] [CrossRef]
- Tang, J.; Bau, H.H. Feedback control stabilization of the no motion state of a fluid confined in a horizontal porous layer heated from below. J. Fluid Mech. 1993, 257, 485–505. [Google Scholar] [CrossRef]
- Zhao, H.; Bau, H.H. Limitations of linear control of thermal convection in a porous medium. Phys. Fluids 2006, 18, 074109. [Google Scholar] [CrossRef]
- Magyari, E. The “butterfly effect” in a porous slab. Transp. Porous Media 2010, 84, 711–715. [Google Scholar] [CrossRef]
- Vadasz, P. Controlling chaos in porous meida convection by using feedback control. Transp. Porous Media 2010, 85, 287–298. [Google Scholar] [CrossRef]
- Straughan, B. Stability and Wave Motion in Porous Media; Applied Mathematical Sciences Series; Springer: New York, NY, USA, 2008. [Google Scholar]
- Sheu, L.-J. An autonomous system for chaotic convection in a porous medium using a thermal non-equilibrium model. Chaos Solitons Fractals 2006, 30, 672–689. [Google Scholar] [CrossRef]
- Roslan, R.; Mahmud, M.N.; Hashim, I. Effects of feedback control on chaotic convection in fluid saturated porous media. Int. J. Heat Mass Transf. 2011, 54, 404–412. [Google Scholar] [CrossRef]
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).