Air Entrainment and Slope Erosion During Overflow on a Levee Covered by Non-Uniform Turfgrass
Abstract
1. Introduction
2. Materials and Methods
3. Results
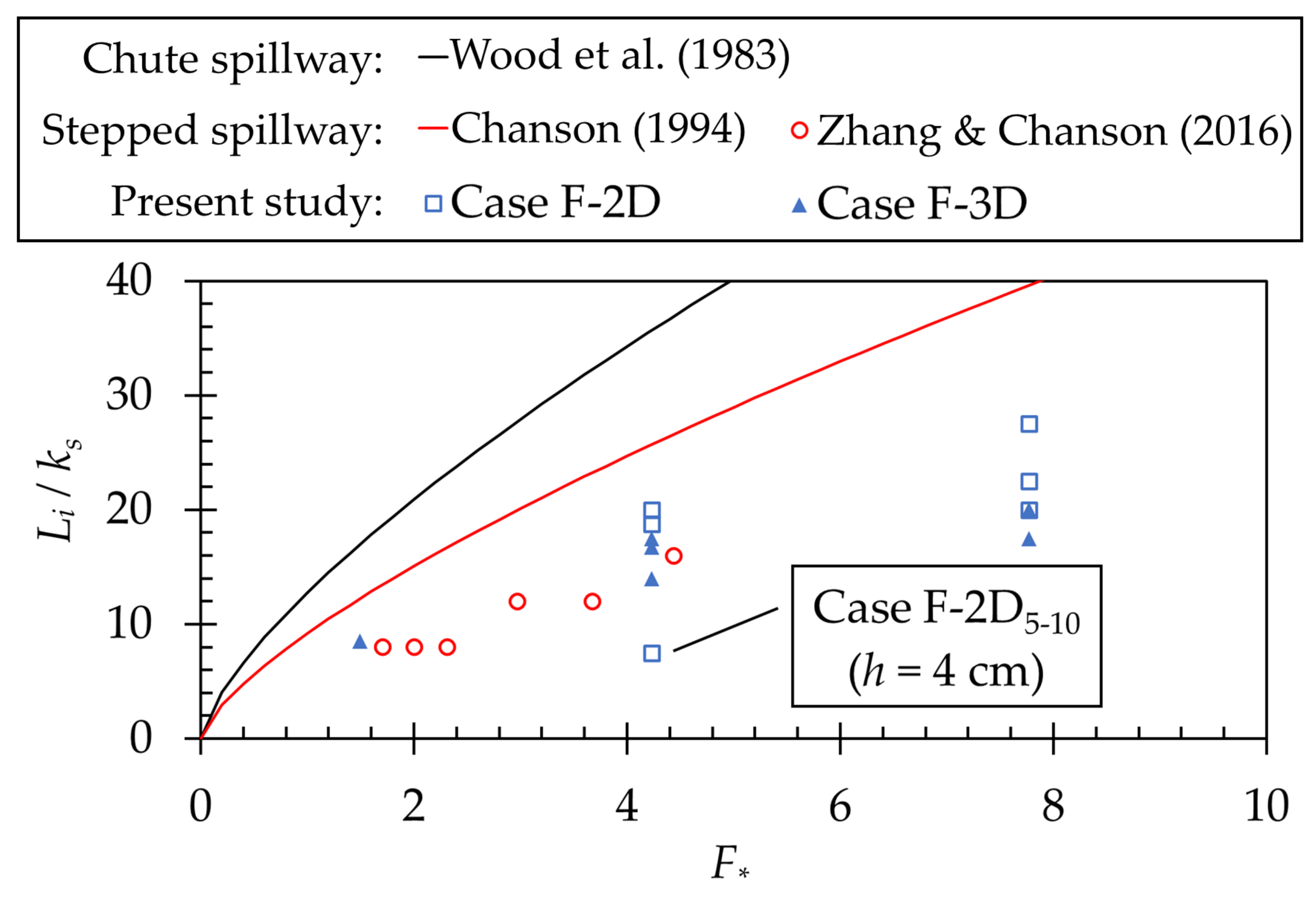
3.1. Flow Conditions and Inception Point of Air Entrainment in Fixed Bed Experiments
3.2. Erosion of the Bare Ground of the Levee Slope in Semi-Mobile Experiments
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MLIT | Ministry of Land, Infrastructure, Transport and Tourism |
References
- Tengbeh, G.T. The Effect of Grass Cover on Bank Erosion. Ph.D. Dissertation, Cranfield Institute of Technology, Bedfordshire, UK, 1989. [Google Scholar]
- De Baets, S.; Poesen, J.; Gyssels, G.; Knapen, A. Effects of grass roots on the erodibility of topsoils during concentrated flow. Geomorphology 2006, 76, 54–67. [Google Scholar] [CrossRef]
- Ali, F.H.; Osman, N. Shear strength of a soil containing vegetation roots. Soils Found. 2008, 48, 587–596. [Google Scholar] [CrossRef]
- Koelewijn, A.R.; Rikkert, S.J.; Peeters, P.; Depreiter, D.; van Damme, M.; Zomer, W. Overflow tests on grass-covered embankments at the Living Lab Hedwige-Prosperpolder: An overview. Water 2022, 14, 2859. [Google Scholar] [CrossRef]
- Wegman, R. Strength of Grass Covers on Dikes. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2020. Available online: https://repository.tudelft.nl/record/uuid:9af2efca-90e7-4006-95a7-8d87180b0709 (accessed on 8 August 2025).
- Hattori, A.; Mochizuki, T.; Fujita, K. Estimation of erosion resistance of the levee slopes covered by vegetation which is managed by two cuttings per year. Proc. Hydraul. Eng. 1997, 41, 367–372, (In Japanese with English Summary). [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, K.; Cen, Y.; Wang, P.; Xia, J. Effects of grass cover on the overland soil erosion mechanism under simulated rainfall. Water Resour. Res. 2025, 61, e2023WR036888. [Google Scholar] [CrossRef]
- Straub, L.G.; Anderson, A.G. Experiments on self-aerated flow in open channels. J. Hydraul. Div. 1958, 84, 1–35. [Google Scholar] [CrossRef]
- Keller, R.J. Field Measurement of Self-Aerated High Speed Open Channel Flow. Ph.D. Thesis, U Canterbury, Christchurch, New Zealand, 1972. [Google Scholar]
- Chanson, H. Air Entrainment in Chutes and Spillways; Research Report. No. CE 133; Dept. of Civil Engineering, The University of Queensland: Brisbane, Australia, 1992; 85p. [Google Scholar]
- Wood, I.R. Uniform region of self-aerated flow. J. Hydraul. Eng. 1983, 109, 447–461. [Google Scholar] [CrossRef]
- Chanson, H. Drag reduction in open channel flow by aeration and suspended load. J. Hydraul. Res. 1994, 32, 87–101. [Google Scholar] [CrossRef]
- Sorensen, R.M. Stepped spillway hydraulic model investigation. J. Hydraul. Eng. 1985, 111, 1461–1472. [Google Scholar] [CrossRef]
- Chanson, H. Hydraulics of skimming flows over stepped channels and spillways. J. Hydraul. Res. 1994, 32, 445–460. [Google Scholar] [CrossRef]
- Briaud, J.L.; Chen, H.C.; Govindasamy, A.V.; Storesund, R. Levee erosion by overtopping in New Orleans during the Katrina Hurricane. J. Geotech. Geoenvironmental Eng. 2008, 134, 618–632. [Google Scholar] [CrossRef]
- Sills, G.L.; Vroman, N.D.; Wahl, R.E.; Schwanz, N.T. Overview of New Orleans levee failures: Lessons learned and their impact on national levee design and assessment. J. Geotech. Geoenvironmental Eng. 2008, 134, 556–565. [Google Scholar] [CrossRef]
- Van der Meer, J.W. Guidance on Erosion Resistance of Inner Slopes of Dikes from 3 Years of Testing with the Wave Overtopping Simulator; Van der Meer Consulting: Leonards, Australia, 2009. [Google Scholar]
- Pan, Y.; Li, L.; Amini, F.; Kuang, C. Influence of three levee-strengthening systems on overtopping hydraulic parameters and hydraulic equivalency analysis between steady and intermittent overtopping. J. Waterw. Port. Coast. Ocean. Eng. 2013, 139, 256–266. [Google Scholar] [CrossRef]
- Ahadiyan, J.; Bahmanpouri, F.; Adeli, A.; Gualtieri, C.; Khoshkonesh, A. Riprap effect on hydraulic fracturing process of cohesive and non-cohesive protective levees. Water Resour. Manag. 2022, 36, 625–639. [Google Scholar] [CrossRef]
- Abbas, F.M.; Tanaka, N. Utilization of geogrid and water cushion to reduce the impact of nappe flow and scouring on the downstream side of a levee. Fluids 2022, 7, 299. [Google Scholar] [CrossRef]
- Yasuda, S.; Shimizu, Y.; Deguchi, K. Investigation of the mechanism of the 2015 failure of a dike on Kinu River. Soils Found. 2016, 56, 581–592. [Google Scholar] [CrossRef]
- Ministry of Land, Infrastructure, Transport and Tourism (MLIT). Study on Resilient River Levees Against Overtopping. 2022. Available online: https://www.mlit.go.jp/river/shinngikai_blog/teibou_kentoukai/dai01kai/pdf/kentou.pdf (accessed on 31 October 2024). (In Japanese).
- Billah, M.M.; Yagisawa, J. Headcut migration in earthen embankment induced by varying sub-surface and seepage state under overflow. Geotech. Geol. Eng. 2023, 41, 4659–4676. [Google Scholar] [CrossRef]
- Sherzai, J.H.; Tanaka, N.; Igarashi, Y.; Onose, R. Effects of Soil Characteristics on Levee Erosion and the Behavior of Twin Eddies in a Scoured Hole Generated by Nappe Flow. Int. J. Civ. Eng. 2025, 23, 1287–1305. [Google Scholar] [CrossRef]
- Afreen, S.; Yagisawa, J.; Binh, V.D.; Tanaka, N. Investigation of scour pattern downstream of levee toe due to overtopping flow. J. Jpn. Soc. Civ. Eng. Ser. B1 2015, 71, I_175–I_180. [Google Scholar] [CrossRef]
- Wood, I.R.; Ackers, P.; Loveless, J. General method for critical point on spillways. J. Hydraul. Eng. 1983, 109, 308–312. [Google Scholar] [CrossRef]
- Zhang, G.; Chanson, H. Hydraulics of the developing flow region of stepped spillways. I: Physical modeling and boundary layer development. J. Hydraul. Eng. 2016, 142, 04016015. [Google Scholar] [CrossRef]
- Dol, S.S.; Wee, S.K.; Yong, T.H.; Sulaiman, S.A. The effects of flexible cylinder structural dynamics to the near wake turbulence. Fluids 2023, 8, 270. [Google Scholar] [CrossRef]
- Igarashi, Y.; Tanaka, N.; Zaha, T. Changes in flow structures and energy reduction through compound tsunami mitigation system with embankment and lined piles. Ocean. Eng. 2018, 164, 722–732. [Google Scholar] [CrossRef]

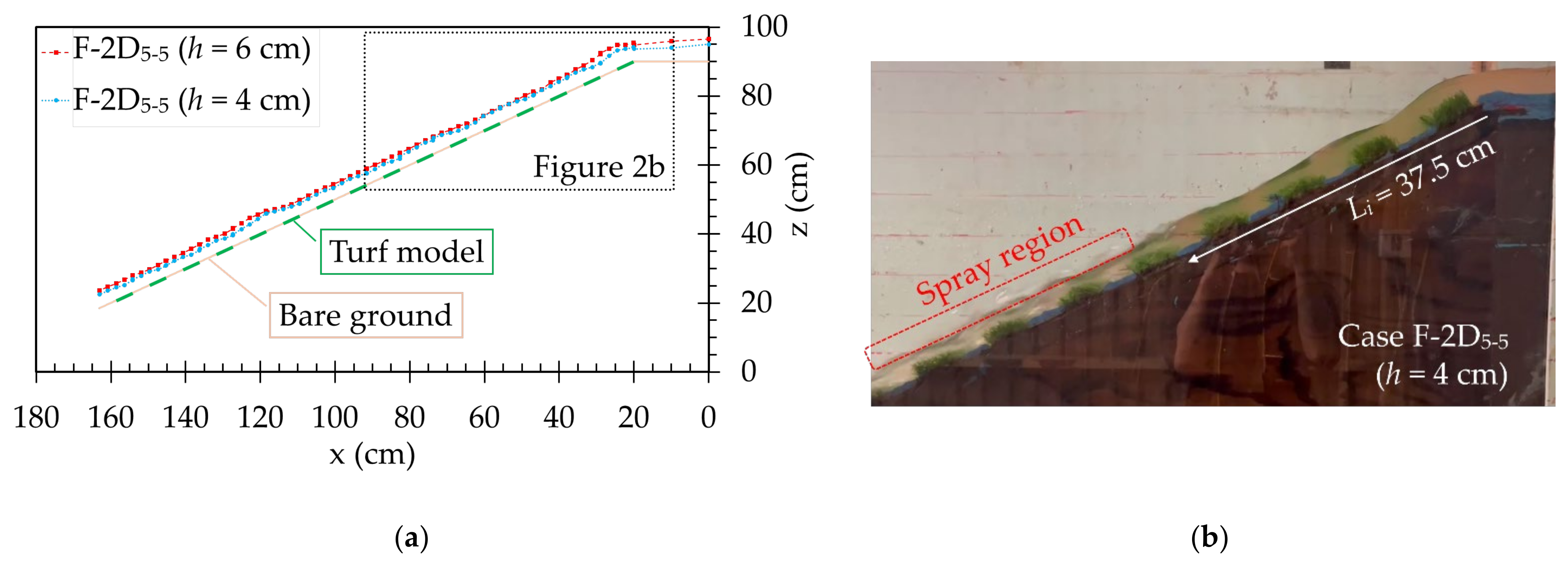
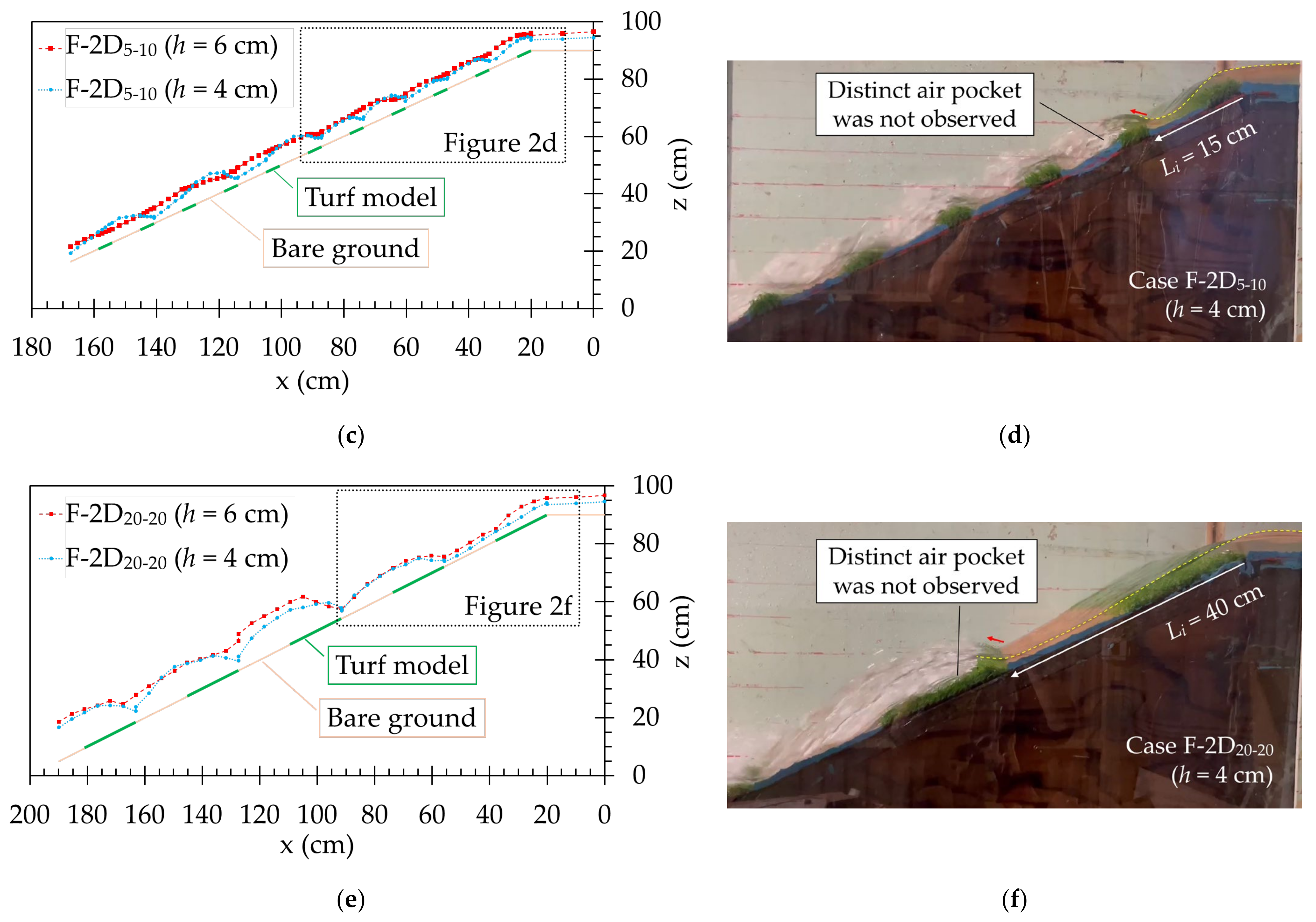

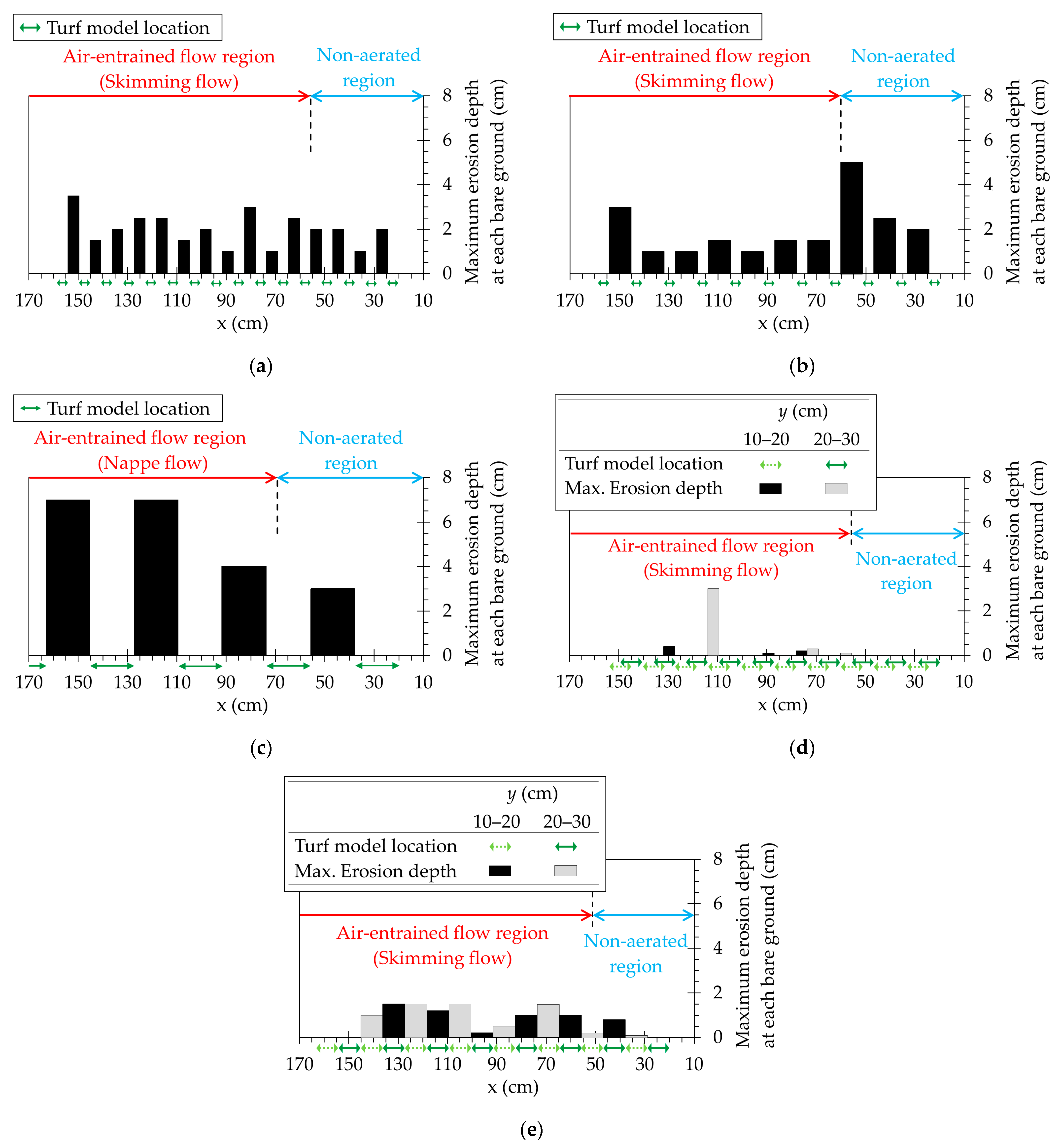
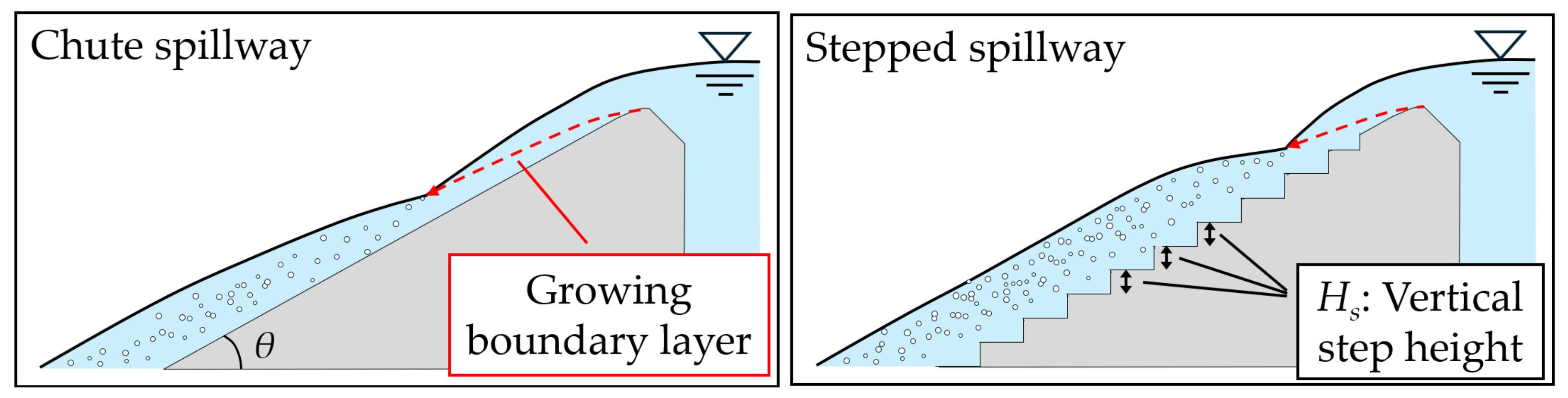
| Case | Slope Condition | h (cm) | Ht (cm) | Lt (cm) | Wt (cm) | Lb (cm) | Wb (cm) | Turf Coverage (%) |
|---|---|---|---|---|---|---|---|---|
| F-2D5-5 | Fixed | 2, 4, 6 | 2 | 5 | 50 | 5 | 50 | 50 |
| F-2D5-10 | Fixed | 2, 4, 6 | 2 | 5 | 50 | 10 | 50 | 33.3 |
| F-2D20-20 | Fixed | 2, 4, 6 | 2 | 20 | 50 | 20 | 50 | 50 |
| F-3D10-5 | Fixed | 2, 4, 6 | 2 | 10 | 10 | 5 | 10 | 66.7 |
| F-3D10-8 | Fixed | 2, 4, 6 | 2 | 10 | 10 | 8 | 10 | 55.6 |
| F-3D10-10 | Fixed | 2, 4, 6 | 2 | 10 | 10 | 10 | 10 | 50 |
| Sm-2D5-5 | Semimobile | 2, 4, 6 | 2 | 5 | 50 | 5 | 50 | 50 |
| Sm-2D5-10 | Semimobile | 2, 4, 6 | 2 | 5 | 50 | 10 | 50 | 33.3 |
| Sm-2D20-20 | Semimobile | 2, 4, 6 | 2 | 20 | 50 | 20 | 50 | 50 |
| Sm-3D10-5 | Semimobile | 2, 4, 6 | 2 | 10 | 10 | 5 | 10 | 66.7 |
| Sm-3D10-10 | Semimobile | 2, 4, 6 | 2 | 10 | 10 | 10 | 10 | 50 |
| h (cm) | Case | Li (cm) | Li/Ht | F∗ (from Equation (2)) |
|---|---|---|---|---|
| 2 | F-2D5-5 | No † | No † | 1.50 |
| F-2D5-10 | No † | No † | ||
| F-2D20-20 | No † | No † | ||
| F-3D10-5 | No † | No † | ||
| F-3D10-8 | No † | No † | ||
| F-3D10-10 | 17 | 8.5 | ||
| 4 | F-2D5-5 | 37.5 | 18.8 | 4.23 |
| F-2D5-10 | 15 | 7.5 | ||
| F-2D20-20 | 40 | 20 | ||
| F-3D10-5 | 35 | 17.5 | ||
| F-3D10-8 | 28 | 11.5 | ||
| F-3D10-10 | 33.5 | 12.5 | ||
| 6 | F-2D5-5 | 55 | 27.5 | 7.77 |
| F-2D5-10 | 45 | 22.5 | ||
| F-2D20-20 | 40 | 20 | ||
| F-3D10-5 | 40 | 20 | ||
| F-3D10-8 | 40 | 20 | ||
| F-3D10-10 | 35 | 17.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Igarashi, Y.; Tanaka, N.; Junjua, M.W.A.; Kobori, T. Air Entrainment and Slope Erosion During Overflow on a Levee Covered by Non-Uniform Turfgrass. Fluids 2025, 10, 212. https://doi.org/10.3390/fluids10080212
Igarashi Y, Tanaka N, Junjua MWA, Kobori T. Air Entrainment and Slope Erosion During Overflow on a Levee Covered by Non-Uniform Turfgrass. Fluids. 2025; 10(8):212. https://doi.org/10.3390/fluids10080212
Chicago/Turabian StyleIgarashi, Yoshiya, Norio Tanaka, Muhammad W. A. Junjua, and Takeharu Kobori. 2025. "Air Entrainment and Slope Erosion During Overflow on a Levee Covered by Non-Uniform Turfgrass" Fluids 10, no. 8: 212. https://doi.org/10.3390/fluids10080212
APA StyleIgarashi, Y., Tanaka, N., Junjua, M. W. A., & Kobori, T. (2025). Air Entrainment and Slope Erosion During Overflow on a Levee Covered by Non-Uniform Turfgrass. Fluids, 10(8), 212. https://doi.org/10.3390/fluids10080212








