Steady Radial Diverging Flow of a Particle-Laden Fluid with Particle Migration
Abstract
1. Introduction
2. Equations of the Present Model
2.1. General Equations of the Model with Particle Migration
2.2. Equations for Steady Plane Radial Flow
- (a)
- Axisymmetric plane viscous radial flow from a point source;
- (b)
- Inviscid radial flow in a diverging channel.
3. Initial Velocity Field with the Uniform Particle Distribution
3.1. Lighter Particles with Higher Inlet Velocity (u0S > u0f)
3.2. Particles and Fluid Have the Same Inlet Velocity
4. Steady Particle Distribution of Plane Radial Diverging Flow
4.1. Light Particles with Higher Inlet Velocity
4.2. Particles and Fluid Have the Same Inlet Velocity
5. Conclusions
- (1)
- In the initial flow field of a particle-fluid suspension with uniformly distributed particles, the relative velocity of particles with respect to the fluid depends on their inlet velocity ratio, the mass density ratio, and the Stokes number of particles. For example, when their inlet velocities are equal (then Stokes drag vanishes at the entrance), the particles heavier (or lighter) than the fluid will move faster (or slower) than the fluid. On the other hand, the particles lighter than the fluid can remain faster than the fluid within a sufficiently long distance, provided that the inlet velocity of lighter particles is much higher than the inlet velocity of the fluid. This result is qualitatively consistent with some known simulations and experiments on gas–liquid bubbly flow in a diverging channel of finite length driven by high-speed injection of gas bubbles into a nearly stationary liquid;
- (2)
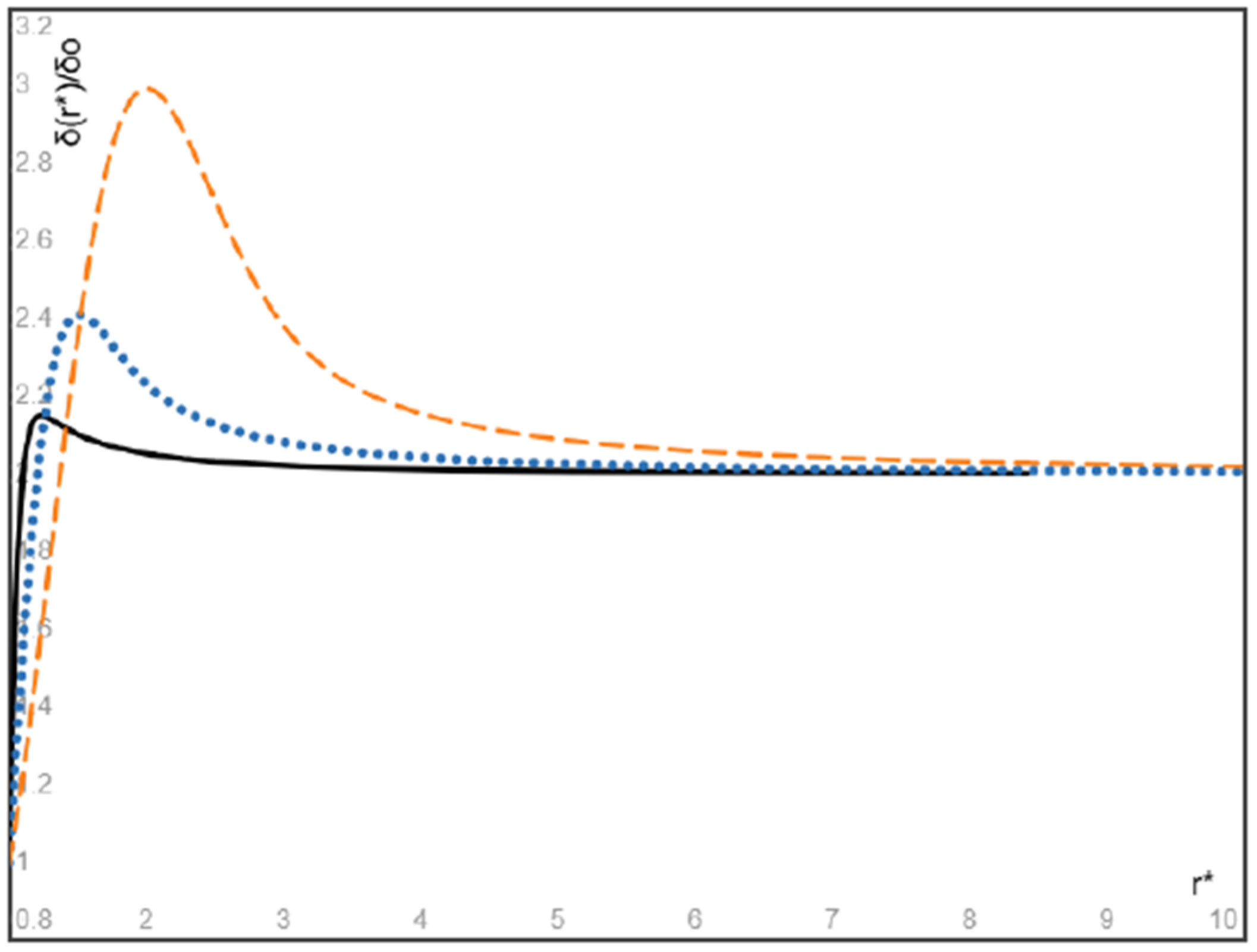
- An explicit expression is obtained for the steady spatial distribution of particles eventually attained as a result of particle migration. In particular, for massless gas bubbles with the inlet velocity higher than the inlet velocity of the fluid, our results show that the volume fraction of bubbles attains its maximum at a location close to the entrance of the flow and after then monotonically decreases with increasing radial coordinate and converges to a finite value determined by the inlet velocity ratio of the bubbles and the fluid. As the Stokes number of bubbles approaches zero, the peak volume fraction decreases and converges to the inlet volume fraction of the bubbles multiplied by the inlet velocity ratio, and the location of peak volume fraction approaches the entrance location of the flow;
- (3)
- When the particles and the fluid have the same inlet velocity, our results show that the steady volume fraction of particles heavier than the fluid attains its minimum at a location close to the entrance of the flow and after then monotonically increases with increasing radial coordinate and converges to a finite value, and as the Stokes number of heavy particles approaches zero, the minimum volume fraction and its location approach the inlet particle volume fraction and the entrance location of the flow, respectively. On the other hand, the steady volume fraction of particles lighter than the fluid attains its maximum at a location close to the entrance of the flow and after then monotonically decreases with increasing radial coordinate and converges to a finite value, and as the Stokes number of lighter particles approaches zero, the maximum volume fraction of light particles and its location approach the inlet particle volume fraction and the entrance location of the flow, respectively.
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Derivation of Equations (A1)–(A5)
References
- Jeffery, G.B. The two-dimensional steady motion of a viscous fluid. Philos. Mag. 1915, 29, 455–465. [Google Scholar] [CrossRef]
- Fraenkel, L.E. Laminar flow in symmetrical channel with slightly curved walls, I. On the Jeffery-Hamel solutions for flow between plane walls. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1962, 267, 119–138. [Google Scholar]
- Eagles, P.M. The stability of a family of Jeffery-Hamel solutions for diverging channel flow. J. Fluid Mech. 1966, 24, 191–207. [Google Scholar] [CrossRef]
- Fujimura, K. On the linear stability of Jeffery-Hamel flow in a converging channel. J. Phys. Soc. 1982, 51, 2000–2009. [Google Scholar] [CrossRef]
- Banks, W.H.H. On perturbations to Jeffery-Hamel flow. J. Fluid Mech. 1988, 186, 559–581. [Google Scholar] [CrossRef]
- Akulenko, L.D.; Georgievskii, D.V.; Kumakshev, S.A. Solutions of the Jeffery-Hamel problem regularly extendable in the Reynolds number. Fluid. Dyn. 2004, 39, 12–28. [Google Scholar] [CrossRef]
- Putkaradze, V.; Vorobieft, P. Instabilities, bifurcations, and multiple solutions in expanding channel flows. Phys. Rev. Lett. 2006, 7, 144502. [Google Scholar] [CrossRef]
- Haines, P.E.; Hewitt, R.E.; Hazel, A.L. The Jeffery-Hamel similarity solution and its relation to flow in a diverging channel. J. Fluid Mech. 2011, 687, 404–430. [Google Scholar] [CrossRef]
- Jotkar, M.R.; Govindarajan, R. Non-modal stability of Jeffery-Hamel flow. Phys. Fluids. 2017, 29, 064107. [Google Scholar] [CrossRef]
- Noureen; Marwat, D.N.K. Double-diffusive convection in Jeffery-Hamel flow. Sci. Rep. 2022, 12, 9134. [Google Scholar] [CrossRef]
- Goli, S.; Saha, S.K.; Agrawal, A. Physics of fluid flow in an hourglass (converging-diverging) microchannel. Phys. Fluids 2022, 34, 052006. [Google Scholar] [CrossRef]
- Kumar, A.; Govindarajan, R. On the intense sensitivity to wall convergence of instability in a channel. Phys. Fluids 2024, 36, 104108. [Google Scholar] [CrossRef]
- Rezaee, D. Linear temporal stability of Jeffery-Hamel flow of nanofluids. Eur. J. Mech. B/Fluids 2024, 107, 1–16. [Google Scholar] [CrossRef]
- Rana, P.; Shukla, N.; Areekara, S.; Pop, I. Multiple solutions and temporal stability for ternary hybrid nanofluid flow between non-parallel plates. J. Appl. Math. Mech. (ZAMM) 2024, 104, e202400124. [Google Scholar] [CrossRef]
- AI-Saedi, A.A.; Verma, L.; Meher, R.; Nikan, O. Study on Jeffery-Hamel nano-fluid flow with uncertain volume fraction using semi-analytical approach. AIP Adv. 2025, 15, 045113. [Google Scholar] [CrossRef]
- Park, H.M. Comparison of the pseudo-single-phase continuum model and the homogeneous single-phase model of nanofluids. Int. J. Heat Mass Transf. 2018, 120, 106–116. [Google Scholar] [CrossRef]
- Saha, G.; Paul, M.C. Investigation of the characteristics of nanofluids flow and heat transfer in a pipe using a single phase model. Int. Commun. Heat Mass Transf. 2018, 93, 48–59. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Single phase nanofluids in fluid mechanics and their hydrodynamic linear stability analysis. Comput. Methods Programs Biomed. 2020, 187, 105171. [Google Scholar] [CrossRef] [PubMed]
- AI-Nimr, M.A.; Hammoudeh, V.A.; Hamdan, M.A. Effect of velocity-slip boundary conditions on Jeffery-Hamel flow solutions. J. Appl. Mech. (ASME) 2010, 77, 041010. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Extending the traditional Jeffery-Hamel flow to stretchable convergent/divergent channel. Comput. Fluids 2014, 100, 196–203. [Google Scholar] [CrossRef]
- Soliman, H.M. Laminar, radial flow of two immiscible fluids in slender wedge-shaped passages. J. Fluids Eng. (ASME) 2017, 139, 081201. [Google Scholar] [CrossRef]
- Sahu, K.C.; Govindarajan, R. Stability of flow through a slowly diverging pipe. J. Fluid Mech. 2005, 531, 325–334. [Google Scholar] [CrossRef]
- Klinkenberg, J.; de Lange, H.C.; Brandt, L. Linear stability of particle laden flows: The influence of added mass, fluid acceleration and Basset history force. Meccanica 2014, 49, 811–827. [Google Scholar] [CrossRef]
- Ru, C.Q. Rotational flow field of a particle-laden fluid on a co-rotating disk. Phys. Fluids 2024, 36, 113356. [Google Scholar] [CrossRef]
- Rubinow, S.I.; Keller, J.B. The transverse force on a spinning sphere moving in a viscous fluid. J. Fluid Mech. 1961, 11, 447–459. [Google Scholar] [CrossRef]
- Saffman, P.G. The lift on a small sphere in a slow shear flow. J. Fluid Mech. 1965, 22, 385–400. [Google Scholar] [CrossRef]
- Boronin, S.A.; Osiptsov, A.N. Stability of a vertical Couette flow in the presence of settling particles. Phys. Fluids. 2020, 32, 024104. [Google Scholar] [CrossRef]
- Li, H.; Ku, X.; Lin, J. Eulerian-Lagrangian simulation of inertial migration of particles in circular Couette flow. Phys. Fluids 2020, 32, 073308. [Google Scholar] [CrossRef]
- Saffman, P.G. On the stability of laminar flow of a dusty gas. J. Fluid Mech. 1962, 13, 120–128. [Google Scholar] [CrossRef]
- Michael, D.H. Kelvin-Helmholtz instability of a dusty gas. Proc. Camb. Philos. Soc. 1965, 61, 569–571. [Google Scholar] [CrossRef]
- Yang, Y. The influence of particles on the spatial stability of two-phase mixing layers. Phys. Fluids 1990, 2, 1839–1845. [Google Scholar] [CrossRef]
- Dimas, A.A.; Kiger, K.T. Linear instability of a particle-laden mixing layer with dynamic dispersed phase. Phys. Fluids 1998, 10, 253957. [Google Scholar] [CrossRef]
- Senatore, G. The effect of non-uniform mass loading on the linear, temporal development of particle-laden shear layers. Phys. Fluids. 2015, 27, 033302. [Google Scholar] [CrossRef]
- Goldshtik, M.A.; Shtern, V.N. Loss of symmetry in viscous flow from a linear source. Fluid Dyn. 1989, 24, 151–199. [Google Scholar] [CrossRef]
- Shusser, M.; Weihs, D. Stability analysis of source and sink flows. Phys. Fluids 1995, 7, 245–2353. [Google Scholar] [CrossRef]
- Putkaradze, V.; Dimon, P. Non-uniform two-dimensional fluid from a point source. Phys. Fluids 2000, 12, 66–70. [Google Scholar] [CrossRef]
- Chemetov, N.V.; Starovoitov, V.N. On a motion of a perfect fluid in a domain with sources and sinks. J. Math. Fluid Mech. 2002, 4, 128–144. [Google Scholar] [CrossRef]
- Taylor, G.I. The viscosity of a fluid containing small drops of another fluid. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1932, 138, 41–48. [Google Scholar]
- Ohie, K. Rheology of dilute bubble suspension in unsteady shear flow. J. Fluid Mech. 2024, 983, A39. [Google Scholar] [CrossRef]
- Auton, T.R.; Hunt, J.C.R.; Prud’homme, M. The forces exerted on body in inviscid unsteady non-uniform rotational flow. J. Fluid Mech. 1988, 197, 241–257. [Google Scholar] [CrossRef]
- Kuo, J.T.; Wallis, G.B. Flow of bubbles through nozzles. Int. J. Multiph. Flow 1988, 14, 547–564. [Google Scholar] [CrossRef]
- Chen, J.; Lei, M.; Lu, S.; Xiao, X.; Yao, M.; Li, Q. Numerical simulation of single bubble motion fragmentation mechanism in Venturi-type bubble generator. Mech. Ind. 2024, 25, 21. [Google Scholar] [CrossRef]
- Zhao, L.; Huang, J.; Chen, C.; Gao, J. Investigations on the near-wall bubble dynamic behaviors in a diverging channel. AIP Adv. 2024, 14, 115014. [Google Scholar] [CrossRef]
- Zeng, X.; Xu, Y.; Cammi, A.; Fan, G.; Wang, J.; Xiao, Y.; Yan, C. Simulation of the vane-type bubble separator using a hybrid Euler-Euler/volume-of-fluid approach. Phys. Fluids 2025, 37, 043330. [Google Scholar] [CrossRef]
- Tribbiani, G. An image-based technique for measuring velocity and shape of air bubbles in two-phase vertical bubbly flows. Fluids 2025, 10, 69. [Google Scholar] [CrossRef]
- Nedeltchev, S. Updated review on the available methods for measurement and prediction of the mass reansfer coefficients in bubble columns. Fluids 2025, 10, 29. [Google Scholar] [CrossRef]
- Magnaudet, J.; Eames, I. The motion of high-Reynolds-Number bubbles. Annu. Rev. Fluid Mech. 2000, 32, 659–708. [Google Scholar] [CrossRef]
- Khan, I. Two-phase bubbly flow simulation using CFD method: A review of models for interfacial forces. Prog. Nucl. Energy 2020, 125, 103360. [Google Scholar] [CrossRef]
- Basagni, G. Computational fluid dynamics modeling of two-phase bubble column: A comprehensive review. Fluids 2023, 8, 91. [Google Scholar] [CrossRef]
- Legendre, D.; Zenit, R. Gas bubble dynamics. Rev. Mod. Phys. 2025, 97, 025001. [Google Scholar] [CrossRef]
- Ru, C.Q. Stability of plane parallel flow revisited for particle-fluid suspensions. J. Appl. Mech. (ASME) 2024, 91, 111005. [Google Scholar] [CrossRef]
- Ru, C.Q. On Kelvin-Helmholtz instability of particulate two-fluid flow. Acta Mech. Sin. 2025, 41, 324143. [Google Scholar] [CrossRef]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ru, C.Q. Steady Radial Diverging Flow of a Particle-Laden Fluid with Particle Migration. Fluids 2025, 10, 200. https://doi.org/10.3390/fluids10080200
Ru CQ. Steady Radial Diverging Flow of a Particle-Laden Fluid with Particle Migration. Fluids. 2025; 10(8):200. https://doi.org/10.3390/fluids10080200
Chicago/Turabian StyleRu, C. Q. 2025. "Steady Radial Diverging Flow of a Particle-Laden Fluid with Particle Migration" Fluids 10, no. 8: 200. https://doi.org/10.3390/fluids10080200
APA StyleRu, C. Q. (2025). Steady Radial Diverging Flow of a Particle-Laden Fluid with Particle Migration. Fluids, 10(8), 200. https://doi.org/10.3390/fluids10080200





