Gas–Liquid Two-Phase Flow in a Hydraulic Braking Pipeline: Flow Pattern and Bubble Characteristics
Abstract
1. Introduction
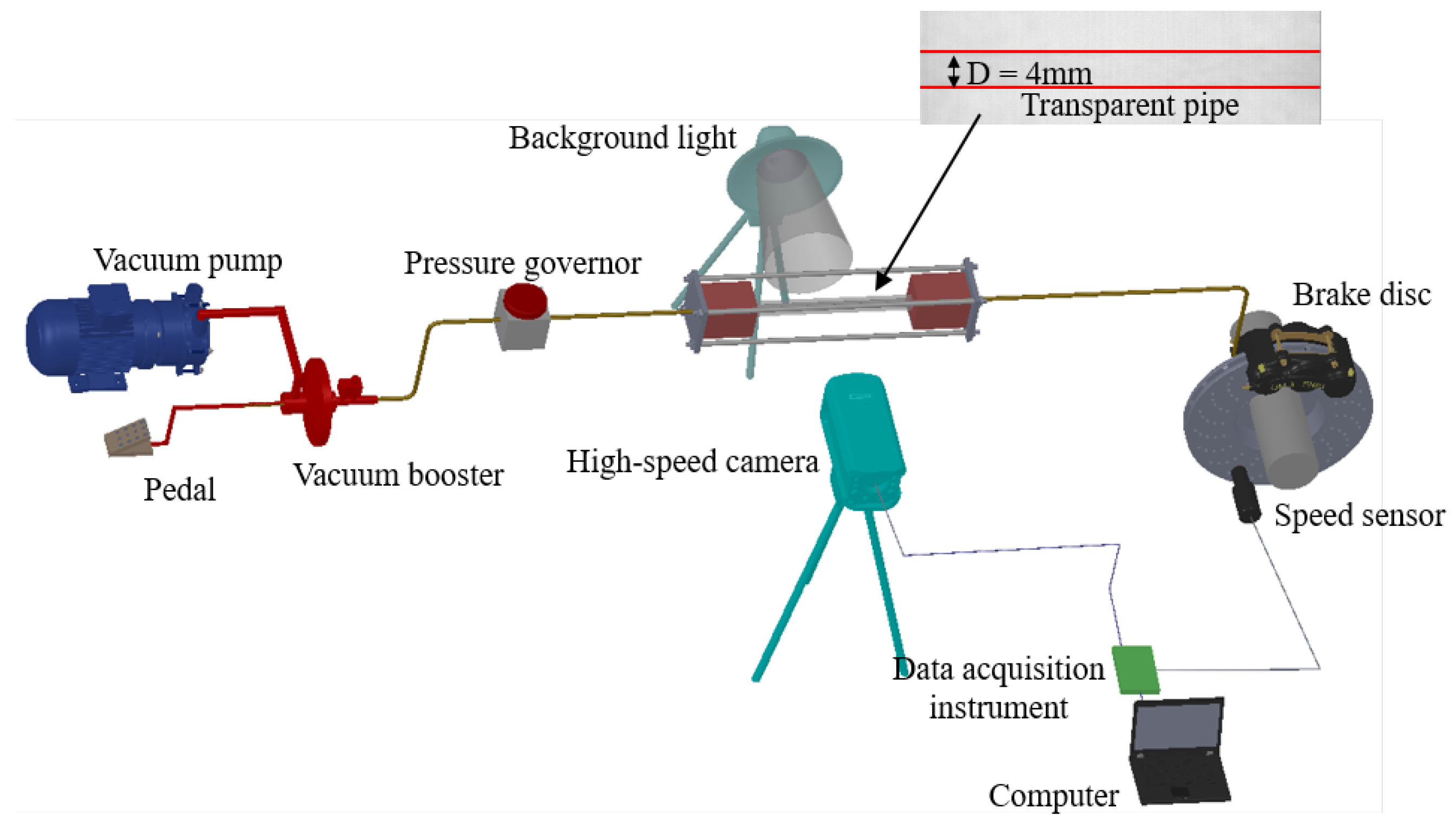
2. Experimental Device and Research Methods
2.1. Experimental Device
2.2. Image Preprocessing
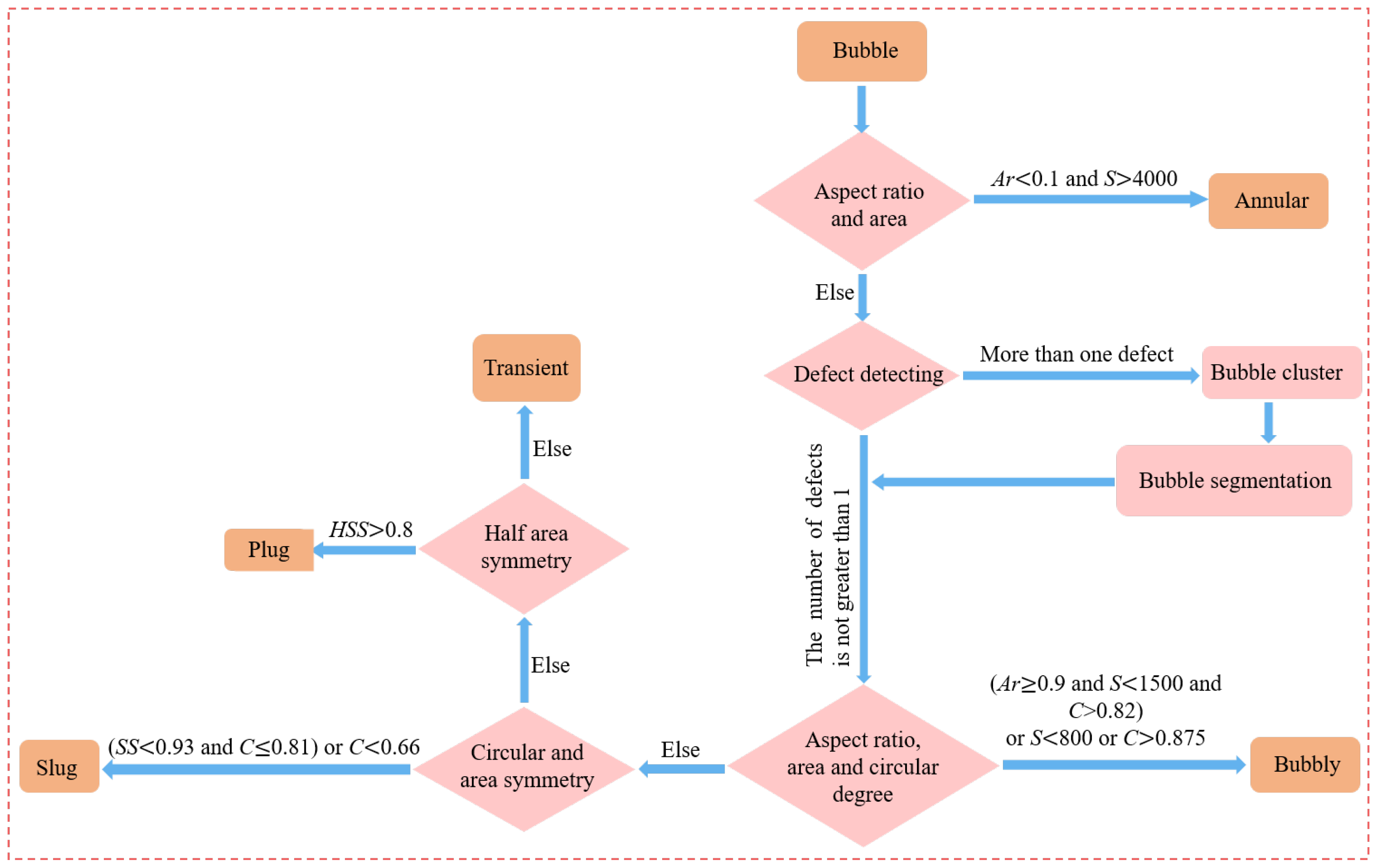
2.3. Bubble Flow Pattern Recognition
2.3.1. Classification of Bubble Flow Pattern
2.3.2. Bubble Classification Criteria
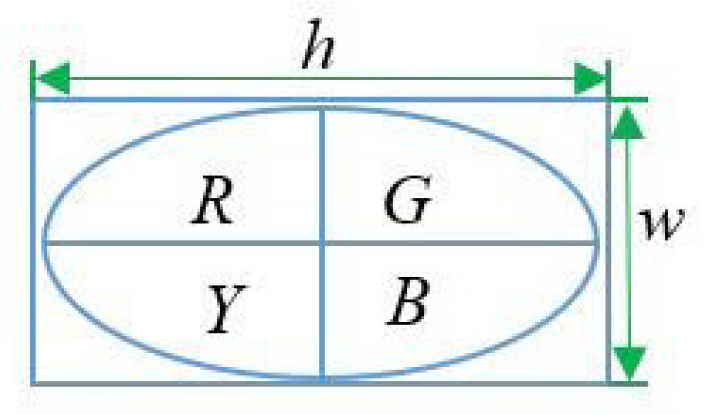
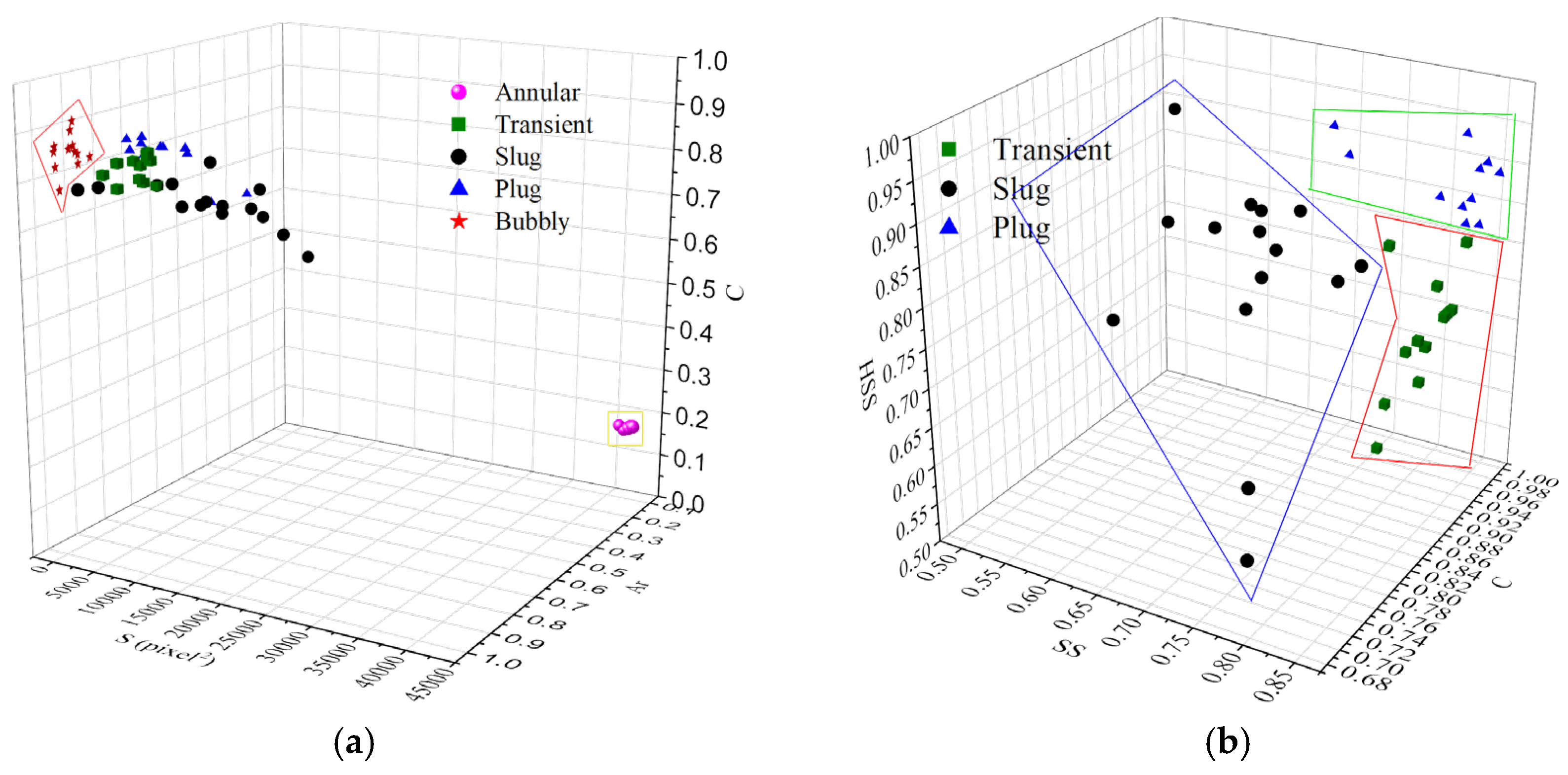
2.3.3. Determination of Classification Characteristics
2.3.4. Visualization of Classification Characteristics
2.3.5. Classification Process
2.4. Calculation of Bubble Volume
2.4.1. Improved Watershed Algorithm
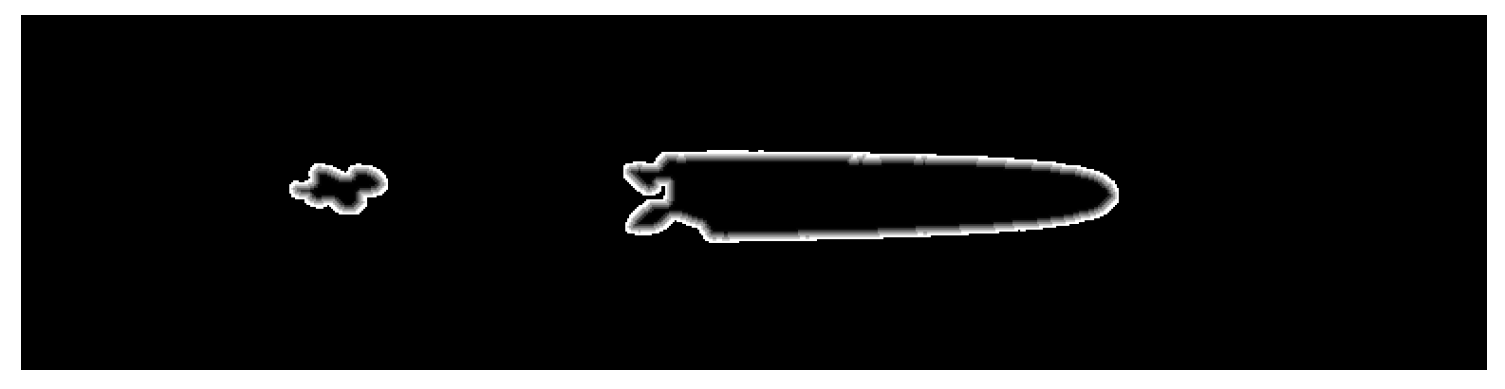
2.4.2. Bubble Segmentation
|
|
|
|
|
|
|
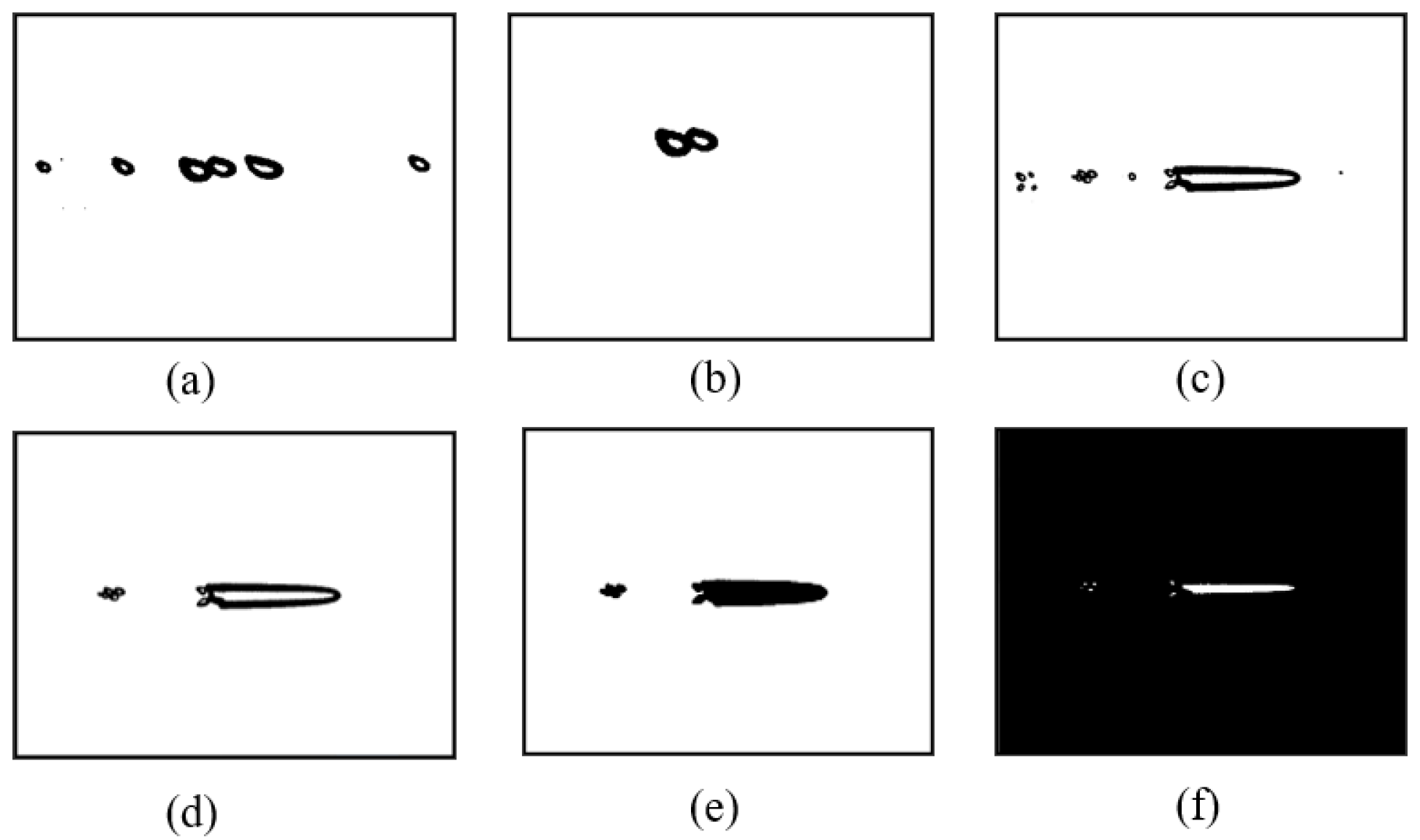
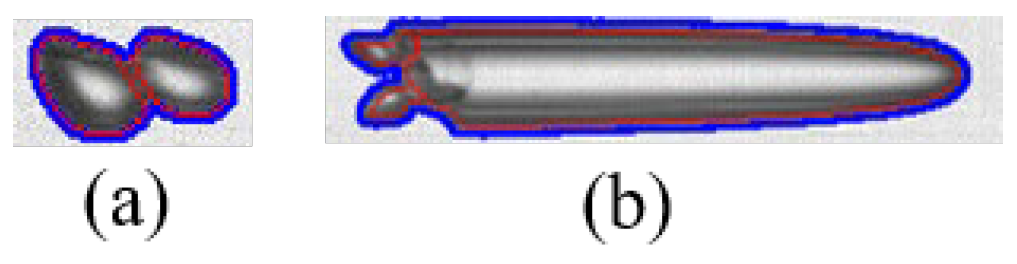
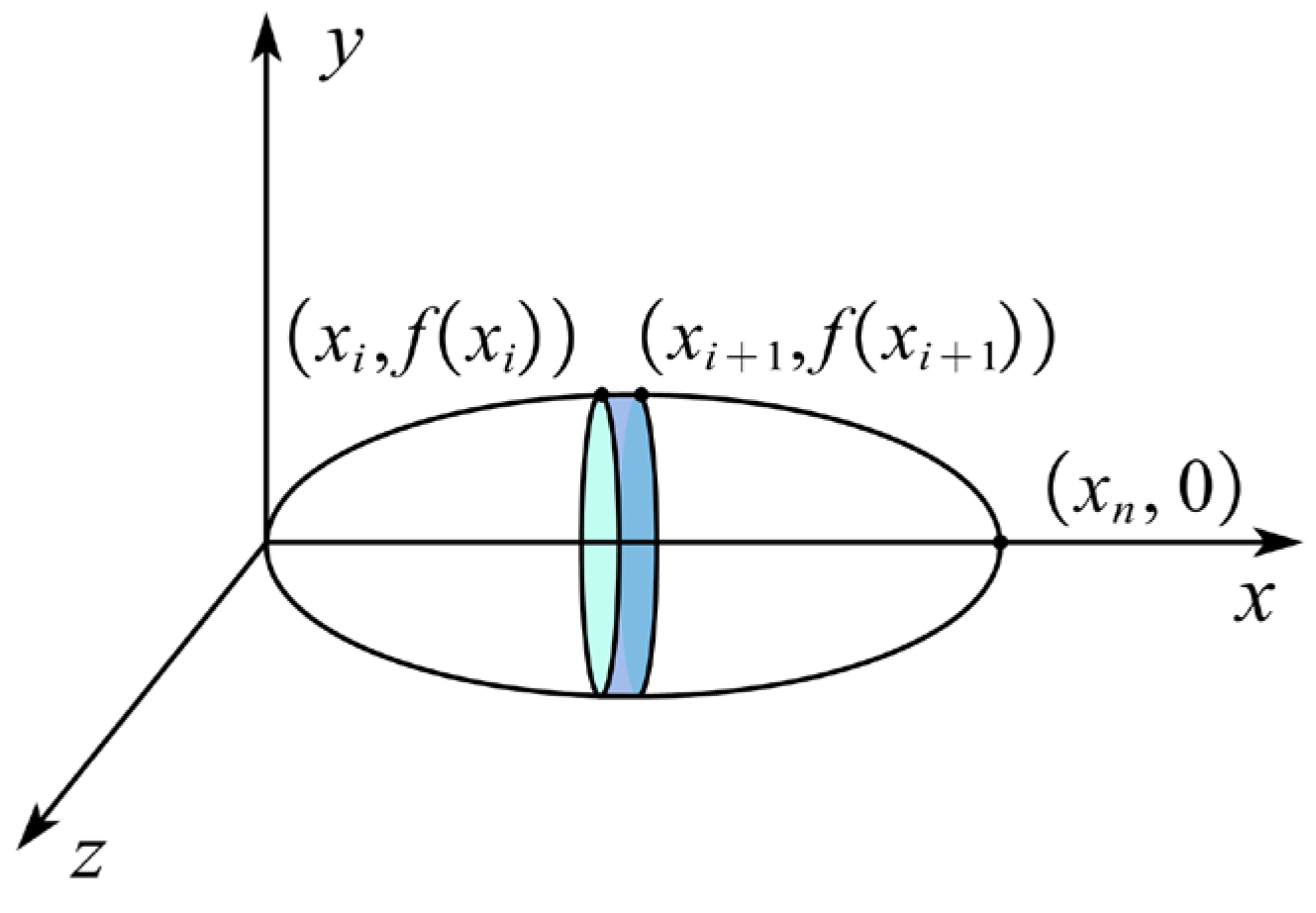
2.4.3. Volume Calculation Method of Isolated Bubble
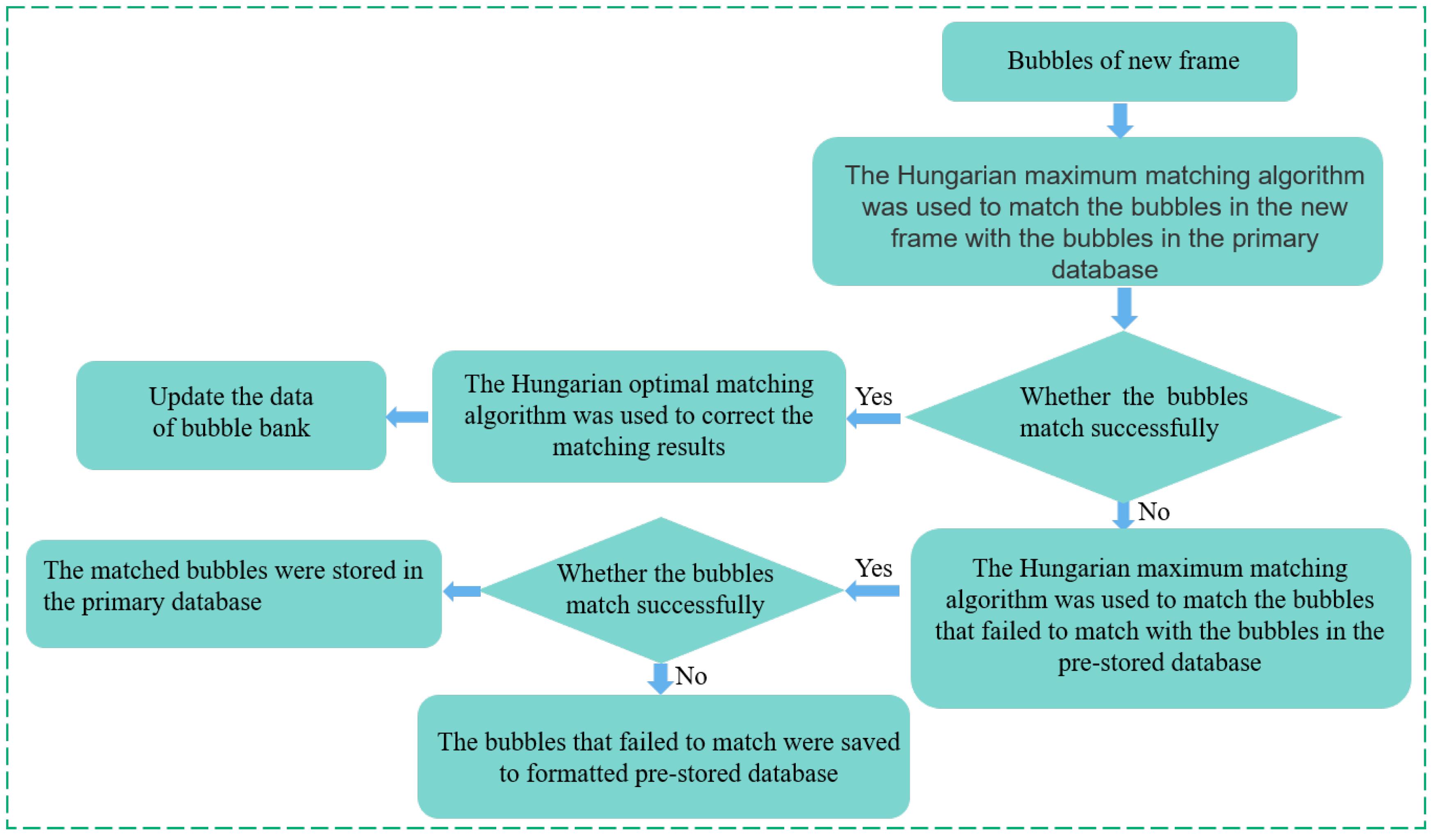
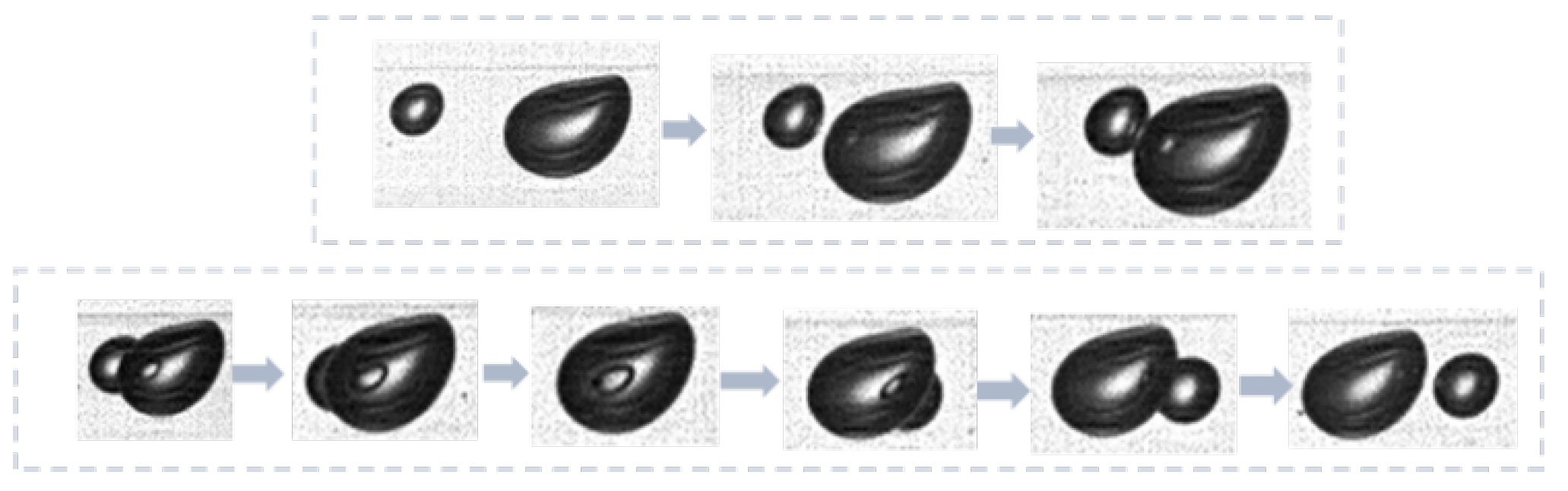
2.5. Bubble Tracking Method
2.5.1. Hungarian Algorithm
2.5.2. Matching Characteristics
- (1)
- Match admission threshold
- (2)
- Characteristic distance
2.5.3. Implementation of Bubble Tracking
2.6. Error Analysis
2.6.1. Error Analysis of Bubble Flow Pattern Recognition
2.6.2. Integral Error of the Bubble Volume Calculation
2.6.3. Error Analysis of Bubble Tracking
3. Experimental Results
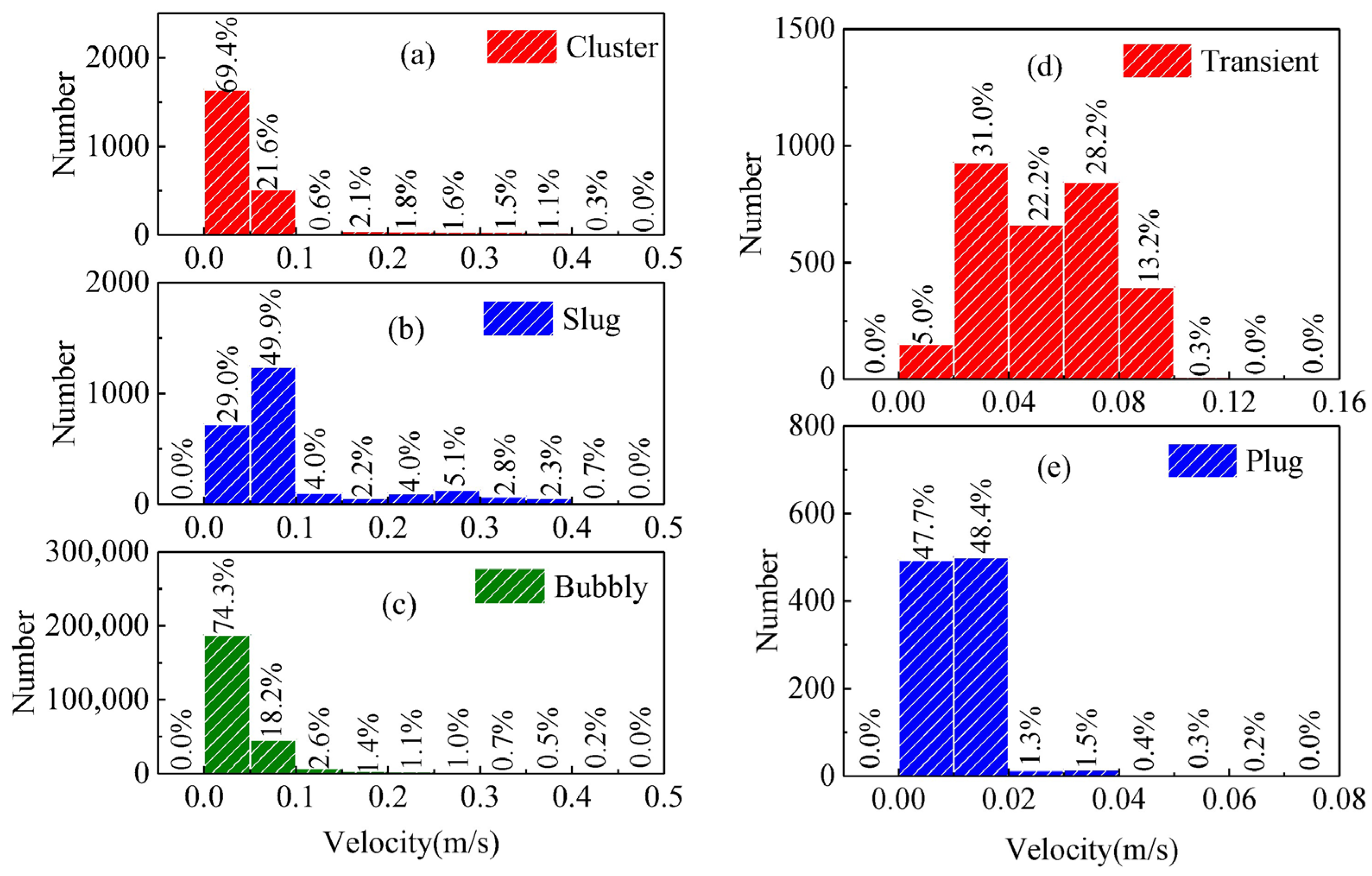
3.1. Bubble Flow Pattern
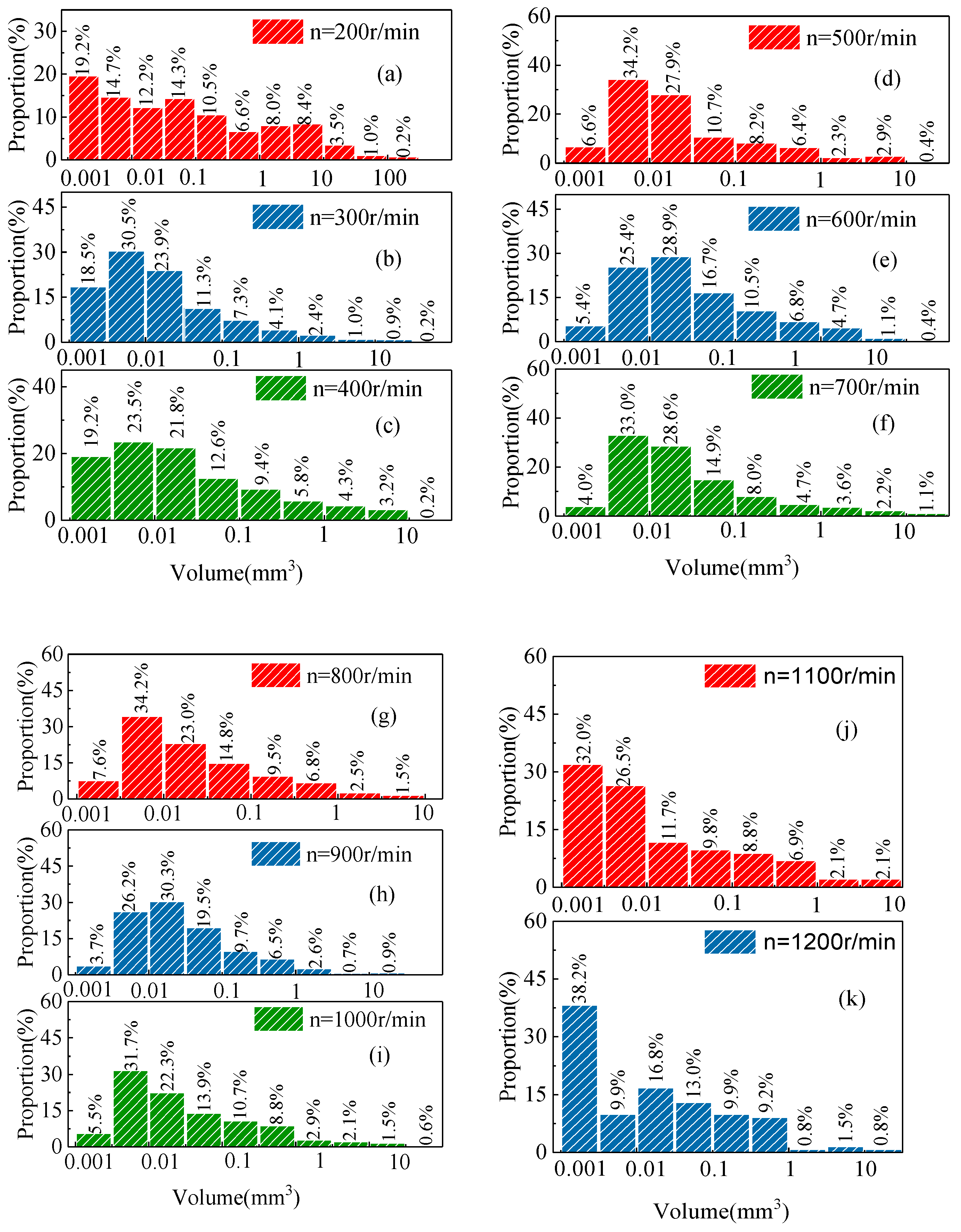
3.2. Bubble Volume
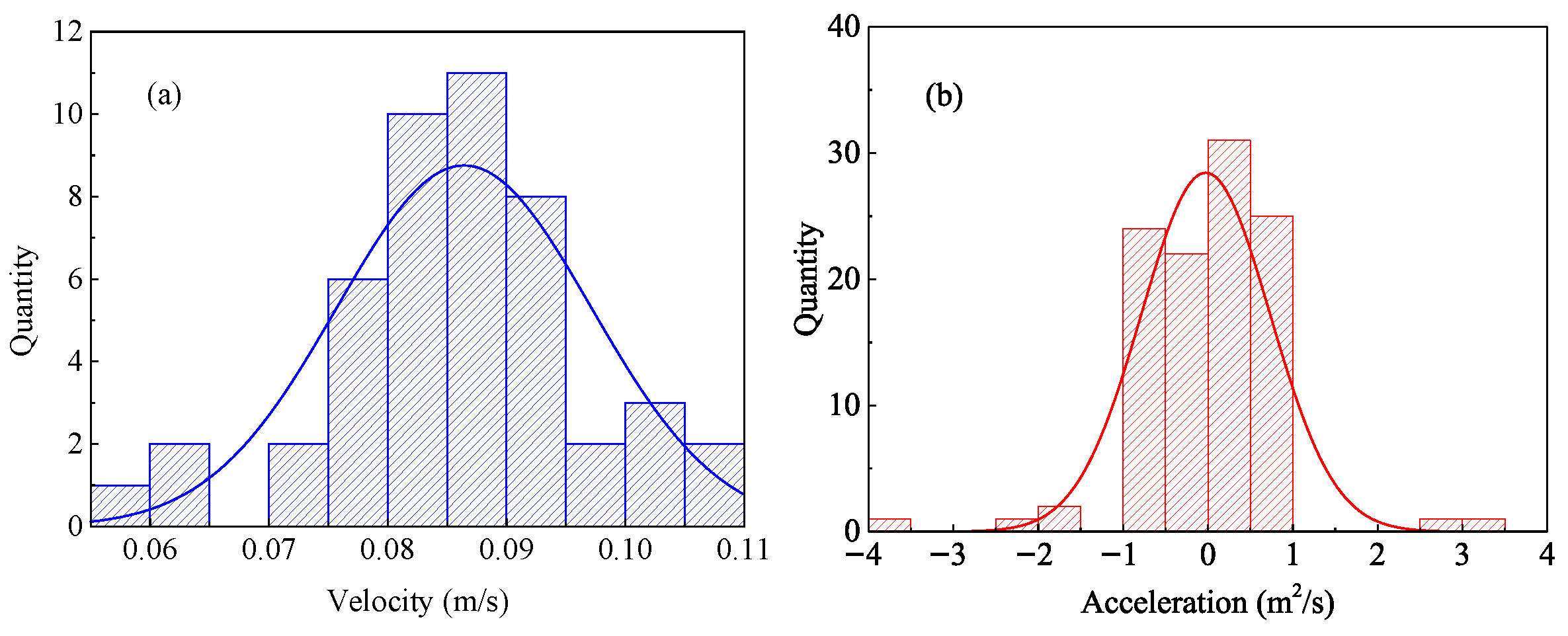
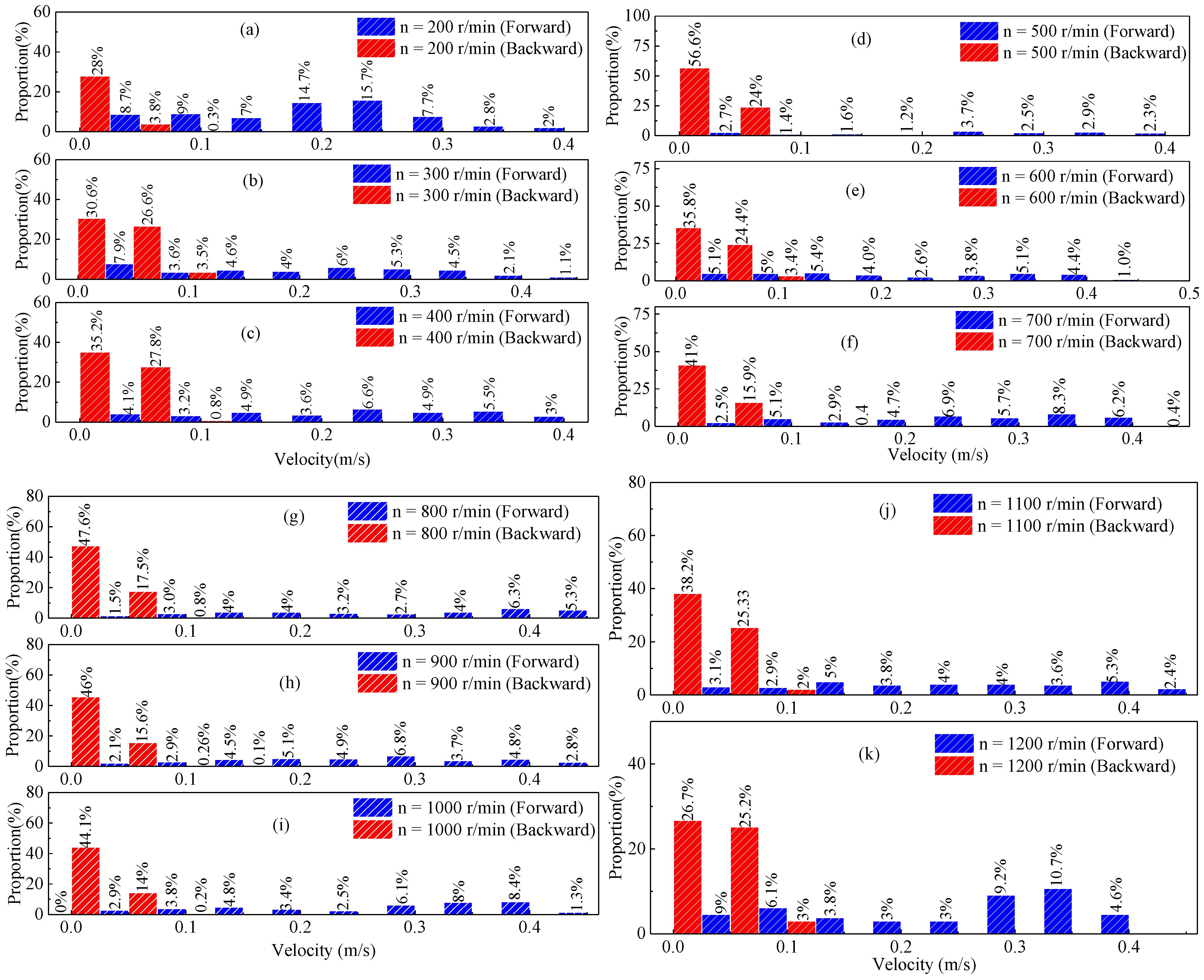
3.3. Velocity of Bubbles
3.3.1. Velocity Distribution of Bubbles in the Transparent Pipe
3.3.2. Velocity Distribution of Bubbles
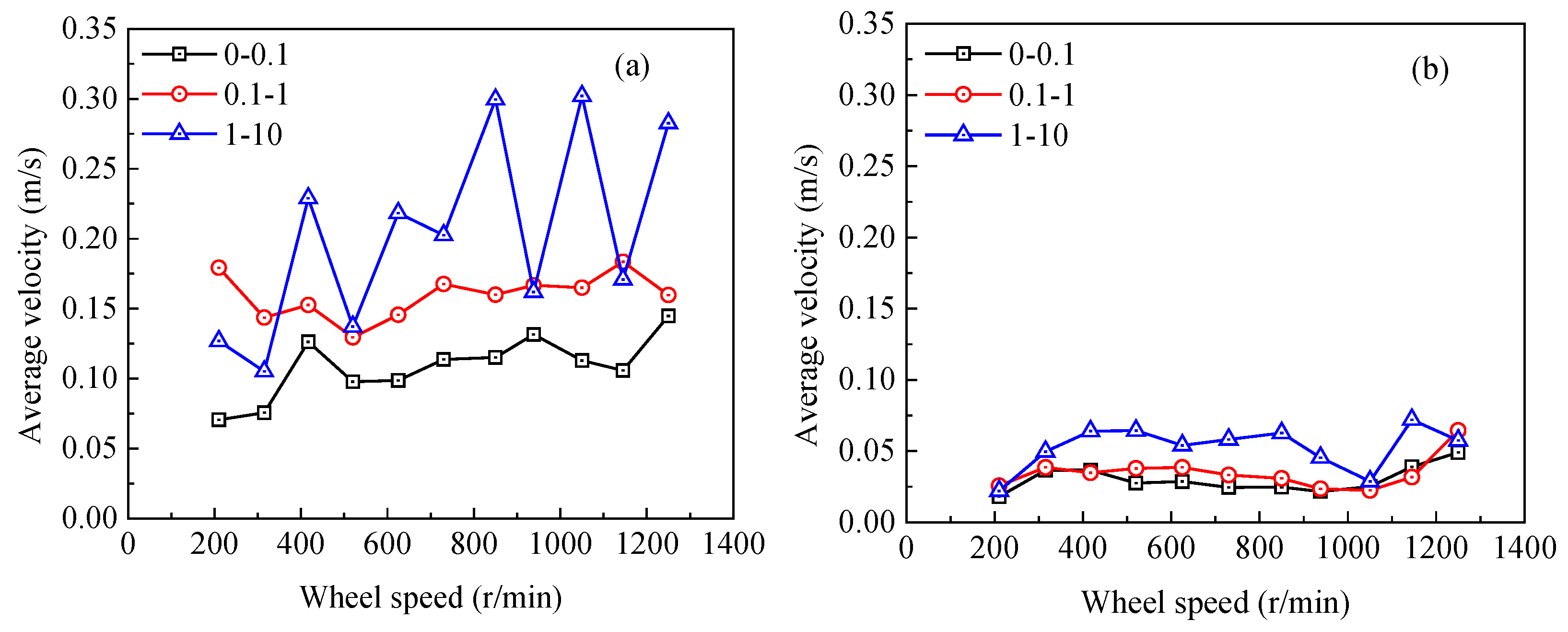
3.3.3. Average Velocity of Different Volume Bubbles
4. Further Discussion
4.1. Distribution of Bubbles
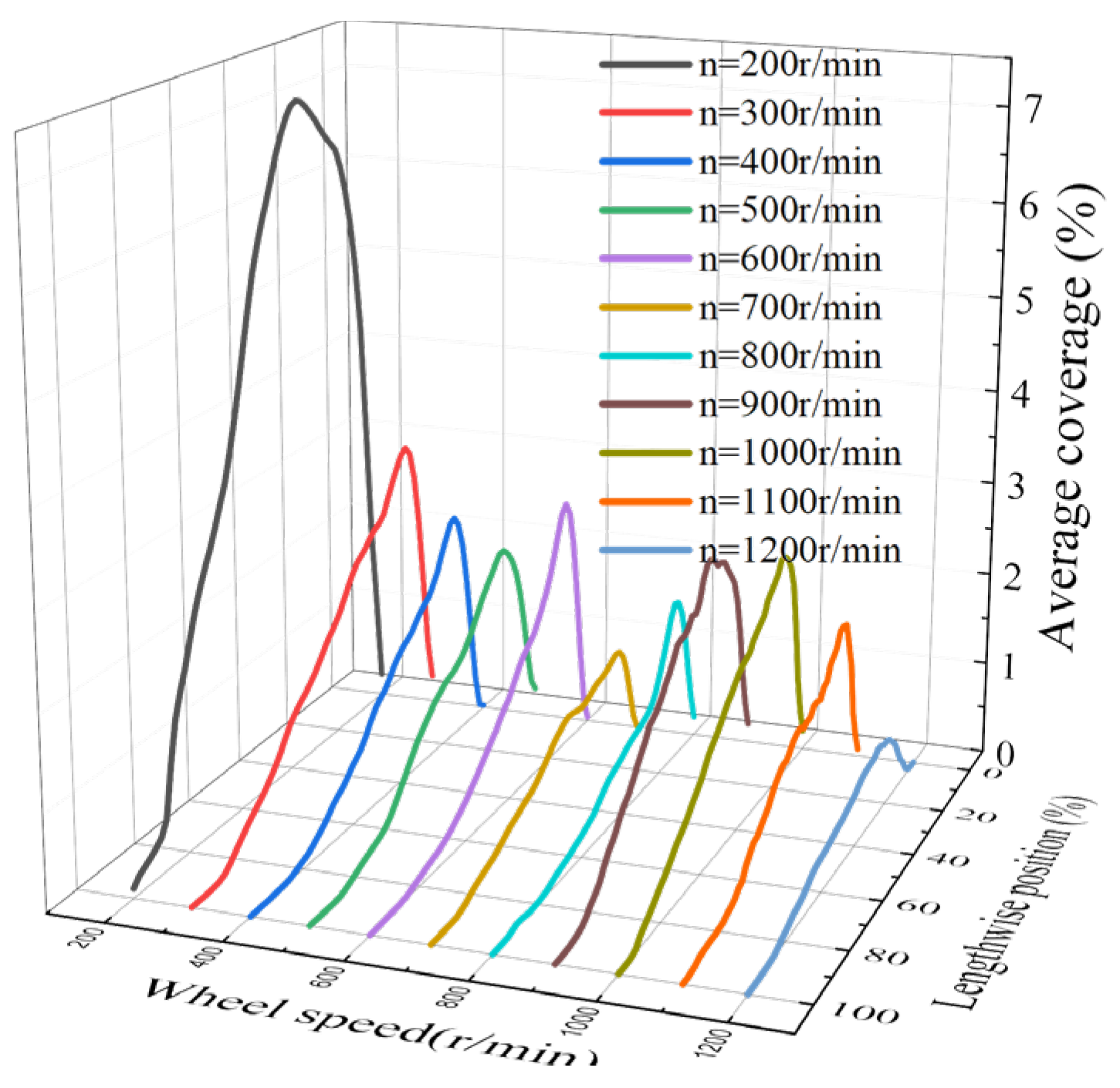
4.2. Average Gas Holdup of Observation Window
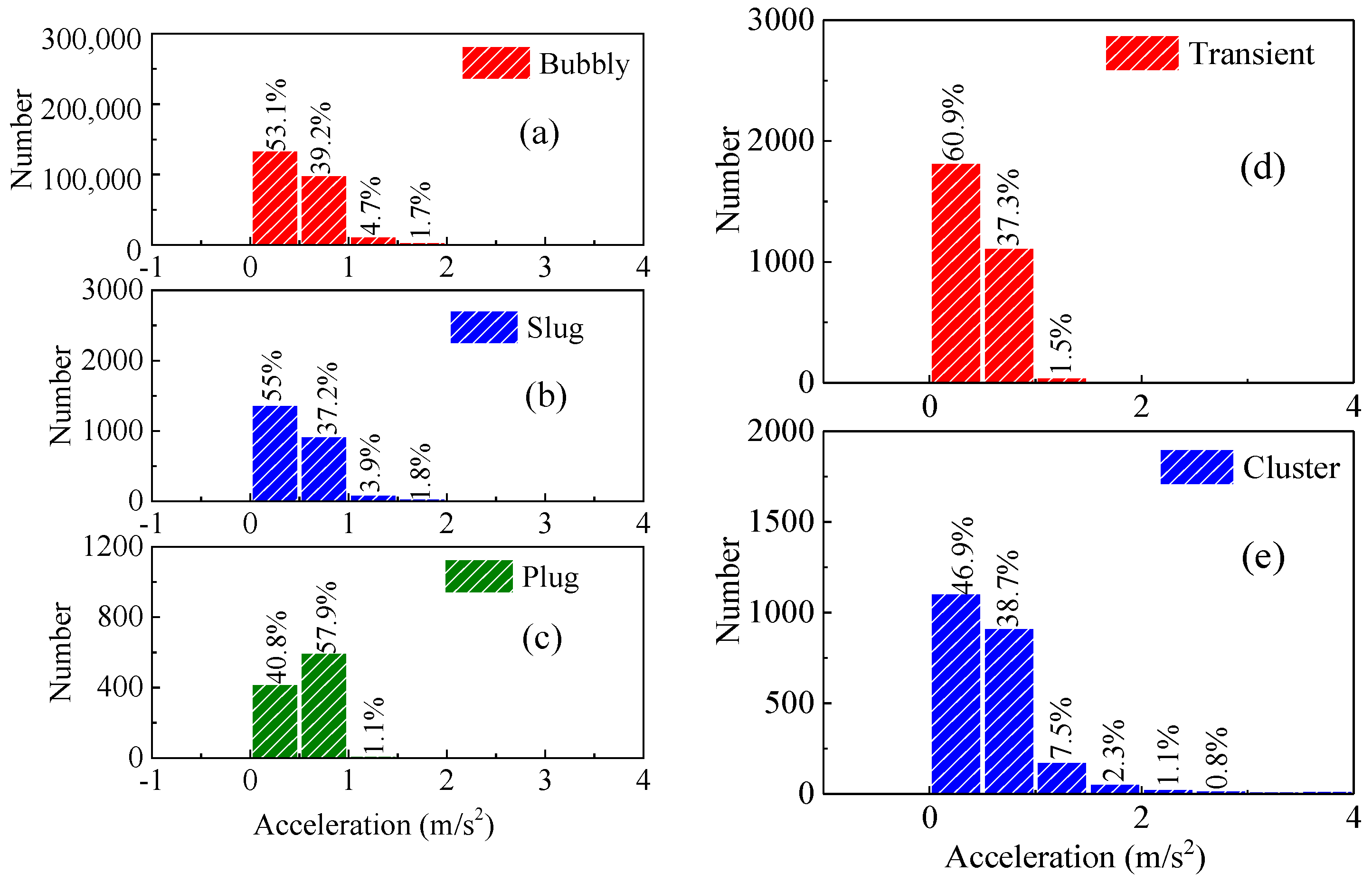
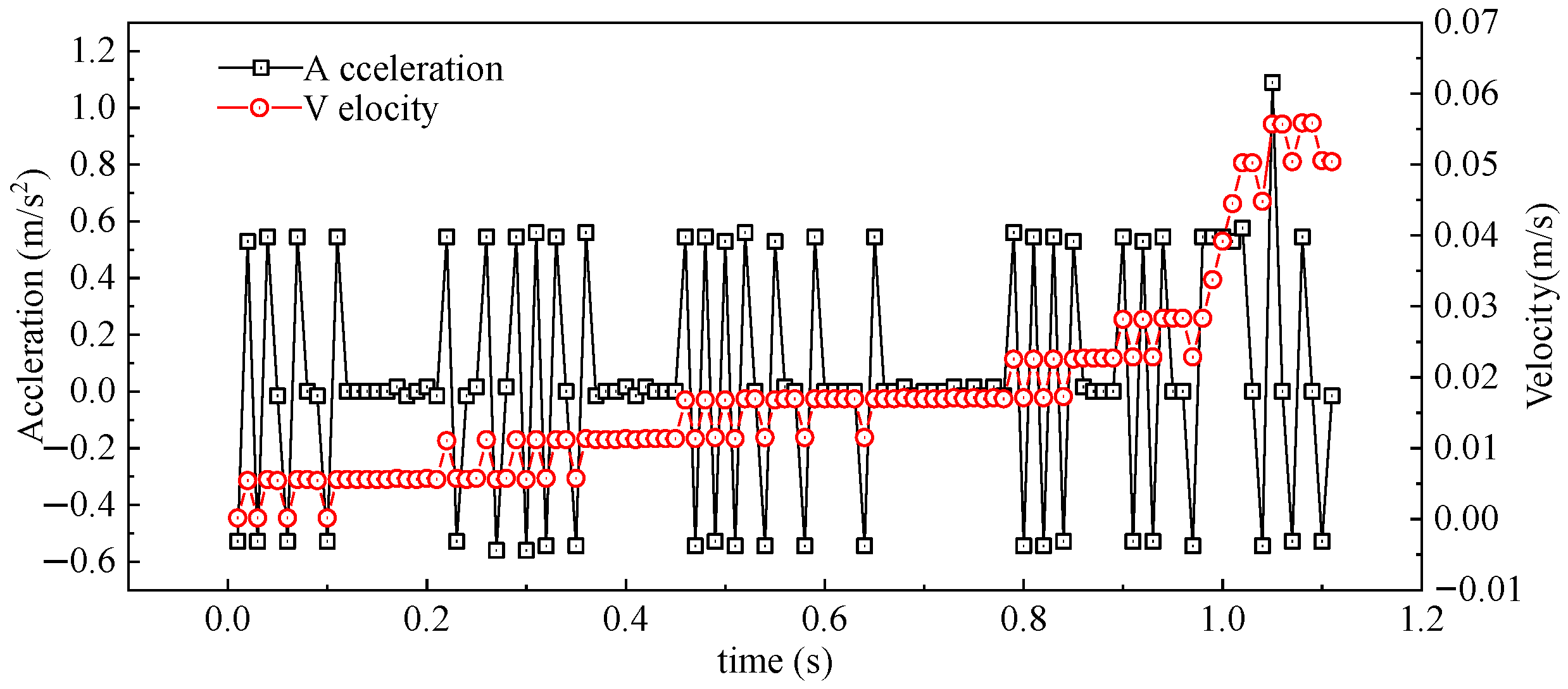
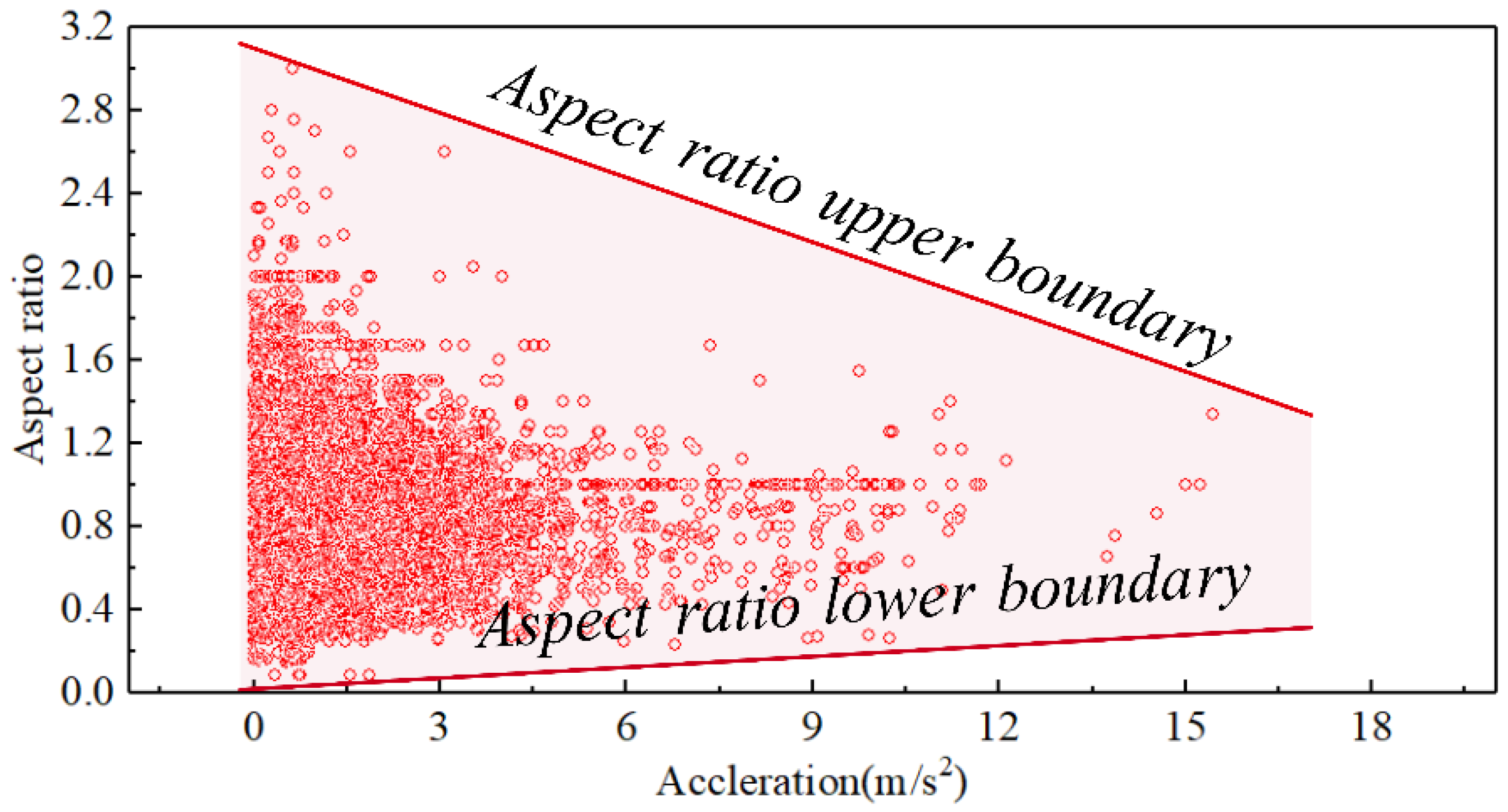
4.3. Bubble Acceleration Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xue, M.H.; Fu, Y.; Geng, X.H.; Sun, S.H.; Lei, Y.L. Integration analysis model of oil-charging system about parallel hydraulic retarder and its response characteristic. Eng. Sci. Technol. Int. J. 2024, 53, 101685. [Google Scholar] [CrossRef]
- Zhang, R.C.; Yu, X.; Hu, Y.L.; Zang, H.J.; Shu, W. Active control of hydraulic oil contamination to extend the service life of aviation hydraulic system. Int. J. Adv. Manuf. Technol. 2018, 96, 1693–1704. [Google Scholar] [CrossRef]
- Hunter, J.E.; Cartier, S.S.; Temple, D.J.; Mason, R.C. Brake fluid vaporization as a contributing factor in motor vehicle collisions. SAE Trans. 1998, 107, 867–885. [Google Scholar]
- Jun, K.J.; Park, T.W.; Jung, S.P.; Lee, S.H.; Yoon, J.W. Development of a numerical method to predict the alpine test result. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2008, 222, 1841–1849. [Google Scholar] [CrossRef]
- Wang, X.Y.; Zhang, Z.; Li, Y.L. Analysis of water coolant pressure fluctuation induced by piston slap. Eng. Fail. Anal. 2020, 112, 104382. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Y.; Li, X.; Xu, C.; Wei, W.; Zhao, J.; Jin, J.; Oppong, F. Spatiotemporal evo- lution of gas in transmission fluid under acoustic cavitation conditions. Appl. Sci. 2024, 14, 6233. [Google Scholar] [CrossRef]
- Chang, Y.J.; Xu, Q.; Zou, S.F.; Zhao, X.Y.; Wu, Q.H.; Wang Thévenin, D.; Guo, L.J. Experiments and predictions for severe slugging of gas-liquid two-phase flows in a long-distance pipeline-riser system. Ocean. Eng. 2024, 301, 117636. [Google Scholar] [CrossRef]
- Le, T.-L.; Chen, J.-C.; Nguyen, H.-B. Numerical study of the thermocapillary droplet migration in a microchannel under a blocking effect from the heated wall. Appl. Therm. Eng. 2017, 122, 820–830. [Google Scholar] [CrossRef]
- Deng, H.W.; Zhang, C.B.; Xu, G.Q.; Tao, Z.; Zhu, K.; Wang, Y.J. Visualization experiments of a specific fuel flow through quartz-glass tubes under both sub- and supercritical conditions. Chin. J. Aeronaut. 2012, 25, 372–380. [Google Scholar] [CrossRef]
- Thaker, J.; Banerjee, J. On intermittent flow characteristics of gas-liquid two-phase flow. Nucl. Eng. Des. 2016, 310, 363–377. [Google Scholar] [CrossRef]
- Al-Safran, E.M. Probabilistic modeling of slug frequency in gas-liquid pipe flow using the Poisson probability theory. J. Pet. Sci. Eng. 2016, 138, 88–96. [Google Scholar] [CrossRef]
- Setyawan, A.; Deendarlianto, I. The effect of the fluid properties on the wave velocity and wave frequency of gas-liquid annular two-phase flow in a horizontal pipe. Exp. Therm. Fluid Sci. 2016, 71, 25–41. [Google Scholar] [CrossRef]
- Al-Kayiem, H.H.; Mohammed, A.O.; Al-Hashimy, Z.I.; Time, R.W. Statistical assessment of experimental observation on the slug body length and slug translational velocity in a horizontal pipe. Int. J. Heat Mass Transf. 2017, 105, 252–260. [Google Scholar] [CrossRef]
- Kajero, O.T.; Abdulkadir, M.; Abdulkareem, L.; Azzopardi, B.J. Experimental study of viscous effects on flow pattern and bubble behavior in small diameter bubble column. Phys. Fluids 2018, 30, 093101. [Google Scholar] [CrossRef]
- Li, X.; Sun, J.; Xu, C.; Li, Y.; Zhang, R.; Qian, L.; Chen, Y. Visualization of bubble flow in the channel of a dimple-type embossing plate heat exchanger under different fluid inlet/outlet ports. Int. J. Heat Mass Transf. 2019, 145, 118750. [Google Scholar] [CrossRef]
- Serra, P.L.S.; Masotti, P.H.F.; Rocha, M.S.; de Andrade, D.A.; Torres, W.M.; de Mesquita, R.N. Two-phase flow void fraction estimation based on bubble image segmentation using Randomized Hough Transform with Neural Network (RHTN). Prog. Nucl. Energy 2020, 118, 103133. [Google Scholar] [CrossRef]
- Karn, A.; Ellis, C.; Arndt, R.; Hong, J. An integrative image measurement technique for dense bubbly flows with a wide size distribution. Chem. Eng. Sci. 2015, 122, 240–249. [Google Scholar] [CrossRef]
- Lau, Y.M.; Deen, N.G.; Kuipers, J.A.M. Development of an image measurement technique for size distribution in dense bubbly flows. Chem. Eng. Sci. 2013, 94, 20–29. [Google Scholar] [CrossRef]
- Honkanen, M.; Saarenrinne, P.; Stoor, T.; Niinimaki, J. Recognition of highly overlapping ellipse-like bubble images. Meas. Sci. Technol. 2005, 16, 1760–1770. [Google Scholar] [CrossRef]
- Javeed, M.A.; Ghaffar, M.A.; Ashraf, M.A.; Zubair, N.; Metwally, A.S.M.; Tag-Eldin, E.M.; Bocchetta, P.; Javed, M.S.; Jiang, X.F. Lane line detection and object scene segmentation using Otsu Thresholding and the Fast Hough Transform for intelligent vehicles in complex road conditions. Electronics 2023, 12, 1079. [Google Scholar] [CrossRef]
- Romanengo, C.; Falcidieno, B.; Biasotti, S. Hough transform based recognition of space curves. J. Comput. Appl. Math. 2022, 415, 114504. [Google Scholar] [CrossRef]
- Li, C. Dangerous posture monitoring for undersea diver based on frame difference method. J. Coast. Res. 2020, 103, 939–942. [Google Scholar] [CrossRef]
- Amoozegar, M.; Akbarizadeh, M.; Bouwmans, T. Robust and efficient FISTA-based method for moving object detection under background movements. Knowl. Based Syst. 2024, 294, 111765. [Google Scholar] [CrossRef]
- Pei, W.J.; Shi, Z.H.; Gong, K. Moving object detection in satellite videos based on an improved ViBe algorithm. Signal Image Video Process. 2024, 18, 2543–2557. [Google Scholar] [CrossRef]
- Zajec, B.; Cizelj, L.; Koncar, B. Effect of mass flow rate on bubble size distribution in boiling flow in temperature-controlled annular test section. Exp. Therm. Fluid Sci. 2023, 140, 110758. [Google Scholar] [CrossRef]
- Riquelme, A.; Desbiens, A.; del Villar, R.; Maldonado, M. Identification of a non-linear dynamic model of the bubble size distribution in a pilot flotation column. Int. J. Miner. Process. 2015, 145, 7–16. [Google Scholar] [CrossRef]
- Shao, S.Y.; Li, C.; Hong, J.R. A hybrid image processing method for measuring 3D bubble distribution using digital inline holography. Chem. Eng. Sci. 2019, 207, 929–941. [Google Scholar] [CrossRef]
- Kong, R.; Rau, A.; Kim, S.; Bajorek, S.; Tien, K.; Hoxie, C. A robust image analysis technique for the study of horizontal air-water plug flow. Exp. Therm. Fluid Sci. 2019, 102, 245–260. [Google Scholar] [CrossRef]
- Bröder, D.; Sommerfeld, M. Planar shadow image velocimetry for the analysis of the hydrodynamics in bubbly flows. Meas. Sci. Technol. 2007, 18, 2513–2528. [Google Scholar] [CrossRef]
- Zhang, W.K.; Liu, D.; Wang, C.J.; Liu, R.T.; Wang, D.Q.; Yu, L.Z.; Wen, S.M. An improved Python-based image processing algorithm for flotation foam analysis. Minerals 2022, 12, 1126. [Google Scholar] [CrossRef]
- Zhou, H.; Niu, X. An image processing algorithm for the measurement of multiphase bubbly flow using predictor-corrector method. Int. J. Multiph. Flow 2020, 128, 103277. [Google Scholar] [CrossRef]
- Zhang, T.; Qian, Y.; Yin, J.; Zhang, B.; Wang, D. Experimental study on 3D bubble shape evolution in swirl flow. Exp. Therm. Fluid Sci. 2019, 102, 368–375. [Google Scholar] [CrossRef]
- Song, Y.C.; Qian, Y.L.; Zhang, T.T.; Yin, J.L.; Wang, D.Z. Simultaneous measurements of bubble deformation and breakup with surrounding liquid-phase flow. Exp. Fluids 2022, 63, 83. [Google Scholar] [CrossRef]
- He, Y.X.; Wang, D.W.; Huang, F.H.; Zhang, R.N.; Min, L.T. A D2I and D2D collaboration framework for resource management in ABS-Assisted Post-Disaster Emergency Networks. IEEE Trans. Veh. Technol. 2024, 73, 2972–2977. [Google Scholar] [CrossRef]
- Feng, Y.L.; Ma, W.; Tan, Y.; Yan, H.; Qian, J.P.; Tian, Z.W.; Gao, A. A note on Hungarian method for solving assignment problem. Appl. Sci. 2024, 14, 1136. [Google Scholar] [CrossRef]
- Anirudh, N.V.; Behera, S.; Sahu, K.C. Coalescence of non-spherical drops with a liquid surface. Int. J. Multiph. Flow 2024, 175, 104800. [Google Scholar] [CrossRef]
- Hua, J.; Zhang, X.B.; Li, H.; Luo, Z.H. Experiment and simulation study on the effect of internals in gas-liquid bubble columns with a low aspect ratio. Ind. Eng. Chem. Res. 2024, 63, 4595–4604. [Google Scholar] [CrossRef]






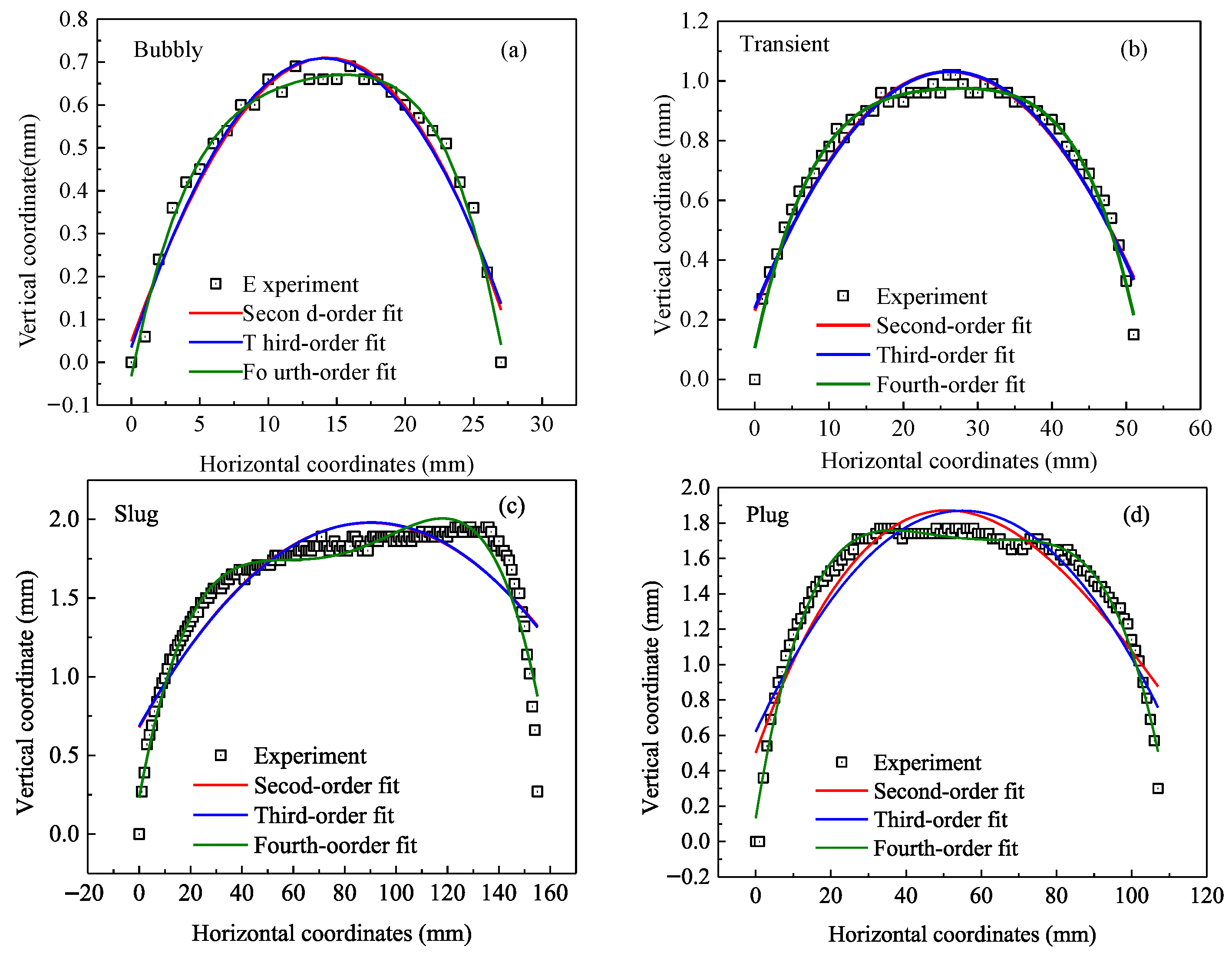

| Pattern | Fourth Order Coefficient | Third Order Coefficient | Second Order Coefficient | First Order Coefficient | Constant Term | Residual |
|---|---|---|---|---|---|---|
| Bubbly | −1.045 | 3.309 | −4.249 | 2.686 | −0.032 | 0.1224 |
| Transient | −0.113 | 0.699 | −1.700 | 1.937 | 0.106 | 0.2048 |
| Slug | −0.016 | 0.216 | −1.055 | 2.185 | 0.132 | 0.5631 |
| Plug | −0.004 | 0.081 | −0.529 | 1.477 | 0.231 | 1.1469 |
| Type | Volume (mm3) | Remainder Term | Error (%) | |
|---|---|---|---|---|
| Bubbly | 1.4679 | 0.0108 | 0.74 | |
| Transient | 6.4176 | 0.0292 | 0.46 | |
| Plug | 46.987 | 0.1675 | 0.36 | |
| Slug | 82.715 | 0.2552 | 0.31 |
| Wheel Speed (r/min) | Bubbly (%) | Slug (%) | Annular (%) | Transient (%) | Cluster (%) | Unsteady (%) |
|---|---|---|---|---|---|---|
| 200 | 81.88 | 4.88 | 0.35 | 0.35 | 2.79 | 9.75 |
| 300 | 96.12 | 0.49 | 0 | 0 | 0.65 | 2.74 |
| 400 | 93.81 | 1.50 | 0 | 0 | 0.56 | 4.13 |
| 500 | 93.37 | 0.78 | 0 | 0 | 0.58 | 5.27 |
| 600 | 94.88 | 0.43 | 0 | 0 | 0.28 | 4.41 |
| 700 | 95.31 | 1.08 | 0 | 0 | 0.36 | 3.25 |
| 800 | 96.41 | 0.21 | 0 | 0 | 0 | 3.38 |
| 900 | 93.42 | 0.34 | 0 | 0 | 0.60 | 5.64 |
| 1000 | 93.90 | 0.38 | 0 | 0 | 0.38 | 5.34 |
| 1100 | 94.13 | 1.41 | 0 | 0 | 0.23 | 4.23 |
| 1200 | 97.73 | 1.52 | 0 | 0 | 0 | 0.75 |
| Bubbly (%) | Slug (%) | Plug (%) | Transient (%) | Cluster (%) |
|---|---|---|---|---|
| 30.5 | 71.5 | 100 | 99 | 86.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Ke, Y.; Xu, C.; Sun, J.; Liang, M. Gas–Liquid Two-Phase Flow in a Hydraulic Braking Pipeline: Flow Pattern and Bubble Characteristics. Fluids 2025, 10, 196. https://doi.org/10.3390/fluids10080196
Li X, Ke Y, Xu C, Sun J, Liang M. Gas–Liquid Two-Phase Flow in a Hydraulic Braking Pipeline: Flow Pattern and Bubble Characteristics. Fluids. 2025; 10(8):196. https://doi.org/10.3390/fluids10080196
Chicago/Turabian StyleLi, Xiaolu, Yiyu Ke, Cangsu Xu, Jia Sun, and Mingxuan Liang. 2025. "Gas–Liquid Two-Phase Flow in a Hydraulic Braking Pipeline: Flow Pattern and Bubble Characteristics" Fluids 10, no. 8: 196. https://doi.org/10.3390/fluids10080196
APA StyleLi, X., Ke, Y., Xu, C., Sun, J., & Liang, M. (2025). Gas–Liquid Two-Phase Flow in a Hydraulic Braking Pipeline: Flow Pattern and Bubble Characteristics. Fluids, 10(8), 196. https://doi.org/10.3390/fluids10080196






