Hybrid Symbolic Regression and Machine Learning Approaches for Modeling Gas Lift Well Performance
Abstract
1. Introduction
1.1. The Importance of Predicting Bottomhole Pressure
1.2. Traditional Prediction Methods
1.3. Machine Learning Models for Predicting BHP
2. Methodology
2.1. Data Collection
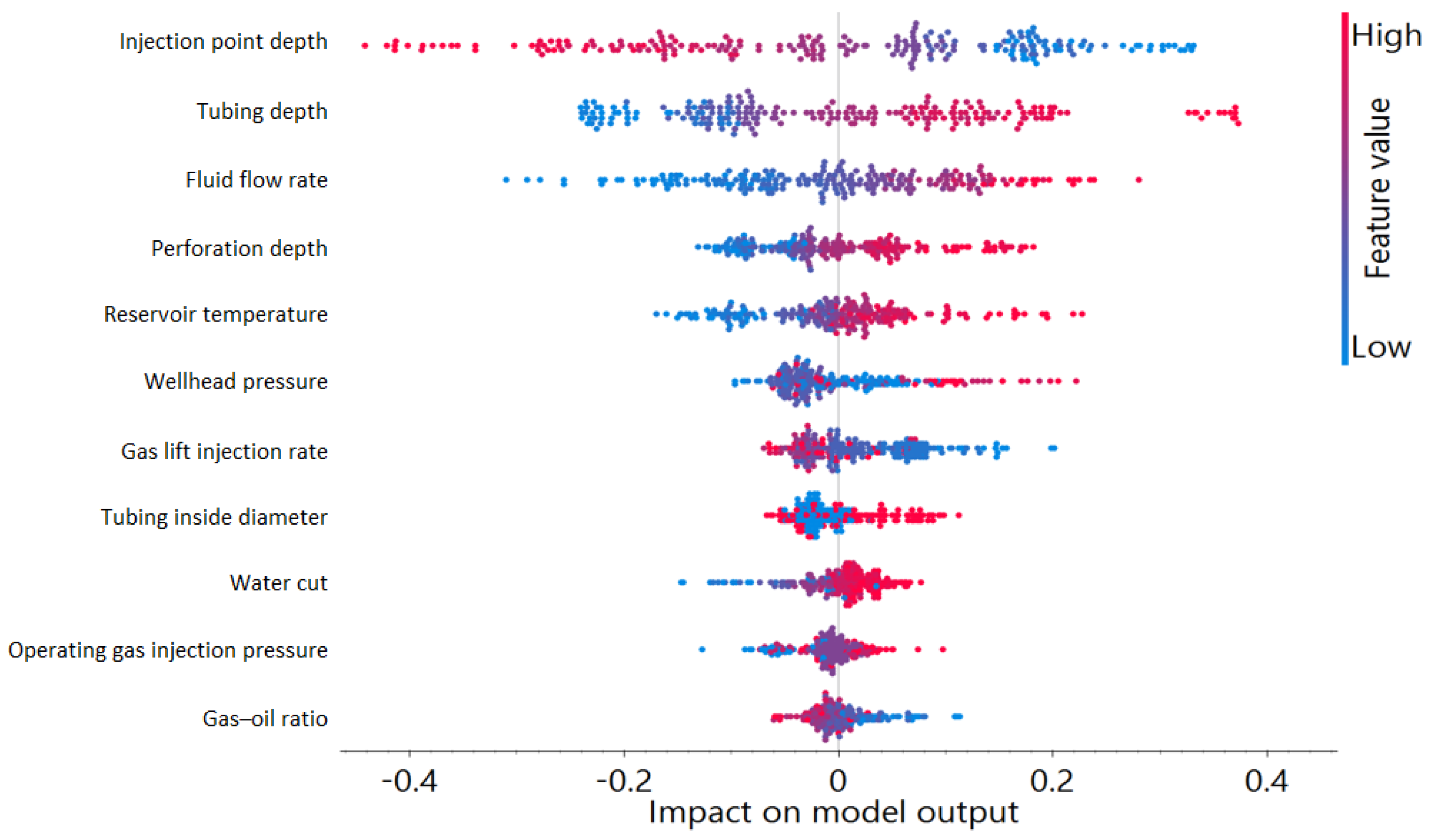
2.2. Feature Ranking
- Xi and Yi are the individual data points;
- and are the means of X and Y;
- The numerator is the covariance of X and Y;
- The denominator is the product of their standard deviations.
- di is the difference between the ranks of corresponding values in X and Y;
- n is the number of data points.
2.3. Data Preprocessing
- is the original value;
- is the minimum value in the feature;
- is the maximum value in the feature;
- is the normalized value (scaled to the range ).
2.4. Models Structure
2.4.1. Traditional Machine Learning and Neural Network-Based Approaches
2.4.2. Genetic Programming-Based Symbolic Regression
3. Results and Discussion
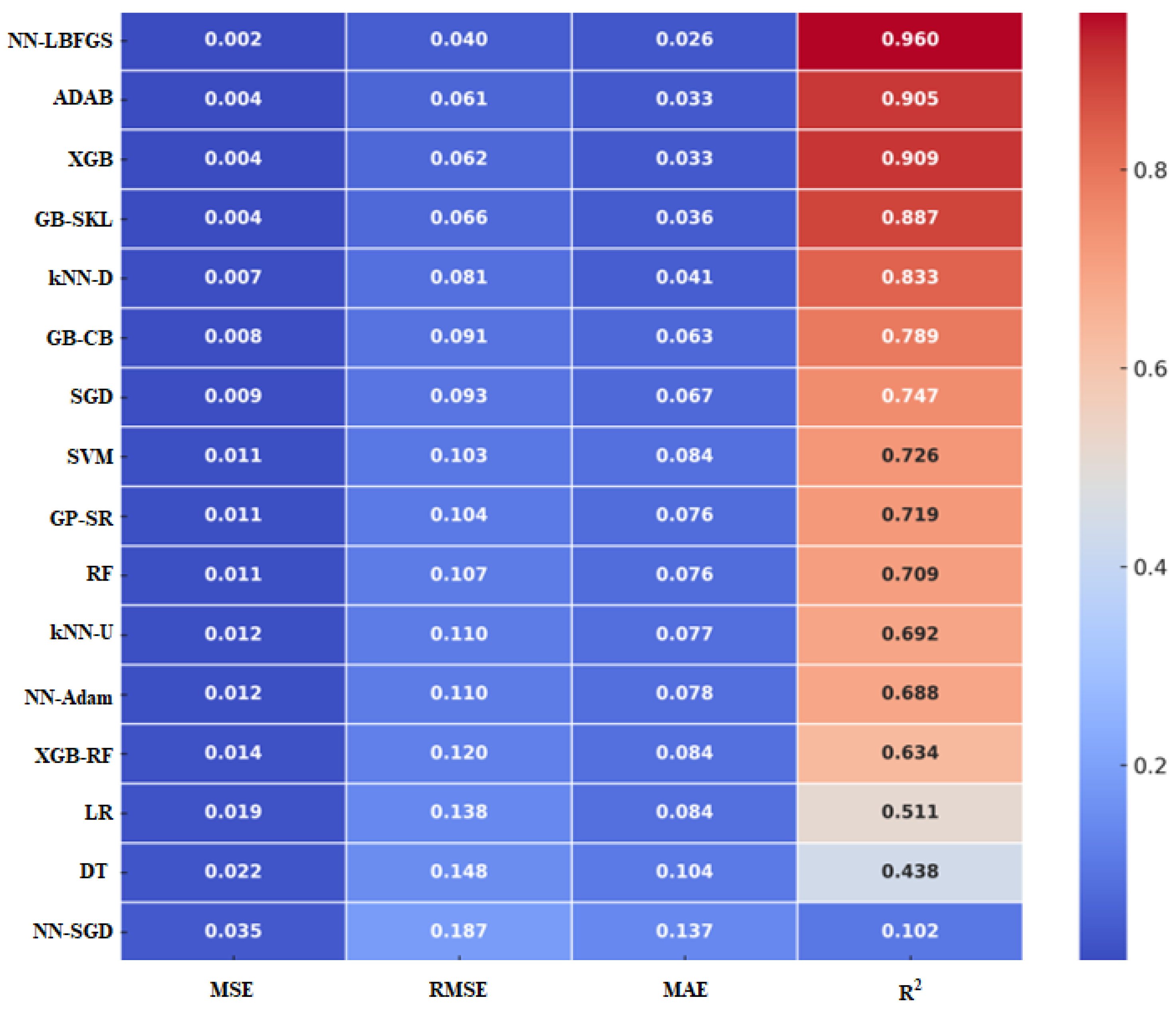
3.1. Model Results
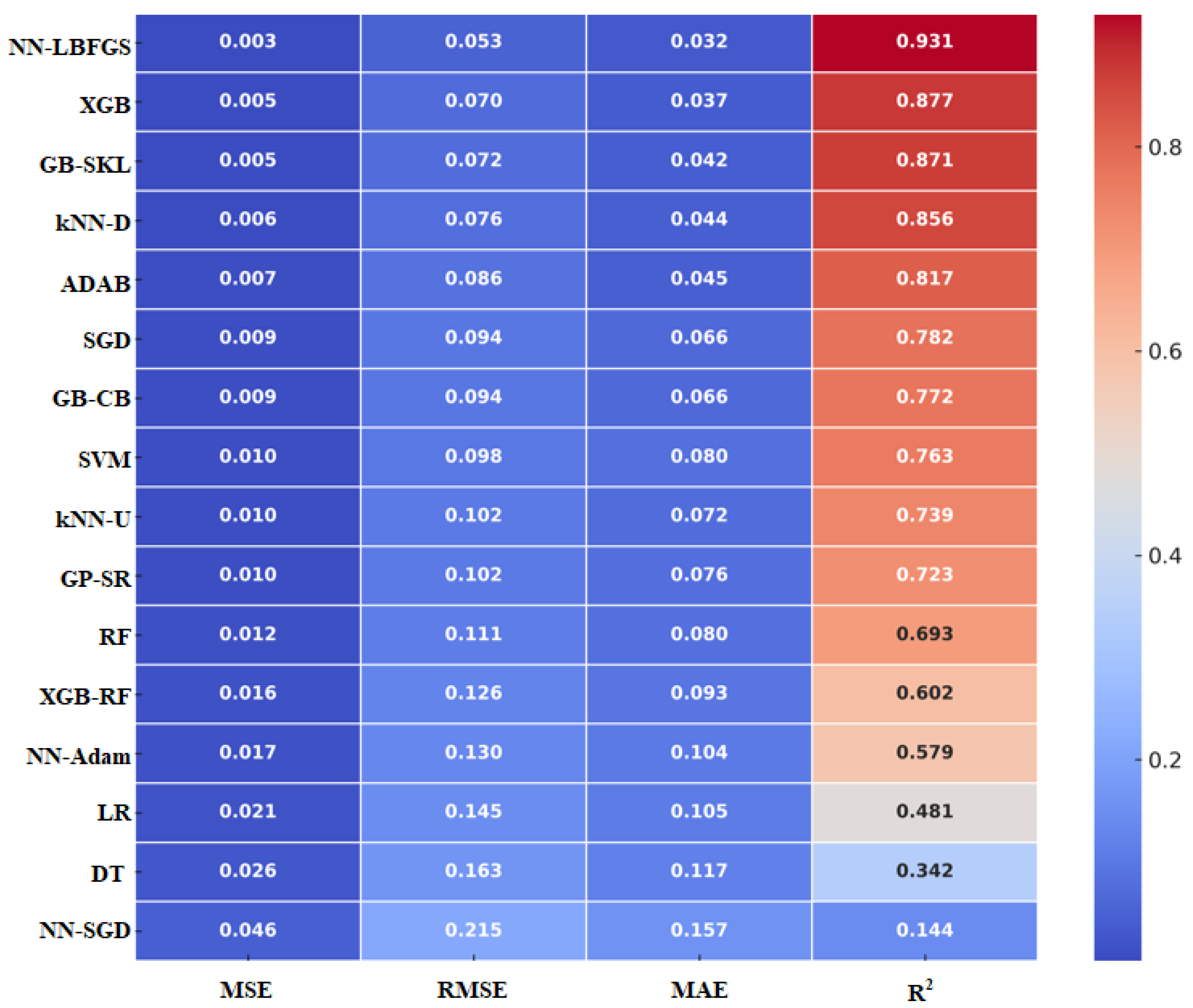
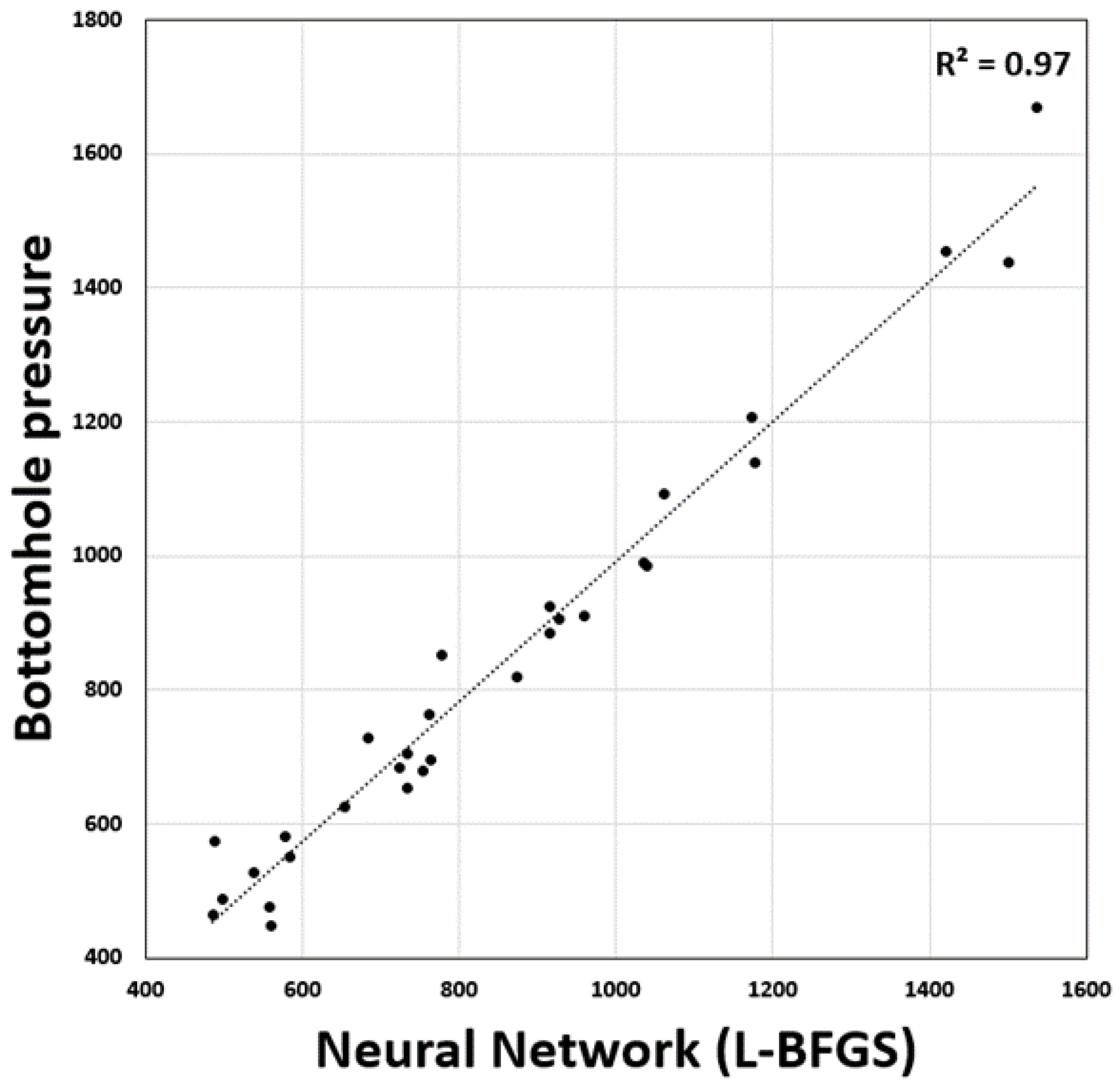
3.2. Model Testing and Validation
3.3. Field Application
3.4. Limitations of Machine Learning Models for BHP Prediction
4. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| AdaBoost | Adaptive Boosting |
| Adam | Adaptive Moment Estimation optimization algorithm |
| BHP | Bottomhole pressure |
| DT | Decision Tree |
| FFR | Fluid flow rate |
| GB-CB | Gradient Boosting (catboost) |
| GB-SKL | Gradient Boosting (scikit-learn) |
| GLIR | Gas lift injection rate |
| GOR | Gas–oil ratio |
| GP-SR | Genetic Programming-based Symbolic Regression |
| IPD | Injection point depth |
| IQR | Interquartile range |
| kNN-D | K-Nearest Neighbor (by distances) |
| kNN-U | K-Nearest Neighbor (uniform) |
| L-BFGS | Limited-memory Broyden–Fletcher–Goldfarb–Shanno optimization algorithm |
| LR | Linear Regression |
| MAE | Mean absolute error |
| MAPE | Mean absolute percent error |
| ML | Machine learning |
| MSE | Mean square error |
| NN | Neural network |
| OGIP | Operating gas injection pressure |
| PD | Perforation depth |
| r | Pearson’s correlation coefficient |
| R2 | Correlation coefficient |
| RF | Random Forest |
| RMSE | Root mean square error |
| RRSCV | Repeated random sampling cross-validation |
| RT | Reservoir temperature |
| SGD | Stochastic Gradient Descent |
| SHAP | SHapley Additive exPlanations |
| SVMs | Support Vector Machines |
| TD | Tubing depth |
| TID | Tubing inside diameter |
| WC | Water cut |
| WHP | Wellhead pressure |
| XGB | Extreme Gradient Boosting (xgboost) |
| XGB-RF | Extreme Gradient Boosting Random Forest (xgboost) |
| ρ | Spearman’s rank correlation coefficient |
References
- Su, S.J.; Ismail, A.M.; Al Daghar, K.; El-Jundi, O.; Mustapha, H. Maximizing the Value of Gas Lift for Efficient Field Development Plan Optimization Through Smart Gas Lift Optimization in a Giant Onshore Carbonate Oilfield. In Proceedings of the ADIPEC, Abu Dhabi, United Arab Emirates, 2 October 2023; p. D012S159R003. [Google Scholar] [CrossRef]
- Moffett, R.E.; Seale, S.R. Real Gas Lift Optimization: An Alternative to Timer Based Intermittent Gas Lift. In Proceedings of the Abu Dhabi International Petroleum Exhibition & Conference, Abu Dhabi, United Arab Emirates, 13 November 2017; p. D021S048R004. [Google Scholar] [CrossRef]
- Zhong, H.; Zhao, C.; Xu, Z.; Zheng, C. Economical Optimum Gas Allocation Model Considering Different Types of Gas-Lift Performance Curves. Energies 2022, 15, 6950. [Google Scholar] [CrossRef]
- Khoshkbarchi, M.; Rahmanian, M.; Cordazzo, J.; Nghiem, L. Application of Mesh Adaptive Derivative-Free Optimization Technique for Gas-Lift Optimization in an Integrated Reservoirs, Wells, and Facilities Modeling Environment. In Proceedings of the SPE Canada Heavy Oil Conference, Virtual, 24 September 2020; p. D041S008R003. [Google Scholar] [CrossRef]
- Suharto, M.A.; Risal, A.R.; Subandi, A.N.; Trjangganung, K.; Zain, A.M.; Ahnap, M.S. Maximizing Oil Production by Leveraging Python for Gas Lift Optimization Through Well Modelling. In Proceedings of the International Petroleum Technology Conference, Kuala Lumpur, Malaysia, 17 February 2025; p. D032S010R016. [Google Scholar] [CrossRef]
- Mammadov, A.V.; Sultanova, A.V.; Mammadov, R.M. Grouping of Gas Lift Wells Based on their Interaction. In Proceedings of the SPE Caspian Technical Conference and Exhibition, Baku, Azerbaijan, 21 November 2023; p. D021S006R008. [Google Scholar] [CrossRef]
- Yan, X.; Dong, J.; Niu, Z.; Liu, D.; Chen, A.; Gunay, A.; Cui, J.; Wang, Y.; Chen, J. Residual Oil Prediction According to Seismic Attributes and Oil Productivity Index Based on PCA and BPNN. In Proceedings of the Fourth International Meeting for Applied Geoscience & Energy, Houston, TX, USA, 26 August 2024; pp. 698–702. [Google Scholar] [CrossRef]
- Amin, R.S.; Abdulwahab, I.M.; Rahman, N.M.A. Maximization of the Productivity Index Through Geometrical Optimization of Multi-Lateral Wells in Heterogeneous Reservoir System. In Proceedings of the International Petroleum Technology Conference, Dhahran, Saudi Arabia, 12 February 2024; p. D021S063R006. [Google Scholar] [CrossRef]
- Alshobaky, A.M.; Abdal, W.S. Productivity Index in Horizontal Well. Malays. J. Ind. Technol. 2024, 8, 1–27. [Google Scholar] [CrossRef]
- Abdullahi, B.A.; Ezeh, M.C. Production Optimization in Oil and Gas Wells: A Gated Recurrent Unit Approach to Bottom Hole Flowing Pressure Prediction. In Proceedings of the SPE Nigeria Annual International Conference and Exhibition, Lagos, Nigeria, 5 August 2024; p. D021S007R004. [Google Scholar] [CrossRef]
- Mohammadpoor, M.; Shahbazi, K.h.; Torabi, F.; Qazvini, A.A. New Methodology for Prediction of Bottomhole Flowing Pressure in Vertical Multiphase Flow in Iranian Oil Fields Using Artificial Neural Networks (ANNs). In Proceedings of the SPE Latin American and Caribbean Petroleum Engineering Conference, Lima, Peru, 1 December 2010; p. SPE-139147-MS. [Google Scholar] [CrossRef]
- Barrufet, M.A.; Rasool, A.; Aggour, M. Prediction of Bottomhole Flowing Pressures in Multiphase Systems Using a Thermodynamic Equation of State. In Proceedings of the SPE Production Operations Symposium, Oklahoma City, Oklahoma, 2 April 1995; p. SPE-29479-MS. [Google Scholar] [CrossRef]
- Gunwant, D.; Kishore, N.; Gogoi, R.; Devshali, S.; Chanchalni, K.L.; Rajak, H.K.; Meena, S.K. Removal of Flow Instability Through the Use of Multiple Converging Gas Lift Ports (MCGLP) in Gas Lift Wells. In Proceedings of the SPE/IATMI Asia Pacific Oil & Gas Conference and Exhibition, Jakarta, Indonesia, 6 October 2023; p. D032S006R001. [Google Scholar] [CrossRef]
- Popov, S.; Chernyshov, S.; Gladkikh, E. Experimental and Numerical Assessment of the Influence of Bottomhole Pressure Drawdown on Terrigenous Reservoir Permeability and Well Productivity. Fluid Dyn. Mater. Process. 2023, 19, 619–634. [Google Scholar] [CrossRef]
- Gharieb, A.; Elshaafie, A.; Gabry, M.A.; Algarhy, A.; Elsawy, M.; Darraj, N. Exploring an Alternative Approach for Predicting Relative Permeability Curves from Production Data: A Comparative Analysis Employing Machine and Deep Learning Techniques. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 29 April 2024; p. D041S054R003. [Google Scholar] [CrossRef]
- Campos, M.C.M.M.; Lima, M.L.; Teixeira, A.F.; Moreira, C.A.; Stender, A.S.; Von Meien, O.F.; Quaresma, B. Advanced Control for Gas-Lift Well Optimization. In Proceedings of the OTC Brasil, Rio de Janeiro, Brazil, 15 October 2017; p. D031S025R006. [Google Scholar] [CrossRef]
- Garg, A.; Sharma, A.; Rajvanshi, S.; Suman, A.; Goswami, B.; Yadav, M.P.; Narayana, D.; Tiwary, R. Optimization of Gas Injection Network Using Genetic Algorithm: A Solution for Intermittent Gas Lift Wells. In Proceedings of the SPE Canadian Energy Technology Conference and Exhibition, Calgary, AL, Canada, 12 March 2024; p. D021S027R003. [Google Scholar] [CrossRef]
- Masud, L.; Cortez, V.L.; Ottulich, M.A.; Valderrama, M.P.; Ghilardi, J.; Sanchez Graff, L.A.; Biondi, J.; Sapag, F. Gas Lift Optimization in Unconventional Wells—Vaca Muerta Case Study. In Proceedings of the SPE Argentina Exploration and Production of Unconventional Resources Symposium, Buenos Aires, Argentina, 20 March 2023; p. D011S004R002. [Google Scholar] [CrossRef]
- Sajjad, F.; Chandra, S.; Wirawan, A.; Dewi Rahmawati, S.; Santoso, M.; Suganda, W. Computational Fluid Dynamics for Gas Lift Optimization in Highly Deviated Wells. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dubai, United Arab Emirates, 15 September 2021; p. D021S032R002. [Google Scholar] [CrossRef]
- Ali, A.M.; Negm, M.N.; Darwish, H.M.; Mansour, K.M. Strategic Modelling Approach for Optimizing and Troubleshooting Gas Lifted Wells: Monitoring, Modelling, Problems Identification and Solutions Recommendations. In Proceedings of the Gas & Oil Technology Showcase and Conference, Dubai, United Arab Emirates, 13 March 2023; p. D021S018R004. [Google Scholar] [CrossRef]
- Ammar, M.; Abdulwarith, A.; Kareb, A.; Paker, D.M.; Dindoruk, B.; Ablil, W.; Altownisi, M.; Abid, E. Optimization of Gas Injection Well Productivity Through Integration of Modified Isochronal Test Including the Impact of Phase Behaviour: A Case Study on Coiled-Tubing Gas Lift for Al-Jurf Offshore Oil Field. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 20 September 2024; p. D021S022R007. [Google Scholar] [CrossRef]
- Akinola, O.; Olufisayo, F.; Ebikeme, A.; Olumide, T.; Aluba, O.; Clement, C. Investigative Approaches to Troubleshooting and Remediating Sub-Optimal Gas Lift Performance in a Dual Completion Well. In Proceedings of the SPE Nigeria Annual International Conference and Exhibition, Lagos, Nigeria, 30 July 2023; p. D031S021R001. [Google Scholar] [CrossRef]
- Elwan, M.; Davani, E.; Ghedan, S.G.; Mousa, H.; Kansao, R.; Surendra, M.; Deng, L.; Korish, M.; Shahin, E.; Ibrahim, M.; et al. Automated Well Production and Gas Lift System Diagnostics and Optimization Using Augmented AI Approach in a Complex Offshore Field. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dubai, United Arab Emirates, 15 September 2021; p. D011S013R001. [Google Scholar] [CrossRef]
- Algarhy, A.; Adel Gabry, M.; Farid Ibrahim, A.; Gharieb, A.; Darraj, N. Optimizing Development Strategies for Unconventional Reservoirs of Abu Roash Formation in the Western Desert of Egypt. In Proceedings of the The Unconventional Resources Technology Conference, Houston, TX, USA, 17 June 2024. [Google Scholar] [CrossRef]
- Zalavadia, H.; Gokdemir, M.; Sinha, U.; Sankaran, S. Optimizing Artificial Lift Timing and Selection Using Reduced Physics Models. In Proceedings of the SPE Oklahoma City Oil and Gas Symposium, Oklahoma City, OK, USA, 17 April 2023; p. D021S003R002. [Google Scholar] [CrossRef]
- Anuar, W.M.; Badawy, K.; Bakar, K.A.; Aznam, M.R.; Salahuddin, S.N.; Mail, M.; Bakar, A.H.; Trivedi, R.; Tri, N.V. Integrated Operations for Gas Lift Optimization: A Successful Story at Peninsular Malaysia Field. In Proceedings of the SPE Asia Pacific Oil and Gas Conference and Exhibition, Brisbane, Australia, 23 October 2018; p. D021S012R002. [Google Scholar] [CrossRef]
- Chanlongsawaitkul, R. An Intelligent System to Recommend Appropriate Correlations for Vertical Multiphase Flow. Master’s Thesis, Chulalongkorn University, Bangkok, Thailand, 2006. [Google Scholar] [CrossRef]
- Sun, H.; Luo, Q.; Xia, Z.; Li, Y.; Yu, Y. Bottomhole Pressure Prediction of Carbonate Reservoirs Using XGBoost. Processes 2024, 12, 125. [Google Scholar] [CrossRef]
- Baryshnikov, E.S.; Kanin, E.A.; Osiptsov, A.A.; Vainshtein, A.L.; Burnaev, E.V.; Paderin, G.V.; Prutsakov, A.S.; Ternovenko, S.O. Adaptation of Steady-State Well Flow Model on Field Data for Calculating the Flowing Bottomhole Pressure. In Proceedings of the SPE Russian Petroleum Technology Conference, Virtual, 26 October 2020; p. D023S007R008. [Google Scholar] [CrossRef]
- Cox, S.A.; Sutton, R.P.; Blasingame, T.A. Errors Introduced by Multiphase Flow Correlations on Production Analysis. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 24 September 2006; p. SPE-102488-MS. [Google Scholar] [CrossRef]
- Campos, D.; Wayo, D.D.K.; De Santis, R.B.; Martyushev, D.A.; Yaseen, Z.M.; Duru, U.I.; Saporetti, C.M.; Goliatt, L. Evolutionary Automated Radial Basis Function Neural Network for Multiphase Flowing Bottom-Hole Pressure Prediction. Fuel 2024, 377, 132666. [Google Scholar] [CrossRef]
- Agwu, O.E.; Alatefi, S.; Alkouh, A.; Azim, R. Artificial Intelligence Models for Flowing Bottomhole Pressure Estimation: State-of-the-Art and Proposed Future Research Directions. Int. J. Adv. Sci. Eng. Inf. Technol. 2024, 14, 1868–1879. [Google Scholar] [CrossRef]
- Obeida, T.A.; Mosallam, Y.H.; Al Mehari, Y.S. Calculation of Flowing Bottomhole Pressure Constraint Based on Bubblepoint-Pressure-vs.-Depth Relationship. In Proceedings of the SPE Middle East Oil and Gas Show and Conference, Manama, Bahrain, 11 March 2007; p. SPE-104985-MS. [Google Scholar] [CrossRef]
- Usov, E.V.; Ulyanov, V.N.; Butov, A.A.; Chuhno, V.I.; Lyhin, P.A. Modelling Multiphase Flows of Hydrocarbons in Gas-Condensate and Oil Wells. Math. Models Comput. Simul. 2020, 12, 1005–1013. [Google Scholar] [CrossRef]
- Marfo, S.A.; Asante-Okyere, S.; Ziggah, Y.Y. A New Flowing Bottom Hole Pressure Prediction Model Using M5 Prime Decision Tree Approach. Model. Earth Syst. Environ. 2022, 8, 2065–2073. [Google Scholar] [CrossRef]
- Chanchlani, K.; Sukanandan, J.; Devshali, S.; Kumar, V.; Kumar, A. Delineating and Decoding the Qualitative Interpretation of Gas Lift Instabilities in the Continuous Gas Lift Wells of Mehsana. In Proceedings of the International Petroleum Technology Conference, Kuala Lumpur, Malaysia, 17 February 2025; p. D022S006R008. [Google Scholar] [CrossRef]
- Soni, D.K.; Mohammed Al Breiki, N. A Case Study of Well Integrity Challenges and Resolutions for the Gas Lift Appraisal Project: How 42 Gas Lift Wells Were Developed Post Mitigation of Well Integrity Challenges to Meet Double Barrier Compliance. In Proceedings of the SPE Middle East Artificial Lift Conference and Exhibition, Manama, Bahrain, 29 October 2024; p. D021S004R004. [Google Scholar] [CrossRef]
- Orudjov, Y.A.; Dadash-zada, M.A.; Mamedov, F.K. Determination of the Critical Value of Bottomhole Pressure during Flow Well Operation. Azerbaijan Oil Ind. 2024, 23–26. [Google Scholar] [CrossRef]
- Molinari, D.; Sankaran, S. Merging Physics and Data-Driven Methods for Field-Wide Bottomhole Pressure Estimation in Unconventional Wells. In Proceedings of the 9th Unconventional Resources Technology Conference, Houston, TX, USA, 26 July 2021. [Google Scholar] [CrossRef]
- Barbosa, M.C.; Rodriguez, O.M.H. Drift-Flux Parameters for High-Viscous-Oil/Gas Two-Phase Upward Flow in a Large and Narrow Vertical and Inclined Annular Duct. J. Energy Resour. Technol. 2022, 144, 033004. [Google Scholar] [CrossRef]
- Yin, B.; Pan, S.; Zhang, X.; Wang, Z.; Sun, B.; Liu, H.; Zhang, Q. Effect of Oil Viscosity on Flow Pattern Transition of Upward Gas-Oil Two-Phase Flow in Vertical Concentric Annulus. SPE J. 2022, 27, 3283–3296. [Google Scholar] [CrossRef]
- Nagoo, A.S.; Vangolen, B.N. Will Gas Lifting in the Heel and Lateral Sections of Horizontal Wells Improve Lift Performance? The Multiphase Flow View. In Proceedings of the SPE Annual Technical Conference and Exhibition, Virtual, 19 October 2020; p. D041S053R007. [Google Scholar] [CrossRef]
- Miranda-Lugo, P.J.; Barbosa, M.C.; Ortiz-Vidal, L.E.; Rodriguez, O.M.H. Efficiency of an Inverted-Shroud Gravitational Gas Separator: Effect of the Liquid Viscosity and Inclination. SPE J. 2023, 28, 429–445. [Google Scholar] [CrossRef]
- Ualiyeva, G.; Pereyra, E.; Sarica, C. An Experimental Study on Two-Phase Downward Flow of Medium Viscosity Oil and Air. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 26 September 2022; p. D021S021R006. [Google Scholar] [CrossRef]
- Xu, L.; Chen, J.; Cao, Z.; Zhang, W.; Xie, R.; Liu, X.; Hu, J. Identification of Oil–Water Flow Patterns in a Vertical Well Using a Dual-Ring Conductance Probe Array. IEEE Trans. Instrum. Meas. 2016, 65, 1249–1258. [Google Scholar] [CrossRef]
- Wu, N.; Luo, C.; Liu, Y.; Li, N.; Xie, C.; Cao, G.; Ye, C.; Wang, H. Prediction of Liquid Holdup in Horizontal Gas Wells Based on Dimensionless Number Selection. J. Energy Resour. Technol. 2023, 145, 113001. [Google Scholar] [CrossRef]
- Luo, C.; Wu, N.; Dong, S.; Liu, Y.; Ye, C.; Yang, J. Experimental and Modeling Studies on Pressure Gradient Prediction for Horizontal Gas Wells Based on Dimensionless Number Analysis. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dubai, United Arab Emirates, 15 September 2021; p. D031S052R006. [Google Scholar] [CrossRef]
- Liu, M.; Bai, B.; Li, X. A Unified Formula for Determination of Wellhead Pressure and Bottom-hole Pressure. Energy Procedia 2013, 37, 3291–3298. [Google Scholar] [CrossRef]
- Xu, Z.; Wu, K.; Song, X.; Li, G.; Zhu, Z.; Pang, Z. A Unified Model to Predict Flowing Pressure and Temperature Distributions in Horizontal Wellbores for Different Energized Fracturing Fluids. In Proceedings of the 6th Unconventional Resources Technology Conference, Houston, TX, USA, 23 July 2018. [Google Scholar] [CrossRef]
- AL-Dogail, A.S.; Gajbhiye, R.N.; AL-Naser, M.A.; Aldoulah, A.A.; Alshammari, H.Y.; Alnajim, A.A. Machine Learning Approach to Predict Pressure Drop of Multi-Phase Flow in Horizontal Pipe and Influence of Fluid Properties. In Proceedings of the Gas & Oil Technology Showcase and Conference, Dubai, United Arab Emirates, 13 March 2023; p. D011S011R002. [Google Scholar] [CrossRef]
- Thabet, S.A.; Elhadidy, A.A.; Heikal, M.; Taman, A.; Yehia, T.A.; Elnaggar, H.; Mahmoud, O.; Helmy, A. Next-Gen Proppant Cleanout Operations: Machine Learning for Bottom-Hole Pressure Prediction. In Proceedings of the Mediterranean Offshore Conference, Alexandria, Egypt, 20 October 2024; p. D021S012R008. [Google Scholar] [CrossRef]
- Asimiea, N.W.; Ebere, E.N. Using Machine Learning to Predict Permeability from Well Logs: A Comparative Study of Different Models. In Proceedings of the SPE Nigeria Annual International Conference and Exhibition, Lagos, Nigeria, 30 July 2023; p. D021S004R005. [Google Scholar] [CrossRef]
- Safarov, A.; Iskandarov, V.; Solomonov, D. Application of Machine Learning Techniques for Rate of Penetration Prediction. In Proceedings of the SPE Annual Caspian Technical Conference, Nur-Sultan, Kazakhstan, 15 November 2022; p. D021S013R002. [Google Scholar] [CrossRef]
- Fan, Z.; Chen, J.; Zhang, T.; Shi, N.; Zhang, W. Machine Learning for Formation Tightness Prediction and Mobility Prediction. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dubai, United Arab Emirates, 15 September 2021; p. D011S018R005. [Google Scholar] [CrossRef]
- Thabet, S.A.; El-Hadydy, A.A.; Gabry, M.A. Machine Learning Models to Predict Pressure at a Coiled Tubing Nozzle’s Outlet During Nitrogen Lifting. In Proceedings of the SPE/ICoTA Well Intervention Conference and Exhibition, The Woodlands, TX, USA, 12 March 2024; p. D021S013R003. [Google Scholar] [CrossRef]
- Mukherjee, T.; Burgett, T.; Ghanchi, T.; Donegan, C.; Ward, T. Predicting Gas Production Using Machine Learning Methods: A Case Study. In Proceedings of the SEG Technical Program Expanded Abstracts 2019, San Antonio, TX, USA, 15 September 2019; pp. 2248–2252. [Google Scholar] [CrossRef]
- Al Shehri, F.H.; Gryzlov, A.; Al Tayyar, T.; Arsalan, M. Utilizing Machine Learning Methods to Estimate Flowing Bottom-Hole Pressure in Unconventional Gas Condensate Tight Sand Fractured Wells in Saudi Arabia. In Proceedings of the SPE Russian Petroleum Technology Conference, Virtual, 26 October 2020; p. D043S032R002. [Google Scholar] [CrossRef]
- Nashed, S.; Moghanloo, R. Replacing Gauges with Algorithms: Predicting Bottomhole Pressure in Hydraulic Fracturing Using Advanced Machine Learning. Eng 2025, 6, 73. [Google Scholar] [CrossRef]
- Gabry, M.A.; Ali, A.G.; Elsawy, M.S. Application of Machine Learning Model for Estimating the Geomechanical Rock Properties Using Conventional Well Logging Data. In Proceedings of the Offshore Technology Conference, OTC, Houston, TX, USA, 24 April 2023; p. D021S028R004. [Google Scholar] [CrossRef]
- El Khouly, I.; Sabet, A.; El-Fattah, M.A.A.; Bulatnikov, M. Integration Between Different Hydraulic Fracturing Techniques and Machine Learning in Optimizing and Evaluating Hydraulic Fracturing Treatment. In Proceedings of the International Petroleum Technology Conference, Dhahran, Saudi Arabia, 12 February 2024; p. D021S084R003. [Google Scholar] [CrossRef]
- Zhuang, X.; Liu, Y.; Hu, Y.; Guo, H.; Nguyen, B.H. Prediction of Rock Fracture Pressure in Hydraulic Fracturing with Interpretable Machine Learning and Mechanical Specific Energy Theory. Rock Mech. Bull. 2025, 4, 100173. [Google Scholar] [CrossRef]
- Yang, C.; Xu, C.; Ma, Y.; Qu, B.; Liang, Y.; Xu, Y.; Xiao, L.; Sheng, Z.; Fan, Z.; Zhang, X. A Novel Paradigm for Parameter Optimization of Hydraulic Fracturing Using Machine Learning and Large Language Model. Int. J. Adv. Comput. Sci. Appl. 2025, 16. [Google Scholar] [CrossRef]
- Gharieb, A.; Gabry, M.A.; Soliman, M.Y. The Role of Personalized Generative AI in Advancing Petroleum Engineering and Energy Industry: A Roadmap to Secure and Cost-Efficient Knowledge Integration: A Case Study. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 20 September 2024; p. D011S007R002. [Google Scholar] [CrossRef]
- Thabet, S.; Elhadidy, A.; Elshielh, M.; Taman, A.; Helmy, A.; Elnaggar, H.; Yehia, T. Machine Learning Models to Predict Total Skin Factor in Perforated Wells. In Proceedings of the SPE Western Regional Meeting, Palo Alto, CA, USA, 9 April 2024; p. D011S004R007. [Google Scholar] [CrossRef]
- Ugoyah, J.C.; Ajienka, J.A.; Wachikwu-Elechi, V.U.; Ikiensikimama, S.S. Prediction of Scale Precipitation by Modelling its Thermodynamic Properties using Machine Learning Engineering. In Proceedings of the SPE Nigeria Annual International Conference and Exhibition, Lagos, Nigeria, 1 August 2022; p. D021S007R005. [Google Scholar] [CrossRef]
- Carpenter, C. Decision Tree Regressions Estimate Liquid Holdup in Two-Phase Gas/Liquid Flows. J. Pet. Technol. 2021, 73, 75–76. [Google Scholar] [CrossRef]
- Thabet, S.; Zidan, H.; Elhadidy, A.; Taman, A.; Helmy, A.; Elnaggar, H.; Yehia, T. Machine Learning Models to Predict Production Rate of Sucker Rod Pump Wells. In Proceedings of the SPE Western Regional Meeting, Palo Alto, CA, USA, 9 April 2024; p. D011S004R008. [Google Scholar] [CrossRef]
- Musorina, A.D.; Ishimbayev, G.S. Optimization of the Reservoir Management System and the ESP Operation Control Process by Means of Machine Learning on the Oilfields of Salym Petroleum Development NV. In Proceedings of the SPE Russian Petroleum Technology Conference, Virtual, 12 October 2021; p. D021S006R004. [Google Scholar] [CrossRef]
- Tan, C.; Chua, A.; Muniandy, S.; Lee, H.; Chai, P. Optimization of Inflow Control Device Completion Design Using Metaheuristic Algorithms and Supervised Machine Learning Surrogate. In Proceedings of the International Petroleum Technology Conference, Kuala Lumpur, Malaysia, 17 February 2025; p. D012S001R007. [Google Scholar] [CrossRef]
- Leem, J.; Mazeli, A.H.; Musa, I.H.; Che Yusoff, M.F. Data Analytics and Machine Learning Predictive Modeling for Unconventional Reservoir Performance Utilizing Geoengineering and Completion Data: Sweet Spot Identification and Completion Design Optimization. In Proceedings of the ADIPEC, Abu Dhabi, United Arab Emirates, 31 October 2022; p. D021S062R002. [Google Scholar] [CrossRef]
- Nashed, S.; Lnu, S.; Guezei, A.; Ejehu, O.; Moghanloo, R. Downhole Camera Runs Validate the Capability of Machine Learning Models to Accurately Predict Perforation Entry Hole Diameter. Energies 2024, 17, 5558. [Google Scholar] [CrossRef]
- Halliburton; Chen, S.; Shao, W.; Halliburton; Sheng, H.; Halliburton; Kwak, H.; Aramco, S. Use of Symbolic Regression for Developing Petrophysical Interpretation Models. In Proceedings of the SPWLA 63rd Annual Symposium Transactions, Stavanger, Norway, 1 March 2022. [Google Scholar] [CrossRef]
- Abdusalamov, R.; Hillgärtner, M.; Itskov, M. Automatic Generation of Interpretable Hyperelastic Material Models by Symbolic Regression. Int. J. Numer. Methods Eng. 2023, 124, 2093–2104. [Google Scholar] [CrossRef]
- Latrach, A.; Malki, M.L.; Morales, M.; Mehana, M.; Rabiei, M. A Critical Review of Physics-Informed Machine Learning Applications in Subsurface Energy Systems. Geoenergy Sci. Eng. 2024, 239, 212938. [Google Scholar] [CrossRef]
- Khassaf, A.K.; Al-hameed, Z.M.; Al-Mohammedawi, N.R.; Al-Mudhafar, W.J.; Wood, D.A.; Abbas, M.A.; Ameur-Zaimeche, O.; Alsubaih, A.A. Physics-Informed Machine Learning for Enhanced Permeability Prediction in Heterogeneous Carbonate Reservoirs. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 28 April 2025; p. D041S049R004. [Google Scholar] [CrossRef]
- Gladchenko, E.S.; Illarionov, E.A.; Orlov, D.M.; Koroteev, D.A. Physics-Informed Neural Networks and Capacitance-Resistance Model: Fast and Accurate Oil and Water Production Forecast Using End-to-End Architecture. In Proceedings of the SPE Symposium Leveraging Artificial Intelligence to Shape the Future of the Energy Industry, Al Khobar, Saudi Arabia, 19 January 2023; p. D021S004R001. [Google Scholar] [CrossRef]
- Abdulwarith, A.; Ammar, M.; Kakadjian, S.; McLaughlin, N.; Dindoruk, B. A Hybrid Physics Augmented Predictive Model for Friction Pressure Loss in Hydraulic Fracturing Process Based on Experimental and Field Data. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 15 April 2024; p. D031S030R006. [Google Scholar] [CrossRef]
- Baki, S.; Dursun, S. Flowing Bottomhole Pressure Prediction with Machine Learning Algorithms for Horizontal Wells. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 26 September 2022; p. D021S038R004. [Google Scholar] [CrossRef]
- Sami, N.A. Application of Machine Learning Algorithms to Predict Tubing Pressure in Intermittent Gas Lift Wells. Pet. Res. 2022, 7, 246–252. [Google Scholar] [CrossRef]
- Rathnayake, S.; Rajora, A.; Firouzi, M. A Machine Learning-Based Predictive Model for Real-Time Monitoring of Flowing Bottom-Hole Pressure of Gas Wells. Fuel 2022, 317, 123524. [Google Scholar] [CrossRef]
- Ahmadi, M.A.; Chen, Z. Machine Learning Models to Predict Bottom Hole Pressure in Multi-phase Flow in Vertical Oil Production Wells. Can. J. Chem. Eng. 2019, 97, 2928–2940. [Google Scholar] [CrossRef]

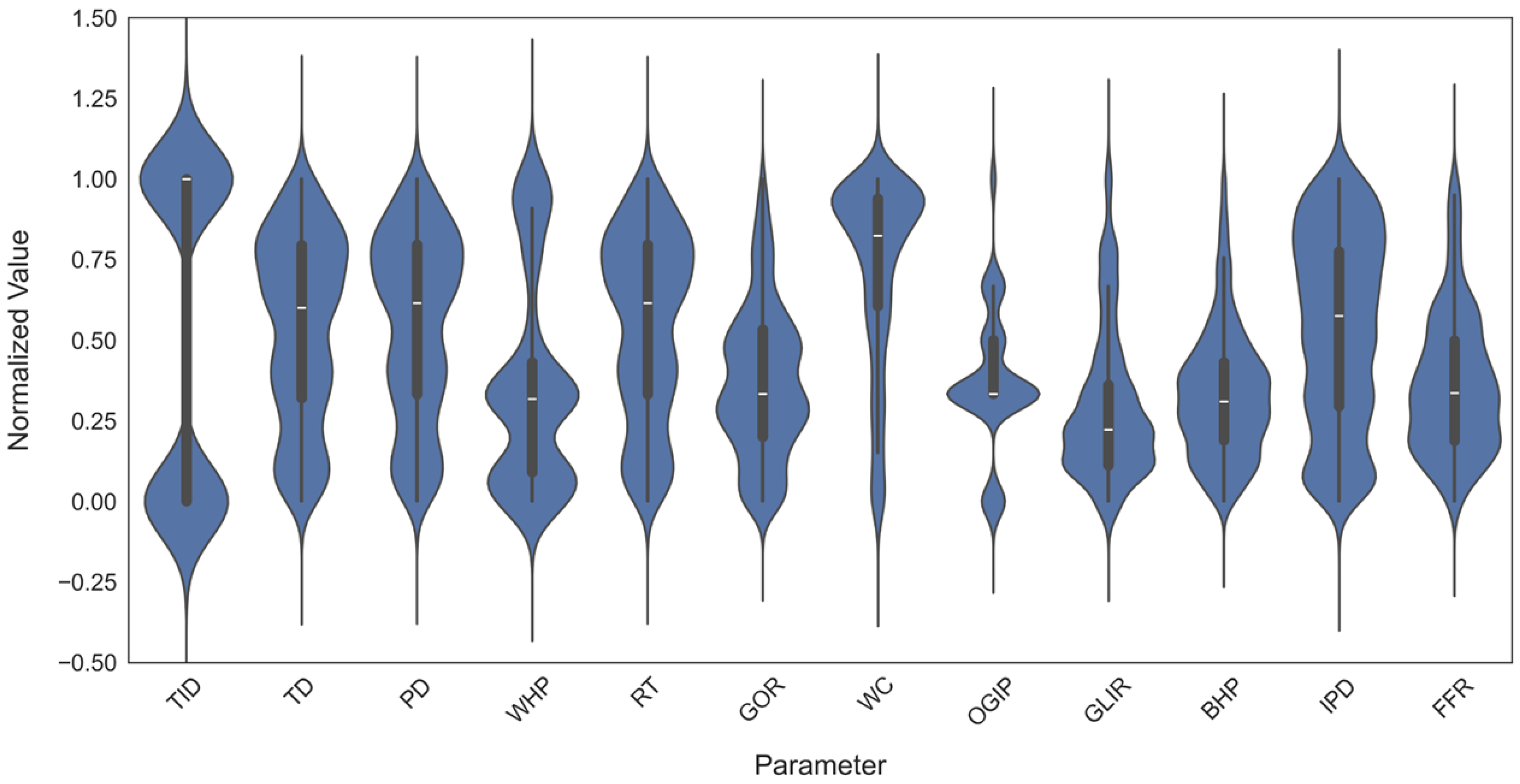
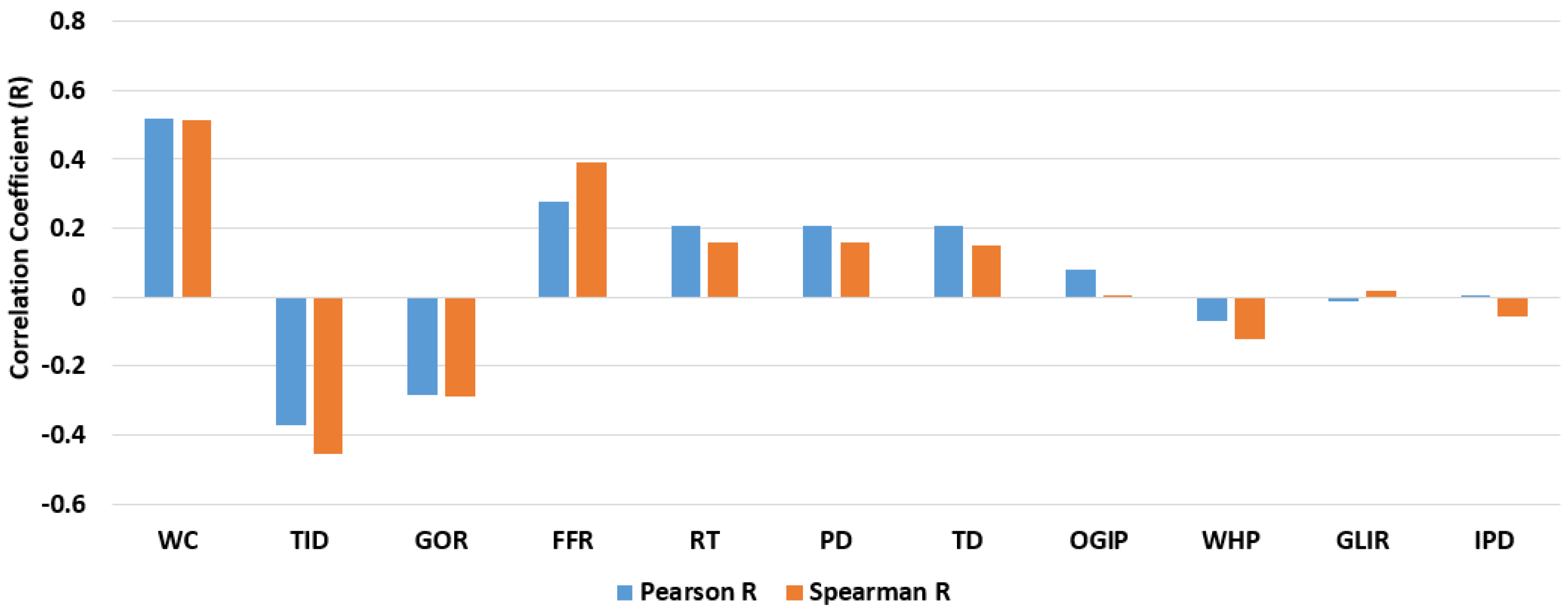
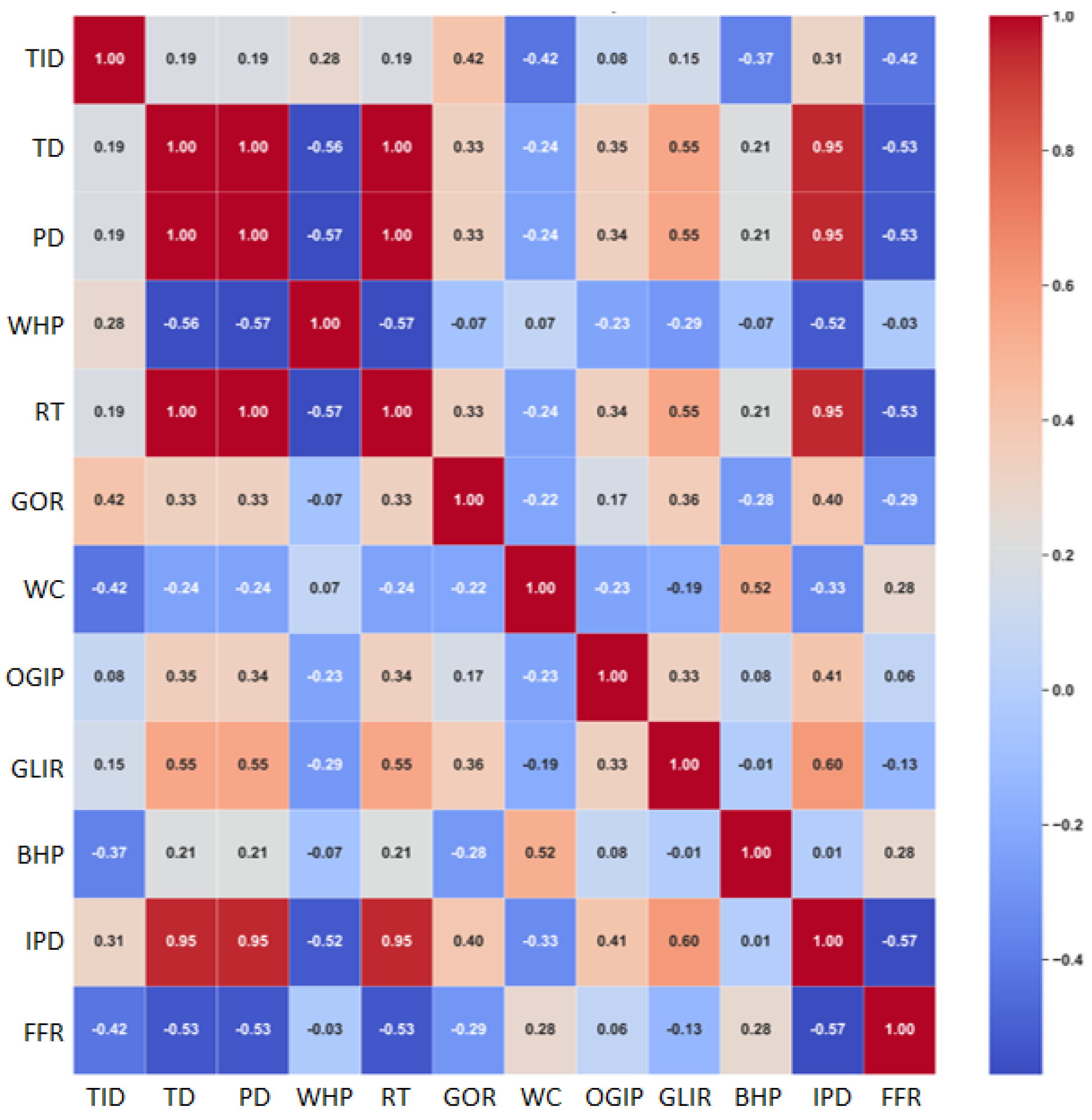
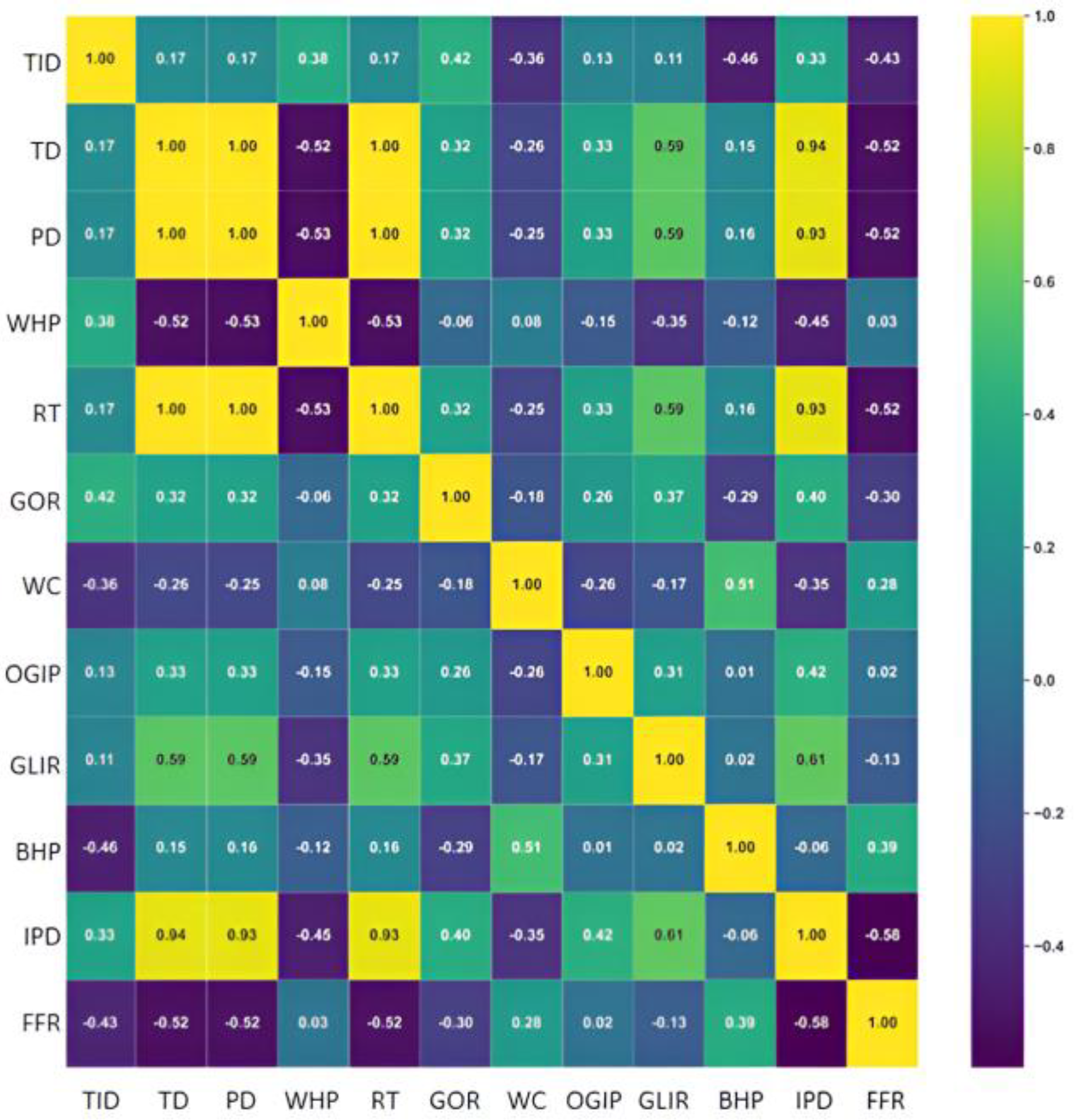
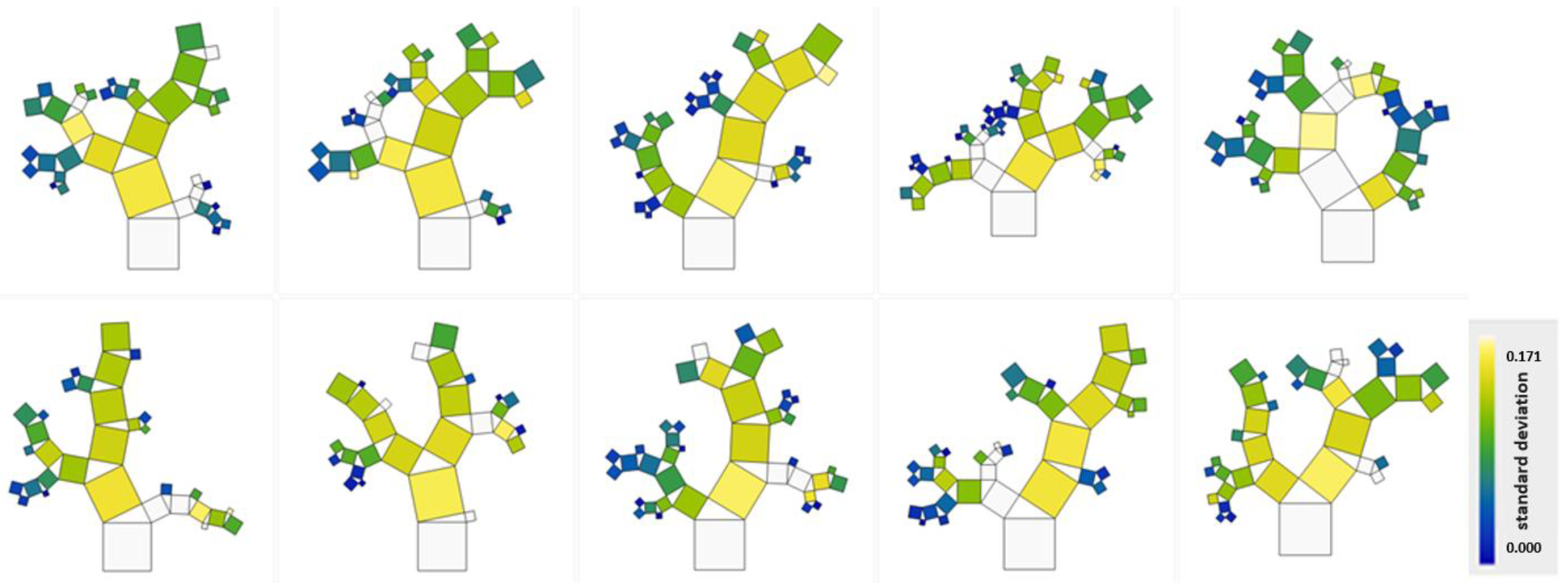
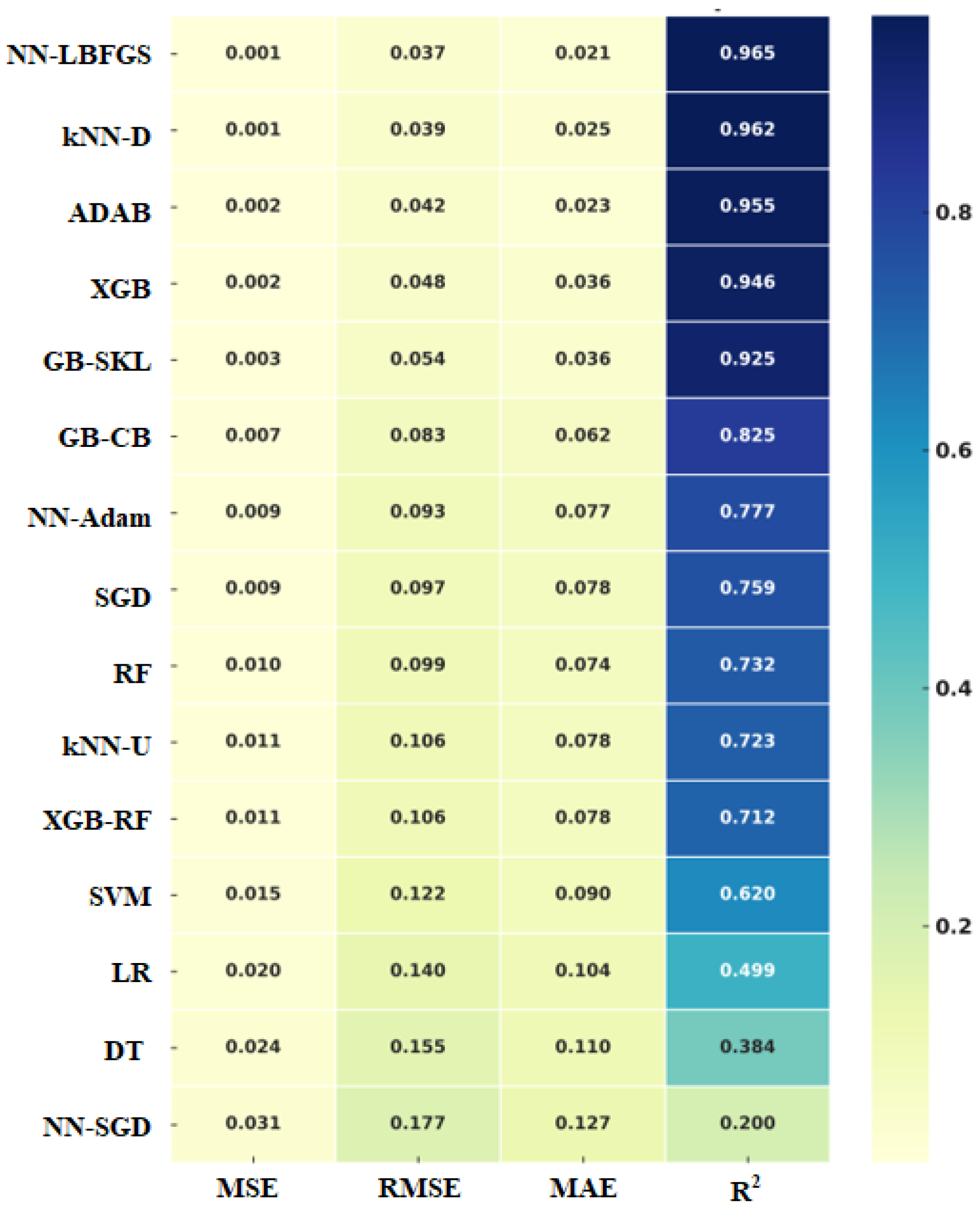
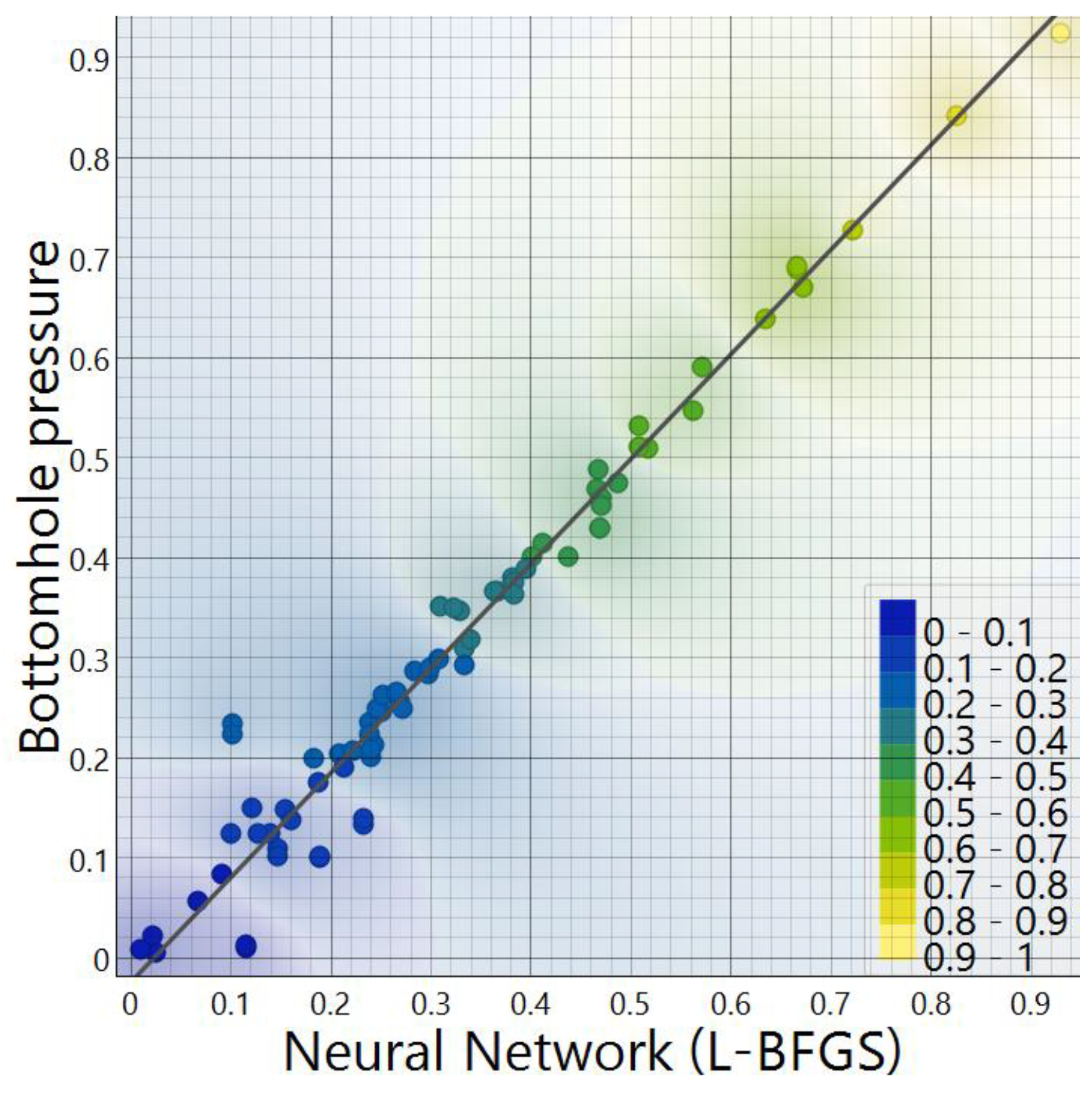
| Parameter | Units | MIN | MAX | AVG | Median |
|---|---|---|---|---|---|
| Tubing inside diameter | inches | 2.441 | 2.992 | 2.731 | 2.992 |
| Tubing depth | ft | 3002 | 10,494 | 7022.441 | 7506 |
| Perforation depth | ft | 3052 | 10,544 | 7116.322 | 7656 |
| Wellhead pressure | psi | 30 | 250 | 109.4079 | 100 |
| Reservoir temperature | f | 110.52 | 185.44 | 151.1632 | 156.56 |
| Gas–oil ratio | scf/stb | 100 | 1600 | 654.9605 | 600 |
| Water cut | % | 0 | 99 | 71.21053 | 81.5 |
| Operating gas injection pressure | psi | 800 | 1100 | 912.5 | 900 |
| Gas lift injection rate | mmscf/d | 0.3 | 1.2 | 0.566447 | 0.5 |
| Bottomhole pressure | psi | 415 | 1669 | 830.2862 | 803.5 |
| Injection point depth | ft | 2304 | 9390 | 6099.862 | 6379.5 |
| Fluid flow rate | stb/d | 22 | 1963 | 730.2566 | 676 |
| Model | Model Parameters |
|---|---|
| GB (scikit-learn) |
|
| EGB (xgboost) |
|
| EGB-RF (xgboost) |
|
| GB (catboost) |
|
| AdaBoost |
|
| RF |
|
| SVMs |
|
| DT |
|
| kNN (distance) |
|
| KNN (uniform) |
|
| LR |
|
| NN (L-BFGS) |
|
| NN (Adam) |
|
| NN (SGD) |
|
| SGD |
|
| Model | Model Parameters |
|---|---|
| GP-SR |
|
| Complexity | Loss | Equation |
|---|---|---|
| 1 | 0.040771 | 0.3271417 |
| 3 | 0.028801 | WC/2.23883 |
| 4 | 0.028639 | Sin (WC) × 0.51090336 |
| 5 | 0.024993 | |
| 6 | 0.024519 | WC/(cos (PD)/0.36379465) |
| 7 | 0.019756 | WC × (TD − IPD + 0.42867288) |
| 8 | 0.016829 | PD − ((WC × −0.37555227) + sin (IPD)) |
| 9 | 0.015375 | (OGIP + WC) × (0.2983757 − (IPD − TD)) |
| 11 | 0.014491 | (WC + OGIP) × (0.24029268 − (IPD − (PD × 1.095866))) |
| 13 | 0.013551 | ((((FFR × 0.2097214) + 0.19042374) × (TD + WC)) + TD) − IPD |
| 14 | 0.012628 | (TD − ((FFR × WC) × −0.55305517)) − (cos (WHP) × (IPD/1.3678912)) |
| 15 | 0.010488 | |
| 16 | 0.010348 | (((WC + TD) × ((FFR × 0.2841561) + 0.13601056)) + TD) − (IPD × cos (WHP)) |
| 17 | 0.009773 | |
| 18 | 0.00901 | |
| 19 | 0.008182 |
| Parameter | Units | MIN | MAX | AVG | Median |
|---|---|---|---|---|---|
| Tubing inside diameter | inches | 2.441 | 2.992 | 2.7165 | 2.7165 |
| Tubing depth | ft | 3200 | 10,318 | 6598.633 | 6220 |
| Perforation depth | ft | 3250 | 10,368 | 6686.3 | 6343 |
| Wellhead pressure | psi | 30 | 250 | 114.3333 | 100 |
| Reservoir temperature | f | 112.5 | 183.68 | 146.863 | 143.43 |
| Gas–oil ratio | scf/stb | 100 | 1500 | 582.5 | 500 |
| Water cut | % | 0 | 99 | 75.66667 | 90 |
| Operating gas injection pressure | psi | 800 | 1100 | 905 | 900 |
| Gas lift injection rate | mmscf/d | 0.4 | 0.9 | 0.52 | 0.5 |
| Bottomhole pressure | psi | 448 | 1661 | 800.2 | 745.5 |
| Injection point depth | ft | 2697 | 9253 | 5737.433 | 4799 |
| Fluid flow rate | stb/d | 50 | 1794 | 780.3667 | 734.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nashed, S.; Moghanloo, R. Hybrid Symbolic Regression and Machine Learning Approaches for Modeling Gas Lift Well Performance. Fluids 2025, 10, 161. https://doi.org/10.3390/fluids10070161
Nashed S, Moghanloo R. Hybrid Symbolic Regression and Machine Learning Approaches for Modeling Gas Lift Well Performance. Fluids. 2025; 10(7):161. https://doi.org/10.3390/fluids10070161
Chicago/Turabian StyleNashed, Samuel, and Rouzbeh Moghanloo. 2025. "Hybrid Symbolic Regression and Machine Learning Approaches for Modeling Gas Lift Well Performance" Fluids 10, no. 7: 161. https://doi.org/10.3390/fluids10070161
APA StyleNashed, S., & Moghanloo, R. (2025). Hybrid Symbolic Regression and Machine Learning Approaches for Modeling Gas Lift Well Performance. Fluids, 10(7), 161. https://doi.org/10.3390/fluids10070161









