Evaluation of Flow-Induced Shear in a Porous Microfluidic Slide: CFD Analysis and Experimental Investigation
Abstract
1. Introduction
2. Mathematical Model and Methods
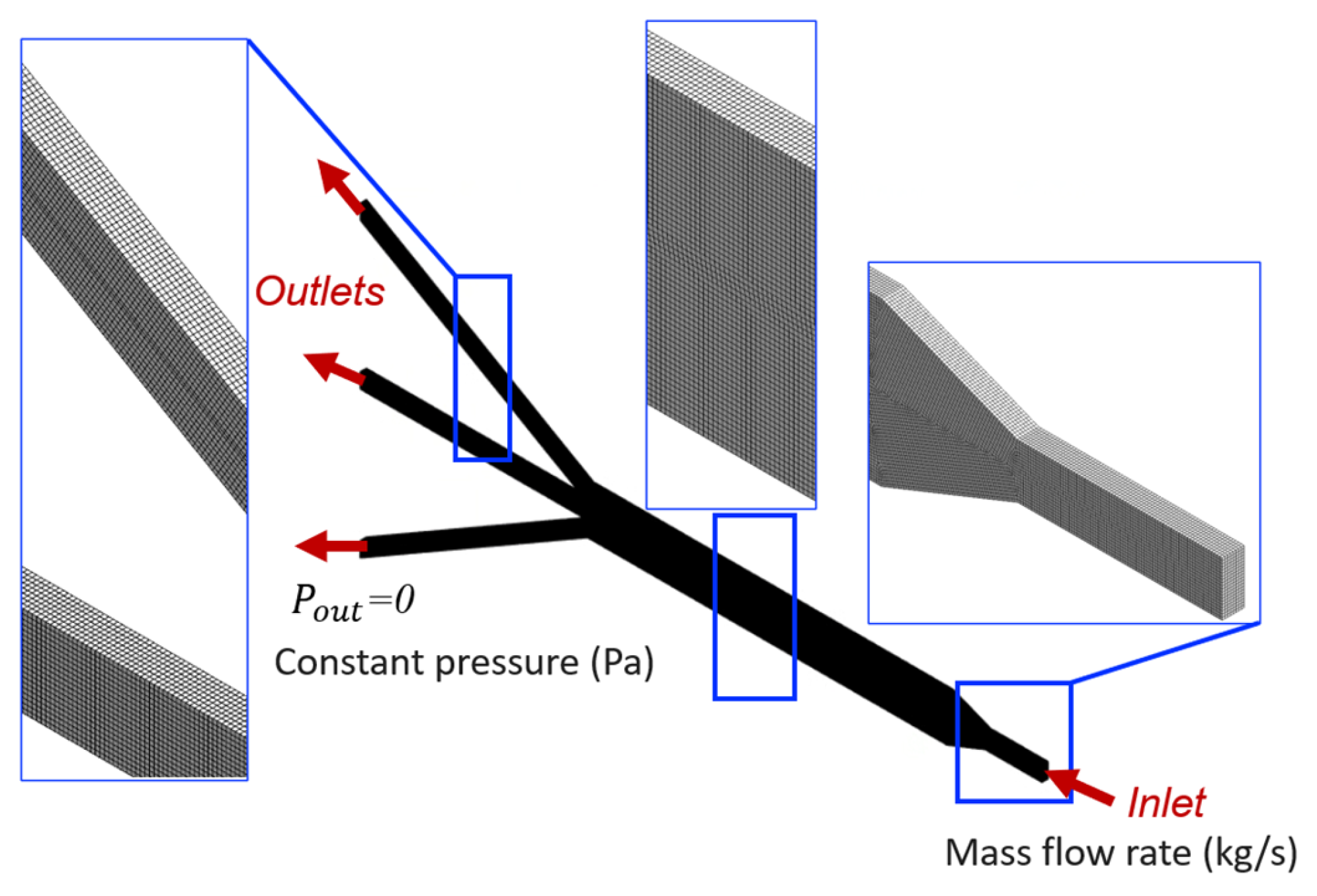
2.1. Problem Description
| Domain | Parameter | Value |
|---|---|---|
| Slide channel geometry (µ-Slide III 3in1) | Outer width | 25.5 mm |
| Outer length | 75.5 mm | |
| Channel length | 45 mm | |
| Total channel volume | 60 µL | |
| Channel height | 0.4 mm | |
| Width of channels thin/thick | 1 mm/3 mm | |
| Culture medium fluid (water) | Density | 998 kg/m3 |
| Dynamic viscosity | 0.001 kg/m.s | |
| Porous matrix (human ECM) | Permeability | 1 × 10−13 m2 (baseline) Refer to Table 2 for range of variation |
| Porosity | 90% | |
| Boundary conditions | Fluid inlet flow rate | 0.01 mL/min (baseline) equal to 1.67 × 10−7 kg/s |
| Fluid outlet pressure | 0 Pa |
| Case 1 (Non-Porous) | Case 2 | Case 3 | Case 4 | Case 5 (Baseline) | Case 6 | |
|---|---|---|---|---|---|---|
| (m2) | (fluid only) | 1 × 10−7 | 1 × 10−9 | 1 × 10−12 | 1 × 10−13 | 1 × 10−15 |
2.2. Flow in µ-Slide Channel: Governing Equations and Modeling Details
2.3. CFD Numerical Simulation Setup
3. Results
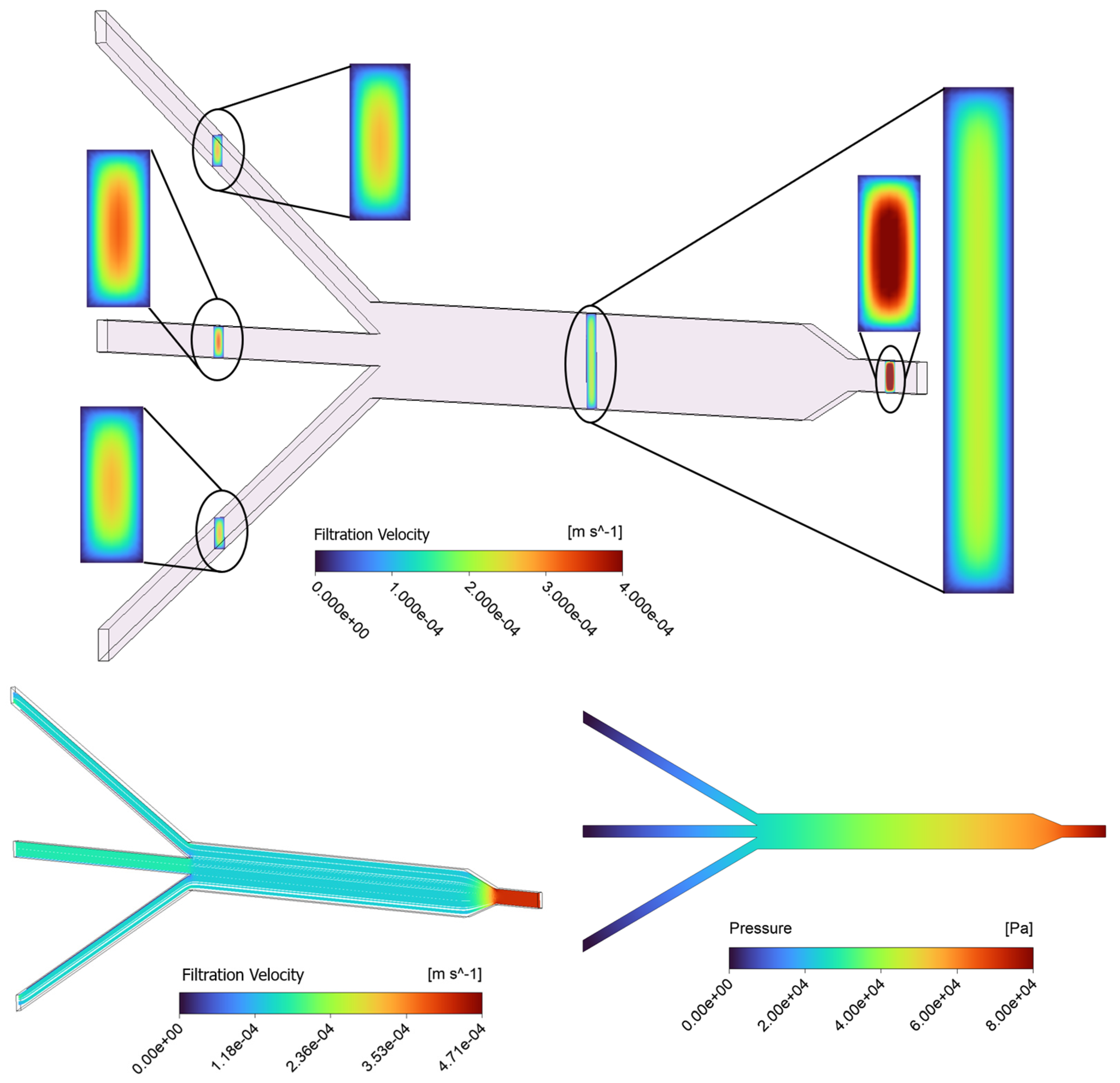
3.1. Fluid Dynamics Within µ-Slide: CFD Measurement of Velocity and Shear Stress
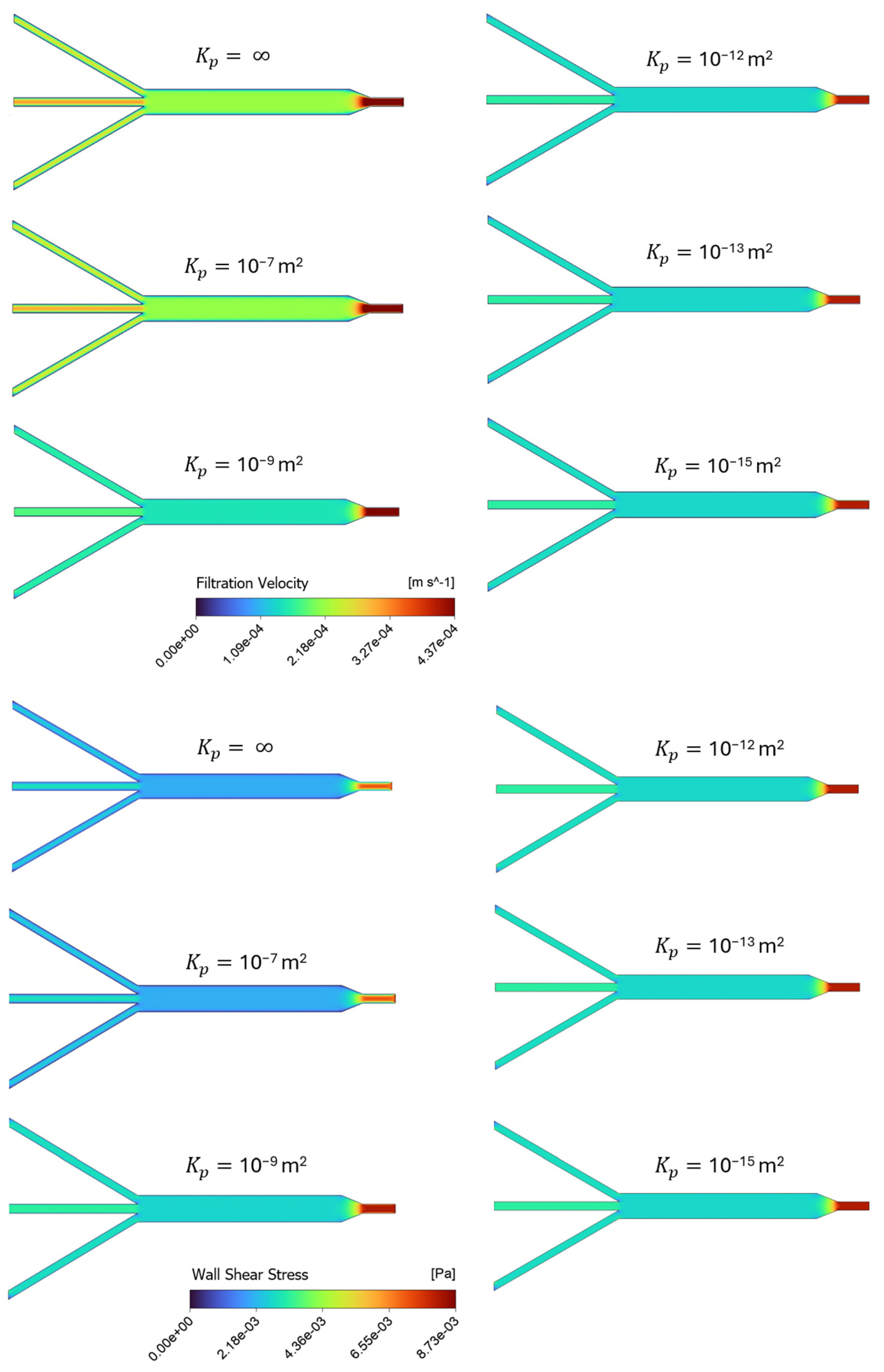
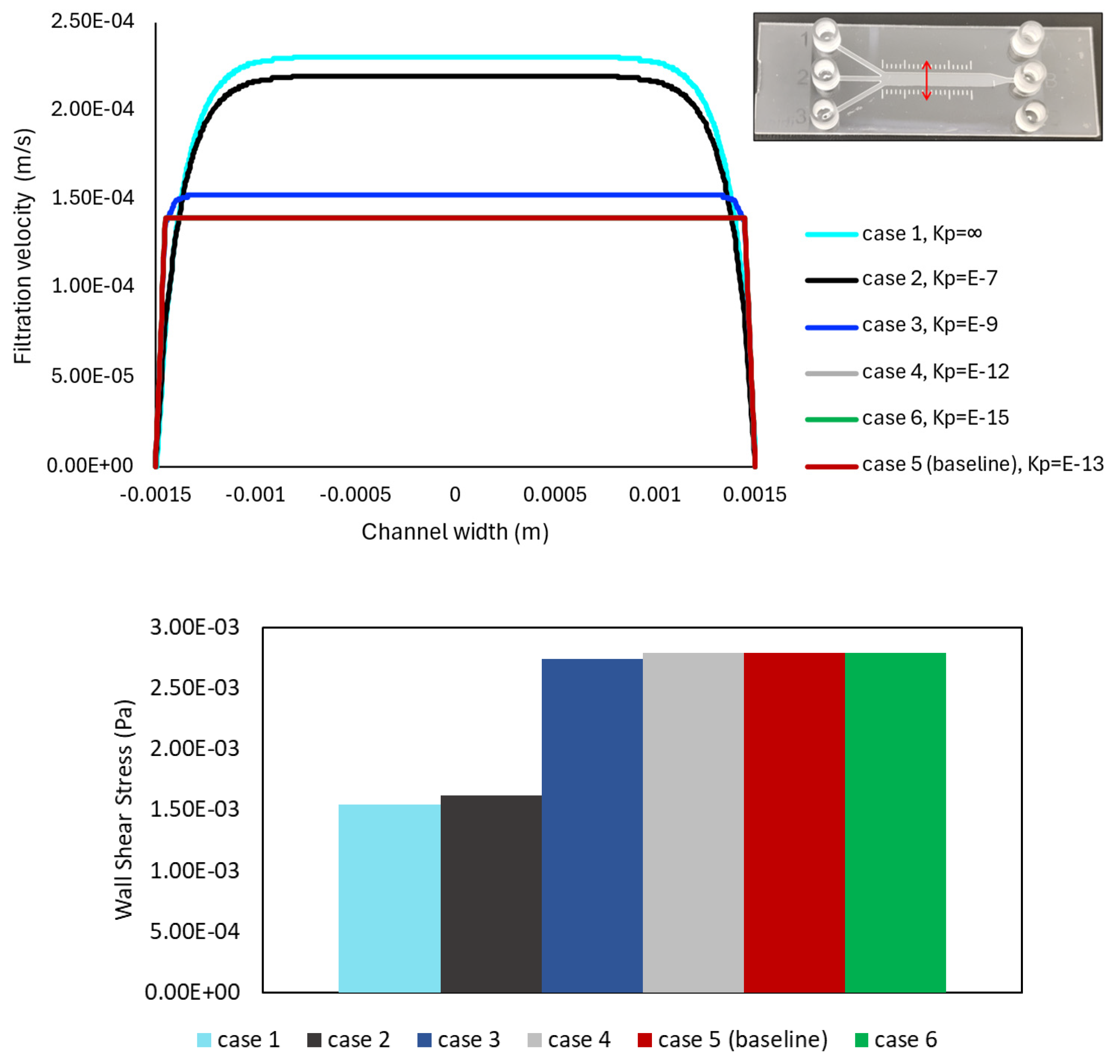
3.1.1. Effect of Matrix Permeability: Filtration Flow and Shear Stress Analysis
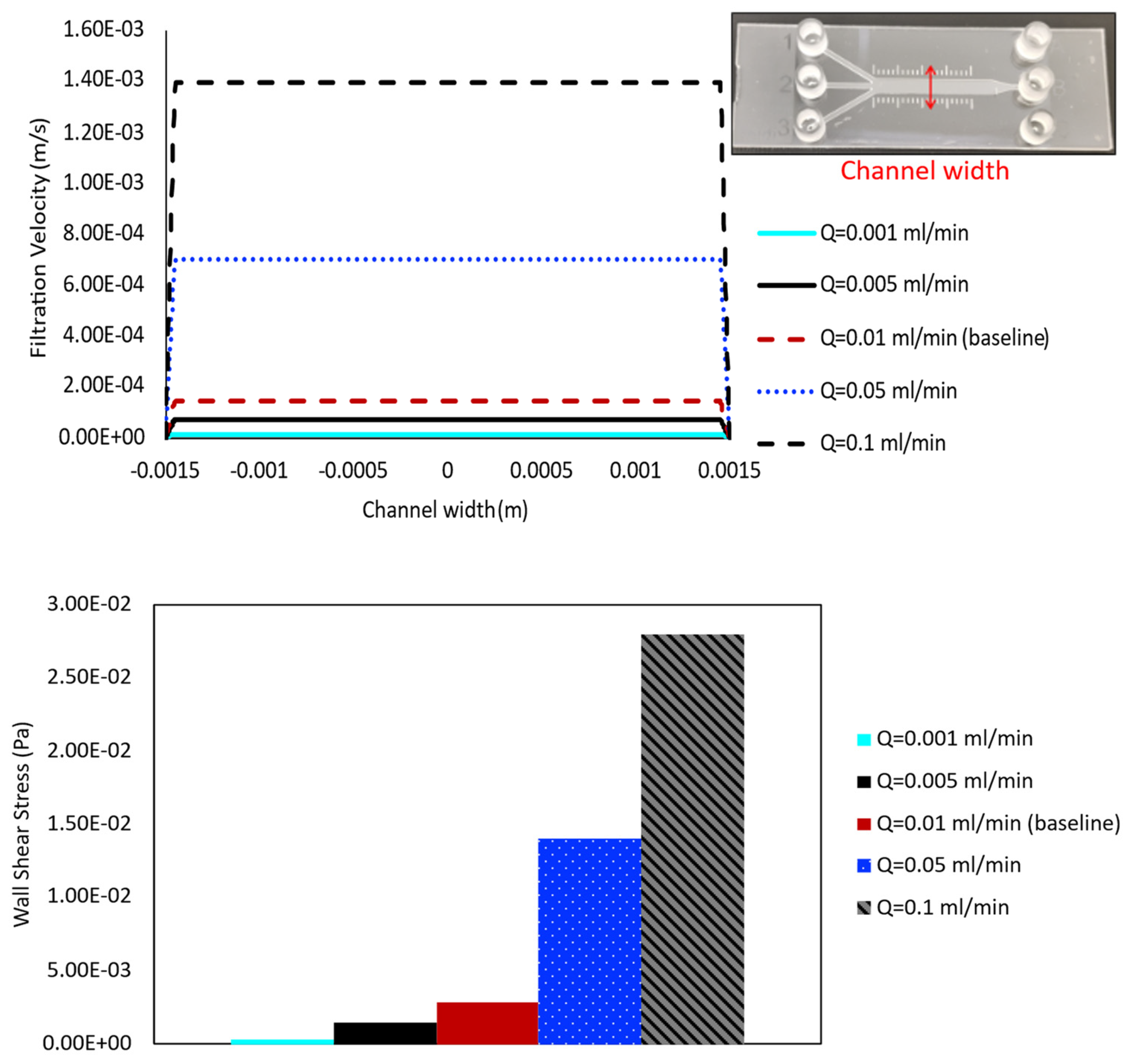
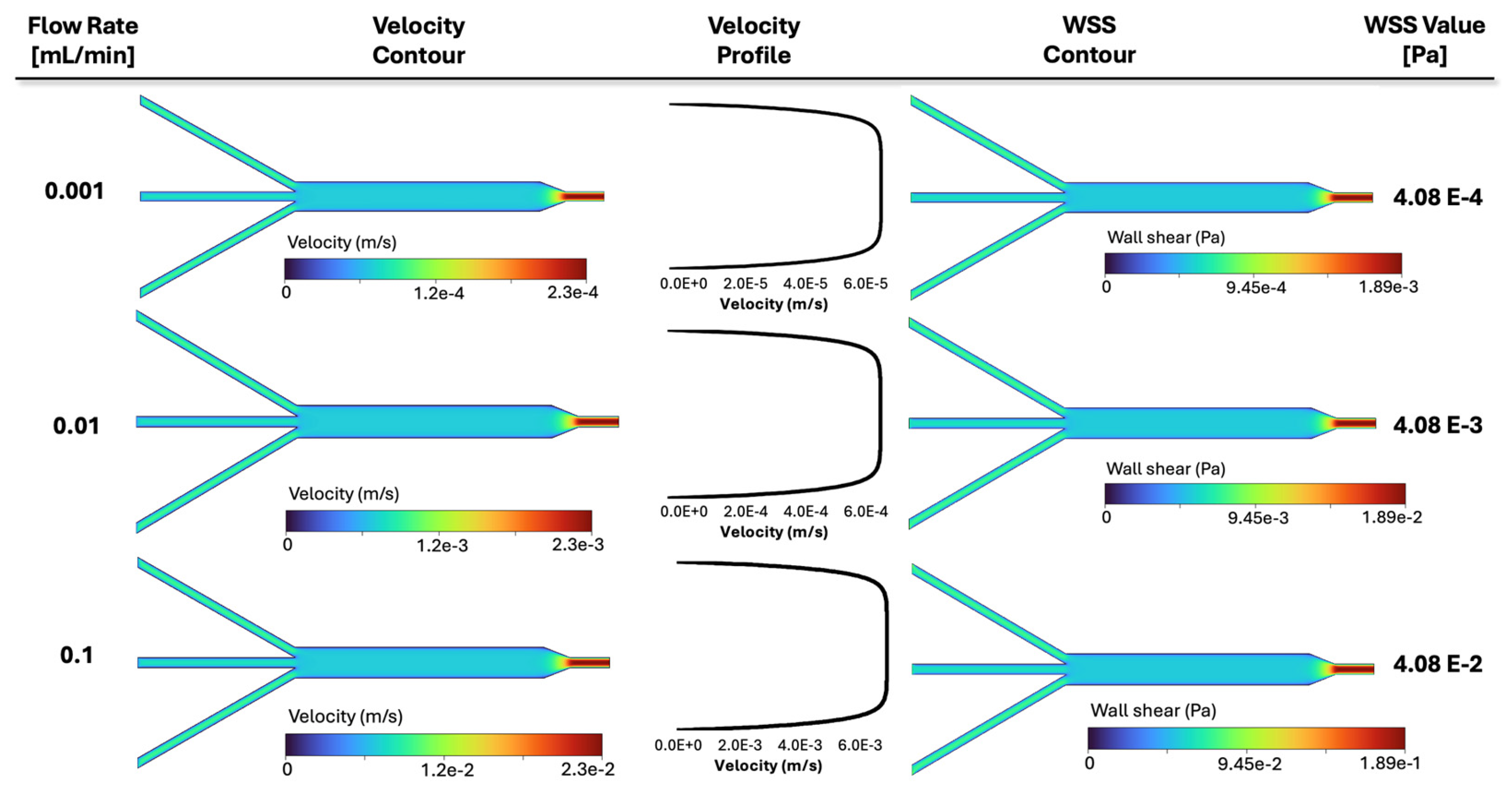
3.1.2. Effect of Perfusion Flow Rate: Filtration Flow and Shear Stress Analysis
3.2. Measuring Filtration Velocity In Vitro
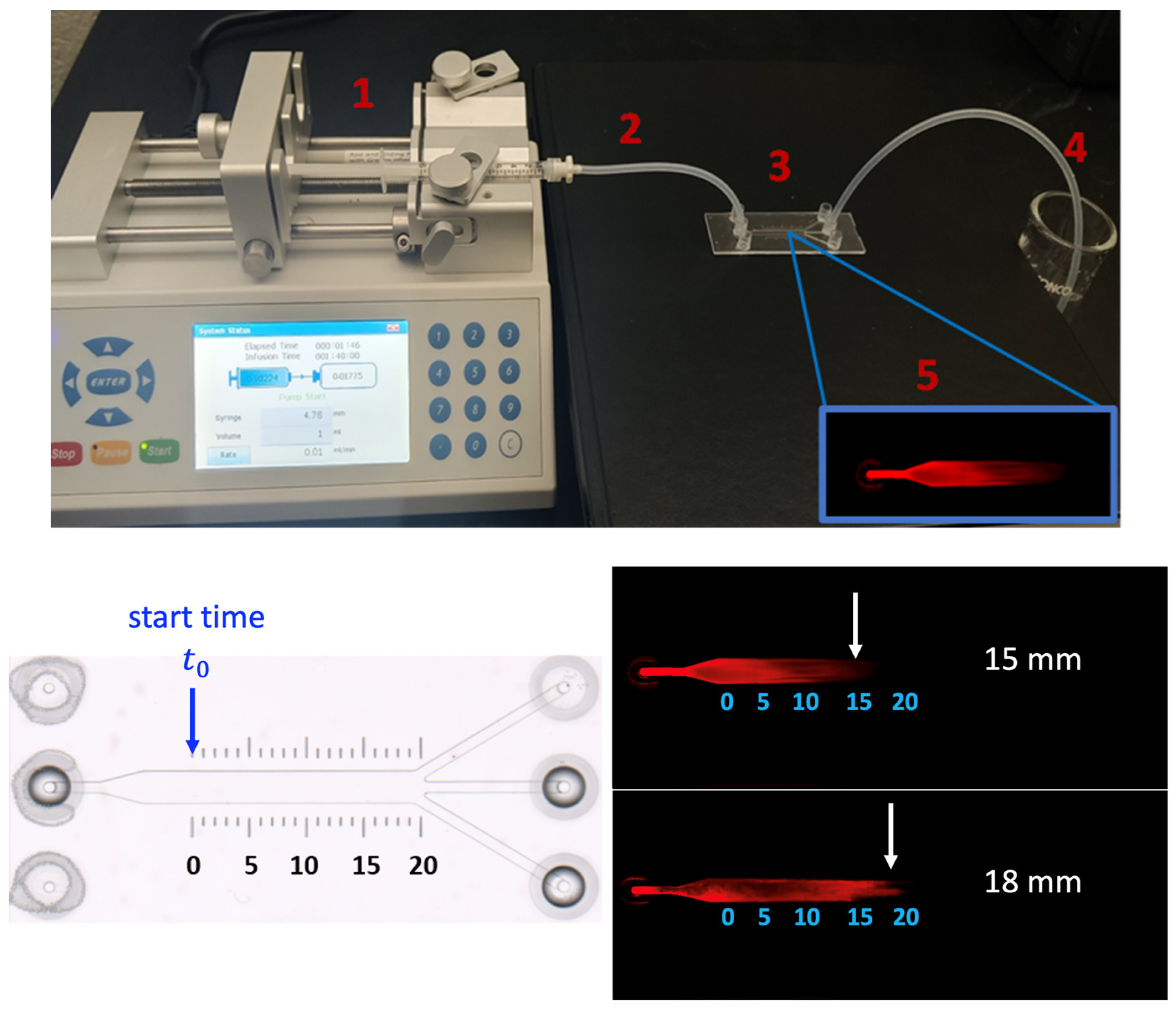
3.2.1. Preparation Process and Details
3.2.2. Experimental Observation and Imaging: Velocity Measurement
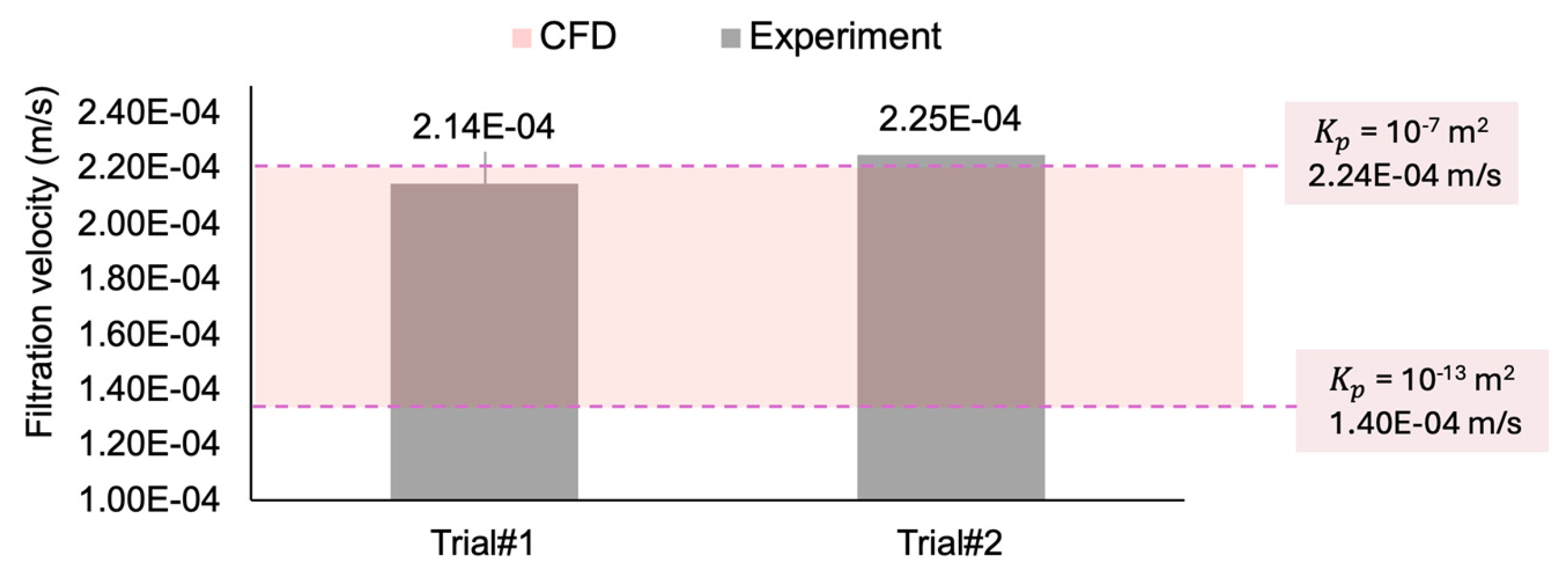
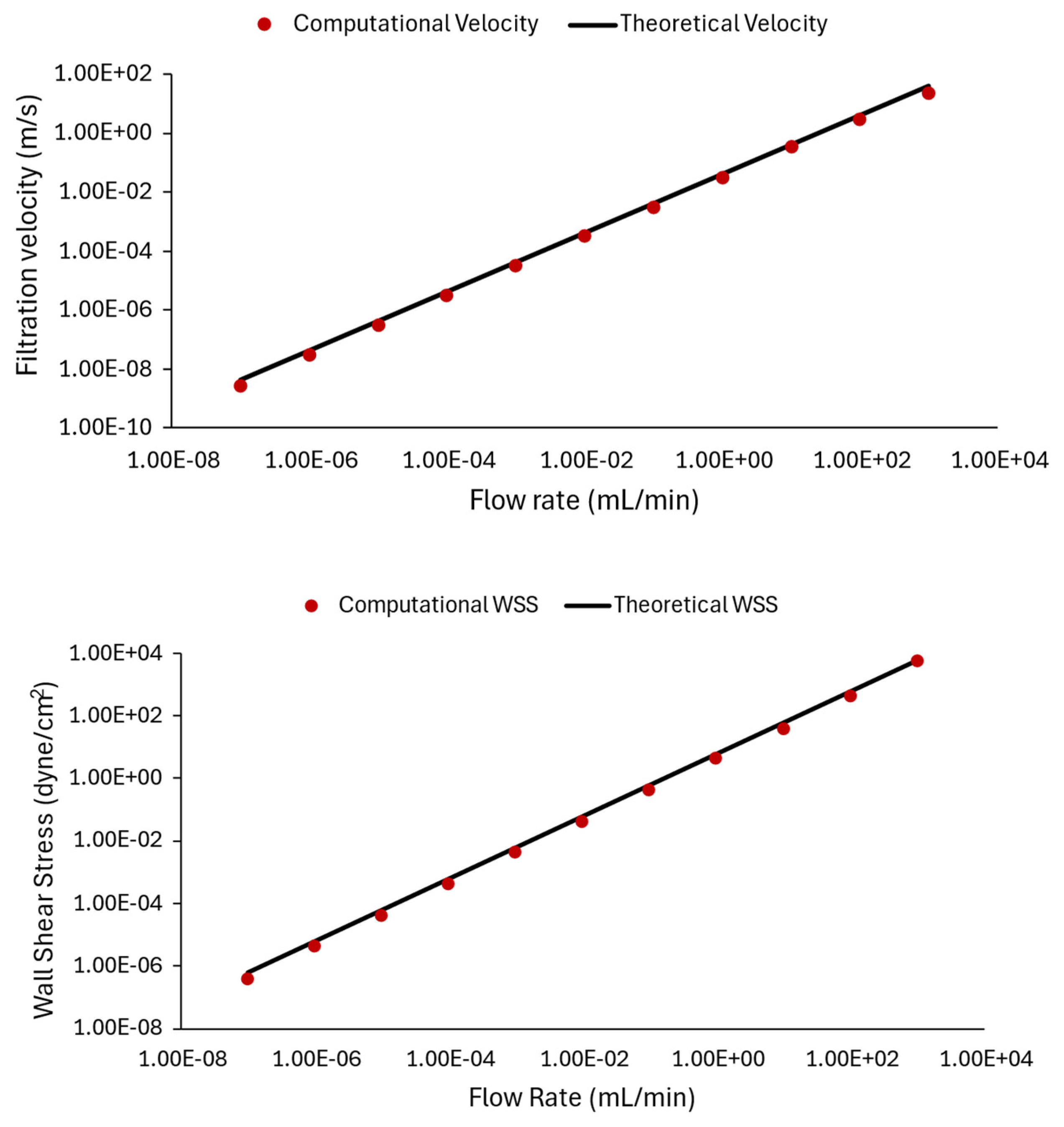
3.3. Validation with Theoretical Calculations
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gimondi, S.; Ferreira, H.; Reis, R.L.; Neves, N.M. Microfluidic devices: A tool for nanoparticle synthesis and performance evaluation. ACS Nano 2023, 17, 14205–14228. [Google Scholar] [CrossRef] [PubMed]
- Shou, Y.; Johnson, S.C.; Quek, Y.J.; Li, X.; Tay, A. Integrative lymph node-mimicking models created with biomaterials and computational tools to study the immune system. Mater. Today Bio 2022, 14, 100269. [Google Scholar] [CrossRef] [PubMed]
- Saorin, G.; Caligiuri, I.; Rizzolio, F. Microfluidic organoids-on-a-chip: The future of human models. In Seminars in Cell & Developmental Biology; Elsevier: Amsterdam, The Netherlands, 2023. [Google Scholar]
- Tehranirokh, M.; Kouzani, A.Z.; Francis, P.S.; Kanwar, J.R. Microfluidic devices for cell cultivation and proliferation. Biomicrofluidics 2013, 7, 051502. [Google Scholar] [CrossRef] [PubMed]
- Peng, J.; Fang, C.; Ren, S.; Pan, J.; Jia, Y.; Shu, Z.; Gao, D. Development of a microfluidic device with precise on-chip temperature control by integrated cooling and heating components for single cell-based analysis. Int. J. Heat Mass Transf. 2019, 130, 660–667. [Google Scholar] [CrossRef]
- Yu, F.; Hunziker, W.; Choudhury, D. Engineering microfluidic organoid-on-a-chip platforms. Micromachines 2019, 10, 165. [Google Scholar] [CrossRef]
- Kanabekova, P.; Kadyrova, A.; Kulsharova, G. Microfluidic Organ-on-a-Chip Devices for Liver Disease Modeling In Vitro. Micromachines 2022, 13, 428. [Google Scholar] [CrossRef]
- Datta, N.; Pham, Q.P.; Sharma, U.; Sikavitsas, V.I.; Jansen, J.A.; Mikos, A.G. In vitro generated extracellular matrix and fluid shear stress synergistically enhance 3D osteoblastic differentiation. Proc. Natl. Acad. Sci. USA 2006, 103, 2488–2493. [Google Scholar] [CrossRef]
- Ali, D.; Ozalp, M.; Blanquer, S.B.; Onel, S. Permeability and fluid flow-induced wall shear stress in bone scaffolds with TPMS and lattice architectures: A CFD analysis. Eur. J. Mech.-B/Fluids 2020, 79, 376–385. [Google Scholar] [CrossRef]
- Esch, M.B.; Post, D.J.; Shuler, M.L.; Stokol, T. Characterization of in vitro endothelial linings grown within microfluidic channels. Tissue Eng. Part A 2011, 17, 2965–2971. [Google Scholar] [CrossRef]
- Huang, M.; Fan, S.; Xing, W.; Liu, C. Microfluidic cell culture system studies and computational fluid dynamics. Math. Comput. Model. 2010, 52, 2036–2042. [Google Scholar] [CrossRef]
- Lindner, M.; Laporte, A.; Block, S.; Elomaa, L.; Weinhart, M. Physiological Shear Stress Enhances Differentiation, Mucus-Formation and Structural 3D Organization of Intestinal Epithelial Cells In Vitro. Cells 2021, 10, 2062. [Google Scholar] [CrossRef] [PubMed]
- Rosa, P.M.; Gopalakrishnan, N.; Ibrahim, H.; Haug, M.; Halaas, Ø. The intercell dynamics of T cells and dendritic cells in a lymph node-on-a-chip flow device. Lab Chip 2016, 16, 3728–3740. [Google Scholar] [CrossRef] [PubMed]
- Delon, L.C.; Guo, Z.; Kashani, M.N.; Yang, C.T.; Prestidge, C.; Thierry, B. Hele Shaw microfluidic device: A new tool for systematic investigation into the effect of the fluid shear stress for organs-on-chips. MethodsX 2020, 7, 100980. [Google Scholar] [CrossRef] [PubMed]
- Bakuova, N.; Toktarkan, S.; Dyussembinov, D.; Azhibek, D.; Rakhymzhanov, A.; Kostas, K.; Kulsharova, G. Design, Simulation, and Evaluation of Polymer-Based Microfluidic Devices via Computational Fluid Dynamics and Cell Culture “On-Chip”. Biosensors 2023, 13, 754. [Google Scholar] [CrossRef]
- Pisapia, F.; Balachandran, W.; Rasekh, M. Organ-on-a-Chip: Design and Simulation of Various Microfluidic Channel Geometries for the Influence of Fluid Dynamic Parameters. Appl. Sci. 2022, 12, 3829. [Google Scholar] [CrossRef]
- Bissoyi, A.; Bit, A.; Singh, B.K.; Singh, A.K.; Patra, P.K. Enhanced cryopreservation of MSCs in microfluidic bioreactor by regulated shear flow. Sci. Rep. 2016, 6, 35416. [Google Scholar] [CrossRef]
- Bahmaee, H.; Owen, R.; Boyle, L.; Perrault, C.M.; Garcia-Granada, A.A.; Reilly, G.C.; Claeyssens, F. Design and Evaluation of an Osteogenesis-on-a-Chip Microfluidic Device Incorporating 3D Cell Culture. Front. Bioeng. Biotechnol. 2020, 8, 557111. [Google Scholar] [CrossRef]
- Bedding-Tyrrell, M.; Khatri, N.; Nithiarasu, P.; Sandnes, B.; Egan, P.; Zhao, F. Data-driven calculation of porous geometry-dependent permeability and fluid-induced wall shear stress within tissue engineering scaffolds. J. Eng. Des. 2024, 1–15. [Google Scholar] [CrossRef]
- Iannetti, L.; D’Urso, G.; Conoscenti, G.; Cutrì, E.; Tuan, R.S.; Raimondi, M.T.; Zunino, P. Distributed and Lumped Parameter Models for the Characterization of High Throughput Bioreactors. PLoS ONE 2016, 11, e0162774. [Google Scholar] [CrossRef]
- Song, M.; Liu, Y.; Hui, L. Preparation and characterization of acellular adipose tissue matrix using a combination of physical and chemical treatments. Mol. Med. Rep. 2018, 17, 138–146. [Google Scholar] [CrossRef]
- Fischer, T.; Hayn, A.; Mierke, C.T. Fast and reliable advanced two-step pore-size analysis of biomimetic 3D extracellular matrix scaffolds. Sci. Rep. 2019, 9, 8352. [Google Scholar] [CrossRef] [PubMed]
- Poon, C. Measuring the density and viscosity of culture media for optimized computational fluid dynamics analysis of in vitro devices. J. Mech. Behav. Biomed. Mater. 2022, 126, 105024. [Google Scholar] [CrossRef] [PubMed]
- Poulsen, M.S.; Rytting, E.; Mose, T.; Knudsen, L.E. Modeling placental transport: Correlation of in vitro BeWo cell permeability and ex vivo human placental perfusion. Toxicol. Vitr. 2009, 23, 1380–1386. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Yuan, T.; Panaitescu, C.; Li, R.; Wu, K.; Zhou, Y.; Zhan, W. Exploring tissue permeability of brain tumours in different grades: Insights from pore-scale fluid dynamics analysis. Acta Biomater. 2024, 190, 398–409. [Google Scholar] [CrossRef]
- Fernandez, M.; Vink, J.; Yoshida, K.; Wapner, R.; Myers, K.M. Direct measurement of the permeability of human cervical tissue. J. Biomech. Eng. 2013, 135, 021024. [Google Scholar] [CrossRef]
- Pilia, M.; Guda, T.; Pollot, B.E.; Aguero, V.; Appleford, M.R. Local microarchitecture affects mechanical properties of deposited extracellular matrix for osteonal regeneration. Mater. Sci. Eng. C 2014, 35, 122–133. [Google Scholar] [CrossRef]
- García-Gareta, E.; Calderón-Villalba, A.; Alamán-Díez, P.; Costa, C.G.; Guerrero, P.E.; Mur, C.; García-Aznar, J.M. Physico-chemical characterization of the tumour microenvironment of pancreatic ductal adenocarcinoma. Eur. J. Cell Biol. 2024, 103, 151396. [Google Scholar] [CrossRef]
- Salavati, H.; Pullens, P.; Debbaut, C.; Ceelen, W. Hydraulic conductivity of human cancer tissue: A hybrid study. Bioeng. Transl. Med. 2024, 9, e10617. [Google Scholar] [CrossRef]
- Armen, J.M.; Schueller, N.R.; Velankar, K.Y.; Abraham, N.; Palchesko, R.N.; Fan, Y.; Gawalt, E.S. Chemically-Induced Cross-Linking of Peptidic Fibrils for Scaffolding Polymeric Particles and Macrophages. Macromol. Biosci. 2021, 21, 2000350. [Google Scholar] [CrossRef]
- Li, N.; Sui, Z.; Liu, Y.; Wang, D.; Ge, G.; Yang, L. A fast screening model for drug permeability assessment based on native small intestinal extracellular matrix. RSC Adv. 2018, 8, 34514–34524. [Google Scholar] [CrossRef]
- Patrawalla, N.Y.; Kajave, N.S.; Albanna, M.Z.; Kishore, V. Collagen and beyond: A comprehensive comparison of human ECM properties derived from various tissue sources for regenerative medicine applications. J. Funct. Biomater. 2023, 14, 363. [Google Scholar] [CrossRef] [PubMed]
- Mano, T.; Grutman, T.; Ilovitsh, T. Versatile ultrasound-compatible microfluidic platform for in vitro microvasculature flow research and imaging optimization. ACS Omega 2023, 8, 47667–47677. [Google Scholar] [CrossRef]
- Kamrava, S.; Sahimi, M.; Tahmasebi, P. Simulating fluid flow in complex porous materials by integrating the governing equations with deep-layered machines. NPJ Comput. Mater. 2021, 7, 127. [Google Scholar] [CrossRef]
- ibidi GmbH Application Note 11: Shear Stress and Shear Rates for ibidi μ-Slides Based on Numerical Calculations. 2022. Version 6.1. Available online: https://ibidi.com/img/cms/downloads/an/AN11_Shear_stress.pdf (accessed on 14 March 2022).
- Zakerzadeh, R.; McCollum, I.; Neves, M. Coupled processes of tissue oxygenation and fluid flow in biphasic vocal folds. Int. J. Heat Mass Transf. 2025, 238, 126494. [Google Scholar] [CrossRef]
- McCollum, I.; Badr, D.; Throop, A.; Zakerzadeh, R. Biotransport in human phonation: Porous vocal fold tissue and fluid–structure interaction. Phys. Fluids 2023, 35, 121909. [Google Scholar] [CrossRef]
- Throop, A.; Badr, D.; Durka, M.; Bukač, M.; Zakerzadeh, R. Analyzing the Effects of Multi-Layered Porous Intraluminal Thrombus on Oxygen Flow in Abdominal Aortic Aneurysms. Oxygen 2022, 2, 518–536. [Google Scholar] [CrossRef]
- Zakerzadeh, R.; Cupac, T.; Durka, M. Oxygen transport in a permeable model of abdominal aortic aneurysm. Comput. Methods Biomech. Biomed. Eng. 2020, 24, 215–229. [Google Scholar] [CrossRef]
- Green, J.V.; Kniazeva, T.; Abedi, M.; Sokhey, D.S.; Taslim, M.E.; Murthy, S.K. Effect of channel geometry on cell adhesion in microfluidic devices. Lab Chip 2009, 9, 677–685. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Neves, M.; Aparnasai Reddy, G.; Niyingenera, A.; Delaney, N.; Meng, W.S.; Zakerzadeh, R. Evaluation of Flow-Induced Shear in a Porous Microfluidic Slide: CFD Analysis and Experimental Investigation. Fluids 2025, 10, 160. https://doi.org/10.3390/fluids10060160
Neves M, Aparnasai Reddy G, Niyingenera A, Delaney N, Meng WS, Zakerzadeh R. Evaluation of Flow-Induced Shear in a Porous Microfluidic Slide: CFD Analysis and Experimental Investigation. Fluids. 2025; 10(6):160. https://doi.org/10.3390/fluids10060160
Chicago/Turabian StyleNeves, Manoela, Gayathri Aparnasai Reddy, Anitha Niyingenera, Norah Delaney, Wilson S. Meng, and Rana Zakerzadeh. 2025. "Evaluation of Flow-Induced Shear in a Porous Microfluidic Slide: CFD Analysis and Experimental Investigation" Fluids 10, no. 6: 160. https://doi.org/10.3390/fluids10060160
APA StyleNeves, M., Aparnasai Reddy, G., Niyingenera, A., Delaney, N., Meng, W. S., & Zakerzadeh, R. (2025). Evaluation of Flow-Induced Shear in a Porous Microfluidic Slide: CFD Analysis and Experimental Investigation. Fluids, 10(6), 160. https://doi.org/10.3390/fluids10060160








