Influence of an Air Slit in Dust Shields on Accumulation of Dust over PV Panels
Abstract
1. Introduction
1.1. Soiling of PV Panels in the MENA Region
1.2. Dust Mitigation Techniques
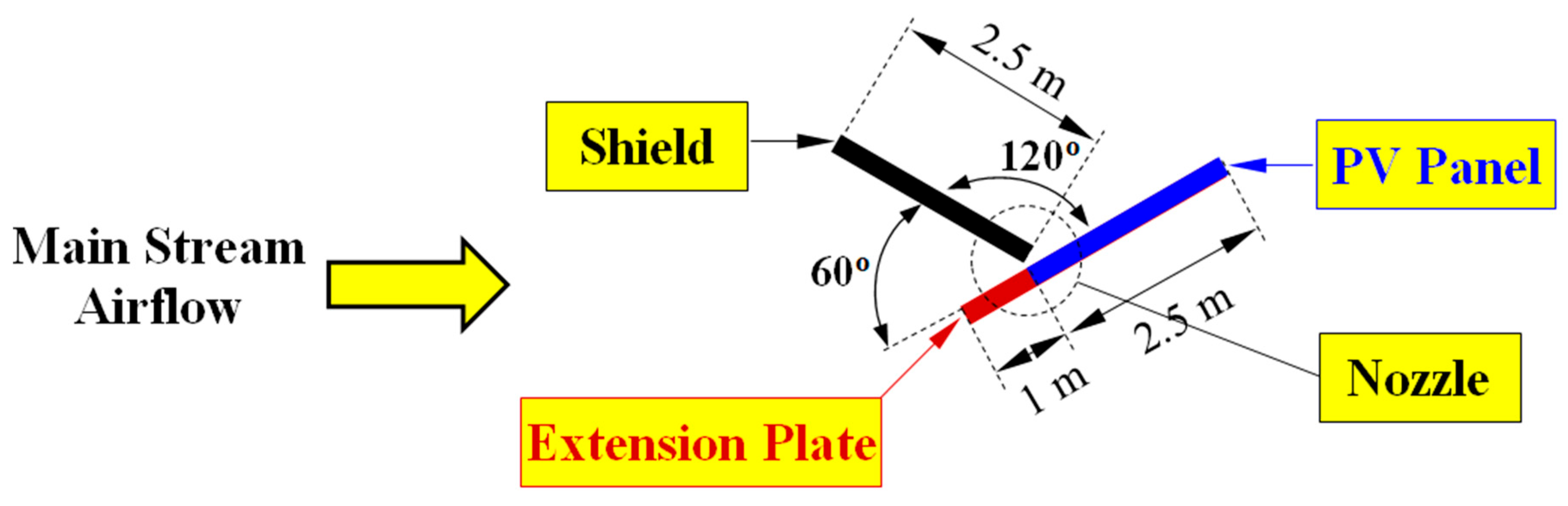
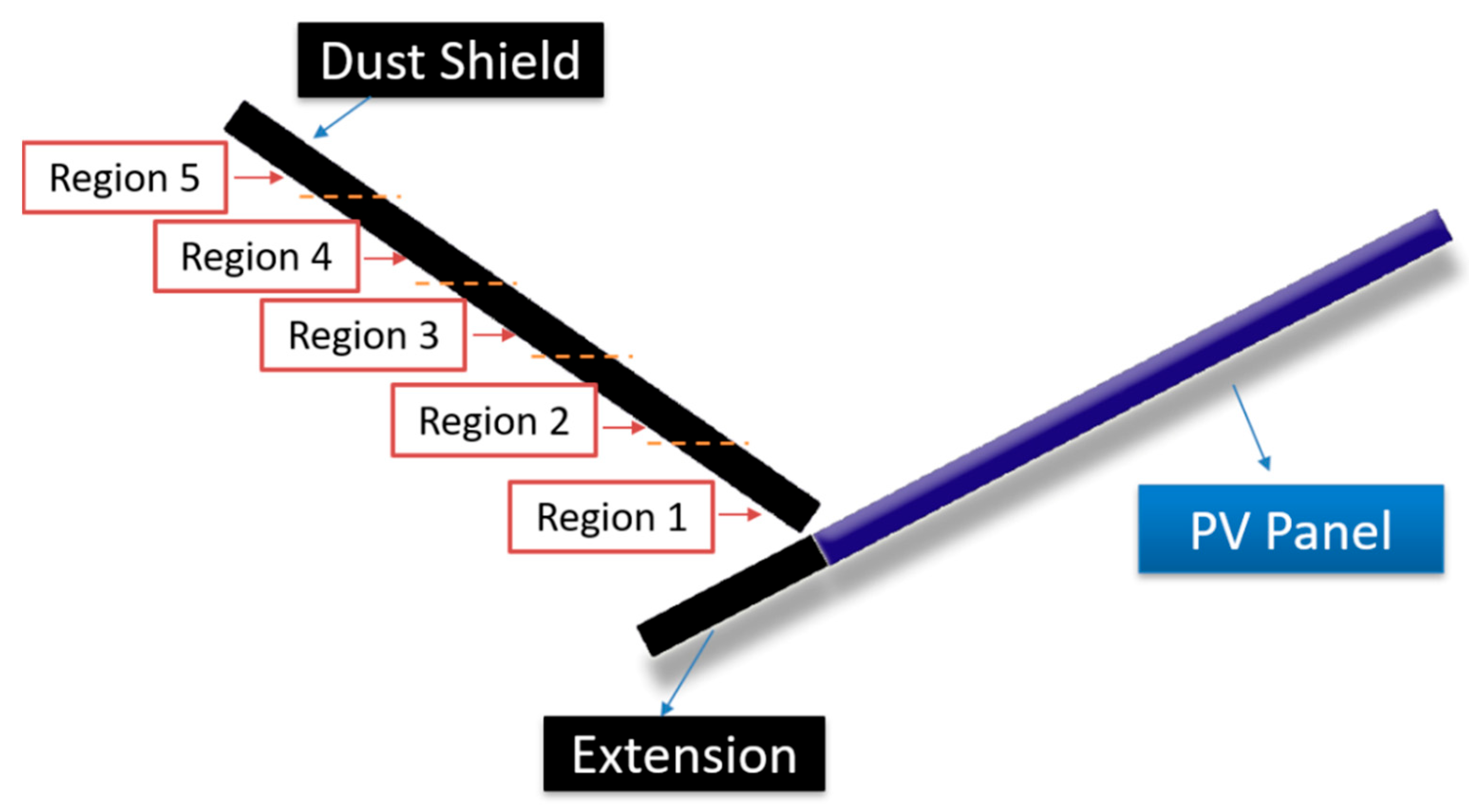
1.3. A New Design of Dust Shields
2. Numerical Methodology
2.1. Numerical Scheme
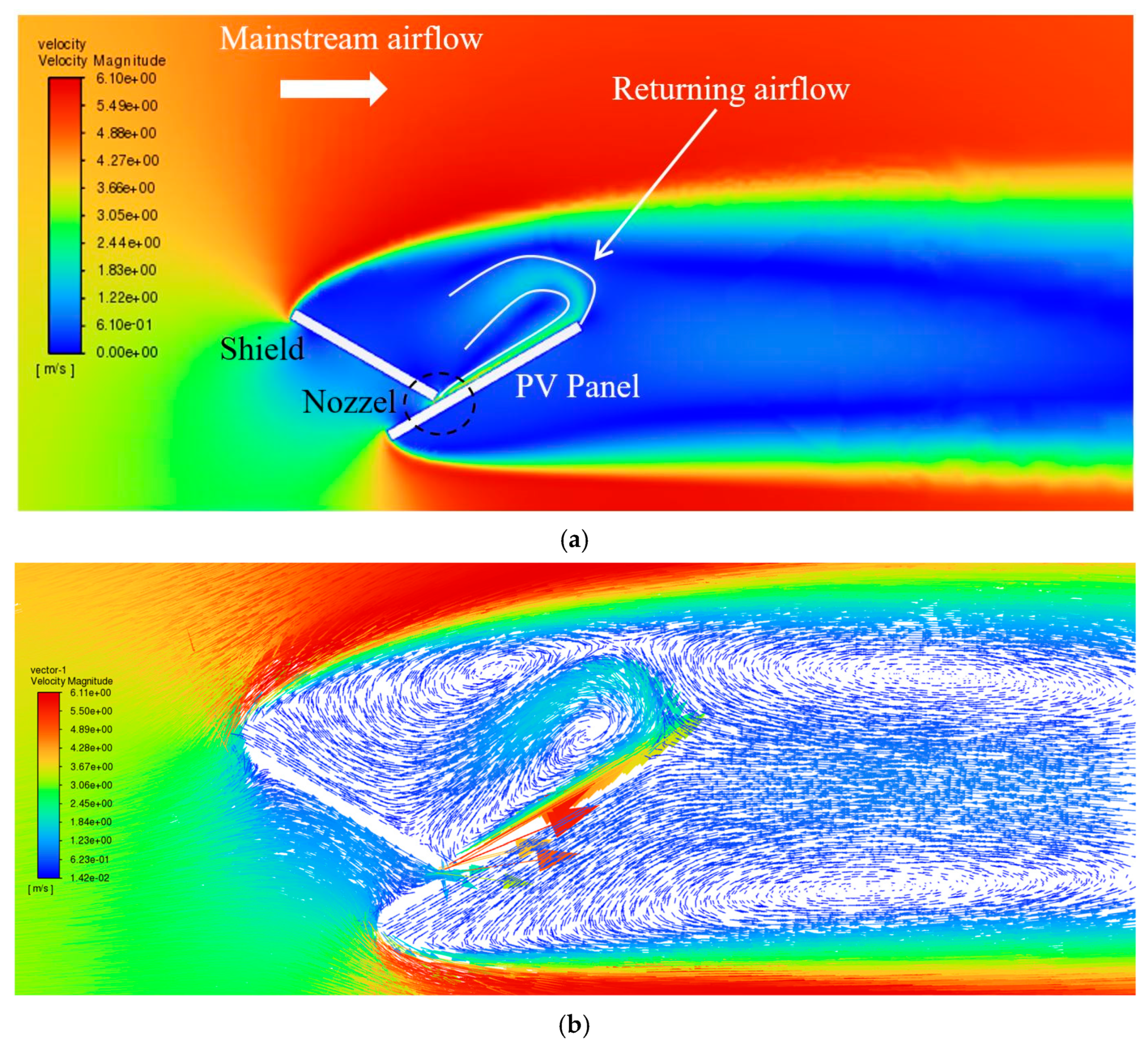
2.2. Airflow Around the PV Panel
2.3. Boundary Conditions
2.4. Dust Deposition Behavior
2.5. Solution Strategy
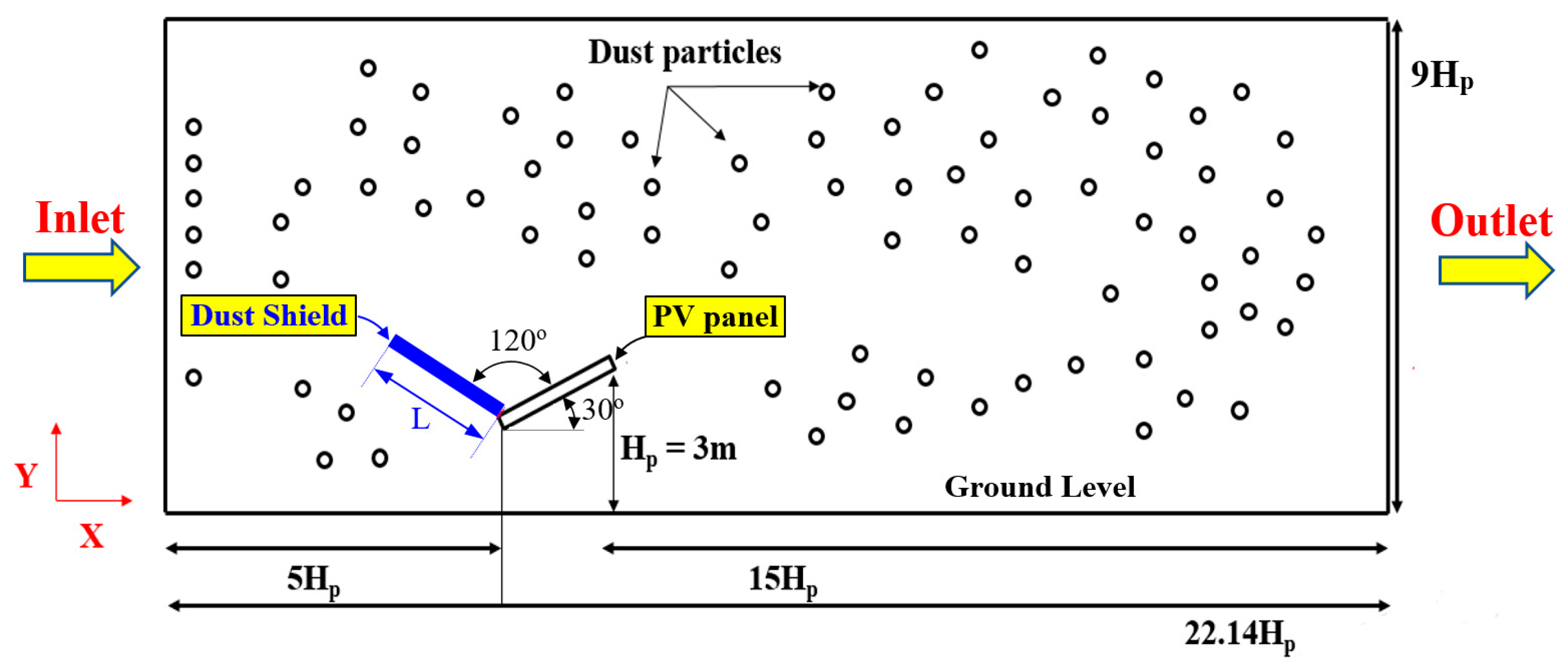
2.6. Model Geometry and Case Description
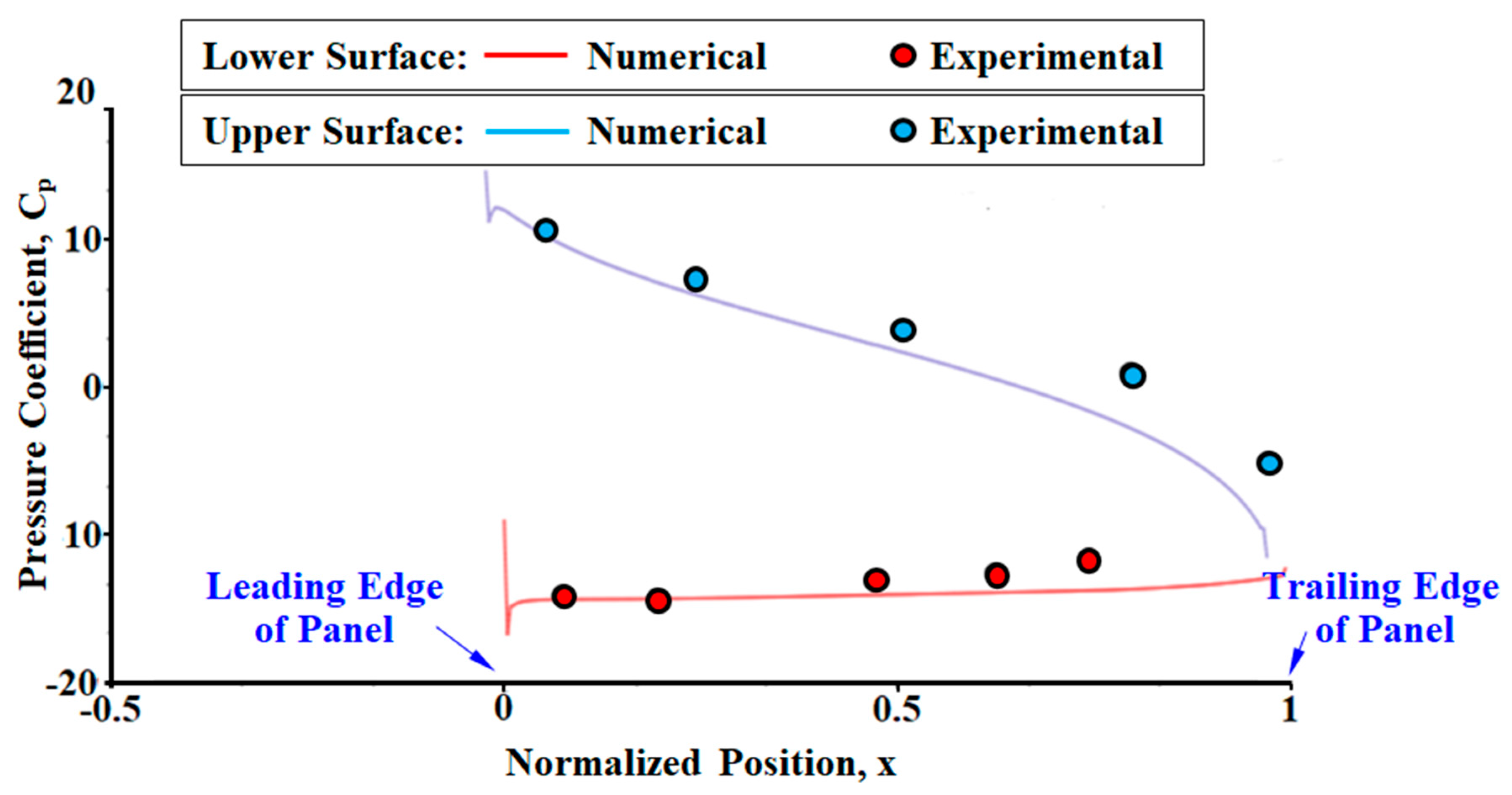
2.7. Grid Independence Study and Numerical Validation
3. Results
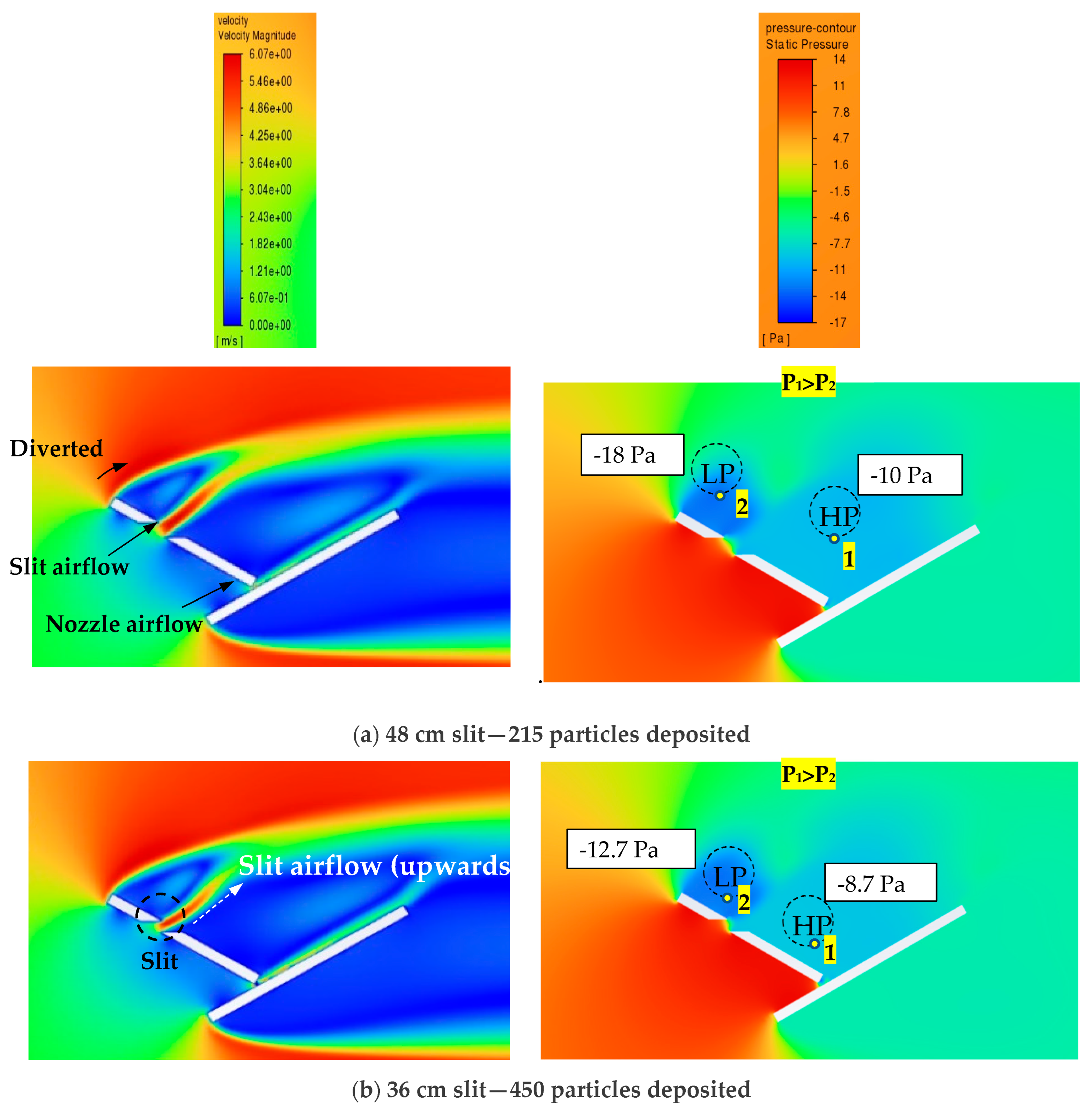
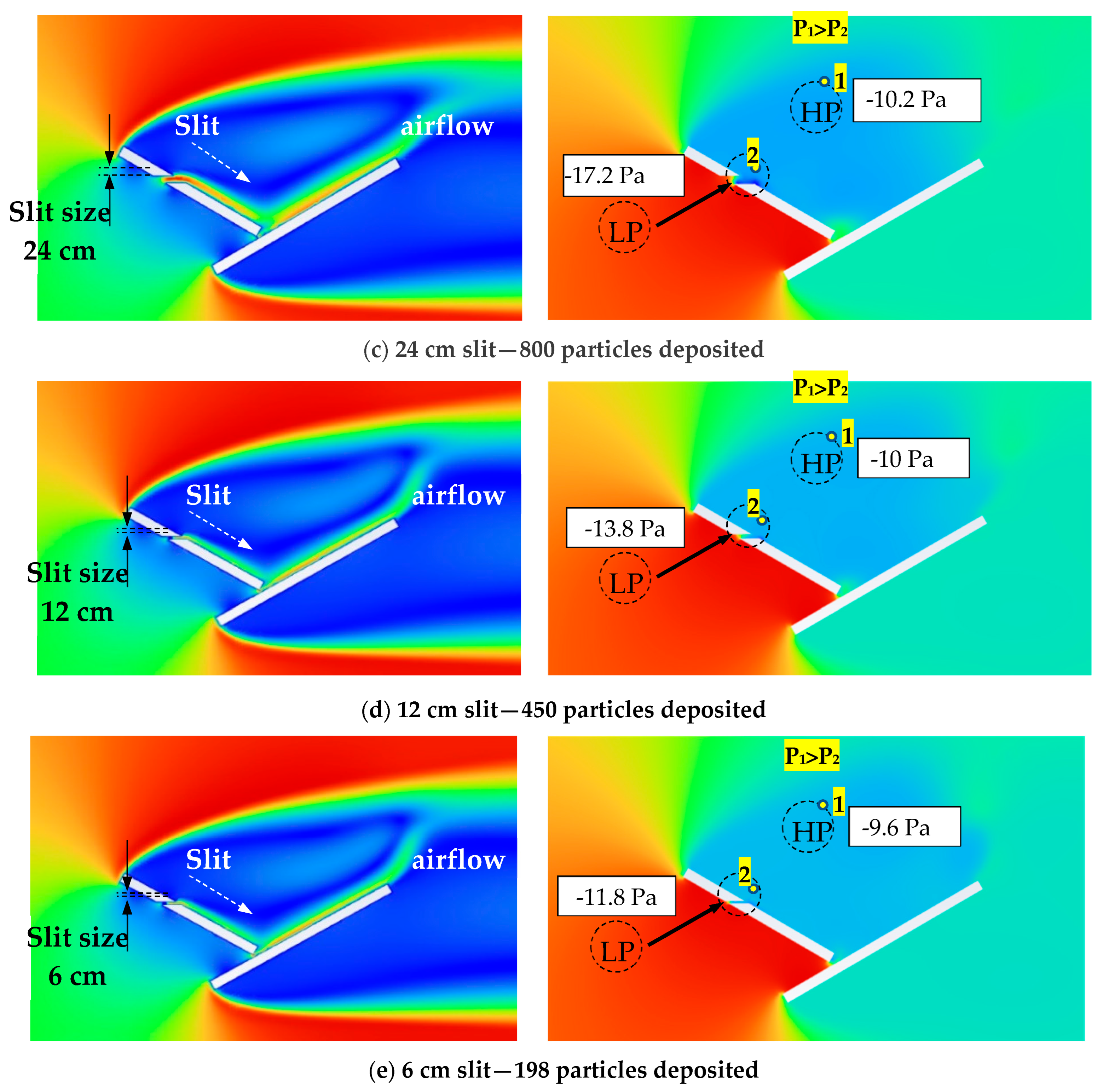
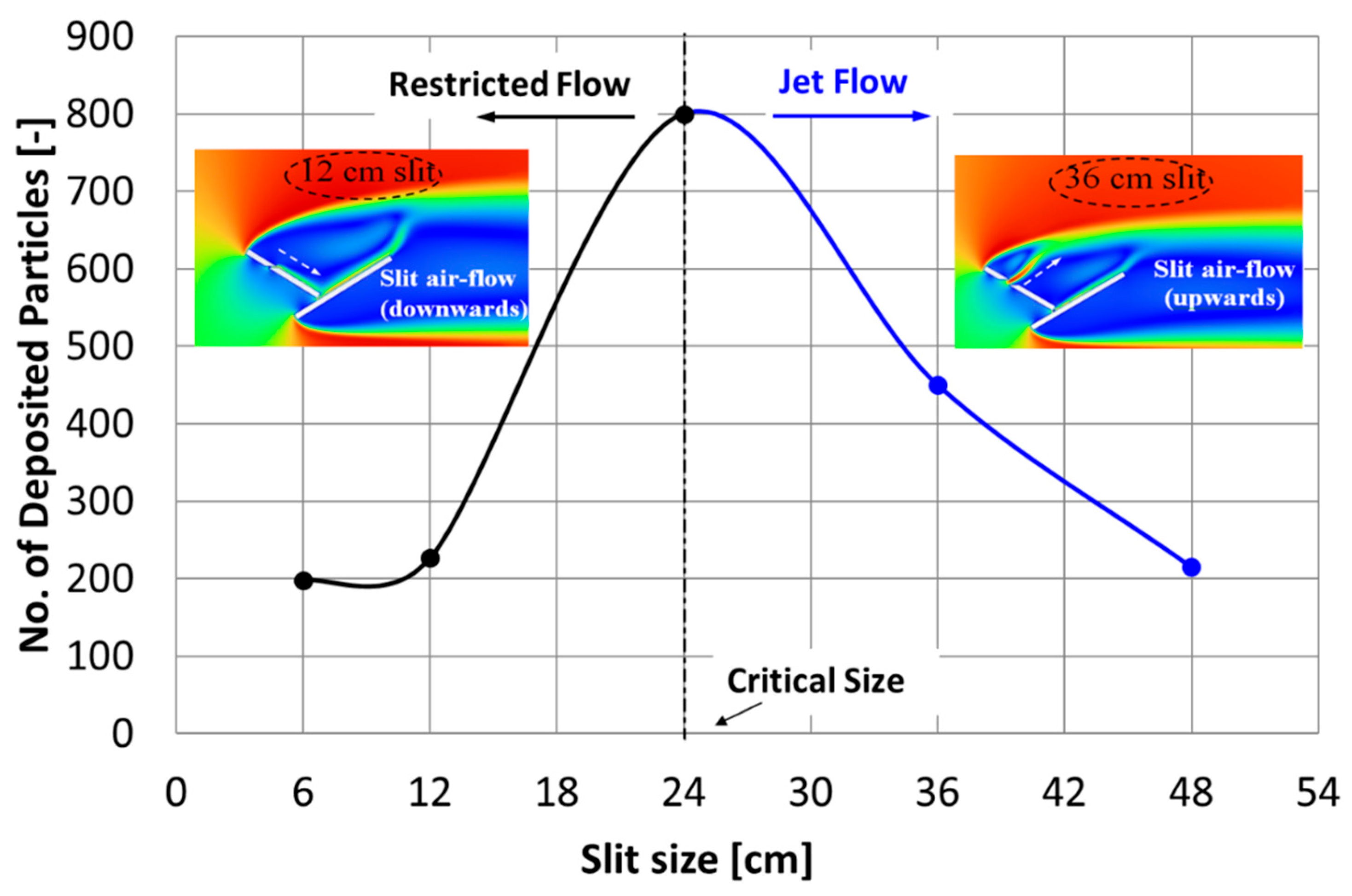
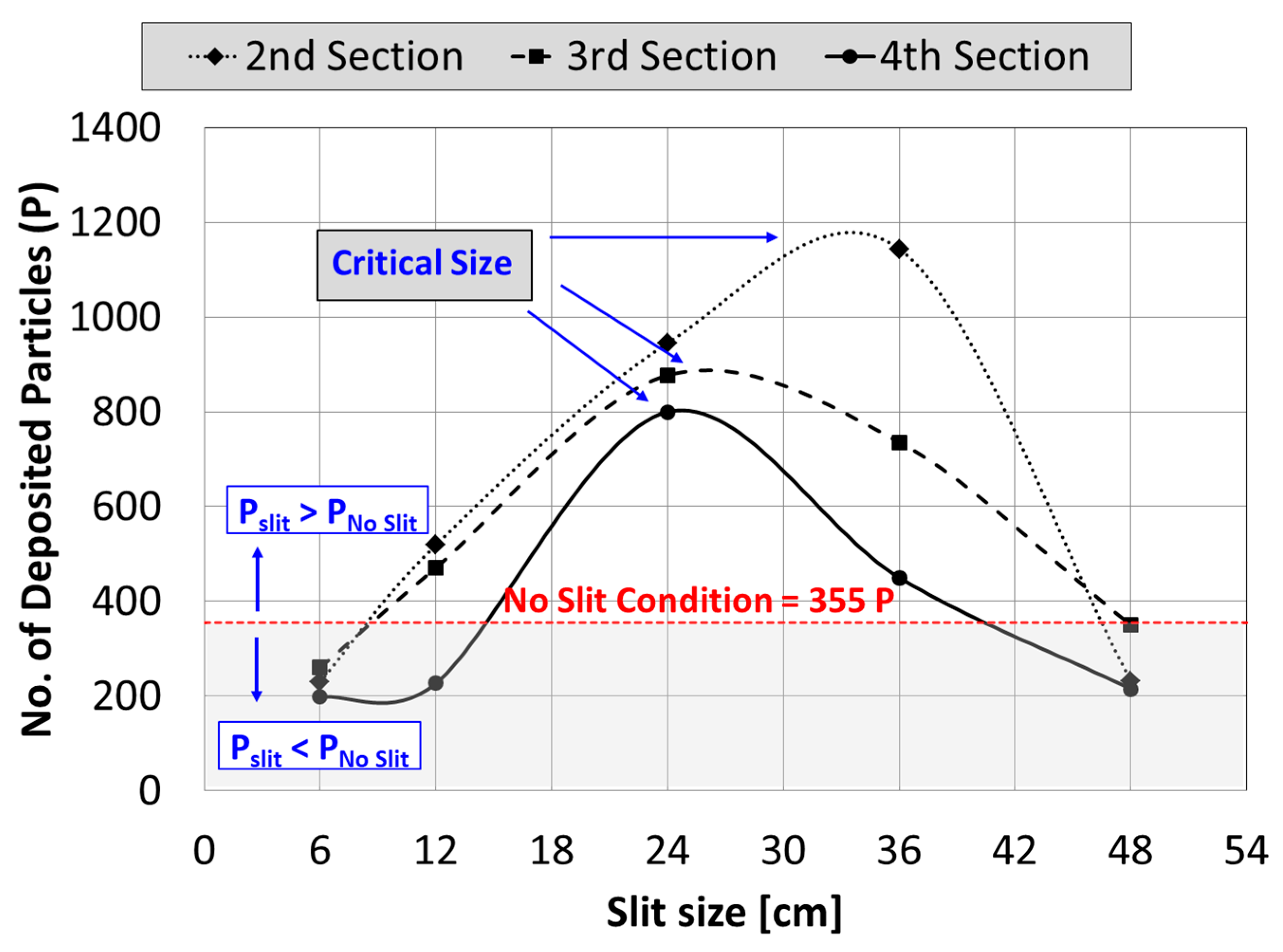
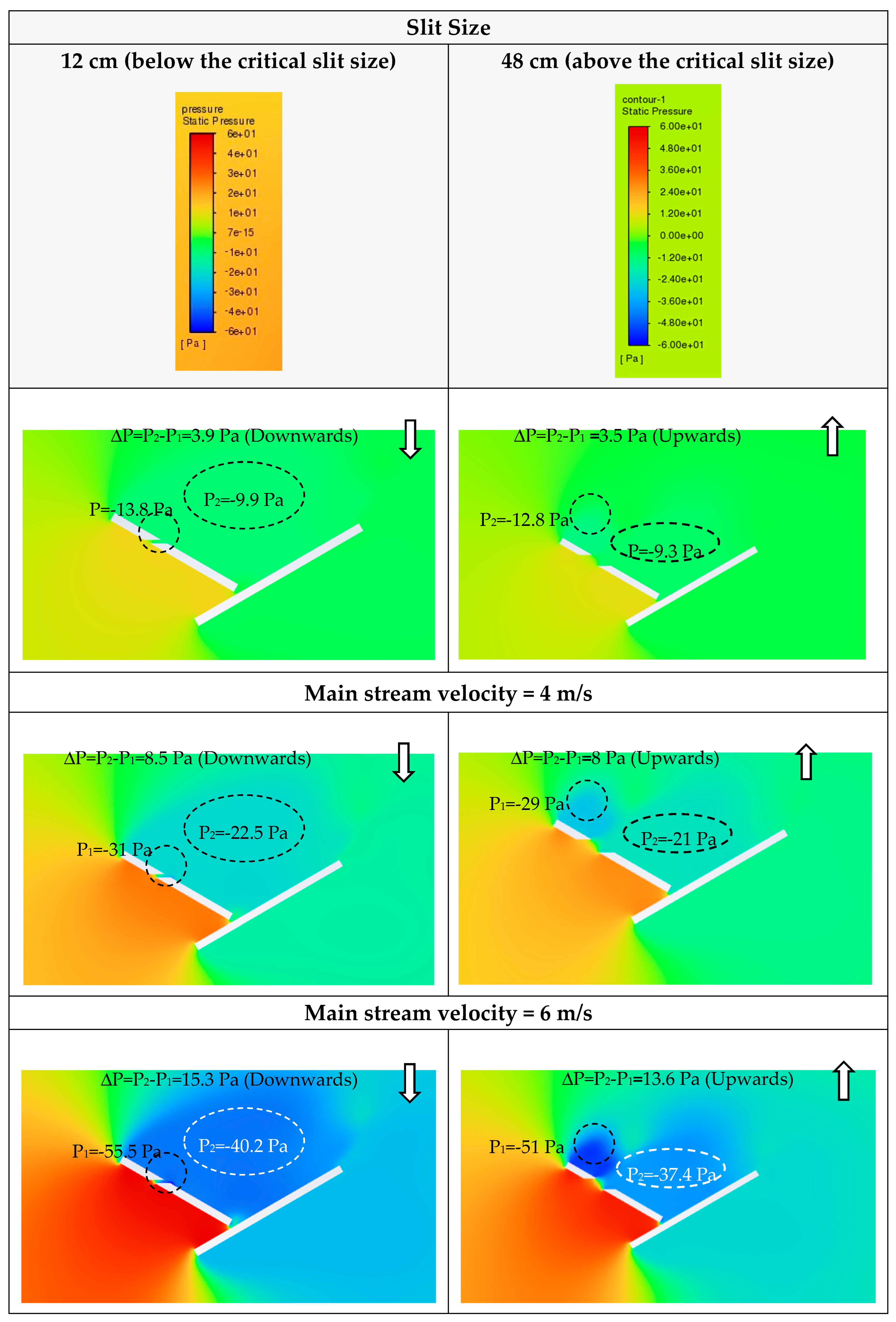
3.1. Influence of Slit Size on Dust Deposition over the PV Panel
3.2. Influence of the Slit Position on Dust Deposition over the PV Panel
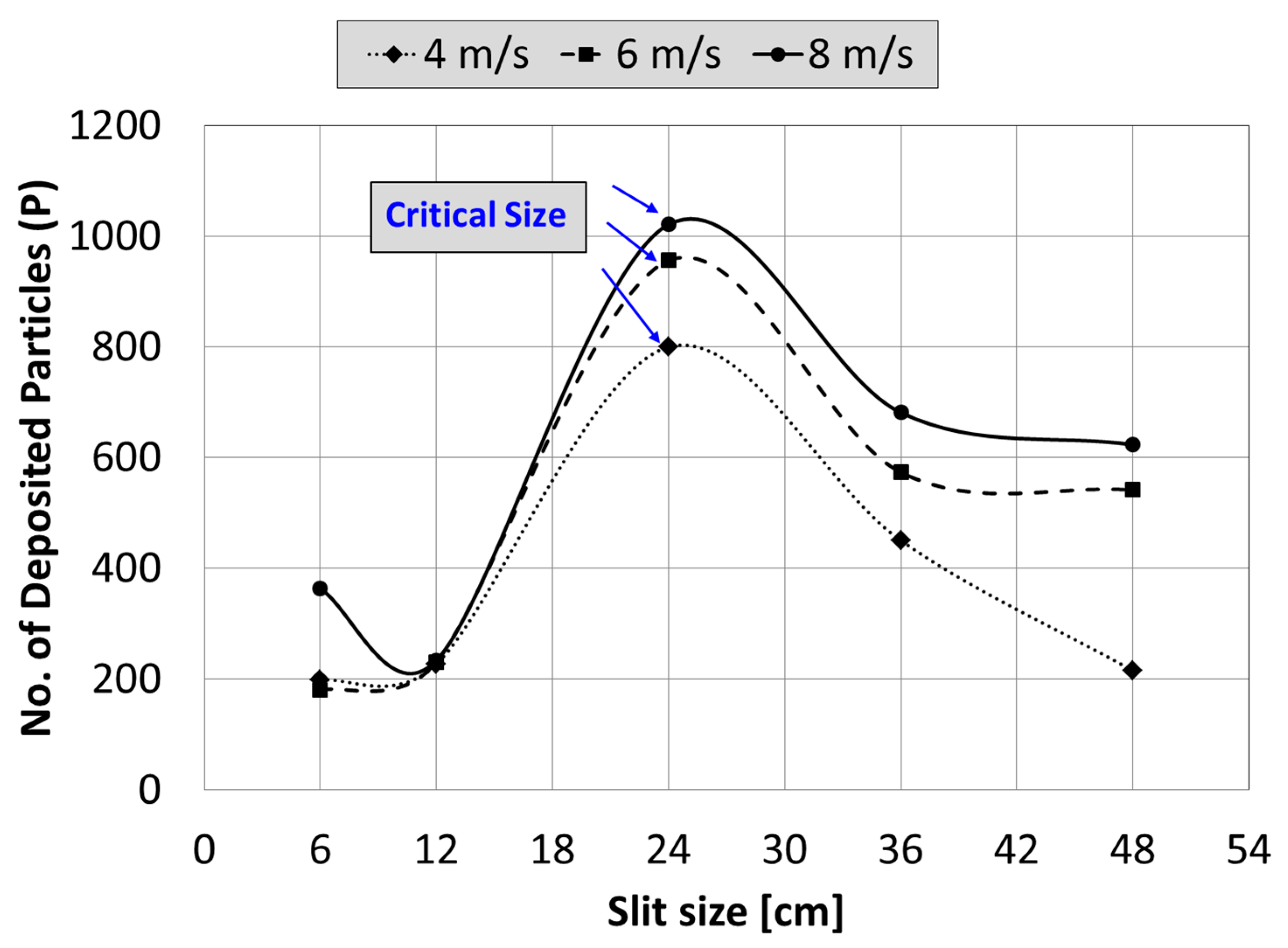
3.3. Influence of the Main Stream Velocity on Dust Deposition over the PV Panel’s Surface
4. Conclusions
- There is a critical slit size, such that below or above that critical size, the number of deposited particles decreases compared to that at the critical size.
- The critical slit size is due to the transition of the airflow from a restricted flow that is intact to the panel’s surface due to the Coanda effect to a free jet flow, which is diverted away from the panel’s surface.
- Positioning the slit too close to the PV panel allows more dust-laden air to reach the panel’s surface, leading to increased dust deposition; conversely, placing the slit far away from the panel reduces dust accumulation.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tawalbeh, M.; Al-Othman, A.; Kafiah, F.; Abdelsalam, E.; Almomani, F.; Alkasrawi, M. Environmental impacts of solar photovoltaic systems: A critical review of recent progress and future outlook. Sci. Total Environ. 2021, 759, 143528. [Google Scholar] [CrossRef]
- Abbasi, K.R.; Shahbaz, M.; Zhang, J.; Irfan, M.; Alvarado, R. Analyze the environmental sustainability factors of China: The role of fossil fuel energy and renewable energy. Renew. Energy 2022, 187, 390–402. [Google Scholar] [CrossRef]
- Cevik, E.I.; Yıldırım, D.Ç.; Dibooglu, S. Renewable and non-renewable energy consumption and economic growth in the US: A Markov-Switching VAR analysis. Energy Environ. 2021, 32, 519–541. [Google Scholar] [CrossRef]
- Bloomberg. US Crosses the Electric-Car Tipping Point for Mass Adoption. 2022. Available online: https://www.bloomberg.com/news/articles/2022-07-09/us-electric-car-sales-reach-key-milestone (accessed on 1 April 2025).
- Saligkaras, D.; Papageorgiou, V.E. On the detection of patterns in electricity prices across European countries: An unsupervised machine learning approach. AIMS Energy 2022, 10, 1146–1164. [Google Scholar] [CrossRef]
- Cavana, G.; Becchio, C.; Bottero, M. Feasibility and evolution studies on renewable energy communities in cities. Renew. Sustain. Energy Rev. 2025, 213, 115477. [Google Scholar] [CrossRef]
- Creutzig, F.; Hilaire, J.; Nemet, G.; Müller-Hansen, F.; Minx, J.C. Technological innovation enables low cost climate change mitigation. Energy Res. Soc. Sci. 2023, 105, 103276. [Google Scholar] [CrossRef]
- Mdallal, A.; Yasin, A.; Mahmoud, M.; Abdelkareem, M.A.; Alami, A.H.; Olabi, A.G. A comprehensive review on solar photovoltaics: Navigating generational shifts, innovations, and sustainability. Sustain. Horiz. 2025, 13, 100137. [Google Scholar] [CrossRef]
- Shenouda, R.; Abd-Elhady, M.S.; Kandil, H.A. A review of dust accumulation on PV panels in the MENA and the Far East regions. J. Eng. Appl. Sci. 2022, 69, 8. [Google Scholar] [CrossRef]
- Abd-Elhady, M.S.; Fazila, A.R.A.; Kandil, H.A.; Khalil, T.; Dahlhaus, D. Modeling the Solar Cells Temperature and Power Output From Photovoltaic Panels Under Dusty Conditions. J. Sol. Energy Eng. 2025, 147, 011008. [Google Scholar] [CrossRef]
- Shenouda, R.; Abd-Elhady, M.S.; Kandil, H.A. Influence of seasonal effect on dust accumulation on Photovoltaic panels that operate light posts. Energy Rep. 2022, 8, 1275–1284. [Google Scholar] [CrossRef]
- Tanaka, T.Y.; Chiba, M. A numerical study of the contributions of dust source regions to the global dust budget. Glob. Planet. Change 2006, 52, 88–104. [Google Scholar] [CrossRef]
- Rashid, M.; Yousif, M.; Rashid, Z.; Muhammad, A.; Altaf, M.; Mustafa, A. Effect of Dust Accumulation on the Performance of Photovoltaic Modules for Different Climate Regions. Heliyon 2023, 9, e23069. [Google Scholar] [CrossRef] [PubMed]
- Rusănescu, C.O.; Rusănescu, M.; Istrate, I.A.; Constantin, G.A.; Begea, M. The effect of dust deposition on the performance of photovoltaic panels. Energies 2023, 16, 6794. [Google Scholar] [CrossRef]
- Ghazi, S.; Sayigh, A.; Ip, K. Dust effect on flat surfaces—A review paper. Renew. Sustain. Energy Rev. 2014, 33, 742–751. [Google Scholar] [CrossRef]
- Adinoyi, M.J.; Said, S.A. Effect of dust accumulation on the power outputs of solar photovoltaic modules. Renew. Energy 2013, 60, 633–636. [Google Scholar] [CrossRef]
- Said, S.A.M.; Al-Aqeeli, N.; Walwil, H.M. The potential of using textured and anti-reflective coated glasses in minimizing dust fouling. Sol. Energy 2015, 113, 295–302. [Google Scholar] [CrossRef]
- Asl-Soleimani, E.; Farhangi, S.; Zabihi, M.S. The effect of tilt angle, air pollution on performance of photovoltaic systems in Tehran. Renew. Energy 2001, 24, 459–468. [Google Scholar] [CrossRef]
- Menoufi, K.; Farghal, H.F.; Farghali, A.A.; Khedr, M.H. Dust accumulation on photovoltaic panels: A case study at the East Bank of the Nile (Beni-Suef, Egypt). Energy Procedia 2017, 128, 24–31. [Google Scholar] [CrossRef]
- Elminir, H.K.; Ghitas, A.E.; Hamid, R.H.; El-Hussainy, F.; Beheary, M.M.; Abdel-Moneim, K.M. Effect of dust on the transparent cover of solar collectors. Energy Convers. Manag. 2006, 47, 3192–3203. [Google Scholar] [CrossRef]
- Moharram, K.A.; Abd-Elhady, S.M.; Kandil, H.A.; El-Sherif, H. Influence of cleaning using water and surfactants on the performance of photovoltaic panels. Energy Convers. Manag. 2013, 68, 266–272. [Google Scholar] [CrossRef]
- Kawamoto, H.; Shibata, T. Electrostatic cleaning system for removal of sand from solar panels. J. Electrost. 2015, 73, 65–70. [Google Scholar] [CrossRef]
- Al-Badra, M.Z.; Abd-Elhady, M.S.; Kandil, H.A. A novel technique for cleaning PV panels using antistatic coating with a mechanical vibrator. Energy Rep. 2020, 6, 1633–1637. [Google Scholar] [CrossRef]
- Abd-Elhady, M.S.; Rana, A.; Elsebaaie, M.A.; Kandil, H.A. A new cleaning method for solar panels inspired from the natural vibrations of tree branches and leaves. Sci. Rep. 2024, 14, 18138. [Google Scholar] [CrossRef] [PubMed]
- Chiteka, K.; Arora, R.; Sridhara, S.N.; Enweremadu, C.C. Optimizing wind barrier and photovoltaic array configuration in soiling mitigation. Renew. Energy 2021, 163, 225–236. [Google Scholar] [CrossRef]
- Raillani, B.; Chaatouf, D.; Salhi, M.; Amraqui, S.; Mezrhab, A. Effect of wind barrier height on the dust deposition rate of a ground-mounted photovoltaic panel. Sustain. Energy Technol. Assess. 2022, 52, 102035. [Google Scholar] [CrossRef]
- Raillani, B.; Chaatouf, D.; Salhi, M.; Bria, A.; Amraqui, S.; Mezrhab, A. The effectiveness of the wind barrier in mitigating soiling of a ground-mounted photovoltaic panel at different angles and particle injection heights. Results Eng. 2022, 16, 100774. [Google Scholar] [CrossRef]
- Raillani, B.; Salhi, M.; Chaatouf, D.; Amraqui, S.; Mezrhab, A. Optimization of a porous wind barrier to reduce soiling and avoid shading losses of photovoltaic panels. Renew. Energy 2022, 189, 510–523. [Google Scholar] [CrossRef]
- Eisa, K.; Shenouda, R.; Abd-Elhady, M.S.; Kandil, H.A.; Khalil, T. Mitigation of dust on PV panels that operate light posts using a wind shield, mechanical vibrations and AN antistatic coating. Ain Shams Eng. J. 2023, 14, 101993. [Google Scholar] [CrossRef]
- Shenouda, R.; Abd-Elhady, M.S.; Kandil, H.A.; Dagher, M. Numerical investigation of the effect of dust shields on accumulation of dust over PV panels. Environ. Sci. Pollut. Res. 2023, 30, 62905–62923. [Google Scholar] [CrossRef]
- Duronio, F.; Lien, H.P.; De Vita, A. CFD unified approach under Eulerian–Lagrangian framework for methanol and gasoline direct injection sprays in evaporative and flash boiling conditions. Int. J. Multiph. Flow 2025, 182, 105048. [Google Scholar] [CrossRef]
- Lu, H.; Zhao, W. CFD Prediction of Dust Pollution and Impact on an Isolated Ground-mounted Solar Photovoltaic System. Renew. Energy 2019, 131, 829–840. [Google Scholar] [CrossRef]
- Tominaga, Y.; Akabayashi, S.I.; Kitahara, T.; Arinami, Y. Air flow around isolated gable-roof buildings with different roof pitches: Wind tunnel experiments and CFD simulations. Build. Environ. 2015, 84, 204–213. [Google Scholar] [CrossRef]
- Karava, P.; Jubayer, C.M.; Savory, E. Numerical modelling of forced convective heat transfer from the inclined windward roof of an isolated low-rise building with application to photovoltaic/thermal systems. Appl. Therm. Eng. 2011, 31, 1950–1963. [Google Scholar] [CrossRef]
- IEM :: Site Wind Roses (iastate.edu). Available online: https://mesonet.agron.iastate.edu/sites/windrose.phtml?station=NUI&network=MD_ASOS (accessed on 1 April 2025).
- Chiteka, K.; Arora, R.; Jain, V. CFD Prediction of dust deposition and installation parametric optimisation for soiling mitigation in non-tracking solar PV modules. Int. J. Ambient Energy 2021, 42, 1307–1320. [Google Scholar] [CrossRef]
- Abd-Elhady, M.S.; Rindt, C.C.M.; Wijers, J.G.; van Steenhoven, A.A. Particulate fouling in waste incinerators as influenced by the critical sticking velocity and layer porosity. Energy 2005, 30, 1469–1479. [Google Scholar] [CrossRef]
- Abiola-Ogedengbe, A.; Hangan, H.; Siddiqui, K. Experimental investigation of wind effects on a standalone photovoltaic (PV) module. Renew. Energy 2015, 78, 657–665. [Google Scholar] [CrossRef]
- Ahmed, N.A. Coanda Effect: Flow Phenomenon and Applications; CRC Press Taylor & Francis Group: Abingdon, UK, 2020; ISBN 978-1-138-33915-6. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gobran, A.M.; Abd-Elhady, M.S.; Kandil, H.A. Influence of an Air Slit in Dust Shields on Accumulation of Dust over PV Panels. Fluids 2025, 10, 153. https://doi.org/10.3390/fluids10060153
Gobran AM, Abd-Elhady MS, Kandil HA. Influence of an Air Slit in Dust Shields on Accumulation of Dust over PV Panels. Fluids. 2025; 10(6):153. https://doi.org/10.3390/fluids10060153
Chicago/Turabian StyleGobran, Ahmed M., Mohamed S. Abd-Elhady, and Hamdy A. Kandil. 2025. "Influence of an Air Slit in Dust Shields on Accumulation of Dust over PV Panels" Fluids 10, no. 6: 153. https://doi.org/10.3390/fluids10060153
APA StyleGobran, A. M., Abd-Elhady, M. S., & Kandil, H. A. (2025). Influence of an Air Slit in Dust Shields on Accumulation of Dust over PV Panels. Fluids, 10(6), 153. https://doi.org/10.3390/fluids10060153





