Influence of Gurney Flap and Leading-Edge/Trailing-Edge Flaps on the Stall Characteristics and Aeroacoustic Performance of Airfoils
Abstract
1. Introduction
2. Numerical Simulation of Flow Around NACA0021 Using DDES
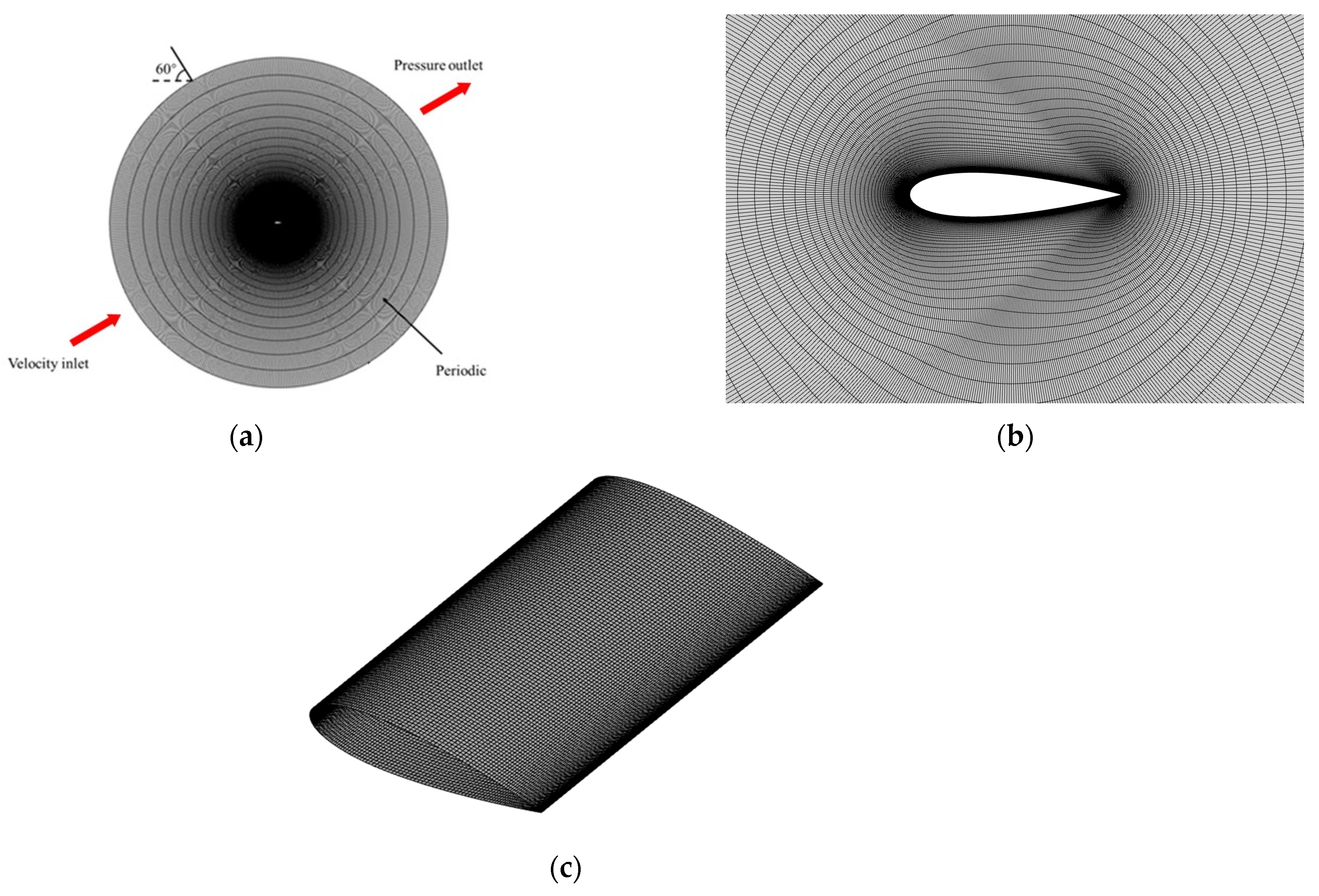
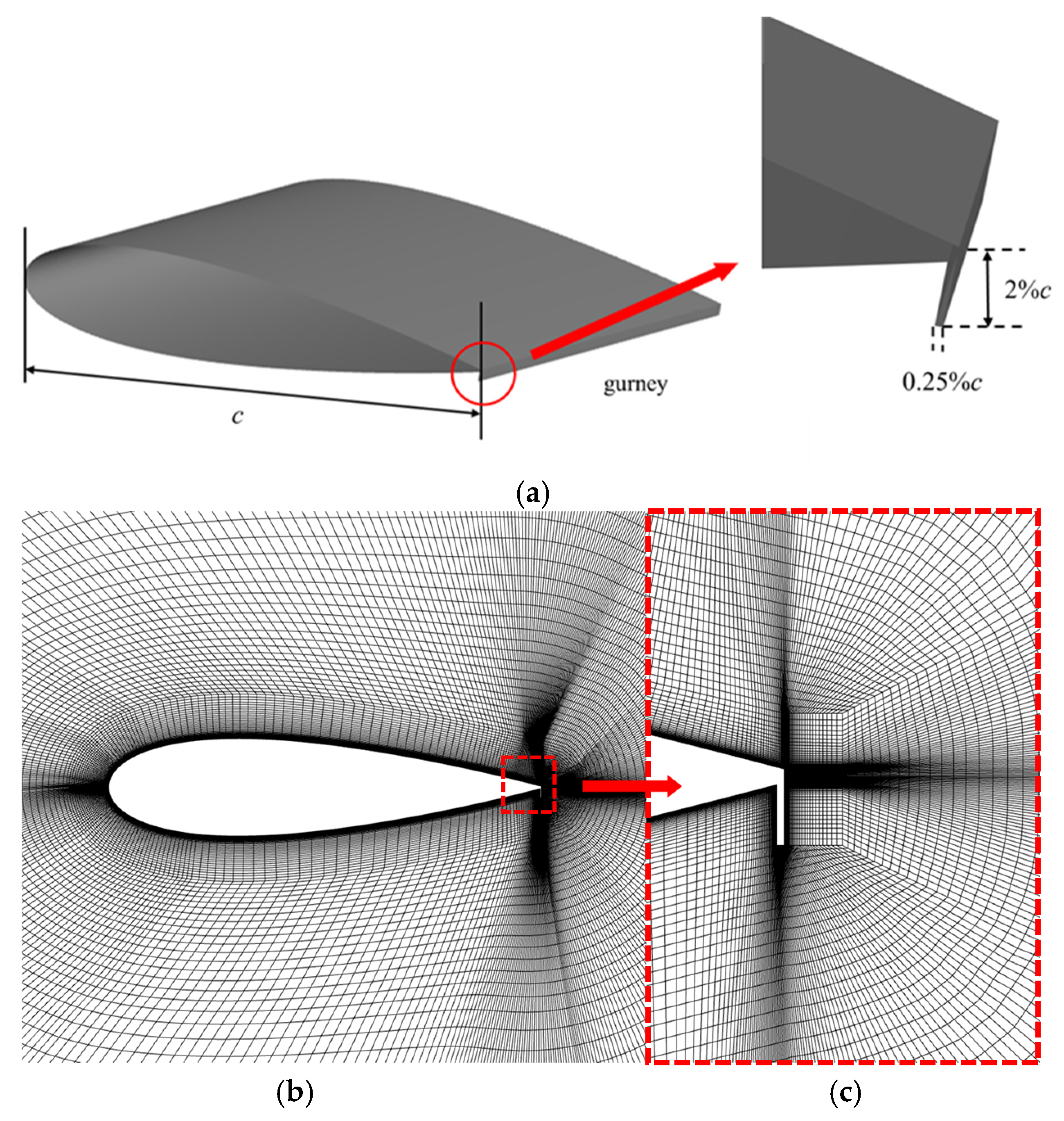
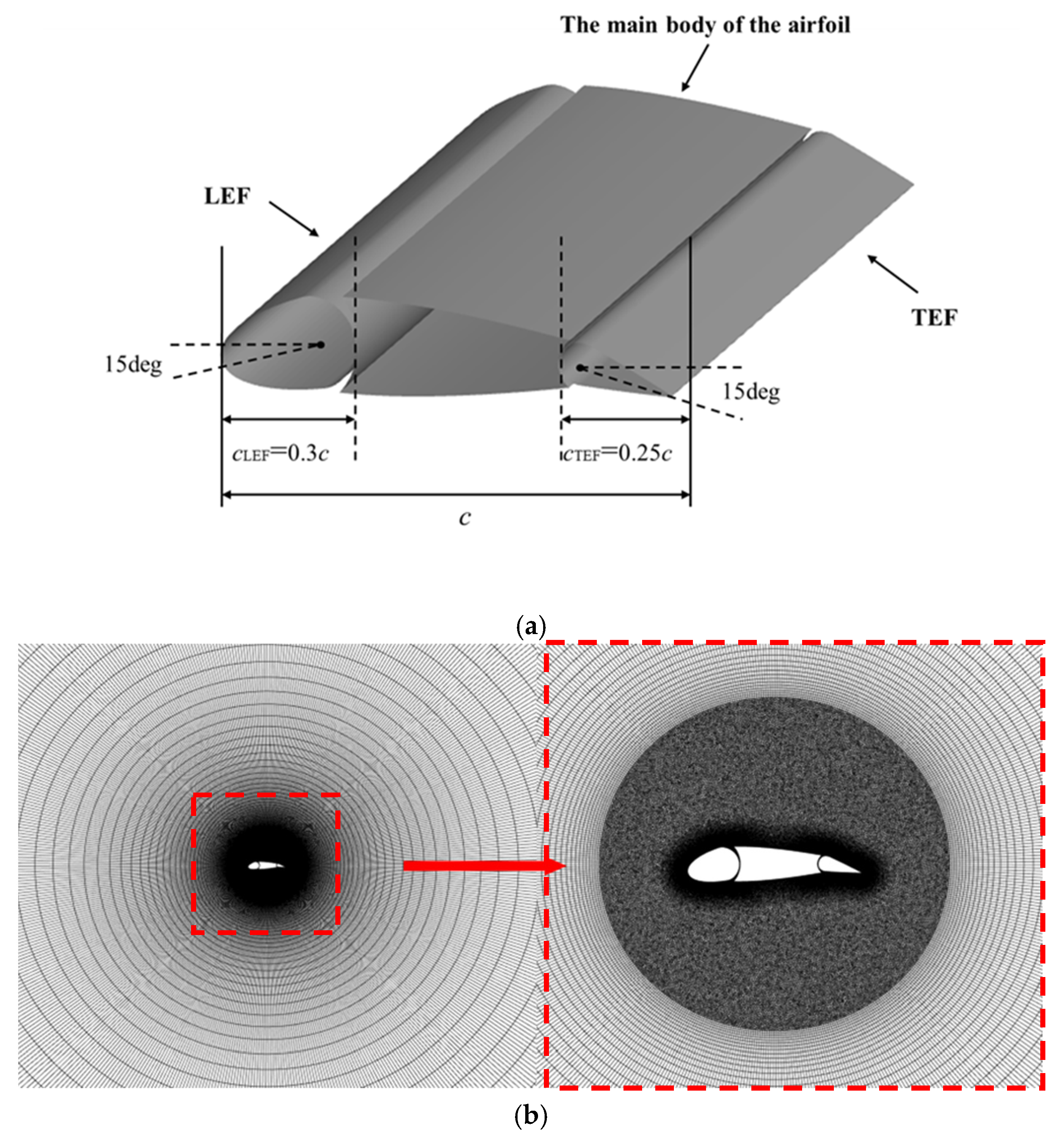
2.1. Computational Modeling and Mesh Generation
- .
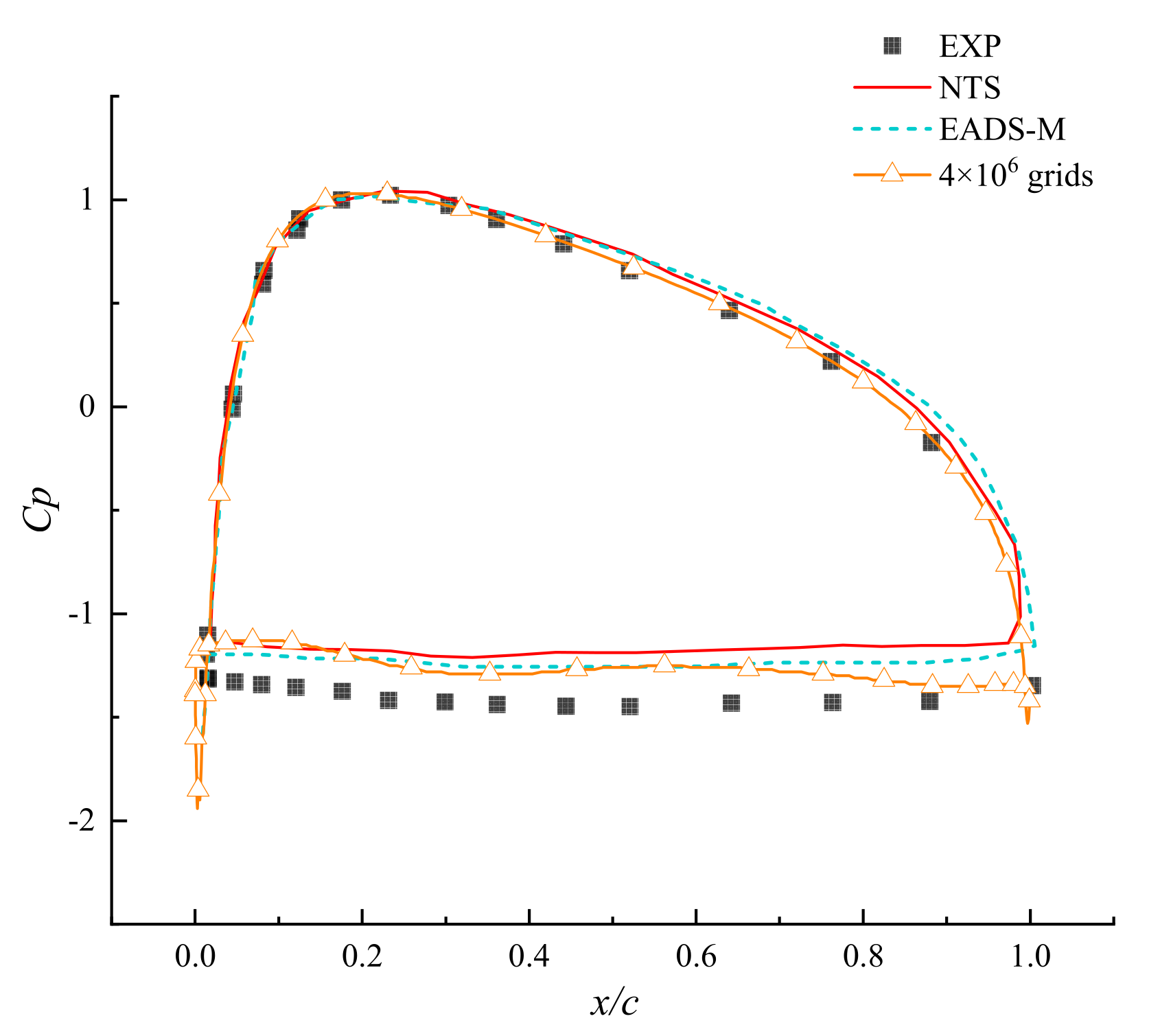
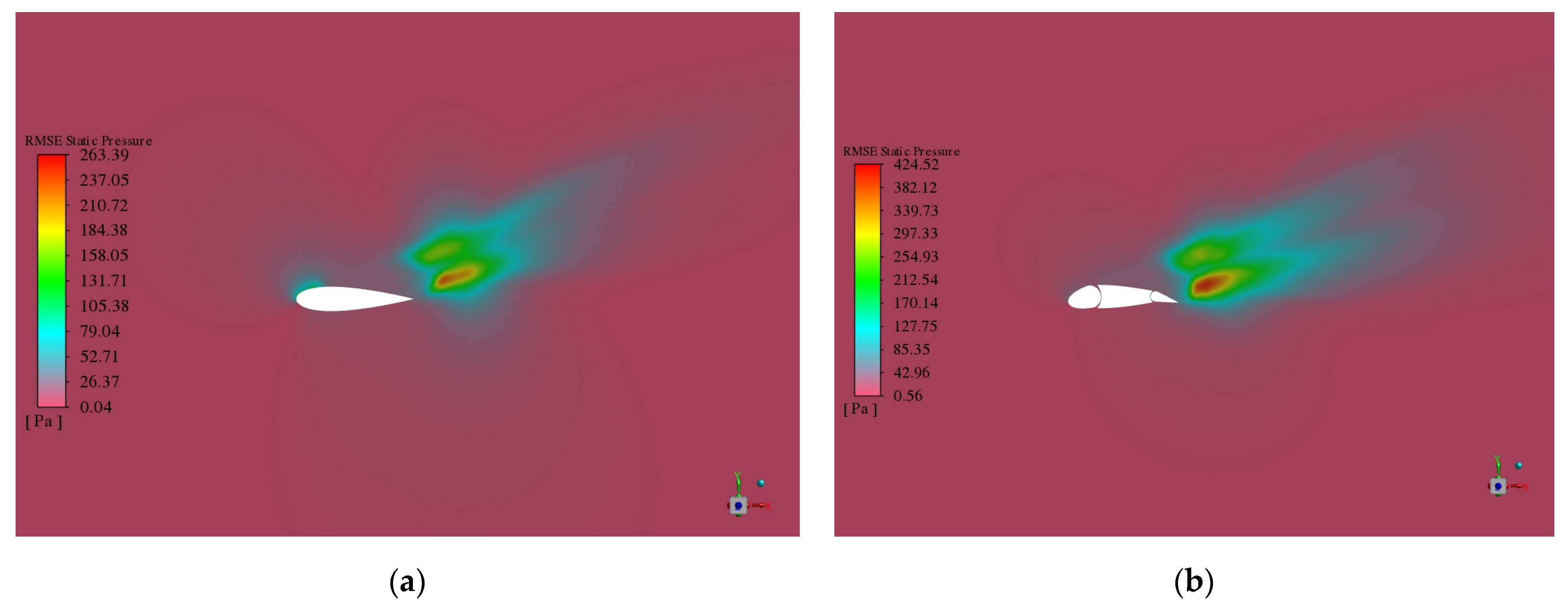
2.2. Grid Independence Verification
2.3. Verification of the Accuracy of Simulation Results
2.4. Simulation Results of Airfoil Model with Gurney Flap Airfoil and Leading- and Trailing-Edge Flap Airfoils
3. Acoustic Noise Analysis
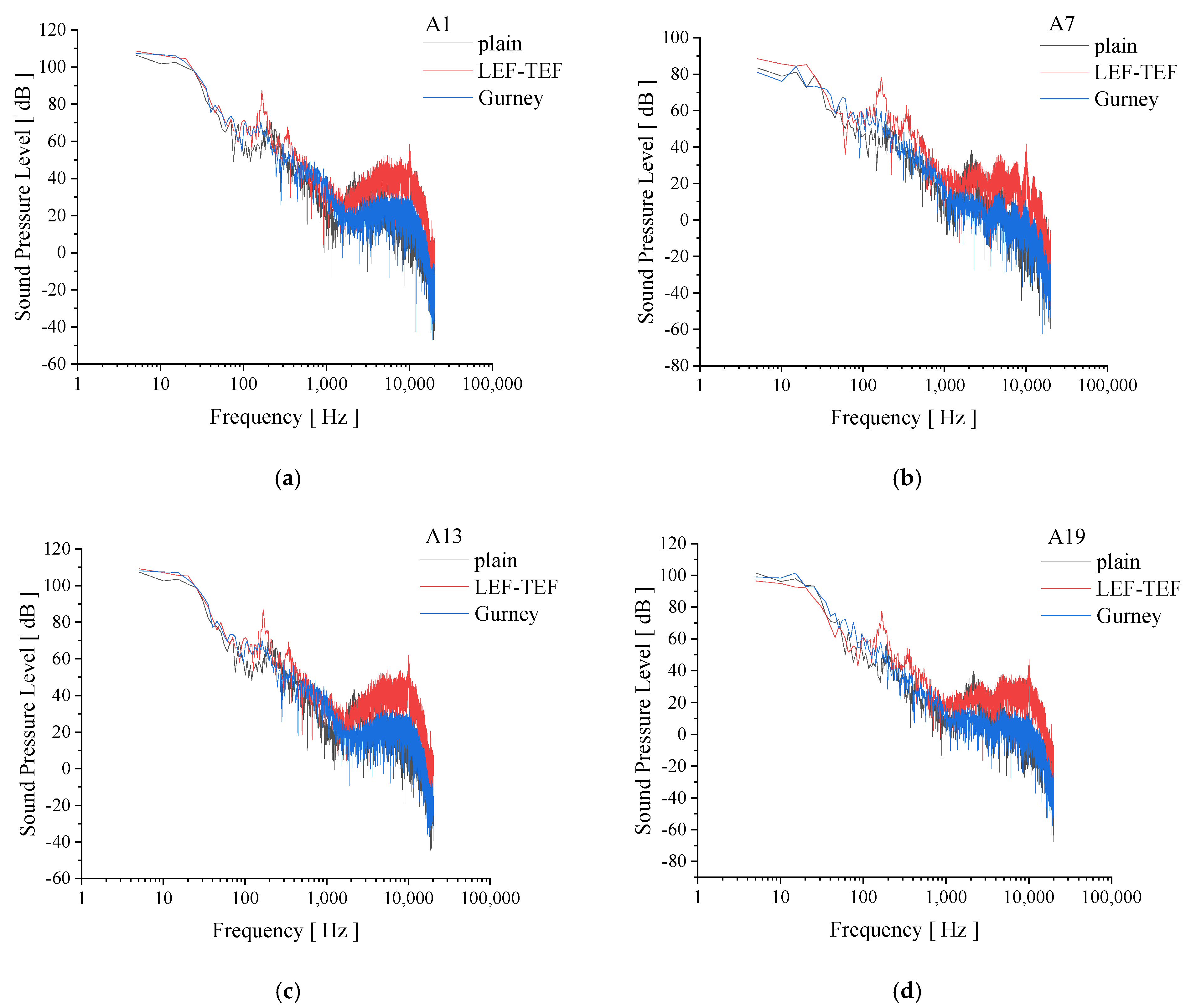
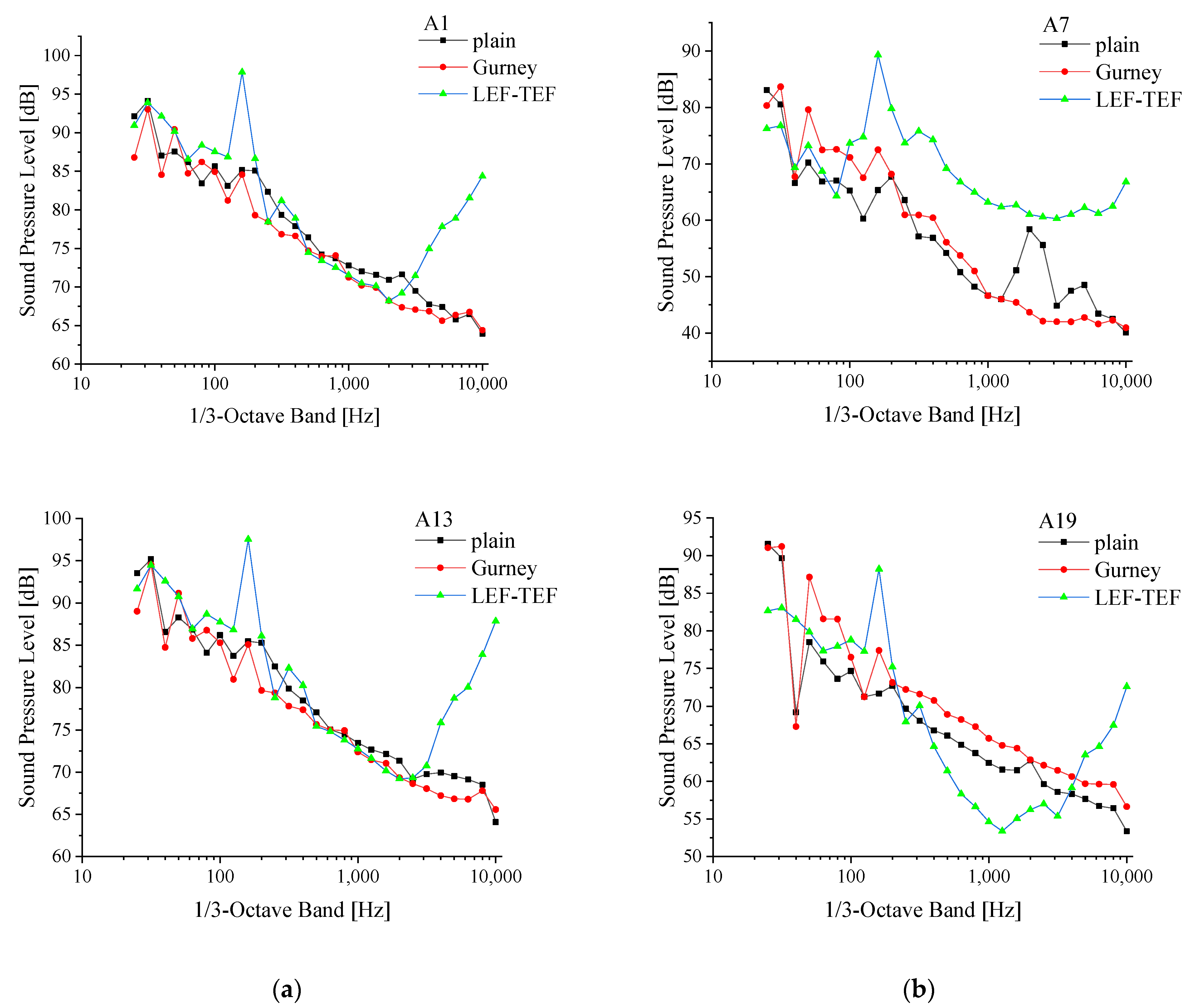
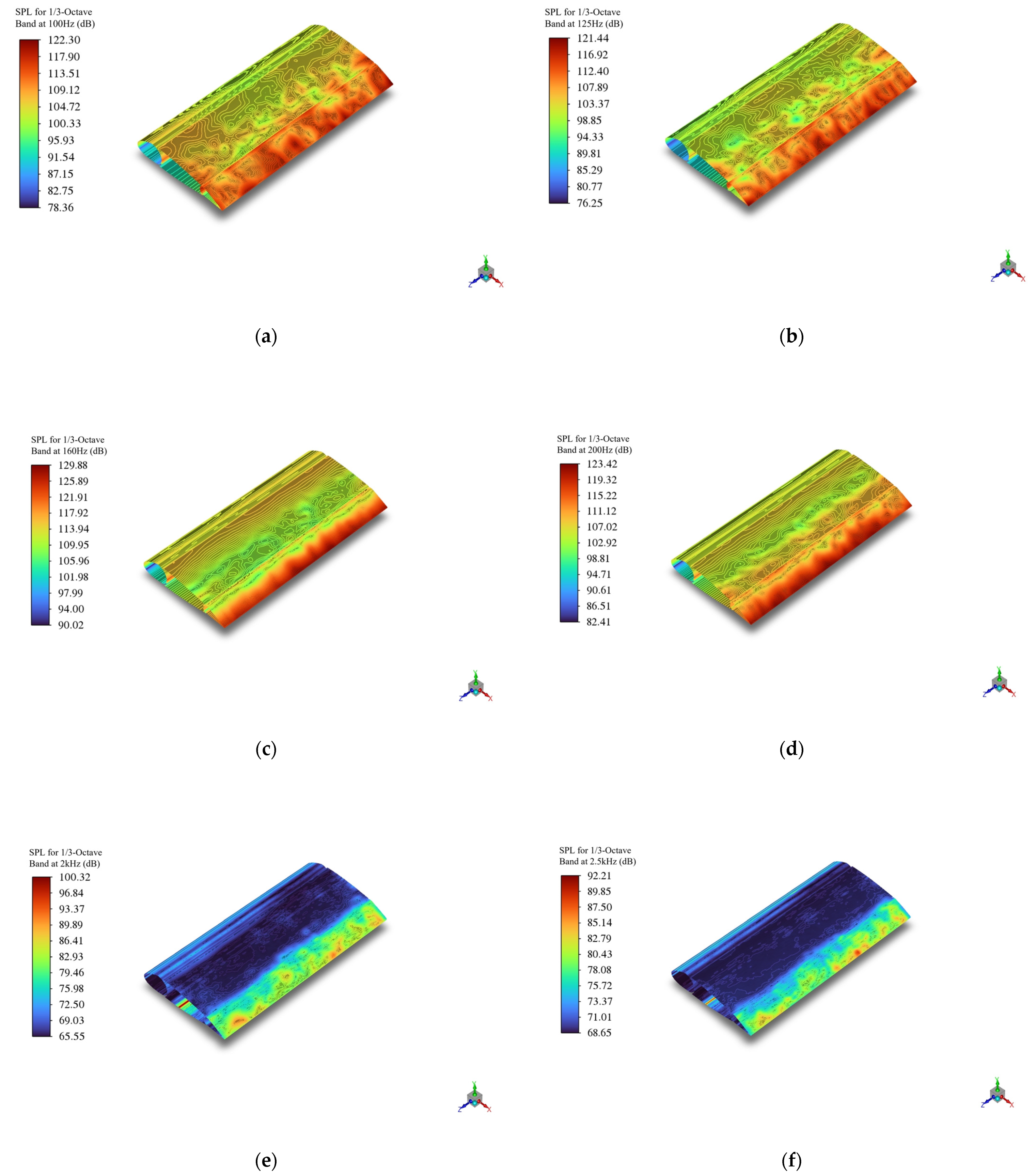
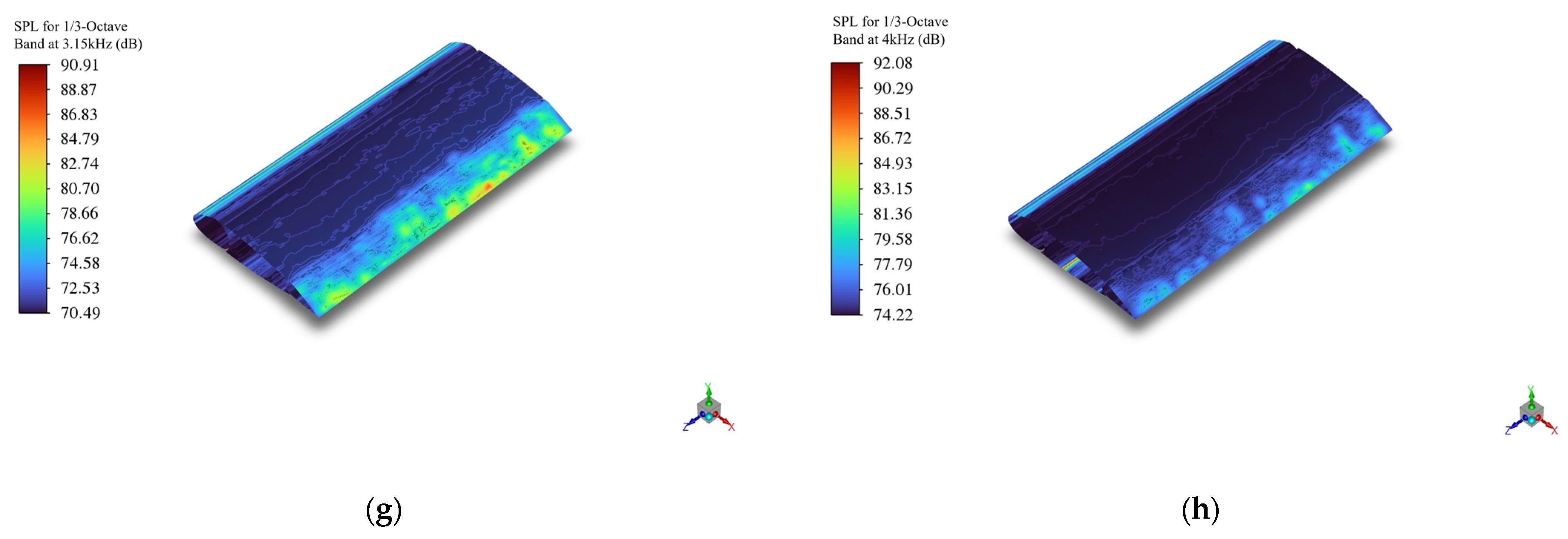
3.1. Noise Spectrum
3.2. Noise Mechanism Analysis of the Gurney Flap Airfoil
3.3. Noise Mechanism Analysis of the Leading-Edge and Trailing-Edge Flap Airfoil
4. Conclusions
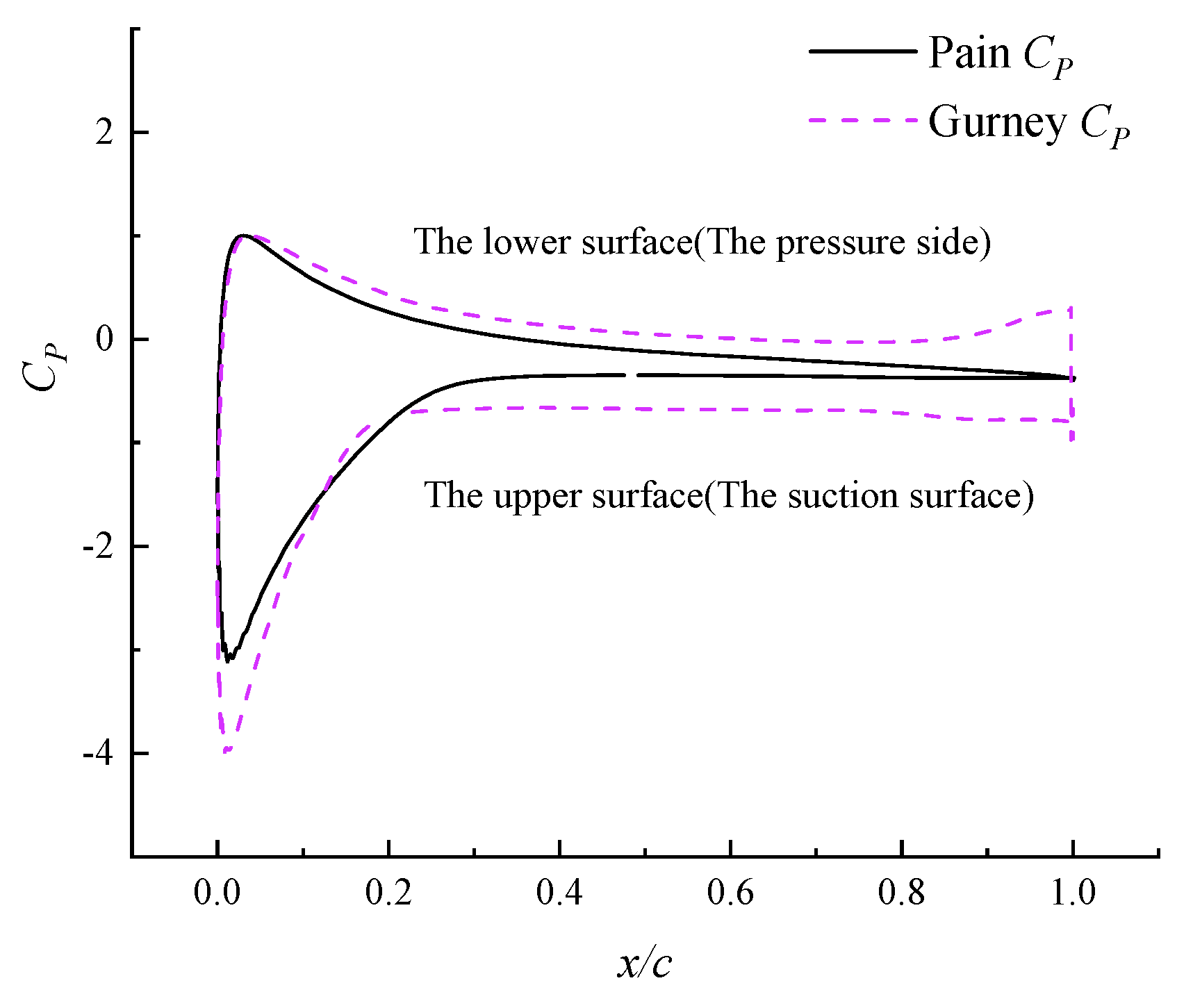
- At an angle of attack of 20°, numerical simulations show that both the Gurney flap airfoil and the leading- and trailing-edge flap airfoil exhibit significant improvements in lift and drag compared to the baseline airfoil. The Gurney flap notably enhances lift with minimal change in drag, resulting in a substantial increase in lift-to-drag ratio. For the airfoil with leading- and trailing-edge flaps, both lift and drag increase considerably, but the lift-to-drag ratio also shows a moderate improvement. The surface pressure coefficient distributions further reveal that the installation of Gurney flaps and leading- and trailing-edge flaps leads to a marked increase in suction-side pressure, thereby contributing to the enhancement of lift.
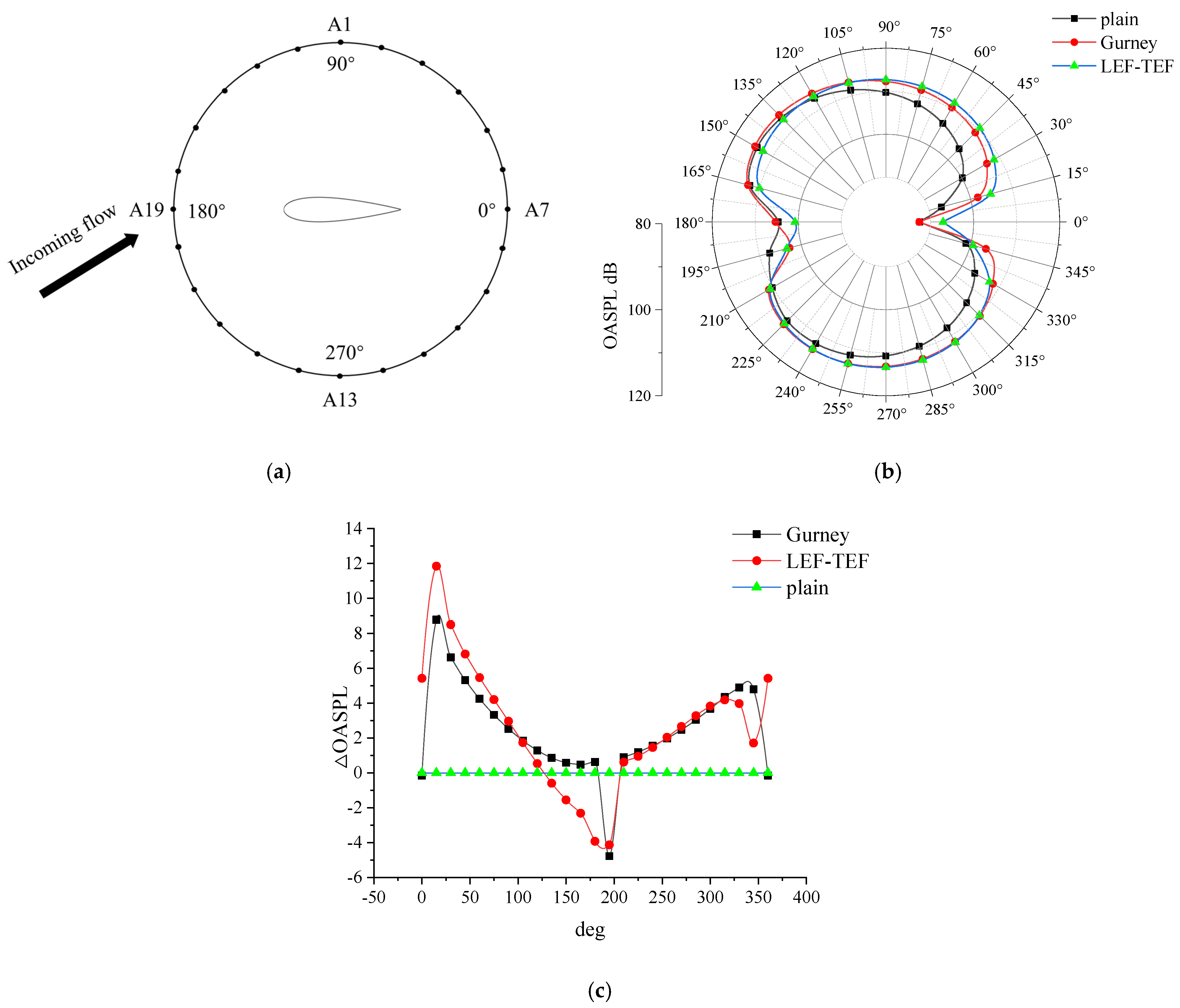
- In terms of spatial radiation characteristics, compared to the baseline airfoil, the Gurney flap airfoil shows a slight reduction of 0.15 dB in overall sound pressure level (OASPL) at the trailing edge (0° azimuth) and a slight increase of 0.63 dB at the leading edge (180° azimuth), indicating minimal changes at these two positions. However, in the regions between 0 and 90° and 270 and 360° azimuth, the OASPL increases by more than 2.5 dB. For the airfoil equipped with leading- and trailing-edge flaps, the OASPL increases at most azimuthal angles, with a maximum rise of up to 11.8 dB. Nevertheless, in the vicinity of the leading edge, specifically within the 135–195° azimuth range, the maximum reduction in OASPL reaches approximately 4.1 dB. These results suggest that both types of flow control generally lead to increased noise across most azimuthal directions, with the leading- and trailing-edge flap configuration causing a more pronounced noise increase near the trailing edge. However, a noise reduction effect is observed near the leading edge for the airfoil with leading- and trailing-edge flaps, with a maximum noise reduction rate of 4.4%.
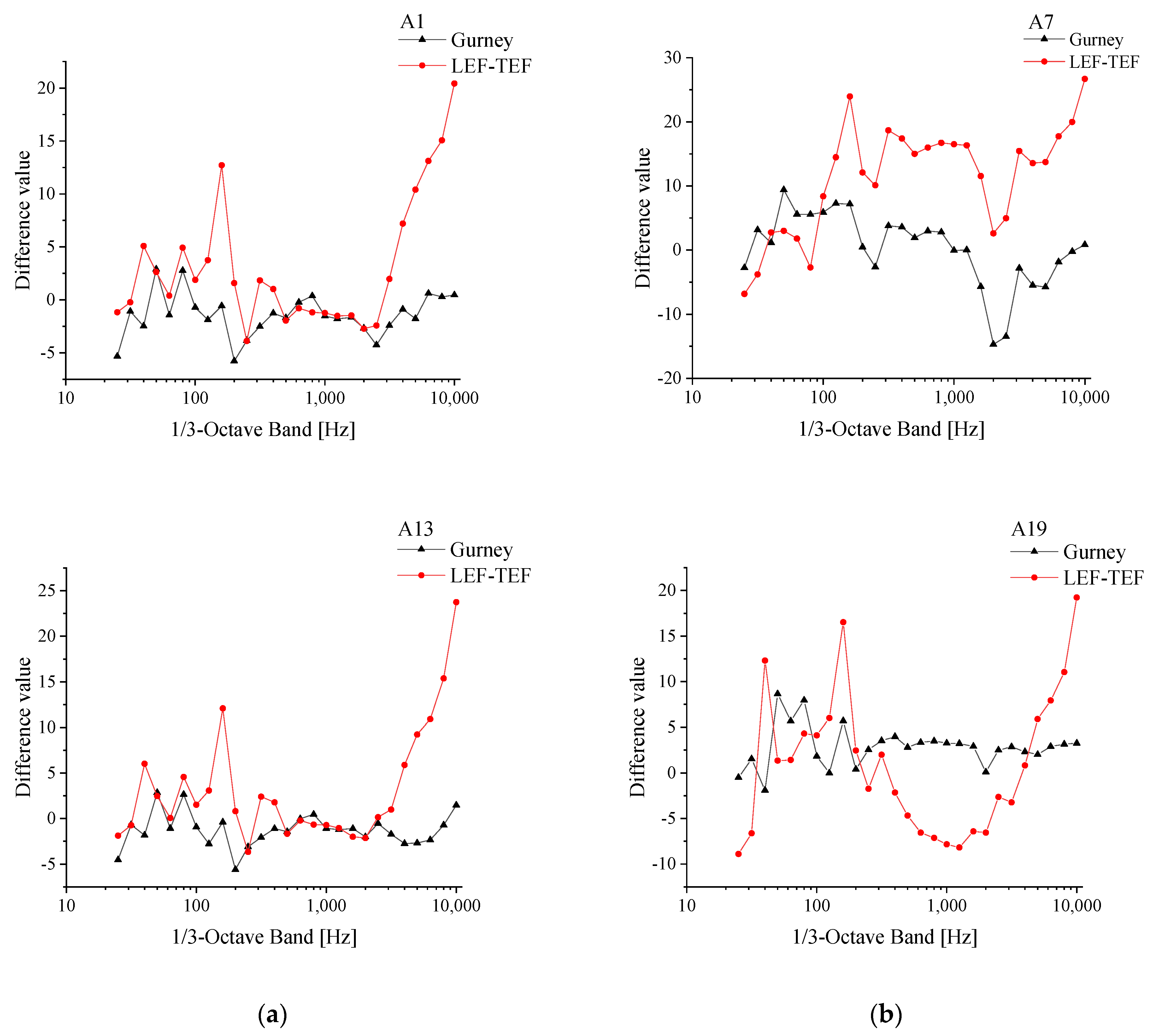
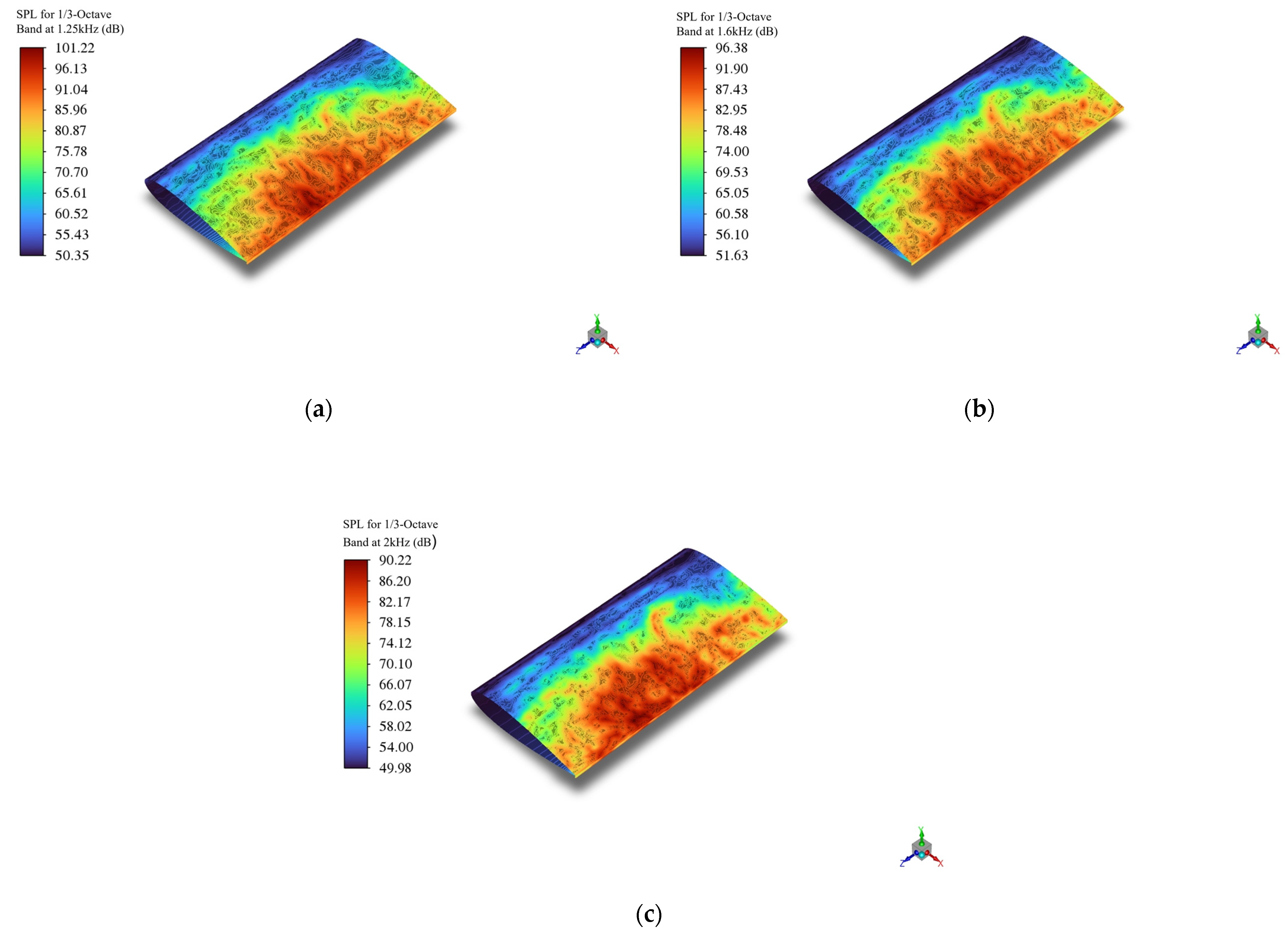
- At an azimuthal angle of 0°, within the low- to mid-frequency range (25–1250 Hz), the Gurney flap airfoil exhibits higher sound pressure levels than the baseline airfoil across most frequencies, with a maximum increase of 9.4 dB observed at 50 Hz. In the mid- to high-frequency range (1250–10,000 Hz), the Gurney flap airfoil shows higher sound pressure only at 10,000 Hz, where it exceeds the baseline by 0.85 dB; at all other frequencies, it exhibits lower sound pressure levels, with a maximum reduction of 14.7 dB at 2000 Hz. This indicates that near the trailing edge, the Gurney flap has a positive effect in suppressing noise in the mid- to high-frequency range. At an azimuthal angle of 180°, within the mid- to high-frequency range (400–3150 Hz), the baseline airfoil displays higher sound pressure levels compared to the airfoil with leading- and trailing-edge flaps, with a maximum increase of 8.19 dB at 1250 Hz. This suggests that near the leading edge, the combined leading- and trailing-edge flaps are effective in suppressing noise within the mid- to high-frequency range.
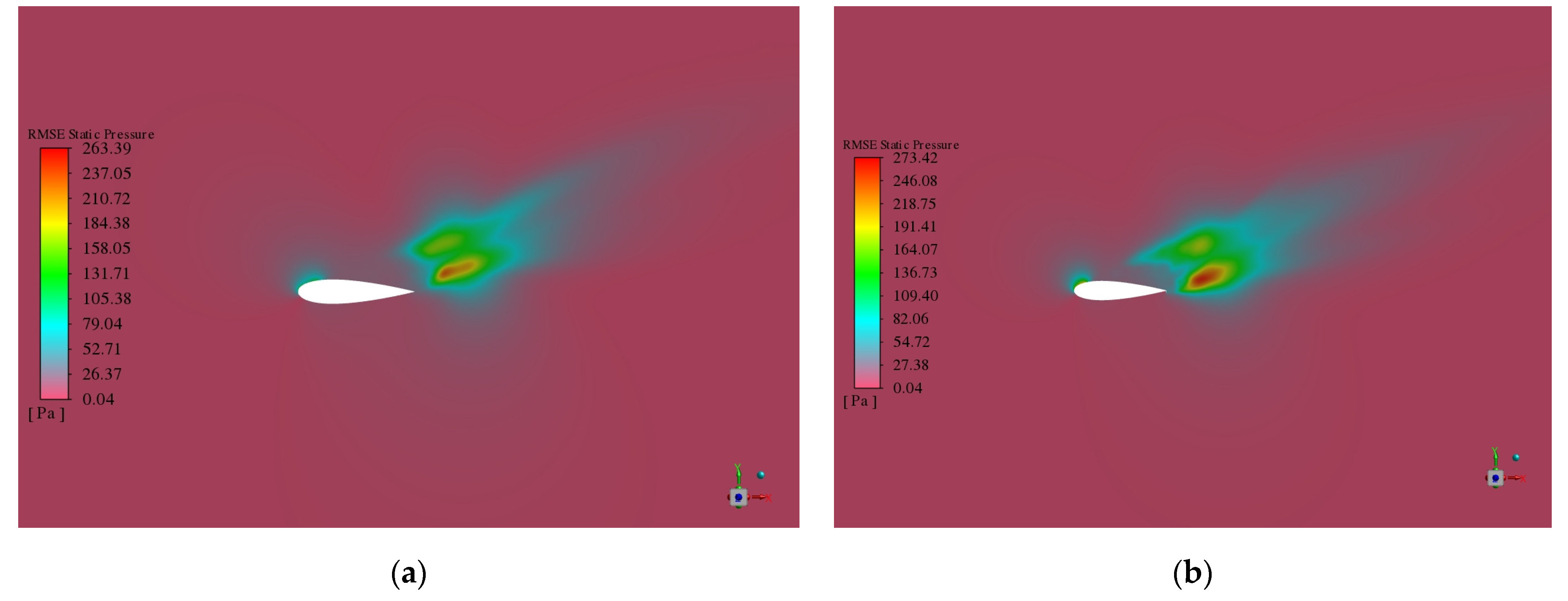
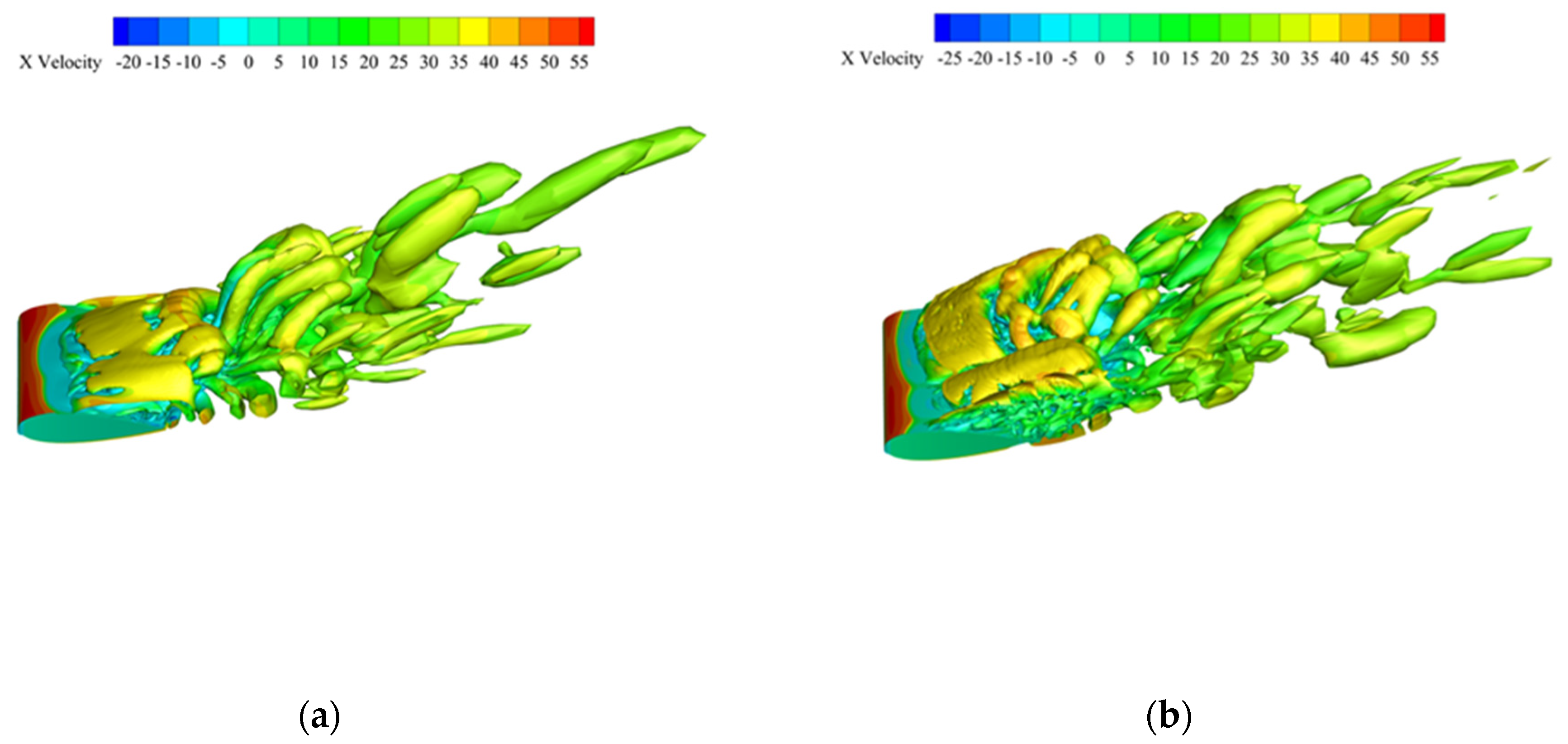
- The pressure fluctuations in the flow field and the surface sound pressure level (SPL) contours of the airfoil were analyzed to better understand the mechanisms by which the two flow control strategies influence noise generation. For the Gurney flap airfoil, the distribution range of peak pressure fluctuations near the trailing edge at 0° azimuth and near the leading edge at 180° azimuth is larger compared to the baseline airfoil. At the trailing edge, noise is mainly generated by the interaction between the airfoil surface and the airflow, constituting the primary source of noise. The presence of the Gurney flap leads to finer and more fragmented wake vortices, thereby reducing the noise contribution from wake vortex interactions within this frequency range. In contrast, for the airfoil equipped with combined leading- and trailing-edge flaps, pressure fluctuations near the leading edge at 180° azimuth are significantly lower than those of the baseline airfoil, resulting in reduced leading-edge noise. However, at the trailing edge, the noise level increases compared to the baseline, with the noise predominantly originating from wake vortex interactions, while the contribution from the interaction between the airfoil surface and the airflow is relatively minor.
- By applying two flow controls to the original airfoil, it can be seen that an increase in the airfoil lift-to-drag ratio is accompanied by an increase in noise generation. Since the Gurney flap airfoil enhances the lift resistance ratio much more than the leading- and trailing-edge flap airfoils in this flow condition, and its influence on the noise generation is smaller compared to the leading- and trailing-edge flap airfoils, it is an excellent flow control method for enhancing lift and controlling noise.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Frankhouser, M.W.; Gregory, J.W. Nanosecond Dielectric Barrier Discharge Plasma Actuator Flow Control of Compressible Dynamic Stall. In Proceedings of the 46th AIAA Plasmadynamics and Lasers Conference, Dallas, TX, USA, 22–26 June 2015. [Google Scholar]
- Maruta, Y.; Kotake, S. Separated Flow Noise of a Flat Plate at Large Attack Angles. J. Sound Vib. 1983, 89, 335–357. [Google Scholar] [CrossRef]
- Wang, T.; Tian, L.; Zhong, W.; Wang, L.; Zhu, C. Advances in Aerodynamic Research for Wind Energy Utilization I: Aerodynamic Characteristics of Wind Turbines. J. Aerodyn. 2022, 40, 1–21. [Google Scholar]
- Choi, H.; Jeon, W.-P.; Kim, J. Control of Flow Over a Bluff Body. Annu. Rev. Fluid Mech. 2008, 40, 113–139. [Google Scholar] [CrossRef]
- Zhao, Y.H.; Liang, H.; Wang, B. Research Progress on Factors Affecting Airfoil Dynamic Stall and Flow Control. Acta Aerodyn. Sin. 2020, 41, 23605. [Google Scholar]
- Fouatih, O.M.; Medale, M.; Imine, O.; Imine, B. Design optimization of the aerodynamic passive flow control on NACA4415 airfoil using vortex generators. Eur. J. Mech.-B/Fluids 2016, 56, 82–96. [Google Scholar] [CrossRef]
- Liu, P.; Li, L.; Xing, Y.; Guo, H. Research Progress on Aerodynamic Noise of High-Lift Devices for Large Aircraft. Acta Aerodyn. Sin. 2017, 35, 472–484. [Google Scholar]
- Amini, Y.; Liravi, M.; Izadpanah, E. The effects of Gurney flap on the aerodynamic performance of NACA0012 airfoil in the rarefied gas flow. Comput. Fluids 2018, 170, 93–105. [Google Scholar] [CrossRef]
- Storms, B.L.; Jang, C.S. Lift enhancement of an airfoil using a Gurney flap and vortex generators. J. Aircr. 1994, 31, 542–547. [Google Scholar] [CrossRef]
- Wang, J.J.; Li, Y.C.; Choi, K.S. Gurney flap—Lift enhancement; mechanisms; applications. Prog. Aerosp. Sci. 2008, 44, 22–47. [Google Scholar] [CrossRef]
- He, X.; Wang, J.; Yang, M.; Ma, D.; Yan, C.; Liu, P. Numerical simulation of Gurney flap on SFYT15thick airfoil. Theor. Appl. Mech. Lett. 2016, 6, 286–292. [Google Scholar] [CrossRef]
- Ye, X.; Hu, J.; Zheng, N.; Li, C. Numerical study on aerodynamic performance and noise of wind turbine airfoils with serrated gurney flap. Energy 2023, 262, 125574. [Google Scholar] [CrossRef]
- Ye, X.; Zheng, N.; Hu, J.; Li, C.; Xue, Z. Numerical investigation of the benefits of serrated Gurney flaps on an axial flow fan. Energy 2022, 252, 124072. [Google Scholar] [CrossRef]
- Zhang, X.; Sciacchitano, A.; Pröbsting, S. Aeroacoustic analysis of an airfoil with Gurney flap based on time-resolved particle image velocimetry measurements. J. Sound Vib. 2018, 422, 490–505. [Google Scholar] [CrossRef]
- Amini, Y.; Emdad, H.; Farid, M. Adjoint shape optimization of airfoils with attached Gurney flap. Aerosp. Sci. Technol. 2015, 41, 216–228. [Google Scholar] [CrossRef]
- Tang, W.; Liu, P.; Hu, T.; Qu, Q.; Guo, H.; Liu, Y.; Akkermans, R.A.D. Effect of gurney flaps on a nonslender delta wing during large-amplitude and high-frequency dynamic pitching. Aerosp. Sci. Technol. 2023, 143, 108715. [Google Scholar] [CrossRef]
- Xie, J.; Yang, X.; Ding, J.; Weng, P. Aeroacoustics evaluation and mechanism of Krueger flap. Aerosp. Sci. Technol. 2025, 161, 110085. [Google Scholar] [CrossRef]
- Qian, Y.; Zhang, Y.; Sun, Y.; Wang, T. Numerical investigations of the flow control effect on a thick wind turbine airfoil using deformable trailing edge flaps. Energy 2023, 265, 126327. [Google Scholar] [CrossRef]
- Liu, Q.; Miao, W.; Li, C.; Hao, W.; Zhu, H.; Deng, Y. Effects of trailing-edge movable flap on aerodynamic performance and noise characteristics of VAWT. Energy 2019, 189, 116271. [Google Scholar] [CrossRef]
- Lee, T.; Gerontakos, P. Unsteady Airfoil with Dynamic Leading- and Trailing-Edge Flaps. J. Aircr. 2009, 46, 1076–1081. [Google Scholar] [CrossRef]
- Samara, F.; Johnson, D.A. Dynamic Stall on Pitching Cambered Airfoil with Phase Offset Trailing Edge Flap. AIAA J. 2020, 58, 2844–2856. [Google Scholar] [CrossRef]
- He, G.; Deparday, J.; Siegel, L.; Henning, A.; Mulleners, K. Stall Delay and Leading-Edge Suction for a Pitching Airfoil with Trailing-Edge Flap. AIAA J. 2020, 58, 5146–5155. [Google Scholar] [CrossRef]
- Jawahar, H.K.; Ai, Q.; Azarpeyvand, M. Experimental and numerical investigation of aerodynamic performance for airfoils with morphed trailing edges. Renew. Energy 2018, 127, 355–367. [Google Scholar] [CrossRef]
- Yang, Z.; Xu, L.; Zhang, K.; Zhu, W. Numerical study on benefits of curved serrations upon suppressing turbulent boundary layer trailing-edge noise. Phys. Lett. A 2025, 530, 130131. [Google Scholar] [CrossRef]
- Wei, R.; Liu, Y. On the shear-layer oscillation and low-frequency tonal noise in a slat cove. Phys. Fluids 2025, 37, 034113. [Google Scholar] [CrossRef]
- Kang, D.; Lee, S. Effect of trailing-edge curvature on airfoil noise source and radiation characteristics. Phys. Fluids 2025, 37, 035134. [Google Scholar] [CrossRef]
- Marouf, A.; Charbonnier, D.; Vos, J.B.; El Akoury, R.; Hoarau, Y.; Braza, M. Morphing of high-lift wing-flap system with cambering and trailing-edge flapping at high Reynolds number towards a full airplane application. J. Fluids Struct. 2024, 127, 104111. [Google Scholar] [CrossRef]
- Shehata, H.M.; Zakaria, M.Y.; Woolsey, C.A.; Hajj, M.R. Lift enhancement by a flapped trailing edge at low Reynolds number: A frequency response approach. J. Fluids Struct. 2022, 110, 103518. [Google Scholar] [CrossRef]
- Lee, T.; Su, Y.Y. Unsteady airfoil with a harmonically deflected trailing-edge flap. J. Fluids Struct. 2011, 27, 1411–1424. [Google Scholar] [CrossRef]
- Wang, L.; Tian, F.-B. Sound generated by the flow around an airfoil with an attached flap: From passive fluid–structure interaction to active control. J. Fluids Struct. 2022, 111, 103571. [Google Scholar] [CrossRef]
- Jawahar, H.K.; Vemuri, S.S.; Azarpeyvand, M. Aerodynamic noise characteristics of airfoils with morphed trailing edges. Int. J. Heat Fluid Flow 2022, 93, 108892. [Google Scholar] [CrossRef]
- Swalwell, K.; Sheridan, J.; Melbourne, W. Frequency analysis of surface pressures on an airfoil after stall. In Proceedings of the 21st AIAA Applied Aerodynamics Conference, Orlando, FL, USA, 24 June 2003; p. 3416. [Google Scholar]
- Ffowcs Williams, J.E.; Hawkings, D.L. Sound generation by turbulence and surfaces in arbitrary motion. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1969, 264, 321–342. [Google Scholar]
- Haase, W.; Braza, M.; Revell, A. DESider–A European Effort on Hybrid RANS-LES Modelling: Results of the European-Union Funded Project, 2004–2007; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Wang, F.M.; Wang, J.C. Relationship and Calculation of 1/3 Octave and Octave Spectrum in Noise Measurement. Noise Vib. Control 1996, 16, 39–41. [Google Scholar]




| EXP | 6 × 106 | 4 × 106 | 2 × 106 | |
| Cl | 0.931 | 0.906 | 0.914 | 0.89 |
| Δ | −2.76% | −1.86% | −4.61% | |
| Cd | 1.517 | 1.467 | 1.473 | 1.436 |
| Δ | −3.41% | −2.99% | −5.64% | |
| EXP | EADS-M | 400w | |
| Cl | 0.931 | 0.889 | 0.914 |
| Δ | −4.51% | −1.86% | |
| Cd | 1.517 | 1.425 | 1.473 |
| Δ | −6.06% | −2.99% | |
| EXP | CFD Plain | CFD Gurney | Enhancement Percentage | |
|---|---|---|---|---|
| Cl | 0.443 | 0.332 | 0.643 | 93.68% |
| Cd | 0.285 | 0.252 | 0.253 | 0.39% |
| Lift-to-Drag Ratio | 1.557 | 1.317 | 2.542 | 93.01% |
| EXP | CFD Plain | CFD LEF&TEF | Enhancement Percentage | |
|---|---|---|---|---|
| Cl | 0.443 | 0.332 | 0.548 | 65.06% |
| Cd | 0.285 | 0.252 | 0.346 | 37.30% |
| Lift-to-Drag Ratio | 1.554 | 1.317 | 1.583 | 20.19% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Li, K.; Sun, X. Influence of Gurney Flap and Leading-Edge/Trailing-Edge Flaps on the Stall Characteristics and Aeroacoustic Performance of Airfoils. Fluids 2025, 10, 152. https://doi.org/10.3390/fluids10060152
Liu Z, Li K, Sun X. Influence of Gurney Flap and Leading-Edge/Trailing-Edge Flaps on the Stall Characteristics and Aeroacoustic Performance of Airfoils. Fluids. 2025; 10(6):152. https://doi.org/10.3390/fluids10060152
Chicago/Turabian StyleLiu, Zelin, Kaidi Li, and Xiaojing Sun. 2025. "Influence of Gurney Flap and Leading-Edge/Trailing-Edge Flaps on the Stall Characteristics and Aeroacoustic Performance of Airfoils" Fluids 10, no. 6: 152. https://doi.org/10.3390/fluids10060152
APA StyleLiu, Z., Li, K., & Sun, X. (2025). Influence of Gurney Flap and Leading-Edge/Trailing-Edge Flaps on the Stall Characteristics and Aeroacoustic Performance of Airfoils. Fluids, 10(6), 152. https://doi.org/10.3390/fluids10060152





