Development of an Anisotropic Porous Model of a Single Cow for Numerical Barn Simulations—A Numerical Study
Abstract
1. Introduction
- Find anisotropic parameters for the pressure drop and heat transfer for a single cow modelled as a porous block as a function of wind speed, cow position, wind direction, and ambient temperature.
- Implement these parameters into the porous media model via regression curves.
- Validate the porous model approach with a random AOZ to compare with modelling using simplified solid cow geometries.
2. Materials and Methods
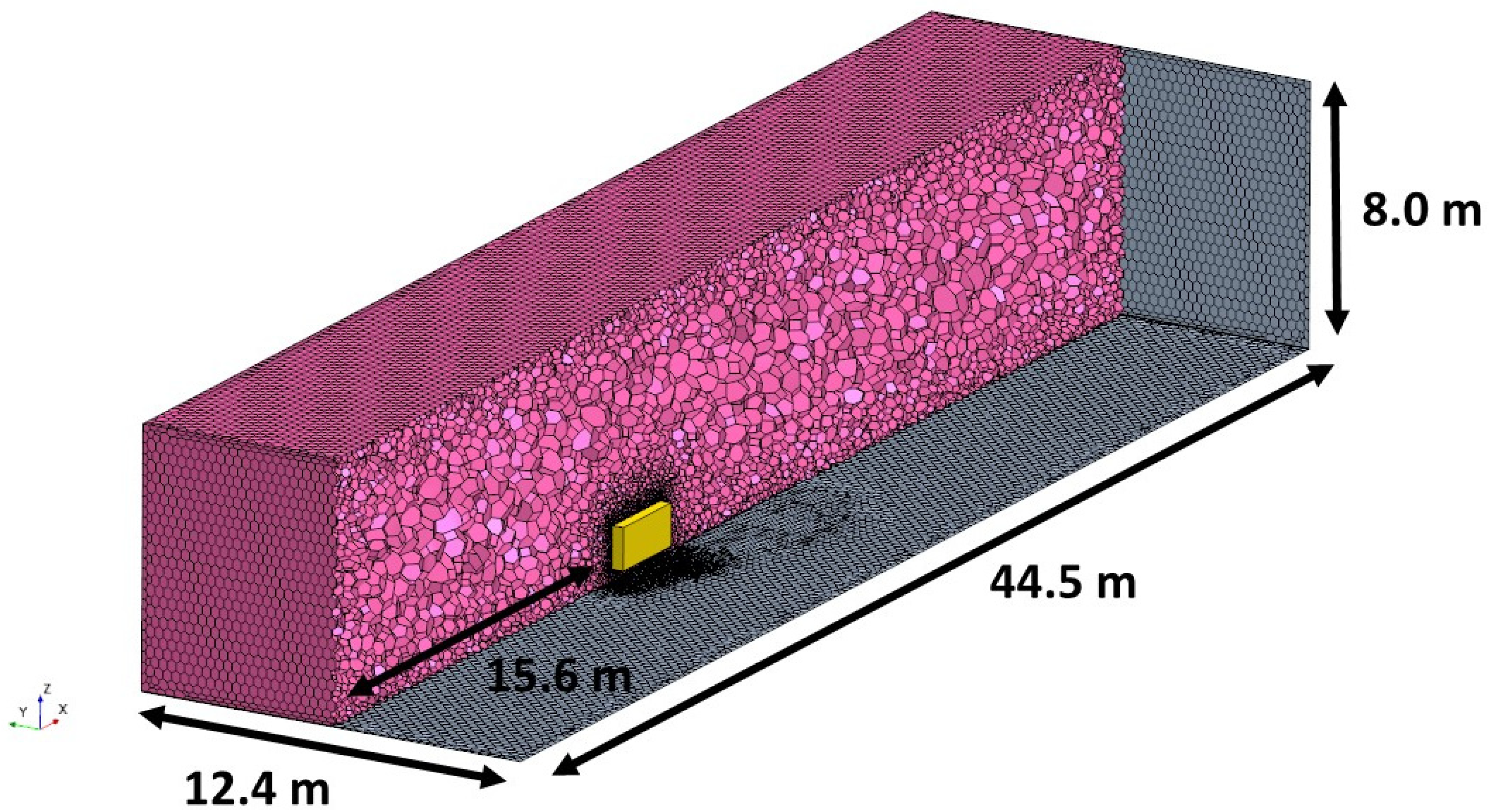
2.1. General Settings for the Simulations
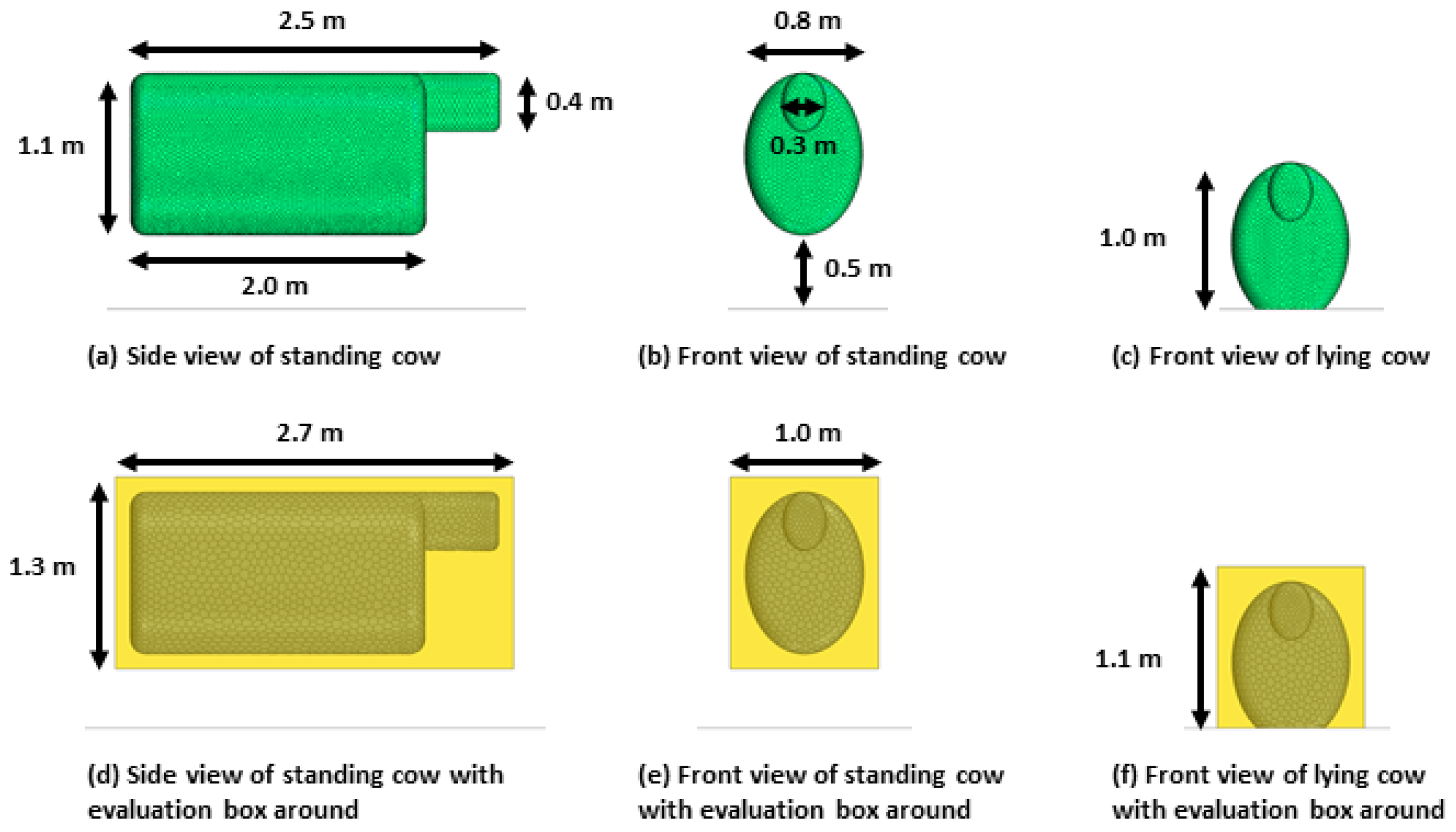
2.2. The Solid and Porous Cow Model
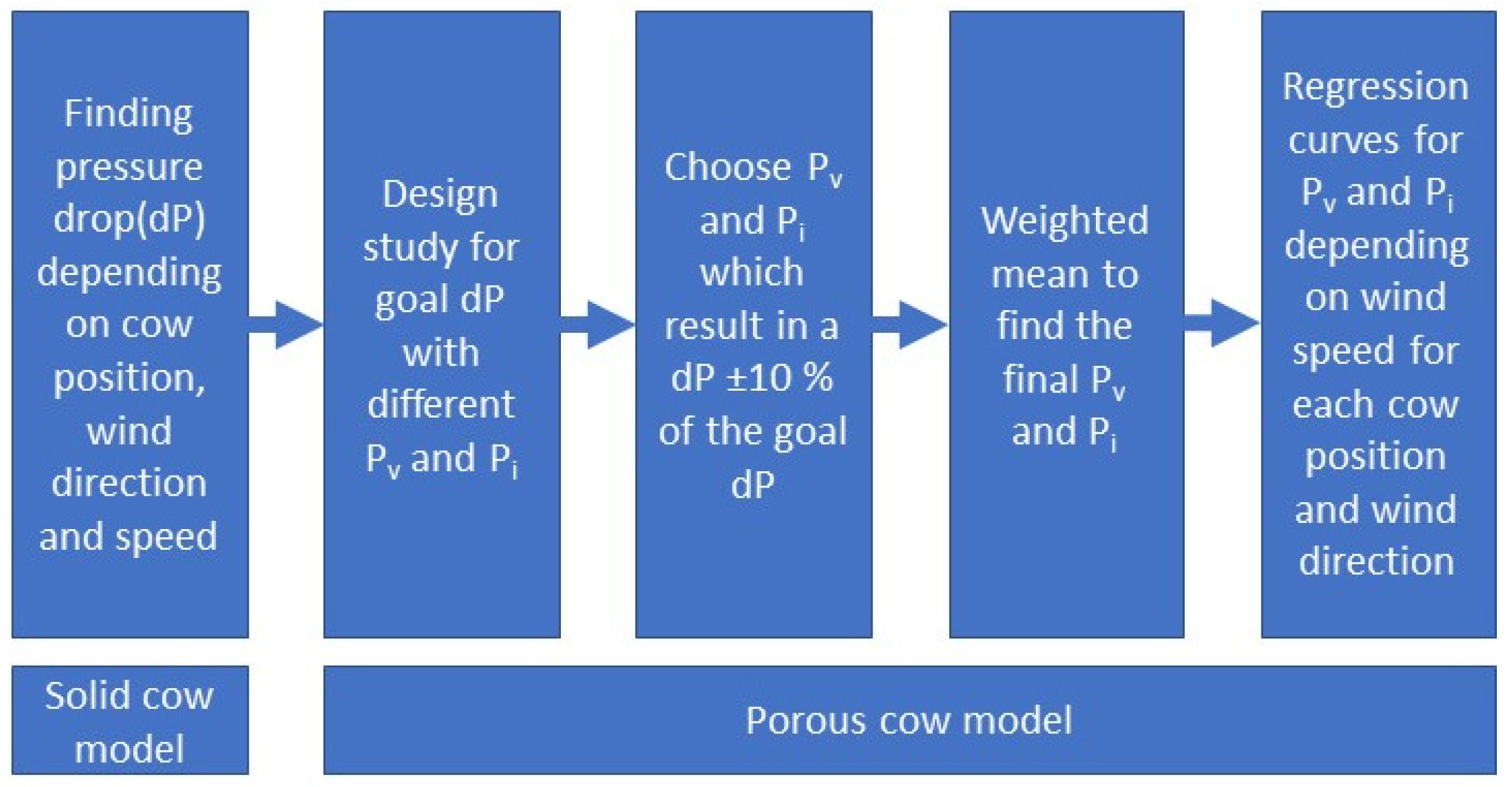
2.3. Porous Media Modelling
2.3.1. Pressure Drop
2.3.2. Heat Transfer
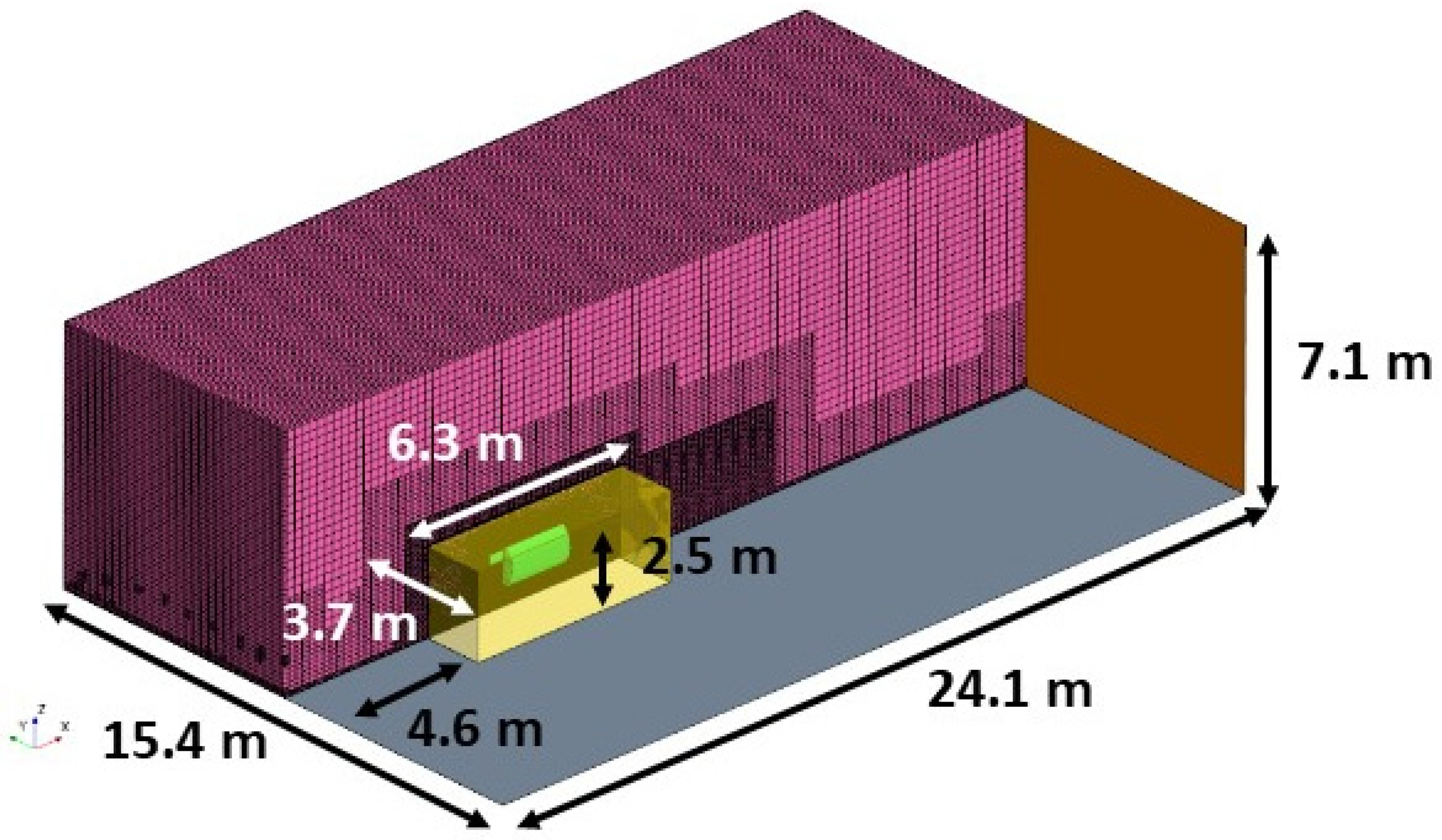
2.4. Validation with a Small AOZ
3. Results and Discussion
3.1. Results for Pressure Drop
3.2. Results for Heat Transfer
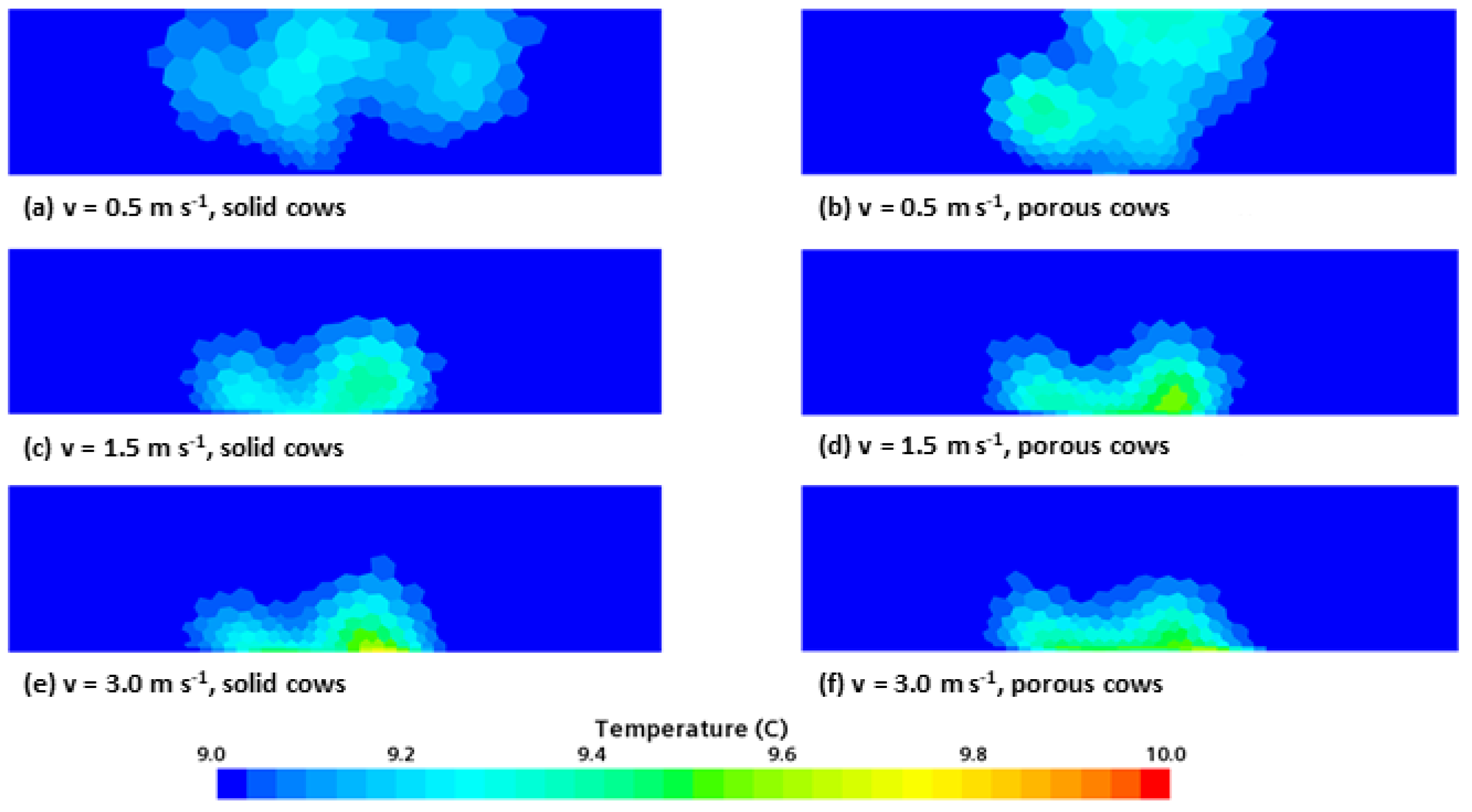
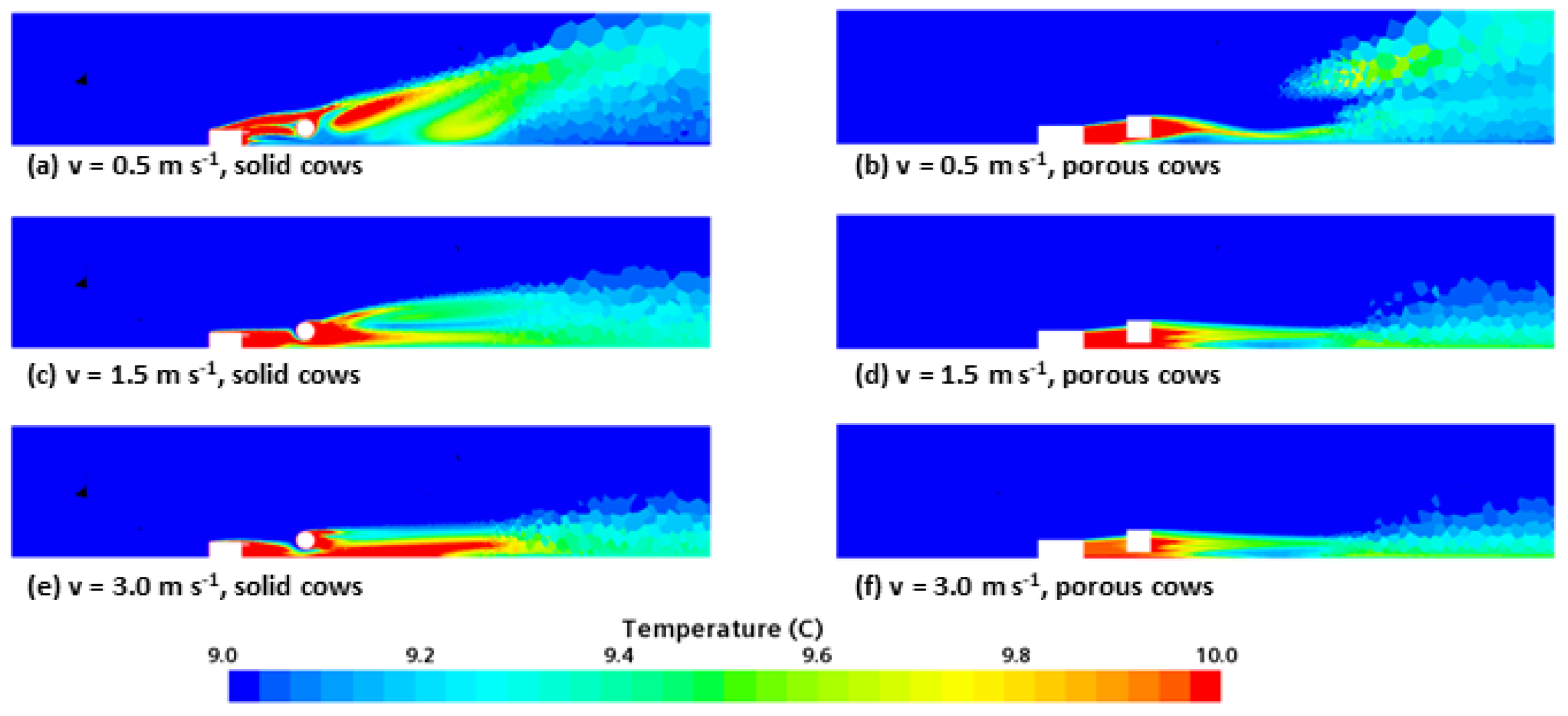
3.3. Results for the Validation with a Small AOZ
3.3.1. Pressure Drop over the AOZ
3.3.2. Heat Transfer of the AOZ
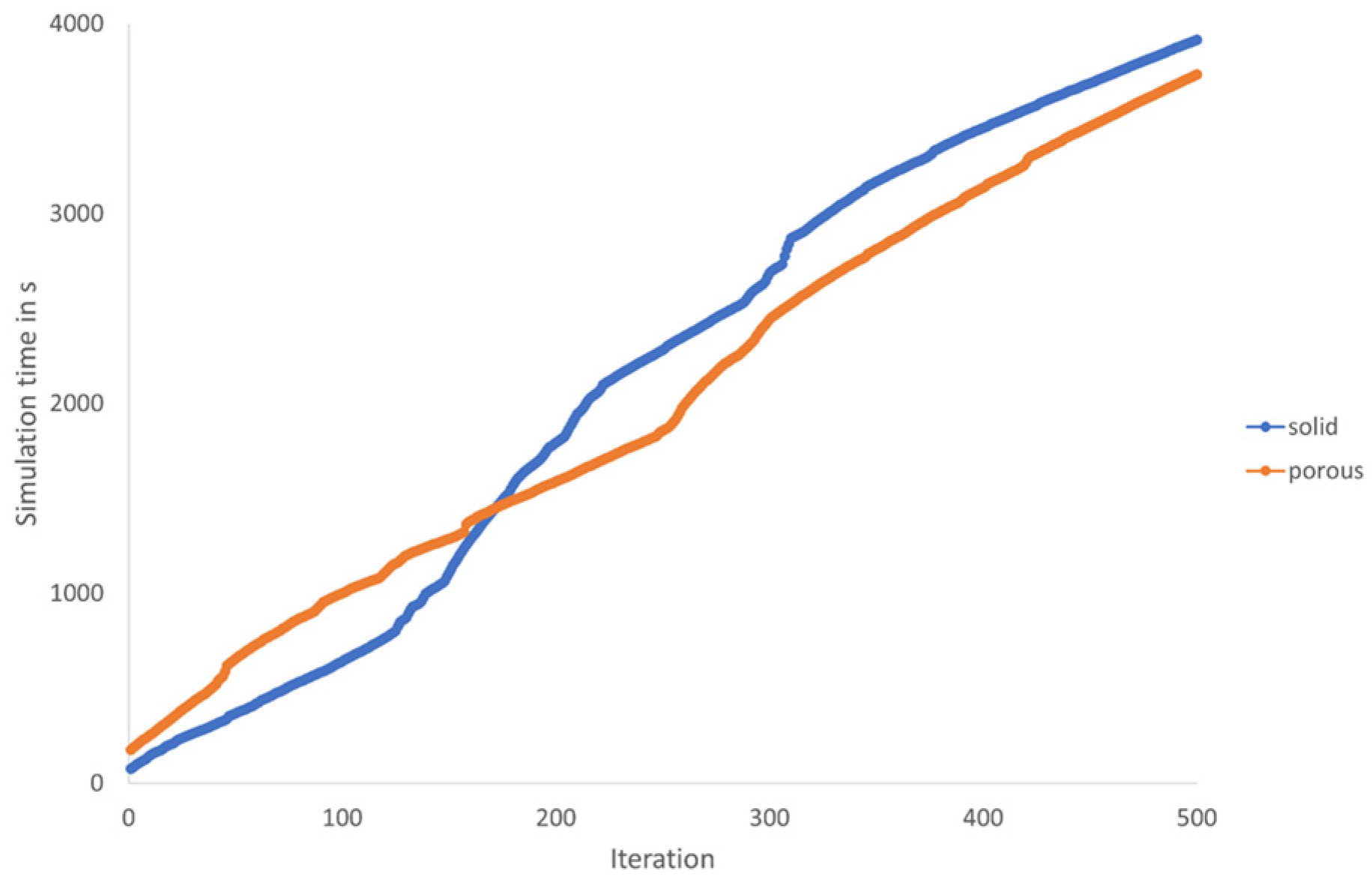
3.3.3. Computational Time and Mesh Size
4. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| A | area (m2) |
| AER | air exchange rate (h−1) |
| AOZ | animal-occupied zone |
| CFD | computational fluid dynamics |
| dP | pressure drop (Pa) |
| haircot | temperature of the haircoat of the cow |
| hc | heat transfer coefficient (W·m−2·K−1) |
| HG | heart girth (m) |
| IAD | interaction area density (m−1) |
| L | characteristic length (m) |
| lc | lying, cross |
| lf | lying, front |
| m | mass-flow-averaged |
| Nu | Nusselt number (-) |
| Pi | porous inertial resistance (kg·m−4) |
| Pv | porous viscous resistance (kg·m−3·s−1) |
| porous | using porous model approach |
| Q | heat flux (W) |
| RANS | Reynolds-averaged Navier–Stokes |
| S | distance from the beginning of the AOZ (m) |
| sc | standing, cross |
| sf | standing, front |
| solid | using a solid model approach |
| T | temperature (°C) |
| v | velocity (m·s−1) |
| W | width of the AOZ (m) |
| w | weight (kg) |
| x | in x-direction |
| y | in y-direction |
| λ | thermal conductivity (W·m−1·K−1) |
| χ | porosity (-) |
| 0 | background |
References
- Janke, D.; Yi, Q.; Thormann, L.; Hempel, S.; Amon, B.; Nosek, Š.; van Overbeke, P.; Amon, T. Direct Measurements of the Volume Flow Rate and Emissions in a Large Naturally Ventilated Building. Sensors 2020, 20, 6223. [Google Scholar] [CrossRef] [PubMed]
- Doumbia, E.M.; Janke, D.; Yi, Q.; Amon, T.; Kriegel, M.; Hempel, S. CFD modelling of an animal occupied zone using an anisotropic porous medium model with velocity depended resistance parameters. Comput. Electron. Agric. 2021, 181, 105950. [Google Scholar] [CrossRef]
- Bjerg, B. Modelling and Design of the Microclimate in Livestock Housing. In Encyclopedia of Smart Agriculture Technologies; Zhang, Q., Ed.; Springer International Publishing: Cham, Switzerland, 2022; pp. 1–15. ISBN 978-3-030-89123-7. [Google Scholar]
- Saha, C.K.; Yi, Q.; Janke, D.; Hempel, S.; Amon, B.; Amon, T. Opening Size Effects on Airflow Pattern and Airflow Rate of a Naturally Ventilated Dairy Building—A CFD Study. Appl. Sci. 2020, 10, 6054. [Google Scholar] [CrossRef]
- Tomasello, N.; Valenti, F.; Cascone, G.; Porto, S.M.C. Development of a CFD Model to Simulate Natural Ventilation in a Semi-Open Free-Stall Barn for Dairy Cows. Buildings 2019, 9, 183. [Google Scholar] [CrossRef]
- Gautam, K.R.; Rong, L.; Iqbal, A.; Zhang, G. Full-scale CFD simulation of commercial pig building and comparison with porous media approximation of animal occupied zone. Comput. Electron. Agric. 2021, 186, 106206. [Google Scholar] [CrossRef]
- Bustos-Vanegas, J.D.; Hempel, S.; Janke, D.; Doumbia, M.; Streng, J.; Amon, T. Numerical simulation of airflow in animal occupied zones in a dairy cattle building. Biosyst. Eng. 2019, 186, 100–105. [Google Scholar] [CrossRef]
- Wu, W.; Zhai, J.; Zhang, G.; Nielsen, P.V. Evaluation of methods for determining air exchange rate in a naturally ventilated dairy cattle building with large openings using computational fluid dynamics (CFD). Atmos. Environ. 2012, 63, 179–188. [Google Scholar] [CrossRef]
- Iqbal, A.; Gautam, K.R.; Zhang, G.; Rong, L. Modelling of animal occupied zones in CFD. Biosyst. Eng. 2021, 204, 181–197. [Google Scholar] [CrossRef]
- Stamou, A.; Katsiris, I. Verification of a CFD model for indoor airflow and heat transfer. Build. Environ. 2006, 41, 1171–1181. [Google Scholar] [CrossRef]
- Rong, L.; Nielsen, P.V.; Bjerg, B.; Zhang, G. Summary of best guidelines and validation of CFD modeling in livestock buildings to ensure prediction quality. Comput. Electron. Agric. 2016, 121, 180–190. [Google Scholar] [CrossRef]
- Zhai, Z.J.; Zhang, Z.; Zhang, W.; Chen, Q.Y. Evaluation of Various Turbulence Models in Predicting Airflow and Turbulence in Enclosed Environments by CFD: Part 1—Summary of Prevalent Turbulence Models. HVACR Res. 2007, 13, 853–870. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, G.; Choi, C.Y. Effect of airflow speed and direction on convective heat transfer of standing and reclining cows. Biosyst. Eng. 2018, 167, 87–98. [Google Scholar] [CrossRef]
- Wu, X.; Shi, Z.; Li, H. Study on the air resistance of pigs in groups based on open-source CFD code: Influence of stocking density and live weight. Biosyst. Eng. 2022, 220, 1–18. [Google Scholar] [CrossRef]
- Mondaca, M.; Choi, C. An Evaluation of Simplifying Assumptions in Dairy Cow Computational Fluid Dynamics Models. Trans. ASABE 2016, 59, 1575–1584. [Google Scholar] [CrossRef]
- Siemens Digital Industries Software. How to Monitor the Pressure Drop. Available online: https://support.sw.siemens.com/knowledge-base/KB000036373_EN_US (accessed on 25 April 2023).
- Marek, R.; Nitsche, K. Praxis der Wärmeübertragung Grundlagen—Anwendungen-Übungsaufgaben; Carl Hanser Verlag GmbH & Co KG: München, Germany, 2015; ISBN 978-3-446-46124-6. [Google Scholar]
- Heinrichs, A.J.; Rogers, G.W.; Cooper, J.B. Predicting body weight and wither height in Holstein heifers using body measurements. J. Dairy Sci. 1992, 75, 3576–3581. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Rong, L.; Zhang, G. Study on convective heat transfer from pig models by CFD in a virtual wind tunnel. Comput. Electron. Agric. 2016, 123, 203–210. [Google Scholar] [CrossRef]
- Mader, T.L.; Davis, M.S.; Kreikemeier, W.M. Case Study: Tympanic Temperature and Behavior Associated with Moving Feedlot Cattle. Prof. Anim. Sci. 2005, 21, 339–344. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, W.; Zhai, Z.J.; Chen, Q.Y. Evaluation of Various Turbulence Models in Predicting Airflow and Turbulence in Enclosed Environments by CFD: Part 2—Comparison with Experimental Data from Literature. HVACR Res. 2007, 13, 871–886. [Google Scholar] [CrossRef]






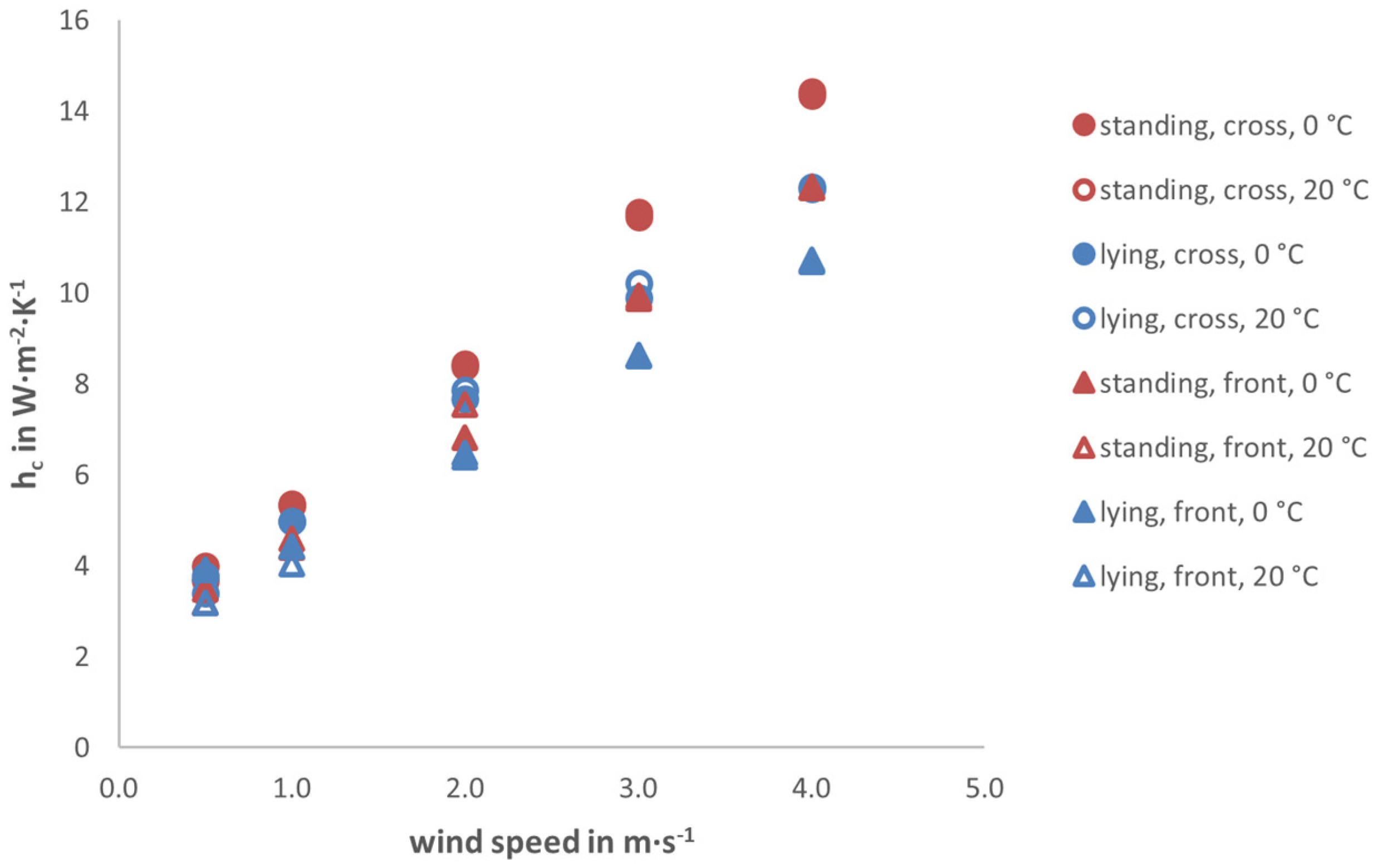
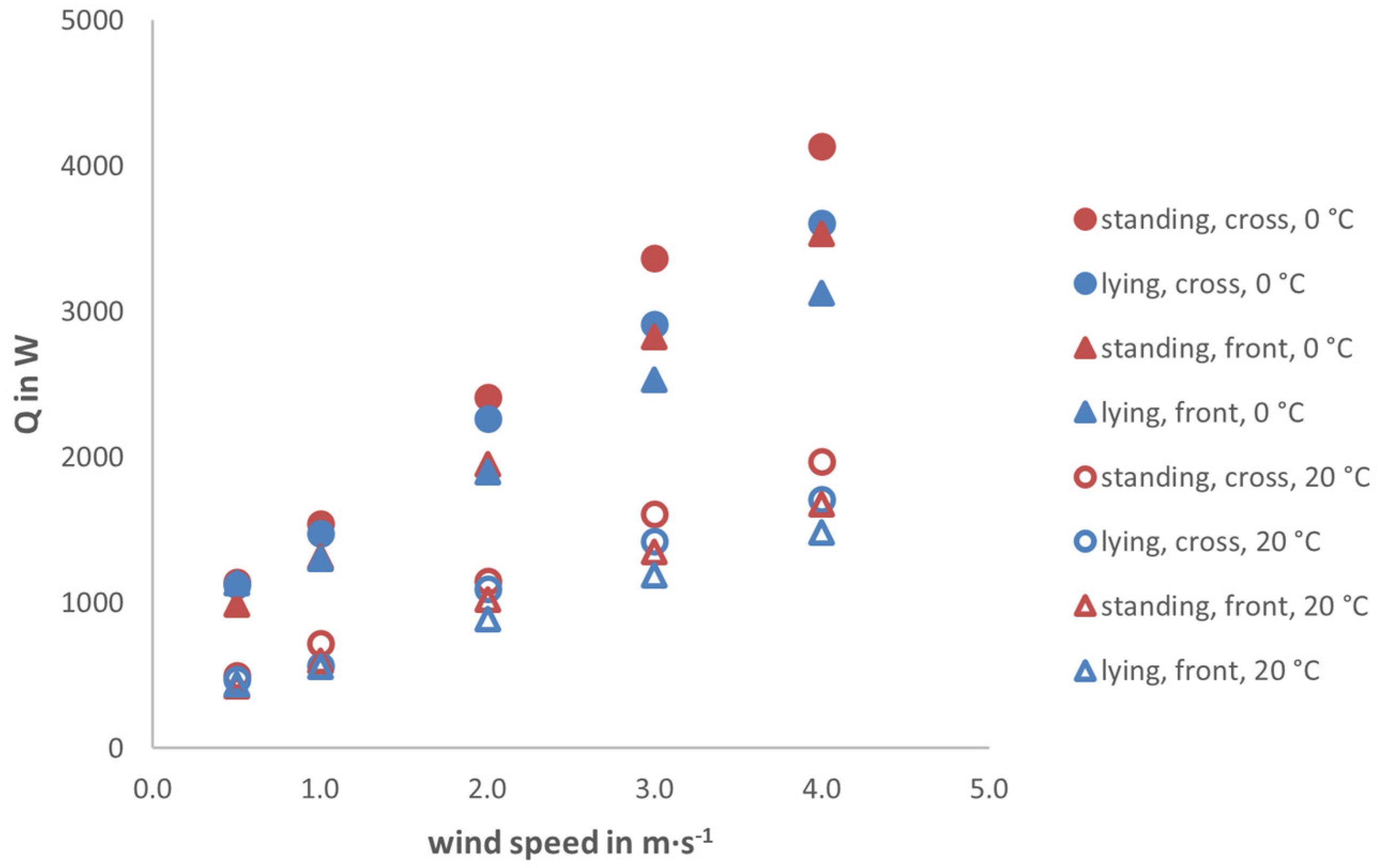
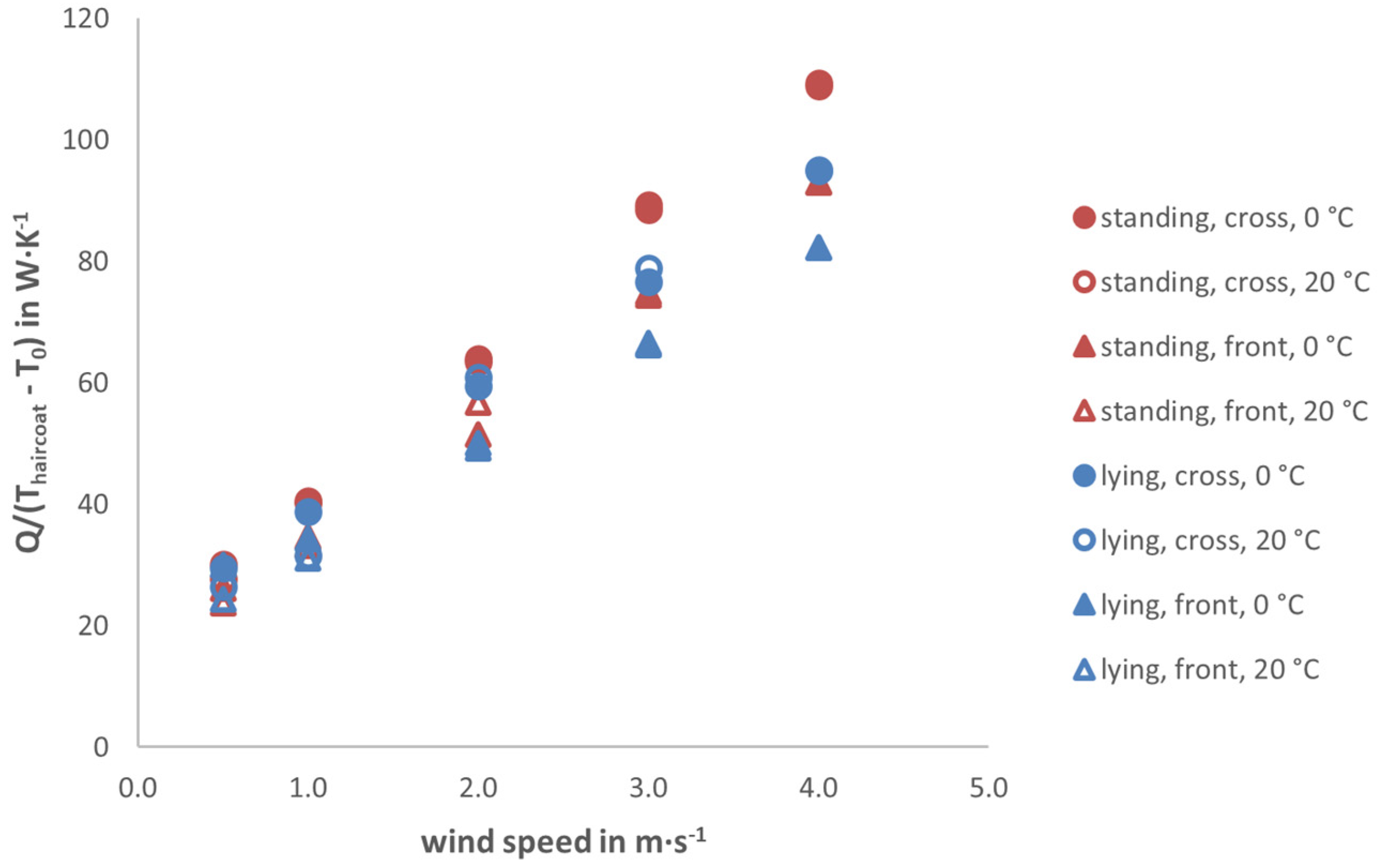
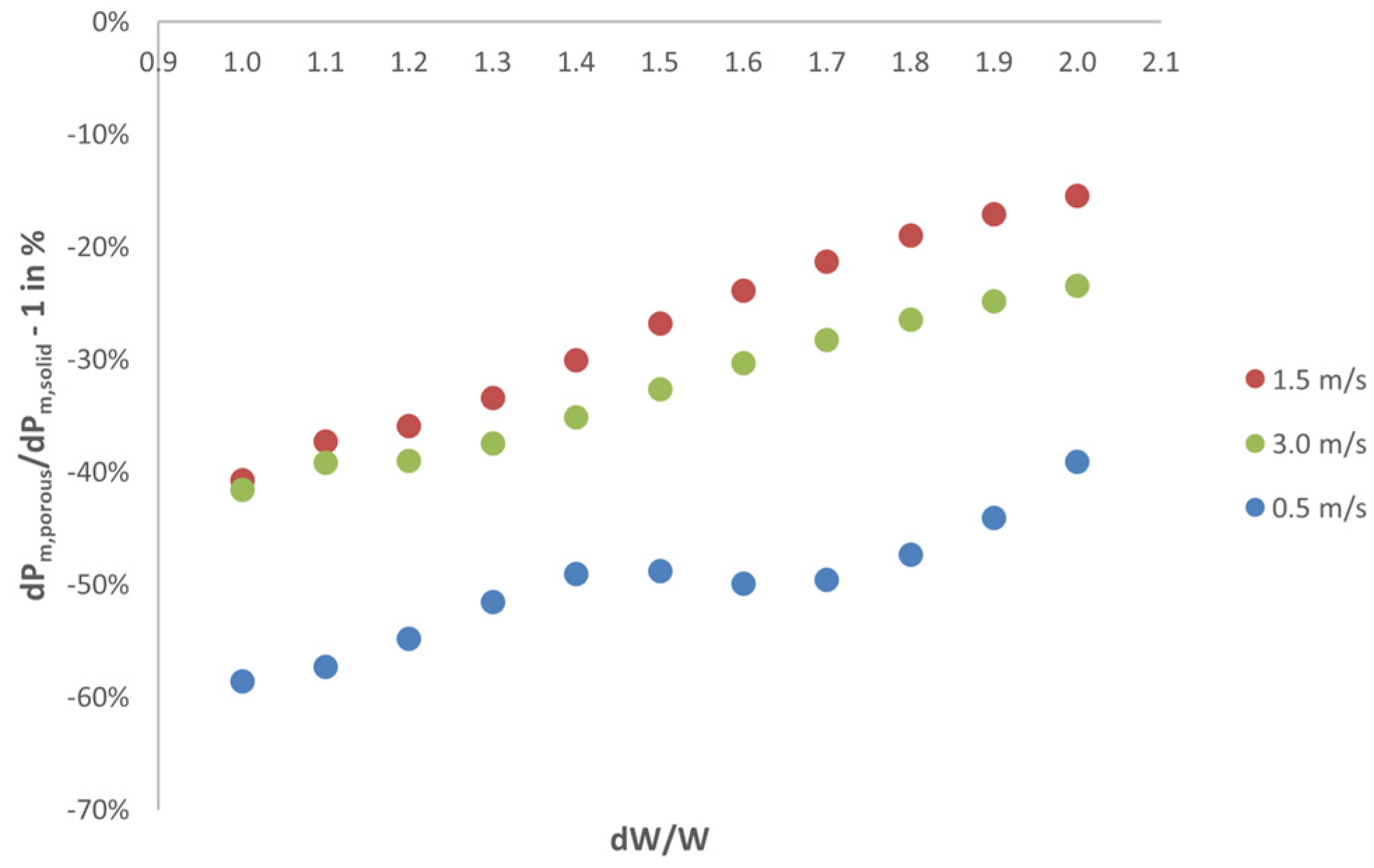



| Cow Position and Flow Direction | Trend Line | R2 |
|---|---|---|
| Lying, cross | 0.98 | |
| 0.98 | ||
| Standing, cross | 0.91 | |
| 0.89 | ||
| Lying, front | 0.97 | |
| 0.97 | ||
| Standing, front | 0.98 | |
| 0.96 |
| Cow Position and Flow Direction | Trend Line | R2 |
|---|---|---|
| standing, cross | 0.99 | |
| lying, cross | 0.99 | |
| standing, front | 0.99 | |
| lying, front | 0.99 |
| Cow Position and Flow Direction | Trend Line | R2 |
|---|---|---|
| standing, cross | 0.99 | |
| lying, cross | 0.99 | |
| standing, front | 0.99 | |
| lying, front | 0.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hartje, J. Development of an Anisotropic Porous Model of a Single Cow for Numerical Barn Simulations—A Numerical Study. Fluids 2025, 10, 142. https://doi.org/10.3390/fluids10060142
Hartje J. Development of an Anisotropic Porous Model of a Single Cow for Numerical Barn Simulations—A Numerical Study. Fluids. 2025; 10(6):142. https://doi.org/10.3390/fluids10060142
Chicago/Turabian StyleHartje, Julian. 2025. "Development of an Anisotropic Porous Model of a Single Cow for Numerical Barn Simulations—A Numerical Study" Fluids 10, no. 6: 142. https://doi.org/10.3390/fluids10060142
APA StyleHartje, J. (2025). Development of an Anisotropic Porous Model of a Single Cow for Numerical Barn Simulations—A Numerical Study. Fluids, 10(6), 142. https://doi.org/10.3390/fluids10060142





