An Application of Upwind Difference Scheme with Preconditioned Numerical Fluxes to Gas-Liquid Two-Phase Flows
Abstract
1. Introduction
2. Numerical Methods
2.1. Governing Equations
2.2. Preconditioned Governing Equations
2.3. Upwinding and Numerical Flux
2.4. Time Integration
3. Numerical Results
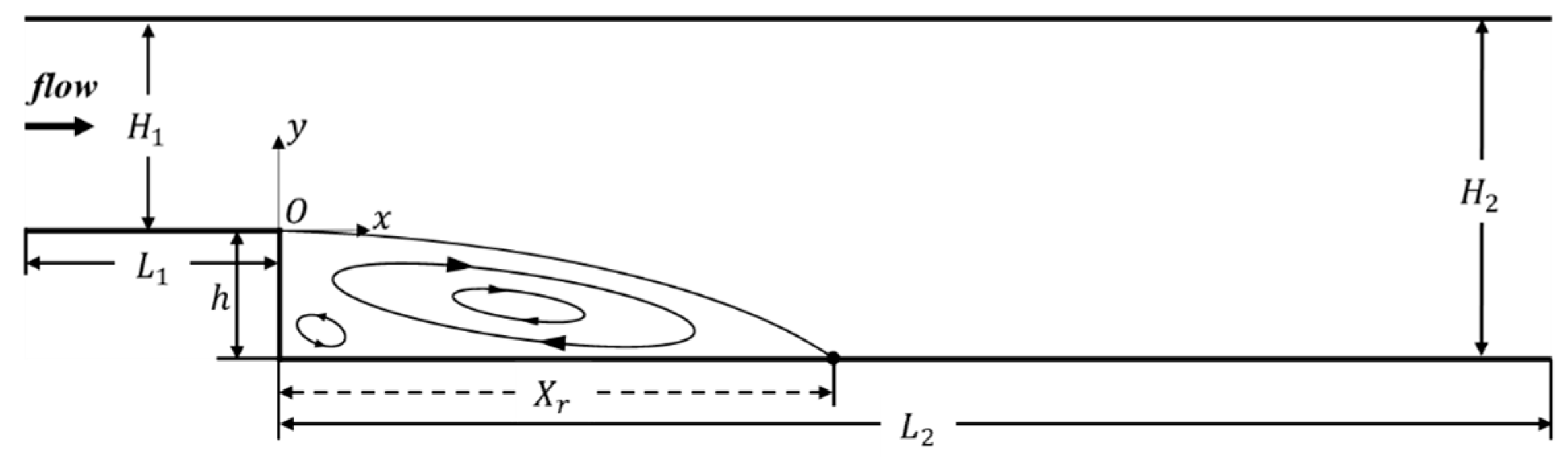
3.1. Computational Setup
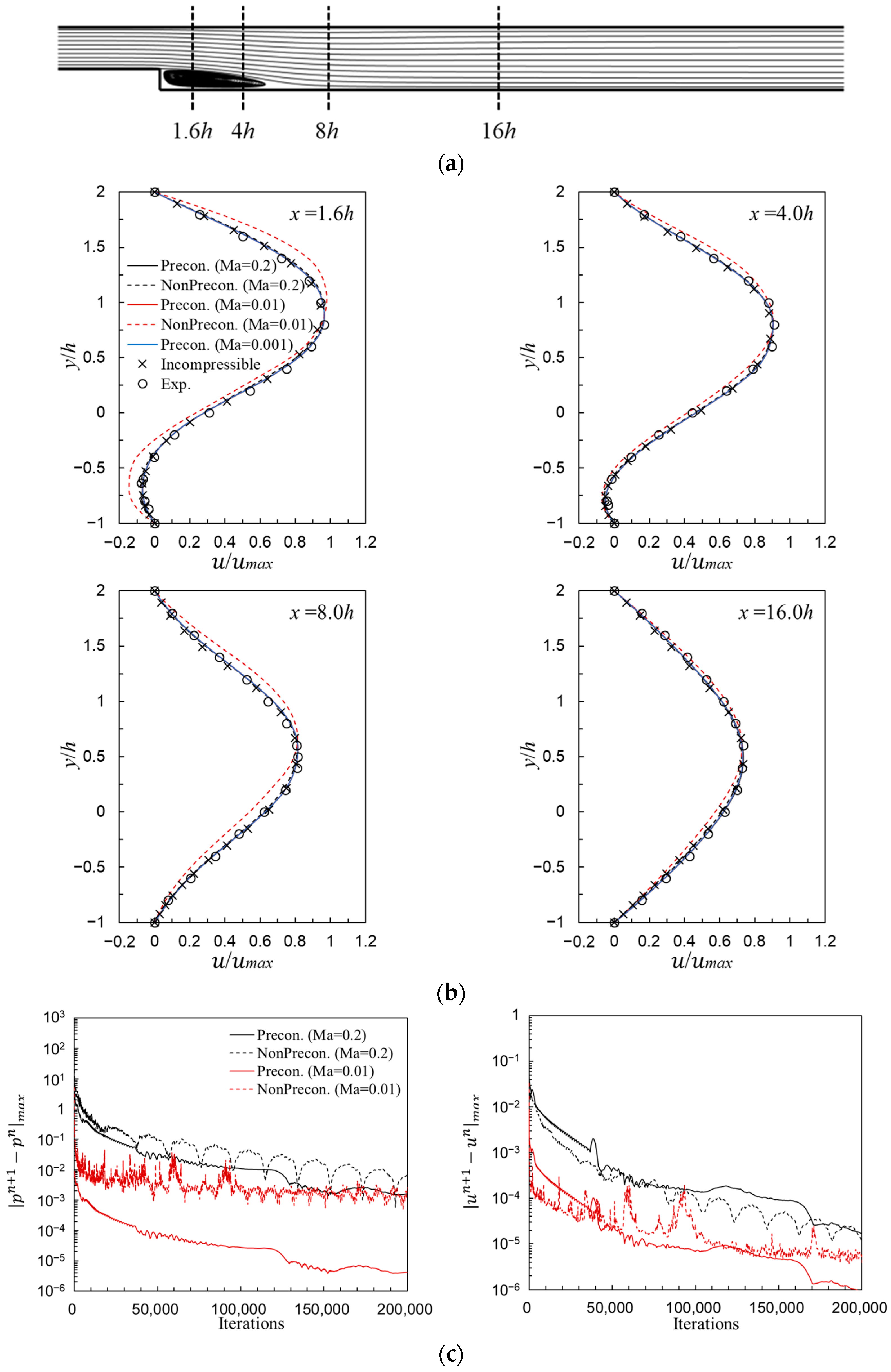
3.2. Low Reynolds Number Flow (Case 1)
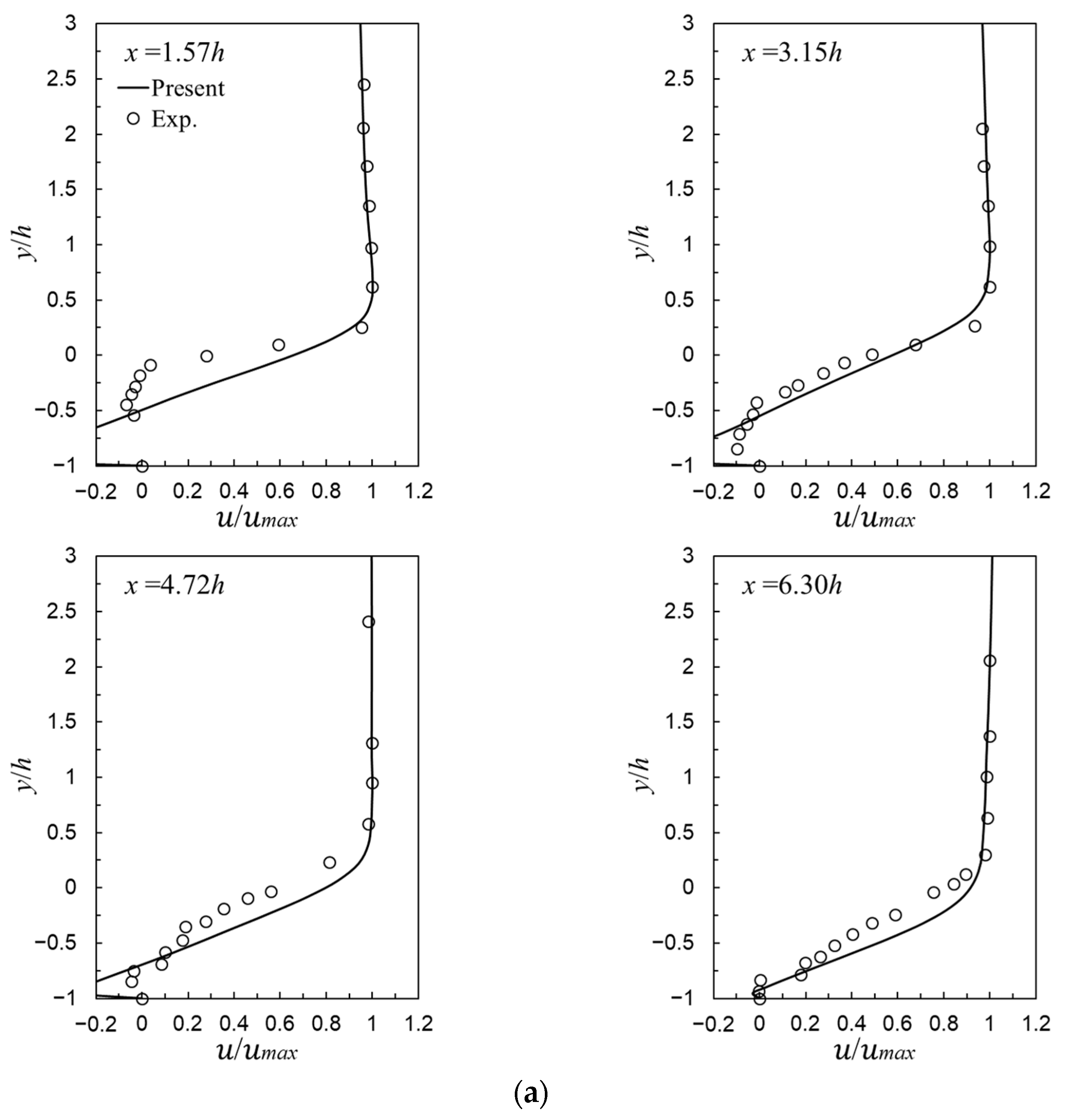
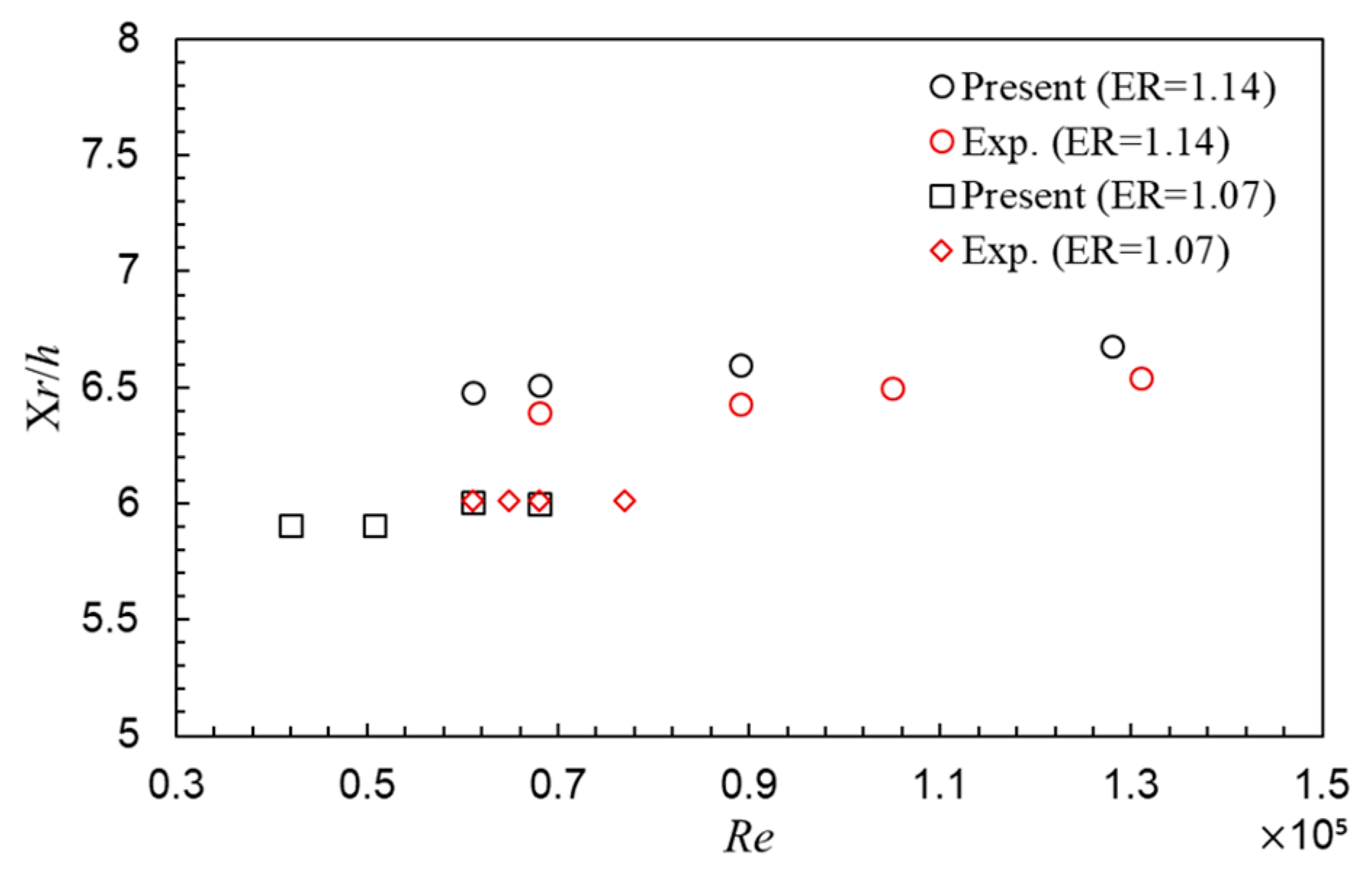
3.3. High Reynolds Number Flow (Cases 2 and 3)
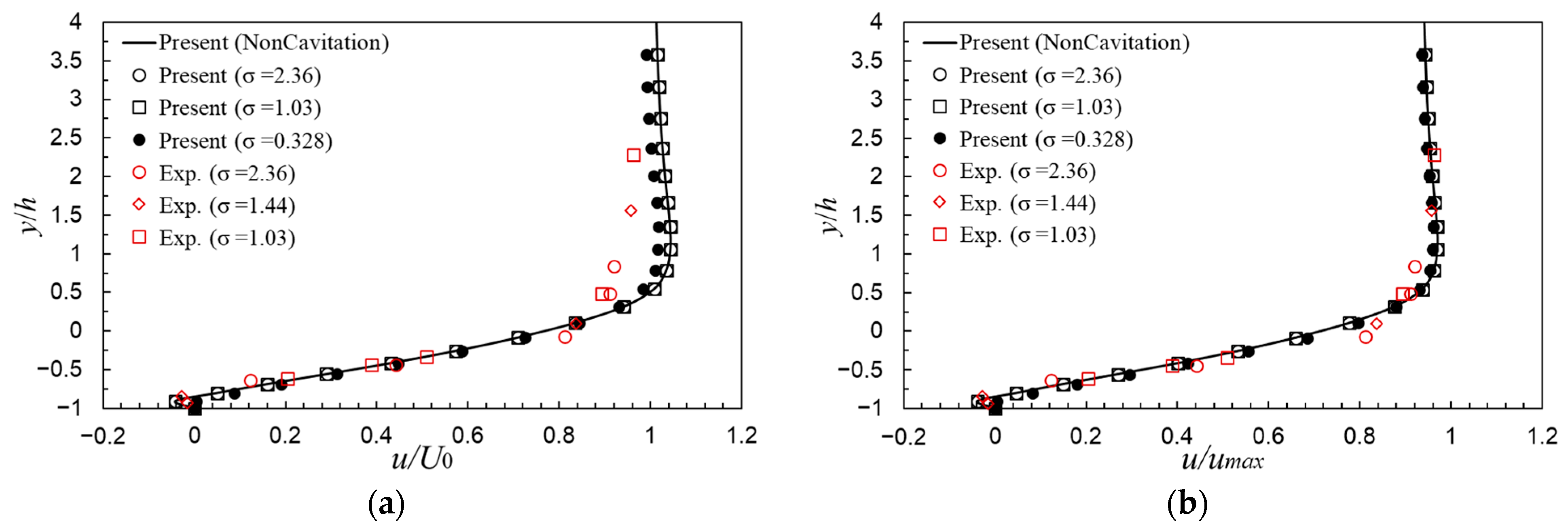
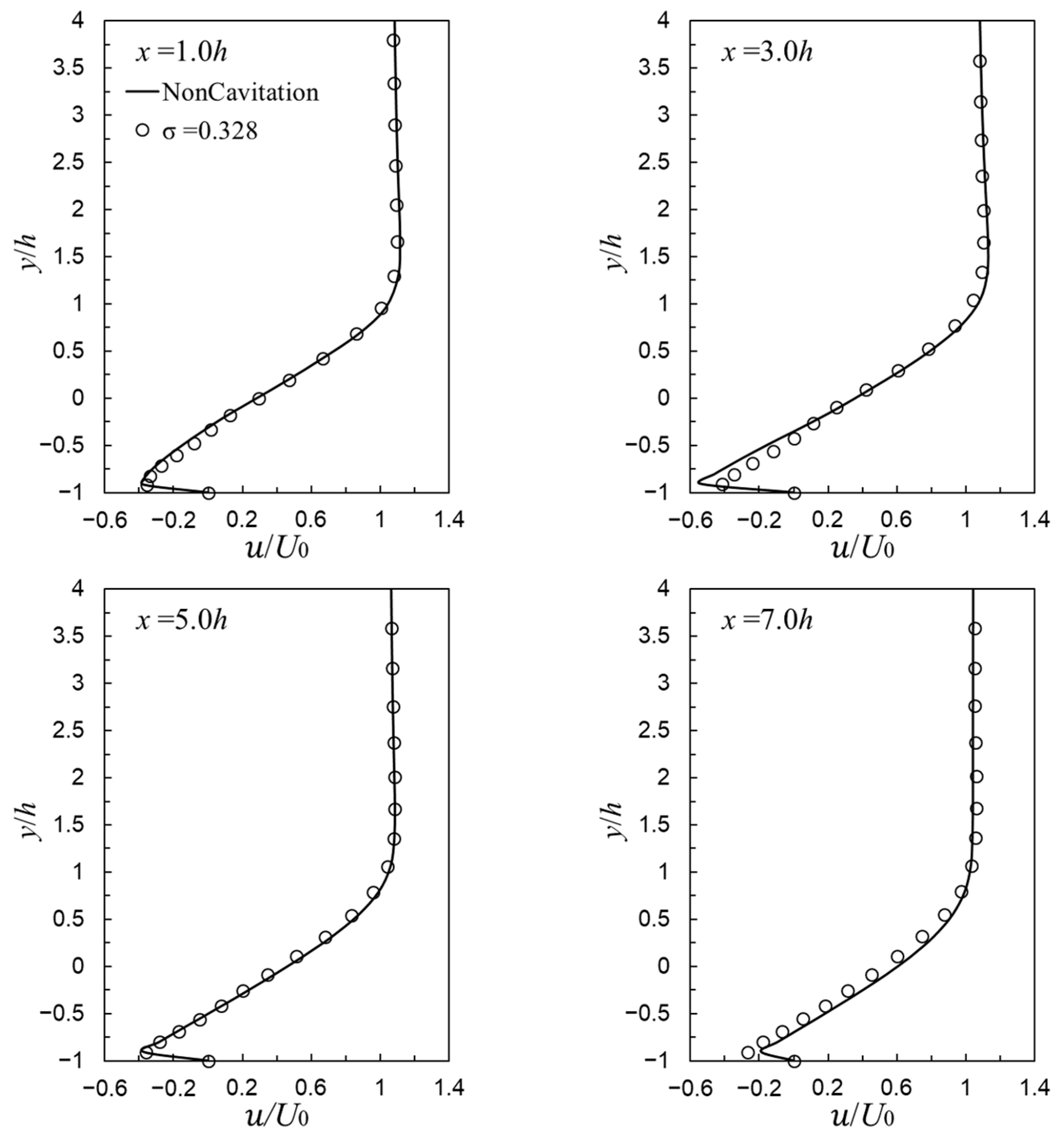
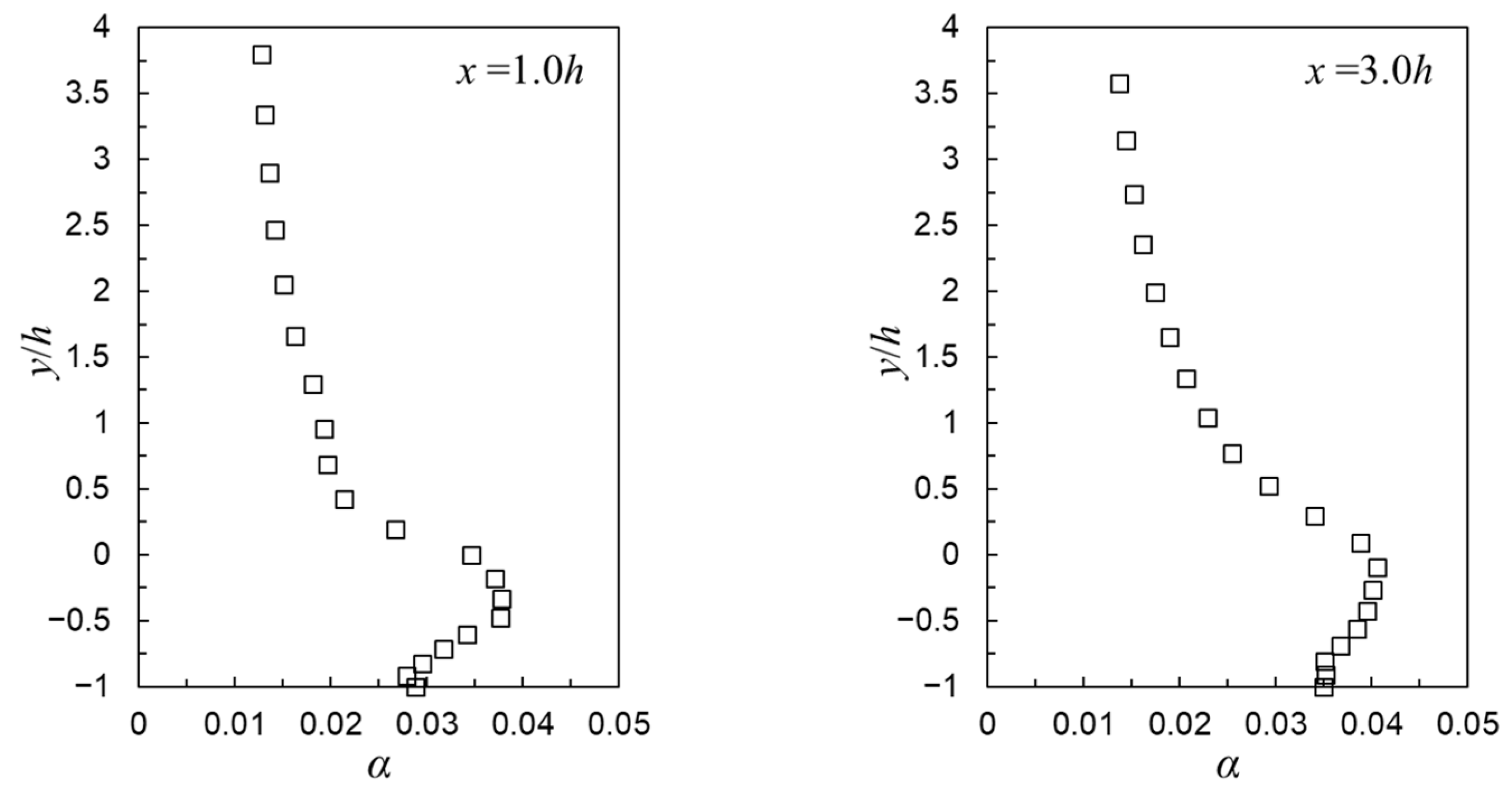
3.4. Gas-Liquid Two-Phase Flows with Cavitation (Case 3)
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Unverdi, S.O.; Tryggvason, G. A Front-tracking Method for Viscous, Incompressible, Multi-Fluid Flows. J. Comput. Phys. 1992, 100, 25–37. [Google Scholar] [CrossRef]
- Nomura, T. ALE Finite Element Computations of Fluid-Structure Interaction Problems. Comput. Methods Appl. Mech. Eng. 1994, 112, 291–308. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of Fluid (VOF) Method for the Dynamics of Free Boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Tomiyama, A.; Sou, A.; Minagawa, H.; Sakaguchi, T. Numerical Analysis of a Single Bubble with VOF Method. Trans. JSME Ser. B 1991, 57, 2167–2173. [Google Scholar] [CrossRef][Green Version]
- Ito, K.; Kunugi, T.; Ezure, T.; Tanaka, M.; Ito, D.; Saito, Y. An Improved Pressure Calculation Method for Simulations of Gas–Liquid Two-Phase Flows on Unstructured Meshes. Multiph. Sci. Technol. 2019, 31, 109–131. [Google Scholar] [CrossRef]
- Sussman, M.; Smereka, P.; Osher, S. A Level Set Approach for Computing Solutions to Incompressible Two-Phase Flow. J. Comput. Phys. 1994, 114, 146–159. [Google Scholar] [CrossRef]
- Turkel, E. Preconditioned Methods for Solving the Incompressible and Low Speed Compressible Equations. NASA LRC Contractor Report, NASA CR-178086; 1986. Available online: https://ntrs.nasa.gov/citations/19860016597 (accessed on 29 January 2025).
- Merkle, C.L.; Feng, J.Z.; Buelow, P.E.O. Computational Modelling of the Dynamics of Sheet Cavitation. In Proceedings of the 3rd International Symposium on Cavitation, Grenoble, France, 7–l0 April 1998. [Google Scholar]
- Edwards, J.R.; Liou, M.-S. Low-diffusion Flux-splitting Methods for Flows at All Speeds. In Proceedings of the 13th Computational Fluid Dynamics Conference, Snowmass Village, CO, USA, 29 June–2 July 1997. [Google Scholar] [CrossRef]
- Seo, J.H.; Moon, Y.J.; Shin, B.R. Prediction of Cavitation Flow Noise by Direct Numerical Simulation. J. Comput. Phys. 2008, 227, 6511–6531. [Google Scholar] [CrossRef]
- Dittakavi, N.; Chunekar, A.; Frankel, S. Large Eddy Simulation of Turbulent-cavitation Interactions in a Venturi Nozzle. ASME J. Fluids Eng. 2010, 132, 121301-1–121301-11. [Google Scholar] [CrossRef]
- Shuen, J.S.; Chen, K.H.; Choi, Y.H. A Time-accurate Algorithm for Chemical Non-equilibrium Viscous Flows at All Speeds. In Proceedings of the 28th Joint Propulsion Conference and Exhibit, Nashville, TN, USA, 6–8 July 1992. [Google Scholar] [CrossRef]
- Weiss, J.M.; Smith, W.A. Preconditioning Applied to Variable and Constant Density Flows. In Proceedings of the 25th AIAA Fluid Dynamics Conference, Colorado Springs, CO, USA, 20–23 June 1994. [Google Scholar] [CrossRef]
- Venkateswaran, S.; Merkle, L. Dual Time Stepping and Preconditioning for Unsteady Computations. In Proceedings of the 33rd AIAA Aerospace Sciences Meeting, Reno, NV, USA, 9–12 January 1995. [Google Scholar] [CrossRef]
- Shin, B.R.; Yamamoto, S.; Yuan, X. Application of Preconditioning Method to Gas–liquid Two-phase Flow Computations. ASME J. Fluids Eng. 2004, 126, 605–612. [Google Scholar] [CrossRef]
- Zhao, T.; Shin, B.R. Upwind Scheme Using Preconditioned Artificial Dissipation for Unsteady Gas–liquid Two-phase Flow and Its Application to Shock Tube Flow. J. Appl. Fluid Mech. 2024, 17, 1806–1819. [Google Scholar] [CrossRef]
- Shin, B.R.; Iwata, Y.; Ikohagi, T. A Numerical Study of Unsteady Cavitating Flows Using a Homogenous Equilibrium Model. Comput. Mech. 2003, 30, 388–395. [Google Scholar] [CrossRef]
- Chorin, A.J. A Numerical Method for Solving Incompressible Viscous Flow Problems. J. Comput. Phys. 1967, 2, 12–26. [Google Scholar] [CrossRef]
- Kwak, D.; Chang, J.L.C.; Shanks, S.P.; Chakravarty, S.R. A three dimensional Incompressible Navier-Stokes Flow Solver Using Primitive Variables. In Proceedings of the 22nd AIAA Aerospace Sciences Meeting, Reno, NV, USA, 9–12 January 1984. [Google Scholar] [CrossRef]
- Choi, Y.H.; Merkle, C.L. The Application of Preconditioning in Viscous Flows. J. Comput. Phys. 1993, 105, 207–223. [Google Scholar] [CrossRef]
- Yoo, Y.-L.; Kim, J.-C.; Sung, H.-G. Homogeneous Mixture Model Simulation of Compressible Multi-phase Flows at All Mach Number. Int. J. Multiph. Flow 2021, 143, 103745. [Google Scholar] [CrossRef]
- Roe, P.L. Approximate Riemann Solvers, Parameter Vectors, and Difference Scheme. J. Comput. Phys. 1981, 43, 357–372. [Google Scholar] [CrossRef]
- van Leer, B. Towards the Ultimate Conservative Difference Scheme (v) A Second-order Sequel to Godunov’s Method. J. Comput. Phys. 1979, 32, 101–136. [Google Scholar] [CrossRef]
- Shin, B.R. Stable Numerical Method Applying a Total Variation Diminishing Scheme for Incompressible Flow. AIAA J. 2003, 41, 49–55. [Google Scholar] [CrossRef]
- Turkel, E.; Fiterman, A.; van Leer, B. Preconditioning and the Limit of the Compressible to the Incompressible Flow Equations for Finite Difference Schemes. In Frontiers of Computational Fluid Dynamics 1994; Caughey, D.A., Hafez, M.M., Eds.; John Wiley and Sons: Chichester, NY, USA, 1995; pp. 215–234. [Google Scholar]
- Liou, M.-S.; Edwards, J.R. Numerical Speed of Sound and its Application to Schemes for All Speeds. In Proceedings of the 14th AIAA Computational Fluid Dynamics Conference, Norfolk, VA, USA, 1–5 November 1999. [Google Scholar] [CrossRef]
- Morgan, K.; Jaques, P.; François, T. Analysis of Laminar Flow Over a Backward Facing Step, Notes on Numerical Fluid Mechanics; Vieweg + Teubner Verlag: Wiesbaden, Germany, 1984; Volume 9, pp. 245–267. [Google Scholar] [CrossRef]
- Kim, J.; Kline, S.J.; Johnston, J.P. Investigation of a Reattaching Turbulent Shear Layer: Flow Over a Backward-facing Step. J. Fluids Eng. 1980, 102, 302–308. [Google Scholar] [CrossRef]
- Balachandar, R. Characteristics of Separated Flows Including Cavitation Effects. Ph.D. Thesis, Concordia University, Montreal, Canada, March 1990. [Google Scholar]
- Kueny, J.L.; Binder, G. Viscous Flow over Backward Facing Steps an Experimental Investigation. In Analysis of Laminar Flow over a Backward Facing Step, Notes on Numerical Fluid Mechanics; Morgan, K., Periaux, J., Thomasset, F., Eds.; Vieweg+Teubner Verlag: Wiesbaden, German, 1984; Volume 9, pp. 32–47. [Google Scholar] [CrossRef]
- Shin, B.R.; Ikohagi, T.; Daiguji, H. An Unsteady Implicit SMAC Scheme for Two-Dimensional Incompressible Navier-Stokes Equations. Trans. JSME Ser. B 1993, 36, 598–606. [Google Scholar] [CrossRef][Green Version]
- Eaton, J.K.; Johnston, J.P. A Review of Research on Subsonic Turbulent Flow Reattachment. AIAA J. 1981, 19, 1093–1100. [Google Scholar] [CrossRef]
- Bhatt, A. Unsteady Cavitation in Separating and Re-attaching Shear Flows. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, January 2021. [Google Scholar]
- Numachi, F. Über die Kavitationsentstehung mit besonderem Bezug auf den Luftgehalt des Wassers. Ing. Arch. 1936, 7, 396–409. [Google Scholar] [CrossRef]





| Case | Expansion Ratio | Inlet Length | Outlet Length | Reynolds Number | Grid Points |
|---|---|---|---|---|---|
| 1 | 1.5 | 100 | 90 × 21 | ||
| 2 | 1.14 | 61,000~128,000 | 201 × 51 | ||
| 3 | 1.07 | 31,000~77,000 | 201 × 51 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, T.; Shin, B. An Application of Upwind Difference Scheme with Preconditioned Numerical Fluxes to Gas-Liquid Two-Phase Flows. Fluids 2025, 10, 38. https://doi.org/10.3390/fluids10020038
Zhao T, Shin B. An Application of Upwind Difference Scheme with Preconditioned Numerical Fluxes to Gas-Liquid Two-Phase Flows. Fluids. 2025; 10(2):38. https://doi.org/10.3390/fluids10020038
Chicago/Turabian StyleZhao, Tianmu, and Byeongrog Shin. 2025. "An Application of Upwind Difference Scheme with Preconditioned Numerical Fluxes to Gas-Liquid Two-Phase Flows" Fluids 10, no. 2: 38. https://doi.org/10.3390/fluids10020038
APA StyleZhao, T., & Shin, B. (2025). An Application of Upwind Difference Scheme with Preconditioned Numerical Fluxes to Gas-Liquid Two-Phase Flows. Fluids, 10(2), 38. https://doi.org/10.3390/fluids10020038






