Towards Efficient Bio-Methanation: A Comparative Analysis of Disperser Designs and Process Optimization in Bubble Columns
Abstract
1. Introduction
1.1. General Disperser Design
1.2. Plates with Holes
1.3. Porous Dispersers Description
1.4. Gas Hold-Up Correlations
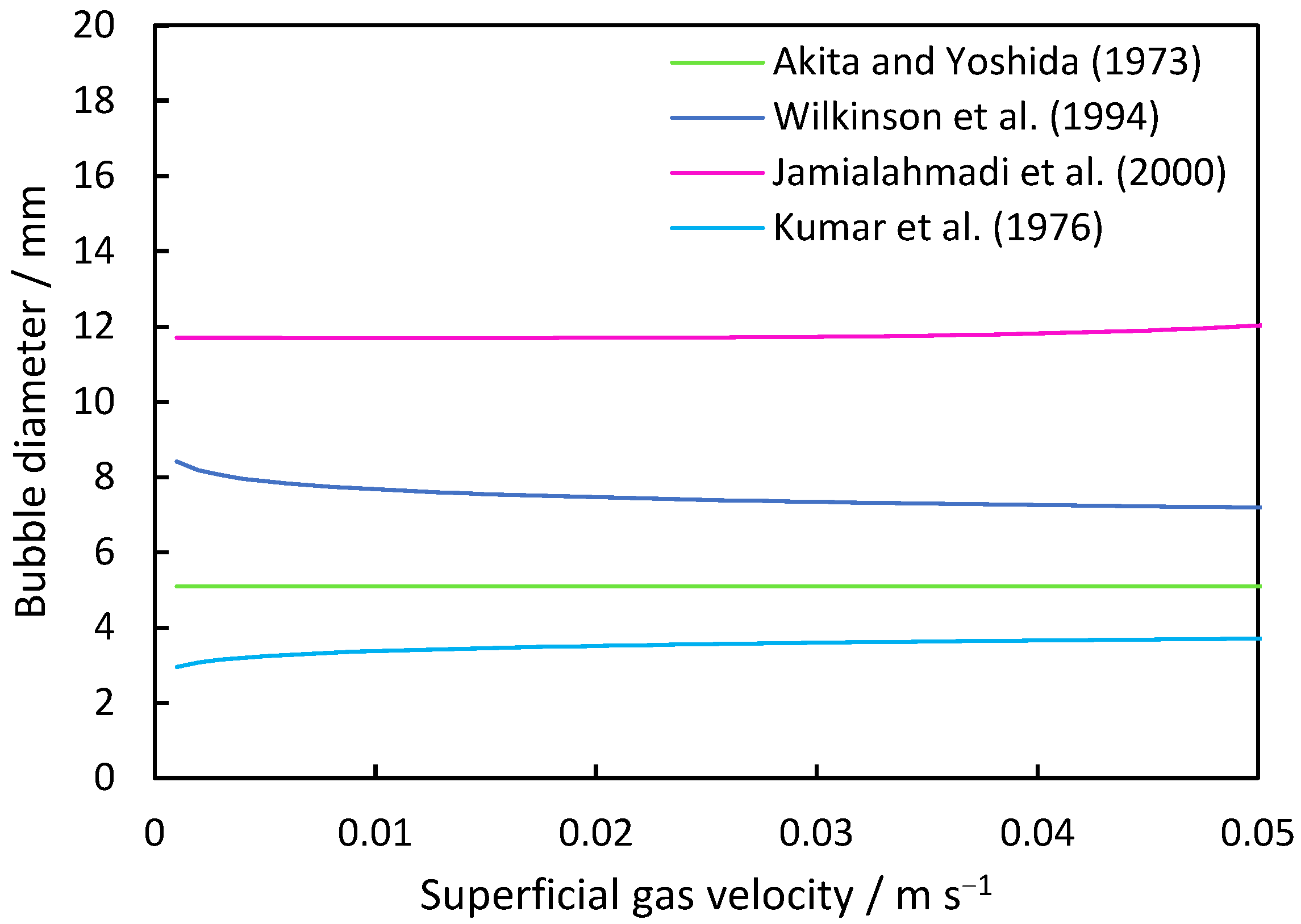
1.5. Bubble Size Correlations
1.6. Aim of This Work
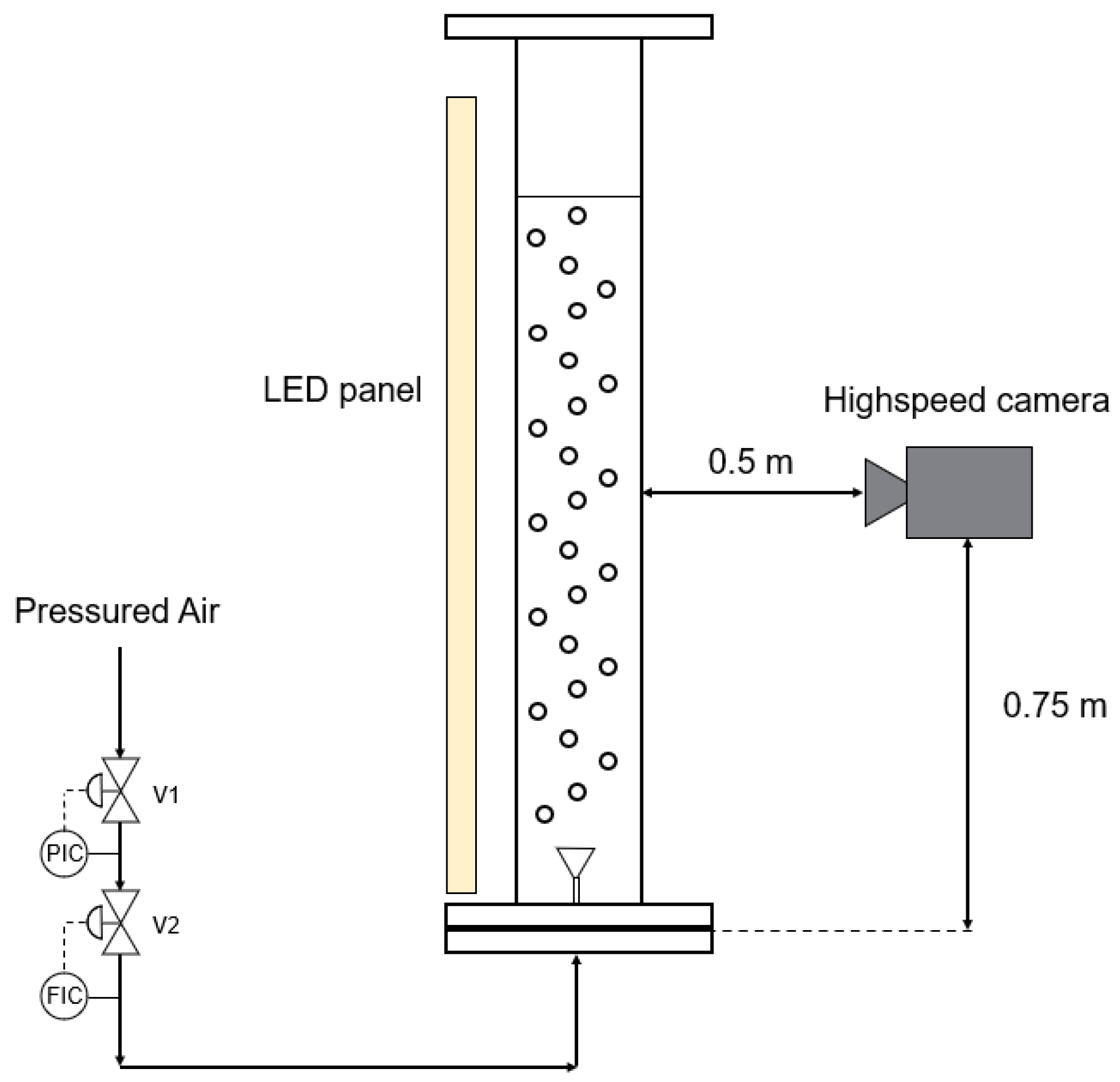
2. Materials and Methods
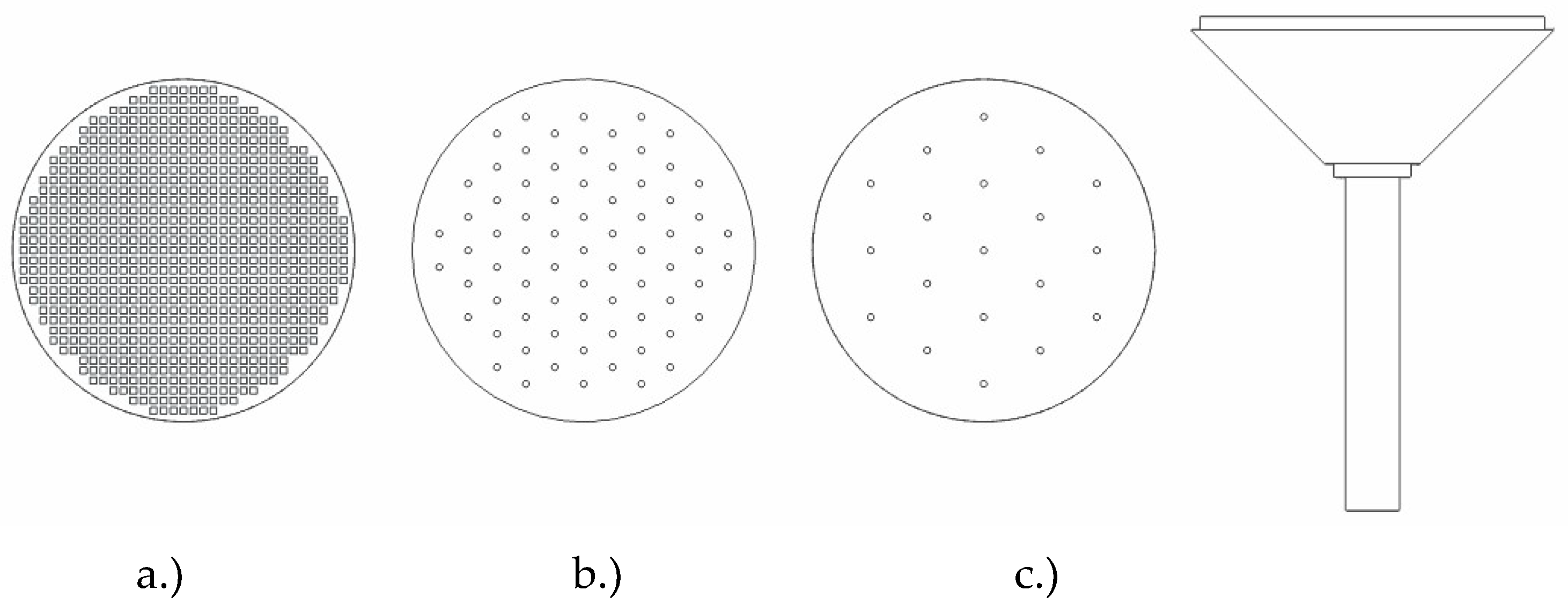
Disperser Designs
3. Results and Discussion
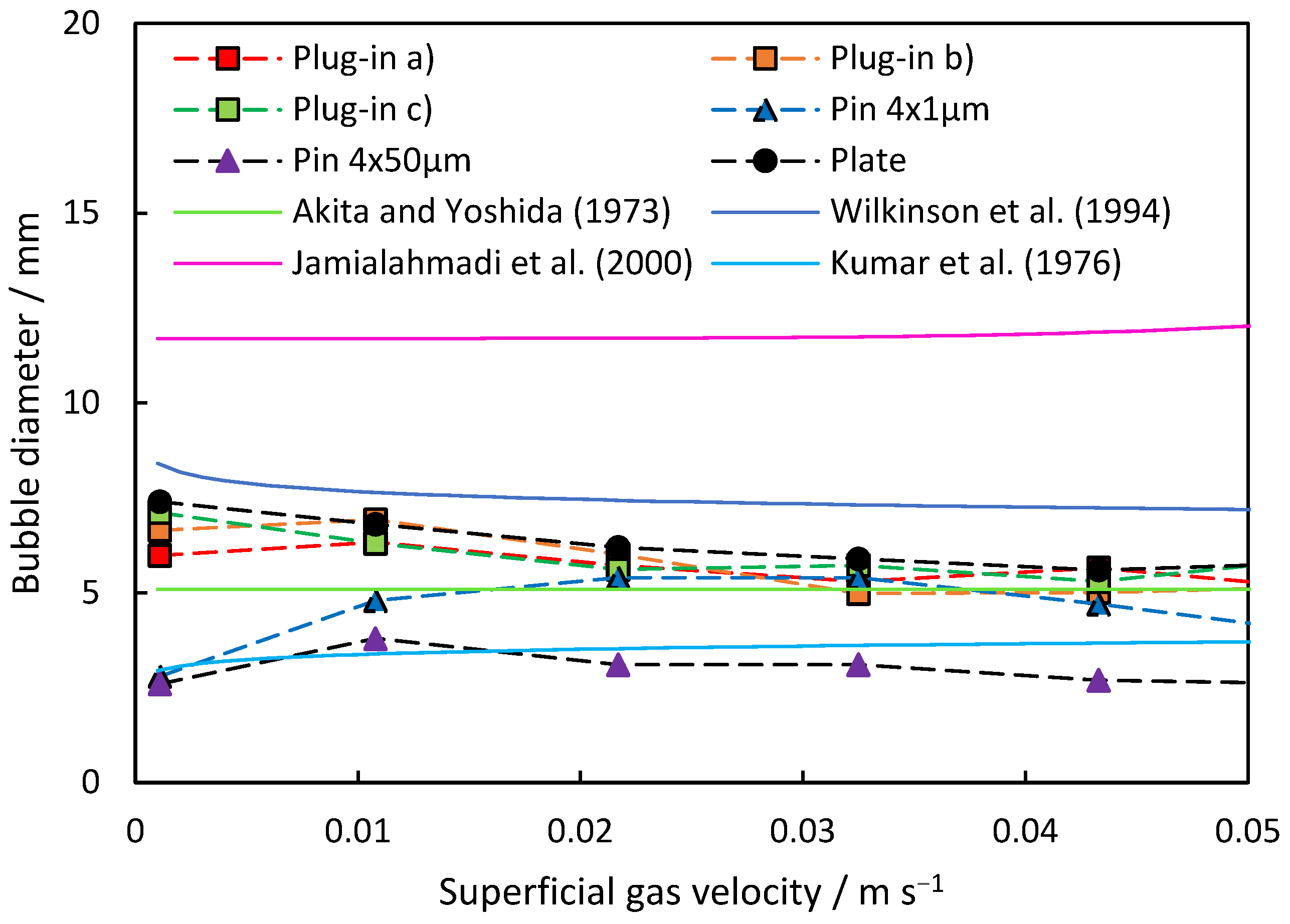
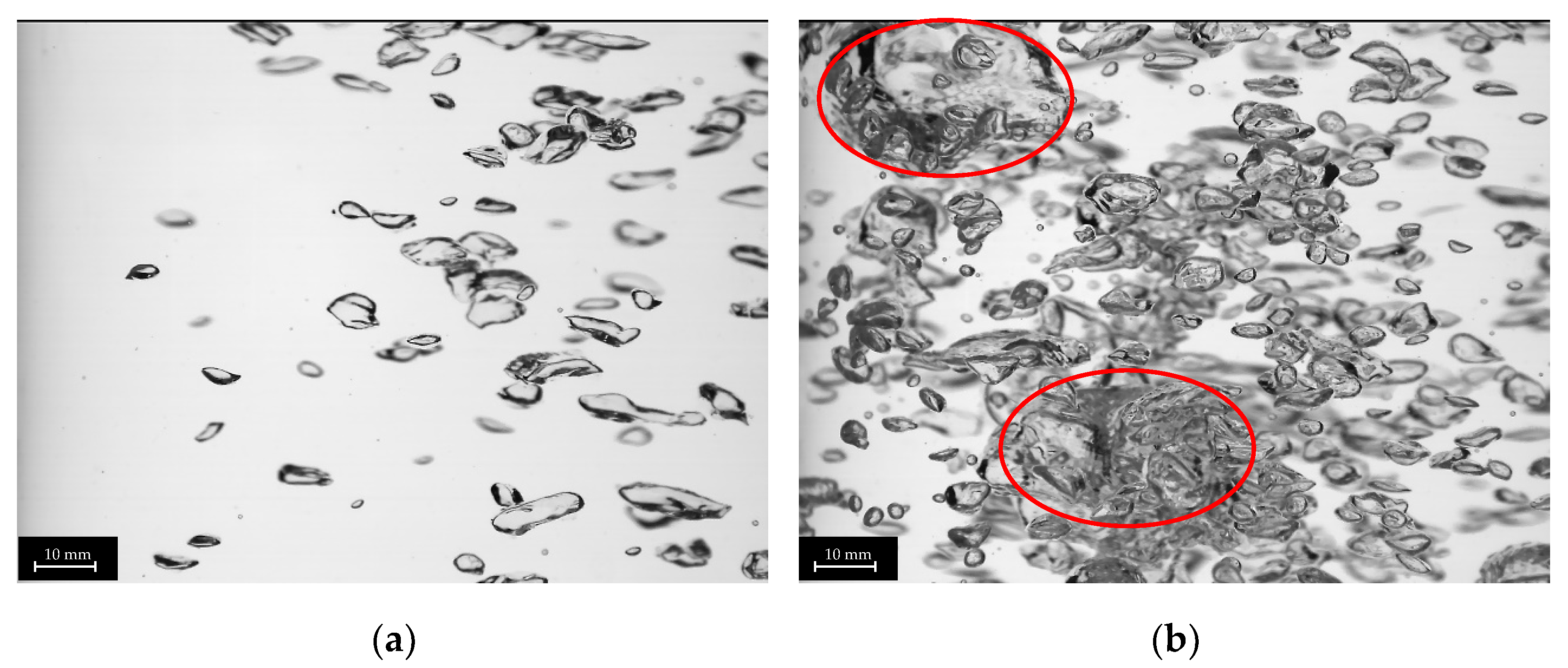
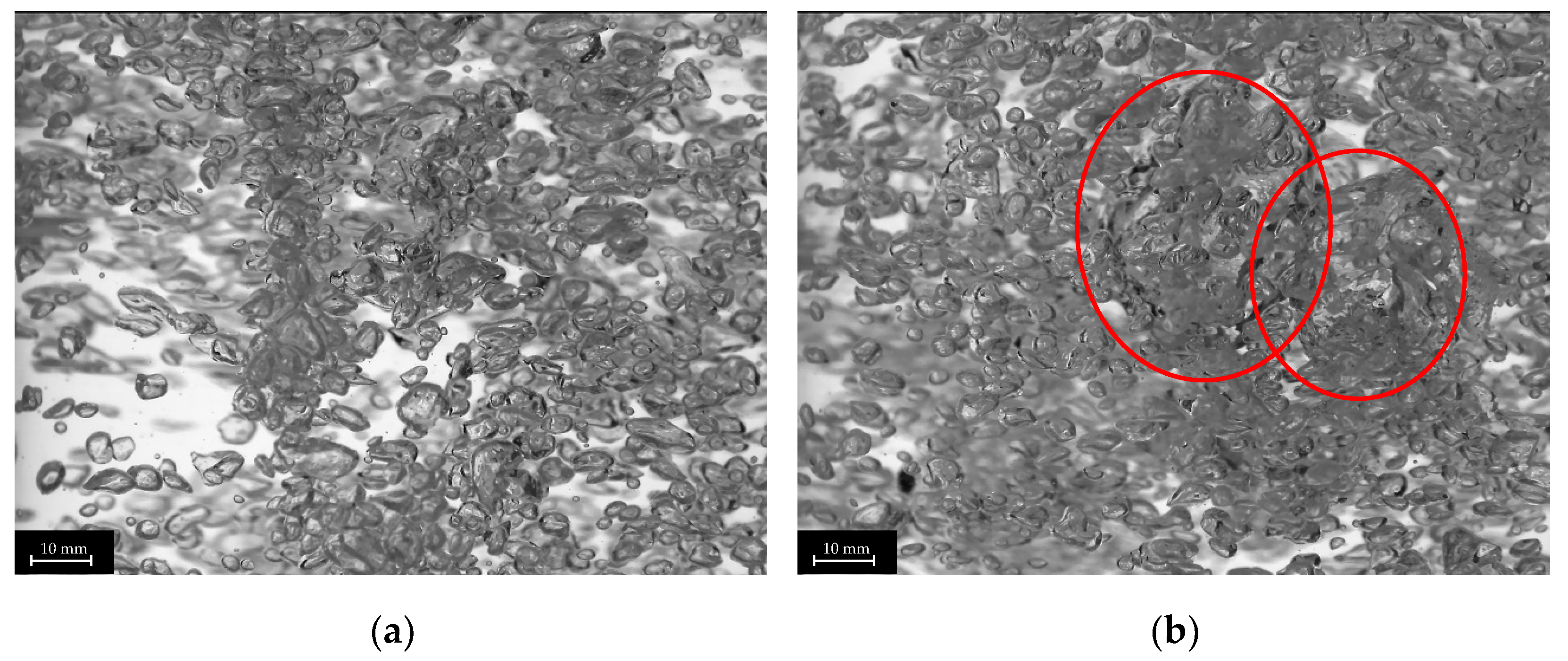
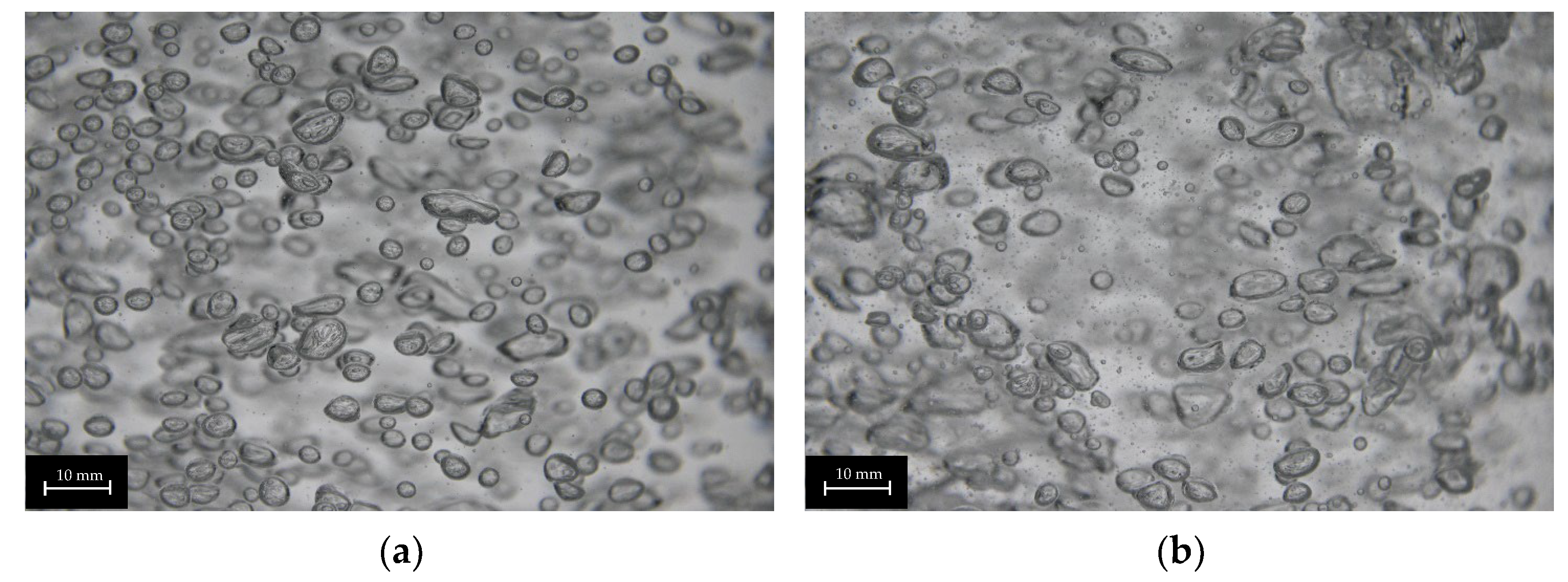
3.1. Bubble Diameter
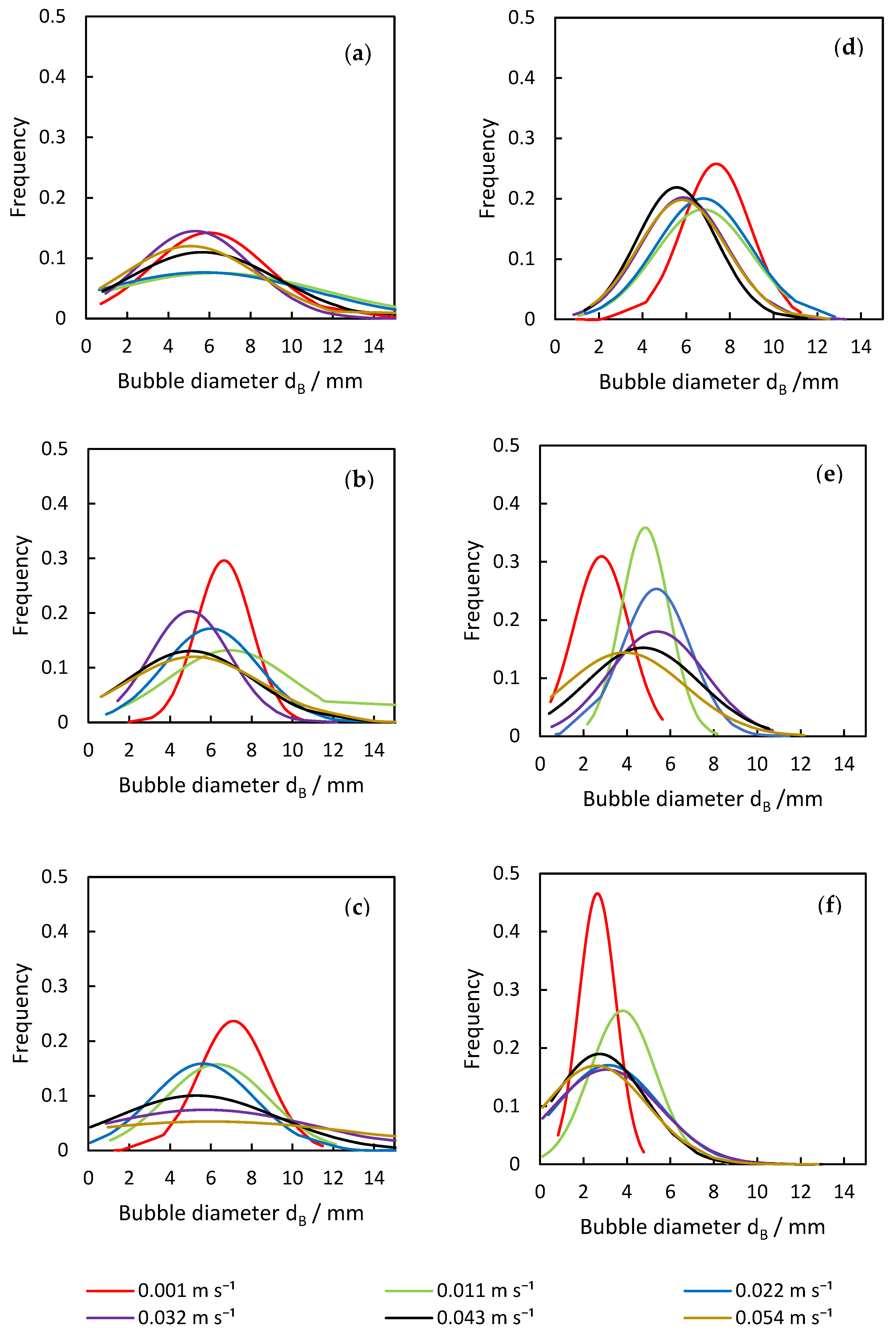
3.2. Bubble Diameter Distribution
3.2.1. Plug-in Dispersers
3.2.2. Porous Dispersers
3.2.3. Plate Disperser
3.3. Gas Hold-Up
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Logroño, W.; Popp, D.; Nikolausz, M.; Kluge, P.; Harms, H.; Kleinsteuber, S. Microbial Communities in Flexible Biomethanation of Hydrogen Are Functionally Resilient Upon Starvation. Front. Microbiol. 2021, 12, 619632. [Google Scholar] [CrossRef] [PubMed]
- Sauerschell, S.; Bajohr, S.; Kolb, T. Methanation Pilot Plant with a Slurry Bubble Column Reactor: Setup and First Experimental Results. Energy Fuels 2022, 36, 7166–7176. [Google Scholar] [CrossRef]
- Mills, G.A.; Steffgen, F.W. Catalytic Methanation. Catal. Rev. 1974, 8, 159–210. [Google Scholar] [CrossRef]
- Er-rbib, H.; Bouallou, C. Methanation catalytic reactor. Comptes Rendus Chim. 2014, 17, 701–706. [Google Scholar] [CrossRef]
- Younas, M.; Loong Kong, L.; Bashir, M.J.K.; Nadeem, H.; Shehzad, A.; Sethupathi, S. Recent Advancements, Fundamental Challenges, and Opportunities in Catalytic Methanation of CO2. Energy Fuels 2016, 30, 8815–8831. [Google Scholar] [CrossRef]
- Stangeland, K.; Kalai, D.; Li, H.; Yu, Z. CO2 Methanation: The Effect of Catalysts and Reaction Conditions. Energy Procedia 2017, 105, 2022–2027. [Google Scholar] [CrossRef]
- Frontera, P.; Macario, A.; Ferraro, M.; Antonucci, P. Supported Catalysts for CO2 Methanation: A Review. Catalysts 2017, 7, 59. [Google Scholar] [CrossRef]
- Bywater, A.; Heaven, S.; Zhang, Y.; Banks, C.J. Potential for Biomethanisation of CO2 from Anaerobic Digestion of Organic Wastes in the United Kingdom. Processes 2022, 10, 1202. [Google Scholar] [CrossRef]
- Grimalt-Alemany, A.; Skiadas, I.V.; Gavala, H.N. Syngas biomethanation: State-of-the-art review and perspectives. Biofuels Bioprod. Biorefining 2018, 12, 139–158. [Google Scholar] [CrossRef]
- Rönsch, S.; Schneider, J.; Matthischke, S.; Schlüter, M.; Götz, M.; Lefebvre, J.; Prabhakaran, P.; Bajohr, S. Review on methanation—From fundamentals to current projects. Fuel 2016, 166, 276–296. [Google Scholar] [CrossRef]
- Hoffstadt, K.; Nikolausz, M.; Krafft, S.; Bonatelli, M.L.; Kumar, V.; Harms, H.; Kuperjans, I. Optimization of the Ex Situ Biomethanation of Hydrogen and Carbon Dioxide in a Novel Meandering Plug Flow Reactor: Start-Up Phase and Flexible Operation. Bioengineering 2024, 11, 165. [Google Scholar] [CrossRef] [PubMed]
- Götz, M.; Koch, A.M.; Graf, F. State of the Art and Prespective of CO2 Methanation Process Concepts for Power-to-Gas Applications. In Proceedings of the International Gas Union Research Conference, Copenhagen, Denmark, 17–19 September 2014; Volume 13. [Google Scholar]
- Thapa, A.; Jo, H.; Han, U.; Cho, S.-K. Ex-situ biomethanation for CO2 valorization: State of the art, recent advances, challenges, and future prospective. Biotechnol. Adv. 2023, 68, 108218. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Chen, J.; Griffin, D.; Li, X.; Henson, M.A. (Eds.) Integrated Metabolic and Process Modeling of Bubble Column Reactors for Gas Fermentation; Elsevier: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Vlaev, S.D.; Fialova, M. Bubble Column Bioreactors: Comparison with Stirred Fermenters Based on Local Gas Hold-up Distribution. Can. J. Chem. Eng. 2003, 81, 535–542. [Google Scholar] [CrossRef]
- Munasinghe, P.C.; Khanal, S.K. Syngas fermentation to biofuel: Evaluation of carbon monoxide mass transfer coefficient (kLa) in different reactor configurations. Biotechnol. Prog. 2010, 26, 1616–1621. [Google Scholar] [CrossRef]
- Yörük, Ö.; Zıraman, D.U.; Uysal, B.Z. Absorption of Sulfur Dioxide by Iron(II) Hydroxide Solution in a Multiplate Bubble Column under Magnetic Field. Chem. Eng. Technol. 2021, 44, 1336–1342. [Google Scholar] [CrossRef]
- Besagni, G.; Inzoli, F.; de Guido, G.; Pellegrini, L.A. Experimental investigation on the influence of ethanol on bubble column hydrodynamics. Chem. Eng. Res. Des. 2016, 112, 1–15. [Google Scholar] [CrossRef]
- Besagni, G.; Inzoli, F.; Ziegenhein, T. Two-Phase Bubble Columns: A Comprehensive Review. ChemEngineering 2018, 2, 13. [Google Scholar] [CrossRef]
- Kraume, M. Transportvorgänge in der Verfahrenstechnik; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Kulkarni, A.A.; Joshi, J.B. Bubble Formation and Bubble Rise Velocity in Gas−Liquid Systems: A Review. Ind. Eng. Chem. Res. 2005, 44, 5873–5931. [Google Scholar] [CrossRef]
- Kougias, P.G.; Treu, L.; Benavente, D.P.; Boe, K.; Campanaro, S.; Angelidaki, I. Ex-situ biogas upgrading and enhancement in different reactor systems. Bioresour. Technol. 2017, 225, 429–437. [Google Scholar] [CrossRef]
- Bassani, I.; Kougias, P.G.; Treu, L.; Porté, H.; Campanaro, S.; Angelidaki, I. Optimization of hydrogen dispersion in thermophilic up-flow reactors for ex situ biogas upgrading. Bioresour. Technol. 2017, 234, 310–319. [Google Scholar] [CrossRef]
- Jensen, M.B.; Kofoed, M.V.W.; Fischer, K.; Voigt, N.V.; Agneessens, L.M.; Batstone, D.J.; Ottosen, L.D.M. Venturi-type injection system as a potential H2 mass transfer technology for full-scale in situ biomethanation. Appl. Energy 2018, 222, 840–846. [Google Scholar] [CrossRef]
- Ngu, V.; Fletcher, D.F.; Kavanagh, J.M.; Rafrafi, Y.; Dumas, C.; Morchain, J.; Cockx, A. H2 mass transfer—A key factor for efficient biological methanation: Comparison between pilot-scale experimental data, 1D and CFD models. Chem. Eng. Sci. 2023, 268, 118382. [Google Scholar] [CrossRef]
- Nada, S.A. Experimental Investigation and Empirical Correlations of Heat Transfer in Different Regimes of Air–Water Two-Phase Flow in a Horizontal Tube. J. Therm. Sci. Eng. Appl. 2017, 9, 021004. [Google Scholar] [CrossRef]
- Besagni, G.; Varallo, N.; Mereu, R. Computational Fluid Dynamics Modelling of Two-Phase Bubble Columns: A Comprehensive Review. Fluids 2023, 8, 91. [Google Scholar] [CrossRef]
- Mândrea, L.; Oprina, G.; Chihaia, O.; El-Leathey, L.-A.; Mirea, R. Theoretical and Experimental Study of Gas Bubbles Behavior. Int. J. Model. Optim. 2017, 7, 145–151. [Google Scholar] [CrossRef][Green Version]
- Lamm, M.; Jarboe, L. Chemical Engineering Separations: A Handbook for Students; Iowa State University Digital Press: Ames, IA, USA, 2020. [Google Scholar]
- Pourtousi, M.; Ganesan, P.; Sandaran, S.C.; Sahu, J.N. Effect of ring sparger diameters on hydrodynamics in bubble column: A numerical investigation. J. Taiwan Inst. Chem. Eng. 2016, 69, 14–24. [Google Scholar] [CrossRef]
- Kulkarni, A.V.; Badgandi, S.V.; Joshi, J.B. Design of ring and spider type spargers for bubble column reactor: Experimental measurements and CFD simulation of flow and weeping. Chem. Eng. Res. Des. 2009, 87, 1612–1630. [Google Scholar] [CrossRef]
- Kulkarni, A.V.; Joshi, J.B. Design and selection of sparger for bubble column reactor. Part I: Performance of different spargers. Chem. Eng. Res. Des. 2011, 89, 1972–1985. [Google Scholar] [CrossRef]
- Şal, S.; Gül, Ö.F.; Özdemir, M. The effect of sparger geometry on gas holdup and regime transition points in a bubble column equipped with perforated plate spargers. Chem. Eng. Process. Process Intensif. 2013, 70, 259–266. [Google Scholar] [CrossRef]
- Kantarci, N.; Borak, F.; Ulgen, K.O. Bubble column reactors. Process Biochem. 2005, 40, 2263–2283. [Google Scholar] [CrossRef]
- Sideman, S.; Hortaçsu, Ö.; Fulton, J.W. Mass Transfer in Gas-Liquid Contacting Systems. Ind. Eng. Chem. 1966, 58, 32–47. [Google Scholar] [CrossRef]
- González-Castaño, M.; Baena-Moreno, F.; De Miguel, J.C.N.; Miah, K.U.; Arroyo-Torralvo, F.; Ossenbrink, R.; Odriozola, J.A.; Benzinger, W.; Hensel, A.; Wenka, A.; et al. 3D-printed structured catalysts for CO2 methanation reaction: Advancing of gyroid-based geometries. Energy Convers. Manag. 2022, 258, 115464. [Google Scholar] [CrossRef]
- Capel, A.J.; Rimington, R.P.; Lewis, M.P.; Christie, S.D.R. 3D printing for chemical, pharmaceutical and biological applications. Nat. Rev. Chem. 2018, 2, 422–436. [Google Scholar] [CrossRef]
- Möller, F.; Seiler, T.; Lau, Y.M.; Weber, M.; Weber, M.; Hampel, U.; Schubert, M. Performance comparison between different sparger plate orifice patterns: Hydrodynamic investigation using ultrafast X-ray tomography. Chem. Eng. J. 2017, 316, 857–871. [Google Scholar] [CrossRef]
- Thorat, B.N.; Kulkarni, A.V.; Joshi, J.B. Design of Sieve Plate Spargers for Bubble Columns: Role of Weeping. Chem. Eng. Technol. 2001, 24, 815–828. [Google Scholar] [CrossRef]
- Schlüter, M. Bildung und Bewegung von Tropfen und Blasen in technischen Apparaten. In Handbuch Vakuumtechnik; Jousten, K., Ed.; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2017; pp. 1–19. [Google Scholar] [CrossRef]
- Springer-Verlag GmbH. VDI-Wärmeatlas; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Akita, K.; Yoshida, F. Bubble Size, Interfacial Area, and Liquid-Phase Mass Transfer Coefficient in Bubble Columns. Ind. Eng. Chem. Proc. Des. Dev. 1974, 13, 84–91. [Google Scholar] [CrossRef]
- Loimer, T.; Machu, G.; Schaflinger, U. Inviscid bubble formation on porous plates and sieve plates. Chem. Eng. Sci. 2004, 59, 809–818. [Google Scholar] [CrossRef]
- Besagni, G.; Brazzale, P.; Fiocca, A.; Inzoli, F. Estimation of bubble size distributions and shapes in two-phase bubble column using image analysis and optical probes. Flow Meas. Instrum. 2016, 52, 190–207. [Google Scholar] [CrossRef]
- Mouza, A.A. Design of bubble columns equipped with porous sparger. Mater. Today Proc. 2018, 5, 27572–27581. [Google Scholar] [CrossRef]
- Jha, A.; Raj Mohan, B.; Chakraborty, S.; Meikap, B.C. Studies on gas holdup in a bubble column using porous spargers with additives. Asia-Pac. J. Chem. Eng. 2008, 3, 417–424. [Google Scholar] [CrossRef]
- Akita, K.; Yoshida, F. Gas Holdup and Volumetric Mass Transfer Coefficient in Bubble Columns. Effects of Liquid Properties. Ind. Eng. Chem. Proc. Des. Dev. 1973, 12, 76–80. [Google Scholar] [CrossRef]
- Wilkinson, P.M.; Haringa, H.; van Dierendonck, L.L. Mass transfer and bubble size in a bubble column under pressure. Chem. Eng. Sci. 1994, 49, 1417–1427. [Google Scholar] [CrossRef]
- Jamialahmadi, M.; Müller-Steinhagen, H.; Sarrafi, A.; Smith, J.M. Studies of Gas Holdup in Bubble Column Reactors. Chem. Eng. Technol. 2000, 23, 919–921. [Google Scholar] [CrossRef]
- Kumar, A.; Degaleesan, T.E.; Laddha, G.S.; Hoelscher, H.E. Bubble swarm characteristics in bubble columns. Can. J. Chem. Eng. 1976, 54, 503–508. [Google Scholar] [CrossRef]
- Schindelin, J.; Arganda-Carreras, I.; Frise, E.; Kaynig, V.; Longair, M.; Pietzsch, T.; Preibisch, S.; Rueden, C.; Saalfeld, S.; Schmid, B.; et al. Fiji: An open-source platform for biological-image analysis. Nat. Methods 2012, 9, 676–682. [Google Scholar] [CrossRef]


| Author | Equation | |
|---|---|---|
| Hughmark (1967) [44] | (2) | |
| Kumar et al. (1976) [45] | (3) | |
| Godbole et al. (1982) [46] | (4) | |
| Zou et al. (1988) [47] | (5) |
| Reference | Correlation | |
|---|---|---|
| Akita and Yoshida [47] | (6) | |
| Wilkinson et al. [48] | (7) | |
| Jamialahmadi et al. [49] | (8) | |
| Kumar et al. [50] | (9) |
| Plug-in a.) | Plug-in b.) | Plug-in c.) | Plate | |
|---|---|---|---|---|
| 818 | 85 | 19 | 144 | |
| 1.0 mm | 1.0 mm | 1.0 mm | 1.0 mm | |
| 40% | 3.4% | 0.8% | 0.7% | |
| 1.5 mm | 5 mm | 10 mm | 10 mm | |
| 2 mm | 2 mm | 2 mm | 5 mm | |
| 2 | 0.725 m s−1 | 0.054 m s−1 | 0.022 m s−1 | 0.108 m s−1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Klapal, F.; Hlawitschka, M.W. Towards Efficient Bio-Methanation: A Comparative Analysis of Disperser Designs and Process Optimization in Bubble Columns. Fluids 2025, 10, 37. https://doi.org/10.3390/fluids10020037
Klapal F, Hlawitschka MW. Towards Efficient Bio-Methanation: A Comparative Analysis of Disperser Designs and Process Optimization in Bubble Columns. Fluids. 2025; 10(2):37. https://doi.org/10.3390/fluids10020037
Chicago/Turabian StyleKlapal, Florian, and Mark Werner Hlawitschka. 2025. "Towards Efficient Bio-Methanation: A Comparative Analysis of Disperser Designs and Process Optimization in Bubble Columns" Fluids 10, no. 2: 37. https://doi.org/10.3390/fluids10020037
APA StyleKlapal, F., & Hlawitschka, M. W. (2025). Towards Efficient Bio-Methanation: A Comparative Analysis of Disperser Designs and Process Optimization in Bubble Columns. Fluids, 10(2), 37. https://doi.org/10.3390/fluids10020037







