Computational Study of a Utility-Scale Vertical-Axis MHK Turbine: A Coupled Approach for Flow–Sediment–Actuator Modeling
Abstract
1. Introduction
2. Governing Equations
2.1. The Hydrodynamic Model
2.2. Turbine Modeling
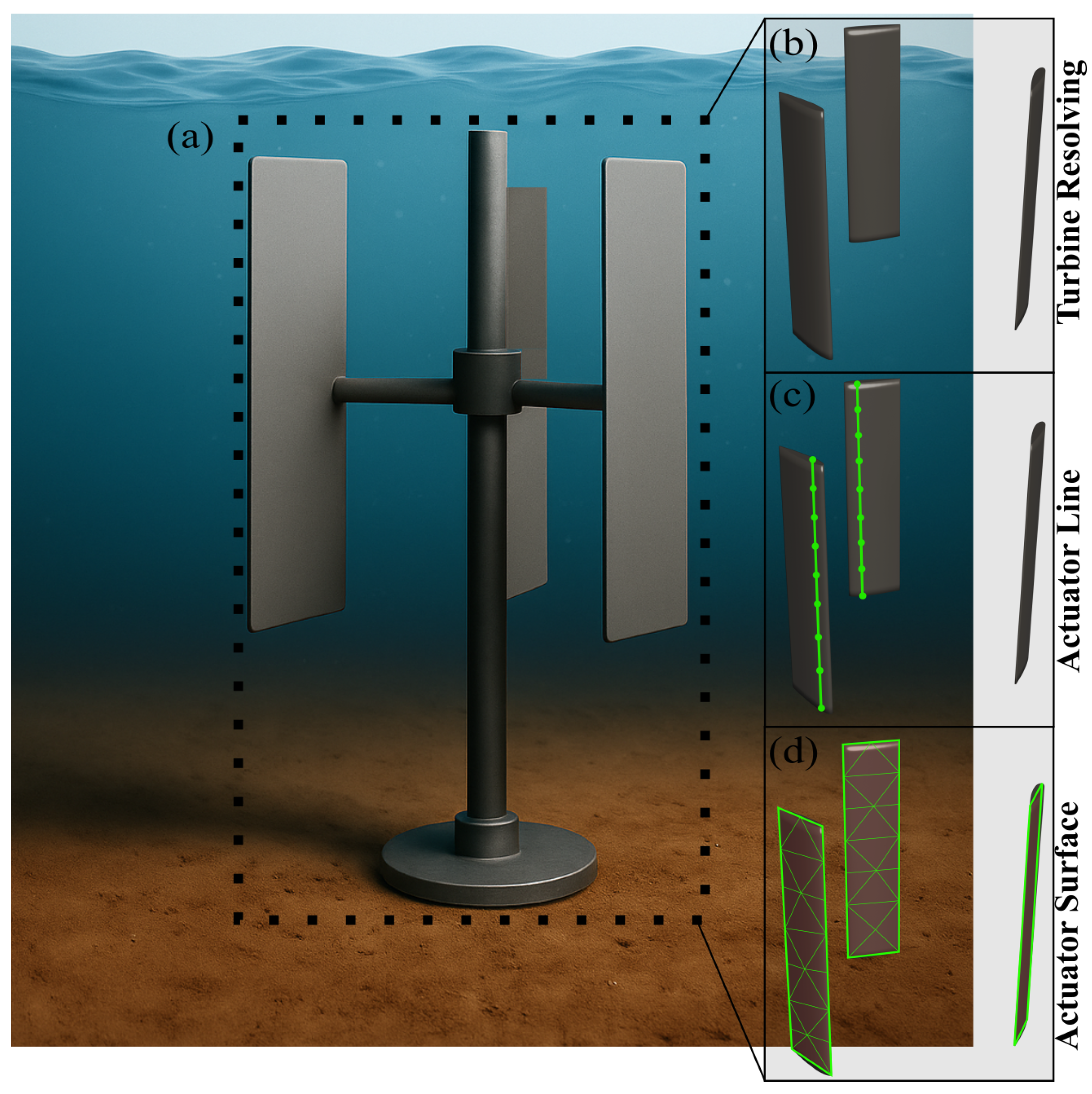
Actuator Surface Method
2.3. Bed Morpho-Dynamics
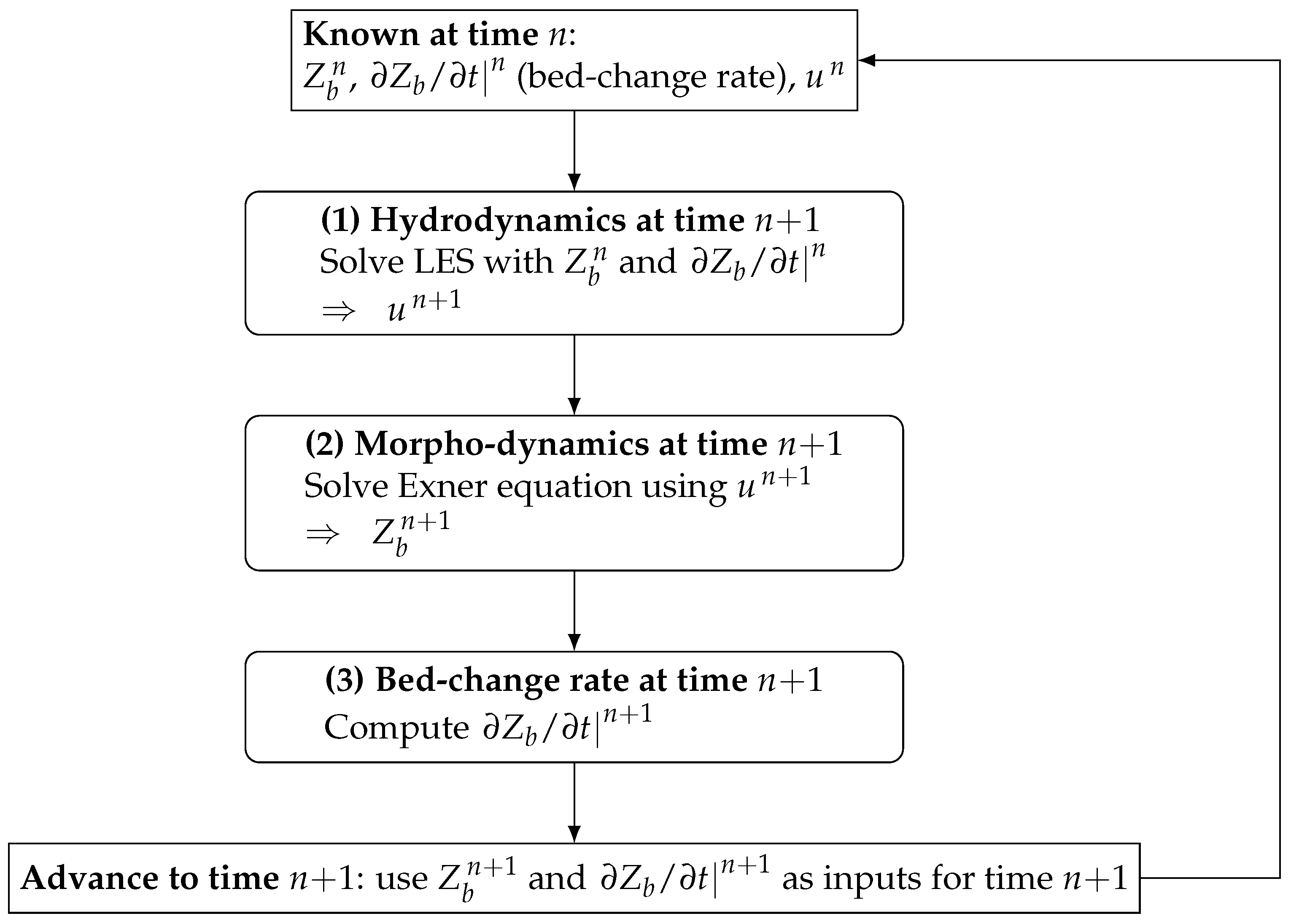
2.4. The Coupled Hydro–Morpho Dynamics
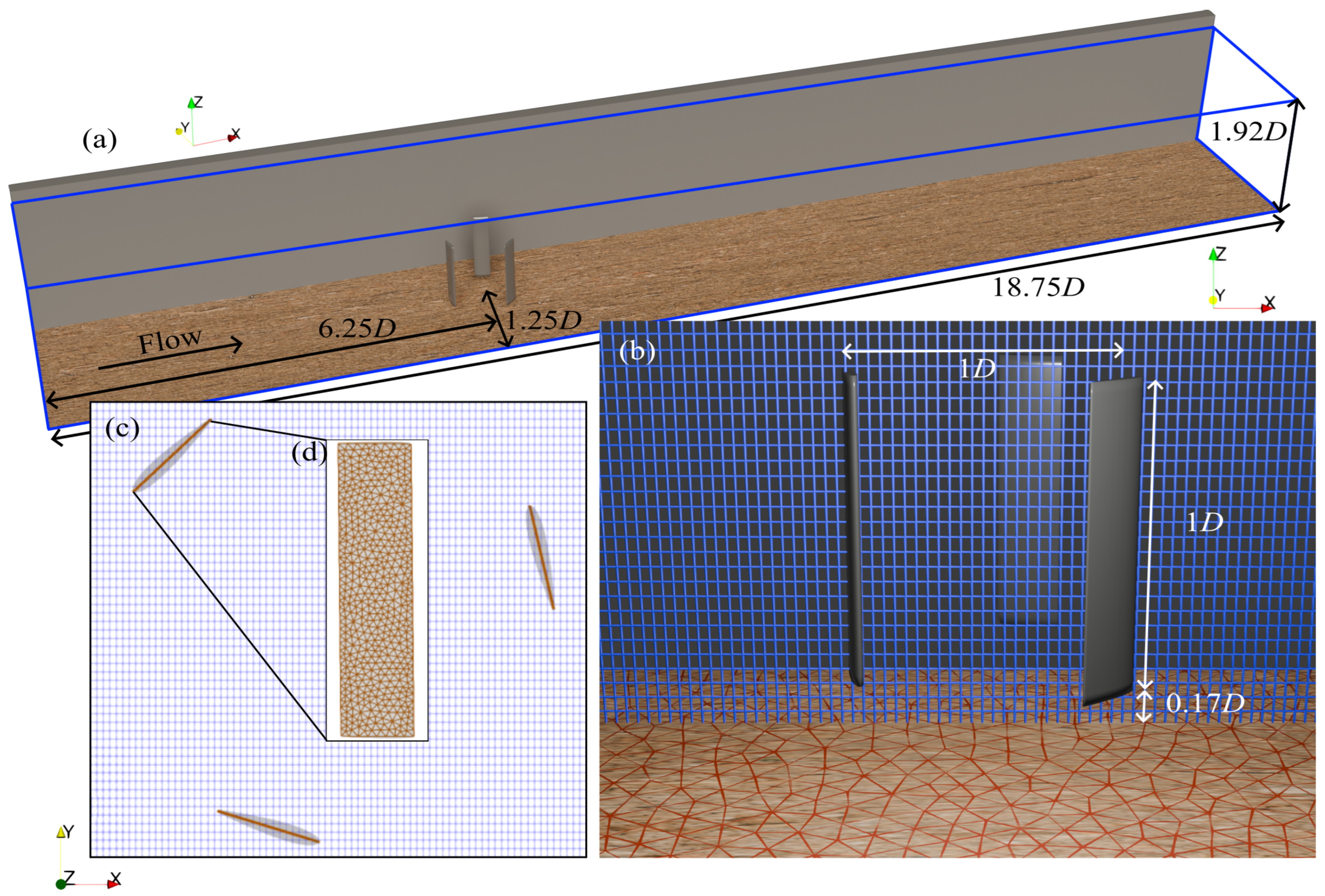
3. Test Case Description and Computational Details
4. Results and Discussions
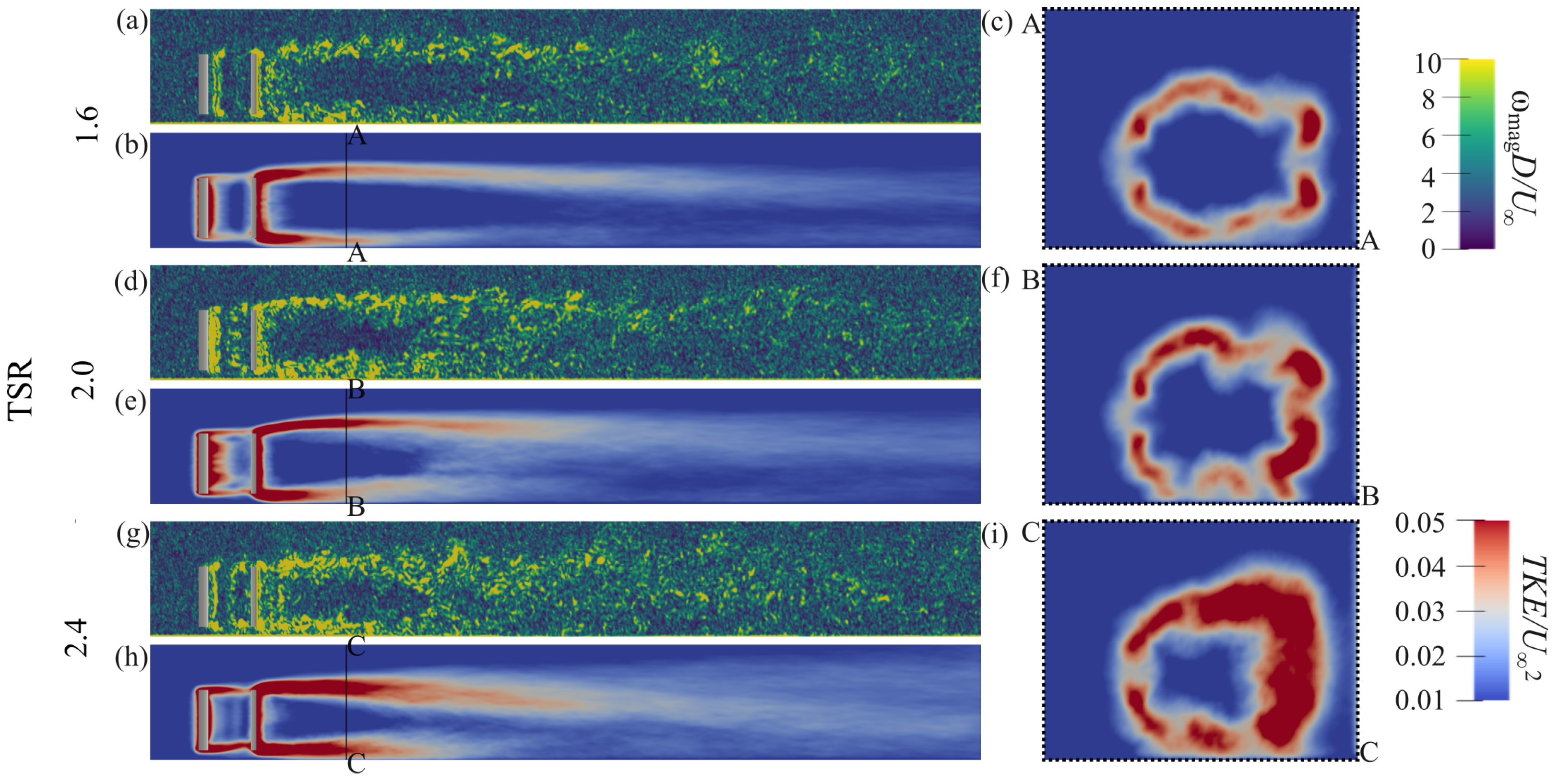
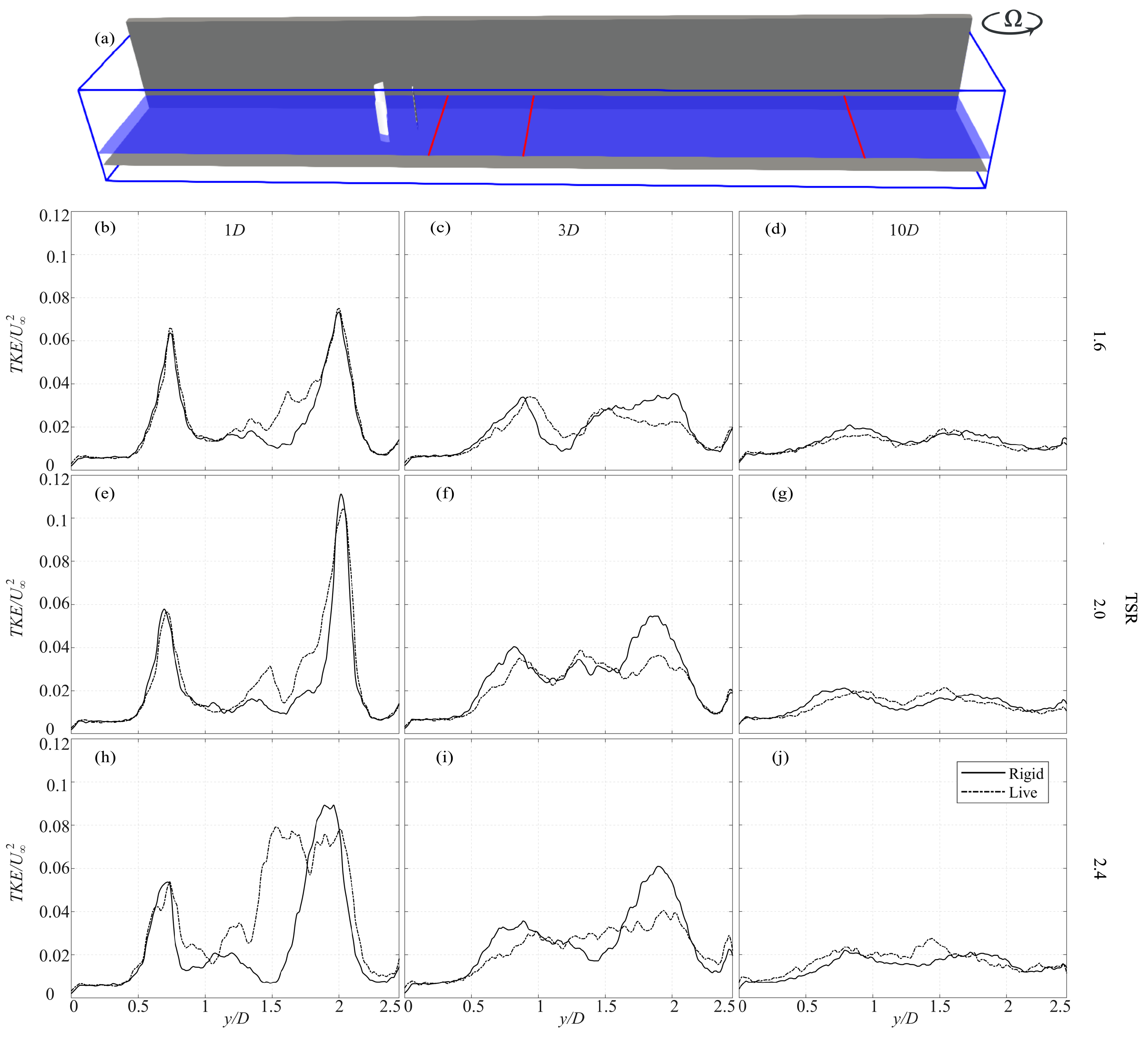
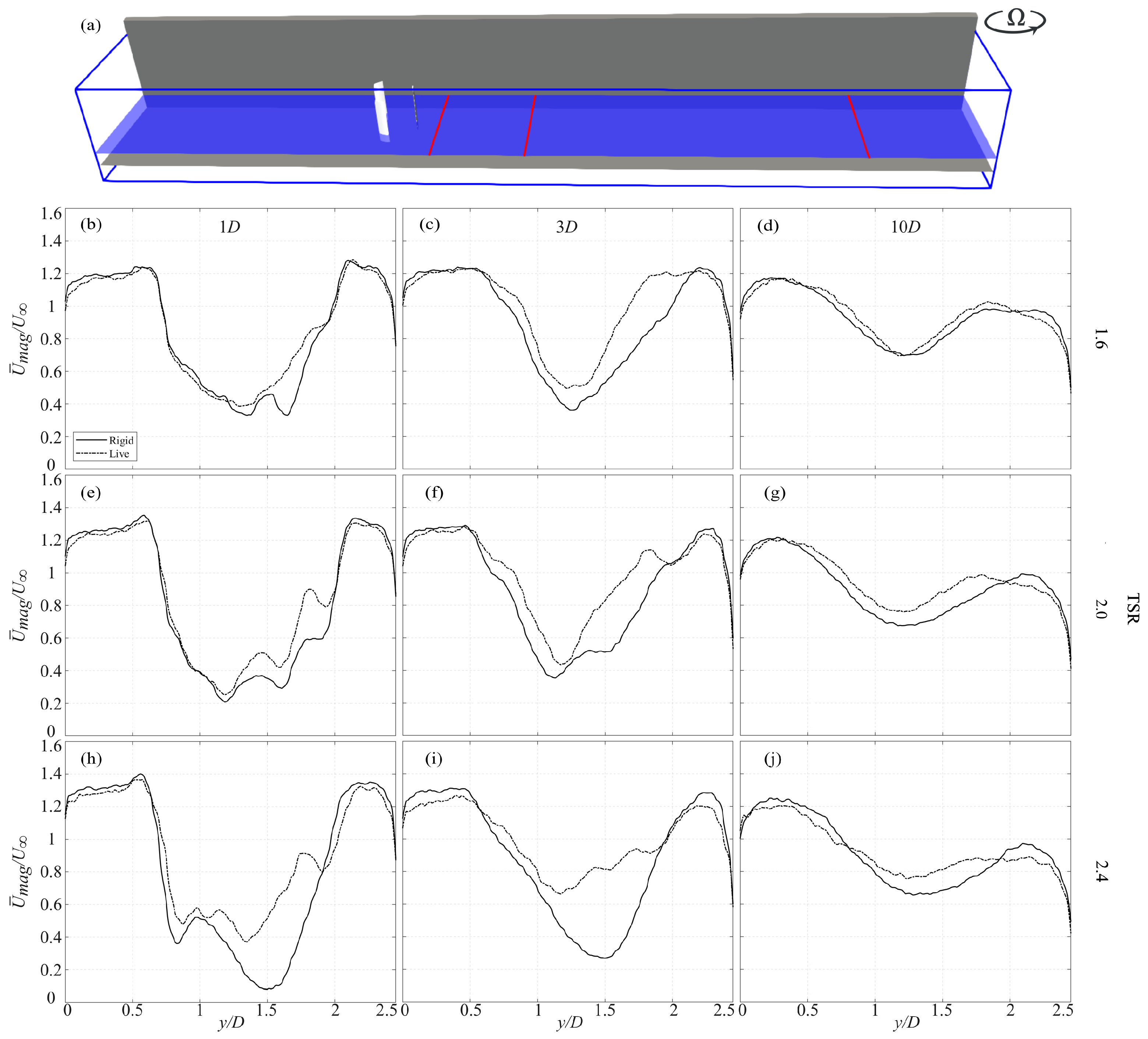
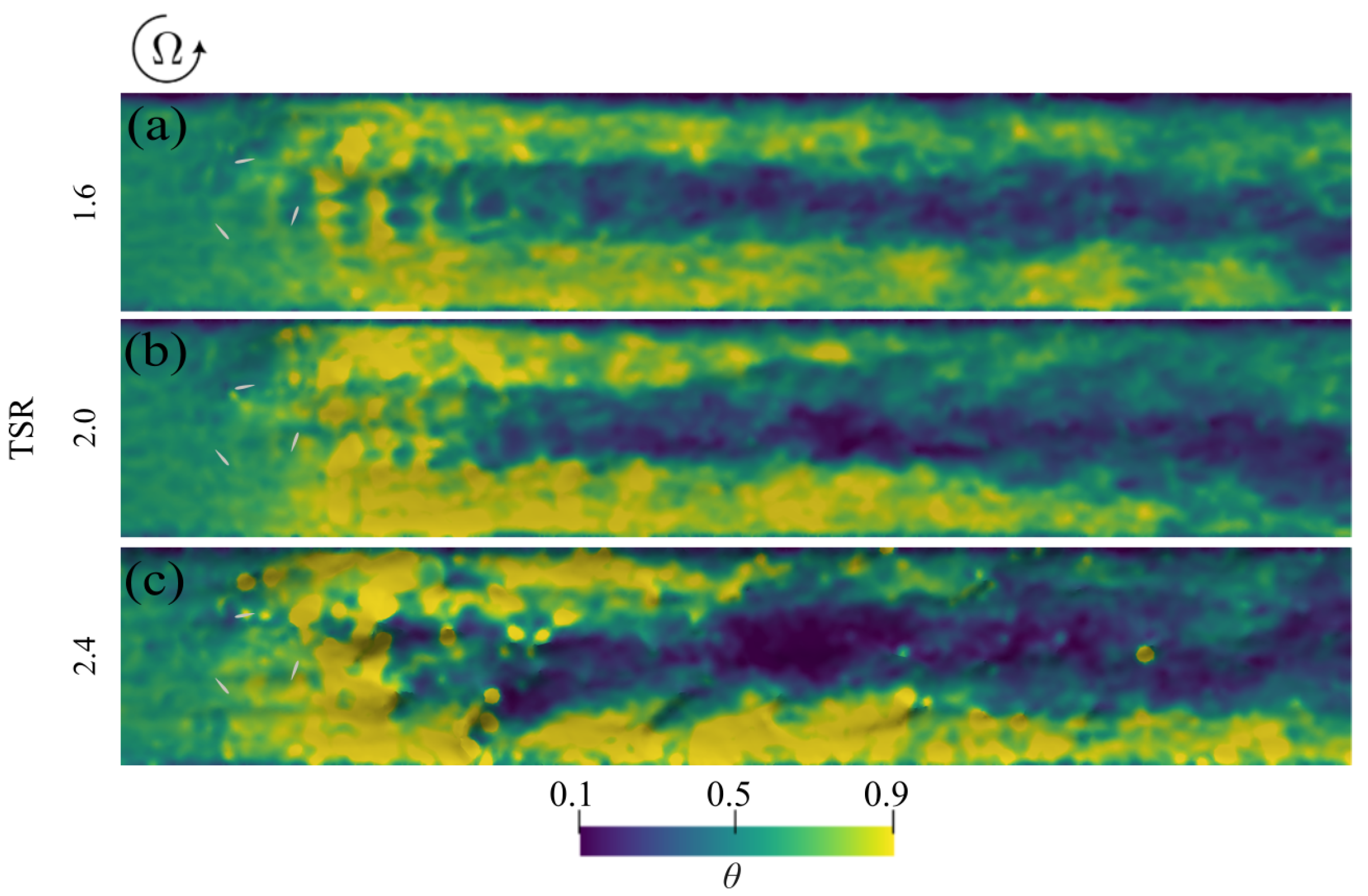
4.1. Wake Flow Under Rigid-Bed Conditions
4.2. Wake Flow Under Live-Bed Conditions
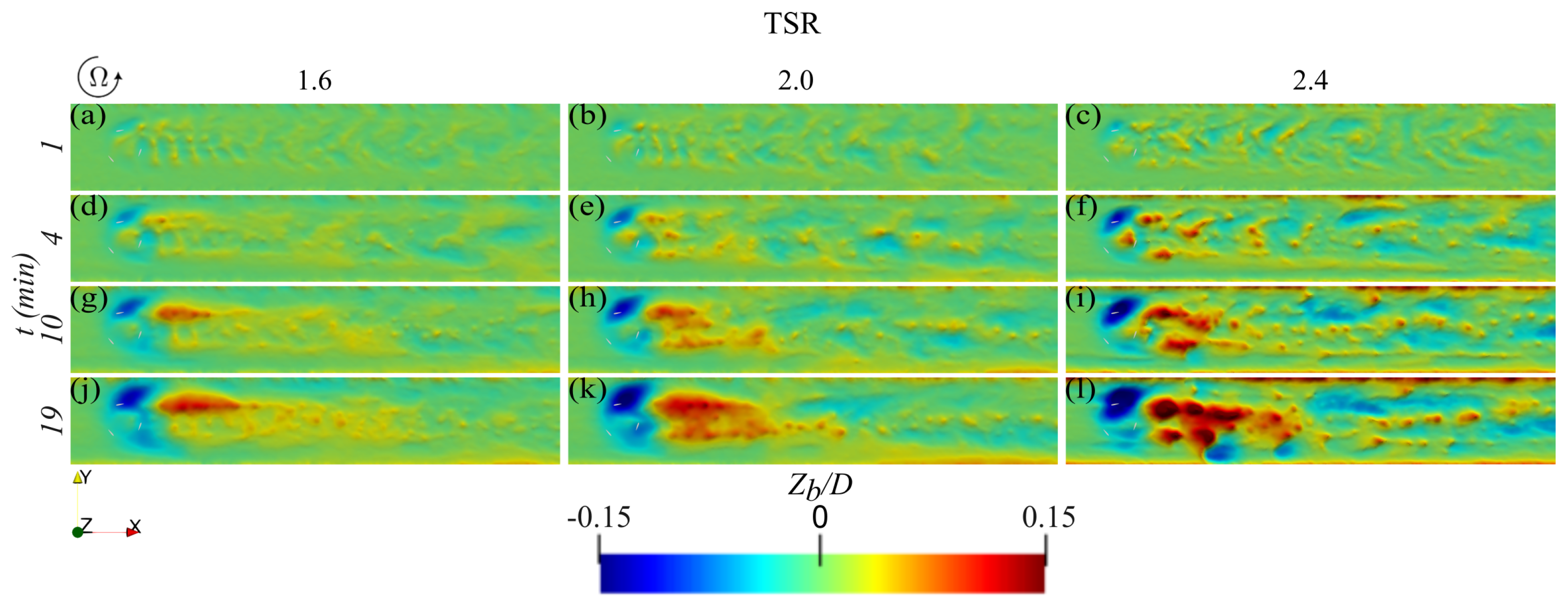
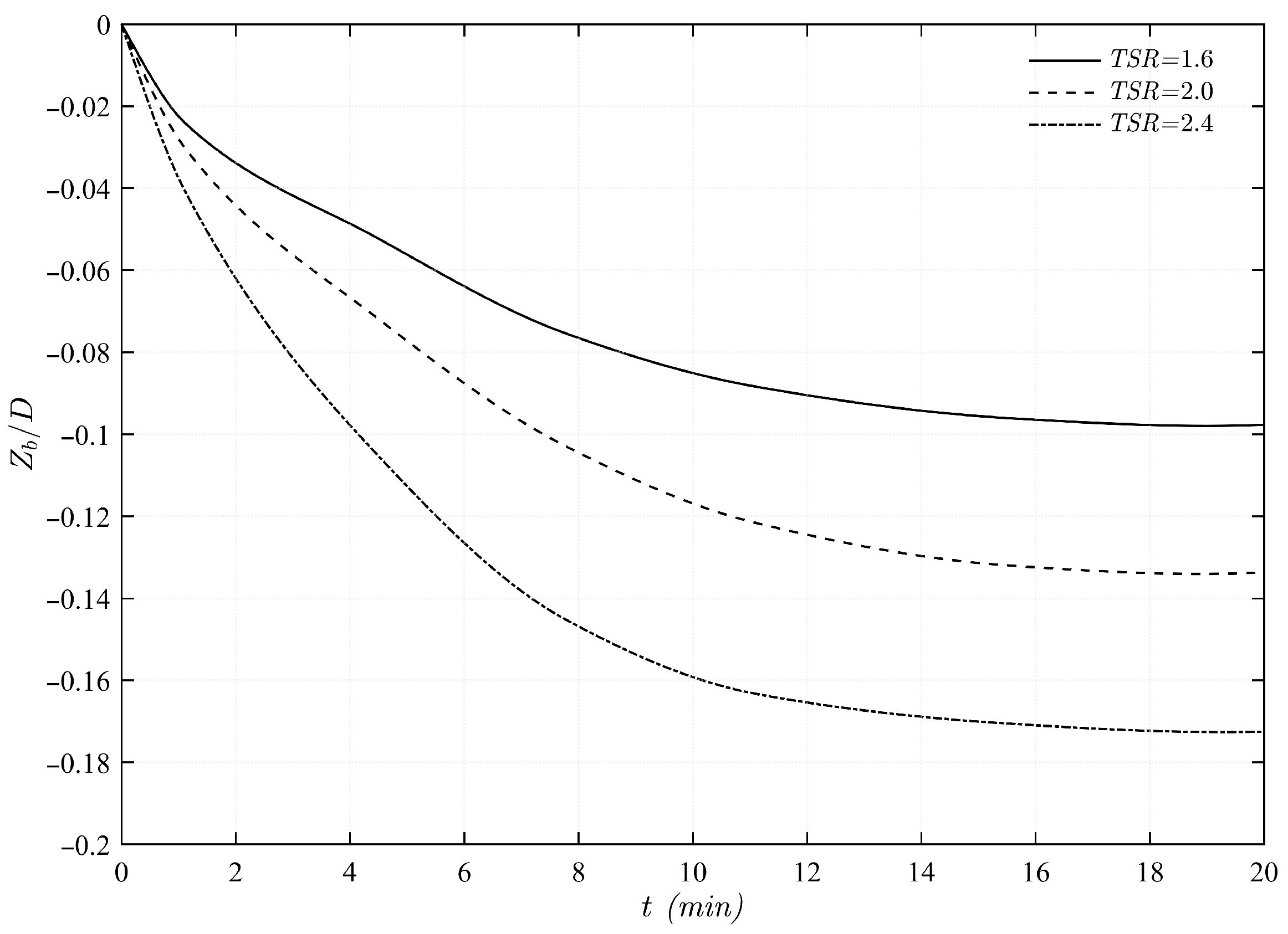
4.3. Sediment Dynamics
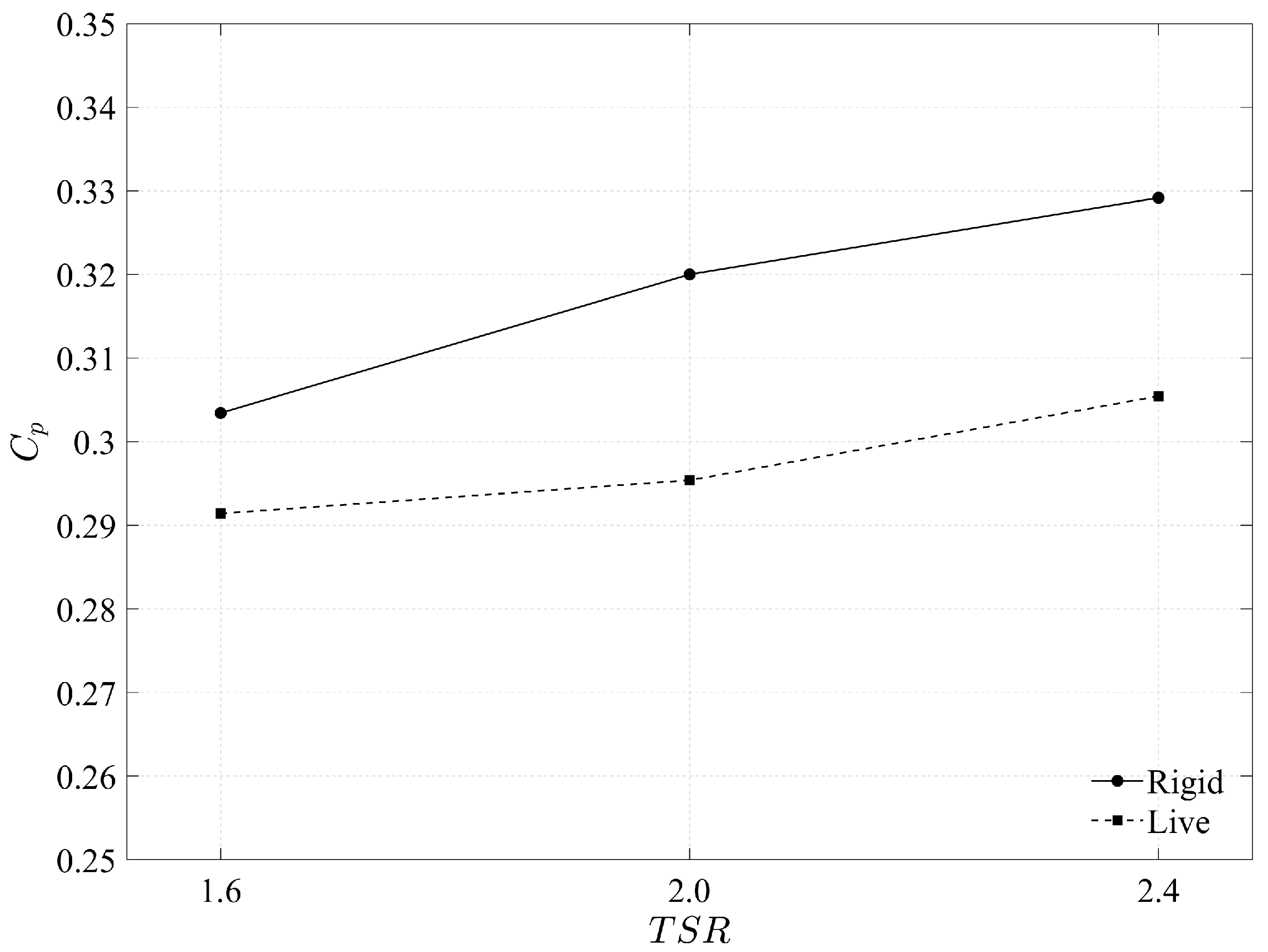
4.4. Turbine Performance
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- International Energy Agency. Renewables 2023; Technical Report; International Energy Agency: Paris, France, 2023. [Google Scholar]
- REN21. Renewables 2024 Global Status Report; Technical Report; Renewable Energy Policy Network for the 21st Century: Paris, France, 2024. [Google Scholar]
- Khan, M.; Bhuyan, G.; Iqbal, M.; Quaicoe, J. Hydrokinetic energy conversion systems and assessment of horizontal and vertical axis turbines for river and tidal applications: A technology status review. Appl. Energy 2009, 86, 1823–1835. [Google Scholar] [CrossRef]
- Behrouzi, F.; Nakisa, M.; Maimun, A.; Ahmed, Y.M. Global renewable energy and its potential in Malaysia: A review of Hydrokinetic turbine technology. Renew. Sustain. Energy Rev. 2016, 62, 1270–1281. [Google Scholar] [CrossRef]
- Kamal, M.M.; Saini, R. A numerical investigation on the influence of savonius blade helicity on the performance characteristics of hybrid cross-flow hydrokinetic turbine. Renew. Energy 2022, 190, 788–804. [Google Scholar] [CrossRef]
- Neill, S.P.; Haas, K.A.; Thiébot, J.; Yang, Z. A review of tidal energy—Resource, feedbacks, and environmental interactions. J. Renew. Sustain. Energy 2021, 136, 062702. [Google Scholar] [CrossRef]
- Kilcher, L.; Fogarty, M.; Lawson, M. Marine Energy in the United States: An Overview of Opportunities; National Renewable Energy Laboratory: Golden, CO, USA, 2021; NREL/TP-5700-78773. [Google Scholar]
- Hussaina, A.; Arifb, S.M.; Aslamc, M. Emerging renewable and sustainable energy technologies: State of the art. Renew. Sustain. Energy Rev. 2017, 71, 12–28. [Google Scholar] [CrossRef]
- Jump, E.; Macleod, A.; Wills, T. Review of tidal turbine wake modelling methods—State of the art. Int. Mar. Energy J. 2020, 3, 91–100. [Google Scholar] [CrossRef]
- Hydropower Explained. 2024. Available online: https://www.eia.gov/energyexplained/hydropower/tidal-power.php (accessed on 10 May 2025).
- Stansby, P.; Ouro, P. Modelling marine turbine arrays in tidal flows. J. Hydraul. Res. 2022, 60, 1–18. [Google Scholar] [CrossRef]
- Fairley, I.; Karunarathna, H.; Masters, I. The influence of waves on morphodynamic impacts of energy extraction at a tidal stream turbine site in the Pentland Firth. Renew. Energy 2018, 125, 630–647. [Google Scholar] [CrossRef]
- Guillou, N.; Thiébot, J.; Chapalain, G. Turbines’ effects on water renewal within a marine tidal stream energy site. Energy 2019, 189, 116113. [Google Scholar] [CrossRef]
- Tidal Energy. 2021. Available online: https://www.pnnl.gov/explainer-articles/tidal-energy (accessed on 10 May 2025).
- Roosevelt Island Tidal Energy (RITE) Project Pilot. 2019. Available online: https://tethys.pnnl.gov/project-sites/roosevelt-island-tidal-energy-rite-project-pilot (accessed on 10 May 2025).
- Cobscook Bay Tidal Energy Test Site. 2024. Available online: https://tethys.pnnl.gov/project-sites/cobscook-bay-tidal-energy-project (accessed on 10 May 2025).
- Wang, T.; Yang, Z. A Tidal Hydrodynamic Model for Cook Inlet, Alaska, to Support Tidal Energy Resource Characterization. J. Mar. Sci. Eng. 2020, 8, 254. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, T.; Branch, R.; Xiao, Z.; Deb, M. Tidal stream energy resource characterization in the Salish Sea. Renew. Energy 2021, 172, 188–208. [Google Scholar] [CrossRef]
- Chawdhary, S.; Angelidis, D.; Colby, J.; Corren, D.; Shen, L.; Sotiropoulos, F. Multiresolution Large-Eddy Simulation of an Array of Hydrokinetic Turbines in a Field-Scale River: The Roosevelt Island Tidal Energy Project in New York City. Water Resour. Res. 2018, 54, 10188–10204. [Google Scholar] [CrossRef]
- Saini, G.; Saini, R.P. A review on technology, configurations, and performance of cross-flow hydrokinetic turbines. Int. J. Energy Res. 2019, 43, 6639–6679. [Google Scholar] [CrossRef]
- Ali, J.; Khan, J.; Khalid, M.S.; Mehmood, N. Harnessing marine energy by horizontal axis marine turbines. In Proceedings of the 2015 12th International Bhurban Conference on Applied Sciences and Technology (IBCAST), Islamabad, Pakistan, 13–17 January 2015. [Google Scholar] [CrossRef]
- Uihlein, A.; Magagna, D. 2014 JRC Ocean Energy Status Report; Technical Report; Publications Office of the European Union: Luxembourg City, Luxembourg, 2015. [Google Scholar] [CrossRef]
- Massie, L.; Ouro, P.; Stoesser, T.; Luo, Q. An Actuator Surface Model to Simulate Vertical Axis Turbines. Energies 2019, 12, 4741. [Google Scholar] [CrossRef]
- Le, T.Q.; Lee, K.S.; Park, J.S.; Ko, J.H. Flow-driven rotor simulation of vertical axis tidal turbines: A comparison of helical and straight blades. Int. J. Nav. Archit. Ocean. Eng. 2014, 6, 257–268. [Google Scholar] [CrossRef]
- Quadrennial Technology Review 2015; Technical Report; United States Department of Energy: Washington, DC, USA, 2015.
- Ouro, P.; Stoesser, T. An immersed boundary-based large-eddy simulation approach to predict the performance of vertical axis tidal turbines. Comput. Fluids 2017, 152, 74–87. [Google Scholar] [CrossRef]
- REN21. Renewables 2016: Global Status Report; Technical Report; Renewable Energy Policy Network for the 21st Century: Paris, France, 2016. [Google Scholar]
- Nachtane, M.; Tarfaoui, M.; Goda, I.; Rouway, M. A review on the technologies, design considerations and numerical models of tidal current turbines. Renew. Energy 2020, 157, 1274–1288. [Google Scholar] [CrossRef]
- Bachant, P.; Wosnik, M. Characterising the near-wake of a cross-flow turbine. J. Turbul. 2015, 16, 392–410. [Google Scholar] [CrossRef]
- Strom, B.; Brunton, S.L.; Polagye, B. Intracycle angular velocity control of cross-flow turbines. Nat. Energy 2017, 2, 17103. [Google Scholar] [CrossRef]
- Roberts, A.; Thomas, B.; Sewell, P.; Khan, Z.; Balmain, S.; Gillman, J. Current tidal power technologies and their suitability for applications in coastal and marine areas. J. Ocean. Eng. Mar. Energy 2016, 2, 227–245. [Google Scholar] [CrossRef]
- Müller, S.; Muhawenimana, V.; Wilson, C.A.; Ouro, P. Experimental investigation of the wake characteristics behind twin vertical axis turbines. Energy Convers. 2021, 247, 114768. [Google Scholar] [CrossRef]
- Müller, S.; Muhawenimana, V.; Sonnino-Sorisio, G.; Wilson, C.A.M.E.; Cable, J.; Ouro, P. Fish response to the presence of hydrokinetic turbines as a sustainable energy solution. Sci. Rep. 2023, 13, 7459. [Google Scholar] [CrossRef]
- Brochier, G.; Fraunie, P.; Beguier, C.; Paraschivoiu, I. Water channel experiments of dynamic stall on Darrieus wind turbine blades. J. Propuls. 2012, 2, 445–449. [Google Scholar] [CrossRef]
- Bachant, P.; Wosnik, M. Performance measurements of cylindrical- and spherical-helical cross-flow marine hydrokinetic turbines, with estimates of exergy efficiency. Renew. Energy 2015, 74, 318–325. [Google Scholar] [CrossRef]
- Tescione, G.; Ragni, D.; He, C.; Simão Ferreira, C.; van Bussel, G. Near wake flow analysis of a vertical axis wind turbine by stereoscopic particle image velocimetry. Renew. Energy 2014, 70, 47–61. [Google Scholar] [CrossRef]
- Araya, D.B.; Colonius, T.; Dabiri, J.O. Transition to bluff-body dynamics in the wake of vertical-axis wind turbines. J. Fluid Mech. 2017, 813, 346–381. [Google Scholar] [CrossRef]
- Ouro, P.; Runge, S.; Luo, Q.; Stoesser, T. Three-dimensionality of the wake recovery behind a vertical axis turbine. Renew. Energy 2019, 133, 1066–1077. [Google Scholar] [CrossRef]
- Nguyen, M.T.; Balduzzi, F.; Goude, A. Effect of pitch angle on power and hydrodynamics of a vertical axis turbine. Ocean Eng. 2021, 238, 109335. [Google Scholar] [CrossRef]
- Yang, M.H.; Gu, Z.T.; Yeh, R.H. Numerical and experimental analyses of the performance of a vertical axis turbine with controllable-blades for ocean current energy. Energy Convers. 2023, 285, 117009. [Google Scholar] [CrossRef]
- Kist, S. America’s First Ocean Energy Delivered to the Grid: ORPC Sells Tidal Power in Maine. 2012. Available online: https://orpc.co/wp-content/uploads/2021/10/americas-first-ocean-energy-delivered-to-the-grid-orpc-sells-tidal-power-in-maine-sept.-13-2012-2012913155.pdf (accessed on 10 May 2025).
- Iida, A.; Kato, K.; Mizuno, A. Numerical Simulation of Unsteady Flow and Aerodynamic Performance of Vertical Axis Wind Turbines with LES. In Proceedings of the 16th Australasian Fluid Mechanics Conference, Crown Plaza, Gold Coast, QLD, Australia, 3–7 December 2007. [Google Scholar]
- Li, C.; Zhu, S.; Xu, Y.; Xiao, Y. 2.5D large eddy simulation of vertical axis wind turbine in consideration of high angle of attack flow. Renew. Energy 2013, 51, 317–330. [Google Scholar] [CrossRef]
- Posa, A.; Parker, C.M.; Leftwich, M.C.; Balaras, E. Wake structure of a single vertical axis wind turbine. Int. J. Heat Fluid Flow 2016, 61, 75–84. [Google Scholar] [CrossRef]
- Elkhoury, M.; Kiwata, T.; Aoun, E. Experimental and numerical investigation of a three-dimensional vertical-axis wind turbine with variable-pitch. J. Wind. Eng. Ind. Aerodyn. 2015, 139, 111–123. [Google Scholar] [CrossRef]
- Posa, A. Wake characterization of coupled configurations of vertical axis wind turbines using Large Eddy Simulation. Int. J. Heat Fluid Flow 2019, 75, 27–43. [Google Scholar] [CrossRef]
- Posa, A. Dependence of the wake recovery downstream of a Vertical Axis Wind Turbine on its dynamic solidity. J. Wind. Eng. Ind. Aerodyn. 2020, 202, 104212. [Google Scholar] [CrossRef]
- Kang, S.; Borazjani, I.; Colby, J.A.; Sotiropoulos, F. Numerical simulation of 3D flow past a real-life marine hydrokinetic turbine. Adv. Water Resour. 2012, 39, 33–43. [Google Scholar] [CrossRef]
- Barnes, A.; Marshall-Cross, D.; Hughes, B.R. Towards a standard approach for future Vertical Axis Wind Turbine aerodynamics research and development. Renew. Sustain. Energy Rev. 2021, 148, 111221. [Google Scholar] [CrossRef]
- Abkar, M.; Dabiri, J.O. Self-similarity and flow characteristics of vertical-axis wind turbine wakes: An LES study. J. Turbul. 2016, 18, 373–389. [Google Scholar] [CrossRef]
- Shamsoddin, S.; Porté-Agel, F. A Large-Eddy Simulation Study of Vertical Axis Wind Turbine Wakes in the Atmospheric Boundary Layer. Energies 2016, 9, 366. [Google Scholar] [CrossRef]
- Mohamed, O.S.; Melani, P.F.; Soraperra, G.; Brighenti, A.; Ferrara, G.; Betti, V.; Schippa, L.; Guerrero, M.; Balduzzi, F.; Bianchini, A. Three-dimensional CFD-ALM-VOF modeling of hydrokinetic turbines in realistic open-channel conditions. Ocean Eng. 2024, 313, 119411. [Google Scholar] [CrossRef]
- Zanforlin, S.; Nishino, T. Fluid dynamic mechanisms of enhanced power generation by closely spaced vertical axis wind turbines. Renew. Energy 2016, 99, 1213–1226. [Google Scholar] [CrossRef]
- Bachant, P.; Goude, A.; Wosnik, M. Actuator line modeling of vertical-axis turbines. arXiv 2018, arXiv:1605.01449. [Google Scholar] [CrossRef]
- Gharaati, M.; Xiao, S.; Wei, N.J.; Martínez-Tossas, L.A.; Dabiri, J.O.; Yang, D. Large-eddy simulation of helical- and straight-bladed vertical-axis wind turbines in boundary layer turbulence. J. Renew. Sustain. Energy 2022, 14, 053301. [Google Scholar] [CrossRef]
- Shchur, I.; Klymko, V.; Xie, S.; Schmidt, D. Design Features and Numerical Investigation of Counter-Rotating VAWT with Co-Axial Rotors Displaced from Each Other along the Axis of Rotation. Energies 2023, 16, 4493. [Google Scholar] [CrossRef]
- Gharib Yosry, A.; Fernández-Jiménez, A.; Álvarez Álvarez, E.; Blanco Marigorta, E. Design and characterization of a vertical-axis micro tidal turbine for low velocity scenarios. Energy Convers. Manag. 2021, 237, 114144. [Google Scholar] [CrossRef]
- Rajagopalan, R.G.; Fanucci, J.B. Finite difference model for vertical axis wind turbines. J. Propuls. Power 1985, 1, 432–436. [Google Scholar] [CrossRef]
- Patankar, S.V. Numerical Heat Transfer and Fluid Flow, 1st ed.; CRC Press: Boca Raton, FL, USA, 1980. [Google Scholar] [CrossRef]
- Rajagopalan, R.G.; Berg, D.E.; Klimas, P.C. Development of a Three-Dimensional Model for the Darrieus Rotor and Its Wake. J. Propuls. Power 1995, 11, 185–195. [Google Scholar] [CrossRef]
- Fortunato, B.; Dadone, A.; Trifoni, V. A Two-Dimensional Methodology to Predict Vertical Axis Wind Turbine Performance. J. Sol. Energy Eng. 1995, 117, 187–193. [Google Scholar] [CrossRef]
- Shen, W.Z.; Zhang, J.H.; Sørensen, J.N. The Actuator Surface Model: A New Navier–Stokes Based Model for Rotor Computations. J. Sol. Energy Eng. 2009, 131, 011002. [Google Scholar] [CrossRef]
- Shamsoddin, S.; Porté-Agel, F. Large Eddy Simulation of Vertical Axis Wind Turbine Wakes. Energies 2014, 7, 890–912. [Google Scholar] [CrossRef]
- Küppers, J.P.; Reinicke, T. Numerical modelling of vertical axis turbines using the actuator surface model. J. Fluids Struct. 2021, 104, 103318. [Google Scholar] [CrossRef]
- Hill, C.; Mirko Musa, M.G. Interaction between instream axial flow hydrokinetic turbines and uni-directional flow bedforms. Renew. Energy 2016, 86, 409–421. [Google Scholar] [CrossRef]
- Shields, M.A.; Woolf, D.K.; Grist, E.P.; Kerr, S.A.; Jackson, A.; Harris, R.E.; Bell, M.C.; Beharie, R.; Want, A.; Osalusi, E.; et al. Marine renewable energy: The ecological implications of altering the hydrodynamics of the marine environment. Ocean Coast. Manag. 2011, 54, 2–9. [Google Scholar] [CrossRef]
- Jacobson, P.T.; Amaral, S.V.; Castro-Santos, T.; Giza, D.; Haro, A.J.; Hecker, G.; McMahon, B.; Perkins, N.; Pioppi, N. Environmental Effects of Hydrokinetic Turbines on Fish: Desktop and Laboratory Flume Studies; Technical Report; Electric Power Research Institute: Palo Alto, CA, USA, 2012. [Google Scholar]
- Lee, J.; Oh, J. A study on the characteristics of organic matter and nutrients released from sediments into agricultural reservoirs. Water 2018, 10, 980. [Google Scholar] [CrossRef]
- Hauer, C.; Kail, J.; Schmütz, C.; Sendzimir, J. The role of sediment and sediment dynamics in the aquatic environment. In Riverine Ecosystem Management: Science for Governing Towards a Sustainable Future; Springer: Cham, Switzernland, 2018; pp. 123–145. [Google Scholar]
- Ross, L.; Sottolichio, A.; Huybrechts, N.; Brunet, P. Tidal turbines in the estuarine environment: From identifying optimal location to environmental impact. Renew. Energy 2021, 169, 700–713. [Google Scholar] [CrossRef]
- Cada, G.; Ahlgrimm, J.; Bahleda, M.; Bigford, T.; Stavrakas, S.D.; Hall, D.; Moursund, R.; Sale, M. Potential Impacts of Hydrokinetic and Wave energy Conversion Technologies on Aquatic environments. Fisheries 2007, 32, 174–181. [Google Scholar] [CrossRef]
- Musa, M.; Heisel, M.; Guala, M. Predictive model for local scour downstream of hydrokinetic turbines in erodible channels. Phys. Rev. Fluids 2018, 3, 024606. [Google Scholar] [CrossRef]
- Copping, A.; Sather, N.; Hanna, L.; Whiting, J.; Zydlewski, G.; Staines, G.; Gill, A.; Hutchison, I.; O’Hagan, A.M.; Simas, T.; et al. Annex IV 2016 State of the Science Report: Environmental Effects of Marine Renewable Energy Development Around the World; Technical Report; Pacific Northwest National Laboratory (PNNL): Richland, WA, USA, 2016. [Google Scholar]
- Yang, X.; Khosronejad, A.; Sotiropoulos, F. Large-eddy simulation of a hydrokinetic turbine mounted on an erodible bed. Renew. Energy 2017, 113, 1419–1433. [Google Scholar] [CrossRef]
- Deng, X.; Zhang, J.; Lin, X. Proposal of actuator line-immersed boundary coupling model for tidal stream turbine modeling with hydrodynamics upon scouring morphology. Energy 2024, 292, 130451. [Google Scholar] [CrossRef]
- Azrulhishama, E.A.; Jamaluddinb, Z.Z.; Azric, M.A.; Yusoff, S.B.M. Potential Evaluation of Vertical Axis Hydrokinetic Turbine Implementation in Equatorial River. In Proceedings of the International Conference on Energy, Electrical and Power Engineering. Journal of Physics: Conference Series, Seoul, Republic of Korea, 15–18 June 2018. [Google Scholar] [CrossRef]
- Jeona, J.; Kima, Y.; Kim, D.; Kang, S. Flume Experiments for Flow around Debris Accumulation at a Bridge. J. Civ. Eng. 2024, 28, 1049–1061. [Google Scholar] [CrossRef]
- Aksen, M.M.; Flora, K.; Seyedzadeh, H.; Anjiraki, M.G.; Khosronejad, A. On the impact of debris accumulation on power production of marine hydrokinetic turbines: Insights gained via LES. Theor. Appl. Mech. Lett. 2024, 14, 100524. [Google Scholar] [CrossRef]
- Aksen, M.M.; Seyedzadeh, H.; Anjiraki, M.G.; Craig, J.; Flora, K.; Santoni, C.; Sotiropoulos, F.; Khosronejad, A. Large eddy simulation of a utility-scale horizontal axis turbine with woody debris accumulation under live bed conditions. Renew. Energy 2025, 239, 122110. [Google Scholar] [CrossRef]
- Wang, C.; Tan, L.; Chen, M.; Fan, H.; Liu, D. A review on synergy of cavitation and sediment erosion in hydraulic machinery. Front. Energy Res. 2022, 10, 1047984. [Google Scholar] [CrossRef]
- Lin, X.; Zhang, J.; Wang, R.; Zhang, J.; Liu, W.; Zhang, Y. Scour around a mono-pile foundation of a horizontal axis tidal stream turbine under steady current. Ocean Eng. 2019, 192, 106571. [Google Scholar] [CrossRef]
- Hill, C.; Kozarek, J.; Sotiropoulos, F.; Guala, M. Hydrodynamics and sediment transport in a meandering channel with a model axial-flow hydrokinetic turbine. Water Resour. Res. 2016, 52, 860–879. [Google Scholar] [CrossRef]
- Chen, L.; Hashim, R.; Othman, F.; Motamedi, S. Experimental study on scour profile of pile-supported horizontal axis tidal current turbine. Renew. Energy 2017, 114, 744–754. [Google Scholar] [CrossRef]
- Musa, M.; Hill, C.; Guala, M. Interaction between hydrokinetic turbine wakes and sediment dynamics: Array performance and geomorphic effects under different siting strategies and sediment transport conditions. Renew. Energy 2019, 138, 738–753. [Google Scholar] [CrossRef]
- Vybulkova, L. A Study of the Wake of an Isolated Tidal Turbine with Application to Its Effects on Local Sediment Transport. Ph.D Thesis, University of Glasgow, Glasgow, UK, 2013. [Google Scholar]
- Lee, J.; Musa, M.; Feist, C.; Gao, J.; Shen, L.; Guala, M. Wake Characteristics and Power Performance of a Drag-Driven in-Bank Vertical Axis Hydrokinetic Turbine. Energies 2019, 12, 3611. [Google Scholar] [CrossRef]
- Gao, J.; Liu, H.; Lee, J.; Zheng, Y.; Guala, M.; Shen, L. Large-eddy simulation and Co-Design strategy for a drag-type vertical axis hydrokinetic turbine in open channel flows. Renew. Energy 2022, 181, 1305–1316. [Google Scholar] [CrossRef]
- Gholami Anjiraki, M.; Aksen, M.M.; Craig, J.; Seyedzadeh, H.; Khosronejad, A. Large eddy simulation of a utility-scale vertical-axis marine hydrokinetic turbine under live-bed conditions. Phys. Fluids 2025, 37, 056609. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, H.; Tang, H.; Zhao, C. Particle size distribution of bed materials in the sandy river bed of alluvial rivers. Int. J. Sediment Res. 2017, 32, 331–339. [Google Scholar] [CrossRef]
- Khosronejad, A.; Limaye, A.B.; Zhang, Z.; Kang, S.; Yang, X.; Sotiropoulos, F. On the Morphodynamics of a Wide Class of Large-Scale Meandering Rivers: Insights Gained by Coupling LES With Sediment-Dynamics. J. Adv. Model. Earth Syst. 2023, 15, e2022MS003257. [Google Scholar] [CrossRef]
- Seyedzadeh, H.; Oaks, W.; Craig, J.; Aksen, M.; Sanz, M.S.; Khosronejad, A. Lagrangian dynamics of particle transport in oral and nasal breathing. Phys. Fluids 2023, 35, 081903. [Google Scholar] [CrossRef]
- Khosronejad, A.; Sotiropoulos, F. Numerical simulation of sand waves in a turbulent open channel flow. J. Fluid Mech. 2014, 753, 150–216. [Google Scholar] [CrossRef]
- Khosronejad, A.; Sotiropoulos, F. On the genesis and evolution of barchan dunes: Morphodynamics. J. Fluid Mech. 2017, 815, 117–148. [Google Scholar] [CrossRef]
- Khosronejad, A.; Kozarek, J.L.; Sotiropoulos, F. Simulation-Based Approach for Stream Restoration Structure Design: Model Development and Validation. J. Hydraul. Eng. 2014, 140, 04014042. [Google Scholar] [CrossRef]
- Zhang, Z.; Gholami Anjiraki, M.; Seyedzadeh, H.; Sotiropoulos, F.; Yang, X.; Khosronejad, A. Predicting Equilibrium Bed Morphology of Large-Scale Meandering Rivers Using a Novel LES-Trained Machine Learning Approach. J. Adv. Model. Earth Syst. 2025, 17, e2024MS004710. [Google Scholar] [CrossRef]
- Seyedzadeh, H.; Anjiraki, M.G.; Sorisio, G.S.; Wilson, C.; Sotiropoulos, F.; Khosronejad, A. On the interaction of fish and marine hydrokinetic turbines: Insights gained through experimental and computational observations. arXiv 2025, arXiv:2508.04558. [Google Scholar] [CrossRef]
- Anjiraki, M.G.; Santoni, C.; Shapourmiandouab, S.; Seyedzadeh, H.; Craig, J.; Sotiropoulos, F.; Khosronejad, A. Wind farm layout optimization using a novel machine learning approach. arXiv 2025, arXiv:2509.07868. [Google Scholar] [CrossRef]
- Flora, K.; Khosronejad, A. Uncertainty quantification of bank vegetation impacts on the flood flow field in the American River, California, using large-eddy simulations. Earth Surf. Process. Landforms 2024, 49, 967–979. [Google Scholar] [CrossRef]
- Germano, M.; Piomelli, U.; Moin, P.; Cabot, W.H. A dynamic subgrid-scale eddy viscosity model. Phys. Fluids Fluid Dyn. 1991, 3, 1760–1765. [Google Scholar] [CrossRef]
- Smagorinsky, J. GENERAL CIRCULATION EXPERIMENTS WITH THE PRIMITIVE EQUATIONS: I. THE BASIC EXPERIMENT. Mon. Weather. Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Yang, X.; Sotiropoulos, F. A new class of actuator surface models for wind turbines. Wind Energy 2018, 1, 285–302. [Google Scholar] [CrossRef]
- Yang, X.; Sotiropoulos, F.; Conzemius, R.J.; Wachtler, J.N.; Strong, M.B. Large-eddy simulation of turbulent flow past wind turbines/farms: The Virtual Wind Simulator (VWiS). Wind Energy 2015, 18, 2025–2045. [Google Scholar] [CrossRef]
- Yang, X.; Kang, S.; Sotiropoulos, F. Computational study and modeling of turbine spacing effects in infinite aligned wind farms. Phys. Fluids 2012, 24, 115107. [Google Scholar] [CrossRef]
- Sørensen, N.N.; Michelsen, J.A.; Schreck, S. Navier–Stokes predictions of the NREL phase VI rotor in the NASA Ames 80 ft × 120 ft wind tunnel. Wind Energy 2002, 5, 151–169. [Google Scholar] [CrossRef]
- Johansen, J.; Sørensen, N.N.; Michelsen, J.A.; Schreck, S. Detached-eddy simulation of flow around the NREL Phase VI blade. Wind Energy 2002, 5, 185–197. [Google Scholar] [CrossRef]
- Sezer Uzol, N.; Long, L. 3-D Time-Accurate CFD Simulations of Wind Turbine Rotor Flow Fields. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006; p. 394. [Google Scholar] [CrossRef]
- Zahle, F.; Sørensen, N.N.; Johansen, J. Wind turbine rotor-tower interaction using an incompressible overset grid method. Wind Energy 2009, 12, 594–619. [Google Scholar] [CrossRef]
- Froude, W. On the Elementary Relation Between Pitch, Slip, and Propulsive Efficiency; Technical Memorandum No. NACA–TM–1; National Advisory Committee for Aeronautics (NACA): Washington, DC, USA, 1920. [Google Scholar]
- Santoni, C.; Khosronejad, A.; Seiler, P.; Sotiropoulos, F. Toward control co-design of utility-scale wind turbines: Collective vs. individual blade pitch control. Energy Rep. 2023, 9, 793–806. [Google Scholar] [CrossRef]
- Santoni, C.; Sotiropoulos, F.; Khosronejad, A. A Comparative Analysis of Actuator-Based Turbine Structure Parametrizations for High-Fidelity Modeling of Utility-Scale Wind Turbines under Neutral Atmospheric Conditions. Energies 2024, 17, 753. [Google Scholar] [CrossRef]
- Zhang, Z.; Santoni, C.; Herges, T.; Sotiropoulos, F.; Khosronejad, A. Time-Averaged Wind Turbine Wake Flow Field Prediction Using Autoencoder Convolutional Neural Networks. Energies 2022, 15, 41. [Google Scholar] [CrossRef]
- Yang, X.; Pakula, M.; Sotiropoulos, F. Large-eddy simulation of a utility-scale wind farm in complex terrain. Appl. Energy 2018, 229, 767–777. [Google Scholar] [CrossRef]
- Van Rijn, L.C. Principles of Sediment Transport in Rivers, Estuaries, and Coastal Seas; Aqua Publications: Telangana, India, 1993. [Google Scholar]
- Paola, C.; Voller, V.R. A generalized Exner equation for sediment mass balance. J. Geophys. Res. Earth Surf. 2005, 110, F04014. [Google Scholar] [CrossRef]
- Borazjani, I.; Ge, L.; Sotiropoulos, F. Curvilinear immersed boundary method for simulating fluid structure interaction with complex 3D rigid bodies. J. Comput. Phys. 2008, 227, 7587–7620. [Google Scholar] [CrossRef]
- Soulsby, R.L.; Whitehouse, R.J. Threshold of Sediment Motion in Coastal Environments. In Pacific Coasts and Ports ’97: Proceedings of the 13th Australasian Coastal and Ocean Engineering Conference and the 6th Australasian Port and Harbour Conference, Volume 1, Christchurch, New Zealand, 7–11 September 1997; Centre for Advanced Engineering, University of Canterbury: Christchurch, New Zealand, 1997. [Google Scholar]
- Chou, Y.J.; Fringer, O.B. A model for the simulation of coupled flow-bed form evolution in turbulent flows. J. Geophys. Res. Ocean. 2010, 115. [Google Scholar] [CrossRef]
- Khosronejad, A.; Rennie, C.D.; Neyshabouri, S.A.A.S.; Townsend, R.D. 3D Numerical Modeling of Flow and Sediment Transport in Laboratory Channel Bends. J. Hydraul. Eng. 2007, 133, 1123–1134. [Google Scholar] [CrossRef]
- Khosronejad, A.; Kang, S.; Borazjani, I.; Sotiropoulos, F. Curvilinear immersed boundary method for simulating coupled flow and bed morphodynamic interactions due to sediment transport phenomena. Adv. Water Resour. 2011, 34, 829–843. [Google Scholar] [CrossRef]
- Khosronejad, A.; Flora, K.; Kang, S. Effect of Inlet Turbulent Boundary Conditions on Scour Predictions of Coupled LES and Morphodynamics in a Field-Scale River: Bankfull Flow Conditions. J. Hydraul. Eng. 2020, 146, 04020020. [Google Scholar] [CrossRef]
- Fujisawa, N.; Shibuya, S. Observations of dynamic stall on Darrieus wind turbine blades. J. Wind Eng. Ind. Aerodyn. 2001, 89, 201–214. [Google Scholar] [CrossRef]
- Posa, A. Influence of Tip Speed Ratio on wake features of a Vertical Axis Wind Turbine. J. Wind Eng. Ind. Aerodyn. 2020, 197, 104076. [Google Scholar] [CrossRef]
- Khosronejad, A.; Diplas, P.; Sotiropoulos, F. Simulation-based optimization of in–stream structures design: Bendway weirs. Environ. Fluid Mech. 2017, 17, 79–109. [Google Scholar] [CrossRef]
- Ouro, P.; Stoesser, T. Wake Generated Downstream of a Vertical Axis Tidal Turbine. In Proceedings of the 12th European Wave and Tidal Energy Conference (EWTEC), Cork, Ireland, 27 August–1 September 2017. [Google Scholar]
- Liu, K.; Yu, M.; Zhu, W. Performance analysis of vertical axis water turbines under single-phase water and two-phase open channel flow conditions. Ocean Eng. 2021, 238, 109769. [Google Scholar] [CrossRef]
- Betz, A. Introduction to the Theory of Flow Machines; Pergamon Press: Oxford, UK, 1966. [Google Scholar]
- Lee, J.; Kim, Y.; Khosronejad, A.; Kang, S. Experimental study of the wake characteristics of an axial flow hydrokinetic turbine at different tip speed ratios. Ocean Eng. 2020, 196, 106777. [Google Scholar] [CrossRef]
- Liu, X.; Li, Z.; Yang, X.; Xu, D.; Kang, S.; Khosronejad, A. Large-Eddy Simulation of Wakes of Waked Wind Turbines. Energies 2022, 15, 2899. [Google Scholar] [CrossRef]
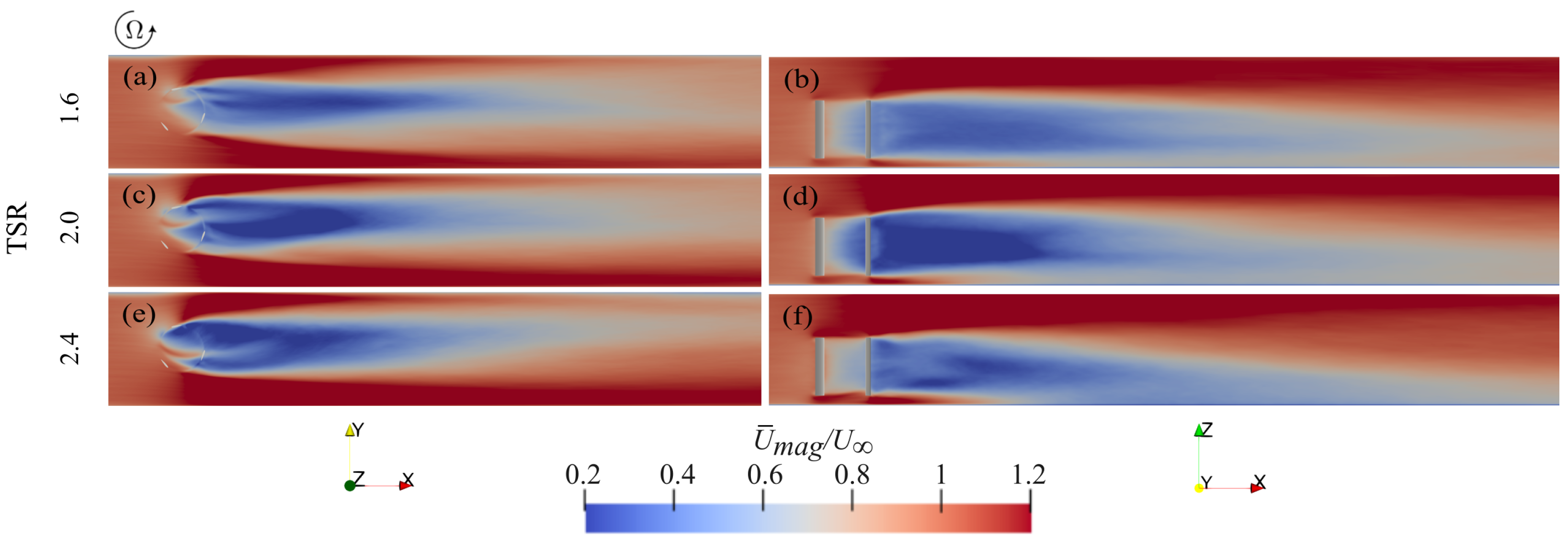
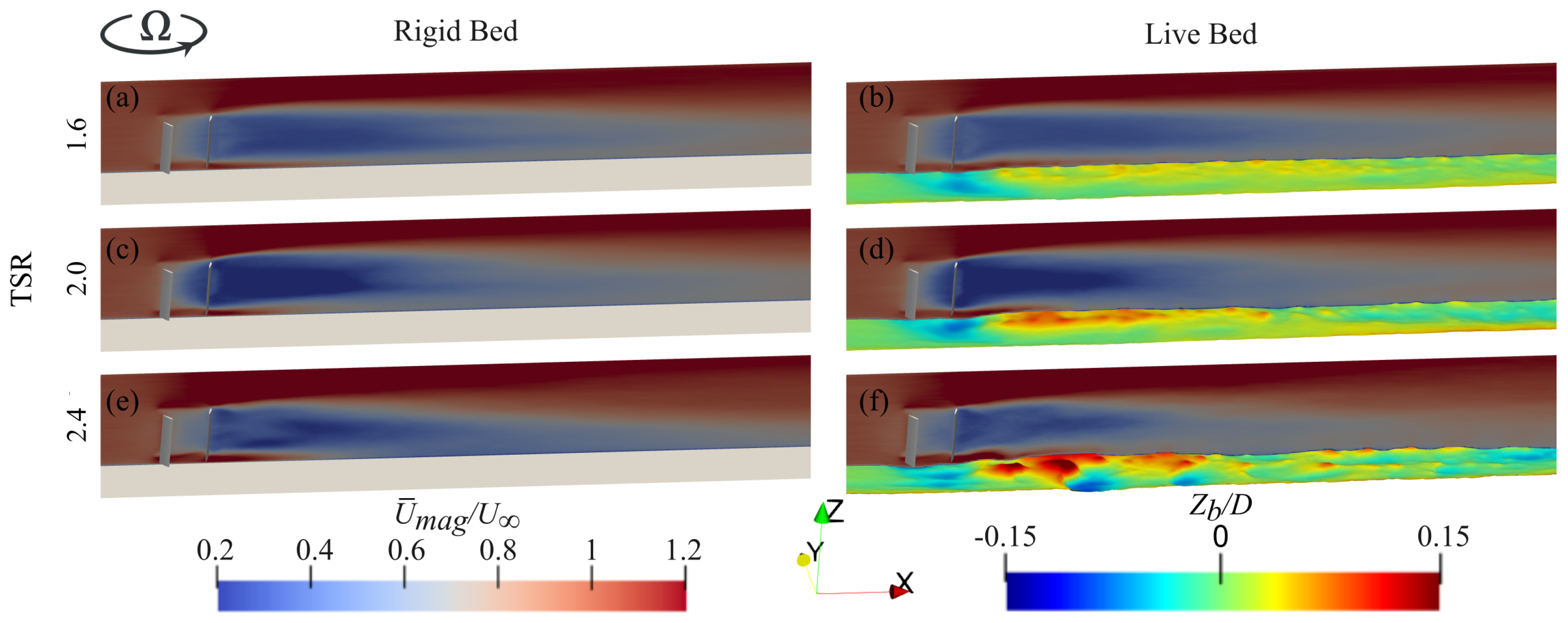
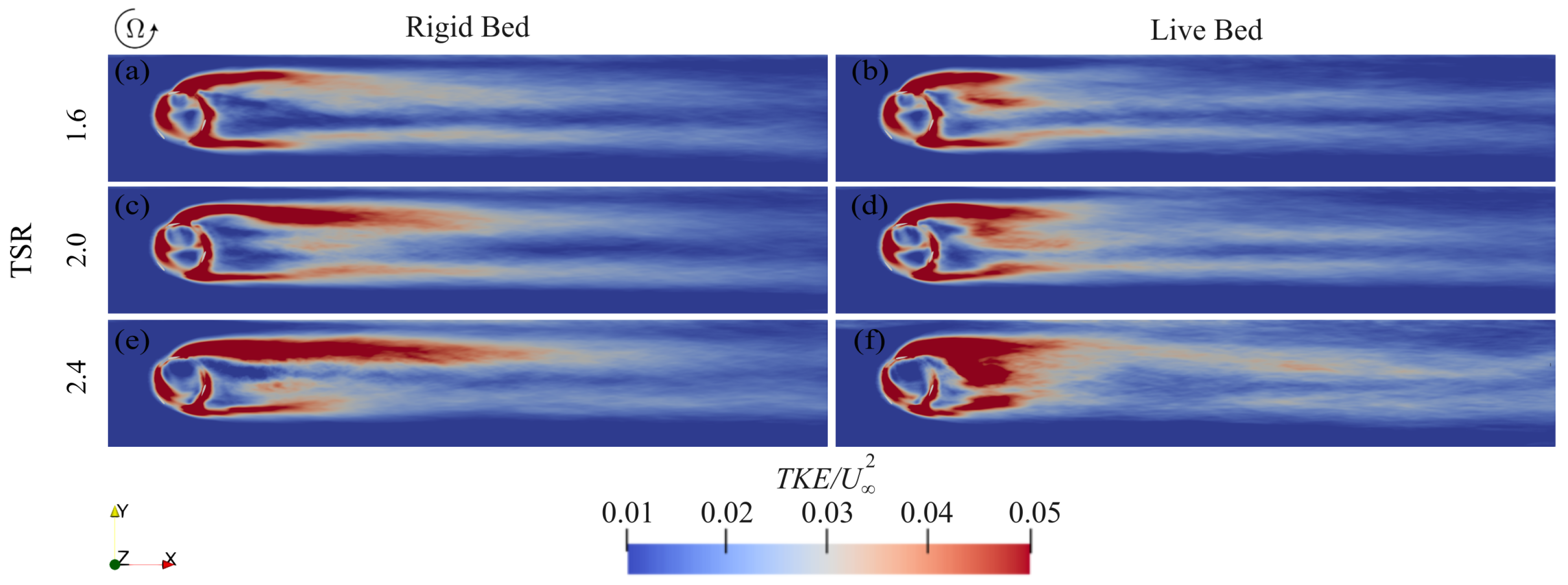
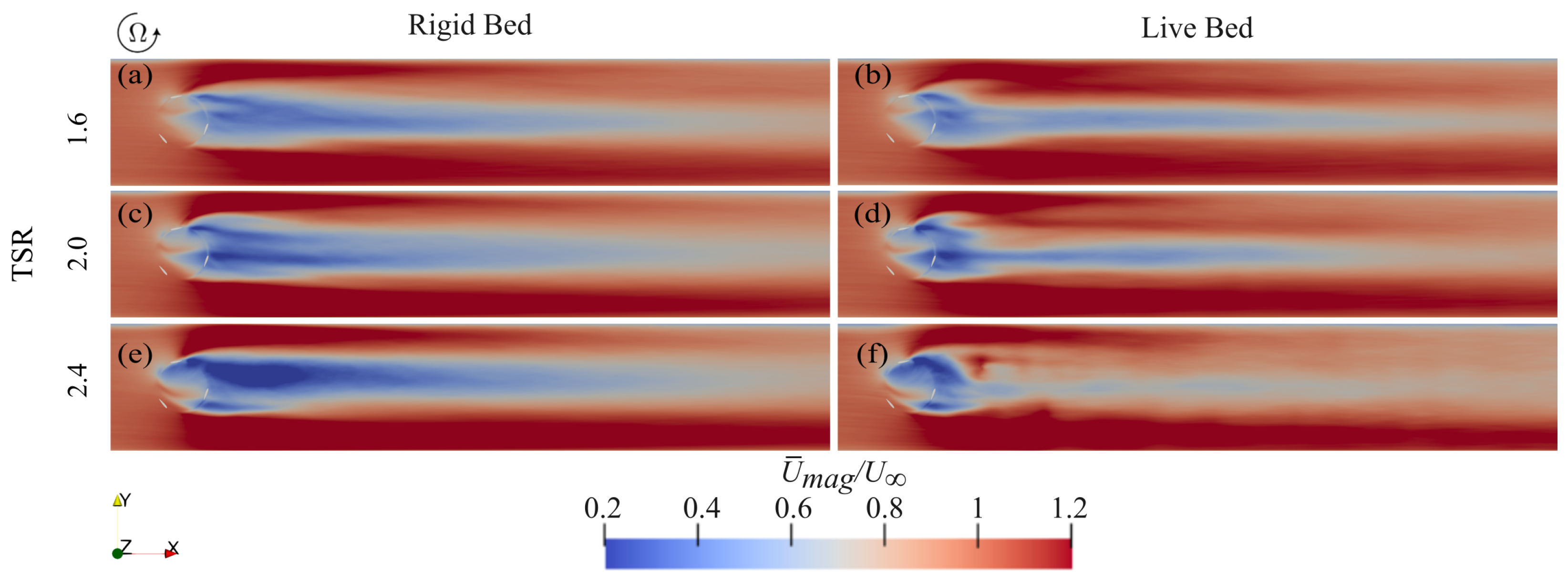
| Test-Case | Mobility | TSR |
|---|---|---|
| 1 | Rigid | |
| 2 | Rigid | |
| 3 | Rigid | |
| 4 | Live | |
| 5 | Live | |
| 6 | Live |
| 1100 | |
| 2650 | |
| (mm) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gholami Anjiraki, M.; Aksen, M.M.; Shapourmiandouab, S.; Craig, J.; Khosronejad, A. Computational Study of a Utility-Scale Vertical-Axis MHK Turbine: A Coupled Approach for Flow–Sediment–Actuator Modeling. Fluids 2025, 10, 304. https://doi.org/10.3390/fluids10120304
Gholami Anjiraki M, Aksen MM, Shapourmiandouab S, Craig J, Khosronejad A. Computational Study of a Utility-Scale Vertical-Axis MHK Turbine: A Coupled Approach for Flow–Sediment–Actuator Modeling. Fluids. 2025; 10(12):304. https://doi.org/10.3390/fluids10120304
Chicago/Turabian StyleGholami Anjiraki, Mehrshad, Mustafa Meriç Aksen, Samin Shapourmiandouab, Jonathan Craig, and Ali Khosronejad. 2025. "Computational Study of a Utility-Scale Vertical-Axis MHK Turbine: A Coupled Approach for Flow–Sediment–Actuator Modeling" Fluids 10, no. 12: 304. https://doi.org/10.3390/fluids10120304
APA StyleGholami Anjiraki, M., Aksen, M. M., Shapourmiandouab, S., Craig, J., & Khosronejad, A. (2025). Computational Study of a Utility-Scale Vertical-Axis MHK Turbine: A Coupled Approach for Flow–Sediment–Actuator Modeling. Fluids, 10(12), 304. https://doi.org/10.3390/fluids10120304






