Numerical Study of Side Boundary Effects in Pore-Scale Digital Rock Flow Simulations
Abstract
1. Introduction
2. Lattice Boltzmann Method for Two-Phase Flow
- The present color-gradient LBM uses the continuous surface force model [27] to capture the effects of surface tension at the fluid interface, and incorporates the forces directly into the lattice Boltzmann equation through a forcing term [9,28]. This will reduce spurious velocities and improve numerical stability.
- The geometrical wetting model [19,23,24] is used to account for the wettability of the solid phase. Compared to the traditional fictitious density wetting model [31], the geometrical wetting model can accurately prescribe the contact angle on complex solid surfaces while avoiding forming non-physical films on the solid surfaces [24].
- A zero-interfacial-force scheme [32] is applied to minimize color gradient near the three-phase contact line, which significantly reduces spurious currents and improve numerical stability.
2.1. The CSF-Based Color-Gradient LBM
2.2. The Geometrical Wetting Boundary Condition
3. Validation
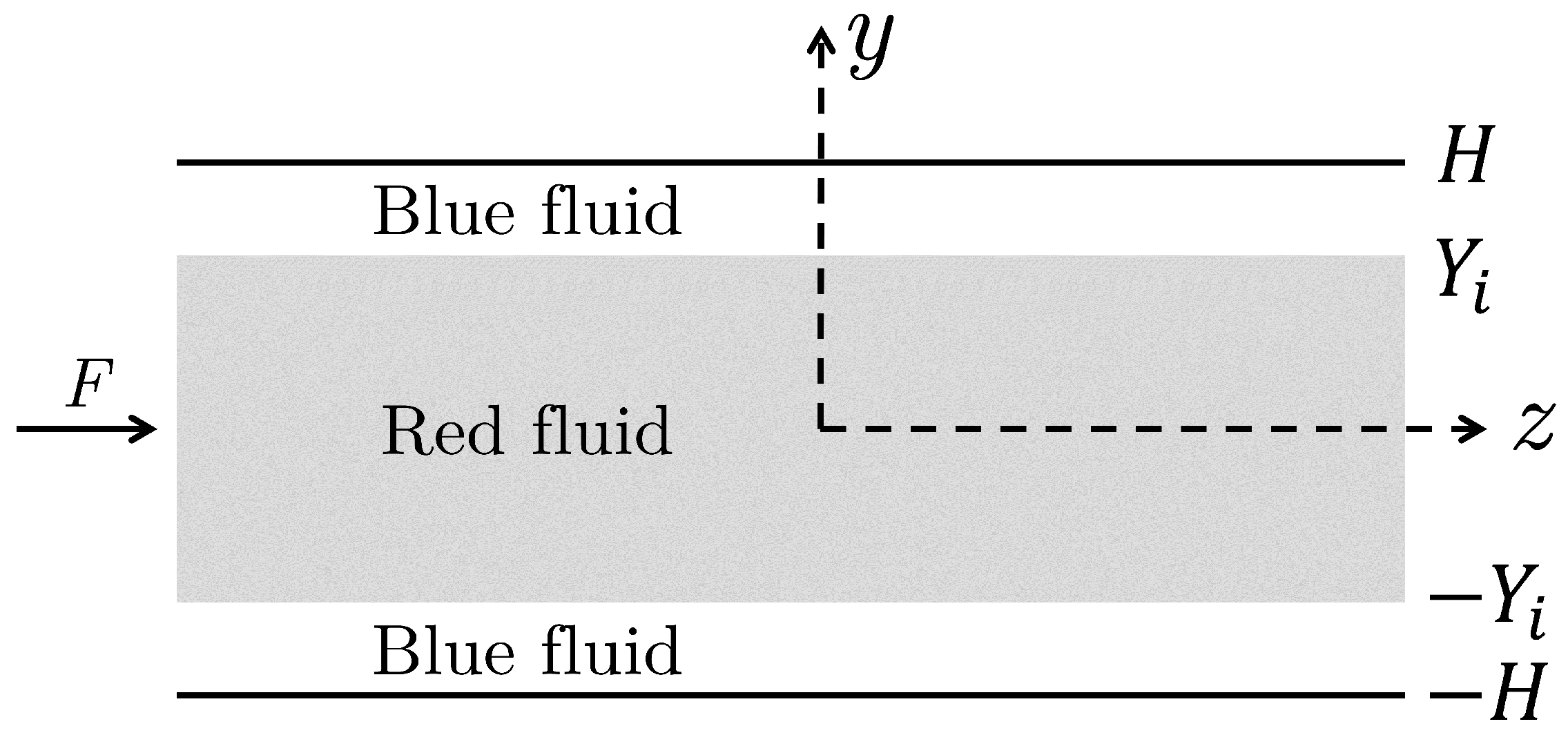
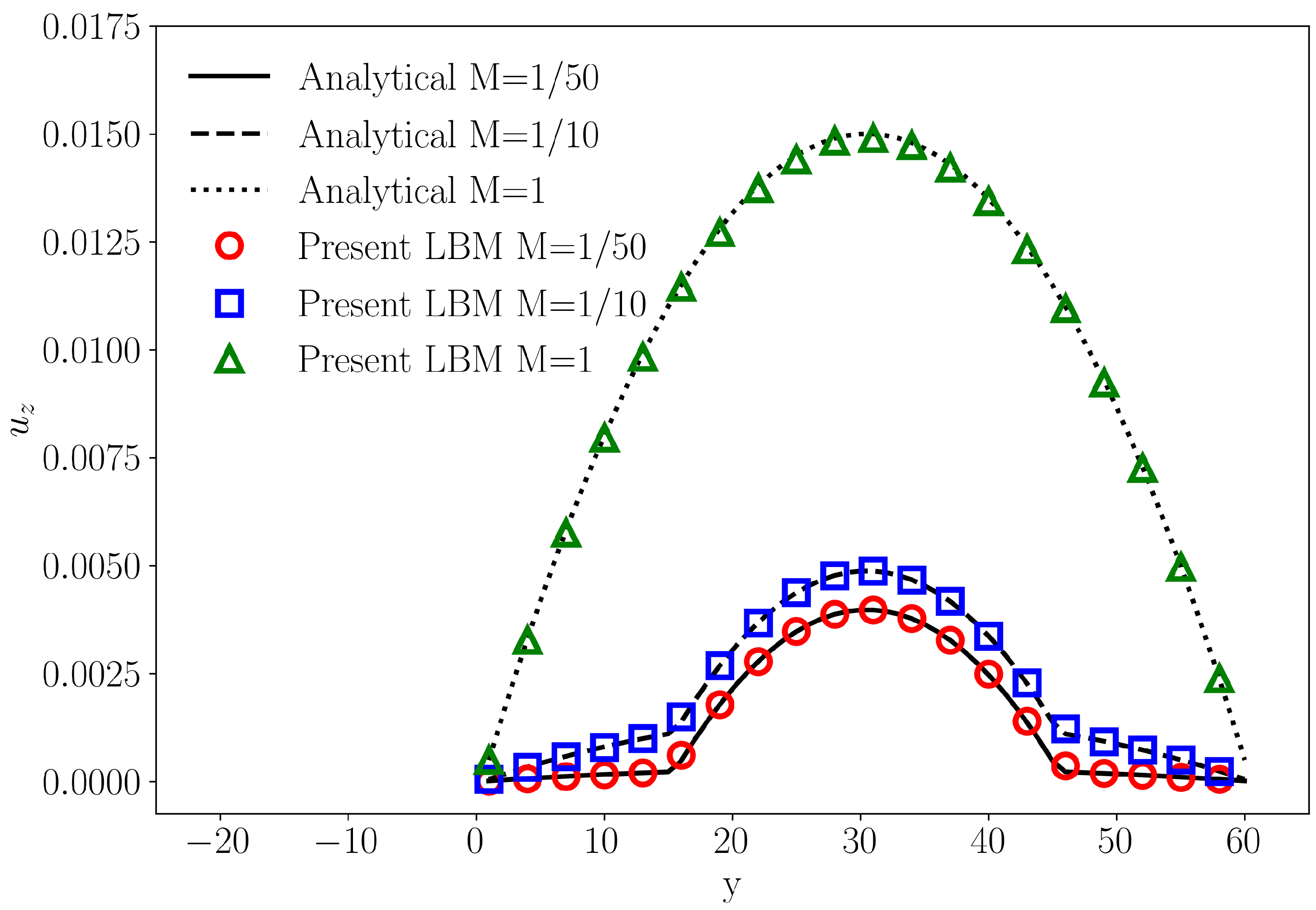
3.1. Two-Phase Layered Flow Between Two Parallel Plates
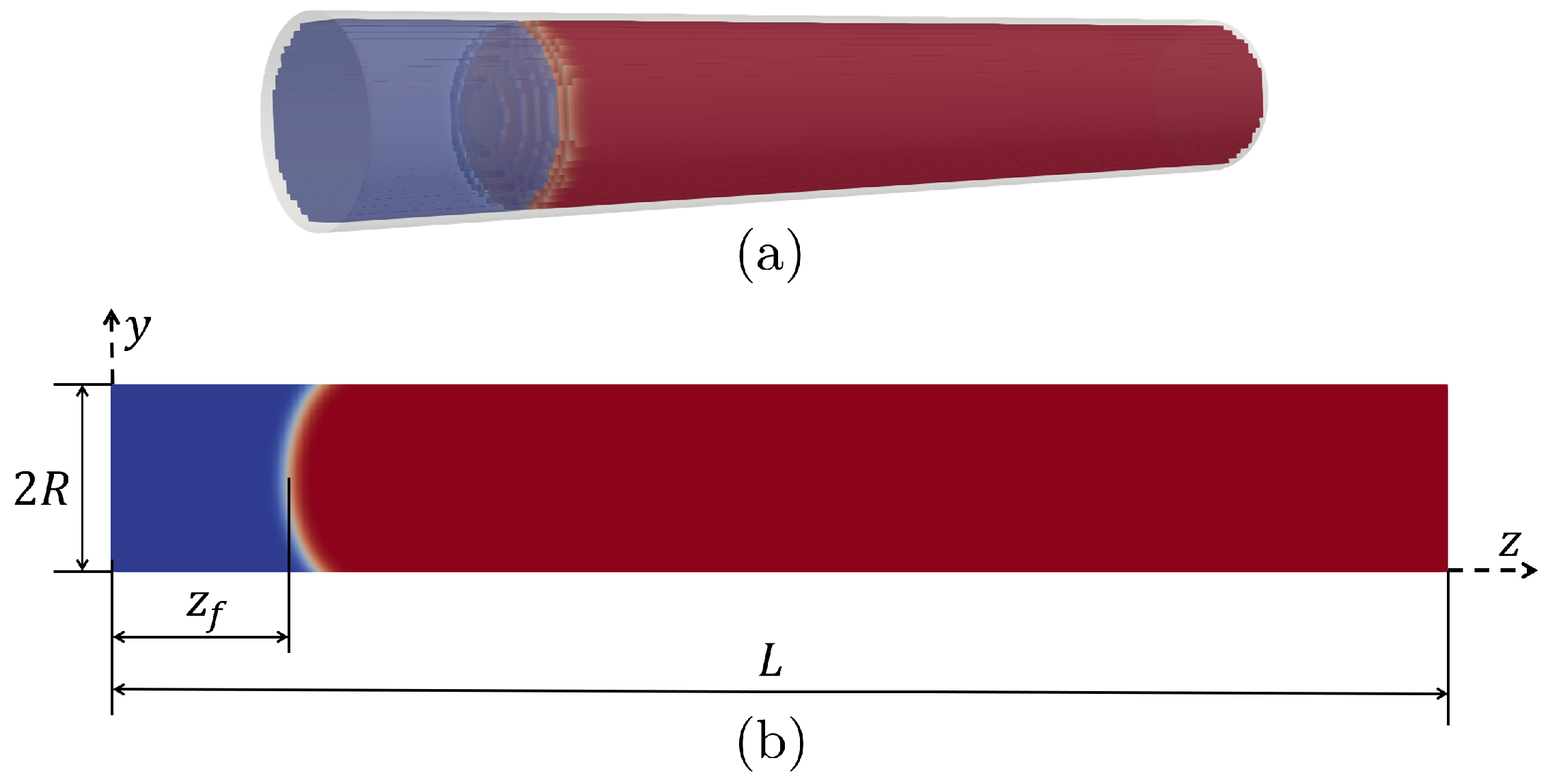
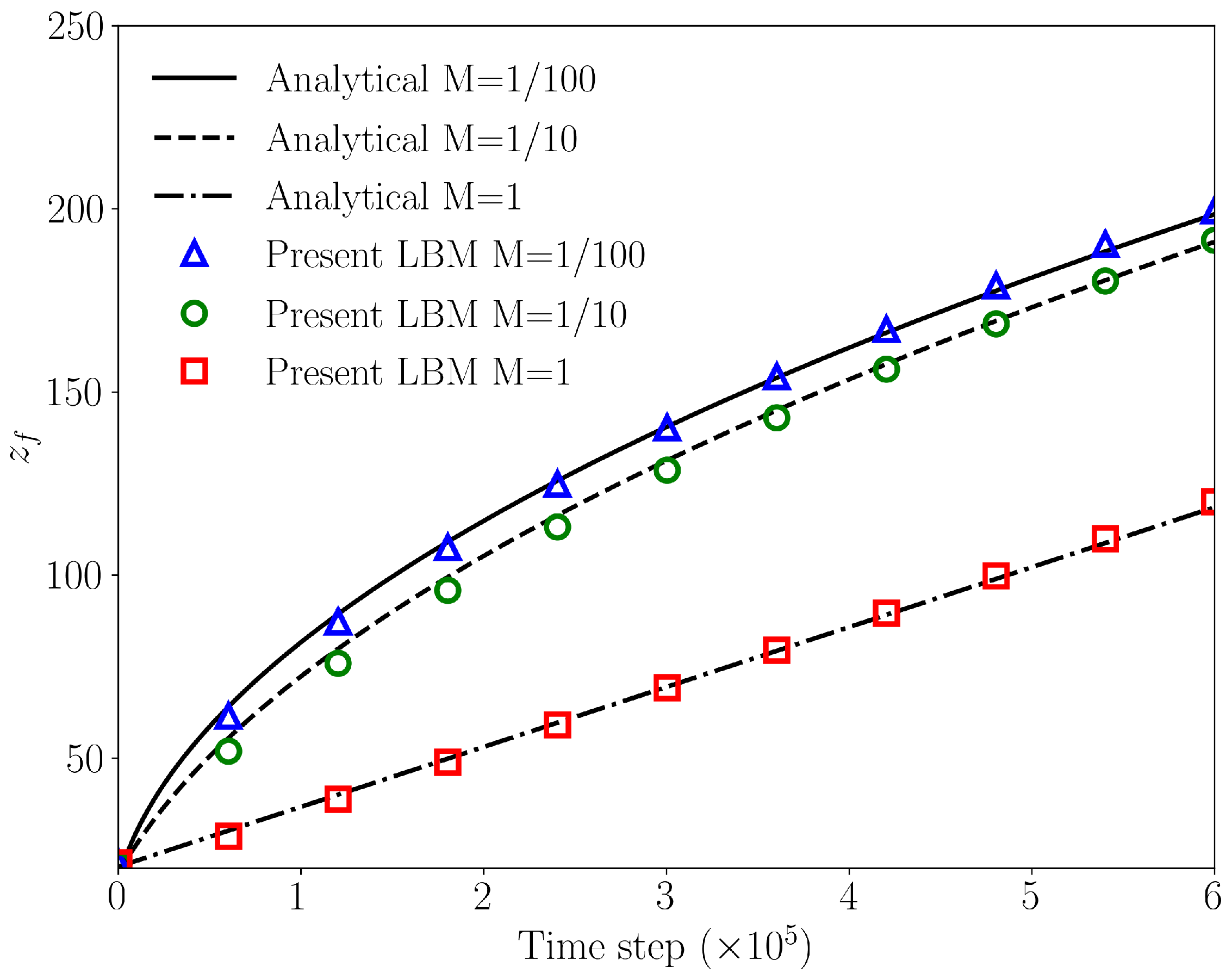
3.2. Three-Dimensional Capillary Intrusion
4. Results
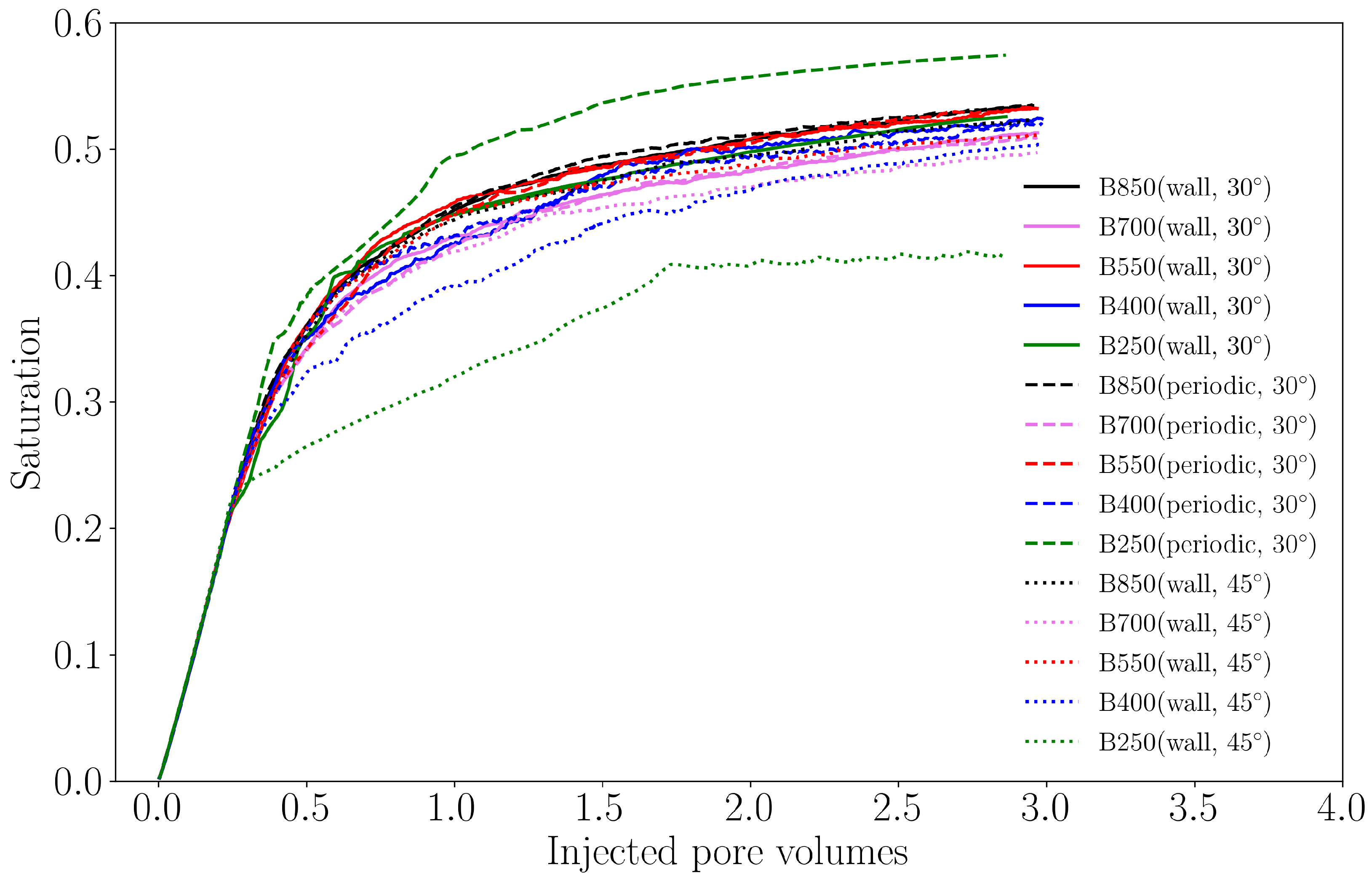
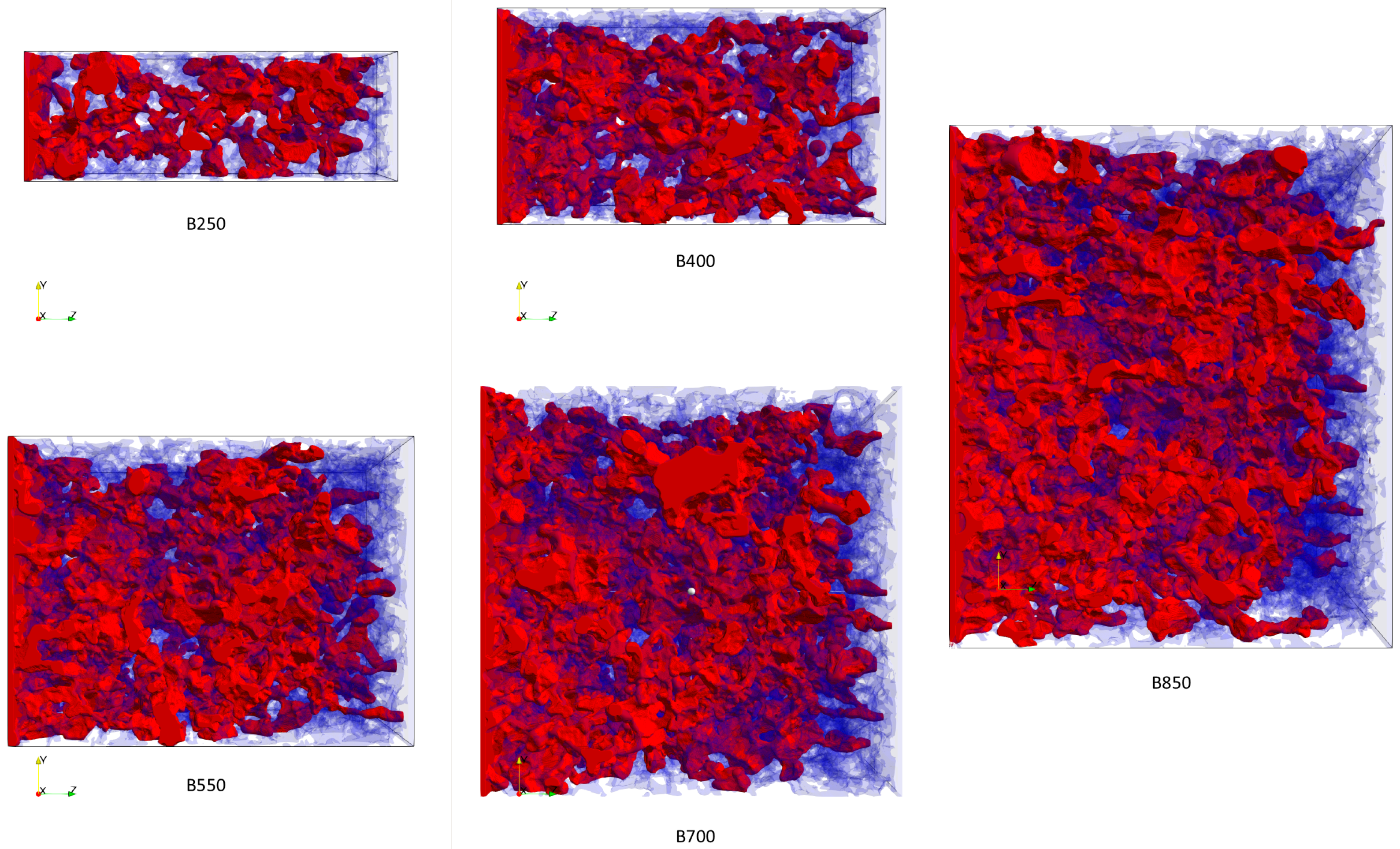
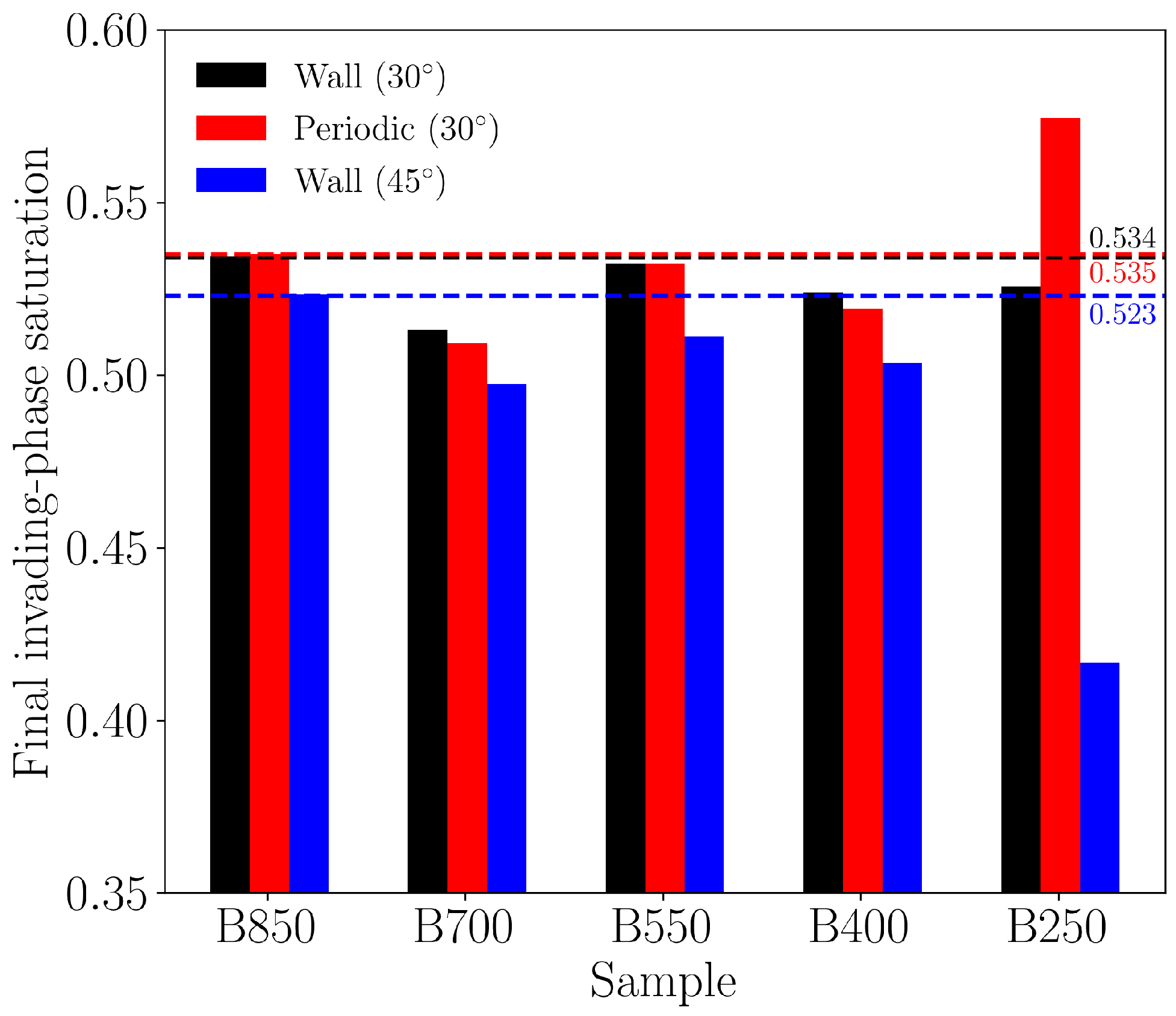
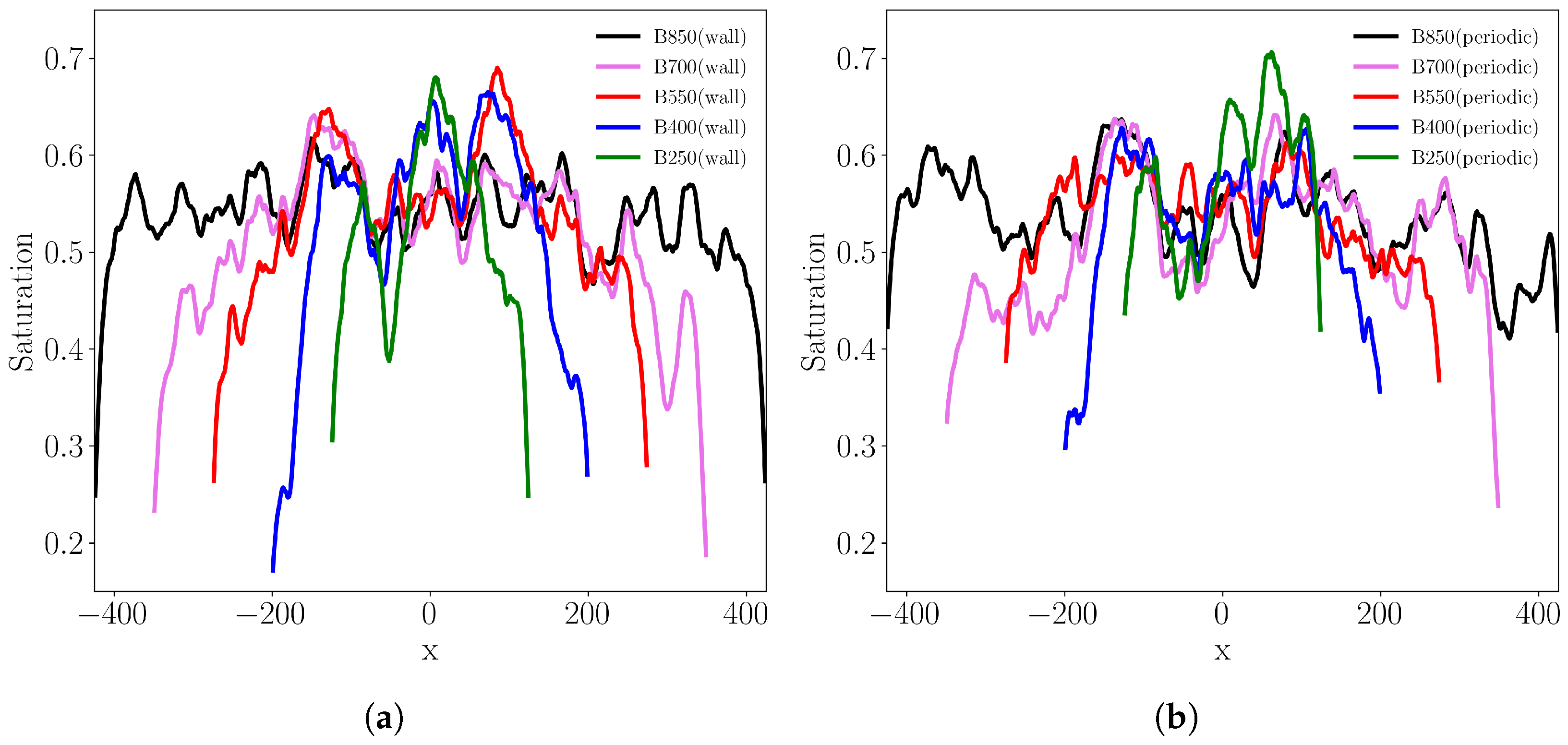
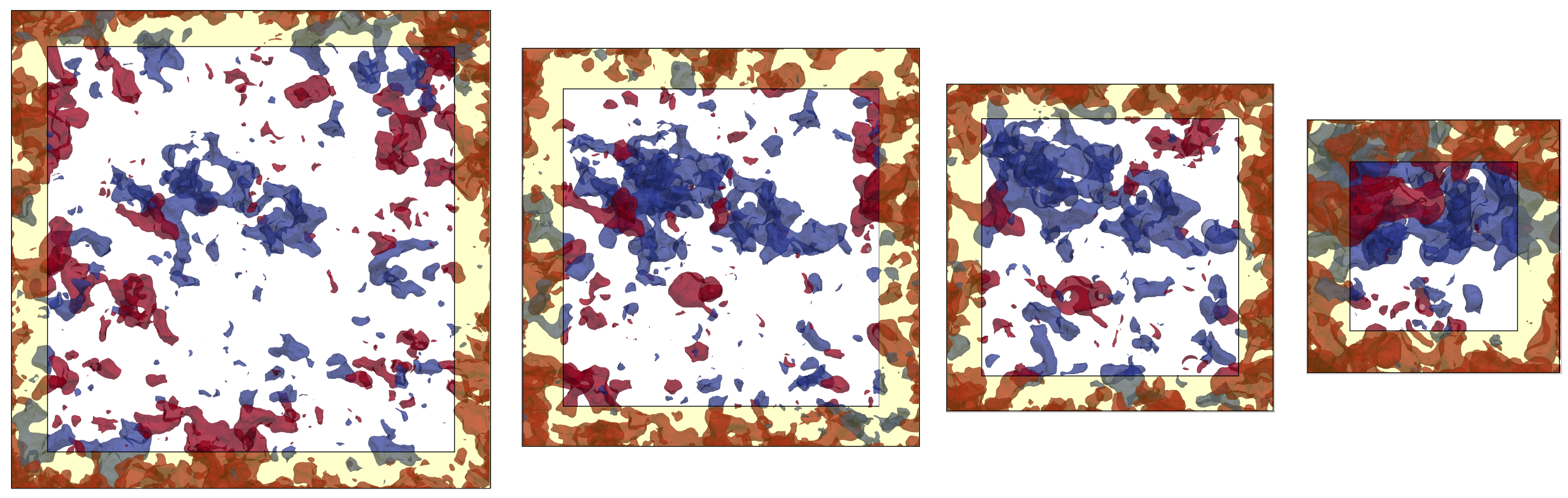
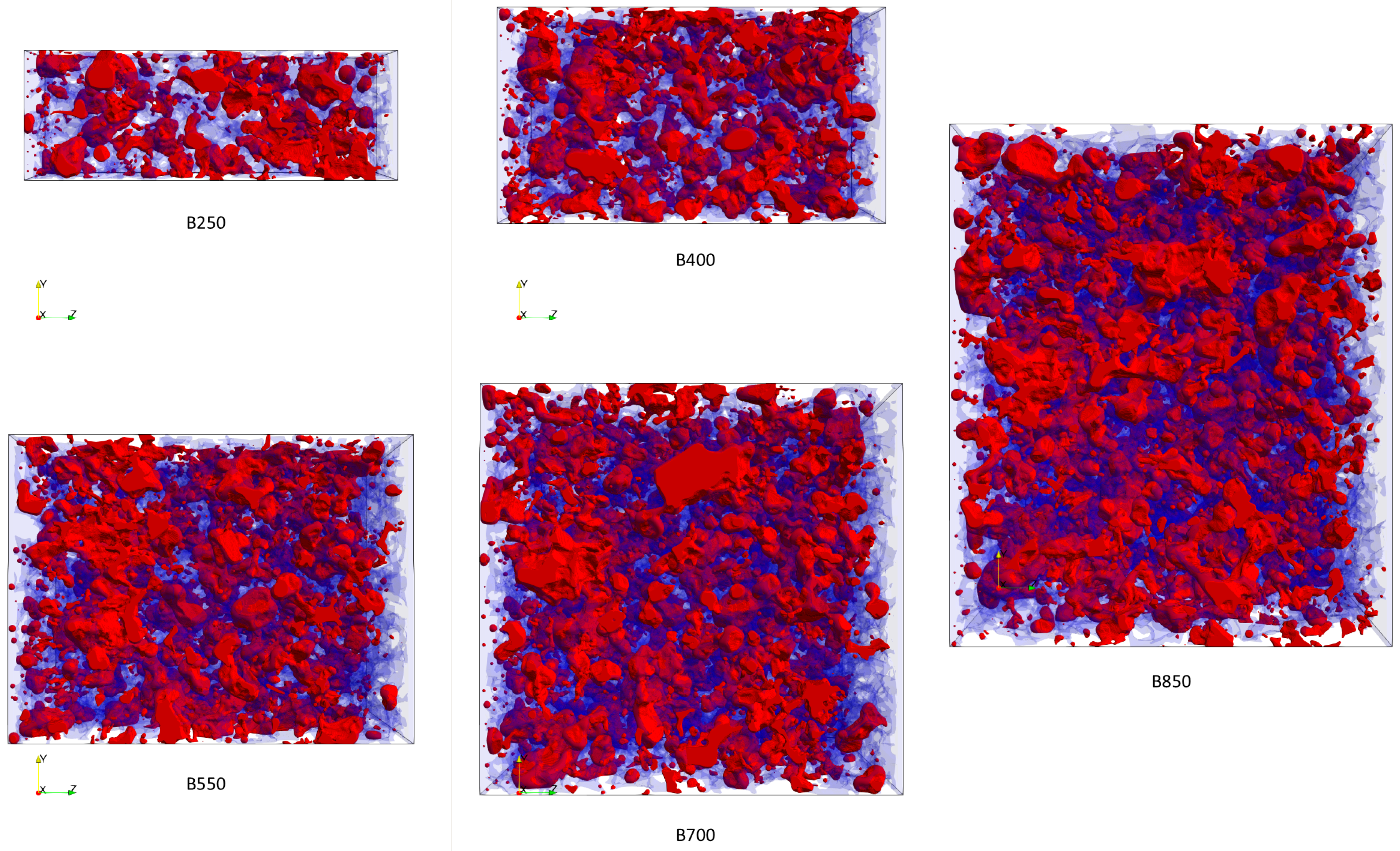
4.1. Two-Phase Flow Simulations on a Bentheimer Sandstone
4.1.1. Simulation Setup
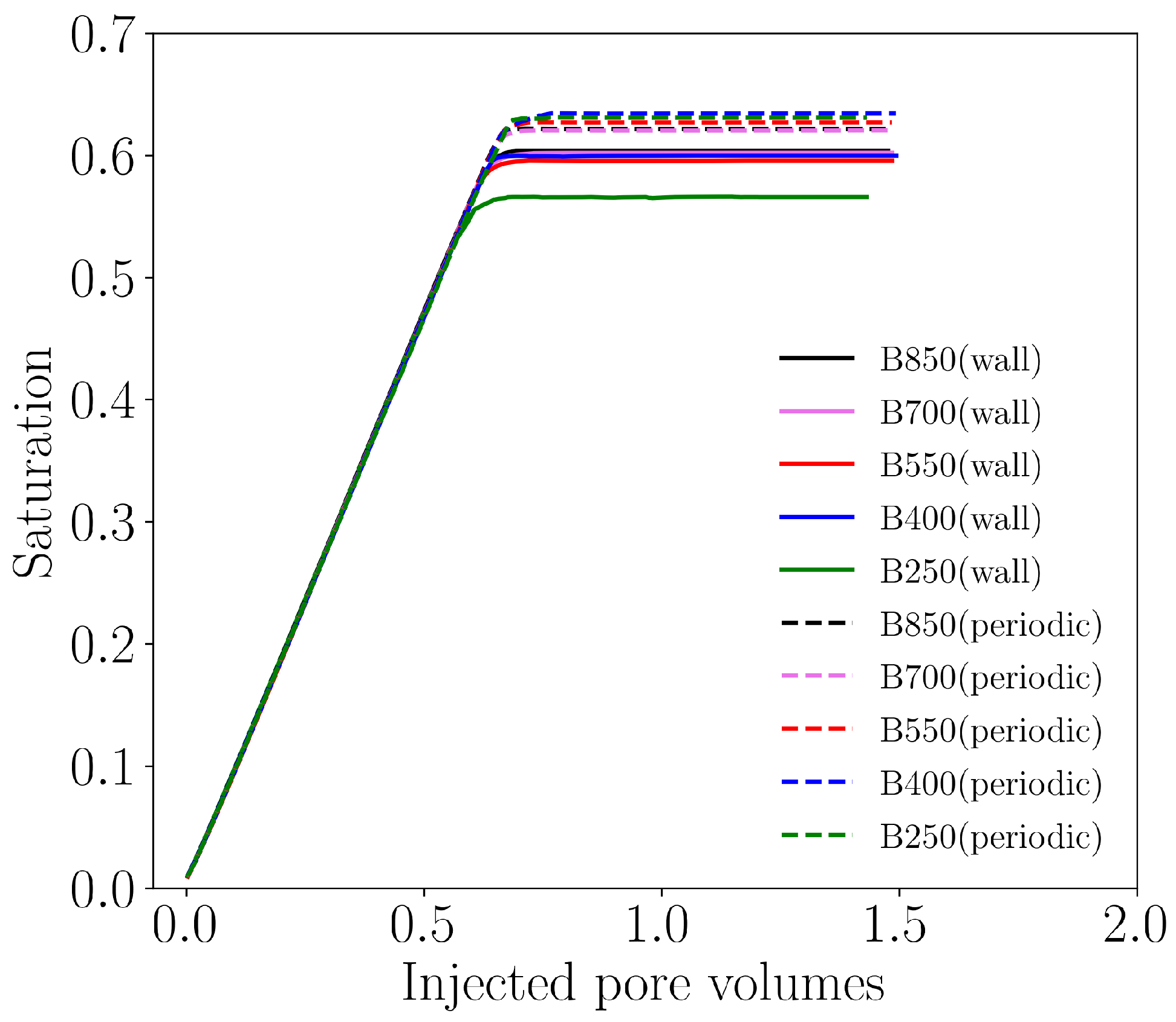
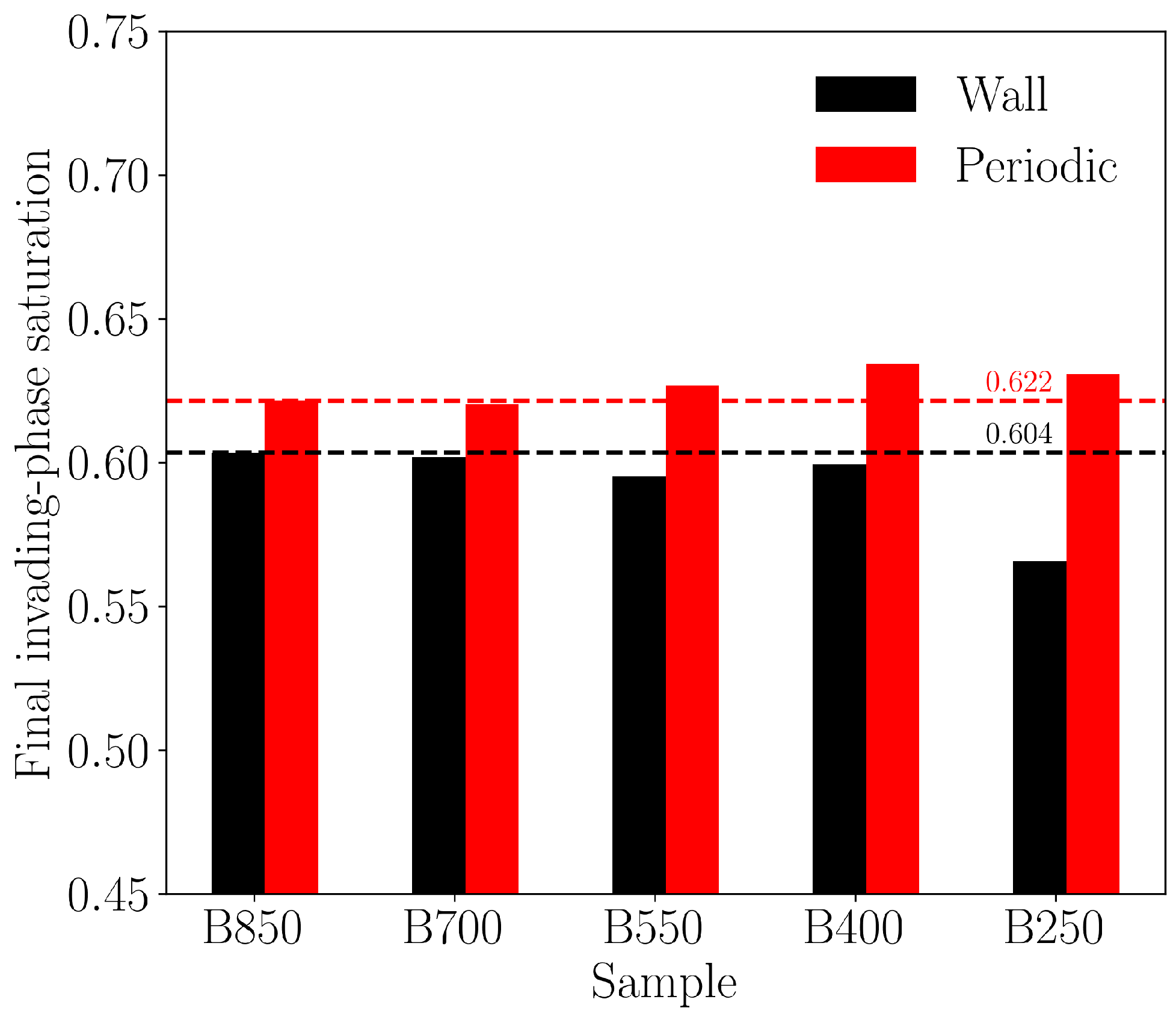
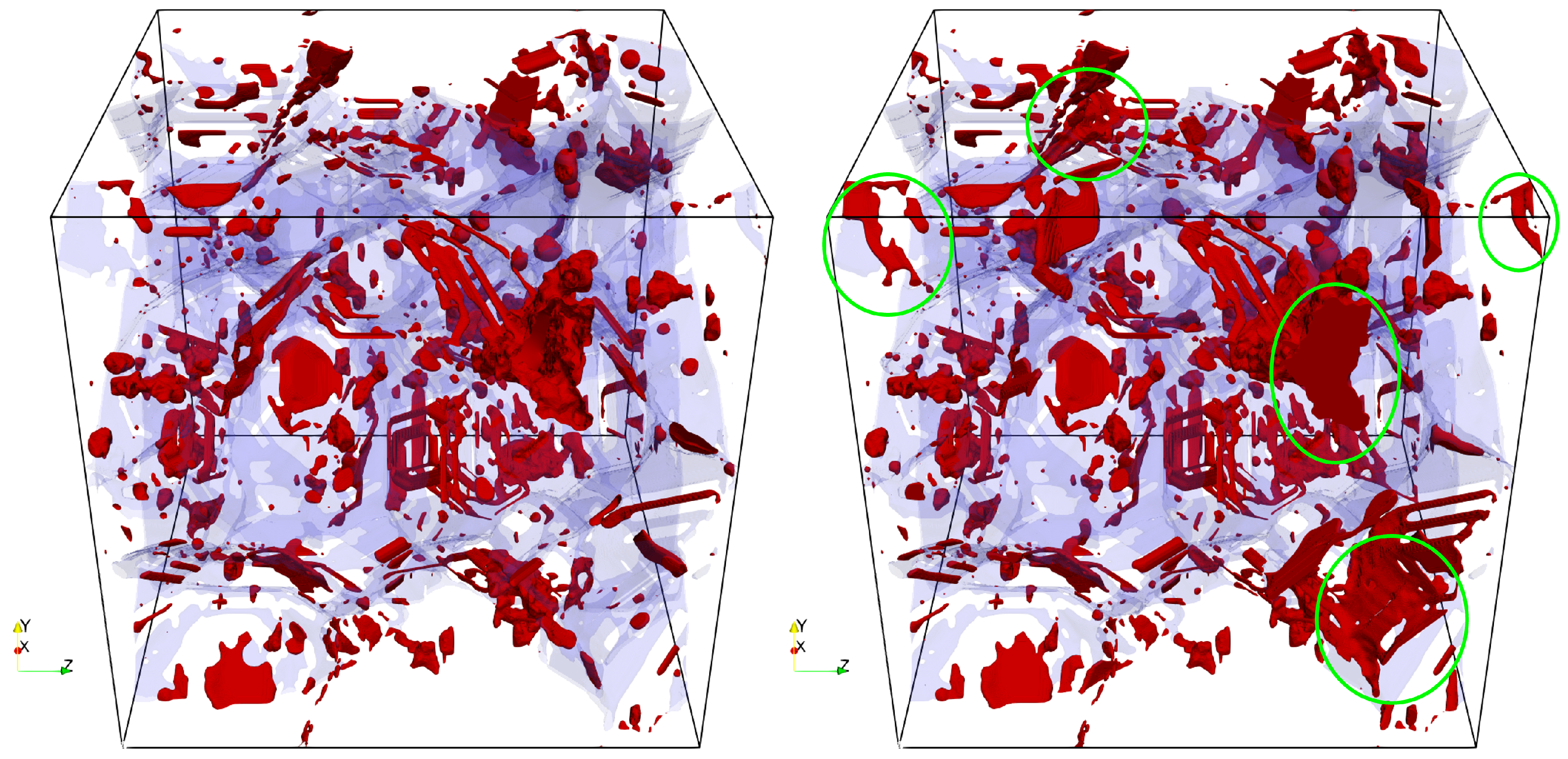
4.1.2. Results of Drainage Simulations
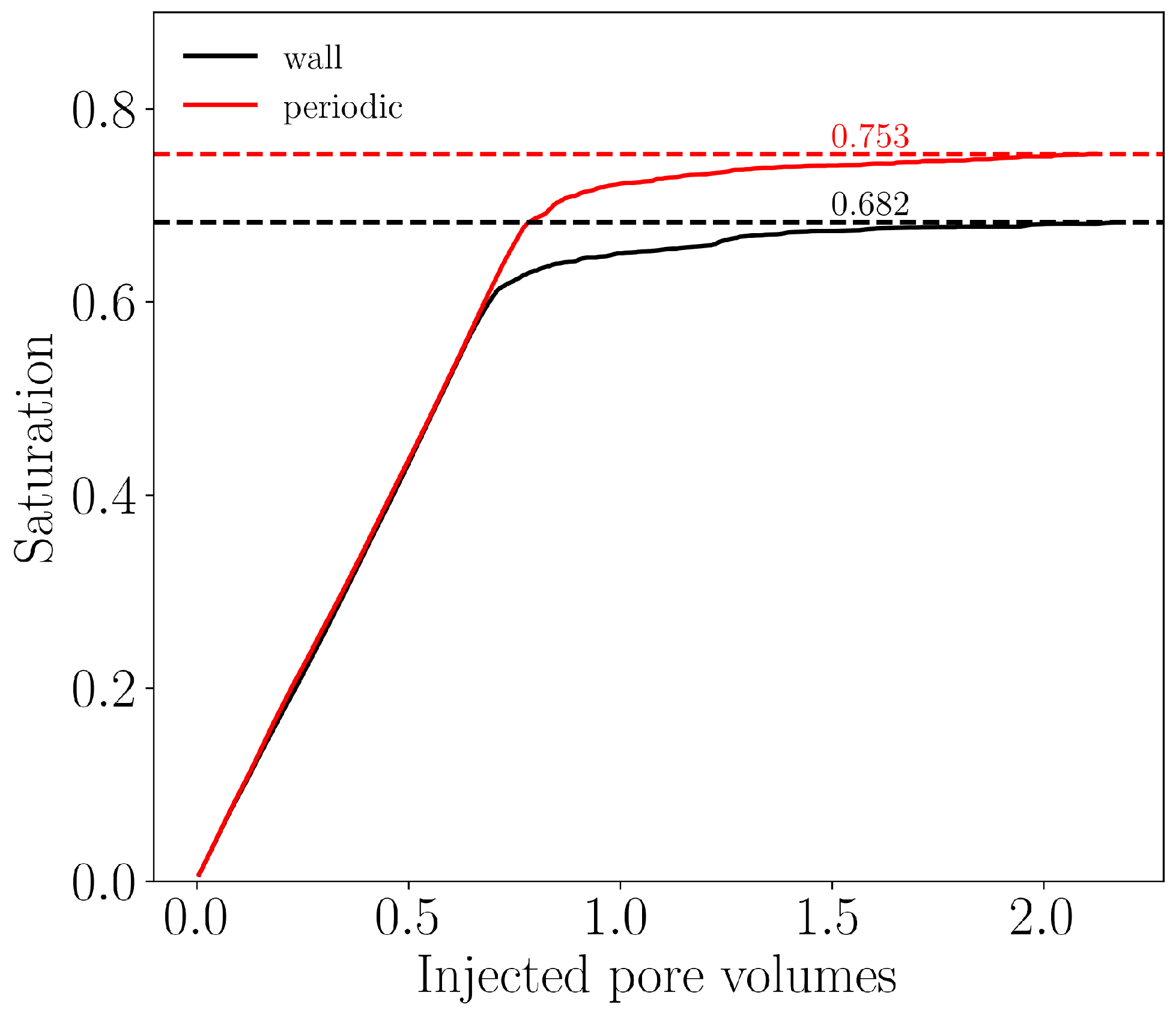
4.1.3. Results of Imbibition Simulations
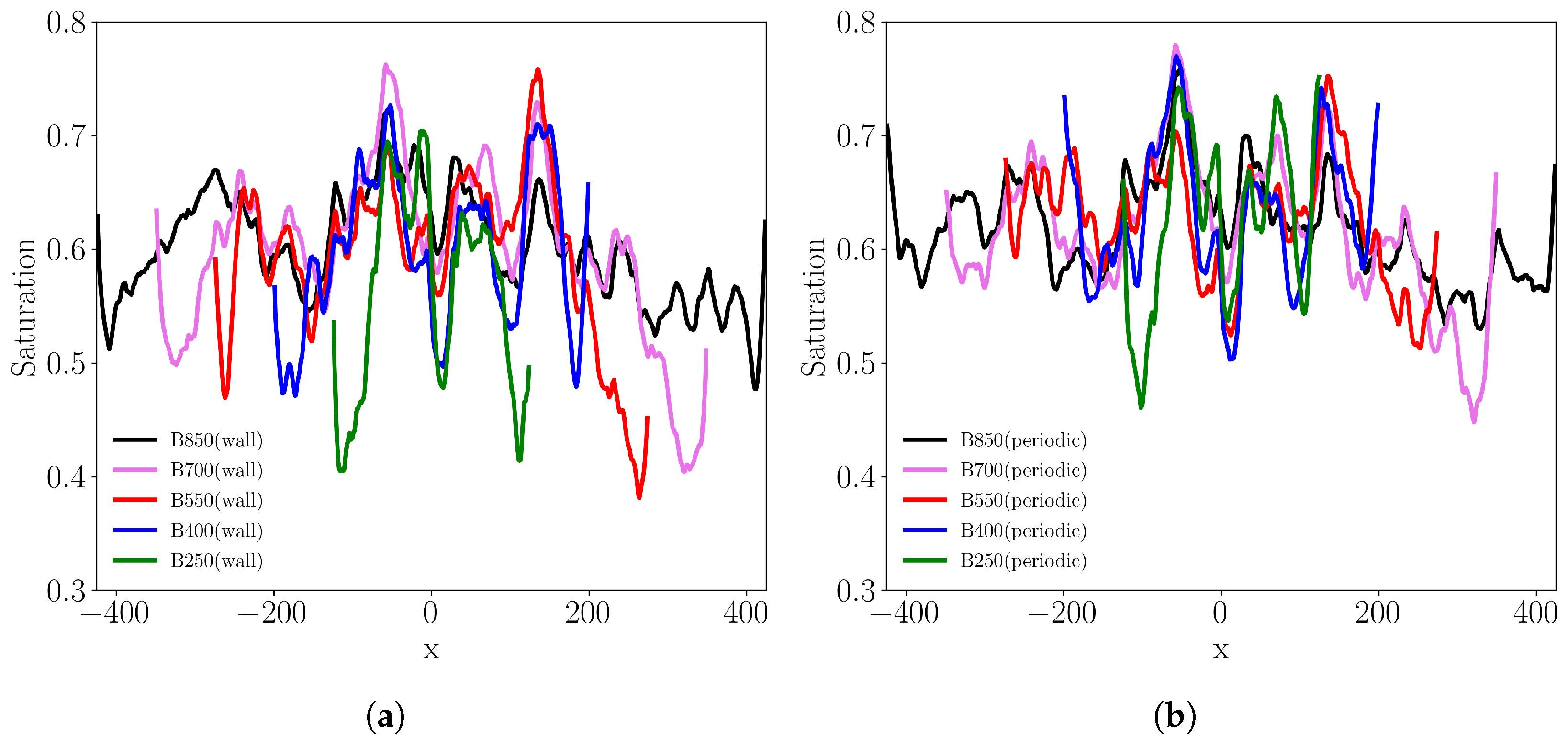
4.2. Two-Phase Flow Simulations on a Synthetic Tight Sandstone
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Blunt, M.J.; Bijeljic, B.; Dong, H.; Gharbi, O.; Iglauer, S.; Mostaghimi, P.; Paluszny, A.; Pentland, C. Pore-scale imaging and modelling. Adv. Water Resour. 2013, 51, 197–216. [Google Scholar] [CrossRef]
- Zhao, B.; MacMinn, C.W.; Primkulov, B.K.; Chen, Y.; Valocchi, A.J.; Zhao, J.; Kang, Q.; Bruning, K.; McClure, J.E.; Miller, C.T.; et al. Comprehensive comparison of pore-scale models for multiphase flow in porous media. Proc. Natl. Acad. Sci. USA 2019, 116, 13799–13806. [Google Scholar] [CrossRef] [PubMed]
- Berg, S.; Ott, H.; Klapp, S.A.; Schwing, A.; Neiteler, R.; Brussee, N.; Makurat, A.; Leu, L.; Enzmann, F.; Schwarz, J.O.; et al. Real-time 3D imaging of Haines jumps in porous media flow. Proc. Natl. Acad. Sci. USA 2013, 110, 3755–3759. [Google Scholar] [CrossRef] [PubMed]
- Geistlinger, H.; Golmohammadi, S.; Zulfiqar, B.; Kuechler, M.; Reuter, D.; Schlueter, S.; Segre, E.; Holtzman, R.; Amro, M. A New Phase Diagram for Fluid Invasion Patterns as a Function of Pore-Scale Heterogeneity, Surface Roughness, and Wettability. Water Resour. Res. 2024, 60, e2023WR036036. [Google Scholar] [CrossRef]
- Raeini, A.Q.; Blunt, M.J.; Bijeljic, B. Modelling two-phase flow in porous media at the pore scale using the volume-of-fluid method. J. Comput. Phys. 2012, 231, 5653–5668. [Google Scholar] [CrossRef]
- Ahrenholz, B.; Tölke, J.; Lehmann, P.; Peters, A.; Kaestner, A.; Krafczyk, M.; Durner, W. Prediction of capillary hysteresis in a porous material using lattice-Boltzmann methods and comparison to experimental data and a morphological pore network model. Adv. Water Resour. 2008, 31, 1151–1173. [Google Scholar] [CrossRef]
- Blunt, M.J. Flow in porous media—pore-network models and multiphase flow. Curr. Opin. Colloid Interface Sci. 2001, 6, 197–207. [Google Scholar] [CrossRef]
- Chen, S.; Doolen, G.D. Lattice Boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef]
- Guo, Z.; Shu, C. Lattice Boltzmann Method and Its Applications in Engineering; World Scientific: Singapore, 2013; Volume 3. [Google Scholar]
- Krüger, T.; Kusumaatmaja, H.; Kuzmin, A.; Shardt, O.; Silva, G.; Viggen, E.M. The Lattice Boltzmann Method; Springer: Berlin/Heidelberg, Germany, 2017; Volume 10. [Google Scholar]
- Liu, H.; Kang, Q.; Leonardi, C.R.; Schmieschek, S.; Narváez, A.; Jones, B.D.; Williams, J.R.; Valocchi, A.J.; Harting, J. Multiphase lattice Boltzmann simulations for porous media applications: A review. Comput. Geosci. 2016, 20, 777–805. [Google Scholar] [CrossRef]
- Tsuji, T.; Jiang, F.; Christensen, K.T. Characterization of immiscible fluid displacement processes with various capillary numbers and viscosity ratios in 3D natural sandstone. Adv. Water Resour. 2016, 95, 3–15. [Google Scholar] [CrossRef]
- Chen, Y.; Valocchi, A.J.; Kang, Q.; Viswanathan, H.S. Inertial effects during the process of supercritical CO2 displacing brine in a sandstone: Lattice Boltzmann simulations based on the continuum-surface-force and geometrical wetting models. Water Resour. Res. 2019, 55, 11144–11165. [Google Scholar] [CrossRef]
- McClure, J.E.; Li, Z.; Berrill, M.; Ramstad, T. The LBPM software package for simulating multiphase flow on digital images of porous rocks. Comput. Geosci. 2021, 25, 871–895. [Google Scholar] [CrossRef]
- TeraFLOP computing on a desktop PC with GPUs for 3D CFD. Int. J. Comput. Fluid Dyn. 2008, 22, 443–456. [CrossRef]
- Akai, T.; Alhammadi, A.M.; Blunt, M.J.; Bijeljic, B. Modeling Oil Recovery in Mixed-Wet Rocks: Pore-Scale Comparison Between Experiment and Simulation. Transp. Porous Media 2019, 127, 393–414. [Google Scholar] [CrossRef]
- Ramstad, T.; Idowu, N.; Nardi, C.; Øren, P.E. Relative permeability calculations from two-phase flow simulations directly on digital images of porous rocks. Transp. Porous Media 2012, 94, 487–504. [Google Scholar] [CrossRef]
- Raeini, A.Q.; Bijeljic, B.; Blunt, M.J. Modelling capillary trapping using finite-volume simulation of two-phase flow directly on micro-CT images. Adv. Water Resour. 2015, 83, 102–110. [Google Scholar] [CrossRef]
- Leclaire, S.; Parmigiani, A.; Malaspinas, O.; Chopard, B.; Latt, J. Generalized three-dimensional lattice Boltzmann color-gradient method for immiscible two-phase pore-scale imbibition and drainage in porous media. Phys. Rev. E 2017, 95, 033306. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Berg, S.; Ju, Y.; Wei, W.; Kou, J.; Cai, J. Systematic investigation of corner flow impact in forced imbibition. Water Resour. Res. 2022, 58, e2022WR032402. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, J.; Wang, J.; Zhang, Q.; Yao, J. Pore-scale numerical simulation of supercritical CO2-brine two-phase flow based on VOF method. Nat. Gas Ind. B 2023, 10, 466–475. [Google Scholar] [CrossRef]
- Galindo-Torres, S.A.; Scheuermann, A.; Li, L. Boundary effects on the Soil Water Characteristic Curves obtained from lattice Boltzmann simulations. Comput. Geotech. 2016, 71, 136–146. [Google Scholar] [CrossRef]
- Xu, Z.; Liu, H.; Valocchi, A.J. Lattice B oltzmann simulation of immiscible two-phase flow with capillary valve effect in porous media. Water Resour. Res. 2017, 53, 3770–3790. [Google Scholar] [CrossRef]
- Akai, T.; Bijeljic, B.; Blunt, M.J. Wetting boundary condition for the color-gradient lattice Boltzmann method: Validation with analytical and experimental data. Adv. Water Resour. 2018, 116, 56–66. [Google Scholar] [CrossRef]
- Chen, Y.; Li, Y.; Valocchi, A.J.; Christensen, K.T. Lattice Boltzmann simulations of liquid CO2 displacing water in a 2D heterogeneous micromodel at reservoir pressure conditions. J. Contam. Hydrol. 2018, 212, 14–27. [Google Scholar] [CrossRef] [PubMed]
- Herschlag, G.; Lee, S.; Vetter, J.S.; Randles, A. Analysis of GPU data access patterns on complex geometries for the D3Q19 lattice Boltzmann algorithm. IEEE Trans. Parallel Distrib. Syst. 2021, 32, 2400–2414. [Google Scholar] [CrossRef]
- Brackbill, J.; Kothe, D.B.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Guo, Z.; Zheng, C.; Shi, B. Discrete lattice effects on the forcing term in the lattice Boltzmann method. Phys. Rev. E 2002, 65, 046308. [Google Scholar] [CrossRef]
- Lallemand, P.; Luo, L.S. Theory of the lattice Boltzmann method: Dispersion, dissipation, isotropy, Galilean invariance, and stability. Phys. Rev. E 2000, 61, 6546–6562. [Google Scholar] [CrossRef]
- d’Humières, D. Multiple-relaxation-time lattice Boltzmann models in three dimensions. Philos. Trans. R. Soc. London Ser. Math. Phys. Eng. Sci. 2002, 360, 437–451. [Google Scholar] [CrossRef]
- Latva-Kokko, M.; Rothman, D.H. Static contact angle in lattice Boltzmann models of immiscible fluids. Phys. Rev. E 2005, 72, 046701. [Google Scholar] [CrossRef]
- Yu, Y.; Liu, H.; Zhang, Y.; Liang, D. Color-gradient lattice Boltzmann modeling of immiscible two-phase flows on partially wetting surfaces. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 232, 416–430. [Google Scholar] [CrossRef]
- Purswani, P.; Guiltinan, E.J.; Chen, Y.; Kang, Q.; Mehana, M.Z.; Neil, C.W.; Germann, T.C.; Gross, M.R. Pore-scale modeling of carbon dioxide and hydrogen transport during geologic gas storage. Geophys. Res. Lett. 2024, 51, e2024GL109216. [Google Scholar] [CrossRef]
- Gunstensen, A.; Rothman, D.; Zaleski, S.; Zanetti, G. Lattice Boltzmann model of immiscible fluids. Phys. Rev. A 1991, 43, 4320–4327. [Google Scholar] [CrossRef]
- Tolke, J.; Krafczyk, M.; Schulz, M.; Rank, E. Lattice Boltzmann simulations of binary fluid flow through porous media. Philos. Trans. A Math. Phys. Eng. Sci. 2002, 360, 535–545. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.; Huang, J.J.; Lu, X.Y. Study of immiscible displacements in porous media using a color-gradient-based multiphase lattice Boltzmann method. Comput. Fluids 2014, 93, 164–172. [Google Scholar] [CrossRef]
- Qian, Y.; d’Humières, D.; Lallemand, P. Lattice BGK models for Navier–Stokes equation. EPL Europhys. Lett. 1992, 17, 479. [Google Scholar] [CrossRef]
- Washburn, E.W. The Dynamics of Capillary Flow. Phys. Rev. 1921, 17, 273–283. [Google Scholar] [CrossRef]
- Herring, A.L.; Andersson, L.; Wildenschild, D. Enhancing residual trapping of supercritical CO2 via cyclic injections. Geophys. Res. Lett. 2016, 43, 9677–9685. [Google Scholar] [CrossRef]
- Ladd, A.J. Numerical simulations of particulate suspensions via a discretized Boltzmann equation. Part 1. Theoretical foundation. J. Fluid Mech. 1994, 271, 285–309. [Google Scholar] [CrossRef]
- Lou, Q.; Guo, Z.; Shi, B. Evaluation of outflow boundary conditions for two-phase lattice Boltzmann equation. Phys. Rev. E 2013, 87, 063301. [Google Scholar] [CrossRef] [PubMed]
- Lai, J.; Wang, G.; Wang, Z.; Chen, J.; Pang, X.; Wang, S.; Zhou, Z.; He, Z.; Qin, Z.; Fan, X. A review on pore structure characterization in tight sandstones. Earth-Sci. Rev. 2018, 177, 436–457. [Google Scholar] [CrossRef]
- Latt, J.; Malaspinas, O.; Kontaxakis, D.; Parmigiani, A.; Lagrava, D.; Brogi, F.; Belgacem, M.B.; Thorimbert, Y.; Leclaire, S.; Li, S.; et al. Palabos: Parallel lattice Boltzmann solver. Comput. Math. Appl. 2021, 81, 334–350. [Google Scholar] [CrossRef]
- Krause, M.J.; Kummerländer, A.; Avis, S.J.; Kusumaatmaja, H.; Dapelo, D.; Klemens, F.; Gaedtke, M.; Hafen, N.; Mink, A.; Trunk, R.; et al. OpenLB—Open source lattice Boltzmann code. Comput. Math. Appl. 2021, 81, 258–288. [Google Scholar] [CrossRef]
- Bauer, M.; Eibl, S.; Godenschwager, C.; Kohl, N.; Kuron, M.; Rettinger, C.; Schornbaum, F.; Schwarzmeier, C.; Thönnes, D.; Köstler, H.; et al. waLBerla: A block-structured high-performance framework for multiphysics simulations. Comput. Math. Appl. 2021, 81, 478–501. [Google Scholar] [CrossRef]
- Geier, M.; Kutscher, K.; Schönherr, M.; Wellmann, A.; Peters, S.; Alihussein, H.; Linxweiler, J.; Krafczyk, M. VirtualFluids–open source parallel LBM solver. Comput. Phys. Commun. 2025, 317, 109810. [Google Scholar] [CrossRef]

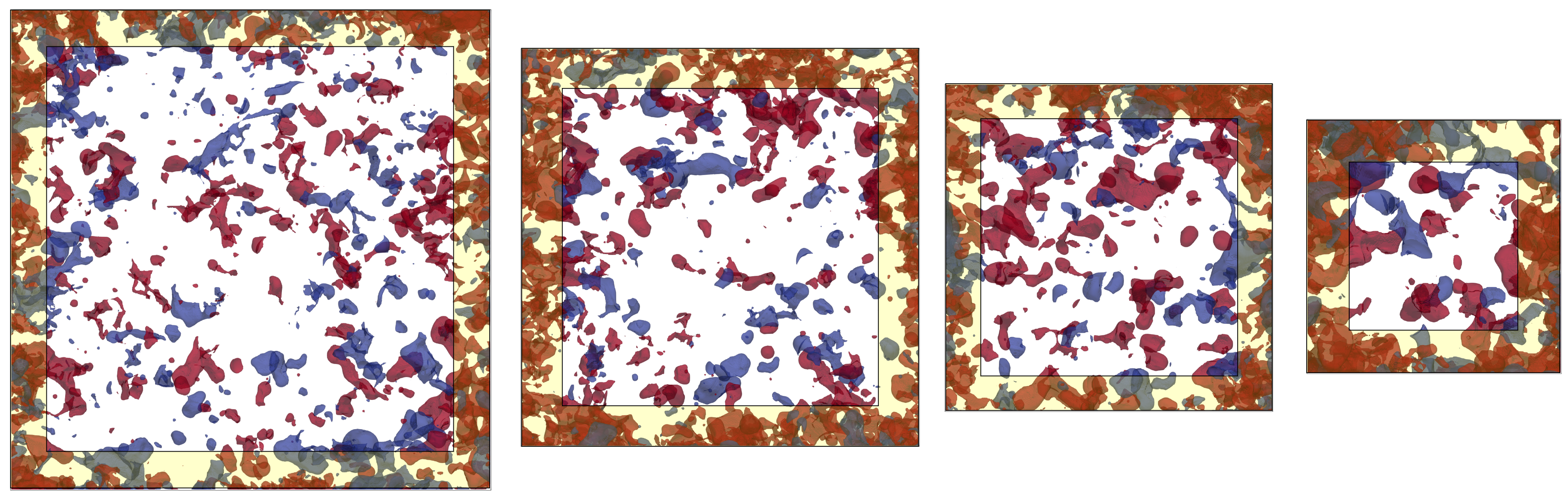

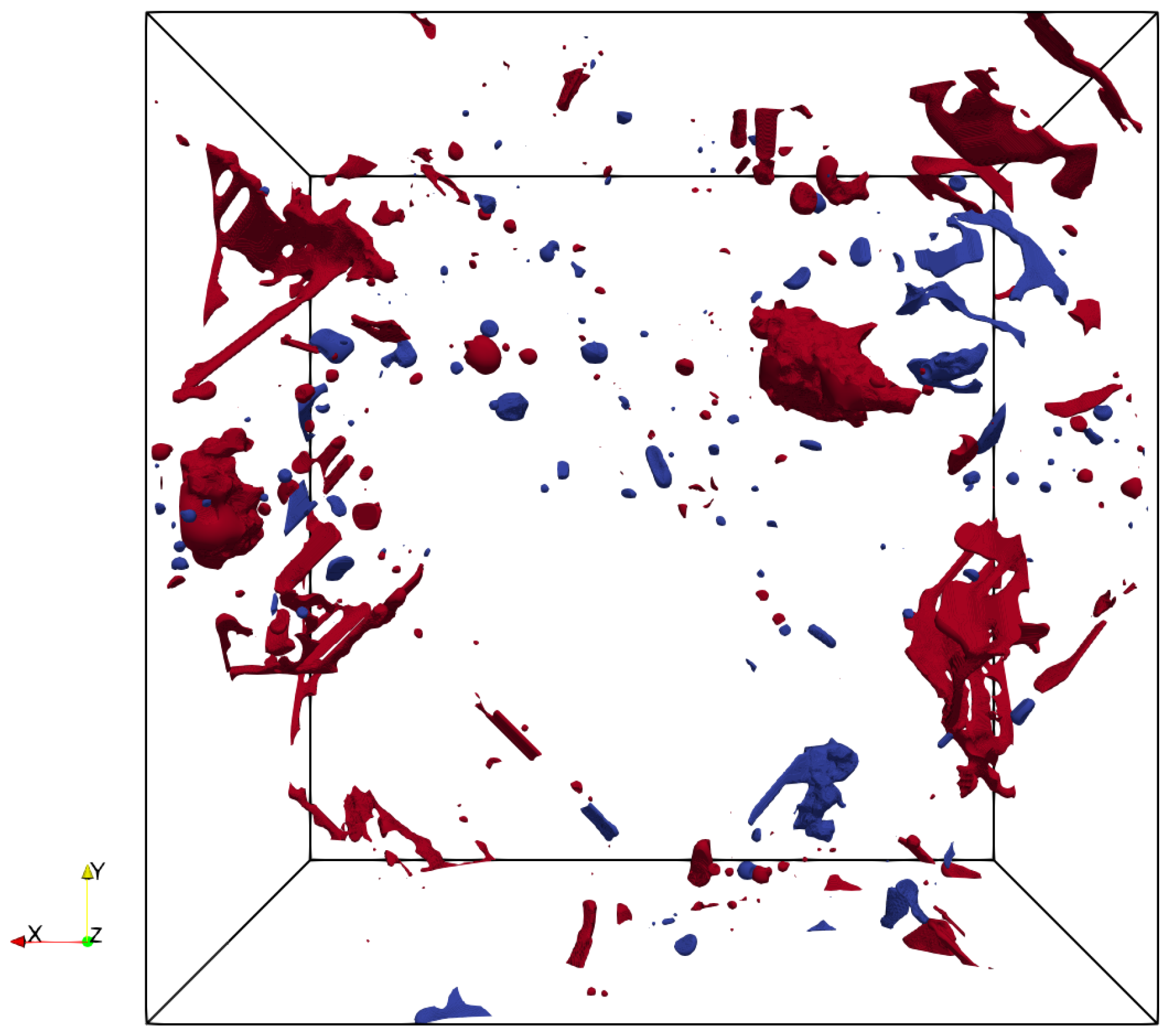
| Reference | Rock Type | Sample Size (Voxels) | Resolution (µm) | Method |
|---|---|---|---|---|
| Ahrenholz et al., 2007 [6] | Beadpack | 200 × 200 × 200 | 11 | LBM |
| Ramstad et al., 2012 [17] | Bentheimer/Berea Sandstone | 256 × 256 × 256 | 6.7/5.3 | LBM |
| Raeini et al., 2015 [18] | Berea Sandstone | 330 × 210 × 210 | 5.5 | VOF |
| Tsuji et al., 2016 [12] | Berea Sandstone | 400 × 200 × 200 | 3.2 | LBM |
| Leclaire et al., 2017 [19] | Berea Sandstone | 400 × 400 × 400 | 5.3 | LBM |
| Chen et al., 2019 [13] | Bentheimer Sandstone | 720 × 720 × 864 | 3.2 | LBM |
| Akai et al., 2019 [16] | Carbonate | 256 × 256 × 200 | 5 | LBM |
| McClure et al., 2021 [14] | Bentheimer Sandstone | 900 × 900 × 1600 | 1.7 | LBM |
| Liu et al., 2022 [20] | Bentheimer Sandstone | 512 × 512 × 512 | 3 | LBM |
| Yang et al., 2023 [21] | Berea | 100 × 100 × 200 | 5.5 | VOF |
| Sample Name | B850 | B700 | B550 | B400 | B250 |
|---|---|---|---|---|---|
| Dimensions (voxels) | 8502 × 720 | 7002 × 720 | 5502 × 720 | 4002 × 720 | 2502 × 720 |
| Porosity | 0.1935 | 0.1924 | 0.1925 | 0.1914 | 0.1996 |
| Permeability (mD) | 1979.8 | 1898.9 | 1826.1 | 1677.7 | 1887.6 |
| Property | Drainage | Imbibition |
|---|---|---|
| Surface tension | 0.04 | 0.04 |
| Invading-phase viscosity | 0.0018 | 0.005 |
| Defending-phase viscosity | 0.0679 | 0.025 |
| Viscosity ratio | 37.7 | 5 |
| Contact angle | 30°, 45° | 150° |
| Inlet velocity | 0.0001 | 0.0001 |
| Capillary number | 4.5 × 10−6 | 1.25 × 10−5 |
| Total iterations | 4 million | 2 million |
| Injected pore volumes | 3.0 | 1.5 |
| Property | Imbibition |
|---|---|
| Surface tension | 0.03 |
| Invading-phase viscosity | 0.08 |
| Defending-phase viscosity | 0.002 |
| Viscosity ratio | 0.025 |
| Contact angle | 45° |
| Inlet velocity | 0.00005 |
| Capillary number | 1.22 × 10−4 |
| Total iterations | 2 million |
| Injected pore volumes | 2.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Liang, M.; Zhang, Y.; Wang, D.; Yang, J.; Chen, Y.; Tang, L.; Pei, X.; Zhou, B. Numerical Study of Side Boundary Effects in Pore-Scale Digital Rock Flow Simulations. Fluids 2025, 10, 305. https://doi.org/10.3390/fluids10120305
Zhang Q, Liang M, Zhang Y, Wang D, Yang J, Chen Y, Tang L, Pei X, Zhou B. Numerical Study of Side Boundary Effects in Pore-Scale Digital Rock Flow Simulations. Fluids. 2025; 10(12):305. https://doi.org/10.3390/fluids10120305
Chicago/Turabian StyleZhang, Qihui, Meijian Liang, Yongbin Zhang, Dong Wang, Jianping Yang, Yu Chen, Liandong Tang, Xuehao Pei, and Bihui Zhou. 2025. "Numerical Study of Side Boundary Effects in Pore-Scale Digital Rock Flow Simulations" Fluids 10, no. 12: 305. https://doi.org/10.3390/fluids10120305
APA StyleZhang, Q., Liang, M., Zhang, Y., Wang, D., Yang, J., Chen, Y., Tang, L., Pei, X., & Zhou, B. (2025). Numerical Study of Side Boundary Effects in Pore-Scale Digital Rock Flow Simulations. Fluids, 10(12), 305. https://doi.org/10.3390/fluids10120305






