Pressure Drops for Turbulent Liquid Single-Phase and Gas–Liquid Two-Phase Flows in Komax Triple Action Static Mixer
Abstract
1. Introduction
2. Experimental Setup
3. Results and Discussion
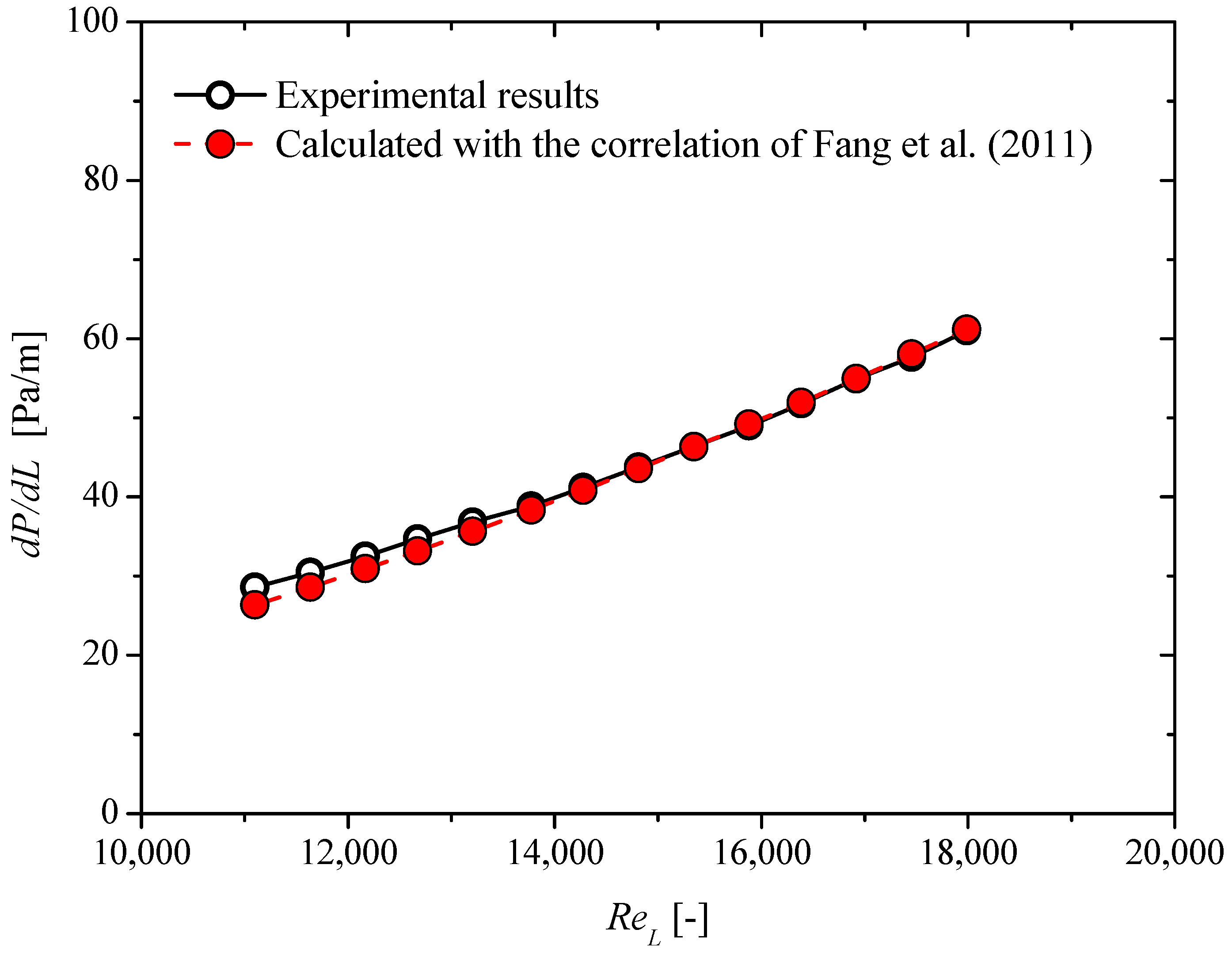
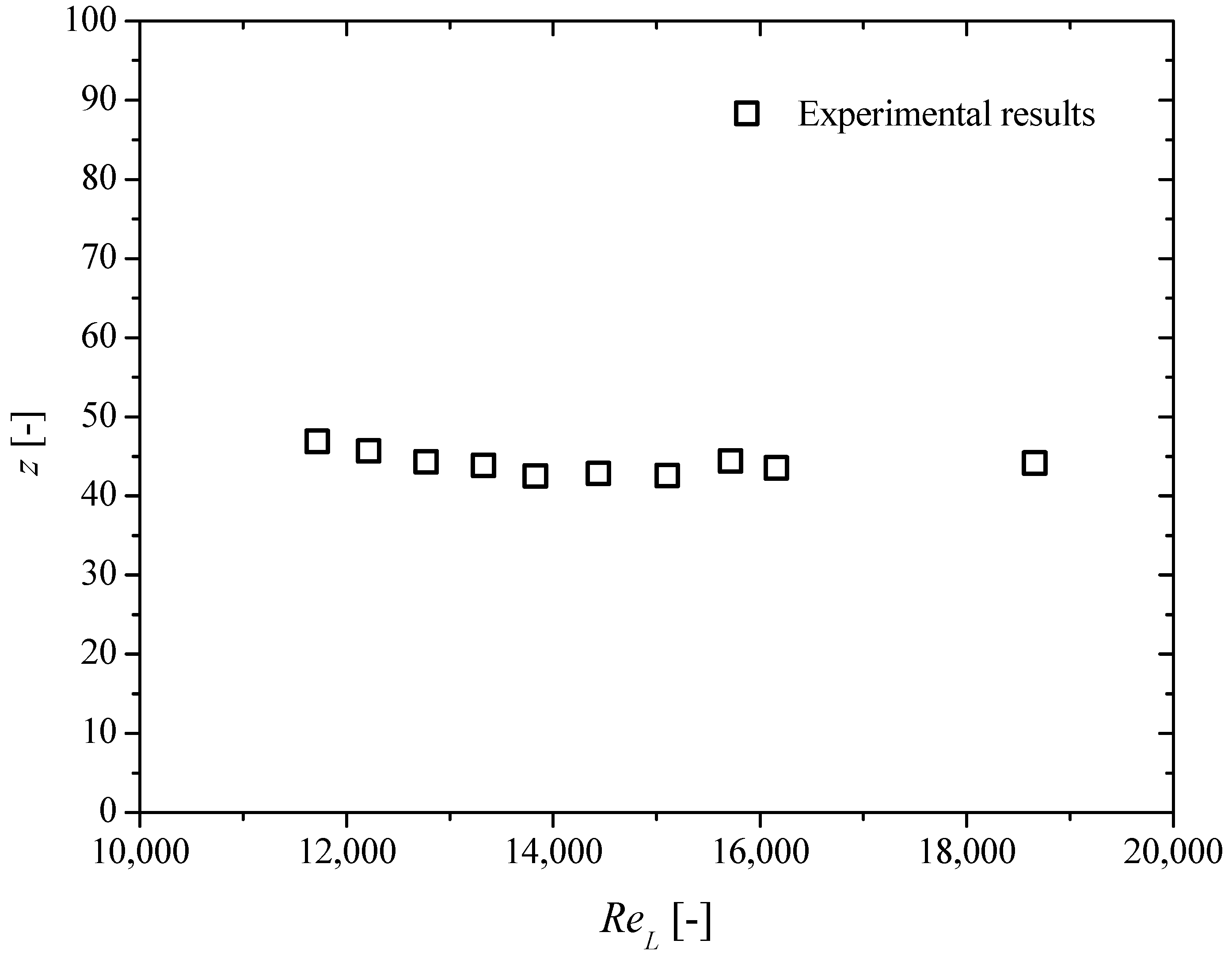
3.1. Liquid Single-Phase Flow
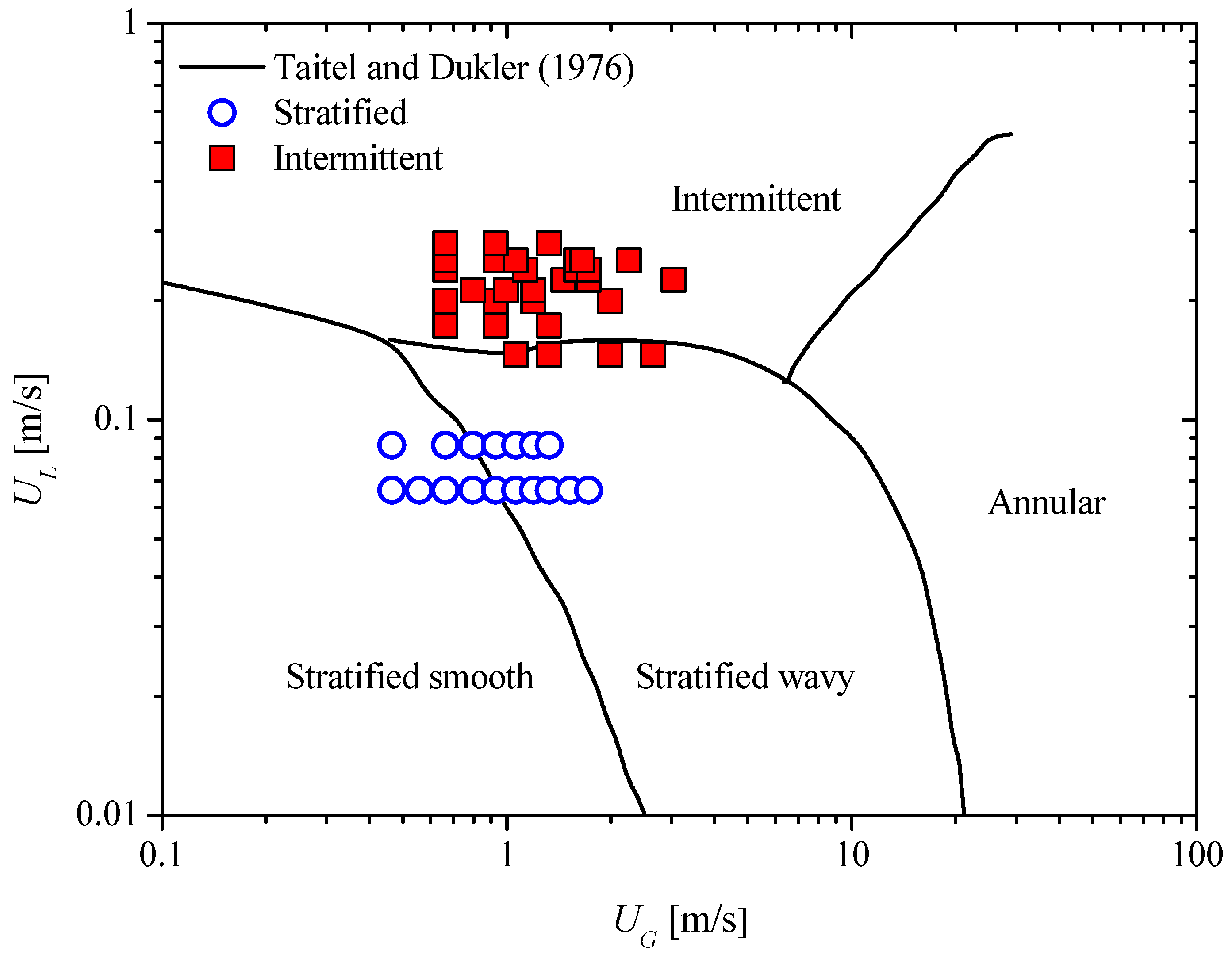
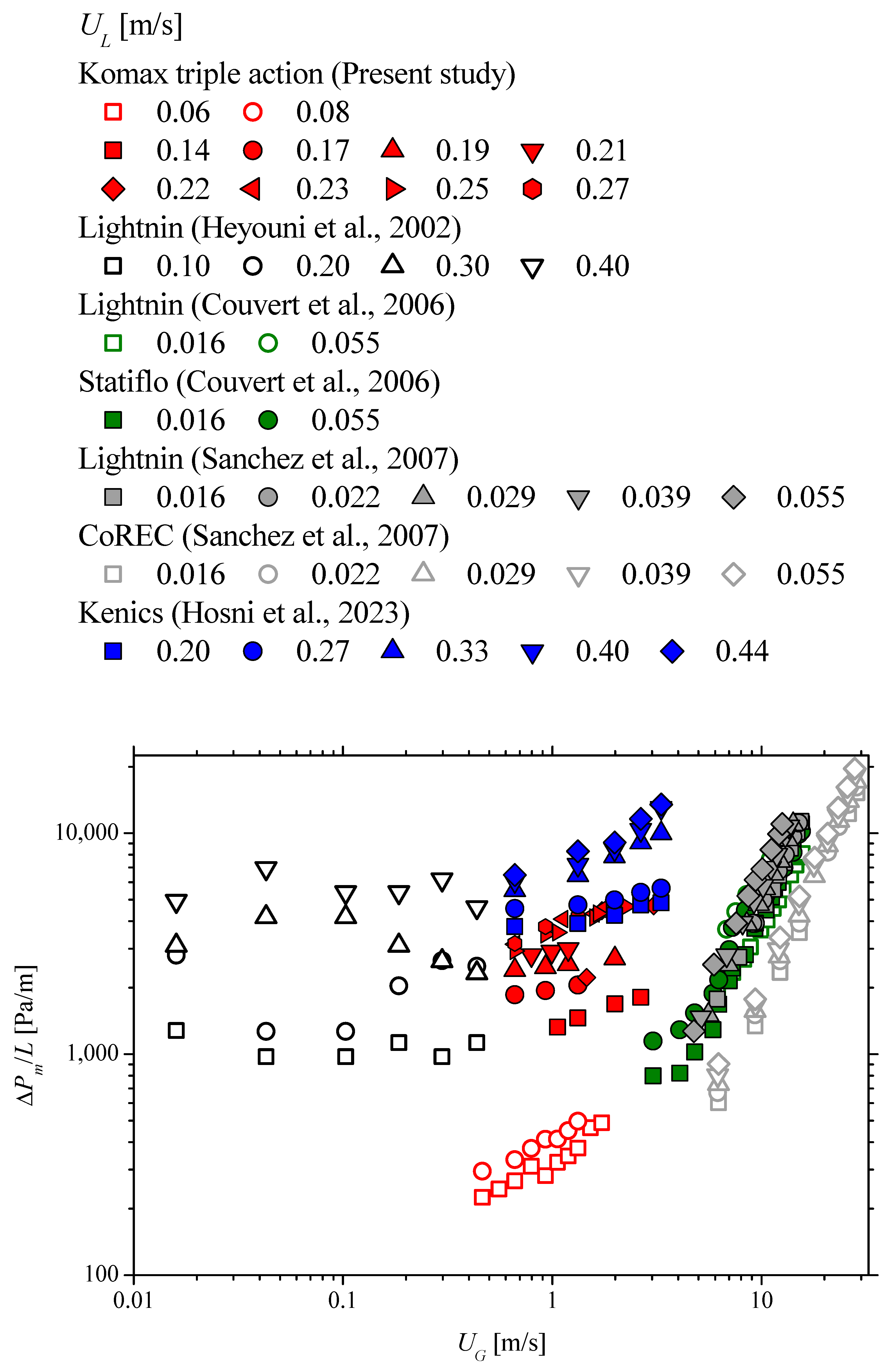
3.2. Gas–Liquid Two-Phase Flow Pressure Drop
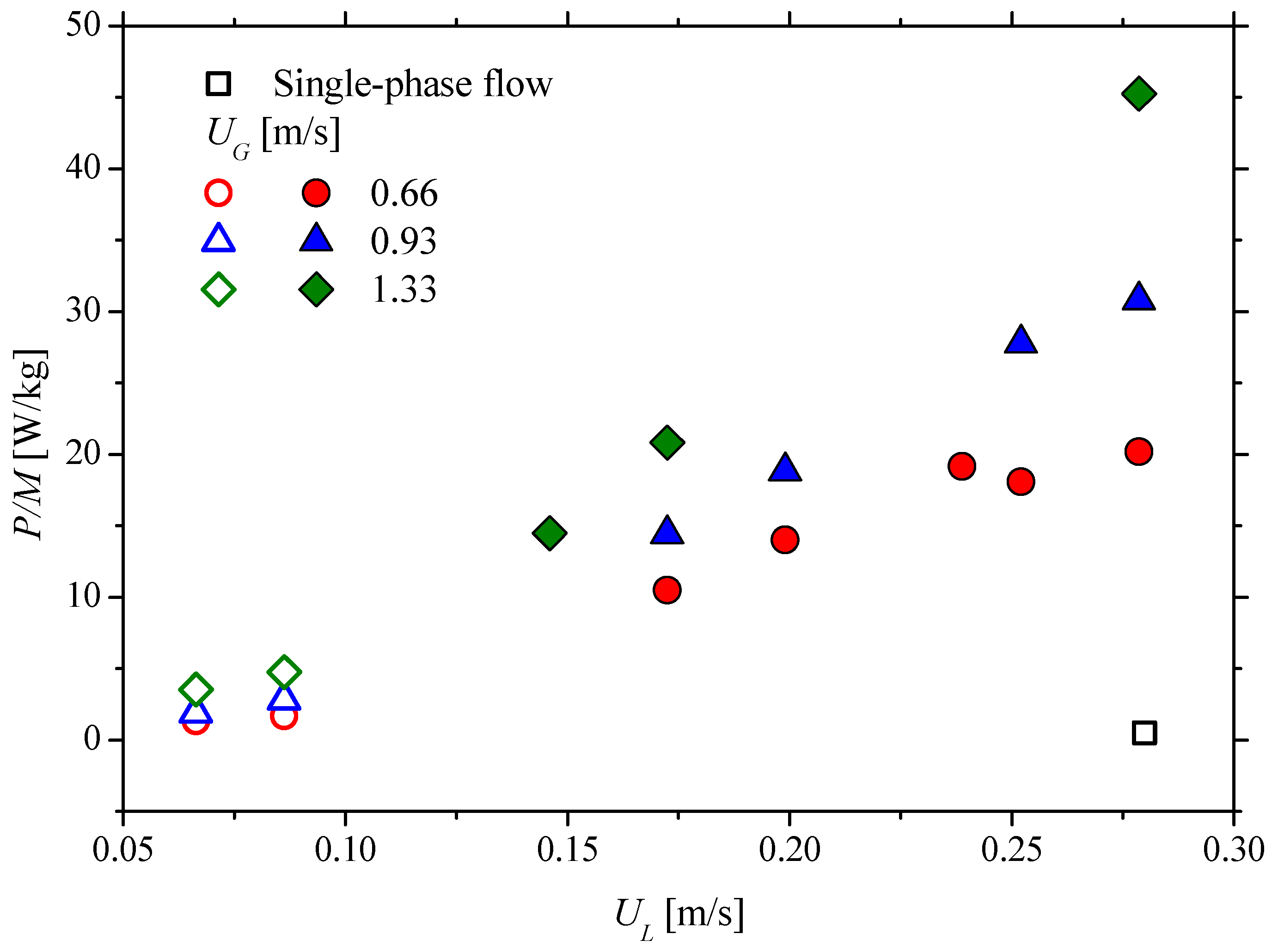
3.3. Power Dissipation
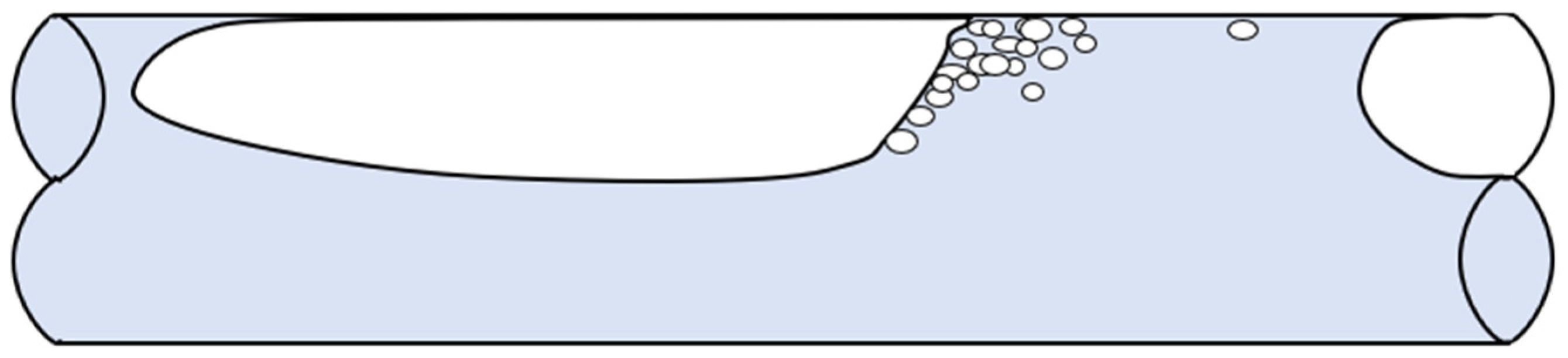
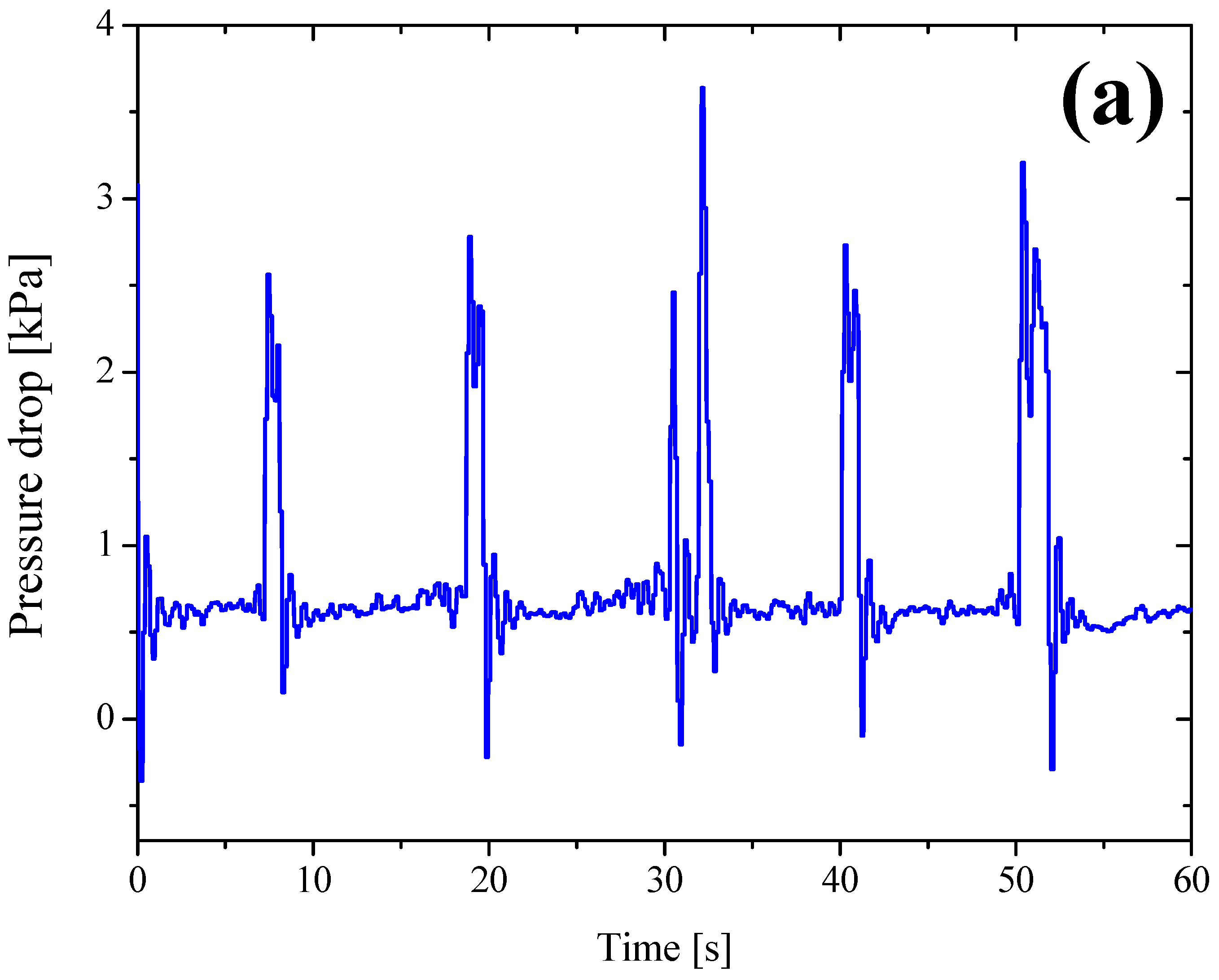
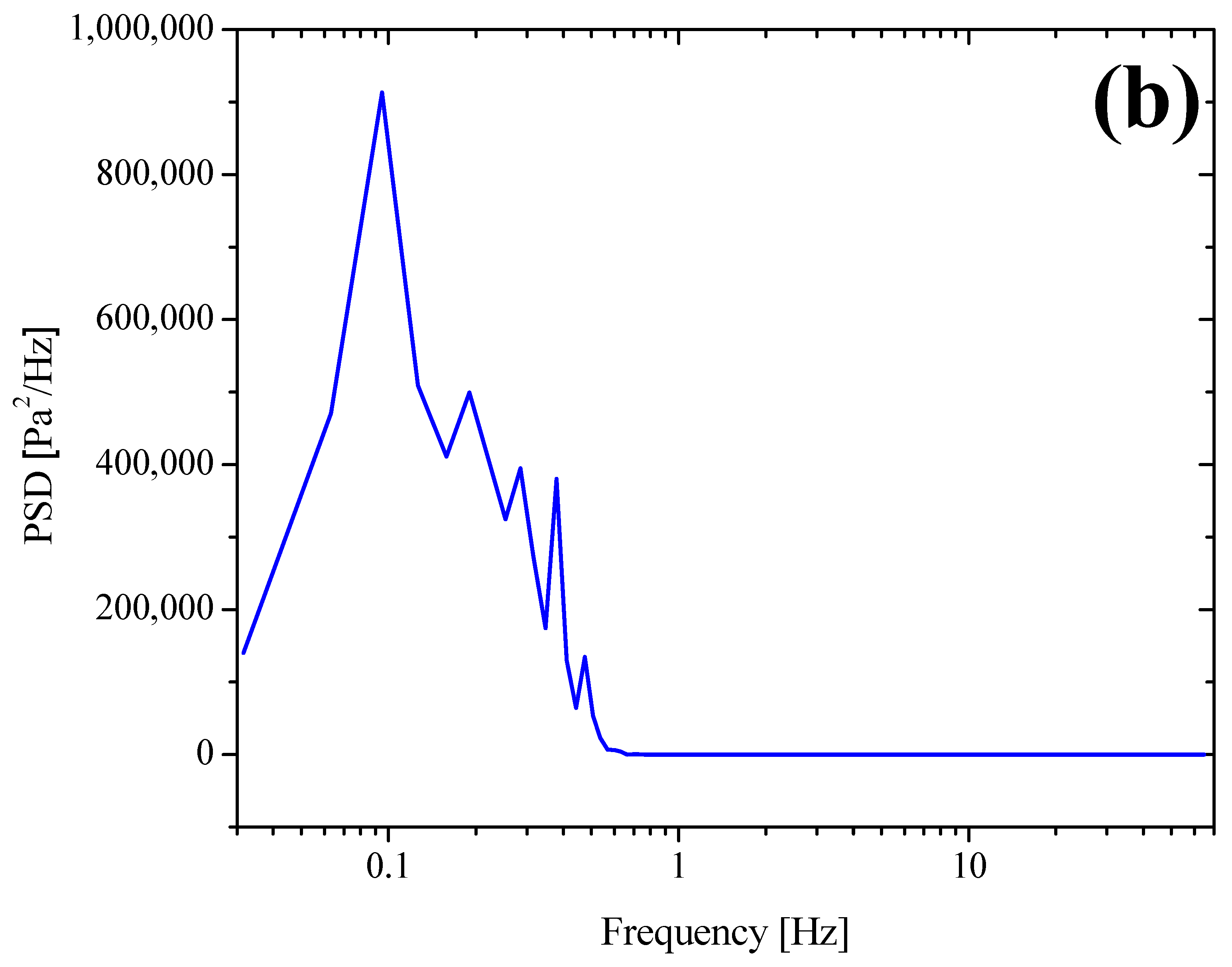
3.4. Characterization of Intermittent Flow Through Komax Triple Action
4. Conclusions
- For turbulent single-phase flow, the friction factor and z-factor are independent of the Reynolds number. The comparison of the presented results with available datasets shows that the Komax triple action generates lower pressure drops.
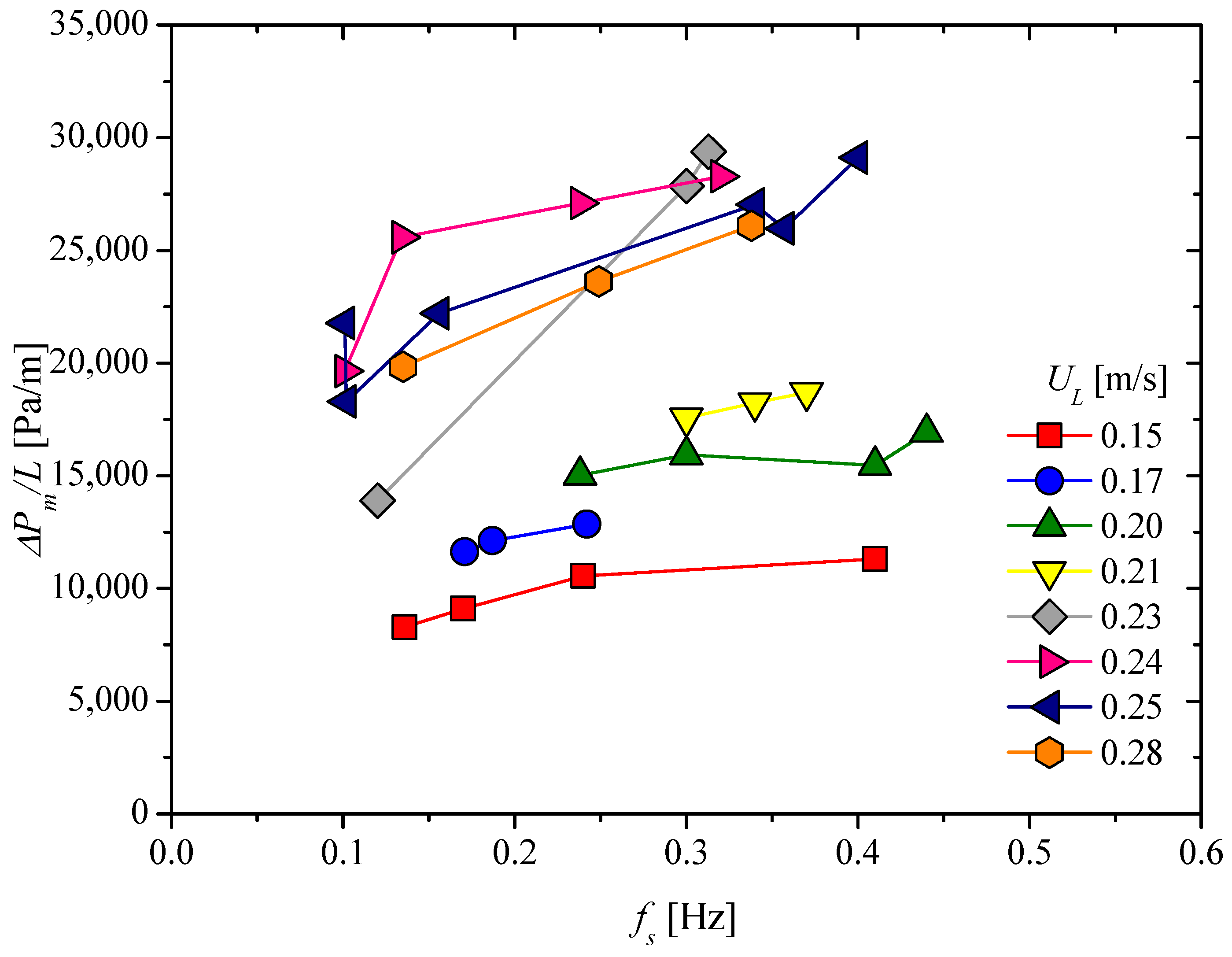
- The pressure drop per unit length in the case of two-phase flow is dependent on both liquid and gas superficial velocities. Meanwhile, the effect of liquid superficial velocity becomes more important when the static mixer is crossed by the intermittent flow.
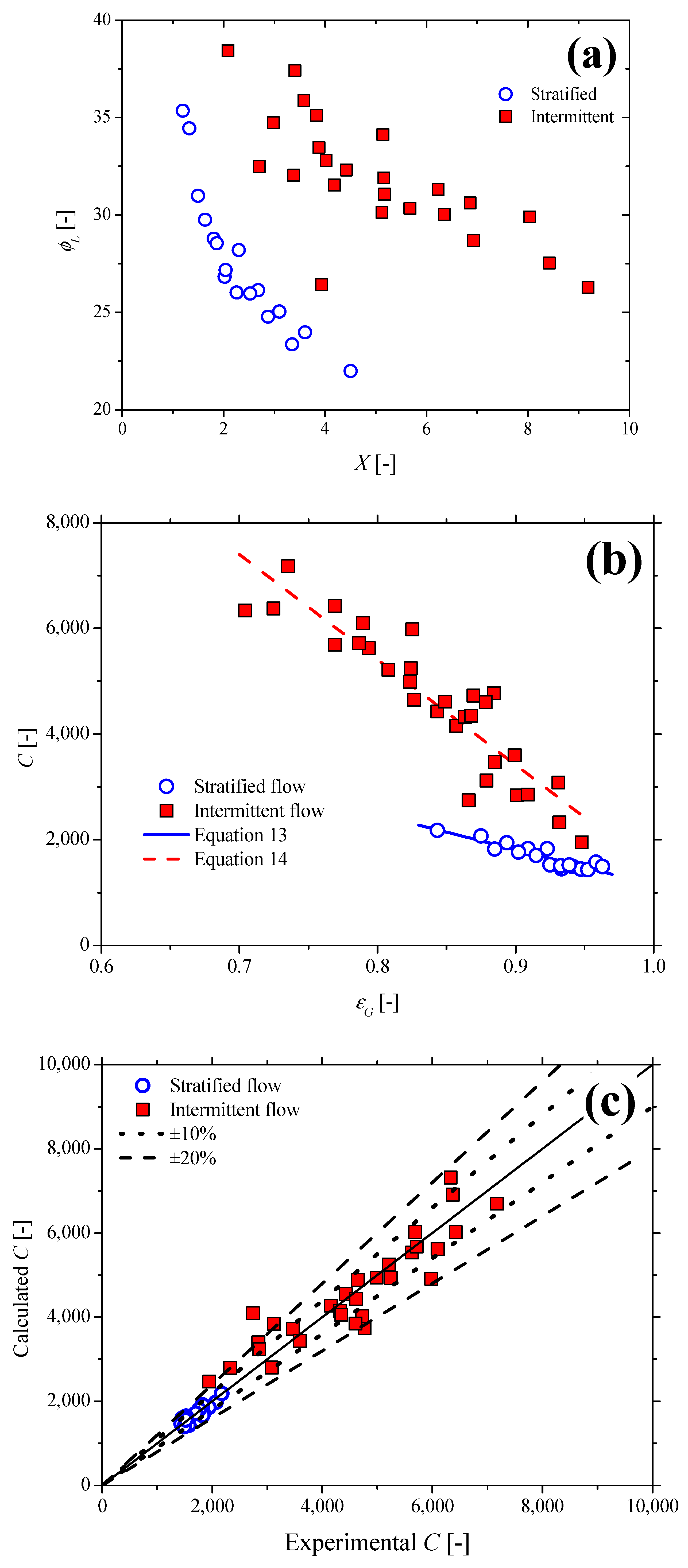
- Application of the Lockhart–Martinelli approach for modeling the two-phase flow pressure drop gives interesting results. By considering the nature of flow regimes, the Chisholm parameter was linearly correlated with the homogenous liquid fraction.
- The study of power dissipation shows that it depends on both the liquid and gas’ superficial velocities.
- The visual observation of images collected shows that the Komax triple action induces the formation of swirling flow when the intermittent flow is observed upstream of the mixer.
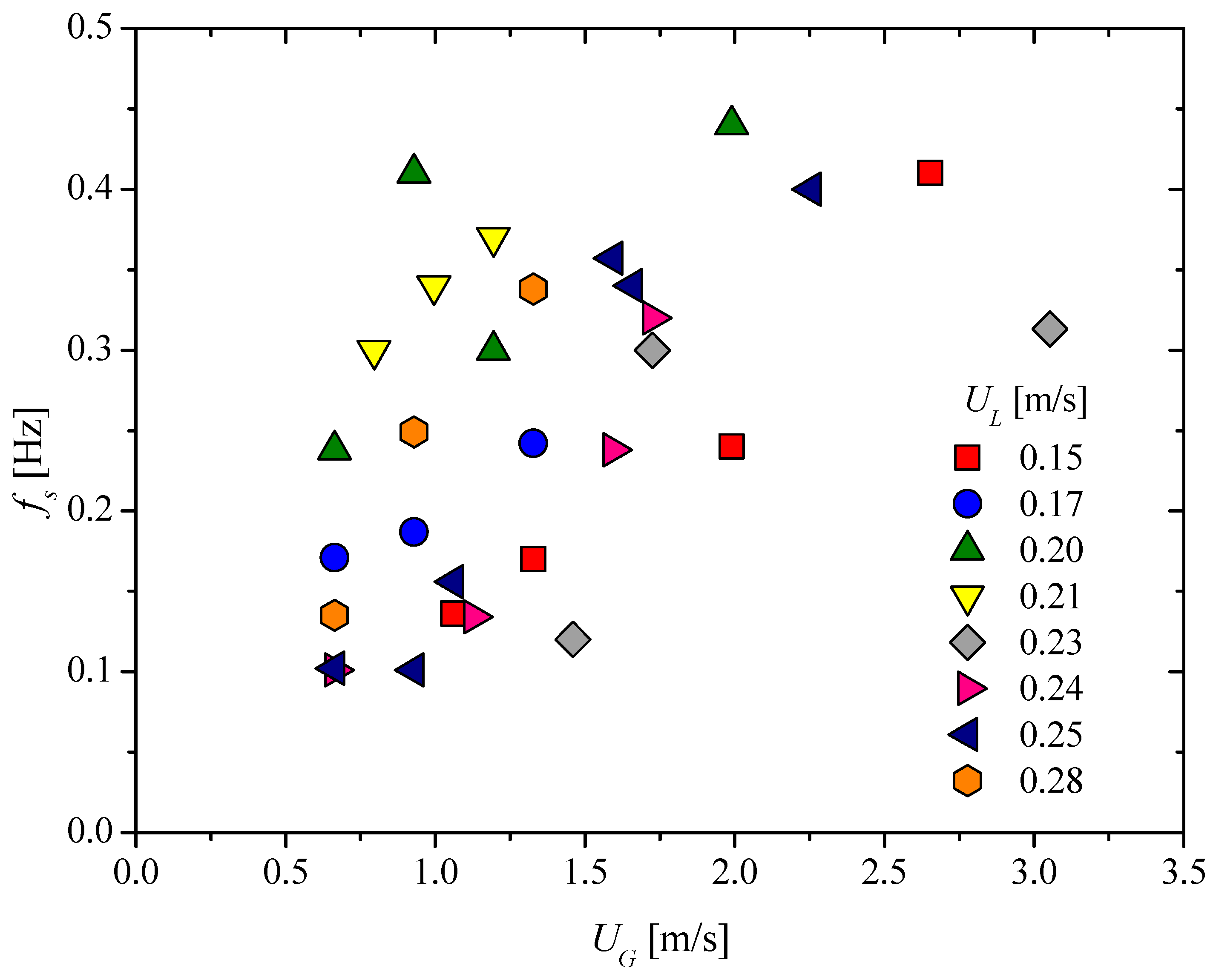
- The measurements of slug frequency showed that it depends on both liquid and gas superficial velocities. Interestingly, an increase in slug frequency induces an increase before a pressure drop stabilization.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CBM | Curved-sheet blade-folded | |
| CFD | Computational fluid dynamics | |
| DEM | Discrete element method | |
| HILDA | ||
| PI | Process intensification | |
| PSD | Power spectral density | |
| SM | Static mixer | |
| TKSM | Static mixer with three twisted leaves | |
| VOF | Volume of fluid | |
| Nomenclature | ||
| C | Chisholm parameter | [-] |
| CoV | Coefficient of variation | [-] |
| D | Pipe diameter | [m] |
| Gas pressure drop gradient | [Pa.m−1] | |
| Liquid pressure drop gradient | [Pa.m−1] | |
| f | Friction factor | [-] |
| fs | Slug frequency | [s−1] |
| HL | Liquid holdup | [-] |
| L | Length of static mixer | [m] |
| M | Mass | [kg] |
| P | Power dissipated | [W] |
| ReL | Liquid Reynolds number | [-] |
| VM | Mixture velocity | [m.s−1] |
| VL | Liquid velocity | [m.s−1] |
| VSM | Volume of static mixer | [m3] |
| UG | Gas superficial velocity | [m.s−1] |
| UL | Liquid superficial velocity | [m.s−1] |
| X | Lockhart–Martinelli parameter | [-] |
| z | Pressure drop ratio | [-] |
| Greek letters | ||
| αSM | Porosity of static mixer | [-] |
| ΔP0 | Pressure drop measured in a straight pipe | [Pa] |
| ΔPL | Liquid Pressure drop | [Pa] |
| ΔPm | Pressure drop generated by static mixer | [Pa] |
| εG | Void fraction | [-] |
| λG | Input gas holdup | [-] |
| µL | Liquid viscosity | [Pa.s] |
| ρL | Liquid density | [kg.m−3] |
| Two-phase multiplier | [-] | |
References
- Haase, S.; Tolvanen, P.; Russo, V. Process intensification in chemical reaction engineering. Processes 2022, 10, 99. [Google Scholar] [CrossRef]
- Paul, E.L.; Atiemo-Obeng, V.A.; Kresta, S.M. Introduction. In Handbook of Industrial Mixing—Science and Practice; John Wiley & Sons: Hoboken, NJ, USA, 2004; Chapter 1; pp. xxxiii–lx. ISBN 0-471-26919-0. [Google Scholar]
- Bowler, A.L.; Bakalis, S.; Watson, N.J. A review of in-line and on-line measurement techniques to monitor industrial mixing processes. Chem. Eng. Res. Des. 2020, 153, 463–495. [Google Scholar] [CrossRef]
- Valdés, J.P.; Kahouadji, L.; Matar, O.K. Current advances in liquid–liquid mixing in static mixers: A review. Chem. Eng. Res. Des. 2022, 177, 694–731. [Google Scholar] [CrossRef]
- Hildner, M.; Lorenz, J.; Zhu, B.; Shih, A. Pressure drop reduction of the impeller spiral static mixer design enabled by additive manufacturing. Chem. Eng. Process.-Process Intensif. 2023, 191, 109486. [Google Scholar] [CrossRef]
- Crittenden, J.C.; Howe, K.J.; Hand, D.W.; Tchobanoglous, G.; Trussell, R.R. Water Treatment: Principles and Design, 2nd ed.; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Thakur, R.K.; Vial, C.; Nigam, K.D.P.; Nauman, E.B.; Djelveh, G. Static mixers in the process industries—A review. Chem. Eng. Res. Des. 2003, 81, 787–826. [Google Scholar] [CrossRef]
- Ghanem, A.; Lemenand, T.; Della Valle, D.; Peerhossaini, H. Static mixers: Mechanisms, applications, and characterization methods–A review. Chem. Eng. Res. Des. 2014, 92, 205–228. [Google Scholar] [CrossRef]
- Hammoudi, M.; Legrand, J.; Si-Ahmed, E.K.; Salem, A. Flow analysis by pulsed ultrasonic velocimetry technique in Sulzer SMX static mixer. Chem. Eng. J. 2008, 139, 562–574. [Google Scholar] [CrossRef]
- Demoz, A. Scaling inline static mixers for flocculation of oil sand mature fine tailings. AIChE J. 2015, 61, 4402–4411. [Google Scholar] [CrossRef]
- Chakleh, R.; Azizi, F. Performance comparison between novel and commercial static mixers under turbulent conditions. Chem. Eng. Process.-Process Intensif. 2023, 193, 109559. [Google Scholar] [CrossRef]
- Yu, Y.; Xiang, K.; Meng, H.; Li, W.; Li, D.; Xia, R.; Han, Z. A comprehensive review of gas–liquid two-phase flow in static mixers. Chem. Eng. Process.-Process Intensif. 2025, 216, 110434. [Google Scholar] [CrossRef]
- Aghamiri, Z.S.; Mehrnia, M.R.; Fatemi, S.; Shojaosadati, S.A.; Yazdian, F. Mathematical modeling of a horizontal tubular loop bioreactor for biomass production from natural gas. Process Biochem. 2010, 45, 1393–1400. [Google Scholar] [CrossRef]
- Li, H.; Yu, X.; Song, Y.; Li, Q.; Lu, S. Experimental and numerical investigation on optimization of foaming performance of the kenics static mixer in compressed air foam system. Eng. Appl. Comput. Fluid Mech. 2023, 17, 2183260. [Google Scholar] [CrossRef]
- Hosseini, S.M.; Razzaghi, K.; Shahraki, F. Design and characterization of a Low-pressure-drop static mixer. AIChE J. 2019, 65, 1126–1133. [Google Scholar] [CrossRef]
- Gavrilescu, M.; Tudose, R.Z. Intensification of transfer processes in biotechnology and chemical engineering using static mixers. Acta Biotechnol. 1995, 15, 3–26. [Google Scholar] [CrossRef]
- Meijer, H.E.; Singh, M.K.; Anderson, P.D. On the performance of static mixers: A quantitative comparison. Prog. Polym. Sci. 2012, 37, 1333–1349. [Google Scholar] [CrossRef]
- Al-Atabi, M. Design and assessment of a novel static mixer. Can. J. Chem. Eng. 2011, 89, 550–554. [Google Scholar] [CrossRef]
- Qiao, Y.; Zheng, L.; Guo, K.; Liu, H.; Zhang, B.; Li, W.; Guo, X.; Liu, C. Numerical study of flow field and mixing performance of a new curved-sheet blade-folded static mixer. Ind. Eng. Chem. Res. 2024, 63, 7836–7852. [Google Scholar] [CrossRef]
- Kresta, S.M.; Krebs, R.; Martin, T. The future of mixing research. Chem. Eng. Technol. Ind. Chem.-Plant Equip.-Process Eng. Biotechnol. 2004, 27, 208–214. [Google Scholar] [CrossRef]
- Haddadi, M.M.; Hosseini, S.H.; Rashtchian, D.; Olazar, M. Comparative analysis of different static mixers performance by CFD technique: An innovative mixer. Chin. J. Chem. Eng. 2020, 28, 672–684. [Google Scholar] [CrossRef]
- Hosni, M.; Hammoudi, M.H.; Si-Ahmed, E.K.; Legrand, J.; Douib, L. Single and two-phase flows in a horizontal pipe with a K enics static mixer: Effect of pressure drop on mixing. Can. J. Chem. Eng. 2023, 101, 828–844. [Google Scholar] [CrossRef]
- Pahl, M.H.; Muschelknautz, E. Statische mischer und ihre anwendung. Chem. Ing. Tech. 1980, 52, 285–291. [Google Scholar] [CrossRef]
- Jovanović, A.; Pezo, M.; Pezo, L.; Lević, L. DEM/CFD analysis of granular flow in static mixers. Powder Technol. 2014, 266, 240–248. [Google Scholar] [CrossRef]
- Rabha, S.; Schubert, M.; Grugel, F.; Banowski, M.; Hampel, U. Visualization and quantitative analysis of dispersive mixing by a helical static mixer in upward co-current gas–liquid flow. Chem. Eng. J. 2015, 262, 527–540. [Google Scholar] [CrossRef]
- Jiang, X.; Yang, N.; Wang, R. Effect of aspect ratio on the mixing performance in the Kenics static mixer. Processes 2021, 9, 464. [Google Scholar] [CrossRef]
- Pezo, L.L.; Pezo, M.; Terzić, A.; Jovanović, A.P.; Lončar, B.; Govedarica, D.; Kojić, P. Experimental and discrete element model investigation of limestone aggregate blending process in vertical static and/or conveyor mixer for application in the concrete mixture. Processes 2021, 9, 1991. [Google Scholar] [CrossRef]
- Li, H.; Yu, X.; Qiu, K.; Yu, X.; Lu, S. Enhanced fire-fighting performance of aqueous film-forming foam (AFFF) by tuning bubble size and expansion ratio with kenics static mixers. Fire Saf. J. 2024, 144, 104117. [Google Scholar] [CrossRef]
- Yao, Z.; Alberini, F.; Montante, G.; Paglianti, A. In-line monitoring of mixing performance for smart processes in tubular reactors. Chem. Eng. Res. Des. 2023, 194, 678–692. [Google Scholar] [CrossRef]
- Maluta, F.; Paglianti, A.; Montante, G. A PBM-Based Procedure for the CFD Simulation of Gas–Liquid Mixing with Compact Inline Static Mixers in Pipelines. Processes 2023, 11, 198. [Google Scholar] [CrossRef]
- Liu, Y.; Gao, M.; Huang, Z.; Wang, H.; Yuan, P.; Xu, X.; Yang, J. Numerical Simulation of the Mixing and Salt Washing Effects of a Static Mixer in an Electric Desalination Process. Processes 2024, 12, 883. [Google Scholar] [CrossRef]
- Wang, L.; Peng, Y.; Yang, X.; Qian, Y.; Wang, H.; Xu, Y.; Xu, Y. Bubble evolution and gas-liquid mixing mechanism in a static-mixer-based plug-flow reactor: A numerical analysis. Chem. Eng. J. 2024, 485, 149899. [Google Scholar] [CrossRef]
- Fonte, C.M.; Leblebici, M.E.; Dias, M.M.; Lopes, J.C.B. The NETmix reactor: Pressure drop measurements and 3D CFD modeling. Chem. Eng. Res. Des. 2013, 91, 2250–2258. [Google Scholar] [CrossRef]
- Jegatheeswaran, S. Using Electrical Resistance Tomography (ERT) and Computational Fluid Dynamics (CFD) to Study the Mixing of Yield-Pseudoplastic Fluids in the SMX Static Mixer. Doctoral Dissertation, Toronto Metropolitan University, Toronto, ON, Canada, 2016. [Google Scholar]
- Nyande, B.W.; Mathew Thomas, K.; Lakerveld, R. CFD analysis of a Kenics static mixer with a low pressure drop under laminar flow conditions. Ind. Eng. Chem. Res. 2021, 60, 5264–5277. [Google Scholar] [CrossRef]
- Wang, C.; Liu, H.; Yang, X.; Wang, R. Research for a non-standard kenics static mixer with an eccentricity factor. Processes 2021, 9, 1353. [Google Scholar] [CrossRef]
- Meng, H.; Meng, T.; Yu, Y.; Wang, Z.; Wu, J. Experimental and numerical investigation of turbulent flow and heat transfer characteristics in the Komax static mixer. Int. J. Heat Mass Transf. 2022, 194, 123006. [Google Scholar] [CrossRef]
- Valdes, J.P.; Kahouadji, L.; Liang, F.; Shin, S.; Chergui, J.; Juric, D.; Matar, O.K. Direct numerical simulations of liquid–liquid dispersions in a SMX mixer under different inlet conditions. Chem. Eng. J. 2023, 462, 142248. [Google Scholar] [CrossRef]
- Patil, P.R.; Dastane, G.G.; Pandit, A.B. Numerical investigation of turbulent flow and heat transfer characteristics in the improved Kenics static mixer. Heat Transf. 2024, 53, 44–72. [Google Scholar] [CrossRef]
- Rakoczy, R.; Masiuk, S.; Kordas, M.; Grądzik, P. The effects of power characteristics on the heat transfer process in various types of motionless mixing devices. Chem. Eng. Process. Process Intensif. 2011, 50, 959–969. [Google Scholar] [CrossRef]
- Revathi, D.; Saravanan, K. Experimental studies on hydrodynamic aspects for mixing of non-Newtonian fluids in a Komax static mixer. Chem. Ind. Chem. Eng. Q. 2020, 26, 329–335. [Google Scholar] [CrossRef]
- Moghaddam, S. Effect of non-Newtonian fluid on mixing quality and pressure drop in several static mixers: A numerical study. Iran. J. Sci. Technol. Trans. Mech. Eng. 2023, 47, 1585–1597. [Google Scholar] [CrossRef]
- Heyouni, A.; Roustan, M.; Do-Quang, Z. Hydrodynamics and mass transfer in gas–liquid flow through static mixers. Chem. Eng. Sci. 2002, 57, 3325–3333. [Google Scholar] [CrossRef]
- Li, G.; Miles, N.J.; Hall, P.; Wang, Z.; Gao, J.; Shen, Y. Dispersion of immiscible liquids in a static mixer without inserted elements: A CFD-PBM study on droplet size reduction and distribution. Powder Technol. 2025, 452, 120547. [Google Scholar] [CrossRef]
- Hammoudi, M.; Si-Ahmed, E.K.; Legrand, J. Dispersed two-phase flow analysis by pulsed ultrasonic velocimetry in SMX static mixer. Chem. Eng. J. 2012, 191, 463–474. [Google Scholar] [CrossRef]
- Martin, N.; Galey, C. Use of static mixer for oxidation and disinfection by ozone. Ozone Sci. Eng. 1994, 16, 455–473. [Google Scholar] [CrossRef]
- Liu, W.; Lv, X.; Jiang, S.; Li, H.; Zhou, H.; Dou, X. Gas–liquid two-phase flow patterns and pressure drop of decaying swirling flow inside a horizontal pipe. Chem. Eng. Sci. 2023, 266, 118281. [Google Scholar] [CrossRef]
- Keshav, T.R.; Somaraju, P.; Kalyan, K.; Saroha, A.K.; Nigam, K.D.P. Liquid phase residence time distribution for gas–liquid flow in Kenics static mixer. Chem. Eng. Process. Process Intensif. 2008, 47, 2275–2280. [Google Scholar] [CrossRef]
- Couvert, A.; Sanchez, C.; Charron, I.; Laplanche, A.; Renner, C. Static mixers with a gas continuous phase. Chem. Eng. Sci. 2006, 61, 3429–3434. [Google Scholar] [CrossRef]
- Sanchez, C.; Couvert, A.; Laplanche, A.; Renner, C. Hydrodynamic and mass transfer in a new co-current two-phase flow gas–liquid contactor. Chem. Eng. J. 2007, 131, 49–58. [Google Scholar] [CrossRef]
- Meng, H.; Hao, Y.; Yu, Y.; Li, Z.; Song, S.; Wu, J. Experimental study of gas-liquid two-phase bubbly flow characteristics in a static mixer with three twisted leaves. Korean J. Chem. Eng. 2020, 37, 1859–1866. [Google Scholar] [CrossRef]
- Hewitt, G.F.; Roberts, D.N. Studies of Two-Phase Flow Patterns by Simultaneous X-Ray And Flast Photography (No. AERE-M-2159); Atomic Energy Research Establishment: Harwell, UK, 1969. [Google Scholar]
- Xu, Y.; Wang, L.; Wang, Y.; Qian, Y.; Wang, H.; Xu, Y.; Yang, X. Gas-liquid flow pattern identification and bubble characteristics analysis in a static mixer based HiPOxTM reactor. Chem. Eng. Sci. 2023, 267, 118269. [Google Scholar] [CrossRef]
- Yu, Y.; Li, B.; Meng, H.; Zhang, J.; Xiang, K.; Yang, P. Multiscale Turbulence Characteristics of Gas–Liquid Pressure Fluctuations in an Industrial Quatro Static Mixer. Ind. Eng. Chem. Res. 2024, 63, 3727–3743. [Google Scholar] [CrossRef]
- Marrocos, P.H.; Fernandes, I.S.; Pituco, M.M.; Lopes, J.C.; Dias, M.M.; Santos, R.J.; Vilar, V.J. CFD and lower order mechanistic models for gas-liquid flow in NETmix: Pressure drop and gas hold-up. Chem. Eng. Sci. 2024, 284, 119478. [Google Scholar] [CrossRef]
- Scala, M.; Gamet, L.; Malbec, L.M.; Li, H.Z. Hydrodynamics of gas-liquid dispersion in transparent Sulzer static mixers SMXTM. Chem. Eng. Sci. 2020, 213, 115398. [Google Scholar] [CrossRef]
- McCowan, M. Developing a Horizontal In-Line Diffused Aeration System for Removing Trihalomethanes from Water Distribution Mains. Master’s Thesis, University of New Hampshire, Durham, NH, USA, 2015. [Google Scholar]
- Ogunsesan, O.A.; Hossain, M.; Droubi, M.G. Computational fluid dynamics modelling of multiphase flows in double elbow geometries. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2021, 235, 1835–1846. [Google Scholar] [CrossRef]
- Holagh, S.G.; Ahmed, W.H. Critical review of vertical gas-liquid slug flow: An insight to better understand flow hydrodynamics’ effect on heat and mass transfer characteristics. Int. J. Heat Mass Transf. 2024, 225, 125422. [Google Scholar] [CrossRef]
- Arabi, A. Contribution à l’étude du Comportement d’un Ecoulement Diphasique Dans une Conduite en Présence d’une Singularité. Ph.D. Thesis, USTHB, Algiers, Algeria, 2019. [Google Scholar]
- Fang, X.; Xu, Y.; Zhou, Z. New correlations of single-phase friction factor for turbulent pipe flow and evaluation of existing single-phase friction factor correlations. Nucl. Eng. Des. 2011, 241, 897–902. [Google Scholar] [CrossRef]
- Saldana, M.; Gallegos, S.; Gálvez, E.; Castillo, J.; Salinas-Rodríguez, E.; Cerecedo-Sáenz, E.; Hernández-Ávila, J.; Navarra, A.; Toro, N. The Reynolds number: A journey from its origin to modern applications. Fluids 2024, 9, 299. [Google Scholar] [CrossRef]
- Almenas, K.; Gasiūnas, S.; Šeporaitis, M.; Pabarčius, R. Shear Number as a Practical Tool for Flow Regime Evaluation and Education. Fluids 2025, 10, 76. [Google Scholar] [CrossRef]
- Stec, M.; Synowiec, P.M. Study of fluid dynamic conditions in the selected static mixers part I-research of pressure drop. Can. J. Chem. Eng. 2017, 95, 2156–2167. [Google Scholar] [CrossRef]
- Taitel, Y.; Dukler, A.E. A model for predicting flow regime transitions in horizontal and near horizontal gas-liquid flow. AIChE J. 1976, 22, 47–55. [Google Scholar] [CrossRef]
- Arabi, A.; Abdul-Majeed, G.H.; Boukrouche, H.B.; Larbi, Z. Pressure recovery model for gas–liquid two-phase flow across sudden expansions. Exp. Comput. Multiph. Flow 2024, 6, 14–27. [Google Scholar] [CrossRef]
- Lockhart, W.R. Proposed correlation of data for isothermal two-phase, two-component flow in pipes. Chem. Eng. Prog. 1949, 45, 39–48. [Google Scholar]
- Chisholm, D. A theoretical basis for the Lockhart-Martinelli correlation for two-phase flow. Int. J. Heat Mass Transf. 1967, 10, 1767–1778. [Google Scholar] [CrossRef]
- Cai, Q.; D’Auria, F.; Umminger, K.; Bestion, D.; Shan, J. Prioritizing pressure drop research in nuclear thermal hydraulics. Prog. Nucl. Energy 2022, 153, 104358. [Google Scholar] [CrossRef]
- Arabi, A.; Salhi, Y.; Zenati, Y.; Si-Ahmed, E.K.; Legrand, J. Identifying the intermittent flow sub-regimes using pressure drop time series fluctuations. Exp. Comput. Multiph. Flow 2024, 6, 28–40. [Google Scholar] [CrossRef]
- Höhn, R.L.; Arabi, A.; Stiriba, Y.; Pallares, J. A review of the measurement of the multiphase slug frequency. Processes 2024, 12, 2500. [Google Scholar] [CrossRef]
- Arabi, A.; Höhn, R.L.; Pallares, J.; Stiriba, Y. Practical aspects of multiphase slug frequency: An overview. Can. J. Chem. Eng. 2025, 103, 2880–2894. [Google Scholar] [CrossRef]
- Woods, B.D.; Hanratty, T.J. Influence of Froude number on physical processes determining frequency of slugging in horizontal gas–liquid flows. Int. J. Multiph. Flow 1999, 25, 1195–1223. [Google Scholar] [CrossRef]
- Dinaryanto, O.; Prayitno, Y.A.K.; Majid, A.I.; Hudaya, A.Z.; Nusirwan, Y.A.; Widyaparaga, A. Experimental investigation on the initiation and flow development of gas-liquid slug two-phase flow in a horizontal pipe. Exp. Therm. Fluid Sci. 2017, 81, 93–108. [Google Scholar] [CrossRef]
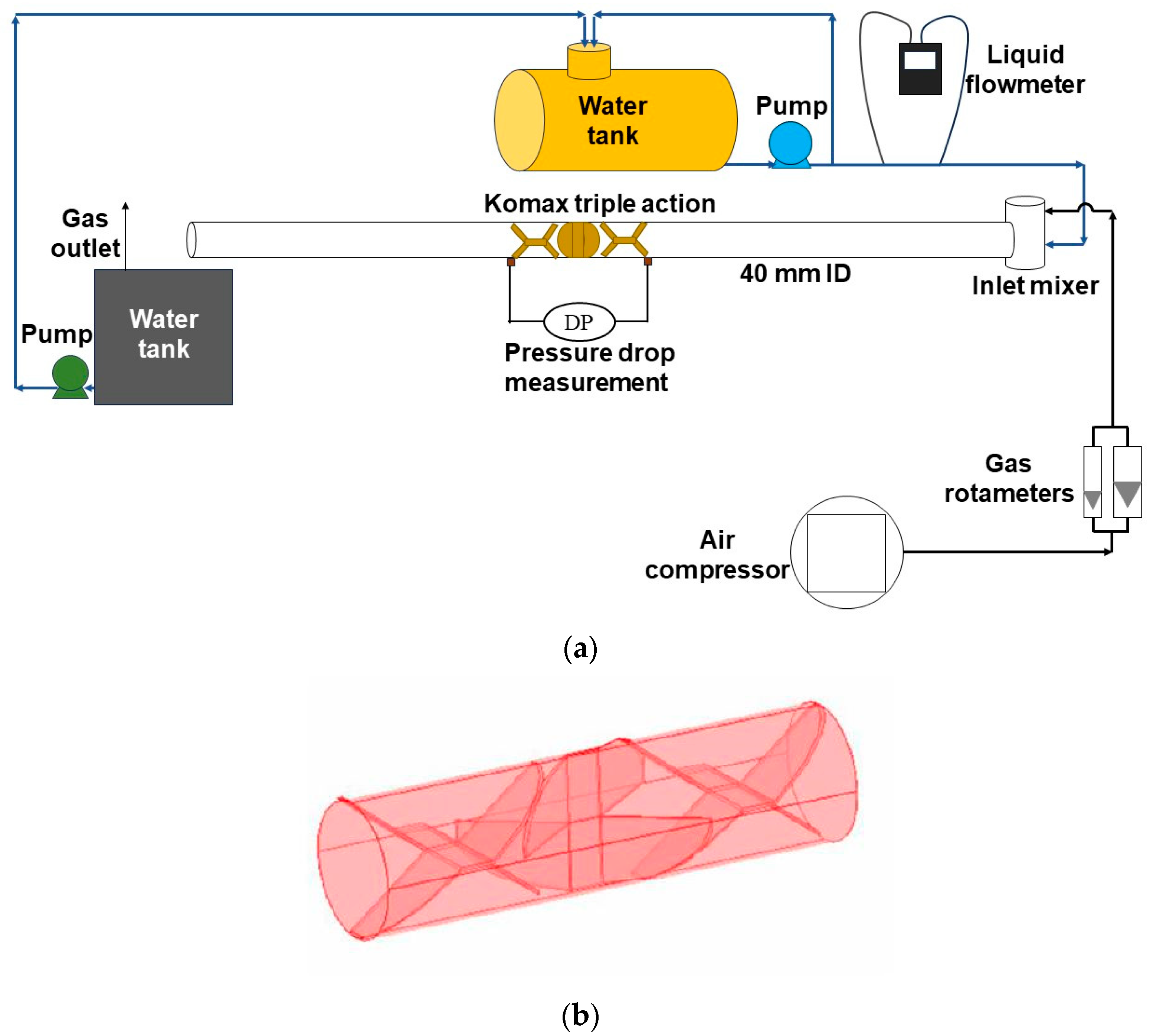



| Diameter (D) | 40 mm |
| Length of static mixer (L) | 160 mm |
| Porosity (αSM) | 92.8% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zenati, Y.; Hammoudi, M.; Arabi, A.; Legrand, J.; Si-Ahmed, E.-K. Pressure Drops for Turbulent Liquid Single-Phase and Gas–Liquid Two-Phase Flows in Komax Triple Action Static Mixer. Fluids 2025, 10, 259. https://doi.org/10.3390/fluids10100259
Zenati Y, Hammoudi M, Arabi A, Legrand J, Si-Ahmed E-K. Pressure Drops for Turbulent Liquid Single-Phase and Gas–Liquid Two-Phase Flows in Komax Triple Action Static Mixer. Fluids. 2025; 10(10):259. https://doi.org/10.3390/fluids10100259
Chicago/Turabian StyleZenati, Youcef, M’hamed Hammoudi, Abderraouf Arabi, Jack Legrand, and El-Khider Si-Ahmed. 2025. "Pressure Drops for Turbulent Liquid Single-Phase and Gas–Liquid Two-Phase Flows in Komax Triple Action Static Mixer" Fluids 10, no. 10: 259. https://doi.org/10.3390/fluids10100259
APA StyleZenati, Y., Hammoudi, M., Arabi, A., Legrand, J., & Si-Ahmed, E.-K. (2025). Pressure Drops for Turbulent Liquid Single-Phase and Gas–Liquid Two-Phase Flows in Komax Triple Action Static Mixer. Fluids, 10(10), 259. https://doi.org/10.3390/fluids10100259








