Reynolds Stresses and Hemolysis in Turbulent Flow Examined by Threshold Analysis
Abstract
:1. Introduction
2. Background
3. Methods
3.1. Modeled Systems
3.2. Computational Procedures
3.2.1. Computational Mesh
3.2.2. Flow Simulation
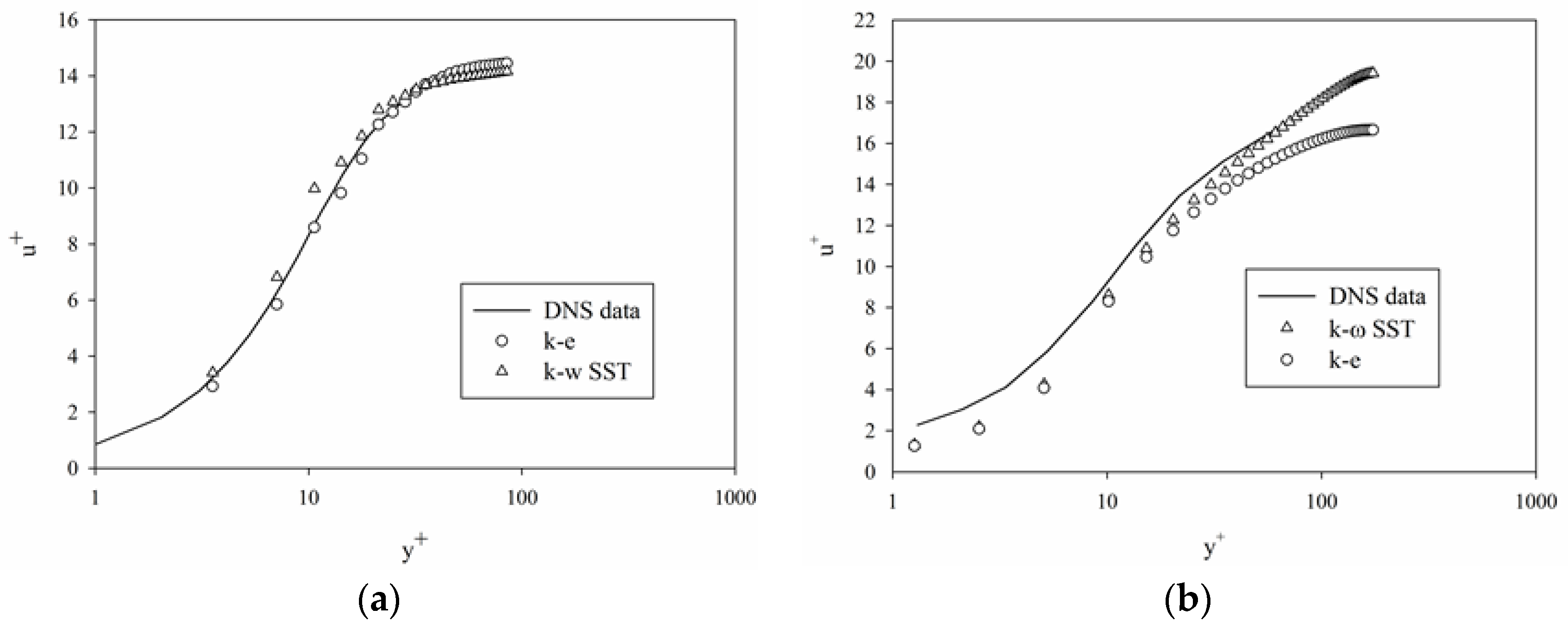
3.2.3. Turbulence Model
3.2.4. Reynolds Stress Calculation
4. Results and Discussion
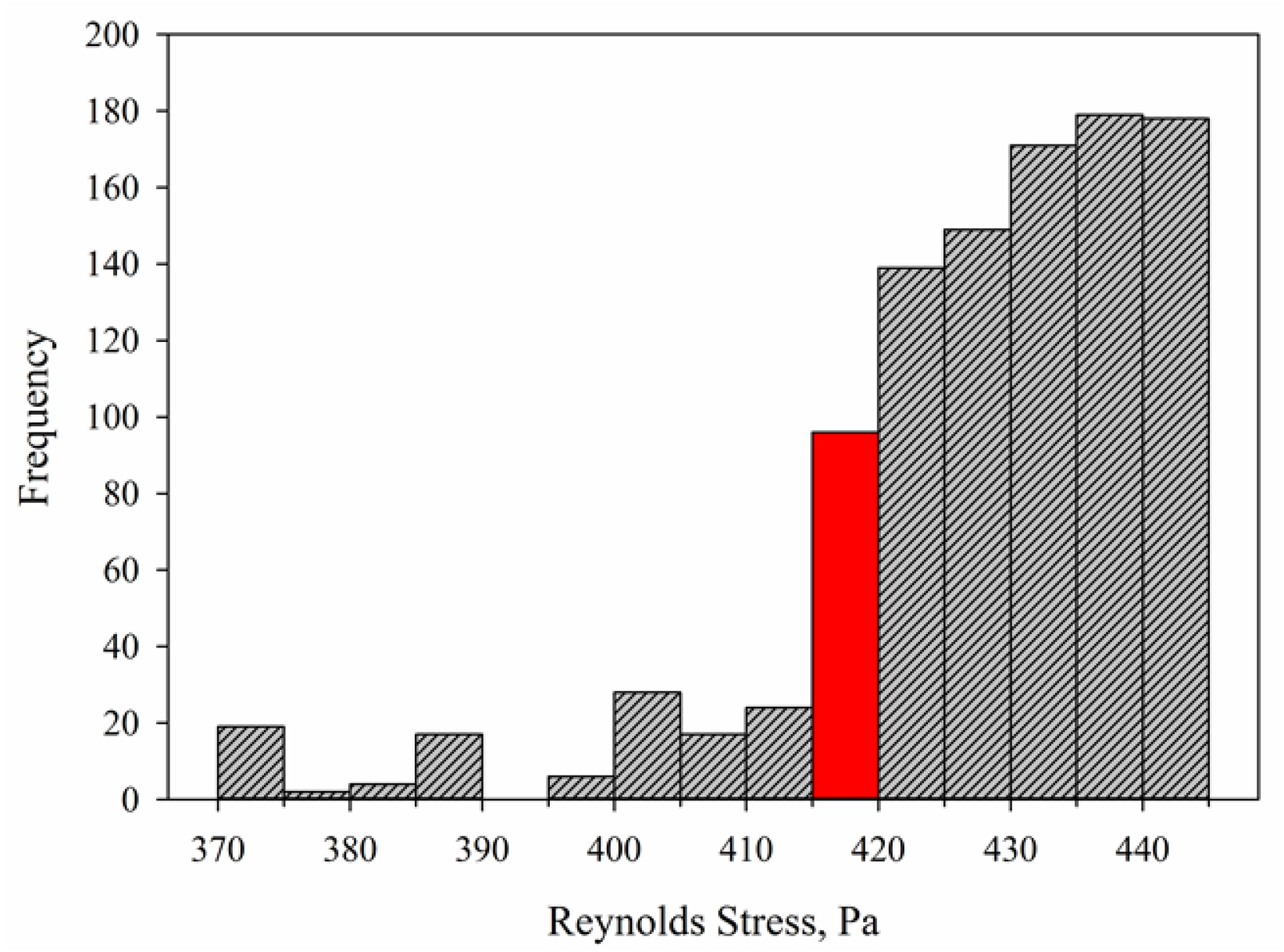
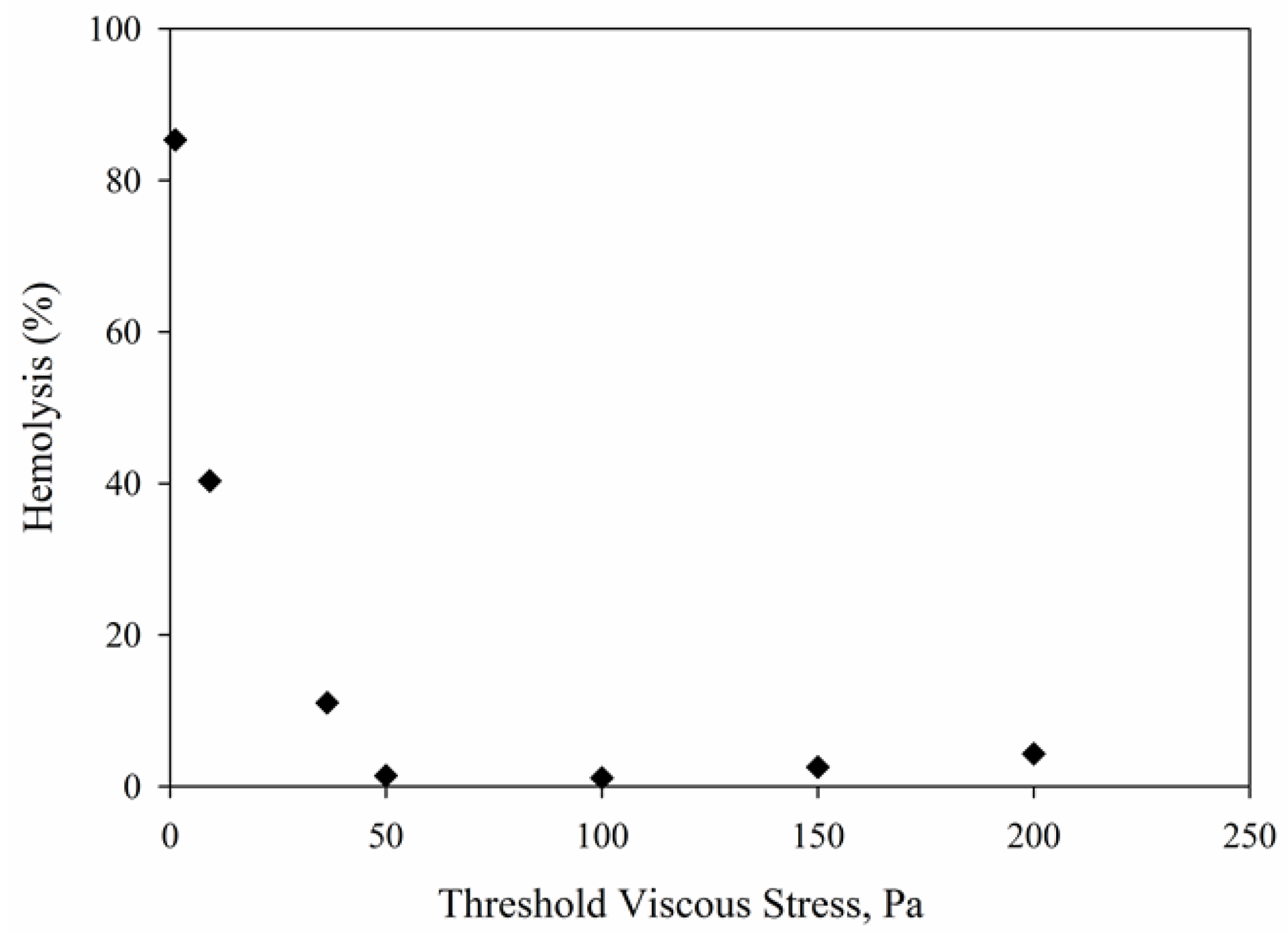
4.1. Reynolds Stress Distributions in Couette Viscometer
4.2. Viscous Stress Distributions in Couette Viscometerr
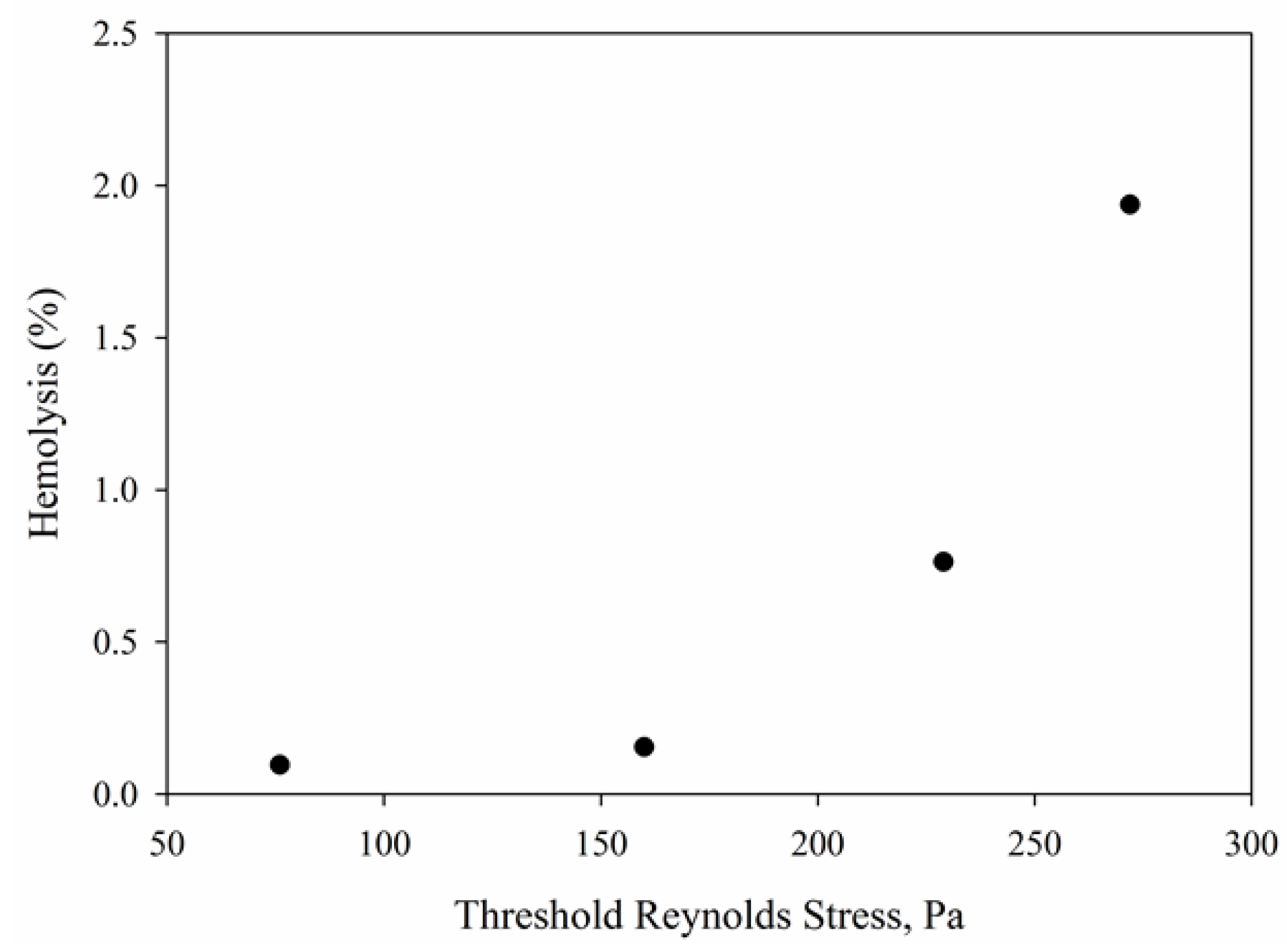
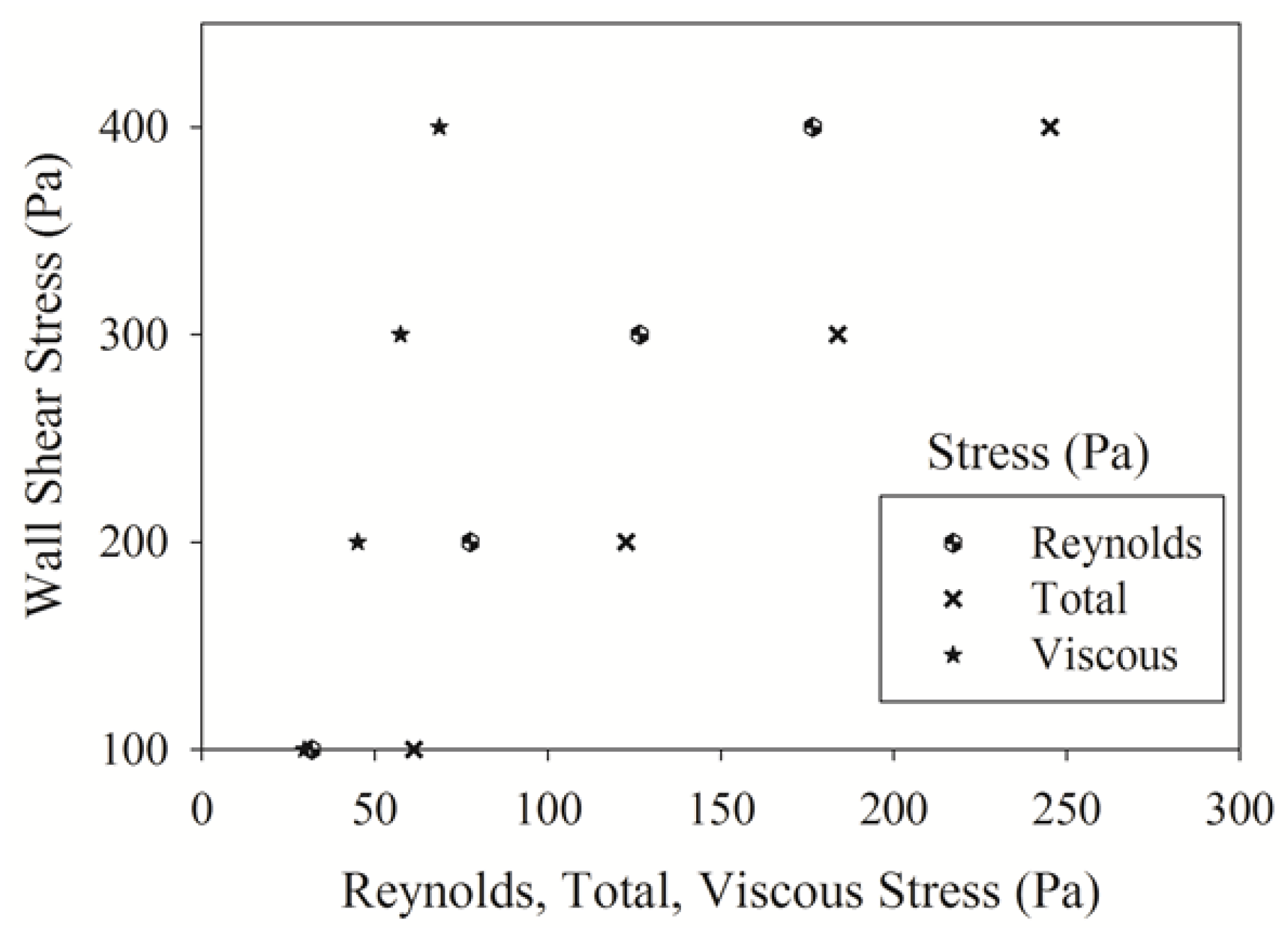
4.3. Reynolds Stress Distributions in Capillary Tube
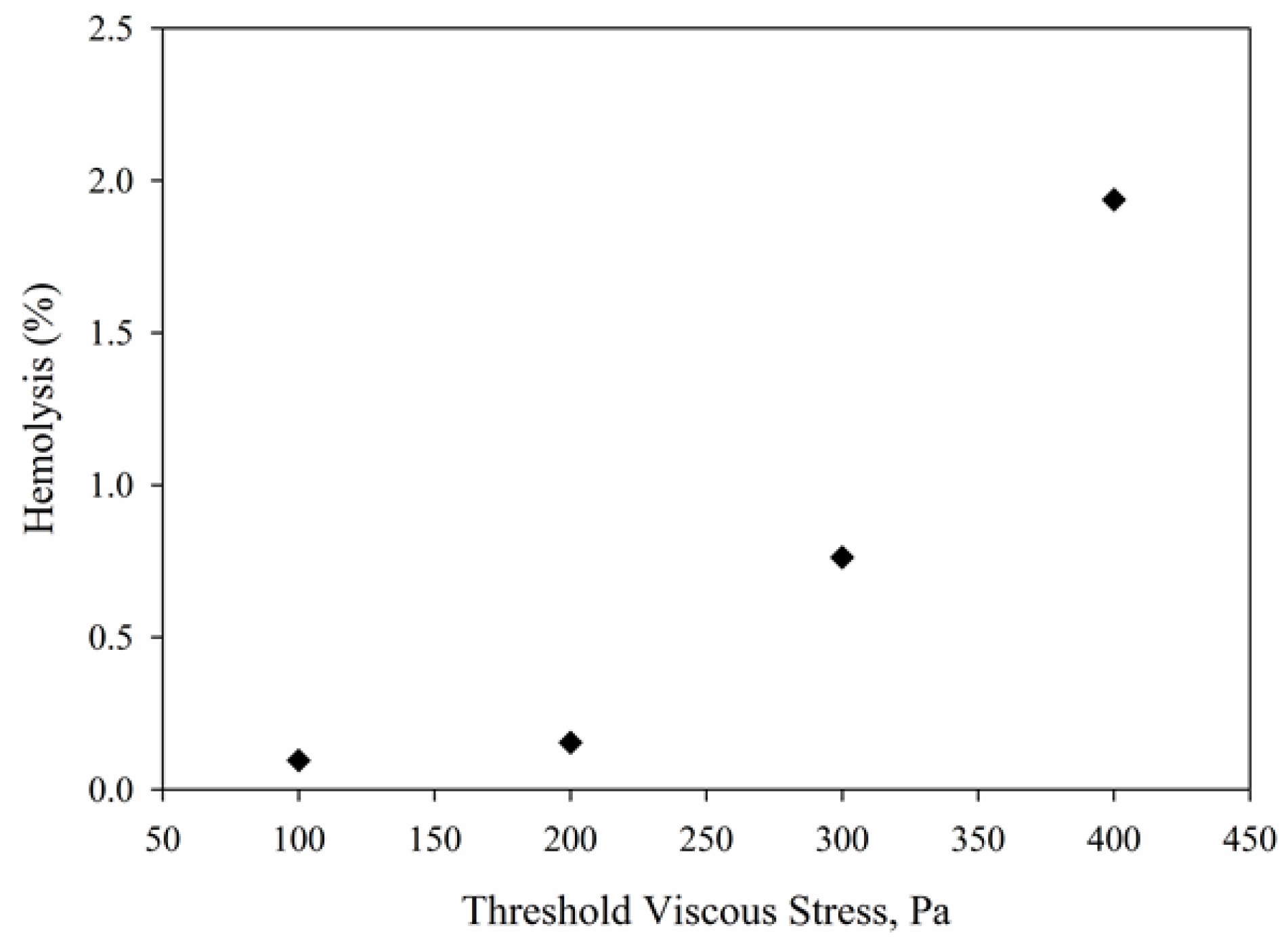
4.4. Viscous Stress Distributions in Capillary Tube
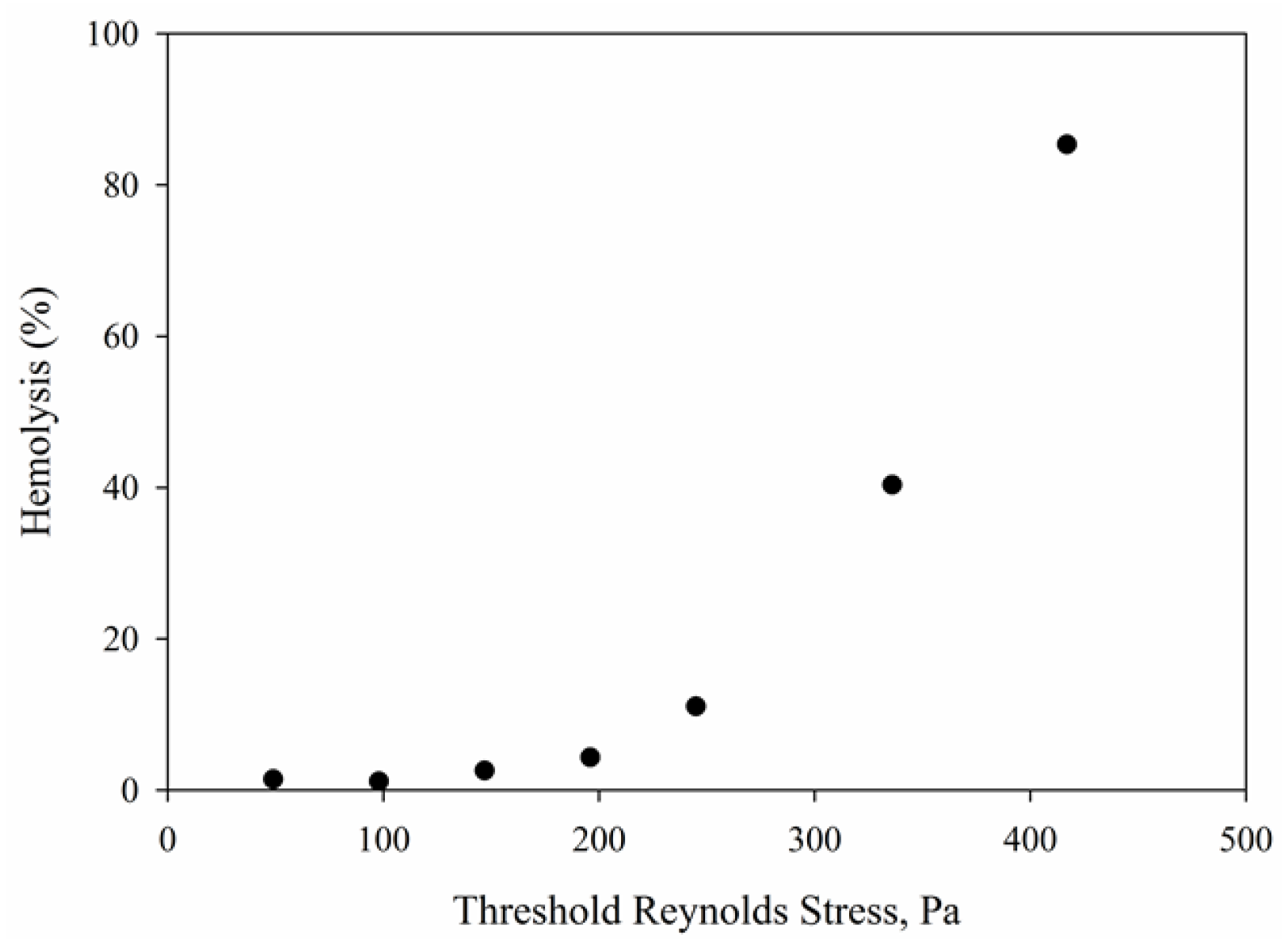
4.5. Hemolysis Calculations Using Power Models
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Fraser, K.H.; Taskin, M.E.; Griffith, B.P.; Wu, Z.J. The use of computational fluid dynamics in the development of ventricular assist devices. Med. Eng. Phys. 2011, 33, 263–280. [Google Scholar] [CrossRef] [PubMed]
- Antiga, L.; Steinman, D.A. Rethinking turbulence in blood. Biorheology 2009, 46, 77–81. [Google Scholar] [PubMed]
- Hund, S.J.; Antaki, J.F.; Massoudi, M. On the representation of turbulent stresses for computing blood damage. Int. J. Eng. Sci. 2010, 48, 1325–1331. [Google Scholar] [CrossRef] [PubMed]
- Kameneva, M.V.; Burgreen, G.W.; Kono, K.; Repko, B.; Antaki, J.F.; Umezu, M. Effects of turbulent stresses upon mechanical hemolysis: Experimental and computational analysis. ASAIO J. 2004, 50, 418–423. [Google Scholar] [CrossRef] [PubMed]
- Aziz, A.; Werner, B.C.; Epting, K.L.; Agosti, C.D.; Curtis, W.R. The cumulative and sublethal effetcs of turbulence on erythrocytes in a stirred-tank model. Ann. Biomed. Eng. 2007, 35, 2108–2120. [Google Scholar] [CrossRef] [PubMed]
- Bludszuweit, C. Three-dimensional numerical prediction of stress loading of blood particles in a centrifugal pump. Artif. Organs. 1995, 19, 590–596. [Google Scholar] [CrossRef] [PubMed]
- Leverett, L.B.; Hellums, J.D.; Alfrey, C.P.; Lynch, E.C. Red blood cell damage by shear stress. Biophys. J. 1972, 12, 257–273. [Google Scholar] [CrossRef]
- Blackshear, P.L. Mechanical Hemolysis in Flowing Blood; Prentice-Hall: Englewood Cliffs, NJ, USA, 1972. [Google Scholar]
- Grigioni, M.; Daniele, C.; Morbiducci, U.; D’Avenio, G.; Benedetto, G.D.; Barbaro, V. The power-law mathematical model for blood damage prediction: Analytical developments and physical inconsistencies. Artif. Organs 2004, 28, 467–475. [Google Scholar] [CrossRef] [PubMed]
- Heuser, G.; Opitz, R. A Couette viscometer for short time shearing of blood. Biorheology 1980, 17, 17–24. [Google Scholar] [PubMed]
- Zhang, T.; Taskin, M.E.; Fang, H.B.; Pampori, A.; Jarvik, R.; Griffith, B.P.; Wu, Z.J. Study of flow-induced hemolysis using novel Couette-type blood shearing devices. Artif. Organs 2011, 35, 1180–1186. [Google Scholar] [CrossRef] [PubMed]
- Marom, G.; Bluestein, D. Lagrangian methods for blood damage estimation in cardiovascular devices—How numerical implementation affects the results. Expert Rev. Med. Devices 2016, 13, 113–122. [Google Scholar] [CrossRef] [PubMed]
- Sheriff, J.; Soares, J.S.; Xenos, M.; Jesty, J.; Bluestein, D. Evaluation of shear-induced platelet activation models under constant and dynamic shear stress loading conditions relevant to devices. Ann. Biomed. Eng. 2013, 41, 1279–1296. [Google Scholar] [CrossRef] [PubMed]
- Soares, J.S.; Sheriff, J.; Bluestein, D. A novel mathematical model of activation and sensitization of platelets subjected to dynamic stress histories. Biomech. Model. Mechanobiol. 2013, 12, 1127–1141. [Google Scholar] [CrossRef] [PubMed]
- Goubergrits, L. Numerical modeling of blood damage: Current status, challenges and future prospects. Expert Rev. Med. Devices 2006, 3, 527–531. [Google Scholar] [CrossRef] [PubMed]
- Sutera, S.P.; Mehrjardi, M.H. Deformation and fragmentation of human red blood cells in turbulent shear flow. Biophys. J. 1975, 15, 1–10. [Google Scholar] [CrossRef]
- Burgreen, G.W.; Antaki, J.F.; Wu, Z.J.; Holmes, A.J. Computational fluid dynamics as a development tool for rotary blood pumps. Artif. Organs 2001, 25, 336–340. [Google Scholar] [CrossRef] [PubMed]
- Fraser, K.H.; Zhang, T.; Taskin, M.E.; Griffith, B.P.; Wu, Z.J. A quantitative comparison of mechanical blood damage parameters in Rotary Ventricular Assist Devices: Shear stress, exposure time, and hemolysis index. J. Biomech. Eng. 2012, 134, 081002. [Google Scholar] [CrossRef] [PubMed]
- Izraelev, V.; Weiss, W.J.; Fritz, B.; Newswanger, E.; Paterson, G.; Snyder, A.; Medvitz, R.B.; Cysyk, J.; Pae, W.E.; Hicks, D.; et al. A passively suspended Tesla pump left ventricular assist device. Am. Soc. Artif. Intern. Organs 2009, 55, 556–561. [Google Scholar] [CrossRef] [PubMed]
- Morsi, Y.S.; Yang, W.; Witt, P.J.; Ahmed, A.M.; Umezu, M. Numerical analysis of the flow characteristics of rotary blood pump. J. Artif. Organs 2001, 4, 54–60. [Google Scholar] [CrossRef]
- Nguyen, V.T.; Kuan, Y.H.; Chen, P.Y.; Ge, L.; Sotiropolous, F.; Yoganathan, A.P.; Leo, H.L. Experimentally validated hemodynamics simulations of mechanical heart valves in three dimensions. Cardiovasc. Eng. Technol. 2012, 3, 88–100. [Google Scholar] [CrossRef]
- Wu, J.; Paden, B.E.; Borovetz, H.S.; Antaki, J.F. Computational fluid dynamics analysis of blade tip clearances on hemodynamic performance and blood damage in a centrifugal ventricular assist device. Artif. Organs 2010, 34, 402–411. [Google Scholar] [CrossRef] [PubMed]
- Giersiepen, M.; Wurzinger, L.J.; Opitz, R.; Reul, H. Estimation of shear stress-related blood damage in heart valve prostheses-in vitro comparison of 25 aortic valves. Int. J. Artif. Organs 1990, 13, 300–306. [Google Scholar] [PubMed]
- Chapra, S.C.; Canale, R.P. Numerical Methods for Engineers; McGraw-Hill: New York, NY, USA, 2010. [Google Scholar]
- Ozturk, M.; O’Rear, E.A.; Papavassiliou, D.V. Hemolysis related to turbulent eddy size distributions using comparisons of experiments to computations. Artif. Organs 2015, 39, E227–E239. [Google Scholar] [CrossRef] [PubMed]
- Vitale, F.; Nam, J.; Turchetti, L.; Behr, M.; Raphael, R.; Annesini, M.C.; Pasquali, M. A multiscale, biophysical model of flow-induced red blood cell damage. Am. Inst. Chem. Eng. J. 2014, 60, 1509–1516. [Google Scholar] [CrossRef]
- Quinlan, N.J.; Dooley, P.N. Models of flow-induced loading on blood cells in laminar and turbulent flow, with application to cardiovascular device flow. Ann. Biomed. Eng. 2007, 35, 1347–1356. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.S.; Lu, P.C.; Chu, S.H. Turbulence characteristics downstream of bileaflet aortic valve protheses. J. Biomech. Eng. 1999, 122, 118–124. [Google Scholar] [CrossRef]
- Li, C.P.; Lo, C.W.; Lu, P.C. Estimation of viscous dissipative stresses induced by a mechanical heart valve using PIV data. Ann. Biomed. Eng. 2010, 38, 903–916. [Google Scholar] [CrossRef] [PubMed]
- Quinlan, N.J. Mechanical Loading of Blood Cells in Turbulent Flow; Springer: New York, NY, USA, 2014. [Google Scholar]
- Yen, J.H.; Chen, S.F.; Chern, M.K.; Lu, P.C. The effect of turbulent viscous shear stress on red blood cell hemolysis. J. Artif. Organs 2014, 17, 178–185. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.; Tatsumi, E.; Taenaka, Y. Experimental study on the Reynolds and viscous shear stress of bileaflet mechanical heart valves in a pneumatic ventricular assist device. ASAIO J. 2009, 55, 348–354. [Google Scholar] [CrossRef] [PubMed]
- Jones, S.A. A relationship between reynolds stresses and viscous dissipation: Implications to red cell damage. Ann. Biomed. Eng. 1995, 23, 21–28. [Google Scholar] [CrossRef] [PubMed]
- Sallam, A.M.; Hwang, N.H.C. Human red blood cell hemolysis in a turbulent shear flow: Contribution of Reynolds shear stresses. Biorheology 1984, 21, 783–797. [Google Scholar] [PubMed]
- Sallam, A.M. An Investigation of the Effect of Reynolds Shear Stress on Red Blood Cell Hemolysis. Ph.D. Thesis, University of Houston, Houston, TX, USA, 1982. [Google Scholar]
- Sallam, A.M.; Hwang, N.H.C. Influence of red blood cell concentrations on the measurement of turbulence using hot-film anemometer. J. Biomech. Eng. 1983, 105, 406–410. [Google Scholar] [CrossRef] [PubMed]
- Ellis, J.T.; Wick, T.M.; Yoganathan, A.P. Prosthesis-induced hemolysis: Mechanisms and quantification of shear stress. J. Heart Valve Dis. 1998, 7, 376–386. [Google Scholar] [PubMed]
- Grigioni, M.; Caprari, P.; Tarzia, A.; D’Avenio, G. Prosthetic heart valves’ mechanical loading of red blood cells in patients with hereditary membrane defects. J. Biomech. 2005, 38, 1557–1565. [Google Scholar] [CrossRef] [PubMed]
- Boehning, F.; Mejia, T.; Schmitz-Rode, T.; Steinseifer, U. Hemolysis in a laminar flow-through Couette shearing device: An experimental study. Artif. Organs 2014, 38, 761–765. [Google Scholar] [CrossRef] [PubMed]
- Paul, R.; Apel, J.; Klaus, S.; Schugner, F.; Schwindke, P.; Reul, H. Shear stress related blood damage in laminar couette flow. Artif. Organs 2003, 27, 517–529. [Google Scholar] [CrossRef] [PubMed]
- Bacher, R.P.; Williams, M.C. Hemolysis in capillary flow. J. Lab. Clin. Med. 1970, 76, 485–496. [Google Scholar] [PubMed]
- ANSYS Inc. ANSYS Fluent 14.0: Theory Guide; ANSYS Inc.: Canonsburg, PA, USA, 2011. [Google Scholar]
- Ge, L.; Dasi, L.P.; Sotiropolous, F.; Yoganathan, A.P. Characterization of hemodynamic forces induced by mechanical heart valves: Reynolds vs. viscous stresses. Ann. Biomed. Eng. 2008, 36, 276–297. [Google Scholar] [CrossRef] [PubMed]
- Puri, A.N.; Kuo, C.Y.; Chapman, R.S. Turbulent diffusion of mass in circular pipe flow. Appl. Math. Model. 1983, 7, 135–138. [Google Scholar] [CrossRef]
- Roberts, P.J.W.; Webster, D.R. Turbulent Diffusion. In Environmental Fluid Mechanics: Theories and Applications; Shen, H.H., Ed.; American Society of Civil Engineers: Reston, VA, USA, 2002. [Google Scholar]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena, 2nd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2002. [Google Scholar]
- Davidson, P.A. Turbulence: An Introduction for Scientists and Engineers; Oxford University Press: New York, NY, USA, 2004. [Google Scholar]
- Pope, S.B. Turbulent Flows; Cambridge University Press: New York, NY, USA, 2000. [Google Scholar]
- Apel, J.; Neudel, F.; Reul, H. Computational fluid dynamics and experimental validation of a microaxial blood pump. ASAIO J. 2001, 47, 552–558. [Google Scholar] [CrossRef] [PubMed]
- Chua, L.P.; Song, G.; Yu, S.C.M.; Lim, T.M. Computational fluid dynamics of gap flow in a biocentrifugal blood pump. Artif. Organs 2005, 29, 620–628. [Google Scholar] [CrossRef] [PubMed]
- Mitoh, A.; Yano, T.; Sekine, K.; Mitamura, Y.; Okamoto, E.; Kim, D.W.; Yozu, R.; Kawada, S. Computational fluid dynamics analysis of an intra-cardiac axial flow pump. Artif. Organs 2003, 27, 34–40. [Google Scholar] [CrossRef] [PubMed]
- Schenkel, A.; Deville, M.O.; Sawley, M.L. Flow simulation and hemolysis modeling for a blood centrifuge device. Comput. Fluids 2013, 86, 185–198. [Google Scholar] [CrossRef]
- Yano, T.; Sekine, K.; Mitoh, A.; Mitamura, Y.; Okamoto, E.; Kim, D.W.; Nishimura, I.; Murabayashi, S.; Yozu, R. An estimation method of hemolysis within an axial flow blood pump by computational fluid dynamics analysis. Artif. Organs 2003, 27, 920–925. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Zhan, Z.; Gui, X.M.; Sun, H.S.; Zhang, H.; Zheng, Z.; Zhou, J.Y.; Zhu, X.D.; Li, G.R.; Hu, S.S.; et al. Design optimization of an axial blood pump with computational fluid dynamics. ASAIO J. 2008, 54, 150–155. [Google Scholar] [CrossRef] [PubMed]
- Al-Azawy, M.; Turan, A.; Revell, A. Investigating the use of turbulence models for flow investigations in a positive displacement ventricular assist devices. In Proceedings of the 6th European Conference of the International Federation for Medical and Biological Engineering, Dubrovnik, Croatia, 7–11 September 2014; pp. 395–398.
- Carswell, D.; McBride, D.; Croft, N.; Slone, A.; Croft, N.; Foster, G. A CFD model for the prediction of haemolysis in micro axial left ventricular assist devices. Appl. Math. Model. 2013, 37, 4199–4207. [Google Scholar] [CrossRef]
- Kido, K.; Hoshi, H.; Watanabe, N.; Kataoka, H.; Ohuchi, K.; Asama, J.; Shinshi, T.; Yoshikawa, M.; Takatani, S. Computational fluid dynamics analysis of the Pediatric tiny centrifugal blood pump (TinyPump). Artif. Organs 2006, 30, 392–399. [Google Scholar] [CrossRef] [PubMed]
- Song, X.; Wood, H.G.; Day, S.W.; Olsen, D.B. Studies of turbulence models in a computational fluid dynamics model os a blood pump. Artif. Organs 2003, 27, 935–937. [Google Scholar] [CrossRef] [PubMed]
- Chin, C.; Monty, J.P.; Ooi, A. Reynols number effects in DNS of pipe flow and comparison with channels and boundary layers. Int. J. Heat Fluid Flow 2014, 45, 33–40. [Google Scholar] [CrossRef]
- Pirro, D.; Quadrio, M. Direct numerical simulation of turbulent Taylor-Couette flow. Eur. J. Mech. B Fluids 2008, 27, 552–566. [Google Scholar] [CrossRef]



| Shear Stress (Pa) | Rotation Rate (rad/s) | Experimental Hemolysis (%) | Taylor Number |
|---|---|---|---|
| 50 | 130 | 1.403 | 2725 |
| 100 | 196 | 1.1364 | 4108 |
| 150 | 240 | 2.5448 | 5030 |
| 200 | 300 | 4.2883 | 6288 |
| 250 | 340 | 11.0547 | 7126 |
| 350 | 400 | 40.3351 | 8383 |
| 450 | 460 | 85.3609 | 9641 |
| Shear Stress (Pa) | Flow Rate (L/min) | Experimental Hemolysis (%) | Reynolds Number | Exposure Times (s) |
|---|---|---|---|---|
| 100 | 0.15 | 0.0954 | 2783 | 0.0230 |
| 200 | 0.23 | 0.1538 | 4253 | 0.0144 |
| 300 | 0.30 | 0.7625 | 5313 | 0.0102 |
| 400 | 0.36 | 1.9375 | 6242 | 0.0086 |
| Root Mean Square Error | Couette Viscometer | Capillary Tube |
|---|---|---|
| k-ε Model | 0.39 | 1.32 |
| k-ω SST Model | 0.65 | 1.04 |
| Power Law Models | Type of Stress | Calculated HI for τw = 100 Pa | Calculated HI for τw = 200 Pa | Calculated HI for τw = 300 Pa | Calculated HI for τw = 400 Pa | Standard Error [24] |
|---|---|---|---|---|---|---|
| Experimental Hemolysis Data [4] | τw | 0.0954 | 0.1538 | 0.7625 | 1.9375 | 0 |
| Giersiepen et al. [23] | τRe | 0.4106 | 3.9302 | 13.8268 | 32.0492 | 6.6658 |
| τt | 2.0132 | 11.8869 | 34.1216 | 70.8037 | 14.8321 | |
| τv | 0.3455 | 1.0587 | 2.0452 | 3.2602 | 0.2485 | |
| τw | 6.5674 | 38.7766 | 111.3085 | 230.9699 | 49.3428 | |
| Heuser et al. [10] | τRe | 0.0051 | 0.0335 | 0.0963 | 0.1944 | 0.3861 |
| τt | 0.0188 | 0.0833 | 0.2028 | 0.3735 | 0.3513 | |
| τv | 0.0044 | 0.0114 | 0.0199 | 0.0296 | 0.4224 | |
| τw | 0.0497 | 0.2208 | 0.5372 | 0.9897 | 0.2126 | |
| Zhang et al. [11] | τRe | 0.0514 | 0.3568 | 1.065 | 2.1868 | 0.0557 |
| τt | 0.1905 | 0.8886 | 2.2428 | 4.2034 | 0.469 | |
| τv | 0.0445 | 0.121 | 0.2203 | 0.3323 | 0.3686 | |
| τw | 0.5049 | 2.3553 | 5.9447 | 11.1413 | 1.9226 | |
| Fraser et al. [18] | τRe | 0.0043 | 0.0274 | 0.0775 | 0.1546 | 0.3947 |
| τt | 0.0155 | 0.0673 | 0.1614 | 0.2943 | 0.3677 | |
| τv | 0.0037 | 0.0094 | 0.0164 | 0.0241 | 0.4234 | |
| τw | 0.0406 | 0.176 | 0.4217 | 0.7692 | 0.267 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ozturk, M.; O’Rear, E.A.; Papavassiliou, D.V. Reynolds Stresses and Hemolysis in Turbulent Flow Examined by Threshold Analysis. Fluids 2016, 1, 42. https://doi.org/10.3390/fluids1040042
Ozturk M, O’Rear EA, Papavassiliou DV. Reynolds Stresses and Hemolysis in Turbulent Flow Examined by Threshold Analysis. Fluids. 2016; 1(4):42. https://doi.org/10.3390/fluids1040042
Chicago/Turabian StyleOzturk, Mesude, Edgar A. O’Rear, and Dimitrios V. Papavassiliou. 2016. "Reynolds Stresses and Hemolysis in Turbulent Flow Examined by Threshold Analysis" Fluids 1, no. 4: 42. https://doi.org/10.3390/fluids1040042
APA StyleOzturk, M., O’Rear, E. A., & Papavassiliou, D. V. (2016). Reynolds Stresses and Hemolysis in Turbulent Flow Examined by Threshold Analysis. Fluids, 1(4), 42. https://doi.org/10.3390/fluids1040042