1. Introduction
Kinematic analysis of geophysically relevant fluid flows has in the past several decades been elevated by dynamical-systems-based methods that enable identification of key material contours or surfaces central to transport and stirring processes. In some cases, the contours are touted as barriers to material transport, and although
any material contour is by definition a barrier, there are some that are particularly significant. For example, a long-lived, coherent eddy is often surrounded by a closed material contour that undergoes minimal material stretching [
1,
2,
3]. The contour does not undergo filamentation or roll-up and therefore can be used to objectively define a boundary that contains fluid that is trapped by the eddy and perhaps transported over large distances [
4]. Another set of significant objects consists of the stable and unstable (attracting and repelling) material manifolds of hyperbolic trajectories. Material manifolds provide a framework for
lobe dynamics, perhaps the most beautiful method of Lagrangian transport analysis. Apparently first applied to the problem of fluid transport by [
5,
6] this approach provides for the visualization and quantification of material transport between qualitatively different regions of a time-varying flow field.
We will present an overview of contributions made roughly over the past two decades, focusing on those that have impacted the field of physical oceanography. The review is not intended to be exhaustive or mathematically rigorous, and the reader should consult the references, particularly [
7,
8], for more formal treatments. The intent of the review is to emphasize accomplishments and limitations, and the latter will lead us to consider an alternative approach that combines elements of Lagrangian analysis with a desire to comprehend property fluxes other than fluid material.
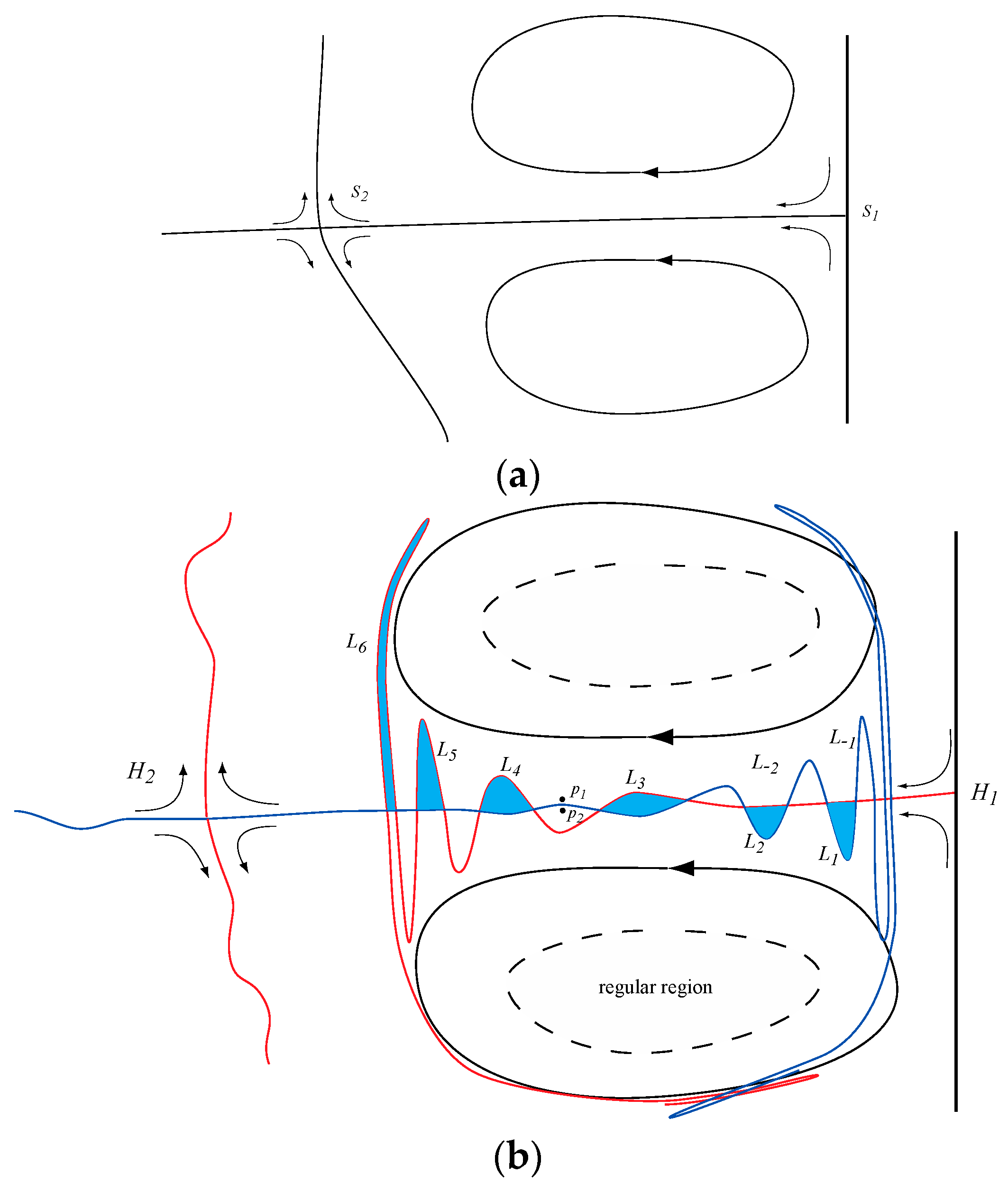
Perhaps the most enduring example of Lagrangian transport analysis in physical oceanography is the computation of exchange between two counter-rotating gyres, depicted in
Figure 1a as the cyclonic and anticyclonic members of a dipole or double-gyre system. In a steady configuration, two hyperbolic stagnation points
S1 and
S2 are connected by a streamline that separates the two members. If a moderately weak, time-periodic disturbance is added to the velocity field,
S1 and
S2 will survive in the form of moving hyperbolic trajectories
H1 and
H2, for which the surrounding flow is, on average, convergent in one direction and divergent in another (
Figure 1b). For example, the flow surrounding
H1 will tend to be convergent, on average, in the along-shore direction and divergent in the offshore direction. The positions of
H1 and
H2 will generally vary with time, but if the disturbance is not too large, both points will linger in the neighborhood of the original stagnations points. If one were to continuously introduce dye into the vicinity of
H1, it would be attracted to
H1 in the along-shore direction, but would be repelled in the offshore direction forming a long streak. This streak would be an approximation of the unstable manifold (also called the “outgoing” manifold) consisting of material that diverges from
H1 (approaches
H1 in backward time). The unstable manifold of
H1 is depicted by red contour in
Figure 1b. Similarly, stable and unstable manifolds can be defined for
H2 as material, time-dependent curves consisting of fluid elements that approach
H2 asymptotically in forward or backward time. All of the manifolds evolve over time and
Figure 1b is just a snap shot, but if the time-dependence is periodic the
shapes will recur periodically.
In the steady case (
Figure 1a) the unstable manifold of
S1 is also a stable manifold of
S2 and can be thought of as a boundary separating the cyclonic and anticyclonic members of the dipole. In the unsteady case, these manifolds are distinct, and it is common for the unstable manifold of
H1 to intersect the stable manifold of
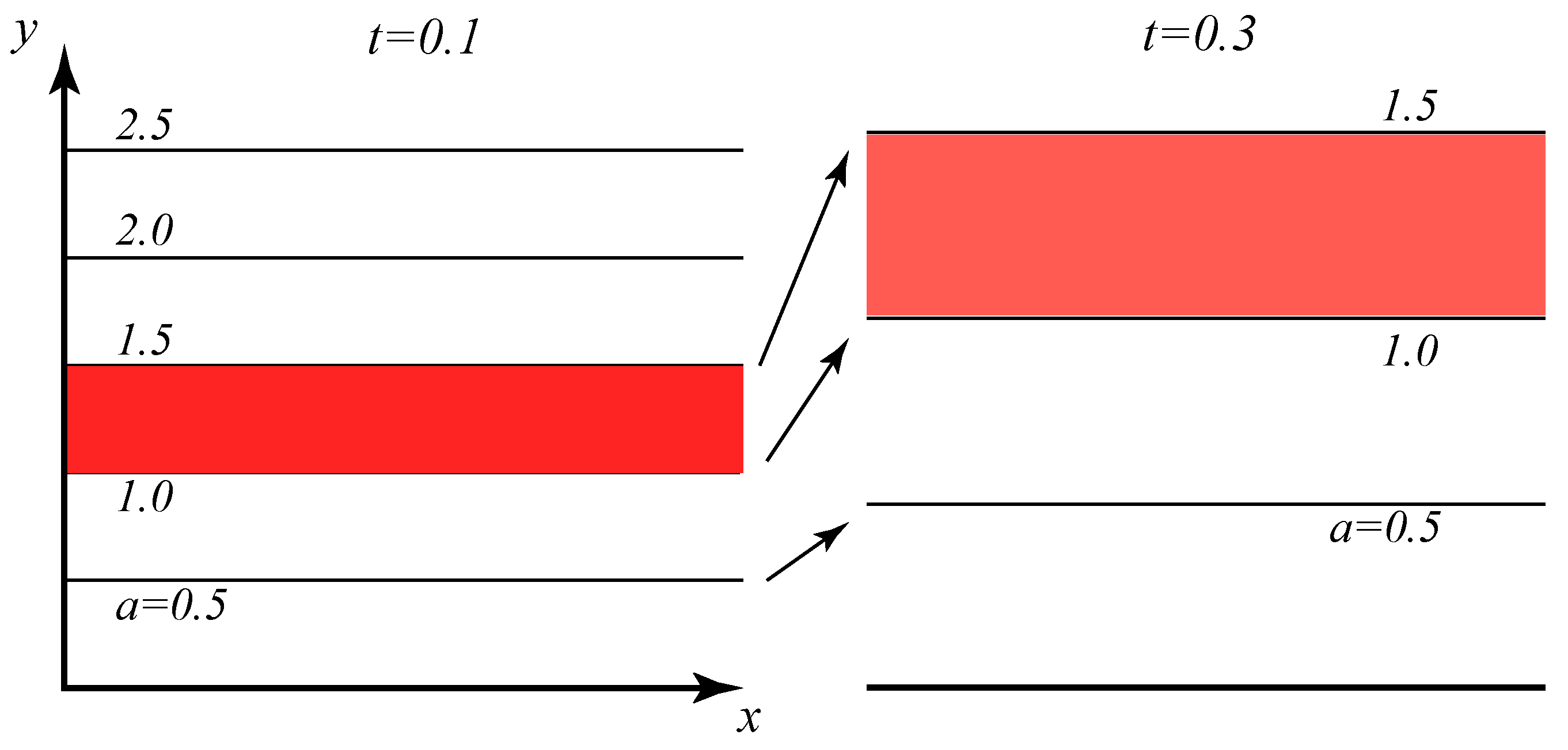
H2. One can identify lobes of fluid
L1,
L2 whose boundaries consist of segments of the intersecting manifolds. As the flow evolves, the lobe
L1 will move from right to left, continuing to be bounded by the same sections of the material curves. If the time dependence is periodic, the shapes of the curves will recur after a single period, and the fluid in
L1 will have moved into the space depicted as
L2 in the figure. After another period the fluid will have moved to the space occupied by
L3 and so on, so there is clearly a transport from the cyclone to the anticyclone. In the same manner, fluid in lobe
L−1 evolves into
L−2 and so on, defining a transport process from the anticyclone to the cyclone. This mechanism leads to exchange between the two gyres, and the lobes are therefore called turnstile lobes. As implied in
Figure 1, the lobes themselves tend to be continuously stretched and folded, so that property gradients within are amplified and irreversible property exchange through diffusion is enhanced. In time-periodic systems, the motion of fluid parcels is often described by a Poincare’ map, in which discrete parcel positions are plotted at the end of each period. In this description, the manifolds in
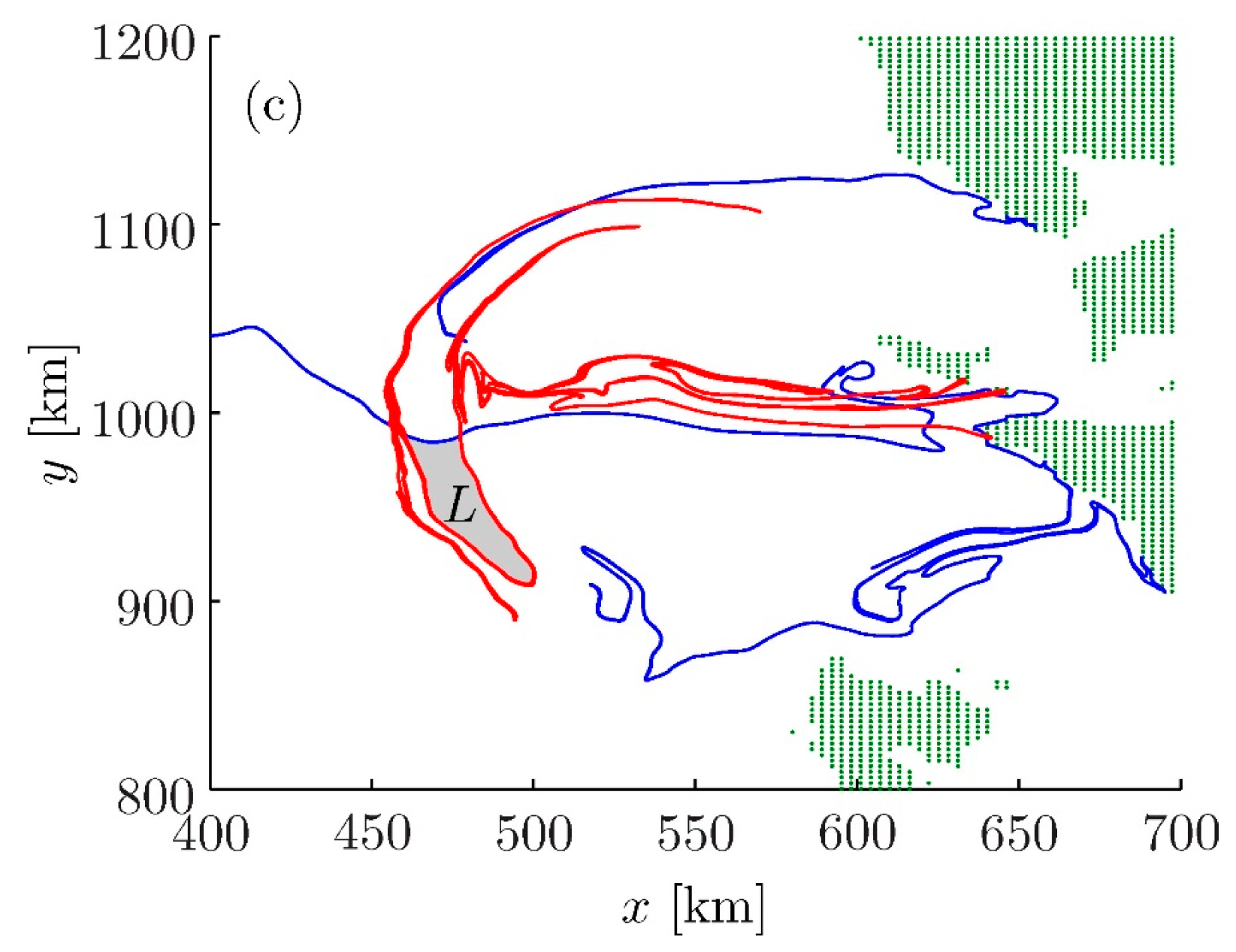
Figure 1b remain frozen, fluid parcels remain on the fixed manifolds as they are mapped from one position to the next, and fluid blobs are mapped from one lobe to another. We prefer to think about the manifolds as time-continuous objects since this picture is relevant to the time aperiodic case, which can be similar in concept and geometry. An example from a numerical simulation of a strongly aperiodic, surface dipole in the Philippine Seas [
9] appears in
Figure 2.
Lobe analysis has been applied to a number of oceanographically relevant flow fields including meandering jets [
10], dipoles and counter rotating gyres [
11,
12,
13,
14,
15], boundary-trapped recirculations [
16], and breaking Rossby waves [
17]. In most cases the velocity field is assumed to be two-dimensional and divergence free, which limits the zoology of stagnation points to just two types: hyperbolic and elliptic. The analysis has been applied [
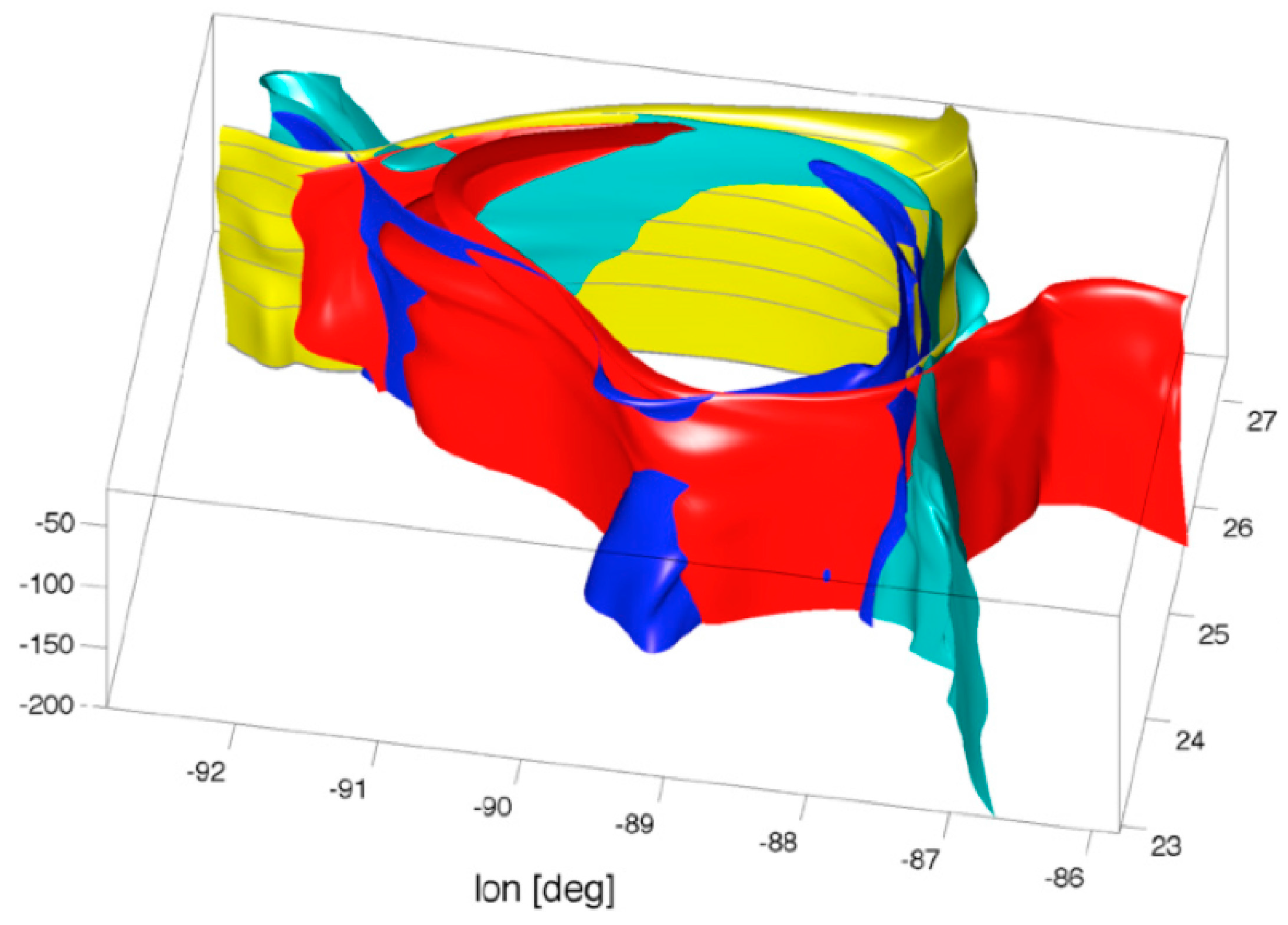
18] to a three-dimensional model of a Gulf of Mexico Loop Current eddy, but the weakness of the vertical velocity implies that the horizontal velocity field is approximately nondivergent at each depth, enabling the authors to construct a 3D picture by stacking a set of 2D analyses at different horizontal levels. The finite time material manifolds now consist of intersecting surfaces (
Figure 3), with finite volume lobes of fluid trapped between. Due to the lengthy analysis involved in making just a single snapshot of the lobes, the authors did not attempt any transport calculations.
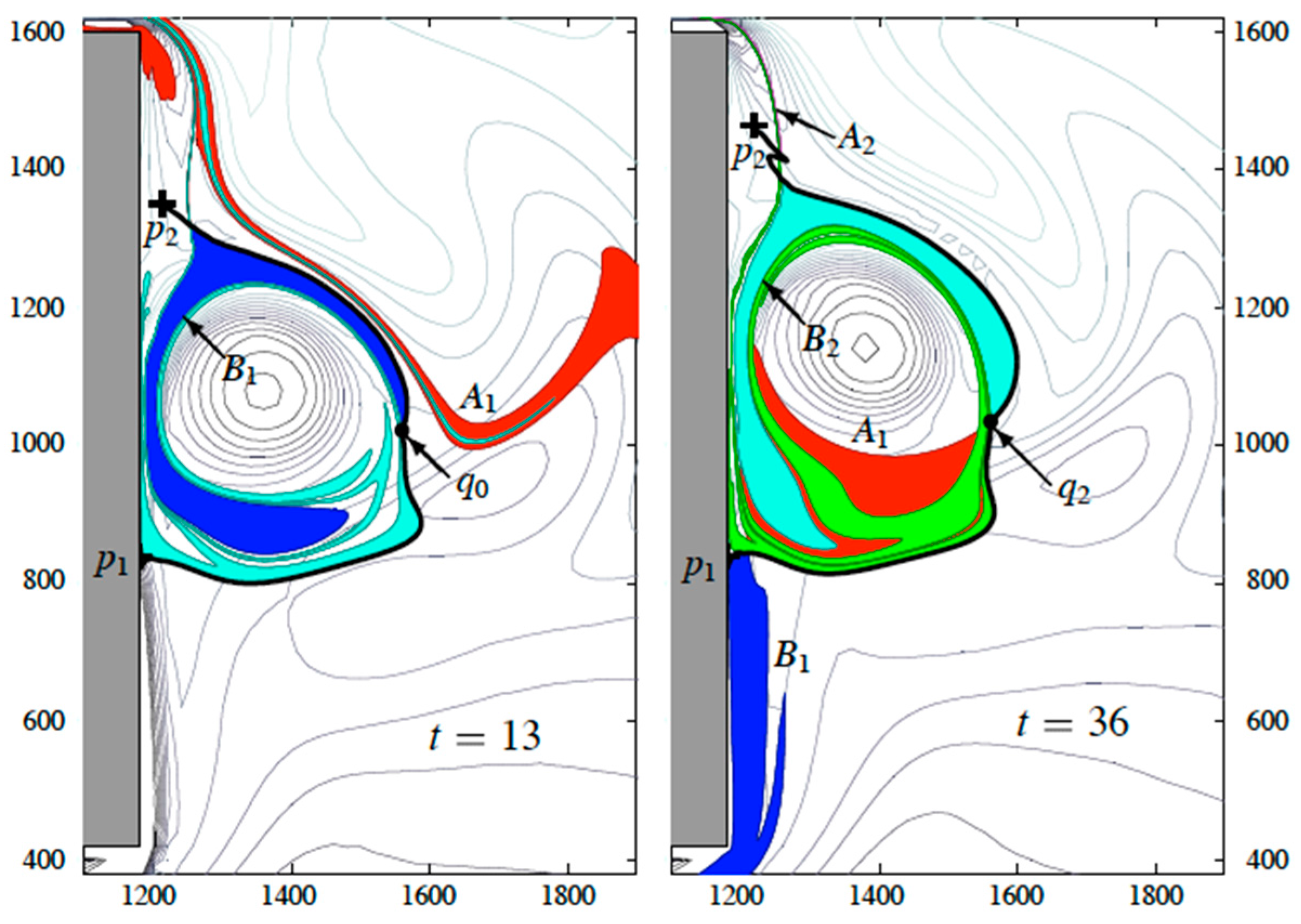
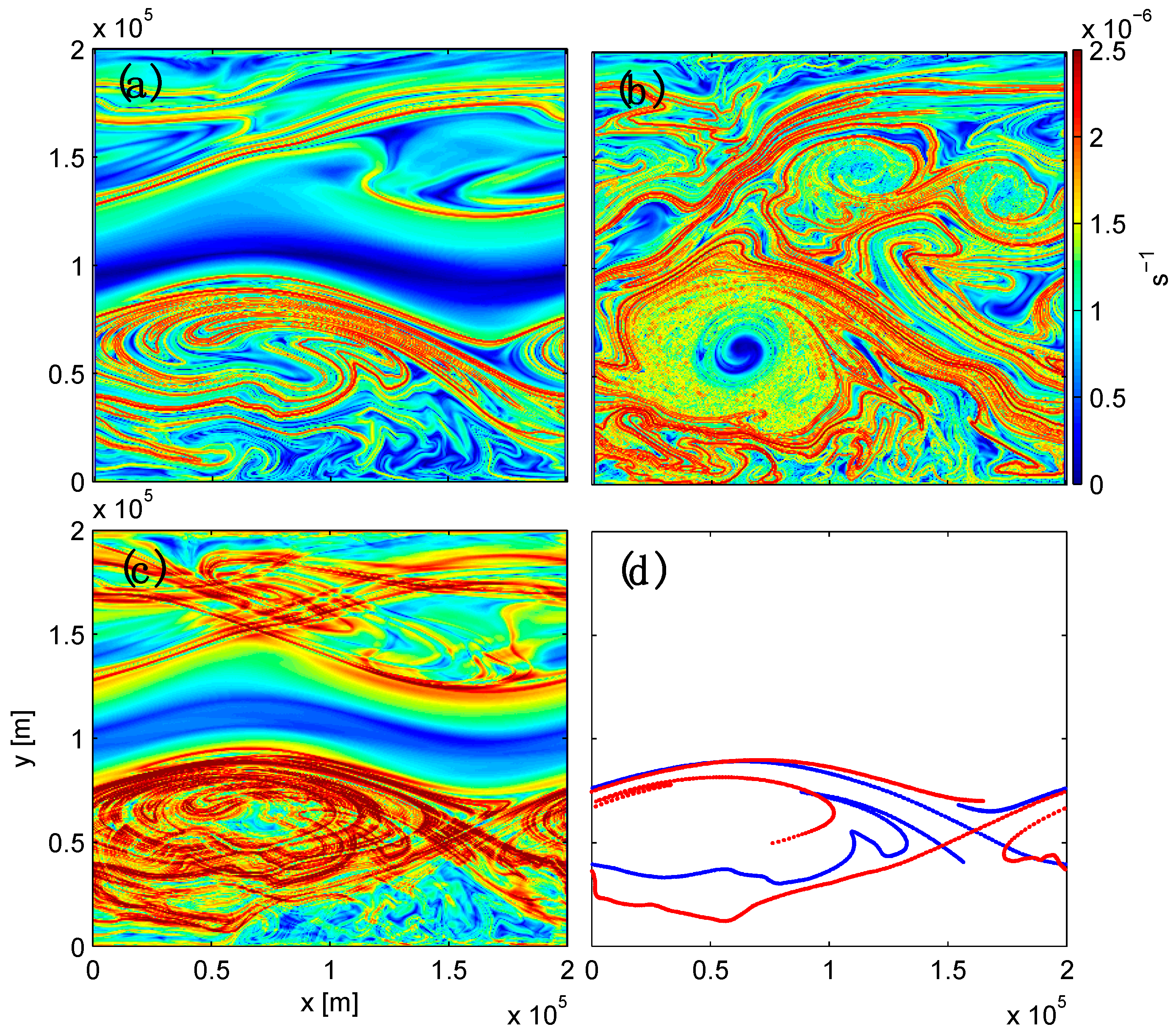
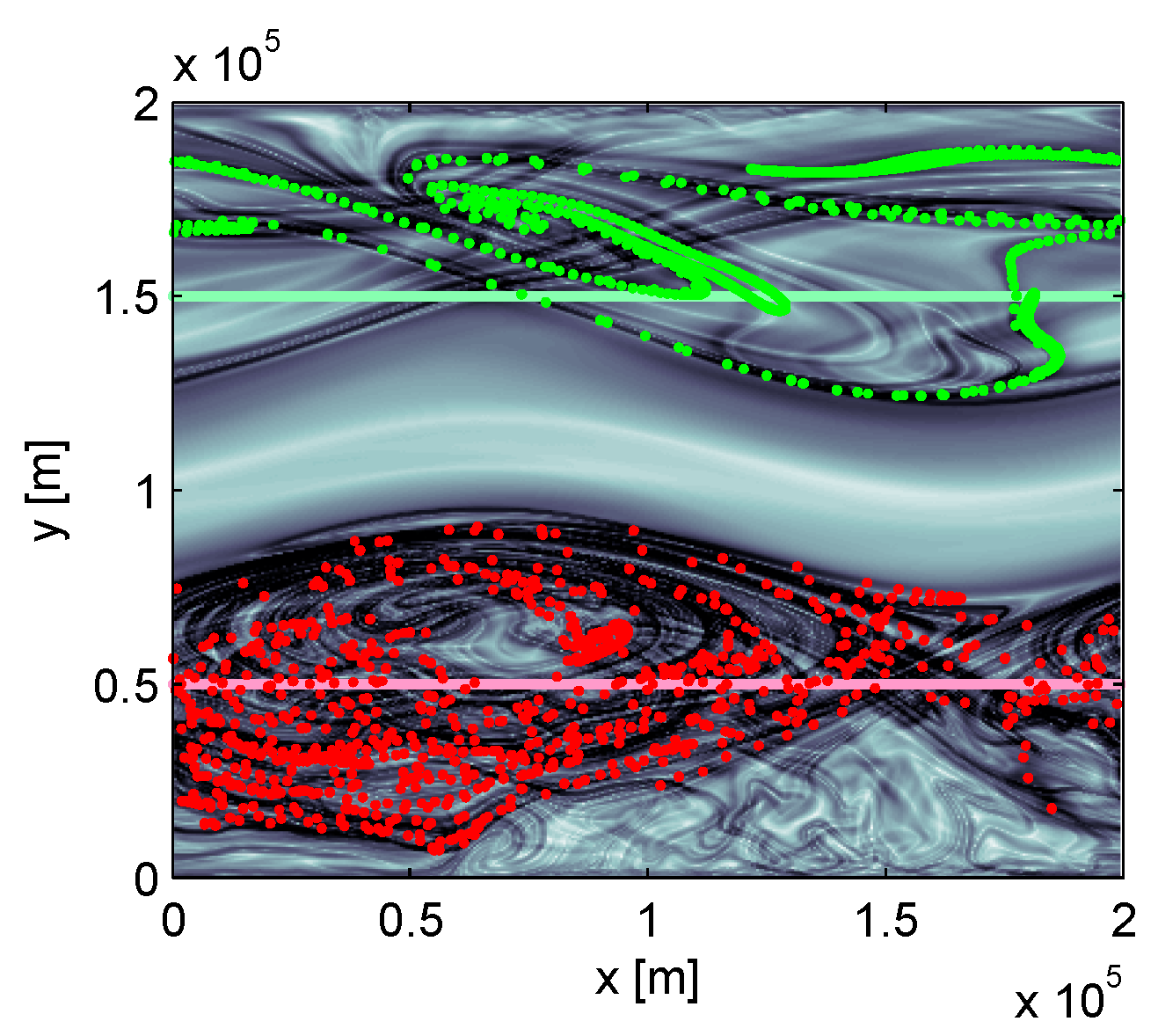
When the velocity fields are known only over finite time, or when strong hyperbolicity is limited to a finite time window, objects similar to stable and unstable material manifolds may still be found. As pointed out in [
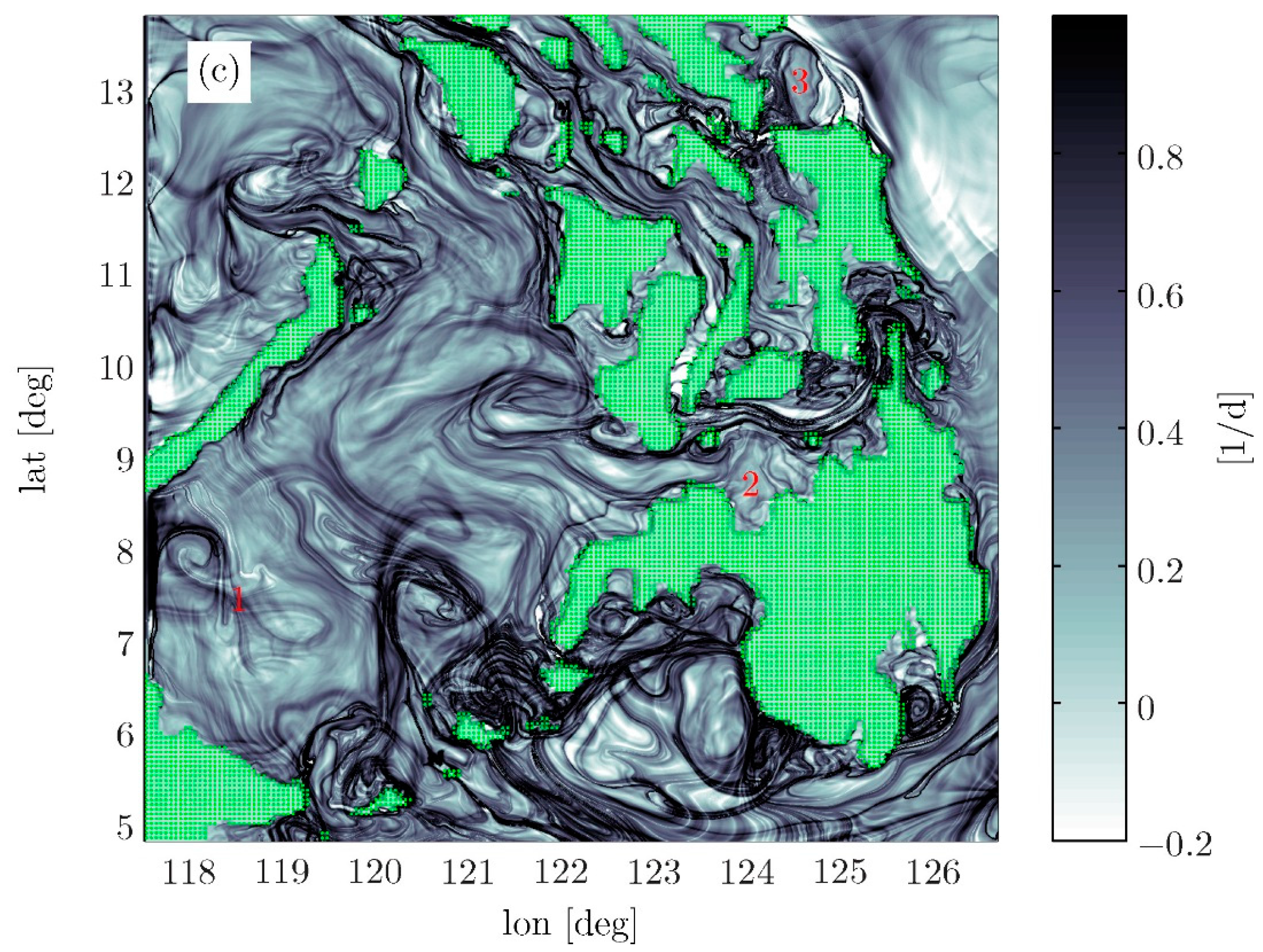
19], persistent hyperbolicity can occur when the Eulerian time scale of the flow is much longer than the Lagrangian time scale. This time scale separation can occur in the so-called chaotic advection regime, when the flow field is dominated by long-lived coherent structures, often in the form of eddies. For example, a concentrated hyperbolic region can form between eddies of like sign and may persist over many eddy winding times (see point “1” in
Figure 4). If a passive tracer is introduced in this region, it will experience contraction in one direction and expulsion in another direction, all in analogy to the stable and unstable directions of a hyperbolic trajectory. Thin material streaks of tracer that emanate from the hyperbolic region in the unstable direction in forward time (or in the stable direction in reverse time) exhibit behavior similar to that typical for invariant manifolds. These objects are collectively known as hyperbolic Lagrangian Coherent Structures [
20], or LCS, that form a skeleton or template for stirring and transport processes due to their attractive/repelling properties. In this paper, we will use the term “finite-time manifolds” loosely to refer to the hyperbolic-type LCS that serve as finite-time analogs of infinite-time invariant manifolds from classical dynamical systems theory. In addition to finite-time manifolds (hyperbolic LCS), relevant finite-time analogs of infinite-time material objects from dynamical systems theory include closed contours defining the boundaries of coherent eddies (elliptic LCS), which are or analogs of KAM tori, and material barriers defined by minimal Lagrangian shear (parabolic LCS), which are analogs of shearless trajectories (e.g., the central axis of a jet) and can exhibit strong stability under perturbation in certain types of Hamiltonian systems [
1]. An example of the latter can be found in [
21]. Even when hyperbolic-type LCS can reasonably be defined in finite time, it may or may not be advantageous to perform a lobe analysis. However, the finite-time LCS themselves still yield valuable information as to which regions of the flow field are being most rapidly stirred and whether barriers to chaotic transport exist. An example of success comes from Monterey Bay [
22], where the circulation has a strong tidal component. Maps of LCS yield information about how the bay is flushed. Other successful applications include the Adriatic Sea [
14], where the circulation is dominated by three coherent gyres, and the Phillipine Sea [
9] where the transport of nutrients from Manila Bay into an offshore dipole can be tracked using manifold-type analysis.
As an example of the type of information that can be gained, consider a plot of 7-day backward and forward, finite-time Lyapunov exponents (FTLEs), computed using a model of the Philippine Seas (
Figure 4) and based on the surface velocity field. The ridges of the FTLE fields are often used to approximate finite-time material manifolds [
20,
23]. (Though regions of strong shear can sometimes result in FTLE ridges that are not associated with hyperbolic-type LCSs, these cases are generally rare in realistic oceanic flows. See [
1] for a more rigorous approach to identifying LCS.) Areas that are densely covered by intersecting curves indicate regions of rapid stretching and folding of material whereas regions that are clear tend to be more slowly stirring, isolated and more regular. Examples of the latter include the interiors of “Figure-eight” separatrix formed by two nearby anticyclonic eddies (marked “1”) and two topographically constrained recirculations (marked “2” and “3”). A more recent approach [
24] to the identification of mixing zones, based on averages of hyperbolicity along trajectories, has been applied to an oil spill in the Gulf of Mexico.
Much of the current interest in Lagrangian dynamical systems analysis is focused on elliptic LCS, closed material contours that exhibit uniform stretching and that can define the boundaries of various types of vortices. The underlying idea is that a boundary that rolls up and develops filaments would undergo non-uniform stretching. Variational methods for computing these objects have been developed [
1,
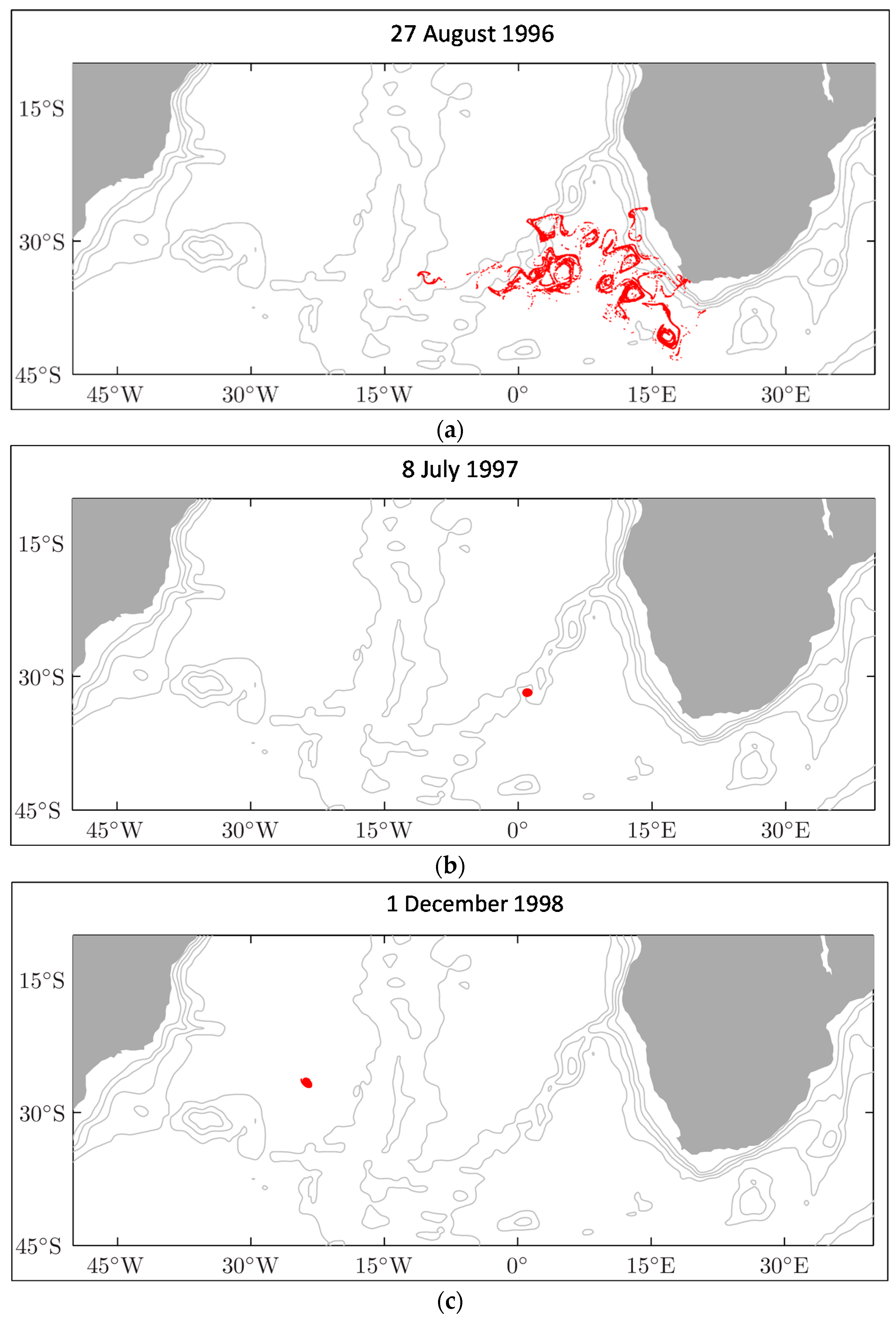
2] and applied to features such as S. Atlantic surface eddies generated in the South African “caldron” [
4]. By defining and computing bounding elliptical contours, the authors have identified eddies that can remain coherent over thousands of km (
Figure 5). Other Lagrangian approaches for the identification and tracking of coherent eddies include transfer operator methods [
25], in which the most coherent sets of trajectories starting from a grid of initial positions are computed. This approach has been successfully used to track 3D Agulhas eddies in numerical simulations [
26]. Koopman mode analysis [
27,
28] also has the potential to identify features that are coherent in a Lagrangian sense. Here, time averages of fixed scalar fields are taken along individual trajectories and clustering algorithms are used to identify those trajectories most similar in terms of Lagrangian averages. Other measures that potentially identify LCS include trajectory arclength [
29,
30] and other measures of trajectory complexity [
30]. There is always debate as to whether objects identified by various methods are material following. If the approach is based on a frame-dependent measure such as Eulerian vorticity, then there is an obligation to demonstrate that the computed object is, in fact, Lagrangian.
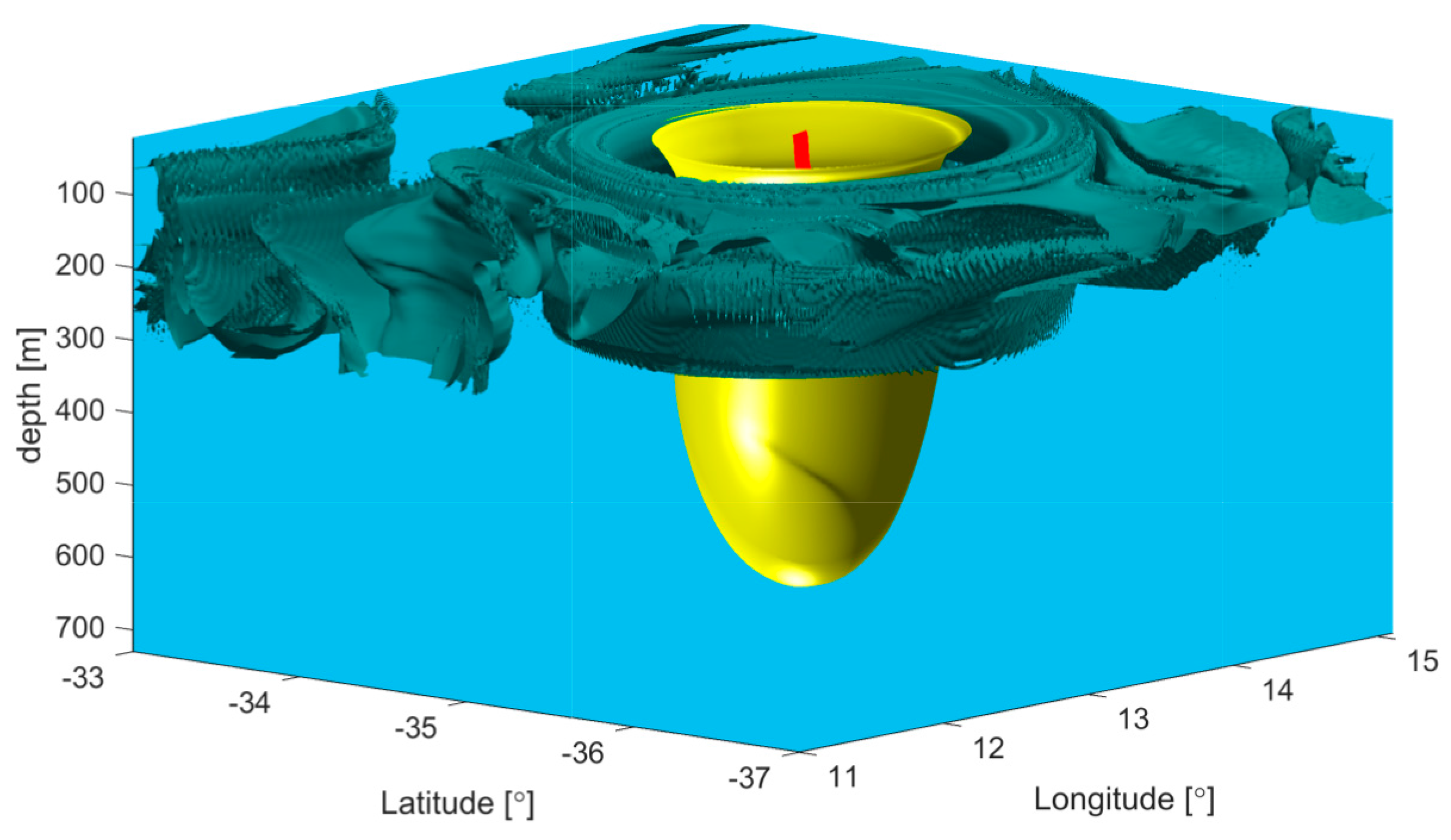
Although elliptic LCS identify coherent structures in the flow field, there is no guarantee that these structure are eddies, at least not in the sense that they are identified with anomalously high vorticity. This has led to a search for boundaries that remain coherent and that are identified by high anomalous Lagrangian-averaged vorticity deviation [
15] (and also see [
31]). An example of a conical boundary surrounding a surface vortex a 3D simulation of the upper ocean is shown in
Figure 6.
Recent attention has been directed towards a better understand of the barriers and chaotic regions of fully 3D flows that have a vertical velocity (
w) that is significant in the sense that vertical derivative of
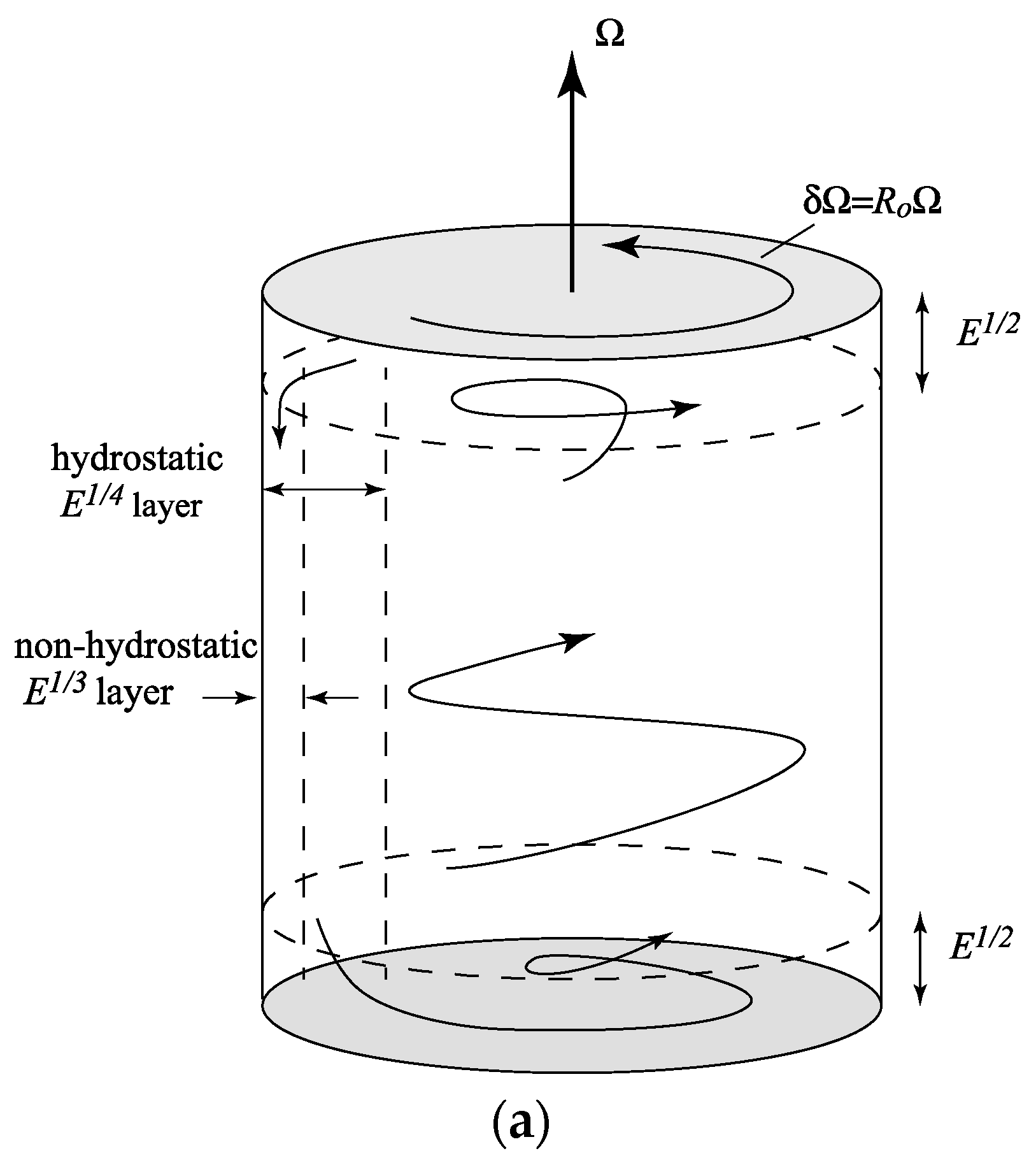
w is as large as the horizontal divergence of the horizontal velocity. This is not the case in quasigeostrophic motion, where the divergence of the horizontal velocity is zero to leading order. In this setting the zoology of stagnation points enlarges to include spiral structures [
33]. Oceanographically relevant flow fields often involve divergent surface and bottom Ekman layers, sub-mesoscale filaments and fronts, and convection cells. Other studies [
34,
35] use idealized but dynamically consistent flow fields. A canonical example that has applications in physical oceanography and engineering, and whose Eulerian characteristics have been studied extensively, is the rotating cylinder flow [
34]. In one of many possible configurations of this flow (
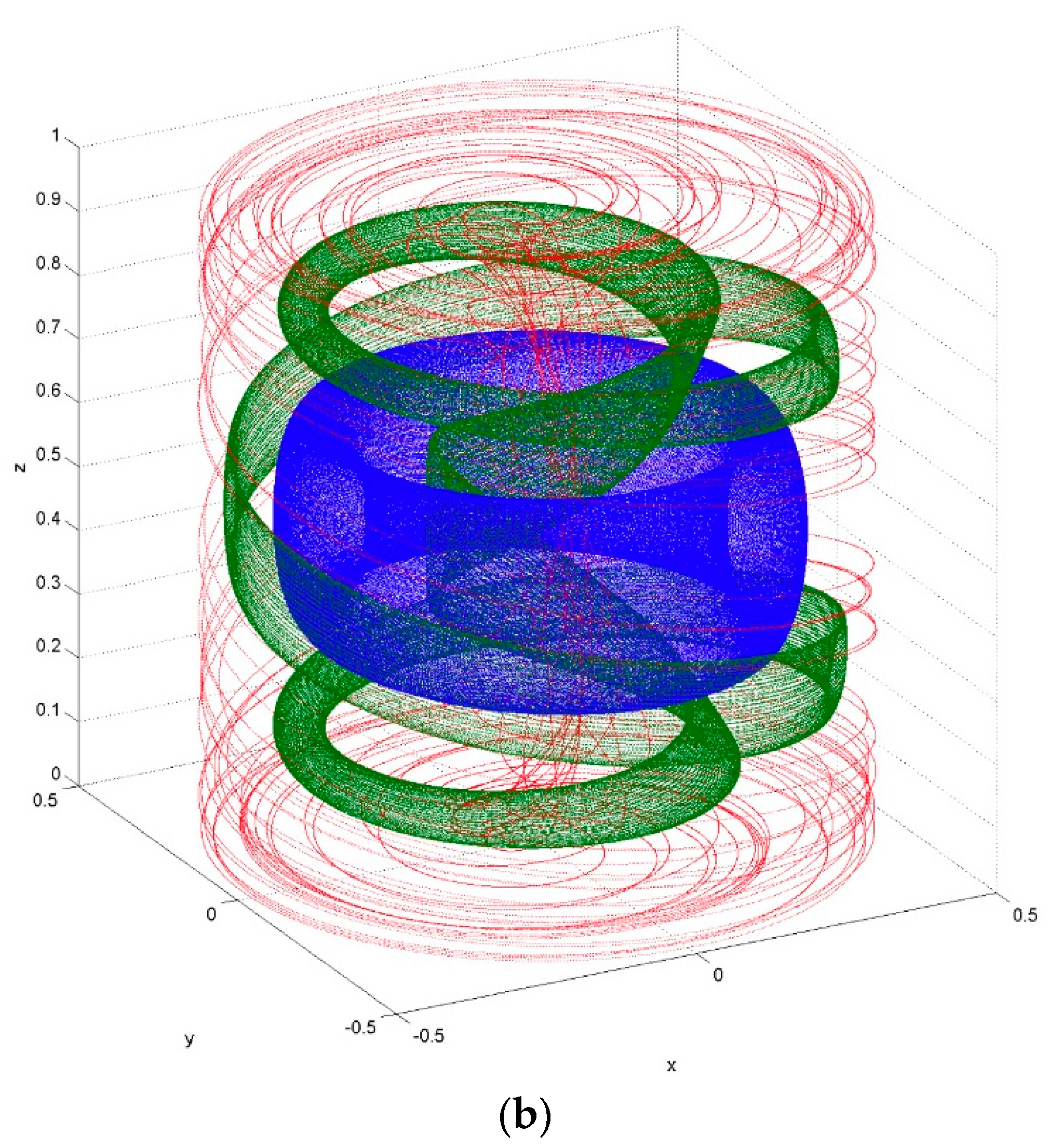
Figure 7a), the circulation in the cylinder is driven by a differential stress distribution at the top surface, and this results in a flow field that has horizontal swirl and vertical overturning, with spiraling trajectories that recirculate on tori. When the axial symmetry of the flow is broken in some manner, some of the tori brake resulting in the formation of chaotic resonant layers, separated by material barriers. These barriers also take the form of tori, as shown by several examples (
Figure 7b). Three dimensional ABC flow [
15,
27] and a kinematic model of neighboring convection cells [
36] form the basis for other commonly-considered 3d examples.
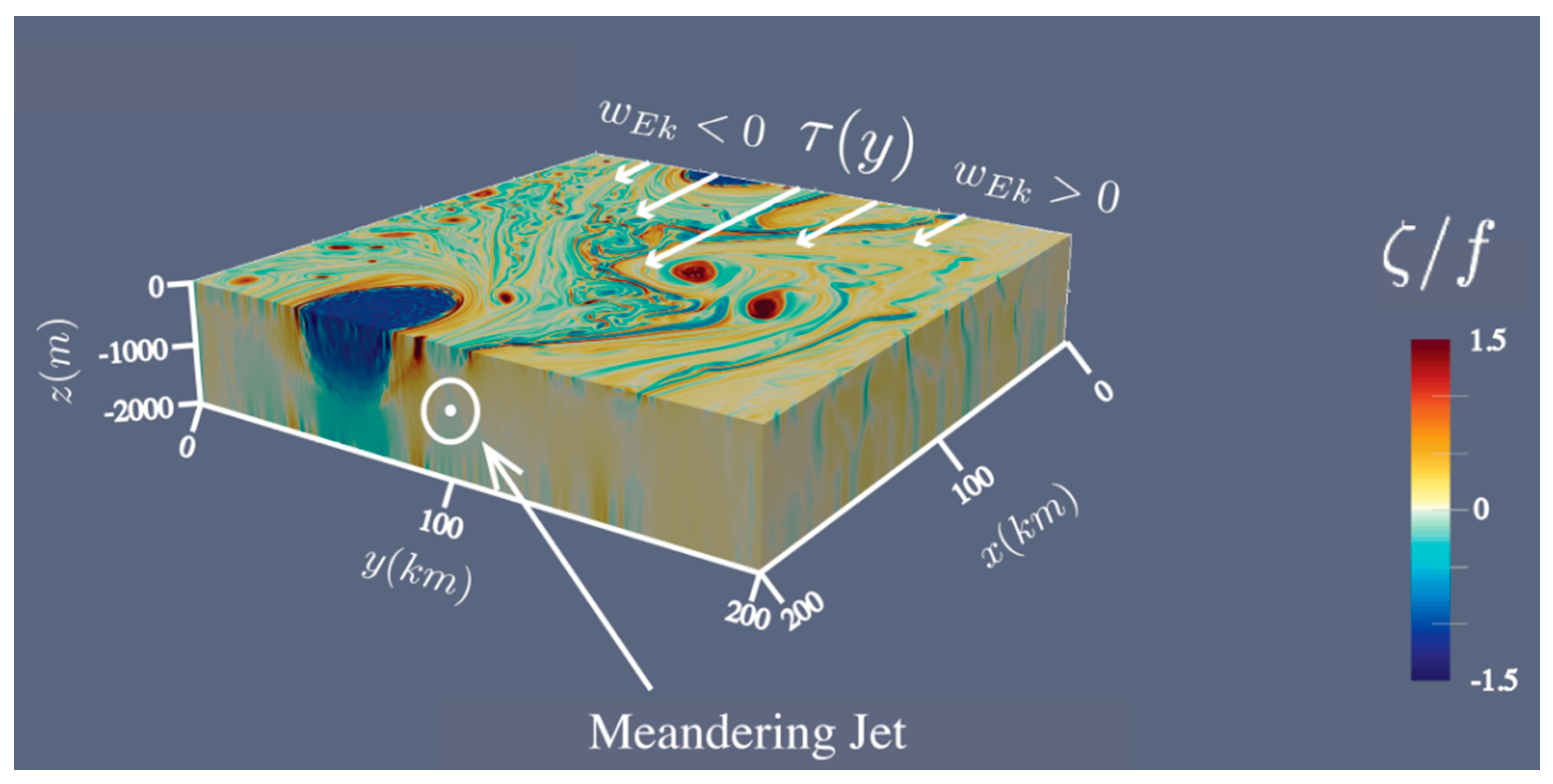
Despite considerable theoretical and computational advances in the identification of important material objects, the field of LCS analysis faces a number of limitations in its application to mainstream physical oceanography. One is that the transport calculations, whether they follow from lobe analysis or from the tracking of elliptic contours or surfaces, give only a volume flux (or area flux in 2D), and while this may be of significance, one is typically more interested in the transports of other scalar properties such as heat, salt, momentum, vorticity, energy, contaminants or chemical and biological tracers. If the scalar is approximately conserved following the fluid, then LCS analysis has direct implications for the scalar flux. However oxygen, momentum components, and other dynamical and biological tracers can be highly non-conservative. An attempt was made [
16] to confront this challenge in the context of an unstable, boundary trapped gyre in a model of wind-driven, barotropic ocean circulation (
Figure 8). At issue are the dynamical mechanisms for driving the circulation in the gyre, which include the wind but also potential vorticity advection into and out of the gyre by eddies. The dynamics can be summarized by writing down the circulation integral for the barotropic flow on a beta plane:
where
is the potential vorticity, ζ is the relative vorticity,
β is the rate of change of Coriolis parameter with latitude,
τ is the surface wind stress, ρ is the (uniform) density,
AH is the horizontal eddy viscosity,
H is the constant ocean depth, and
u is the horizontal velocity. The contour integrals are taken about the boundary
of a region
R that contains the gyre. The integrals on the right-hand side of Equation (1) measure the advection of potential vorticity across
, the tangential component of stress on
, and the horizontal frictional stress acting along
. The sum of these terms can cause the gyre to spin up or down, as measured by the rate of change of circulation (first term in the left-hand side), and/or cause the mean latitude
y of the gyre to increase or decrease (second term in the left-hand side). By constructing a time-dependent boundary
using pieces of stable and unstable manifolds, the authors were able to quantify the advection of
q into and out of the gyre as a lobe exchange processes. The approach requires that one first computes the manifolds and lobes, then separately calculates the amount of area-integrated
q for each lobe entering or leaving the gyre at irregular intervals.
In a more recent attempt [
37,
38] to calculate scalar property fluxes using lobe analysis, the velocity and scalar tracer fields are partitioned into a time mean and a time-varying perturbation. The boundary across which the tracer transport is computed is chosen as a mean streamline and the flux is associated with “psuedo lobes” formed by a material contour that initially coincides with a mean streamline but that begins to meander back and forth across it as the result of transverse motion. The method is formulated based on perturbation theory and hence requires variations (i.e., perturbations) about the means of the velocity and tracer field to be small. The method can be used as a diagnostic tool for Lagrangian transport and is applied by the authors to the problem of exchange of a passive tracer between two gyres.
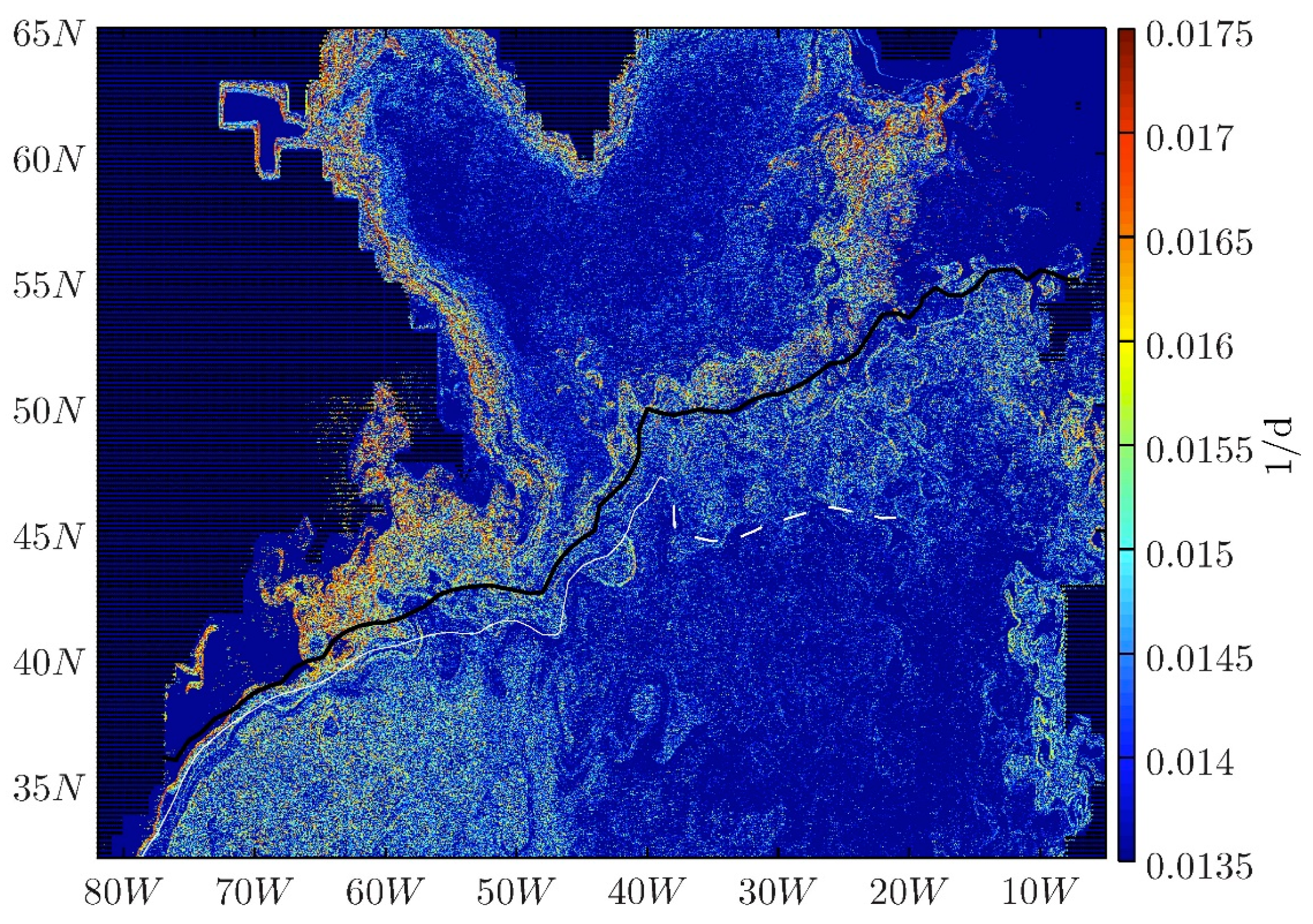
The second limitation is that eddy resolving flow fields are often so complex that computation of Lagrangian material transport would require a prohibitively intricate level of bookkeeping. This is evident, for example, in a study of transport between the Atlantic Ocean subtropical and subpolar gyres ([
39] and
Figure 9). There the intersecting finite-time stable and unstable manifolds (approximated by FTLE ridges) are extremely complex and spring from numerous hyperbolic trajectories. In another study [
40], manifold proxies are computed in models of increasing resolution and it is shown that the presence of submesoscale motions causes otherwise smooth LCS to rapidly filament and acquire a level of complexity that would surely undermine the type of mesoscale lobe computations presented in [
18]. Of course, these findings are dependent on the model’s representation of submesoscales, a feature that is difficult to validate. In fact, some studies [
41,
42] have found good agreement between observed surface drifter motion and LCS computed from altimeter-based velocities.
This all begs the question of whether it is possible to develop an approach that retains some of the flavor and intuition afforded by LCS analysis, that yields direct information about fluxes of specific physical properties, and that can somehow avoid bookkeeping difficulties that can arise in intricate flow fields. To accomplish the latter, the method must treat some smoothed version of the flow and yield fluxes that are meaningful. The approach developed below is a possible step in that direction and our purpose here is to describe it and point out some strengths and weaknesses. As with most other types of Lagrangian analysis, it is completely diagnostic and requires that the fluid velocity and tracer fields are known in advance. In the case of a dynamically active tracer such as buoyancy or vorticity, the flux is determined by the velocity and thermodynamic variables (pressure, density, temperature, etc.), all of which are part of the model output. If the tracer is passive, then a separate calculation is required, perhaps with an advection-diffusion equation, in order to establish the tracer fields, with different distributions following from different initial conditions.