1. Introduction
Theory of heat and mass transfer by small-scale transient motions constitutes a large and important component of numerous physical sciences, including fields as diverse and seemingly unrelated as oceanography, astrophysics, geology and materials science. The key challenge in small-scale mixing theory, in all its forms and applications, is the analysis and prediction of mean turbulent transport for a given large-scale distribution of properties. Most small-scale mixing processes in fluids that are nominally stably stratified—with density decreasing upwards—can be broadly classified into mechanically-driven and double-diffusive categories. An example of a common mechanically-driven phenomenon is the intermittent generation of small-scale turbulence by shear associated with internal gravity waves. Double-diffusive phenomena, on the other hand, are caused by unequal molecular diffusion rates of two (or more) individual density components, such as temperature and salt in the oceanic context.
Recent years have witnessed a substantial progress in our understanding of both double-diffusive and turbulent phenomena. In particular, reliable parameterizations have been developed for double-diffusion in astrophysical [
1,
2] and oceanographic [
3] contexts. These parameterizations express the vertical fluxes
of diffusing properties
as a function of the corresponding large-scale gradients using Fick’s diffusion model:
where the eddy diffusivities
themselves are not uniform but assumed to depend on the density ratio
, where
are the expansion/contraction coefficients.
The purpose of this communication is to discuss one fundamental yet mostly overlooked distinction in the dynamics and consequences of double-diffusive and mechanically-driven mixing. In addition to the vertical transport of diffusing properties (e.g., temperature and salinity) which the flux-gradient laws (Equation (1)) attempt to represent, numerous applications require knowledge of the corresponding volume or mass transport across mean density surfaces. Following oceanographic nomenclature, the velocity component normal to the density surfaces () will be referred to as the diapycnal velocity and the associated volume flux as the diapycnal transport. It is the analysis of diapycnal transport which reveals some rather unique properties of double-diffusion that have no direct counterpart in one-component turbulent flows. In particular, we argue that in double-diffusive flows, diapycnal volume transport is dramatically reduced relative to that in turbulent systems with comparable mixing rates of density components. When both double-diffusion and turbulence are present, diapycnal velocity is restricted to a finite range, which is controlled by the relative contributions of double-diffusion and turbulence to overall mixing.
Much of the motivation for the analysis of diapycnal volume transport [
4,
5,
6,
7] stems from the role it plays in the theory of thermohaline circulation in the ocean. Thermohaline circulation—the system of large-scale flows driven by the sea-water density variation—is an essential regulator of the Earth’s climate. Nevertheless, several aspects of it have not been fully explained. The classical view [
8,
9,
10,
11] emphasizes the role of small-scale mixing and associated water mass transformation in the ocean interior. This idea was challenged by studies advocating an alternative adiabatic view [
12,
13,
14] which invokes isopycnal advection as the key mechanism for maintenance of the Meridional Overturning Circulation (MOC). While the exact contributions of different circulation components remain a source of debate, there is a general consensus that the diabatic mode, driven by diapycnal fluxes, can be substantial. Radko et al. [
15] for instance, estimate that the diabatic mode of circulation accounts for approximately one third of the Meridional Overturning Circulation (MOC) in the global ocean. Another uncertain aspect of the theory of thermohaline circulation concerns the relative role of shallow overturning cells in the main thermocline and deep circulation in the abyssal ocean. Earlier efforts [
9,
16] were mostly focused on the abyssal dynamics. However, an interesting suggestion was made [
17] that the meridional transport of heat is controlled by the processes operating in the upper ocean. In an attempt to quantify partitioning of the oceanic heat flux between the deep and shallow overturning cells, these authors introduced the “heatfunction”, a quantity which identifies the components of circulation which contribute to the total meridional heat flux. Boccaletti et al. [
17] have shown that the heatfunction represents a surface-intensified flow largely limited to the main thermocline. Therefore meridional heat transport is dominated by the contribution from the upper branch of the MOC where double-diffusion is most active. For instance, as much as 95% of the Atlantic thermocline is double-diffusively unstable [
18]. Thus, the link between double-diffusion and diapycnal volume transport can have potentially critical ramifications for thermohaline circulation and should be explored much further.
In order to rationalize the tendency of double-diffusion to suppress the diapycnal volume transport, we propose two arguments. The first argument applies to the strongly diabatic regime representative of the lower (diffusive) thermocline that is often described by Munk’s [
9] vertical advection-diffusion balance. We find that steady one-dimensional solutions in double-diffusive systems are possible only for a very narrow range of diapycnal velocities. The second argument is more relevant for the central thermocline, where double-diffusive processes are most common. Dynamics of the main thermocline are fundamentally three-dimensional [
19]. The overall water-mass distribution is set by large-scale advection whereas diapycnal mixing is relatively weak. Nevertheless, in this regime it is still possible to predict the impact of higher order diabatic processes on cross-isopycnal transfer using a technique originally developed by Rhines and Young [
20]. The crux of this approach is the integration of governing equations along closed streamlines, which effectively eliminates the zero order advective terms in integral balances. Adapting this procedure to the double-diffusive problem allows us to evaluate the average diapycnal velocity in regions bounded by closed streamlines and, ultimately, to explain the insulation effect from first principles. Thus, for both advectively-dominated and diffusively-dominated regimes, there are theoretical reasons to expect the suppression of diapycnal volume flux by double-diffusion.
The paper is set as follows. Our starting point (
Section 2) is an analysis of a one-dimensional vertical advective-diffusive balance of temperature and salinity of Munk’s [
9] type. This analysis, albeit highly idealized, suggests that fundamental differences may exist in the way turbulent and double-diffusive mixing affect diapycnal volume transport. Motivated by this possibility, we perform a series of large-scale three-dimensional multi-century numerical simulations (
Section 3), which also consistently reflect the tendency of double-diffusion to constrain diapycnal volume transport. In
Section 4, we develop an analytical model of the double-diffusive insulation in a three-dimensional setting. We summarize and conclude in
Section 5.
2. Preliminary Considerations
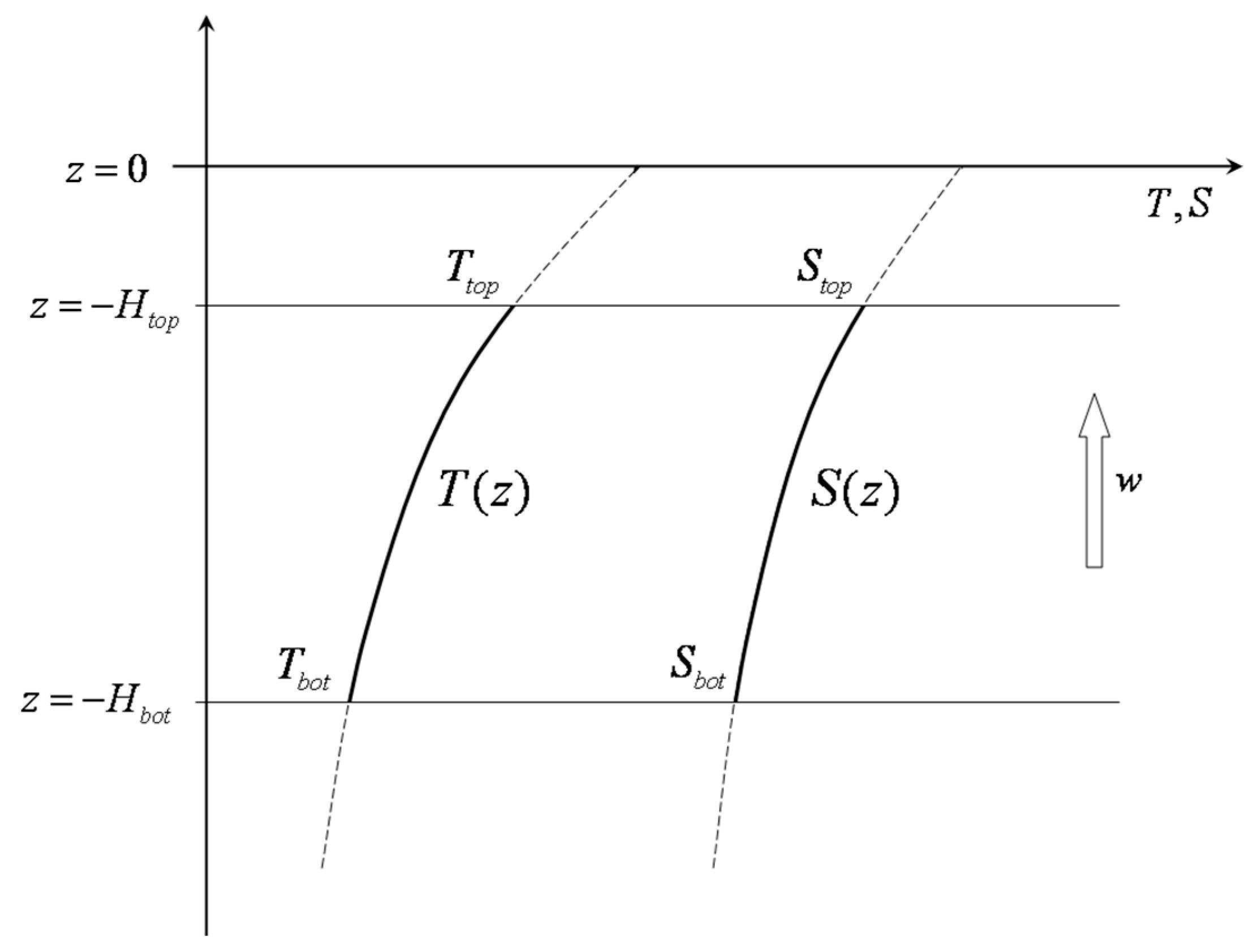
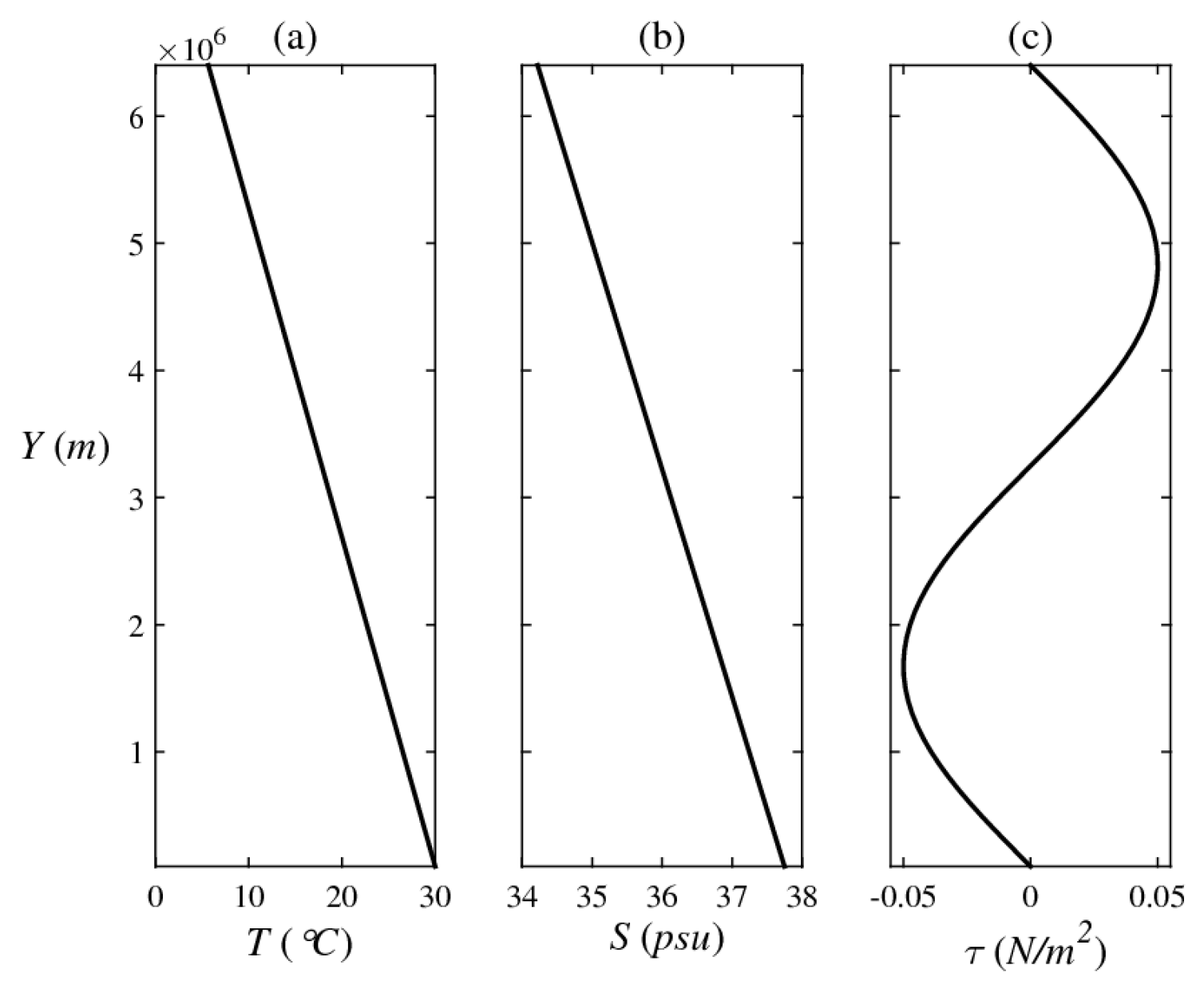
Our inquiry into the link between double-diffusive mixing and the associated diapycnal volume transport was originally motivated by the following fairly abstract problem. Consider a one-dimensional model consisting of the steady state temperature and salinity equations:
where
and
are the large-scale temperature and salinity of the sea-water;
is the upward vertical velocity. The temperature and salinity fluxes
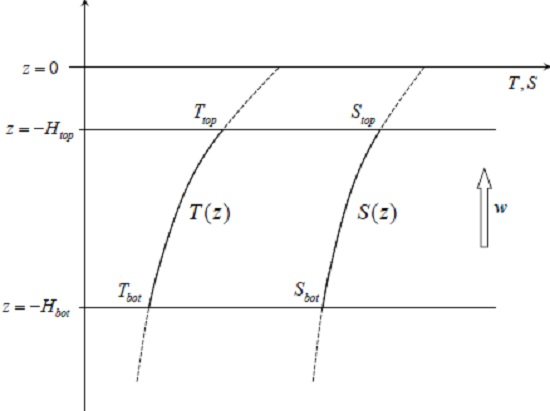
are attributed to small-scale mixing processes and related to large-scale gradients through Equation (1). We are interested in solving Equation (2) for given boundary conditions:
where
, (
) represents the top (bottom) of the mixing zone and
is its thickness (see the schematic in
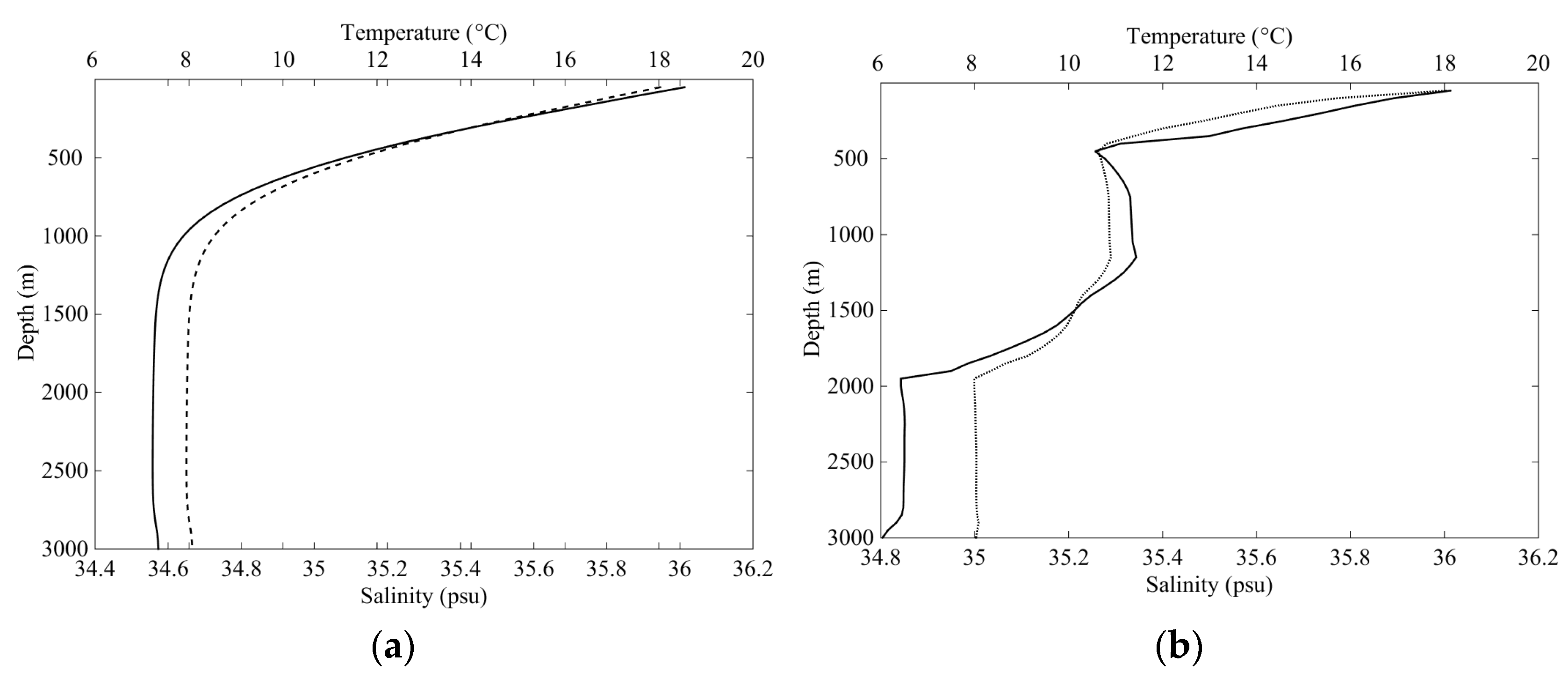
Figure 1. In particular, we are concerned by the differences in the solutions of Equations (2) and (3) for cases in which vertical mixing is controlled by: mechanical turbulence, double-diffusion, and a combination thereof.
2.1. Turbulent Mixing
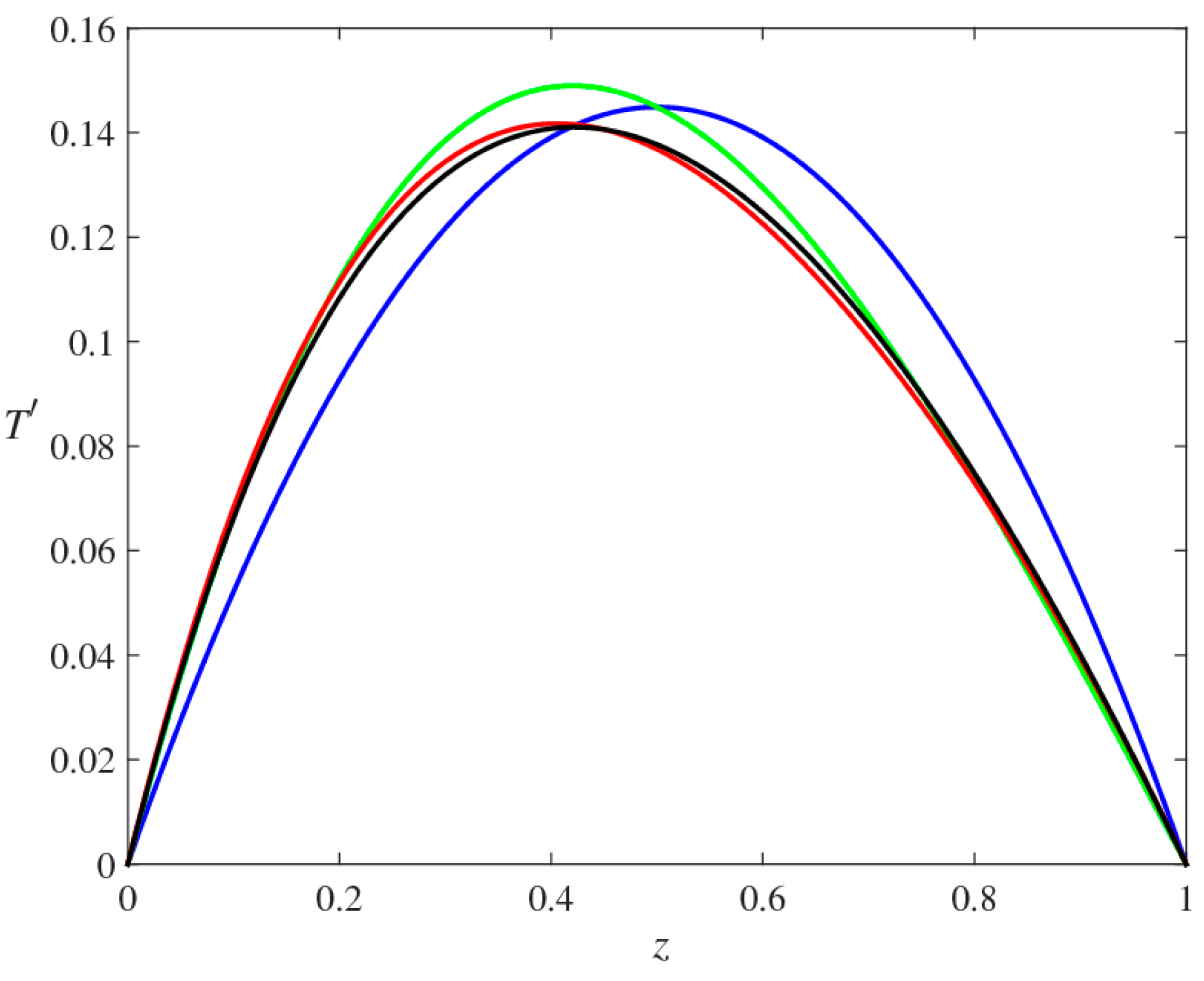
To illustrate the basic properties of the 1D system (Equation (2)), consider first the simplest model of turbulent mixing characterized by constant and equal eddy diffusivities of heat and salt:
In this case, Equations (2) and (3) can be solved for any value of diapycnal velocity (
):
and
Thus, the turbulent mixing model (Equation (4)) represents an extreme case of a completely passive system which offers no restrictions on diapycnal velocity. For any value of
w it is possible to construct a consistent solution of the
T-
S advection-diffusion equations satisfying the boundary conditions at
and
. It should be noted that the advective-diffusive balance (Equation (2)) remains passive even when the diffusivities of heat and salt are spatially uniform but not equal to each other (
). The latter model can be used to represent differential diffusion, the preferential turbulent mixing of temperature relative to salinity under certain conditions [
21,
22]. In order to demonstrate that the passive character of the advective-diffusive balance is not necessarily realized in other types of mixing, we now turn to a very different configuration which demands a unique value of
—the constant flux ratio model of double-diffusion.
2.2. Double-Diffusion: The Constant Flux Ratio Model
Double-diffusion comes in two distinct forms, fingering and diffusive convection. The fingering regime is commonly realized in the subtropical thermocline where warm and salty water overlies cold and fresh. Diffusive convection is more prevalent in high-latitude oceans, where temperature and salinity frequently increase downward. While we believe that the analysis in this paper is relevant for both forms of double-diffusion, to be specific, the discussion is focused on the salt-finger regime.
The single most significant parameter controlling diapycnal mixing in regions of active double-diffusion is the local density ratio
where
and
are the expansion/contraction coefficients in the linear equation of state—see the discussion in Schmitt [
18,
23] and Radko [
24]. Double-diffusive parameterizations typically assume that the eddy diffusivities of heat and salt
are determined by
. It is also common to approximate the ratio of thermal and haline density fluxes, so-called flux ratio (
), by a constant value:
Particular examples of such parameterizations can be found in, for example, Schmitt [
25], Zhang et al. [
26], and Merryfield et al. [
27].
Combining Equations (2) and (8), we arrive at
To maintain fingering convection, the loss of potential energy stored in salt stratification should exceed the energy gain by heat stratification and therefore
. The density ratio, on the other hand, has to exceed unity in order for density to decrease upward. Hence,
and therefore Equation (9) can be satisfied only if
. Thus, in contrast with the turbulent mixing model, the double-diffusive system actively controls diapycnal velocity. Of course, the selection of a unique
in this model could be a consequence of the chosen flux laws; of particular concern is the constant flux ratio approximation (Equation (8)). However, even when the assumption of constant flux ratio is relaxed (
Appendix) by considering typical finite variations in
we still find that the range of permitted diapycnal velocities is rather narrow:
.
2.3. Combined Effects of Double-Diffusion and Turbulence
Because small-scale mixing in the ocean is controlled by a combination of double-diffusion and mechanically generated turbulence, it is of interest to examine the constraints on diapycnal velocity in a model which includes both mixing processes. For that, we extend the foregoing analyses by considering the following closure:
which assumes equal and uniform diffusivities of heat and salt due to turbulence (
). Note that this simplified conceptual model does not take into account the possibility of direct influence of turbulence on double-diffusion [
28,
29].
There have been at least two attempts to evaluate the flux ratio based on oceanographic field measurements [
30,
31]. Both estimates were mutually consistent, suggesting the flux ratio of
The individual values of salt finger fluxes, and particularly the pattern of their variation with
, are more difficult to infer from observations. Therefore, we adopt the parameterization proposed by Radko and Smith [
3] on the basis of high-resolution DNS:
where
and
We assume parameter values representative of mid-latitude thermocline:
where
. Next, we systematically vary
in an attempt to determine how it affects the range of diapycnal velocities.
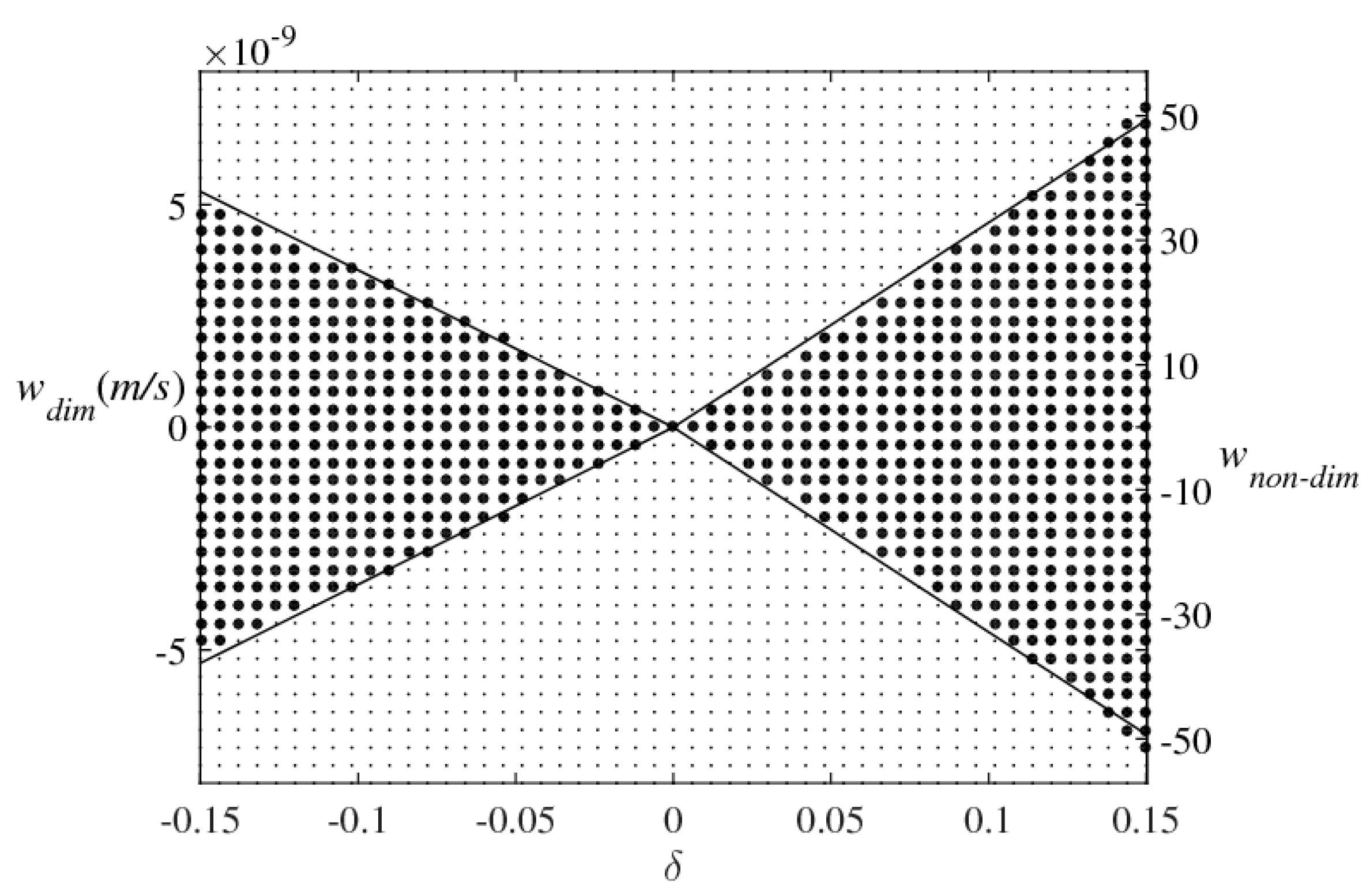
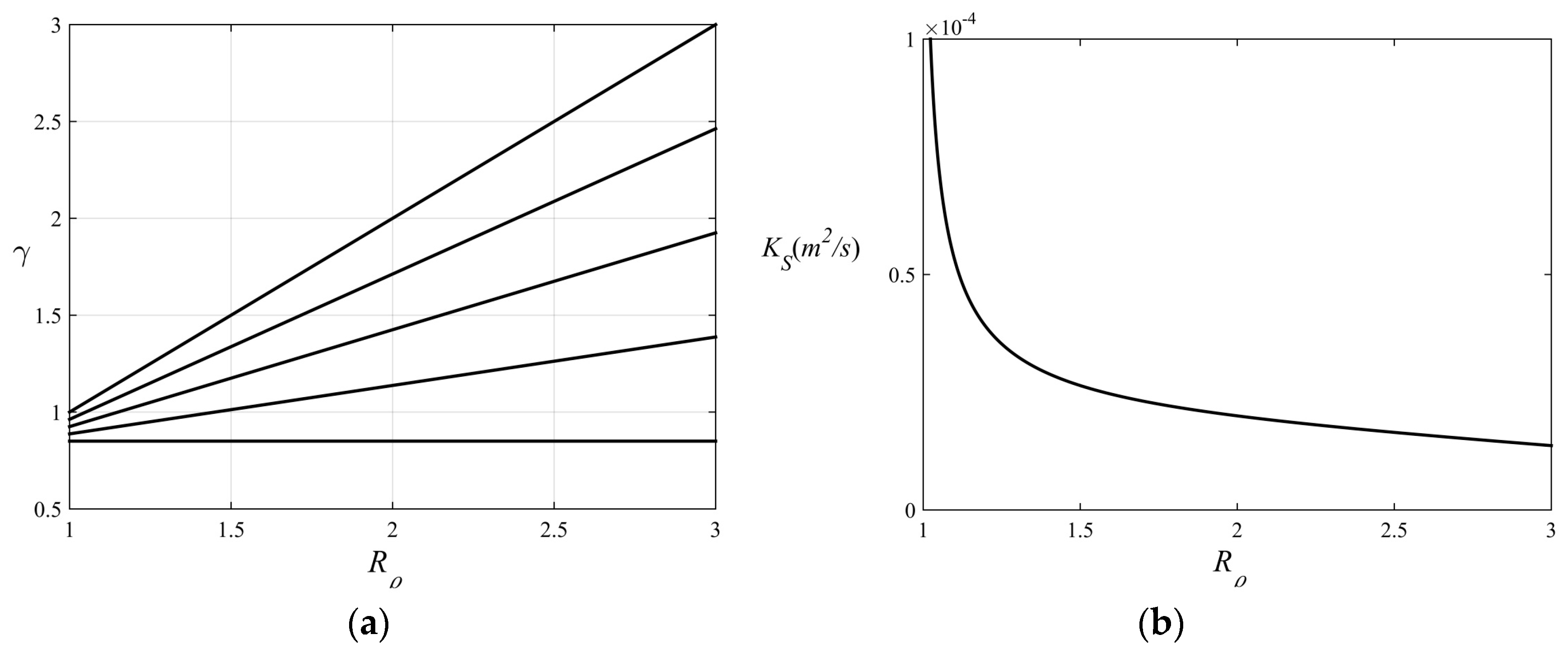
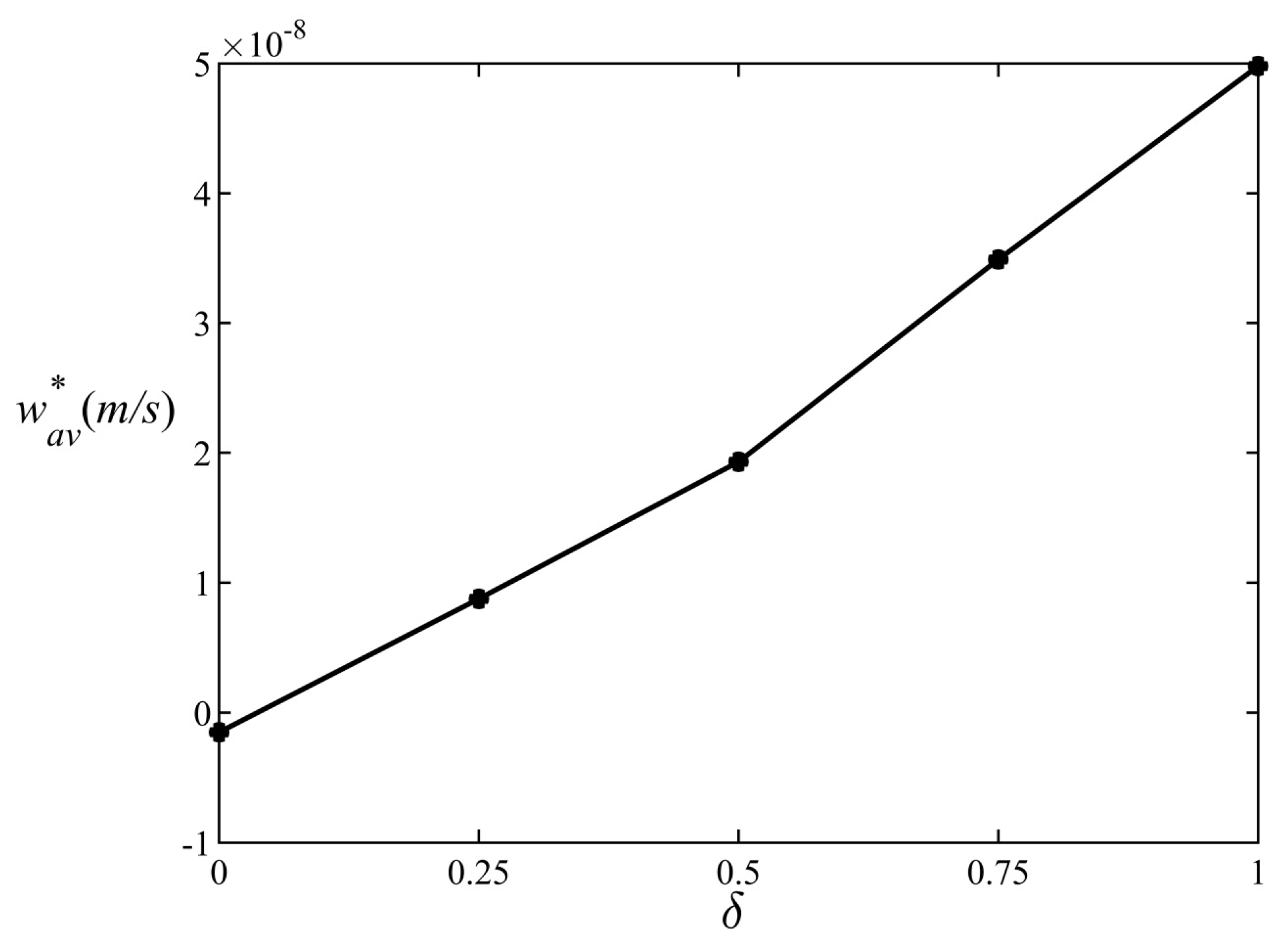
The system consisting of Equation (2) and Equations (11)–(14) was coded in Maple software package and solutions were sought for a range of
. Note that in the context of the one-dimensional model, in which all field variables are assumed to vary in z only, the continuity equation
reduces to the requirement that
. This feature simplifies the exploration of the parameter space and the results are shown in
Figure 2. Calculations resulting in regular solutions are indicated by the heavy dots and the light dots represent conditions under which no solutions were found.
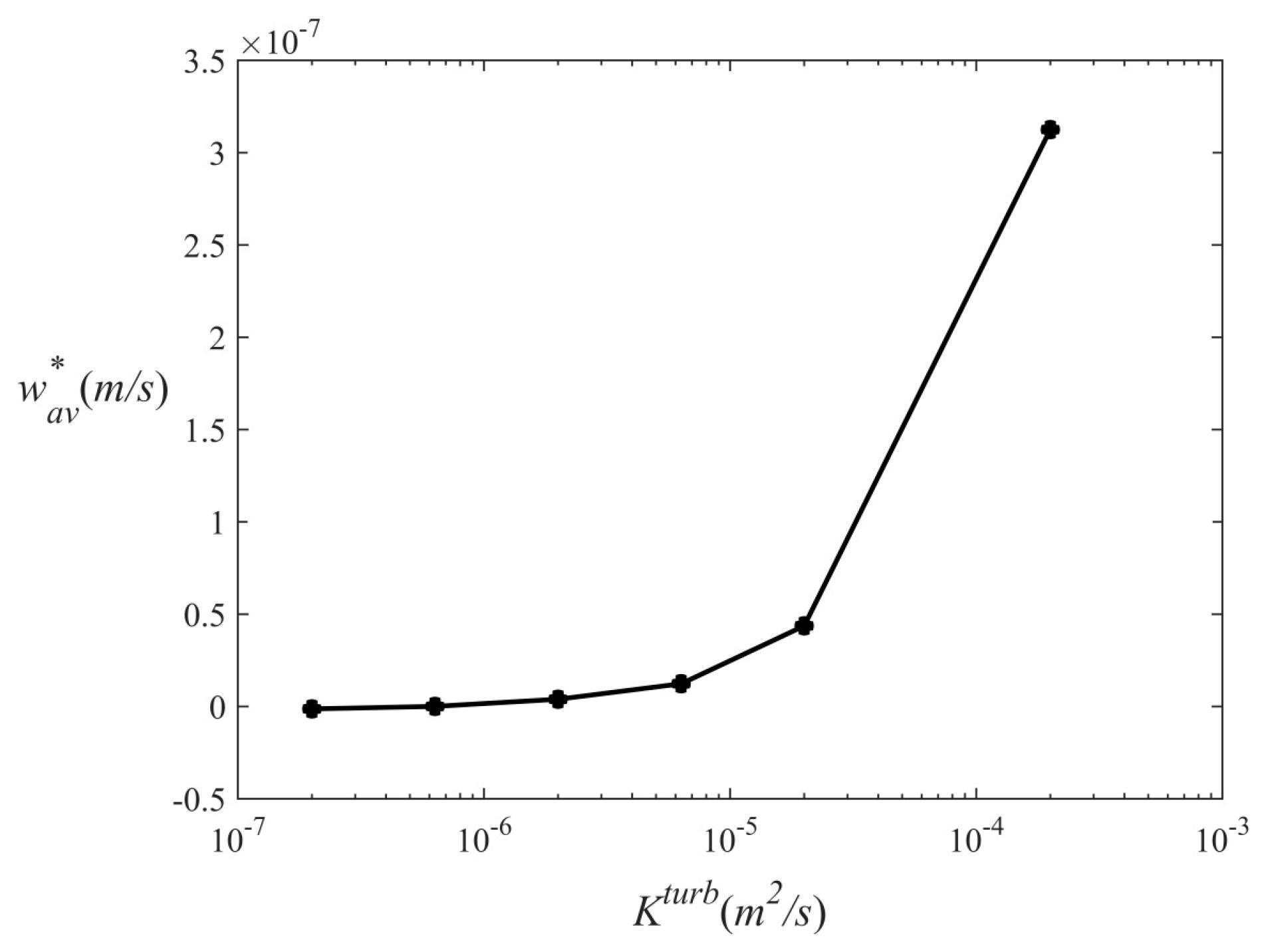
Figure 2 indicates that the constraints on diapycnal velocity loosen (tighten) with the increase (decrease) in
—a quantity measuring the relative contributions from turbulence and double-diffusion to the net mixing.
Despite considerable uncertainties in the estimated magnitudes of double-diffusive and turbulent mixing, it is plausible that in the central thermocline of the Atlantic Ocean their diffusivities are comparable [
32]. For
we obtain the following constraint on the (dimensional) diapycnal velocity:
which is similar to the data-based estimates of the diapycnal velocity in regions susceptible to both double-diffusive and turbulent mixing [
32].
In summary, the foregoing calculations indicate that (i) in the turbulent model, the assumed vertical T-S balances do not impose any internal constraints on diapycnal transport; (ii) in the double-diffusive model the diapycnal transport is zero; and (iii) the hybrid model, which takes into account both double-diffusion and turbulence, allows only a finite range of diapycnal velocities. These findings, of course, should be interpreted with great caution—the ability of any one-dimensional model to reflect the inherently three-dimensional dynamics of ocean circulation is suspect. Perhaps it is most profitable to interpret these one-dimensional solutions as the result of the averaging of the advection-diffusion equations along isopycnal surfaces, although this conceptualization raises the question whether such averaging is physically justified. Nevertheless, the profound differences in the way various mixing models affect diapycnal volume transport provide a compelling reason to launch a more comprehensive investigation of this phenomenon using more realistic—three-dimensional and time-dependent—models. We now proceed with the analysis of double-diffusive insulation based on a series of large-scale numerical simulations.
4. Theoretical Model of Double-Diffusive Insulation
Numerical simulations (
Section 3) indicate that double-diffusive insulation occurs over most of the thermocline and it is not limited to Munk’s regions characterized by vertical advective-diffusive balance. Therefore our next step represents an attempt to rationalize this phenomenon without relying on the highly restrictive one-dimensional assumption used in
Section 2. Over much of the main thermocline, small-scale mixing constitutes a numerically small component of the full advective-diffusive balance of temperature and salinity. Yet, this component is responsible for the diabatic water-mass transformation and, ultimately, for the selection of diapycnal velocity. Diabatic dynamics can be brought to the fore and analyzed theoretically using a procedure analogous to the one used by Rhines and Young [
20], albeit in a very different context.
Consider a zero-order steady state of the ocean in the absence of mixing. This state is characterized by exact conservation of temperature, salinity, density and potential vorticity. This ideal basic state is slightly perturbed by including weak diapycnal fluxes of heat and salt in the advection-diffusion equations of motion. It is assumed that the perturbation results in only slight (first order) modification of the corresponding ideal zero order solution. The perturbed state is governed by
where
and
is given in Equation (23).
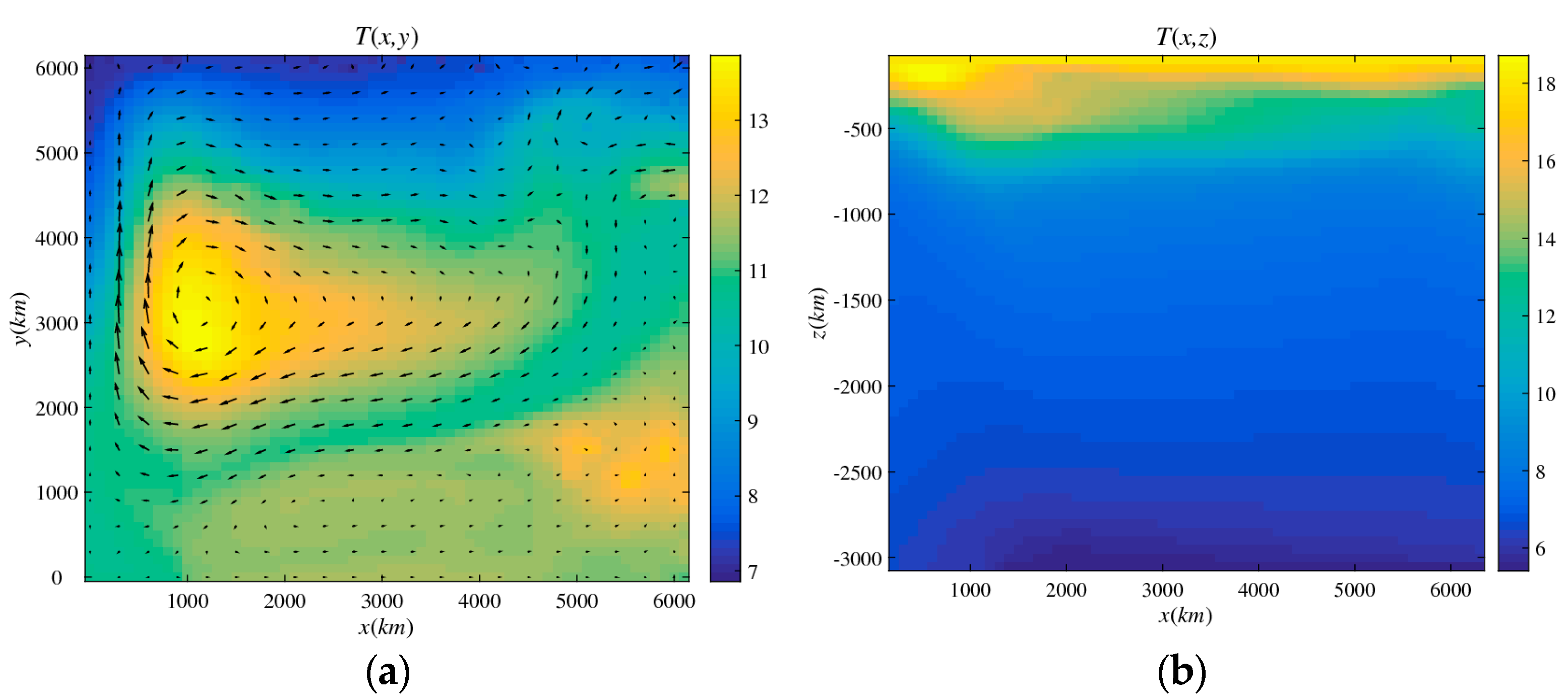
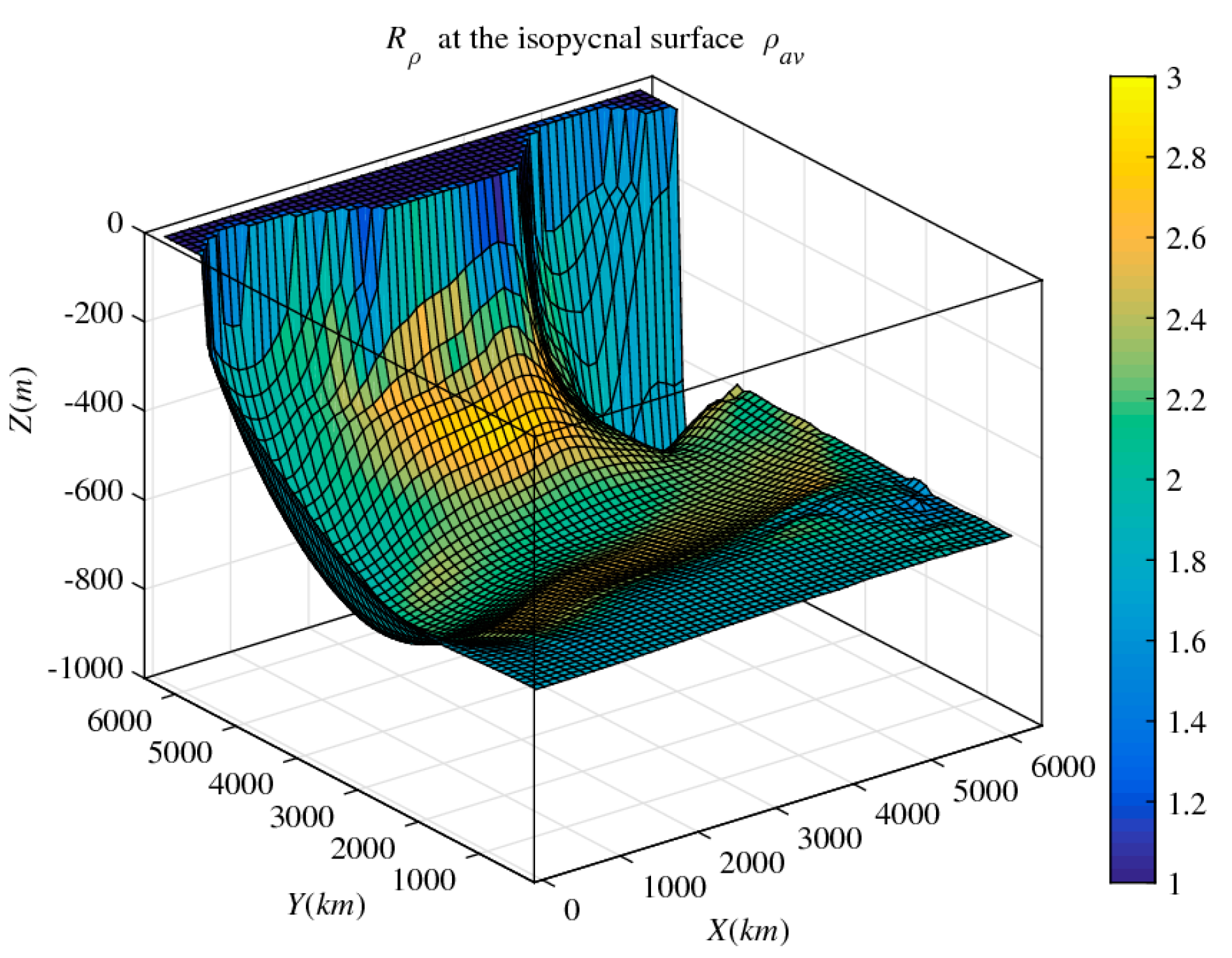
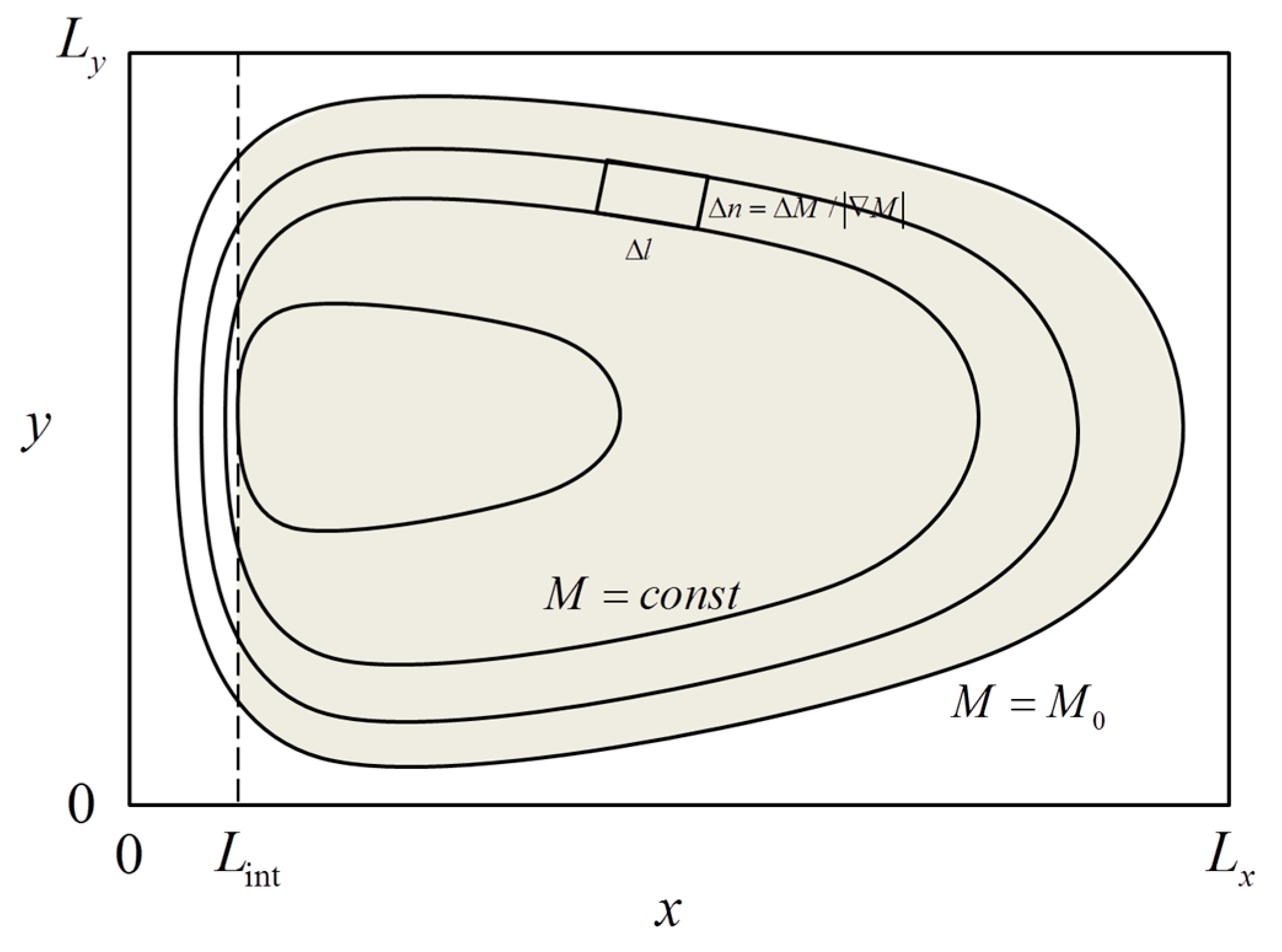
Figure 13 represents the typical circulation pattern in the subtropical ocean on an arbitrarily chosen isopycnal surface
. On this surface, we select a closed temperature contour (
). Since temperature, salinity and density are assumed to be uniquely related through the linear equation of state, it follows that salinity is also constant along the chosen contours (
). These contours closely follow the corresponding streamlines of the ideal basic state on which
are conserved exactly.
The following analysis is pivoted about the time integrals of Equation (28) along such closed contours:
The major simplification here is achieved by elimination of the zero order advective terms. Combining Equation (29) with the double-diffusive parameterization (Equation (8)), we arrive at
The next step is the change of the integration variable from time (
t) to the length coordinate measured along the contours (
l), which reduces Equation (30) to
where
is the absolute value of horizontal velocity. The mid-latitude circulation patterns (e.g.,
Figure 12) consist of two distinct regions: relatively slow geostrophic interior (
) and swift western boundary currents (
). The inspection of Equation (31) indicates that even if a streamline passes through both regions (
Figure 13), the dominant contribution to Equation (31) comes from the interior geostrophic region, where
is much less (by a factor
) than the velocity in the boundary current. Neglecting the small contribution from the region of western intensification allows us to focus exclusively on geostrophic dynamics and express the horizontal velocity components as follows:
where
M is the Montgomery potential. This system (Equation (32)) indicates that the contours of integration in Equation (31) at the leading order coincide with the isopleths of
M. Another simplification brought by geostrophic approximation is that the Ertel potential vorticity in this case takes a relatively simple form
where
C is any conservative tracer. Recall that the perturbed solution is assumed to be only slightly different from its adiabatic counterpart, which conserves temperature, salinity, and potential vorticity in the Lagrangian sense. Thus, we conclude that at the leading order (i) potential vorticity
q is conserved along the contours of integration and (ii) the tracer
C can be represented by any combination of temperature and salinity. Given the structure of the line integral (Equation (31)), we expect significant simplifications to occur for
Since potential vorticity is approximately uniform along each streamline, we divide Equation (31) by
q, entering it directly into the integrand, which reduces the line integral to
Here, the notation “
int” is used to emphasize that the integration is carried out only over the geostrophic interior. By virtue of Equation (32), we further simplify Equation (35) to
The final step is the transition from the line integrals to the area integrals over the regions bounded by closed contours of the Montgomery potential (
):
Equation (37) shows that there could be no net diapycnal transport across broad regions on the isopycnal surfaces laterally bounded by closed streamlines, which confirms and rationalizes the double-diffusive insulation effect discussed and numerically modeled in
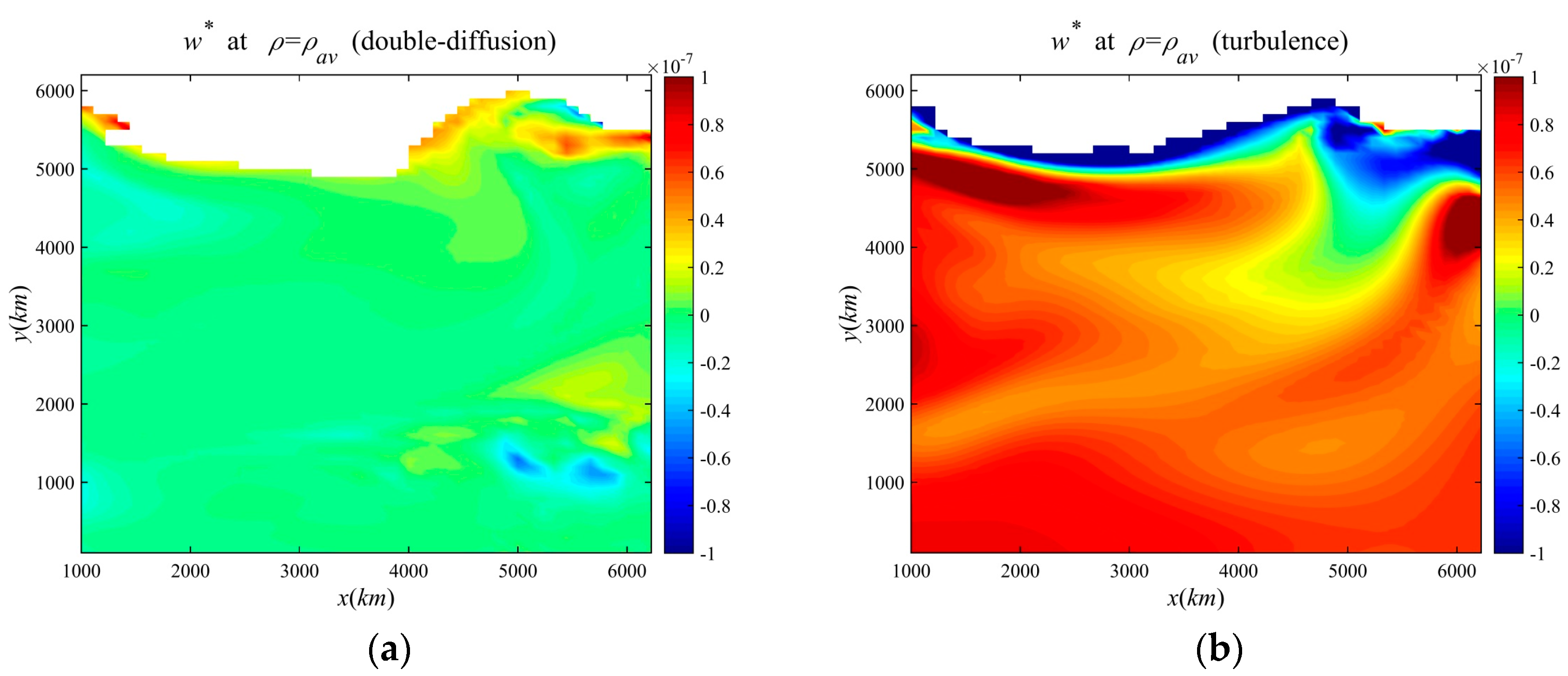
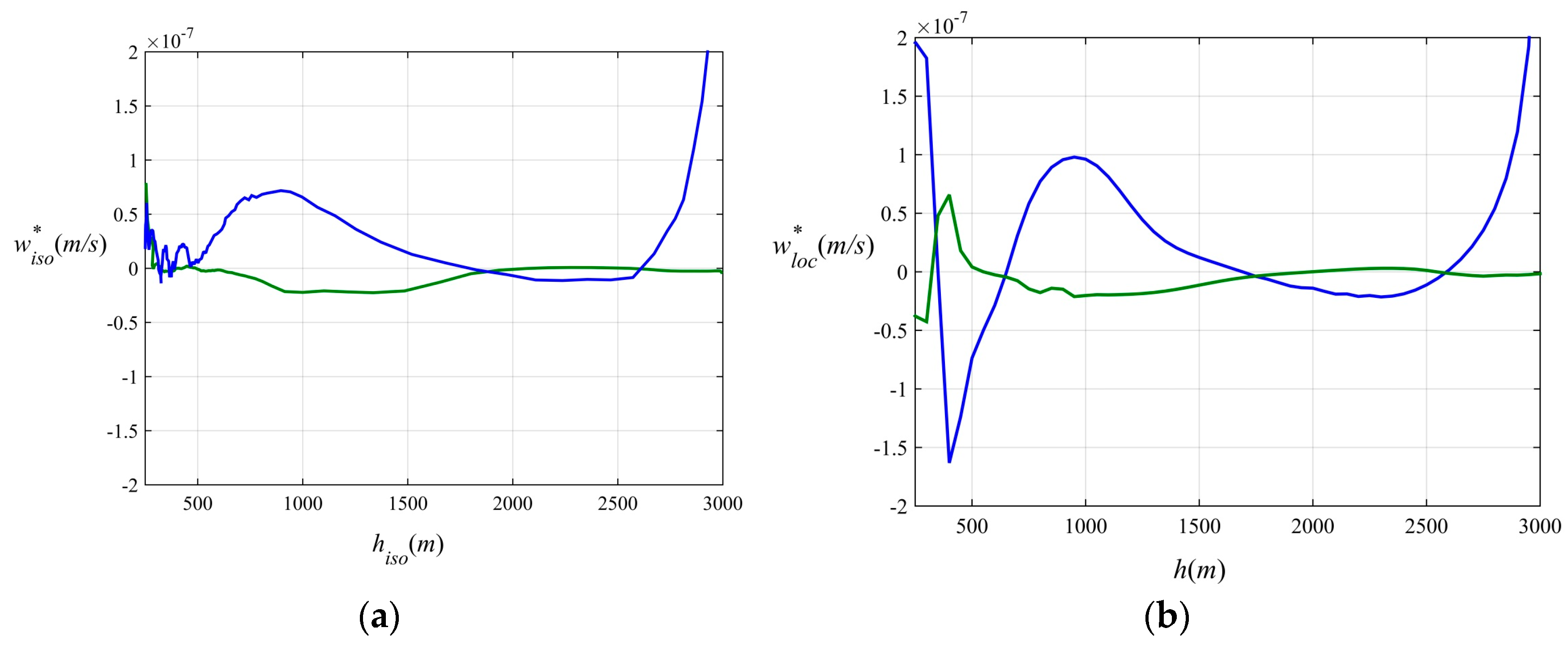
Section 3. The foregoing arguments are certainly not relevant for the turbulent ocean. In the turbulent case, the flux laws do not satisfy Equation (8) and therefore Equation (30)—and all that follows—does not apply. Hence, no analogous constraints on diapycnal velocity are expected to arise in purely turbulent systems.
5. Discussion
This communication draws attention to the dramatic differences in the dynamics of diapycnal transport realized when the dominant mixing agent is double-diffusion and when mixing is controlled by mechanically-generated turbulence. Double-diffusion occurs in numerous geophysical and astrophysical fluid systems. In the ocean, nearly half of water masses are potentially affected by double-diffusive mixing [
42]. Double-diffusion is also likely to play a major role in the dynamics of massive stars and giant planets [
43,
44]. Unlike mechanically-generated turbulence, double-diffusion is characterized by unequal eddy diffusivities of density components, which depend on the background density ratio. This feature is ultimately responsible for rather unique properties of double-diffusive mixing, such as its ability to actively constrain diapycnal volume transport—all smooth steady solutions of the
T-
S advection-diffusion equations are necessarily characterized by low diapycnal velocities. This property is contrasted with the passive behavior of systems dominated by mechanically generated turbulence, where it is possible to construct consistent steady-state solutions for an arbitrarily wide range of diapycnal velocities.
Our interest in the problem of diapycnal volume transport was ignited by the need to fully understand dynamics of the oceanic thermohaline circulation and associated meridional overturning. The classical view [
9] ascribes small-scale diapycnal mixing a critical role for its establishment and maintenance. This notion has profoundly affected the evolution of physical oceanography. It motivated development of the extensive small-scale mixing research program, largely aimed at quantification of the average diapycnal diffusivity in the ocean [
16,
45]. It is commonly assumed that the increase in diapycnal diffusion of temperature and salinity necessarily amplifies the diabatic component of the meridional overturning [
46]. Our study presents a peculiar counter-example of this tendency by showing that mixing can have an adverse impact on overturning. Using a suite of basin-scale simulations and theoretical models, we demonstrate that the inclusion of double-diffusion can place rather severe constraints on the magnitude of vertical diapycnal velocity. In the extreme case when vertical mixing is dominated by double-diffusion, typical values of diapycnal velocity (
) are less, by at least an order of magnitude, than
driven by mechanically-generated turbulence with comparable
T-
S diffusivities. Simulations indicate that these constraints are realized both locally and in the isopycnal-average sense. In essence, double-diffusion acts to seal the thermocline by preventing the leakage of seawater (both upward and downward) across the isopycnal surfaces on which double-diffusion is a dominant mixing process. Mechanically generated turbulence, on the other hand, offers no restrictions on diapycnal velocity. When both double-diffusion and turbulence are present, the constraints on
loosen (tighten) with the increase (decrease) of the fraction of the overall mixing attributed to turbulence.
When the contributions to mixing from double-diffusion and turbulence are comparable—the regime which is perhaps realized in the central Atlantic thermocline [
32]—the maximum diapycnal velocity is on the order of
. This value is comparable to current estimates of diapycnal velocity, which raises an intriguing possibility that diapycnal transport could be controlled by constraints on
imposed by double-diffusion. This suggestion is distinct from the ideas expressed by mainstream models of thermohaline circulation [
47] in which the
T-
S advective-diffusive dynamics constitute only a part of the problem. Ultimately, diapycnal velocity is selected by invoking three-dimensional large-scale balances involving both momentum and density. It should be realized, however, that the latter proposition is based on mixing models with uniform and equal vertical diffusivity
. The examples in this paper indicate that such models may not capture all the relevant dynamics and therefore we urge caution in conceptualizing the thermohaline circulation based on oversimplified mixing parameterizations.
Our attempts to force the double-diffusive thermocline by applying a large vertical velocity which lies outside of the permitted range—the range in which smooth regular solutions can be found—have led to rather dramatic transformations of the stratification into a series well-defined convective layers separated by stratified interfaces. In this regard, it should be noted that one of the most interesting and controversial problems of double-diffusive theory concerns the origin and dynamics of so-called thermohaline staircases—stepped structures in the vertical temperature and salinity profiles. Several hypotheses have been proposed to explain the formation mechanisms [
39,
48] and our analysis of the “forced” experiments (
Section 3.5) may add another candidate to the list. Thermohaline staircases could form as a response to strong externally imposed vertical advection, provided that the magnitude of vertical velocity is such that the advective-diffusive balance of Munk’s [
9] type can only be satisfied by discontinuous step-like solutions.
Of course, there are a number of uncertainties in the presented model, particularly with regard to its ability to incorporate all relevant dynamics of the oceanic circulation. For instance, it is not clear how resilient the double-diffusive insulating blanket is in the presence of active mesoscale variability, which can also impact diapycnal transport [
38]. The processes discussed in this study could be affected by the nonlinearities of the equation of state [
49]. Thus, the quantitative accuracy of double-diffusive insulation theory is readily questioned. However, the differences in the way double-diffusion and turbulence affect diapycnal transport identified here are suggestive and are likely to be realized in Nature. In this regard, it should be emphasized that large-scale modeling studies which take into account double-diffusion [
26,
27,
50] report systematic reduction in the strength of meridional overturning. Although the extent of this reduction varies considerably between models, it is possible that these results can be attributed to the double-diffusive insulation effect. Finally, it should be mentioned that while the specific solutions in this paper are based on the assumed parameterizations of double-diffusive fluxes, which require further refinements and testing, additional experiments (not shown) indicate that our results are not particularly sensitive to the choice of the functional relations for
and
. Therefore, we expect our qualitative conclusions to be sufficiently robust.